1 Introduction

The investigation of bone tissue behaviour from an engineering point of view has been one of the most important tasks in biomechanics. The statement pertains to both cortical and trabecular tissue of both animal and human origin. Such investigation might be conducted in two ways, i.e. by performing experimental strength tests or numerical simulations. The former requires proper tools and sophisticated environmental conditions, the latter needs a mathematical model of bone tissue. Usually, formulation of the mathematical models cannot be completed without experimental studies, such as uniaxial compression/tensile tests, biaxial tests, bending or torsion. By “mathematical model”, we mean here an equation relating stress with strain, i.e. a constitutive equation.

Most of the constitutive models of bone have been formulated on a macroscale with farfetched assumptions. In the macroscale approach, some very important features of bone and phenomena can be neglected or considered in a simplified manner. Investigation of the tissue on a microscale, i.e. studies on the basic units of bone which are osteons (cortical bone) and trabeculae (cancellous bone), gives us an opportunity to model more accurately specific properties of bone. For instance, we can adopt or formulate any constitutive equation to describe the mechanical behaviour of a trabecula and consider interstitial fluid flow, which altogether makes bone tissue on macroscale a viscoelastic material. In addition, the anisotropic properties of bone resulting from its microscopic and mesoscopic architecture can be taken into account.

One of the first attempts to formulate a multi-scale model of bone is presented in [1]. The author proposed a model to predict the influence of mineral volume fraction and particle aspect ratio on the elastic modulus of bone. The bone was considered as mineralised polymer composite with high aspect ratio filler particles. The model was based on tensile tests conducted on macroscopic samples. Although it was formulated for cortical tissue, the author claims that the model can be extended to include the effect of porosity in trabecular bone. In 2009 Ghanbari and Naghdabadi proposed a hierarchical multi-scale model for cortical bone [2]. They presented a model which predicts mechanical properties of the tissue, such as the Young modulus, shear modulus and Poisson’s ratio. They used a homogenisation scheme to calculate macroscopic stress from stress distribution on the microscale and transfer it back to the macroscale. The authors concluded that their method could be used to determine the mechanical properties of cortical bone. Jaziri et al. developed a model for bovine trabecular bone describing the elastoplastic behaviour of the tissue under compression loading [3]. They used a homogenisation method to define the elastic properties of the bone and proposed a constitutive plastic-damage model to describe its response. The material parameters in the model, i.e. the Young modulus and the yield stress, were calibrated based on tensile tests conducted on macroscopic samples. A homogenisation approach is also presented in [4] to evaluate the influence of resorption cavities on the mechanical properties of cortical bone and by Atthapreyangkul et al., who performed multi-scale finite element analysis to determine the effect of geometrical changes at multiple structural scales on the mechanical properties of cortical bone [5]. Rahmoun et al. proposed a micromechanical formula to model the elastic response of the human humerus [6]. The authors coupled a two-phase micromechanical approach by using a homogenisation scheme for cylindrical voids in the bone and nanoindentation measurements to determine the elastic modulus of the bone matrix phase.

In the present paper, a different approach is presented. The constitutive model is formulated at a microscale, i.e. for trabeculae of human cancellous bone. The model takes into account the nonlinear viscoelastic properties of bone as the time-dependent properties of bone seem to play a significant role in the tissue behaviour under various loads [7,8,9]. A material indicates nonlinear viscoelastic behaviour when the stress distribution depends on both time and strain, as it is in the case of bone tissue. Such description allows us to capture a hysteresis loop in the loading-unloading mechanical tests, as it will be proved below. The material constants in our constitutive law were identified based on microindentation tests conducted on trabeculae and stress relaxation tests in compression performed on a macroscopic trabecular bone sample. The constitutive model was implemented in a commercial finite element method (FEM) software—ANSYS. The purely elastic response of the bone was modelled by means of Mooney–Rivlin two-parameter hyperelastic material model. The viscoelastic behaviour of the tissue was captured by Prony Shear Relaxation option. Our model was then validated by comparing the experimental results of compression tests conducted on macroscopic samples and the results of the FEM simulations of the tests. The original aspect of this study lies in nonlinear viscoelastic model formulation for a trabecula and application of the constitutive law in macroscopic simulations of trabecular bone structure. In addition, as the material constants were calibrated for a range of indentation force rates, our model covers a relatively broad span of bone deformation rate, which is also a novel aspect in multi-scale modelling of trabecular bone.

An alternative approach in modelling of cancellous bone might be the application of a homogenisation method, as it was already presented above. Some comments on this topic are provided in Discussion section.

2 Materials and methods

2.1 Preparation of trabecular bone sample and µCT imaging

The human trabecular bone specimen was extracted from the femoral head of one patient during a hip replacement surgery after approval of the Bioethics Committee of Military Medicine Institute. The patient was 63 years old male who suffered from arthritis. From the specimen, a cuboid bone sample with dimensions of 9.6 x 9.6 x 9.8 mm was cut out with a saw blade such that two cutting surfaces were perpendicular and the other four surfaces were parallel to the main direction of the trabeculae. The following parameters of the cutting process were applied: (i) saw blade shaft speed n = 3300 rpm, (ii) saw blade feed f = 0.17 mm/s, (iii) blade appropriate to cut materials of hardness 50–400 HV. The first parameter indicates how fast a saw blade rotates, the second is how fast a blade moves forward, and the third is the range of hardness on the Vickers scale. After cutting, the marrow was removed. The cuboid sample was stored in 95% ethanol at a temperature of 4 ºC.

Subsequently, a high-resolution micro-computed tomography (µCT) scan was taken of the cuboid sample using a Skyscan 1172 µCT scanner. The following scan parameters were used: (i) voxel resolution 16.86 µm, (ii) source voltage 100kV, (iii) current 100 µA [10]. The images were converted into the 3D model using Mimics software. To decrease the number of triangles in the 3D model, triangle reduction with the preservation of the original shape of the trabeculae structure was used. The 3D model also allowed to investigate the porosity, which was 75% and was typical for trabecular bone from the femoral head [11, 12].

2.2 Microindentation tests

The measurements were carried out on the CSM Microhardness Tester with the diamond spherical indenter tip of a diameter of 200 µm. The tests were conducted with three values of maximum load \(P_{\max }\) = 300 mN, 500 mN and 700 mN and with two loading/unloading rates V = 500 mN/min and 1000 mN/min, which gave six pairs of test parameters. Tests included both loading and unloading phases with no hold at peak force. The measured force P as a function of microindentation depth h enabled us to obtain hysteresis loops. Young’s modulus was determined directly from indentation curves by the Oliver-Pharr method [13]. The value of the trabecular bone Poisson ratio \(\nu \) was assumed to be 0.3 [14, 15].

Before the tests, the bone sample was drained from ethanol in a controlled environment (temperature of 20º  ± 5º  and humidity 32% ± 5%) for an hour. Three measurements on the same trabecula were performed within each pair of test parameters, giving a total number of 18 microindentations. The region of interest for indentations was selected arbitrarily.

2.3 Compression tests

Compression tests consisted of two phases: stress relaxation test and uniaxial compression test. Both stages were carried out on the same bone sample on MTS Bionix Systems. The bone was drained for an hour at room temperature before every test. During the stress relaxation test, the sample was compressed to the strain value 0.01 within 160 s. The process of stress relaxation was registered for 500 s. After this test bone sample was stored in 95% ethanol at a temperature of 4 ºC for two days. The uniaxial compression test was conducted with the same strain value as the relaxation test. Both the loading and unloading phases lasted 100 s.

2.4 Formulation of the constitutive model

The constitutive equation that was used in this study was developed in our previous study [16]. Trabecular bone was assumed as a nonlinear viscoelastic material. In nonlinear viscoelasticity, the constitutive model can be formulated as a convolution of strain-dependent function \(\mathrm {\textbf{S}}^{\mathrm {\textbf{s}}}\left( \lambda \right) \, \)and a time-dependent function \(g\left( t \right) \):

$$\begin{aligned} \mathrm {\textbf{S}}\left( \lambda ,t \right) =\mathrm {\, }\mathrm {\textbf{S}}^{\mathrm {\textbf{s}}}\left( \lambda \right) *g\left( t \right) \end{aligned}$$
(1)

where: \(\mathrm {\textbf{S}}\) – second Piola–Kirchhoff stress tensor, \(\mathrm {\textbf{S}}^{\mathrm {\textbf{s}}}\) – elastic second Piola–Kirchhoff stress tensor, \(\lambda \) is stretch ratio along the loading direction, t represents time. The time-dependent function may be defined by means of Prony series:

$$\begin{aligned} g\left( t \right) =g_{\infty }+\sum \limits _{i=1}^n {g_{i}\cdot e^{-\frac{t}{\tau _{i}}},} \end{aligned}$$
(2)

where: \(\tau _{i}\) – relaxation times, \(g_{i}\) – viscoelastic constants,

$$\begin{aligned} g_{\infty }=1-\sum \nolimits _{i=1}^n g_{i} \end{aligned}$$
(3)

Relaxation times and viscoelastic constants are identified based on the experimental data.

Equation (1) can also be written as:

$$\begin{aligned} {\varvec{S}}\left( \lambda ,t \right) =\int \limits _0^t {g(t-s)\frac{\partial {\varvec{S}}^{{\varvec{s}}}(\lambda )}{\partial s}} \text {d}s. \end{aligned}$$
(4)

Equation (4) can be split into elastic and viscoelastic terms:

$$\begin{aligned} {\varvec{S}}\left( \lambda ,t \right) = \underbrace{g_{\infty }{{\varvec{S}}}^{{\varvec{s}}}(\lambda )}_{\hbox {elastic term}}+ \underbrace{\sum \limits _{i=1}^{n}\int \limits _{0}^{t} g_{i}\cdot e^{-\frac{t-s}{\tau _{i}}} \frac{\partial {{\varvec{S}}}^{{\varvec{s}}}(\lambda )}{\partial s} \text {d}s,}_{\hbox {viscoelastic term}} \end{aligned}$$
(5)

where: s – represents the historical time variable. To calculate \({\varvec{S}}\left( t\right) \) the strain history must be known. Note that strain is represented here by stretch ratio \(\lambda \). The elastic part of the second Piola–Kirchhoff stress is calculated by means of Eq. (6):

$$\begin{aligned} S_{ij}^{s}=2\partial \varPsi /\partial C_{ij}, \end{aligned}$$
(6)

where: \(C_{ij}, (i, j = 1, 2, 3)\) are components of the right Cauchy deformation tensor C.

The strain energy function \(\varPsi \) can be written in general form [17]:

$$\begin{aligned} \varPsi =\varPsi _\textrm{iso}+\varPsi _\textrm{v}, \end{aligned}$$
(7)

where: \(\varPsi _\textrm{iso}\) represents the isochoric part of strain energy function and \(\varPsi _\textrm{v}\) represent volumetric part. In this constitutive equation \(\varPsi _\textrm{iso}\) takes the form of the hyperelastic Mooney–Rivlin model [18]:

$$\begin{aligned} \varPsi _{iso}=c_{10}\left( \bar{I}_{1}-3 \right) +c_{01}\left( \bar{I}_{2}-3 \right) , \end{aligned}$$
(8)

where: \(\bar{I}_{1}\) and \(\bar{I}_{2}\,\) are the first and second invariants of tensor \(\bar{C}\mathrm {\mathbf {=}}J^{\mathrm {-}\textrm{2}/\textrm{3}}\mathrm {\textbf{C}}\), J is the determinant of the deformation gradient tensor, \(c_{10}\) and \(c_{01}\,\) are hyperelastic constants which are identified on the basis of experimental data.

The volumetric strain energy function \(\varPsi _{v}\) takes the form [17]:

$$\begin{aligned} \varPsi _{v}=\frac{1}{D}\left( J-1 \right) ^{2}. \end{aligned}$$
(9)

The constant D is the compressibility parameter, which for incompressible materials has to be very small. In this study, D assumed to be \(1\cdot {10}^{-5}\, \textrm{MPa}^{-1}\).

The hereditary integral in (4) was determined using an algorithm based on finite increments of time [19]. By means of this algorithm, the stress in (4) can be computed using the formula:

$$\begin{aligned} {\varvec{S}}\left( t+1 \right) =g_{\mathrm {\infty }}{\varvec{S}}^{{\varvec{s}}}\left( t\mathrm {+1} \right) \mathrm {+}\sum \limits _{\mathrm {i=1}}^\textrm{n} {\left( \textrm{e}^{\frac{\mathrm {-}\varDelta t}{\tau _{i}}}{\mathrm {\cdot \textbf{Q}}}_{\mathrm {\textbf{i}}}\mathrm {(t)+}g_{i}\frac{\mathrm {1-}\textrm{e}^{\frac{\mathrm {-}\varDelta t}{\tau _{i}}}}{\frac{\varDelta t}{\tau _{i}}}\left( {\varvec{S}}^{\textbf{s}}\left( t\mathrm {+1} \right) \mathrm {-}{\varvec{S}}^{{\varvec{s}}}\left( t \right) \right) \right) .} \end{aligned}$$
(10)

In Eq. (10), \(\varDelta t\) is the time increment, \(\mathrm {\textbf{Q}}_{\mathrm {\textbf{i}}}\mathrm {(t)}\) represents the stress at the previous time step, n is a number of relaxation times \(\tau _{i}\) and viscoelastic constants \(g_{i}\, (i=1,\, \ldots ,\, n)\). As the initial stress and strain in the material are known, the stress at time \(t > 0\) can be calculated.

2.5 The constants calibration

The number n and values of relaxation times were determined using data from the stress relaxation test performed on the cuboid sample taking advantage of the algorithm described in detail in [20]. The algorithm is based on iterative calibration. The relaxation times \(\tau _{i}\, (i=1,\ldots ,\, n)\) were calibrated by fitting the curve described by Eq. 10 to the relaxation part of the curve obtained from the experiment. The process of the calibration was conducted in MATLAB.

The hyperelastic constants \(c_{10}\) and \(c_{01}\), as well as viscoelastic constants \(g_{i}\, (i=1,\, \ldots ,\, n)\) were calibrated using the indirect method based on finite element analyses. These constants were calibrated by fitting the curves obtained from simulations to the experimental curves. To make the process of calibration possible, the constitutive equation was implemented into Ansys by means of two model options, i.e. Mooney–Rivlin hyperelastic model (purely elastic response) and Prony Shear Relaxation series (viscoelastic properties).

The implementation allowed us to simulate tests performed on trabecular bone. In the three-dimensional analyses of microindentation, the spherical indenter was modelled as an elastic material (the Young modulus \(2\cdot {10}^{5}\) MPa, the Poisson ratio 0.3), and the trabecula was modelled by means of the formulated constitutive equation. Models of trabecula and indenter were designed in SolidWorks as half of the sphere with a diameter of 200 µm and a cuboid with dimension \(340 \times 340 \times 120\, \mu \) m, saved as a STEP file and then imported into ANSYS. In ANSYS, the model of the indenter was meshed with tetrahedron elements with a dimension of 20 µm., while the model of trabecular bone was meshed with hexahedron elements with two different sizes: 7 µm near the area of contact and 15 µm (Fig. 1). The mesh study was conducted to find the best mesh density. In analyses, the whole load and unload cycle was considered with the same test parameters as in the experiment, i.e. maximum load and load/unload rate. It gave a total number of 18 unique simulations, the same amount as microindentations.

Fig. 1
figure 1

Meshed models of indenter and trabecula

Full size image

To validate the constitutive equation simulations of stress relaxation test and uniaxial compression test with identified material constants were performed.

3 Results

3.1 Identification of relaxation times

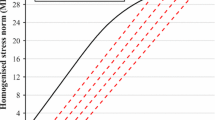
The relaxation times determine how quickly the tissue recovers from the applied load. Based on the material model that resulted from the fit procedure, four relaxation times were needed to properly describe the basic shape of the stress curve during the stress relaxation test. It means that n in Eq. (4) is equal to 4. The result of the curve-fitting process is presented in Fig. 2. The curve obtained from the stress relaxation test is shown by means of squares, and the theoretical curve described by Eq. 10 is shown by a solid line. The curve-fitting is satisfactory. The identified values of the relaxation times are as follows: \(\tau _{1}=1\, \textrm{s}, \tau _{2}=7\, \textrm{s}, \tau _{3}=59\, \textrm{s}, \tau _{4}=500\, \textrm{s}.\)

Fig. 2
figure 2

Model curve fitted to the stress relaxation results

Full size image

3.2 Identification of hyperelastic and viscoelastic constants

In Fig. 3 graphical representation of the microindentation curve-fitting process is shown. Curves from the experiments are represented by squares, while curves described by the constitutive model and obtained from the simulations are shown by a solid line.

Fig. 3
figure 3

Curves from simulations fitted to the microindentation results for: a P  = 300 mN and V = 500 mN/min, b P = 300 mN and V = 1000 mN/min, c \(P\,\) = 500 mN and V = 500 N/min, d P  = 500 mN and V = 1000 mN/min, e P = 700 mN and V = 500 mN/min, f P = 700 mN and V = 1000 mN/min

Full size image

In the curve-fitting process, two criteria of fit were established: the error of fitting the areas of hysteresis loops obtained from experiment \(A_\textrm{exp}\) and simulation \(A_\textrm{sim}\) had to be under 15%, and the error of position of the curves’ peaks from experiment \(h_\textrm{exp}\) and simulation \(h_\textrm{sim}\) had to be under 15%. The area of the hysteresis loop, which is also an indentation work W, was determined numerically from force-displacement curves using a trapezoidal integration rule. The areas-fitting error was determined by means of the following formula:

$$\begin{aligned} \textrm{err}=\left| \frac{A_\textrm{sim}-A_\textrm{exp}}{A_\textrm{exp}} \right| \cdot 100\% . \end{aligned}$$
(11)

The values of the error are presented in Table 1.

In the second criteria, only the maximum depth of microindentation from the experiment and simulation was taken into account because the maximum load in the experiment and in the corresponding simulation was the same. The error was determined using the formula:

$$\begin{aligned} \textrm{err}=\left| \frac{h_\textrm{sim}-h_\textrm{exp}}{h_\textrm{exp}} \right| \cdot 100\% . \end{aligned}$$
(12)

The values of the error are presented in Table 2.

Using Mooney–Rivlin hyperelastic strain energy function we calculated values of Young Modulus E by means of the following formula (13):

$$\begin{aligned} E=2G\left( 1+\nu \right) , \end{aligned}$$
(13)

where: G is the Kirchhoff modulus and \(\nu \) is a Poisson’s ratio. The value of Poisson’s ratio was assumed to be 0.3 while the Kirchhoff modulus was calculated using Eq. (14)

$$\begin{aligned} G=2\left( c_{10}+c_{01} \right) . \end{aligned}$$
(14)

The values of the Young modulus measured during microindentation tests and calculated from Eq. (13) are shown in Table 3.

Table 1 Values of areas-fitting error
Full size table
Table 2 Values of error of position of the curves’ peaks
Full size table
Table 3 Values of elastic modulus measured in the experiments and predicted by the constitutive model
Full size table

The calibrated hyperelastic and viscoelastic constants are shown in Table 4. The constants \(c_{10}\) and \(c_{01}\) determined elastic behaviour of trabecular bone while \(g_{1},\, g_{2},\, g_{3},\, g_{4}\) determined the width of the hysteresis loop.

Table 4 Values of the identified material constants
Full size table

From all 18 sets of material constants, averaged values were calculated: \(c_{10}=2720, c_{01}=-1834,\, g_{1}=0.17,\, g_{2}=0.20, g_{3}=0.31,\, g_{4}=0.04\). To check if these parameters properly describe the investigated trabecular bone simulations with the same six pairs of test parameters as before were performed.

Results from these simulations compared with experimental results are shown in Fig. 4. Curves from the experiments are represented by squares, while curves obtained from the simulations calculated with averaged constants are shown by a solid black line.

Fig. 4
figure 4

Curves from simulations with averaged constants compared with the microindentation results for: a P  = 300 mN and V = 500 mN/min, b P  = 300 mN and V = 1000 mN/min, c P  = 500 mN and V = 500 N/min, d P  = 500 mN and V = 1000 mN/min, e P  = 700 mN and V = 500 mN/min, f P  = 700 mN and V = 1000 mN/min,

Full size image

The comparison shows that averaged material constants could be treated as representative for this trabecular bone. In four cases, curves from simulations are very well fitted to experimental results. In two cases, the curves obtained from the simulations with averaged constants differ from those obtained from the experiments. This is, however, acceptable since even measurements performed on the same trabecula can differ from each other (Fig. 4a and e). This is due to the fact that trabecular bone is not homogeneous.

3.3 The model validation

Simulations of the stress relaxation test and uniaxial compression test were performed with averaged constants. Relaxation times were taken from identification based on the stress relaxation test. The 3D model of the cuboid trabecular bone sample made from µCT images used in these simulations is shown in Fig. 5. Simulations were performed in Ansys.

Fig. 5
figure 5

The 3D model of trabecular bone sample

Full size image

In order to validate the formulated constitutive equation for human trabecular bone, results from simulations of the stress relaxation test and uniaxial compression test with experimental results were graphically compared (Fig. 6). The curves obtained from the experiments are shown by means of squares, while the FE analysis curves are shown as solid lines.

Fig. 6
figure 6

The comparison of results from: a stress relaxation test simulation and from experiment, b uniaxial compression test simulation and from experiment

Full size image

In the relaxation part curves are very similar. The relaxation in the simulation happened to occur quicker than that in the experiment, and through the rest of the simulation stress was on the same level. During the experiment, relaxation lasted till the end of the test. The maximum stress in the simulation, which resulted from the given initial strain, was \({-}\) 7.32 MPa and was 0.3 MPa higher than that in the experiment.

The curve from the simulation of the uniaxial compression test is well fitted to the experimental result. The maximum depth of the compression is almost the same, i.e. 0.068 in simulation and 0.066 in the experiment. The depth after unloading was 0.017 and 0.023, respectively.

4 Discussion

In the paper, a new multi-scale constitutive model for human trabecular bone tissue is presented. Its formulation is based on nanoindentation tests conducted on trabeculae. The constitutive law considers the nonlinear viscoelastic behaviour of bone at a microscopic scale, which is manifested by the hysteresis loop in the force-displacement line graphs, and the sensitivity of the tissue response to various deformation rates. In addition, the model also describes very well the stress relaxation phenomenon. Our constitutive equation proved to be useful in macroscale as it reflects relatively well trabecular bone behaviour under compression.

As it was stated before, the material constants calibration was based on nanoindentation tests performed on trabeculae. Instrumented nanoindentation proved to be a very effective tool to determine the mechanical properties of bone [21,22,23]. We conducted the tests on non-extracted trabeculae, i.e. the indented trabeculae were not resected from the bone samples. This allowed us to minimise the effect of trabecula bending during indentation. The experiments were conducted to three levels of indentation force, i.e. 300 mN, 500 mN and 700 mN (three indentations for each force level) with two rates, i.e. 500 mN/min and 1000 mN/min (altogether 18 measurements). The results presented in Fig. 3 show that the response of the bone, i.e. the indentation depth, was different for the three cases, which seems to be reasonable. However, we also observed that the depth was also different within one set of particular measurement parameters, i.e. the assumed force level and rate. The observation proves that a single trabecula is not homogeneous. In addition, the various values of penetration permitted us to formulate a constitutive model that describes the tissue behaviour at multiple length scales. It has been shown that indenting bone to various depths allows one to determine its mechanical properties in a wide span of structural features [24,25,26].

The indentation tests were performed with a spherical tip. We chose that tip shape to minimise plastic effects during trabecula deformation. The studies reported in [27], where a spherical tip was also utilised, showed that plasticity begins to be predominating in bone deformation at depths of 20 \(\mu \)m and below. In our experimental test, the tip indented maximally 7 \({\mu }\)m in trabeculae. This justifies the assumption of the nonlinear viscoelastic response of bone in the studied range of deformation. Even though there is the residual deformation in every curve in Fig. 3, it does not mean plastic deformation in the bone. After some time after unloading, bone undergoes a relaxation process and returns to the original shape. The phenomenon is related to the viscoelastic properties of the trabecular bone. On the other hand, some researchers take into consideration plastic effects in their mathematical modelling of bone for the cases of low indentation depths [28, 29]. However, the modelling was based on the results from nanoindentation tests conducted with a Berkovich (three-sided pyramid) tip. In our research, we decided to study nonlinear viscoelastic effects in trabecular tissue in indentation tests conducted at various loading rates. We did not consider a load hold phase, which is usually done to minimise the viscous effects during deformation. In addition, we determined relaxation times and purely viscoelastic constants that characterised the tissue response to stress relaxation tests.

The identification of the purely elastic and viscoelastic constants was conducted by means of the indentation force-depth curve fitting method. Analysis of Fig. 3 proves that the model is able to mimic the bone response very well. However, it has to be critically stated that the constants were calibrated with some errors, which are presented in Tables 1 and 2. The accuracy of the values of the constants was estimated by comparing the areas within the hysteresis loops defined by our model and that obtained from the indentation tests. As that factor would not be sufficient to assess the calibration accuracy, another criterium was proposed, namely the error of the loop peaks convergence. Generally, the values of the errors are low, especially those related to the position of the peaks. The areas-fitting error seems to be high in the case of some measurements. A close analysis of the curves in Fig. 3 allows one to observe that the highest curve-fitting error related to the hysteresis loop areas was calculated for the measurements where in the initial phase of indentation there was a slight increase in force with progressing indentation depth. Such an effect is obtained when the indenter is immersed into the non-demineralised layer of trabecula, or the force and depth registration begin too quickly. In most of the measurements, we managed to eliminate that effect and our model seems to describe the trabecula response accurately. Nevertheless, in our opinion, the curve-fitting error was rather low given the fact that our model was fitted to experiments conducted on biological tissue. Also, a comparison of results from simulations with averaged hyperelastic and viscoelastic parameters to experimental curves, which can be seen in Fig. 4, proves that our approach was correct.

Figure 6 shows that our model, which was formulated on a microscopic scale, can be applied to model trabecular bone response on a macroscale. The figures present a comparison of the stress relaxation test (Fig. 6a) and compression test (Fig. 6b) conducted on a trabecular bone sample to the numerical bone response obtained by means of our model. We can observe good agreement between the numerical and experimental results. This proves the high ability of our constitutive model to simulate trabecular bone behaviour also on a macroscopic scale where the tissue indicates anisotropic behaviour. The anisotropy of trabecular bone on a macroscale depends, however, on the architecture of the trabecular structure [23]. Therefore, our multi-scale constitutive equation can be also utilised to model trabecular bone in a macroscale.

An alternative method of bone behaviour modelling in multi-scale is the application of a homogenisation technique. Those methods are related to the idea of representative volume element (RVE) definition. On the scale of an RVE, bone is considered as homogeneous material and on the lower scales—it is treated as a heterogeneous tissue. The homogenisation procedure can be successfully utilised in modelling poroelastic media, see e.g. [30,31,32], to which bone tissue might be classified. The homogenisation method consists of the application of averaging techniques to determine stress in the RVE. The technique has been applied in cortical bone modelling [33, 34]. One limitation is that gradient elasticity effects are not taken into account [35, 36] and another limitation of this technique is its strong dependency on boundary conditions. Moreover, the method idealises the trabecular bone structure by assuming its periodic strut network. In spite of this, one can address some research where the homogenisation technique is applied to a trabecular bone to model its basic properties [37,38,39,40].

Our model has some limitations. Firstly, calibration of the purely viscoelastic constants was based on stress relaxation tests conducted on macroscopic bone samples. This introduced some inaccuracy as the constants correspond to a porous structure with biological fluid inside the pores and not to a single trabecula. Secondly, plastic deformation seems to play an important role. Thus, it seems quite fundamental to consider plasticity in the constitutive formulation [41,42,43]. Thirdly, the rest of the constants were identified based on nanoindentation tests. In our opinion, including the results of uniaxial tension/compression tests or torsion tests conducted on a single trabecula would highly improve the constitutive model. However, some problems related to the accuracy of curve-fitting might arise.

5 Conclusions

Our study showed that the adopted method of multi-scale modelling to formulate a constitutive equation for human trabecular bone is correct. The model was formulated on a microscale as the parameters in the proposed mathematical model were identified based on nanoindentation experiments. Our further investigations showed that the constitutive equation could be successfully applied in modelling the mechanical behaviour of trabecular bone on a macroscale, e.g. bone adaptation to new loads [44,45,46,47], bone ingrowth in special implants utilised in bone healing process [48] or trabecular bone repair with use of granular medium [41, 49]. Numerical simulations with an application of our model can be very useful in the prediction of bone behaviour after a surgical intervention, e.g. implantation of a prosthesis or scaffold.