The Typical Cell of a Voronoi Tessellation on the Sphere

Abstract

The typical cell of a Voronoi tessellation generated by $n+1$ uniformly distributed random points on the d-dimensional unit sphere $\mathbb {S}^d$ is studied. Its f-vector is identified in distribution with the f-vector of a beta’ polytope generated by n random points in $\mathbb {R}^d$. Explicit formulas for the expected f-vector are provided for any d and the low-dimensional cases $d\in \{2,3,4\}$ are studied separately. This implies an explicit formula for the total number of k-dimensional faces in the spherical Voronoi tessellation as well.

1 Introduction

Let E be a metric space and $\{x_i:i\in I\}$ a finite (or, more generally, locally finite) collection of points in E, where I is some index set. The Voronoi cell of a point $x_i$ is the set of all points in E whose distance to $x_i$ is not greater than the distance to any other point $x_j$ with $i\ne j$. The Voronoi tessellation or Voronoi diagram associated with the set $\{x_i:i\in I\}$ is then just the collection of all such Voronoi cells. The study of Voronoi tessellations has attracted a lot of attention in computational as well as in stochastic geometry. To a great extent this is because of their various applications ranging from the modeling of biological tissues or polycrystalline microstructures in metallic alloys to classification problems in machine learning. We refer the reader to the monographs [4, 28,29,30] for details and many more references.

In this note we consider Voronoi tessellations of the unit sphere that are generated by a (finite) collection of uniformly distributed, independent random points. Unlike their Euclidean counterparts, for which there exists an extensive literature (see [29, 30, 34, 35] and the references cited there), the mathematical properties of spherical Voronoi tessellations are poorly understood. Just a few results for Voronoi tessellation on the 2-dimensional unit sphere are available in the classical reference [27]. On the other hand, Voronoi tessellations induced by points on a general manifold become increasingly important in computational geometry, see [4, 11]. Our goal is to partially fill the resulting gap by considering the combinatorial structure of what is called the typical cell of a Voronoi tessellation on the d-dimensional unit sphere for general $d\ge 2$. More precisely, we shall study the f-vector of the typical spherical Voronoi cell. We do this by establishing and exploiting a new connection of such typical Voronoi cells with the classes of random beta and beta’ polytopes. These have recently been under intensive investigation [6, 7, 10, 14, 20,21,22,23,24,25]. In fact, as it will turn out, the f-vector of the typical spherical Voronoi cell can be identified in distribution with the f-vector of (the dual of) a particular random beta’ polytope. Also, explicit expected values can be determined from this distributional identity and some known results for beta’ polytopes. We establish in addition a link between the expected f-vector of typical spherical Voronoi cells and that of a special beta polytope. Of special interest are the low-dimensional cases $d\in \{2,3,4\}$ which will be examined separately.

We would like to point out that our paper continues a recent line of research in stochastic geometry which focuses on the study of non-Euclidean geometric random structures. As examples we mention the studies of random convex hulls in spherical convex bodies or on half-spheres [3, 5, 21, 23], the results on random tessellations by great hyperspheres [1, 16, 17, 27], the central and non-central limit theorems for Poisson hyperplanes in hyperbolic spaces [15], the papers [12, 18] on splitting tessellations on the sphere, the asymptotic investigation of Voronoi tessellations on general Riemannian manifolds [9], and the general limit theory for stabilizing functionals of point processes in manifolds [32].

Fig. 1

Simulations of spherical Voronoi tessellations on $\mathbb {S}^2$ with 50 cells (left) and 200 cells (right)

2 The Typical Voronoi Cell and Its f-Vector

2.1 The Typical Voronoi Cell

We are now going to introduce our framework. Let $\mathbb {S}^d$ be the d-dimensional unit sphere, which we think of being embedded in $\mathbb {R}^{d+1}$ in such a way that it is centered at the origin of $\mathbb {R}^{d+1}$. A generic point in $\mathbb {R}^{d+1}$ is denoted by $x=(x_0,x_1,\ldots ,x_d)$. The dimension of the sphere, $d\in \mathbb {N}$, is fixed once and for all. The normalized spherical Lebesgue measure on $\mathbb {S}^d$ is denoted by $\sigma _d$. Let $X_1,\ldots ,X_n$ be $n\in \mathbb {N}$ independent random points sampled on $\mathbb {S}^d$ according to $\sigma _d$ and defined over some underlying probability space $(\Omega ,\mathcal {A},\mathbb {P})$. The binomial process $\xi _{n}:=\{X_1,\ldots ,X_n\}$ is the point process on $\mathbb {S}^d$ with atoms at $X_1,\ldots ,X_n$. We can now construct the spherical Voronoi tessellation based on $\xi _{n}$ as follows. If $\rho (\,{\cdot }\,,\,{\cdot }\,)$ denotes the geodesic distance on $\mathbb {S}^d$, we let $C_{i,n}$ be the Voronoi cell of a point $X_i\in \xi _n$, that is,

$$\begin{aligned} C_{i,n} := \bigl \{z\in \mathbb {S}^d:\rho (X_i,z)\le \rho (X_j,z)\text { for all } j\in \{1,\ldots ,n\}\bigr \},\qquad i\in \{1,\ldots ,n\}. \end{aligned}$$

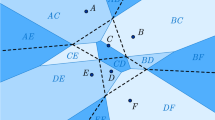
As in the Euclidean case (see [34, Chap. 10]), one shows that the sets $C_{1,n},\ldots ,C_{n,n}$ are in fact spherical polytopes covering $\mathbb {S}^d$ and having disjoint interiors. Here, we recall that a spherical polytope is defined as an intersection of $\mathbb {S}^d$ and a polyhedral convex cone, and that the latter is defined as an intersection of finitely many closed half-spaces whose bounding hyperplanes contain the origin. The collection $\{C_{1,n},\ldots ,C_{n,n}\}$ of all Voronoi cells of points of $\xi _{n}$ is what we call the spherical Voronoi tessellation $\mathfrak {m}_{n,d}$, see Fig. 1 for two sample realizations.

In this note we are interested in the typical cell of such a spherical Voronoi tessellation. Roughly speaking, the typical cell arises by picking one of the cells $C_{i,n}$ uniformly at random and rotating it so that its “center” $X_i$ becomes the north pole $e:=(1,0,\ldots ,0)$ of $\mathbb {S}^d$. To make this precise, let $N=N_{n}$ be a random variable with uniform distribution on the set $\{1,\ldots ,n\}$ and assume that N is independent of the binomial process $\xi _{n}$. Also, for every point $v\in \mathbb {S}^d$ we fix some orthogonal transformation $O_v:\mathbb {R}^{d+1}\rightarrow \mathbb {R}^{d+1}$ such that $O_vv=e$ and assume that the matrix elements of $O_v$ are Borel functions of v. Then, the typical cell of the Voronoi tessellation $\mathfrak {m}_{n, d}$ is a random spherical polytope $\mathscr {V}_{n,d}$ defined by

$$\begin{aligned} {\mathscr {V}_{n,d} := O_{X_N} C_{N,n}.} \end{aligned}$$

(2.1)

Since $X_1,\ldots ,X_n$ are exchangeable, the tuple $(\xi _n,X_N)$ has the same joint law as $(\xi _n,X_1)$ and we arrive at the following distributional equality:

$$\begin{aligned} \mathscr {V}_{n,d} {\mathop {=}\limits ^{\text{ d }}}O_{X_1} C_{1,n}. \end{aligned}$$

In the following, it will be more convenient to consider a binomial process with $n+1$ rather than with n points. The next proposition states that the typical Voronoi cell $\mathscr {V}_{n+1,d}$ of the binomial process $\xi _{n+1}$ has the same distribution as the Voronoi cell of the north pole e in the point process ${\xi _n\cup \{e\}}$. Note that it also proves that the distribution of the typical cell does not depend on the choice of the family of orthogonal transformations $(O_v)_{v\in \mathbb {S}^d}$.

Proposition 2.1

We have the distributional equality

$$\begin{aligned} \mathscr {V}_{n+1,d} {\mathop {=}\limits ^{\text{ d }}}\bigl \{z\in \mathbb {S}^d: \rho (e,z)\le \rho (X_j,z) \text { for all } j\in \{1,\ldots ,n\}\bigr \}. \end{aligned}$$

(2.2)

Proof

Conditioning on $X_1=v$ and integrating over all $v\in \mathbb {S}^d$, we can write the distribution of $\mathscr {V}_{n+1,d}$ as follows:

$$\begin{aligned} \mathbb {P}[\mathscr {V}_{n+1,d} \in B] = \int _{\mathbb {S}^d}\mathbb {P}\bigl [O_{X_1} C_{1,n+1} \in B \big | X_1 = v\bigl ]\, \sigma _d(\text{ d }v), \end{aligned}$$

for every Borel set B in the space of compact subsets of $\mathbb {S}^d$ endowed with the usual Hausdorff distance. Recalling the definition of $C_{1,n+1}$, we can write

$$\begin{aligned}&\mathbb {P}\bigl [O_{X_1} C_{1,n+1} \in B \big | X_1 = v\bigl ]\\&\quad =\mathbb {P}\Bigl [O_{v} \Bigl \{z\in \mathbb {S}^d:\rho (v,z)\le \min _{j=2,\ldots ,n+1}\rho (X_j,z)\Bigr \} \in B\Bigr ]\\&\quad =\mathbb {P}\Bigl [\Bigl \{y\in \mathbb {S}^d:\rho (v,O_v^{-1} y)\le \min _{j=2,\ldots ,n+1}\rho (X_j,O_v^{-1} y)\Bigr \} \in B\Bigr ]\\&\quad =\mathbb {P}\Bigl [\Bigl \{y\in \mathbb {S}^d:\rho (e,y) \le \min _{j=2,\ldots ,n+1}\rho (O_v X_j,y)\Bigr \} \in B\Bigr ]\\&\quad =\mathbb {P}\Bigl [\Bigl \{y\in \mathbb {S}^d:\rho (e,y) \le \min _{j=1,\ldots ,n}\rho (X_j,y)\Bigr \} \in B\Bigr ], \end{aligned}$$

where we defined $y:= O_v z$ and used that $(O_v X_2,\ldots ,O_v X_{n+1})$ has the same joint law as $(X_1,\ldots ,X_{n})$. Since the right-hand side does not depend on $v\in \mathbb {S}^d$, we arrive at

$$\begin{aligned} \mathbb {P}[\mathscr {V}_{n+1,d} \in B] = \mathbb {P}\Bigl [\Bigl \{y\in \mathbb {S}^d:\rho (e,y) \le \min _{j=1,\ldots ,n}\rho (X_j,y)\Bigr \}\in B\Bigr ], \end{aligned}$$

which completes the proof. $\square$

For stationary tessellations in the Euclidean space $\mathbb {R}^d$, where the number of cells is almost surely infinite, one usually defines the typical cell using the concept of Palm distribution, which is a common device in stochastic geometry [34]. The Palm approach can be applied on the sphere, too. Following [33], the Palm distribution $\mathbf {P}_{\xi _{n+1}}^e$ of the binomial process $\xi _{n+1}$ with respect to a fixed point on the sphere (which we choose to be the north pole e) can formally be defined as follows. For $v\in \mathbb {S}^d$ we let $\Theta _v$ denote the set of all orientation-preserving orthogonal transformations $O:\mathbb {R}^{d+1}\rightarrow \mathbb {R}^{d+1}$ such that $Ov=e$. Note that $\Theta _e$ is a group which can be identified with $\text {SO}(d)$. By $\nu _e$ we denote the unique Haar probability measure on $\Theta _e$ and define the image measure $\nu _v(A):=\nu _e(\{OO_v^{-1}:O\in A\})$, $A\subset \Theta _v$, on $\Theta _v$, where $O_v\in \Theta _v$ is arbitrary (in fact, the definition is independent of the choice of $O_v$, see [33]). The Palm distribution $\mathbf {P}_{\xi _{n+1}}^e$ with respect to the point e is given by

$$\begin{aligned} \mathbf {P}_{\xi _{n+1}}^e(\,{\cdot }\,):=\frac{1}{n+1}\,\mathbb {E}\!\sum _{v\in \xi _{n+1}}\int _{\Theta _v}\!\mathbf{1}(O^{-1} \xi _{n+1}\in \,{\cdot }\,)\,\nu _v(\text{ d }O). \end{aligned}$$

From [26, Lem. 6.14] it is known that

$$\begin{aligned} \mathbf {P}_{\xi _{n+1}}^e(\,{\cdot }\,)=\mathbf {P}_{\xi _n}(\xi _{n}\cup \{e\}\in \,{\cdot }\,), \end{aligned}$$

where $\mathbf {P}_{\xi _{n}}$ denotes the distribution of the binomial process $\xi _{n}$. This is the analogue for binomial processes of the celebrated Slivnyak–Mecke theorem for Poisson processes [26, Lem. 6.15]. In particular, it shows that the definition of the typical cell given above coincides with the definition based on the Palm approach.

2.2 Total Number of Faces

Our goal is to describe the f-vector of the typical Voronoi cell $\mathscr {V}_{n,d}$. More precisely, consider a spherical polytope $P\subset \mathbb {S}^d$ represented as an intersection of $\mathbb {S}^d$ and a polyhedral convex cone C. The k-dimensional faces of P are defined as intersections of $(k+1)$-dimensional faces of C with $\mathbb {S}^d$, where $k\in \{0,1,\ldots ,d\}$. We denote by $\mathcal F_k(P)$ the set of k-dimensional faces of P and by $f_k(P):=|\mathcal F_k(P)|$ their number.¹ Here, |A| stands for the number of elements of a set A. The d-dimensional vector $(f_0(P),f_1(P),\ldots ,f_{d-1}(P))$ is called the f-vector of P.

Before stating the results on the expected f-vector of the typical Voronoi cell, let us point out its connection to another natural quantity. The total number of k-dimensional faces of the tessellation $\mathfrak {m}_{n, d}$ is denoted by

$$\begin{aligned} f_k(\mathfrak {m}_{n, d}) := \left| \bigcup _{i=1}^n \mathcal F_k(C_{i,n})\right| , \qquad k\in \{0,1,\ldots ,d\}. \end{aligned}$$

Note that even if some face F belongs to more than one cell $C_{i,n}$, it is counted only once in the above definition.

Proposition 2.2

For all $n\ge d+1$ and $k\in \{0,\ldots ,d\}$, we have

$$\begin{aligned} \mathbb {E}f_k (\mathfrak {m}_{n, d}) = \frac{n}{d-k+1}\,\mathbb {E}f_k(\mathscr {V}_{n,d}). \end{aligned}$$

Proof

We use a double-counting argument. Let $M:=\sum _{i=1}^nf_k(C_{i,n})$ be the number of pairs $(C_{i,n},F)$, where $C_{i,n}$ is a cell of the tessellation $\mathfrak {m}_{n,d}$, and $F\subset C_{i,n}$ a k-dimensional face of $C_{i,n}$. On the one hand, the above definition (2.1) of the typical cell implies that

$$\begin{aligned} \mathbb {E}f_k(\mathscr {V}_{n,d})&=\mathbb {E}f_k(O_{X_N}C_{N,n})=\mathbb {E}f_k(C_{N,n})\\&=\frac{1}{n}\sum _{i=1}^n\mathbb {E}f_k(C_{i,n})=\frac{1}{n}\,\mathbb {E}\sum _{i=1}^n f_k(C_{i,n})=\frac{\mathbb {E}M}{n}. \end{aligned}$$

On the other hand, the spherical Voronoi tessellation is normal, that is, every k-dimensional face belongs to $d-k+1$ cells of dimension d, with probability one (cf. [34, Thm. 10.2.3] for a similar statement in the Euclidean case). It follows that almost surely

$$\begin{aligned} M = (d-k+1) f_k(\mathfrak {m}_{n,d}). \end{aligned}$$

By taking the expectations and comparing both identities, we arrive at the claim. $\square$

2.3 Reduction to Beta’ Polytopes

As anticipated above, our goal will be to identify the expected f-vector of the typical Voronoi cell $\mathscr {V}_{n+1,d}$ generated by $n+1$ uniformly distributed random points on the d-dimensional unit sphere. We do this first in terms of the f-vector of random beta’ polytopes, a notion we are going to explain next. For $\beta >d/2$ we define the probability density $\tilde{f}_{d,\beta }$ on $\mathbb {R}^d$ by

$$\begin{aligned} \tilde{f}_{d,\beta }(x):=\tilde{c}_{d,\beta }(1+\Vert x\Vert ^2)^{-\beta },\qquad \ \tilde{c}_{d,\beta }=\frac{\Gamma (\beta )}{\pi ^{d/2}\Gamma (\beta -d/2)}, \end{aligned}$$

(2.3)

where $\Vert \,{\cdot }\,\Vert$ denotes the Euclidean norm in $\mathbb {R}^d$. We let $\tilde{P}_{n,d}^\beta :={\text {conv}}{(\tilde{X}_1,\ldots ,\tilde{X}_n)}$ be the convex hull of $n\in \mathbb {N}$ independent random points $\tilde{X}_1,\ldots ,\tilde{X}_n$ distributed in $\mathbb {R}^d$ according to the density $\tilde{f}_{d,\beta }$. This random polytope is known as a so-called beta’ polytope. In our notation we follow [22, 24, 25], where these polytopes were studied. As in the spherical case, we denote by $(f_0(P),f_1(P),\ldots ,f_{d-1}(P))$ the f-vector of a polytope $P\subset \mathbb {R}^d$, where $f_k(P)$, $k\in \{0,1,\ldots ,d\}$, is the number of k-dimensional faces of P. Our main result relates the f-vector of $\mathscr {V}_{n+1,d}$ to that of $\tilde{P}_{n,d}^\beta$ with $\beta =d$ and can be formulated as follows. The proof is postponed to Sect. 4.

Theorem 2.3

For each $n\ge d+1$ we have that

$$\begin{aligned} \bigl (f_k(\mathscr {V}_{n+1,d})\bigr )_{k=0}^{d-1}\overset{\text{ d }}{=} \bigl (f_{d-k-1}(\tilde{P}_{n,d}^d)\bigr )_{k=0}^{d-1}, \end{aligned}$$

where $\overset{\text{ d }}{=}$ denotes equality in distribution of random vectors.

2.4 Reduction to Beta Polytopes

Recall that $X_1,\ldots ,X_{n}$ are independent and uniformly distributed random points on $\mathbb {S}^d$. Denote their convex hull in $\mathbb {R}^{d+1}$ by $P_{n,d+1}^{-1}:={\text {conv}}{(X_1,\ldots ,X_n)}$. This random polytope is a particular case of a beta polytope with parameter $\beta =-1$ studied in [22, 24, 25]. We follow the notation used there. Our next theorem expresses the expected f-vector of $\mathscr {V}_{n,d}$ in terms of that of $P_{n,d+1}^{-1}$.

Theorem 2.4

For each $n\ge d+1$ and $k\in \{0,1,\ldots ,d\}$ we have that

$$\begin{aligned} \mathbb {E}f_k(\mathscr {V}_{n,d}) = \frac{d-k+1}{n}\, \mathbb {E}f_{d-k}(P_{n,d+1}^{-1}). \end{aligned}$$

Remark 2.5

There is a duality between the faces of the spherical Voronoi tessellation $\mathfrak {m}_{n,d}$ and the faces of the convex hull of $X_1,\ldots ,X_n$, which was stated already in the work of Edelsbrunner and Nikitenko [13, pp. 3226–3227]. It says that for arbitrary $\ell \in \{0,\ldots ,d\}$ and $1\le i_0<\ldots <i_\ell \le n$, the convex hull of $X_{i_0},\ldots ,X_{i_\ell }$ is a face of the convex hull of $X_1,\ldots ,X_n$ if and only if the spherical Voronoi cells $C_{i_0,n},\ldots ,C_{i_\ell ,n}$ have a non-empty intersection. This intersection is then a common face of these cells of dimension $d-\ell$, with probability 1. In the proof given below, we provide a detailed explanation of this duality based on [34, pp. 472–473].

Proof of Theorem 2.4

First of all, let us provide a general representation for the faces of the spherical Voronoi tessellation $\mathfrak {m}_{n,d}$. Take some $i\in \{1,\ldots ,n\}$ and consider the cell

$$\begin{aligned} C_{i,n}=\mathbb {S}^d \cap \bigl \{y\in \mathbb {R}^{d+1}: \langle y, X_i\rangle \ge \langle y, X_j\rangle \text { for all } j\in \{1,\ldots ,n\} \bigr \}. \end{aligned}$$

(2.4)

Here, $\langle \,{\cdot }\,,\,{\cdot }\,\rangle$ stands for the standard scalar product in $\mathbb {R}^{d+1}$. In order to represent the relative interiors of the faces of this cell, we need to turn some of the inequalities $\langle y,X_i\rangle \ge \langle y,X_j\rangle$ into equalities, while making the remaining inequalities strict; see, e.g., [31, 7.2(e) on p. 135]. Thus, the relative interiors of the faces of $\mathfrak {m}_{n,d}$ admit a representation of the form

$$\begin{aligned} S := \bigl \{y\in \mathbb {S}^{d}: \langle y, X_{i_0}\rangle = \ldots = \langle y, X_{i_\ell }\rangle > \langle y, X_j\rangle \text { for all } j\notin \{i_0,\ldots ,i_\ell \}\bigr \} \end{aligned}$$

(2.5)

for some $\ell \in \{0,\ldots , n\}$ and $1\le i_0<\ldots <i_\ell \le n$. Conversely, any set S of the above form (2.5) is a relative interior of a face of $\mathfrak {m}_{n,d}$ provided $S\ne \varnothing$. Observe that for $\ell >d$ the vectors $X_{i_1}-X_{i_0},\ldots ,X_{i_\ell }-X_{i_0}$ linearly span $\mathbb {R}^{d+1}$ with probability 1 and hence the only solution of $\langle y, X_{i_0}\rangle = \ldots = \langle y, X_{i_\ell }\rangle$ is $y=0$ (implying that $S=\varnothing$). Thus, we may assume that $\ell \in \{0,\ldots , d\}$. Then, the vectors $X_{i_1}-X_{i_0},\ldots ,X_{i_\ell }-X_{i_0}$ are linearly independent almost surely and hence the dimension of the set S defined in (2.5) is $d-\ell$, provided $S\ne \varnothing$.

Let us now provide a description of the faces of the polytope ${\text {conv}}{(X_1,\ldots ,X_n)}$. For $\ell \in \{0,\ldots ,d\}$ and $1\le i_0<\ldots <i_\ell \le n$ let E be the affine subspace through the points $X_{i_0},\ldots ,X_{i_\ell }$. In the following, we exclude an event of probability 0 and assume that E is $\ell$-dimensional. Let $E_0$ be the translate of E passing through the origin of $\mathbb {R}^{d+1}$, that is, $E_0$ is the linear hull of $X_{i_1}-X_{i_0}, \ldots , X_{i_\ell }-X_{i_0}$. Put

$$\begin{aligned} F=E_0^\perp =\{y\in \mathbb {R}^{d+1}: \langle y, X_{i_0}\rangle = \ldots = \langle y, X_{i_\ell }\rangle \} \end{aligned}$$

and note that F is a linear subspace of dimension $d+1-\ell$. The intersection of F with $\mathbb {S}^d$ is a $(d-\ell )$-dimensional great subsphere of $\mathbb {S}^d$ consisting of all points $y\in \mathbb {S}^d$ having equal geodesic distances to $X_{i_0},\ldots ,X_{i_\ell }$. For $y\in F\cap \mathbb {S}^d$ write $r(y):=\rho (y,X_{i_0})=\ldots =\rho (y,X_{i_\ell })$. Denote by $\mathrm{Cap}(y,r(y)):=\{z\in \mathbb {S}^d:\rho (y,z)\le r(y)\}$ the closed spherical cap centered at y with geodesic radius r(y) and put

$$\begin{aligned} S :=\bigl \{y\in F\cap \mathbb {S}^d:\mathrm{Cap}(y,r(y))\cap \{X_1,\ldots ,X_n\}= \{X_{i_0},\ldots , X_{i_\ell }\}\bigr \}, \end{aligned}$$

(2.6)

which is just an equivalent form of (2.5).

We now claim that $S\ne \varnothing$ if and only if ${\text {conv}}{(X_{i_0},\ldots ,X_{i_\ell })}$ is a face of ${\text {conv}}{(X_1,\ldots ,X_n)}$. Indeed, if $S\ne \varnothing$, then there is $y\in \mathbb {S}^d$ such that $a=\langle y,X_{i_0}\rangle =\ldots =\langle y, X_{i_\ell }\rangle$ and $\langle y,X_j\rangle >a$ for all indices $j\notin \{i_0,\ldots , i_\ell \}$. Consider the hyperplane $H:=\{z\in \mathbb {R}^{d+1}:\langle z,y \rangle =a\}$. Then, H is a supporting hyperplane for ${\text {conv}}{(X_1,\ldots ,X_n)}$ and ${\text {conv}}{(X_{i_0},\ldots ,X_{i_\ell })}={\text {conv}}{(X_1,\ldots ,X_n)}\cap H$ is the corresponding face of ${\text {conv}}{(X_1,\ldots ,X_n)}$, thus proving the forward direction of the claim. To prove the backward direction, one assumes that ${\text {conv}}{(X_{i_0},\ldots ,X_{i_\ell })}$ is a face of ${\text {conv}}{(X_1,\ldots ,X_n)}$ corresponding to some supporting hyperplane H which must be of the form $H:=\{z\in \mathbb {R}^{d+1}:\langle z,y\rangle =a\}$ for some $y\in \mathbb {S}^d$ and $a\in \mathbb {R}$. It follows that $a=\langle y,X_{i_0}\rangle =\ldots =\langle y, X_{i_\ell }\rangle$ and (without restriction of generality) $\langle y,X_j\rangle >a$ for all $j\notin \{i_0,\ldots ,i_\ell \}$. This proves our claim. Although we shall not need it, notice also the following consequence of (2.5) and (2.4): the closure of S coincides with $C_{i_0,n}\cap \cdots \cap C_{i_\ell ,n}$.

Summarizing, we proved that there is a bijective correspondence between the $(d-\ell )$-dimensional faces of $\mathfrak {m}_{n,d}$, the $\ell$-dimensional faces of ${\text {conv}}{(X_1,\ldots ,X_n)}$, and the tuples $1\le i_0<\ldots <i_\ell \le n$ for which the set S defined in (2.5) or (2.6) is non-empty. Thus, taking $\ell :=d-k$ we conclude that

$$\begin{aligned} f_{d-k}(P_{n,d+1}^{-1}) = f_k(\mathfrak {m}_{n,d}) \quad \ \text {almost surely}. \end{aligned}$$

(2.7)

On the other hand, by Proposition 2.2 we have

$$\begin{aligned} \mathbb {E}f_k (\mathfrak {m}_{n,d}) = \frac{n}{d-k+1}\,\mathbb {E}f_k(\mathscr {V}_{n,d}). \end{aligned}$$

Putting these results together completes the proof of Theorem 2.4. $\square$

3 Explicit Formulas and Special Cases

3.1 Explicit Formula for the Expected f-Vector

The expected f-vectors of beta and beta’ polytopes have been explicitly determined in the series of works [19,20,21,22, 25]. The main results we shall rely on are stated in [22, Thms. 7.1 and 7.3]. Combining these formulas with Theorems 2.3 or  2.4 we arrive at the following explicit expression for the f-vector of the typical Voronoi cell $\mathscr {V}_{n+1,d}$.

Theorem 3.1

For all $d\ge 2$, $n\ge d+1$, and $\ell \in \{1,\ldots ,d\}$ we have

$$\begin{aligned}&\mathbb {E}f_{d-\ell } (\mathscr {V}_{n+1,d})=\frac{1}{\pi }\biggl (\frac{\Gamma (({d+1})/{2})}{\sqrt{\pi }\, \Gamma (d/2)}\biggr )^{\!n-\ell }\!\!\!\!\sum _{\begin{array}{c} m\in \{\ell ,\ldots ,d\} \\ m\equiv d \;(\mathrm {mod}\,2) \end{array}}\!\!\!\tilde{I}_d(n,m) (md-1) \tilde{J}_d(m,\ell ) \end{aligned}$$

(3.1)

$$\begin{aligned}&=\frac{1}{\pi }\biggl (\frac{\Gamma (({d+1})/{2})}{\sqrt{\pi }\, \Gamma (d/2)}\biggr )^{\!n-\ell }\!\!\!\!\sum _{\begin{array}{c} m\in \{\ell ,\ldots ,d\} \\ m\equiv d \;(\mathrm {mod}\,2) \end{array}}\!\!\!I_{d-1}(n,m) ((m+1)(d-1)+1) J_{d-1}(m,\ell ) , \end{aligned}$$

(3.2)

where

$$\begin{aligned} \tilde{I}_d(n,m)&:=\left( {\begin{array}{c}n\\ m\end{array}}\right) \int _{-\pi /2}^{+\pi /2} (\cos x)^{d m -1} (\tilde{F}_d(x))^{n-m} \,\text{ d }x,\\ \tilde{J}_d(m,\ell )&:=\left( {\begin{array}{c}m\\ \ell \end{array}}\right) \int _{-\infty }^{+\infty } (\cosh y)^{-d m + 1} (\tilde{F}_d({\mathrm{i}}y))^{m-\ell } \,\text{ d }y,\\ I_{d-1}(n,m)&:=\left( {\begin{array}{c}n\\ m\end{array}}\right) \int _{-\pi /2}^{+\pi /2} (\cos x)^{(d-1)(m+1)} (F_{d-1}(x))^{n-m} \,\text{ d }x,\\ J_{d-1}(m,\ell )&:=\left( {\begin{array}{c}m\\ \ell \end{array}}\right) \int _{-\infty }^{+\infty } (\cosh y)^{-(d-1)(m+1) - 2} (F_{d-1}({\mathrm{i}}y))^{m-\ell } \,\text{ d }y,\\ \tilde{F}_d(z)=F_{d-1}(z)&:=\int _{-\pi /2}^z (\cos y)^{d-1} \,\text{ d }y, \qquad z\in \mathbb {C}. \end{aligned}$$

Remark 3.2

Note that the imaginary unit ${\mathrm{i}}=\sqrt{-1}$ appears because the J-quantities are related to the analytic continuation of the I-quantities [22]. The integral in the definition of $\tilde{F}_d(z)=F_{d-1}(z)$ is taken along any contour connecting $-\pi /2$ and z. Observe also that the quantities $\tilde{J}_d(m,\ell )$ and $J_{d-1}(m,\ell )$ are real-valued as one can see by making the substitution $y\mapsto -y$ in the defining integrals and using the fact that $\tilde{F}_d({\mathrm{i}}y)$ is the complex conjugate of $\tilde{F}_d(-{\mathrm{i}}y)$, for all $y\in \mathbb {R}$.

Proof of Theorem 3.1

We can give two proofs based on reduction of the spherical Voronoi tessellation to beta’ and beta polytopes. These proofs yield (3.1) and (3.2), respectively. Let us start with the approach based on beta’ polytopes. By Theorem 2.3, we have

$$\begin{aligned} \mathbb {E}f_{d-\ell } (\mathscr {V}_{n+1,d}) = \mathbb {E}f_{\ell -1}(\tilde{P}_{n,d}^d). \end{aligned}$$

By [22, Thm. 7.3] applied with $\alpha = \beta =d$, we obtain

$$\begin{aligned} \mathbb {E}f_{\ell -1}(\tilde{P}_{n,d}^d)&= \frac{2\cdot n!}{\ell !}\biggl (\frac{\Gamma (({d+1})/{2})}{d \sqrt{\pi }\, \Gamma (d/2)}\biggr )^{\!n-\ell }\\&\quad \,\times \,\sum _{\begin{array}{c} m\in \{\ell ,\ldots ,d\} \\ m\equiv d \;(\mathrm {mod}\,2) \end{array}}\!\!\!\tilde{b}\{n,m\} \biggl (m-\frac{1}{d}\biggr )\tilde{a}\biggl [m-\frac{2}{d}, \ell - \frac{2}{d}\biggr ], \end{aligned}$$

where

$$\begin{aligned} \tilde{b}\{n,m\}&=\frac{d^{n-m}}{(n-m)!} \int _{-\pi /2}^{+\pi /2} (\cos x)^{d m -1} (\tilde{F}_d(x))^{n-m} \,\text{ d }x,\\ \tilde{a}\biggl [m-\frac{2}{d},\ell - \frac{2}{d}\biggr ]&= \frac{d^{m-\ell +1}}{(m-\ell )!} \cdot \frac{1}{2\pi } \int _{-\infty }^{+\infty } (\cosh y)^{-d m +1} (\tilde{F}_d({\mathrm{i}}y))^{m-\ell }\,\text{ d }y, \end{aligned}$$

and where $\tilde{F}_d$ is as above. After straightforward transformations, we arrive at (3.1).

On the other hand, we can give an alternative proof based on Theorem 2.4 which states that

$$\begin{aligned} \mathbb {E}f_{d-\ell }(\mathscr {V}_{n+1,d}) = \frac{\ell +1}{n+1} \, \mathbb {E}f_{\ell }(P_{n+1,d+1}^{-1}). \end{aligned}$$

The expected f-vector of the beta polytope is given explicitly in [22, Thm. 7.1]. Applying this theorem with $\beta =-1$ and $\alpha =d-1$, we obtain

$$\begin{aligned} \mathbb {E}f_{\ell }(P_{n+1,d+1}^{-1})&=\frac{2\cdot (n+1)!}{(\ell +1)!} \biggl (\frac{\Gamma (({d-1})/{2})}{2\sqrt{\pi }\, \Gamma ({d}/{2})}\biggr )^{\!n-\ell }\\&\quad \times \!\! \sum _{\begin{array}{c} m\in \{\ell ,\ldots ,d\} \\ m\equiv d \;(\mathrm {mod}\,2) \end{array}}\!\!\!b\{n+1,m+1\} \biggl (m + 1 + \frac{1}{d-1}\biggr )\\&\qquad \qquad \qquad \quad \times \,a\biggl [m+1+\frac{2}{d-1}, \ell + 1 + \frac{2}{d-1}\biggr ], \end{aligned}$$

where

$$\begin{aligned} b\{n+1,m+1\}&=\frac{(d-1)^{n-m}}{(n-m)!} \int _{-\pi /2}^{+\pi /2} (\cos x)^{(d-1)(m+1)} (F_{d-1}(x))^{n-m} \,\text{ d }x,\\&a\biggl [m+1 + \frac{2}{d-1}, \ell + 1 + \frac{2}{d-1}\biggr ]\\&= \frac{(d\!-\!1)^{m-\ell +1}}{(m-\ell )!} \cdot \frac{1}{2\pi } \int _{-\infty }^{+\infty } (\cosh y)^{-(d-1)(m+1)-2} (F_{d-1}({\mathrm{i}}y))^{m-\ell } \,\text{ d }y. \end{aligned}$$

After some transformations, we arrive at (3.2). $\square$

Remark 3.3

In particular, we obtained an indirect proof that the right-hand sides of (3.1) and (3.2) are equal. Finding a direct proof of this equality seems non-trivial. Let us also mention that, according to our numerical computations, the individual summands in (3.1) and (3.2) are, in general, not equal.

Proposition 3.4

Let $d\ge 2$, $n\ge d+2$, and $k\in \{0,\ldots ,d-1\}$. If d is even, then $\mathbb {E}f_k(\mathscr {V}_{n,d})$ is a rational number. If d is odd, then $\mathbb {E}f_k(\mathscr {V}_{n,d})$ is a linear combination of the numbers $\pi ^{-2r}$, where $r=0,1,\ldots , \lfloor ({n-d+k-1})/{2}\rfloor$, with rational coefficients.

Proof

This follows from Theorem 2.4 together with [22, Thm. 7.2]. The same result could be deduced by combining Theorem 2.3 with [22, Thm. 7.4]. $\square$

Remark 3.5

Along with the Voronoi tessellation it is natural to consider the so-called spherical hyperplane tessellation which is defined as follows. As before, let $X_1,\ldots ,X_n$ be n independent, uniformly distributed random points on $\mathbb {S}^d$, where $n\ge d+1$. Let $X_i^{\bot }=\{z\in \mathbb {R}^{d+1}:\langle z,X_i\rangle =0\}$ be the hyperplane orthogonal to $X_i$. The hyperplanes $X_1^{\bot },\ldots , X_n^{\bot }$ dissect the sphere $\mathbb {S}^d$ into spherical polytopes which constitute the spherical hyperplane tessellation. The spherical Crofton cell $\mathcal Z_{n,d}$ is defined as the almost surely unique cell of this tessellation that contains the north pole e. We have $\mathcal Z_{n,d}=\mathbb {S}^d\cap (G_1\cap \cdots \cap G_n)$, where $G_i$ is the half-space bounded by $X_i^{\bot }$ and containing the north pole e. The expected f-vector of the spherical Crofton cell $\mathcal Z_{n,d}$ can be computed as follows. We observe that the dual of the convex cone $G_1\cap \cdots \cap G_n$ is the positive hull $D_n:={\text {pos}}{(X_1^{-},\ldots ,X_{n}^-)}$ of the points $X_i^-:=-X_i\cdot {\text {sgn}}{\langle X_i,e\rangle }$. The points $X_1^-,\ldots ,X_n^-$ are independent and uniformly distributed on the lower half-sphere $\mathbb {S}^d_-:=\{z\in \mathbb {S}^d:\langle z,e\rangle \le 0\}$. The corresponding f-vectors satisfy

$$\begin{aligned} \mathbb {E}f_k (\mathcal Z_{n,d}) = \mathbb {E}f_{k+1} (G_1\cap \cdots \cap G_n) = \mathbb {E}f_{d-k} (D_n)=\mathbb {E}f_{d-k-1} (\mathbb {S}^d\cap D_n) \end{aligned}$$

for all $k\in \{0,\ldots ,d-1\}$. The expected face numbers of the random spherical polytopes $\mathbb {S}^d\cap D_n$ that appear on the right-hand side have been explicitly computed in [21]. These polytopes are also closely related to the beta’ polytopes $\tilde{P}_{n,d}^{\beta }$, but this time with $\beta =({d+1})/{2}$, see [21, 23].

3.2 Low-Dimensional Cases

Let us consider the low-dimensional cases separately. For example, in dimension $d=2$, if we take $\ell =1$ in Theorem 3.1 we arrive at the following result of Miles [27].

Corollary 3.6

For $d=2$ and $n\ge 3$ we have

$$\begin{aligned} \mathbb {E}f_0(\mathscr {V}_{n+1,2}) = \mathbb {E}f_1(\mathscr {V}_{n+1,2}) = 6 \cdot \frac{n-1}{n+1} = 6\biggl (1-\frac{2}{n+1}\biggr ). \end{aligned}$$

(3.3)

Proof

According to Theorem 3.1, $\mathbb {E}f_1(\mathscr {V}_{n+1,2})=\tilde{I}_2(n,2)\cdot 3\cdot \tilde{J}_2(2,1)/(\pi 2^{n-1})$. Moreover, $\tilde{F}_2(z)=1+\sin z$, which implies that $\tilde{J}_2(2,1)=\pi$. In addition,

$$\begin{aligned} {n\atopwithdelims ()2}^{\!-1}\tilde{I}_2(n,2)&= \int _{-\pi /2}^{\pi /2}(\cos x)^3(1+\sin x)^{n-2}\,\text{ d }x\\&=\sum _{k=0}^{n-2} {\left( {\begin{array}{c}n-2\\ k\end{array}}\right) } \int _{-\pi /2}^{\pi /2}(\cos x)^3(\sin x)^k\,\text{ d }x\\&=\sum _{k=0}^{n-2}{\left( {\begin{array}{c}n-2\\ k\end{array}}\right) } {2(1+(-1)^k)\over (k+1)(k+3)} = {2^{n+1}\over n(n+1)}, \end{aligned}$$

which implies

$$\begin{aligned} \mathbb {E}f_1(\mathscr {V}_{n+1,2})={3\over 2^{n-1}}{n\atopwithdelims ()2}{2^{n+1}\over n(n+1)}=6\cdot {n-1\over n+1}. \end{aligned}$$

$\square$

As observed already by Miles [27], it is not surprising that $\mathbb {E}f_0(\mathscr {V}_{n+1,2})\rightarrow 6$, as $n\rightarrow \infty$, which is the expected number of vertices of the typical cell of a Poisson–Voronoi tessellation in the plane, see [34, Thm. 10.2.5].

Remark 3.7

We note that (3.3) can alternatively be obtained by purely combinatorial means. Indeed, by the Euler relation and the fact that the Voronoi tessellation on the sphere is almost surely simple (which, for $d=2$, means that each vertex of the tessellation belongs to exactly three edges), we have

$$\begin{aligned} f_2(\mathfrak {m}_{n+1,d}) - f_1(\mathfrak {m}_{n+1,d})+f_0(\mathfrak {m}_{n+1,d}) = 2 \quad \text { and }\quad 2 f_1(\mathfrak {m}_{n+1,d})=3f_0(\mathfrak {m}_{n+1,d}) \end{aligned}$$

almost surely. Also, $f_2(\mathfrak {m}_{n+1,d}) = n+1$ since each cell corresponds to its center. Altogether, it follows that

$$\begin{aligned} f_0(\mathfrak {m}_{n+1,d}) = 2(n-1)\quad \text { and }\quad f_1(\mathfrak {m}_{n+1,d}) = 3(n-1) \end{aligned}$$

almost surely. Taking the expectations and recalling Proposition 2.2 yields (3.3).

Table 1 Exact and approximate values for the expected number of vertices of the typical Voronoi cell generated by $n\in \{4,\ldots ,9\}$ random points on $\mathbb {S}^3$ and $n\in \{5,\ldots ,9\}$ random points on $\mathbb {S}^4$

On the other hand, in dimensions $d>2$ the f-vector of $\mathfrak {m}_{n+1,d}$ is not deterministic. For $d=3$ and $d=4$, we present exact formulas for the expected f-vector of the typical spherical Voronoi cell and refer to Table 1 for some exact and numerical values for small values of n.

Corollary 3.8

For $d=3$ and all $n\ge 4$ we have

$$\begin{aligned} \mathbb {E}f_0(\mathscr {V}_{n+1,3})&={256\over 35\pi }\biggl (\frac{1}{2\pi }\biggr )^{\!n-3}\left( {\begin{array}{c}n\\ 3\end{array}}\right) \int _{-\pi /2}^{+\pi /2}(\cos x)^8(2 x+\sin 2x+\pi )^{n-3}\,\text{ d }x,\\ \mathbb {E}f_1(\mathscr {V}_{n+1,3})&=\frac{3}{2}\, \mathbb {E}f_0(\mathscr {V}_{n+1,3}),\qquad \mathbb {E}f_2(\mathscr {V}_{n+1,3})=\frac{1}{2}\, \mathbb {E}f_0(\mathscr {V}_{n+1,3}) + 2. \end{aligned}$$

Proof

The first formula follows from Theorem 3.1 with $d=3$ and $\ell =3$:

$$\begin{aligned} \mathbb {E}f_0(\mathscr {V}_{n+1,3}) = {1\over \pi }\biggl ({2\over \pi }\biggr )^{\!n-3}\tilde{I}_3(n,3)\cdot 8 \cdot \tilde{J}_3(3,3). \end{aligned}$$

It remains to note that $\tilde{F}_3(z)=(2z+\sin 2z+\pi )/4$, which implies that $\tilde{J}_3(3,3)={32/35}$ and

$$\begin{aligned} \tilde{I}_3(n,3) = \biggl ({1\over 4}\biggr )^{\!n-3}{n\atopwithdelims ()3}\int _{-\pi /2}^{+\pi /2}(\cos x)^8(2x+\sin 2x+\pi )^{n-3}\,\text{ d }x. \end{aligned}$$

Since $\mathscr {V}_{n+1,3}$ is a simple polytope with probability one, we have that almost surely $2f_1(\mathscr {V}_{n+1,3})=3f_0(\mathscr {V}_{n+1,3})$. Finally, the formula for $\mathbb {E}f_0(\mathscr {V}_{n+1,3})$ follows from Euler’s relation, which says that almost surely $f_0(\mathscr {V}_{n+1,3})-f_1(\mathscr {V}_{n+1,3})+f_2(\mathscr {V}_{n+1,3})=2$.

$\square$

Corollary 3.9

For $d=4$ and all $n\ge 5$ we have

$$\begin{aligned} \mathbb {E}f_0(\mathscr {V}_{n+1,4})&=\frac{6435}{2048}\biggl ({3\over 48}\biggr )^{\!n-4}\left( {\begin{array}{c}n\\ 4\end{array}}\right) \int _{-\pi /2}^{+\pi /2}(\cos x)^{15}(8+9\sin x+\sin 3x)^{n-4}\,\text{ d }x,\\ \mathbb {E}f_1(\mathscr {V}_{n+1,4})&=2\mathbb {E}f_0(\mathscr {V}_{n+1,4}),\qquad \mathbb {E}f_2(\mathscr {V}_{n+1,4})=6{n-1\over n+1}+{6\over 5}\,\mathbb {E}f_0(\mathscr {V}_{n+1,4}),\\ \mathbb {E}f_3(\mathscr {V}_{n+1,4})&=6{n-1\over n+1}+{1\over 5}\,\mathbb {E}f_0(\mathscr {V}_{n+1,4}). \end{aligned}$$

Proof

The identity for $\mathbb {E}f_0(\mathscr {V}_{n+1,4})$ follows from Theorem 3.1. In fact, taking $d=4$ and $\ell =4$ we obtain

$$\begin{aligned} \mathbb {E}f_0(\mathscr {V}_{n+1,4}) = {1\over \pi }\biggl ({3\over 4}\biggr )^{\!n-4}\tilde{I}_4(n,4)\cdot 15\cdot \tilde{J}_4(4,4). \end{aligned}$$

Moreover, $\tilde{F}_4(z)=(8+9\sin z+\sin 3z)/12$, which in turn implies that $\tilde{J}_4(4,4)={429\,\pi /2048}$ and

$$\begin{aligned} \tilde{I}_4(n,4)=\biggl ({1\over 12}\biggr )^{\!n-4}{n\atopwithdelims ()4}\int _{-\pi /2}^{+\pi /2}(\cos x)^{15}(8+9\sin x+\sin 3x)^{n-4}\,\text{ d }x . \end{aligned}$$

To derive the other identities, we use the three linearly independent Dehn–Sommerville equations for simplicial 5-dimensional polytopes [8, Cor. 17.8]. Applied to $P_{n+1,5}^{-1}$ they say that almost surely

$$\begin{aligned}&2 = f_0(P_{n+1,5}^{-1}) - f_1(P_{n+1,5}^{-1}) + f_2(P_{n+1,5}^{-1}) - f_3(P_{n+1,5}^{-1}) + f_4(P_{n+1,5}^{-1}),\\&2f_1(P_{n+1,5}^{-1}) = 3f_2(P_{n+1,5}^{-1})-6f_3(P_{n+1,5}^{-1})+10 f_4(P_{n+1,5}^{-1}),\\&5f_4(P_{n+1,5}^{-1}) = 2f_3(P_{n+1,5}^{-1}). \end{aligned}$$

Using (2.7) these identities translate into the almost sure relations

$$\begin{aligned}&2 = f_4(\mathfrak {m}_{n+1,4}) - f_3(\mathfrak {m}_{n+1,4}) + f_2(\mathfrak {m}_{n+1,4}) - f_1(\mathfrak {m}_{n+1,4}) + f_0(\mathfrak {m}_{n+1,4}),\\&2f_3(\mathfrak {m}_{n+1,4}) = 3f_2(\mathfrak {m}_{n+1,4}) - 6f_1(\mathfrak {m}_{n+1,4}) + 10 f_0(\mathfrak {m}_{n+1,4}),\\&5f_0(\mathfrak {m}_{n+1,4}) = 2f_1(\mathfrak {m}_{n+1,4}) \end{aligned}$$

for the random Voronoi tessellation $\mathfrak {m}_{n+1,4}$ on $\mathbb {S}^4$. In addition, we have that almost surely $f_4(\mathfrak {m}_{n+1,4})=n+1$, since each cell of $\mathfrak {m}_{n+1,4}$ corresponds to its center. This implies that $f_1(\mathfrak {m}_{n+1,4})$, $f_2(\mathfrak {m}_{n+1,4})$, and $f_3(\mathfrak {m}_{n+1,4})$ can be expressed in terms of $f_0(\mathfrak {m}_{n+1,4})$ only. In fact, we have that almost surely

$$\begin{aligned} f_1(\mathfrak {m}_{n+1,4})= & {} {5f_0(\mathfrak {m}_{n+1,4})\over 2},\qquad f_2(\mathfrak {m}_{n+1,4})= 2(n-1) + 2f_0(\mathfrak {m}_{n+1,4}),\\ f_3(\mathfrak {m}_{n+1,4})= & {} 3(n-1) + {f_0(\mathfrak {m}_{n+1,4})\over 2}. \end{aligned}$$

We finally apply Proposition 2.2 to conclude that $5\mathbb {E}f_0(\mathfrak {m}_{n+1,4})=(n+1)\mathbb {E}f_0(\mathscr {V}_{n+1,4})$ and

$$\begin{aligned} \mathbb {E}f_1(\mathscr {V}_{n+1,4})= {4\over n+1}\,\mathbb {E}f_1(\mathfrak {m}_{n+1,4}) = {4\over n+1}\cdot {5\over 2}\cdot \mathbb {E}f_0(\mathfrak {m}_{n+1,4}) = 2\mathbb {E}f_0(\mathscr {V}_{n+1,4}). \end{aligned}$$

The identities for $\mathbb {E}f_2(\mathscr {V}_{n+1,4})$ and $\mathbb {E}f_3(\mathscr {V}_{n+1,4})$ follow similarly:

$$\begin{aligned} \mathbb {E}f_2(\mathscr {V}_{n+1,4})&= {3\over n+1}(2(n-1)+2\mathbb {E}f_0(\mathfrak {m}_{n+1,4}))=6{n-1\over n+1}+{6\over 5}\,\mathbb {E}f_0(\mathscr {V}_{n+1,4}),\\ \mathbb {E}f_3(\mathscr {V}_{n+1,4})&= {2\over n+1}\biggl (3(n-1)+{1\over 2}\,\mathbb {E}f_0(\mathfrak {m}_{n+1,4})\biggr )=6{n-1\over n+1} + {1\over 5}\,\mathbb {E}f_0(\mathscr {V}_{n+1,4}). \end{aligned}$$

This completes the argument. $\square$

Remark 3.10

It is interesting to note that if we applied the Dehn–Sommerville equations directly to the typical Voronoi cell $\mathscr {V}_{n+1,4}$ (which is almost surely a simple polytope), this would not yield enough relations to express all $\mathbb {E}f_i(\mathscr {V}_{n+1,4})$ through $\mathbb {E}f_0(\mathscr {V}_{n+1,4})$. It is known [8, § 17] that both, in dimensions 4 and 5, the f-vectors of simplicial (and simple) polytopes depend on two free parameters. Applying the Dehn–Sommerville relations to the 5-dimensional beta polytope has the advantage that we know the number of vertices to be $n+1$, which reduces the number of free parameters to 1.

4 Proof of Theorem 2.3

4.1 Preliminaries

Let us first introduce some notation. Recall that $\xi _n=\{X_1,\ldots ,X_n\}$ is a binomial process on $\mathbb {S}^d$ induced by $n\in \mathbb {N}$ independent random points $X_1,\ldots ,X_n$ with the uniform distribution $\sigma _d$. For each $i\in \{1,\ldots ,n\}$ we let $h_i\in [-1,1]$ be the projection of $X_i$ onto the 0-th coordinate of $\mathbb {R}^{d+1}$ which is shown as the vertical direction in Fig. 2. Also, we denote by $\theta _i\in [0,\pi ]$ the angle between $e=(1, 0,\ldots ,0)$ and $X_i$. Formally,

$$\begin{aligned} h_i = \langle X_i,e\rangle = \cos \theta _i, \end{aligned}$$

where $\langle \,{\cdot }\,,\,{\cdot }\,\rangle$ denotes the standard scalar product in $\mathbb {R}^d$. We can then decompose $X_i$ as follows:

$$\begin{aligned} X_i = e \cos \theta _i + U_i \sin \theta _i, \qquad i\in \{1,\ldots ,n\}, \end{aligned}$$

(4.1)

where $U_i$ is a suitable unit vector in the d-dimensional hyperplane $e^{\bot } = \{x_{0} = 0\}$ which we identify with $\mathbb {R}^d$. The next lemma, which is well known, characterizes the joint distribution of $h_i$ and $U_i$. It is just a probabilistic restatement of the slice integration formula for spheres, see [2, Cor. A.5]. The density of $h_i$ can be found in [23, Lem. 7.6] or deduced from [24, Lem. 4.4].

Lemma 4.1

For each $i\in \{1,\ldots ,n\}$ the random variable $h_i$ has density

$$\begin{aligned} f(h) = {\Gamma ({(d+1)/2})\over \sqrt{\pi }\,\Gamma ({d/2})}\,(1-h^2)^{{d/2}-1},\qquad h\in [-1,1], \end{aligned}$$

with respect to the Lebesgue measure on $[-1,1]$. The random variable $U_i$ is uniformly distributed on the unit sphere in ${\{x_{0}=0\}\equiv \mathbb {R}^d}$. Finally, $h_i$ and $U_i$ are independent.

Fig. 2

Illustration of the construction used in the proof of Theorem 2.3

4.2 Proof of Theorem 2.3

The starting point of our proof is the representation of the typical Voronoi cell on $\mathbb {S}^d$ given in Proposition 2.1:

$$\begin{aligned} \mathscr {V}_{n+1,d}{\mathop {=}\limits ^{\text{ d }}} \bigcap _{i=1}^n\{z\in \mathbb {S}^d: \rho (e,z)\le \rho (X_i,z)\}. \end{aligned}$$

Recalling that the geodesic distance on $\mathbb {S}^d$ is given by $\rho (x,y)=\arccos {\langle x,y\rangle }$, $x,y\in \mathbb {S}^d$, and using that the function $u\mapsto \arccos u$ is decreasing on $[-1,1]$, we can write the above representation as

$$\begin{aligned} \mathscr {V}_{n+1,d} {\mathop {=}\limits ^{\text{ d }}} \bigcap _{i=1}^n (L_i^+ \cap \mathbb {S}^d), \end{aligned}$$

(4.2)

where $L_1^+,\ldots ,L_n^+\subset \mathbb {R}^{d+1}$ are half-spaces defined by

$$\begin{aligned} L_i^+&:=\{z\in \mathbb {R}^{d+1}:\langle e,z\rangle \ge \langle X_i,z\rangle \}\\&=\{z\in \mathbb {R}^{d+1}:\langle X_i-e,z\rangle \le 0\},\qquad i\in \{1,\ldots ,n\}. \end{aligned}$$

The bounding hyperplane of $L_i^+$ is denoted by

$$\begin{aligned} L_i :=\{z\in \mathbb {R}^{d+1}: \langle X_i-e,z\rangle = 0 \}, \qquad i\in \{1,\ldots ,n\}; \end{aligned}$$

see Fig. 2. Note that $L_i$ passes through the origin of $\mathbb {R}^{d+1}$ and that $e\in L_i^+$. Consider the convex random polyhedral cone

$$\begin{aligned} C_n := \bigcap _{i=1}^n L_i^+ \subset \mathbb {R}^{d+1}; \end{aligned}$$

see Fig. 3. By definition, the k-dimensional faces of the spherical polytope $C_n\cap \mathbb {S}^d$ (which is the right-hand side of (4.2)) are in bijective correspondence with the $(k+1)$-dimensional faces of the polyhedral cone $C_n$. Thus, we arrive at the distributional equality

$$\begin{aligned} \bigl (f_k(\mathscr {V}_{n+1,d})\bigr )_{k=0}^{d-1}{\mathop {=}\limits ^{\text{ d }}} \bigl (f_{k}(C_n \cap \mathbb {S}^d)\bigr )_{k=0}^{d-1}=\bigl (f_{k+1}(C_n)\bigr )_{k=0}^{d-1}. \end{aligned}$$

(4.3)

Fig. 3

Illustration of the cones $C_n$ and $C_n^\circ$ as well as the random polytope $Q_n$

The dual or polar of the convex cone $C_n$ is defined as

$$\begin{aligned} C_n^\circ := \{x\in \mathbb {R}^{d+1}:\langle x,y\rangle \le 0\text { for all }y\in C_n\}. \end{aligned}$$

Since the $(k+1)$-dimensional faces of $C_n$ are in bijective correspondence with the $(d-k)$-dimensional faces of $C_n^\circ$, it follows from (4.3) that

$$\begin{aligned} \bigl (f_k(\mathscr {V}_{n+1,d})\bigr )_{k=0}^{d-1} {\mathop {=}\limits ^{\text{ d }}} \bigl (f_{d-k}(C_n^\circ )\bigr )_{k=0}^{d-1}. \end{aligned}$$

(4.4)

Since $C_n$ is defined as the intersection of the half-spaces $L_1^+,\ldots ,L_n^+$, the dual cone is the positive hull of the outward normal vectors of these half-spaces, that is

$$\begin{aligned} C_n^\circ = {\text {pos}}{ (X_1-e,\ldots ,X_n-e)}. \end{aligned}$$

Since the 0-th coordinates of the vectors $X_i-e$ are strictly negative almost surely, it follows that $C_n^\circ \setminus \{0\}$ is contained in $\{x_0<0\}$ almost surely. Recall from (4.1) that $X_i-e=e (\cos \theta _i-1)+U_i\sin \theta _i$. We may ignore the case when some $\theta _i=0$ because it has probability 0. Normalizing the vectors spanning $C_n^\circ$ in such a way that their 0-th coordinate becomes $-1$, we get

$$\begin{aligned} C_n^\circ = {\text {pos}}{\biggl (-e + \frac{U_1}{R_1},\ldots ,-e + \frac{U_n}{R_n}\biggr )}, \end{aligned}$$

where

$$\begin{aligned} R_i := \frac{1 - \cos \theta _i}{\sin \theta _i} = \tan {\theta _i\over 2}, \qquad i\in \{1,\ldots ,n\}. \end{aligned}$$

It follows from $C_n^\circ \setminus \{0\}\subset \{x_0<0\}$ that almost surely the $(d-k)$-dimensional faces of $C_n^{\circ }$ are in one-to-one correspondence with the $(d-k-1)$-dimensional faces of the polytope obtained by intersecting $C_n^\circ$ with the tangent space to $\mathbb {S}^d$ at its south pole $-e$. Define the polytope

$$\begin{aligned} Q_n := (C_n^\circ \cap \{x_0 = -1\}) + e = {\text {conv}}{\biggl (\frac{U_1}{R_1},\ldots , \frac{U_n}{R_n}\biggr )}\subset \{x_0=0\}. \end{aligned}$$

(4.5)

Recalling (4.4) we can write

$$\begin{aligned} \bigl (f_k(\mathscr {V}_{n+1,d})\bigr )_{k=0}^{d-1} {\mathop {=}\limits ^{\text{ d }}} \bigl (f_{d-k-1}(Q_n)\bigr )_{k=0}^{d-1}. \end{aligned}$$

(4.6)

To complete the proof of Theorem 2.3, it remains to verify that the random polytope $Q_{n}$ has the same distribution as the beta’ polytope $\tilde{P}_{n,d}^d$ in $\mathbb {R}^d$ with parameter $\beta =d$.

Lemma 4.2

For each $i\in \{1,\ldots ,n\}$ the random variable $R_i$ has density

$$\begin{aligned} g(r) = {2^d\,\Gamma ({(d+1)/2})\over \sqrt{\pi }\,\Gamma ({d/2})}\cdot {r^{d-1}\over (1+r^2)^d},\qquad r\ge 0, \end{aligned}$$

(4.7)

with respect to the Lebesgue measure on $[0,\infty )$. Also, we have $R_i\overset{\text{ d }}{=} 1/R_i$.

Proof

The identity

$$R_i = \frac{1-\cos \theta _i}{\sin \theta _i}=\frac{\sin \theta _i}{1+\cos \theta _i}$$

implies that

$$\begin{aligned} R_i^2 = \frac{1-\cos \theta _i}{\sin \theta _i} \cdot \frac{\sin \theta _i}{1+\cos \theta _i} = \frac{1-\cos \theta _i}{1+\cos \theta _i} = \frac{1-h_i}{1+h_i}. \end{aligned}$$

(4.8)

Since $h_i$ has the same distribution as $-h_i$ by Lemma 4.1, we have $R_i\overset{\text{ d }}{=} 1/R_i$. Furthermore, for each $r\ge 0$,

$$\begin{aligned} \mathbb {P}[R_i\ge r]&= \mathbb {P}\biggl [\sqrt{1-h_i\over 1+h_i}\ge r\biggr ] = \mathbb {P}\biggl [h_i\le {1-r^2\over 1+r^2}\biggr ]\\&= {\Gamma ({(d+1)/2})\over \sqrt{\pi }\,\Gamma ({d/2})}\!\int _0^{(1-r^2)/(1+r^2)}(1-h^2)^{{d/2}-1}\,\text{ d }h, \end{aligned}$$

where the last identity comes from Lemma 4.1. Differentiation with respect to r thus proves that the density of $R_i$ is

$$\begin{aligned} g(r)&= {\Gamma ({(d+1)/2})\over \sqrt{\pi }\,\Gamma ({d/2})}\,\biggl (1-\biggl ({1-r^2\over 1+r^2}\biggr )^{\!2}\biggr )^{\!{d/2}-1}\,{4r\over (1+r^2)^2}\\&= {2^d\,\Gamma ({(d+1)/2})\over \sqrt{\pi }\,\Gamma ({d/2})}\cdot {r^{d-1}\over (1+r^2)^d}, \end{aligned}$$

which completes the argument. $\square$

We are now in position to complete the proof of Theorem 2.3. Recall from Lemma 4.1 that $U_1,\ldots ,U_n$ are i.i.d. and uniformly distributed on the unit sphere in $\mathbb {R}^d$. The same Lemma 4.1 (see also (4.8)) states that this family is independent of the collection $R_1,\ldots ,R_n$ of random variables which are also i.i.d. and have density g(r) given by (4.7). Altogether, recalling (4.5), it follows that

$$\begin{aligned} Q_{n} \overset{\text{ d }}{=} {\text {conv}}{\biggl (U_1 R_1,\ldots , U_nR_n\biggr )}, \end{aligned}$$

and that $U_1R_1,\ldots ,U_nR_n$ are independent random points in $\mathbb {R}^d$ with Lebesgue density

$$\begin{aligned} \tilde{f}_{d, d}(x) := {\Gamma (d)\over \pi ^{d/2}\Gamma (d/2)} (1+\Vert x\Vert ^2)^{-d},\qquad x\in \mathbb {R}^d. \end{aligned}$$

(The value of the constant follows from the Legendre duplication formula but is actually not needed for the argument). This is the beta’ density from (2.3) with $\beta =d$. Hence, $Q_{n}$ has the same distribution as the beta’ polytope $\tilde{P}_{n,d}^d$, and the proof of Theorem 2.3 is complete.

Remark 4.3

As a byproduct of the above proof, note that the beta’ distribution with $\beta =d$ stays invariant under inversion with respect to the unit sphere.