Abstract
We give a full classification of vertex-transitive zonotopes. We prove that a vertex-transitive zonotope is a \(\Gamma \)-permutahedron for some finite reflection group \(\Gamma \subset {{\,\mathrm{O}\,}}(\mathbb {R}^d)\). The same holds true for zonotopes in which all vertices are on a common sphere, and all edges are of the same length. The classification of these then follows from the classification of finite reflection groups. We prove that root systems can be characterized as those centrally symmetric sets of vectors, for which all intersections with half-spaces, that contain exactly half the vectors, are congruent. We provide a further sufficient condition for a centrally symmetric set to be a root system.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A (convex) polytope is the convex hull of finitely many points. The zonotopes form a special class of polytopes for which several equivalent definitions are known (see e.g. [13, Sect. 7.3]):
Definition 1.1
A zonotope is a polytope \(Z\subset \mathbb {R}^d\) that satisfies any of the following equivalent conditions:
-
(i)
Z is a projection of a \(\delta \)-dimensional cube.
-
(ii)
Z is a Minkowski sum of line segments.
-
(iii)
Z has only centrally symmetric faces.
-
(iv)
Z has only centrally symmetric 2-faces.
A polytope \(P\subseteq \mathbb {R}^d\) is called vertex-transitive if its (Euclidean) symmetry group \({{\,\mathrm{Aut}\,}}P\subseteq {{\,\mathrm{O}\,}}(\mathbb {R}^d)\) acts transitively on its vertex set \(\mathscr {F}_0(P)\). While many classes of symmetric polytopes have been classified in the past (e.g. regular polyopes, edge- and vertex-transitive polyhedra), a classification of general vertex-transitive polytopes is probably infeasible: almost every finite group is isomorphic to the symmetry group of some vertex-transitive polytope [1, 6] (the only exceptions are certain abelian groups and dicyclic groups). This endeavor can therefore be compared with classifying all finite groups (and their real representations).
We can now impose further restrictions on this class to obtain a new, still interesting, but tractable classification problem. One well-studied sub-class is formed by the uniform polytopes (see e.g. [3, 8]). Another large class of polytopes are the zonotopes, which have seemingly not been probed for their vertex-transitive members before. In fact, we show that a full classification of vertex-transitive zonotopes can be achieved, and is immediately linked to the classification of finite reflection groups and their root systems.
The first examples of vertex-transitive zonotopes are usually the following: cubes, prisms, and permutahedra. All these belong to the more general class of \(\Gamma \)-permutahedra (see Definition 3.1), which contains further examples of vertex-transitive zonopes. We were able to show that these are all the vertex-transitive zonotopes that exist. Surprisingly (but in fact easier to prove), the same holds for zonotopes for which all vertices are on a common sphere and all edges are of the same length (no symmetry requirements are necessary). We shall call them homogeneous zonotopes.
As a side product of this classification we obtain further interesting characterizations of root systems. For example, for a finite centrally symmetric set \(R\subset \mathbb {R}^d\setminus \{0\}\) consider the intersection of R with a half space that contains exactly half the elements of R (these intersections will be called semi-stars, see Definition 2.2). For root systems, such “half-sets” are known as positive roots, and it is well known that the Weyl group acts transitively on these. We prove an inverse: if in a finite and centrally symmetric set all semi-stars are congruent, then it is a root system. We also prove a further sufficient condition using only the length of the sum of the vectors in the semi-stars.
1.1 Overview
Sections 2 and 3 recap the relevant definitions and preliminary results that are known from the literature. In Sect. 2 we define the generators of a zonotope (i.e., a canonical way to write the zonotope as a Minkowski sum of line segments) and recall how these determine its faces. We also show that the generators determine the symmetries of the zonotope. Section 3 recalls permutahedra, reflection groups, and root systems. We included a proof for the following fact: permutahedra are exactly the zonotopes generated by root systems. This is the core property exploited in the following sections.
In Sect. 4 we provide a proof of our main result (Theorem 4.11): the vertex-transitive zonotopes are exactly the \(\Gamma \)-permutahedra, where \(\Gamma \subset {{\,\mathrm{O}\,}}(\mathbb {R}^d)\) is some finite reflection group. We also show that a homogeneous zonotope (all vertices on a common sphere, all edges of the same length) is necessarily a \(\Gamma \)-permutahedron. These results enable a complete classification of vertex-transitive/homogeneous zonotopes, detailed in Sect. 4.4.
In Sect. 5 we apply the classification of the previous sections to give alternative characterizations of root systems (Corollary 5.1 and Theorem 5.2).
2 Generators, Faces, and Symmetries
Throughout this paper \(Z\subset \mathbb {R}^d\) with \(d\ge 2\) shall always denote a full-dimensional zonotope. The cases \(d\in \{0,1\}\) are trivial and will not be considered here. Zonotopes are centrally symmetric and we shall assume \(Z=-Z\).
2.1 Generators
By Definition 1.1 (ii), Z is the Minkowski sum of line segments, and so there is a finite centrally symmetric set \(R\subset \mathbb {R}^d\setminus \{0\}\) with
We use the convention \({{\,\mathrm{Zon}\,}}\varnothing :=\{0\}\). Conversely,
is a finite, centrally symmetric set with \({{\,\mathrm{Zon}\,}}{({{\,\mathrm{Gen}\,}}Z)}=Z\). The elements of \({{\,\mathrm{Gen}\,}}Z\) will be called generators of Z.
For this section, let \(R\subset \mathbb {R}^d\setminus \{0\}\) be a finite centrally symmetric set.
Definition 2.1
R is called reduced if \({{\,\mathrm{span}\,}}{\{r\}}\cap R=\{-r,r\}\) for all \(r\in R\).
The set \({{\,\mathrm{Gen}\,}}Z\) is always reduced. If R is reduced, then it is centrally symmetric, and \(R={{\,\mathrm{Gen}\,}}{({{\,\mathrm{Zon}\,}}R)}\), that is, R is the set of generators of some zonotope.
Definition 2.2
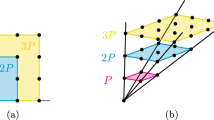
We consider the following two kinds of subsets of R (see Fig. 1):
-
(i)
A subset \(S\subseteq R\) is a semi-star, if it contains exactly half the elements of R, and can be written as the intersection of R with a half-space.
-
(ii)
A subset \(F\subseteq R\) is a flat, if it can be written as the intersection of R with a linear subspace of \(\mathbb {R}^d\), or alternatively, if \(R\cap {{\,\mathrm{span}\,}}F=F\).
The name “semi-star” is motivated by the occasional use of the term “star” for centrally symmetric sets \(R\subset \mathbb {R}^d\setminus \{0\}\). Note that a semi-star of R contains exactly one element from \(\{-r,r\}\subseteq R\) for each \(r\in R\).
2.2 Faces
We describe how to infer information about the faces of Z from its generators \({{\,\mathrm{Gen}\,}}Z\). The main features of this description (Propositions 2.3 and 2.4) are well known and can be found e.g. in the introduction of [12]. As a general rule of thumb, the shapes of the faces are determined by the flats of \({{\,\mathrm{Gen}\,}}Z\), and the positions of the vertices are determined by the semi-stars of \({{\,\mathrm{Gen}\,}}Z\). It follows from (2.1) that a vertex \(v\in \mathscr {F}_0(Z)\) can be written as
However, not every subset \(S\subseteq {{\,\mathrm{Gen}\,}}Z\) gives rise to a vertex in that way, but only if S is a semi-star of \({{\,\mathrm{Gen}\,}}Z\). This correspondence is one-to-one:
Proposition 2.3
The vertices \(\mathscr {F}_0(Z)\) are in one-to-one correspondence with the semi-stars \(S\subset {{\,\mathrm{Gen}\,}}Z\) via the bijection \(S \mapsto v_S:=\sum _{r\in S}r\).
The faces \(\sigma \in \mathscr {F}(Z)\) are themselves zonotopes (though in contrast to Z itself, they are not centered at the origin). Their shapes are determined by their generators which are exactly the flats in \({{\,\mathrm{Gen}\,}}Z\):
Proposition 2.4
The following holds:
-
(i)
For each face \(\sigma \in \mathscr {F}(Z)\), \({{\,\mathrm{Gen}\,}}\sigma \subseteq {{\,\mathrm{Gen}\,}}Z\) is a flat.
-
(ii)
For each flat \(F\subseteq {{\,\mathrm{Gen}\,}}Z\) there is a face \(\sigma \in \mathscr {F}(Z)\) with \({{\,\mathrm{Gen}\,}}\sigma =F\).
2.3 Symmetries
\({{\,\mathrm{Zon}\,}}(\,{\cdot }\,)\) and \({{\,\mathrm{Gen}\,}}(\,{\cdot }\,)\) are compatible with invertible linear transformations in the sense that for each \(T\in {{\,\mathrm{GL}\,}}(\mathbb {R}^d)\) holds
In particular, this holds for orthogonal \(T\in {{\,\mathrm{O}\,}}(\mathbb {R}^d)\), and it follows immediately that
Proposition 2.5
\({{\,\mathrm{Aut}\,}}Z={{\,\mathrm{Aut}\,}}{({{\,\mathrm{Gen}\,}}Z)}\).
Proof
If \(T\in {{\,\mathrm{Aut}\,}}Z\) is a symmetry of Z, then
and thus, \(T\in {{\,\mathrm{Aut}\,}}{({{\,\mathrm{Gen}\,}}Z)}\). The proof of the other direction is analogous. \(\square \)
For later use we prove
Proposition 2.6
For \(T\in {{\,\mathrm{O}\,}}(\mathbb {R}^d)\) hold:
-
(i)
If \(T\in {{\,\mathrm{Aut}\,}}R\), then T maps semi-stars onto semi-stars.
-
(ii)
If \(TS\subseteq R\) for at least one semi-star \(S\subset R\), then \(T\in {{\,\mathrm{Aut}\,}}R\).
Proof
The semi-stars \(S\subset R\) are exactly the subsets of R of the form
for which \(c\in \mathbb {R}^d\setminus \{0\}\) is non-orthogonal to all \(r\in R\). For (i) compute
which is a semi-star since \(\langle r,Tc\rangle =\langle T^{-1}r,c\rangle \) cannot be zero, as \(T^{-1}r\in R\).
For (ii), assume \(TS\subseteq R\). For any vector \(r\in R\), either \(r\in S\), and then \(Tr\in R\) by assumption, or \(-r\in S\), then \(Tr=-T(-r)\in -R=R\) by central symmetry. Thus \(TR=R\) and \(T\in {{\,\mathrm{Aut}\,}}R\). \(\square \)
3 Permutahedra and Root Systems
The standard \((d-1)\)-dimensional permutahedron is obtained as the convex hull of all coordinate permutations of the vector \((1,2,\dots ,d)\in \mathbb {R}^{d}\). These polytopes, and certain generalizations for the other finite reflection groups (the \(\Gamma \)-permutahedra), provide well-known examples of vertex-transitive zonotopes.
3.1 \(\Gamma \)-Permutahedra and Reflection Groups
In the following \(\Gamma \subset {{\,\mathrm{O}\,}}(\mathbb {R}^d)\) shall denote a finite reflection group, that is, a matrix group
where \(R\subset \mathbb {R}^d\setminus \{0\}\) is some finite set of vectors and \(T_r\in {{\,\mathrm{O}\,}}(\mathbb {R}^d)\) denotes the reflection on the hyperplanes \(r^\bot \). Let \(\mathscr {E}\) denote the union of the reflection hyperplanes \(r^\bot \), \(r\in R\). The connected components of \(\mathbb {R}^d\setminus \mathscr {E}\) are called Weyl chambers of \(\Gamma \). It is well known that \(\Gamma \) acts regularly (i.e., transitively and freely) on these chambers [10, Sect. 4.6].
Definition 3.1
A \(\Gamma \)-permutahedron is a polytope \(P\subset \mathbb {R}^d\) that satisfies any of the following equivalent conditions:
-
(i)
\(\Gamma \) acts regularly on the vertices of P.
-
(ii)
P is the orbit polytope \({{\,\mathrm{Orb}\,}}(\Gamma ,v):={{\,\mathrm{conv}\,}}{\Gamma v}\) of a point \(v\in \mathbb {R}^d\setminus \mathscr {E}\) in some Weyl chamber of \(\Gamma \).
Definition 3.1 describes a special case of Wythoff’s kaleidoscopic construction [2], which can be used to construct a larger class of polytopes. Because of our special choice to have v in \(\mathbb {R}^d\setminus \mathscr {E}\), we find that \({{\,\mathrm{Orb}\,}}(\Gamma ,v)\) has exactly \(|\Gamma |\) vertices. For later use we note specifically the following:
Remark 3.2
A \(\Gamma \)-permutahedron has exactly one vertex per Weyl chamber of \(\Gamma \), and no vertices in \(\mathscr {E}\) (such a vertex would be fixed by a reflection).
A further remarkable property of \(\Gamma \)-permutahedra is that their combinatorial type does not depend on the exact choice of \(v\in \mathbb {R}^d\setminus \mathscr {E}\) [4, Proposition 3], and so any choice of \(\Gamma \) provides us essentially with a single type of generalized permutahedron.
\(\Gamma \)-permutahedra are not necessarily zonotopes (some faces might be not centrally symmetric). However, there is always a point \(v\in \mathbb {R}^d\setminus \mathscr {E}\) such that \({{\,\mathrm{Orb}\,}}(\Gamma , v)\) is a zonotope (see, e.g. the construction in Remark 3.5). Furthermore, among these points there is always one for which the zonotope has all edges of the same length. The resulting polytopes are classically known as the omnitruncated uniform polytopes [8].
The finite reflection groups are completely classified [10]. The irreducible ones are denoted by \(I_1\), \(I_2(p)\), \(A_d\), \(B_d\), \(D_d\), \(H_3\), \(H_4\), \(F_4\), \(E_6\), \(E_7\), and \(E_8\) (\(d,p\ge 3\), the sub-index always denotes the dimension). The reducible ones are obtained as direct sums of the irreducible ones. See Fig. 2 for the \(\Gamma \)-permutahedra generated from \(A_3\) (resp. \(D_3\)), \(B_3\), and \(H_3\).
Clearly, if P is a \(\Gamma \)-permutahedron then \(\Gamma \subseteq {{\,\mathrm{Aut}\,}}P\). However, \({{\,\mathrm{Aut}\,}}P\) might be strictly larger than \(\Gamma \). This happens exactly for \(\Gamma \in \{I_2(p),A_d,F_4, E_6\}\) because these reflection groups have additional symmetries that are not part of the group itself. Adding these symmetries results in the so-called extended reflection groups (see [9, Sect. 11.6]).
3.2 Root Systems
Root systems bridge between zonotopes and reflection groups. We shall work with a minimalistic version of the definition (no crystallographic or reducedness restrictions):
Definition 3.3
A root system is a finite set \(R\subset \mathbb {R}^d\setminus \{0\}\) for which \(T_r R=R\), for all vectors \(r\in R\).
We can give an alternative definition of \(\Gamma \)-permutahedron using root systems: a zonotope is a \(\Gamma \)-permutahedron if and only if \({{\,\mathrm{Gen}\,}}Z\) is a root system (we provide a proof for completeness in Lemmas 3.4 and 3.6). The Weyl group of a root system R is the group
This is a finite reflection group. Note that \(\Gamma \subseteq {{\,\mathrm{Aut}\,}}R\) by definition of root system.
Lemma 3.4
If \({{\,\mathrm{Gen}\,}}Z\) is a root system, then Z is a \(\Gamma \)-permutahedron, where \(\Gamma \) is the Weyl group of \({{\,\mathrm{Gen}\,}}Z\).
Proof
It holds \(\Gamma \subseteq {{\,\mathrm{Aut}\,}}{({{\,\mathrm{Gen}\,}}Z)}\) by definition of root system, and therefore \(\Gamma \subseteq {{\,\mathrm{Aut}\,}}Z\) by Proposition 2.5. The proof proceeds in two steps: first, we show that \(\Gamma \) acts transitively on \(\mathscr {F}_0(Z)\). This shows that \(\mathscr {F}_0(Z)\) is an orbit of \(\Gamma \). Second, we show that no \(T_r,r\in {{\,\mathrm{Gen}\,}}Z\), fixes a vertex of Z. The vertices must then lie in the interior of the Weyl chambers of \(\Gamma \), and \(\Gamma \) must act regularly on them.
Step 1: The edge graph of Z is connected. So, for any two vertices \(v,w\in \mathscr {F}_0(Z)\) the edge graph contains a path \(v_0v_1{\ldots }v_k\) between \(v=v_0\) and \(w=v_k\). That means, \(e_i:={{\,\mathrm{conv}\,}}{\{v_{i-1},v_i\}}\) is an edge of Z for all \(i\in \{1,\ldots ,k\}\). Choose \(r_i\in {{\,\mathrm{Gen}\,}}Z\) parallel to \(e_i\). The reflection \(T_{r_i}\) fixes \(e_i\) and exchanges its end vertices \(v_{i-1}\) and \(v_i\). The map \(T:=T_{r_k}\!\cdots T_{r_1}\in \Gamma \) now satisfies \(Tv=w\). This proves vertex-transitivity.
Step 2: For \(v\in \mathscr {F}_0(Z)\), there is a unique semi-star \(S\subset {{\,\mathrm{Gen}\,}}Z\) whose elements sum up to v (Proposition 2.3). For any generator \(r\in {{\,\mathrm{Gen}\,}}Z\) exactly one element of \(\{-r,r\}\) is in S. Since \(T_r (\pm r)=\mp r\), the reflection \(T_r\) cannot fix S but maps it to a different semi-star (by Proposition 2.6 (i)). Since the semi-star is unique for v, \(T_r\) cannot fix v either. \(\square \)
Remark 3.5
For any finite reflection group \(\Gamma \), there exists a \(\Gamma \)-permutahedron which is a (vertex-transitive) zonotope. To see this, choose a reduced root system R that generates \(\Gamma \) (e.g. build R from the normals of the mirror hyperplanes of \(\Gamma \)). Then, \({{\,\mathrm{Zon}\,}}R\) is a zonotope and a \(\Gamma \)-permutahedron by \({{\,\mathrm{Gen}\,}}{({{\,\mathrm{Zon}\,}}R)}=R\) and Lemma 3.4.
Lemma 3.6
If Z is a \(\Gamma \)-permutahedron, then \({{\,\mathrm{Gen}\,}}Z\) is a root system.
Proof
Choose a generator \(r\in {{\,\mathrm{Gen}\,}}Z\) and let \(e\in \mathscr {F}_1(Z)\) be an r-parallel edge. There is at most one vertex per Weyl chamber of \(\Gamma \) (Remark 3.2), hence the end vertices of e cannot be in the same chamber. Therefore, e must cross one of the reflection hyperplanes of \(\Gamma \). These are symmetry hyperplanes of Z, and if e crosses one, it must be perpendicular to it. Thus, this hyperplane is \(r^\bot \). We have shown that \(T_r\in {{\,\mathrm{Aut}\,}}Z={{\,\mathrm{Aut}\,}}{({{\,\mathrm{Gen}\,}}Z)}\) for all \(r\in R\), and therefore, \({{\,\mathrm{Gen}\,}}Z\) is a root system. \(\square \)
4 Vertex-Transitive and Homogeneous Zonotopes
The goal of this section is to prove Theorem 4.11 that all vertex-transitive (and homogeneous, Definition 4.4) zonotopes are \(\Gamma \)-permutahedra.
4.1 Roadmap
We briefly describe the roadmap to the proof. The idea is to prove the statement for 2-dimensional zonotopes (Sect. 4.2), and then, transfer this result to general dimensions (Sect. 4.3). This is possible by the following result (Theorem 4.2): if all 2-faces of a zonotope are vertex-transitive, then it is a \(\Gamma \)-permutahedron.
We cannot immediately see that the 2-faces of our vertex-transitive zonotopes are vertex-transitive (this is true, but not obvious, and it is false for general polytopes). We therefore prove an auxiliary result (Proposition 4.3) which further weakens the condition of vertex-transitivity of the 2-faces.
In Sect. 4.3 we define homogeneous zonotopes (all vertices on a sphere, all edges of the same length), and prove that these are \(\Gamma \)-permutahedra (Corollary 4.6). The proof is surprisingly simple: their 2-faces are regular polygons, hence vertex-transitive. To transfer the result to vertex-transitive zonotopes, we define the normalization of a zonotope (Definition 4.7), which transforms any vertex-transitive zonotope into a homogeneous one. This transformation preserves the edge-directions of the zonotope, so that with the help of Proposition 4.3 we can show that all 2-faces of the initial zonotope must have been vertex-transitive. Applying Theorem 4.2 then proves the main result, Theorem 4.11.
4.2 2-Dimensional Zonotopes
A 2-dimensional zonotope is a centrally symmetric 2n-gon. Such one is vertex-transitive, if either
-
(i)
it is a regular 2n-gon, or
-
(ii)
n is even, and it has alternating edge lengths, as seen in Fig. 3.
This list is complete: every vertex-transitive polygon is an orbit polytope of a cyclic group or dihedral group. These orbit polytopes are contained in the list above.
If Z is a 2n-gon as listed in (i) or (ii), \({{\,\mathrm{Gen}\,}}Z\) consists of 2n vectors in \(\mathbb {R}^2\), equally spaced by an angle of \(\pi /n\), and in the case (ii), these vectors alternate in length (see Fig. 3). These are exactly the root systems that correspond to the reflection group \(I_2(n)\) (if \(n\ge 3\)), or \(I_1\oplus I_1\) (if \(n=2\)). Applying Lemma 3.4, we obtain the classification in dimension two.
Corollary 4.1
A 2-dimensional vertex-transitive zonotope is a \(\Gamma \)-permutahedron.
This already finishes the case of 2-dimensional vertex-transitive zonotopes. This case is important for the following reason: investigating vertex-transitive zonotopes in general dimensions boils down to the study of their 2-faces:
Theorem 4.2
If all 2-faces of Z are vertex-transitive, then Z is a \(\Gamma \)-permutahedron.
Proof
Choose generators \(r,s\in {{\,\mathrm{Gen}\,}}Z\). We show \(T_{r}s\in {{\,\mathrm{Gen}\,}}Z\), establishing that \({{\,\mathrm{Gen}\,}}Z\) is a root system and Z is a \(\Gamma \)-permutahedron by Lemma 3.4. The case \(r=\pm s\) is trivial. We therefore assume that
is 2-dimensional. In particular, \(R\subseteq {{\,\mathrm{Gen}\,}}Z\) is a 2-dimensional flat of \({{\,\mathrm{Gen}\,}}Z\). By Proposition 2.4 there exists a 2-face \(\sigma \in \mathscr {F}_2(Z)\) with \({{\,\mathrm{Gen}\,}}\sigma =R\). By assumption, \(\sigma \) is vertex-transitive, and R therefore a root system (Corollary 4.1). Conclusively, \(T_r s\in R\subseteq {{\,\mathrm{Gen}\,}}Z\). \(\square \)
In order to apply Theorem 4.2, we need that all 2-faces of Z are vertex-transitive. This does not follow immediately (even though it is true) from the fact that we start from a vertex-transitive zonotope. Instead, we use the following helper result:
Proposition 4.3
If \(Z\subset \mathbb {R}^2\) is a 2-dimensional zonotope that
-
(i)
has all vertices on a common circle, and
-
(ii)
has the same edge directions as a regular 2n-gon,
then Z is vertex-transitive.
This statement is elementary. We sketch its proof:
The exterior angles of a (convex) polygon always add up to \(2\pi \) (used in the proof of Proposition 4.3)
Proof of Proposition 4.3
A (convex) polygon has at most two edges of the same direction, and if it is centrally symmetric, it has exactly two of each. A regular 2n-gon has n edge directions, and by (ii), so has Z. Since Z is centrally symmetric, it must be a 2n-gon as well.
Let \(\alpha _i\in \mathbb {R}\) be the exterior angle of the i-th vertex of Z (see Fig. 4). By (ii) we have \(\alpha _i=k_i\pi /n\), where \(k_i\in \mathbb N\) is an integer \(\ge 1\). The exterior angles of a (convex) polygon add up to \(2\pi \), and so we estimate
and conclude that \(k_i=1\). That is, all exterior and interior angles are equal.
For simplicity, assume that Z, and all polygons mentioned in the following paragraph, are of circumradius one. Let \(\ell \) be the length of the shortest edge of Z. Then, \(\ell \) is no longer than the edge length of a regular 2n-gon. This ensures that there exists a vertex-transitive 2n-gon with an edge of length \(\ell \) (consider an appropriately chosen orbit polytope of \(I_2(n)\), resp. \(I_1\oplus I_1\)). But a polygon satisfying (i) and with prescribed identical interior angles at every vertex is already uniquely determined by placing a single edge (the placement of both incident edges follows uniquely from the set restrictions, and this iteratively determines the whole polygon). Therefore, Z must be this vertex-transitive polygon.\(\square \)
4.3 The General Case
Definition 4.4
A zonotope is said to be homogeneous, if all its vertices are on a common sphere, and all its edges are of the same length.
Homogeneity is a hereditary property:
Observation 4.5
The faces of a homogeneous zonotope Z are homogeneous: all edges of a face \(\sigma \in \mathscr {F}(Z)\) are of the same length. All vertices of Z are on a sphere \(\mathscr {S}\), and all vertices of \(\sigma \) are on an affine subspace of \(\mathbb {R}^d\). All vertices of \(\sigma \) are on the intersection of this subspace with \(\mathscr {S}\), which is itself a sphere.
The 2-faces of homogeneous zonotopes are homogeneous, and homogeneous 2-faces are regular, thus vertex-transitive. With Theorem 4.2 we conclude
Corollary 4.6
If Z is homogeneous, then Z is a \(\Gamma \)-permutahedron.
We apply this to vertex-transitive zonotopes via the following construction:
Definition 4.7
The normalization of Z is the zonotope
The normalized zonotope has the same edge directions as Z, but all edges are of the same length. We further need to understand how vertex-transitivity is determined by \({{\,\mathrm{Gen}\,}}Z\):
Proposition 4.8
Z is vertex-transitive if and only if all semi-stars of \({{\,\mathrm{Gen}\,}}Z\) are congruent.
Proof
Consider two vertices \(v,v'\in \mathscr {F}_0(Z)\) determined by semi-stars \(S,S'\subseteq {{\,\mathrm{Gen}\,}}Z\) (via Proposition 2.3).
A symmetry \(T\in {{\,\mathrm{Aut}\,}}Z\) that maps v onto \(v'\), maps S onto a semi-star whose elements add up to \(v'\) (Proposition 2.6). But the semi-star with this property is unique by Proposition 2.3, and therefore must equal \(S'\). Thus, \(TS=S'\), and T is a congruence between the semi-stars.
On the other hand, if \(T\in {{\,\mathrm{O}\,}}(\mathbb {R}^d)\) maps the semi-star S onto \(S'\subset {{\,\mathrm{Gen}\,}}Z\), then it also maps v onto \(v'\). And \(T\in {{\,\mathrm{Aut}\,}}Z\) by Proposition 2.6 (ii). \(\square \)
Corollary 4.9
If Z is vertex-transitive, then so is its normalization \(Z^*\).
Proof
If all semi-stars of \({{\,\mathrm{Gen}\,}}Z\) are congruent, then this certainly stays valid when normalizing all vectors in \({{\,\mathrm{Gen}\,}}Z\).\(\square \)
Corollary 4.10
If Z is vertex-transitive, then \(Z^*\) is a \(\Gamma \)-permutahedron.
Proof
By Corollary 4.9, \(Z^*\) is vertex-transitive, in particular, all vertices are on a common sphere. Furthermore, all edges of \(Z^*\) have the same length. Thus, \(Z^*\) is homogeneous, and a \(\Gamma \)-permutahedron by Corollary 4.6.\(\square \)
We can finally prove the main result:
Theorem 4.11
A vertex-transitive zonotope Z is a \(\Gamma \)-permutahedron.
Proof
In Corollary 4.10 we saw that \(Z^*\) is a \(\Gamma \)-permutahedron, and \({{\,\mathrm{Gen}\,}}Z^*\) therefore a root system by Lemma 3.4. For each 2-face \(\sigma \in \mathscr {F}_2(Z)\), the set
is a 2-dimensional flat subset of the root system \({{\,\mathrm{Gen}\,}}Z^*\). As such, it is a root system itself. A 2-dimensional root system consists of vectors that are equally spaced by an angle \(\pi /n\) for some \(n\in \mathbb {N}\), or in other words, the elements of \(R^*\) are the edge directions of a regular 2n-gon. The 2-face \(\sigma \) has the edge direction (but not necessarily the edge lengths) from \(R^*\), hence, the same edge direction as a regular 2n-gon.
Additionally, as a face of a vertex-transitive polytope, \(\sigma \) has all vertices on a common sphere. By Proposition 4.3, \(\sigma \) is vertex-transitive. We found that all 2-faces of Z are vertex-transitive. Theorem 4.2 provides that Z is a \(\Gamma \)-permutahedron. \(\square \)
We summarize the results in the following theorem:
Theorem 4.12
If Z is a zonotope, then the following are equivalent:
-
(i)
Z is vertex-transitive.
-
(ii)
All semi-stars of \({{\,\mathrm{Gen}\,}}Z\) are congruent.
-
(iii)
\({{\,\mathrm{Gen}\,}}Z\) is a root system.
-
(iv)
Z is a \(\Gamma \)-permutahedron.
Proof
\(\text {(ii)}\;{\mathop {\Longleftrightarrow }\limits ^{\tiny {4.8}}}\; \text {(i)}\;{\mathop {\Longleftrightarrow }\limits ^{{\tiny {3.1+4.11}}}}\; \text {(iv)}\;{\mathop {\Longleftrightarrow }\limits ^{{\tiny {3.4+3.6}}}}\;\text {(iii)}\). \(\square \)
We list some consequences of this classification, none of which holds for general polytopes:
Corollary 4.13
The following holds:
-
(i)
The faces of a vertex-transitive zonotope are vertex-transitive.
-
(ii)
A homogeneous zonotope (i.e., it has all vertices on a common sphere, and all edges of the same length) is vertex-transitive.
-
(iii)
A zonotope in which all faces (in fact, all 2-faces) are homogeneous (resp. vertex-transitive) is itself homogeneous (resp. vertex-transitive).
Proof
If Z is vertex-transitive, then \({{\,\mathrm{Gen}\,}}Z\) is a root system (Theorem 4.11). By Proposition 2.4, for every face \(\sigma \in \mathscr {F}(Z)\), its generators \({{\,\mathrm{Gen}\,}}\sigma \subseteq {{\,\mathrm{Gen}\,}}Z\) are a flat subset of the root system \({{\,\mathrm{Gen}\,}}Z\), hence, a root system as well. Hence, \(\sigma \) is a \(\Gamma \)-permutahedron and vertex-transitive. This proves (i).
Part (ii) follows immediately from Corollary 4.6. Part (iii) follows from Theorem 4.2 (a homogeneous 2-face is regular, hence also vertex-transitive). \(\square \)
4.4 The Classification of Vertex-Transitive/Homogeneous Zonotopes
We apply the results in Corollary 4.6 and Theorem 4.11 to compile a list of all vertex-transitive/homogeneous zonotopes.
We restrict the enumeration to the irreducible cases, that is, to those which result from irreducible reflection groups. The other vertex-transitive, resp. homogeneous, zonotopes (the reducible ones) are obtained as cartesian products of the irreducible ones. The most recognizable reducible vertex-transitive, resp. homogeneous, zonotopes are the hypercubes and prisms.
We obtain the following list of irreducible homogeneous zonotopes:
-
infinitely many 2-dimensional homogeneous zonotopes (the regular 2n-gons),
-
for each \(d\ge 3\), the d-dimensional zonotopes generated by reflection groups \(A_d\), \(B_d\), and \(D_d\) (which are distinct if and only if \(d>3\)), and
-
six exceptional zonotopes to the reflection groups \(H_3\), \(H_4\), \(F_4\), \(E_6\), \(E_7\), and \(E_8\) in their respective dimensions \(d\in \{3,4,6,7,8\}\).
Each of these is uniquely determined up to scale and orientation. The polytopes in that list are also classically known as the omnitruncated uniform polytopes. This terminology, and many related names were coined by Norman Johnson [8]. By definition, the \(\Gamma \)-permutahedron has \(|\Gamma |\) vertices. Furthermore, each \(\Gamma \)-permutahedron is simple (i.e., its vertex degree matches its dimension), and it therefore has \(d|\Gamma |/2\) edges. See Table 1 for the precise numbers.
The (irreducible) vertex-transitive zonotopes differ from the homogeneous ones in three cases: the zonotopes that correspond to the root systems \(I_2(2n)\) (the 4n-gons), \(B_d\) and \(F_4\) are not uniquely determined up to scale and orientation, but each case forms a continuous 1-dimensional family of combinatorially equivalent zonotopes (see e.g. Fig. 5 for the case \(B_3\)). Typically, the vectors of a root system form a single orbit under the action of the associated Weyl group, except in the cases \(I_2(2n)\), \(B_d\), and \(F_4\) in which they form two orbits [7, Sect. 2.11]. The lengths of the vectors in these orbits can be chosen independently from each other, giving these zonotopes one degree of freedom that manifests in two (possibly) different edge lengths. Such degrees of freedom are also present in all reducible vertex-transitive zonotopes. For example, the d-cubes (the cartesian product of line segments) belong to the continuous family of d-orthotopes with d degrees of freedom. We give some further information on some of the families:
4.4.1 The Family \(A_d\)
The generated zonotope is the standard permutahedron. For \(d=3\), this zonotope is called truncated octahedron (Fig. 2), which coincides with the zonotope obtained from \(D_3\) (this is the only pair of coinciding zonotopes). The classical name for this family is omnitruncated d-simplices.
4.4.2 The Family \(B_d\)
The vertices of a general \(B_d\)-permutahedron are formed by the coordinate permutations and sign selections of some vector
If the \(x_i\) form a linear sequence \(x_i=x_0 + \epsilon (i-1)\) for some fixed \(x_0\), \(\epsilon >0\), then the corresponding polytope is a zonotope. The quotient \(\epsilon /x_0\) parametrizes the 1-dimensional family (see Fig. 5), and \(\epsilon /x_0=\sqrt{2}\) corresponds to the homogeneous representative. Clasically, the homogeneous zonotopes of this family are called omnitruncated d-cubes.
4.4.3 The Family \(D_d\)
The vertex-coordinates of the \(D_d\)-zonotope are as in (4.1) with setting \(x_0=0\) in the linear sequence (see Fig. 5). For \(d=3\), this zonotope coincides with the \(A_3\)-permutahedron (the truncated octahedron). For \(d=4\), this zonotope is known as the truncated 24-cell. Classically, the zonotopes of this family are called omnitruncated d-demicubes.
4.4.4 Exceptional Zonotopes
In dimensions \(d\in \{3,4,6,7,8\}\) the following exceptional vertex-transitive zonotopes exist:
-
For \(d=3\), there exists the omnitruncated icosahedron/dodecahedron to the reflection group \(H_3\) (see Fig. 2).
-
For \(d=4\), there exists the continuous 1-dimensional family of \(F_4\)-zonotopes (the homogeneous member is called omnitruncated 24-cell), as well as the omnitruncated 120-cell/600-cell to the reflection group \(H_4\).
-
For \(d\in \{6,7,8\}\), there exist the omnitrucation of the uniform \(E_d\)-polytope (also known as \(2_{21}\), \(3_{21}\), and \(4_{21}\)).
4.4.5 Summary
All in all, we obtain the following numbers of irreducible homogeneous zonotopes (aka combinatorial types of irreducible vertex-transitive zonotopes) per dimension.
d | \(\#\) | groups |
|---|---|---|
2 | \(\infty \) | \(I_2(n),n\ge 2\) |
3 | 3 | \(A_3 \text { or } D_3, B_3, H_3\) |
4 | 5 | \(A_4, B_4, D_4, F_4, H_4\) |
5 | 3 | \(A_5, B_5, D_5\) |
6 | 4 | \(A_6, B_6, D_6, E_6\) |
7 | 4 | \(A_7, B_7, D_7, E_7\) |
8 | 4 | \(A_8, B_8, D_8, E_8\) |
\(\ge 9\) | 3 | \(A_d, B_d, D_d\) |
5 Characterizing Root Systems
Our results on vertex-transitive and homogeneous zonotopes enable us to give interesting alternative characterizations for root systems:
Corollary 5.1
If \(R\subset \mathbb {R}^d\setminus \{0\}\) is finite and reduced, then the following are equivalent:
-
(i)
R is a root system, and
-
(ii)
all semi-stars of R are congruent.
Proof
R is reduced, hence the set of generators of \({{\,\mathrm{Zon}\,}}R\). We can apply (ii) \(\Leftrightarrow \) (iii) from Theorem 4.12.\(\square \)
The statement of Corollary 5.1 still holds true, even if R is not reduced, but we leave that to the reader. The norm of a semi-star shall be the norm of the sum of its elements. It follows from Corollary 5.1 that a root system has all semi-stars of the same norm. We prove a weaker form of a converse:
Theorem 5.2
Let \(R\subset \mathbb S^d\) be a finite centrally symmetric set of unit vectors. If all semi-stars of R have the same norm, then R is a root system.
Proof
Recall that each vertex of \({{\,\mathrm{Zon}\,}}R\) can be written as the sum of the vectors in some semi-star of R (Proposition 2.3). The norm of that semi-star therefore equals the distance of that vertex from the origin.
Since all semi-stars have the same norm, \({{\,\mathrm{Zon}\,}}R\) has all vertices on a common sphere around the origin. Furthermore, R is centrally symmetric, and all vectors in R are of the same length, i.e., all edges of \({{\,\mathrm{Zon}\,}}R\) are of the same length. Thus, \({{\,\mathrm{Zon}\,}}R\) is homogeneous, and by Corollary 4.6 it is a \(\Gamma \)-permutahedron.
Since R is centrally symmetric and consists of unit vectors, it is reduced. Conclusively, \(R={{\,\mathrm{Gen}\,}}({{\,\mathrm{Zon}\,}}R)\) is a set of generators of a \(\Gamma \)-permutahedron, and therefore a root system. \(\square \)
It is unclear to the author whether dropping the assumption of central symmetry in Theorem 5.2 allows other, essentially different vector configurations (see Question 6.4). On the other hand, condition \(R\subset \mathbb {S}^{d}\) is certainly necessary, as there are inscribed zonotopes with edges of distinct lengths and that are not permutahedra (see Fig. 6 and Sect. 6).
Three inscribed zonotopes obtained as projections of higher-dimensional \(\Gamma \)-permutahedra. Left: projection of the \(A_4\)-zonotope, combinatorially equivalent to the \(A_3\)-zonotope, but not vertex-transitive. Middle: projection of the \(D_4\)-zonotope. Right: projection of the homogeneous \(F_4\)-zonotope. The latter two are not combinatorially equivalent to a \(\Gamma \)-permutahedron
6 Related Problems and Open Questions
The vertex-transitive zonotopes belong to the larger class of inscribed zonotopes (that is, all vertices are on a common sphere). If we put no restrictions on the edges (as in the homogeneous case), we obtain a class with much unclearer properties.
It is clear that not all inscribed zonotopes can be \(\Gamma \)-permutahedra: it is easy enough to find an inscribed centrally symmetric 2n-gon that is not vertex-transitive. It is harder to construct examples in three or more dimensions. One might be tempted to conjecture that an inscribed zonotope is at least combinatorially equivalent to a \(\Gamma \)-permutahedron. However, counterexamples were provided by Raman Sanyal and Sebastian Manecke (personal communication): the orthogonal projection of a \(\Gamma \)-permutahedron along one of its edge directions is again inscribed, but not necessarily combinatorially equivalent to a \(\Gamma \)-permutahedron (see Fig. 6). In general, the projection of an inscribed zonotope along an edge direction is again inscribed. There are further known examples which cannot be obtained as such repeated projections of \(\Gamma \)-permutahedra, but all those are still combinatorially equivalent to one which was obtained as a projection.
Question 6.1
(Sanyal and Manecke) Are there inscribed zonotopes that are not combinatorially equivalent to a \(\Gamma \)-permutahedron or the repeated projection of such one along edge directions?
Zonotopes have a known relation to real hyperplane arrangement. The results of this paper immediately yield the following: a hyperplane arrangement whose symmetry group acts transitively on its chambers must be a reflection arrangement. A more general question was asked by Caroline J. Klivans and Ed Swartz [11, Problem 13], and we shall repeat it here:
Question 6.2
(Klivans and Swartz) If all chambers of a real hyperplane arrangement are congruent, is it a reflection arrangement?
One finds that such an arrangement must be central and simplicial. The answer to Question 6.2 is known to be affirmative in dimensions \(d\in \{2,3\}\) [5], but is open in \(d\ge 4\). Dualizing again, the analogous question for zonotopes is the following:
Question 6.3
If all vertex-figures of a zonotope are identical, is it combinatorially equivalent to a \(\Gamma \)-permutahedron, or more precisely, is its normalization (see Definition 4.7) a \(\Gamma \)-permutahedron?
Another question, for which no immediate answer was found, is whether it is necessary to assume central symmetry in Theorem 5.2, or whether the following stronger version of the theorem holds:
Question 6.4
Let \(S\subset \mathbb S^d\) be a finite set of unit vectors, in which all semi-stars have the same norm. Is \(S\cup -S\) necessarily a root system?
Note that S alone is not necessarily a root system: let S be the set of vertices of a regular triangle centered at the origin, then all semi-stars have the same norm, but S is not a root system. However, \(S\cup -S\) is the root system of \(I_2(3)\).
Finally, zonotopes can also be thought of as spherical tilings with zonotopal tiles. This can be generalized to plane (or even hyperbolic) tilings with zonotopal tiles. A classification of such seems equally unfeasible as a classification of zonotopes, and so asking for the vertex-transitive tilings might be interesting.
Question 6.5
Can we classify the vertex-transitive plane (resp. hyperbolic) tilings with zonotopal tiles? Do these have similar relations to the affine (resp. hyperbolic) reflection groups?
References
Babai, L.: Symmetry groups of vertex-transitive polytopes. Geometriae Dedicata 6(3), 331–337 (1977)
Coxeter, H.S.M.: Wythoff’s construction for uniform polytopes. Proc. Lond. Math. Soc. 38, 327–339 (1935)
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P.: Uniform polyhedra. Philos. Trans. R. Soc. Lond. Ser. A 246(916), 401–450 (1954)
Dutour Sikirić, M., Ellis, G.: Wythoff polytopes and low-dimensional homology of Mathieu groups. J. Algebra 322(11), 4143–4150 (2009)
Ehrenborg, R., Klivans, C., Reading, N.: Coxeter arrangements in three dimensions. Beitr. Algebra Geom. 57(4), 891–897 (2016)
Friese, E., Ladisch, F.: Affine symmetries of orbit polytopes. Adv. Math. 288, 386–425 (2016)
Humphreys, J.E.: Reflection Groups and Coxeter Groups. Cambridge Studies in Advanced Mathematics, vol. 29. Cambridge University Press, Cambridge (1990)
Johnson, N.W.: The Theory of Uniform Polytopes and Honeycombs. PhD thesis, University of Toronto (1966)
Johnson, N.W.: Geometries and Transformations. Cambridge University Press, Cambridge (2018)
Kane, R.: Reflection Groups and Invariant Theory. CMS Books in Mathematics, vol. 5. Springer, New York (2001)
Klivans, C.J., Swartz, E.: Projection volumes of hyperplane arrangements. Discrete Comput. Geom. 46(3), 417–426 (2011)
McMullen, P.: On zonotopes. Trans. Am. Math. Soc. 159, 91–109 (1971)
Ziegler, G.M.: Lectures on Polytopes. Graduate Texts in Mathematics, vol. 152. Springer, New York (1995)
Acknowledgements
The author gratefully acknowledges the support by the funding of the European Union and the Free State of Saxony (ESF). The author also thanks Raman Sanyal and Sebastian Manecke for insightful discussions, as well as the two anonymous referees for their constructive comments.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: János Pach
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Winter, M. Classification of Vertex-Transitive Zonotopes. Discrete Comput Geom 66, 1446–1462 (2021). https://doi.org/10.1007/s00454-021-00303-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-021-00303-6