Open Sets Avoiding Integral Distances

Abstract

We study open point sets in Euclidean spaces $\mathbb{R }^d$ without a pair of points an integral distance apart. By a result of Furstenberg, Katznelson, and Weiss such sets must be of Lebesgue upper density $0$. We are interested in how large such sets can be in $d$-dimensional volume. We determine the exact values for the maximum volumes of the sets in terms of the number of their connected components and dimension. Here techniques from diophantine approximation, algebra and the theory of convex bodies come into play. Our problem can be viewed as a counterpart to known problems on sets with pairwise rational or integral distances. It possibly opens a new research direction with strong links to topology and measure theory.

1 Introduction

Is there a dense set $S$ in the plane so that all pairwise Euclidean distances between the points are rational? This famous open problem was posed by Ulam in 1945, see e.g. [18, 39]. Unlike this, a construction of a countable dense set in the plane avoiding rational distances is not hard to find, see e.g. [27, Problems 13.4, 13.9]. If all pairwise distances between the points in $S$ are integral and $S$ is non-collinear, i.e. not all points are located on a line, then $S$ is finite [2, 17]. Having heard of this result, Ulam guessed that the answer to his question would be in the negative. Of course the rational numbers form a dense subset of a coordinate line with pairwise rational distances; also, on a circle there are dense sets with pairwise rational distances, see e.g. [1, 2]. It was proved by Solymosi and De Zeeuw [37] that the line and the circle are the only two irreducible algebraic curves containing infinite subsets of points with pairwise rational distances. Point sets with rational coordinates on spheres have been considered in [34]. There is interest in a general construction of a planar point set $S(n,k)$ of size $n$ with pairwise integral distances such that $S(n,k)=A\cup B$ where $A$ is collinear, $|A|=n-k$, $|B|=k$, and $B$ has no three collinear points. The current record is $k=4$ [11]. And indeed, it is very hard to construct a planar point set, no three points on a line, no four points on a circle, with pairwise integral distances. Kreisel and Kurz [28] found such a set of size 7, but it is unknown if there exists one of size 8.

The present paper is concerned with a problem that may be considered as a counterpart to those just described, namely with large point sets in $\mathbb{R }^d$ without a pair of points an integral distance apart. We write $f_d(n)$ for the supremum of the volumes $\lambda _d(\mathcal{P })$ of open point sets ${\mathcal{P }}\subset \mathbb{R }^d$ with $n$ connected components without a pair of points whose distance apart is a positive integer. We determine the exact values of the function $f_d(n)$ for all $d$ and $n$.

This problem is related to the famous Hadwiger–Nelson open problem of determining the (measurable) chromatic number of $\mathbb{R }^{d}$, see e.g. [12, Problem G10]. Here one can also ask for the highest density of one color class in such a coloring, that is, we may ask for the densest set without a pair of points a distance $1$ apart. In [31] such a construction in $\mathbb{R }^3$ has been given. In the plane the best known example, due to Croft [13], consists of the intersections of hexagons with circles and attains a density of $0.2294$. The upper bounds are computed in [5, 14]. Point sets avoiding a finite number $k$ of prescribed distances are considered e.g. in [10] and [12, Problem G4], so the point sets avoiding all distances that are positive integers correspond to the case with an infinite number $\kappa$ of excluded distances. It is known [21] that for each subset $\mathcal U$ of the plane with positive density, there is a constant $d(\mathcal U )$ such that all distances greater than $d$ occur between the points of $\mathcal U$. The same result is true in higher dimensions [33]. It follows that in every dimension $d\ge 2$, the Lebesgue measurable sets avoiding integral distances, which are of interest here, must be of upper density $0$, so we consider the supremum of their volumes instead.

The paper is organized as follows: in Sect. 2 we introduce the basic notation and provide characterizations of arbitrary open point sets without pairs of points an integral distance apart. After stating first relationships between the upper bounds for the maximum volumes of those sets with different numbers of connected components we continue in Sect. 3 by considering a relaxed problem. We evaluate the maximum volumes of sets avoiding integral distances in the special case where the connected components of the sets are open balls. In our crucial constructions we make use of Weyl’s theorem from diophantine approximation and the fact, we derived from Mann’s theorem, that the lengths of the diagonals of a regular $p$-gon are linearly independent over $\mathbb Q$ whenever $p$ is a prime. In Sect. 4 we approach the main problem of evaluating the function $f_d(n)$ in the general case. For two-component opens sets ($n=2$) we provide a complete solution in Sect. 4.1. Motivated by the necessary conditions for open point sets to avoid integral distances we consider $d$-dimensional open sets with $n$ connected components of diameter at most $1$ each whose intersection with every line has a total length of at most $1$. At the end of Sect. 4.1 we state a conjecture on the exact values of $l_d(n)$ which bears a strong resemblance to the problems of geometric tomography, see e.g. [22]. In Sect. 4.2 we provide some upper bounds for $l_d(2)$ with $d\ge 2$. The main problem of generally evaluating $f_d(n)$ is finally settled in Sect. 4.3. In Sect. 5 we give a summary of the results obtained and draw the appropriate conclusions.

2 General Observations and Basic Notation

Denote by $\text{ dist }(x,y)$ the Euclidean distance between two points $x,y\in \mathbb{R }^d$ and by $\text{ dist }(V,W):=\inf \{\text{ dist }(x,y)\mid x\in V,\,y\in W\}$ the distance between two subsets $V$ and $W$ of $\mathbb{R }^d$. The minimal width of $V$, i.e. the minimum distance between parallel support hyperplanes of the closed convex hull of $V$, will be denoted by $\text{ width }(V)$, and $\lambda _d$ will stand for the Lebesgue measure in $\mathbb R ^d$.

At first we observe that the diameter of any connected component of an open set avoiding integral distances, i.e. having no points an integral distance apart, is at most $1$.

Lemma 1

Let $\mathcal{P }\subseteq \mathbb R ^d$ be an open set avoiding integral distances. Then for every connected component $\mathcal{C }$ of $\mathcal{P }$ we have $\mathrm{{diam}}(\mathcal{C })\le 1$.

Proof

Suppose there is a connected component $\mathcal{C }$ with $\text{ diam }(\mathcal{C })> 1$, then there exist $x_1,x_2\in \mathcal{C }$ such that $\text{ dist }(x_1,x_2)>1$. Since $\mathcal{C }$ is open, it is path connected, so there is a point $x$ on the image curve of a continuous path in $\mathcal{C }$ joining $x_1$ and $x_2$ such that $\text{ dist }(x_1,x)=1$. $\square$

By the isodiametric inequality the open ball $B_d\subset \mathbb{R }^d$ centered at the origin with unit diameter has the largest volume among measurable sets in $\mathbb{R }^d$ of diameter at most $1$, see e.g. [19], [6], Chap. 2]. Thus we have

$$\begin{aligned} f_d(1)=\lambda _d \big (B_d\big )=\frac{\pi ^{d/2}}{2^d\cdot \Gamma \big (\frac{d}{2}+1\big )}= \left\{ \begin{array}{l@{\quad }l} \frac{\pi ^{\frac{d}{2}}}{2^d\big (\frac{d}{2}\big )!} &{} \quad \text{ for }\; d\; \text{ even },\\ \frac{\big (\frac{d-1}{2}\big )!\ \cdot \ \pi ^{\frac{d-1}{2}}}{d!}&{}\quad \text{ for }\; d \;\text{ odd }.\end{array}\right. \end{aligned}$$

The first few values are given by $\lambda _1(B_1)=1$, $\lambda _2(B_2)=\frac{\pi }{4}$, $\lambda _3(B_3)=\frac{\pi }{6}$, and $\lambda _4(B_4)=\frac{\pi ^2}{32}$. We remark that the volume of the scaled ball $B$ with diameter $m$ in $\mathbb{R }^d$ is $\lambda _d(B)=m^d\lambda _d(B_d)$.

Next we characterize 1-dimensional open sets containing a pair of points an integral distance apart.

Lemma 2

A non-empty open set $\mathcal{P }\subseteq \mathbb{R }$ contains a pair of points $x,y\in \mathcal{P }$ with $\mathrm{{dist}}(x,y)\in \mathbb{N }$ if and only if either $\lambda _1(\mathcal{P })>1$ or there is a pair of connected components (i.e. disjoint open intervals) $\mathcal{C }_1$, $\mathcal C _2$ of $\mathcal{P }$ such that $\mathrm{{dist}}(\mathcal{C }_1,\,\mathcal{C }_2)\notin \mathbb{N }$ and $\lambda _1(\mathcal{C }_1\cup \mathcal{C }_2)> \lceil \mathrm{{dist}}(\mathcal{C }_1,\,\mathcal{C }_2)\rceil -\mathrm{{dist}}(\mathcal{C }_1,\,\mathcal{C }_2)$. If $\lambda _1(\mathcal{P })\le 1$, then there exists a shift $f: x\mapsto x+a$ of $\mathbb R$ such that $f(\mathcal{P })\cap \mathbb{Z }=\emptyset$.

Proof

The restriction of the canonical epimorphism $\phi : \mathbb{R }\rightarrow \mathbb{R }/\mathbb{Z }$, $x\mapsto x+\mathbb{Z } =(x-\lfloor x\rfloor )+\mathbb{Z }$, to the interval $[0,1)$ is a continuous bijection of $[0,1)$ onto the 1-dimensional torus $\mathbb{T }=\mathbb{R }/\mathbb{Z }$, the inverse map $\phi |_{[0,1)}^{-1}$ being continuous at all points except $\phi (0)=0+\mathbb{Z }=\mathbb{Z }\in \mathbb{T }$. We consider the retraction $\phi _1:=\phi |_{[0,1)}^{-1}\circ \phi : \mathbb{R }\rightarrow [0,1)$, that is, $\phi _1(x)=x-\lfloor x\rfloor$ for all $x\in \mathbb R$ (i.e. $\phi _1(x)=x\,\text{ mod }\, 1$ is the fractional part of $x$). We observe that the image under $\phi _1$ of any open interval $(x,y)$ of length $y-x<1$ is either the open interval $(\phi _1(x),\,\phi _1(y))=(x-n,y-n)$ of the same length $\phi _1(y)-\phi _1(x)=(x-n)-(y-n)=y-x$, whenever both $x$ and $y$ are in $(n,n+1)$, for some $n\in \mathbb{Z }$, or the union of two disjoint connected components

$$\begin{aligned}{}[0,\phi _1(y))\cup (\phi _1(x),1)=[0,y-n)\cup (1-(n-x),1) \end{aligned}$$

of the same total length $(y-n)+(n-x)=y-x$, whenever $x<n<y$, for some $n\in \mathbb{Z }$. If $y-x=1$, then similarly either $\phi _1((n,n+1))=(0,1)$ or $\phi _1((x,y))=[0,y-n)\cup (1-(n-x),1)=[0,1)\setminus \{y-n\}$ whenever $x<n<y$ for some $n\in \mathbb{N }$. Hence, in general, the total length of the connected components of $\phi _1((x,y))$ is $y-x$, whenever $y-x\le 1$.

Let $\mathcal{P }$ be the disjoint union of open intervals $\mathcal{C }_i$, say, with total length $\lambda _1(\mathcal{P })=\sum _i\lambda _1(\mathcal{C }_i)>1$. Then by Lemma 1 $i\ge 2$ and $\lambda _1(\mathcal{C }_i)\le 1$ for all $i$. We thus have from above that the total length of the connected components of all the images $\phi _1(\mathcal{C }_i)$ equals $\sum _i\lambda _1(\mathcal{C }_i)>1$. Hence at least two images $\phi _1(\mathcal{C }_k)$ and $\phi _1(\mathcal{C }_j)$ must overlap, so there exists $z\in \phi _1(\mathcal{C }_k)\cap \phi _1(\mathcal{C }_j)$, that is, $x_0-\lfloor x_0\rfloor =y_0-\lfloor y_0\rfloor$ for some $x_0\in \mathcal{C }_k$ and $y_0\in \mathcal{C }_j$. Thus $x_0-y_0=\lfloor x_0\rfloor -\lfloor y_0\rfloor \in \mathbb{Z }\setminus \{0\}$, hence $\text{ dist }(x_0,y_0)\in \mathbb{N }$.

If $\lambda _1(\mathcal{C }_1\cup \mathcal C _2)>\alpha$ for some connected components $\mathcal{C }_1=(a,b)$ and $\mathcal{C }_2=(c,d)$ of $\mathcal{P }$ with $\text{ dist }(\mathcal{C }_1,\,\mathcal{C }_2)=c-b=m-\alpha$, where $m\in \mathbb{N }$, $0<\alpha <1$, so that $\lceil \text{ dist }(\mathcal{C }_1,\,\mathcal{C }_2)\rceil - \text{ dist }(\mathcal{C }_1,\,\mathcal{C }_2)=\alpha$, we can take a point $x$ in the leftmost interval, say $x\in \mathcal{C }_1$ and a point $y\in \mathcal{C }_2$ so that the length of $(x,b)\cup (c,y)$ is $\alpha <\lambda _1(\mathcal{C }_1\cup \mathcal C _2)=(b-a)+(d-c)$. Then

$$\begin{aligned} \text{ dist }(x,y)=(b-x)+m-\alpha +(y-c)=\alpha +m-\alpha =m\in \mathbb{N }. \end{aligned}$$

Conversely, suppose there are $x,y\in \mathcal{P }$ with $\text{ dist }(x,y)=k\in \mathbb{N }$. If $x$ and $y$ lie in the same connected component $\mathcal C _i$ of $\mathcal{P }$, then $\lambda _1(\mathcal{C }_i)>k\ge 1$ because $\mathcal{C }_i$ is open, hence $\lambda _1(\mathcal{P })>1$. Suppose $x$ and $y$ lie in distinct connected components of $\mathcal{P }$, say $x<y$ and $x\in \mathcal{C }_1=(a,b)$, $y\in \mathcal{C }_2=(c,d)$, and let $\lambda _1(\mathcal{P })\le 1$. Then $(b-a)+(d-c)\le 1$ as well whence the distance between the components is $\text{ dist }(\mathcal{C }_1,\,\mathcal{C }_2)=c-b\notin \mathbb{N }$, because $c-b<\text{ dist }(x,y)<c-b+[(b-a)+(d-c)]\le c-b+1$. Let $c-b=m-\alpha$ where $m\in \mathbb{N },$ $0<\alpha <1$. Then

$$\begin{aligned} \alpha&= m+b-c<m+1+b-c<(d-a)+(b-c)\\&= (b-a)+(d-c)=\lambda _1(\mathcal{C }_1\cup \mathcal C _2), \end{aligned}$$

since $m+1<d-a$ because $m+1\le k<d-a$. Thus either $\lambda _1(\mathcal{P })>1$ or there is a pair of required connected components of $\mathcal{P }$.

If $\lambda _1(\mathcal{P })\le 1$, then $\lambda _1(\mathcal{C }_i)\le 1$ for all $i,$ so the total length of the connected components of all the images $\phi _1(\mathcal{C }_i)$ equals $\sum _i\lambda _1(\mathcal{C }_i)=\lambda _1(\mathcal{P })$, as shown previously. If $\lambda _1(\mathcal{P })< 1$, then clearly, $\phi _1(\mathcal{P })\ne [0,1)$. If $\lambda _1(\mathcal{P })=1$, then again $\phi _1(\mathcal{P })\ne [0,1)$, whenever the images ${\phi _1(\mathcal C }_i)$ are not pairwise disjoint. Suppose all the images ${\phi _1(\mathcal C }_i)$ are pairwise disjoint and $\mathcal{P }\cap \mathbb{Z }\ne \emptyset$. Then there is exactly one $\mathcal{C }_j=(a,b)$ that meets $\mathbb{Z }$. Hence the complement $[0,1)\setminus \phi _1(\mathcal{C }_j)=[\phi _1(b),\phi _1(a)]$ is a non-open set in $\mathbb R$ that cannot be covered by the images $\phi _1(\mathcal{C }_i)$ of the other connected components of $\mathcal{P }$, since they are all open intervals, so $\phi _1(\mathcal{P })\ne [0,1)$ as well. Thus in all the cases we have $\phi _1(\mathcal{P })\ne [0,1)$. Take $\phi _1(a)\in [0,1)\setminus \phi _1(\mathcal{P })$, $a\in \mathbb R$, that is, $\phi _1(a)\cap \phi _1(\mathcal{P })=\emptyset$. Then $\phi (a)\cap \phi (\mathcal{P })=\emptyset$, i.e. $(a+\mathbb{Z })\cap (\mathcal{P }+\mathbb{Z })=\emptyset ,$ so $(\mathcal{P }-a)\cap \mathbb{Z }=\emptyset$ and the required shift is $f:x\mapsto x+(-a)$. $\square$

Applying Lemma 2 we establish a criterion for an open set to avoid integral distances in all dimensions.

Theorem 1

An open point set $\mathcal{P }\subseteq \mathbb R ^d$ does not contain a pair of points with integral distance if and only if for every line $\mathcal{L }$

• (i) $\lambda _1(\mathcal{P }\cap \mathcal{L })\le 1$ and

• (ii) if $\mathcal{L }$ hits a pair of distinct connected components $\mathcal{C }_1$, $\mathcal C _2$ of $\mathcal{P }$ in the intervals $\mathcal{C }_1\cap \mathcal{L },\,\mathcal{C }_2\cap \mathcal{L }$ with $\mathrm{{dist}}(\mathcal{C }_1\cap \mathcal{L }, \mathcal{C }_2\cap \mathcal{L })=r\notin \mathbb N$, then $\lceil r\rceil -r\ge \lambda _1((\mathcal{C }_1\cup \mathcal C _2)\cap \mathcal{L })$.

Another criterion, which we will also be using is:

Lemma 3

Let $\mathcal{P }$ be a $d$-dimensional disconnected open set all of whose connected components are of diameter of at most $1$. Then $\mathcal{P }$ contains a pair of points with integral distance if and only if

$$\begin{aligned} \big (\mathrm{{dist}}(\mathcal{C }_1,\,\mathcal{C }_2),\;\mathrm{{diam}}(\mathcal{C }_1\cup \mathcal{C }_2)\big )\cap \mathbb{N }\ne \emptyset \end{aligned}$$

for some of its connected components.

Proof

Since all connected components of $\mathcal{P }$ are open with diameter at most $1$, any two distinct points of $\mathcal{P }$ with integral distance must be in two different components, say $\mathcal{C }_1$ and $\mathcal{C }_2$. Let $x\in \mathcal{C }_1$, $y\in \mathcal{C }_2$ with $d(x,y)=n\in \mathbb{N }$. We then select two small closed balls $\overline{B}(x,\varepsilon _1)\subsetneq \mathcal{C }_1$ and $\overline{B}(y,\varepsilon _2)\subsetneq \mathcal{C }_2$ centered at $x$ and $y$ respectively with radii $\varepsilon _1,\,\varepsilon _2>0$. The line $\mathcal{L }$ through $x$ and $y$ meets the two balls in the intervals, say $[x_1,x_2]\subsetneq \overline{B}(x,\varepsilon _1)$ and $[y_1,y_2]\subsetneq \overline{B}(y,\varepsilon _2)$, where $x_1,x_2\in \mathcal{C }_1$ and $y_1,\,y_2\in \mathcal{C }_2$. With this we have

$$\begin{aligned}&\text{ dist }(\mathcal{C }_1,\,\mathcal{C }_2)<\min _{1\le i,j\le 2}d(x_i,y_j)<d(x,y)\\&\qquad =n<\max _{1\le i,j\le 2}d(x_i,y_j)< \text{ diam }(\mathcal{C }_1\cup \mathcal C _2). \end{aligned}$$

Conversely, if $\text{ dist }(\mathcal{C }_1,\,\mathcal{C }_2)<n<\text{ diam }(\mathcal{C }_1\cup \mathcal C _2)$ for an integer $n$, then there exist $x_1,\,x_2\in \mathcal{C }_1$ and $y_1,\,y_2\in \mathcal{C }_2$ such that

$$\begin{aligned} \text{ dist }(\mathcal{C }_1,\,\mathcal{C }_2)<d(x_1,y_1)<n<d(x_2,y_2)<\text{ diam }(\mathcal{C }_1\cup \mathcal C _2). \end{aligned}$$

Joining $x_1$ with $x_2$ in $\mathcal{C }_1$ and $y_1$ with $y_2$ in $\mathcal{C }_2$ by continuous paths, we can find $x\in \mathcal{C }_1$ and $y\in \mathcal{C }_2$ on the image curves of these paths with $d(x,y)=n$. $\square$

In some situations it is helpful if we are able to assume that the components of the point sets in question are not too close to each other. Specifically, we will be using the fact that in such cases the connected components of the sets have disjoint closures.

Lemma 4

Let $\mathcal{C }_1$, $\mathcal C _2$ be distinct connected components of a $d$-dimensional open point set $\mathcal{P }$ without a pair of points an integral distance apart. If $\lambda _d(\mathcal{C }_1\cup \mathcal{C }_2)>\lambda _d\big (B_d\big )$, then $\mathrm{{dist}}(\mathcal{C }_1,\,\mathcal{C }_2)\ge 1$.

Proof

Making use of the isodiametric inequality we deduce from $\lambda _d(\mathcal{C }_1\cup \mathcal C _2)>\lambda _d\!\big (B_d\big )$ that $\text{ diam }(\mathcal{C }_1\cup \mathcal C _2)>1$. By Lemma 1 we have $\text{ diam }(\mathcal{C }_1)\le 1$ and $\text{ diam }(\mathcal{C }_2)\le 1$. So we can choose $x_1\in \mathcal{C }_1$, $x_2\in \mathcal{C }_2$ with $\text{ dist }(x_1,x_2)>1$. If $\text{ dist }(\mathcal{C }_1,\,\mathcal{C }_2)<1$, then there exist $\bar{x}_1\in \mathcal{C }_1$ and $\bar{x}_2\in \mathcal{C }_2$ such that $\text{ dist }(\bar{x}_1,\bar{x}_2)<1$. Since $\mathcal{C }_1$ and $\mathcal C _2$ are open, they are path connected, hence we can join $x_1$ and $\bar{x}_1$ by a continuous path in $\mathcal{C }_1$ and similarly $x_2$ and $\bar{x}_2$ in $\mathcal{C }_2$ and on the image curves of these paths we then find $x_1^{\prime }\in \mathcal{C }_1$ and $x_2^{\prime }\in \mathcal{C }_2$ such that $\text{ dist }(x_1^{\prime },x_2^{\prime })=1$, but $\mathcal{P }$ avoids integral distances, a contradiction. Thus we have $\text{ dist }(\mathcal{C }_1,\,\mathcal{C }_2)\ge 1$. $\square$

As Lemma 1 and Theorem 1(i) will be our main tools in estimating upper bounds for $f_d(n)$, we denote by $l_d(n)$ the supremum of the volumes $\lambda _d(\mathcal{P })$ of open point sets $\mathcal{P }\subseteq \mathbb{R }^d$ with $n$ connected components of diameter at most $1$ each (condition (a)), and with total length of the intersection with every line at most $1$ (condition (b)). Clearly $l_d(1)=f_{d}(1)=\lambda _d\big (B_d\big )$ and $f_d(n)\le l_d(n)$ for all $d$ and $n$. We remark that omitting condition (b) trivializes the problem of estimating the extreme volumes, the extremal configurations obviously consist of $n$ disjoint open $d$-dimensional balls of diameter $1$. Dropping condition (a) makes the problem more challenging. It turns out that there are open connected $d$-dimensional point sets $\mathcal{P }$ with infinite volume $\lambda _d(\mathcal{P })$ and diameter $\text{ diam }(\mathcal{P })$ even though the length of the intersection of $\mathcal{P }$ with every line $\mathcal{L }$ is at most $1$, i.e. $\lambda _1(\mathcal{P }\cap \mathcal{L })\le 1$ for all $\mathcal{L }$.

Example 1

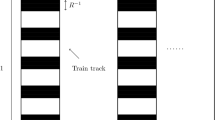
For integers $n\ge 1$ and $d\ge 2,$ denote by $\mathcal{A }_n^d$ the $d$-dimensional open spherical shell, or annulus, centered at the origin with inner radius $n$ and outer radius $n+\frac{1}{dn^d}$, i.e. $\mathcal{A }_n^d$ are bounded by concentric $(d-1)$-dimensional spheres centered at the origin. These shells will guarantee that the volume of their union is unbounded as $n$ tends to infinity. So far the constructed point set is disconnected. To obtain a connected point set, we denote by ${\mathcal{B }}_n^d$ the $d$-dimensional open spherical shell centered on the $y$-axis at $n+\frac{3}{4}$ with inner radius $1$ and outer radius $1+\frac{1}{n^4}$. With this $\mathcal{P }=\cup _{n\ge 30} \big (\mathcal{A }_n^d\cup \mathcal{B }_n^d\big )$ is open and connected with infinite volume and diameter even though the length of its intersection with every line is at most $1$. In Fig. 1 we depicted such a configuration in dimension $d=2$ containing the first few annuli. The detailed computations demonstrating the assertions claimed are provided in the appendix, see Sect. A.1.

Fig. 1

Concentric annuli with infinite area but finite lengths of line intersections (color figure online)

In order to make the problem of evaluating the functions $f_d(n)$ and $l_d(n)$ more tractable, we consider both problems in the special case, where the connected components are restricted to $d$-dimensional open balls. We denote the corresponding maximum volumes by $f^\circ _d(n)$ and $l^\circ _d(n)$ respectively. Clearly we have $f^\circ _d(n)\le f_d(n)$ and $f^\circ _d(n)\le l^\circ _d(n)\le l_d(n)$. In Sect. 3 we determine the exact values of both functions $l^\circ _d(n)$ and $f^\circ _d(n)$ for all $d$ and $n$.

Based on a simple averaging argument, any given upper bound on one of the four introduced maximum volumes for $n$ components yields an upper bound for $k\ge n$ connected components in the same dimension.

Lemma 5

For each $k\ge n$ we have $l_d(k)\le \frac{k}{n}\cdot \Lambda _1$ whenever $l_d(n)\le \Lambda _1$ and $f_d(k)\le \frac{k}{n}\cdot \Lambda _2$ whenever $f_d(n)\le \Lambda _2$.

Proof

Let $\mathcal{P }$ be a $d$-dimensional open set with corresponding property in either case and $k\ge n$ connected components. The volume of each of the ${k \atopwithdelims ()n}$ different unions of $n$ connected components inheriting these properties is at most $\Lambda _i$. Since each component occurs exactly ${{k-1}\atopwithdelims (){n-1}}$ times in those unions, the stated inequalities hold. $\square$

3 Unions of Open $d$-Dimensional Balls

Here we consider open point sets $\mathcal{P }$ that are unions of $n$ disjoint $d$-dimensional open balls of diameter at most $1$ each such that they either do not contain a pair of points with integral distance or intersect each line in the intervals with total length at most $1$. As introduced in the previous section we denote the supremum of possible volumes of such $\mathcal{P }$ by $f_d^\circ (n)$ and $l_d^\circ (n)$ respectively.

In dimension $1$ we can consider one open interval of length $1-\varepsilon$ and $n-1$ open intervals of length $\frac{\varepsilon }{n}$, where $1>\varepsilon >0$, arranged in a unit interval so that they are pairwise disjoint. The set does not have a pair of points an integral distance apart and the total length of the $n$ intervals tends to $1$ as $\varepsilon$ approaches $0$. It follows from Theorem 1 that $f^\circ _1(n)=l^\circ _1(n)=1$ for all $n$. For $n=1$, by the isodiametric inequality, only the volumes of $d$-dimensional open balls of diameter $1$ attain the maximum values $f^\circ _d(1)=l^\circ _d(1)=\lambda _d\!\big (B_d\big )$.

Lemma 6

For $d,n\in \mathbb{N }$, we have $l^\circ _d(n)\le \max \!\big (1,\frac{n}{2^d}\big )\cdot \lambda _d \big (B_d\big )$.

Proof

Consider $n$ disjoint open $d$-dimensional balls with diameters $X_1\le 1,\ldots ,X_n\le 1$, where we can assume w.l.o.g. that $X_1\le \cdots \le X_n\le 1$. Clearly in dimension $1$ we have $l_1^{\circ }(n)=l_1(n)=1=\lambda _1(B_1)$ for all $n\in \mathbb{N }$ and for all dimensions $d$, we have $l_d^{\circ }(1)=l_d(1)=\lambda _d(B_d)$, so in the cases where either $d$ or $n$ is $1$ the stated inequality holds, hence we can assume that $d\ge 2$ and $n\ge 2$. Then by Theorem 1 we have $X_i+X_j\le 1$ for all $1\le i<j\le n$. If $X_n\le \frac{1}{2}$, then $\sum \nolimits _{i=1}^n X_i^d \le \frac{n}{2^d}$ so the required inequality holds. Otherwise we have $X_i\le 1-X_n$ and it remains to maximize the function $g_d(x):=x^d+(n-1)(1-x)^d$ with domain $[\frac{1}{2},1]$. Since $g_d(x)^{\prime \prime }=d(d-1)x^{d-2}+d(d-1)(n-1)(1-x)^{d-2}>0$, every inner local extremum of $g_d$ is a minimum, so the global maximum of $g_d$ is attained at the boundary of the domain. Finally, we compute $g_d(1)=1$, $g_d\big (\frac{1}{2}\big )=\frac{n}{2^d}$, hence the lemma follows. $\square$

Remark

The special case of balls of diameter $\frac{1}{2}$ is directly related to point sets with pairwise integral distances. Let $\mathcal{P }$ be the union of $n$ $d$-dimensional open balls of diameter $\frac{1}{2}$ each without a pair of points an integral distance apart. Then the distance between the centers of the balls must be of the form $d_{i,j}+\frac{1}{2}$ for some integers $d_{i,j}$. By dilation with a factor of two we obtain the set of $n$ centers of the balls with pairwise odd integral distances. However, it has been shown in [23] that for such sets $n\le d+2$, where equality is possible if and only if $d+2\equiv 0\pmod {16}$. The exact maximum number of odd integral distances between points in the plane has been determined in [32].

Theorem 2

We have $l_d^\circ (n)=\max \,\big (1,\frac{n}{2^d}\big )\cdot \lambda _d\big (B_d\big )$ for all $d\ge 2$.

Proof

By Lemma 6 it suffices to provide configurations (asymptotically) attaining the upper bound.

For an arbitrary $1>\varepsilon >0$ we consider the union of $1$ $d$-dimensional open ball of diameter $1-\varepsilon$ and $n-1$ disjoint open balls of diameter $\frac{\varepsilon }{n-1}$ arranged in the interior of an open ball of diameter $1$. As $\varepsilon$ tends to $0$, the volume of the union tends to $\lambda _d\!\big (B_d\big )$.

For the remaining part we consider the union of $n$ open $d$-dimensional balls with diameter $\frac{1}{2}$ centered at the vertices of a regular $n$-gon with circumradius $k$. Clearly, for $k$ large enough, every line hits at most two balls. $\square$

Another construction consists of $n$ open $d$-dimensional balls with centers $\big (i\cdot k,i^2,0,\ldots ,0\big )$ and diameter $\frac{1}{2}$ for $1\le i \le n$. If $k$ is large enough then again there is no line intersecting three or more balls.

Corollary 1

We have $f_d^\circ (n)=l_d^\circ (n)=\lambda _d\big (B_d\big )$ for $d\ge 2$ and $n\le 2^d$.

It turns out that, in fact, the equalities $f_d^\circ (n)=l_d^\circ (n)=\max \!\big (1,\frac{n}{2^d}\big )\cdot \lambda _d\!\big (B_d\big )$ hold in all dimensions $d\ge 2$. To explain the underlying idea, we first consider the special case where $d=2$ and $n=5$, i.e. the first case that is not covered by Corollary 1.

Lemma 7

$$\begin{aligned} f_2^\circ (5)=\frac{5\pi }{16}\approx 0.9817477. \end{aligned}$$

Proof

For each integer $k\ge 2$ and $\frac{1}{7}>\varepsilon >0$, we consider a regular pentagon $P$ with side length $\frac{1}{2}-2\varepsilon +k$. At each of the vertices of $P$ we place an open circle of diameter $\frac{1}{2}-2\varepsilon$, see Fig. 2. Since each component has diameter less than $1$, there is no pair of points at integral distance inside one of the five components. For two points $a$ and $b$ from different components we either have

$$\begin{aligned} k<\mathrm{dist }(a,b)<k+1, \end{aligned}$$

whenever the discs are adjacent with their centers located on an edge of $P$, or

$$\begin{aligned} \Big (\frac{1+\sqrt{5}}{2}\Big )\cdot k+\frac{\sqrt{5}-1}{4}-2\varepsilon <\mathrm{dist }(a,b)< \Big (\frac{1+\sqrt{5}}{2}\Big )\cdot k+ \frac{3+\sqrt{5}}{4}-5\varepsilon \end{aligned}$$

otherwise.

Fig. 2

Integral distance avoiding open set for $d=2$ and $n=5$

Let $[\alpha ]$ denote the positive fractional part of a real number $\alpha$, i.e. there exists an integer $l$ with $\alpha =l+[\alpha ]$ and $0\le [\alpha ]<1$. If, given $\varepsilon >0$, one can find an integer $k$ such that

$$\begin{aligned} \Big [\Big (\frac{1+\sqrt{5}}{2}\Big )\cdot k +\frac{\sqrt{5}-1}{4}-2\varepsilon \Big ]<3\varepsilon , \end{aligned}$$

then the point set with parameters $k$ and $\varepsilon$ does not contain a pair of points with integral distance.

Since $\frac{1+\sqrt{5}}{2}$ is irrational, we can apply the equidistribution theorem, see e.g. [38, 40], to deduce that $\big (\frac{1+\sqrt{5}}{2}\big )\cdot \mathbb{N }$ is dense (even uniformly distributed) in $[0,1)$. The same holds true if we shift the set by the fixed real number $\frac{\sqrt{5}-1}{4}-2\varepsilon >0$. Thus we can find a suitable integer $k$ for each $\varepsilon >0$. As $\varepsilon$ tends to $0$, the total area of the five components approaches $\frac{5\pi }{16}$ which is best possible by Lemma 6. $\square$

We illustrate this by a short list of suitable values of $k$:

$$\begin{aligned} \Big [\frac{\sqrt{5}-1}{4}+\Big (\frac{1+\sqrt{5}}{2}\Big )\cdot \mathbf{{6}}\Big ]\approx 0.01722,\\ \Big [\frac{\sqrt{5}-1}{4}+\Big (\frac{1+\sqrt{5}}{2}\Big )\cdot \mathbf{{61}}\Big ]\approx 0.00909,\\ \Big [\frac{\sqrt{5}-1}{4}+\Big (\frac{1+\sqrt{5}}{2}\Big )\cdot \mathbf{{116}}\Big ]\approx 0.00096,\\ \Big [\frac{\sqrt{5}-1}{4}+\Big (\frac{1+\sqrt{5}}{2}\Big )\cdot \mathbf{{1103}}\Big ]\approx 0.00051, \end{aligned}$$

and

$$\begin{aligned} \Big [\frac{\sqrt{5}-1}{4}+\Big (\frac{1+\sqrt{5}}{2}\Big )\cdot \mathbf{{2090}}\Big ]\approx 0.00005. \end{aligned}$$

We shall generalize Lemma 7 to an arbitrary dimension $d\ge 2$ and arbitrary number $n$ of connected components. The idea is to locate the centers of $n$ small $d$-dimensional balls of diameter slightly less than $\frac{1}{2}$ at some points $C_i$ in a two-dimensional sub-plane so that the set of different pairwise distances $\alpha _i$ between their centers are linearly independent over the rational numbers. So either the distances coincide or they are rationally independent. The appropriate candidates for the center points $C_i$ would be the vertices of a regular $p$-gon, where $p$ is an odd prime. We use a theorem of Mann, see [29], to prove the desired property of the distances. The condition that the point set in question avoids integral distances can be translated into a system of inequalities of the form $[\alpha _1\cdot k]<\varepsilon ,\ldots ,[\alpha _l\cdot k]<\varepsilon$, where $k\in \mathbb{N }$, and we are looking for an integer $k$ such that the above fractional parts of the scaled pairwise distances are arbitrarily small. By a theorem of Weyl, see e.g. [40], Satz 3] or a textbook on Diophantine Approximation like e.g. [9], such systems have solutions if the $\alpha _i$ are irrational and linearly independent over $\mathbb Q$ (Weyl actually proves equidistribution while we only need denseness, a weaker result that Weyl himself attributes to Kronecker).

We remark that a similar construction, using the vertices of a regular hexagon does not work. Here the lengths of the occurring diagonals are given by $1$, $\sqrt{3}$, and $2$. The necessary inequalities

$$\begin{aligned} \Big [\Big (k+\frac{1}{2}-2\varepsilon \Big )\cdot l_i-\Big (\frac{1}{2}-2\varepsilon \Big )\Big ]=\Big [k\cdot l_i+\Big (\frac{1}{2}l_i-\frac{1}{2}\Big )+(2-2l_i)\cdot \varepsilon \Big ]<3\varepsilon , \end{aligned}$$

where $l_i$ denote the lengths of the diagonals, are trivially satisfied for $l_i=1$, but cannot hold for $l_i=2$ and small $\varepsilon$. We remark that very recently Mann’s theorem was used in another problem from discrete geometry see [15, 35].

Theorem 3

(Mann [29]) Suppose we have

$$\begin{aligned} \sum \limits _{i=1}^ka_i\zeta _i=0, \end{aligned}$$

with $a_i\in \mathbb{Q }$, the $\zeta _i$ roots of unity, and no sub-relations $\sum \nolimits _{i\in I}a_i\zeta _i=0$, where $\emptyset \ne I\subsetneq [k]$. Then

$$\begin{aligned} \big (\zeta _i/\zeta _j\big )^m=1 \end{aligned}$$

for all $i,j$, with $m=\prod \nolimits _{p\le k\,\text{ prime }} p$.

The vertices of a regular $p$-gon with a circumcircle of radius $1$ centered at the origin are given by

$$\begin{aligned} \Big (\cos \Bigl (\frac{j\cdot 2\pi }{p}\Bigr ),\,\sin \Bigl (\frac{j\cdot 2\pi }{p}\Bigr )\Big ) \end{aligned}$$

for $0\le j\le p-1$. Using complex notation they coincide with the $p$th roots of unity

$$\begin{aligned} \zeta _j^{\prime }=\cos \Bigl (\frac{j\cdot 2\pi }{p}\Bigr )+i\cdot \sin \Bigl (\frac{j\cdot 2\pi }{p}\Bigr ). \end{aligned}$$

The distance between vertices $0$ and $j$ is given by $2\sin \bigl (\frac{j\cdot 2\pi }{2p}\bigr )$. Since $\sin (\pi -\alpha )=\sin (\pi )$, there are only $(p-1)/2$ distinct distances in a regular $p$-gon, attained for $1 \le j \le (p-1)/2$. We remark that this is not too far away from the minimal number of distinct distances in the plane, which is bounded below by $c\cdot \frac{p}{\log p}$ for a suitable constant $c$, see [24]. We can express these distances in terms of $2p$th roots of unity

$$\begin{aligned} \zeta _j=\cos \Bigl (\frac{j\cdot 2\pi }{2p}\Bigr )+i\cdot \sin \Bigl (\frac{j\cdot 2\pi }{2p}\Bigr ) \end{aligned}$$

via

$$\begin{aligned} 2\sin \Bigl (\frac{j\cdot 2\pi }{2p}\Bigr )=\frac{\zeta _j-\zeta _{2p-j}}{i} \end{aligned}$$

for all $1\le j\le \frac{p-1}{2}$.

Lemma 8

Given an odd prime $p$, let

$$\begin{aligned} \alpha _j=\frac{\zeta _j-\zeta _{2p-j}}{i} \quad {\text{ for }}\quad 1\le j\le \frac{p-1}{2}, \end{aligned}$$

where the $\zeta _j$ are $2p$th roots of unity. Then the $\alpha _j$ are irrational and linearly independent over $\mathbb Q$.

Proof

A folklore result, see e.g. [30], states that $\sin (\pi q)$, where $q\in \mathbb{Q }$, is a rational number if and only if $\sin (\pi q)\in \big \{-1,-\frac{1}{2},\, 0,\,\frac{1}{2},1\big \}$. Since $p$ is odd this cannot occur in our context. It remains to show that the $\alpha _j$ are linearly independent over $\mathbb Q$. Suppose to the contrary that there are rational numbers $b_j$ for $1\le j\le l\le \frac{p-1}{2}$ with $\sum \nolimits _{j=1}^{l} b_j\alpha _j=0$. We then have

$$\begin{aligned} \sum \limits _{j=1}^{l}\big (b_j\zeta _j-b_j\zeta _{2p-j}\big )=0. \end{aligned}$$

Now let $J$ be a subset of those indices $j$, $2p-j$ such that $\sum \nolimits _{j\in J} a_j\zeta _j=0$, where $a_j\in \{\pm b_j\}$, and no sub-relation adds up to $0$. We have $|J|\le p-1$. Hence by Mann’s Theorem $(\zeta _{j_1}/\zeta _{j_2})^2=1$ for all $j_1,j_2\in J$, since

$$\begin{aligned} \gcd \Bigl (2p,\prod _{t\le p-1\,\text{ prime }} t\Bigr )=2. \end{aligned}$$

With this we obtain $j_2=j_1+p$ for $j_1<j_2$. Since $J$ is a subset of

$$\begin{aligned} \Big \{1,\ldots ,\frac{p-1}{2}\Big \}\cup \Big \{2p-\frac{p-1}{2},\ldots ,2p-1\Big \}, \end{aligned}$$

this is impossible and the $\alpha _j$ have to be linearly independent over $\mathbb Q$. $\square$

Theorem 4

For $d\ge 2$ we have $f^\circ _d(n)=\max \big (1,\frac{n}{2^d}\big )\cdot \lambda _d\big (B_d\big )$.

Proof

Since $f_d^\circ (n)\le l_d^\circ (n)$ we conclude from Theorem 2 the upper bound $f^\circ _d(n)\le \max \big (1,\frac{n}{2^d}\big )\cdot \lambda _d\big (B_d\big )$. For the construction we fix an odd prime $p$ with $p\ge n$. For each integer $k\ge 2$ and each $\frac{1}{4}>\varepsilon >0$ we consider a regular $p$-gon $P$ with side lengths $2k\cdot \sin \big (\frac{\pi }{p}\big )$, i.e. with radius $k$. At $n$ arbitrarily chosen vertices of the $p$-gon $P$ we place the centers of $d$-dimensional open balls with diameter $\frac{1}{2}-2\varepsilon$. Since each of the $n$ components has a diameter less than $1$ there is no pair of points at integral distance inside one of these $n$ components. Next we consider two points $a$ and $b$ from two different components. By $\alpha$ we denote the distance of the centers of the corresponding open balls. From the triangle inequality we conclude

$$\begin{aligned} \alpha -\Big (\frac{1-4\varepsilon }{2}\Big )<\text{ dist }(a,b)<\alpha +\Big (\frac{1-4\varepsilon }{2}\Big ). \end{aligned}$$

Since the occurring distances $\alpha$ are given by $2k\sin \big (\frac{\pi }{p}\big ))$ for $1\le j\le \frac{p-1}{2}$ we look for a simultaneous solution of the system

$$\begin{aligned} \Big [2k\cdot \sin \,\Big (\frac{j\pi }{p}\Big )-\frac{1}{2}+2\varepsilon \Big ]\le 4\varepsilon \end{aligned}$$

with $k\in \mathbb{N }$. By Lemma 8 the factors $2\sin \!\big (\frac{j\pi }{p}\big )$ are irrational and linearly independent over $\mathbb Q$, so by Weyl’s Theorem [40] the systems admit a solution for all $\varepsilon$.

Therefore, for every $0<\varepsilon <\frac{1}{4}$ we can choose a suitable value of $k$ and construct a point set without pairs of points an integral distance apart with a volume of $n\big (\frac{1}{2}-2\varepsilon \big )^d\cdot \lambda _d(B_d)$. As $\varepsilon$ approaches $0$ this volume tends to $\frac{n}{2^d}\cdot \lambda _d(B_d)$. For small values of $n$ we consider, for an arbitrary $\varepsilon >0$, one open $d$-dimensional ball of diameter $1-\varepsilon$ and $d-1$ open $d$-dimensional balls of diameter $\frac{\varepsilon }{d}$ arranged in an open $d$-dimensional ball of diameter $1$, see the proof of Theorem 2. As the diameter of the whole set is less than $1$ there is no pair of points with integral distance. $\square$

Thus, in the case of spherical components the values of $l_d^\circ (n)$ and $f_d^\circ (n)$ are completely determined. For general components the problem is more challenging for $n\ge 2$ and will be addressed in the following section.

4 Bounds for $l_d(n)$ and the Exact Value of $f_{d(n)}$

In dimension $1$ we can consider one open interval of length $1-\varepsilon$ and $n-1$ open intervals of length $\frac{\varepsilon }{n}$, where $1>\varepsilon >0$, arranged in the unit interval so that they are pairwise non-intersecting. Obviously there is no pair of points with integral distance and the total length of the $n$ intervals tends to $1$ as $\varepsilon$ approaches $0$. Thus we can conclude $f_1(n)=l_1(n)=1$ from Theorem 1. For $n=1$ component the unique example achieving the maximum volume of $f_d(1)=l_d(1)=\lambda _d\big (B_d\big )$ is the $d$-dimensional open ball with diameter $1$. For $n,d\ne 1$ the problem gets more involved. In Sect. 4.1 we treat the case of $n=2$ components. In general we are only able to obtain some lower and upper bounds, which is executed in Sect. 4.2 for $l_d(n)$ and in Sect. 4.3 the exact value of $f_d(n)$ is determined.

4.1 Two Components

At first we will start to obtain an upper bound in the case of two components. To this end, we remark that we can reformulate the condition of Lemma 3 as $\text{ diam }(\mathcal{C }_1\cup \mathcal{C }_2)\le \big \lfloor \text{ dist }(\mathcal{C }_1,\,\mathcal{C }_2)\big \rfloor +1$. Next we use Lemmas 3 and 4 to deduce some structural information on the pairs of connected components $\mathcal{C }_1$, $\mathcal{C }_2$ in a $d$-dimensional integral distance avoiding set $\mathcal{P }$. Due to Lemma 4 there exist parallel hyperplanes ${\mathcal{H }}_2$ and $\mathcal{H }_3$ such that, after a possible relabeling of the components, $\mathcal{C }_1$ is on the left hand side of ${\mathcal{H }}_2$, $\mathcal{C }_2$ is on the right hand side of $\mathcal{H }_3$, and $\mathcal H _2$ is on the left hand side of $\mathcal{H }_3$. W.l.o.g. we assume $\text{ dist }(\mathcal{H }_2,\,\mathcal{H }_3)\le \text{ dist }(\mathcal{C }_1,\,\mathcal{C }_2)$. By Lemma 3 there exist two further hyperplanes $\mathcal{H }_1$, $\mathcal{H }_4$ being parallel to $\mathcal{H }_2$ and $\mathcal{H }_3$ such that $\mathcal{C }_1$ is on the right hand side of $\mathcal{H }_1$ and $\mathcal{C }_2$ is on the left hand side of $\mathcal{H }_4$. In other words, $\mathcal{C }_1$ lies between $\mathcal{H }_1$ and $\mathcal{H }_2$, and $\mathcal{C }_2$ lies between $\mathcal{H }_3$ and $\mathcal{H }_4$. W.l.o.g. we can assume $\text{ dist }(\mathcal{H }_1,\,\mathcal{H }_4)\le \text{ diam }(\mathcal{C }_1\cup \mathcal C _2)$. Thus for $d_1:=\text{ dist }(\mathcal{H }_1, \,\mathcal{H }_2)$ and $d_2:=\text{ dist }(\mathcal{H }_3,\,\mathcal{H }_4)$ we have $d_1+d_2\le 1$ by Theorem 1(i). Clearly $d_1$ and $d_2$ are upper bounds for the width of $\mathcal{C }_1$ and $\mathcal{C }_2$, respectively.

For a convex body $\mathcal K$ in $\mathbb{R }^d$ with diameter $D$ and minimal width $\omega$ an upper bound on its $d$-dimensional volume $V$ has been found in [25, Theorem 1], namely:

$$\begin{aligned} V\le \lambda _{d-1}(B_{d-1})\cdot D^d\int \limits _0^{\arcsin \frac{\omega }{D}}\cos ^d\theta \,\text{ d }\theta . \end{aligned}$$

(1)

Equality holds if and only if $\mathcal K$ is the $d$-dimensional spherical symmetric slice with diameter $D$ and minimal width $\omega$. In the planar case some more inequalities relating several descriptive parameters of a convex set can be found in [36]. Since we will extensively use $d$-dimensional spherical symmetric slices with diameter $1$ and width $\frac{1}{2}$, we denote them by $S_d$. Viewing $S_d$ as a truncated $d$-dimensional ball of unit diameter we denote the two isomorphic cut-off bodies by $C_d$ and call them caps, i.e. we have $\lambda _d(B_d)=\lambda _d(S_d)+2\cdot \lambda _d(C_d)$.

$$\begin{aligned} \lambda _d(S_d)&= \lambda _{d-1}(B_{d-1})\int \limits _0^{\frac{\pi }{6}}\cos ^d\theta \,\text{ d }\theta ,\end{aligned}$$

(2)

$$\begin{aligned} \lambda _d(C_d)&= \frac{1}{2}\cdot \big (\lambda _d(B_d)-\lambda _d(S_d)\big ). \end{aligned}$$

(3)

In Table 1 we give the first exact volumes and refer to the Appendix, i.e. Sect. A.2, for further equivalent expressions.

Table 1 Values of $\lambda _d(S_d)$ and $\lambda _d(C_d)$ for small dimensions

Lemma 9

For $d\ge 2$, we have $f_d(2)\le 2\lambda _d(S_d)$.

Proof

With the notation as introduced above we estimate the total volume of the closed convex hulls of the two connected components $\text{ conv }(\overline{\mathcal{C }}_1),\text{ conv }(\overline{\mathcal{C }}_2)$,

$$\begin{aligned} \lambda _d(\text{ conv }(\mathcal{C }_1))+\lambda _d(\text{ conv }(\mathcal{C }_2)), \end{aligned}$$

where both components have a diameter of at most $1$, $\mathcal{C }_1$ has a width of at most $d_1$, and $\mathcal{C }_2$ has a width of at most $d_2$, using Inequality (1). We thus have

$$\begin{aligned} \lambda _d(\text{ conv }(\mathcal{C }_1))\le \lambda _d(B_{d-1})\int \limits _0^{\arcsin d_1}\cos ^d\theta \,\text{ d }\theta \end{aligned}$$

and

$$\begin{aligned} \lambda _d(\text{ conv }(\mathcal{C }_2))\le \lambda _d(B_{d-1})\int \limits _0^{\arcsin d_2}\cos ^d\theta \,\text{ d }\theta . \end{aligned}$$

Since both right hand sides are strictly monotone in $d_1$, $d_2$, respectively, we can assume w.l.o.g. that $d_1+d_2=1$. So it suffices to maximize the function

$$\begin{aligned} \int \limits _0^{\arcsin x}\cos ^d\theta \,\text{ d }\theta +\int \limits _0^{\arcsin (1-x)}\cos ^d\theta \,\text{ d }\theta \end{aligned}$$

for $x\in [0,1]$. After a straightforward calculation we conclude that the unique maximum is attained at $x=\frac{1}{2}$. $\square$

Lemma 10

$$\begin{aligned} f_d(2)\ge 2\cdot \lambda _d(S_d). \end{aligned}$$

Proof

For an arbitrary integer $k\ge 5$ we place a $d$-dimensional ball with diameter $1-\frac{2}{k}$ at the origin and cut off the spherical cap at the hyperplanes with value $\pm \big (\frac{1}{4}-\frac{1}{k}\big )$ of the first coordinate. By $\mathcal S _1$ we denote the resulting truncated ball. Another such truncated ball $\mathcal S _2$ is located with a shift of $dk+\frac{1}{2}-\frac{2}{k}$ in the direction of the first coordinate (see Fig. 3 for a drawing of the two-dimensional case). Both $\mathcal S _1$ and $\mathcal{S }_2$ have a diameter less than $1$ for all $k\in \mathbb{N }$ so that they contain no pair of points with integral distance. For two points $a\in \mathcal{S }_1$ and $b\in \mathcal{S }_2$ we have

$$\begin{aligned} dk<\text{ dist }(a,b)<\sqrt{(d-1)\Big (1-\frac{2}{k}\Big )^2+\Big (dk+1-\frac{4}{k}\Big )^2}\le dk+1, \end{aligned}$$

so that $\mathcal{S }_1\cup \mathcal{S }_2$ contains no pair of points with integral distance.

Fig. 3

Truncated circles—a construction of two components without integral distances

Finally we remark that the volume of $\mathcal{S }_1\cup \mathcal{S }_2$ approaches $2\cdot \lambda _d(S_d)$ as $k$ tends to $\infty$. $\square$

Combining Lemma 9 with Lemma 10 yields:

Corollary 2

For $d\ge 2$ we have $f_d(2)=2\lambda _d(S_d)$.

One might conjecture that the upper bound from Lemma 9 is also valid for $l_d(2)$, see Conjecture 1. Technically, we have used Lemmas 3 and 4, but it might be possible to come up with another approach which does not rely on these properties. In this context we would like to remark that related problems can be quite complicated, e.g. it is quite hard to determine the equilateral $n$-gon with diameter $1$ and maximum area [3, 4].

Conjecture 1

For $n\ge 2$ and $d\ge 2$ we have $l_d(n)=n\cdot \lambda _d(S_d)$.

4.2 Bounds for $l_{d(n)}$

Using exhaustion over lines, we can conclude two first upper bounds for $l_d(n)$.

Lemma 11

For $d\ge 2$, we have $l_d(2)\le \lambda _{d-1}\,\big (B_{d-1}\big )\cdot \big (\sqrt{\frac{2d}{d+1}}\big )^{d-1}$.

Proof

By Lemma 1 both connected components, denoted by $\mathcal{C }_1$ and $\mathcal{C }_2$, are of diameter at most $1$, so Jung’s theorem [16, 26] yields the enclosing balls $\mathcal{B }_1$, $\mathcal B _2$ for these components of diameter $\sqrt{\frac{2d}{d+1}}$. So there is an enclosing cylinder, having a $(d-1)$-dimensional ball of diameter $\sqrt{\frac{2d}{d+1}}$ as its base, containing the closed convex hull $\text{ conv }(\overline{\mathcal{B }_1\cup \mathcal B _2})$. The diagram is depicted in Fig. 4, where we remark that the two enclosing balls $\mathcal{B }_1$, $\mathcal{B }_2$ might intersect in general. By exhausting the cylinder with the lines parallel to the line trough the centers of $\mathcal{B }_1$ and $\mathcal{B }_2$, i.e. using a suitable Riemann integral or Fubini’s theorem, and applying Theorem 1(i) we conclude that the volume of $\mathcal{C }_1\cup \mathcal{C }_2$ is at most $\lambda _{d-1}\,\big (B_{d-1}\big )\cdot \big (\sqrt{\frac{2d}{d+1}}\big )^{d-1}$. $\square$

Fig. 4

Two $3$-dimensional components with the enclosing balls and enclosing cylinder

The estimates for the first few upper bounds of $l_d(2)$ in Lemma 11 are:

$$\begin{aligned} l_2(2)\le \frac{2}{\sqrt{3}}\approx 1.1547,\quad l_3(2)\le \frac{3\pi }{8}\approx 1.1781,\\ l_4(2)\le \frac{8\sqrt{2}\pi }{15\sqrt{5}}\approx 1.0597, \quad l_5(2)\le \frac{25\pi ^2}{288}\approx 0.8567 \end{aligned}$$

and $l_d(2)$ tends to $0$ as the dimension $d$ approaches infinity.

The enclosing balls are a bit wasteful. The universal cover problem, first stated in a personal communication of Lebesgue in 1914, asks for the minimum area $A$ of a convex set $U$ containing a congruent copy of any planar set of diameter $1$, see [8]. For the currently best known bounds $0.832\le A\le 0.844$ and generalizations to higher dimensions we refer the interested reader to [7], Sect. 11.4]. In this paper we will not use this concept. The restriction to $d$-dimensional open balls as components has already been treated in Sect. 3.

In dimension $d=2$ the upper bound from Lemma 11 can be improved easily.

Lemma 12

$$\begin{aligned} l_2(2)\le 1. \end{aligned}$$

Proof

Let $\mathcal{P }$ be a planar open point set consisting of two components $\mathcal{C }_1$ and $\mathcal{C }_2$ each of diameter at most $1$. If one of them is contained in the closed convex hull of the other, see Fig. 5 for an example, then we have $\lambda _2(\mathcal{P })\le \lambda _2(B_2)=\frac{\pi }{4}<1$. Otherwise, we select any support line $\mathcal{L }$ through the boundary points of $\mathcal{C }_1$ and $\mathcal{C }_2$ so that both regions are in the same half-plane determined by $\mathcal{L }$. We then consider the strip parallel to this line with smallest possible width $w$ containing both regions, see Fig. 6. Since both $\mathcal{C }_1$ and $\mathcal{C }_2$ have diameter at most $1$ we have $w\le 1$. By exhausting the strip with the lines parallel to $\mathcal{L }$ and applying Theorem 1 we conclude that the area of $\mathcal{C }_1\cup \mathcal{C }_2$ is at most $1$.   $\square$

Fig. 5

A component contained in the convex hull of another

Fig. 6

Two components between two parallel lines

4.3 The Exact Value of ${f}_{d(n)}$

By combining Lemmas 9 and 5 we obtain the upper bound $f_d(n)\le n\lambda _d\,\big (S_d\big )$. In the remaining part of this subsection we will describe a construction which asymptotically achieves this upper bound.

As a first step we remark that we can improve slightly the construction from Theorem 4. For $d\ge 2$ we choose a prime $p\ge n$ and locate $n$ open balls of diameter $1-2\varepsilon$, where $\varepsilon$ is suitably chosen, at $n$ out of the $p$ vertices of the regular $p$-gon. For each two balls we cut off spherical caps in the directions of the lines connecting two centers resulting in a width of $\frac{1}{2}-2\varepsilon$. If the radius of the regular $p$-gon approaches infinity we can assume that $\varepsilon$ can tend to $0$. So to compute the asymptotic volume of this construction it suffices to consider a regular $p$-gon $P$ of fixed radius $>2$, where we locate $n$ open balls at the vertices of $P$ and cut off spherical caps such that the components have a width of $\frac{1}{2}$ in the direction of each line connecting two used vertices, i.e. the centers of the $n$ balls. For future reference we call this construction the $p$-gon construction. An example with $p=n=5$ in dimension $d=2$ is depicted in Fig. 7.

Fig. 7

$p$-gon Construction: integral distance avoiding point set for $d=2$ and $p=n=5$

Theorem 5

For $d\ge 2$ and $n\ge 2$ we have $f_d(n)=n\lambda _d(S_d)$.

Proof

Lemmas 9 and 5 yield the upper bound $f_d(n)\le n\lambda _d(S_d)$. By Lemma 10 we can assume that $n\ge 3$. For arbitrary $\varepsilon$ let $S_{d,\varepsilon }$ be a $d$-dimensional spherical symmetrical slice with diameter $1-2\varepsilon$ and minimal width $\frac{1}{2}-2\varepsilon$. As $\varepsilon$ tends to $0$, the volume of $S_{d,\varepsilon }$ approaches $\lambda _d(S_d)$. In the following we provide a construction of an open $n$-component point set $\mathcal{P }^{\prime }$ avoiding integral distances each of whose connected $n$ components contains a congruent copy of $S_{d,\varepsilon }$.

Consider a regular $p$-gon $P$ with circumradius $k$, the parameters $p$ and $k$ to be specified. We enumerate clockwise the vertices of $P$ from $1$ to $p$ and assume w.l.o.g. that the line through vertices $1$ and $2$ is the $x$-axis. At each vertex $1\le i\le n\le p$ we place the center of an open $d$-dimensional ball of diameter $1-\varepsilon$. For each pair of the $n$ balls we cut off spherical caps in the direction of the lines through their centers resulting in a width of $\frac{1}{2}-\varepsilon$. We denote the union of the resulting $n$ open sets by $\mathcal{P }$.

Consider further all $2\cdot {n \atopwithdelims ()2}$ cutting hyperplanes that cut off the spherical caps from the initial open balls. As the number $p$ of vertices of the $p$-gon $P$ increases, with $n$ fixed, all those hyperplanes tend to be orthogonal to the $x$-axis. Now choose a prime $p$ large enough so that each connected component of $\mathcal{P }$ contains a $d$-dimensional spherical symmetrical slice with diameter $1-2\varepsilon$ and minimal width $\frac{1}{2}-2\varepsilon$ whose cutting hyperplanes are orthogonal to the $x$-axis. By $\mathcal{P }^{\prime }$ we denote the subset of $\mathcal{P }$ which is the union of those $S_{d,\varepsilon }$’s.

There exists a number $k_1$ such that for $k\ge k_1$ each line hits at most two connected components of $\mathcal{P }^{\prime }$. Since the diameter of each of its connected components is at most $1-2\varepsilon$, the pairwise distances between the points within the same component are non-integral. Let $a$ and $b$ be two points in different connected components. By the construction the distance between the corresponding centers is given by $2k\cdot \sin \!\big (\frac{j\pi }{p}\big )$ for a suitable integer $j$. Thus

$$\begin{aligned} \text{ dist }(a,b)\ge 2k\cdot \sin \,\Big (\frac{j\pi }{p}\Big )-\frac{1}{2}+\varepsilon . \end{aligned}$$

There exists a number $k_2$ such that for $k\ge k_2$, we have

$$\begin{aligned} \text{ dist }(a,b)\le 2k\cdot \sin \,\Big (\frac{j\pi }{p}\Big )+\frac{1}{2}-\varepsilon , \end{aligned}$$

since all the lines joining the centers of the connected components of $\mathcal{P }^{\prime }$ then to be horizontal, as $k$ increases (compare the proof of Lemma 10).

Thus, provided that $k\ge \max (K_1,k_2)$, the system of inequalities

$$\begin{aligned} \Big [2k\cdot \sin \!\Big (\frac{j\pi }{p}\Big )-\frac{1}{2}+\varepsilon \Big ]\le 2\varepsilon \end{aligned}$$

has a solution, the distance $\text{ dist }(a,b)$ cannot be integral, so $\mathcal{P }^{\prime }$ does not contain a pair of points with integral distance. By Lemma 8 and the Weyl theorem the above system admits indeed a solution. $\square$

5 Conclusion

Problems related to point sets with pairwise rational or integral distances were one of Erdős’ favorite subjects in combinatorial geometry. In the present paper we study some kind of a counterpart to this type of problems by asking for the largest open $d$-dimensional set $\mathcal{P }$ of points without a pair of points an integral distance apart, i.e. that with the largest possible volume $f_d(n)$, where $n$ denotes the number of connected components of $\mathcal{P }$. As a relaxation we have also considered $d$-dimensional open point sets consisting of $n$ connected components, each having a diameter at most $1$, such that the intersection with every line has a total length of at most $1$. The corresponding maximum volume was denoted by $l_d(n)$. While the assumption on diameters of the connected components seems to be a bit technical, geometrical objects with specified intersections with lines or higher-dimensional subspaces are interesting in their own right. So far we were not able to prove that the maximum volumes $l_d(n)$ are bounded if we drop the condition on the diameters. In this context we just mention the famous Kakeya problem of whether a Kakeya set in $\mathbb{R }^d$, i.e. a compact set containing a unit line segment in every direction, has Hausdorff dimension $d,$ see e.g. the review [41] or [12, Problem G6].

By restricting the shapes of the connected components to $d$-dimensional balls, we were able to determine the exact values of the corresponding maximum volumes $f^\circ _d(n)$ and $l^\circ _d(n)$, respectively. Also the values of $f_d(n)$ could be determined exactly, while for $l_d(n)$ we only have the lower bound $l_d(n)\ge f_d(n)$, which we conjecture to be tight.

Appendix

In order to keep the main part of the paper more accessible we have moved some side remarks and technical calculations to this appendix.

1.1 A. 1 Details of the Annuli Construction

We have to ensure that Construction 1 satisfies the proposed properties. First we remark that both $\mathcal{A }_n^d$ and $\mathcal{A }_{n+1}^d$ meet $\mathcal{B }_n^d$ for $n\ge 1$. Thus $\mathcal{P }$ is a connected open set in $\mathbb{R }^d$. The volume $\lambda _d\big (\mathcal{A }_n^d\big )$ is given by

$$\begin{aligned}&\lambda _d(B_d)\cdot \Big (\big (2n+\frac{2}{dn^d}\big )^d-(2n)^d\Big )\nonumber \\&\quad =\lambda _d(B_d)\cdot 2^d\cdot \Big (\big (n+\frac{1}{dn^d}\big )^d-n^d\Big )\ge \lambda _d(B_d)\cdot 2^d\cdot \frac{1}{n}. \end{aligned}$$

Since the harmonic series diverges to infinity, the $d$-dimensional volume of $\mathcal{P }$ is unbounded.

Now we consider the intersection of a line $\mathcal{L }$ with a $d$-dimensional annulus $\mathcal{C }_d(r_1,r_2)$ with inner radius $r_1$ and outer radius $r_2$ centered at the origin. Due to symmetry we can assume that $\mathcal{L }$ is parallel with the $x$-axis, i.e.

$$\begin{aligned} \mathcal{L }=\big \{\begin{pmatrix}1&0&\dots&0\end{pmatrix}^T\cdot \lambda + \begin{pmatrix}0&a_2&\dots&a_d\end{pmatrix}^T\mid \lambda \in \mathbb{R }\big \}. \end{aligned}$$

By symmetry we can further assume $a_i\ge 0$ for all $2\le i\le d$. To ease notation we set $l :=\sqrt{\sum \nolimits _{i=2}^d a_i^2}$. We remark $\mathcal{C }_d(r_1,r_2)\cap \mathcal{L }=\emptyset$ for $l^2>r_2^2$. The $x$-coordinates of the intersections of $\mathcal{L }$ with the $d$-dimensional sphere of radius $r_1$ are given by $\pm \sqrt{r_1^2-l^2}$, as long as $l^2\le r_1^2$. Similarly the $x$-coordinates of the intersections of $\mathcal{L }$ and the $d$-dimensional sphere of radius $r_2$ are given by $\pm \sqrt{r_2^2-l^2}$, as long as $l^2\le r_2^2$. For $l^2\le r_1^2$ we have

$$\begin{aligned} \lambda _1\big (\mathcal{C }_d(r_1,r_2)\cap \mathcal{L }\big )=2\cdot \underset{=:h_1(a_2,\dots ,a_d)}{ \underbrace{\Big (\sqrt{r_2^2-\sum \nolimits _{i=2}^d a_i^2}-\sqrt{r_1^2-\sum \nolimits _{i=2}^d a_i^2}\Big )}}. \end{aligned}$$

Since

$$\begin{aligned} \frac{\partial h_1}{\partial a_i}(a_2,\dots ,a_d)=a_i\cdot \Big (\frac{1}{\sqrt{r_1^2-\sum \nolimits _{i=2}^d a_i^2}}- \frac{1}{\sqrt{r_2^2-\sum \nolimits _{i=2}^d a_i^2}}\Big )\ge 0, \end{aligned}$$

we can assume $l^2\ge r_1^2$ for the maximum length of the intersection. If the $a_i$ are restricted by an inequality $l^2\le k^2\le r_1^2$ the maximum length of the intersection is bounded from above by $2\sqrt{r_2^2-k^2}-2\sqrt{r_1^2-k^2}$.

For $r_1^2\le \sum \nolimits _{i=2}^d a_i^2\le r_2^2$ we have

$$\begin{aligned} \lambda _1\big (\mathcal{C }_d(r_1,r_2)\cap \mathcal{L }\big )=2\cdot \underset{=:h_2(a_2,\dots ,a_d)}{ \underbrace{\sqrt{r_2^2-\sum \nolimits _{i=2}^d a_i^2}}} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial h_1}{\partial a_2}(a_2,\ldots ,a_d)=-a_i\cdot \frac{1}{\sqrt{r_2^2-\sum \nolimits _{i=2}^d a_i^2}}\le 0, \end{aligned}$$

so that the extremal values are taken at $\sum \nolimits _{i=2}^d a_i^2=r_1^2$ where we have $\lambda _1\big (\mathcal{C }_d(r_1,r_2)\cap \mathcal{L }\big ) \le 2\sqrt{r_2^2-r_1^2}$.

Thus for an arbitrary line $\mathcal{L }$ we have

$$\begin{aligned} \lambda _1\big (\cup _{n\ge 30}\mathcal{B }_n^d\cap \mathcal{L }\big )\le \sum \limits _{n=30}^\infty 2\sqrt{\big (1+\frac{1}{n^4}\big )^2-1^2}\le \sum \limits _{n=30}^\infty \frac{2\sqrt{3}}{n^2}<0.12. \end{aligned}$$

For the remaining part we restrict ourselves on lines being parallel to the $x$-axis. If $l<30$ then

$$\begin{aligned} \lambda _1\big (\cup _{n\ge 30}\mathcal{A }_n^d\cap \mathcal{L }\big )&\le 2\sqrt{\big (30+\frac{1}{d\cdot 30^d}\big )^2-30^2}\\&\quad + \sum \limits _{n=31}^\infty 2\sqrt{\big (n+\frac{1}{dn^d}\big )^2-l^2}-2\sqrt{n^2-l^2}\\&\le 0.366+2\sum \limits _{n=31}^\infty \frac{\frac{2}{n}}{2\sqrt{n^2-30^2}}<0.47. \end{aligned}$$

For $l\ge 30$ we have

$$\begin{aligned} \lambda _1\big (\cup _{n\ge 30}\mathcal{A }_n^d\cap \mathcal{L }\big )&\le 4\sqrt{\big (\lfloor l\rfloor +\frac{1}{d\cdot \lfloor l\rfloor ^d}\big )^2-\lfloor l\rfloor ^2}\\&\quad + \sum \limits _{n=\lfloor l+2\rfloor }^\infty 2\sqrt{\big (n+\frac{1}{dn^d}\big )^2-l^2}-2\sqrt{n^2-l^2}\\&\le 0.732++2\int \limits _{\lfloor l+1\rfloor }^\infty \frac{1}{x\sqrt{x^2-l^2}}\mathrm{d }x \\&= 0.732+\frac{2}{l}\cdot \arcsin \Big (\frac{l}{\lfloor l+1\rfloor }\Big )\\&\le 0.732 +\frac{2}{l} \cdot \frac{\pi }{2}<0.84. \end{aligned}$$

Since $0.12+\max (0.47,0.84)<1$ we have $\lambda _1(\mathcal{P }\cap \mathcal{L })<1$ for each line $\mathcal{L }$.

1.2 A. 2 Volumes of Truncated Balls and Caps

In Table 1 we have stated the volumes of truncated $d$-dimensional balls of unit diameter $S_d$ and the cutt-off bodies, i.e. caps, $C_d$ for small dimensions $d$. Due to Eqs. (2) and (3) it suffices to compute the values $v(d):=\int \nolimits _{0}^{\frac{\pi }{6}}\cos ^{\text{ d }}(x)\,\mathrm{d }x$. The first few values are given by $v(1) = \frac{1}{2}$, $v(2) = \frac{1}{8}\cdot \sqrt{3}+\frac{1}{12}\cdot \pi$, $v(3) = \frac{11}{24}$, and $v(4) = \frac{9}{64}\cdot \sqrt{3}+\frac{1}{16}\cdot \pi$. Using integration by parts we can immediately compute

$$\begin{aligned} v(d)=\left\{ \begin{array}{ll} \frac{(2m-1)!!}{(2m)!!}\cdot \big (\frac{1}{2}\cdot \sum \nolimits _{k=0}^{m-1}\frac{(2k)!!}{(2k+1)!!}\cdot \frac{\sqrt{3}}{2}\cdot \big (\frac{3}{4}\big )^{k} +\frac{\pi }{6}\big )&{}\quad \text{ for } \; d=2m,\\ \frac{(2m)!!}{(2m+1)!!}\cdot \frac{1}{2}\cdot \sum \nolimits _{k=0}^m \frac{(2k-1)!!}{(2k)!!}\cdot \big (\frac{3}{4}\big )^{k} &{}\quad \text{ for } \; d=2m+1. \end{array}\right. \end{aligned}$$

Given the integer sequence A091814 from the “On-line encyclopedia of integer sequences” $v(d)$ can be written as

$$\begin{aligned} \frac{A091814(d))\cdot \big (\frac{d-1}{2}\big )!}{d!\cdot 2^{\frac{d+1}{2}}} \end{aligned}$$

for all odd $d$. Benoit Cloitre contributed the following second order recursion formula: $v(1)=\frac{1}{2}$, $v(3)=\frac{11}{24}$, and

$$\begin{aligned} v(2n-1)=\frac{1}{8n-4}\cdot ((14n-17)\cdot v(2n-3)-6(n-2)\cdot v(2n-5)) \end{aligned}$$

for $n\ge 3$. A similar recursion formula can be obtained for even $d$, where $v(d)$ can be written as

$$\begin{aligned} q(d)\cdot \sqrt{3}+\frac{{{d-1}\atopwithdelims (){\frac{d}{2}}}}{2^d\cdot 3}\cdot \pi \end{aligned}$$

for rational numbers $q(d)$.

Additionally one can compute the corresponding ordinary generating function:

$$\begin{aligned}&F(z):=\sum \limits _{k=0}^\infty v(k)z^k=\sum \limits _{k=0}^\infty \int \limits _0^{\frac{\pi }{6}} (z\cos t)^k\,\mathrm{d }t= \int \limits _0^{\frac{\pi }{6}}\frac{\mathrm{d }t}{1-z\cos t}\\&\qquad \quad =\frac{2}{\sqrt{1-z^2}}\arctan \!\Big (\sqrt{\frac{1+z}{1-z}}\cdot \tan \frac{\pi }{12}\Big ). \end{aligned}$$

We will apply singularity analysis in order to determine the asymptotic behavior of $a_n:=F_\alpha (z)[z^n]$, where slightly more generally

$$\begin{aligned} F_\alpha (z):= \frac{2}{\sqrt{1-z^2}}\arctan \!\Big (\sqrt{\frac{1+z}{1-z}}\cdot \alpha \Big ),\end{aligned}$$

see e.g. [20], chapter VI]. The main singularity is at $z=1$ since there is a compensation for $z=-1$. From

$$\begin{aligned} \arctan \!\Big (\sqrt{\frac{1+z}{1-z}}\cdot \alpha \Big )&= \frac{\pi }{2}+O\bigl ((1-z)^\frac{1}{2}\bigr ),\\ \frac{2}{\sqrt{1+z}}&= \sqrt{2} +O(1-z),\quad \text{ and }\\ \bigl [z^n\bigr ]\frac{1}{\sqrt{1-z}}&= \frac{1}{\sqrt{\pi n}}+O\!\big (\frac{1}{n^{\frac{3}{2}}}\big ) \end{aligned}$$

we conclude

$$\begin{aligned} a_n=\sqrt{\frac{\pi }{2n}}+O\!\big (\frac{1}{n^{\frac{3}{2}}}\big ). \end{aligned}$$

So we have $v(d)\sim \sqrt{\frac{\pi }{2d}}$.