Mafic explosive volcanism at Llaima Volcano: 3D x-ray microtomography reconstruction of pyroclasts to constrain shallow conduit processes

Abstract

Mafic volcanic activity is dominated by effusive to mildly explosive eruptions. Plinian and ignimbrite-forming mafic eruptions, while rare, are also possible; however, the conditions that promote such explosivity are still being explored. Eruption style is determined by the ability of gas to escape as magma ascends, which tends to be easier in low-viscosity, mafic magmas. If magma permeability is sufficiently high to reduce bubble overpressure during ascent, volatiles may escape from the magma, inhibiting violent explosive activity. In contrast, if the permeability is sufficiently low to retain the gas phase within the magma during ascent, bubble overpressure may drive magma fragmentation. Rapid ascent may induce disequilibrium crystallization, increasing viscosity and affecting the bubble network with consequences for permeability, and hence, explosivity. To explore the conditions that promote strongly explosive mafic volcanism, we combine microlite textural analyses with synchrotron x-ray computed microtomography of 10 pyroclasts from the 12.6 ka mafic Curacautín Ignimbrite (Llaima Volcano, Chile). We quantify microlite crystal size distributions (CSD), microlite number densities, porosity, bubble interconnectivity, bubble number density, and geometrical properties of the porous media to investigate the role of magma degassing processes at mafic explosive eruptions. We use an analytical technique to estimate permeability and tortuosity by combing the Kozeny-Carman relationship, tortuosity factor, and pyroclast vesicle textures. The groundmass of our samples is composed of up to 44% plagioclase microlites, > 85% of which are < 10 µm in length. In addition, we identify two populations of vesicles in our samples: (1) a convoluted interconnected vesicle network produced by extensive coalescence of smaller vesicles (> 99% of pore volume), and (2) a population of very small and completely isolated vesicles (< 1% of porosity). Computed permeability ranges from 3.0 × 10⁻¹³ to 6.3 × 10⁻¹² m², which are lower than the similarly explosive mafic eruptions of Tarawera (1886; New Zealand) and Etna (112 BC; Italy). The combination of our CSDs, microlite number densities, and 3D vesicle textures evidence rapid ascent that induced high disequilibrium conditions, promoting rapid syn-eruptive crystallization of microlites within the shallow conduit. We interpret that microlite crystallization increased viscosity while simultaneously forcing bubbles to deform as they grew together, resulting in the permeable by highly tortuous network of vesicles. Using the bubble number densities for the isolated vesicles (0.1-3⁻³ × 10⁴ bubbles per mm³), we obtain a minimum average decompression rate of 1.4 MPa/s. Despite the textural evidence that the Curacautín magma reached the percolation threshold, we propose that rapid ascent suppressed outgassing and increased bubble overpressures, leading to explosive fragmentation. Further, using the porosity and permeability of our samples, we estimated that a bubble overpressure > 5 MPa could have been sufficient to fragment the Curacautín magma. Other mafic explosive eruptions report similar disequilibrium conditions induced by rapid ascent rate, implying that syn-eruptive disequilibrium conditions may control the explosivity of mafic eruptions more generally.

Introduction

The volume of erupted magma is dominated by products from effusive to mildly explosive mafic eruptions (Parfitt 2004). However, mafic Plinian-style eruptions can occur, generating destructive pyroclastic currents and widespread ash fall (La Spina et al. 2020). The most powerful examples include the basaltic Plinian deposits of ∼60 ka Fontana Lapilli and ∼2 ka Masaya Triple Layer at Masaya Volcano in Nicaragua (Constantini et al. 2009; Constantini et al. 2010; Bamber et al. 2020; Pérez et al. 2020); the 122 BC eruption of Etna, Italy (Coltelli et al. 1998; Houghton et al. 2004; Sable et al. 2006); and the 1886 Tarawera eruption, New Zealand (Houghton et al. 2004; Sable et al. 2006; Shea 2017; Moitra et al. 2018).

In general, explosive eruptions are modulated by the conditions of volatile exsolution that lead to vesiculation. Vesiculation is a process in which volatiles originally dissolved in the magma exsolve into gas bubbles due to a decrease in the pressure-dependent solubility during magma ascent (Yoshimura et al. 2019). The exsolution of volatiles within a magma is controlled by decompression rate, the degree of volatile saturation, availability of nucleation sites, surface tension, and viscosity of magma (Mangan et al. 2004; Cassidy et al. 2018). The resulting bubbles undergo decompression-induced expansion, reducing the bulk mixture density of the magma and enhancing buoyancy (Cassidy et al. 2018). As bubbles expand, they may coalesce to form permeable pathways connecting the dispersed volatile phase (Klug and Cashman 1996). If the resulting permeability is sufficiently high to limit bubble overpressure during ascent, the volatiles may escape from the magma, reducing the chance of violent explosive activity. In contrast, if the permeability is low enough to largely trap the gas phase within the magma during ascent, overpressure in bubbles may drive magma fragmentation, producing an explosive eruption (Mueller et al., 2008; Degruyter et al. 2012; Cashman and Scheu 2015; Cassidy et al. 2018).

Many studies show that there is a link between mafic explosive volcanism, rapid ascent, and syn-eruptive disequilibrium conditions in both the gas and solid phases (La Spina et al., 2016; Polacci et al. 2018; Arzilli et al. 2019; Bamber et al. 2020; Namiki et al. 2021; Colombier et al. 2021). When decompression rate is high, the volatiles may not degas from the magma under equilibrium conditions. Such disequilibrium degassing may lead to volatile supersaturation, late vesiculation, and high bubble overpressures (Mangan and Sisson 2000). Similarly, crystallization kinetics are controlled by water content, degassing, and decompression rates (La Spina et al. 2016; Befus and Andrews 2018; Arzilli et al. 2019). High degrees of disequilibrium due to rapid ascent result in high crystal nucleation and growth rates (Befus and Andrews 2018). The rapid increase of the magma bulk viscosity may further prevent gas loss, promoting the conditions necessary for explosive volcanism (Arzilli et al. 2019; Colombier et al. 2021).

The bubble and crystal textures of magmas are critical in determining their rheology and eruptive behavior (Gonnermann and Manga, 2007; Polacci et al., 2018). Rapid crystallization due to disequilibrium degassing triggers profound rheological changes in ascending magmas (Vona et al. 2011; Arzilli et al. 2019). Indeed, pyroclasts from mafic Plinian eruptions typically display high microlite number densities and high crystallinities (Houghton et al. 2004; Sable et al. 2006; Sable et al. 2009; Murch and Cole 2019; Bamber et al. 2020), suggesting that changes in rheology due to rapid crystallization may be responsible for triggering highly explosive basaltic volcanism (Sable et al. 2006).

Pyroclasts from explosive eruptions record the state of the volatile phase in the conduit prior to fragmentation (Degruyter et al. 2010). Thus, if post-fragmentation vesiculation is negligible, pyroclast vesicle textures can be used to constrain magma permeability at the time of fragmentation, as well as ascent rate and fragmentation conditions (Mueller et al. 2005; Toramaru 2006; Polacci et al. 2010).

The most common approach to investigate vesicle texture is using 2D images from scanning electron microscope (SEM) imaging of thin sections. However, this technique cannot image the 3D internal vesicle structures that govern permeability (Saar and Manga 1999; Polacci et al. 2010; Giachetti et al. 2011). Even with 3D analysis, permeability and tortuosity estimates often require lab measurements or numerical models, which may not be an option due to pyroclast size (too small for lab permeameters) and computational challenges to accurately simulate a large enough volume to be representative. For these reasons, this study uses an alternative methodology to calculate pyroclast permeability of lapilli size pyroclasts, which are commonly too small for lab permeameters.

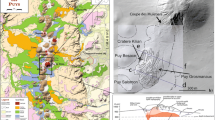
The objective of this study is to understand why mafic magma erupted explosively at Llaima Volcano (38° 41′ 45 S, 71° 43′ 54 W). We focus on pyroclasts produced by the large volume 12.6 ka mafic explosive eruption responsible for the extensive Curacautín Ignimbrite (Fig. 1; Naranjo and Moreno 1991; Lohmar 2008; Schindlbeck et al. 2014; Marshall et al. 2021). The Curacautín Ignimbrite is a massive, poorly sorted, and matrix-supported coarse ash to fine lapilli tuff. The eruption produced four flow units of variable thickness with SiO₂ content between 50.7 and 57.6 wt.% (Marshall et al. 2021). We collected 10 samples stratigraphically (Units 1–4) from the most complete exposure, which is located southeast of the summit (Fig. 1).

Fig. 1

(A) Map showing Curacautín deposits and the most complete exposure, which is located southeast of the summit (yellow rectangle). (B) Photo of Unit 1 showing sample locations. Unit 1 is the thickest deposit in the sequence. The base is not exposed. (C) Photo showing the contact between Unit 1, Unit 2, and Unit 3. Samples L12 (top of Unit 1) and L18 (Unit 4) are not visible in these photos

Previous work shows that Curacautín pyroclasts are coarse ash to lapilli size, subrounded, micro-vesicular with low phenocryst contents (2–3%; Marshall et al. 2021). The groundmass is microlite-rich, mostly plagioclase (volume fraction between 0.36 and 0.44), and contains little to no glass (8.0–18.4 × 10⁶ plagioclase microlites per mm³. Fig. 2; Table 2). 2D analyses suggest that vesicles shapes are controlled by an abundance of plagioclase microlites (Fig. 2).

Fig. 2

SEM image of a pyroclast from the Curacautín Ignimbrite. (A) Sample L1, Unit 1. (B) Sample L8, Unit 2. The groundmass is microlite rich, mostly plagioclase (volume fraction between 0.36 and 0.44) and contains little to no glass. The vesicle shapes appear controlled by the high amount of plagioclase microlites

Here we use plagioclase microlite textures and plagioclase crystal size distributions (CSDs) to identify changes in decompression pathways and rates of microlite crystallization. We also report 3D results using x-ray microtomography of porosity, bubble number density, surface areas, tortuosity, and permeability of pyroclasts from the Curacautín Ignimbrite. We then estimate decompression rates, the degree of coupling between the gas phase and the magma, and the evolution of vesiculation during ascent to investigate the role of magma degassing processes during mafic explosive eruptions. Finally, we discuss the consequences of disequilibrium conditions induced by high decompression rates and compare our results with other basaltic explosive eruptions. We recognize that post-fragmentation vesiculation may occur, but for this study makes the simplifying assumption that post-fragmentation vesiculation was negligible, primarily due to our inability to constrain the degree to which it affected final pyroclast textures.

Methodology

To understand the processes that led to fragmentation, we use several complementary measurements and models.

Microlite texture analysis

Plagioclase microlite textures were measured using backscattered electron (BSE) images of Curacautín pyroclasts collected on a Teneo FEI Field Emission Scanning Electron Microscope (FESEM) at the Boise State University Center for Materials Characterization using a beam current of 6.4 nA and 15 kV accelerating voltage. BSE images were acquired at 1500–2000 × magnifications.

In order to calculate crystal size distributions (CSDs), microlites need to be assigned a crystal habit that describes their shape based on their short, intermediate, and long axes (S:I:L). We obtained crystal habits using the stereological conversion program CSDslice v.5 (Morgan and Jerram 2006). Because of their acicular nature in two dimensions, we measured > 250 plagioclase microlites per pyroclast to ensure correct determination of crystal habit (Morgan and Jerram 2006). Crystal habits calculated from CSDslice v.5 were used as inputs for CSDcorrections v.1.6 (Higgins 2000) to generate CSD plots. The crystal roundness was set to 0.1, and we used a shape measurement of parallelepiped for stereological conversions. Images were corrected for sample vesicularity measured in ImageJ.

Crystallization times τ_c can be calculated from the CSDs using

$$\mathrm{slope}=-\frac{1}{G\times{\tau }_{c}},$$

(1)

where “slope” is the slope of the CSD linear regression and G is the microlite growth rate (Cashman and Marsh 1988). We calculated τ_c using growth rates of 10⁻⁴ mm s⁻¹ (Arzilli et al. 2019), 2 × 10⁻⁵ mm s⁻¹ (Arzilli et al. 2015), 10⁻⁶ mm s⁻¹ (Shea and Hammer 2013), and 10⁻⁷ mm s⁻¹ (Arzilli et al. 2015) to investigate the variability of fast versus slow crystallization (Bamber et al. 2020).

The y-intercept n° of CSD linear regressions is the nucleation density (mm⁻⁴). Cashman and Marsh (1988) showed that the nucleation rate J can be calculated from

$$J=n^\circ \times G,$$

(2)

where G is the mean linear growth rate.

Synchrotron x-ray microtomography

Lapilli size pyroclasts were picked, cleaned, and sorted by density (Marshall et al. 2021). We chose the mean and median density pyroclasts from each sample for 3D analysis and drilled 3.4 mm diameter cores for further microtomography imaging. We only imaged intact and visually undamaged cores. Cores were immersed in an ultrasonicator water bath for 25 min to remove powder produced by coring, then dried in an oven at 95 °C. Due to the micro-vesicularity of our samples, no loss of internal structure is expected.

X-ray microtomography was performed on beamline 8.3.2 at the Advanced Light Source, Lawrence Berkeley National Lab. 3D data was acquired over five sessions between September 2017 and October 2018. Owing to differences in beam stability and small changes in setup, scanning parameters varied slightly between sessions to optimize image quality. Images were acquired with 25–30 keV monochromatic x-rays and 200 ms exposure times. One thousand twenty-five to 2625 projections were imaged with a PCO edge camera, a 5× Mitutoyo lens, and a 50 mm LuAG scintillator over a 180° continuous rotation of the sample. Isotropic pixel size was 1.3 microns. A subset of 5 samples were imaged at 0.64 microns/pixel for comparison. Image reconstruction was performed with Xi-cam (Pandolfi et al. 2018), including center of rotation optimization along with ring and outlier removal.

3D data processing

Image processing, volume rendering, and geometric computations were generated using the Dragonfly software, Version 2020.1.0.797 for Windows 10 (Object Research Systems (ORS) Inc, Montreal, Canada, 2018; software available at http://www.theobjects.com/dragonfly). We stacked 820 2D images (2560 × 2560 pixels) per sample to reconstruct the 3D microstructures (Supplementary Material B.1A). Due to the size of the resulting volume (22.2 GB; Supplementary Material B.1A) and the computational challenges to process that amount of data, four cubic sub volumes of 820 × 820 × 820 voxels (~ 1.21 mm³) per sample were extracted as Volumes of Interest (VOI; Supplementary Material B.1). These VOIs have linear dimensions that are more than an order of magnitude greater than microlite and vesicle dimensions, and hence are large enough to sample the complexity and heterogeneity of the samples, but small enough to not overwhelm the computing resources available for this project (Baker et al. 2012; Degruyter et al. 2010). We selected four sub volume locations vertically throughout each core sample to reduce ring errors (maximum at the center of the sample) and avoid the cylindrical boundaries of the 2D images (Supplementary Material B.1B). Using four VOIs also provides a sensitivity analysis, enabling uncertainty estimates related to sample heterogeneity.

In order to analyze and visualize the pore network, the VOIs were segmented using Dragonfly’s segmentation toolkit. This process partitions the volume into groups of voxels of each phase of interest. For simplicity, we defined two phases of interest: pores and solid rock. We utilized a global segmentation criterion based on a brightness/grayscale histogram threshold (Histogram segmentation in Dragonfly), where the darker voxels correspond to vesicles or pores and the brighter ones correspond to the solid phase (Supplementary Material B.2). Commonly, this process generates artifacts and errors due to the heterogeneities in voxel brightness (Baker et al. 2012; Degruyter et al. 2010; Ketcham and Carlson 2001; Ketcham 2005; Shanti et al. 2014). Thus, a cleaning procedure was performed using morphological operations, part of Dragonfly’s segmentation toolkit, to “Erode,” “Dilate,” and “Smooth,” effectively removing artifacts such as islands and holes smaller than 9 voxels. This process was repeated as many times as necessary until a clear, bimodal image was produced maintaining the main internal morphologies of the sample (confirmed by a visual inspection, Supplementary Material B.2). Once the segmentation was successful, we separated the vesicle phase (Supplementary Material B.2). Every separated vesicle was counted and identified, followed by the computation of geometrical properties including volume and surface area (Supplementary Material A.1).

Quantification of 2D and 3D vesicle textures in terms of vesicularity (volumetric fraction of vesicles), bubble number densities (number of vesicles per unit volume), vesicle volume, surface areas, and connectivity (volume fraction of the vesicle network) were performed with the same software (Table 1, Supplementary Material A.1). Additionally, we extracted 3D visualizations of the skeletonization (Fig. 3D), segmented phases (Fig. 3B), and separated phases (Fig. 3C). The final 3D segmented data volumes were converted to binary images for tortuosity analysis.

Table 1 Results of plagioclase CSD analyses. Four values of τ_c are provided using different experimentally derived growth rates. Letter in parentheses for samples is the CSD segment. Multiple J and τ values correspond to their respective G values. Note that the units for τ vary for different G. Three images were analyzed per sample, and their average was used for CSDs, timescale calculations, and nucleation rate calculations

Fig. 3

3D visualization of L4. All three volumes have the same size and correspond to one VOI. (A) 3D reconstruction of L4. Darker voxels correspond to vesicles and the brighter ones correspond to the solid phase (B) Segmentation of the porous media represented in cyan color. (C) Separation of the vesicle phase. Every color represents a single bubble. (D) 3D visualization of the skeletonization of sample L4. The convoluted shape and the chaotic distribution of the purple matrix structure make it difficult to calculate classically defined tortuosity

3D tortuosity factor

Tortuosity factors (${\tau }^{*}$) were calculated using the MatLab application TauFactor (Cooper et al. 2016). TauFactor calculates the changes in diffusive transport produced by contortions and heterogeneities of the interconnected pore space (Eq. 3; Backeberg et al. 2017; Cooper et al. 2016). The effective diffusivity (D_eff) is related to the tortuosity factor,

$${D}_{\mathrm{eff}} ={D}_{0}\frac{\phi }{{\tau }^{*}} ,$$

(3)

where D₀ is the intrinsic diffusivity of the conductive phase and $\phi$ is the volume fraction of the pore phase. TauFactor calculates the directional tortuosity factor along three mutually perpendicular axes of interconnected “diffusive phases” (or porous phases) through a 3D volume generated by stacking binary or trinary 2D images (Supplementary Material B.3).

It is important to note that tortuosity factor and tortuosity ($\tau )$ are two different parameters with different definitions in governing equations, although both characterize the relationship between the geometry and length of interconnected phases. In porous media, tortuosity is defined as the ratio between the flow-path length and a straight-line length in the direction of flow, which has been commonly used to quantify flow, or diffusion along porous media (Suman and Ruth 1993; Shanti et al. 2014; Backeberg et al. 2017; Cooper et al. 2016). Tortuosity is measured from skeletonized data using finite element analysis or finite difference calculation on meshed data (Shanti et al. 2014). Unfortunately, the skeletonization of the porous network of our samples is too complex and chaotic for this type of calculation (Fig. 3D). As such, a tortuosity factor calculation is better suited for modelling more complex pore networks such as those in our clasts (Backeberg et al. 2017; Cooper et al. 2016).

In a system where the cross-sectional area of the flow path remains constant, tortuosity factor is equal to the square of tortuosity (Tjaden et al. 2016; Backeberg et al. 2017). Given an average variation of ~ 13% in the cross-sectional area of the flow represented by the 2D porosity changes (Supplementary Material B.4), we use Eq. 4 as an approximation.

$${\tau }^{*}\simeq {\tau }^{2}.$$

(4)

The tortuosity factor and tortuosity both increase as pathways become more contorted. Both parameters approach 1 when the cross-sectional area of the flow pathways remains constant and the direction of flow follows the axis that is orthogonal to that cross-sectional area (Backeberg et al. 2017).

TauFactor also computes 2D volume fractions, 3D phase volume fraction (vesicularity), effective diffusivity (${D}_{\mathrm{eff}}$), directional percolation, tortuosity factor (${\tau }^{*}$), and a provides a visual representation of the flux during steady state (an example is shown in Supplementary Material B.3).

Permeability calculations

One of the most widely used relationships between permeability and tortuosity is the Kozeny‐Carman relation for the Darcian permeability k₁ (Kozeny 1927; Carman 1937; Yokoyama and Takeuchi 2009; Matyka et al. 2008; Farquharson et al. 2015; Berg 2014; Bernard et al. 2007; Wei et al. 2018),

$${k}_{1}=\frac{{\phi }^{3}}{c{\tau }^{2}{S}^{2}},$$

(5)

where $\phi$ is the porosity, $\tau$ is the tortuosity, S is the surface area per unit volume, and c is the Kozeny constant. Bernabe et al. (2010) define two idealized Kozeny constants: a crack-controlled medium where c = 12, and a pore-controlled medium where c = 8 (Farquharson et al. 2015). We use c = 8 due to the nature of the porous network. Given the complexity of the porous media observed in the skeletonized data (Fig. 3D) and the low variation in the cross-sectional area of the flow path, we combined Eq. (4) and Eq. (5) to find a relationship between permeability and tortuosity factor

$${k}_{1}\simeq \frac{{\phi }^{3}}{c{\tau }^{*}{S}^{2}}$$

(6)

We compare our estimates of permeability based on the Kozeny-Carman model (5), and the measured vesicularity and estimated tortuosity, with direct numerical simulation of 3D flows in one of the VOIs using the Palabos open-source lattice Boltzmann flow solver (Latt et al. 2021). Lattice Boltzmann methods have often been used to compute the pore-scale flow field in volcanic porous media to estimate permeability from direct numerical simulations (e.g., Wright et al. 2009; Polacci et al. 2009; Degruyter et al. 2010). The flow simulation is conducted with a prescribed pressure gradient on the OSCAR computer cluster at Brown University. The flow field was simulated until it converged (Supplementary Material B.4). For this comparison, and owing to memory limitations, we chose one VOI from sample L4 (closest sample parameters to the average results calculated for Unit 1) reducing the volume by a factor of 2 to a domain of 820 × 820 × 410 voxels for both the TauFactor and lattice Boltzmann calculations. This comparison does not address whether the imaging resolution is sufficient for a meaningful estimate of permeability but does address whether the Kozeny-Carman model is a good model for our samples as imaged.

Decompression and discharge rates

Given the lack of clear evidence for shear-induced coalescence (no preferential elongation of vesicles or preferential orientation of microlites), we use the bubble number density decompression rate meter proposed by Toramaru (2006) to calculate decompression rates (dP/dt) from volumetric bubble number densities (N_v) for basaltic magmas undergoing heterogeneous nucleation (Shea 2017; Toramaru 2006):

$$\frac{dP}{dt}={\left(\frac{{N}_{v}}{5\left(\pm 3.5\right)\times {10}^{3}}\right)}^\frac{2}{3}$$

(7)

Additionally, if we assume a cylindrical conduit geometry, we can estimate mass discharge rates $(\dot{m)}$ as a function of bulk magma density $({\rho }_{m})$, decompression rate, pressure gradient in the conduit (dP/dz), and conduit radius (r) (Shea 2017):

$$\dot{m}= {\rho }_{m}{\left(\frac{dP}{dz}\right)}^{-1}\left(\frac{dP}{dt}\right)\pi {r}^{2}.$$

(8)

We approximate the pressure gradient in the conduit with the magmastatic gradient. For a mafic magma at 1200 °C, dP/dz = 0.026 MPa m⁻¹ (Cas and Simmons 2018). We used the bulk magma density $({\rho }_{m})$ (i.e., melt + bubbles + crystals) as the average density of our pyroclasts for Unit 1, ${\rho }_{bulk} \sim 1290 \mathrm{kg }{\mathrm{m}}^{-3}$(Marshall et al. 2021). For the radius, we considered that Plinian eruptions require larger conduits radius, between 10 and 150 m, to explain the relationship between mass discharge and decompression rates (Shea 2017). To address uncertainty in r, we calculated three discharge rates for radii of 25, 50, and 100 m.

Forchheimer and Stokes numbers

We calculated the Stokes and Forchheimer numbers for Unit 1 following Degruyter et al. (2012) to compare our results with other explosive eruptions. The Stokes number (St) is a non-dimensional number that represents the ratio of the magma response time scale and the gas phase characteristic flow time, in this case, the flow of gas through the permeable magma,

$$\mathrm{St}=\frac{\frac{{\rho }_{m}{k}_{1}}{{\mu }_{g}}}{\frac{r}{{U}_{o}}}$$

(9)

where μ_g is the viscosity of the gas phase, r is the conduit radius, and U₀ is the velocity. Velocity is calculated as the ratio between the mean decompression rate and the magmastatic gradient in the conduit. When St is small, magma and gas are coupled and ascend at similar velocities, limiting gas loss from the magma. For larger St, the degree of coupling decreases permitting gas loss (Degruyter et al. 2012; La Spina et al. 2017). The Forchheimer number (Fo) is the ratio of the inertial and viscous term in Forchheimer’s law (Eq. 10; Degruyter et al. 2012; La Spina et al. 2017)

$$\mathrm{Fo}= \frac{{\rho }_{g0}{k}_{1}{U}_{o}}{{k}_{2}{\mu }_{g}}$$

(10)

where the density of the gas ρ_g0 is calculated from the ideal gas law

$${\rho }_{g0}= \frac{{P}_{0}}{RT}$$

(11)

and k₂ is the inertial permeability, P₀ is the pressure in the conduit at a certain depth, and R is the specific gas constant. The inertial permeability is calculated using the Gonnermann et al. (2017) relationship between Darcian and Inertial permeabilities (in SI units)

$${\mathrm{log}}_{10}\left({k}_{2}\right)=1.353{\mathrm{log}}_{10}\left({k}_{1}\right)+8.175.$$

(12)

For small Fo, outgassing is controlled by the viscous permeability (Darcian). For larger Fo, the inertial permeability dominates (Degruyter et al. 2012; La Spina et al. 2017).

In order to obtain values of Fo and St, we assumed that the temperature in the conduit is constant. We used a temperature of 1100 °C (1375 K), which represents the mean temperature for the Curacautín Ignimbrite pre-eruptive magma (Lohmar 2008). Gas viscosity and velocity throughout the conduit are assumed constant as well, while conduit radius and reference depth are variable between 25 and 100 m, and between 100 and 1000 m, respectively.

Results

Each measurement and analysis provide distinct results. The joint analysis and interpretation of the complementary measurements are provided in the discussion.

Plagioclase microlite number densities and crystal size distributions

Plagioclase microlite CSD results are summarized in Table 1. We analyzed three pyroclasts for Unit 1, and one pyroclast each for Units 2, 3, and 4. Unit 1 plagioclase have tabular to rectangular prism habits and S:I:L axes between 1:6:10 and 1:8:10 (R² = 0.68–0.83). Units 2 and 3 microlites have rectangular prism habits and S:I:L axes of 1:6:10 (R² = 0.80 and 0.85, respectively). Unit 4 plagioclase have a tabular habit and S:I:L axes of 1:6:10 (R² = 0.86). Plagioclase microlite number densities are available in Table 2.

Table 2 Summary of x-ray microtomography results of vesicle textural analysis. Microlite number densities and density values extracted from Marshall et al. (2021)

All CSD curves are concave up (Fig. 4). We identified two size populations of microlites based on linear regression. The first regression (segment A, Fig. 4) is fit to the smallest crystal size population and produces the steepest slopes. The second regression (segment B, Fig. 4) is fit to the largest crystal size population and has shallower slopes. The y-intercept n° is the nucleation density (mm⁻⁴). All CSDs exhibit a downturn at the smallest size bins (i.e., abrupt decrease in microlite CSD; Fig. 4). Because our data were collected at 1500–2000× magnifications, these downturns likely reflect the reduced probability of intercepting small crystals and not inadequate image resolution (Cashman 1998; Marsh 1998). Data from downturns are not included in segment A regressions (Fig. 4).

Fig. 4

Curacautín CSDs for (A) Unit 1, (B) Unit 2, (C) Unit 3, and (D) Unit 4, where ln n° represents the natural log of the nucleation density. Regressions in (A) are the average of all Unit 1 samples. Segment A reflects shallow conduit and/or syn-eruptive crystallization, whereas segment B reflects crystallization deeper in the conduit. Segments are labeled in panel D but apply to all panels

Reconstruction and measurements of vesicle textures in 3D

We analyzed 40 VOIs from 10 representative pyroclasts, 4 VOIs per sample. The reconstructed volumes obtained using synchrotron x-ray microtomography allow us to visualize and quantify the vesicle network of Llaima pyroclasts in 3D (Fig. 5). All samples show high vesicle interconnectivity (99%) and no clear signs of preferential vesicle elongation. From a gas transport perspective, there are two main populations of vesicles: (1) a contorted connected vesicle network produced by coalescence of smaller vesicles (> 99% of porosity network, yellow color in Fig. 5A), and (2) a population of very small and completely isolated vesicles (< 1% of total porosity; Fig. 5B). The contorted vesicle network has irregular shapes and rough surfaces. In contrast, some of the smallest isolated vesicles are moderately spherical, whereas the larger isolated vesicles have irregular to polylobate shapes (Supplementary Material B.6).

Fig. 5

(A) 3D visualization of L4 vesicle network and isolated vesicles. Each vesicle is assigned a distinct color. Yellow shows the main convoluted connected vesicle network. All voids correspond to the solid phase. (B) 3D visualization of L4 isolated vesicles

Quantitative textural parameters including 2D and 3D vesicularities, bubble number densities (BND), and specific surface area are summarized in Table 2. Individual 3D measurements of vesicularities are shown in Supplementary Materials B.5. Average 3D vesicularities, correlated stratigraphically in Fig. 6A, and BND are presented in Table 2. The BND results are based on the number of small, isolated vesicles, and do not include the (uncountable) number of vesicles that are part of the interconnected network. The reported BND is thus a lower bound. No correlation between BND and vesicularity is observed.

Fig. 6

Results summarized with respect to their locations in the stratigraphic column. (A) Porosity. (B) Tau factor. (C) Darcian permeability. (D) Minimum decompression rates. (E) Minimum discharge rates for conduit radii r of 25, 50, and 100 m

Average specific surface area calculations, a key measurement for the Kozeny-Carman model Eq. (5) and defined as the ratio between surface area and volume (Maroof et al. 2020), are also presented in Table 2. These values were calculated for the contorted connected phase through which gas flowed and represent 99% of the vesicle phase (Fig. 5A, yellow interconnected vesicle).

Tortuosity factor

We compute tortuosity factors in three orthogonal directions following the axis of our VOIs. Results are presented in Table 2 and correlated stratigraphically in Fig. 6B. We observe low directional variability, implying that there is no preferred flow direction for the gas flux. We also observe an inverse relationship between vesicularity and tortuosity, and a strong direct correlation with specific surface area (Supplementary Material A.1).

Permeability calculations

Darcian permeabilities were calculated using Eq. (6) assuming a pore-controlled medium with c = 8 (Bernabe et al. 2010; Farquharson et al. 2015). Similar to the tortuosity factor calculations, we computed permeability values in three orthogonal directions following the axes of our VOIs. Computations of average Darcian permeability are presented in Table 3 and correlated stratigraphically in Fig. 6C. Calculated permeabilities have an inverse correlation with tortuosity, a direct correlation with vesicularity, and a strong inverse correlation with the specific surface area. We calculated inertial permeabilities using the Darcian permeability results and Eq. (12) (Gonnermann et al. 2017). Average values of inertial permeabilities are also presented in Table 3, and show similar correlations to Darcian permeabilities. The computed permeabilities are the result of many stages of analysis, from image reconstruction to segmentation to the use of the Kozeny-Carman model. Error in our calculated permeabilities can be introduced at all stages.

Table 3 Summary of results for Darcian and inertial permeabilities, decompression rates, discharge rates, and fragmentation threshold

The permeability estimates from the tortuosity calculations (6.26 × 10⁻¹³ m²) and the lattice Boltzmann numerical simulation (5.1 × 10⁻¹³ m²) are in good agreement (Supplementary Material B.4). The 19% difference between the estimates is encouraging given limitations in spatial resolution in both numerical simulations and the assumption that tortuosity and specific surface area can be used as a proxy for permeability in the Kozeny-Carman model.

Decompression and discharge rates

Due to the large amount of microlites and the absence of glass in our samples (Marshall et al. 2021; Fig. 2), we propose a heterogeneous nucleation regime for the formation of the small isolated bubbles (Fig. 5B). Therefore, we calculated decompression rates using Eq. (7) proposed by Toramaru (2006) for basaltic magmas undergoing heterogeneous nucleation (Shea 2017). Using the BND based on isolated vesicles, the minimum decompression rates for all samples range from 0.36 to 2.6 MPa s⁻¹ (Table 3; Fig. 6D). Figure 7, which compares our results with other basaltic eruptions (Toramaru 2006; Shea 2017), shows that the minimum estimated decompression rates for the Curacautín magma are close to decompression rates calculated for Tarawera 1886AD and Etna 122BC. Finally, in order to calculate and contrast the minimum discharge rates with other basaltic eruptions, we use Eq. (8) for three different conduit radius (Table 3 and Fig. 6E). Minimum average discharge rates are between 1.6 × 10⁸ and 2.2 × 10⁹ kg s⁻¹ (Fig. 6E; Eq. 8).

Fig. 7

Minimum average decompression rates (MPa/s) vs BND (mm⁻³) for Units 1–4 using Eq. (6) (Toramaru 2006, Shea 2017). The blue dashed line corresponds to the equation shown in the top left corner for basaltic rocks (Shea  2017). Historic basaltic eruptions (gray symbols) are extracted from Shea 2017

Forchheimer and Stokes numbers

We calculated Fo and St for Unit 1 following Eqs. (9–12) using the reference parameters in Table 4 (Degruyter et al. 2012; La Spina et al. 2017). The (St, Fo) results for Unit 1 overlap with the (St, Fo) values for the 1980 Mount St. Helens (MSH) Plinian eruption reported by Degruyter et al. (2012) (Fig. 8). Both areas are in the low St and high Fo regions, indicating that the magma and gas were well coupled, ascending at similar (but not equal) velocities, and the outgassing was turbulent (Degruyter et al. 2012). Higher permeabilities lead to higher and lower values of St and Fo, respectively, increasing the outgassing efficiency but not enough to decouple the gas phase from the magma. Conversely, lower permeabilities lead to lower and higher values of St and Fo, respectively, enhancing the coupling between magma and the gas phase. Figure 8 also shows how increasing certain parameters influence the St and Fo numbers. The threshold (dashed line in Fig. 8) separating conditions that lead to explosive and effusive eruptions was determined in Degruyter et al. (2012) using numerical simulations of magma ascent. These simulations depend on details of magma composition, how rheology evolves during ascent, and the fragmentation mechanism. Performing equivalent simulations is hindered by a lack of constraints on how rheology of Llaima magma evolves as it ascends and how crystallinity and vesicularity change. However, based on the results in Degruyter et al. (2012), the threshold is unlikely to change by more than an order of magnitude. Furthermore, the key parameters that determine St and Fo are those we can measure from the pyroclasts and the ascent velocity which is constrained by the mass eruption rate. We thus added question marks to the dashed line to highlight the uncertainty, but note that Llaima magma erupted with conditions that most likely lie well within conditions that promote fragmentation.

Table 4 Reference parameters and results for calculation of Stokes and Forchheimer numbers

Fig. 8

Stokes (St) vs Forchheimer (Fo) number. The dark gray region represents the (Fo, St) results for Unit 1 using the parameters listed in Table 4. The light gray area corresponds to the (Fo, St) values for the 1980 Mount St. Helens Plinian eruption (Degruyter et al. 2012). The dashed line represents a boundary between effusive (below) and explosive (above) computed for Mount St. Helens (Degruyter et al. 2012) and includes question marks because the crystallization kinetics and rheology are not well enough constrained to perform equivalent numerical calculations for Curacautín pyroclasts. The arrows indicate how the results would change by increasing different parameters

Discussion

Microlite texture analysis

CSDs are useful for identifying changing decompression pathways in the subsurface (Fig. 4). For example, CSDs that form a straight line reflect continuous decompression while concave up CSDs reflect differing depths and rates of crystallization (Marsh 1998). In the shallow subsurface, nucleation-dominated crystallization is driven by high decompression rates and high undercooling (ΔT). Conversely, larger microlites and phenocrysts form deeper in the conduit and magma chamber where they have time to grow before their final ascent to the surface.

The two segments in our CSDs (Fig. 4) identified from separate linear regressions are most simply explained by a change in decompression histories during ascent of the Curacautín magma (Murch and Cole 2019; Bamber et al. 2020). Bamber et al. (2020) determined that G values of 10⁻⁴ mm s⁻¹ (Arzilli et al. 2019) and 2 × 10⁻⁵ mm s⁻¹ (Arzilli et al. 2015) are most appropriate for crystallization in the conduit, while 10⁻⁶ mm s⁻¹ (Shea and Hammer 2013) and 10⁻⁷ mm s⁻¹ (Arzilli et al. 2015) are appropriate for phenocrysts or larger microlites crystallizing within the magma reservoir. Thus, segment A (Fig. 4) documents the shallow, rapid decompression or syn-eruptive crystallization where nucleation-dominated crystallization prevailed (Geschwind and Rutherford 1995; Hammer et al. 1999; Blundy and Cashman 2008). Segment B (Fig. 4) records the larger sizes of crystals that nucleated deeper in the conduit. Note that 85–93% of plagioclase microlites in our samples are < 10 μm, suggesting that even though a subpopulation of microlites crystallized deeper, most plagioclase crystals had little time to grow. We therefore interpret our CSDs as primarily reflecting disequilibrium crystallization conditions produced by rapid ascent and rapid crystallization of microlites at shallow depths.

Calculations of τ_c from segment A linear regression in Fig. 4D indicate that the Curacautín magma reached high microlite crystallinities in seconds to minutes (Table 1). We interpret that such rapid crystallization could only result from high degrees of undercooling (ΔT, Arzilli et al. 2019). High degrees of undercooling are further reflected in the dominantly acicular to hopper microlite textures, which form under disequilibrium crystallization conditions (Shea and Hammer 2013).

Our microlite textures and CSDs indicate varying degrees of microlite nucleation, decompression rate, and ascent dynamics between the four units. There is a general increase in n° and J of segment A from Unit 1 into Units 2, 3, and 4 suggesting that the ascent rates of later eruptive episodes increased along with nucleation rates. Therefore, we suggest that our CSDs reflect mid- to shallow conduit conditions and syn-eruptive crystallization, likely accompanying and following the onset of bubble nucleation, rather than conditions and processes in the magma reservoir. A more quantitative assessment would require a set of laboratory decompression experiments using Curacautín magma, which is beyond the scope of this paper.

Vesicle network analysis

The 3D reconstructions allow us to investigate the pyroclast vesicle textures in detail and extract vesicularity, surface areas, interconnectivity, and number of vesicles, all of which are more challenging to interpret in 2D slices. For example, we observe an average variation of ~ 13% for the 2D vesicularities considering all our VOIs (Supplementary Material B.4). That variation decreases to less than ~ 3% if we compare the 3D vesicularity between the four VOIs per sample (Table 2). This increment of accuracy suggests that the selected VOI is sufficient to account for the major textural heterogeneity of our samples. In addition, vesicles have more than 99% interconnectivity in all our samples, a feature that would be impossible to conclude with 2D section analyses.

Similar to the microlite texture interpretations, BND results suggest that the magma rose at fast decompression rates, similar to other basaltic explosive eruptions reported in the literature (Shea 2017). Specifically, Unit 1 has a minimum average decompression rate of 1.4 MPa s⁻¹ (Eq. 7), similar to the 1.5 and 2.0 MPa s⁻¹ reported for Tarawera 1886AD and Etna 122BC, respectively (Fig. 7; Shea 2017). Although the lack of more samples for Units 2, 3, and 4 adds additional uncertainty to the results, their calculated minimum decompression rates show a similarly rapid ascent. We estimate minimum average discharge rates between 1.6 × 10⁸ and 2.2 × 10⁹ kg s⁻¹ (Fig. 6E; Eq. 8), close to the 1.4 × 10⁸ kg s⁻¹ and 5–8.5 × 10⁸ kg s⁻¹ reported for Fontana Lapilli Masaya 60 ka and Etna 122BC, respectively (Shea 2017).

Decompression experiments show that rapid ascent rates lead to high degrees of disequilibrium, promoting rapid nucleation of plagioclase microlites at shallow depths (Brugger and Hammer 2010; Befus and Andrews 2018). As discussed in the previous section, our samples are rich in microlites, with plagioclase microlite number densities of 7.95–18.4 × 10⁸ per mm³ (Table 2), evidencing high degrees of disequilibrium crystallization. Microlite nucleation may have shifted the solubility conditions of the remaining melt (Gonnermann et al. 2012), causing exsolution and vesiculation. Such vesiculation would have enhanced the buoyancy of the bulk magma, driving magma acceleration (Cassidy et al. 2018). Simultaneously, rapid crystallization of microlites increased the viscosity of the magma and may have restricted the expansion of the first population of bubbles forcing them to deform as they grew toward each other and resulting in a tortuous but still well-connected (99% connectivity) bubble network structure (Fig. 2; Arzilli et al. 2019; deGraffenried et al. 2019).

The presence of a well-connected, albeit convoluted, vesicle network and a population of small vesicles suggest that there was a change in the coalescence efficiency prior fragmentation. The larger vesicles that are part of the connected network have irregular shapes and rough surfaces suggesting that they had more time to evolve. In contrast, some of the smallest isolated vesicles are moderately spherical. The contorted vesicle network shape and the abundance of microlites between vesicles could hinder diffusion of the remaining dissolved volatiles to existing bubbles, enabling heterogeneous nucleation on microlites and leading to the formation of the disconnected group of bubbles (Hajimirza et al. 2021). We interpret that the population of small, isolated vesicles (~ 1% of vesicularity; Fig. 5B) was the last to form and might be the result of a syn-eruptive crystallization of microlites induced by high decompression rates (La Spina et al. 2016). Given the high vesicle connectivity (⁓99%), it is likely that this final stage of vesiculation occurred after the main vesicle network reached the percolation threshold (Lindoo et al. 2017).

Fo and St calculations for Unit 1 (Eqs. 10 and 11; Fig. 8) suggest that the gas phase was well coupled with the magma during ascent (Degruyter et al. 2012). We propose that, despite the well-connected network of bubbles promoted by crystallization (Lindoo et al. 2017) and evidence for the Curacautín magma reaching the percolation threshold, the permeability of the convoluted bubble network remained low enough for gas to remain well coupled with the magma during its ascent. That is, the minimum decompression rate inferred from the population of small, isolated vesicles is high enough that gas loss through the interconnected network of bubbles was suppressed, leading to the overpressure needed to promote fragmentation (Fig. 8). Furthermore, rapid crystallization of microlites induced by high decompression rates increased viscosity of the magma and limited gas loss through the permeable network. We interpret that this promoted gas overpressure and brittle fragmentation, similar to the conditions reported for other mafic explosive eruptions (Moitra et al. 2018; Arzilli et al. 2019; Colombier et al. 2021). Given the evidence for rapid ascent rates, shear-induced fragmentation may also have played a role. However, we see no evidence of preferential elongation or orientation of the interconnected vesicle network or the isolated vesicles which we might expect from high strain rates and large strains. Nor do we see any obvious microlite preferred orientation that would result from shear.

As a preliminary validation for our permeability model, the calculations presented herein indicate that pyroclast permeability of our samples is similar to, but slightly lower than, those of other basaltic explosive eruptions (Colombier et al. 2021; Fig. 9) and similar to basaltic scoria (Saar and Manga 1999). Additionally, our results fall within the wide empirical bounds provided by Mueller et al. (2005) for explosive volcanic rocks. Furthermore, our values are similar to those measured on samples generated experimentally in crystallizing and vesiculating basaltic andesites (Lindoo et al. 2017).

Fig. 9

Porosity vs Darcian permeability results. Black dots correspond to the values calculated for the 12.6 ka Curacautín Ignimbrite (Eq. 4). Gray and white dots correspond to values measured on pyroclasts for Tarawera 1886AD and Etna 122BC, respectively (Colombier et al. 2021). The area between the dashed lines shows the Mueller et al. (2005) model for explosive eruptions

Following the methods of Mueller et al. (2008), we calculate the minimum bubble overpressure needed to lead fragmentation (ΔP_fr)

$$\Delta {P}_{\mathrm{fr}}= \frac{a\sqrt{{k}_{1}}+ {\sigma }_{m}}{\phi }$$

(13)

where a and σ_m are constants equal to 8.21 × 10⁵ MPa m⁻¹ and 1.54 MPa, respectively. Our results show that a bubble overpressure greater than ~ 5 MPa could have been sufficient to fragment the Curacautín magma (Fig. 10; Table 3).

Fig. 10

The 3D curve represents the minimum overpressure required to achieve fragmentation at given sample porosity and permeability (Mueller et al. 2008). Red stars represent our results for permeability and porosity. Our results show that a bubble overpressure greater than ~ 5 MPa could have been sufficient to fragment the Curacautín magma (Table 3)

Lastly, low variations of microstructural properties (CSDs, BND, vesicularity, permeability) in the stratigraphic sequence (Fig. 6) support the assertion of Marshall et al. (2021) that the Curacautín Ignimbrite is the result of one eruptive event with perhaps several discrete explosive pulses, resulting in the four flow units.

Conclusions

We investigated the 12.6 ka explosive mafic eruption at Llaima Volcano, Chile, that produced the extensive Curacautín ignimbrite. The objective of this study was to use microlite and vesicle textural analysis to explore the conditions that promoted the strong explosivity of the Curacautín magma. We use microlite number densities and CSDs to constrain ascent rates and crystallization rate paths, and vesicle textures to constrain vesicle tortuosity, permeabilities, decompression rates, the degree of coupling between the gas phase and the magma, and the evolution of vesiculation during ascent. We validate permeability estimates using a full three-dimensional lattice Boltzmann simulation. The analytical calculations provide an approach for quantifying the permeability and tortuosity of pyroclast vesicle networks in samples too small to use laboratory techniques like traditional permeameters.

The CSD analyses combined with our 3D vesicle texture results suggest rapid ascent rates that induced disequilibrium crystallization of microlites during ascent at shallow depths. Simultaneously, microlite crystallization increased magma bulk viscosity and confined bubbles during expansion. This rapid crystallization forced bubbles to deform as they grew toward each other, resulting in the convoluted interconnected vesicle network. Despite reaching the percolation threshold, it appears the decompression rate was too high for the Curacautín magma permeability to promote outgassing; instead, the volatile phase remained well coupled with the magma, which inhibited outgassing and promoted an increase in bubble overpressure. Our permeability and vesicularity results suggest that a minimum bubble overpressure of ⁓5 MPa was required to induce fragmentation of the magma.

The conditions that led to explosive mafic volcanism at Llaima Volcano are similar to other basaltic explosive eruptions (Tarawera 1886AD, Etna 122BC, and Fontana Lapilli Masaya 60 ka). Our results provide further evidence that mafic explosive volcanism at Llaima Volcano, as well as other mafic centers, is driven by rapid magma ascent. Rapid ascent induces disequilibrium crystallization conditions and rapid crystallization of microlites at shallow depths. Crystallization increases viscosity of the magma, inhibiting gas escape and driving bubble overpressure, promoting explosive behavior. The question that remains is – why was the decompression rate so high? A combination of decompression experiments to quantitatively assess decompression rates, rheology experiments to constrain the physical parameters of the magma as it crystallized, fragmentation experiments on Curacautín pyroclasts, and conduit modelling to explore different geometries may yield more insight into this fundamental question.