Abstract
Spatial variations in the thickness and grain-size characteristics of tephra fall deposits imply that tephra depositional processes cannot be fully captured by models of single-particle sedimentation from the base of the eruption plume. Here, we document a secondary thickness maximum in a ∼9.75 ka tephra fall deposit from Chaitén volcano, Chile (Cha1 eruption). This secondary thickness maximum is notably coarser-grained than documented historical examples, being dominated by medium-grained ash, and an origin via particle aggregation is therefore unlikely. In the region of secondary thickening, we propose that high levels of atmospheric turbulence accelerated particles held within the mid- to lower-troposphere (0 to ∼6 km) towards the ground surface. We suggest that this enhancement in vertical atmospheric mixing was driven by the breaking of lee waves, generated by winds passing over elevated topography beneath the eruption plume. Lower atmospheric circulation patterns may exert a significant control on the dispersal and deposition of tephra from eruption plumes across all spatial scales, particularly in areas of complex topography.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The grain-size and thickness characteristics of tephra fall deposits reflect a range of processes that influence particle settling from explosive eruption plumes. Particle transport distance is primarily related to particle size (and hence settling rate; cf. Pyle 1989; Bonadonna et al. 1998), the height of particle injection into the atmosphere, and the atmospheric wind field (Walker 1973; Suzuki 1983; Carey and Sparks 1986). Thus, idealised settling relationships predict that deposits become thinner and finer-grained with increasing distance from source. However, many tephra fall deposits deviate from this simple thinning relationship (e.g. Scasso et al. 1994; Durant et al. 2009), providing evidence of spatial variability in the rate at which particular particle size-fractions are deposited from an eruption plume.
Many mathematical models of tephra dispersal do not fully account for processes that modify single-particle settling laws (cf. Folch et al. 2010). Such models, developed from theories of eruptive column behaviour and atmospheric particle dispersal (e.g. Suzuki 1983; Woods 1988; Bonadonna et al. 1998), are widely used to predict patterns of tephra deposition or to estimate eruption parameters from deposit measurements (e.g. Armienti et al. 1988; Connor et al. 2001; Costa et al. 2006). To improve the predictive capability of tephra dispersal models, it is important to capture the full spectrum of processes that characterise tephra sedimentation.
Aggregation, which produces particle clusters with higher fall velocities than individual grains, is one process that can enhance the settling rate of sub-millimetre scale tephra (Brown et al. 2012). Aggregation has been widely used to explain the regions of tephra fall deposits that depart from an attenuation of thickness and grain-size with distance from source (Sorem 1982; Textor et al. 2006; Durant et al. 2009), even when aggregated clasts have not been directly observed in the deposits (cf. Carazzo and Jellinek 2013). Convective instabilities, developed within the plume, may provide an alternative process for accelerating the deposition of finer-grained particles and have recently been used to explain the depositional patterns of fine-grained ash in some historical eruption deposits (Carazzo and Jellinek 2013; Durant 2015).
An extensive and rapid onset of aggregation enhances tephra deposition and may produce a region of downwind thickening in a tephra fall deposit, commonly referred to as a secondary or distal thickness maximum. If aggregation is generally more pervasive across a deposit, or if other processes such as convective instabilities enhance fine-particle deposition, then the result may not be a well-developed secondary thickness maximum but a stretching or distortion of the isopachs, altering the rate at which the deposit thins with distance (whether this rate is described by multi-segment exponential, power-law or Weibull thickness decay patterns; cf. Pyle 1989; Bonadonna et al. 1998; Bonadonna and Phillips 2003; Bonadonna and Costa 2012). The grain-size distribution of any bulk sample from a fall deposit affected by aggregation is expected to be a composite of multiple grain-size populations (spanning multiple phi intervals, and potentially forming multimodal distributions in relatively proximal deposits) and enriched in fine grains (i.e. reflecting both the single-particle settling population and the poorly sorted aggregate population; Durant and Rose 2009; Durant et al. 2009). In contrast, single-particle settling alone generally produces relatively narrow unimodal grain-size distributions, although some complexities may originate from variable particle densities.
Here, we show that lower atmospheric circulation patterns may produce complex grain-size and thickness relationships within tephra fall deposits, implying that deposits displaying such characteristics have not necessarily been affected by aggregation (cf. Carazzo and Jellinek 2013). We document an anomalously thick and poorly sorted region of the Cha1 fall deposit, from Chaitén volcano, Chile (42.83°S, 72.65°W) (Fig. 1). This region of the Cha1 deposit is much closer to source, and relatively coarser-grained, than the thickened regions of historical deposits inferred to have formed via aggregation (e.g. Durant et al. 2009). We first describe the deposit characteristics in the region of anomalous thickening and then discuss processes for its origin. We propose a model whereby atmospheric turbulence associated with complex topography, rather than particle aggregation, may have locally enhanced tephra deposition.
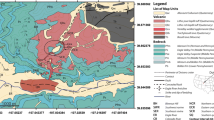
Isopach map of the northward-distributed lobe of the Cha1 fall deposit, shown on SRTM2.1 topography (https://lta.cr.usgs.gov/SRTM2). The 20 cm isopach shows a secondary thickness maximum, apparent as a sharp increase in deposit thickness downwind of Yate volcano, consistently present across multiple field sites. Grain-size sampling sites A to F are labelled; other field sites are shown as black dots (see Electronic supplementary material data for full site details)
The Cha1 fall deposit
The Cha1 eruption occurred at ∼9.75 ka (Watt et al. 2011) and produced ∼5.5 km3 of aphyric rhyolitic pumice. The eruption deposited an elongate lobe of tephra to the north of Chaitén (Naranjo and Stern 2004; Watt et al. 2011; comprising ∼3.5 km3), with additional deposition to the east from poorly mapped explosive phases (Amigo et al. 2013; Fontijn et al. 2014). Overall, the exposure of the deposit is relatively sparse, but it has been identified in several road cuttings 15–30 km north of Chaitén and in the Hualaihue region, 90–160 km north of Chaitén (Watt et al. 2011). In the Hualaihue region, an absence of the deposit in road cuttings to the east and west suggests a relatively narrow deposit width and a northerly axis of deposition (Fig. 1). This is consistent with proximal exposures (Naranjo and Stern 2004) and is supported by the identification of the Cha1 deposit in lakes around Villarrica, approximately 400 km north of Chaitén (K. Fontijn, personal communication 2013). Taken together, these observations suggest that plume transport approximately followed the continental coastline, on a bearing of 010°. Fortuitously, this zone of deposition overlaps with the regional road network and means that the Cha1 deposit has been mapped over a much larger area than other pre-historic tephra deposits in southern Chile (Naranjo and Stern 2004; Watt et al. 2011). Correlation of the deposit across 28 sites has been based on bulk- and glass-chemical compositions, deposit appearance, stratigraphic position, sedimentological characteristics, and radiocarbon dates (cf. Watt et al. 2011 and Electronic supplementary material data).
Mapping of the Cha1 deposit in the Hualaihue region reveals an increase in deposit thickness away from source, in an along-axis direction, thus forming a secondary thickness maximum. The thickening occurs immediately north of Yate volcano (41.76°S, 72.40°W), a substantial edifice with a peak elevation of 2,187 m located 120 km from Chaitén (Fig. 1). The deposit has a thickness of 16 cm 36 km south of Yate and a thickness of 15–18 cm 15 km north of Yate. It is this thickening pattern that we seek to explain in this paper.
The Cha1 deposit is unusually well exposed in the Hualaihue region, where deposit thickness has been mapped across 16 measurement sites at a mean spacing of <5 km. This spacing compares favourably with the sampling density of well-mapped historical deposits (Scasso et al. 1994; Watt et al. 2009). For example, the Mount St. Helens 1980 secondary maximum is mapped at a site spacing of ∼30 km across the plume axis and 60–120 km in a downwind direction, meaning that mapping of the secondary maximum is based on ∼10 sites (Durant et al. 2009). The systematic nature of the Cha1 deposit thickness and grain-size patterns in the Hualaihue region suggests a primary depositional origin and strengthen the identification of the secondary thickness maximum. Our dataset also suggests that a denser site spacing than is often attainable may be required to reveal complexities within tephra fall deposits.
The exposure of Cha1 is sparse over other parts of the deposit. In particular, a lack of across-axis measurements means that isopach and isopleth shapes are difficult to constrain, inhibiting assessment of wind speed and plume height. Some inferences can be made from the absence of deposit identification in road cuts where it might otherwise be expected, but this is a relatively weak criterion. Although the poor constraints on eruption parameters limit the precision with which we can simulate the event, there are still sufficient data to investigate the origin of the anomalous depositional patterns in the Hualaihue region.
The Cha1 tephra deposit volume of 5.5 km3 (Amigo et al. 2013) was derived from multiple isopachs modified from Watt et al. (2011; two of which are shown in Fig. 1). These isopachs assume a simple symmetrical shape, in the absence of any data to justify further complexities. The increase in isopach width around the secondary thickness maximum is an attempt to fit the variable thickness data, but the precise isopach shape in this region is poorly defined. A simple isopach shape for the Cha1 deposit is supported by the nature of the proximal deposit, which comprises a single unit of well-sorted rhyolitic pumice, with slight reverse grading at the base, suggesting that the eruption (or at least the stage that generated the lobe shown in Fig. 1) involved a single sustained Plinian explosive phase. This relative simplicity contrasts, for example, with the multiple overlapping units that form the 2008 Chaitén eruption deposit (Watt et al. 2009; Alfano et al. 2011), where deposition from multiple eruptive phases at a single site obscures depositional complexities arising from other processes. The latter event was far smaller than Cha1; for comparison, at a distance of 135 km, the thickest part of the 2008 deposit comprises 1 cm of medium-grained ash, compared with 15–18 cm of fine lapilli on the dispersal axis of the Cha1 deposit. The northward distribution of the Cha1 deposit makes it an ideal case to investigate spatial variability in particle deposition. Southerly winds are relatively uncommon in this region, tending to occur as brief (<48 h) episodes in the Austral winter (H. Moreno, pers. comm. 2015; such a wind direction marked the initial stage of the Hudson 1991 eruption (Naranjo 1991)). The northward transport of the plume is likely to have meant that deposition was not complicated by additional phases of the Cha1 eruption (as suggested by the simple deposit characteristics), which followed prevailing wind directions towards the east (Amigo et al. 2013).
In common with the isopachs, the Cha1 isopleth width drawn in Watt et al. (2011) is poorly constrained but may be used to estimate column height using the nomograms of Carey and Sparks (1986). The elongate deposit shape suggests a strong wind-field, and based on the 10 and 50 mm deposit isopleths, Figure 16 of Carey and Sparks (1986) suggests a plume top elevation of 25–30 km and a wind speed of 17–20 m s−1 (this compares to a plume top estimate of 25–36 km under no-wind conditions and 25–32 km in a 30 m s−1 cross-wind, derived from separate plots). A more robust estimate can be made using our maximum clast-size data and the predictive model of Burden et al. (2011), which does not require any interpretation of isopleths but provides a direct statistical fit to the available data. Uncertainties remain large within the Burden et al. (2011) approach, due to a low number of data points, but the best estimate produced by this statistical fit, of 26–29 km in a wind of 18–23 m s−1, is in good agreement with the Carey and Sparks (1986) nomograms.
Grain-size distributions
The grain-size distributions of six samples from Cha1, in a 56-km axial transect spanning the secondary thickness maximum, have been measured by sieving at 0.5 phi intervals from −2 to 4 phi (Fig. 2). Samples are pure rhyolitic pumice or glass shards; the juvenile material is aphyric and lithics are absent. Large pumice clasts are highly vesicular with a density of 480 ± 70 kg m−3 (based on water immersion estimates from twelve ∼5-cm diameter clasts collected 20 km from source). Higher densities are likely for finer grain sizes, especially at size fractions where glass shards, rather than vesicular grains, dominate (cf. Eychenne and Le Pennec 2012).
a Cumulative grain-size distributions for samples A to F. The relative shapes of A to C and D to F are similar, defining two groups. b Comparison of the mean cumulative grain-size distributions for A–C and D–F, overlapped at the median. The coarse limbs of the two grain-size distributions match closely, but the increased proportion of relatively fine-grained particles is clear for sites D–F. c Spline curves (Fig. 3) fitted to each grain-size distribution
The modal grain-size (i.e. the peak of the overall grain-size distribution) for sites A to C is ∼2.7 phi and ∼2.9 phi for D to F. This decrease is consistent with an expected reduction in mean particle size with distance from source. However, there is a clear difference in the shape of the grain-size distributions for samples A to C, which lie upwind of the secondary maximum, relative to sites D to F, which lie within the region of secondary thickening. The grain-size distributions of A to C have a very steep fine grain-size limb (Fig. 2 inset), in contrast to the more gentle fine grain-size limb and greater spread of D to F. The two distinct sets of cumulative distribution curves (Fig. 2) confirm this pattern.
All the grain-size distributions have a tail of fine-grained material (for example, from 1.5 to 5 phi in A to C; Fig. 2). For A to C, this material accounts for a very small proportion of the total deposit and may reflect small amounts of fine-grained ash accreted on the surface of larger grains (i.e. a form of aggregation, perhaps associated with moisture within the plume). In samples D to F, the 1.5–4 phi interval accounts for a much larger proportion of the total deposit (again, there is a minor tail of very fine material, from 4 to 5 phi). The increased proportion of medium- to fine-grained ash (1.5–4 phi) deposition coincides with the position of the Cha1 secondary thickness maximum and occurs consistently within all our samples. This spatial consistency argues against the formation of these complex grain-size distributions via post-depositional remobilisation or winnowing.
Grain-size sub-populations
To explore changes in tephra deposition around the secondary thickness maximum, we have deconvolved the grain-size data into a series of log-normal distributions (cf. Durant et al. 2009). We used the SFT software (Wohletz et al. 1989) to fit a spline curve to the sieved mass-intervals and then fitted log-normal distributions, aiming to achieve a fit to the data with a residual of <10 % (Fig. 3). This approach is partially subjective but allows us to understand the visual differences between the two groups of grain-size curves. Given the more simple shape of curves A to C, we fitted log-normal distributions to these first. They can all be very well described by two log-normal sub-populations. We did not attempt to fit the minor, fine-grained tail, and there is thus a residual to our fitted log-normal sub-populations of slightly over 10 %. The modal values and standard deviations of the sub-populations are similar across A to C, with very little change in the overall deposit grain-size characteristics. There are no clear visual differences in grain type that can be used to define the two sub-populations. The presence of multiple log-normal grain-size populations, even in apparently simple fall deposits, has been observed previously (Durant et al. 2009).
Grain-size distributions of the Cha1 deposit at sites a to f, based on sieved mass fractions and shown as grey bars. Fitted spline curves are shown in black, and divided into constituent log-normal sub-populations (coloured lines) with the residual to the fit shown in red. a to c are well described by two log-normal sub-populations; d to f require the fitting of two additional finer-grained sub-populations. Details of the fitted sub-populations are provided as an Electronic supplementary material table
Given the consistent presence of two sub-populations in A to C, we assume that similar sub-populations, albeit with a finer modal grain-size, are present in the grain-size distribution of D to F. Thus, we start by fitting the coarse tail of D to F with sub-population 1, aiming to keep a similar standard deviation to that in A to C, and then continue by fitting sub-population 2. This leaves a large proportion of fine-grained material unaccounted for, but we find that this can be well fitted by two further log-normal sub-populations. The first (sub-population 3) has a similar standard deviation to sub-populations 1 and 2, and a constant mode of 1.5 phi across sites D to F. The second is broader and has a mode that reduces in grain-size from 2.5 to 3 phi downwind, from samples D to F.
We suggest that sub-populations 3 and 4 represent particles that settled more rapidly than expected from the eruption plume, thus producing a secondary thickness maximum in the Cha1 deposit north of Yate. To test this inference, we plot the variation in deposit thickness with distance for all Cha1 measurement sites (Fig. 4). Thickness decay rates in proximal to medial portions of pyroclastic fall deposits (i.e. those dominated by deposition of particles with a Reynolds number >500 (fine lapilli to coarse ash); Bonadonna et al. 1998; Bonadonna and Phillips 2003) are close to exponential, even when wind-advected (Pyle 1989; Sparks et al. 1992, 1997; departures from a single exponential trend occur in the most proximal and in more distal regions (Bonadonna et al. 1998)). Given the axial trend of our measurement sites, thickness measurements should therefore define a straight line on a log (thickness) versus distance plot. This is indeed the case for all samples upwind of Yate (discounting the more rapid increase in thickness for the most proximal sites, which is expected; cf. Bonadonna et al. 1998). However, deposit thickness increases abruptly downwind of Yate, to define a separate exponentially decreasing trend (Fig. 4). In this part of the deposit, for sites D to F, we can calculate the proportional thickness accounted for by sub-populations 1 and 2 (these sub-populations account for 51–59 wt% of the total grain-size population at these sites). These recalculated thickness values (i.e. 51–59 % of the measured thicknesses) lie very close to the exponential trend defined by sites upwind of Yate (Fig. 4). Thus, there is good evidence that the increase in tephra deposition downwind of Yate is entirely accounted for by the deposition of sub-populations 3 and 4. Again, the consistent proportions of different grain-size populations across multiple sites, and their correlation with expected thinning relationships, suggest that the observed patterns reflect primary depositional processes rather than post-depositional reworking of the Cha1 deposit.
Deposit thickness against distance from Chaitén volcano for all Cha1 measurement sites. Data are well-described by exponential thinning, but with a sharp increase in deposit thickness at Yate. Sub-populations 1 and 2 follow the trend of data upwind of Yate; the increase in thickness north of Yate is accounted for by deposition of sub-populations 3 and 4. The grey elevation profile at the base of the graph marks the topography along the plume axis, indicated by the arrow in Fig. 1
Causes of enhanced ash deposition
Our results indicate that the Cha1 secondary thickness maximum is due to the relatively early fallout of grains in the 1 to 4 phi size range (sub-populations 3 and 4; Fig. 5). The deposition of these grain-sizes has a sharp onset and occurs immediately north of Yate volcano. We examine three potential explanations for the enhanced deposition of these grain-size fractions. The first possibility is that aggregation processes resulted in enhanced settling rates and produced a secondary maximum of the same type observed in other deposits from large explosive eruptions (e.g. Durant et al. 2009). In this instance, the spatial association of the secondary maximum with the elevated topography at Yate volcano would be coincidental. Alternative possibilities are that the topography at Yate played a role in enhancing the deposition of grain-sizes within sub-populations 3 and 4. This enhancement may have been via rapid wet aggregation driven by orographic precipitation, or by the breaking of topographically induced gravity waves that accelerated particles towards the ground in this region. In addition, at the finer end of the 1 to 4 phi size range, it has been proposed that within-cloud convective instabilities may enhance particle deposition (Carazzo and Jellinek 2013). However, this latter process is not well tested, would not be expected to produce a sharp change in deposit thickness and grain-size distribution, as observed for the Cha1 deposit, and would not be expected to strongly influence the deposition of the medium-grained ash particles that characterise sub-population 3 (Durant 2015).
“Normal” aggregation: comparison with other secondary thickness maxima
Well-developed secondary thickness maxima occurred in the tephra fall deposits of Hudson, Chile, in 1991 (Scasso et al. 1994), and Mount St. Helens, U.S.A., in 1980 (Durant et al. 2009), which were both of comparable magnitude to the Cha1 eruption. In these and other instances (e.g. Durant and Rose 2009), the formation of secondary maxima has been attributed to aggregation processes, whereby grains form clusters with a larger overall size and a higher settling velocity. For eruption columns that reach the upper troposphere or stratosphere, observations and models suggest that large proportions of particles <125 μm (3 phi) in diameter are deposited as aggregates (Carey and Sigurdsson 1982; Bonadonna and Phillips 2003).
Several recent studies have investigated aggregation (e.g. James et al. 2003; Textor et al. 2006; Durant et al. 2009), but our understanding of when aggregates develop within a plume remains limited. The wide range of volcanic aggregate morphologies (Brown et al. 2012) suggests that a variety of processes may lead to their formation. In general, the availability of liquid appears to allow efficient and extensive aggregation (Woods 1993; Gilbert and Lane 1994; Textor et al. 2006; Durant et al. 2009), although dry aggregation may be highly significant in driving the fallout of particles <70 μm (∼4 phi) in diameter (James et al. 2003). The water content of eruption plumes is not simply determined at source, but may vary during transit due to lower atmospheric mixing and circulation processes. In addition, phase changes of water as plume elevation decreases can significantly affect aggregate formation and fallout (e.g. Durant et al. 2009). Thus, the extent and timing of aggregation may vary as an eruption plume is transported within the atmosphere.
In contrast to other known examples, the Cha1 secondary maximum occurs relatively proximally (and is correspondingly thick, in absolute terms) and via the enhanced deposition of medium- to coarse-grained ash (modal grain-size of 1.5 phi), as opposed to very fine-grained ash (modal grain-size of ∼5 phi). This is well illustrated by comparison with well-documented historical examples (Table 1): The secondary maxima at Hudson and Mount St. Helens occurred at ∼450 km and ∼325 km, respectively, and involved gradual downwind thickening towards the secondary maxima, over a distance of >150 km. In contrast, the Cha1 secondary maximum occurs at a distance of 120 km and involves thickening over a distance of ≤10 km (based on the distance between sampling points that lie on discrete exponential thinning trends; Fig. 4). Although these contrasts in distance could partially result from differences in column height and wind-field, the distinction between the Cha1 secondary maximum and other documented examples is clear from their grain-size distributions. Grain-size distributions from the Hudson and Mount St. Helens secondary maxima are distinctly bimodal, because the aggregating population is much finer-grained than the population deposited by single-particle sedimentation (the modes are separated by several phi intervals, compared with ∼1 phi interval for Cha1). For the eruptions in Table 1, there are rough correlations between the thickness of the secondary maxima and the eruption volumes, and also the distance to the secondary maxima and the eruption column heights. However, the Cha1 secondary maximum is relatively more proximal, involves much coarser grain-sizes and forms a thicker deposit than historical examples, suggesting that it did not form via the same process. We thus consider alternative mechanisms, focusing on the spatial association of the secondary maximum with the elevated topography at Yate volcano.
Topographic influences on ash deposition
The tephra grains that form fall deposits are transported as suspended particles in a gravitationally spreading and wind-advected volcanic plume (Bursik et al. 1992; Sparks et al. 1997), before undergoing sedimentation from the base of the plume. From this point, the time to deposition is determined by particle size, shape and density, and by atmospheric density (Bonadonna et al. 1998). Advection due to atmospheric motions continues during downward transport, controlling the particle transport distance (Bursik et al. 1992; Bonadonna and Phillips 2003). In a laterally invariant wind-field, advection leads to a simple relationship between grain-size and transport distance, with the coarsest grains depositing first. Similarly, above any single ground position, a vertical stratification in grain-size is present in the atmosphere, with the highest fall-velocity particles (i.e. with higher densities or grain sizes) closest to the surface (Fig. 6). However, variable atmospheric circulation in both vertical and horizontal dimensions may affect the rate of particle deposition.
Orographic precipitation and liquid-pellet formation
The typical particle diameter within most types of ash aggregate is ∼30 μm (Brown et al. 2012), which corresponds well with grain sizes across all documented examples of secondary thickness maxima (Table 1). For the coarser-grained Cha1 secondary maximum, deposition via liquid pellets (the AP3 aggregate type in Brown et al. 2012) is a possible aggregation mechanism. In liquid pellets, grain-sizes up to 1 mm in diameter are transported within rain droplets. Liquid pellets are poorly documented, since the water disperses on deposition and leaves little evidence in terms of deposit structures. Although descriptions of liquid-pellet deposition refer to condensation-driven precipitation within the plume (Woods 1993; Gilbert and Lane 1994), a similar process may also take place if settling particles interact with lower altitude weather systems. Direct observations of rain-enhanced tephra deposition have been observed in both proximal (Lane et al. 1995) and distal (Stevenson et al. 2013) settings, and rainfall-enhanced tephra deposition has been proposed for the origin of some poorly sorted ash-rich deposits with variable thickness (Talbot et al. 1994).
Decreases in temperature (adiabatic cooling) induced as air rises over topography can cause condensation and precipitation, referred to as orographic rainfall. Particle sizes that lay within the atmospheric height-range affected by this condensation and precipitation would thus be rapidly deposited at the surface, while finer-grained particles, higher in the atmosphere, would be advected further downwind. However, although the topography of Yate is the most significant along the axis of the northward directed plume, it remains a relatively small topographic barrier, and it is unlikely that orographic rainfall would be so localised. Additionally, orography is expected to drive rainfall on the windward side of a topographic barrier, but we only observe enhanced tephra fallout on the leeward side of Yate. Thus, although rainfall-enhanced tephra deposition is a plausible process, the spatial pattern of the Cha1 secondary maximum does not support enhanced deposition via orographic rainfall. An alternative driver of liquid-pellet formation may have been the interaction of the eruption plume with a wet-weather (i.e. storm) system north of Yate. The location of the secondary maximum would be coincidental in such a case.
Accelerated deposition via breaking lee waves
There is no direct evidence of wet aggregation in the Cha1 deposit (i.e. splash marks, clustered grains), although such textures may not be preserved. An alternative explanation for the early, en-masse deposition of medium-ash size fractions, without the need for either water or aggregation, is provided by the formation and subsequent breaking of lee waves (also referred to as mountain waves, a type of atmospheric gravity wave) (Smith 1979; Wurtele et al. 1996). Lee waves form when stably stratified air is forced up over topographic obstacles, resulting in oscillations downwind of the obstacle. Their magnitude, wavelength and horizontal extent is influenced by the height and lateral extent of the underlying topographic feature and is also a function of the vertical variation in wind-speed and air temperature in the lower troposphere at a height of a few kilometres, where the breaking of lee waves is initiated. Lee-wave breaking is often associated with downslope windstorms and hydraulic jumps on the lee side of the topographic obstacle (Wurtele et al. 1996; Jiang and Doyle 2004). It results in extreme air turbulence and significant enhancement of vertical atmospheric mixing, and could therefore drive rapid downward acceleration and deposition of particles. Under certain conditions, the instabilities initiated by the breaking of lee waves can propagate upwards, even entering the stratosphere (Smith et al. 2008).
The effects of lee waves have been extensively reported through observations (Jiang and Doyle 2004; Doyle et al. 2005; Smith et al. 2007; Lane et al. 2009; Jiang et al. 2010). Some early theoretical studies (Long 1953; Miles and Huppert 1968) elucidated the nonlinear mechanisms for an early stage of the wave breaking processes. Understanding of these mechanisms has been significantly enriched through numerical experiments (Laprise and Peltier 1989; Lin and Wang 1996; Jiang et al. 2004; McHugh and Sharman 2013). For a highly simplified case of uniform stratification and wind profile, a Mountain Froude number (cf. Smolarkiewicz and Rotunno 1988), Fr = U/(Nh), where N is the Brunt-Väisälä frequency (the natural oscillation frequency of the stable air), h is the mountain height, and U is the wind speed, is known to be a crucial parameter for the condition of wave breaking. Lee-wave breaking occurs when Fr is about equal to or smaller than unity (e.g. Lin and Wang 1996). The condition of Fr ∼ 1 is not an unusual one; for example, if we take a climatological lapse rate of 0.006 K m−1 for the troposphere (NOAA 1976; Wallace and Hobbs 2006), which gives N ≈ 0.0117 s−1, a wind speed of U = 12 m s−1, and a mountain with h = 1,000 m, the Mountain Froude number is Fr ≈ 1.02.
Mountains do not need to be particularly prominent to initiate lee-wave breaking (e.g. 550 m in Laprise and Peltier 1989). The horizontal extent of the wave-breaking region may extend from the peak of the mountain to several tens of kilometres downwind. For relatively unstable lee waves, a wavelength of 6–10 km is typical. The parameters of lee-wave breakdown therefore agree well with the region of enhanced particle deposition on the downwind side of Yate. In a vertical direction, wave breaking may extend to two to three times the obstacle height above ground level, which equates to ∼6 km for Yate (Fig. 6). Enhanced deposition within the wave-breaking region can be explained by resonant amplification theory (Clark and Peltier 1984; Scinocca and Peltier 1993). This theory is built upon the hypothesis that an elevated wave-breaking layer (with high Richardson number) reflects upward propagating gravity waves back towards the ground and that resonance of the reflected waves with the upward propagating waves can lead to extreme mixing in the region between the ground and the upper wave-breaking layer. In the scenario of the Cha1 plume, enhanced vertical mixing associated with this process would causing rapid downward transport of tephra particles (and subsequent deposition) within the tropospheric height range of 0 to ∼6 km, in the region downwind of Yate (Fig. 6). Enhanced mixing may also have been promoted by wind funnelling and the generation of high boundary-layer turbulence along the Reloncaví fjord (Fig. 1), which is bounded to the east and west by mountains reaching 2,000 m.
The process outlined above promotes particle deposition via enhanced tropospheric vertical mixing and does not require the presence of moisture and associated particle aggregation. However, if moist air was present then it would simply facilitate deposition, because condensation within the region of lee-wave breaking would promote particle clustering. Although air on the lee side of mountains is generally dry, moist air may have entered the system in this particular scenario from the west, along the Reloncaví fjord. In general, however, we suggest that lee-wave processes can enhance tephra deposition in dry conditions, without the need for wet aggregation.
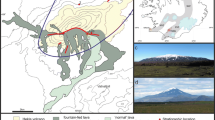
In order to test whether the topography around Yate could generate lee waves with dimensions that are compatible with our hypothesis, we have performed numerical simulations using the ALYA code, following a method developed by Avila et al. (2013). We do not aim to replicate atmospheric conditions during the Cha1 eruption or to simulate tephra transport but to simply obtain an insight of how the topography around Yate influences lower atmospheric movements under plausible meteorological conditions. Our model uses a computational fluid dynamics code that has been adapted to atmospheric flows for wind energy applications. The model solves the turbulent Reynolds Averaged Navier-Stokes equations, including Coriolis effects, a limitation of the mixing length and a modification of the standard κ-ε turbulence model to adapt it to atmospheric boundary-layer flows. The model requires wind and potential temperature profiles as boundary and initial conditions, which can either be provided by mesoscale meteorological models or extracted from ideal profiles (i.e. one-dimensional solutions of the equations for a flat terrain and constant roughness). For the Chaitén case, contemporaneous atmospheric conditions are unconstrained, so we derive boundary conditions from ideal stable atmospheric profiles. The computational domain lies between 100 and 140 km from Chaitén along the plume axis and includes topographic relief at a resolution of 100 m. Wind and potential temperature profiles are fixed at inflow and were used to investigate conditions of lee wave formation downwind of Yate. The example in Fig. 7 has a fixed inflow wind speed of 17.5 m s−1 at 6.5 km elevation and is calculated with a lapse rate of 0.0018 K m−1 and surface temperature of 300 K. Numerical results show lee-wave formation and downward acceleration ∼10 km downwind of Yate, with downward velocities (which are substantially higher than particle terminal fall velocities) extending to heights of ∼6 km (Fig. 7). These results are fully compatible with our hypothesis. The breaking of the modelled lee waves would lead to the enhanced deposition of particles held within this tropospheric height range.
Numerical model results across a NS transect passing over Yate volcano (shown with no vertical exaggeration). Topography has not been considered north of the Reloncaví fjord in order to provide a flat outflow condition. a Vertical wind velocity contours show alternate positive (upwards) and negative (downwards) values with a strong downward movement north of Yate. b Potential temperature contours. c Wind velocity contours. Note the acceleration zone downwind of Yate
Enhanced particle deposition in the region immediately north of Yate may have led to a relative reduction in deposition further along the axis if the atmosphere returned to more stably stratified conditions. We cannot test this idea, due to a lack of deposit exposure beyond the northern end of the Reloncaví fjord. Along the fjord itself, the thickness and grain-size properties of the Cha1 deposit follow a consistent pattern and suggest that the region influenced by lee wave breaking extended for at least 40 km beyond Yate.
Atmospheric height range of enhanced grain deposition
To further test whether the lee-wave breaking in the mid to lower troposphere could lead to the enhanced deposition of particle sizes in the Cha1 sub-populations 3 and 4 (Fig. 5), we estimate the atmospheric height range at which these particles would have resided in the region of Yate. The process that generated the secondary maximum did not promote the fallout of particles finer than ∼80 μm and thus presumably operated across a limited height range. From our explanation above, we expect the depositing particles to lie within the lower ∼6 km of the atmosphere.
The transport distance of individual particles from the Cha1 plume is dependent on the initial column height and wind field. The top of the eruption column (H t ) reaches significantly higher than the neutral buoyancy height (H b ) (Carey and Sparks 1986). H b defines the height of lateral particle transport, and the height at which particles fall from the base of the spreading plume (H cb ) can be approximated as 0.6H t (Bonadonna and Phillips 2003). Based on the estimates in “The Cha1 fall deposit” Section (26–29 km plume top height), we use a basal plume height (H cb ) of 16 km. A simple estimate of particle transport distance can be made from the terminal fall velocity of spherical particles (cf. Brown and Lawler 2003; Durant et al. 2009) in a standard atmosphere (NOAA 1976). Many relevant parameters are poorly constrained, but an approximate calibration of our estimates can be obtained from the modal grain-size upwind of Yate, where we assume deposition occurred via single-particle sedimentation. The estimate of transport distance is most sensitive to particle density and the vertical variation in the wind speed; because particles fall relatively rapidly at higher atmospheric levels (due to lower viscosity and density values), the estimates are less sensitive to the basal height of the plume. Using the above approach in a constant wind-field of 20 m s−1 and release from the base of the plume (16 km), particles with a diameter of 700 μm (the approximate modal grain-size at sites A to C) and densities of 500–1,000 kg m−3 reach sea level at 75–120 km from source. This neglects advection before particles fall out from the base of the plume but provides a rough estimate that is in good agreement with the observed peak depositional region of this particle size (100 km from source). For the same conditions, particles in sub-populations 3 and 4 (modal grain-sizes of 350 and 150 μm, respectively) reside at atmospheric elevations of 2–6 km and 9–11 km, respectively, at the distance corresponding to Yate.
The above estimates suggest that the major proportion of particles that account for the Cha1 secondary thickness maximum (sub-population 3) lay within the region of lee-wave generation (up to ∼6 km) in the vicinity of Yate (Fig. 6). It is thus plausible that rapid vertical mixing and downward acceleration, associated with lee-wave breaking, caused the early deposition of these particles and generated the Cha1 secondary thickness maximum. However, the origin of sub-population 4 is less clear. The estimates made above are relatively crude, and many parameters are unconstrained. It is possible that this population represents denser clasts, which would have resided at lower atmospheric levels than estimated above, and may therefore have lain within the same region as sub-population 3. Alternatively, if the above elevation estimates are correct, then a process is required that enhanced downward particle transport across a broader height range, reaching ∼10 km. Possibilities include the interaction of the ash cloud with a storm system or the propagation of lee waves to higher elevations. However, given their co-deposition, the simplest explanation is that sub-populations 3 and 4 lay within the same atmospheric height range.
Implications and further discussion
There are few examples of secondary maxima in pre-historic tephra deposits, and even for historical events, only a few deposits have been mapped in sufficient spatial detail to reveal depositional complexities. Recognition of anomalous thickening patterns is most likely in deposits from large eruptions dispersed over land (e.g. Stern 2008) that are well exposed and sampled on spatial scales of a few kilometres or less. Even in such instances, depositional complexities arising from atmospheric processes (whether it be turbulence, aggregation or within-cloud convective instabilities) may still obscured by the overlap of deposits from multiple eruptive phases (i.e. as in the Chaitén 2008 eruption; Watt et al. 2009) or by post-depositional compaction and erosion. Generally, only deposition in continental regions allows fall deposits to be measured in detail, which explains why most of the examples in Table 1 are from the Americas, where prevailing winds commonly lead to eastward tephra dispersal. Even for historical eruptions, very few tephra deposits have been mapped in sufficient detail to reveal depositional complexities, despite the fact that such complexities hold important clues to atmospheric controls on tephra dispersal, as well as information about atmospheric processes at the time of deposition. Logistical challenges can inhibit such mapping; for example, although the distal portion of the Chaiten 2008 deposit, in Argentina, is very well mapped, the more proximal region of deposition in the Andes, where the complex topography may have influenced deposition, is virtually unmapped due to limited accessibility (Watt et al. 2009; Alfano et al. 2011). For smaller explosive eruptions, rapid post-eruption sampling is required to produce comprehensive tephra depositional datasets. Such studies have the potential to reveal significant spatial complexities in deposition, indicating departures from statistically simple thinning relationships and potential evidence for processes that modify sediment settling rates (e.g. Ruapehu, New Zealand 1996; Bonadonna et al. 2005).
The Cha1 secondary maximum is observable because it occurs relatively proximally, in a correspondingly thick deposit and because the regional road network fortuitously overlaps with the deposit axis, which allowed detailed sampling from fresh road cuttings. However, a significant role of lower atmospheric turbulence on tephra deposition, as implied by the Cha1 deposit, may be more widespread. Even if a secondary maximum is not well developed, a stretching or distortion of isopachs may arise from localised spatial variability in the rate of ash fallout and is not necessarily the result of source complexities in eruption intensity (i.e. multiple eruptive phases). Volcanic eruptions often occur in regions of complex, mountainous topography, and it is plausible that local atmospheric turbulence can strongly impact ash fall, even for small explosive eruption plumes. Complex isopach shapes are commonly observed in well-mapped deposits. For example, recent deposits from Unzen (Watanabe et al. 1999) and Tungurahua (Bernard et al. 2013) show anomalous thickening around coastlines or mountain bodies that may reflect an influence of air movement over topography on particle deposition. Similarly, distortions of isopachs from the Huaynaputina (1600; Adams et al. 2001) eruption roughly follow the downwind edges of local mountain ranges.
More generally, changes in air temperature and pressure (and associated weather systems) occurring at transitions between land and sea (e.g. Anthes 1978; Steele et al. 2013) could potentially influence tephra deposition. The Cha1 secondary maximum, as well as coinciding with Yate, lies at the point where the plume moves from sea to land. Secondary maxima in the Hekla (Iceland,1970; Thorarinsson and Sigvaldason 1972) and Hudson (1991; Scasso et al. 1994) deposits lie close to coastlines and may have been influenced by interfaces between air masses in these regions.
It is notable that the different portions of the Cha1 deposit (i.e. the portion deposited by normal single-particle sedimentation and the portion experiencing accelerated deposition) are each described by two sub-populations, rather than one. Although log-normal distributions are not necessarily the most appropriate description of a population of fragmented grains (Wohletz et al. 1989), it is clear from the variable asymmetry of the Cha1 grain-size distributions that a single statistical distribution cannot describe every sample. Thus, the occurrence of distinct grain-size populations, even at sites upwind of Yate, appears to be real. This is consistent with observations from other historical eruptions (e.g. Durant and Rose 2009; Durant et al. 2009) and suggests that multiple sub-populations can exist in a deposit without the need for aggregation. Possible explanations for this include distinct populations based on variation in grain type (e.g. pumice, crystals; Bursik et al. 1992; Durant et al. 2009), or vesicularity (i.e. density; Carey and Sigurdsson 1987), discrete eruption phases with overlapping deposition (Watt et al. 2009), and convective instabilities and associated plume stratification derived from the eruption column (Carazzo and Jellinek 2013; Durant 2015). Furthermore, different grain-size populations could be preferentially scavenged during aggregation, depending on the process. For example, in liquid pellets, one population may represent the maximum diameter than can be carried within a liquid drop, and a second, finer-grained population may be carried on the surface as a result of surface tension forces.
The dispersal and fallout of tephra following explosive volcanic eruptions has major impacts on human activities, including the disruption of air transport (Prata and Tupper 2009) and impacts on infrastructure (Wilson et al. 2012) and human health (Horwell and Baxter 2006). Mitigating such impacts relies, in part, on accurately forecasting patterns of tephra deposition. This requires constraints on all processes that influence the atmospheric residence time of particles. In addition, accurate reconstruction of past events, an important component of hazard assessments, relies on knowledge of the processes that produced the preserved deposits.
The ideas presented here suggest that future tephra dispersal models should aim to account for atmospheric circulation patterns on relatively localised scales. Lower atmospheric circulation patterns vary widely, and meteorological observations provide long-term datasets that can be analysed to model eruptive scenarios across a variety of plausible atmospheric conditions. Atmospheric influences may be particularly important for particle transport following relatively small explosive eruptions, where moderate column heights (i.e. mid- to lower-troposphere) lead to direct particle injection at heights characterised by spatially variable atmospheric circulation patterns. In such cases, patterns of local tephra deposition may depart strongly from simple models. Fully characterising air movement in regions of variable topography remains a challenge, because the predictability of mountain wave turbulence is still not well established (Sharman et al. 2012). In order to characterise tephra dispersal and deposition from explosive eruptions at all scales, an improved awareness of the topographic influence on atmospheric circulation is required, as well as the integration of this information into tephra transport models.
Conclusions
The Cha1 secondary thickness maximum is notable both for its relative proximity to source (and corresponding deposit coarseness/thickness) and geographic position downwind of a topographic obstacle, formed by Yate volcano. In these respects, it differs from historical examples of secondary maxima. It was caused by the accelerated deposition of medium- to fine-grained ash (100 to 500 μm), in contrast to the extremely fine ash (25 μm) of historical examples. Deposition by the formation of liquid pellets, driven by rainfall, is a possible cause of the secondary maximum. A more likely alternative is that accelerated deposition was driven by the breaking of lee waves, generated in the lower troposphere as air passed over the elevated topography of Yate. Such a process would be dry and shows that complex deposit grain-size distributions may arise without aggregation. Turbulent air circulation in the lower troposphere, particularly in regions of complex topography, may cause localised variability in the rate of ash deposition, potentially representing an important process across all scales of eruption plumes. This may be manifested in relatively subtle depositional patterns but may nevertheless form a significant control on the atmospheric residence time and distribution of tephra from explosive eruption plumes.
References
Adams NK, de Silva SL, Self S, Salas G, Schubring S, Permenter JL, Arbesman K (2001) The physical volcanology of the 1600 eruption of Huaynaputina, southern Peru. Bull Volcanol 62:493–518
Alfano F, Bonadonna C, Volentik ACM, Connor CB, Watt SFL, Pyle DM, Connor LJ (2011) Tephra stratigraphy and eruptive volume of the May, 2008, Chaitén eruption, Chile. Bull Volcanol 73:613–630
Amigo A, Lara LE, Smith VC (2013) Holocene record of large explosive eruptions from Chaitén and Michinmahuida Volcanoes, Chile. Andean Geol 40:227–248
Anthes RA (1978) The height of the planetary boundary layer and the production of circulation in a sea breeze model. J Atmos Sci 35:1231–1239
Armienti P, Macedonio G, Pareschi MT (1988) A numerical-model for simulation of tephra transport and deposition—applications to May 18, 1980, Mount-St-Helens eruption. J Geophys Res 93:6463–6476
Avila M, Folch A, Houzeaux G, Eguzkitza B, Prieto L, Cabezón D (2013) A parallel CFD model for wind farms. Proc Comput Sci 18:2157–2166
Bernard B, Bustillos J, Wade B, Hidalgo S (2013) Influence of the wind direction variability on the quantification of tephra fallouts: December 2012 and March 2013 Tungurahua eruptions. Avances 5:A14–A21
Bonadonna C, Costa A (2012) Estimating the volume of tephra deposits: a new simple strategy. Geology 40:415–418
Bonadonna C, Houghton BF (2005) Total grain-size distribution and volume of tephra-fall deposits. Bull Volcanol 67:441–456
Bonadonna C, Phillips JC (2003) Sedimentation from strong volcanic plumes. J Geophys Res 108:2340–2368
Bonadonna C, Ernst GGJ, Sparks RSJ (1998) Thickness variations and volume estimates of tephra fall deposits: the importance of particle Reynolds number. J Volcanol Geotherm Res 81:173–187
Bonadonna C, Phillips JC, Houghton BF (2005) Modeling tephra sedimentation from a Ruapehu weak plume eruption. J Geophys Res 110:B08209
Brown PP, Lawler DF (2003) Sphere drag and settling velocity revisited. J Environ Eng 129:222–231
Brown RJ, Bonadonna C, Durant AJ (2012) A review of volcanic ash aggregation. Phys Chem Earth 45–46:65–78
Burden RE, Phillips JC, Hincks TK (2011) Estimating volcanic plume heights from depositional clast size. J Geophys Res 116:B11206
Bursik MI, Carey SN, Sparks RSJ (1992) A gravity current model for the May 18, 1980 Mount St. Helens Plume. Geophys Res Lett 19:1663–1666
Carazzo G, Jellinek AM (2013) Particle sedimentation and diffusive convection in volcanic ash-clouds. J Geophys Res 118:1–18
Carey S, Sigurdsson H (1982) Influence of particle aggregation on deposition of distal tephra from the May 18, 1980 eruption of Mount St. Helens Volcano J Geophys Res 87:7061–7072
Carey S, Sigurdsson H (1985) The May 18, 1980 eruption of Mount St. Helens volcano 2. Modeling of the dynamics of the Plinian phase. J Geophys Res 90:2948–2958
Carey S, Sigurdsson H (1987) Temporal variations in column height and magma discharge rate during the 79 ad eruption of Vesuvius. Geol Soc Am Bull 99:303–314
Carey SN, Sparks RSJ (1986) Quantitative models of the fallout and dispersal of tephra from volcanic eruption columns. Bull Volcanol 48:109–125
Clark TL, Peltier WR (1984) Critical-level reflection and the resonant growth of nonlinear mountain waves. J Atmos Sci 41:3122–3134
Connor CB, Hill BE, Winfrey B, Franklin NM, La Femina PC (2001) Estimation of volcanic hazards from tephra fallout. Nat Hazard Rev 2:33–42
Costa A, Macedonio G, Folch A (2006) A three-dimensional Eulerian model for transport and deposition of volcanic ashes. Earth Planet Sci Lett 241:634–647
Doyle JD, Shapiro MA, Jiang Q, Bartels DL (2005) Large-amplitude mountain wave breaking over Greenland. J Atmos Sci 62:3106–3126
Durant AJ (2015) Toward a realistic formulation of fine-ash lifetime in volcanic clouds. Geology 43:271–272
Durant AJ, Rose WI (2009) Sedimentological constraints on hydrometeor enhanced particle deposition: 1992 eruptions of Crater Peak, Alaska. J Volcanol Geotherm Res 186:40–59
Durant AJ, Rose WI, Sarna-Wojcicki AM, Carey S, Volentik ACM (2009) Hydrometeor-enhanced tephra sedimentation: constraints from the, 18 May, 1980 eruption of Mount St. Helens J Geophys Res 114:B03204
Eychenne J, Le Pennec J-L (2012) Sigmoidal particle density distribution in a subplinian scoria fall deposit. Bull Volcanol 74:2243–2249
Folch A, Costa A, Durant A, Macedonio G (2010) A model for wet aggregation of ash particles in volcanic plumes and clouds: 2. Model Appl J Geophys Res 115:B09202
Fontijn K, Lachowycz SM, Rawson H, Pyle DM, Mather TA, Naranjo JA, Moreno-Roa H (2014) Late Quaternary tephrostratigraphy of southern Chile and Argentina. Quat Sci Rev 89:70–84
Gilbert JS, Lane SJ (1994) The origin of accretionary lapilli. Bull Volcanol 56:398–411
Hildreth W, Drake RE (1992) Volcan Quizapu, Chilean Andes. Bull Volcanol 54:93–125
Horwell J, Baxter PJ (2006) The respiratory health hazards of volcanic ash: a review for volcanic risk mitigation. Bull Volcanol 69:1–24
James MR, Lane SJ, Gilbert JS (2003) Density, construction, and drag coefficient of electrostatic volcanic ash aggregates. J Geophys Res 108:2435
Jiang Q, Doyle JD (2004) Gravity wave breaking over the Central Alps: role of complex terrain. J Atmos Sci 61:2249–2266
Jiang Q, Doyle JD, Grubišić V, Smith RB (2010) Turbulence characteristics in an elevated shear layer over Owens Valley. J Atmos Sci 67:2355–2371
Lane SJ, Gilbert JS, Kemp AJ (1995) Electrical and chemical properties of eruption plumes at Sakurajima volcano, Japan. In: 8th report of geophysical and geochemical observations at Sakurajima Volcano, pp 105–107
Lane TP, Doyle JD, Sharman RD, Shapiro MA, Watson CD (2009) Statistics and dynamics of aircraft encounters of turbulence over Greenland. Mon Weather Rev 137:2687–2702
Laprise R, Peltier WR (1989) The structure and energetics of transient eddies in a numerical simulation of breaking mountain waves. J Atmos Sci 46:565–585
Lin YL, Wang TA (1996) Flow regimes and transient dynamics of two-dimensional stratified flow over an isolated mountain ridge. J Atmos Sci 53:139–158
Long RR (1953) Some aspects of the flow of stratified fluids I. A theoretical investigation. Tellus A 5:42–58
McGimsey RG, Neal CA, Riley CM (2001) Areal distribution, thickness, mass, volume, and grain size of tephra-fall deposits from the 1992 eruptions of Crater Peak vent, Mt. Spurr volcano, Alaska. USGS open-file report 01–370
McHugh J, Sharman R (2013) Generation of mountain wave-induced mean flows and turbulence near the tropopause. Q J R Meteor Soc 139:1632–1642
Miles JW, Huppert HE (1968) Lee waves in a stratified flow. Part 2. Semi-circular obstacle. J Fluid Mech 33:803–814
Naranjo JA (1991) Major eruption reported in Chile. Eos Transl AGU 72:393–394
Naranjo JA, Stern CR (2004) Holocene tephrochronology of the southernmost part (42°30′–45°S) of the Andean Southern Volcanic Zone. Rev Geol Chile 31:224–240
NOAA (1976) U.S. Standard Atmosphere, 1976. National Oceanic and Atmospheric Administration, National Aeronautics and Space Administration, and U.S. Air Force, U.S. Government Printing Office, Washington, D.C. 227
Prata AJ, Tupper A (2009) Aviation hazards from volcanoes: the state of the science. Nat Hazards 51:239–244
Pyle DM (1989) The thickness, volume and grainsize of tephra fall deposits. Bull Volcanol 51:1–15
Scasso RA, Corbella H, Tiberi P (1994) Sedimentological analysis of the tephra from the 12–15 August 1991 eruption of Hudson volcano. Bull Volcanol 56:121–132
Scinocca JF, Peltier WR (1993) The instability of Long’s stationary solution and the evolution toward severe downslope windstorm flow. Part 1: nested grid numerical simulations. J Atmos Sci 50:2245–2263
Sharman RD, Trier SB, Lane TP, Doyle JD (2012) Sources and dynamics of turbulence in the upper troposphere and lower stratosphere: a review. Geophys Res Lett 39:L12803
Smith RB (1979) The influence of mountains on the atmosphere. Adv Geophys 21:87–230
Smith RB, Doyle JD, Jiang Q, Smith SA (2007) Alpine gravity waves: lessons from MAP regarding mountain wave generation and breaking. Q J R Meteor Soc 133:917–936
Smith RB, Woods BK, Jensen J, Cooper WA, Doyle JD, Jiang Q, Grubišić V (2008) Mountain waves entering the stratosphere. J Atmos Sci 65:2543–2562
Smolarkiewicz PK, Rotunno R (1988) Low Froude number flow past three-dimensional obstacles. Part I: baroclinally generated lee vortices. J Atmos Sci 46:1154–1164
Sorem RK (1982) Volcanic ash clusters: tephra rafts and scavengers. J Volcanol Geotherm Res 13:63–71
Sparks RSJ, Bursik MI, Ablay GJ, Thomas RME, Carey SN (1992) Sedimentation of tephra by volcanic plumes. 2. Controls on thickness and grain-size variations of tephra fall deposits. Bull Volcanol 54:685–695
Sparks RSJ, Bursik MI, Carey SN, Gilbert JS, Glaze LS, Sigurdsson H, Woods AW (1997) Volcanic plumes. Wiley, Chichester
Steele CJ, Dorling SR, von Glasow R, Bacon J (2013) Idealized WRF model sensitivity simulations of sea breeze types and their effects on offshore windfields. Atmos Chem Phys 13:443–461
Stern CR (2008) Holocene tephrochronology record of large explosive eruptions in the southernmost Patagonian Andes. Bull Volcanol 70:435–454
Stevenson JA, Loughlin SC, Font A, Fuller GW, MacLeod A, Oliver IW, Jackson B, Horwell CJ, Thordarson T, Dawson I (2013) UK Monitoring and deposition of tephra from the May 2011 eruption of Grímsvötn, Iceland. J Appl Volcanol 2:3
Suzuki T (1983) A theoretical model for dispersion of tephra. In: Shimozuru D, Yokoyama I (eds) Arc volcanism, physics and tectonics. Terra Scientific Publishing Company, Tokyo, pp 95–113
Talbot JP, Self S, Wilson CJN (1994) Dilute gravity current and rain-flushed ash deposits in the 1.8 ka Hatepe Plinian deposit, Taupo, New Zealand. Bull Volcanol 56:538–551
Textor C, Graf HF, Herzog M, Oberhuber JM, Rose WI, Ernst GGJ (2006) Volcanic particle aggregation in explosive eruption columns. Part I: parameterization of the microphysics of hydrometeors and ash. J Volcanol Geotherm Res 150:359–377
Thorarinsson S, Sigvaldason GE (1972) The Hekla eruption of 1970. Bull Volcanol 36:269–288
Walker GPL (1973) Explosive volcanic eruptions—a new classification scheme. Geol Rundsch 62:431–446
Wallace JM, Hobbs PV (2006) Atmospheric science—an introductory survey. Academic Press, 2nd edition, 504
Watanabe K, Ono K, Sakaguchi K, Takada A, Hoshizumi H (1999) Co-pyroclastic density current ash-fall deposits of the 1991 eruptions of Fugen-dake, Unzen Volcano, Japan. J Volcanol Geotherm Res 89:95–112
Watt SFL, Pyle DM, Mather TA, Martin RS, Matthews NE (2009) Fallout and distribution of volcanic ash over Argentina following the May 2008 explosive eruption of Chaitén, Chile. J Geophys Res 114:B04207
Watt SFL, Pyle DM, Naranjo JA, Rosqvist G, Mella M, Mather TA, Moreno H (2011) Holocene tephrochronology of the Hualaihue region (Andean southern volcanic zone, ∼42°S), southern Chile. Quat Int 246:324–343
Wiesner MG, Wetzel A, Catane SG, Listanco EL, Mirabueno HT (2004) Grain size, areal thickness distribution and controls on sedimentation of the, 1991 Mount Pinatubo tephra layer in the South China Sea. Bull Volcanol 66:226–242
Wilson TM, Stewart C, Sword-Daniels V, Leonard GS, Johnston DM, Cole JW, Wardman J, Wilson G, Barnard ST (2012) Volcanic ash impacts on critical infrastructure. Phys Chem Earth A/B/C 45–46:5–23
Wohletz KH, Sheridan MF, Brown WK (1989) Particle size distributions and the sequential fragmentation/transport theory applied to volcanic ash. J Geophys Res 94:15703–15721
Woods AW (1988) The dynamics and thermodynamics of volcanic eruption columns. Bull Volcanol 50:169–191
Woods AW (1993) Moist convection and the injection of volcanic ash into the atmosphere. J Geophys Res 98:17627–17636
Wurtele MG, Sharman RD, Datta A (1996) Atmospheric lee waves. Annu Rev Fluid Mech 28:429–476
Acknowledgments
We acknowledge support from the Natural Environment Research Council (UK) via NE/I02044X/1 (SFLW) and the VANAHEIM Consortium (NE/I015612/1; JCP). We are grateful to Costanza Bonadonna, Adam Durant, Raffaello Cioni and an anonymous reviewer for their constructive comments on the manuscript. We thank Ana Abarzua, Karen Fontijn and Jasper Moernaut for sharing data on the distal Cha1 deposit and Matias Ávila for assisting in the CFD simulations using the ALYA code.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editorial responsibility: C. Bonadonna
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary Data
Two tables are provided in a single MS Excel file. Table 1 provides grain-size data for sites A to F and statistics of the fitted sub-populations; Table 2 gives details for all sites where the Cha1 deposit has been identified. (XLSX 15 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Watt, S.F.L., Gilbert, J.S., Folch, A. et al. An example of enhanced tephra deposition driven by topographically induced atmospheric turbulence. Bull Volcanol 77, 35 (2015). https://doi.org/10.1007/s00445-015-0927-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00445-015-0927-x