Abstract
The eighth-century Latin manuscript Milan, Veneranda Biblioteca Ambrosiana, L 99 Sup. contains fifteen palimpsest leaves previously used for three Greek scientific texts: a text of unknown authorship on mathematical mechanics and catoptrics, known as the Fragmentum Mathematicum Bobiense (three leaves), Ptolemy's Analemma (six leaves), and an astronomical text that has hitherto remained unidentified and almost entirely unread (six leaves). We report here on the current state of our research on this last text, based on multispectral images. The text, incompletely preserved, is a treatise on the construction and uses of a nine-ringed armillary instrument, identifiable as the “meteoroscope” invented by Ptolemy and known to us from passages in Ptolemy's Geography and in writings of Pappus and Proclus. We further argue that the author of our text was Ptolemy himself.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The manuscript Milan, Veneranda Biblioteca Ambrosiana, L 99 Sup., an 8th-century Latin manuscript of Isidore of Seville's Etymologiae that previously formed part of the medieval library of the Abbey of St. Columbanus at Bobbio, was discovered by Angelo Mai to contain palimpsested Greek scientific texts some two hundred years ago. In the brief appendix on the manuscript that Mai inserted in his 1819 publication of fragments of the Gothic Bible recovered from other palimpsests in the Ambrosiana, he reported having found, and partially transcribed, Greek mathematical texts with diagrams on thirty pages (paginas omnino triginta), a facsimile of one of which (p. 124, a passage of “mechanical” mathematics concerning balancing of weights and centers of gravity) was provided at the end of the volume.Footnote 1 Mai's unpublished transcriptions, preserved in Biblioteca Apostolica Vaticana, Vat. Lat. 9556, ff. 229r–234v, came from thirteen pages, and he recorded another thirteen as bearing Greek text that he did not attempt to copy.Footnote 2 It was almost certainly Mai who applied a reagent to these twenty-six pages and six more, with the result that by 1880, when Christian Belger inspected the manuscript, the difficulty of deciphering the erased texts had been compounded by the dark brown stains left by the chemicals.Footnote 3 Nevertheless Belger succeeded in making an almost complete facsimile of two more pages, 113–114 (concerning the mathematical optics of curved mirrors), which he assumed to belong to the same text as p. 124. This text had been given the name Fragmentum mathematicum Bobiense by Diels in 1877.Footnote 4
A substantial advance came with J. L. Heiberg's discovery and edition in 1895 of twelve pages containing parts of Ptolemy's On the Analemma, a short treatise on geometrical constructions related to the theory of sundials. The identification was made possible by their correspondence to passages of the late thirteenth-century Latin translation by William of Moerbeke, made from a since-lost Greek codex, that was up to that time the only form in which On the Analemma was known.Footnote 5 Heiberg transcribed the Analemma pages to the fullest extent that he was able without further application of reagents—the destructive method commonly employed to enhance palimpsests' legibility earlier in the nineteenth century—or the 20th technique of illumination and photography by ultraviolet light and more recent advanced imaging technologies. It is in fact astonishing how much he succeeded in reading, a testament to his sharp eye and philological acumen, though assisted of course by the availability of the hyper-literal Latin version by William of Moerbeke.
Heiberg also improved the text of the three Fragmentum mathematicum pages previously known from the published facsimiles and provided the first published survey of all thirty pages bearing Greek text.Footnote 6 Six pages could now be assigned to the Fragmentum mathematicum (whose author Heiberg believed to be Anthemius of Tralles, an attribution that now appears doubtful) and twelve to On the Analemma. Heiberg argued from the extensive use of abbreviations and compendia in the Fragmentum mathematicum, but not in the On the Analemma, that the two groups of pages had been recycled from different manuscripts. As for the remaining twelve palimpsest pages, despite his being unable to read more than a few brief and disjointed passages, Heiberg noticed expressions and terminology that seemed similar to that of On the Analemma, so that he raised the possibility that the medieval Latin translation as it is preserved is missing the end of the work, with these palimpsest pages belonging to this lost portion.Footnote 7
One of the present authors (Jones) examined the manuscript in 1984, finding that more could be read on some of the pages by autopsy than Heiberg managed; subsequently, still more proved to be recoverable using simple digital manipulation of photographs from old microfilms. While not enough of an advance to merit publication, these findings suggested that more powerful imaging techniques such as multispectral imaging should be attempted, though it was not clear to what extent the chemical staining of the pages might be an impediment. And in fact two of the Fragmentum mathematicum pages and one from the Analemma (113, 123, and 144) were experimentally subjected to multispectral imaging and processing by the company Fotoscientifica s.n.c. di Parma in the early 2000s, and a single published processed image of p. 123 shows a substantial amount of traced text.Footnote 8 This project was not continued, however, and it gave rise to no published scholarship toward editing and interpreting the text.
Finally, in January 2020, the palimpsest pages were subjected to UV fluorescence and multispectral reflectance imaging funded by Sorbonne Université and carried out by the French company Lumière Technology under the direction of Pascal Cotte (see Appendix). Additional processing of these images was generously undertaken in 2021 by Keith Knox of the Early Manuscripts Electronic Library. In June 2022, further multispectral imaging was funded by Sorbonne Université and carried out under the direction of Michael Phelps by a team from the Early Manuscripts Electronic Library, the Rochester Institute of Technology, and MegaVision, Inc.Footnote 9 Using these images (for examples see Figs. 3, 4, 5 and 6 in Sect. 5), we have been able to recover significant amounts of text that had hitherto remained illegible. New editions of Ptolemy’s On the Analemma and the Fragmentum mathematicum are currently in preparation. However, the most significant textual discovery has been the discovery of parts of Ptolemy’s treatise on the instrument called Meteoroscope (ὄργανον μετεωροσκοπεῖον or μετεωροσκοπικόν).Footnote 10 Ptolemy's precise title for this book is unknown, but we will provisionally call it On the Meteoroscope. Since a critical edition of the remains of On the Meteoroscope is a difficult task whose completion is still some way off, we provide here a preliminary discussion of the work, its state of preservation, and our basis for attributing it to Ptolemy.
2 The palimpsest
The Greek texts are distributed as follows:
-
Fragmentum mathematicum Bobiense: pp. 113–114 and 123–124 (constituting a single bifolium), and 197–198. Note that pp. 114 and 124 were not overwritten with Latin text.
-
Ptolemy, On the Analemma: pp. 117–120 (a single bifolium), 129–130 and 139–140 (a single bifolium), and 143–144 and 157–158 (a single bifolium).
-
Ptolemy, On the Meteoroscope: pp. 189–190 and 195–196 (a single bifolium), 235–236 and 241–242 (a single bifolium) and 249–252.
Imaging has confirmed that pp. 187–188, which are part of the same bifolium as pp. 197–198 and exhibit traces of chemical reagents, do not contain palimpsested text—the staining is evidence that Mai took into consideration the codicological structure of the manuscript in his search for palimpsest pages. No other pages were subjected to imaging, there being no reason to believe that they contained erased text. Furthermore, autoptic examination by Gysembergh and Zingg (December 2021) revealed that pp. 249–250 and 251–252 do not belong to the same bifolium, as one might have expected, but to two separate bifolia; the other halves of these bifolia, which came after p. 252, were cut out. This appears to have happened after Mai’s discovery, at a time when the folios were unbound, because reagent stains are visible along the binding that seem to have extended beyond the cut. No information is available regarding the possible whereabouts of the two lost pages. However, we have no reason to believe that the missing halves contained Greek text. They probably served as guards to the Latin manuscript and were not, or not densely, covered with Latin text. Therefore, Mai could easily have taken notice of any Greek text on them, which he evidently did not. (We will return below to the possible significance of these presumed blank pages for the structure of the Greek text.)
As we can see from the summary above, each bifolium is devoted to just one of the three texts (i.e., the “mechanical” Fragmentum mathematicum, the Analemma, and the Meteoroscope), while in the composition of the present codex the bifolia belonging to each text were scrambled with each other and with non-palimpsest bifolia, so that it is not clear whether the order in which they come in the manuscript tells us anything about their original order in the source manuscript or manuscripts. Moreover, the bifolium comprising pp. 189–190 and 197–198 was turned the other way up when it was reused, so that the Greek text now appears upside-down relative to the overwritten Latin. And while the present odd-numbered page of each leaf necessarily always immediately preceded its even-numbered page in its source manuscript, we cannot assume that the two conjugate leaves of each bifolium as bound now are in the same order they had in the source manuscript. In fact, we know that each of the three bifolia of the Analemma is now bound so that the leaf that came second in the source manuscript now comes first.
The pages with the Meteoroscope text normally have thirty lines of text, whereas the Analemma pages commonly have twenty-nine and the Fragmentum mathematicum pages thirty-six.Footnote 11 The sloping majuscule hands of all three are similar; indeed, based both on autoptic examination by Gysembergh and Zingg, and on decipherment of the images, no significant difference has appeared between the handwriting and layout of the Meteoroscope text and the handwriting and layout of Ptolemy's On the Analemma (except for the minor difference in the number of lines per page), supporting the hypothesis that this pair of texts derive from a single source manuscript. The hand of the Fragmentum has been variously dated to the sixth or seventh century, while Heiberg estimated a seventh century date for all the Greek texts. Unlike the Analemma, the Meteoroscope is divided into chapters—apparently rather short ones on the order of a page or two long—with titles indented from both margins. When the end of a chapter is followed by the title of the next chapter on the same page, a row of dashes separates them, and such a row at least sometimes comes between a title and the chapter that it introduces. There is just one preserved diagram, at the bottom of p. 249 following the chapter to which it pertains.
The Latin text of Isidore's Etymologiae has a slightly broader line-spacing than the underlying Meteoroscope text, so that runs of consecutive lines of Greek that have little or no overwriting alternate with runs of lines that more or less coincide with the Latin, and so are much harder to read. This is a constant phenomenon applying similarly to all the pages. On the other hand, the thoroughness with which the ink of the Greek was washed off during the process of recycling, and the susceptibility of the remaining traces to being brought out in photographs taken at various wavelengths are highly variable. An additional impediment to reading is the frequency of orthographic anomalies and textual omissions and errors, which are sometimes corrected in small interlinear or marginal annotations.
3 Evidence for Ptolemy's meteoroscope and his treatise concerning it
In Geography 1.3, after briefly recounting how his predecessors had attempted to determine the size of the terrestrial globe in terms of mundane units of distance by observing the elevation of the north celestial pole in two localities lying some surveyed distance apart along a single terrestrial meridian, Ptolemy asserts that he had established a method of carrying out this determination for any two localities separated by a surveyed great-circle distance in any direction “by means of the construction of a meteoroscopic instrument” (διὰ κατασκευῆς ὀργάνου μετεωροσκοπίου or μετεωροσκοπικοῦ).Footnote 12 Nothing is said about this instrument's structure or how one operated it, but we are told that it could do the following:
-
determine the elevation of the north celestial pole for the place one is observing on an arbitrary day or night;
-
determine the direction of the meridian circle for the place of observation, and the directions of routes of travel from that place relative to the meridian in the form of the angle between the meridian and another great circle passing through the zenith point;
-
using the foregoing data, display on the meteoroscopic instrument itself the sought arc between the two localities; and
-
display the arc of the equator cut off between the meridians through the two localities.
Hence, the “meteoroscopic instrument,” presented by Ptolemy as his personal invention, functioned both as an instrument of observation and as an analogue computer for calculations in spherical astronomy. There is no explicit allusion to a separate text devoted to it.
Proclus, Hypotyposis 6.2, prefaces his account of the seven-ringed “astrolabe” or armillary instrument (τὸν διὰ τῶν ἑπτὰ κύκλων ἀστρολάβον) described by Ptolemy in Almagest 5.1 with the remark:
The meteoroscope (μετεωροσκοπεῖον) differs from this astrolabe inasmuch as all the things that can be sighted (θηρᾶν) by means of the latter can also (be sighted) by means of the former, as well as many other things useful for astronomy. For the number of rings of which (the meteoroscope subsists) is larger—since it is fashioned with nine rings—and it has been constructed in a more systematic (εὐμεθοδώτερον) way.
Theon of Alexandria (Commentary on Almagest Book 1, ed. Rome p. 419) likewise couples the meteoroscope (μετεωροσκόπιον) with the armillary of Almagest 5.1 as examples of the armillary spheres Ptolemy mentions in Almagest 1.4. Neither Proclus nor Theon explicitly ascribes the meteoroscope to Ptolemy or mentions a text.
Pappus, however, does this in his effort to fill out Ptolemy's rather terse description of the seven-ringed armillary (Commentary on Almagest Book 5, ed. Rome pp. 4–6 and 12). He writes:
(Ptolemy) does not disclose the sizes of the rings; but in the constructed (διακατασκευασμένῳ—a hapax legomenon if the word is not corrupt) instrument that is named meteoroscope (μετεωροσκοπεῖον) he makes a clear statement; hence before the detailed guide to the other matters we will deal with the subject of the proportionality (συμμετρίας) of the rings and the specific construction and use of the instrument.
He takes up this promise a few lines later, offering specific numerical ratios that should subsist between the rings' radii and their radial depth and thickness and a specific radius of 1 cubit for the largest ring where the Almagest just asks for rings of “appropriate size” (συμμέτρους… τῷ μεγέθει). He goes on:
For in the meteoroscope, he makes the entire size of the instrument up to the ability of the person constructing it, but such that the diameter of the bearer (τοῦ φέροντος) and largest ring should not be less than 12 fingers (δάκτυλοι, a unit of length). He defines the depth of the equal rings that are (mounted) at their diameters, (namely) the “revolver” (πολεύοντος) and zodiac (rings), as being 2 units, the breadth of the “revolver” 2 1/2 (unit), that of the zodiac 1 1/2 (units), such that the radius of either extending as far as its convex circumference is 49 (units).
Thus, this account by Ptolemy of the meteoroscope went into considerable quantitative detail about the instrument's constituent parts in a way that he never does in the descriptions of instruments in the Almagest. Among these parts, the outermost ring is designated the “bearer” (φέρων) and a ring conjoined to the ring representing the zodiac or ecliptic is designated the “revolver” (πολεύων), terms that do not occur in the Almagest.
Drawing on the information Pappus provides about the meteoroscope's construction and Ptolemy's list of possible uses of the instrument in the Geography, Rome conjectured two alternative reconstructions of the nine-ring armillary, neither of which turns out to match the reconstruction we offer below.Footnote 13
4 The contents of the Meteoroscope text and the structure of the instrument
The pages bearing Meteoroscope text contain two kinds of material: instructions for fashioning an armillary instrument (pp. 249, 251, and 252), apparently not subdivided into chapters, and a series of chapters giving instructions for carrying out various observations or measurements using the instrument (the rest of the pages). Since p. 250, containing a chapter concerning applications of the instrument, was the immediate successor of p. 249, we have in pp. 251, 252, and 249 (in that order) the end of the part on the construction, which we may call the introductory section, and in p. 250 the beginning of the part on its uses. If we are correct in our belief that the lost conjugate leaves of these pages did not bear any Greek text, they must have been blanks preceding the treatise, so that probably two bifolia of the treatise are lost at the beginning, on the assumption that the manuscript consisted of quires of four bifolia. In what remains of this introductory section, the author, proceeding from the inside out, describes how the rings are connected to each other. He then adds information about the rings' dimensions. At the end of the introduction, at the bottom of p. 249, is a small diagram, the letters of which connect it with the concluding passage about dimensions.
The first short chapter that follows the introductory section bears the title “How the arc of the meridian between the tropic (circles) is obtained, as well as the elevation of the pole at the place of observation” (p. 250, ll. 1–5: π̣ῶς ἡ μ̣ετα̣ξὺ τ̣[ῶ]ν̣ τ̣ρ̣ο̣π̣ι[κῶ]ν̣ τοῦ μεσημβρ̣ι̣ν̣ο̣ῦ̣ περιφ̣έ̣ρ̣ε̣ι̣[α] λαμβάνεται καὶ τ̣ὸ ἐν τῷ τόπῳ̣ τῆ̣ς̣ τηρήσεως τ̣ο̣ῦ̣ πόλου ἔξαρμα).Footnote 14 It is worth noting in passing that the second task is precisely one of those that Ptolemy lists in Geography 1.3. Taken together with information in the pages of the introductory section, this chapter is important for reconstructing the instrument, by allowing deductions about the name, function, and position of each of its rings (listed here from the outside in, see Figs. 1, 2):
-
1.
ὁ φέρων
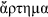 , “the (ring) bearing a suspension/hanger,” or simply φέρων, “bearer.” This is a fixed meridian ring representing the local meridian in a horizon-based frame of reference. The name seems to imply that for certain purposes the instrument was positioned by dangling it from some kind of supporting apparatus, similarly to a third- or fourth-century portable armillary sundial found at Philippi.Footnote 15
, “the (ring) bearing a suspension/hanger,” or simply φέρων, “bearer.” This is a fixed meridian ring representing the local meridian in a horizon-based frame of reference. The name seems to imply that for certain purposes the instrument was positioned by dangling it from some kind of supporting apparatus, similarly to a third- or fourth-century portable armillary sundial found at Philippi.Footnote 15 -
2.
ἑκτήμορος, hektemoros (literally “six-parter”). This is a ring in the vertical plane perpendicular and fixed to the bearer and intersecting it at the zenith and nadir, equal in dimensions to the bearer.
-
3.
ὁρίζων, “horizon.” This is a ring in the plane of the local horizon, fixed to the bearer and hektemoros at the cardinal points.
-
4.
μεσημβρινός, “meridian,” representing the local meridian in an equatorial frame of reference. It is immediately inside the bearer and kept in the bearer's plane by flanges, but can be set in any orientation in that plane according to the terrestrial latitude.
-
5.
πολεύων, “revolver,” representing the solstitial colure. It is immediately inside the meridian ring and pivots on the points of the meridian ring that represent the celestial poles.
-
6.
ζῳδιακός, “zodiac,” representing the ecliptic. It is equal in dimensions to the revolver and fixed to it at right angles at the points of the revolver that represent the solstitial points.
-
7.
ἀστρολάβος, “astrolabe,” immediately inside the revolver and zodiac rings and pivoting on the points of the revolver that represent the poles of the ecliptic.
-
8.
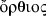 , “upright,” immediately inside the astrolabe ring and pivoting on the points of the revolver that represent the celestial poles. This ring can represent an arbitrary meridian for any locality.
, “upright,” immediately inside the astrolabe ring and pivoting on the points of the revolver that represent the celestial poles. This ring can represent an arbitrary meridian for any locality. -
9.
παγκλινής, “all-tilter,” immediately inside the upright ring, and pivoting on the points of the upright ring that represent the intersections of the arbitrary meridian with the equator. This ring can represent the horizon for any locality; its name reflects the fact that it can be set in any plane.
Outermost six rings of the meteoroscope, not to scale. Nh, Sh, Eh, and Wh are cardinal points of the horizon; Ne and Se are the north and south celestial poles; Nz and Sz are the north and south poles of the ecliptic; and Z is the zenith. In the color online version, the “meridian” ring establishing the equatorial frame of reference is in darker blue, and the “revolver” and “zodiac” rings establishing the ecliptic frame of reference are in lighter blue (color figure online)
Hence, we are dealing with a nine-ring armillary sphere, which immediately brings to mind Ptolemy's meteoroscope, especially since some of the distinctive ring names are also mentioned by Pappus. There is no evidence for any other Greek astronomers having independently developed such an instrument, although Theon of Alexandria arguably wrote a treatise about Ptolemy’s instrument.
The combined tasks of measuring both the meridian arc bounded by the tropic circles (i.e., double the obliquity of the ecliptic) and the elevation of the celestial pole (i.e., one's terrestrial latitude) recall Almagest 1.12, in which Ptolemy describes the use of meridian shadow-casting instruments to determine both these quantities. In that context, however, measuring the obliquity is a fundamental empirical step that must be taken prior to deducing the system of quantified celestial models that is the object of the Almagest, whereas to construct an armillary sphere that incorporates a ring representing the ecliptic one must already know the obliquity. Hence, there is no scientific use in measuring the obliquity by means of the meteoroscope, unless it would be to confirm the accuracy of the assumed value or perhaps to study its constancy or variation over centuries—but in this case, rather than a comparatively small armillary sphere, it would be preferable to use a meridian ring or quadrant of the largest possible size in order to obtain the greatest possible accuracy. Thus, the treatise, and the instrument it was about, appears to have served a twofold purpose: for practitioners, to carry out measurements, and for teachers, to demonstrate how some well-established results had been arrived at.
At present, it is not possible to establish the sequence of the chapters following the first one. Another chapter's title is “How to find the elevation of the pole and the meridian in every place and on every day” (p. 241, ll. 25–27: Π̣[ῶς] ἐ̣ν̣ [ἑκ]ά̣[στῳ] τ̣ό̣πῳ καὶ πάσῃ ἡμέρᾳ τό τε̣ τοῦ̣ πόλου ἔξαρμα εὑρίσκεται καὶ ἡ μεσημβρ̣ία). Based on its beginning, this chapter may have been the fourth after the introduction. Its title is again reminiscent of Ptolemy's description of the meteoroscope in Geography I, 3, 3 where he writes that with it:
(…) we can easily obtain, among many other extremely useful things, the elevation of the north [celestial] pole at the place of observation on any day or night, and at any hour the direction of the meridian (…). (Transl. J.L. Berggren and A. Jones)
The chapter immediately before this (perhaps the third), of which only the ending has been deciphered to date, is said to be connected with the problem of determining the epoch of the sun's mean motion as well as its monthly and daily course, and more generally the hypotheses for the sun's motion. Although the procedure has not been recovered yet, its aim was apparently to measure the sun's longitude; in any case, the result arrived at was the “degree of the zodiac” (p. 241, l. 16: [μ]οῖραν τοῦ ζῳδιάκου) of a certain celestial body.
At an uncertain place in the treatise, a short chapter which has been almost entirely deciphered deals with determining certain angles that are called katabatikos and antiskios. We will discuss this chapter in the next section. Finally, immediately following this chapter appears the title of another chapter on “How to measure angles in the plane of the meridian and in the plane of the zenith” (p. 190, ll. 28–30: Π̣ῶ̣ς λ̣[ηπ]τ̣[έον] γ̣ω̣ν̣ί̣α̣ς καὶ τὰς ἐν τῷ τ̣ὸ (l. τοῦ) μ̣ε̣σ̣η̣μ̣β̣ρινοῦ ἐπιπέδῳ καὶ τὰς ἐν τῷ τοῦ κατὰ κορυφὴν ἐπιπέδῳ). The body of the chapter has not yet been recovered.
5 The authorship of the Meteoroscope text
Page 190 was among those on which Heiberg managed to read a small amount of text by autopsy; his transcription of the top three lines is as followsFootnote 16:
. . . . τινα τροπον επεσκεπται ον . . . . .
. . . . τας τε καταβατικας και αντι . . . .
. . . σκιους
The dots show that he did not realize that these lines, being a chapter title, are indented from the margins so that his readings constitute a stretch of unbroken text. We are now able to read and translate lines 1–4 in their entirety:
-
1
τίνα τρόπον ἐπισκεπταῖον (l. ἐπισκεπτέον).
-
2
τάς τε κατ̣αβατικὰς καὶ ἀντι-
-
3
σκίους γω̣νίας ἐπὶ τοῦ ὑποτι-
-
4
[θ]εμένου κλ̣ί̣ματος.
-
1
In what manner one should examine.
-
2
the katabatikê and anti-
-
3
skios angles at the hypo-
-
4
thesized klima (i.e., terrestrial latitude).
The chapter itself occupies lines 6–26 and is followed by another chapter title cited above (lines 28–30).Footnote 17 The topic is a computational, not an observational, procedure. It is presupposed that the Sun's longitude has been set for a given date using some kind of marker on the zodiac ring and that the revolver ring has been rotated so that the Sun is at the appropriate ascensional distance from the meridian for the given time. Then, the all-tilter ring is manipulated so that it passes through both the zenith and the Sun's position (in the text this is called τὸ κατὰ κορυφὴν ἐπίπεδον, “the plane through the zenith,” in modern terminology a vertical circle). The text continues (lines 14–23; for images see Figs. 3, 4, 5, 6 and 7):
ἥ τε ἀπολαμβανομένη α̣ὐτοῦ π̣εριφέ̣ρε̣ι̣α̣ ἡ̣ μεταξὺ τοῦ τε ἡλίου καὶ τοῦ κατὰ κορυφὴν (about 3 incompletely legible words) ὑ̣π̣ο̣τ̣[ί]ν̣ο̣υ̣σ̣α̣ (l. ὑποτείνουσα) [τὴν] γωνί̣αν τη̣ν̣ ὑ̣φ᾿ ἡμῶν καλουμένην κ̣αταβατι̣κὴν κα̣ὶ τὴν λείπουσαν εἰς τὴν μίαν ὀρθὴ̣ν̣ ⟨ἣν⟩ οὕτως ὠνόμ̣ασαν οἱ̣ πρὸ̣ ἡμῶν, καὶ ἔτι ἡ ἀπ̣ολαμβανομένη περιφέρεια τοῦ ὁρίζοντος μεταξὺ τοῦ τε μεσημβρινοῦ καὶ τοῦ παγκλινοῦς, ὑποτίνουσα (l. ὑποτείνουσα) καὶ αὐτὴ τὴν γωνίαν <τὴν> ὑπὸ τῶν παλαιῶν ἀντίσκιον καλουμένην …
… the arc of it (scil. the all-tilter) cut off between the Sun and the zenith (about 3 incompletely legible words) which subtends the angle named by us katabatikê (“downward-heading”) and the remaining (angle to complete) one right angle, to which our predecessors gave this name (scil. katabatikê), and moreover the arc of the horizon cut off between the meridian and the all-tilter, which itself subtends the angle that was named antiskios (“counter-shadow”) by the old ones…
Ambrosianus L 99 sup., p. 190, ll. 14–23, multispectral logarithmic color image by the Early Manuscripts Electronic Library, processed by Keith T. Knox. Upside-down Latin overtext in brown and enhanced traces of the Greek undertext.
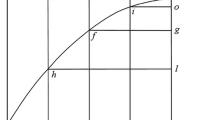
In Fig. 8, which shows the configuration of the rings schematically, C is the center point of the instrument, S the Sun, Z the zenith, M the southernmost point of the horizon, E the easternmost point of the horizon, and H the intersection of the all-tilter—here functioning as a vertical circle—with the horizon. The angle that the author calls katabatikê and the one that the author says his predecessors called katabatikê are, respectively, k1 and k2; and a is the angle that, according to the author, his predecessors called antiskios.
These angles are familiar from Ptolemy's Analemma as being part of the specialized terminology of the mathematical theory of sundials (gnomonics), and crucially, the distinction between names that our text's author makes between his own nomenclature and that of earlier writers agrees precisely with how Ptolemy modifies his predecessors’ coordinate system in On the AnalemmaFootnote 18; see especially ed. Heiberg p. 191, l. 27–34:
Instead of the angle bounded by the gnomon and the ray, they use (the angle) lacking (to complete) one right angle, and call this the descensivum (William's Latin rendering of katabatikê, cf. ed. Heiberg p. 191, ll. 5–6: circulum quem uocamus katauaticum id est descensiuum). Instead of the angle which is bounded by the inclination of the katabatikê (arc) to the zenith circle (i.e., the great circle through the zenith and the easternmost and westernmost points of the horizon), they use the one comprised by its inclination to the meridian and call it the antiskios, which means “opposite the shadow.” (ed. Heiberg p. 191, l. 27–34—the last phrase is William's gloss)
The content of this chapter thus provides the strongest evidence to date that the new text’s author is Ptolemy.Footnote 19 Moreover, it supplements our information concerning the chronological sequence of his works.Footnote 20 We already could presume that the instrument, and the treatise describing it, postdate the Almagest (which itself was completed after AD 146/147, the date of the Canobic Inscription) since the meteoroscope is clearly a development on the seven-ringed armillary. To this, we now can add the strong likelihood that On the Meteoroscope was written after On the Analemma, whose place relative to Ptolemy's other writings was hitherto entirely undetermined. A probable terminus ante quem is the composition of Ptolemy’s Geography, which refers to the meteoroscope as an established thing that the reader could learn more about elsewhere.
There is also considerable linguistic evidence that this text was written by Ptolemy. Most striking is the overlap between the phrase ὥστε… καὶ μίαν ἐπιφάνειαν ποιεῖν τῶν τε κυρτῶν ἐμ μέρει καὶ τῶν κοίλων ἐπιφανειῶν (“so that… it makes a single surface out of both the convex, respectively, and the concave surfaces,” p. 251, ll. 1–4) and the nearly identical ὥστε… καὶ μίαν ἐπιφάνειαν ποιεῖν κατά τε τὴν κυρτὴν καὶ τὴν κοίλην in Pappus’ description of the meteoroscope (ed. Rome p. 7, ll. 3–4). Of great import as well are syntagms that bear no relation to the astronomical subject-matter: thus, ἐφεξῆς δὲ καί (p. 251, l. 11) is unattested before the 2nd c. CE, and rare afterwards except for massive use by Galen, a contemporary of Ptolemy; Ptolemy and Alexander of Aphrodisias both use it twice, and no other ancient author uses it more than once. ἕνεκεν δὲ τοῦ + infinitive (p. 249, ll. 6–7) and the aorist form παρεσημειωσάμεθα (p. 249, l. 9) are also “verbal fingerprints” of Ptolemy. While not specific to Ptolemy, φέρε εἰπεῖν (p. 195, ll. 28–29) is used often by him (12 times).
Characteristic astronomical phrases can also be identified by corpus-wide TLG searches, like ἡ ὑπόθεσις τῆς κινήσεως αὐτοῦ (scil. τοῦ ἡλίου), “the hypothesis for its motion (sc. of the sun)” (p. 241, ll. 21–22). Ptolemy in his known works uses such a phrase no less than five times, while no other author uses it more than once, and all of those who use it are heavily influenced by Ptolemy (i.e., Porphyry, Theon of Alexandria, Proclus, Manuel Bryennius and Theodorus Metochites). In other authors, the same idea is expressed with less abrupt syntax, e.g., αἱ περὶ τὰς κινήσεις ὑποθέσεις (Aristotle, Simplicius) or αἱ ὑποθέσεις δι᾽ ὧν ποιεῖται τὰς κινήσεις (Theon of Alexandria). The words μοιρογραφία (p. 251, l. 23) and ἐμπολίζειν (p. 249, ll. 13, 15, and 27–28; p. 251, l. 25; p. 252, l. 11) and the phrase ἡ τοῦ κόσμου θέσις (p. 190, l. 9), while not exclusive to Ptolemy, are also characteristic of his style.
Finally, we may also argue by elimination. The three most plausible candidates for authorship are Ptolemy and his commentators Pappus and Theon of Alexandria. But Pappus, who provides many details about Ptolemy's armillary spheres, nowhere says or implies that he wrote a separate text about the meteoroscope. On the other hand, two Arabic manuscripts contain closely related versions of a text about a nine-ring armillary sphere and ascribe it to Theon.Footnote 21 In the 9th c., Ibn Wāḍiḥ al-Ya‘qūbi in his Chronicle (Ta’rīkh, p. 154–157 Houtsma) summarized a closely related text, and ascribed it to Ptolemy (p. 154–157 Houtsma).Footnote 22 The armillary sphere described in the Arabic texts of ‘Theon’ and al-Ya‘qūbi is assembled in precisely the same way as in the Milan palimpsest. However, the Greek text, although it has the same general structure (an introduction about the instrument, followed by a series of chapters with practical instructions for measurements), exhibits many differences from the Arabic text. The most reasonable explanation, already given by Richard Lorch, is that the Arabic text was translated (with some elements of paraphrase) from a work by Theon on Ptolemy's meteoroscope, and that al-Ya‘qūbi misunderstood the ascription of the text he summarized.Footnote 23
Taken together, the evidence demonstrates that the newly deciphered text from Ambrosianus L 99 Sup. is Claudius Ptolemy’s treatise about his meteoroscope, consistently with the text's content and language, and with its being contained in the same codex as Ptolemy's treatise On the Analemma. Work on this new text is ongoing: following a second imaging session, further progress in decipherment and interpretation is to be expected.
Notes
Mai 1819. Note that L 99 sup. is paginated with page numbers, not folio numbers, so that e.g. pp. 113 and 114 are the recto and verso of a single leaf.
The partially transcribed pages are 113–114, 117, 120, 124, 130, 139, 144, 157, 190, 236, 249, and 251; the others are 118–119, 123, 129, 140, 143, 158, 189, 197–198 (apparently—Mai wrote these numbers but subsequently crossed them out), 235, 250, and 252. Mai's transcriptions are unfortunately too slight and inaccurate to be of any use as a supplement to what can now be read by means of the imaging reported in the present article. In a note preceding the transcriptions, replacing an initial thought that the author was Philo of Byzantium, he speculates that the texts might come from the lost portions of Pappus's Collection.
Belger 1881. The additional stained pages are pp. 187–188 (which in fact bear no Greek text, but constitute the conjugate leaf of the palimpsested 197–198), 195–196 (the conjugate of 189–190), and 241–242 (the conjugate of 241–242).
Diels 1877.
Heiberg 1895, 4–6. Parts of this material were later included in somewhat different form in Heiberg 1907, clxxix and 1927, 87–92. (For the Fragmentum mathematicum see also Huxley 1959.) Heiberg included his edition of the Latin translation and the Greek fragments of On the Analemma in Heiberg 1907, 189–223; for a reedition of the Latin, see Edwards 1984.
As Heiberg 1895, 5 noted, Delambre 1817, 2.60 had already supposed that the Latin On the Analemma was lacking its end, a hypothesis that finds support from the fact that the text in the archetype, William of Moerbeke's autograph of the translation in Biblioteca Apostolica Vaticana, Ottob. Lat. 1850, cuts off at the bottom of the verso of the last leaf of a quire (f. 64v) without the dated colophon that William provided at the end of the other translations in this codex. On the other hand, Jones 1986, 1.12, speculated that the text on the remaining twelve palimpsest pages might have been the Analemma of Diodorus (first century BC) or Pappus's commentary on that work.
The 2020 and 2022 imaging campaigns were kindly authorized by the Veneranda Biblioteca Ambrosiana. Our thanks are extended to the Library’s Director, Federico Gallo, and to its staff, in particular Stefano Serventi and Vittorio Bergnach, for their support and hospitality.
The discovery was announced at the 26th International Congress of History of Science and Technology: Gysembergh et al. 2021.
Exceptions: (Meteoroscope) p. 249 has 28 lines followed by a diagram, p. 190 may have a row of dashes below line 30, and pp. 235 and 242 are not well enough preserved to allow line counting; (Analemma) pp. 119, 120, and 139 have 28 lines; (Fragmentum) p. 198, which may be the text's final page, has 32 lines.
The reading ὀργάνου μετεωροσκοπίου is offered by several authoritative manuscripts including Vat. gr. 191, f. 130r, and Urb. gr. 82, f. 3r, though editors have tended to prefer ὀργάνου μετεωροσκοπικοῦ. Later in the same passage the instrument is called simply μετεωροσκόπιον.
Rome 1927.
Following papyrological conventions, which are more appropriate than those of classical text editions for transcribing a manuscript of this nature, underdots indicate uncertainly read letters; square brackets indicate letters that we cannot see but believe were written; and angle brackets indicate letters we believe were accidentally omitted (or that were already missing in the exemplar). Our explanatory glosses are in parentheses.
Jones 2016, 28 and 31, fig. I-8.
Heiberg 1895, 5.
Our lineation follows the standard 30-line page layout, so that lines 5 and 27 are vacant except for the rows of dashes separating titles from main text.
In Ptolemy's system, instead of the angle that the earlier authors called antiskios, Ptolemy uses its complement (designated ἡ τοῦ ὁρίζοντος, cf. ed. Heiberg p. 206, ll. 15–16 of the Greek), though this relation is somewhat obscured by the way he defines it in the Analemma passage just quoted. This angle, h in Fig. 1, may have been mentioned in our text following p. 190 l. 23.
On the chronology see Jones 2020, 25–27.
We thank Flora Vafea, who is preparing the princeps edition of this text, for sharing her work with us. The manuscripts are lstanbul, Topkapı Sarayı, Ahmet III 3505, ff. l17r–133v, and Bombay, Mulla Firuz 86, ff. 58r–72r.
Cf. Lorch 1981.
Cotte and Simonot 2020.
References
Belger, C. 1881. “Ein neues Fragmentum mathematicum Bobiense (hierzu zwei Facsimiletafeln).” Hermes 16, 261–284 and plates 1–2.
Berggren, J.L., and A. Jones. 2000. Ptolemy’s geography: an annotated translation of the theoretical chapters. Princeton: Princeton University Press.
Cotte, P., and M. Dupouy. 2001. “A high resolution device for digitizing large size documents.” US Patent No. 6,603,582 B1.
Cotte, P., and M. Dupouy. 2003. “CRISATEL high resolution multispectral system.” PICS 2003: Image Processing, Image Quality, Image Capture Systems Conference. Rochester, NY, 161–165.
Cotte, P., and D. Dupraz. 2006a. “Spectral imaging of Leonardo Da Vinci’s Mona Lisa: A true color smile without the influence of aged varnish.” CGIV 2006 3rd European Conference on Colour in Graphics. Leeds, 311.
Cotte, P., and D. Dupraz. 2006b. “Spectral imaging of Leonardo Da Vinci’s Mona Lisa: An authentic smile at 1523 dpi with additional infrared data.” Archiving 2006. Ottawa, 228–235.
Cotte, P., and L. Simonot. 2020. Mona Lisa’s spolvero revealed. Journal of Cultural Heritage 45: 1–9.
Delambre, J. B. 1817. Histoire de l'astronomie ancienne. 2 vols. Paris: Courcier.
Diels, H. 1877. “Das Fragmentum mathematicum Bobiense”. Hermes 12: 421–425.
Edwards, D. R. 1984. Ptolemy’s Περὶ ἀναλήμματος. PhD Dissertation, Brown University. 1984.
Gordon, M. S., C.F. Robinson, E.K. Rowson, and M. Fishbein, eds. 2018. The Works of Ibn Wāḍiḥ al-Ya‘qụ̄bi. An English Translation. Vol. 2. Leiden: Brill.
Gysembergh, V., A. Jones, and E. Zingg. 2021. “Greek Texts by and Related to Ptolemy Recovered from the Late Antique Palimpsest Ambrosiana L 99 Sup.” Conference paper, 26th International Congress of History of Science and Technology, 26 July 2021.
Heiberg, J.L. 1890. “Neue Studien über Archimedes”. Abhandlungen Zur Geschichte Der Mathematik 5: 1–84.
Heiberg, J.L. 1895. “Ptolemäus de Analemmate”. Abhandlungen Zur Geschichte Der Mathematik 7: 1–30.
Heiberg, J. L. 1907. Claudii Ptolemaei Opera quae exstant omnia, volumen II: Opera astronomica minora. Leipzig: Teubner.
Heiberg, J. L. 1927. Mathematici graeci minores. Det Kgl. Danske Videnskabernes Selskab, Historisk-filologiske Meddelelser 13.3. Copenhagen: Høst.
Houtsma, M. Th. 1883. Ibn-Wādhih qui dicitur al-Jaʿqubī. 2 vols. Leiden: Brill.
Huxley, G. L. 1959. Anthemius of Tralles: A Study of Later Greek Geometry. Cambridge, MA: Eaton Press.
Jones, A. 1986. Pappus of Alexandria: Book 7 of the Collection. 3 vols. New York: Springer.
Jones, A. 2016. “Introduction.” in A. Jones, ed., Time and Cosmos in Greco-Roman Antiquity. New York: Institute for the Study of the Ancient World. 19–43.
Jones, A. 2020. “The Ancient Ptolemy.” in D. Juste et al., eds. Ptolemy's Science of the Stars in the Middle Ages. Ptolemaeus Arabus et Latinus Studies 1. Turnhout: Brepols. 13–34.
Klamroth, M. 1888. “Über die Auszüge aus griechischen Schriftstellern bei al-Ja‘qūbi. IV. Mathematiker und Astronomen”. Zeitschrift Der Deutschen Morgenländischen Gesellschaft 42: 1–44.
Lorch, R. 1981. “The ‘Meteoroscope’ Attributed to Theon of Alexandria. A Study of the Arabic Sources.” I. International Congress on the History of Turkish-Islamic Science and Technology. Istanbul: İ.T.Ü. Mimarlık Fakültesi Baskı Atölyesi. 33–38.
Luckey, P. 1927. “Das Analemma des Ptolemäus”. Astronomische Nachrichten 230 (5498): 17–46.
Mai, A. 1819. Ulphilae partium ineditarum in Ambrosianis palinsestis ab Angelo Maio repartarum specimen. Milan: Regiis typis.
Neugebauer, O. 1975. A History of Ancient Mathematical Astronomy, vol. 3. Berlin: Springer.
Pasini, C. 2005. “I palinsesti greci all’Ambrosiana”. Biblioteche Oggi, Maggio 2005: 30–33.
Pasini, C. 2008. “I palinsesti greci all'Ambrosiana: risultati di un indagine complessiva.” In Libri palinsesti greci: conservazione, restauro digitale, studio. Atti del Convegno internazionale […] 21–24 aprile 2004. Rome. 223–229 with plate 1.
Rome, A. 1927. “L’Astrolabe et le Météoroscope d’après le commentaire de Pappus sur le 5e livre de l’Almageste”. Annales De La Société Scientifique De Bruxelles, Série A 47: 77–102.
Acknowledgements
The multispectral imaging of the manuscript was funded by Sorbonne Université. Emanuel Zingg's research was generously supported by Sorbonne Université and an Alexander von Humboldt Research Fellowship for Experienced Scholars with the Institut für Alte Geschichte und Epigraphik in Munich as host institution. We thank the administration of the Veneranda Biblioteca Ambrosiana in Milan, who made the imaging and the autopsy of the palimpsest possible, especially Federico Gallo, Stefano Serventi, and Vittorio Bergnach. We also thank the members of the two teams that provided multispectral images of the palimpsest and processed them for us: Pascal Cotte and Salvatore Apicella of Lumière Technology; Michael Phelps, Damianos Kasotakis and Keith T. Knox of the Early Manuscripts Electronic Library; Roger L. Easton Jr. of the Rochester Institute of Technology; and Ken Boydston of MegaVision, Inc. Finally, we thank Flora Vafea for sharing her work on the Arabic text ascribed to Theon, and Cesare Pasini for responding to queries about past imaging of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare.
Additional information
Communicated by Jed Buchwald.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper is authored by Victor Gysembergh, Alexander Jones, and Emanuel Zingg, except for the Appendix which is by Pascal Cotte and Salvatore Apicella.
Appendices
Appendix
Multispectral digitization of the palimpsest L99 Sup. of the Biblioteca Ambrosiana in Milan
Pascal Cotte and Salvatore Apicella
A1. Hardware
The multispectral scanning system (Fig. 9) consists of the Lumière Technology cameraFootnote 24 placed on a tripod, a lighting device with two xenon sources and a book support.
The camera uses: a linear CCD sensor of 12,000 pixels which moves inside the camera to constitute a 240 Mp matrix; a barrel with 10 soft-coating filters of bandwidth (B.P.) 40 nm which cover the visible domain from 380 to 760 nm and 3 N.I.R. filters of B.P. 100 nm at 800, 900 and 1000 nm; a motorized 210 mm optic. The optical center of the camera is placed at a distance of 157 cm from the page, ensuring a resolution of 600 dpi (42.3 µm pixels).
The 450-W xenon light sources are at the focus of elliptical mirrors in the horizontal direction. They project a vertical line of semi-collimated light that scans the page in synchronization with the CCD movement.
The whole (CCD, filters, optics, light sources) ensures a dynamic range of images at 79 dB with a C.T.F. / M.T.F. above 80%.
The book stand (Fig. 10) maintains in a vertical position the page to be digitized, which is placed behind a quartz glass.
UV fluorescence images at 600 dpi are made separately on the same book support with a Nikon 50 Mp camera and two UV sources at 350 nm.
A2. Procedure
Each page to be scanned is positioned by hand behind the glass, a ribbon holds the opposite page (Fig. 10). Multispectral scanning with filter changes, individual focus and 16-bit file recording are automated. The scanning time for one page is about 30 min. The scanning in UV fluorescence is done in a second step on the same book stand.
A3. Image processing
The final color image is calculated from CIELAB D65 after applying flat-fields, resizing on the reference image at 560 nm, and normalizing with the reference white (Teflon).
To facilitate the reading of the palimpsests, we apply the algorithms of the Layer Amplification Method (L.A.M.),Footnote 25 which combine all the filters, several formulas with several parameters to obtain 1650 images reflecting light/matter interaction at different depths in the thickness of the parchment.
The U.V. fluorescence images are superimposed on the L.A.M. images to help decipher the most difficult cases.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gysembergh, V., Jones, A., Zingg, E. et al. Ptolemy’s treatise on the meteoroscope recovered. Arch. Hist. Exact Sci. 77, 221–240 (2023). https://doi.org/10.1007/s00407-022-00302-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-022-00302-w




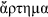 , “the (ring) bearing a suspension/hanger,” or simply φέρων, “bearer.” This is a fixed meridian ring representing the local meridian in a horizon-based frame of reference. The name seems to imply that for certain purposes the instrument was positioned by dangling it from some kind of supporting apparatus, similarly to a third- or fourth-century portable armillary sundial found at Philippi.
, “the (ring) bearing a suspension/hanger,” or simply φέρων, “bearer.” This is a fixed meridian ring representing the local meridian in a horizon-based frame of reference. The name seems to imply that for certain purposes the instrument was positioned by dangling it from some kind of supporting apparatus, similarly to a third- or fourth-century portable armillary sundial found at Philippi.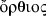 , “upright,” immediately inside the astrolabe ring and pivoting on the points of the revolver that represent the celestial poles. This ring can represent an arbitrary meridian for any locality.
, “upright,” immediately inside the astrolabe ring and pivoting on the points of the revolver that represent the celestial poles. This ring can represent an arbitrary meridian for any locality.








