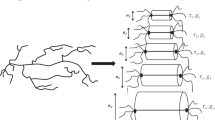
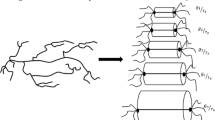
Abstract
Hydrogen bonding is the most common noncovalent reversible interaction leading to supramolecular polymeric assemblies. Shabbir et al. (Macromolecules 48:5988–5996, 2015) reported both linear and nonlinear rheological data for a model system consisting of pure poly(n-butyl acrylate) (PnBA) homopolymer and three PnBA-poly(acrylic acid) (PnBA-PAA) copolymers with different numbers of acrylic acid (AA) side groups. Hydrogen bonds between the AA groups not only cause the storage and loss modulus to shift in the direction of a power law scaling of 0.5 in the terminal relaxation regime, but also the elongational viscosity shows increasing strain hardening with a strongly nonlinear dependence on the number of hydrogen bonding groups. Based on the “Sticky Rouse” model and a constitutive equation of the Doi-Edwards type with consideration of chain stretch, we model the effect of hydrogen bonding on the elongational viscosity of the PnBA-AA copolymers. We show that the elongational viscosity data are consistent with a Sticky Rouse relaxation modulus of the AA associations characterized by a constant modulus \(G_{A}\) and a constant sticker life time \(\tau_{A}\), while the complexity of the hydrogen assemblies as quantified by the Sticky Rouse time increases with the concentration of AA groups from the order of seconds (3% AA) to hours (6%AA) and to 1 day (13%AA), and leads to extreme strain hardening. The elongational stress shows a steady state at large strains and the stretch reaches a limiting value independent of strain rate. At the highest concentration of AA groups investigated (38%AA), the PnBA-AA copolymer is a weak gel fracturing at a critical strain, and the sticker life time loses its significance. The effect of the Sticky Rouse time on self-healing is discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The rheology of supramolecular polymers is of increasing interest as this class of polymers offers interesting material properties for applications such as adhesives, coatings, cosmetics, and printing. Supramolecular polymers are a broad class of materials that include all polymers whose monomeric units can associate via secondary interactions. Hydrogen bonding is the most common noncovalent reversible interaction leading to supramolecular polymeric assemblies. A particularly useful characteristic of hydrogen bonds is that the association strength and dynamics of hydrogen bonds can be significantly altered by temperature: At high temperatures, the association strength is significantly reduced, and thus the presence of hydrogen bonds has little to no effect on material properties. At low temperatures, the association strength is large, and the life time is such that the bonds act like weak cross-links between chains. This ability to thermally control the association strengths of hydrogen bonds allows for easy processing of such materials for various applications.
Although a large body of work on the synthesis of H-bonding supramolecular polymers exists in the literature [see e.g. Stadler and de Lucca Freitas 1988; Brunsveld et al. 2001, Feldmann et al. 2009; Chen et al.. 2013; Lewis et al. 2014], very few studies have examined the rheological properties of these polymers in the melt state, and most of these studies were mainly concerned with the linear-viscoelastic properties. A notable exception is the work of Shabbir et al. (2015), who reported both linear and nonlinear rheological data for a model system of poly(n-butyl acrylate) (PnBA) homopolymer and three PnBA-poly(acrylic acid) (PnBA-PAA) copolymers with different number of acrylic acid (AA) side groups. The copolymers were synthesized via hydrolysis of the pure PnBA homopolymer. Therefore, all polymers studied have the same backbone length. Shabbir et al. (2015) showed that hydrogen bonding affects linear viscoelasticity at frequencies below the inverse reptation time of PnBA. More specifically, with increasing concentration of hydrogen bonds, the storage (G′) and loss (G″) modulus as a function of frequency shift to a power law scaling of 0.5 in the terminal regime. In addition, they demonstrated that the nonlinear elongational viscosity shows extreme strain hardening and that the magnitude of elongational stress has a strongly nonlinear dependence on the number of hydrogen bonding groups.
In the present paper, we analyze the elongational viscosity data of Shabbir et al. (2015). While the rheology of the unbounded PnBA fraction can be accounted for by the Doi-Edwards model [Doi and Edwards 1978, 1979], strain hardening is caused by the viscoelastic contribution of the temporary network of PnBA-AA chain strands created by AA associations. The linear-viscoelastic dynamics of the network is assumed to follow the “Sticky Rouse” model [Baxandall 1989], while stretching of the temporary network strands follows affine stretch until a limiting stretch value has been reached.
The paper is organized as follows: We first give a short report of sample preparation and linear-viscoelastic characterization, followed by a presentation of the model. Then, comparison of experimental data and model predictions for start-up of elongational flow is presented, followed by Conclusions.
Experimental data
Sample preparation and characterization is reported in detail by Shabbir et al. (2015). The PnBA investigated had a number average molecular weight of Mn = 121 kg/mol, a weight average molecular weight of Mw = 166 kg/mol, and a polydispersity index of PDI = 1.375. According to Jullian et al. (2010) , the entanglement molecular weight of PnBA is Me = 32 kg/mol, and therefore the number of entanglements of the pure PnBA is Z ≈ 5. Three partially hydrolyzed samples of PnBA were produced by converting n-butyl acrylate (nBA) side groups to acrylic acid (AA) side groups. The PnBA-AA copolymers so produced had increasing number of acrylic acid groups with 6% AA, 13% AA, and 38% AA side groups per chain. The percentage of AA was determined post hydrolysis using NMR spectroscopy and is presented in Table 1.
Table 1 shows that with Z ≈ 5, even for the reference or “pure” PnBA, there are several AA groups per entanglement section.
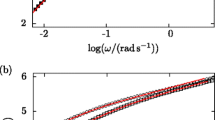
The linear-viscoelastic (LVE) properties of the PnBA-AA copolymers were investigated by small-amplitude oscillatory shear (SAOS) rheology. For the samples of PnBA and AA6, the LVE data were measured between − 25 and 45 °C, and time–temperature superposition (TTS) was used to create mastercurves for storage (G′) and loss (Gʺ) modulus (Fig. 1). Samples with acrylic acid content above 6% do not follow TTS above temperatures of 30 °C, and therefore for samples AA13 and AA38, only the LVE data measured between − 15 and 30 °C were used to create mastercurves. Shabbir et al. (2015) reported that the contribution of hydrogen bonding to linear viscoelasticity is restricted to the terminal regime, i.e., hydrogen bonding leads to branching which in turn hinders reptation of the entangled chains. As shown in Fig. 1, deviation from the expected low-frequency scaling of G′ is already observed for the reference PnBA. At the highest concentration of AA side groups (AA38) a weak gel with G′ = Gʺ is formed.
Storage (G′) and loss modulus (G″) of PnBA-AA copolymers. The lines in (a) represent the expected power law dependence of G′ and G″ in the low-frequency terminal regime. Reprinted with permission from Shabbir et al. (2015). Copyright [2015], American Chemical Society. (a) PnBA (b) AA6, 6% AA (c) AA13, 13% AA (d) AA38, 38% AA
From the mastercurves of G′ and G″ at T = 21.5 °C, parsimonious relaxation spectra were obtained for characterization of the linear-viscoelastic relaxation modulus \(G(t)\) with partial moduli \(g_{i}\) and relaxation times \(\tau_{i}\),
The relaxation spectra for PnBA, AA6 and AA13 were determined by the IRIS software (Winter and Mours 2006; Poh et al. 2022) and are summarized in Table 2. For AA38, the relaxation spectrum as reported by Shabbir et al. (2015) was used and is also included in Table 2.
The elongational stress growth coefficient as a function of time was measured using a filament stretching rheometer [Bach et al. 2003]. Measurements were performed at a constant Hencky strain rate imposed at the mid-filament diameter using an online control scheme [Marin et al. 2013]. All experiments were performed at 21.5 °C. The imposed strain rates were varied from 0.0006 to 1 s−1. All samples except AA38 were relatively fluid-like and were formed into cylindrical test specimen. Since sample AA38 had an extremely long relaxation time, it was formed and annealed at 80 °C under a nitrogen-rich environment and was allowed to relax for up to 2 h before the test.
Modelling elongational flow of supramolecular PnBA-AA copolymers
Shabbir et al. (2015) estimated the Rouse time of pure PnBA to be approximately \(\tau_{R} = 0.038s\). Thus, no strain hardening in elongational flow is expected for Hencky strain rates of \(\dot{\varepsilon } \le 13s^{ - 1}\). Therefore, when restricting attention to elongation flows with Weissenberg numbers \(Wi = \dot{\varepsilon }\tau_{R} < 1\), the fraction of “free” molecules in the PnBA-AA copolymers, i.e., those PnBA-AA molecules which are not associated to form supramolecular structures, should follow the tube model of Doi and Edwards (1978, 1979). The relaxation modulus \(G_{PnBA} (t)\) of the free PnBA-AA molecules is an integral part of the relaxation modulus \(G(t)\) according to Eq. (1) and Table 2, which represents the combined linear-viscoelastic response of both the free and the associated PnBA-AA molecules. The free molecules will only be oriented in the flow, but not stretched. Using the independent alignment (IA) assumption of the Doi-Edwards model (DEIA), the extra stress tensor \({{{\upsigma}}}_{PnBA} (t)\) of the free PnBA-AA molecules is given by a history integral of the form:
t the time of observation when the stress is measured, and t’ indicates the time when a tube segment was created by reptation. The strain measure \({\mathbf{S}}_{DE}^{IA}\) represents the contribution to the extra stress tensor originating from the affine rotation of the tube segments and is given by
with \({\mathbf{S}}(t,t^{\prime})\) being the relative second order orientation tensor. \({\mathbf{u}}^{\prime}{\mathbf{u}}^{\prime}\) is the dyad of a deformed unit vector \({\mathbf{u}}^{\prime} = {\mathbf{u}}^{\prime}(t,t^{\prime})\),
\({\mathbf{F}}_{t}^{ - 1} = {\mathbf{F}}_{t}^{ - 1} (t,t^{\prime})\) is the relative deformation gradient tensor, and \(u^{\prime}\) is the length of \({\mathbf{u}}^{\prime}\). The orientation average is indicated by < … > 0,
i.e., an average over an isotropic distribution of unit vectors \({\mathbf{u}}\).
On the other hand, strain hardening is caused by the fraction of associated molecules in the PnBA-AA copolymers, i.e., those PnBA-AA molecules which due to hydrogen bonds are associated to form temporary 3D network structures. We characterize the linear-viscoelastic effect of the supramolecular assemblies by a relaxation modulus \(G_{e} (t)\), which is also partly represented by the terminal regime of \(G(t)\) as given by Eq. (1) and Table 2, although the full terminal regime with slopes of 1 (Gʺ) and 2 (G′) has not been reached experimentally by SAOS as shown in Fig. 1, and therefore the very long relaxation times of \(G_{e} (t)\) are not included in \(G(t)\). As reptation is suppressed by sticky side-chains, the relaxation modulus \(G_{e} (t)\) of the supramolecular complexes is modeled by the “Sticky Rouse” model [Baxandall 1989] as
with
n is the number density of network strands with relaxation time \(\tau_{A} (N/p)^{2}\) created by AA associations and n is assumed to be independent of p, k is the Boltzmann constant and T the absolute temperature. \(\tau_{A}\) is the life time of a hydrogen bond (“sticker”), and the summation is over all network strands from p = 1 to p = N created by AA associations. N characterizes the width of the relaxation spectrum of the supramolecular assemblies and thereby their complexity, and the maximal or “Sticky Rouse” time \(\tau_{RA}\) is given by,
The nonlinear viscoelasticity of the supramolecular AA associations is modeled by
The Doi-Edwards strain measure \({\mathbf{S}}_{DE}^{IA}\) in combination with a suitable stretch function has been used earlier successfully to model the stress–strain behavior of crosslinked rubbers. The use of \({\mathbf{S}}_{DE}^{IA}\) takes into account the non-affine deformation of rubber network strands as shown by Wagner and Schaeffer (1993) and Wagner (1994). We use \({\mathbf{S}}_{DE}^{IA}\) here for modeling of the stress–strain behavior of the temporary network of the supramolecular complexes created by AA associations. While Eq. (9) is similar to the Molecular Stress Function (MSF) model [see e.g. Wagner et al. 2001; Rolón-Garrido 2014; Narimissa and Wagner 2019], the stretch function \(\lambda (t,t^{\prime})\) is not related to the tube diameter of an entangled polymer melt, but rather represents the relative stretch of the temporary network strands formed by the AA associations. An on-average affine stretch of network strands leads to an evolution equation for the stretch \(\lambda\) of the form
with \({\mathbf{K}} = \nabla {\mathbf{v}}\) being the velocity gradient. The dependence on t and t’ is understood, and the initial condition is \(\lambda (t = t^{\prime},t^{\prime}) = 1\). Integration gives the following expression for the stretch,
We note that \(\lambda \approx < u^{\prime}(t,t^{\prime}) >\) with \(< u^{\prime}(t,t^{\prime}) >\) being the average stretch of unit vectors \({\mathbf{u}}\) representing the isotropic orientation of network strands before deformation. We also note that \(\lambda^{2}\) is proportional to the strain energy of network strands, \(w_{s} = 3kT\lambda^{2}\).
The analysis of the elongational behavior of the PnBA-AA copolymers reveals that the elongational stress reaches a steady state at larger Hencky stains, as shown for PnBA and AA6 in Figs. 2a and c. The stretching of the temporary network strands is largely independent of the strain rate as demonstrated by scaling the stress stress–strain curves by vertical shifts in Fig. 2b and d, thereby creating approximately strain-rate independent mastercurves. (The deviations from the mastercurve of AA6 shown in Fig. 2d are due to the linear-viscoelastic stress contribution of the free PnBA-AA molecules, which depends on strain rate.) A possible explanation of this behavior may be found in the results of recent molecular dynamics simulations of associating polymer melts performed by Mohottalalage et al. (2022). They showed that increasing elongation leads to increasing breakup of associating clusters. According to their analysis, the additional dissipation due to the work of breaking associations converges towards a common value independent of association strength and strain rate.
Elongational stress \(\sigma_{E}^{ + } (\varepsilon )\) of PnBA (a) and AA6 (c) as a function of Hencky strain. (b) Scaled by vertical shift b with b = 0.5, 0.65, 1, 2.8 for \(\dot{\varepsilon } = 3,\;2,\;1,\;0.3s^{ - 1} \;\), respectively. (c) Scaled by vertical shift b with b = 1, 3, 10, 30, 73 for \(\dot{\varepsilon } = \;1,\;0.1,0.01,0.03,0.001s^{ - 1} \;\), respectively
Figure 2b and d demonstrates that the strain-rate independent stretching of network strands created by AA associations is limited by a maximal stretch \(\lambda_{\infty }^{{}}\) corresponding to a maximal strain energy which can be stored in the network strands, i.e., stretching ceases when \(\lambda^{2} = \lambda_{\infty }^{2}\). This condition is satisfied by the evolution equation,
which depends only on strain, not strain rate, in the same way as Eq. (10). Integration leads to
with parameter \(\lambda_{\infty }^{{}}\) and dependence on t and t’ understood. At large strains, the stretch is approaching the limiting stretch \(\lambda_{\infty }^{{}}\) and a limiting strain energy of network strands of \(w_{s} = 3kT\lambda_{\infty }^{2}\). We note for later use that \(\lambda_{\infty }^{{}}\) is related to a corresponding Hencky strain [Wagner et al. 2018],
The full constitutive equation considering the stress contributions of both the supramolecular PnBA-AA associations, \({{\boldsymbol{\upsigma}}}_{e} (t)\) from Eq. (9), and the un-associated (“free”) PnBA-AA, \({{\boldsymbol{\upsigma}}}_{PnBA} (t)\) according to Eq. (2), is then given by
We assume now that the relaxation modulus of the associated (\(G_{e} (t)\)) and of the free (\(G_{PnBA} (t)\)) PnBA-AA copolymers are additive, i.e., \(G(t) = G_{e} (t) + G_{PnBA} (t)\), and eliminate \(G_{PnBA} (t) = G(t) - G_{e} (t)\) from Eq. (15). The stress equation can, therefore, be expressed in the experimentally accessible window as
i.e., the effect of the AA associations on the stress via \(G_{e} (t)\) is only measurable in the nonlinear regime, when \(\lambda (t,t^{\prime}) > 1\).
In summary, the model requires the relaxation modulus \(G(t)\) of the PnBA-AA copolymers obtained from LVE characterization plus the parameters \(G_{A}\), \(\tau_{A}\), N, and \(\lambda_{\infty }^{{}}\). We expect a hierarchical increase in the size of the supramolecular assemblies with increasing concentration of AA groups and therefore an increase of the Sticky Rouse time \(\tau_{RA} = \tau_{A} N^{2}\). The parameters \(G_{A}\) and \(\tau_{A}\) should be the same for PnBA, AA6, and AA13, because the supramolecular assemblies are created by the same unit processes of association and dissociation, when a free PnBA-AA molecule is associated to the temporary network or an associated PnBA-AA molecule is released from the network. For the gel AA38, the sticker life time will lose its significance and the value of the effective sticker relaxation time \(\tau_{A}\) is expected to be much larger than for the sols PnBA, AA6 and AA13.
Comparison of experimental data and model predictions
In the following, we compare predictions of the model, stress tensor Eq. (16) and relaxation modulus \(G_{e} (t)\) according to Eq. (6), with experimental evidence in elongational flow.
Figures 3, 4, 5, and 6 present the data (symbols) of the elongational stress growth coefficient \(\eta_{E}^{ + } (t)\) as a function of time t, and of the elongational stress \(\sigma_{E}^{ + } (\varepsilon )\) as a function of Hencky strain \(\varepsilon\). Also shown in Figs. 3a, 4a, 5a, and 6a are the LVE elongational start-up viscosity (short-dashed line) and the elongational stress growth coefficient \(\eta_{E}^{ + } (t)\) according to the DEIA model (long-dashed lines), i.e., assuming no stretch (\(\lambda = 1\)) in Eq. (16) and only orientation. Predictions for affine stretch of network strands according to the evolution Eq. (11) of the stretch are indicated in Figs. 3, 4, 5, and 6 by long-short dashed lines, while predictions using evolution Eq. (13) are shown as full lines. The model parameters are summarized in Table 3.
Comparison of data (symbols) of PnBA and predictions (lines) of (a) elongational stress growth coefficient \(\eta_{E}^{ + } (t)\) and (b) elongational stress \(\sigma_{E}^{ + } (\varepsilon )\) according to Eq. (16) and evolution Eq. (11) (affine stretch, long-short dashed lines) and Eq. (13) (limiting stretch \(\lambda_{\infty }^{{}} = 22\), full lines). In (a), short-dashed and long-dashed lines indicate LVE elongational start-up viscosity and predictions of the DEIA model, respectively
Comparison of data (symbols) of AA6 and predictions (lines) of (a) elongational stress growth coefficient \(\eta_{E}^{ + } (t)\) and (b) elongational stress \(\sigma_{E}^{ + } (\varepsilon )\) according to Eq. (16) and evolution Eq. (11) (affine stretch, long-short dashed lines) and Eq. (13) (limiting stretch \(\lambda_{\infty }^{{}} = 11\), full lines). In (a), short-dashed and long-dashed lines indicate LVE elongational start-up viscosity and predictions of the DEIA model, respectively
Comparison of data (symbols) of AA13 and predictions (lines) of (a) elongational stress growth coefficient \(\eta_{E}^{ + } (t)\) and (b) elongational stress \(\sigma_{E}^{ + } (\varepsilon )\) according to Eq. (16) and evolution Eq. (11) (affine stretch, long-short dashed lines) and Eq. (13) (limiting stretch \(\lambda_{\infty }^{{}} = 11\), full lines). In (a), short-dashed and long-dashed lines indicate LVE elongational start-up viscosity and predictions of the DEIA model, respectively
Comparison of data (symbols) of AA38 and predictions (lines) of (a) elongational stress growth coefficient \(\eta_{E}^{ + } (t)\) and (b) elongational stress \(\sigma_{E}^{ + } (\varepsilon )\) according to Eq. (16) and evolution Eq. (11) (affine stretch, long-short dashed lines) and FENE (Eq. (18) with maximal stretch \(\lambda_{m}^{{}} = 2.5\), full lines). In (a), short-dashed and long-dashed lines indicate LVE elongational start-up viscosity and predictions of the DEIA model, respectively
Excellent agreement of data and model predictions is obtained for PnBA with values of modulus \(G_{A} = 100\,Pa\) and sticker life time \(\tau_{A} = 0.44\,s\) (Fig. 3). With N = 5, this combination of values for \(G_{A}\) and \(\tau_{A}\) resulted in the lowest Sticky Rouse time \(\tau_{RA} = \tau_{A} N^{2} = 11s\), which is in agreement with the experimental data. As expected, using the same values for \(G_{A}\) and \(\tau_{A}\), the Sticky Rouse time increases strongly with increasing concentration of AA groups to \(\tau_{RA} = \tau_{A} N^{2} = 2475s\) corresponding to N = 75 for AA6 with 6% AA (Fig. 4). Again, excellent agreement of data and model predictions is achieved. As shown in Figs. 3 and 4, the start-up of the elongational stress growth coefficient \(\eta_{E}^{ + } (t)\) as well as of the elongational stress \(\sigma_{E}^{ + } (\varepsilon )\) are accurately predicted by the affine stretch assumption according to Eq. (11). At larger strains, a steady-state of elongational viscosity and stress is reached, which corresponds to a limiting value of the stretch, \(\lambda_{\infty }^{{}} = 22\) for PnBA (Fig. 3) and \(\lambda_{\infty }^{{}} = 11\) for AA6 (Fig. 4), respectively. The agreement of data and model validates the Sticky Rouse relaxation modulus, Eq. (6), as well as the stretch evolution Eq. (12), which expresses the strain-rate independence of the stretch of network strands as demonstrated by the existence of the (approximate) mastercurves shown in Fig. 2b and d. As already noted, the molecular simulations of Mohottalalage et al. (2022) also revealed that increasing elongation leads to increasing breakup of associating clusters, independent of strain rate.
Figure 5 presents comparison of data of AA13 with model predictions using again the same values of modulus \(G_{A} = 100\,Pa\) and sticky life time \(\tau_{A} = 0.44\,s\) as for PnBA and AA6. The Sticky Rouse time of the associations increases to \(\tau_{RA} = \tau_{A} N^{2} = 7.04 \cdot 10^{4} s\) corresponding to N = 400. While, in general, good agreement between data and model is achieved, disagreement between data and prediction is observed at the highest strain rate of \(\dot{\varepsilon } = 1s^{ - 1}\), and for the lowest strain rates of \(\dot{\varepsilon } = 0.001s^{ - 1}\) and \(\dot{\varepsilon } = 0.0006s^{ - 1}\) at high strains. This may be due to deficiencies of the model at high AA group concentration shortly before the gel point with G′ approaching Gʺ (Fig. 1), but we remark that in addition the LVE characterization of AA13 may be insufficient as the range of time–temperature superposition is restricted for AA13 and AA38 as reported earlier, and the terminal relaxation regime has not been fully resolved. At larger strains, while there is an indication that a steady-state elongational stress is approached as quantified by \(\lambda_{\infty }^{{}} = 11\) (Fig. 5b), the samples of AA13 fractured at Hencky strains of \(\varepsilon \approx 4.5\) or earlier. This may be related to the increasing breakup of associating clusters leading in the case of high association strength eventually to cavitation effects as shown by the recent molecular dynamics simulations of associating polymer melts (Mohottalalage et al. 2022).
Comparison of data and model predictions for the gel AA38 is presented in Fig. 6. For a gel, there are always many continuous molecular pathways from one side of the sample to the other. Therefore, the individual life time of a sticker loses its significance and is replaced by an effective relaxation time \(\tau_{A} = 440s\) (Table 3), i.e., a factor of 1000 higher than for the sols. With \(G_{A} = 100\,Pa\) and N = 260, excellent agreement of the start-up of the elongational stress growth coefficient \(\eta_{E}^{ + } (t)\) and the elongational stress \(\sigma_{E}^{ + } (\varepsilon )\) is obtained by use of the affine stretch assumption according to Eq. (11). For Hencky strains larger than \(\varepsilon \approx 1\), the stress increases stronger than predicted by the affine stretch assumption and the samples break at a Hencky strain of \(\varepsilon \approx 2\), except for the strain rate \(\dot{\varepsilon } = 1s^{ - 1}\), where fracture is observed experimentally at a somewhat higher strain. We note that in contrast to the sols PnBA, AA6 and AA13, which besides the supramolecular complexes also contain free PnBA molecules, deformation is directly applied to the gel AA38, and the enhanced increase of the stress is due to the finite extensible nonlinear elasticity (FENE) of the network strands of the gel. We model this by a nonlinear spring with relative tension \(f = c\lambda\), where c represents a relative Padé inverse Langevin function [Cohen 1991] with
The maximal stretch is taken as \(\lambda_{m}^{{}} = 2.5\), and \(\lambda^{2}\) in the stress tensor Eq. (15) is replaced by \(f\lambda = c\lambda^{2}\) leading to
Taking FENE into account does not only result in excellent agreement with the experimental data, but also reproduces the fracture observed at \(\varepsilon \approx 2\).
Conclusions
Based on the relaxation modulus of the “Sticky Rouse” model, Eq. (6), and a single integral constitutive equation of the Doi-Edwards IA type with chain stretch, Eq. (16), the effect of hydrogen bonding on the elongational viscosity of PnBA-AA copolymers can be quantified. The elongational viscosity data reported by Shabbir et al. (2015) are consistent with a Sticky Rouse relaxation modulus \(G_{e} (t)\) of the AA associations characterized by a constant modulus \({G}_{A}=100Pa\) and a constant sticker life time \(\tau_{A} = 0.44s^{ - 1}\). The longest Sticky Rouse time \(\tau_{RA} = \tau_{A} N^{2}\) of the supramolecular assemblies increases strongly with the concentration of AA groups, from \(\tau_{RA} = 11s\) for PnBA with 3% of AA groups to \(\tau_{RA} = 2475s\) for AA6 with 6% AA groups, and to \(\tau_{RA} = 7 \cdot 10^{4} s\) for AA13 with 13% AA groups (Table 3), i.e., from seconds to the order of nearly 1 h and to 1 day, respectively. The increase in the Sticky Rouse time is caused by an increasing supramolecular complexity as expressed by the number N of Rouse modes, which increases from 5 (PnBA) to 75 (AA6) and to 400 (AA13). The width of the Sticky Rouse relaxation modulus \(G_{e} (t)\) increases in proportion to N2, and this has important consequences for the modeling of the self-healing potential of these materials: Experiments on supramolecular self-healing dynamics as reported e.g. by by Hinton et al. (2019) suggest that there are two important process time scales, the waiting time \(\tau_{W}\) and the healing time \(\tau_{H}\). During the waiting time, i.e., before the two parts of the fractured sample are recontacted, the material evolves toward a state which may differ from that of the undamaged material. The ability of the material to heal is significantly decreased the more so the longer the parts of the fractured sample remain separated. The healing time begins when the two halves are reconnected, and the material recovers some degree of its undamaged mechanical properties. In addition to diffusion, the effects of both \(\tau_{W}\) and \(\tau_{H}\) on self-healing are governed by the dynamics of the AA associations as expressed by the Sticky Rouse relaxation modulus. Hinton et al. (2019) reported an equilibration time \(\tau_{eq} = 2000s\) for AA6, i.e., the time for open stickers to reach equilibrium with the network. While this is in satisfactory agreement with the Sticky Rouse time of \(\tau_{RA} = 2475s\) for this copolymer, it may be necessary for models of supramolecular self-healing to take into account the width of the Sticky Rouse relaxation spectrum explicitly. The assumption of an average or characteristic association bond life time may not be sufficient for quantitative modeling.
The increase in the Sticky Rouse time of the supramolecular assemblies leads to extreme strain hardening. The elongational stress \(\sigma_{E} (\dot{\varepsilon })\) shows a steady state at large strains and the stretch reaches a limiting value \(\lambda_{\infty }\) independent of strain rate. \(\sigma_{E}\) increases with increasing strain rate as shown in Fig. 7a, where \(\sigma_{E}\) is plotted as a function of the Weissenberg number \(Wi_{RA} = \dot{\varepsilon }\tau_{RA}\). The elongational stress calculated from Eqs. (16) and (13) is mainly due to the stretch of the temporary network strands created by the supramolecular assemblies. The Sticky Rouse relaxation modulus \(G_{e} (t)\) of the supramolecular assemblies for \(\tau_{A} < t < \tau_{RA}\) can be expressed as [Narimissa and Wagner 2020]
Steady-state elongational stress \(\sigma_{E}\) (a) and dimensionless reduced elongational viscosity \(\eta_{E} /(G_{A} \tau_{RA} )\) (b) as a function of Weissenberg number \(Wi_{RA} = \dot{\varepsilon }\tau_{RA}\) calculated by Eqs. (16) and (13). Dashed lines show the asymptotic contribution of the AA associations to the elongational stress (Eq. (22)) and to the reduced elongational viscosity (Eq. (23)) with slope of ½ and − ½, respectively
and the elongational true start-up stress \(\sigma_{EA}^{ + }\) of the AA associations from Eq. (9) is given by
\(S_{11} - S_{33}\) is the orientation function in the flow direction, and \(\varepsilon\) and \(\varepsilon ^{\prime}\) are the Hencky strain at observation time \(t = \varepsilon /\dot{\varepsilon }\) and at creation time \(t^{\prime} = \varepsilon ^{\prime}/\dot{\varepsilon }\) of strands, respectively. For sufficiently high strain rates and strains, when the network strands are fully oriented with \((S_{11} - S_{33} )_{\varepsilon ,\varepsilon ^{\prime}} = 1\) and have reached their limiting stretch \(\lambda_{\infty }\) at \(\varepsilon = \varepsilon_{\infty }\), the asymptotic steady-state elongational stress \(\sigma_{EA}\) can be approximated (for details see Narimissa and Wagner 2020) by,
With \(\varepsilon_{\infty }\) from Eq. (14), this results in
corresponding to a dimensionless reduced viscosity
Predictions of Eqs. (22) and (23) are shown in Fig. 7 by dashed lines. The asymptotic elongational stress \(\sigma_{EA}\) of the supramolecular assemblies depends on the modulus \(G_{A}\), the maximal stretch \(\lambda_{\infty }\), and the Weissenberg number \(Wi_{RA}\). Even at high \(Wi_{RA}\), \(\sigma_{EA}\) is slightly lower than the steady-state elongational stress \(\sigma_{E}\) as calculated by Eqs. (16) and (13), which also contains a minor stress contribution of the free PnBA-AA molecules due to their orientation in the flow field. The higher stress \(\sigma_{E}\) of PnBA compared to AA6 and AA13 at the same Weissenberg number is mainly related to the higher value of \(\lambda_{\infty }^{{}} = 22\) for PnBA compared to \(\lambda_{\infty }^{{}} = 11\) for AA6 and AA13. At higher Weissenberg numbers, slopes of ½ and − ½ are reached for \(\sigma_{E}\) and \(\eta_{E}\), respectively, as indicated by the dashed lines in Fig. 7. This is the signature of the Sticky Rouse relaxation spectrum of the supramolecular assemblies as expressed by Eq. (19), which is reflected in the elongational stress data. With increasing Weissenberg number \(Wi_{RA}\), network strands with shorter and shorter relaxation times are stretched up to the limiting stretch \(\lambda_{\infty }\) and contribute to the elongational stress, whereby the stress increases in proportion to \(Wi_{RA}^{1/2}\). Obviously, the approximation of Eq. (19) loses its significance for Weissenberg numbers \(Wi_{RA} = \dot{\varepsilon }\tau_{RA} = \dot{\varepsilon }\tau_{A} N^{2} > N^{2}\), i.e., when the shortest Sticky Rouse mode with \(\tau_{A} = 0.44s\) has reached the limiting stretch \(\lambda_{\infty }\). With \(N^{2} = 25\) for PnBA, \(N^{2} = 5625\) for AA6 and \(N^{2} = 1.6 \cdot 10^{5}\) for AA13 (see Table 3), this transition to a different scaling is outside the experimental window. Also, with the estimated Rouse time of pure PnBA of \(\tau_{R} = 0.038s\) (Shabbir et al. 2015), stretching of the free PnBA-AA molecules is expected to occur for Hencky strain rates of \(\dot{\varepsilon } > 13s^{ - 1}\). This would also affect the scaling for elongational flows with \(Wi = \dot{\varepsilon }\tau_{R} > 1\), which are not considered here.
In summary, the analysis of the elongational flow data of the PnBA-AA copolymers allows a quantification of the dynamics of the supramolecular complexes created by AA associations, which is not immediately apparent by LVE characterization. The nonlinear effect of hydrogen bonds in the sol state can be quantified by a Sticky Rouse relaxation modulus with the three parameters \(G_{A}\), \(\tau_{A}\), and N; two of them (\(G_{A}\) and \(\tau_{A}\)) being the same for PnBA, AA6, and AA13, i.e., independent of the concentration of the AA groups. It is important to note that the limiting stretch parameter \(\lambda_{\infty }^{{}}\) does not depend on the elongation rate, and that the strain energy stored by network strands created by AA associations depends only on strain. The PnBA-AA copolymer AA38 with the highest concentration of AA groups investigated is a weak gel, and the sticker life time loses its significance. The longest Rouse time of AA38 is of the order of \(3 \cdot 10^{7} s\) or close to a year, although shorter relaxation modes down to the order of several minutes still allow for partial self-healing of any crack as shown by Hinton et al. (2019).
As hydrogen bonding is the most common noncovalent reversible interaction leading to supramolecular polymeric assemblies, the detailed understanding of the elongational rheology can have considerable impact on the formulation of hydrogen-bonded supramolecular polymers and the future developments of this important class of polymers with interesting application potential.
References
Bach A, Rasmussen HK, Hassager O (2003) Extensional viscosity for polymer melts measured in the filament stretching rheometer. J Rheol 47:429–441
Baxandall LG (1989) Dynamics of reversibly cross-linked chains. Macromolecules 22:1982–1988
Brunsveld L, Folmer BJB, Meijer EW, Sijbesma RP (2001) Supramolecular polymers. Chem Rev 101:4071–4098
Chen Y, Wu W, Himmel T, Wagner MH (2013) Structure and rheological behavior of thermoreversible supramolecular polymers with weak multiple hydrogen bonds. Macromol Mater Eng 298:876–887
Cohen A (1991) A Padé approximant to the inverse Langevin function. Rheol Acta 30:270–273
Doi M, Edwards SF (1978) Dynamics of concentrated polymer systems. Part 3.- the constitutive equation. J. Chem. Soc. Faraday Trans. 74:1818–1832
Doi M, Edwards SF (1979) Dynamics of concentrated polymer systems. Part 4.- rheological properties. J. Chem. Soc. Faraday Trans 75:38–54
Feldman KE, Kade MJ, Meijer EW, Hawker CJ, Kramer EJ (2009) Model transient networks from strongly hydrogen-bonded polymers. Macromolecules 42:9072–9081
Hinton ZR, Shabbir A, Alvarez NJ (2019) Dynamics of supramolecular self-healing recovery in extension. Macromolecules 52:2231–2242
Jullian N, Leonardi F, Grassl B, Peyrelasse J, Derail C (2010) Rheological characterization and molecular modeling of poly(n– butyl acrylate). Appl Rheol 20:1–11
Lewis C, Stewart K, Anthamatten M (2014) The influence of hydrogen bonding side-groups on viscoelastic behavior of linear and network polymers. Macromolecules 47:729–740
Marín JMR, Huusom JK, Alvarez NJ, Huang Q, Rasmussen HK, Bach A, Skov AL, Hassager O (2013) A control scheme for filament stretching rheometers with application to polymer melts. J Non-Newtonian Fluid Mech 194:14–22
Mohottalalage SS, Senanayake M, Clemmer JT, Perahia D, Grest GS, O’Connor T (2022) Nonlinear elongation flows in associating polymer melts: from homogeneous to heterogeneous flow. Phys Rev X 12:021024
Narimissa E, Wagner MH (2019) Review on tube model based constitutive equations for polydisperse linear and long-chain branched polymer melts. J Rheology 63:361–375
Narimissa E, Wagner MH (2020) Modeling nonlinear rheology of unentangled polymer melts based on a single integral constitutive equation. J Rheology 64:129–140
Poh L, Narimissa E, Wagner MH, Winter HH (2022) Interactive shear and extensional rheology - 25 years of IRIS Software. Rheol Acta 61:259–269
Rolón-Garrido (2014) The molecular stress function (MSF) model in rheology. Rheol Acta 2014(53):663–700
Shabbir A, Goldansaz H, Hassager O, van Ruymbeke E, Alvarez NJ (2015) Effect of hydrogen bonding on linear and nonlinear rheology of entangled polymer melts. Macromolecules 48:5988–5996
Stadler R, de Lucca Freitas L (1988) Dynamics of hydrogen bond complexes in polymer melts. Colloid and Polymer Science Colloid Polym. Sci 266:1102–1109
Wagner MH (1994) The origin of the C2 term in rubber elasticity. J Rheology 38:655–679
Wagner MH, Schaeffer J (1993) Rubbers and polymer melts: universal aspects of nonlinear stress-strain relations. J Rheology 37:643–661
Wagner MH, Rubio P, Bastian H (2001) The molecular stress function model for polydisperse polymer melts with dissipative convective constraint release. J Rheology 45:1387–1412
Wagner MH, Narimissa E, Huang Q (2018) On the origin of brittle fracture of entangled polymer solutions and melts. J Rheology 62:221–223
Winter HH, Mours M (2006) The cyber infrastructure initiative for rheology. Rheol Acta 45:331–338
Acknowledgements
EN acknowledges the financial support from the Ministry of Science and Technology of China (MOST, Grant no.: QN2021030003L)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wagner, M.H., Narimissa, E. & Shabbir, A. Modelling the effect of hydrogen bonding on elongational flow of supramolecular polymer melts. Rheol Acta 61, 637–647 (2022). https://doi.org/10.1007/s00397-022-01352-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00397-022-01352-1