Modelling elongational viscosity overshoot and brittle fracture of low-density polyethylene melts

Abstract

The Hierarchical Multi-mode Molecular Stress Function (HMMSF) model predicts the elongational and multiaxial extensional viscosities of polydisperse linear polymer melts based exclusively on their linear viscoelastic characterization and a single nonlinear material parameter, the so-called dilution modulus ${G}_{D}$. For long-chain branched (LCB) polymer melts such as low-density polyethylene (LDPE), the HMMSF model describes quantitatively the elongational stress growth coefficient up to the maximum of the elongational viscosity but fails to predict the existence of the maximum and the following steady-state viscosity. By taking into account branch point withdrawal in elongational flow of LCB melts, we extend the HMMSF model and show that the maximum of the elongational viscosity can be characterized by a single additional parameter, the characteristic stretch ${\overline{\lambda }}_{m}$, while the steady-state tensile stress and the elongational viscosity depend only on the dilution modulus ${G}_{D}$ as in the case of linear polydisperse melts. Comparison of predictions of the Extended Hierarchical Multi-mode Molecular Stress Function (EHMMSF) model to experimental data of 5 LDPE melts with widely different molecular weights, polydispersities and densities, and a model polystyrene pom-pom polymer shows good agreement within experimental accuracy in constant elongational-rate flow as well as stress relaxation after steady and reversed elongational flow. For the LCB melts considered, we report differences in the specific Hencky strain at the maximum of the tensile stress as quantified by the characteristic stretch ${\overline{\lambda }}_{m}$, and we discuss correlations between polydispersity, dilution modulus ${G}_{D}$, and strain hardening potential of the LDPE melts. We also extend the fracture criterion for brittle fracture of monodisperse polymer melts to the case of polydisperse polymers and find reasonable agreement with experimental evidence.

Introduction

Low-density polyethylene (LDPE) is among the most complex examples of entangled polymer systems. LDPEs are not only highly polydisperse but also contain short- and long-chain branched macromolecules with widely different structures such as hyperbranched structures with branch-on-branch topologies. One may say that in a macroscopic sample, not a single molecule has the structure of any other molecule. It is therefore highly challenging to predict the rheological behavior of LDPEs, especially the nonlinear behavior in elongational flow. While monodisperse and polydisperse linear polymer melts show a monotonously increasing elongational stress growth coefficient with increasing time or deformation reaching finally a steady-state elongational viscosity, long-chain branched (LCB) polymers display an overshoot in the transient elongational viscosity. Raible et al. (1979) presented the first measurements concerning the existence of an elongational viscosity overshoot for a polydisperse LDPE melt. Many years later, Rasmussen et al. (2005) measured the transient elongational viscosity of two LDPE melts, Lupolen 1840D and 3020D, using the filament stretch rheometer (FSR), and confirmed the existence of elongational viscosity overshoot. Combining constant elongation rate and constant stress experiments, Alvarez et al. (2013) could rule out the possibility of the overshoot being an experimental artefact. Nielsen et al. (2006) demonstrated that a nearly monodisperse polystyrene (PS) pom-pom melt with two branch points and 2 to 3 arms per branch point also shows indication of elongational viscosity overshoot. It has long been suspected that LCB macromolecules become quasilinear by aligning the arms in strong extensional flows (see, e.g., Ianniruberto and Marrucci (2013)). Mortensen et al. (2018) could demonstrate by small-angle neutron scattering studies of a three-armed polystyrene star polymer that upon exposure to large elongational flow, the star polymer indeed changes its conformation. All three arms are oriented parallel to the flow, one arm being either in positive or negative stretching direction, while the two other arms are oriented parallel, right next to each other in the direction opposite to the first arm.

On the theoretical side, some early constitutive equations were able to predict the viscosity overshoot of LDPE followed by a steady viscosity (see, for instance, Wagner et al., 1979). However, constitutive equations for branched polymer melts developed later, such as the pom-pom model of McLeish and Larson (1998) based on the idea of “branch point withdrawal,” i.e., the branch points and side arms are withdrawn into the backbone tube, and the molecular stress function (MSF) model of Wagner et al. (2001, 2003) predicted a monotone increase of the transient elongational viscosity. Wagner and Rolón-Garrido (2008) modified the MSF model by considering branch point withdrawal and obtained agreement with the pom-pom polystyrene data of Nielsen et al. (2006). Later Hoyle et al. (2013) and Hawke et al. (2015) introduced branch point withdrawal and entanglement stripping into the pom-pom model and achieved reasonable agreement with elongational data of LDPE DOW 150R, albeit at the cost of a large number of fitting parameters. The significance of the nonlinear viscoelastic rheological modelling of polydisperse polymeric systems for quantitative flow simulations in polymer processing has prompted Narimissa et al. (2015a, 2016a, b, c) to develop the Hierarchical Multi-mode Molecular Stress Function (HMMSF) model capable of predicting the rheological behaviors of linear and long-chain branched polymers for various categories of flow, i.e., uniaxial extensional, multiaxial extensional, and shear deformations, based on the linear viscoelastic (LVE) characterization of the melt and only two free nonlinear parameters (i.e. 1 in extensional flows and 2 in shear flow). The basic idea in the development of the model has been to recognize that the rheological effects of the complex (and in the case of long-chain branched polymers often unknown) molecular structures are already contained in the linear viscoelastic spectrum of relaxation times of the polymer and that only a limited number of well-defined constitutive assumptions concerning the nonlinear rheology is needed, thereby reducing the number of adjustable free nonlinear material parameters to a minimum. The HMMSF model is based on the linear viscoelastic relaxation modulus, and the basic ideas of hierarchical relaxation, dynamic dilution, and interchain tube pressure. It was shown to predict the elongational and multiaxial extensional viscosity as well as the shear viscosity of several polydisperse linear polymer melts based exclusively on their linear viscoelastic characterization by use of a single nonlinear material parameter, the so-called dilution modulus ${G}_{D}$, for extensional flows, and in addition a constraint release parameter for shear flow. For long-chain branched polymer melts, the HMMSF describes accurately the elongational stress growth coefficient up to the maximum of the elongational viscosity but fails to predict the existence of a maximum and the following steady-state viscosity at higher strain rates.

The objectives of this contribution is to present an Extended Hierarchical Multi-Mode Molecular Stress Function (EHMMSF) model, which captures the maximum in the elongational viscosity of LDPE melts and also assesses the brittle facture of polydisperse polymer melts at high strain rates. We will concentrate on elongational deformations and will not discuss shear flow here. The paper is organized as follows: the “Hierarchical multi-mode molecular stress function model” section gives a short account of the HMMSF model for extensional flows, which is followed by the “Extended hierarchical multi-mode molecular stress function model and brittle fracture” section which presents the EHMMSF model and the fracture criterion. The molecular and linear viscoelastic characteristics of the LDPEs considered and of a model PS pom-pom polymer are summarized in the “Materials” section. In the “Comparison between model predictions and elongational data” section, an extensive comparison between experimental elongational data and model predictions is given, followed by discussion and conclusions in the “Discussion and conclusions” section.

Hierarchical multi-mode molecular stress function model

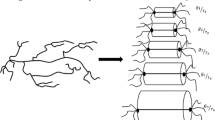
From the basic idea of the pom-pom model, an LCB polymer can be represented by a series of individual pom-pom macromolecules with two branch points, characterized by the parameters $\left\{{\tau }_{i}, {g}_{i}\right\}$ of a discrete relaxation spectrum (Narimissa and Wagner 2015). Figure 1 displays a schematic illustration of the proposed conversion of an LCB macromolecule into a hierarchical series of pom-pom polymers, where the pom-poms with short relaxation times dynamically dilute those with longer relaxation times. As shown schematically, the tube diameter a_i and the contour length grow with increasing relaxation time, when the already relaxed pom-poms with shorter relaxation times dilute the ones with longer relaxation times.

Fig. 1

Schematic representation of a long-chain branched polymer by a hierarchical series of pom-pom polymers with ${\tau }_{i+1}>{\tau }_{i}$ and ${a}_{1}<{a}_{2}<\cdots {a}_{n}$ For details, see text. Reprinted from Narimissa and Wagner (2016c), Copyright (2016), with permission from Elsevier

In the case of linear polymers, similarly an ensemble of entangled linear chains can be represented by a series of segments with hierarchically increasing tube diameters (Narimissa and Wagner 2016b).

The extra stress tensor of the Hierarchical Multi-mode Molecular Stress Function (HMMSF) model (Narimissa and Wagner 2015) is given as,

$$\sigma\left(t\right)=\sum_i\limits \int\limits_{-\infty}^{+\infty}\frac{\partial G_i\left(t-t'\right)}{\partial t'}f_i^2\left(t,t'\right)\mathbf{S}_{DE}^{IA}\left(t,t'\right)dt'$$

(1)

Here, ${\mathbf{S}}_{DE}^{IA}$ is the Doi and Edwards orientation tensor assuming an independent alignment (IA) of tube segments (Doi and Edwards 1978), which is five times the second-order orientation tensor S,

$$\mathbf{S}_{DE}^{IA}\left(t,t'\right)\equiv\langle\frac{\mathbf{u'} \mathbf{u'}}{u^{'2}}\rangle=5 \mathbf{S}\left(t,t'\right)$$

(2)

u΄ presents the length of the deformed unit vector $\mathbf{u'}$, and the bracket denotes an average over an isotropic distribution of unit vectors at time t΄, u(t΄), which can be expressed as a surface integral over the unit sphere,

(3)

The relative deformation gradient tensor, ${\mathbf{F^{-1}}}\left(t,t\right)$, signifies the deformation of the unit vector u at observation time t to $\mathbf{u'}$ according to affine deformation assumption,

$${\mathbf{u'}\left(t,t'\right)}=\mathbf{F^{-1}}\left(t,t'\right).\mathbf{u}\left(t'\right)$$

(4)

The molecular stress functions ${f_i=f}_i\left(t,t'\right)$ are the inverse of the relative tube diameters a_i of each mode i,

$$f_i\left(t,t'\right)=a_{i0}/a_i\left(t,t'\right)$$

(5)

$f_i=f_i\left(t,t'\right)$ is a function of both the observation time t and the time $t'$ of creation of tube segments by reptation. The relaxation modulus G(t) of the melt is represented by discrete Maxwell modes with partial relaxation moduli ${g}_{i}$ and relaxation times ${\tau }_{i}$,

$$G\left(t\right)=\sum_{j=1}^{n}\limits {G}_{j}\left(t\right)=\sum_{j=1}\limits ^{n}{g}_{j}exp \left(-t/{\tau }_{j}\right)$$

(6)

It is important realizing that the hierarchical relaxation and dilution of the tube segments according to Fig. 1 is already embedded in the linear viscoelastic relaxation spectrum and can therefore be extracted from the spectrum, as shown in the following.

In contrast to the case of monodisperse and bidisperse polymer melts, where dynamic dilution starts from the plateau modulus ${G}_{N}^{0}$ (Narimissa and Wagner 2016b), two dilution regimes exist during the relaxation process of polydisperse polymers: the regime of permanent dilution and the regime of dynamic dilution. Permanent dilution occurs due to the presence of oligomeric chains and un-entangled (fluctuating) chain ends. As shown in Fig. 2, we assume that the onset of dynamic dilution starts as soon as the relaxation process has reached the dilution modulus ${G}_{D}\le {G}_{N}^{0}$. The dilution modulus ${G}_{D}$ is a free parameter of the model, which needs to be fitted to nonlinear viscoelastic experimental evidence, since the mass fraction of oligomeric chains and un-entangled chain ends is in general not known a priori. However, for model polymers, the dilution modulus may be inferred from the known topology of the polymer as shown below for a model PS pom-pom melt. The time t when G(t) has relaxed to the value of ${G}_{D}$, i.e., $t={\tau }_{D}$, denotes the commencement of the dynamic dilution zone, while at relaxation times $t\le {\tau }_{D}$, the chain segments are assumed to be permanently diluted. Hence, the relaxation time $t={\tau }_{D}$ separates the zone of permanent dilution from the zone of dynamic dilution.

Fig. 2

Relaxation modulus and dilution-dependent weight fractions of a chain segment with relaxation time ${\tau }_{i}$ in view of the permanent and dynamic dilution mechanisms of the HMMSF model. Reprinted with permission from Narimissa and Wagner (2016b). Copyright [2016], The Society of Rheology

The weight fraction ${w}_{i}$ of dynamically diluted linear or LCB polymer segments with relaxation time ${\tau }_{i}>{\tau }_{D}$ is determined by considering the ratio of the relaxation modulus at time ${t =\tau }_{i}$ to the dilution modulus, ${G}_{D}=G\left(t={\tau }_{D}\right)$

$$\begin{array}{ll}{w}_{i}^{2}=\frac{G\left(t={\tau }_{i}\right)}{{G}_{D}}=\frac{1}{{G}_{D}}\sum \limits_{j=1}^{n}{g}_{j}exp\left(-{\tau }_{i}/{\tau }_{j}\right)& \mathrm{for}\; {\tau }_{i}>{\tau }_{D}\\ {w}_{i}^{2}=1& \mathrm{for}\; {\tau }_{i}\le {\tau }_{D}\end{array}$$

(7)

It is assumed that the value of ${w}_{i}$ obtained at $t={\tau }_{i}$ can be attributed to the chain segments with relaxation time ${\tau }_{i}$. Segments with ${\tau }_{i}<{\tau }_{D}$ are considered to be permanently diluted, i.e., their weight fractions are fixed at ${w}_{i}=1$. Although this may seem to be a very rough estimate, it was shown to be a sufficiently robust assumption to model the rheology of broadly distributed polymers, largely independent of the number of discrete Maxwell modes used to represent the relaxation modulus G(t) (Narimissa and Wagner 2015).

The evolution equation for the molecular stress function of each mode is expressed as (Wagner and Narimissa 2016c),

$$\frac{\partial {f}_{i}}{\partial t}={f}_{i}\left(\mathbf{K:S}\right)-\frac{{f}_{i}-1}{\alpha {\tau }_{i}}\left(1-\frac{2}{3}{w}_{i}^{2}\right)-\frac{2}{3}\frac{{f}_{i}^{2}\left({f}_{i}^{3}-1\right)}{3\alpha {\tau }_{i}}{w}_{i}^{2}$$

(8)

with the initial conditions $f\left(t=t',t'\right)=1$. The first term on the right-hand side represents an on average affine stretch rate with ${\mathbf{K}}$ the velocity gradient tensor, the second term takes into account Rouse relaxation in the longitudinal direction of the tube, and the third term limits molecular stretch due to the interchain tube pressure in the lateral direction of a tube segment (Wagner et al. 2005; Wagner and Rolón-Garrído 2009a,b). The effect of dynamic dilution is entering Eq. (8) via the square of the weight fractions ${w}_{i}^{2}$ and takes into account that the effect of dynamic dilution vanishes in fast flows as discussed in Wagner (2011). The topological parameter $\alpha$ depends on the topology of the melt (Narimissa and Wagner 2019) with,

$$\begin{array}{ll}\alpha =1& \mathrm{for}\; \mathrm{LCB}\; \mathrm{Melts}\\ \alpha =1/3& \mathrm{for}\; \mathrm{polydisperse}\; \mathrm{linear}\; \mathrm{melts}\end{array}$$

(9)

Thus, the HMMSF model for polydisperse polymer melts consists of the multi-mode stress Eq. (1), a set of evolution equations for the molecular stresses ${f}_{i}$, Eq. (8), and a hierarchical procedure to quantify the fraction of dynamically diluted chain segments according to Eq. (7) with only one free nonlinear parameter, the dilution modulus ${G}_{D}$. Once the linear viscoelastic relaxation spectrum of a polydisperse polymer melt is known, the weight fractions $w_{i}$ in the evolution Eq. (8) can be obtained by fitting the value of ${G}_{D}$ to the elongational viscosity. The parameter ${G}_{D}$, in conjunction with the relaxation times ${\tau }_{i}$, determines the extent of strain hardening. This one free parameter is sufficient for modelling extensional flows, while for shear flow an additional constraint release parameter is needed (Narimissa and Wagner 2016b).

We add a note on Finite Extensible Nonlinear Elasticity (FENE) here. The maximum stretch ${\lambda }_{max}$ of monodisperse polyethylene is given by (see, e.g., Rolón-Garrído et al. 2006),

$${\lambda }_{max}=0.82\sqrt{\frac{{M}_{e}/{M}_{b}}{{C}_{\infty }}}$$

(10)

With ${M}_{e}=1.1kg/mol$ for the entanglement molar mass, ${M}_{b}=14g/mol$ for the molar mass of a carbon-link, and ${C}_{\infty }=7.5$ for the characteristic ratio (Fetters et al. 2002), the maximum stretch of monodisperse polyethylene is given by ${\lambda }_{max}=2.65$ or ${\lambda }_{max}^{2}\cong 7$. However, in polydisperse and long-chain branched polymer systems, the “long” chains (i.e., those chain segments which feature long relaxation times) are permanently diluted by short chains and chain ends. When the relaxation modulus $G\left(t\right)$ reaches the dilution modulus ${G}_{D}={G}_{N}^{0}{w}_{D}^{2}$ (see Fig. 2), the short chains have already relaxed and the remaining weight fraction of long chains still relaxing is given by ${w}_{D}=\sqrt{{G}_{D}/{G}_{N}}$. Considering that the plateau modulus of polyethylene is ${G}_{N}^{0}=2.5MPa$ (Fetters et al. 2002) and the dilution modulus of LDPE is typically of the order of ${G}_{D}=2.5\bullet {10}^{4}Pa$, these long chains are permanently diluted to the order of ${w}_{D}=\sqrt{{G}_{D}/{G}_{N}}\cong 0.1$, and the effective ${\lambda }_{max}^{2}$ of the long chains of LDPE is ${\lambda }_{max}^{2}\cong 7/{w}_{D}\cong 70$. In addition, due to further dynamic dilution of the long chains and the resulting small values of, ${w}_{i}$ FENE effects can be neglected for LDPEs as long as elongation rates are sufficiently small so that short chains are not stretched. Therefore, the Gaussian assumption is used in the following.

Extended hierarchical multi-mode molecular stress function model and brittle fracture

At sufficiently large and fast deformations, branch point withdrawal will occur in LCB melts; i.e., branch points and side arms will be withdrawn into the backbone tube and the number of effective entanglements carrying stress will decrease. We model this effect by dimensionless functionals ${H}_{i}$ representing the percentage of entanglements with relaxation times ${\tau }_{i}$ surviving a given deformation history. The stress tensor Eq. (1) is therefore modified to

$$\sigma\left(t\right)=\sum_i\limits \int\limits_{-\infty}^t\frac{\partial G_i\left(t-t'\right)}{\partial t'}H_i\left(t,t'\right)f_i^2\left(t,t'\right)\mathbf{S}_{DE}^{IA}\left(t,t'\right)dt'$$

(11)

with

$$H_i\left(t,t'\right)={Min}_{t''=t'}^{t''=t}\left[1+\frac{w_i\tau_i\left(\mathbf{K}\left(t''\right):\mathbf{S}\left(t'',t'\right)\right)}{1+\left({\overline\lambda}_m/\overline\lambda\left(t'',t'\right)\right)^4}\right]^{-1}$$

(12)

$\overline\lambda\left(t'',t'\right)$ is the average affine stretch of an entanglement segment between the times t’ and t’’ without the consideration of stretch relaxation (see e.g. Wagner et al. 2001),

$$\overline\lambda(t'',\;t')=exp(<\ln u'(t'',t')>_0\;)$$

(13)

$\overline\lambda\left(t'',t'\right)$ can also be considered as a normalized strain energy function and is a frame invariant quantity. The parameter ${\overline{\lambda }}_{m}$ represents a measure of the characteristic stretch (or strain energy) defining the maximum of the elongational viscosity. At small deformation rates and/or deformations, the functionals ${H}_{i}$ reduce to ${H}_{i}\to 1$, and the HMMSF model is recovered. With increasing deformation rate, ${H}_{i}$ decreases as soon as $\overline\lambda\left(t'',t'\right)>{\overline\lambda}_m$, and the survival probability of entanglements of type i decreases, the more so the larger the strain rate and the larger the value of the weight fraction ${w}_{i}$. Due to the minimum functional in Eq. (12), the lowest value of ${H}_{i}$ is retained, i.e., the lowest value of ${H}_{i}$ between creation of an entanglement segment at time t’ and the stress measurement at time t. This is equivalent to the assumption of the irreversibility of branch point withdrawal: Once side chains of a branch point have been withdrawn in the tube of the backbone (Fig. 1), the branch point will not reappear later in case the deformation decreases. The approach is similar to the irreversibility assumption in temporary network models (Wagner and Stephenson 1979) and will become important in reversing flows (see below). For $\overline\lambda\left(t'',t'\right)\gg{\overline\lambda}_m$ and elongational flow with constant elongation rate $\dot{\varepsilon }$, ${H}_{i}$ reduces to

$${H}_{i}=\frac{1}{1+{w}_{i}{\tau }_{i}\dot{\varepsilon }}$$

(14)

At small values of ${w}_{i}$, branch points are only marginally embedded in the temporary polymer network due to large dynamic dilution by chain segments with shorter relaxation times. According to Eq. (14), for small Weissenberg numbers ${Wi}_{i}={\tau }_{i}\dot{\varepsilon }$ the effect of branch point withdrawal is then relatively small. Only at larger values of ${Wi}_{i}$ branch point withdrawal becomes important. Therefore, the quantity relevant for branch point withdrawal is the product of ${w}_{i}$ and ${Wi}_{i}$. While the time-dependent elongational stress as determined from Eq. (11) depends also on the characteristic stretch parameter ${\overline{\lambda }}_{m}$, the steady-state stress depends only on strain rate, LVE characterization and weight fractions ${w}_{i}$. Thus, the only nonlinear material parameter determining the steady-state of elongational stress and viscosity is the dilution modulus ${G}_{D}$ according to Eq. (7). In the asymptotic limit of fast elongational flow, the steady-state elongational stress is given by,

$$\sigma \cong \frac{15}{2}\sum_{i}\limits \frac{{g}_{i}}{{w}_{i}}{H}_{i}\sqrt{2{\tau }_{i}\dot{\varepsilon }}\cong \frac{15}{2}\sum_{i}\limits\frac{{g}_{i}}{{w}_{i}}\frac{\sqrt{2{Wi}_{i}}}{1+{w}_{i}{Wi}_{i}}\cong \frac{15\sqrt{2}}{2}\sum_{i}\limits \frac{{g}_{i}}{{w}_{i}^{2}}{\left({Wi}_{i}\right)}^{-1/2}$$

(15)

and the elongational viscosity by,

$${\eta }_{E}\approx \frac{15\sqrt{2}}{2}\sum_{i}\limits\frac{{g}_{i}{\tau }_{i}}{{w}_{i}^{2}}{\left({Wi}_{i}\right)}^{-3/2}$$

(16)

However, because of brittle fracture (see below), it is not possible to reach the asymptotic scaling of stress and viscosity. Nevertheless, Eqs. (15) and (16) demonstrate that with increasing Weissenberg numbers ${Wi}_{i}={\tau }_{i}\dot{\varepsilon }$, the contribution of chain segments with long relaxation times to elongational stress and viscosity decreases strongly due to branch point withdrawal.

To model brittle fracture of LDPE melts, we adjust the fracture criterion for monodisperse polymers (Wagner et al. 2018, 2021a,b,c) by assuming that fracture occurs as soon as the entanglement segments corresponding to one relaxation mode fracture, i.e., when these segments reach the critical value ${W}_{c}$ of the strain energy,

$${W}_{c}=3kT{f}_{i,c}^{2}{w}_{i}=U$$

(17)

$U$ is the bond-dissociation energy of a single carbon–carbon bond in hydrocarbons. As explained in [12], the strain energy of a diluted chain segment (neglecting FENE) is given by ${W}_{c}=3kT{f}_{i,c}^{2}{w}_{i}$, and the ratio of bond-dissociation energy $U$ to thermal energy $3kT$ is approximately $U/3kT\approx 35$ at a temperature of T = 130 °C, $U/3kT \approx 33$ at T = 150 °C, and $U/3kT \approx 32$ at T = 160 °C (Table 1 and 2). When the strain energy of the entanglement segment reaches the critical energy $U$, the total strain energy of the chain segment will be concentrated on one C–C bond by thermal fluctuations, and this bond then ruptures. Equation (17) defines the square of the critical stretch ${f}_{i,c}$ at fracture,

$${f}_{i,c}^{2}=\frac{U}{3kT}\frac{1}{{w}_{i}}$$

(18)

and for all polymer melts investigated here, fracture is triggered by the mode with the longest relaxation time.

Table 1 Characterization and relaxation spectra of LDPE A, LDPE B, and LDPE C

Table 2 Characterization and relaxation spectra of DOW 150R, Lupolen 3020D, and model PS pom-pom

Materials

To demonstrate the versatility and accuracy of the EHMMSF model, we present in the following a comparison of model predictions of Eq. (11) and elongational data for a variety of commercial LDPE melts with a wide range of molecular weight, polydispersity, and density. We consider LDPE A, LDPE B, and LDPE C investigated by Huang et al. (2016), low-density polyethylene DOW 150R of Hawke et al. (2015), and Lupolen 3020D of Huang et al. (2012).

Table 1 and Table 2 display weight average molecular weight (M_w), polydispersity index (M_w/M_n), testing temperature (T), ratio of carbon–carbon bond energy to thermal energy (U/3kT), room temperature density (ρ_RT), zero shear viscosity (η₀) at testing temperature calculated from the relaxation spectrum, melt flow rate (MFR), and activation energy (E_a) obtained by standard time–temperature shifting. For details, please refer to the original publications. Also, the dilution modulus G_D and the parameter ${\overline{\lambda }}_{m}$ of the EHMMSF model (as obtained by fitting of the elongational data) are summarized.

The LVE characterization of the melts was performed by small amplitude oscillatory shear (SAOS) measurements, and from the mastercurves of storage and loss modulus, parsimonious spectra were obtained by use of the IRIS software (Winter and Mours 2016). The partial moduli g_i and relaxation times ${\tau }_{i}$ resulted in excellent agreement with the SAOS data and are also reported in Table 1 and 2.

The elongational rheological measurements were conducted by a homemade filament stretching rheometer (DTU-FSR) (Bach et al. 2003), and a commercial filament stretching rheometer (VADER-1000) from Rheo Filament (Huang et al. 2016). Details of sample preparation and measurements are given in Huang et al. (2016), Hawke et al. (2015), and Huang et al. (2012).

In addition to the LDPE melts, we consider the elongational viscosity data of the model polystyrene pom-pom melt reported by Nielsen et al. (2006). The sample has well-defined pom-pom architecture with two branch points (Fig. 1). The weight-average molecular weight of the backbone and of the arm is ${M}_{b}=140kg/mol$ and ${M}_{a}=28kg/mol$, respectively, with polydispersities M_w/M_n of 1.08 and 1.06 (Table 2). According to the detailed analysis of Nielsen et al. (2006), each branch point has an average of q = 2.5 arms.

Comparison between model predictions and elongational data

Figures 3 and 4 compare experimental data of the tensile stress $\sigma$ as a function of Hencky strain $\varepsilon$ and the elongational stress growth coefficient ${\eta }_{E}\left(t\right)$ of LDPE A and LDPE C to predictions of the HMMSF and the EHMMSF model. Within experimental accuracy, the tensile stress and elongational stress growth coefficient are well described by the HMMSF model up to the maximum in the elongational stress and the viscosity (Fig. 3a, b and Fig. 4a, b) by use of a dilution modulus of ${G}_{D}={3.10}^{4} Pa$. However, while the HMMSF model predicts a monotonous transition to steady-state values at higher Hencky strains, the experimental data of LDPE A and LDPE C show a maximum in the tensile stress and the viscosity at higher strain rates, which is more pronounced and occurs at smaller Hencky strains with increasing strain rate, followed by a steady-state tensile stress and elongational viscosity at sufficiently high strains. This behavior is well captured by the EHMMSF model as demonstrated in Fig. 3c, d and Fig. 4c, d. We note that the maximum in the elongational stress occurs at smaller Hencky strains for LDPE A than LDPE C, which is reflected by a value of ${\overline{\lambda }}_{m}=70$ for LDPE A and ${\overline{\lambda }}_{m}=90$ for LDPE C.

Fig. 3

Comparison of experimental data (symbols) of tensile stress $\sigma$ as a function of Hencky strain $\varepsilon$ (a and c) and elongational stress growth coefficient ${\eta }_{E}\left(t\right)$ (b and d) of LDPE A to predictions (lines) of the HMMSF (a and b) and the EHMMSF model (c and d). Elongation rates $\dot{\varepsilon: }$ 2.5, 1.0, 0.6, 0.4, 0.25, 0.15, 0.1, 0.06, 0.04, 0.025, and 0.01 s⁻¹. Short-dotted line in (b) and (d) indicates the linear viscoelastic start-up viscosity

Fig. 4

Comparison of experimental data (symbols) of tensile stress $\sigma$ as a function of Hencky strain $\varepsilon$ (a and c) and the elongational stress growth coefficient ${\eta }_{E}\left(t\right)$ (b and d) of LDPE C to predictions (lines) of (a) and (b) the HMMSF model, Eq. (1), and (c) and (d) the EHMMSF model, Eq. (11). Elongation rates $\dot{\varepsilon: }$ 2.5, 1.0, 0.6, 0.4, 0.25, 0.15, 0.1, 0.06, 0.04, 0.025, and 0.01 s⁻¹. Short-dotted line in (b) and (d) indicates the linear viscoelastic start-up viscosity

The EHMMSF model predicts brittle fracture of LDPE A and LDPE C at a strain rate of $\dot{\varepsilon }=2.5{s}^{-1}$. While the experimental data of LDPE A seem to reach a steady-state value of stress and viscosity at this strain rate, we note that there is already a significant discrepancy between start-up of the data and the predictions, which might indicate that the sample has not seen the full deformation at the strain rate of $\dot{\varepsilon }=2.5{s}^{-1}$ and which might be due to an issue of the control system of the FSR at high strain rates. In the case of LDPE C, there is a similar discrepancy, and in addition to the absence of a steady-state the sample shows an increase of the stress after reaching a minimum, indicating again a possible issue of the control system.

Figure 5 compares the steady-state elongational viscosity ${\eta }_{E}$ of LDPE A and LDPE C with predictions of the EHMMSF model in the strain rate range up to $\dot{\varepsilon }={1s}^{-1}$, where steady-state values could be determined from the experimental data with some confidence. The elongational viscosities of LDPE A and LDPE C are quite similar, in spite of the difference in the zero strain rate viscosities, and show a maximum at about $\dot{\varepsilon }={0.1s}^{-1}$. Within experimental accuracy, model predictions are in good agreement with the experimental data. We note again that both polymer melts feature the same dilution modulus ${G}_{D}={3.10}^{4} Pa$, and the difference seen in the elongational viscosity ${\eta }_{E}$ is the consequence of the difference in the LVE relaxation spectra of the two melts.

Fig. 5

Comparison of steady-state elongational viscosity data (symbols) of LDPE A and LDPE C with predictions (lines) of the EHMMSF model, Eq. (11)

LDPE B (Fig. 6) does not show a maximum of the tensile stress and the stress growth coefficient in the experimentally investigated Hencky strain and strain rate range. However, we note that the apparent steady-state is reached already at smaller Hencky strains experimentally when the strain rate is increased, and the strain range investigated is not large enough to guarantee the existence of a true steady-state. Again, the HMMSF model gives a quantitative account of the start-up of tensile stress and elongational stress growth coefficient using a dilution modulus ${G}_{D}={3.10}^{4} Pa$ (Fig. 6a, b), but overpredicts the experimentally observed maximal values at higher strain rates. The EHMMSF model with stretch parameter ${\overline{\lambda }}_{m}=70$ predicts a shallow overshoot of stress and stress growth coefficient at the highest strain rate of $\dot{\varepsilon }={1s}^{-1}$ (Fig. 6c, d), which is in reasonable agreement with the maximal values observed experimentally.

Fig. 6

Comparison of experimental data (symbols) of tensile stress $\sigma$ as a function of Hencky strain $\varepsilon$ (a and c) and the elongational stress growth coefficient ${\eta }_{E}\left(t\right)$ (b and d) of LDPE B to predictions (lines) of (a) and (b) the HMMSF model, Eq. (1), and (c) and (d) the EHMMSF model, Eq. (11). Elongation rates $\dot{\varepsilon }$: 1.0, 0.4, 0.15, 0.1, and 0.04 s⁻¹. Short-dotted line in (b) and (d) indicates the linear viscoelastic start-up viscosity

We note that LDPE B features the same dilution modulus ${G}_{D}={3.10}^{4} Pa$ as LDPE A and C as well as the same stretch parameter ${\overline{\lambda }}_{m}=70$ as LDPE A. However, surprisingly it shows weak (if any) overshoot of the stress growth coefficient $\eta_{E} (t)$ in comparison to LDPE A and C. As shown in Fig. 7, the storage and loss modulus of LDPE B are lower than the corresponding moduli of LDPE A and C in the terminal regime (Fig. 7a). When converted to the relaxation modulus G(t) (Fig. 7b), it is obvious that below the dilution modulus ${G}_{D}={3.10}^{4} Pa$ the relaxation modulus of LDPE B has a similar shape as the relaxation modulus of LDPE A, but the time ${\tau }_{D}$, i.e., the time ${t=\tau }_{D}$ when $G\left(t\right)={G}_{D}$ (see Fig. 2), is shifted to smaller times by a factor of about 4. This agrees approximately with the ratio of the zero-shear viscosities of LDPE A and B, i.e., $31.4kPas/7.1kPas\approx 4$ (Table 1). In spite of its high weight-average molar mass of ${M}_{w}=320kg/mol$ (Table 1), which is twice the ${M}_{w}$ of LDPE A, relaxation of LDPE B is faster than relaxation of LDPE A. In view of the larger polydispersity of LDPE B in comparison to LDPE A, this means that LDPE B contains a larger fraction of short molecules, which shift the relaxation times ${\tau }_{i}$ of LDPE B to lower values in comparison to LDPE A. According to Eq. (14), the overshoot in the tensile stress and the viscosity is small if the product ${w}_{i}{Wi}_{i}$ is small. Compared at the same elongation rate $\dot{\varepsilon }$, the Weissenberg numbers ${Wi}_{i}$ of LDPE B are smaller by a factor of 4 than the corresponding ${Wi}_{i}$ of LDPE A, and consequently the viscosity overshoot of LDPE B is shifted to higher strain rates, outside the experimentally investigated strain rate range.

Fig. 7

a Storage (G’, full symbols) and loss modulus (G’’, open symbols) and b relaxation modulus G(t) of LDPE A, B, and C. Horizontal line in (b) indicates dilution modulus ${G}_{D}={3.10}^{4} Pa$

A comparison of the EHMMSF model with dilution modulus ${G}_{D}={3.10}^{4} Pa$ and stretch parameter ${\overline{\lambda }}_{m}=40$ to experimental data of tensile stress and elongational stress growth coefficient of LDPE DOW 150R is shown in Fig. 8, and reasonable agreement between model and data is obtained. The maxima in the tensile stress occur at significantly smaller Hencky strains than for LDPE A and C, as quantified by the lower stretch parameter ${\overline{\lambda }}_{m}$. Brittle fracture is observed experimentally and predicted for the highest strain rate of $\dot{\varepsilon }={0.3s}^{-1}$. Figure 9 presents stress relaxation experiments after steady extension with strain rates of $\dot{\varepsilon }={0.01s}^{-1}$, ${0.03s}^{-1}$ and ${0.1s}^{-1}$ to Hencky strains of ${\varepsilon }_{0}=3$ and $4.5$. The corresponding constant strain rate data of Fig. 8 are also shown by open symbols in Fig. 9. These agree reasonably well with the stress growth data of the relaxation experiments at ${\varepsilon }_{0}=3$, but at ${\varepsilon }_{0}=4.5$, some discrepancy of the experimental data is seen. In the case of $\dot{\varepsilon }={0.01s}^{-1}$ stress relaxation at ${\varepsilon }_{0}=4.5$ starts slightly before or at the maximal stress, and the relaxation curves of ${\varepsilon }_{0}=3$ and $4.5$ do not cross in the experimental window. This is different for the strain rates $\dot{\varepsilon }={0.03s}^{-1}$ and ${0.1s}^{-1}$, where stress relaxation at ${\varepsilon }_{0}=4.5$ starts definitely after the maximum in the elongational stress growth coefficient, and stress relaxation starting at ${\varepsilon }_{0}=4.5$ is clearly faster than stress relaxation starting at ${\varepsilon }_{0}=3$, i.e., the two relaxation curves cross each other. The predictions of the EHMMSF model agree qualitatively though not quantitatively with the experimental stress relaxation data: At the lowest strain rate, the predicted relaxation curves starting at ${\varepsilon }_{0}=3$ and ${\varepsilon }_{0}=4.5$ do not cross in the experimental window, while they do cross each other the sooner the higher the strain rate.

Fig. 8

Comparison of experimental data (symbols) of a tensile stress $\sigma$ as a function of Hencky strain $\varepsilon$ and b elongational stress growth coefficient ${\eta }_{E}\left(t\right)$ of DOW 150R to predictions (lines) of the EHMMSF model, Eq. (11). Short-dotted line in (b) indicates the linear viscoelastic start-up viscosity

Fig. 9

Comparison of experimental data (symbols) of elongational stress growth and relaxation coefficient ${\eta }_{E}\left(t\right)$ of DOW 150R to predictions (lines) of the EHMMSF model, Eq. (11). Open symbols indicate the elongational stress growth coefficients ${\eta }_{E}\left(t\right)$ from Fig. 7

The experimental data of tensile stress and elongational stress growth coefficient of LDPE Lupolen 3020D are compared to predictions of the EHMMSF model with dilution modulus ${G}_{D}={5.10}^{3} Pa$ and stretch parameter ${\overline{\lambda }}_{m}=25$ in Fig. 10. Again, good agreement between model and data is obtained. At the highest strain rate of $\dot{\varepsilon }={0.3s}^{-1}$ brittle fracture is observed experimentally and predicted by the model, although the model predicts a larger Hencky strain at fracture than observed. Further evidence of infinite elongational flow versus brittle fracture is presented in Fig. 11, which in addition to the constant strain rate data shows data of constant stress (Wagner and Rolón-Garrído 2013) and constant force experiments (Wagner and Rolón-Garrído 2012) for Lupolen 3020D. Details of the experimental set-up and conditions are given in the original publications. Constant stress (also called creep) experiments with $\sigma =1.1\bullet {10}^{5} Pa$ and $\sigma =1.5\bullet {10}^{5} Pa$ reveal that elongations up to $\varepsilon =7$ are possible without fracture of the samples. These stresses correspond approximately to the steady-state stresses of constant strain rate experiments with $\dot{\varepsilon }={0.03s}^{-1}$ and $\dot{\varepsilon }={0.1s}^{-1}$, respectively. Similar creep experiments by Alvarez et al. (2013) with constant stresses $\sigma$ in the range of $0.8\bullet {10}^{5} Pa$ to $2.0\bullet {10}^{5} Pa$ demonstrated the existence of steady flow after a maximum in both constant stress and constant strain rate experiments. In contrast, samples in constant force experiments with constant engineering stresses (stress per area of undeformed cross-section) of $\sigma =4\bullet {10}^{4} Pa$ and $\sigma =8\bullet {10}^{4} Pa$ fail by brittle fracture at Hencky deformations of $\varepsilon =3.7$ and $\varepsilon =3.4$, respectively, and tensile stresses in the range of 1 to 2 MPa in agreement with the reported rupture stress of LDPE melts in Rheotens experiments (see, e.g., Wagner et al. 1996; Bastian 2001). For a certain range of Hencky strains (called “regime 2” in Wagner and Rolón-Garrído 2012), constant force extension of LCB polymers is approximately equivalent to constant strain rate deformation: Constant force extension with $\sigma =4\bullet {10}^{4} Pa$ corresponds approximately to constant strain rate elongation data and model prediction for a constant strain rate of $\dot{\varepsilon }={0.3s}^{-1}$, and model prediction for a constant strain rate of $\dot{\varepsilon }={1s}^{-1}$ coincides with constant force extension at $\sigma =8\bullet {10}^{4} Pa$ (Fig. 11).

Fig. 10

Comparison of experimental data (symbols) of a tensile stress $\sigma$ as a function of Hencky strain $\varepsilon$ and b elongational stress growth coefficient ${\eta }_{E}\left(t\right)$ of Lupolen 3020D to predictions (lines) of the EHMMSF model, Eq. (11). Short-dotted line in (b) indicates the linear viscoelastic start-up viscosity

Fig. 11

Experimental data (symbols) of tensile stress $\sigma$ as a function of Hencky strain $\varepsilon$ for constant strain rate $\dot{\varepsilon }$, constant stress $\sigma$, and constant force experiments with engineering stress ${\sigma }_{0}$. Lines are predictions of the EHMMSF model, Eq. (11), for constant strain rate experiments

In Fig. 12, stress relaxation data after steady extension at strain rate $\dot{\varepsilon }={0.03s}^{-1}$ to Hencky strains of ${\varepsilon }_{0}=2$, $3$ and $4.5$ are presented. Predictions of the EHMMSF model agree nearly quantitatively with the experimental stress relaxation data. Stress relaxation predicted at ${\varepsilon }_{0}=4.5$, i.e., after the maximum in the stress growth coefficient, is faster than stress relaxation at ${\varepsilon }_{0}=3$ and even ${\varepsilon }_{0}=2$, in agreement with experimental evidence.

Fig. 12

Comparison of experimental data (symbols) of elongational stress growth and relaxation coefficient ${\eta }_{E}\left(t\right)$ of DOW 150R for $\dot{\varepsilon }=0.03{s}^{-1}$ to predictions (lines) of the EHMMSF model, Eq. (11)

Figure 13 presents tensile stress data and predictions of the EHMMSF model for reversing elongational flows, i.e., steady elongation with elongation rate $\dot{\varepsilon }={0.03s}^{-1}$ up to Hencky strains of $2\le {\varepsilon }_{0}\le 4.5$, followed by compression of the sample with elongation rate $\dot{\varepsilon }={0.03s}^{-1}$. For experimental details, refer to Huang et al. (2012). The agreement of data and predictions can be rated as excellent. This agreement can only be achieved by assuming the irreversibility of branch point withdrawal as expressed by the minimum functional in Eq. (12): When side chains of a branch point have been withdrawn in the tube of the backbone during elongational flow, the branch point will not reappear when the deformation is reversed during the compression part of the flow.

Fig. 13

Tensile stress data (symbols) for reversing elongational flows, i.e., steady elongation with elongation rate of $\dot{\varepsilon }=0.03{s}^{-1}$ up to Hencky strains of $2\le {\varepsilon }_{0}\le 4.5$, followed by compression of the sample with elongation rate $\dot{\varepsilon }=-0.03{s}^{-1}$. Lines are predictions of the EHMMSF model, Eq. (11), for stress relaxation experiments starting at Hencky strains of $2\le {\varepsilon }_{0}\le 5.5$

The strain recovery ${\varepsilon }_{r}$, i.e., the difference of the strain ${\varepsilon }_{0}$ and the residual strain $\varepsilon$ at ${\sigma }=0$ in the compression regime, is shown in Fig. 14 for reversing elongational flow experiments at $\dot{\varepsilon }={0.01s}^{-1}$, ${0.03s}^{-1}$, and ${0.1s}^{-1}$. ${\varepsilon }_{r}$ increases with increasing ${\varepsilon }_{0}$ until the maximal value of the stress is reached, and then decreases drastically after the maximum. Predictions of the EHMMSF model are in agreement with experimental evidence within experimental accuracy.

Fig. 14

Strain recovery ${\varepsilon }_{r}$ for reversing elongational flow experiments at strain rates of $\dot{\varepsilon }=0.01{s}^{-1}$, $0.03{s}^{-1}$, and $0.1{s}^{-1}$. Experimental data (symbols) and predictions (lines) of EHMMSF model, Eq. (11)

As a final test of the EHMMSF model, we consider the elongational viscosity data of a model polystyrene pom-pom melt as reported by Nielsen et al. (2006). The sample has a pom-pom architecture with two branch points, and each branch point has an average of q = 2.5 arms. The weight-average molecular weight of the backbone and of the arm is ${M}_{b}=140kg/mol$ and ${M}_{a}=28kg/mol$, respectively (Table 2). As side chain relaxation and backbone relaxation are well separated, side chain relaxation leads to permanent dilution of the backbone chain on the time scale of the backbone. This is true as long as the elongation rate is smaller than the inverse stretch relaxation time of the arms. The weight fraction ${w}_{D}$ of the backbone is therefore,

$${w}_{D}=\frac{{M}_{b}}{{M}_{b}+2q{M}_{a}}=0.5$$

(19)

With the plateau modulus of polystyrene of ${G}_{N}^{0}=2.5\bullet {10}^{5} Pa$, the dilution modulus ${G}_{D}$ is obtained as (see Fig. 2 and Eq. (7))

$${G}_{D}={G}_{N}{w}_{D}^{2}=6\bullet {10}^{4}Pa$$

(20)

Experimental data of the tensile stress $\sigma \left(\varepsilon \right)$ and of the elongational stress growth coefficient ${\eta }_{E}\left(t\right)$ of the pom-pom polymer are compared to predictions of the HMMSF and EHMMSF model in Fig. 15. Tensile stress and elongational stress growth coefficient are well described by the HMMSF model up to an elongation rate of $\dot{\varepsilon }=0.01{s}^{-1}$. At the three highest elongation rates, there is indication of a maximum in the experimental data of stress and viscosity, while predictions of the HMMS model continue increasing monotonously until the steady-state is reached or brittle fracture is predicted (Fig. 15a, b). With a stretch parameter of ${\overline{\lambda }}_{m}=30$, the EHMMSF model provides a good description of the maxima in tensile stress and elongational viscosity within experimental accuracy (Fig. 15c, d). Note that in this case of a well-defined topology of the polymer, the stretch parameter ${\overline{\lambda }}_{m}$ is the only nonlinear fitting parameter of the model. At these early times of the development of the filament stretching rheometer, the control loop was not yet fast enough to capture the strong downturn in tensile stress and viscosity, and therefore the conclusion regarding brittle fracture remains inconclusive.

Fig. 15

Comparison of experimental data (symbols) of tensile stress $\sigma$ as a function of Hencky strain $\varepsilon$ (a and c) and the elongational stress growth coefficient ${\eta }_{E}\left(t\right)$ (b and d) of model PS pom-pom melt to predictions (lines) of (a) and (b) the HMMSF model, Eq. (1), and (c) and (d) the EHMMSF model, Eq. (11). Short-dotted line in (b) and (d) indicates the linear viscoelastic start-up viscosity

Discussion and conclusions

The Hierarchical Multi-mode Molecular Stress Function (HMMSF) model is based on the fact that the rheological effect of polydispersity and, in the case of LCB polymers, the effect of the often unknown molecular branching topology are already contained in the linear viscoelastic spectrum of relaxation times of the polymer. Therefore, only a very limited number of well-defined constitutive assumptions concerning the nonlinear rheology is needed, thereby reducing the number of adjustable free nonlinear material parameters to a minimum. The HMMSF model is based on the linear viscoelastic relaxation modulus, and the basic concepts of hierarchical relaxation, dynamic dilution, and interchain tube pressure. Through hierarchical relaxation, dynamic dilution results in larger tube diameters of chain segments with smaller partial relaxation moduli ${g}_{i}$. Dynamic dilution starts when the relaxation process reaches the dilution modulus ${G}_{D}\le {G}_{N}^{0}$ (Fig. 2), and in nonlinear elongational flow the “dynamic” part of dilution (as quantified by the dilution modulus ${G}_{D}$) decreases with increasing Weissenberg number ${Wi}_{Ri}=\dot{\varepsilon }{\tau }_{Ri}$. Stretch and orientation dynamics of the HMMSF model are coupled through a tube diameter which decreases with increasing deformations. A decreasing tube diameter in turn leads to an increasing interchain tube pressure, which sets a limit on the minimum tube segment diameter, and thereby the maximum stretch of the chain segment for a given deformation rate. The HMMSF model, with only one nonlinear material parameter, the dilution modulus ${G}_{D}$, has been shown to quantitatively model the extensional viscosities of linear polymer melts at all deformation rates investigated (Narimissa and Wagner 2016b). For long-chain branched polymer melts, the HMMSF model describes accurately the elongational stress growth coefficient up to the maximum of the elongational viscosity but fails to predict the maximum and the following steady-state viscosity at higher strain rates. For the LDPEs investigated here, the values of the dilution modulus ${G}_{D}$ are in the range of $5 \bullet 10^{3}$ to $3\bullet {10}^{4}Pa$. Due to the permanent dilution by short chains and chain ends, the weight fraction of the “long” chains (i.e., those chain segments which feature long relaxation times and which are dynamically diluted) is of the order of ${w}_{D}=\sqrt{{G}_{D}/{G}_{N}}\cong 0.1$ or smaller, i.e., only about 10% or less of the total molar mass of the LDPE polymer. This is different for the model PS pom-pom melt, where ${w}_{D}$ is defined by the topology of the polymer at ${w}_{D}=0.5$.

By introducing dimensionless functionals ${H}_{i}$ representing the percentage of entanglements with relaxation times ${\tau }_{i}$ surviving a given deformation, the Extended Hierarchical Multi-mode Molecular Stress Function (EHMMSF) model takes into account branch point withdrawal in elongational flow of LCB melts and allows quantifying the maximum in the elongational viscosity of LDPE melts observed at higher strain rates and the following steady-state elongational viscosity at high strains. The functionals ${H}_{i}$ depend on strain rate, relaxation time ${\tau }_{i}$, weight fraction ${w}_{i}$, and a stretch parameter ${\overline{\lambda }}_{m}$. For the LDPEs and the PS pom-pom polymer investigated, the range of the stretch parameter is $25\le {\overline{\lambda }}_{m}\le 90$. We note that ${\overline{\lambda }}_{m}$ can be converted in good approximation into an equivalent characteristic Hencky strain ${\varepsilon }_{m}=1+ln\left({\overline{\lambda }}_{m}\right)$ (Wagner et al. 2018). The larger the value of ${\overline{\lambda }}_{m}$, the larger is the Hencky strain at which the maximum in the tensile start-up stress $\sigma (\varepsilon )$ or in the elongational stress growth coefficient ${\eta }_{E}\left(t\right)$ is reached. It is the first time that for different LCB melts differences in the Hencky strains at the maximum of the tensile stress are noted, and we show that they can be quantified by the single parameter ${\overline{\lambda }}_{m}$. According to Eq. (12), at constant ${\overline{\lambda }}_{m}$, the maximum will be reached at smaller Hencky strains with increasing strain rate and will be more pronounced. We speculate that a large value of ${\overline{\lambda }}_{m}$ is associated with a polymer topology featuring a large number and/or rather long side chains with possibly branch-on-branch topology resulting in large deformations and thereby large tensile forces needed in the backbone chain for branch point withdrawal.

While the maximum of the elongational stress growth coefficient ${\eta }_{E}\left(t\right)$ is characterized by the stretch parameter ${\overline{\lambda }}_{m}$, the steady-state tensile stress and viscosity in the limit of high strains depends only on the dilution modulus ${G}_{D}$ and the LVE relaxation spectrum of the melt. Figure 16 shows the strain hardening potential ${\eta }_{E}/{\eta }_{0}$ of the LDPEs analyzed as a function of tensile stress ${\sigma }_{E}$. This is a temperature-invariant representation. Starting from the Trouton relation of ${\eta }_{E}/{\eta }_{0}=3$, the 3 LDPEs with the largest value of ${G}_{D}$, i.e., LDPE A, B, and C $\left({G}_{D}=3\bullet {10}^{4}Pa\right)$, show the strongest strain hardening behavior reaching maximal ratios of ${\eta }_{E}/{\eta }_{0}$ between approximately 20 and 30. Interestingly, LDPE B with the highest weight-average molecular weight ${M}_{w}$ but the largest polydispersity and the lowest zero-shear viscosity features the strongest strain hardening, followed by LDPE C and LDPE A. LDPE DOW150R has the same polydispersity as LDPE A, but a lower dilution modulus ${G}_{D}=1\bullet {10}^{4}Pa$, and therefore shows a smaller strain hardening potential than LDPE A. The polymer with the smallest polydispersity and the lowest value of the dilution modulus $\left({G}_{D}=3\bullet {10}^{4}Pa\right)$, LDPE 3020D, displays the weakest strain hardening potential with a maximum of ${\eta }_{E}/{\eta }_{0}=8$.

Fig. 16

Trouton ratio as a function of tensile stress for the LDPE melts investigated. Predictions of EHMMSF model, Eq. (11)

The comparison of predictions of the EHMMSF model in elongational flow including stress relaxation after steady elongational flow as well as reversed elongation to experimental data of 5 LDPE melts with widely different molecular weights, polydispersities, and densities shows good agreement within experimental accuracy. Hence, starting from the linear viscoelastic relaxation modulus G(t), it is possible to characterize the nonlinear viscoelastic elongational flow properties of LDPE melts by only two material parameters, the dilution modulus ${G}_{D}$ and the stretch parameter ${\overline{\lambda }}_{m}$. This can be of considerable importance for polymer processing simulations. The EHMMSF model is further validated by comparison to elongational data of a model PS pom-pom melt (Nielsen et al 2006). In this case, the dilution modulus is unambiguously defined by the mass fraction of the backbone, and the stretch parameter ${\overline{\lambda }}_{m}$ is the only nonlinear parameter of the model.

We also extended the fracture criterion for brittle fracture of monodisperse polymer melt to the case of polydisperse polymers. According to this criterion, a polydisperse polymer will fail by brittle fracture when the stretch energy of one relaxation mode reaches the bond-dissociation energy of a single carbon–carbon bond. For LDPE A and C as well as DOW150R and 3020D, this fracture criterion was reached at the highest strain rate investigated, and while for LDPE A and C the evidence of brittle fracture remained inconclusive, brittle fracture was observed experimentally at the highest strain rate for DOW 150R and Lupolen 3020D in agreement with predictions. Brittle fracture of Lupolen 3020D is confirmed by comparison to data of constant force extension (Wagner and Rolón-Garrído 2012).