ENSO phase space dynamics with an improved estimate of the thermocline depth

Abstract

The recharge oscillator model of the El Niño Southern Oscillation (ENSO) describes the ENSO dynamics as an interaction between the eastern tropical Pacific sea surface temperatures (T) and subsurface heat content (thermocline depth; h), defining a dynamical cycle with different phases. h is often approximated on the basis of the depth of the 20 °C isotherm (Z₂₀). In this study we will address how the estimation of h affects the representation of ENSO dynamics. We will compare the ENSO phase space with h estimated based on Z₂₀ and based on the maximum gradient in the temperature profile (Z_mxg). The results illustrate that the ENSO phase space is much closer to the idealised recharge oscillator model if based on Z_mxg than if based on Z₂₀. Using linear and non-linear recharge oscillator models fitted to the observed data illustrates that the Z₂₀ estimate leads to artificial phase dependent structures in the ENSO phase space, which result from an in-phase correlation between h and T. Based on the Z_mxg estimate the ENSO phase space diagram show very clear non-linear aspects in growth rates and phase speeds. Based on this estimate we can describe the ENSO cycle dynamics as a non-linear cycle that grows during the recharge and El Nino state, and decays during the La Nina states. The most extreme ENSO states are during the El Nino and discharge states, while the La Nina and recharge states do not have extreme states. It further has faster phase speeds after the El Nino state and slower phase speeds during and after the La Nina states. The analysis suggests that the ENSO phase speed is significantly positive in all phases, suggesting that ENSO is indeed a cycle. However, the phase speeds are closest to zero during and after the La Nina state, indicating that the ENSO cycle is most likely to stall in these states.

1 Introduction

The dynamics of the El Nino Southern Oscillation (ENSO) are often analysed in the context of the recharge oscillator (ReOsc) model [Burgers et al. 2005; Jin 1997; Timmermann et al. 2018]. In this model the interannual variations of ENSO are described by the interaction between the eastern equatorial Pacific sea surface temperatures (SST) and the thermocline depth of the whole equatorial Pacific (h). Here, h is assumed to be measuring the thickness of the upper ocean layer also referred to as the upper ocean warm water volume (WWV). It marks the point in the temperature profile with the strongest gradients (Z_mxg), see Fig. 1.

Fig. 1

Idealised temperature profiles with estimates of the thermocline depth by the maximum temperature gradient (Z_mxg) and the 20 °C isotherm (Z₂₀). The thermocline depth is the same in all profiles

Studies of ENSO dynamics often estimate h based on the 20 °C isotherm [Z₂₀; e.g., Smith 1995; Kessler 2002; Timmermann et al. 2018; Vijayeta and Dommenget 2018; Burgers et al. 2005]. The Z₂₀ is considered a good approximation of Z_mxg, as it is roughly on the same depth as Z_mxg for most of the equatorial Pacific and covaries with Z_mxg on seasonal to interannual time scales. However, it does have some important limitations in the context of ENSO dynamics. First, as illustrated in Fig. 1, the Z₂₀ can change due to warming of the whole or a part of the temperature profile even though Z_mxg has not changed. This is an important problem for climate change studies, as pointed out in [Yang and Wang 2009; Dommenget and Vijayeta 2019; Vijayeta 2020; Izumo and Colin 2022].

Further, dynamical changes that do not affect Z_mxg can have an effect on Z₂₀ (Fig. 1). In the context of ENSO dynamics, the interaction between SST and h is of particular interest, which could potentially be different for Z₂₀ and Z_mxg. Dommenget and Al-Aasari [2022; here after DA22] presented an extended discussion of the ENSO phase space statistics based on Z₂₀ estimates. They concluded that much of the phase dependent characteristics of the ENSO phase space can be linked to an artificial cross-correlation between Z₂₀ and T. This posed a problem when trying to interpret the phase dependent structures of the ENSO phase space.

The study of Izumo and Colin [I2022] approached the problem of estimating h for the analysis of the ENSO dynamics by statistically improving the estimate of h. They statistically optimized the orthogonality between T and h using sea level data as a proxy for WWV or h.

Here we focus on the temperature profile as an estimate for WWV. By approximating the WWV using the temperature profile, Z₂₀ can have a different dynamical behaviour in ENSO variability from that of Z_mxg since they measure by construction different aspects of the temperature profile.

The aim of this study is to evaluate how the representation of ENSO dynamics change when the thermocline depth estimates are changed from a Z₂₀ to a maximum gradient estimate (Z_mxg). In the following section we will shortly describe the data, the methods of estimating Z₂₀ and Z_mxg, the ReOsc model and how its parameters are estimated and the statistical methods for analysing the ENSO phase space. The first result section will focus on comparing the statistics of Z₂₀ and Z_mxg, which is followed by an analysis of how they co-vary with the SST. We then focus on the analysis of the ENSO phase space diagram in Sect. 5 building up on the results from DA22. This discussion is further explored by the analysis of linear and non-linear ReOsc models fitted to the observed data in Sects. 6 and 7. The study is concluded with a summary and discussion section.

2 Data and methods

Observed data for this study is mostly limited by the subsurface ocean data and we therefore limit the analysis to the time from 1980 to 2021. SST is taken from HADISST 1.1 data set for the period 1980 to 2019 [Rayner et al. 2003]. The temperature index for the ReOsc model is based on monthly mean SST in the NINO3 region (150°W–90°W, 5°S–5°N).

Upper ocean temperature observations for the estimation of Z₂₀ and Z_mxg are based on several ocean analysis data sets: the ocean analysis of the UK Met Office from 1980–2021 [Good et al. 2013], SODA3 1980–2017 [Carton and Giese 2008], CHOR AS and RL ocean reanalysis 1980–2010 [Yang et al. 2017]. The four different datasets are combined to one long time series repeating each common year several times to better capture the variability.

The temperature profiles are based on coarse vertical resolutions with vertical gaps between data points of 5 m or more, see Fig. 2 for examples. For the estimation of Z_mxg and Z₂₀ we use a spline fit interpolation with a vertical resolution of 0.1 m. At the upper and lower end of the data profiles we add additional help points to avoid artificial curves of the spline fit near the ends of the profile. For the upper help point we add a point at depth 0 m with the same temperature as the most upper data point in the profile. At the lower end of the profile, we add another data point below the last data point with the same depth and temperature difference as between the last two points, thus we linearly interpolate. Z_mxg is defined as the depth of the interpolated point with the largest gradient and Z₂₀ as the depth with the interpolated point closest to the 20 °C isotherm, see Fig. 2 for examples.

Fig. 2

Examples of Observed temperature profiles along the equatorial Pacific together with estimates of the Z₂₀ (red dashed line) and Z_mxg (blue dashed line) values. They show the observed data points (black circles), the help points at the ends of the profiles (red triangles), the spline-fitted temperature profile (red lines) and the gradients of the spline-fitted temperature profile (blues lines) in values of [0.02 °C/m] in reference to the 18 °C value on the x-axis

The equatorial mean thermocline depth (h) is defined as the averaged over the equatorial Pacific (130°E–80°W, 5°S–5°N) for both estimates. Some statistics for T and h are shown in Table 1. The ReOsc model, as discussed in this study follows Burgers et al. [2005]. It is presented by two tendency equations:

Table 1 Parameters of the PDF for observed and modelled T and h

$$\frac{dT\left(t\right)}{dt}={a}_{11}T\left(t\right)+{a}_{12}h\left(t\right)+{\zeta }_{T}$$

(1)

$$\frac{dh\left(t\right)}{dt}={a}_{21}T\left(t\right)+{a}_{22}h\left(t\right)+{\zeta }_{h}$$

(2)

The model describes the tendencies of T and h as function of T and h, and some white noise forcing terms (${\zeta }_{T}$ and ${\zeta }_{h}$). It has four important parameters: the growth rates of T (${a}_{11}$) and h (${a}_{22}$), and the coupling parameters (${a}_{12}$ and ${a}_{21}$). They are estimated for the combined observations by multivariate linear regression the monthly mean tendencies of T and h against monthly mean T and h, respectively [Burgers et al. 2005; Jansen et al. 2009; Vijayeta and Dommenget 2018]. h is estimated by either Z_mxg or Z₂₀, resulting into two different estimates of the ReOsc model parameters. The residual of the linear regression fit are interpreted as the random noise forcing terms (${\zeta }_{T}$ and ${\zeta }_{h}$), with the standard deviation (stdv) of the residuals being the stdv of ${\zeta }_{T}$ and ${\zeta }_{h}$. The values of all parameters are shown in Table 2.

Table 2 ReOsc model parameters as they result from different fits to observations

The ReOsc model with different parameter fits can be integrated for 10⁴yrs with white noise forcing for ${\zeta }_{T}$ and ${\zeta }_{h}$, to evaluate the effect on the statistics for T and h. In the following analysis will discuss a number of different ReOsc model fits. Some statistics for T and h for the different fits are given in Table 1.

The analysis of the ENSO phase space is based on monthly mean values of T and h, and follows the approach of DA22. T is presented on the x-axis versus h on the y-axis. This Cartesian coordinate system is transformed into a spherical coordinate system with the phase angle $\varphi = {0}^{o}$ in the h (y-direction) and ${90}^{o}$ in the T (x-direction). $\varphi$ follows a clockwise rotation. T and h are normalized by their respective standard deviation (Table 1) to get a non-dimensional presentation of the variables (T_n and h_n). This normalization is also applied to the ReOsc model parameters (Table 2). The ENSO system anomaly, S, is a vector with the two cartesian coordinates T_n and h_n. In the spherical coordinate system the magnitude of S is constant for a constant radius and is not a function of the phase $\varphi$. Thus, the ENSO system is now described by the magnitude of S and $\varphi$.

The tendencies of the ENSO system in the spherical coordinate system are described by the radial and tangential components. The radial component describes the tendency to move away from the origin (positive values) or towards it (negative values). The tangential component describes the tendency of the system to circle around the origin, with positive values indicating clockwise motion and negative values indicating anti-clockwise motion.

We can define a phase dependent growth rate based on the radial tendencies divided by the magnitude of S. It should be noted that this statistical definition of the growth rate is different from the growth rates ${{\varvec{a}}}_{11}$ and ${{\varvec{a}}}_{22}$, as it includes the dynamical growth and the growth by noise forcing (see DA22for details). A phase dependent phase speed is defined based on the tangential tendencies divided by the magnitude of S. The mean period of an ENSO cycle can be estimated based on integrating the phase speed from 0° to 360°.

In an idealized ReOsc model we would expect all normalized model parameters being symmetrical for T_n and h_n, leading to symmetrical eqs. [1–2]. That is, the growth rates, coupling and strength of the noise forcing are the same magnitudes for both T_n and h_n. Following DA22 we define an idealized ReOsc model reference with the parameters:

$${a}_{11}={a}_{22}=-0.048 \,{mon}^{-1} \quad \mathrm{ and } \quad {a}_{12}={-a}_{21}=0.16 \,{mon}^{-1}$$

(3)

This idealized ReOsc model serves as a reference against which we can evaluate different estimates of the observed ReOsc model, assuming that the observed ENSO is indeed a symmetric, damped oscillation between SST and some subsurface heat content index. Thus, a presentation of ENSO that is closer to the idealised ReOsc model is likely to be a better presentation of the underlying dynamics of ENSO.

3 Comparison of Z ₂₀ and Z _mxg statistics

The Z₂₀ estimate is designed to approximate the variability and mean of Z_mxg. While it is often very close to Z_mxg, it can clearly be different from the Z_mxg for individual profiles (e.g., Fig. 1a).

This can also be illustrated by the example profiles shown in Fig. 2. The nature of the two estimation procedures can lead to different characteristics in their variability. The Z₂₀ estimate is a robust estimate that cannot vary much for small changes in the temperature profile, but it is sensitive to warming of the whole or parts of the profile.

In turn, the Z_mxg is based on gradients that are not sensitive to warming of the whole profile or some parts of it, but it can lead to significant changes in Z_mxg for small changes in the temperature profile that affect the maximum gradient. For instance, the temperature profiles often have a region of 50 m or longer in which the temperature gradients are not substantially different (e.g., Fig. 2a and c). A small change in this region of the profile can lead to substantial changes in Z_mxg but would have very little impact on Z₂₀. This can lead to higher variance in Z_mxg for high frequency variability in small regions or local profiles.

The vertical resolution of the temperature profile and the spline fit used in this approach can affect the estimates, but are unlikely to be a primary problem, assuming we have 10 m or better vertical resolution. The Z₂₀ has little sensitivity to the changes in the resolution from 10 m to much higher resolution, while the Z_mxg estimate can be a bit more sensitive due to the above-mentioned regions of long sections in the profile with nearly constant temperature gradients. Here higher vertical resolution would make the Z_mxg estimate more variable, as it would capture smaller changes in gradients. Therefore, the spline fit of the coarse resolution data acts as a smoothing of the gradients.

The relationship between Z₂₀ and Z_mxg, as Fig. 3 illustrates by the maps of the mean and the standard deviation of Z₂₀ and Z_mxg for the tropical Pacific, varies regionally. The overall pattern and values in the mean are similar for both estimates near the equator (from 5^oS to 5^oN) but disagree further away from the equator. Z₂₀ is generally a bit deeper in the west and shallower in the east equatorial Pacific.

Fig. 3

Comparison of the mean (left column) and standard deviation (right column) of the thermocline estimates Z₂₀ (c, d) and Z_mxg (a, b), and the differences between the two (e, f) in percentages of the Z_mxg values. The correlation between Z₂₀ and Z_mxg are shown in (g)

The standard deviation is enhanced on the equator relative to the off-equatorial regions in particular for the central to eastern Pacific, and more clearly for Z₂₀ than for Z_mxg. The variability in the western equatorial Pacific is stronger for Z_mxg than for Z₂₀ and it is weaker for Z_mxg than for Z₂₀ in the far eastern equatorial Pacific. The correlation between Z₂₀ and Z_mxg is relatively high in the central equatorial Pacific and lower at higher latitudes, see Fig. 3g.

For the dynamics of ENSO, as discussed in the context of the ReOsc model, the thermocline depth of the whole equatorial Pacific (h) is a dynamical variable of importance. Figure 4a shows the time series of h, as estimated by Z₂₀ and Z_mxg. We can note that they are highly correlated and that the standard deviation of both is very similar.

Fig. 4

a Time series of h estimated by Z₂₀ (red) and Z_mxg (blue). The correlation value r and the ratio in the standard deviations are shown too. b Power spectra of Z₂₀ (red) and Z_mxg (blue) and the cross-spectral power between the two estimates (black). c Cross-spectral coherence and d cross-spectral phase between the two estimates

The power spectra of the two estimates of h show that Z_mxg has more variance than the Z₂₀ on nearly all frequencies, but in particular on the high frequencies (Fig. 4b). This can reflect the nature of the physical processes causing the variability in these two variables, but it may also reflect the nature of how the two variables are defined (see discussion above).

A more important difference in the variability of Z₂₀ and Z_mxg can be noted in the cross-power spectrum between the two estimates, see Fig. 4b-d. For lower frequencies (smaller than 1/yr), for which the variability of the two estimates is highly coherent, we can note that the Z_mxg estimates leads the time evolution of Z₂₀ by about 25°. Thus, variations in Z_mxg appear significantly earlier in time than they do in Z₂₀. Such differences in the timing of the variability is important for the ENSO phase space discussions, as they focus on the phase relations between T and h.

4 Co-variability with T

The idealised ReOsc model suggests that T and h should have a perfectly out-of-phase cross-correlation, with zero correlation at lag zero and opposite cross-correlations at lags of opposite signs, Fig. 5. In the following analysis we will use the idealised ReOsc model as a reference against which we evaluate the different estimates of h, assuming that the estimate that more closely follows the idealised ReOsc model is more accurate.

Fig. 5

Cross-correlation between T and h based on Z₂₀ (red) and Z_mxg (blue), and for the idealised ReOsc model simulation (black). The 90% confidence interval (shaded area) is based on 40yrs long time series of the idealised ReOsc model simulation

The Z_mxg does follow this out-of-phase cross-correlation of the idealised ReOsc model for time lags near zero very well but does show some significant deviations for lags < − 12 mon and lags > 3 mon. The mismatch between the observed Z_mxg estimate and the idealised ReOsc model is much stronger when h leads T than when T leads h. This asymmetry is unexpected from the idealised ReOsc model.

The Z₂₀ estimate, however, does not appear to fit to the idealised ReOsc model on any time lag. The cross-correlation at lag zero is strongly positive and the lag-lead time evolution of the cross-correlation is clearly shifted towards negative time lags.

The cross-power spectrum between T and h provides an alternative way of evaluating the cross-relation between T and h, see Fig. 6. Both estimates have very similar behaviour for the cross-spectral amplitude and coherence, but different phase relations for longer time scales. The cross spectral amplitude for both estimates is higher than that of the idealised ReOsc model for frequencies away for the peak amplitude frequency, and it is lower at frequencies near the peak amplitude for both estimates (Fig. 6a). The coherence is also a bit higher for frequencies away for the peak amplitude frequency for both estimates than expected from the idealised ReOsc model (Fig. 6b). The phase relation of the Z_mxg estimate appears to be largely in agreement with the expected 90° relation found in the idealised ReOsc model. However, the Z₂₀ estimate has a significant deviation from the 90° relation for interannual frequencies, suggesting a closer in-phase relation between Z₂₀ and T than expected from the idealised ReOsc model. This is consistent with the cross-correlation at lag zero being positively correlated between Z₂₀ and T.

Fig. 6

Cross-spectral analysis between T and h based on Z₂₀ (red) and Z_mxg (blue), and for the idealised ReOsc model simulation (black). The 90% confidence interval (shaded area) is based on 40yrs long time series of the idealised ReOsc model simulation. a Cross-spectral amplitude, b coherence and c phase

The fact that the Z₂₀ estimate does not have the 90° out-phase relationship with T could potentially be related to the assumption that h should be the mean over the whole equatorial Pacific. The mean thermocline depth over the whole equatorial Pacific is a balance of thermocline depth in the western equatorial Pacific, which tends to have a negative correlation (at lag zero) to T, and the thermocline depth in the east, which tends to have a positive correlation to T [Meinen et al. 2000; Izumo and Colin 2022; Jin 1997]. A change in the regional weighting of the western and eastern equatorial Pacific could potentially improve the phase relation between Z₂₀ and T. Due to the different strength of variability of the Z_mxg and Z₂₀ estimates in different regions of the tropical Pacific (Fig. 3), they effectively have different weightings of the west and east tropical Pacific in the arithmetic mean thermocline. depth over the whole equatorial Pacific (h). The Z_mxg estimate has more variability in the western Pacific relative to the Z₂₀ estimate (Fig. 3), which shifts the balance away from the east and further to the west, if compared against the Z₂₀ estimates, effectively being more shifted towards a negative correlation with T.

However, this regional shift in variance it not the most important difference between the two estimates, as the estimates are by construction different in nature. We now test the role of the regional weighting along the equatorial Pacific by estimating h with Gaussian weighting function, see Fig. 7a. The weighting function has different weights as function of longitudes with a width of the Gaussian function of 20° longitudes. For each estimate we shift the peak of the distribution by 10° longitudes. This effectively tests how the cross-relation between T and h depends on the relative weighting between the western and eastern equatorial Pacific thermocline depth.

Fig. 7

Statistics of longitudinal weighted estimated of h based on Z₂₀ (red) and Z_mxg (blue): a weighting functions used to estimate h. b correlation between T and h. c Mean phase between T and h for frequencies < 1/yr. d Correlation between dT/dt and h. The x-axis values in b-d mark the longitude of the peak value of the weighting functions. Panels b-d also show the values of the idealised ReOsc model (solid black line), of the Z₂₀ (red dotted) and Z_mxg (blue dotted) estimates based on the whole equatorial Pacific without a weighting function

Figure 7b shows the cross-correlation between T and h as function of the longitude with the maximum weighting for h. For both estimates we find a clear transition from a negative correlation in the western equatorial Pacific towards a positive correlation in the eastern equatorial Pacific, consistent with findings from previous studies. Thus, there is a longitude for both estimates at which the correlation between T and h is zero, which is further to the west for Z₂₀ than for Z_mxg. For most of the equatorial Pacific the Z₂₀ estimate has a larger (more positive) correlation than Z_mxg, indicating that Z₂₀ is generally more strongly correlated with T than the Z_mxg. The Z₂₀ estimate is also more sensitive to the longitude of the weighting function, as the correlation varies more strongly from the western to the eastern equatorial Pacific.

The idealised ReOsc model suggests that T and h should have a 90° phase relationship for frequencies smaller than 1/yr. Figure 7c shows the mean phase for both estimates as function of the longitude with the maximum weighting for h. Similarly, to the cross-correlation results we can note a transition from the west to the east towards a more in-phase (phase zero) relation between T and h. Again, there is a longitude at which both estimates have the expected 90° phase relationship, but for both estimates this is slightly different from the longitude at which the cross-correlation is zero (compare Fig. 7b and c). The mean phase of Z₂₀ is also more sensitive to the longitude of the weighting than for Z_mxg.

A key idea of the idealised ReOsc model is that h forces the tendencies of T (eq. [1]), with positive h leading to positive tendencies in T and vice versa for negative h. Thus, we would expect that there is a positive correlation between dT/dt and h. In the idealised ReOsc model this correlation is 0.48. For the mean equatorial Pacific estimates of h with Z₂₀ and Z_mxg the values are 0.36 and 0.43, respectively. Indicating that Z_mxg is closer to the idealised ReOsc model expectation than Z₂₀. These values vary substantially for the longitude with the maximum weighting for h, see Fig. 7d. Both estimates peak at a similar longitude in the central Pacific, but the correlation is higher at all longitudes for Z_mxg.

In addition to the sensitivity of h to the longitudes over which it is estimated there is also a potential sensitivity of h to the latitudes over which it is estimated. We therefore estimate h with different width in latitudes centred around the equator, ranging from 1° to 20°, see Fig. 8. For width ranging from 1° to about 7° the Z_mxg estimate tends to be closest to what we would expect from the idealised ReOsc model. For width larger than the cross correlation.between T and h, and between dT/dt and h clearly point out that the estimates are drifting away from the expected idealised ReOsc model, suggesting these estimates are not relevant for ENSO dynamics. Again, the Z₂₀ estimates are clearly further away from the expect statistics for the idealised ReOsc model than the Z_mxg estimates, suggesting that the Z_mxg estimates are the better estimates for the analysis of ENSO dynamics.

Fig. 8

Statistics of h based on Z₂₀ (red) and Z_mxg (blue) with different latitudinal width: a correlation between T and h. b mean phase between T and h for frequencies < 1/yr. c correlation between dT/dt and h. The x-axis values mark the latitudinal width for the estimation of h. The idealised ReOsc model is shown with a solid black line for comparison

5 The ENSO phase space

We now focus on the ENSO phase space, which highlights the dynamics between T and h, as a cycle of an oscillation between T and h. In an idealised linear ReOsc model the phase space should present T and h as a perfect circle with clockwise phase propagation through all phases [DA22].

Figure 9 shows the ENSO phase space base on the Z₂₀ and Z_mxg estimates. The Z₂₀ estimate is essentially the same as the one discussed in DA22 and is marked by a preferred likelihood to be along the diagonal quarters Q1 to Q3 due to the correlation between Z₂₀ and T as discussed in DA22. The Z_mxg estimate is more circular and does not appear to be stretched along the diagonal from Q1 to Q3.

Fig. 9

Observed ENSO phase space based on Z₂₀ (left) and Z_mxg (right). The times series of $\overrightarrow{\mathrm{S}}$ are shown as grey lines and the vectors are the mean tendencies of T_n and h_n within a range of ± 0.4 to the reference point in the phase space (starting point of the vector). A vector of unit length is a tendency of 1 mon⁻¹ and the scale of the vector is proportional to the magnitude of the tendencies. Vectors are only shown for S < 3.5 and where there is actual data. The red line marks the mean value of $\overrightarrow{\mathrm{S}}$ for each angle within an angle range of ± 20°. In addition to the Cartesian coordinates T_n and h_n, the spherical coordinates for the radius ($\overrightarrow{\mathrm{S}}$) values [2,3,4] and angle ($\mathrm{\varphi }$) in clockwise notation are given

The mean S and the probability of S > 2 as function of phase are shown in Fig. 10a and b. Both estimates have similar mean S with a high correlation (see r-value in Fig. 10a), but with the Z_mxg estimates showing larger values in the Q2 quarter and the Z₂₀ estimate being more pronounced in the Q1 and Q3 relative to the Q2 and Q4 quarters.

Fig. 10

Statistics of the ENSO phase space for the Z₂₀ (red) and Z_mxg (blue) estimates in comparison to idealised ReOsc model statistics. a mean value of $\overrightarrow{\mathrm{S}}$ for each angle within an angle range of ± 20°. b Probability for S > 2 as function of angle within a range of ± 20°. Probability values are in arbitrary units. c growth rate in [1/mon]. d phase speed in [1/mon]. The idealised ReOsc model values are shown in panels a-c as black lines and with a 90% confidence interval (grey shaded area) assuming a 40yrs long time series. In d the uncoupled ReOsc model is shown (black lines) as a reference with an expected zero phase speed. Again a 90% confidence interval, assuming a 40yrs long time series, is shown as a grey shaded area. The mean period of the ENSO cycle based on the phase speed integrated over all phases are shown for Z₂₀ (red) and Z_mxg (blue) estimates in panel d. The correlation between the Z₂₀ and Z_mxg estimates are shown as the r-values in each panel

More pronounced differences between Z₂₀ and Z_mxg are noted for the extreme values of S > 2. Here the Z_mxg estimate shows a very clear picture with the extremes being focussed on the Q2 quarter, which is somewhat expected from the skewness of T and Z_mxg (Table 1). The Z₂₀ estimate is clearly stretched out to the Q1 and Q3 quarters due to the positive correlation between Z₂₀ and T.

An important aspect that the phase diagram allows to analyse is the phase dependence of the growth rate and phase speed of the ENSO dynamical system. Figure 10c and d show the growth rate and phase speed as function of phase. The two estimates do have only modest similarity, but indeed show some important differences.

The growth rate of the Z_mxg estimate shows positive growth rates from shortly after the La Nina state (~ 300°) until shortly after the El Nino state (~ 130°) and negative growth for the rest of the cycle. The growth rate of the Z₂₀ estimate is more complex with positive growth rates around the recharge and discharge states (0° and 180°) and negative growth rate near the Nina state and El Nino states (90° and 270°). This pattern is again strongly related to the positive correlation between Z₂₀ and T, as discussed in DA22.

The phase speed shows substantial differences between the two estimates. The Z₂₀ estimate shows very strong variations with fastest transitions in the Q2 and Q4 quarters and slowest in quarter Q3, which are again a result of the correlation between Z₂₀ and T (see discussion in DA22). This result is in quite contrast to the literature discussion, which state that the ENSO cycle is slowest or least clear in quarter Q2 [e.g., Kessler 2002].These variations in phase speed are also much larger than those in the Z_mxg estimate, however they lead to a similar estimate of the mean cycle period (see values in Fig. 10d).

The Z_mxg estimate has the fastest transition after an El Nino state (100° to 160°) and the slowest between the La Nina and the recharge states (270° to 30°) consistent with the discussion in Kessler [2002]. Further, both estimates have mean phase speeds significantly different from zero for all phases suggesting that ENSO is indeed a cycle. This is more clearly the case for Z_mxg than for Z₂₀.

6 Fit of the linear ReOsc model

The characteristics of the ENSO phase space diagram can best be understood in the context of the ReOsc model. We therefore fitted the linear ReOsc model to the Z₂₀ and Z_mxg data with the same T values for both, resulting into two different sets of estimated ReOsc model parameters corresponding to the Z₂₀ and Z_mxg, respectively (see methods section for details). It should be noted here that the multi-variate approach does lead to changes in all parameter, not just the ones directly related to h. The model parameters are listed in Table 2.

Given that Z₂₀ and Z_mxg have different standard deviations, we expect the model parameters, which are related to h, to be different for the two estimates. To be able to better compare the different ReOsc models estimates we can focus on the non-dimensional, normalised model parameters (see Table 2). The normalized model parameters also allow us to compare the dynamics of the tendency equations of T and h irrespective of the physical units of T and h.

The Z₂₀ estimate of the normalized ReOsc model parameters are very similar (symmetric) for T and h for all aspects, but not for the growth rate. The growth rate in T is strongly damped, whereas the growth rate in h is weakly positive. This asymmetry is a result of the positive correlation between T and Z₂₀, as discussed in DA22. The ReOsc model fit of the Z_mxg estimate is much more symmetric in all aspects of the tendency equations, including the growth rates, which are nearly identical for T and h. Here both growth rates are equally strongly damped (negative). This fit is very similar to the idealised ReOsc model (Eq. 3).

The differences in the fitted ReOsc model parameters result into very different statistics of the ENSO phase space, as can be shown by integrating eqs. (1,2) with white noise forcing for 10⁴yrs, see Table 1 and Fig. 11. The linear model with the Z_mxg estimate has very little to no phase dependencies, whereas the linear ReOsc model with the Z₂₀ estimate has very clear phase decencies resulting from the asymmetry in the growth rate of T, which is a result of the correlation between T and Z₂₀. The linear ReOsc model with the Z₂₀ estimate has good correlation with the observed statistics, suggesting that much of these observed statistics can be explained by the correlation between T and Z₂₀. Thus, it is unlikely that these characteristics mark true underlying structure of the ENSO recharge oscillator dynamics. They are most likely just a limitation, resulting from the artificial correlation between T and Z₂₀. The results of the ENSO phase space statistics of the Z_mxg estimate in turn suggest that basically all the observed phase dependent characteristics are unrelated to linear dynamics. Thus, they must result from some non-linear ENSO dynamics.

Fig. 11

Statistics of the ENSO phase space for the Z₂₀ (left) and Z_mxg (right) estimates, as in Fig. 10, but in comparison to the fitted linear ReOsc model statistics. Each panel shows the observed statistics (blue lines), the linear ReOsc model fit (red lines) and the idealised ReOsc model reference (black lines) with the 90% confidence interval in shaded grey areas. The correlation between the observed and the fitted ReOsc model values are shown as the r-values in each panel

7 Fit of a non-linear ReOsc model

The analysis of the linear ReOsc model fitted to the observed Z_mxg estimate in the previous section suggests that the phase dependent characteristics of the observed ENSO phase space are potentially resulting from non-linear interactions between T and h, and their tendencies. Previous studies have suggested several different processes that could contribute to non-linear interactions between T and h, including non-linear growth of T or h, state-dependent noise, non-linear response of wind stress to SST or non-linear coupling of T or h [e.g., Frauen and Dommenget 2010; Kim and An 2020; Levine et al. 2016]. It is beyond the scope of this study to fully explore what non-linear aspect of ENSO may explain the ENSO phase space characteristics, but similar to the approach in DA22 we like to give some indication of how non-linear processes can potentially explain the observed ENSO phase space characteristics.

We follow the approach in DA22 and focus on a non-linear growth rate of T assuming a quadratic function. We replaced eq. (1) of the ReOsc model to include a non-linear growth rate of T:

$$\frac{dT\left(t\right)}{dt}={a}_{11-2}{T}^{2}\left(t\right)+{a}_{11-1}T\left(t\right)+{a}_{11-0}+{a}_{12}h\left(t\right)+{\zeta }_{T}$$

(4)

A Nelder-Mead optimization scheme is used to estimate the non-linear model parameters (${a}_{11-2},{a}_{11-1},{a}_{11-0})$. The cost function for this optimization is based on integrating the model for 1000yrs and estimate the monthly mean distribution parameters of T and h. The parameters of this non-linear model for Z₂₀ and Z_mxg estimates are shown in Table 2. For both models we have a stronger negative feedback for large negative T values, and a weaker or positive feedback for large positive T values. This is qualitatively similar to models suggested in previous studies [e.g., Frauen and Dommenget 2010; Kim and An 2020; Geng et al. 2019; DA22]. We integrate this model with the same noise forcing as for the linear model. We refer to this model as the non-linear ReOsc model. Statistics for T and h for Z₂₀ and Z_mxg estimates are listed in Table 1.

Figure 12 shows the statistics of the ENSO phase space of the non-linear fits for the Z₂₀ and Z_mxg estimates. First, we can note that in general the non-linear ReOsc model fits better to the observed data for both estimates than the linear model (compare correlation values in Figs. 11 and 12). This is essentially expected, since we optimised the non-linear model to fit to the observations, and the non-linear model has more parameters to be optimized than the linear model. Second, we can again notice that the non-linear model fits are substantially different between the two estimates, highlighting that the two estimates give very different presentations of the ENSO dynamics (see correlation values in Fig. 12).

Fig. 12

Statistics of the ENSO phase space for the Z₂₀ (left) and Z_mxg (right) estimates, as in Fig. 11, but in comparison to the fitted non-linear ReOsc model statistics. For each panel in the right column the correlation between the statistics of the fitted non-linear ReOsc model for the Z₂₀ and Z_mxg estimates are shown as the red r-values

The non-linear fit for the Z₂₀ estimate is closer to the observed data than the linear fit, but it is not substantially different, suggesting that much of the structure in the phase space diagram is resulting from linear dynamics.

Focussing on the Z_mxg estimate we can notice that the non-linear model fit does capture parts of the phase dependent mean S and the probability of S > 2 (Fig. 12b,d) much better than the linear fit. The non-linear ReOsc model can capture well the asymmetry in the mean El Nino (90°) and La Nina states (270°), with larger means for the El Nino state, but it has larger than observed mean S for the recharge state (0°) and smaller than observed mean discharge states (180°).

This mismatch in the asymmetries along the h-axis become clearer for the extreme values of S > 2 (Fig. 12d). Here the observed data shows a very strong non-linearity towards extreme discharge states. This is not captured by the non-linear ReOsc model fit. This marks a strong limitation of the non-linear ReOsc model fit.

The strongest mismatch between the non-linear model fit and the observed Z_mxg estimate is in the growth rates. Here there is essentially no match between the two. The non-linear ReOsc model fit has positive growth rates during the El Nino state and negative growth rates during the La Nina state. This is what is expected since we constructed the non-linear model with a non-linearity in the growth rate of T only. However, this does not match very well with the observed, both in terms of the phase space structure, as measured by the correlation, and in terms of the overall strength in the variations with different phases, which is much stronger in the observed than in the non-linear model.

The phase transition speed variations with the phases are also not well captured by the non-linear ReOsc model. The model fails to capture the faster phase transitions after an El Nino state and suggests the fastest transitions during the discharge state (180°), which is not observed.

Overall, we have to conclude from this non-linear model fit, that the observed variations in the ENSO phase space are only moderately well capture by a model with non-linear growth rate in T, and that there are important aspects of the ENSO phase space that remain unexplained by this approach. Most importantly, these are asymmetries along the h axis, between the recharge and discharge states.

8 Summary and discussion

In this study we looked at the differences in the representation of the ENSO dynamics, as represented in the phase space, if based on Z₂₀ and Z_mxg. While the statistics of equatorial mean variability of Z₂₀ and Z_mxg estimates are very similar in many aspects, they do have substantially different representations of the ENSO phase space. The Z₂₀ estimated is more in-phase correlated with T, which results into ENSO phase space diagrams that are dominated by this correlation, but in turn does not present important non-linear aspects of ENSO very well. The Z_mxg estimated presents the ENSO phase space much more as expected from an idealised ReOsc model, with clear out-of-phase relations between T and h.

We further evaluated the longitudes and latitudes over which h should be estimated. We find that for both estimates there exist a region along the equatorial Pacific for which there is a perfect out-of-phase relation between T and h. However, the Z₂₀ estimate is more sensitive to the region over which it is estimated and has in general a lower correlation with the tendencies of T than the Z_mxg estimate.

A Fit of linear and non-linear ReOsc models to the observed data of T, Z₂₀ and Z_mxg also showed substantial differences between the two estimates. The Z_mxg estimate suggests that phase dependent ENSO statistics results entirely from non-linear dynamics, while in the Z₂₀ estimate much of the phase dependent ENSO statistics result from linear ReOsc dynamics related to the in-phase correlation between T and Z₂₀. Based on the non-linear ReOsc model using the Z_mxg estimate we find that a non-linear growth rate of T can only capture some elements of the non-linear ENSO phase space, but misses out on substantial non-linear behaviour for the variability in h. It also has only limited skill in capturing the observed phase dependent aspects of the growth rate and phase speeds. This suggest that other processes than the growth rate of T must contribute to the non-linear behaviour of ENSO.

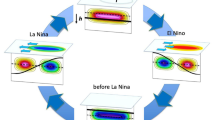
Using the more realistic presentation with the Z_mxg estimate we can use the ENSO phase space diagram to describe the typical (mean) ENSO cycle, see sketch in Fig. 13. Starting at the recharge state: this state has, in the mean, relatively weak values and rarely has any extreme values. However, it is the phase of the ENSO cycle that is in average most unstable (positive growth rates) and will therefore lead to growth in the ENSO anomalies. At the same time the phase speed is slower than in average, allowing the ENSO anomalies to grow. This will lead to relatively strong El Nino states, which can have some of the most extreme ENSO anomalies.

Fig. 13

Sketch illustrating the idealised observed ENSO phase space. Shading indicates the probability density distribution, the green band marks the mean cycle and the arrows the mean phase speed

After the El Nino state comes a phase with relative fast phase transition speed and positive growth rates. This leads to a transition into strong discharge states. Indeed, the discharge state, is the state with the most extreme ENSO anomalies. The transition from the discharge state to the La Nina state is marked by negative growth rates and moderate phase transition speeds. This leads to relatively weak mean La Nina states and rarely any extreme La Nina states.

The transition from a La Nina state to the recharge state starts with a phase of negative growth rate and a slow phase transition. This leads into the phases of the ENSO cycle with the weakest mean ENSO anomalies and the absence of any extreme values. Despite the ENSO cycle slowing down and weakening in these phases, there is still a significant mean phase transition to the next phase, the recharge state, completing the cycle. Thus, ENSO is a cycle with clear phase transitions through all phases. The La Nina to recharge transition is, however, the phase which is most likely to stall, allowing the ENSO cycle to break.

In summary, the ENSO phase space analysis using the Z_mxg estimate provides a very powerful statistical analysis of ENSO dynamics. It can provide analysis of growth rate and phase speed as function of the ENSO phase, including non-linear aspects of ENSO. A key signature of the analysis of a phase space is that it presents the system as a cycle, which allows to clearly study how the system evolves from one phase to the next. This is an aspect that previous linear statistics of ENSO, such as lag-lead cross-correlations (Fig. 5) or composite time evolutions of events (e.g. Figures 2–4 in Okumura and Deser 2010 of Figs. 5 and 7 in Dommenget et al. 2013) do not capture as well.

This concept of phase space analysis as presented in this work is not limited to ENSO studies, but it has general application for the analysis of climate modes. A phase space, for instance, have been used in the context of the Madden–Julian Oscillation [MJO; Wheeler and Hendon 2004]. This can in general be extended to any climate mode. It will require to find a 2-dimensional presentation of the climate mode by two out-of-phase variables that transition into one another as it is the case for T and Z_mxg for ENSO or the two leading EOF-modes for the multivariate MJO-index [Wheeler and Hendon 2004].

The above discussion of the ENSO phase space has also illustrated that it is not always clear what are the best variables to present the dynamical phase space. While the phase space based on for T and Z_mxg shows good characteristics of presenting the ENSO dynamics, it is not necessarily a perfect presentation of ENSO dynamics. Other studies suggested different ways to present the ENSO phase space [e.g., Wang and Wang 2000; Izumo and Colin 2022]. In the context of tropical basin interactions, it also needs to be considered that ENSO dynamics are partly controlled by the other tropical ocean basins [e.g., Dommenget and Yu 2017; Cai et al. 2019]. Further studies are needed to further explore how an ENSO phase space can be presented in an optimal way.