1 Introduction

It has now become quite clear that the emission into the atmosphere of huge amounts of CO\(_2\) from the combustion of fossil fuels by humankind, together with other changes such as deforestation and intensive agriculture, is altering the climate, with rising temperatures over most of the planet (Cubasch et al. 2013). One concern for society and its policymakers is that higher average temperatures may enhance the risk of extreme events such as heatwaves. These are associated with effects that can be lethal for humans, and, even below lethality, can have adverse impacts on their livelihoods (Field et al. 2012). Examples of such heatwaves were those that occurred in Southern Europe in 2003 (García-Herrera et al. 2010), Russia in 2010 (Barriopedro et al. 2011), and Canada in 2021 Thompson et al. (2022).

The best tools with which to project the future evolution of these extreme events are global climate models (GCMs) that take account of forcing from greenhouse gas emissions (see for example (Randall et al. 2007)). At present however, these models are too coarse to properly represent atmospheric properties such as temperature or precipitation at the local scale as would be needed for adaptive planning and policy making. This issue is usually addressed by downscaling the GCMs using Regional Climate Models (RCMs) (see for example (Xu et al. 2019; Tapiador et al. 2020) and references therein). An RCM is a limited-area weather model embedded in a GCM, or a higher resolution reanalysis that takes inhomogeneities of the Earth’s surface into account as well as other properties not covered by the coarser GCMs. Obviously, if an RCM is to be used to study the future state of the climate then it must describe reasonably well the current state. The variable on which the present study will focus is that of extreme temperatures.

There are two main ways to approach the study of extreme meteorological and climate events. One is to use extreme indices such as some high percentile of the probability distribution function (Zhang et al. 2010; Peterson et al. 2001; Peterson 2005). The other is to apply the branch of statistics known as extreme value theory (EVT). An important advantage of the latter is that the technique is more informative than that of the extreme indices since, by obtaining the parameters of the distribution function, one can estimate the likelihood of as-yet unobserved events—the 100-year return level for example. This feature is widely used for engineering design purposes. The main drawback of EVT is probably the requirement for independence of the data which is needed to estimate the parameters of the distribution. But Coles (2001), among others, have shown that under conditions of weak dependence between the variables, the EVT can still be applied. The present work in particular applies the GEV formulation of EVT in order to get a climatological picture of extreme temperature events through estimating the parameters of the corresponding extreme value distribution. Given the spatial character of temperature as a variable, it seemed appropriate to use the theory of spatial extremes to study it. Three approaches have typically been used to address the problem of spatial extremes—max-stable random fields, copulas, and Bayesian hierarchical models (Davison et al. 2012)—and it is this last approach we shall take in the present work. One of the more important benefits of using a spatial extremes theory instead of modeling each observatory individually is the increased precision when estimating the parameters of the statistical distribution. Indeed, one of the difficulties one faces in a statistical study of extreme data is that, by their very nature, extreme data are ‘rare’, i.e., there are usually so few data that one must expect to get a large uncertainty in the parameters that describe the tail of the statistical distribution. One way to mitigate the consequences of this lack of data and to increase the precision of the parameter estimates is to trade space for time, pooling information from different observatories (see, for example, (Casson and Coles 1999; Cooley et al. 2007; Schliep et al. 2010)). Also, as pointed out by Renard (Renard 2011), a spatial theory allows the parameters of the extreme distribution to be estimated at an ungauged or poorly gauged site. This important advantage allows one to address the so-called change of support problem in spatial statistics (see (Gelfand et al. 2001; Fuentes et al. 2003)). This problem arises when one tries to compare data coming from sources at different spatial scales. In our case, we want to compare the extreme value distribution obtained from a model defined at a grid-cell scale with that obtained at a meteorological observatory defined at a local scale. Moreover, the use of Bayesian statistics allows one to account properly for the uncertainties that naturally arise when modeling meteorological phenomena (see Epstein (1985)).

Most published studies dealing with extreme weather and climate events obtained from GCM/RCM models used extreme indices (Sillmann et al. 2013a, b; Bartolomeu et al. 2016; Deng et al. 2016; Jiang et al. 2015; Lorenz et al. 2016; Zollo et al. 2016). Far fewer have used EVT. As one example of applying EVT, Kharin and Zwiers (2005) made a study of extreme temperature and precipitation in a GCM for the period 1990–2100, considering several scenarios using a GEV distribution. Also, Tomassini and Jacob (2009) made an analysis of extreme precipitation in Germany using a non-homogeneous Poisson point process to determine the GEV parameters. Both cases, however, fitted the statistical model to the results obtained at each grid point individually. On the other hand, Schliep et al. (2010) used a spatial hierarchical model in a study of extreme precipitation obtained from six different RCMs. That study used a multivariate intrinsic autoregressive (IAR) spatial model—a kind of Gaussian Markov Random Field model. While this type of model is computationally well suited to fitting the gridded output of a climate model, it is less suitable for making a prediction at a ‘non-observed’ site. A model closer to the one used in the present work is that of Craigmile and Guttorp (2013) who studied extreme minimum temperatures obtained in Sweden from an RCM. The main problem we have found in that paper is that the analysis does not take the altitude dependence of the temperature into account, a dependence that is now included in the present model.

The objective of the present study was therefore twofold—firstly, to simulate the present climate in our region by means of an RCM, specifically, the WRF v4.0 model using ERA Interim reanalysis boundary conditions, and secondly, to produce a statistical model which can be used to characterize summer extreme temperatures produced by the RCM for the region of Extremadura (Spain). This statistical model will then be used to assess whether the RCM can correctly describe the region’s observed extreme temperatures.

The paper is organized as follows. The data used are described in Sect. 2, the details of the statistical model are presented in Sect. 3, and the results in Sect. 4. Finally, some conclusions are drawn and discussed in Sect. 5.

2 Data

The temperature data used come from a simulation of the climate using the community WRF model (version 4.0.1) (Skamarock et al. 2008) forced with ERA Interim (Dee et al. 2011) reanalysis. The period for the simulation was 1980–2015. The simulation used two two-way nested domains centred in the Iberian Peninsula. The larger external domain’s resolution was 36 km, and the internal one’s was 9 km. Figure 1 shows the position of the two domains. The number of vertical levels is 50.

Fig. 1
figure 1

The blue boxes in the map shows the position of the two domains used in the simulation. The larger external domain’s resolution was 36 km, and the internal one’s was 9 km

Full size image

Every 6 h, the boundary conditions, including Sea Surface Temperature (SST) and deep-soil temperature updates, were provided, and analysis nudging was applied in the external domain beyond the Planetary Boundary Layer (PBL). The WRF physical configuration was: Microphysics—WRF Single-Moment 6-class (Hong and Lim 2006); Longwave/Shortwave Radiation—RRTMG (Iacono et al. 2008); Surface Layer—MM5 similarity (Jiménez et al. 2012); Planetary Boundary Layer—Yonsei University (Hong et al. 2006; Hong 2010); Land Surface—Noah Land Surface Model (Chen and Dudhia 2001); Cumulus Parametrization—Grell-Freitas (Grell and Freitas 2014). The model was run at intervals of 6 years, disregarding the first as a spin-up, and combining the results at the end. The version of WRF used was that modified by (Fita et al. 2019) which allows the user to obtain extreme values from the data simulated at each step of the modeling process.

In the inner domain, we focused on the region of Extremadura (Fig. 2).

Fig. 2
figure 2

Location of the Extremadura region in the Iberian Peninsula (left). Topographic map of Extremadura as seen by the WRF model (right) with the scale in the colorbar in metres above sea level (m.a.s.l.)

Full size image

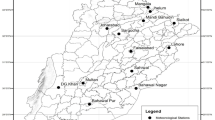
For comparison with the results obtained with our statistical model, a set of extreme temperatures in the period 1981–2015 observed at 28 meteorological observatories sited in the aforecited region of Extremadura was used. Table 1 lists the code, name, and geographic coordinates of these observatories. Figure 3 shows their positions within the region of Extremadura.

Table 1 Code, name, and geographical coordinates of the meteorological observatories used in the study
Full size table
Fig. 3
figure 3

Location within the Extremadura region of the meteorological observatories

Full size image

For both the WRF model and the observed data, the extreme temperature is the highest temperature during the summer season (June–July–August).

We also used the Stead database developed by Serrano-Notivoli, Begueria, and De Luis Serrano-Notivoli et al. (2019) to compare the climatology of the maximum daily summer (June–July–August) temperatures given by the WRF model.

3 Statistical model

As was noted in the Introduction, we shall use a Bayesian hierarchical model framework in which to address the problem of estimating the parameters of a spatial Extreme Value model. In this framework (see Berliner (2003); Cressie (2011)), in the first stage, denoted ‘data model’, it is assumed that the observed noisy data are random variables that depend on a latent (unknown) process plus various parameters. In the second stage, denoted ‘process model’, a model is proposed for the latent process through a conditional probability distribution. It is in this second stage that scientific models are usually introduced. The third stage, denoted ‘parameter model‘, can be considered the Bayesian part of the hierarchical model. In it, the parameters are considered random variables with a probability distribution function to take into account the uncertainties about them.

Stage 1 (data model):

\(\textbf{P}( \text {data} \ \ \vert \ \text {process},\ \text {parameters} )\)

Stage 2 (process model):

\(\textbf{P}(\text {process}\ \ \vert \ \text {parameters})\)

Stage 3 (parameter model):

\(\textbf{P}(\text {parameters})\)

Bayes’ theorem allows one to determine the distribution of the model’s parameters once the data have been observed. The corresponding relationship is

$$\begin{aligned}{} & {} \textbf{P} ( \textrm{process}, \ \textrm{parameters}\ \vert \ \textrm{data} ) \nonumber \\{} & {} \quad \propto \textbf{P} (\textrm{data} \ \vert \ \textrm{process}, \ \textrm{parameters}) \cdot \textbf{P} ( \textrm{process} \ \vert \ \textrm{parameters} ) \nonumber \\{} & {} \quad \cdot \textbf{P} ( \textrm{parameters} ). \end{aligned}$$
(1)

The distribution on the left hand side of Equation (1) is termed the posterior distribution, the distribution \(\textbf{P}(\textrm{parameters})\) on the far right the prior distribution, and the distribution \(\textbf{P}(\textrm{data}\vert \textrm{process}, \textrm{parameters})\) in the middle the likelihood. One of the problems with Equation (1) is that the proportionality constant is unknown. Its evaluation is only feasible in simple cases. The introduction of numerical techniques such as Markov chain Monte Carlo (MCMC) methods ( Gilks et al. (1996)), however, has allowed numerical simulation of the posterior distribution of the parameters, in particular by obtaining a sample of the parameters of interest. In the following subsections, we shall describe the proposed model in greater detail.

This hierarchical model may be placed in a more specifically climatological context (see for example Berliner (2003), Cooley et al. (2007)). It is well known that the weather, i.e., the state of the atmosphere at a given time and place, may be regarded as a random process and the relevant weather variables (pressure, temperature, etc) as random variables. The values of these random variables are expressed by probability distributions whose parameters may be considered to represent the climate of that place. This process corresponds to Stage 1 of the hierarchical model. Furthermore, in Stage 2, the climate, represented by the parameters of the distribution, is itself regarded as a random process expressed by a probability distribution. Finally, in Stage 3, a probability distribution is proposed for the prior of the parameters that appear in Stage 2.

3.1 First stage (data model)

In the first stage, we assume that the block extreme data at observatory s, \(Y_s\) follow a GEV distribution, where the probability distribution function can be expressed as

$$\begin{aligned}{} & {} \textbf{P}(Y_s \le y \vert \mu _s, \sigma _s, \xi _s ) =\;\; \exp \left\{ -\left[ 1+\xi _s \left( \frac{y-\mu _s}{\sigma _s}\right) \right] ^{-1/\xi _s} \right\} , \nonumber \\{} & {} \quad 1+\xi _s \left( \frac{y-\mu _s}{\sigma _s}\right) > 0. \end{aligned}$$
(2)

In the present study, the block extreme data are maximum temperatures in the summer season (June-July-August). It is also assumed that, conditional on \(\mu _s\), \(\sigma _s\) and \(\xi _s\), the block extremes are spatially and temporally conditionally independent, i.e., the block extreme at observatory s conditional on \(\mu _s\), \(\sigma _s\), and \(\xi _s\) is independent of the block extreme at observatory \(s'\), and that the block extreme observed at time t is independent of that observed at time \(t'\). The scale parameter \(\sigma _s\) represents the spread of the distribution, with a greater value representing greater dispersion of the maximum temperature. The shape parameter \(\xi _s\) represents the tail behaviour of the extreme distribution—a negative parameter corresponds to a bounded tail, otherwise the tail is unbounded.

3.2 Second stage (process model)

In the second stage, the parameters of the GEV distribution are assumed to follow a spatio-temporal model, i.e., to depend on spatial coordinates \(\textbf{s}\) and time t. At this point, it is important to distinguish between stationary and non-stationary models. In the former, the GEV parameters do not depend on time, while in the latter they do. In the stationary case, the parameters of the GEV distributions are assumed to take the form

$$\begin{aligned} \mu (\textbf{s})=\; & {} X_\mu (\textbf{s}) \cdot \pmb \alpha _\mu + W_\mu (\textbf{s}) + \epsilon _\mu \end{aligned}$$
(3)
$$\begin{aligned} \sigma (\textbf{s})=\; & {} X_\sigma (\textbf{s}) \cdot \pmb \alpha _\sigma + W_\sigma (\textbf{s}) + \epsilon _\sigma \end{aligned}$$
(4)
$$\begin{aligned} \xi (\textbf{s})=\; & {} X_\xi (\textbf{s}) \cdot \pmb \alpha _\xi + W_\xi (\textbf{s}) + \epsilon _\xi \end{aligned}$$
(5)

where \(X_{\mu , \sigma , \xi }(\textbf{s})\) are p spatial covariates (geographical coordinates) that may be different for each parameter, \(\pmb \alpha _{\mu , \sigma , \xi }\) is a set of p regression parameters, \(W_{\mu , \sigma , \xi }(\textbf{s})\) are spatial models capturing the associations between different sites (grid cells), and \(\epsilon _{\mu , \sigma , \xi }\) represent noise unaccounted for in the spatial models (generally known in the spatial data community as the nugget effect), and \(\textbf{s}\) denotes a spatial coordinate. In the non-stationary case, a linear time dependence is included in the location parameter:

$$\begin{aligned}{} & {} \mu ({\textbf{s}},t) = X_\mu (\textbf{s}) \cdot \pmb \alpha _\mu + W_\mu (\textbf{s}) + (X'_\mu (\textbf{s}) \cdot \pmb \gamma _\mu \nonumber \\{}\;\; & {} \quad\;\;\;\; + W'_\mu + \epsilon '_\mu ) (t-t_0)+ \epsilon _\mu . \end{aligned}$$
(6)

This equation can be rewritten as

$$\begin{aligned} \mu ({\textbf{s}}, t) = \mu _0(\textbf{s}) + \mu _1(\textbf{s}) (t-t_0). \end{aligned}$$
(7)

In Eq. (6), it has been assumed that the temporal-trend coefficient may depend on geographical factors through the covariates \(X'_\mu\), and that nearer sites could show a stronger temporal relationship through the spatial model \(W'_\mu\). The spatial models \(W_\kappa (\textbf{s}),\kappa =\mu , \sigma , \xi ; W'_\mu (\textbf{s})\) are assumed to be of the form

$$\begin{aligned} W_\kappa (\textbf{s}) = Z \Psi _\kappa (\mathbf {s'}); \qquad \kappa =\mu , \sigma , \xi \end{aligned}$$
(8)

where Z is an \(n\times r\) matrix and \(\Psi _\kappa (\mathbf {s'})\) is a spatial process of dimension r. This spatial process is modeled as a multivariate Gaussian process with zero mean and covariance matrix \(\mathbf {\Sigma }\), i.e.,

$$\begin{aligned} \Psi _\kappa (\mathbf {s'}) \sim MVN(\textbf{0}; \mathbf {\Sigma }_\kappa ); \qquad \kappa =\mu , \sigma , \xi \end{aligned}$$
(9)

The \(r\times r\) covariance matrix defines the covariance among the r spatial locations, and is assumed to be of the form

$$\begin{aligned} \mathbf {\Sigma }_\kappa (s',s') = \beta _{\kappa 1}^2 \exp (-\Vert s'_i - s'_j\Vert )/\beta _{\kappa 2}) = \beta _{\kappa 1}^2 R_\kappa (\beta _{\kappa 2}) \end{aligned}$$
(10)

where \(R_\kappa\) is the correlation matrix. The parameter \(\beta _{\kappa 2}\) (also called the range parameter) defines the strength of the association in the relationships among the spatial sites. The variance parameter \(\beta ^2_{\kappa 1}\) is also known as the sill in the geostatistics community. The residual noise \(\epsilon _{\kappa }\) is modeled as a Gaussian process of zero mean and variance \(\tau _{\kappa }^2\) which is assumed to be constant everywhere.

The reason for the introduction into our model of a matrix Z that transforms an r-spatial process into an n-spatial process is the following. The number of grid cells increases enormously as the resolution of the model increases. For example, for our region of Extremadura and with a WRF resolution of 9 km, there are 957 grid cells. Such a large number of cells makes the numerical problem nearly unfeasible (the covariance matrix would be 957\(\times\)957 and we would have to invert such a large matrix at each MCMC step). To lighten the numerical burden, we followed the method proposed in Banerjee et al. (2008), and modified in Finley et al. (2009) (see also Eidsvik et al. (2012)). Those authors proposed replacing the \(W_\kappa\) process by what they called a predictive process \(\tilde{W}_\kappa\), defined as

$$\begin{aligned} \tilde{W}_\kappa (s)=\;\; & {} E(W_\kappa (s) \vert \Psi _\kappa (s'))=\;\;\;\mathbf {\Sigma }_\kappa (s,s')\cdot \mathbf {\Sigma }_\kappa ^{-1}(s',s')\nonumber \\ \Psi _\kappa (s')= & {} Z_\kappa \Psi _\kappa (s'), \end{aligned}$$
(11)

where \(\mathbf {\Sigma }_\kappa (s, s')\) is the \(n\times r\) covariance matrix between an s-site and an s’-site. With a value \(r \ll n\), the problem of inverting an \(n\times n\) matrix at each MCMC step reduces to that of inverting an \(r\times r\) matrix. In this work, we have subsampled the WRF grid every three rows and columns, which yields an r-matrix of 110\(\times\)110 elements. The substitution of the \(W_\kappa\) process by the predictive \(\tilde{W}_\kappa\) process has the consequence of reducing the variance of the spatial process. To compensate for this, Finley et al. (2009) proposes increasing the nugget variance \(\tau ^2 I\) by the amount

$$\begin{aligned} \text {Diagonal}(I-\mathbf {\Sigma }_\kappa (s,s')\mathbf {\Sigma }_\kappa ^{-1}(s',s') \mathbf {\Sigma }_\kappa (s',s)). \end{aligned}$$

To close this second stage, Equation (3) may be expressed as normal distributions: for the stationary model,

$$\begin{aligned} \mu (\textbf{s})\sim & {} N(\textbf{X}_\mu (\textbf{s}) \cdot \pmb \alpha _\mu + W_\mu (\textbf{s}), \hat{\tau }_\mu ^2) \\ \sigma (\textbf{s})\sim & {} N(\textbf{X}_\sigma (\textbf{s}) \cdot \pmb \alpha _\sigma + W_\sigma (\textbf{s}), \hat{\tau }_\sigma ^2)\\ \xi (\textbf{s})\sim & {} N(\textbf{X}_\xi (\textbf{s}) \cdot \pmb \alpha _\xi + W_\xi (\textbf{s}), \hat{\tau }^2_\xi ), \end{aligned}$$

and for the non-stationary model,

$$\begin{aligned} \mu _1(\textbf{s})\sim & {} N(\textbf{X}_\mu (\textbf{s}) \cdot \pmb \alpha _\mu + W_\mu (\textbf{s}), \hat{\tau }_\mu ^2) \\ \mu _2(\textbf{s})\sim & {} N(\mathbf {X'}_\mu (\textbf{s}) \cdot \pmb \gamma _\mu + W'_\mu (\textbf{s}), \hat{\tau }'^2_\mu) \\ \sigma (\textbf{s})\sim & {} N(\textbf{X}_\sigma (\textbf{s}) \cdot \pmb \alpha _\sigma + W_\sigma (\textbf{s}), \hat{\tau }_\sigma ^2) \\ \xi (\textbf{s})\sim & {} N(\textbf{X}_\xi (\textbf{s}) \cdot \pmb \alpha _\xi + W_\xi (\textbf{s}), \hat{\tau }^2_\xi ), \end{aligned}$$

where the \(\hat{\tau }_i\) represent the increased nugget variances.

3.3 Third stage (prior model)

In the third stage, prior distributions have to be provided for the parameters used in the previous two stages, in particular, for the spatial regression coefficients \(\pmb \alpha _\kappa\), the parameters of the covariance model \(\beta ^2_{\kappa 1}, \beta _{\kappa 2}\), the nugget variances \(\tau ^2_\kappa\), and, in the non-stationary case, the trend parameters \(\pmb \gamma _\kappa , \beta '^2_{\kappa 1}, \beta '_{\kappa 2}, \tau '^2_\kappa\). As the present study area is not too large, we took as covariates X the grid cell heights provided by the WRF topography (see Fig. 2, right). Therefore, the term \(X(\textbf{s})\cdot \pmb \alpha _\kappa\) can be written as \(\alpha _{\kappa 0} + h_s \alpha _{\kappa 1}\), so that we need to provide priors for \(\alpha _{\kappa 0}, \alpha _{\kappa 1}\). Gaussian distributions were used for both cases:

$$\begin{aligned} \alpha _{\kappa j} \sim N(a_{\alpha _{\kappa j}}, b_{\alpha _{\kappa j}}^2), \qquad \kappa =\{\mu ,\sigma ,\xi \}, j=\{0,1\}, \end{aligned}$$

where the hyperparameters of mean (\(a_{\alpha _{\kappa j}}\)) and variance (\(b_{\alpha _{\kappa j}}^2\)) were chosen appropriately in such a way that the distribution was either non- or only weakly informative with no extra information about the parameters, e.g., \(\alpha _{\mu j} \sim N(0, 10 000)\). A similar model (Gaussian) was selected for the trend parameter \(\pmb \gamma\) in the non-stationary model. The sill parameters \(\beta ^2_{\kappa 1}\) and the nugget variances \(\tau ^2_\kappa\) were parametrized by inverse gamma distributions. A uniform distribution was chosen for the range \(\beta _{\kappa 2}\).

3.4 Parameter estimation

Pulling together the different parts of the hierarchical model, and taking into account Bayes’ theorem as expressed in Equation (1), for the stationary model, the posterior distribution of the parameters is given by the expression

$$\begin{aligned}{} & {} \textbf{P}\big (\pmb {\mu },\pmb {\sigma },\pmb \xi , \textbf{W}_\mu , \textbf{W}_\sigma , \textbf{W}_\xi , \pmb {\alpha }_{\mu }, \pmb {\alpha }_{\sigma },\pmb {\alpha }_{\xi }, \varvec{\beta }_{\mu }, \varvec{\beta }_{\sigma }, \varvec{\beta }_{\xi }, \tau _\mu ^2, \tau _\sigma ^2,\tau _\xi ^2 \ \vert \ \pmb {Y}, \pmb {X}\big ) \nonumber \\\propto & {} \prod _{s=1}^{ngrid} \prod _{t=1}^{ndat} \textbf{GEV}(y_{ts}\vert \pmb {\mu },\pmb {\sigma },\pmb {\xi })\nonumber \\&\cdot&\textbf{P}\big (\pmb {\mu }\vert \pmb {X}_\mu , \pmb {\alpha }_{\mu }, W_\mu , \tau ^2_\mu \big )\textbf{P}\big (\pmb {\sigma }\vert \pmb {X}_\sigma , \pmb {\alpha }_{\sigma }, W_\sigma , \tau ^2_\sigma \big ) \textbf{P}\big (\pmb {\xi }\vert \pmb {X}_\xi , \pmb {\alpha }_{\xi }, W_\xi , \tau ^2_\xi \big ) \nonumber \\&\cdot&\textbf{P}\big (\mathbf {\Psi }_\mu \vert \pmb {\beta }_{\mu }\big )\textbf{P}\big (\mathbf {\Psi }_\sigma \vert \pmb {\beta }_{\sigma }\big )\textbf{P}\big (\mathbf {\Psi }_\xi \vert \pmb {\beta }_{\xi }\big ) \nonumber \\&\cdot&\textbf{P}(\alpha _{\mu 0})\textbf{P}(\alpha _{\mu 1})\textbf{P}(\alpha _{\sigma 0})\textbf{P}(\alpha _{\sigma 1})\textbf{P}(\alpha _{\xi 0}) \textbf{P}(\alpha _{\xi 1})\nonumber \\&\cdot&\textbf{P}(\beta _{\mu 0}^2)\textbf{P}(\beta _{\mu 1})\textbf{P}(\beta _{\sigma 0}^2)\textbf{P}(\beta _{\sigma 1})\textbf{P}(\beta _{\xi 0}^2)\textbf{P}(\beta _{\xi 1}) \textbf{P}(\tau ^2_\mu )\textbf{P}(\tau ^2_\sigma )\textbf{P}(\tau ^2_\xi ), \end{aligned}$$
(12)

where \(W_{\kappa }, \kappa =\mu , \sigma , \xi\) has been estimated by its definition \(W_\kappa = Z\Psi _\kappa\). For the non-stationary model, the posterior distribution is given by the expression

$$\begin{aligned}{} & {} \textbf{P}\left( \pmb {\mu },\pmb {\sigma },\pmb \xi , \textbf{W}_\mu , \mathbf {W'}_\mu , \textbf{W}_\sigma , \textbf{W}_\xi , \pmb {\alpha }_{\mu }, \pmb {\gamma }_{\mu },\pmb {\alpha }_{\sigma }, \pmb {\alpha }_{\xi },\right. \nonumber \\{} & {} \left. \varvec{\beta }_{\mu }, \varvec{\beta '}_{\mu }\varvec{\beta }_{\sigma }, \varvec{\beta }_{\xi }, \tau _{\mu ^{2}}, \tau '^2_\mu, \tau _\sigma ^2,\tau _\xi ^2 \ \vert \ \pmb {Y}, \pmb {X}, f(t) \right) \nonumber \\\propto & {} \prod _{s=1}^{ngrid} \prod _{t=1}^{ndat} \textbf{GEV}(y_{ts}\vert \pmb {\mu },\pmb {\sigma },\pmb {\xi }, f(t))\nonumber \\&\cdot&\textbf{P}\big (\pmb {\mu _1}\vert \pmb {X_\mu }, \pmb {\alpha }_{\mu }, W_\mu , \tau ^2_\mu \big ) \textbf{P}\big (\pmb {\mu _2}\vert \pmb {X'_\mu }, \pmb {\gamma }_{\mu }, W'_\mu , \tau '^2_\mu \big ) \nonumber \\&\cdot&\textbf{P}\big (\pmb {\sigma }\vert \pmb {X_\sigma }, \pmb {\alpha }_{\sigma }, W_\sigma , \tau ^2_\sigma \big ) \textbf{P}\big (\pmb {\xi }\vert \pmb {X_\xi }, \pmb {\alpha }_{\xi }, W_\xi , \tau ^2_\xi \big ) \nonumber \\&\cdot&\textbf{P}\big (\mathbf {\Psi }_\mu \vert \pmb {\beta }_{\mu }\big ) \textbf{P}\big (\mathbf {\Psi '}_\mu \vert \pmb {\beta '}_{\mu }\big ) \nonumber \\&\cdot&\textbf{P}\big (\mathbf {\Psi }_\sigma \vert \pmb {\beta }_{\sigma }\big )\textbf{P}\big (\mathbf {\Psi }_\xi \vert \pmb {\beta }_{\xi }\big ) \nonumber \\&\cdot&\textbf{P}(\alpha _{\mu 0})\textbf{P}(\alpha _{\mu 1})\textbf{P}(\gamma _{\mu 0})\textbf{P}(\gamma _{\mu 1})\textbf{P}(\alpha _{\sigma 0})\textbf{P}(\alpha _{\sigma 1})\textbf{P}(\alpha _{\xi 0}) \textbf{P}(\alpha _{\xi 1})\nonumber \\&\cdot&\textbf{P}(\beta _{{\mu 0}^2})\textbf{P}(\beta _{\mu 1})\textbf{P}(\beta '_{{\mu 0}^2})\textbf{P} (\beta '_{\mu 1})\textbf{P}p(\beta _{\sigma 0}^2)\textbf{P}(\beta _{\sigma 1}) \textbf{P}(\beta _{\xi 0}^2) \textbf{P}(\beta _{\xi 1})\nonumber \\&\cdot&\textbf{P}(\tau ^2_\mu )\textbf{P}(\tau '^2_\mu )\textbf{P}(\tau ^2_\sigma )\textbf{P}(\tau ^2_\xi ), \end{aligned}$$
(13)

where \(\pmb \mu = \pmb \mu _0 + f(t) \pmb \mu _1\), with \(f(t)=(t-t_0)\) being the linear temporal-trend function.

The simulation of the posterior distribution was carried out by means of an MCMC method, in particular using a Gibbs sampler with embedded Metropolis-Hastings steps (see Gilks et al. (1996) for more details about MCMC methods). The MCMC was iterated for 50 000 samples with a burn-in period of 30 000 samples to allow the MCMC to reach the stationary state. To avoid the autocorrelation that appears in the MCMC, we kept one out of ten samples for the subsequent calculations. To test the convergence of the chains, four chains were constructed starting with different values of the parameters being simulated. The Gelman–Rubin diagnostic convergence test (see Cowles and Carlin (1996)) was used to evaluate the convergence of these four chains. In most cases, that burn-in period was sufficient for convergence to be reached.

A preliminary study of the spatial models revealed that the spatial-trend coefficient \(\pmb \alpha _\xi\) for the shape parameter \(\xi\) is not significantly different from zero. For this reason, and given that the shape parameter is the most difficult to estimate Sang and Gelfand (2009); Cooley and Sain (2010) we shall assume this shape parameter to be constant throughout the domain.

The code used to carry out the simulations was written in FORTRAN, following quite closely the procedure in Finley et al. (2015). For the Gelman-Rubin diagnostic test, the CODA package of the R language was used, and the maps and figures were prepared using the R packages fields and sp.

3.5 Checking the models

An important step in a statistical analysis is to assess whether the observed data are indeed fitted by the proposed statistical model or models. A two-step procedure was followed. In the first step, the models were ranked according to the WAIC (Widely Applicable Information Criterion) model comparison tool (Gelman et al. 2014). In the second step, the chosen model was contrasted with the data by means of a Bayesian p-value procedure. In both steps the posterior predictive distribution was used. The posterior predictive distribution (PPD) is defined as (Gelman et al. 1996)

$$\begin{aligned} \textbf{P} (y^{\text {rep}}\vert M, y) = \int \textbf{P}(y^{\text {rep}}\vert M,\theta ) \textbf{P} (\theta \vert M, y) d\theta , \end{aligned}$$
(14)

which gives the probability of obtaining new replicated data given the model M and the observed data y. In this equation, \(\theta\) represents the parameters of the model, \(\textbf{P} (\theta \vert M, y)\) the posterior distribution, and \(\textbf{P}(y^{\text {rep}}\vert M,\theta )\) the likelihood.

The WAIC criterion to rank the models is defined by the equation

$$\begin{aligned} \text {WAIC}=-2\log \left( \prod _{i=1} ^{n} \textbf{P} (y_i) \right) +p_{\text {waic}} = -2 \sum _{i=1}^{n} \log \left( \textbf{P} (y_i) \right) +p_{\text {waic}}, \end{aligned}$$
(15)

where \(\textbf{P}(y_i)\) is the PPD given by Equation (14), and \(p_{\text {waic}}\) is a term that measures both the bias introduced into the test from using the data twice—once to estimate the parameters, and a second time to use them in the test (see Gelman et al. (2014))—and the complexity of the model (penalizing models with more parameters). The term \(-2 \sum _{i=1}^{n} \log \left( \textbf{P} (y_i) \right)\) is estimated by the equation

$$\begin{aligned} -2 \sum _{i=1}^{n} \log \left( \textbf{P} (y_i) \right) \approx -2 \sum _{i=1}^{n} \log \left[ \frac{1}{J} \sum _{j=1}^{J} \left( \textbf{P}(y_i\vert \theta ^j)\right) \right] \end{aligned}$$
(16)

where J is the number of samples taken from the MCMC method and \(\theta ^j\) are the estimated parameters of the model. The \(p_{\text {waic}}\) parameter is defined by the expression

$$\begin{aligned} p_{\text {waic}} = \sum _{i=1}^{n} \text {var}_{\text {post}}\left[ \log \left( \textbf{P} (y_i) \right) \right] \end{aligned}$$
(17)

where \(\text {var}_{\text {post}}\) is the operator variance and is estimated as

$$\begin{aligned} \text {var}_{\text {post}}(x) = \frac{1}{J-1} \sum _{j=1}^{J}(x_j - \bar{x}); \qquad x_j = \log \left( \textbf{P} (y_i\vert \theta ^j) \right) . \end{aligned}$$
(18)

As before, J is the number of samples taken from the MCMC. The choice of the WAIC criterion is motivated by the fact that it is easy to calculate from the MCMC and that it has the property of being asymptotically equivalent to a leave-one-out cross-validation (LOO-CV) test (see Gelman et al. (2014)).

In the second step, the Bayesian p-value was evaluated as follows. Let T(y) be some feature of the data we are interested in, for example, the skewness of the data, and we want to see whether the model predicts this feature reasonably well. A measure of the agreement is the Bayesian p-value defined by Lynch and Bruce (2004)

$$\begin{aligned} p_b(y) = \textbf{P} \big (T(y^{\text {rep}}) \ge T(y) \ \vert \ M, y\big ). \end{aligned}$$
(19)

A \(p_b\)-value that is too small or too large would indicate that the model does not reproduce the data (or at least some features of the data) well. One way to calculate the \(p_b\)-value is from the MCMC. As was noted above, an MCMC method allows one to obtain values of the parameter \(\theta\) from the posterior distribution \(\textbf{P}(\theta \vert y)\). For each simulated \(\theta\) value, a \(y^{\text {rep}}\) value is simulated by using the posited model, and then the statistic \(T(y^{\text {rep}})\) is computed. Evaluating the number of times that \(T(y^{\text {rep}}) \ge T(y)\) gives the \(p_b\)-value as

$$\begin{aligned} p_b = \frac{\# \big (T(y^{\text {rep}}) \ge T(y)\big )}{J}, \end{aligned}$$
(20)

with J being the number of samples of \(\theta\) taken from the Markov chain.

3.6 Prediction at a non-grid site

Once we have fitted the model, we are in a position to predict variables of interest at a non-grid site. In particular, we are interested in predicting the parameters of the GEV distribution \(\pmb \mu , \pmb \sigma , \pmb \xi\) in order to estimate, for example, the T-year return levels at those non-grid sites. We shall illustrate the method developed for the location parameter \(\pmb \mu\). Based on Equation (3), we shall assume that if \(\mu _0\) is the location parameter at a non-grid site then the joint statistical distribution of the location parameter at the grid and non-grid sites is given by

$$\begin{aligned} \begin{pmatrix} \mu _0 \\ \pmb \mu \end{pmatrix} \sim {\textbf {MVN}} \begin{pmatrix} &{} m_0 &{} \vert &{} \sigma _0 &{} \pmb \Sigma _{0n}\\ &{}\textbf{m} &{} \vert &{} \pmb \Sigma _{n0} &{} \pmb \Sigma _{nn} \end{pmatrix} \end{aligned}$$
(21)

where \({\textbf {MVN}}\) represents the multivariate normal distribution, \(m_0, \textbf{m}\) are the means of the distributions at the non-grid site and grid sites respectively, \(\sigma _0\) is the variance at the non-grid site, \(\pmb \Sigma _{nn}\) is the \(n\times n\) covariance matrix at the grid sites, and \(\pmb \Sigma _{0n}, \pmb \Sigma _{n0}\) are the \(1\times n, n\times 1\) covariance matrices between the non-grid and grid sites. A result from multinormal distribution theory allows us to say that the conditional distribution of \(\mu _0\) given \(\pmb \mu\), i.e., \(P(\mu _0\vert \pmb \mu )\), is normal with mean given by

$$\begin{aligned} m_1 = m_0 + \pmb \Sigma _{0n}\pmb \Sigma ^{-1}_{nn} (\pmb \mu - \textbf{m}) \end{aligned}$$
(22)

and variance

$$\begin{aligned} \sigma _1 = \sigma _0 - \pmb \Sigma _{0n}\pmb \Sigma ^{-1}_{nn}\pmb \Sigma _{n0}. \end{aligned}$$
(23)

Once the mean \(m_1\) and variance \(\sigma _1\) have been estimated, one can take samples of the location parameter at the non-grid site. According to Eqs. (3) to (5), the \(\pmb \mu\) distribution is

$$\begin{aligned} \pmb \mu \sim {\textbf {MVN}}( X\cdot \pmb \alpha _u+ W_\mu , \tau _\mu ^2 {\textbf {I}} ) \end{aligned}$$
(24)

where \(W_\mu\) is the spatial process given by \(W_\mu = Z\Psi _\mu\), with Z being an \(n\times r\) matrix and \(\Psi _\mu\) an \(r\times r\) MVN process with zero mean and variance \(\pmb \Sigma _\mu\) (Eqs. (8) and (9)). Integrating in \(\Psi _\mu\), the above distribution may be expressed as

$$\begin{aligned} \pmb \mu \sim {\textbf {MVN}}( X\cdot \pmb \alpha _\mu , Z\, \pmb \Sigma _\mu Z^{T} + \tau ^2_\mu {\textbf {I}} ). \end{aligned}$$
(25)

From this expression, one can take \({\textbf {m}}= X \cdot \pmb \alpha _\mu\) and \(m_0= X_0\cdot \pmb \alpha _\mu\). Taking into account Eq. (10), the \(r\times r\) covariance matrix \(\pmb \Sigma _\mu\) is given by

$$\begin{aligned} \mathbf {\Sigma }_{\mu }(\textbf{s}',\textbf{s}') = \beta _{\mu 1}^2 \exp (-\Vert \textbf{s}'_i - \textbf{s}'_j\Vert )/\beta _{\mu 2}), \qquad i,j=1, \cdots , r. \end{aligned}$$
(26)

The Z matrix is given by (see Eq. (11)):

$$\begin{aligned} Z= \mathbf {\Sigma }_\mu (\textbf{s},\textbf{s}')\cdot \mathbf {\Sigma }_\mu ^{-1}(\textbf{s}',\textbf{s}'). \end{aligned}$$
(27)

Lastly, the covariance between the non-grid and a grid site is taken as

$$\begin{aligned} \mathbf {\Sigma }_{n0} = \beta _{\mu 1}^2 \exp (-||\textbf{s}_i - \textbf{s}_0||)/\beta _{\mu 2}), \end{aligned}$$
(28)

and \(\sigma _0= \tau ^2_\mu\).

4 Results

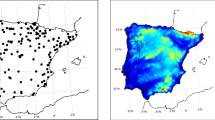
First of all, it is important to know whether the climate of the region (represented by the summer maximum temperature) is well described by the WRF model. Figure 4 shows a map of the mean summer extreme temperatures for the study period (1981–2015) given by the Stead database Serrano-Notivoli et al. (2019) (left) and by the WRF model (right). As can be seen, the spatial distribution of the maximum temperature is quite similar in the two maps, so that we have reasonable confidence in the results given by the WRF model.

Fig. 4
figure 4

Mean of the summer extreme temperature during the period 1981–2015 given by the WRF model (right) for the Iberian Peninsula and during the period 1981–2014 given by Stead database for Spain. Scales are in \(^\circ\)C

Full size image

Moving to the statistical model, one first needs to establish the external covariate term X. Because the spatial domain is not too large, and given the influence of altitude on temperature, we chose the height of the grid cell to be our covariate. Prior to their introduction into the model, the heights were linearly normalized to the interval (0, 1). With this choice of covariate, the spatial-trend term in the location parameter \(\pmb \mu\) (stationary models) and \(\pmb \mu _0\) (non-stationary models) is

$$\begin{aligned} \textbf{X}_\mu (s) \cdot \pmb \alpha _\mu = \alpha _0 + h_s \alpha _1, \end{aligned}$$
(29)

and in the temporal-trend coefficient \(\pmb \mu _1\) is

$$\begin{aligned} \textbf{X}'_\mu (s) \cdot \pmb \gamma _\mu = \gamma _0 + h_s \gamma _1. \end{aligned}$$
(30)

Prior to its use in the model, the linear temporal-trend function \(f(t) = t- t_0\) was also linearly normalized to the interval (− 1, 1).

We posited various models depending on whether or not there exists a temporal trend in the location parameter, and, within them, whether there exists a dependence on height in both the location and the scale parameters. As mentioned above, to rank the proposed models, the WAIC criterion was used. The results are presented in Table 2.

Observing column \(p_{\text {waic}}\), one sees that as the complexity of the models increases so does the complexity parameter. The results in the last column lead to non-stationary models fitting better than stationary models, with model 2110 performing the best. Therefore, this model was chosen for the next step—the assessment of the model against the data using the Bayesian p-value.

As noted above, to apply the Bayesian p-value we need to choose a statistic T(y) of the data that can help determine which model best explains some feature of the data. Because we are considering a time dependence in the models, we took the Mann-Kendall test as the feature to explain. This is a non-parametric test used to determine whether a uniform trend exists in a set of independent data. The test statistic is given by the expression Gallego et al. (2011)

$$\begin{aligned}{} & {} T(y) = \frac{1}{\sqrt{n(n-1)(2n+5)/18}} \nonumber \\{} \;\;\;& {} \quad \left( \sum _{i=1}^{n-1} \sum _{j=i+1}^n \textrm{sgn}(y_j - y_i) - \textrm{sgn}(T)\right) , \end{aligned}$$
(31)

where \(\textrm{sgn}(x)\) is the sign function defined as \(+1\) if \(x>0\), \(-1\) if \(x<0\), and 0 if \(x=0\), and n is the number of data for each grid cell. We calculated the \(p_b\)-value by evaluating this statistic for the ‘observed’ and the replicated data. To simulate replicated data according to the PPD given by expression (14), an instance of the \(\mu , \sigma , \xi\) parameters is taken from the MCMC chain, and a sample of n elements is extracted using the GEV distribution. The statistic \(T(y^{\text {rep}})\) is then evaluated from this sample. This procedure is repeated for each element of the chain, obtaining a sample of J replicated Mann-Kendall statistics. This statistic is also evaluated for the observed data. From the replicated sample and the observed datum, the \(p_b\) value is calculated as the percentile of the observed \(T(y^{\text {obs}})\) in the J replicated Mann-Kendall statistics. Values of \(p_b\) that are too large or too small mean that the replicated data do not explain that feature of the observed data well. If there are N grid cell elements in the domain, we obtain N \(p_b\) values. From this set, we calculated, by way of synthesis, the minimum, the 25, 50, and 75 percentiles, and the maximum. For the chosen 2110 model, these values were 0.1870, 0.4080, 0.4470, 0.5440, 0.9500, respectively. Values of the 25, 50, and 75 percentiles are close to 0.5, which means that for most sites the 2110 model explains quite well the temporal trend observed in the results given by the RCM.

Table 2 Summary of the values of the WAIC information criterion
Full size table
Fig. 5
figure 5

Spatial-regression coefficients \(\alpha _0\) (left) and \(\alpha _1\) (right). The red line shows the interval (2.5%, 97.5%)

Full size image

Let us now consider this model’s results in greater detail. Firstly, Fig. 5 shows the spatial regression coefficients \(\alpha _0, \alpha _1\). The right-hand panel shows that the height-trend coefficient is negative with a mean value of \(-\)15.1\(^\circ\)C. Therefore, given that the heights were normalized, and considering that the maximum altitude in the model is 1794.8 m and the minimum is 134.8 m, one has the result that \(\alpha _1 = -9.35\;^\circ \text {C/km}\), which is quite close to the theoretical adiabatic coefficient of \(-9.8\;^\circ \text {C/km}\). It is important to bear in mind that the data correspond to summer when the temperatures are the highest and the atmospheric boundary layer is in nearly adiabatic equilibrium. This result lends added confidence to the proposed model.

Secondly, we shall show the results for the temporal-trend coefficients \(\gamma _0, \gamma _1\). Although the chosen model only has the \(\gamma _0\) coefficient, an analysis of that model with \(\gamma _1\) present showed that coefficient to not differ from zero, i.e., the temporal-trend coefficient has no height dependence. Figure 6 shows a density plot of \(\gamma _{0}\). The mean (2.5%, 97.5%) is \(-\)0.26 (\(-\)0.39, \(-\)0.12). From the aforementioned linear temporal-trend function, one finds a temporal trend of \(-\)0.15 \(^\circ\)C per decade with a 2.5–97.5% interval of (\(-\)0.21 \(^\circ\)C, \(-\)0.10 \(^\circ\)C ) per decade. This is a surprising result because one would expect an increase in temperature due to climate change. Figure 7 shows a plot of the temporal-trend regression coefficient (\(^\circ\)C/year) obtained by the Sen method (Sen 1968; Hirsch and Smith 1982) for the summer extreme 2-metre-height temperature in the ERA Interim reanalysis used to externally force the WRF model in the study period 1981–2015. The ERA Interim reanalysis shows a predominantly positive trend for the study period (1981–2015), mainly in the central area of the Iberian Peninsula. However, this positive trend tends to decrease towards the west of the IP, with some regions showing a negative, although small, trend. Also, one can see from the figure that the WRF model shows a negative trend throughout the west, including the study region, and a positive trend in the center of the IP. It is possible, however, that internal variability and model variability in the WRF model which persist after the constraint of the boundary conditions given by the external reanalysis (Alexandru et al. 2009; Hawkins and Sutton 2009) lead to the enhanced, although small, negative trends in extreme temperatures appearing in a simulation as short as that of the present work (35 years).

Fig. 6
figure 6

Temporal-trend coefficients \(\gamma _0\). The red line shows the interval (2.5%, 97.5%)

Full size image
Fig. 7
figure 7

Temporal-trend regression coefficient (\(^\circ\)C/year) obtained by the Sen method for summer extreme 2-metre-height temperature in the ERA Interim reanalysis (left) and in the WRF model (right)

Full size image

Some previous studies on temporal trends in RCM simulations have shown the difficulty these models have in estimating these trends. In Lorenz and Jacob (2010), temporal trends in 2-m seasonal and annual average temperatures were simulated by 13 RCMs driven by ERA40 reanalysis for the period 1960–2000 within the framework of the ENSEMBLES EU-Project. The trends of the annual average temperature obtained with the RCMs were found to underestimate the observed trends in all regions, and in most regions they also underestimated the trends given by the ERA40 reanalysis dataset. Bukovsky (2012) analysed temporal trends in 2-m seasonal average temperatures obtained from six RCMs driven by NCEP-2 reanalysis for the period 1980–2003 within the framework of the North American Regional Climate Change Assessment Program (NARCCAP). According to those authors’ own words: ‘There are no clear conclusions about the behaviour of the RCMs because some of the models cannot capture certain seasonal trends over portions of the domain’ Min et al. (2013).

An interesting parameter to study is the shape parameter, which provides information on the shape of the extreme temperature probability distribution function (PDF). A positive value indicates that there is no upper bound on the extreme temperatures, and a negative value that there is an upper bound. Figure 8 shows the posterior distribution of this parameter for the chosen model.

Fig. 8
figure 8

Shape parameter \(\xi\). The red line shows the interval (2.5%, 97.5%)

Full size image

The mean (2.5%, 97.5%) is \(-\)0.994 (\(-\)0.092, \(-\)0.106), thus supporting a bound on the extreme temperatures for the region under study. The negative value of the shape parameter in the GEV and Generalized Pareto Distribution used to fit the extreme temperature distribution seems to be a universal feature because several other works have found similar negative values for different parts of the world (see, for example, Salleh and Hasan (2018) for Malaysia, García-Cueto et al. (2013) for Mexico, Furrier et al. (2010) for USA, Brown et al. (2008) for different parts of the world, Nogaj et al. (2006) for the North Atlantic, and Parey et al. (2007) for France).

It is important to note that we also performed the model’s calculations with other subsampling values (2\(\times\)2, 4\(\times\)4), obtaining results similar to those just shown for the 3\(\times\)3 subsampling case.

Once the parameters of the GEV distribution are known, one could already display maps of them. From the perspective of field practitioners, however, it would be more interesting to combine them and display return level maps. The T-year return level is the quantile for which the probability that the annual maximum exceeds this quantile is 1/T (see Kharin and Zwiers (2005) and Cooley (2013) for a definition of the T-year return level and T-year return period in a non-stationary context). From the GEV distribution, one gets the expression

$$\begin{aligned} y_{p}(s) = \mu _s - \frac{\sigma _s}{\xi _s} \left( 1- (-\log (1-p))^{-\xi _s} \right) , \end{aligned}$$
(32)

with \(p=1/T\). For the non-stationary model (Equation (7)), the T-year return level is

$$\begin{aligned} y_{p}(s, t) = \mu _{0s} + \mu _{1s}\cdot f(t)- \frac{\sigma _s}{\xi _s} \left( 1- (-\log (1-p))^{-\xi _s} \right) . \end{aligned}$$
(33)

From this equation, one can evaluate the difference between the end and the beginning of the period,

$$\begin{aligned} \Delta y_p(s) = 2\mu _{1s}, \end{aligned}$$
(34)

considering the normalization used in f(t).

Fig. 9
figure 9

Mean of the 40-year return level for t=0 (left), and \(\Delta y_{0.05}\) (right). Scales are in \(^\circ\)C

Full size image

Figure 9 (left) shows a map of the 40-year (97.5 percentile) return level. As may be appreciated by comparing this figure with that of the topography (Fig. 2), the spatial distribution of the 40-year return level is completely determined by the topography as should be expected for a variable such as temperature. We also calculated the difference in the 40-year return level between the end and the beginning of the study period. The resulting map is shown in Fig. 9 (right). One sees that, for most of the region, there is a decrease in the return level by about 0.8 \(^\circ\)C to 1.0 \(^\circ\)C, except at the eastern edge of the region where the decrease approaches 0 \(^\circ\)C

One of the advantages of having a spatial model such as that used in this work is the possibility of predicting the GEV distribution parameters at a non-observed site. In this sense, we evaluated the T-year return period for a set of 28 weather stations in the region under study. To obtain values of the location and scale parameters, we drew from a normal distribution with mean and variance given by Equations (22) and (23), and with Equation (32) we got the T-year return period. Figure 10 is a scatter plot of the predicted versus observed 40-year return levels, together with the regression line through the origin \(y \sim x\) (blue) and the 1:1 line (black). The observed 40-year return level was obtained by fitting a GEV model to each observed data set using the R package ismev ( Coles (2001)). The regression coefficient is 0.96 (±0.014), the bias (observed - predicted) is 1.66 \(^\circ\)C, and the RMS is 2.30\(^\circ\)C. The results seem quite promising, although the predicted values are underestimates of those observed.

Fig. 10
figure 10

Scatter plot of the predicted and ‘observed’ 40-year return levels for 28 observatories in the region. The black line is the 1:1 line, and the blue line the \(y \sim x\) linear regression. Scales are in \(^\circ\)C

Full size image

5 Summary and conclusions

In the present work, we have described a two-step study of extreme temperatures in the region of Extremadura (Spain). In the first step, we used the WRF model to obtain a set of extreme temperatures for the period 1981–2015 in our region. The boundary conditions needed by the model were obtained from ECMWF’s ERA Interim data. In the second step, a statistical study was made of the extreme temperature data obtained in the region. To this end, a Bayesian hierarchical spatio-temporal model with a GEV parametrization of the extreme event data was used. Two advantages of this kind of model are that it reduces the uncertainty in the parameters of the statistical distribution by pooling data among ‘observatories’ in a consistent way, and that it can project important features of the statistical distribution, such as the T-year return level, to non-observing sites.

The spatial-trend parameter given by the model chosen was quite consistent with that corresponding to the dry adiabatic gradient, i.e., the gradient one would expect in the summer season when adiabatic conditions are prevalent in the atmospheric boundary layer. The negative trend in the location parameter is consistent with the negative trend that the WRF model shows for the extreme temperature in the western part of the Iberian Peninsula which has enhanced the trend given by ERA Interim for the same region. A possible reason for this result may lie in the internal and model uncertainties in using the WRF model. The shape parameter of the GEV model was negative, showing that there is an upper bound to the extreme temperatures over the region.

An important product we have obtained from the statistical model is that of obtaining return levels at non-observing sites. A comparison of the 40-year return levels of observed temperatures with those predicted by the statistical model showed a bias (observed minus predicted) of 1.66\(^\circ\)C.