A Bayesian hierarchical spatio-temporal model for summer extreme temperatures in Spain

Abstract

A statistical study was made of the summer extreme temperatures over peninsular Spain in the last forty years. Records from 158 observatories regularly distributed over Iberia with no missing data were available for the common period from 1981 to 2020. For this purpose, a hierarchical spatio-temporal model with a Gaussian copula and a generalized extreme value parametrization of the extreme events was used. The temporal trend in maximum extreme temperatures was studied making use of both a stationary model and a nonstationary one that takes into account the influence of anthropogenic climate change on extreme temperatures using the global mean temperature as a function of time for the study period. The results led to a better fit of the nonstationary model, with there being a 3.5-fold greater increase in the 20-year return level of the extreme temperatures than in that corresponding to the global mean temperature.

1 Introduction

The IPCC in its 6AR Technical Summary (Arias et al. 2021) established that the global mean temperature has increased by 1.09 [0.95–1.20]$^\circ$C from 1850–1900 to 2011–2020, and that, considering land only, the increase has been 1.59 [1.34–1.83]$^\circ$C. It seems logical to expect that, associated with this increase in the mean temperature, there should be an increase in the frequency and intensity of hot temperature events. These hot events can have severely damaging effects on human health and livelihoods as occurred with the events in southern Europe in 2003 (García-Herrera et al. 2010), Russia in 2010 (Barriopedro et al. 2011), and Canada in 2021 (Thompson et al. 2022), to cite just three examples. It is also expected that, with the increase in temperature in the 21st century, the frequency and severity of these events will also increase. However, due to the Earth’s inhomogeneities, these changes will be different around the world, so that it is interesting to study the evolution of the temperature at a regional or local scale where the effects of the changes will be more sharply distinguishable. This paper studies the extreme temperatures in peninsular Spain over the last forty years. This period is used in order to consider the greatest number of temperature time series with the minimum proportion of lost data.

There have been two main paths taken to address the study of extreme weather and climate events. One is by means of extreme indices such as a high percentile of the probability distribution function, see for example Zhang et al. (2010), Peterson et al. (2001), Peterson (2005). The other is by using the statistics of extreme value theory (EVT). This second path is that taken in this paper. Given the spatial character of the variable under study, temperature, it seems appropriate to use the theory of spatial extremes to study it. There exist, see the review papers by Davison et al. (2012), Ribatet et al. (2016), Huser and Wadsworth (2022), several approaches to the study of spatial extreme, among which we can cite: extreme copulas, max-stable models, r-Pareto models, Bayesian hierarchical models. It is this last approach the one we shall take in the present work. Although using Bayesian hierarchical models is inappropriate for applications where the joint behaviour of the random vector is required, however, as was pointed out by Davison et al. (2012) and Ribatet et al. (2016), if one is mainly interested in the study of the marginal behaviour this approach is a good choice due to its feasibility when one has a large number of observation sites and their flexibility to capture complex spatio-temporal trends.

It is frequently assumed, when using Bayesian hierarchical models, that the data are spatially independent given the values of the parameters of their distribution. However, as was pointed out by Renard (2011), this hypothesis is questionable since the spatial dependence of the parameters and the spatial dependence of the data arise from different processes. The spatial dependence of the parameters is related to the climate of the region, while the spatial dependence of the data could be interpreted as weather dependence (Cooley et al. 2007; Renard 2011). Moreover, these dependence structures have different impacts on the regional model, while climate dependence allows transferring information to non-observed sites from observed sites, the main effect of the weather dependence is to decrease the information content of the data taken at nearby sites (Renard 2011). To take into account this double dependence, following Renard and Lang (2007) and Renard (2011), we shall model the data by means of a Gaussian copula, see also Sang and Gelfand (2010), Bracken et al. (2016), Ossandón et al. (2022) for other studies using this copula in the same context of extreme analysis. Although the Gaussian copula does not correspond to a multivariate extreme value distribution (Cooley et al. 2012), there is a twofold motivation for this choice: it is applicable to a marginal GEV model, and its use is feasible when one has hundreds of locations to model, as in the present case.

One of the more important benefits of using a spatial extremes theory instead of modeling each observatory individually is the increased precision in the estimation of the parameters of the statistical distribution. Indeed, one of the difficulties encountered when one carries out a statistical study of extreme data is that extreme data are by their very nature ‘rare’ – there are usually not enough data, so that one must expect to get a large uncertainty in the parameters describing the tail of the statistical distribution. One way to mitigate the consequences of this lack of data and to increase the precision in the estimation of the parameters is to trade space for time, pooling information from different observatories – see for example Casson and Coles (1999), Cooley et al. (2007), Schliep et al. (2010). Also, as pointed out by Renard (2011), a spatial theory allows the parameters of the extreme distribution to be estimated at an ungauged or poorly gauged site.

Several studies have been carried out using extreme indices to analyse the maximum temperatures observed in the Iberian Peninsula. Among them we can cite Rio et al. (2011), El Kenawy et al. (2012), Fernández-Montes and Rodrigo (2012), Espírito-Santo et al. (2014), Fonseca et al. (2016), Barbosa and Scotto (2022) all of which found positive trends in the indices used. For a study using EVT, we can cite Acero et al. (2014) who used a peak over threshold (POT) analysis for each meteorological observatory individually, finding that there exists a positive trend in the 20-year return level, and Garcia et al. (2021) who used the same methodology as in the present work although with the study being limited to the region of Extremadura and using a temporally stationary model. Moreover, recently published papers has brought to light that Spain has experienced a significant increase in extreme heat waves and very intense droughts during the summer months (Serrano-Notivoli et al. 2023, Serrano-Notivoli et al. 2022; Espín-Sánchez  and Conesa-García 2021). Besides, Mediterranean region is warming 20% faster than the global average so Spain is especially sensitive to increases in extreme temperatures. Therefore, any statistical study on extreme temperatures in this country is specially interesting. The present paper studies the temporal trend in maximum extreme temperatures, so that we shall be going to extend the previously mentioned temporally stationary model (Garcia et al. 2021) to a temporally nonstationary model spanning the whole of peninsular Spain. The first aim is to analyze the effect of the climate change on Spain by studying the influence of the increase in global mean temperature on extreme temperatures. The second aim is focused on the elaboration of non-stationary return level maps for a complete region from the data recorded in a set of observatories belonging to that region.

The paper is organized as follows. Data used are described in Sect. 2, the details of the statistical model are presented in Sect. 3, and the results in Sect. 4. Finally, some conclusions are drawn and discussed in Sect. 5.

2 Data

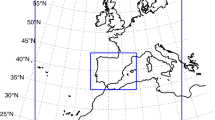
Summer (JJA) maximum temperatures recorded in 158 observatories distributed over Spain were used, The study period spans from 1981 to 2020. Those observatories with more than three lost data were eliminated. These time series were taken from an extensive database of daily temperature series provided by Spain’s National Weather Agency (AEMET). The map on the left in Fig. 1 shows the location of the observatories used, and that on the right is the topographic map of Spain seen by the Weather Research Pre-Processing System (WPS) of the Weather, Research and Forecasting (WRF) model at 9-km resolution.

Fig. 1

Location of the meteorological observatories used in the study (left). Topographic map of Spain seen by the Weather Research Pre-Processing System (WPS) of the Weather, Research and Forecasting (WRF) model at 9-km resolution (right). The scale is in metres above sea level

Also used in this study is the global mean summer (JJA) anomaly temperature (with respect to the 1951–1980 period) (GMSAT) obtained from the NASA GISS Surface Temperature Analysis version 4 (GISTEMP v4, https://data.giss.nasa.gov/gistemp/) for the period 1981–2020. This global temperature anomaly is taken as a proxy for anthropogenic climate change. To eliminate the effect of the ENSO phenomenon, the anomaly data were smoothed with a 5-year moving average. The minimum value of the smoothed series appears in 1984 with 0.14$^\circ$C, and the maximum value in 2020 with 0.89$^\circ$C.

3 Model

As was noted in the Introduction, we shall use a Bayesian hierarchical modeling technique to estimate the parameters of the model. The main goal of the this technique is to factorize a complex statistical problem into pieces consisting of more elementary conditional models by estimating the parameters that appear in it following a Bayesian formalism (see Berliner (1996), Wikle et al. (1998) and Cressie and Wikle (2011)). Usually, factorization of the model is done in three stages. In the first, called the data stage, the observed data are assumed to follow a univariate generalized extreme value distribution (GEV) at each observatory individually, with parameters that change in space and time. In the second, the process stage, a space-time regression model is proposed for the parameters of the GEV distribution. And in the third, a prior distribution is proposed for the parameters that appear in the regression model, followed by calculation of the posterior distribution of the parameters using Bayes’ theorem.

In the first stage, it is supposed that the data are distributed according to a Gaussian copula distribution with GEV marginals at each site. Let $Y_{st}$ represent the variable of interest, in our case, the summer extreme temperature at site s in year t. Therefore, according to our hypothesis, the distribution function at each observatory follows a univariate GEV distribution, that is,

$$\begin{aligned}{} & {} P(Y_{st} < y) = GEV(y|\mu _{st}, \sigma _{st}, \xi _{st}) \\{} & {} \quad = \exp \left\{ -\left[ 1 + \xi _{st} \left( \frac{y-\mu _{st}}{\sigma _{st}} \right) \right] ^{-1/\xi _{st}} \right\} \end{aligned}$$

whose parameters, location $\mu _{st}$, scale $\sigma _{st}$ and shape $\xi _{st}$ depends on the site s and time t. For the M sites the multivariate distribution function is given by the Gaussian copula (Renard and Lang 2007)

$$F_{{GC}} (y_{1} , \cdots ,y_{M} ) = \Phi _{M} (\phi ^{{ - 1}} (GEV_{1} (y_{1} |\mu _{{s_{1} t}} ,\sigma _{{s_{1} t}} ,\xi _{{s_{1} t}} )),{\text{ }} \cdots ,\phi ^{{ - 1}} (GEV_{M} (y_{M} |\mu _{{s_{M} t}} ,\sigma _{{s_{M} t}} ,\xi _{{s_{M} t}} ))$$

where $\Phi _M$ represent a M-dimensional Gaussian distribution function with mean $\textbf{0}$ and correlation matrix $\mathcal {C}$ and $\phi$ a standard (0,1) gaussian distribution function.

The corresponding distribution density function may be expressed as

$$\begin{aligned} f_{{GC}} \left( {y_{1} ,{\mkern 1mu} ...,{\mkern 1mu} y_{M} } \right) = & \frac{{\prod\limits_{{i = 1}}^{M} {f_{{GEV}} \left( {y_{i} |\mu _{{s_{i} t}} ,\sigma _{{s_{i} t}} ,\xi _{{s_{i} t}} } \right)} }}{{\prod\limits_{{i = 1}}^{M} {f_{N} \left( {u_{i} } \right)} }}{\mkern 1mu} \quad \\ \cdot {\mkern 1mu} f_{{N_{M} }} \left( {u_{1} ,{\mkern 1mu} ...,{\mkern 1mu} u_{M} |{\mathcal{C}}} \right), \\ \end{aligned}$$

(1)

where $f_{GEV}$ represents the GEV probability density distribution function, $f_{N}$ the probability density distribution function of the standard normal distribution, and $f_{N_M}$ the probability density distribution function of the M-dimensional normal distribution with correlation matrix $\mathcal {C}$, and $u_{i}$ the quantile of $P(Y_{s_i t} \le y_i )$ of the standard normal distribution for $i = 1,...,M$.

Following Renard (2011), the correlation matrix $\mathcal {C}$ is assumed to be of the form

$${\mathcal{C}}_{{ij}} = {\text{ }}c_{0} \cdot \exp \left\{ { - \frac{{\parallel {\mathbf{x}}\left( {s_{i} } \right) - {\mathbf{x}}\left( {s_{j} } \right)\parallel }}{{c_{1} }}} \right\} + (1 - c_{0} ) \cdot \exp \left\{ { - \frac{{\parallel {\mathbf{x}}\left( {s_{i} } \right) - {\mathbf{x}}\left( {s_{j} } \right)\parallel }}{{c_{2} }}} \right\}$$

(2)

where $c_0, c_1, c_2$ are unknown parameters, $\textbf{x} \left( s \right)$ is the geographical position (longitude, latitude) of the site $s \in S$, and $\parallel \textbf{x} \left( s_i \right) - \textbf{x} \left( s_j \right) \parallel$ are the distances between the sites $s_i$ and $s_j$, for $i, j = 1,..,M$. Also, independence is assumed between observations $\left( Y_{s_1 t}, \ldots , Y_{s_M t} \right)$ and $\left( Y_{s_1 t'}, \ldots , Y_{s_M t'} \right)$ for $t, t' \in T$ such that $t \ne t'$. In Renard’s paper, this dependence-distance model is called a “dependogram”.

In the second stage of the hierarchical model, as noted above, the parameters of the GEV($\mu ,\sigma ,\xi$) distribution are assumed to be functions of space and time. More specifically, here we shall assume that the location parameter $\mu$ is temporally nonstationary, having the following form

$$\begin{aligned} \mu \left( \textbf{s}, t\right) = \mu _0 \left( \textbf{s} \right) + \mu _1 \left( \textbf{s} \right) f(t) \end{aligned}$$

(3)

where

$$\begin{aligned} \mu _0 \left( \textbf{s} \right) = \textbf{X}_0 \left( \textbf{s} \right) \cdot {\varvec{\alpha }}_{\mu _0} + W_{\mu _0} \left( \textbf{s} \right) +\epsilon _{\mu _0} \left( \textbf{s} \right) \end{aligned}$$

(4)

$$\begin{aligned} \mu _1 \left( \textbf{s} \right) = \textbf{X}_1 \left( \textbf{s} \right) \cdot {\varvec{\alpha }}_{\mu _1} + W_{\mu _1} \left( \textbf{s} \right) +\epsilon _{\mu _1} \left( \textbf{s} \right) \end{aligned}$$

(5)

with $\textbf{X}_0, \textbf{X}_1$ being external covariates, ${\varvec{\alpha }}_{\mu _0}, {\varvec{\alpha }}_{\mu _1}$ are vectors of regression parameters, $W_{\mu _0}, W_{\mu _1}$ are the residual of the regression model and may be seen as spatial fields capturing the association among the location parameters at different meteorological sites not taken into account by the regression model, and $\epsilon _{\mu _0}, \epsilon _{\mu _1}$ representing local noise not included in the spatial field. Lastly, f(t) is a function of time. Usually, a linear time function is used for f(t). However, in order to analyse the influence of anthropogenic climate change on extreme temperatures over peninsular Spain, we shall use as a proxy for it the 5-year moving average global mean surface temperature.

For the scale parameter $\sigma$, the model is assumed to be stationary, having the form

$$\begin{aligned} \log {\sigma \left( \textbf{s} \right) }= \textbf{X}_0 \left( \textbf{s} \right) \cdot {\varvec{\alpha }}_{\sigma } + W_{\sigma } \left( \textbf{s} \right) +\epsilon _{\sigma } \left( \textbf{s} \right) \end{aligned}$$

(6)

The use of a logarithm is in order to keep the scale parameter positive. The external covariates are the same as for the location parameter: height and latitude.

The shape parameter $\xi$ is taken to be the same over the whole domain.

The spatial fields $W_\kappa (\textbf{s})$ ($\kappa \equiv \mu _0, \mu _1, \sigma$) are Gaussian random fields, with mean $\textbf{0}$ and covariance ${\varvec{\Sigma }}_\kappa$, i.e.,

$$\begin{aligned} W_\kappa (\textbf{s}) \sim MVN(\textbf{0}, {\varvec{\Sigma }}_\kappa ) \end{aligned}$$

(7)

where the symbol $\sim$ means distributed as. The covariance $\Sigma _\kappa$ between sites i, j is taken to be of the form

$$\begin{aligned} \Sigma _\kappa (s_i, s_j) = \beta _{\kappa 1}^2 \exp (-||s_i - s_j||/\beta _{\kappa 2}) \end{aligned}$$

(8)

A hypothesis of the proposed model is that the dependence parametrized by the Gaussian copula only affects the spatial data, i.e., the maximum temperatures recorded in one year are independent of those recorded in another. Under this hypothesis, using Bayes’ theorem, the posterior distribution of the parameters given by the observed data and covariates may be written as

$$\begin{aligned} \begin{aligned}&P \left( c_0, c_1, c_2, \mu _0 \left( \textbf{s} \right) , \mu _1 \left( \textbf{s} \right) , \sigma \left( \textbf{s} \right) , \xi , W_{\mu _0} \left( \textbf{s} \right) , W_{\mu _1} \left( \textbf{s} \right) , W_{\sigma } \left( \textbf{s} \right) , {\varvec{\alpha }}_{\mu _0}, {\varvec{\alpha }}_{\mu _1}, \alpha _{\sigma }, \right. \\&\left. \qquad \qquad \qquad \qquad \qquad \qquad \beta _{\mu _0 0}, \beta _{\mu _0 1}, \beta _{\sigma 0}, \beta _{\sigma 1}, \tau _{\mu _0}^2, \tau _{\mu _1}^2, \tau _{\sigma }^2 \, | Y, X \left( \textbf{s} \right) \right) \\ {}&\propto \ \prod _{t=1}^{t=N} P \left( Y_t(\textbf{s}) | \, c_0, c_1, c_2, \mu _0 \left( \textbf{s} \right) , \mu _1 \left( \textbf{s} \right) , \sigma \left( \textbf{s} \right) , \xi \right) \cdot P \left( c_0 \right) \cdot P \left( c_1 \right) \cdot P \left( c_2 \right) \cdot P \left( \xi \right) \\ {}&\qquad \qquad \cdot P \left( \mu _0 \left( \textbf{s} \right) \, | \, X_0 \left( \textbf{s} \right) , W_{\mu _0} \left( \textbf{s} \right) , {\varvec{\alpha }}_{\mu _0}, \beta _{\mu _0 0}, \beta _{\mu _0 1}, \tau _{\mu _0}^2 \right) \\ {}&\qquad \qquad \cdot P \left( \mu _1 \left( \textbf{s} \right) \, | \, X_1 \left( \textbf{s} \right) , W_{\mu _1} \left( \textbf{s} \right) , {\varvec{\alpha }}_{\mu _1}, \beta _{\mu _1 0}, \beta _{\mu _1 1}, \tau _{\mu _1}^2 \right) \\ {}&\qquad \qquad \cdot P \left( \sigma \left( \textbf{s} \right) \, | \, W_{\sigma } \left( \textbf{s} \right) , \alpha _{\sigma }, \beta _{\sigma 0}, \beta _{\sigma 1}, \tau _{\sigma }^2\right) \\ {}&\qquad \qquad \cdot P \left( W_{\mu _0} \left( \textbf{s} \right) \, | \, \beta _{\mu _0 0}, \beta _{\mu _0 1} \right) \cdot P \left( W_{\mu _1} \left( \textbf{s} \right) \, | \, \beta _{\mu _1 0}, \beta _{\mu _1 1} \right) \cdot P \left( W_{\sigma } \left( \textbf{s} \right) \, | \, \beta _{\sigma 0}, \beta _{\sigma 1} \right) \\ {}&\qquad \qquad \cdot P \left( {\varvec{\alpha }}_{\mu _0} \right) \cdot P\left( {\varvec{\alpha }}_{\mu _1} \right) \cdot P \left( \alpha _{\sigma } \right) \cdot P \left( \beta _{\mu _0 0} \right) \cdot P \left( \beta _{\mu _0 1} \right) \cdot P \left( \beta _{\mu _1 0} \right) \cdot P \left( \beta _{\mu _1 1} \right) \\ {}&\qquad \qquad \cdot P \left( \beta _{\sigma 0} \right) \cdot P \left( \beta _{\sigma 1} \right) \cdot P \left( \tau _{\mu _0}^2 \right) \cdot P \left( \tau _{\mu _1}^2 \right) \cdot P \left( \tau _{\sigma }^2 \right) . \end{aligned} \end{aligned}$$

(9)

The local noise $\epsilon _\kappa$, also termed as nugget in the geostatistics real, is modeled as a Gaussian process of zero mean and variance $\tau _\kappa ^2$ which is assumed to be constant everywhere.

$$\begin{aligned} \epsilon _\kappa (\textbf{s}) \sim MVN(\textbf{0}; \textbf{I}\tau _\kappa ^2 ); \qquad \textbf{I}\quad \text {being the identity matrix}. \end{aligned}$$

The simulation of the posterior distribution was carried out by means of a Markov chain Monte Carlo (MCMC) method, using a Gibbs sampler with embedded Metropolis-Hastings steps. In all cases uninformative priors were used. See Gilks et al. (1996) for more details about MCMC methods. In this work, 4 chains with 60 000 samples each were run with a burn-in of 30 000 samples. The Gelman-Rubin diagnostic convergence test was evaluated using software that appears in the book by Kruschke (2015). Once convergence is reached, only every 10th draw was retained to avoid autocorrelation problems.

To test the statistical significance of the different parameters that appear in the model, the bayestestR package was used (see Makowski et al. (2019), Makowski et al. (2019)). In particular, the probability of direction test ($p_d$) was used. This is a measure of a parameter being greater or less than zero depending on whether its median is greater or less than zero. This parameter has a direct correspondence with the frequentist p-value because the one- and two-sided p-values can be estimated through the relationship

$$\begin{aligned} p_{one-sided}= 1 - p_d \end{aligned}$$

or

$$\begin{aligned} p_{two-sided}= 2(1-p_d) \end{aligned}$$

3.1 Inference

Once the model has been fitted, one is in a position to predict variables of interest at an ungauged site. Our particular interest is in predicting the parameters of the GEV distribution, $\pmb \mu , \pmb \sigma , \pmb \xi$, in order for example to estimate T-year return levels at those ungauged sites. We shall illustrate the method developed for the location parameter $\pmb \mu _0$. A similar procedure was carried out for $\pmb \mu _1$.

From Eq. (4), the parameter $\pmb \mu _0$ is distributed as an MVN distribution

$$\begin{aligned} \pmb \mu _0\sim {\textbf {MVN}}( X\cdot \pmb \alpha _{\pmb \mu _0}+ W_{\pmb \mu _0}, \tau _{\pmb \mu _0}^2 {\textbf {I}} ) \end{aligned}$$

(10)

where again the symbol $\sim$ means distributed as. Integrating in $W_{\pmb \mu _0}$, the above distribution may be expressed (Bishop 2006) as

$$\begin{aligned} \pmb \mu _0 \sim {\textbf {MVN}}( X\cdot \pmb \alpha _{\pmb \mu _0}, \pmb \Sigma _{\pmb \mu _0} + \tau ^2_{\pmb \mu _0} {\textbf {I}} ) \end{aligned}$$

(11)

Based on Eq. (11), we shall assume that if $\mu ^{0}_0$ is the location parameter at an ungauged site, the joint statistical distribution of the location parameter at the gauged and ungauged sites is given by

$$\begin{aligned} \begin{pmatrix} \mu ^0_0 \\ \pmb \mu _0 \end{pmatrix} \sim {\textbf {MVN}} \begin{pmatrix} &{} m^0_0 &{} | &{} \sigma ^{0}_0 &{} \pmb \Sigma _{0M}\\ &{}\textbf{m}_0 &{} | &{} \pmb \Sigma _{M0} &{} \pmb \Sigma _{MM} + \tau ^2_{\pmb \mu _0} I_{MM} \end{pmatrix} \end{aligned}$$

(12)

where $m^0_0, \textbf{m}_0$ are the means of the distributions at the ungauged site and gauged sites respectively, $\sigma ^{0}_0$ is the variance at the ungauged site, $\pmb \Sigma _{MM}$ is the $M\times M$ covariance matrix at the gauged sites (Eq. (8)), and $\pmb \Sigma _{0M}, \pmb \Sigma _{M0}$ are the $1\times M, M\times 1$ covariance matrices between the ungauged and gauged sites. From Eq. (11), one can take ${\textbf {m}}_0= X \cdot \pmb \alpha _{\pmb \mu }$ and $m^0_0= X_0\cdot \pmb \alpha _{\pmb \mu }$. Lastly, the covariance between the ungauged and a gauged site is taken as

$$\begin{aligned} \Sigma _{M0}(s_i, s_0) = \beta ^2_{\pmb \mu _00} \exp (-||s_i - s_0||)/\beta _{\pmb \mu _01}) \end{aligned}$$

(13)

and $\sigma ^0_0= \tau ^2_{\mu _0} + \beta ^2_{\mu _0 0}$.

A result of MVN distribution theory allows one to consider that the conditional distribution of $\mu ^{0}_0$ given $\pmb \mu _0$, i.e., $P(\mu ^{0}|\pmb \mu _0)$, is normal with a mean given by

$$\begin{aligned} m^1_0 = m^{0}_0 + \pmb \Sigma _{0M}\left( \pmb \Sigma _{MM}+\tau ^2_{\pmb \mu _0} I_{MM}\right) ^{-1}(\pmb \mu _0 - \textbf{m}_0) \end{aligned}$$

(14)

and variance

$$\begin{aligned} \sigma ^{1}_0 = \sigma ^{0}_0 - \pmb \Sigma _{0M}\left( \pmb \Sigma _{MM}+\tau ^2_{\pmb \mu _0} I_{MM}\right) ^{-1}\pmb \Sigma _{M0} \end{aligned}$$

(15)

Once the mean $m^1_0$ and variance $\sigma ^{1}_0$ have been estimated, one can draw samples of the location parameter at the ungauged site.

We can also estimate observations at an ungauged site taking into account the dependence with other gauged sites given by the Gaussian copula. Now we can use the posterior predictive distribution (Gelman et al. 1996; Lynch and Bruce 2004)) to obtain replicate data $y^{\text {rep}}$, which can be regarded as predictions of the model. The posterior predictive distribution at an ungauged site is given by (Gelman et al. 1996)

$$\begin{aligned} \begin{aligned}&P(y(s_0)|Y) = \int P\left( y(s_0)|\mu (s_0), \sigma (s_0), \xi (s_0)\right) \\ {}&\qquad \qquad \qquad \qquad \cdot P\left( \mu (s_0), \sigma (s_0), \xi (s_0)|\mu (s), \sigma (s), \xi (s), Y\right) \\ {}&\qquad \qquad \qquad \qquad \cdot P\left( \mu (s), \sigma (s), \xi (s)| Y\right) d\mu (s) d\sigma (s) d\xi (s) \end{aligned} \end{aligned}$$

(16)

3.2 Ranking the models

To check which version of the model, stationary or nonstationary, best fits the data, the widely applicable information criterion (WAIC) (see Gelman et al. (1996)) was used. This criterion is based on the posterior predictive distribution given by Eq. (16), and is defined by the equation

$$\begin{aligned} {\text{WAIC}} = & - 2\log \left( {\prod\limits_{{i = 1}}^{n} {\mathbf{P}} (y_{i} )} \right) + 2*p_{{{\text{waic}}}} \quad \\ = - 2\sum\limits_{{i = 1}}^{n} {\log } \left( {{\mathbf{P}}(y_{i} )} \right) + 2*p_{{{\text{waic}}}} , \\ \end{aligned}$$

(17)

where $\textbf{P}(y_i)$ is the PPD given by Eq. (16), and $p_{\text {waic}}$ is a term that measures both the bias introduced into the test from using the data twice – once to estimate the parameters, and a second time to use them in the test (see Gelman et al. (2014)) – and the complexity of the model (penalizing models with more parameters). The term $-2 \sum _{i=1}^{n} \log \left( \textbf{P} (y_i) \right)$ is estimated by the equation

$$\begin{aligned} -2 \sum _{i=1}^{n} \log \left( \textbf{P} (y_i) \right) \approx -2 \sum _{i=1}^{n} \log \left[ \frac{1}{J} \sum _{j=1}^{J} \left( \textbf{P}(y_i\vert \theta ^j)\right) \right] \end{aligned}$$

(18)

where J is the number of samples taken from the MCMC method and $\theta ^j$ are the estimated parameters of the model. The $p_{\text {waic}}$ parameter is defined by the expression

$$\begin{aligned} p_{\text {waic}} = \sum _{i=1}^{n} \text {var}_{\text {post}}\left[ \log \left( \textbf{P} (y_i) \right) \right] \end{aligned}$$

(19)

where $\text {var}_{\text {post}}$ is the operator variance and is estimated as

$$\begin{aligned} \text {var}_{\text {post}}(x) = \frac{1}{J-1} \sum _{j=1}^{J}(x_j - \bar{x})^2; \qquad x_j = \log \left( \textbf{P} (y_i\vert \theta ^j) \right) . \end{aligned}$$

(20)

As before, J is the number of samples taken from the MCMC. The choice of the WAIC criterion is motivated by the fact that it is easy to calculate from the MCMC and that it has the property of being asymptotically equivalent to a leave-one-out cross-validation (LOO-CV) test (see Gelman et al. (2014)).

3.3 Prediction

We can obtain replicate data $y(s_0)$ which follows the above distribution via composition sampling by means of the following steps for each element (l) of the Markov chain:

• 1. Following the aforementioned procedure, evaluate the parameters of the GEV distribution at the ungauged site given the parameters at a gauged site.

• 2. Generate a value of the Gaussian copula $\{u_{s_1}^{(l)},...,u_{s_M}^{(l)},u_{s_0}^{(l)}\}$ with the $(M+1)\times (M+1)$ correlation matrix $\mathcal {C}^{(l)}$ given by Eq. (2)

• 3. Invert the copula value according to the expression

  $$\begin{aligned} y_s^{(l)} = F_{GEV}^{-1}(u_s^{(l)}|\mu _s^{(l)}, \sigma _s^{(l)}, \xi _s^{(l)}) \end{aligned}$$

  for all $s_1, s_2, \ldots , s_0$, thus obtaining the vector $\left( y_{s_1}^{(l)}, y_{s_2}^{(l)}, \ldots , y_{s_M}^{(l)}, y_{s_0}^{(l)} \right)$

3.4 Return levels

An important climatological parameter of particular interest for engineering purposes is the T-year return level. In a stationary climate, this is defined as the high quantile for which the probability that the annual maximum exceeds this quantile is 1/T. Let $M_y$ be the maximum extreme of the random variable of interest y

$$\begin{aligned} Pr(M_y > r_l) = 1/T \Rightarrow Pr(M_y \le r_l) = 1-\frac{1}{T} \end{aligned}$$

i.e.,

$$\begin{aligned} GEV(r_l |\mu ,\sigma ,\xi ) = 1-\frac{1}{T} \end{aligned}$$

(21)

from which we can get $r_l$. An equivalent definition is that, on average, the time one has to wait for an event greater than m is T. From the above equation the return level $r_l$ may be evaluated by the expression

$$\begin{aligned} r_l=\mu + \frac{\sigma }{\xi } \left\{ \left( - \frac{1}{\log \left( 1-\frac{1}{T} \right) }\right) ^\xi -1 \right\} \end{aligned}$$

(22)

Several methods have been proposed to estimate the return level in the nonstationary case. See for example Parey et al. (2010), Cooley (2013), Salas and Obeysekera (2014) and Yan et al. (2017). Among them, we have used in the present paper the expected number of events (ENE) which is defined as the level $r_l$ for which the expected number of exceedances in T years after year t is one. It can be shown (see the references just cited) that this $r_l$ level can be evaluated as the solution of the equation

$$\begin{aligned} 1= \sum _{t=1}^{t=T}(1-GEV(r_l|\mu _t, \sigma _t, \xi _t)) \end{aligned}$$

(23)

The software used to carry out the simulations was written in the FORTRAN language. The map figures were prepared using the R packages fields and sp. The code is available upon request.

4 Results

Before addressing the nonstationary temporal model, we fitted our data to a stationary one. Given that temperature depends on elevation and latitude, these two variables after prior linear normalization to the interval (0,1) were used as covariates $X(\textbf{s})$ in the location and scale parameters. Then

$$\begin{aligned} \mu _0= & {} \alpha _{\mu _{0_1}} + \alpha _{\mu _{0_2}} h + \alpha _{\mu _{0_3}} lat + W_{\mu } \left( \textbf{s} \right) +\epsilon _{\mu } \left( \textbf{s} \right) \\ \sigma= & {} \exp \left( \alpha _{\sigma _{1}} + \alpha _{\sigma _{2}} h + \alpha _{\sigma _{3}} lat + W_{\sigma } \left( \textbf{s} \right) +\epsilon _{\sigma } \left( \textbf{s} \right) \right) \end{aligned}$$

with the $\xi$ parameter kept constant throughout the domain. The mean value(95% credibility interval (CI)) for $\alpha _{\sigma _{3}}$ is 0.26($-$0.38, 0.90) with a directional probability ($p_d$) of 78.8%, which means that it is not statistically significant and can therefore be ignored. The model is fitted again excluding this term in the scale parameter. Figure 2 shows the density plots of the coefficients $\alpha _{\mu _{2}}, \alpha _{\mu _{3}}$, and $\alpha _{\sigma _{2}}$.

Fig. 2

Density plot for the $\alpha _{\mu _{2}}, \alpha _{\mu _{3}}$ coefficients (left and center) and for $\alpha _{\sigma _{2}}$ (right). The red line shows the interval (2.5%, 97.5%) percentiles

The coefficient $\alpha _{\mu _{2}}$, which represents the dependence on the elevation of the location parameter, is negative with a mean(2.5%, 97.5% percentiles) value of $-$9.55($-$11.89, $-$7.13)$^\circ$C, so that, taking into account that the elevations were normalized to the interval (0,1) and the highest meteorological site is 2195 m asl and the lowest one is 1 m asl, the corresponding value is $-$4.35($-$5.42, $-$3.25)$^\circ$C km$^{-1}$. The coefficient $\alpha _{\mu _{3}}$, which represents the dependence on the latitude of the location parameter, is negative with a mean(2.5%, 97.5% percentiles) value of $-$6.54($-$14.50, 1.00)$^\circ$C. In this case, the greatest latitude is 5180 km and the least is 4413 km,¹ so that the coefficient becomes $-$8.55($-$18.91, 1.30)$^\circ$C (1000 km)$^{-1}$. There stands out in this case the high uncertainty in the parameter leading the credible interval to contain the value zero. However, a $p_d$ value of 95.2% indicates that, with this statistical significance, it can be said that this parameter is negative with a mean value of $-$8.55$^\circ$C (1000 km)$^{-1}$. This result makes physical sense because the decrease of temperature with latitude is well known. Finally, the coefficient $\alpha _{\sigma _{2}}$ is $-$0.15($-$0.34, 0.018) km$^{-1}$. Again, the confidence interval contains the value zero, but, since the $p_d$ value is 96.3%, at this level of statistical significance it can be said that this coefficient is negative with a mean value of $-$0.15 km$^{-1}$. As the scale parameter is a measure of the variability of the distribution, this result shows that the variability of the maximum extreme temperature in the study area decreases with elevation. This variability is higher in places with low altitude, but as the elevation of the study area increases, the variability of the extreme temperatures decreases.

The shape parameter provides information about the shape of the extreme temperature probability distribution function. Positive values mean that there is no upper bound on the extreme temperatures while negative values lead to an upper bound. Figure shows the density plot for the shape parameter. The mean (2.5%, 97.5%) is $-$0.223 ($-$0.205,$-$0.241), thus supporting a bound on the extreme temperatures for the study area.

After this analysis of the parameters for the stationary model, let us move on to analyse the nonstationary model by introducing into the stationary model the term $\mu _1$ given by Eq. (5). This is an important term because it parametrizes the influence of anthropogenic climate change on the extreme temperatures in peninsular Spain. First, let us show a map of the regression of the maximum extreme temperature versus the global mean temperature: Figure 3 is a map of the Sen regression coefficients,

Fig. 3

Map of the Sen regression coefficients of the maximum extreme temperature versus the mean global temperature (top figures). Histogram plot of the Sen regression coefficients for all gauges is also shown. The right-hand figure shows only those with a statistically significant trend

where the slope is calculated by taking the median of the slopes between each pair of points in the data (Sen 1968). The mean trend is 0.59 with a standard deviation of 2.22; 82 observatories show a positive trend and 76 a negative one. Most of the negative trends are located in the northeastern part of the Peninsula, corresponding to the Ebro valley and the Pyrenees.

Initially we assumed that $\mu _1$ depends on elevation and latitude, i.e.,

$$\begin{aligned} \mu _1\left( \textbf{s} \right) = \alpha _{\mu _{11}} + \alpha _{\mu _{12}} h + \alpha _{\mu _{13}} lat + W_{\mu _1} \left( \textbf{s} \right) +\epsilon _{\mu _1} \left( \textbf{s} \right) \end{aligned}$$

The mean value of $\alpha _{\mu _{13}}$, which represents the latitude dependency, is $-$0.74 ($-$2.48, 1.21) with a $p_d$ of 78.24%. It can therefore be ignored, thus ignoring the dependence on latitude of the trend term $\mu _1\left( \textbf{s} \right)$. The model is fitted again but excluding this term.

Figure 4 shows density plots of the coefficients $\alpha _{\mu _{11}}$ and $\alpha _{\mu _{12}}$ of the model without the latitude term.

Fig. 4

Density plots for the $\alpha _{\mu _{11}}, \alpha _{\mu _{12}}$ coefficients. The red line shows the (2.5%, 97.5% percentiles) interval

The $\alpha _{\mu _{11}}$ coefficient with a mean value of 2.98(1.75, 3.72) is significantly different from zero, and, while $\alpha _{\mu _{12}}$ with a mean value of $-$1.55($-$3.13, 0.09) contains zero, it has a $p_d$ value of 96.8% suggesting that we keep this term in the model. The negative sign of the term corresponds to a decrease with elevation of the influence of the global temperature on the maximum extreme temperature in peninsular Spain.

We want now to compare which model, stationary or nonstationary, better fits the data. Table 1 presents the results of applying the WAIC. The better fit is with the nonstationary model (smaller WAIC parameter), although its $p_{\text {waic}}$ parameter, which measures the complexity of the model, is greater.

Table 1 Summary of the values of the WAIC information criterion for the stationary and nonstationary models

The parameter $\pmb \mu _1(\textbf{s})$ represents the influence of climate change as given by the GMSAT measure on the extreme temperatures over the Iberian Peninsula. The model gives us this parameter for the gauged sites. However, the theory in Sect. 3.1 applied for each MCMC sample allows us to estimate the distribution of the $\mu _1$ coefficient for each of the 17760 grid cells of the Iberian Peninsula obtained from the topographic map shown in Fig. 1. Figure 5 shows the maps of the mean and the masked mean values of the $\mu _1\left( \textbf{s} \right)$ parameter (upper row) and of the 2.5% and 97.5% percentiles (lower row). The masked values are those grid cells with a directional probability $p_d$ less than 95%. All the parameters shown include the constant used to normalize the global mean temperature to the interval (0,1). This means that for each degree Celsius that the global temperature increases or decreases with respect to the minimum value of 1984, the location parameter $\mu _1\left( \textbf{s} \right)$ increases or decreases by the value shown in the map.

Fig. 5

Maps of the mean and masked mean (upper row) and 2.5% and 97.5% percentiles (lower row) of the $\mu _{1}$ location parameter

In the figure, the lowest values (which were found not to be statistically significant) correspond to the highest mountain ranges in the Peninsula (see the map in Fig. 1) – the Pyrenees in the northeast, the Sistema Central in the centre of the Peninsula, the Sistema Betico in the south, and the Cordillera Cantabrica in the north. The effect of climate change measured by the increase in global average temperature is smaller in mountainous areas.

4.1 Model diagnostics

Figure 6 shows the temporal evolution of the maximum annual values of temperature for a randomly chosen set of 9 of the 158 observatories together with the mean and 2.5% and 97.5% percentiles of the simulation obtained with the statistical model. As can be seen, most of the observed temperatures (represented by dots) lie within the 95% margin of error (blue lines).

Fig. 6

Temporal plots of observed and simulated data for 9 randomly chosen sites. Dots show observed maximum annual values during summer months. For the simulated temperatures, the red line is the mean and the blue lines the 2.5% and 97.5% percentiles

To measure the ability of the model to reproduce the data used to fit it, the posterior predictive distribution given in Sect. 3.3 was applied. As a measure of the deviation from the observed maximum extreme temperatures, the error

$$\begin{aligned} E= \hat{y}(s,t)- y(s,t) \end{aligned}$$

and absolute error

$$\begin{aligned} ABE = |\hat{y}(s,t)- y(s,t)| \end{aligned}$$

were evaluated, with $\hat{y}(s,t), y(s,t)$ being the mean (taken over the samples) of the simulated values and the observed value, respectively, for each site s and time t.

Figure 7 shows a density plot of the error and the absolute error between the observed and the simulated data of the maximum extreme temperatures. The mean error is 0.26$^\circ$C and the mean absolute error 1.43$^\circ$C. These results show that the model slightly overestimates the extreme temperatures.

Fig. 7

Density plot of the error (left) and absolute error (right) between the observed and the simulated data

Given the nonstationarity of the model, to compare the statistical distributions of the observed and simulated data we followed Renard’s suggestion (Renard 2011) to convert the observations into a probability space by the transformation

$$\begin{aligned} \pi _{s,t} = GEV(y(s,t)|\mu (s,t), \sigma (s), \xi ), \end{aligned}$$

which is also termed the probability integral transform (Gneiting et al. 2007), and then plotting $\pi _{s,t}$ against the quantiles of the uniform (0,1) distribution. Figure 8 shows these probability-probability plots of the simulated data. The lowest quantiles indicate

Fig. 8

Probability plots of the simulated data versus the uniform (0,1) distribution for the sites used: each site individually (left), and pooled (right)

where the model underestimates the temperatures, but the highest ones indicate overestimates. One can see that, in general, the model follows the 1:1 line reasonably well.

4.2 Spatial dependendence

As mentioned in the introduction, the association among the extreme temperature observed in different sites comes from two sources, one associated with climate variation along the region represented by the regression model of the GEV parameters and another associated with what has been called weather association and represented by the copula model. In this sense, the noise $W_\kappa (s)$ introduced by Eqs. (4), (5) and (6) represents the association due to the variation of the climate along the region not taken into account by the regression model. The degree of association is given by the correlation matrix $\Sigma _\kappa$ and the range parameter $\beta _{\kappa 2}$ gives the rate at which the correlation decreases with the distance. Figure 9 shows a plot of the dependogram given by Eq. (2) and the correlation of the spatial model of the parameters in the GEV distribution given by Eq. (8) and Table 2 gives the median and the (2.5%, 97.5%) percentiles of the range parameters $c_1, c_2$ that appear in Eq. (2), and the parameters $\beta _{\mu 0_2}, \beta _{\mu 1_2}, \beta _{\sigma _2}$ that appear in Eq. (8). Units are km.

Fig. 9

Spatial dependence of the data and GEV‘s parameters. Dependogram (top left); location $\mu _0$ (top right); location $\mu _1$ (bottom left) and scale parameter (bottom right). The red line shows the mean values and the dotted blue ones the 2.5% and 97.5% percentiles

Table 2 Median and (2.5%, 97.5%) percentiles of range parameters for the dependogram (Eq. 2 ) and the spatial model for the GEV distribution (Eq. 8)

As it may be seen from the figure, the dependence among the data is quite high even for observatories 1000 km apart. The model slightly overestimates the correlations among the data at the largest distances. The high dependence among the data justifies the introduction of a copula in the model. We can see from the figure and from Table 2 that within the spatial dependence of the GEV parameters, the shorter range corresponds to the non-stationary time trend $\beta _{\mu 1_2}$ and the largest one to the scale parameter $\beta _{\sigma _2}$. This result suggests that the regression model for the trend location parameter $\mu _1$ explains better its spatial variation than the regression model for location $\mu _0$ and scale $\sigma$ parameters.

4.3 Prediction

Because of their missing values, 20 meteorological observatories were left out of the calculations. They are now used to test the model’s predictive capacity. Following the steps presented in Sect. 3.1, the GEV parameters of the new observatories were obtained, and the steps set out in Sect. 3.3 were used to get estimates of the observations at the new sites. This was done for each of the samples of the Markov chain. As before, the error and absolute error were evaluated (Fig. 10).

Fig. 10

Temporal plot of simulated and observed data for 9 prediction sites chosen at random. The red line is the mean and the blue lines the 2.5% and 97.5% percentiles of the simulated temperatures

Figure 11 shows density plots of the two errors. The mean error is 0.09$^\circ$C and the mean absolute error 1.86$^\circ$C. There is, therefore, an overestimation of the extreme temperature given by the model, although lower than that corresponding to the observed sites. The absolute error is greater, leading to a greater uncertainty.

Fig. 11

Density plot of the error (left) and absolute error (right) for the prediction sites

Fig. 12

Probability plot of the observed data versus the uniform distribution (0,1) for the prediction sites for each site individually (left), and pooled (right)

Figure 12 shows the probability plot for the prediction sites. Generally, there is an underestimation for the highest temperatures and an overestimation for the lower ones with a larger dispersion than that obtained with the observation sites. The mathematical model does not explain well the behavior of temperatures over their full range of variation.

4.4 Return level

As mentioned before, the expected number of events (ENE) in T-years is used to evaluate the return level (RL). The main problem with this approach is that one needs T years of data after the year t in which to evaluate RL. For example, to evaluate the 20-year RL in the year 2020, 20 subsequent years are required. But the span of the time series used is only up to that year. To resolve this drawback, the smoothed global mean temperatures of the period 1985–2020 were fitted to a straight line. Figure 13 shows a scatterplot of the smoothed global mean temperature versus time together with that straight line fit. As one can see, the fit is quite good. Supposing, business as usual, a linear evolution of the global mean temperature, the straight line is a projection for the next 20 years to allow for the uncertainty in the evolution of the future climate. Solving Equation (22), the return levels for the years 2000 and 2020 were evaluated for each of the samples of the Markov chain and for each cell.

Fig. 13

Scatterplot of the smoothed global mean temperature versus time

Fig. 14

Maps of the mean of the 20-year return level beginning in the year 2000 (top left), and beginning in the year 2021 (top right), and the difference between the return levels for the two dates (bottom left) and the masked difference (bottom right)

The averages (means) of the samples are shown in Fig. 14 together with the differences and the masked differences. There is an increase in the return level over the whole Iberian Peninsula with a mean(2.5%,97.5% percentiles) of 1.4(0.9,1.6)$^\circ$C. Obviously, this differences map agrees quite well with the $\mu _1$ location map shown in Fig. 5. Given a trend of 0.0185$^\circ$C year$^{-1}$ in the global mean temperature, during the 20 years that elapse between the evaluation of the two return levels, the global mean temperature has increased by 0.37$^\circ$C, while the mean 20-year return level over the Iberian Peninsula has increased by 1.4$^\circ$C, i.e., more than 3.5 times as much. The return levels for the year 1981 were also evaluated and the differences between the values obtained in 2021 and 1981 lead to a similar spatial distribution over the study area but a different scale. The maximum difference between 2021 and 2000 is 1.8$^\circ$C, and between 2021 and 1981 is 3.3$^\circ$C.

5 Summary and conclusions

This work has presented a statistical study of the summer maximum extreme temperature observed at a set of 158 meteorological sites located in peninsular Spain for the period 1981–2020. The statistical tool used to model the data was a hierarchical spatio-temporal Bayesian model with a GEV parametrization of the extreme events. A Gaussian copula was applied to take into account the correlations among the observed temperatures at the different observatories. The main advantages of models of this kind are that they allow the uncertainty in the parameters of the statistical distribution to be reduced by pooling information from different observatories, and that they can interpolate important features of the statistical distribution, such as the T-year return level, to non-observing sites. Two models, one stationary and one nonstationary, were used. Because our interest was in analysing the possible influence of anthropogenic climate change on the extreme temperatures in Spain, in the nonstationary model we used as a function of time the 5-year smoothed mean global temperature for the study period.

The results showed that the nonstationary model fits the observations better than the stationary one. The location parameter $\mu _0\left( \textbf{s}\right)$ of the GEV distribution shows a negative dependence on elevation and latitude, which is the expected dependence for the temperature. The scale parameter $\sigma \left( \textbf{s}\right)$ and the trend coefficient $\mu _1\left( \textbf{s} \right)$ also showed a decrease with elevation, leading to a decrease in the variability of the extreme temperature with elevation as well as a lower influence of the increase in global mean temperature for higher locations. The shape parameter was negative, which seems to be a universal behaviour for maximum temperatures since all the known works report a negative value for this parameter. The negative value of the shape parameter reveals that the tail of the distribution cannot be greater than a threshold value which may be different for each location.

The model in general overestimates the observed lowest temperatures and underestimates the highest ones. On average, the bias (a measure of simulated minus observed) is positive, i.e., the simulated temperature is higher than the observed one.

The results also show an increase in the 20-year RL over most of the Iberian Peninsula except for a region in northeastern Spain where the increase is not statistically significant.

An improved model considering anisotropy in the covariance function would be a significant advance over the current model. It would be interesting to use other types of copulas valid for extremes, but they are not easy to implement when the spatial dimension of the model is large, as happens for climatological data with scales of the size of the Iberian Peninsula.