Understanding CMIP6 biases in the representation of the Greater Horn of Africa long and short rains

Abstract

The societies of the Greater Horn of Africa (GHA) are vulnerable to variability in two distinct rainy seasons, the March–May ‘long’ rains and the October–December ‘short’ rains. Recent trends in both rainy seasons, possibly related to patterns of low-frequency variability, have increased interest in future climate projections from General Circulation Models (GCMs). However, previous generations of GCMs historically have poorly simulated the regional hydroclimate. This study conducts a process-based evaluation of simulations of the long and short rains in CMIP6, the latest generation of GCMs. Key biases in CMIP5 remain or are worsened, including long rains that are too short and weak and short rains that are too long and strong. Model biases are driven by a complex set of related oceanic and atmospheric factors, including simulations of the Walker Circulation. Biased wet short rains in models are connected with Indian Ocean zonal sea surface temperature (SST) gradients that are too warm in the west and convection that is too deep. Models connect equatorial African winds with the strength of the short rains, though in observations a robust connection is primarily found in the long rains. Model mean state biases in the timing of the western Indian Ocean SST seasonal cycle are associated with certain rainfall timing biases, though both biases may be due to a common source. Simulations driven by historical SSTs (AMIP runs) often have larger biases than fully coupled runs. A path towards using biases to better understand uncertainty in projections of GHA rainfall is suggested.

1 Introduction

The Greater Horn of Africa (GHA), comprising eleven countries in East Africa, is a region of both climatic extremes and related societal vulnerability. It comprises the driest area of the tropics, while its societies are heavily dependent on the rainfall cycle. Around 75% of the population in Ethiopia, Kenya, and Tanzania are smallholder farmers primarily working on rainfed lands (Salami et al. 2019; Biazin et al. 2012), and around 60% of the Somali population practice pastoralism in arid and semi-arid water-stressed regions (UNDP 2019). Consequently, droughts are often associated with threats to food security—for example, the 2011 East African Drought led to the United Nations declaring a famine in southern Somalia, where 2.8 million people needed ‘life-saving assistance’ (NASA Earth Observatory 2011).

A notable characteristic of the regional climate is the presence of two distinct rainy seasons in the coastal plains of Ethiopia, Somalia, Kenya, and Tanzania: the stronger ‘long’ rains, known locally as the gu in Somali or masika in Swahili, occur in the boreal spring, and the generally weaker but more variable ‘short’ rains, known locally as the deyr in Somali or vuli in Swahili, occur in the boreal fall (these will be referred to as the ‘long’ and ‘short’ rains, respectively, throughout this paper). Drought extremes that contribute to famines often result from a mistiming or a complete loss of a rainy season such as during the fall 2010 drought (FEWSNET 2011), in which the short rains largely failed. Conversely, particularly wet seasons can cause destructive flooding, such as during the record short rains associated with the 1997–1998 El Niño, which resulted in over 1300 deaths and 270,000 displacements in Somalia alone (IRIN 97).

Recent trends in the observational records in both rainy seasons have heightened concerns about the impact of climate change on rainfall variability in the GHA region. Declines in total annual rainfall since 1983 and specifically during the long rains have been found in studies examining satellite data, station records, satellite-station hybrid datasets, and in farmer recollections (Diem et al. 2014, 2019; Ssentongo et al. 2018; Cattani et al. 2018; Salerno et al. 2019). These changes are associated with a decrease in the rainy season length, with both later onsets and earlier demises (Wainwright et al. 2019). The frequency of droughts during the long rains seems to have increased since 1998, which may be the consequence of natural or forced variability attributable to changes in Pacific Ocean SSTs (Lyon 2014; Vigaud et al. 2017; Funk et al. 2018; Gebremeskel Haile et al. 2019). An increase in the zonal SST gradient in the tropical Pacific in particular, which is not well-captured in CMIP5 and CMIP6 models, may be due to a response to radiative forcing (Seager et al. 2019, 2022), and could be favoring La Niña conditions, a stronger Walker circulation and drought over the GHA. Conversely, similar research has found increases in the strength of the short rains in parts of the region (Diem et al. 2014; Cattani et al. 2018; Gebremeskel Haile et al. 2019).

Consequently, many recent studies have used climate models to project changes in rainfall characteristics under global warming scenarios. Modeling studies predict wetter, more intense, and later short rains (e.g. Dunning et al. (2018); Otieno and Anyah (2013); Wainwright et al. (2021)) and wetter long rains (e.g., Wainwright et al. (2021)). These projections may be at odds with recent decreases in boreal spring rainfall, an ‘East African Paradox’ likely related to internal variability in the system (e.g. Lyon and Vigaud (2017)) or possible modeling deficits.

Climate models are increasingly used to project the impacts of regional climate change into the future (e.g. Hsiang et al. (2017); Carleton et al. (2019)). In East Africa, recent studies have for example used CMIP5-era models to project the impact of global warming on maize and beans production in Ethiopia (Abera et al. 2018; Thornton et al. 2010), groundwater resources (Taylor et al. 2013), and metrics of fisheries, flood management, urban infrastructure, and urban health (Bornemann et al. 2019), among others. Climate model studies are also routinely cited in government documents such as Kenya’s National Climate Action Plan Government of Kenya (2018), Ethiopia’s National Adaptation Plan (Federal Democratic Republic of Ethiopia 2019), or Somalia’s communications to the UN Framework Convention on Climate Change (Office of the Prime Minister, the Federal Republic of Somalia 2018).

However, despite their heavy use in both academic and government sources, climate models historically have a poor record in simulating rainfall in East Africa. CMIP5 models have well-known biases in simulating both the strength and the timing of the long and short rains in East Africa. The long rains in CMIP5 models start 19 days later on average than in observations (Dunning et al. 2017); the long rains are generally too weak and the short rains too strong in models, leading to the short rains being stronger than the long rains (Yang et al. 2014).

A process-based model evaluation is however particularly complex in the GHA due to the many regional and large-scale processes that affect local rainfall. Both the long and short rains in the GHA are affected by the behavior of the large-scale circulation over the global tropics and the Indian Ocean basin. In its long-term average state, the atmosphere above the Indian Ocean is formed into a zonal overturning circulation referred to in the recent literature as the Indian Ocean Walker Cell or Walker-type circulation due to its similarities with the Pacific Ocean Walker Cell pattern over the Pacific Ocean. The Indian Ocean pattern mirrors its Pacific Ocean counterpart; the climatological circulation involves near-surface westerlies, high-level easterlies, ascent over the eastern Indian Ocean and Indo-Pacific Warm Pool, and descent over the GHA (Nicholson 2017). This descent suppresses convection and is present to a certain extent even during the climatological average short rain period (Nicholson 2017; King et al. 2019).

The long and short rains occur during the temporary reprieve of this climatological descent in the ‘shoulder’ seasons between the summer and winter monsoons. The long rains generally begin in late March or early April as the Arabian High dissipates and the strong surface northerlies of the boreal winter weaken and turn southerly, and end as the Mascarene High intensifies, reversing the low-level meridional geopotential height gradient, and strong southerly winds feed into the broader Indian Monsoon circulation (Riddle and Cook 2008; Vizy and Cook 2020; Camberlin et al. 2010). The short rains generally begin in late September, as these strong southerly winds weaken and reverse once more (Vizy and Cook 2020).

The wet seasons are both characterized by seasonal peaks in offshore sea surface temperatures (SSTs), positive anomalies in large-scale instability as measured by the difference between surface moist static energy (MSE) $h_s$ and saturation MSE $h^*$ in the free troposphere and rising motion in the atmosphere above the GHA (Yang et al. 2015a). They feature weak, onshore surface winds bringing warm, wet air onto the GHA. During the long rains, additional moisture may be entrained from the Congo Basin through westerly zonal wind anomalies in equatorial Africa (Finney et al. 2020; Walker et al. 2020). The dry seasons are characterized by seasonal minima in offshore SSTs, large-scale descent through the middle and upper troposphere, negative anomalies in $h_s-h^*$, and surface winds that are both parallel to the shore and dry (Yang et al. 2015a; Nicholson 2017).

Studies that have taken a process-based approach to evaluating previous generations of models have developed a series of dynamical metrics for model rainfall behavior. For example, Yang et al. (2015b) examined SSTs over the western Indian Ocean and aspects of MSE in CMIP5 models, finding that biases in near-surface MSE modulated by biases in SSTs can explain differences between historical and AMIP runs of the MRI-CGCM3 model. King et al. (2019) focused on mid-tropospheric ascent over the GHA to diagnose Kenyan rainfall. Dyer and Washington (2021), focusing on the Kenyan long rains, developed a series of diagnostic metrics for model evaluation.

This complex system suggests the influence of both oceanic and atmospheric factors; studies tracing the interannual variability of the long and short rains have found corresponding influences from both. This variability is particularly strong in the short rains, which, despite being weaker on average than the long rains, contribute more to the overall interannual precipitation variability in the region (Camberlin and Philippon 2002).

It is likely possible to learn about origins of model biases by examining in observations and models the processes that lead to interannual variability of the rains. For example, if some state of the climate system causes anomalously wet rains, then models that are biased towards that state in the mean may be expected to also be biased to rains that are too wet. To this effect, anomalies representing a strengthening of the mean structure of the Indian Ocean Walker Cell are associated with drier rainy seasons in the GHA and vice-versa in observations (e.g., Funk et al. (2018); Zhao and Cook (2021)). Stronger low-level westerlies over the Indian Ocean are negatively correlated with the strength of the short rains (Nicholson 2017). Conversely, low-level easterlies, often associated with the positive phase of the Indian Ocean Dipole (IOD), a mode of the zonal SST gradient, are often associated with particularly strong short rains (Liebmann et al. 2014; Nicholson 2017; Blau and Ha 2020). Mid-tropospheric vertical velocity, corresponding to the descending limb of the Walker Cell, has also been connected to regional rainfall; for example, models that overestimate the strength of the descending limb tend to be biased dry during both the long and short rains in Kenya (King et al. 2019) and models that explicitly resolve convection over the GHA reduce timing biases in both seasons (Wainwright et al. 2021). The influence of the direction of the high-level zonal winds above the GHA is complex; weaker easterlies may indicate a weaker Walker Cell (e.g. King et al. (2019); Limbu and Tan (2019); Hastenrath et al. (2011)) and divergence aloft associated with convective activity in the western Indian Ocean and wetter seasons (Camberlin and Philippon 2002; Limbu and Tan 2019); conversely, during the long rains in particular, stronger easterlies may be associated with the Asian monsoon anticyclone and drying of the GHA (Liebmann et al. 2017).

Given their connection to the interannual variability in the GHA rainy seasons, simulations of the surface SSTs and the Indian Ocean Walker Circulation are logical targets for diagnostic metrics of model behavior. We consequently develop metrics based on two aspects of the oceanic state: the Indian Ocean zonal SST gradient and western Indian Ocean SSTs (WIOSSTs); and four aspects of the atmospheric circulation: zonal winds aloft, ascent, and MSE over the GHA, and mid-tropospheric zonal winds over equatorial Africa, to identify these sources.

Warmer WIOSSTs and a stronger SST zonal gradient with warm western and cold eastern Indian Ocean temperatures during the rainy seasons are expected to correlate with stronger rainy seasons; later peaks of the SST seasonal cycle in both variables may be indicative of broader biases in a model’s large-scale seasonal cycles and may therefore correlate with later peaks in the rainy seasons. Given the IOD’s connection to interannual variability in the short rains in particular, metrics of the zonal SST gradient are expected to particularly correlate with metrics of the short rains in models.

Stronger high-level easterlies above the GHA may be an indicator of the development of a convective center in the western Indian Ocean. This connection may be particularly strong in the short rains when the coherence of the Walker Cell is stronger (Hastenrath et al. 2011), though studies have shown easterly anomalies aloft for March-April in years in which the long rains seem to be particularly affected by the ENSO cycle (Camberlin and Philippon 2002) and have found a role for the Walker Cell in recent long rain droughts (Vigaud et al. 2017; Funk et al. 2018). If connected to western Indian Ocean convection in models, easterly anomalies during the rainy seasons may therefore correlate with wetter seasons, particularly during the short rains. Liebmann et al. (2017) on the other hand find suppressed easterlies to be a pre-condition for the onset, and strengthened easterlies for the demise, of the long rains, relating to modulation of large-scale descent over the GHA; in this paradigm, westerly anomalies in the boreal spring would therefore be expected to correlate with wetter long rains.

The difference between surface MSE and saturation MSE in the free troposphere $h_s-h^*$ is expected to be correlated with stronger rainy seasons, particularly during the short rains. During the long rains, this connection may be weaker since $h_s-h^*$ does not directly capture the impact of mid-level entrainment from the Congo Basin not captured through $h_s$. This process would be more easily identified through a connection between westerly anomalies over equatorial Africa and MSE h in the mid-troposphere and stronger long rains.

Finally, stronger ascent, an indicator of convective activity, is expected to be tightly correlated with both stronger long and short rains, as is later ascent with later rainy seasons; biases in these metrics could diagnose problems with model convection simulations.

CMIP6 models are now available, and offer higher resolutions, more explicitly modeled physical processes, and improvements in key dynamics for the Indian Ocean basin (e.g., Gusain et al. (2020)). Increased CMIP6 model resolution does not remedy biases in precipitation over East Africa (Akinsanola et al. 2021), suggesting that orography is not the primary driver of biases, at least within the resolution range of CMIP6 models ($0.70^\circ -2.8^\circ$ per grid cell). Consequently, the source of model biases is likely in their ability to simulate the large-scale dynamics of the region. A necessary but insufficient condition for users of CMIP6 output to be confident in their projections is the models’ ability to reproduce key aspects of the climate variability in the historical record related to the task at hand (see e.g., the discussion in Nissan et al. (2020)). Since these models will likely be extensively used to create projections of the impacts of climate change on East Africa in the coming years, this paper seeks to understand whether these models accurately represent the characteristics of the seasonal cycles in the double rainy season area of the GHA, and whether they replicate key physical drivers of regional rainfall gleaned from the literature and derived from observations.

The rest of this paper is structured as follows: Sect.  2 will introduce the daily observational and CMIP6 data used; Sect. 3 introduces the methodology for calculating seasonal and dynamical metrics. Section 4 will detail issues in CMIP6 representations of GHA rainfall. Sections 5 and 6 will investigate to what extent metrics of the ocean and the atmospheric circulation can explain biases in seasonal characteristics, respectively. Finally, Sect. 7 summarizes conclusions and charts a path forward for how this information can be used to interpret projections of the rainy seasons in the GHA.

2 Data

Daily data are used throughout this study to accurately characterize the timing of the rainy seasons. Not only are rainy seasons often less than two months long, but sub-seasonal variability apparent even in monthly data suggests that higher resolution data are needed to fully resolve the relevant dynamics (e.g., Camberlin and Okoola (2003); Camberlin and Philippon (2002)).

To cover the longest timeframe included in all observational and modeling data products used, all analysis involving rainfall and atmospheric variables is conducted over the years 1981–2014 for climatological averages. Analysis for individual years is limited to the period 1981–2013, to account for the demise of the short rains sometimes occurring after the Gregorian New Year. Analysis involving SSTs is conducted over the years 1982–2014 to account for the later start of the ocean observations used.

2.1 Observational data

To characterize precipitation in the Horn of Africa, we use daily rainfall data from the Climate Hazards Infrared Precipitation with Stations (CHIRPS) dataset (Funk et al. 2015). CHIRPS combines satellite data from the TRMM satellite with interpolated rain gauge products and an elevation model. Though evaluation is complicated by the lack of a dense rain gauge network in the region (e.g. Dinku (2018)), studies have shown CHIRPS to outperform other commonly used datasets in the GHA; while it overestimates the occurrence of rainfall, rainfall in those extra events tends to be minimal (e.g. Diem et al. (2019); Ayehu et al. (2018)).

Daily sea surface temperatures (SSTs) from the Daily Optimum Interpolation Sea Surface Temperature (OISST) record, version 2.1 (Huang et al. 2021) are used to construct the ocean metrics. OISST is a 0.25-degree gridded product blending in situ ship and buoy measurements with satellite-derived estimates from the Advanced Very High Resolution Radiometer (AVHRR). Though the Indian Ocean in OISST is biased slightly low compared to in situ measurements (e.g., $\sim 0.08^\circ$ C vs. Argo floats in Huang et al. (2021)), having gridded daily data allows for a direct comparison to model output. OISST begins on September 1, 1981; we use data from 1982 to 2014.

250 hPa and 700 hPa zonal velocity, 250 hPa and 500 hPa vertical pressure velocity, and surface and 700 hPa specific humidity and temperature from the ERA5 reanalysis product are used to analyze historical circulation patterns (Hersbach et al. 2020). Data were downloaded in ERA5’s native hourly format and daily averages were taken to obtain daily data.

Table 1 Circulation metrics analyzed

2.2 Model data

This study examines biases in models from the 6th edition of the Coupled Model Intercomparison Project (CMIP6; Eyring et al. (2016)). Compared to the previous generation of climate models (CMIP5), CMIP6 models on average have slightly higher resolution and directly simulate more physical processes. Precipitation, SSTs, zonal velocity at 250 hPa and 700 hPa, vertical pressure velocity at 250 hPa and 500 hPa, and surface and 700 hPa specific humidity and temperature from any CMIP6 model with daily data for that variable (not every model has daily data for each variable, see Table 2) are used.

Table 2 Models analyzed in this study

This study analyses three types of climate model experiments. The bulk of the analysis focuses on each model’s ‘historical’ experiment, in which models are forced using historical observed atmospheric compositions, solar forcings, and land use patterns (Eyring et al. 2016). In Sect. 5.3, to isolate the impact of SST biases on the biases in the GHA rainy seasons, daily precipitation data from CMIP6 model runs forced by historical SSTs are additionally analyzed, and referred to as ‘AMIP’ runs (‘atmospheric model intercomparison project’) throughout. From both sets of model output, the years 1981–2014 are used in analyses of precipitation and other atmospheric variables, spanning from the start of the CHIRPS dataset to the end of the ‘historical’ forcing scenario in the CMIP6 project. For analyses of SSTs, 1982-2014 are used to span the spread of the OISST dataset. In Sect.  7, to illustrate the challenges in using current biases to partition future model projections, precipitation from model runs using the SSP3 scenario (O’Neill et al. 2016), representing high challenges to mitigation and adaptation, are used as well.

3 Methods

3.1 Study area

This study focuses on the area of the GHA that experiences two distinct rainy seasons (hereafter referred to as the “double-peaked region”). In calculations of seasonal statistics, we consider every land grid cell in observations or models between $32^\circ$ E and the Indian Ocean and between $-3^\circ$ S and $12.5^\circ$ N for which the second harmonic is larger than the first harmonic. This region is similar to commonly-used geographic subsets for studies of East African rainfall, see e.g., the regions studied by Wainwright et al. (2021) or Yang et al. (2014). Some authors use a smaller region centered on Southern Somalia (e.g. Camberlin et al. (2010); Liebmann et al. (2014)); we show our results are robust to the particular region studied.

Fig. 1

Study area in CHIRPS observations and CMIP6 models. The red contour shows the area with a double-peaked rainfall structure over GHA land in CHIRPS; note that CHIRPS is a land-only data product and rainfall observations over the ocean are not considered in this study. Darker shading means more CMIP6 models have a double-peaked rainfall climatology in that location. All models are shown at their native resolutions; grid cells may only partially overlap between models. Most models place the double-peaked region along the coastal plains of Somalia, Kenya, and southeastern Ethiopia, consistent with observations. For the remainder of this study, statistics of the rainy seasons (and ascent) are averaged over each data product’s double-peaked region over land

Each model is evaluated based on its own reality—i.e., the study area is calculated separately for each model and for observations. Models do differ in the exact geographic area in which a double-peaked rainfall climatology is simulated (Fig.  1); however, models generally place this region in the coastal plains of Somalia, southeast Ethiopia, and northern Kenya, consistent with observations. Many models also show a region with a single dominant summer peak in rainfall along the Somali coast. Such a region does exist in observations along the coast between roughly 42$^\circ$ E and 45$^\circ$ E, including the cities of Kismayo and Mogadishu, where peak rainfall is in June, though its extent is more limited than in models. In the literature, this rainy season is sometimes classified as an extension of the long rains (e.g., Camberlin and Planchon (1997) for its occurrence farther south in Kenya), though these rains are referred to as occurring during the hagaa or xagaa dry season in the rest of Somalia by UN bulletins (e.g., OCHA (2020)), or during a separate, local rainy season called the hhagaayo by e.g. Galaal (1992). The factors causing these differences in geographic locations of the rainy seasons may be important for understanding model behavior in this region, but are beyond the scope of this paper. In Sect. 4, we additionally perform analysis on only the part of the GHA where more than 40 models and CHIRPS observations show a double-peaked region; results are consistent to this subset.

Different areas in the double-peaked region have phenomenologically similar rainy seasons; however, geographic differences in the strength and timing of the rainy seasons are well-known. The long rains tend to begin earlier in the south and later in the north, and vice-versa, and the north tends to be drier than the south. Geographic subsets of the GHA are to a certain extent always arbitrary, given the number of different precipitation regimes discovered. Nicholson (2017) lists studies that found between 3 and 26 distinct rainfall regions, given the strong spatial homogeneity in interannual variability, particularly during the short rains. To ensure that focusing on each model’s own reality does not bias results due to geographical differences in the march of the seasons, in Sect. 4 we additionally conduct our analysis on 7 separate subsets of the region and note differences where applicable.

3.2 Seasonal definitions

Throughout this paper, we use the seasonal definitions by Dunning et al. (2016) based on inflection points in the cumulative precipitation rate. This method was specifically designed for African regions with a double-peaked rainfall climatology, and is designed to reduce the likelihood of ‘false starts’—early-season storms followed by prolonged periods of dryness—that may be particularly damaging to recently-planted crops (Huho et al. 2012; Dunning et al. 2016). Notably, however, it is derived from the data itself, and therefore may not overlap with local agricultural or pastoral definitions of the seasons. These may emphasize different aspects of the season, other variables such as soil moisture content, or use threshold-based definitions that are easier to measure using local information (e.g., Goddard et al. (2010); Lala et al. (2020)).

For each grid cell in the study area, the onset and demise of the 1981-2014 climatological rainfall is determined using the Dunning et al. (2016) method, as is the onset and demise of the rainy seasons in each individual year from 1981 to 2013 (see Sect. S1 for full details).

3.3 Seasonal metrics

For each season, seasonal characteristics are calculated based on the onset and demise determined using the methodology detailed above. The ‘duration’ of each season is defined as the simple difference in days between the onset and demise, and the ‘total integrated rainfall’ or ‘strength’ as the total sum of daily rainfall between the onset and demise. The ‘peak timing‘ is the day of peak rainfall, while the ‘peak amount‘ is the amount of rain on that day.

3.4 Definition of circulation variables

We develop diagnostic metrics for the strength and timing of the rainy seasons based on two aspects of the oceanic state—IOD and western Indian Ocean SSTs, and four aspects of the atmospheric circulation—upper-tropospheric zonal winds above the GHA, ascent over the GHA, mid-tropospheric zonal winds over equatorial Africa, and moist static energy over the GHA (see Table 1 for summary). We examine circulation metrics from both fully coupled simulations from each model’s “historical” experiment run, and from simulations forced by historical sea surface temperatures, referred to as AMIP (Atmospheric Model Intercomparison Project) runs throughout.

Western Indian Ocean SSTs (WIOSSTs). Following the region used in Yang et al. (2015a), average SSTs in the western Indian Ocean (referred to as WIOSSTs) are calculated as the average from 10$^\circ$ S to 12$^\circ$ N and 38$^\circ$ E to 55$^\circ$ E. For each year, the day of peak WIOSSTs and the peak WIOSSTs are calculated using daily OISST data, for days 30–250 to compare to the long rains, and 250–30 of the following year to compare to the short rains.

Indian Ocean zonal SST gradient. The IOD is characterized by the zonal gradient in Indian Ocean SSTs, using the same regions as those used for the Dipole Mode Index (DMI) developed by Saji et al. (1999) and used e.g. in Lyon (2020). To be able to measure model mean differences, we use the raw difference between SSTs in the West (average in the box 10$^\circ$ S to 10$^\circ$ N, 50$^\circ$-70$^\circ$ E) and East (average in the box 10$^\circ$ S - 0$^\circ$ S, 90$^\circ$-110$^\circ$ E) Indian Ocean. Note that this is different from the DMI, which is the gradient in anomalies vs. the seasonal cycle; in Sect. 5.2.2 we note differences in results between the two metrics. If this metric is positive, then SSTs in the western Indian Ocean are higher than in the eastern Indian Ocean. For each year, the day of the peak gradient and the peak gradient are calculated using daily OISST data, for the days 30–230 to compare to the long rains, and 230–30 of the following year to compare to the short rains.

Zonal winds aloft. The average 250 hPa zonal velocity above the study area (3$^\circ$ S to 12.5$^\circ$ N and 32$^\circ$ E to 52$^\circ$ E) is used to characterize the zonal circulation aloft. For each year, the day of peak westerlies and the peak westerly strength are calculated using daily ERA5 data, for the days 30–230 to compare to the long rains, and 230–30 of the following year to compare to the short rains.

Moist Static Energy. We analyze three metrics of MSE. In addition to MSE h at 700 hPa (Dyer and Washington 2021), following Yang et al. (2015a), the large-scale stability in the atmosphere is characterized by the difference between surface moist static energy $h_s$ and saturation moist static energy $h^*$ at 700 hPa:

$$\begin{aligned} \begin{aligned} h&= c_pT + L_vq + gz \\ h_s&= c_pT_s + L_vq_s + gz_s\\ h^*&= c_pT + L_vq^* + gz \\ \text {where } q^*&= f(T) \\ \end{aligned} \end{aligned}$$

for temperature T in K, specific humidity q, and height z above a reference value (in this case, mean sea level) in m, with the subscript s denoting surface values. $c_p$ is the specific heat capacity of air at constant pressure $1004.6\ J/(kg\cdot K)$, $L_v$ is the latent heat of vaporization of water $2.257\times 10^6\ J/kg$, and g is the gravitational constant $9.807\ m/s^2$. The saturation specific humidity $q^*$ is a function of temperature alone and is calculated using the approximation by Murray (1967).

$h_s-h^*$ is therefore

$$\begin{aligned} \begin{aligned} h_s-h^*&= c_p(T_s-T) + L_v(q_s-q^*) + g(z-z_s) \end{aligned} \end{aligned}$$

where $(z-z_s)$ is the height difference between the local topography and the pressure level of interest, which in this case is 700 hPa. Note that $h_s-h^*$ ignores the effect of possible mid-tropospheric entrainment, which has been suggested as an important source of convective energy for the long rains (Walker et al. 2020; Finney et al. 2020); consequently, following Dyer and Washington (2021), $h_s-h^*$ is analyzed in conjunction with h at 700 hPa, which depends on both temperature and specific humidity.

h, $h_s$, and $h^*$ are analyzed as the mean across all grid cells in the double-peaked region.

Ascent. To directly diagnose ascent in the GHA, the average 500 and 250 hPa vertical pressure velocities across grid cells in the double-peaked region are used to characterize mid-level and upper-level ascent, respectively. For each year, the day of peak ascent and the peak vertical velocity using daily ERA5 data, for the days 50–250 to compare to the long rains, and 250–50 of the following year to compare to the short rains.

Mid-tropospheric zonal winds over equatorial Africa.

To further diagnose the possible impact of moisture entrainment from west of the GHA, mid-tropospheric zonal winds over equatorial Africa are analyzed. Following the region used in Walker et al. (2020), the average 700 hPa zonal velocity over equatorial Africa is calculated as the average from 5$^\circ$ S to 5$^\circ$ N and $10^\circ$ W to $30^\circ$ E). For each year, the day of peak westerlies and the peak westerly strength are calculated using daily ERA5 data, for the days 30–230 to compare to the long rains, and 230–30 of the following year to compare to the short rains.

3.5 Characterizing circulation variables

Fig. 2

Rainfall (blue) and key variable (red) climatologies in observations (CHIRPS for rainfall, OISST for SST variables) or reanalysis (ERA5 for circulation variables). Light green shading is the geographical average long (centered on May) and short (centered on October) rainy seasons. Note that this shading shows the average onset and demise across grid cells and not the onset and demise of the rainfall climatology shown in blue. See Fig. 3 for composite climatologies

Connections between statistics of the rainy seasons as defined above and diagnostic statistics of the broader circulation are investigated. Each variable, except for equatorial African zonal winds, has a similar double-peaked seasonal cycle to the rainy seasons (Figs. 2, 3). For these variables, the analysis focuses primarily on two metrics defined independently from the rainy seasons—the day on which the variable peaks, referred to as the ‘peak timing,’ and the value of the variable on that peak day, referred to as the ‘peak amount,’ for either the first or second portion of the calendar year. For each metric, this cutoff point between the boreal spring and fall seasons is chosen ad hoc to encompass the inflection points for each CMIP6 model and the observations. The boreal spring peak timing and amount values are compared to metrics for the long rains, and the boreal fall values with the metrics for the short rains. All metrics are calculated both as a climatological mean and individually for all years in the sample, after each time series has been smoothed using a Gaussian filter with a 30-day width.

Fig. 3

Seasonal composites of key variables in observations (OISST for SST variables) or reanalysis (ERA5 for circulation variables). Values are the average across years relative to CHIRPS seasonal onset (1981–2013); the average peak day of each season is shown in dotted lines and the average end of each season in a solid line. All variables peak roughly around the GHA rainy seasons, though peaks generally correspond more closely to rainfall peaks during the long rains. See Fig. 2 for raw (not composite) climatologies

When possible, we choose definitions of circulation metrics that are independent of the definitions of the rainy seasons—i.e., using the peak timing and peak magnitude. This is to avoid defining explanatory variables using characteristics of the rainy seasons they may be imperfectly related to. This is not feasible for variables such as equatorial African zonal winds, the climatology of which does not have a similar double-peaked seasonal cycle to the rainy seasons; consequently, we use their seasonal mean value over the long or short rains as defined using the onset and demise calculated as in Sect. 3.2, and do not investigate their relationship to the timing of the seasons. Furthermore, to verify the robustness of the results to the metric definition, we also investigate the seasonal mean of variables with a double-peaked seasonal cycle; results are compared to those calculated using the peak value alone.

3.6 Analysis

To understand the magnitude and cause of CMIP6 biases in the GHA rainy seasons, first the biases compared to CHIRPS observations in the onset, demise, duration, peak timing, peak strength, and total strength of the long and short rains in each model’s ‘historical’ experiment are analyzed in Sect. 4, following the methodology detailed above in Sects. 3.2 and 3.3.

Then, in Sects. 5, 6, we use the circulation metrics defined above in Sect. 3.4 to study whether models replicate observed relationships between the rainy seasons and the large-scale dynamics of the region. To do so, the timing and magnitude of the circulation variables are compared with the timing and strength of the rainy seasons in both models and observations. For the rest of this paper, ‘correlations’ refer to Pearson’s correlation coefficients. First, interannual correlations in observations $\rho ^{OI}$ between these circulation metrics and their precipitation counterparts are calculated, which reveals whether these facets of the circulation are associated with characteristics of the rainy seasons in the historical record (see Sect. S3.1 for a detailed derivation). Significance is reported based on two-sided confidence 95% confidence intervals for correlation calculations.

Interannual correlations between the circulation metrics and their precipitation counterparts $\rho ^{MI,mod}$ for each individual model mod are then calculated, revealing whether these facets of the circulation are associated with characteristics of the rainy seasons within a given model (Sect. S3.2). Finally, the correlation between model climatological means of these circulation and rainy season metrics $\rho ^{MM}$ is calculated, which gives insight into whether the mean state of the model is associated with the biases in these metrics (Sect. S3.3).

We report $\rho ^{OI}$, $\rho ^{MI,mod}$, and $\rho ^{MM}$ for all circulation metrics for both long and short rains, even if a certain dynamical process is only associated with either the long or short rains in observations. This is to capture possible model errors in seasonal connections; for example, in Sect. 6.4 we show how mid-tropospheric winds over equatorial Africa are more associated with the short than the long rains in models, whereas no connection is found in observations with the short rains.

In each section, model behavior in metrics that particularly well explain interannual or intermodel variability in CMIP6 models (i.e., high $\rho ^{MI,mod}$s or $\rho ^{MM}$) are then analyzed to specifically diagnose underlying model issues. Furthermore, when analyzing the impact of ocean SSTs on the rainy seasons, biases from fully coupled models are compared to biases from the same models’ AMIP configurations.

Whether a model is truly simulating the right processes for the right reasons is a combination of both low biases in variables of interest and good performance at replicating the dynamical factors that affect these variables in the observational record. Though evaluation metrics calculated for previous generations of models have poorly partitioned future projections (Rowell et al. 2016), whether relationships are robustly mirrored in both models and observations may be a first identifier for metrics useful for diagnosing model performance of CMIP6 models.

4 Precipitation biases in CMIP6 models

Previous generations of models tended to begin the long rains too late, produce too little rain in the long rains, and produce too much rain in the short rains (Yang et al. 2014; Dunning et al. 2017). These biases remain largely unchanged in the CMIP6 generation of models.

4.1 Timing biases

The average model long rains across CMIP6 models begin 24 ± 18  days late (with ± expressing one standard deviation across model-years) compared to the average onset in the study area in CHIRPS data (Fig.  4a). This bias is of similar magnitude to biases in CMIP5 ($19\pm 13$ in Dunning et al. (2017)). The bias in the onset of the short rains, on the other hand, is minor across models; the ensemble model-year bias is $2\pm 9$ days too early.

Fig. 4

Key characteristics of the long and short rains in the study region in CMIP6 models (light blue) and CHIRPS observations (red). Each dot shows a model-year (CMIP6) or an observation-year (CHIRPS) between 1981 and 2013. Box plots show the median (notch), 0.25 and 0.75 quartiles (box), up to $1.5\times IQR$ beyond the 0.25 and 0.75 quartiles (whiskers), and outliers beyond this limit (circles). The range of models is biased versus observations for almost every characteristic, except for the onset of the short rains (panel a, x-axis). Otherwise, models tend to be too late in their demise and peak timing, rain too little on the wettest days, overestimate the length and strength of the short rains, and underestimate the length and strength of the long rains

The peak day of the rainy seasons is also too late in both the long and the short rains, but more consistently so between rainy seasons than in the onset ($19\pm 18$ days and $14\pm 13$ days, respectively; Fig. 4d), with more late outliers during the short rains.

Models tend to be late on the demise of both rainy seasons—and similarly so; models that are late on the demise in the long rains also tend to be late on the demise of the short rains. Note that the perceived relationship between the demise of the long and short rains in Fig. 4b is largely between models rather than across years; individual years in models or observations with a late demise of the long rains do not tend to have a late demise of the short rains or vice-versa. Given that the demise of the long rains has been connected in observations to the onset of the Indian Monsoon (Camberlin et al. 2010), a pattern unique to the boreal summer, the robust intermodel connection with the demise of the short rains before the boreal winter is surprising.

These factors combine to make model long rains slightly too short on average, and short rains significantly too long on average (Fig. 4c), and are likely connected to the biases in relative strength of the rainy seasons, since rainy season strength is largely modulated by its length rather than average or peak rate (Camberlin et al. 2009; Wainwright et al. 2019).

4.2 Strength biases

As in CMIP5 models (Yang et al. 2015b), CMIP6 models also overestimate the strength of the short rains and underestimate the strength of the long rains (Fig. 4f). The average ratio of the amount of rain in the long rains to the short rains in models is 0.7, compared to 1.3 in the observations. Like in CMIP5 models, this discrepancy arises both from an underestimation of the strength of the long rains (29 ± 93 mm too dry) and an overestimation of the strength of the short rains (129 ± 152 mm too wet). In the amount of both long and short rains, there is however substantial overlap with the range of observations (Fig. 4f).

Models tend to underestimate peak rainfall of both rainy seasons (Fig. 4e), which is consistent with existing biases in CMIP3 and CMIP5-generation models (e.g. Sun et al. (2015)). In the short rains in particular, which are biased wet in models, this result underscores that biases in the strength of the rainy seasons are not primarily driven by biases in peak rainfall intensity. These biases may more generally be related to model treatment of rainfall extremes, which is beyond the scope of this study.

4.3 Geographic variation in biases

The long and short rains are not identical everywhere within the double-peaked region. In observations, the long rains tend to be spatially less coherent (Nicholson 2017), and generally begin towards the west and south earlier than towards the east and north, for example, while the short rains tend to progress from north to south (Fig. S1). To investigate the regional coherence in model behavior, we additionally calculate model biases in rainy season metrics in geographic subsets of the double-peaked region (Figs. S1–S3). Though the rainy season metrics show geographical variation, biases tend to be geographically coherent across the region; the median model long rains are too short and the median model short rains too long in every studied subset, for example (Figs. S2–S3). A notable exception is models’ inability to capture the much earlier onset and demise of the short rains in the subset of the GHA including the Golis, Cal Madow, and Cal Miskaad mountain ranges parallel to the Gulf of Aden (the ‘North’ region in Fig. S1).

Fig. 5

Regional context of GHA precipitation biases. Figure shows the multi-model mean (MMM) bias vs. CHIRPS in rainfall during the GHA long (top) or short (bottom) rains, averaged across the years 1981 to 2014, for the 35 models in the sample with both a fully coupled run and an AMIP run. Figure shows results for both fully coupled (left) and AMIP (right) model runs. The red line shows the extent of the study area for which seasonal definitions were derived, for reference. Dotted areas indicate lower model agreement; in those regions, fewer than 28 out of 35 models agree on the sign of the bias. Each model’s own seasonal definitions is used, taking into account the different timings of the seasons between models and observations. Note that as a result biases shown in this figure largely reflects timing biases relative to the rainfall climatologies in the rest of the continent; for example, during the long rains, which tend to be late in models, rainfall is biased high in the Sahel and low in southern Africa, in line with the rain band having moved farther North by the time the long rains start in models compared to observations. See Fig. S5 for a version of this map using monthly averages, i.e., consistent time periods across datasets

Regionally, model biases are not limited to the double-peaked area alone (Fig. 5). During the long rains, nearly all models are also too dry in an arc from Tanzania via the rift valleys to the southern Democratic Republic of the Congo and Angola (Fig.  5 top left). During the short rains, nearly all models are also too wet in most of southeastern Africa (Fig.  5 bottom left). These coherent biases are due to the timing biases in the model long and short rains; since model rainy seasons tend to be too late compared to observations, at the time of the rainy seasons, the rain band in the rest of the continent is farther north than in observations during the long rains and farther south during the short rains (Fig. S4). Examining instead March–April–May (MAM) and October–November–December (OND) means, as is often done in studies of East African rainfall, extraregional biases are less coherent across models (Figure S5). During OND, most models are too wet in Tanzania and the Ethiopian Highlands in addition to the GHA (Fig. S5 bottom left).

5 SST representations

5.1 Expected impact of SSTs

To diagnose the impact of model SST biases on GHA rainfall biases, the relationships between WIOSSTs and the IOD and the GHA rainy seasons are investigated. Given connections found between the interannual variability of SSTs and the GHA rainy seasons in observations, models with WIOSSTs and IODs that are too strong may be expected to have rainy seasons that are biased wet, or dry for models with WIOSSTs and IODs that are too weak. Connections between SSTs and the timing of the rainy seasons are more tenuous—forecast skill is connected more to atmospheric variables (e.g., MacLeod (2018))—but a recent study has connected onset variability in the short rains to SST anomalies in the Indian Ocean (Gudoshava et al. 2022).

Like rainfall in the double-peaked region, both variables climatologically peak twice a year (see Fig. 2 for climatologies, and Fig. 3 for composite climatologies relative to the onset of each season), though the average SST peak during the short rains is notably a few weeks after the average end of the season. Since most of the interannual variability of the IOD is concentrated in the boreal fall, analyses have generally focused on its impact on the short rains; however, a west-east temperature gradient generally also forms in the boreal spring, peaking along with the average long rains.

Biases in the IOD and in WIOSSTs may point to errors in different, but related underlying processes. The IOD is closely related to the structure of the Indian Ocean Walker Cell—a positive IOD (warm west, cool east) is generally associated with low pressure in the western Indian Ocean and surface easterly winds that advect warm, moist air onto the GHA. A positive IOD generally involves anomalously positive WIOSSTs; however, several studies have also suggested a role for offshore SSTs in encouraging moisture convergence over central East Africa, regardless of the presence of a dipole event (e.g., Liu et al. (2020)).

5.2 SSTs and the rainy seasons

For each SST metric and each rainy season, six correlations are calculated – the interannual correlation in observations $\rho ^{OI}$, the interannual correlation in an individual model $\rho ^{MI,mod}$ for every model mod separately, and correlations across model means $\rho ^{MM}$ for ‘strength’ (correlation between peak value of the variable and total rainfall in a season) and the ‘timing’ of the rainy seasons (correlation between peak timing of the variable and peak timing of the rainy season) (see Sect. S3 for derivations). The correlations across model means $\rho ^{MM}$ are based on climatological values of each metric, while the interannual correlations $\rho ^{OI}$ in observations and $\rho ^{MI}$ in models are calculated across values for each individual year. Figure 6a-b shows $\rho ^{OI}$, $\rho ^{MI,mod}$, and $\rho ^{MM}$ between the two diagnostic SST metrics and the strength and timing of the rainy seasons. Correlations are relatively robust to the GHA subset chosen (Fig. S12).

Fig. 6

Correlations between statistics of the GHA rainy seasons and statistics of peak WIOSSTs (a), the peak zonal SST gradient (b), seasonal mean equatorial Africa 700 hPa zonal winds (c), peak GHA 250 hPa zonal winds (d), peak GHA $h_s-h^*$ (e), and peak GHA 250 hPa pressure velocity (f) in models and observations. For each sub-panel, the leftmost column (red dot) shows the correlation between years of the variable and the rainy season in observations (‘observation-year’ correlation), the center column (blue dots) shows the correlation between years of the variable and the rainy season for each model (‘model-year’ correlation), and the rightmost column (blue bar) shows the correlation between model means of the variable and the rainy season (‘model-means’ correlation). Black vertical lines show 95% confidence intervals; for individual models and observations, darker blue or red dots show significant Pearson’s correlation coefficients at the $p<0.05$ level. For each peak variable and season, correlations between two sets of statistics are shown: ‘timing’ means the correlation between the peak day of the rainy season and the peak day of the variable, ‘amount’ means the correlation between the total amount of rain in that season and the peak magnitude of the variable. See Figure S11 for a comparison between correlations calculated either using the peak magnitude or seasonal mean of circulation variables. In panel c., we show statistics of seasonal mean equatorial Africa u, but no timing, since the metric does not have a double-peaked climatology. Correlations are robust to different subsets of the GHA; see Fig.  S12 for the same calculations over a smaller box centered on southeastern Somalia

5.2.1 Mean state biases in WIOSSTs correlate with mean state biases in model rainy seasons

Though the observed climatology of WIOSSTs closely matches that of the long rains (Figs. 2a, 3a), neither their peak magnitude nor the peak timing are significantly correlated with the total rainfall or peak timing of the long rains in observations (Fig. 6a, light red dots). During the boreal fall, the WIOSST climatology peaks over a month after the short rains (Fig. 3a); no interannual correlation is found with the peak timing of the short rains. The peak magnitude of boreal fall WIOSSTs does correlate with the total rainfall, or strength, of the short rains, which may be related to the zonal SST gradient (see below).

A handful of models, however, show significant interannual correlations across years between WIOSSTs and both the timing and strength of the long rains (Fig. 6a, blue dots). In line with this interannual correlation and the fact that model long rains’ onset, peak, and demise are all late on average compared to observations (Fig. 4a, b, d), the average model WIOSSTs tend to peak 13 ± 7 days too late during the boreal spring as well (Fig. S6; compare to the model long rain peaks being 19 ± 18 days late). Models that find a strong interannual correlation between WIOSSTs and the timing and strength of the long rains may be producing a coupling between SSTs and rains that is not mirrored in observations.

Models generally correctly replicate both the interannual correlation of the total strength of the short rains with the peak magnitude of WIOSSTs and the lack of a correlation between the timing of peak of WIOSSTs and the timing of peak rainfall. Model WIOSSTs tend to peak on average 12 ± 15 days too early in the boreal fall, but the lack of an interannual connection in models and the fact that model short rains tend to happen too early suggests that the WIOSST seasonal cycle is not at fault for short rain timing biases.

However, model mean state biases in the timing and magnitude of peak WIOSSTs in both the boreal spring and fall are correlated with model mean state biases in the strength and timing of the long and short rains, respectively (Fig. 6a, blue bars), despite interannual correlations only being significant in some models and not at all in observations for the long rains and the timing of the short rains. This combination suggests that while the direct relationship between WIOSSTs and the rainy seasons may be weak in many models, mean-state biases easily visible in the SST seasonal cycle may nevertheless be indicative of common drivers of both SST and GHA rainfall biases. A model that is particularly suggestive of this mean-bias relationship is KIOST-ESM, which has the lowest mean state bias in the timing of the boreal spring SST peak, one of the lowest biases in the strength of the boreal spring SST peak, and one of the lowest biases in the timing and strength of the long rains (Fig. S7).

5.2.2 IOD strength biases associated with model short rain biases

Generally, the westward magnitude of the zonal SST gradient—meaning how much warmer the western Indian Ocean is than the eastern Indian Ocean, or how much the state of the Indian Ocean resembles positive IOD conditions—and the WIOSSTs peak are strongly correlated with the strength of the short rains in all metrics; i.e., $\rho ^{OI}$, $\rho ^{MM}$, and $\rho ^{IM}$ for many models are generally positive and significant (right-most columns in Fig. 6a–b). The correlation is stronger with the zonal gradient than with WIOSSTs by themselves, in line with previous studies connecting the zonal gradient to the short rains in observations on interannual timescales. Correlations are similar when calculated using the DMI instead of the raw zonal gradient (Fig. S18). The high correlation between the zonal SST gradient and short rain strength across model years suggests that models on average are reproducing this well-known ocean-atmosphere relationship. One notable outlier to this strong relationship is AWI-ESM-1-1-LR, for which the magnitude of the zonal SST gradient is entirely uncorrelated and the magnitude of the DMI is significantly negatively correlated with the strength of the short rains; AWI-ESM-1-1-LR also has the largest dry bias in the short rains among models studied.

These relationships in both models and observations seem to suggest the use of the IOD as a diagnostic variable for model simulation of processes that affect the strength of the short rains in the double-peaked region. In particular, some of the models with the most prominent mean state wet biases in the short rains also systematically create climatological SST gradients that are too westward;¹ i.e., the western Indian Ocean is much too warm compared to the eastern Indian Ocean. For many models, the western Indian Ocean is warmer than the east even in the climatological mean, a reversal of the mean gradient in observations, which is climatologically eastward (Fig. S6, top right). Models with low mean state IOD magnitude biases in the boreal fall tend to also have low biases in the strength of the short rains. A notable exception is IPSL-CM6A-LR, which has a low strength bias in the magnitude of the zonal SST gradient despite overestimating the strength of the short rains by a factor of more than 2, suggesting that this low bias may mask structural errors in the model simulation of the region (Fig. S8).

The strong relationship between model mean-state biases in the IOD and corresponding biases in the rainy seasons are in line with the findings of Hirons and Turner (2018), who show that many CMIP5 models have climatological low-level equatorial easterlies in the Indian Ocean instead of observed westerlies and associated zonal SST gradients that are too anomalously westward—i.e., the west is too warm compared to the east—during the short rains; these models subsequently cannot correctly capture the dynamics of moisture advection onto East Africa during IOD events in the boreal fall.

Interestingly, the timing of the peak zonal SST gradient in the boreal spring is positively correlated with the timing of the long rains in several models, though it is insignificant in observations. The correlation is once again strongest for model means (i.e., $\rho ^{MM}>\rho ^{OI},\rho ^{MI}$), further suggesting that the mean state of the SST seasonal cycle may be related to rainfall biases in the double-peaked region. However, since the corresponding timing correlation across model means for WIOSSTs is larger, it is possible that this correlation may be capturing the effect of WIOSSTs by themselves, which are generally higher during IOD events and are more frequently connected to long rain variability (e.g., Yang et al. (2015a)).

5.3 Evidence from atmosphere-only runs

Do the mean state correlations imply that the SST biases are the primary driver of rainy season biases or, perhaps, that both SST and rainy season biases are affected by a common driver? To investigate this connection, we take advantage of “AMIP” runs—versions of the studied CMIP6 models that replace their ocean component with historical SSTs. These runs can simulate to a certain extent how the model would behave if it perfectly simulated the ocean, though important atmosphere-ocean feedbacks are removed by prescribing SSTs. We recalculate model biases in the rainy seasons and compare them to biases in the same models run in their fully coupled mode (Fig. 7). Forcing CMIP6 models with historical SSTs only improves biases under certain conditions; instead, for many models and metrics, biases are increased, particularly concerning the peak timing and demises of the GHA rainy seasons (Fig. 8, S10), suggesting the relationship between SST and rainfall biases may be more complex.

Fig. 7

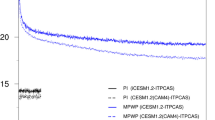
Key characteristics of the long and short rains in the study region (as in Fig. 4), for models with available daily rainfall data from both fully coupled runs (light blue) and runs forced with historical SSTs (dark blue). Coupling doesn’t uniformly reduce biases. AMIP runs tend to end the long rains later, leading to an increase in the duration bias, and begin the short rains later than fully coupled runs, leading to a decrease in the duration bias. In both rainy seasons, the late bias in the timing of the rainy season peak is increased compared to the fully coupled runs. In line with the changes in duration bias, the average model-year total amount is too strong in the AMIP long rains, but the positive rainfall bias is decreased in the short rains. In line with observations, the AMIP long rains are now stronger than the short rains

Correlations between the model mean SST peak timing and the model mean rainy season timing in coupled models have suggested a role for mean state biases in the seasonal cycle in the modulation of the rainy seasons (Fig. 6a, b blue bars). The average WIOSSTs in a CMIP6 model’s coupled run peak too late compared to observations during the long rains, but too early during the short rains (Fig.  S6); however, forcing models with historical SSTs does not lead to a consistent shift in the timing of the rains across most models, nor a consistent reduction in the magnitude of the timing bias in the peak timing and demise of the rains. The bias in the demise of the long rains is in fact worsened, from 9 days on average in coupled runs to 30 days in AMIP runs on average (Fig.  7b, x axis) and up to a factor of 10 in one model, BCC-CSM2-MR (Fig. 8 and S10, ‘demise’ column in left panel). Given that the demise of the long rains is tightly correlated with the start of the Indian Monsoon in Kerala in observations (e.g., Camberlin et al. (2010)), this bias may therefore be related to changes in monsoon dynamics brought on by the lack of interactive atmosphere-ocean coupling in AMIP runs. In fact, Yang et al. (2015b) show that coupling-induced biases in GHA rainy seasons in CMIP5 models can appear jointly with dry biases in the Indian Monsoon.

Fig. 8

Change in bias between fully coupled and AMIP runs. Each dot represents the climatological bias difference |AMIP|— |coupled|, scaled by the average climatological bias of the fully coupled runs for the long (L) and short (R) rains. A value of 0 means the AMIP and coupled biases are identical; a value of 1 means the AMIP bias is larger than the coupled bias by an amount equal to the average coupled bias, a value of -1 means the opposite. AMIP models do not uniformly decrease (or increase) biases; the long rain demise bias in particular is worsened in most models. See Fig. S10 for a version with the raw fractional change instead

In one of the few robust improvements in biases in AMIP runs, the subset of coupled models that are most biased in the timing of the early year peak of WIOSSTs also tend to have the largest reductions in the bias of the onset of the long rains in their AMIP runs (Fig. 9, L panel). A similar pattern is seen during the short rains; in AMIP runs, the SST peak in the second half of the year is pushed back compared to coupled runs (WIOSSTs are biased early; Fig. S2), and the onset of the short rains is biased late on average in AMIP runs instead of early in coupled runs.

Fig. 9

Examples of metrics in which fully coupled runs tend to have stronger biases than AMIP runs. Points show model means. Y axes represent the change in the absolute bias between AMIP and coupled runs (negative values mean AMIP runs have lower biases) in a given metric; x axes represent the early year WIOSST timing bias (L panel) or the late year IOD strength bias (R panel) in the fully coupled run. Shading shows coupled model bias. Models whose WIOSSTs peak the latest compared to observations tend to see the biggest improvements in the late onset bias seen in the most models’ long rains (L panel). Similarly, the models with the largest positive IOD biases (the 8 models in the red box in the R panel) show the largest improvements in short rain strength biases when forced with historical SSTs

Given that a similar number of models have improved or worsened biases in the onset and demise of the rainy seasons (Fig.  8), geographic patterns of intermodel mean African rainfall biases during each model’s long and short rains, which are largely driven by the timing mismatch between models and observations, are similar between AMIP and historic runs (Fig. 5 right column).

AMIP runs have long rains that are longer and stronger than the short rains, a reversal of a key bias in CMIP6 models; now, the ratio of the climatological model strength of the long rains to the short rains is 1.4 compared to 1.3 in observations and 0.7 in fully coupled runs. Biases in the mean strength of the rainy seasons are moderately correlated between coupled and AMIP runs (correlations of 0.55 for the long rains, and 0.59 for the short rains). In all but one model, AMIP runs are wetter than coupled runs, though this represents an increase in model bias for many models (Fig. S10). AMIP long rains are now too long and too strong compared to observations. (Fig. 7c, f; dots to the right and below the dotted 1:1 line show model- or observation-years in which the long rains are wetter than the short rains). These two processes are likely linked; the total rainfall in a season is more modulated by the rainy season’s length than the average intensity of rainfall in observations (Wainwright et al. 2019). It is important to emphasize however that these improvements in the biases in the strength of the rainy seasons in AMIP runs were the result of increased timing biases, and underscores the point that models may produce the right metrics, but for the ‘wrong’ reasons.

Furthermore, the coupled models with the largest boreal fall IOD biases have the largest reduction in the strength biases of the short rains in their AMIP runs (Fig. 9, R panel). These coupled models have zonal SST gradients that are substantially too westward—i.e., the west being too warm compared to the east—and correspondingly tend to produce short rains that are too powerful as well. As a result, particularly unphysical values of the mean state IOD in a model may be a useful diagnostic to determine model skill in simulating the East African short rains.

5.4 Conclusions on ocean-driven biases

SST biases play a role in some, but not all facets of the biases in the rainy seasons in East Africa, in line with the highly coupled nature of the regional dynamics. Model mean correlations between mean state biases in SSTs and rainfall metrics that are not borne out in model interannual correlations suggest certain SST biases are driven by the same underlying patterns that produce erroneous long and short rains in the GHA in models. AMIP runs tend to substantially reduce biases only in limited situations, for example, in models whose climatological IODs are 100–400% too strong during the short rains, or for models whose SST seasonal cycle is particularly out of phase with observations. Instead, many biases are worsened in AMIP runs, implying either that the coupling between the atmosphere and ocean is crucial to the regional dynamics affecting those aspects of the GHA rainy seasons, or that competing atmosphere-ocean biases in different aspects of the model may have fortuitously ‘cancelled out’ in the fully coupled runs.

These findings are only partially consistent with those of Lyon (2020), which suggested that SST biases are the primary driver of both timing and strength biases of the East African rainy seasons, though that study used only one model which was not present in our sample. They are, however, consistent with previous studies showing that AMIP runs did not substantially fix biases in the rainy seasons in CMIP5, the previous generation of models (Hirons and Turner 2018; King et al. 2019). Furthermore, the substantial differences in the long rain biases between fully coupled and AMIP runs confirm that despite the weak correlations between the long rains and SSTs in most parts of the global ocean (e.g., Liebmann et al. (2017)) aspects of ocean-atmosphere coupling are nevertheless crucial to the dynamics of the long rains in models.

6 Circulation representations

6.1 Expected impact of circulation biases

Circulation metrics have been found to explain more variability in GHA precipitation than ocean variables (Nicholson 2017), and the moisture budget is affected more by the circulation than the humidity cycle in observations (Yang et al. 2015a), making aspects of the circulation useful foci for diagnosing biases in the processes driving the rainy seasons.

The climatological circulation pattern over the Indian Ocean Basin, particularly during the dry seasons, consists of ascent in the East over the Maritime Continent, easterlies aloft, descent over the western Indian Ocean and GHA, and surface westerlies along the equator. Strong descent over the GHA inhibits convection for most of the year.

During the rainy seasons, this pattern reverses around the GHA: there is anomalous ascent over the GHA, anomalous westerlies aloft, anomalous large-scale instability, and anomalous easterlies close to the GHA coast. The seasonal reversal of the winds aloft, $h_s-h^*$, and the vertical motion over the GHA roughly track GHA rainfall, exhibiting a clear double-peaked structure (Figs.  2d–f, 3d–f); all three of these are associated with an eastward shift in the descending arm of the Indian Ocean Walker Circulation during the rainy seasons, reducing its ability to suppress convection over the GHA (e.g. King et al. (2019); Hastenrath et al. (2011)).

Surface easterlies are also strongly correlated with the short rains in Kenya in observations (e.g. $\sim 0.85$ in Hastenrath et al. (1993) or $\sim 0.82$ for the start of the long rains in Dyer and Washington (2021)); however, their influence decreases farther north in the double-peaked region where the surface circulation is less zonal, and are not considered in this analysis.

Zonal velocity aloft (at 250mb), vertical velocity, and $h_s-h^*$ over the GHA are therefore examined to diagnose biases in the circulation processes associated with the vertical structure of the atmosphere during the rainy seasons.

More recently, authors have also noted a connection between zonal winds over equatorial Africa and the GHA, with westerly anomalies over the Congo Basin and the Gulf of Guinea associated with wetter long rains in observations (Finney et al. 2020; Walker et al. 2020; Dyer and Washington 2021) and in future CMIP5 model projections (Giannini et al. 2018). Following Dyer and Washington (2021), 700 hPa zonal winds over equatorial Africa and h are therefore examined to characterize this connection.

6.2 High-level zonal winds are associated with the strength of short rains

During the long rains, Liebmann et al. (2017) show that rainfall begins when upper-level easterlies weaken, and ends when easterlies strengthen with the onset of the monsoonal anticyclone, and associate the recent decrease in the strength of the long rains with an increase in the strength of upper-level easterlies. In observations, the climatology of 250 hPa u over the double-peaked region closely matches the rainfall climatology, with winds turning westerly as the rains begin and peaking with the long rains. However, this relationship is not observed in our sample across years; $\rho ^{OI}$ and $\rho ^{MI}$ in most models are insignificant for the timing of the rainy seasons (Fig. 6d.), which suggest a better metric for this relationship may have to be developed. Most models and observations do have a positive correlation between peak westerly anomalies and stronger long rains, though this is only significant in a handful of models. The peak seems to be a better diagnostic than the average u over the season in models (Fig. S11c.). Models generally tend to simulate the climatology of the upper-level zonal winds during the boreal spring relatively well (Fig. S6).

During the short rains, the Walker circulation is more coherent (Hastenrath et al. 2011) and expected to play a larger role in the interannual variability of the region. In observations, the strength of the short rains are significantly negatively correlated with the peak zonal wind value in the second half of the year (Fig. 6c); i.e., wetter short rains are associated with stronger easterly anomalies. Strong easterlies directly above the GHA may be related to a reversal of the structure of the Indian Ocean Walker Cell, with a convective center in the Indian Ocean off the coast of the GHA and upper-level divergence, as Limbu and Tan (2019) found in the OND climatology. This relationship is robust across model means as well (significant $\rho ^{MM}$), and is present across years in most models, though it is only significant in 6 models. The one model with a significant positive correlation (a positive $\rho ^{MI}$), i.e., where wetter short rains are associated with weaker easterlies across years, INM-CM4-8, also has the largest wet bias in the short rains. Furthermore, only one model, BCC-CSM2-MR, has strong westerlies during the short rains on average together with a substantial wet bias. Models however simulate the range of peak 250 hPa zonal winds relatively well (Fig. S6); biases in the upper-level zonal winds are therefore unable to well partition models based on short rain performance.

6.3 Models overestimate the depth of short rain convection

Vertical velocity is closely related to convection processes in observations and models. Rainfall in the double-peaked region tends to occur when the processes that inhibit convection, such as descent associated with the Walker Cell or the import of cool, dry air leading to strong static stability, weaken (King et al. 2019; Hastenrath et al. 2011; Yang et al. 2015a). Correspondingly, ascent, especially in the mid-troposphere, tends to closely track the development of both rainy seasons (Figs.  2f, 3f).

As expected, peak ascent at both 500mb and 250mb is strongly correlated with the strength of both the long and short rains in observations (Fig. 6f, red dot and S13 for 500 mb), and peak timing of ascent with the timing of the long rains. As with other metrics, the timing of the short rains tends to not be strongly correlated with the timing of ascent in observations or models, though one model is a particularly prominent outlier (CanESM5), for which later onsets are significantly associated with earlier peaking of ascent.

Models generally replicate this strong relationship between peak ascent and peak strength of the rainy seasons, both across years in individual models and across mean states in different models (blue dots and bars in Fig. 3f). Biases in ascent are therefore expected to translate directly to rainfall biases; this seems particularly relevant in the case of biases in the depth of convection during the short rains. In observations, convection during the average short rains is much shallower than during the long rains and tends to not reach 250 hPa (Fig.  12, red bars). The average model, however, produces ascent at 250 hPa during the short rains (Fig.  12); in particular, models that produce climatological ascent at 250 hPa during the short rains are on average 150 mm too wet, compared to 11 mm too dry for those that don’t. Models overestimate ascent in the long rains on average as well (left panel in Fig. 12), but this discrepancy is weaker.

Fig. 10

Difference between the mean u in the ten wettest long (L) and short (R) rains from 1981 to 2013 and the mean u in the average long and short rains in the CMIP6 multi-model mean (top) and in ERA5 reanalysis (bottom). Stippling in top indicates areas where fewer than 21 models have the same anomaly during wet years. Though models correctly show westerly anomalies during wet long rains over the Congo Basin, these are weaker and more geographically constrained than in observations on average. During wet short rains, nearly all models coherently show westerly anomalies over the Gulf of Guinea and the Congo Basin which are not seen in observations

In other words, the strength biases of the short rains may manifest through model convection being too deep. In particular, models whose convection is not too deep tend to have short rains closer to observed strengths, though even within this group, biases range from 140 mm too dry to 157 mm too wet. This signal is visible in other metrics as well; for example, the same models that are particularly biased in their vertical velocity also tend to be the models producing an IOD that is too powerful (see above in Sect.  5). Since the strength bias in the short rains is reduced in those models’ AMIP runs, the deep convection in the short rains is likely connected to the same overall structural error in these models that produces too much boreal fall convection in the western Indian Ocean.

6.4 Models associate equatorial westerlies with the short rains instead of the long rains

In observations, westerly anomalies over the Gulf of Guinea and the Congo Basin are strongly correlated with wetter long rains, but uncorrelated with the strength of the short rains (Fig.  6c), as has been previously found by e.g., Walker et al. (2020). Though some models correctly replicate the relationship during the long rains, the majority of models only have a significant correlation between westerlies and the strength of the short rains instead (Fig. 6c). During the short rains, most models produce anomalous westerlies in a geographic region similar to that in which anomalous westerlies are present during particularly wet long rains in observations (Fig.  10). During the long rains, most models correctly associate wet years with anomalous westerlies over the Congo Basin, but fail to replicate the same over the Gulf of Guinea.

6.5 Models produce too much surface moisture in the GHA

In observations, years in which $h_s-h^*$ peaks later during the boreal spring have long rains that peak later, and years in which $h_s-h^*$ is larger during the boreal fall have stronger short rains; the connection between $h_s-h^*$ timing and the short rains or magnitude and the long rains is weaker (Fig.  6e.). A strong connection between $h_s-h^*$ and the timing but not the strength of the long rains is consistent with a possible role of mid-tropospheric entrainment by Congo Basin moisture during the boreal spring proposed by e.g. Finney et al. (2020); $h_s-h^*$ does not consider mid-tropospheric moisture, but higher values are associated with unstable conditions that could be amplified by mid-tropospheric entrainment. Correlations across years in observations between the magnitude of h at 700 hPa and the strength of the long rains are higher (Fig. S16), though a strong correlation would be expected regardless of any additional moisture advection above the boundary layer due to convective moisture ascent.

Models largely reproduce this relationship, with one prominent exception: the correlation between peak $h_s-h^*$ and the model long rains is much higher in all models studied than in observations (Fig. 6e.). Since the lower correlation in observations may be related to mid-tropospheric entrainment not captured by $h_s-h^*$, this bias is consistent with models not fully replicating the connection between equatorial African moisture and the long rains, as analyzed in Sect. 6.4. Many models have lower correlations between the strength of the long rains and 700 hPa h than do observations, which may indicate a less prominent role for entrainment above the boundary layer (Fig. S16c.).

More generally, however, the peak and average magnitude of $h_s-h^*$ is highly correlated with the strength of both the long and short rains in most models, suggesting it is a useful diagnostic of large-scale stability. On average, $h_s-h^*$ is too high for most of the year over the GHA (Fig. 11) in all CMIP6 models analyzed. The bias is particularly high during the short rains, in line with higher biases in the strength of the short rains. The general magnitude of $h_s-h^*$ biases, and the positive biases during the long rains despite the long rains being on average too dry in models, suggest that models require more instability to produce the same amount of rainfall in the region. This may be related to model convection schemes; Wainwright et al. (2021) show that a convection-resolving model fixes many key GHA biases, including strength biases in the model in question.

Fig. 11

1981–2014 Climatologies of $h_s-h^*$ and its components in CMIP6 models (light blue) and ERA5 reanalysis (red). Positive biases in $h_s-h^*$ arise from models overestimating $h_s$ (top middle) during both seasons, largely due to positive biases in surface moisture $q_s$ (bottom R). During the short rains, the $h_s-h^*$ bias is enhanced by negative biases in $h^*$

Positive $h_s-h^*$ biases in models are largely driven through substantial positive biases in surface moisture (Fig.  6), though most models additionally underestimate $h^*$ during the short rains. Together, these biases are consistent with the too deep convection identified in model short rains in Sect. 6.3. Similar biases had been identified in CMIP5 models by Yang et al. (2015b), who identified their source as positive WIOSST biases. In CMIP6 models, most, but not all CMIP6 models have WIOSSTs that are too high during the short rains; however, all models save one have too high surface moisture during the short rains, suggesting that SST biases alone cannot explain this discrepancy. Similarly, during the long rains, almost all models have too high surface moisture, but many models have WIOSSTs that are too cold, suggesting a role for discrepancies in the model circulations causing increased moisture transport.

7 Conclusions and discussion

In conclusion, models continue to produce poor simulations of the rainy seasons in the GHA double-peaked region. As in the CMIP5 generation of models, in CMIP6 the timing of both the long and short rains tends to be late, the short rains tend to be too strong, and the long rains tend to be too weak. These biases decrease confidence in projections of the evolution of future rainfall in the GHA, particularly since many are connected to problems simulating the underlying large-scale processes of the Indian Ocean Basin and equatorial Africa.

Model performance in the short rains is affected by a cascade of likely interrelated biases. WIOSSTs are too high and the zonal SST gradient is too westward, leading to anomalously high surface moisture over the double-peaked region, increased $h_s$, and decreased large-scale stability through positive $h_s-h^*$ biases. Consequently, convection over the GHA is too deep, likely helped by moisture entrainment from the Congo Basin by equatorial westerlies, which are correlated with the short rains in models but not observations.

During the long rains, many models fail to replicate the observed relationship between equatorial westerly anomalies and the strength of the rainy season. Less entrainment from the Congo Basin may explain part of the dry bias; however, surface moisture and $h_s-h^*$ are both too high in nearly all models, suggesting that moisture availability alone cannot account for this discrepancy.

Increased moisture advection from the Congo Basin has been identified as a driver of wetter GHA rainy seasons in future projections in CMIP5 models (Giannini et al. 2018). These results suggest that CMIP6 models have short rains that are already more susceptible to the circulation patterns associated with this moisture advection in their historical simulations. However, there is little evidence that models that correctly lack a relationship between equatorial Africa u and the short rains are less biased in their strength of the short rains, or that those with a strong relationship are more biased (Fig. S15). The same is largely true in reverse for the long rains, though the models that are most biased wet tend to have a significant $\rho ^{MI}$ between easterly anomalies and the strength of the long rains (Fig. S15).

Mean state biases in the timing and strength of peak SSTs in the boreal spring and fall are correlated with biases in the timing and strength of the long and short rains, respectively, suggesting that biases in the large-scale seasonal cycle may be affecting the GHA rainy seasons.

Though many of these biases are related to simulations of SSTs, most rainy season biases in models are not reduced by fixing ocean biases; timing biases in particular are increased in AMIP runs in many models. Consequently, improvements to the performance of ocean models in GCMs alone may not be sufficient to improve model performance over the GHA. Nevertheless, due to their connection with both the long and short rains, particularly significant mean state biases in the timing of the WIOSST cycle and the magnitude and sign of the zonal SST gradient may still be used as diagnostics for general biases in the simulation of the overall seasonal cycle of the basin.

Model biases may therefore be particularly susceptible to issues in the simulation of broader circulation patterns. Peak zonal winds in the boreal fall aloft above the GHA are indeed significantly correlated with the strength of the short rains across years in observations and across model means, with stronger easterlies or weaker westerlies associated with wetter seasons, but the same correlation only appears across years in a subset of models. This suggests that biased simulation of the Indian Ocean Walker Cell may exacerbate rainfall biases, which is consistent with the findings of King et al. (2019) for CMIP5 models, who also highlight the importance of improving Walker Cell dynamics in future modeling efforts.

Finally, ascent over the double-peaked region itself, which is predictably connected with the strength of both the long and short rains, is a useful diagnostic of biases in model representations of convection. Despite the average 250 hPa vertical pressure velocity being positive, i.e., descending, in observations, models produce high-level ascent on average, that is, convection that is too deep. The models with the biggest ascent bias are also the models with the largest positive bias in the zonal Indian Ocean SST gradient, suggesting an anomalously strong Bjerknes-type feedback, as had previously been found in CMIP3 and CMIP5 models by Cai and Cowan (2013). The models are also those with the largest strength bias in the short rains.

A logical next step in evaluating model behavior would be to identify the drivers of model biases in Walker Cell dynamics. For example, studies have found recent connections between warm northwest Pacific SSTs and dry long rains, a connection brokered through a strengthened Walker Cell (Vigaud et al. 2017; Funk et al. 2018). In line with this explanation, models whose SSTs are biased particularly low in the northwest Pacific Ocean tend to have AMIP long rains that are dryer than those in their coupled configuration (Fig. S17), a result consistent with a previous modeling study by Lyon and DeWitt (2012) using an ensemble of runs from a CMIP3-generation model. Given the complexity of and internal variability in this connection over the study time period in observations (Vigaud et al. 2017; Funk et al. 2018), a more targeted study may be needed to diagnose how this connection interacts with CMIP6 simulations of the GHA rainy seasons.

Our results also show that relying solely on monthly averages can result in misleading results about model behavior in the GHA. Since seasonal timing can be radically different between models, the same calendar month can represent wholly different stages of a given model’s seasonal cycle. Rather, such results should be interpreted using the additional help of seasonal composites that take into account the actual onset and demise dates of the seasons in observations and each model, which in this case has shown more coherent results across models. Differences in seasonal timing also complicate the evaluation of subseasonal variability in models, which is often done using day-of-year or month-of-year cutoffs developed from observations (e.g., Dyer and Washington (2021)). More work will be needed to consistently generalize the evaluation of known subseasonal patterns of variability to models.

Ideally, a process-based model evaluation such as this one can be used to diagnose whether models are simulating the rainy seasons correctly for the ‘right’ reasons. A logical direction for future research would be to determine whether CMIP6 models that replicate observed relationships between the rainy seasons in East Africa and aspects of the atmospheric and ocean circulations produce different projections of future rainfall than those that don’t. However, climate models in the GHA are rarely consistently ‘good’ or ‘bad’ across metrics and seasons (Akinsanola et al. 2021). More broadly, metrics-based approaches to model subsetting have failed to reduce projection uncertainty in CMIP5 models (Rowell et al. 2016). CMIP6 models may run into a similar issue, illustrated through a sample model partitioning based on IOD behavior. Figure 13 shows changes in characteristics of the GHA rainy seasons between the historical period and end of century (2066–2098) in SSP370 (see Figure S19 for future values), with models with the largest historical bias in the strength of the IOD shown in green (the 5 models with available SSP370 data of the 8 models in the box in Fig. 9). These models’ changes are relatively clustered in the short rains (as would be expected given the increased relevance of the IOD to the short rains), particularly in their onset, demise and total rainy season amount changes. Similar to historical simulations, these models tend to be show some of the wettest future short rains as well (Fig.  S19). However, plausible ranges of future changes in seasonal metrics are not well-constrained by this subset, despite the unrealistic simulation of the Indian Ocean in the removed models.

Fig. 12

Peak strength of vertical pressure velocity ($\omega$) over the double-peaked region in models and observations. Models tend to produce deeper convection than observations in the short rains (vertical axes; model bias in pressure velocity is stronger at 250  hPa, where observations rarely show strong upward motion, than at 500 hPa)

Fig. 13

Changes in GHA rainy season characteristic between models’ historical runs (1981–2013) and SSP370 (2066–2098) runs. Green dots highlight models with IOD biases above 1.5 K. Projections of future changes in onset, demise, peak daily amount, and total amount for the short rains in particular seem to be similar across models with particularly biased historical IODs; however, three of these models are variants from the same modeling group (EC-Earth), which may explain the clustering

Future research will need to verify whether this lack of clear partitioning extends towards other aspects of CMIP6 biases as well. Nevertheless, even if easy partitions are unrealistic, process-based model evaluations remain important for understanding the sources of model biases in ‘expert judgment’ approaches suggested by Rowell et al. (2016). Studying the biases in underlying processes is particularly crucial to identifying models that may have a low bias in the rainy seasons despite having an unrealistic simulation of the broader circulation; these models may have the ‘right’ rainy seasons, but for the ‘wrong’ reasons.

More generally, studies that use climate model projections to estimate the impact of climate change on society should verify that the models are adept at simulating not just the variables of interest, but the processes that affect them. This is particularly important for rainfall, which is often poorly simulated, and in regions with complex dynamics such as the GHA, where biases in rainy seasons may have many causes.