1 Introduction

The mid-Piacenzian Warm Period (MPWP, 3.264–3.025 Ma) is the most recent geological interval when climate was persistently warmer while atmospheric CO2 concentrations were close to today. In addition, various characteristics of this period are similar to present, increasing transferability of inferences drawn from MPWP climate to a modern perspective, such as the distribution of continents (Dowsett et al. 2016). Therefore, interest in the MPWP stems from it being a possible reference for future climate (Dowsett et al. 2016; Burke et al. 2018; Chandan and Peltier 2018; Sun et al. 2018, 2024; McClymont et al. 2020).

Reconstructions using environmental proxies and numerical simulations are the two main ways to study past climates. Fruitful collaboration between these two disciplines has shed light on Pliocene climate. Noteworthy are continued effort of the Pliocene Research, Interpretation and Synoptic Mapping (PRISM) project over the past 30 years (Dowsett 1991; Dowsett et al. 1994, 1996, 1999, 2009, 2010, 2012, 2013a, b, 2016; Dowsett and Robinson 2009) that have provided the paleoclimatic framework for model-data comparison and ample information on paleogeography that has been provided to the modeling community as boundary conditions for simulations of Pliocene climate. The paleogeographic reconstructions of PRISM3 (Dowsett et al. 2010) and PRISM4 (Dowsett et al. 2016) have served as boundary conditions for the Pliocene Model Intercomparison Project, an international climate modeling initiative to study and understand climate and environments of the MPWP (Haywood et al. 2021) that has conducted two successful phases PlioMIP1 (Haywood et al. 2011), PlioMIP2 (Haywood et al. 2016), and has recently entered its third phase PlioMIP3 (Haywood et al. 2023).

Overall, the large-scale warm and wet conditions indicated by MPWP climate reconstructions are reproduced by most PlioMIP models. The increase in MPWP surface air temperature (SAT) relative to the pre-industrial inferred from proxy reconstructions improved from PlioMIP1 (∼1.8–3.6 °C) to PlioMIP2 (∼1.7–5.2 °C) (Haywood et al. 2013, 2020) as did total precipitation (0.09–0.18 mm/day in PlioMIP1 (Haywood et al. 2013), 0.07–0.37 mm/day in PlioMIP2 Haywood et al. 2020). In addition to the large-scale patterns, PlioMIP models also simulate important regional climate features, including weakened tropical atmospheric circulation (Sun et al. 2013), reduced El Niño variability (Oldeman et al. 2021), increased monsoon rainfall (Zhang et al. 2013; Sun et al. 2016, 2018, 2024; Li et al. 2020; Berntell et al. 2021; Han et al. 2021; Williams et al. 2021), an overall poleward migration of storm tracks (Baatsen et al. 2022), Arctic warmth (Zheng et al. 2019; de Nooijer et al. 2020), and the enhancement of Atlantic Meridional Overturning Circulation (AMOC) (Zhang et al. 2021). Although much progress has been made in improving simulations in comparison to the geologic record, some basic scientific issues remain (Tindall et al. 2022). For example, high-latitude warmth shown in proxy records persists in being generally underestimated by simulations, despite efforts to resolve data-model inconsistencies by altering the orbital parameters (Prescott et al. 2014; Samakinwa et al. 2020), increasing CO2 concentration (Stepanek et al. 2020), including enhanced concentrations of non-CO2 (i.e. CH4) trace gases (Hopcroft et al. 2020), and enhancing the poleward heat transport via closure of the Bering Strait (Chandan and Peltier 2017; Hunter et al. 2019; Chan and Abe-Ouchi 2020; Stepanek et al. 2020; Tan et al. 2020; Weiffenbach et al. 2022). In essence, the widespread underestimation of polar amplification in climate simulations persists in PlioMIP2. Given the widespread interest in future changes in tropical atmospheric circulation and the associated uncertainties, there is an increasing focus on studying past geological warm periods to gain insights into how tropical atmospheric circulation has evolved in the past, thus contributing to the understanding of future changes (Sun et al. 2013; Zhang et al. 2023, 2024). However, the validity of a common attribution of the weakening of tropical atmospheric circulation during warm periods to the enhancement of static stability has recently been questioned (Zhang et al. 2024). Furthermore, while water-isotope enabled simulations have been used in the study of the Quaternary (Zhu et al. 2017; Tabor et al. 2018; Hu et al. 2019; Falster et al. 2021; He et al. 2021) and of the Eocene (Zhu et al. 2020), there is a lack of consideration of stable water- isotopes in climate simulations of the Pliocene, hampering direct comparison of model- output to oxygen-isotope-based proxy-records as there is necessity for the use of transfer functions. Furthermore, the ability of stable water-isotopes to be used as a tracer for dynamics in the hydrological cycle has so far been lacking for the Pliocene.

With this in mind, we studied the large-scale features of the MPWP using iCESM1.2-ITPCAS following the PlioMIP2 protocols, in anticipation of new findings that increase our understanding of this quasi-analog of future climate conditions and that supplement inferences gained from the PlioMIP2. Our findings indicate that (1) enhanced polar amplification is observed when utilizing a distinct ocean initialization, setting our study apart from the majority of previous research; (2) precipitation response in the latitude band [~ 30°S–10°N] differs between iCESM1.2-ITPCAS and PlioMIP2 primarily due to the predominant influence of different physical processes (dynamic vs. thermodynamic); (3) Diabatic processes provide a more fundamental explanation for a spatial response of tropical atmospheric circulation to MPWP warmth, including Hadley cells and the tropical Pacific Walker cell; (4) two additional water-isotope enabled experiments help us to decipher the decomposition of δ18Op response during the MPWP.

2 Model description and simulation for mid-piacenzian climate

2.1 Model description

The model used for the MPWP simulation is the fully coupled water isotope-enabled version of the Community Earth System Model version 1 (iCESM1.2) (Brady et al. 2019). The four model components that make up this model are: atmosphere (CAM5.3, resolution 1.9° latitude\(\times\)2.5° longitude), land surface (CLM4, 1.9°\(\times\)2.5°), ocean (POP2, ~ 1.0°\(\times\)1.0°), and sea ice (CICE4, same resolution as POP2). All components of iCESM1.2 exchanges relevant fluxes via a coupler (CPL7). The model codes are available to the public via an open access publication of source files (https://github.com/NCAR/iCESM1.2).

As assessed by the work of Nusbaumer et al. (2017) and Brady et al. (2019), iCESM1.2 has good performance in representing the observed distribution of stable isotopes of oxygen (δ18Op) in precipitation, and thus it is widely used in paleoclimate simulations (Zhu et al. 2017, 2020).

2.2 Experimental designs

Following PlioMIP2 protocols, this study used iCESM1.2-ITPCAS to carry out MPWP climate simulations under the enhanced boundary conditions from PRISM4 (Dowsett et al. 2016; Haywood et al. 2016). Given the open-source nature of iCESM1.2 and its application by various different modeling groups, we added the suffix ITPCAS to the article title and diagrams, distinguishing our study from other groups potentially using this model version for PlioMIP simulations. The main experimental parameters in the MPWP simulation (Eoi400; Haywood et al. 2016) are configured as follows: (1) CO2 concentrations in the atmosphere are set to 400 ppm; (2) changes in the topography and bathymetry include closure of the Canadian Archipelago and Bering Strait, and a reduction in land ice cover that comes with major changes of the land-sea-mask in the western Antarctic; (3) prescribed vegetation is provided by the PRISM3 reconstruction as described in Salzmann et al. (2008); and (4) the solar constant and orbital forcing are the same as the pre-industrial condition. In addition to the MPWP experiment, the pre-industrial experiment (PI, E280) is performed for comparison with the MPWP simulation. The MPWP experiment was run for 2500 model years whereas the PI experiment was restarted from a previously obtained equilibrium state (Zhu et al. 2017, 2020) and then ran for another 300 model years.

To illustrate the advantage of the iCESM1.2-ITPCAS compared with other PlioMIP2 models in simulating high latitude warmth, we conducted PlioMIP2 core experiments also using the CESM1.2 (CAM4)-ITPCAS (motivation for specification of the model version is as for iCESM1.2-ITPCAS) following the same experimental configuration as the iCESM1.2-ITPCAS and compare results in Fig. 1. The CESM1.2-ITPCAS configuration used in this work differs from that of Feng et al. (2020) in that the atmospheric model used in their study is CAM version 5 (CAM5) at the horizontal resolution of 0.9° along latitudes and 1.25° along longitudes, whereas we employ CAM version 4 (CAM4) at the horizontal resolution of 1.9° latitude by 2.5° longitude.

Fig. 1
figure 1

Time series of global annual mean surface air temperature (SAT in °C) in the simulations of mid-Piacenzian warm period (MPWP, blue line) and pre-industrial reference period (PI, black line). Solid and dashed lines used to distinguish simulation of iCESM1.2-ITPCAS and CESM1.2(CAM4)-ITPCAS. The ITPCAS suffix is used to distinguish our simulations from PlioMIP2 simulations performed by other groups using CESM.

Full size image

Due to increased equilibrium climate sensitivity (ECS) from CAM4 to CAM5 (Feng et al. 2020), this could be the primary reason for our simulated difference in MPWP surface warmth between iCESM1.2-ITPCAS and CESM1.2 (CAM4)-ITPCAS (i.e., iCESM1.2-ITPCAS simulates higher warmth than CESM1.2 (CAM4)-ITPCAS). The model version (CESM 1.0.5), a model not featuring high ECS, can simulate MPWP surface conditions that are among the warmest found from PlioMIP2 models, including those with higher ECS, if it is initialized from a warmer ocean state as opposed to starting from PI or present-day conditions (Baatsen et al. 2022). We similarly used warm model initialization (same salinity and slightly higher ocean temperature) for iCESM1.2-ITPCAS and CESM1.2 (CAM4)-ITPCAS in the expectation of higher magnitude of MPWP surface warmth at higher latitude that was so far underestimated by the models (Dowsett et al. 2013a; Salzmann et al. 2013). This, of course, has the side effect of overestimating some of the reconstructed temperatures in the tropics. We note that different types of proxies appear to disagree on temperatures in the tropics of the Pliocene, and that particularly cold tropical temperatures could potentially be related to biases in the proxy recorder (e.g. McClymont et al. 2020). For detailed initial values of temperature and salinity, please refer to the data set that has been made available online (file ts_init_b20.681_1100-01_s_35.60level.dat.orig, source: https://github.com/CESM-Development/paleoToolkit/tree/master/cesm1/ocn/ic/).

Considering the potential impact of intrinsic decadal variability on the results (Parsons et al. 2020), the last 100 years of each simulation were used for analysis. It’s noteworthy that the time span for calculating the mean climate state is variable across different studies, and averaging periods over 20 (He et al. 2021; IPCC et al. 2013), 30 (Arguez and Vose 2011; Haywood et al. 2013; Salzmann et al. 2013; Sun et al. 2018, 2021, 2023), 50 (IPCC 2013; Hawkins et al. 2017), or even 100 years (Haywood et al. 2020; Stepanek et al. 2020) have been used. For a simulated climate in equilibrium, the choice of the time length over which climatological results are derived should not affect results too much if the average is made over at least a period of multiple decades and as long as it can be shown that significant impact of multi-decadal to multi-centennial variability is absent.

2.3 Diagnostic methodology

2.3.1 Decomposition of surface temperature changes

Causes of differences between simulations were examined by decomposing MPWP surface air temperature (SAT) anomaly into several physical processes by means of an analysis of the surface energy budget, following the work of Lu and Cai (2009).

$$4\sigma {\overline{T}}_{s}^{3}\varDelta T\approx -(\varDelta \alpha) \left(\overline{{S}^{\downarrow }}+\varDelta {S}^{\downarrow }\right)+\varDelta CR{F}_{s}+\left(1-\overline{\alpha }\right)\varDelta {S}^{\downarrow ,clr}+\varDelta {F}^{\downarrow ,clr}-\varDelta Q-\varDelta \left(SH+LH\right)$$
(1)

where overbar indicates time means, \({S}^{\downarrow }\) and \({S}^{\uparrow }\) are surface downward and upward shortwave radiation fluxes, \(\alpha\) is the surface albedo calculated as the ratio of \({S}^{\uparrow }\) to \({S}^{\downarrow }\) at surface, F is net longwave radiation flux at the surface derived from differences between \({F}^{\downarrow }\) (downward longwave radiation flux) and \({F}^{\uparrow }\) (upward longwave radiation flux), the superscript \({\left(\cdot \right)}^{clr}\) denotes clear sky (clr) condition, \({CRF}_{s}\) is cloud radiative forcing at the surface, Q is heat storage, SH and LH are sensible heat and latent heat fluxes, respectively, and a \(\varDelta \left(\cdot \right)\) notation denotes variable differences between two data sets (i.e. different simulated climate states in our case). Thus, the surface temperature difference of MPWP climate vs. a reference climate can be approximately decomposed into the sum of partial temperature changes due to the following seven processes (from left to right): surface albedo feedback (SAF) (\(\varDelta {T}_{SAF}\)), cloud radiative forcing (\(\varDelta {T}_{CRE}\)), non-SAF-induced change in clear-sky short wave radiation (\(\varDelta {T}_{\text{non}\_\text{SAF}\_\text{SW}}\)), downward clear-sky long wave radiation fluxes (\(\varDelta {T}_{\text{r}\text{l}\text{d}\text{s}\_\text{c}\text{l}\text{r}}\)), heat storage (\(\varDelta {T}_{Q}\)), surface sensible fluxes (\(\varDelta {T}_{SH}\)), and surface latent fluxes (\(\varDelta {T}_{LH}\)).

2.3.2 Water vapor budget

Before we continue, we must keep in mind that there are several formulations for the water vapor balance equation, and we have chosen one of the more commonly used expressions (Seager et al. 2010; Chou and Lan 2012).

$$P=E-\langle \nabla \cdot q{\overrightarrow{V}}_{H}\rangle+Res$$
(2)

where P is precipitation, E is evaporation, q is the atmospheric specific humidity, \({\overrightarrow{V}}_{H}\) is the horizontal wind, ∇∙ its divergence, and Res accounts for the residual term, encompassing transient eddy effects and deformation of surface moisture transport due to the surface pressure gradient (D’Agostino and Lionello, 2020; Sun et al. 2021; Sun et al. 2023). The bracket notation denotes the vertical integral in the atmospheric column across the troposphere and is defined as \(\langle\cdot\rangle=\frac1{{gp}_w}\int_0^{P_s}\cdot dp\), where Ps is the surface pressure, ρw is the density of water, and g is the gravitational acceleration. The difference in water vapor budget between two climate states, considering changes in the divergence of water vapor flux (\(-\delta \langle \nabla \cdot q{\overrightarrow{V}}_{H}\rangle\)) for thermodynamic and dynamic decompositions, can be expressed as follows:

$$\begin{array}{l}\delta P=\delta E-\delta \langle \nabla \cdot q{\overrightarrow{V}}_{H}\rangle+\delta Res\\\approx \delta E-\langle \nabla \cdot {\overrightarrow{V}}_{H}\delta q\rangle-\langle \nabla \cdot q\delta {\overrightarrow{V}}_{H}\rangle+\delta Res\\\equiv \delta E+\delta TH+\delta DY+\delta Res\end{array}$$
(3)

The above defined thermodynamic (\(\delta \text{TH}\)) and dynamic (\(\delta \text{DY}\)) components of changes in divergence of water vapor flux (\(-\delta \langle \nabla \cdot q{\overrightarrow{V}}_{H}\rangle\)) that affect precipitation difference between MPWP and PI can be written as follows:

$$\delta\text{TH}=-\langle\nabla\cdot{\overrightarrow V}_H\delta q\rangle=-\frac1{g\rho_w}\int_0^{P_s}\;\nabla\cdot{\overrightarrow V}_H \ \delta q \ dp$$
(4)
$$\delta\text{DY}=-\langle\nabla\cdot q{\delta\overrightarrow V}_H\rangle=-\frac1{g\rho_w}\int_0^{P_s}\;\;\nabla\cdot{q\delta\overrightarrow V}_H \ dp$$
(5)

Application of the water vapor budget can be summarized as follows: (1) examining the physical processes controlling precipitation during two different periods (Eqs. 2), (2) evaluating relative contributions of different components to the response of precipitation to MPWP warmth (Eq. 3), and (3) further elucidating relative magnitudes of thermodynamic and dynamic processes in water vapor transport through thermodynamic and dynamic decompositions (Eqs. 4 and 5).

2.3.3 Decomposition of the response of δ18Op

To identify controls on δ18O in precipitation (δ18Op), two additional stable water-isotopes experiments were conducted where sea surface temperature and sea ice distribution from the last 100 years of the PI and MPWP experiments were prescribed as a lower boundary condition to the stand-alone iCAM5. Each simulation ran for 40 years, analysis of climate state and model dynamics being conducted on the last 30 years of each simulation. A mathematical expression for δ18Op at any grid cell can be formulated as the weighted sum of oxygen isotopes in precipitation from all source areas, following the methods described in the work of Tabor et al. (2018), Hu et al. (2019) and He et al. (2021).

$$\mathbf\delta^{\mathbf{18}}{\mathbf O}_{\mathbf p}=\sum\nolimits_{i=1}^N\delta^{18}O_{pi}\times\frac{p_i}{p_{total}}$$
(6)

where \({\delta }^{18}{O}_{pi}\) and \({p}_{i}\) represent \({\delta }^{18}{O}_{p}\) and precipitation from the source region “i” \(and \ {p}_{total}\) is total precipitation at each grid cell. Equation 6 describes the calculation for δ18Op, considering contributions from multiple source regions weighted by their respective precipitation amounts. The δ18O transported by water vapor (δ18Owv, i) from a specified source region “i” to the formation of δ18O in precipitation at a grid cell (δ18Opi) involves three distinct characteristics and processes: the isotopic signal of water vapor at the source region δ18Owv, i and isotopic depletion δ18Owvsink, i and enrichment en route due to rainout and condensation.The relation of δ18Opi with the three aforementioned characteristics and processes can be expressed as follows:

$$\mathrm\delta^{18}{\mathrm O}_{\mathrm{pi}}=(\mathrm\delta^{18}{\mathrm{Owv}}_{\mathrm{source},\;\mathrm i})+(\;\mathrm\delta^{18}{\mathrm{Owv}}_{\mathrm{sink},\;\mathrm i}-\mathrm\delta^{18}{\mathrm{Owv}}_{\mathrm{source},\;\mathrm i})+(\mathrm\delta^{18}{\mathrm O}_{\mathrm{pi}}\;-\mathrm\delta^{18}{\mathrm{Owv}}_{\mathrm{sink},\;\mathrm i})$$
(7)

The δ18Op difference between MPWP and PI periods can be attributed to four distinct processes (Eq. 8).

$$\begin{array}{c}{\varDelta (\delta }^{18}{O}_{p})=\sum\limits_{i=1}^{N}{\varDelta (\delta }^{18}{O}_{pi})\times \frac{{p}_{i}}{{p}_{total}}+\sum\limits_{i=1}^{N}{\delta }^{18}{O}_{pi}\times \varDelta \left(\frac{{p}_{i}}{{p}_{total}}\right)\\=\sum_{i=1}^N\Delta\left\{\underbrace{\left(\delta^{18}O_{WVsource,i}\right)}_{\mathrm{Source}\;\mathrm{composition}}+\underbrace{\left(\delta^{18}O_{WVsink,i}-\delta^{18}O_{WVsource,i}\right)}_{\mathrm{Rainout}}\right.\\+\left.\underbrace{\left(\delta^{18}O_{pi}-\delta^{18}O_{WV\sin k,i}\right)}_{\mathrm{Condensation}}\right\}\times\frac{p_i}{p_{total}}+\underbrace{\sum_{i=1}^N\delta^{18}O_{pi}\times\Delta\left(\frac{p_i}{p_{total}}\right)}_{\mathrm{Source}\;\mathrm{location}\;\mathrm{changes}}\end{array}$$
(8)

Please note that annual mean δ18Op is calculated by weighing monthly precipitation amount (Eq. 9).

$${\delta }^{18}{O}_{p}=\sum\nolimits_{mon=1}^{12}{\delta }^{18}{O}_{pmon}\times \frac{{p}_{mon}}{{p}_{ann}}$$
(9)

where \({\delta }^{18}{O}_{pmon}\) is monthly δ18Op, pmon is monthly precipitation, pann is annual total precipitation.

In our study, we divide the investigation into eight regions, seven being located across the ocean, and one covering the global terrestrial realm (Fig. 7b). This approach enables regionally discrete quantification of contributions of three physical processes (source composition, rainout, condensation) and of the spatially heterogeneous isotopic composition at different source regions to the variations of δ18Op around the tropical Indian Ocean and the Tibetan Plateau (TP) in response to MPWP warmth.

2.3.4 Diabatic processes and tropical atmospheric circulation

In the tropics, the thermodynamic equations describing atmospheric motion can be simplified as follows:

$$Q\approx \omega \cdot \sigma$$
(10)

where \(\omega\) is the vertical motion of air and \(\sigma\) is the static stability of the atmosphere. This means that the tropical atmosphere is in equilibrium between diabatic heating (cooling) and adiabatic rising (sinking) (Mitas and Clement 2006). First of all, the climatic means of tropical diabatic heating and cooling correspond spatially well with the rising and sinking of the tropical atmosphere (Figs. S4-S5). Next, changes in diabatic processes in the tropics (\(\delta Q\)) and their decomposition into dynamic (\(\delta {Q}_{DY}=\sigma \cdot \delta \omega\)) and thermodynamic contributions (\(\delta {Q}_{TH}=\omega \cdot \delta \sigma\)) due to respective changes by vertical circulation and dry static stability are further used to study the Hadley circulation and Walker circulation changes in response to MPWP warmth.

2.3.5 Mass stream function for Hadley circulation and stream function for Walker circulation

The Hadley circulation’s conventional metric, the mass stream function (MSF), is determined as the vertical integral of the zonal mean meridional wind throughout the troposphere (Oort and Yienger 1996). The calculation is expressed by the equation:

$${\uppsi }\left(\varnothing ,p\right)=\frac{2\pi a \ \text{cos} \ \varnothing }{g}\int_{0}^{p}v\left(\varnothing ,p\right)dp$$
(11)

In this equation, a represents Earth’s radius, ∅ signifies latitude, g stands for acceleration due to gravity, p denotes pressure, and v represents meridional velocity.

The edges of the northern and southern Hadley cells, labeled NHCE and SHCE respectively, represent the latitudinal positions where the MSF reaches zero at 500 hPa within the subtropical regions of the northern and southern hemispheres (Sun et al. 2013; Zhang et al. 2024).

We can obtain the zonal overturning circulation that characterizes the Walker circulation by vertically integrating the divergence component of the zonal wind average over 30°S-30°N (Sun et al. 2013; Zhang et al. 2024). It is expressed as:

$${\uppsi }\left(\lambda ,p\right)=\frac{2\pi a}{g}\int_{0}^{p}{u}_{d}(\lambda ,p)dp$$
(12)

Here, Ψ denotes the zonal stream function, \(\lambda\) represents longitude, p represents pressure, and \({u}_{d}\) represents the divergence component of the zonal wind.

2.3.6 Aridity index

The aridity index (AI) is commonly defined as the ratio of precipitation (P) to potential evapotranspiration (PET), expressed as AI = P/PET. It serves as a direct and effective indicator for quantifying land dryness and is widely employed in drought research (Su et al. 2018). Potential evapotranspiration is often calculated using the Penman formula (Allen et al. 1998):

$$PET=\frac{0.408\varDelta \left({R}_{n}-G\right)+\gamma \frac{900}{{T}_{a}+273}{U}_{2}\left({e}_{s}-{e}_{a}\right)}{\varDelta +\gamma \left(1+0.34{U}_{2}\right)}$$
(13)

Where:

∆ is the slope of saturation vapor pressure curve at the given air temperature (kPa \(^\circ \mathrm C^{-1}\)), Rn is the net radiation at the surface (W m−2), G is the soil heat flux (W m−2), γ is the psychrometric constant (kPa\(^\circ \mathrm C^{-1}\)), Ta denotes the 2-meter air temperature, U2 represents the 2-meter wind speed, es stands for the saturation vapor pressure (kPa), and ea represents the actual vapor pressure (kPa), which can be calculated from es and relative humidity.

Therefore, PET comprehensively considers the combined effects of near-surface temperature, relative humidity, surface energy, and other factors, providing a good reflection of the evapotranspiration capacity under different underlying surface thermal conditions. A lower AI value indicates a drier climate. According to the classification standards of the United Nations Environment Programme (Middleton and Thomas 1992), drought severity is categorized into four levels based on AI values: AI < 0.05 indicates a hyper-arid region, 0.05 ≤ AI < 0.2 represents an arid region, 0.2 ≤ AI < 0.5 denotes a semi-arid region, and 0.5 ≤ AI < 0.65 characterizes a dry sub-humid region. As a rule, the annual average AI index is used to describe the average annual dry and humid conditions of a region. The seasonal AI is then used to describe the seasonal variations in regional dry and wet conditions (Zhao et al. 2019; Pour et al. 2020; Kumar et al. 2021).

3 Results

3.1 Surface temperature

Figure 2 shows annual and seasonal SAT anomalies (Fig. 2, middle panel) of MPWP compared with the PI period as simulated with iCESM1.2-ITPCAS. For the latter, absolute values are shown in Fig. 2 (left panel). The simulated global average SAT of mean annual, boreal winter (December-January-February, DJF) and boreal summer (June-July-August, JJA) is 4.98 °C, 4.81 °C and 5.16 °C above the PI period, respectively. Surface warmth during the MPWP is far from globally uniform, as manifested by pronounced positive temperature anomalies in the high latitudes of the Northern and Southern Hemispheres and a weak rise of SAT in the tropics (Fig. 2b-e-h). Latitudinal heterogeneity of SAT changes reduces the meridional (equator-to-pole) thermal contrast in both hemispheres (Fig. 2b-e-h and c-f-i); the potential effect of non-uniform distribution of warmth on tropical atmospheric circulation is further addressed in Section 3.3.

Fig. 2
figure 2

Climatology of surface air temperature (SAT, units: °C) in the PI period (left panel) and differences between MPWP and PI period (middle panel) in terms of annual (top), boreal winter (December-January-February, DJF, middle) and boreal summer (June-July-August, JJA, bottom). Left and middle panels show results derived with iCESM1.2-ITPCAS. The right panel shows for the various simulations changes in meridional temperature gradients with regard to PI that are computed from zonal averages of the anomaly MPWP vs. PI. The red curve on the right panel is for iCESM1.2- -ITPCAS, shown along with CESM1.2 (CAM4)-ITPCAS (orange curves) and PlioMIP2 multi-model ensemble (MME) (black cures). Gray and green bands are the width of one standard deviation of the zonal mean derived from iCESM1.2-ITPCAS and PlioMIP2 MME. Dotted areas in the middle panel are differences above the 1% significance level. Colored circles in b represent reconstructed annual mean SAT during PRISM (~ 3.3-3.0 Ma), from Salzmann et al. (2013)

Full size image

Compared with the results of PlioMIP2 multi-model ensemble mean (MME) (black curves in Fig. 2c-f-i) and CESM1.2 (CAM4)-ITPCAS (orange curves in Fig. 2c-f-i), the simulations of iCESM1.2-ITPCAS (red curves in Fig. 2c-f-i) show positive temperature anomalies to be more pronounced at high-latitudes in both hemispheres thereby better representing findings derived from reconstructions during the MPWP (Salzmann et al. 2013).

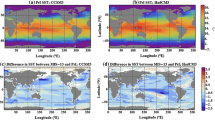
In addition to changes in SAT, sea surface temperature (SST) simulated using iCESM1.2-ITPCAS also shows a significant positive anomaly at high latitudes (Fig. 3, top panel). This is consistent with the results of the PlioMIP2 MME (Fig. 3, bottom panel). Compared to the PlioMIP2 MME, pronounced high latitude warmth in the iCESM1.2-ITPCAS is more in line with proxy data for the MPWP (Dowsett et al. 2013a).

Fig. 3
figure 3

As in Fig. 2, except for the simulation of sea surface temperature (SST, units: °C) anomalies derived from iCESM1.2-ITPCAS (top panel) and PlioMIP2 multi-model ensemble (bottom panel) in comparison with proxy data by McClymont et al. (2020) (colored circles)

Full size image

Decomposition shows that the simulated MPWP surface warmth is mainly controlled by changes in downward clear-sky long wave radiation fluxes (\(\varDelta {T}_{\text{r}\text{l}\text{d}\text{s}\_\text{c}\text{l}\text{r}}\)) in both iCESM1.2-ITPCAS and CESM1.2 (CAM4)-ITPCAS (Fig. 4). Yet, iCESM1.2-ITPCAS simulates a larger contribution of\(\varDelta {T}_{\text{r}\text{l}\text{d}\text{s}\_\text{c}\text{l}\text{r}}\) to high latitude surface warmth than the CESM1.2 (CAM4)-ITPCAS simulation (Fig. 4). In addition, contributions by heat storage (\(\varDelta {T}_{Q}\)) and cloud radiative forcing (\(\varDelta {T}_{CRE}\)) to high latitude surface warmth during the MPWP are much higher in the iCESM1.2-ITPCAS simulation than in the CESM1.2 (CAM4)-ITPCAS simulation. This could explain the reason for MPWP surface warmth at high latitudes as simulated by iCESM1.2-ITPCAS is much closer to PRISM4 reconstructions than the results derived from CESM1.2 (CAM4)-ITPCAS (Fig. 2).

Fig. 4
figure 4

Decomposition of (a) SAT anomaly (units: °C) during the MPWP relative to the PI into partial temperature changes due to surface albedo feedback (SAF) (\(\varDelta {T}_{SAF}\)), changes in cloud radiative forcing (\(\varDelta {T}_{CRE}\)), the non-SAF-induced change in clear-sky short wave radiation (\(\varDelta {T}_{\text{n}\text{o}\text{n}\_\text{S}\text{A}\text{F}\_\text{S}\text{W}}\)), the change in downward clear-sky long wave radiation fluxes (\(\varDelta {T}_{\text{r}\text{l}\text{d}\text{s}\_\text{c}\text{l}\text{e}\text{a}\text{r}\text{s}\text{k}\text{y}}\)), the change in heat storage (\(\varDelta {T}_{Q}\)), the change in surface sensible fluxes (\(\varDelta {T}_{SH}\)), the change in surface latent fluxes (\(\varDelta {T}_{LH}\)), and (b) the sum of the seven decomposed terms. Top and bottom panels show the decomposition of iCESM1.2-ITPCAS and CESM1.2 (CAM4)-ITPCAS, respectively. The dotted areas in each subfigure are differences above the 1% significance level

Full size image

3.2 Precipitation and δ18Op

In addition to simulating a warmer MPWP (Figs. 2 and 3), iCESM1.2-ITPCAS simulates MPWP climate that is wetter compared to the PI period (Fig. 5b-e-h and a-d-g). Global average precipitation was higher in the MPWP by 0.33 mm/day, 0.31 mm/day, 0.35 mm/day for the annual, boreal winter, and boreal summer means, respectively. While precipitation in the MPWP was higher overall, there is obvious regional modulation (Fig. 5b-e-h). For example, MPWP precipitation is generally higher outside the tropics. Within the tropics there is a mixed response, with higher precipitation mainly in the monsoon regions, especially in the Asian-Australian monsoon zone, and reduced precipitation in the equatorial region (Fig. 5b-e-h).

Fig. 5
figure 5

As in Fig. 2, except for precipitation (mm/day). The right panel shows differences in the meridional gradient of precipitation for iCESM1.2-ITPCAS (blue) and PlioMIP2 multi model ensemble (MME) (green). PlioMIP2 MME precipitation anomalies in rightmost panel are derived from Sun et al. 2024

Full size image

Signs of precipitation changes are largely consistent between iCESM1.2-ITPCAS and PlioMIP2 MME (Fig. 5c-f-i) in most parts of both hemispheres, except for regions around the equator and the southern tropics (Fig. 5c-f-i). That is, precipitation patterns are similar between iCESM1.2-ITPCAS and PlioMIP2 MME with respect to wetter middle to high latitudes in each hemisphere, more pronounced dry regions in the northern subtropics, and wetter northern tropics. In contrast, both models produce opposite signs of precipitation change during the MPWP over the tropical regions [~ 30 S°–10\(^\circ\)N]. In the PlioMIP2 MME we find increased precipitation near the equator [~ 10 S°–10\(^\circ\)N] and drying in tropical regions south of the equator [~ 30 S°–10\(^\circ\)S], while in iCESM1.2-ITPCAS there is a decreased precipitation near the equator and increased rainfall in tropical regions of both hemispheres the equator, straddling the equator.

Analysis of water vapor budgets in iCESM1.2-ITPCAS and PlioMIP2 MME, depicted in Fig. 6, helps us to understand precipitation responses to MPWP surface warmth and to identify associated physical processes. Relative to the PI, the increase in global mean precipitation (\(\delta P\)) during the MPWP primarily links to increased evaporation (\(\delta E\)) that is the dominant component across seasons. While providing strong signals at regional scale, other water vapor budget components (\(\delta TH\), \(\delta DY\), \(\delta Res\)) have rather minor impact on global mean precipitation changes in iCESM1.2-ITPCAS and negligible effects in PlioMIP2 MME (Table 1; Fig. 6). At regional scale, however, both in iCESM1.2-ITPCAS and PlioMIP2 MME simulations, dynamic effects (\(\delta DY\)) contribute more to precipitation anomalies than thermodynamic effects (\(\delta TH\)), notably within the tropics and subtropics (Fig. 6). For iCESM1.2-ITPCAS we find a more pronounced response of MPWP precipitation than for PlioMIP2 MME. This owes to stronger physical processes (\(\delta E, \delta TH\), \(\delta DY\), \(\delta Res\)) governing precipitation in iCESM1.2-ITPCAS (Table 1; Fig. 6). Notably, contrasting regional precipitation responses between iCESM1.2-ITPCAS and PlioMIP2 MME, particularly within [~ 30 S°–10°N], arise due to differing dominant effects of \(\delta DY\) and \(\delta TH\). iCESM1.2-ITPCAS emphasizes \(\delta DY\) control, while PlioMIP2 MME attributes regional precipitation changes more to \(\delta TH\) (Fig. 6), although the difference in contribution is for PlioMIP2 MME not so clear due to comparably small overall contribution by both processes (Fig. 6; Table 1).

Table 1 Global average water vapor budget differences (mm/day) between MPWP and PI (iCESM1.2-ITPCAS/PlioMIP2 MME).
Full size table
Fig. 6
figure 6

Comparative analysis of changes in the components of the water vapor budget (δE, δTH, δDY, δRes) that influence differences in precipitation (δP) between the MPWP and the PI. This analysis uses iCESM1.2-ITPCAS and PlioMIP2 MME simulations over annual, DJF and JJA periods

Full size image

Stable oxygen isotopes (δ18O) simulation in iCESM1.2-ITPCAS enables us to study the dynamic response of precipitation to MPWP warmth. Here we show that PI δ18Op in iCESM1.2-ITPCAS captures the spatial pattern of observed annual, DJF and JJA δ18Op (Fig. 7a-d-g). For the MPWP more negative δ18Op is found over the tropical Indian Ocean and its surrounding landmasses, while remaining regions largely exhibit positive δ18Op anomalies (Fig. 7c-f-i). To clarify controls for more negative δ18Op over the tropical Indian Ocean and its surrounding land masses during the MPWP, Fig. 8 illustrates the combined effects of individual physical processes in all regions for annual (left panel), DJF (middle panel) and JJA (right panel) δ18Op response. These include contributions from changes in source composition (row 1 of Fig. 8), rainout (row 2), condensation (row 3), and source location (row 4).

Fig. 7
figure 7

As Fig. 5, except for the spatial distribution of δ18Op in PI and MPWP periods, along with differences between MPWP and PI (units: permille). Within panel b, black rectangle boxes highlight the regions accountable for the differences in δ18Op at areas of interest that are denoted by red curve (Tibetan Plateau) and rectangle (tropical Indian Ocean) in panel c

Full size image
Fig. 8
figure 8

Sum of individual physical process in all regions that contribute to the annual (left panel) δ18Op response in the MPWP (units: permille), as well as responses during DJF (middle panel) and JJA (right panel), including changes in source composition (row 1), rainout (row 2), condensation (row 3), and source locations (row 4)

Full size image

We find that negative δ18Op over the tropical Indian Ocean and its surrounding land masses is mainly driven by condensation processes (Fig. 8g-h-i) followed by the impact of source location (Fig. 8j-k-l). We also find that condensation is (together with source composition) the primary factor for more positive δ18Op over the TP during DJF (Fig. 8b-h) and (together with source location) for negative deviations during JJA (Fig. 8i-l). Annual variations in δ18Op over the TP are primarily influenced by changes in source location (Fig. 8j). By quantifying the relative contributions of the four physical processes from the 8 considered regions, we conclude that the significant negative δ18Op (annual, DJF and JJA) during the MPWP in the Tropical Indian Ocean is mainly attributed to local condensation processes in the TIO region (Figs. S1C2, S2C2 and S3C2), although source location changes in other regions outside the TIO also contribute (Figs. S1-S2-S3, row5).

3.3 Tropical Atmospheric circulation (Hadley and Walker cells)

3.3.1 A weakened and expanded Hadley circulation

The Hadley Circulation in the MPWP is generally weakened compared to the PI period, and its spatial variation represented by mass stream function is not uniform, characterized by opposite changes in its tropical and subtropical components (Fig. 9). Specifically, anomalous counterclockwise and clockwise circulations are present in the tropics of the Northern and Southern Hemispheres, respectively (shading Fig. 9 left). This is contrary to the spatial distribution of climatological Hadley circulation (i.e., counterclockwise tropical circulation in the Southern Hemisphere, clockwise tropical circulation in the Northern Hemisphere) (contours, Fig. 9 left). In contrast, in the subtropics of both hemispheres anomalous circulation is of the same sense of rotation as the climatological Hadley circulation., i.e. clockwise in the Northern Hemisphere, counterclockwise in the Southern Hemisphere, with the change in the Northern Hemisphere dominating (shading, Fig. 9 left). A weakened mass streamfunction in the tropics of both hemispheres leads to reduced intensity of Northern and Southern Hadley cells; on the other hand, intensified mass stream function in the subtropics of both hemispheres leads a MPWP Hadley circulation that is shifted poleward compared to the PI (Fig. 10).

Fig. 9
figure 9

Leftmost panel: mass stream function used to quantify differences in Hadley circulation (HC) during the MPWP (shading; \({10}^{10}\) kg\({\cdot s}^{-1}\)) compared to the PI (contours; \({10}^{10}\) kg\({\cdot s}^{-1}\)). Blue solid (sky blue dashed) contours indicate absolute stream function of clockwise (counterclockwise) Northern (Southern) Hadley cell, shadings illustrate changes. Remaining panels: impact of differences in diabatic processes (shadings) in the tropics (column 2: \(\delta Q\), \({10}^{-6}\) K\({\cdot s}^{-1}\) ) on HC (colored contours, same as the shadings in leftmost panel) and separate contributions of dynamics (column 3: \(\delta {Q}_{DY}\)) and thermodynamics (column 4: \(\delta {Q}_{TH}\)) due to changes in vertical motion and dry static stability, respectively. Areas with a significance above the 5% level are stippled

Full size image
Fig. 10
figure 10

a) Hadley cell boundaries shown via the northern Hadley Cell extent (NHCE) and Southern Hadley Cell extent (SHCE) in the two climate states and b) poleward shift of southern and northern edges of Hadley Circulation during the MPWP compared to PI

Full size image

As mentioned above, both the weakened intensity of Hadley circulation and its poleward shift are due to spatially non-uniform response of the mass stream function to the surface warmth of the MPWP. Therefore, the physical processes explaining the spatially non-uniform response of the mass stream function serve as a logical explanation for the weakening of the Hadley circulation and expansion of its boundaries during the MPWP. Tropical diabatic processes can adequately characterize the climatology of the Hadley circulation for PI and MPWP periods across the annual cycle (Fig. S4); i.e., diabatic heating coincides with tropical rise (Fig. S4, warm colors) and extratropical diabatic cooling matches subtropical sinking (Fig. S4, cool colors).

Moreover, spatial distribution of changes in diabatic processes during the MPWP compared to the PI can usefully depict the anomalous regional meridional cell characterized by anomalies in the mass stream function (Fig. 9, 2nd column). The response of atmospheric diabatic processes to MPWP warmth is not uniformly distributed in the meridional session (from south to north). There is extratropical Southern Hemisphere cooling, tropical Southern Hemisphere heating, Northern Hemisphere cooling south of 10\(^\circ\)N, tropical Northern Hemisphere heating, and extratropical Northern Hemisphere cooling. As the atmosphere rises with heating and sinks with cooling, anomalous regional meridional cells thus develop from south to north in counterclockwise, clockwise, counterclockwise, and clockwise directions. Thus, heterogeneity of atmospheric diabatic processes in the meridional response to MPWP warmth explains the weakened intensity of the Hadley circulation and expansion of its boundaries across the year. Further decomposition of the change in atmospheric diabatic processes into two partial contributions − (1) dynamic contribution (\(\delta {Q}_{DY}\)) due to a change in circulation with no change in potential temperature (Fig. 9, 3rd column), and (2) thermodynamic contribution (\(\delta {Q}_{TH}\)) due to a change in potential temperature with no change in circulation (Fig. 9, 4th column) – shows that dynamical processes (\(\delta {Q}_{DY}\)) dominate spatial heterogeneity of tropical atmospheric diabatic processes in response to MPWP warmth. Thus, dynamical processes determine spatial heterogeneity of the HC anomaly, MPWP relative to PI, and as well are drivers of weakened intensity and extended boundaries of MPWP Hadley circulation across the year.

As we know, subtropical arid zones in both hemispheres correspond approximately to the sinking branch of the Hadley circulation. Therefore, it is expected that in the context of ongoing climate change migration of the Hadley circulation would lead to a poleward shift in the extent of the subtropical arid zone (e.g. Hu et al. 2018). To test this hypothesis for the MPWP we compare the aridity index (AI) for the two periods (Fig. 11). Obviously, the northern extent of the northern subtropical arid regions generally moves northward to the northern shores of the Mediterranean Sea. This is expected to impact on the distribution of vegetation in the region. Indeed, one PlioMIP2 model showed that MPWP savanna is expanded northward at the expense of the extent of the Sahara (Stepanek et al. 2020). Similarly, the extent of hyper-arid and arid zones in Central Asia increases (Fig. 11). In the annual and JJA condition, the northern extent of Hadley circulation shifts much more than the southern extent. For this reason, the poleward shift of the southern Hadley cell and its potential linkage to changes in the subtropical arid zone in the Southern Hemisphere are not addressed.

Fig. 11
figure 11

Aridity index (AI) for the two simulated climate states: PI (left panel) and MPWP (right panel). Blue curve in each plot outlines the Central Asia domain

Full size image

In addition, anomalous tropical clockwise circulation in the Southern Hemisphere, and anomalous counterclockwise circulation in the Northern Hemisphere, which weaken MPWP Hadley circulation, have common sinking branches near the equator (shading, Fig. 9, 1st column). These common sinking branches reduce ascending motion, and thus lead to decreased precipitation near the equator [~ 10 S°–10\(^\circ\)N] (Fig. 5b-e-h and c-f-i).

3.3.2 Strengthening and westward shift of Walker circulation over the tropical Pacific Ocean

In addition to analyzing differences in MPWP meridional atmospheric circulation with respect to today, we examine the tropical zonal atmospheric circulation (Walker circulation) in response to MPWP warmth. In the iCESM1.2-ITPCAS MPWP simulation we compare the PI Walker circulation over the tropical Pacific Ocean, which is characterized by the rising branch in the Indo-Pacific warm pool and by the sinking branch in the equatorial eastern Pacific Ocean (contours, Fig. 12, 1st column) to the circulation regime that establishes under MPWP climate conditions. Compared with the PI period, the MPWP annual mean Walker circulation is, overall, enhanced across the tropical Pacific Ocean (Fig. 12, 1st column). This enhancement is mainly due to the contribution of the overall intensification of Walker circulation during boreal summer (Fig. 12, 1st column). In contrast, for Walker circulation during boreal winter we see significant enhancement only for the ascending branch. We identify this enhancement during the boreal winter season as the main contributor to the enhanced ascending branch of annual mean Walker circulation (Fig. 12, 1st column). Overall enhancement in Walker circulation, and increased intensity of the ascending branch, would lead to an increase in strength, and to a westward shift, of Walker circulation. In brief, strengthening and westward shift of annual mean Walker circulation are caused by enhancement of Walker circulation in distinct regions in boreal summer and winter, respectively.

Fig. 12
figure 12

As Fig. 9, but for quantification of the Walker circulation (WC) during the MPWP (shading; \({10}^{10}\) kg\({\cdot s}^{-1}\)) compared to the PI (contours;\({10}^{10}\) kg\({\cdot s}^{-1}\)). We show impacts on MPWP WC associated with differences in diabatic processes in the tropics. These are partitioned into dynamic (\(\delta {Q}_{DY}\), 3rd column) and thermodynamic (\(\delta {Q}_{TH}\), 4th column) components to quantify the relative contribution of dynamic (\(\delta {Q}_{DY}\)) and thermodynamic (\(\delta {Q}_{TH}\)) processes

Full size image

Different expressions of diabatic processes in the MPWP compared to the PI serve to understand the strengthening of the Walker circulation and of the westward shift of its boundary. First, diabatic heating is in good agreement with the mean ascending branch of the Walker circulation, from the tropical Indian Ocean to the tropical western Pacific. In contrast, subsidence of Walker circulation in the eastern Pacific is spatially well matched with tropical diabatic cooling (Fig. S5).

Regional clockwise circulation anomalies are due to a rise of diabatic heating in the Indo-Pacific warm pool region and subsidence of cooling in the central-eastern Pacific; such clockwise circulation anomalies are superimposed on the climatologically clockwise Walker circulation in the Pacific, leading to a relatively increased intensity of the MPWP Walker circulation across the year (Fig. 12, 2nd column). There is a clear seasonal modulation of the intensity of diabatic heating in the MPWP in the Indian Ocean-West Pacific. In DJF heating is centered at 60\(^\circ\)E -120\(^\circ\)E, whereas during JJA the largest heating occurs in the regions from 60\(^\circ\)E-90\(^\circ\)E and from 150\(^\circ\)E-180\(^\circ\). This finding explains seasonal dependency of westward shift and of overall enhancement of Walker circulation, where westward shift occurs mainly in boreal winter while enhancement is mainly found during boreal summer. Decomposing tropical diabatic processes into the various contributors that shape a MPWP Walker circulation that is different from its modern counterpart, i.e. into dynamic (Fig. 12, 3rd column) and thermodynamic processes (Fig. 12, 4th column), shows that the anomalous diabatic heating and cooling, which determines enhancement of the Walker circulation and westward shift of its ascending branch, depends mainly on contributions from dynamic processes (Fig. 12, 3rd and 4th column).

3.4 Global and Atlantic Ocean Meridional overturning circulation

Figure 13a-b and c-d compare PI and MPWP patterns of global Meridional Overturning Circulation (MOC) and of Atlantic Meridional Overturning Circulation (AMOC) with each other. Well-known large-scale features of MOC and of AMOC are well represented in the simulations. This includes the characteristic northward transport of warmer surface waters towards deep-water formation regions in the Northern Hemisphere’s mid to high latitudes. There, the water cools and sinks, before being transported southwards as underlying cold water, finally reaching Southern Hemisphere mid-latitudes where a part of the water again and rises to the surface (Fig. 13a-b and c-d). For the MPWP simulation with iCESM1.2-ITPCAS we find an overall increase in the upper branches of both MOC and AMOC strength compared to the PI period (Fig. 13e-f). This finding is consistent with the enhancement of AMOC in most PlioMIP2 models due to closure of the Bering Strait (Zhang et al. 2021). It is noteworthy that we also find relatively higher Antarctic Bottom Water in the MPWP (Fig. 13e), indicating that enhanced circulation has not been limited to the uppermost 3000 m of the water column but extended far into the deep ocean.

Fig. 13
figure 13

Global meridional overturning circulation (MOC, left panel) and Atlantic meridional overturning circulation (AMOC, right panel) in units of Sverdrup simulated by iCESM1.2-ITPCAS for the two climate states: PI (top panel) and MPWP (middle panel). The anomaly between MPWP and PI is shown in the bottom panel. Positive values imply clockwise circulation. Areas with a significance above the 1% level are stippled

Full size image

4 Summary and conclusions

We used the water isotope-enabled Community Earth System Model (iCESM1.2- ITPCAS) to simulate large-scale features of the MPWP - a time, when distribution of continents and oceans and the level of CO2 concentrations, was similar to present day. Our findings do not only reproduce large-scale features of MPWP climate as observed from the PlioMIP2 MME. Results derived in our study with iCESM1.2-ITPCAS but also provide further insights. Highlights of the work presented here are: (1) we have mapped the spatial distribution of oxygen isotopes in precipitation δ18Op during this period and explained the isotopic response to MPWP warmth, revealing detailed mechanistic insights using the water tag-region method for areas with significant responses; (2) iCESM1.2-ITPCAS shows higher warmth at high latitudes compared to the PlioMIP2 MME; (3) our study provides a comprehensive mechanistic understanding for differences in temperature, precipitation and tropical atmospheric circulation in the MPWP with respect to today – these key indicators have been extensively studied in climate change research. Our key findings are summarized as follows:

  1. 1.

    A quantitative data–model comparison reveals reduction in the meridional thermal contrast due to heterogeneity of surface warmth during the MPWP, that is characterized by more pronounced warm anomalies at high latitudes than at tropical low latitudes. Compared to the PlioMIP2 MME, iCESM1.2-ITPCAS better simulates the, by models routinely underestimated, high latitude warmth. i.e., the high-latitude MPWP surface temperature simulated by iCESM1.2-ITPCAS is close to the magnitude derived from the reconstruction. Enhanced high-latitude warmth in iCESM1.2-ITPCAS is attributed to two potential factors: (1) its higher climate sensitivity compared to most PlioMIP2 models and (2) utilization of an ocean initialization approach distinctly different from that employed by most previous studies. These differences may result in a larger amplification of high-latitude warmth during the MPWP, that is caused by a modulation of downward clear-sky long wave radiation fluxes (\(\varDelta {T}_{\text{r}\text{l}\text{d}\text{s}\_\text{c}\text{l}\text{r}}\)) in iCESM1.2-ITPCAS compared to PlioMIP2.

  2. 2.

    iCESM1.2-ITPCAS simulates a MPWP that is wetter compared to the PI period. This finding is similar to results from the PlioMIP2 MME, but the precipitation anomaly is certainly larger in iCESM1.2-ITPCAS. Though precipitation is largely similar between our results and those from PlioMIP2 from the viewpoint of global precipitation, regional differences exist between iCESM1.2-ITPCAS and PlioMIP2 MME. In particular, iCESM1.2-ITPCAS simulates a drier equatorial region [~ 10 S°–10\(^\circ\)N] and wetter Southern Hemisphere tropics [~ 30 S°–10\(^\circ\)S]. Differences in regional precipitation responses between iCESM1.2-ITPCAS and PlioMIP2 MME are driven by different relative importance of physical processes for simulated climate patterns. iCESM1.2-ITPCAS emphasizes the control of dynamic processes (δDY), while the PlioMIP2 MME attributes regional precipitation anomalies with regard to PI mainly to thermodynamic processes (δTH).

  3. 3.

    Overall we find positive δ18Op anomalies over most of the world, with the exception of a more negative δ18Op that is observed over the tropical Indian Ocean and on surrounding landmasses. Decomposition of the δ18Op response to MPWP warmth reveals that changes in local condensation emerges as a dominant driver for pronounced negative δ18Op in this region.

  4. 4.

    The MPWP shows distinct differences in tropical zonal and meridional atmospheric circulations in comparison to PI. These include a weakening and a poleward shift in Hadley circulation, and a strengthening and a westward shift of the tropical Pacific Walker circulation. We attribute these changes in circulation patterns to tropical diabatic processes, which we consider to be a more fundamental explanation for MPWP circulation patterns than static stability. Furthermore, compared to thermodynamic effects (\(\delta {Q}_{TH}\)), changes in diabatic processes induced by circulation changes (dynamic effects, \(\delta {Q}_{DY}\)) play a crucial role in determining variations in diabatic processes (\(\delta Q\)) and determine the spatial response of the tropical atmospheric circulation.

  5. 5.

    Surface warmth during the MPWP reinforces subtropical aridity via a poleward shift of the subtropical arid zone that follows from poleward expansion of Hadley circulation during the MPWP. Meanwhile, northward contraction of the southern extent of the Sahara Desert may be related to the northward expansion of the North African monsoon region.

  6. 6.

    With iCESM1.2-ITPCAS we simulate enhanced global ocean and Atlantic ocean meridional overturning circulation during the MPWP that is consistent with the results of the PlioMIP2 MME.