Abstract
The effect of anthropogenic climate change in the ocean is challenging to project because atmosphere-ocean general circulation models (AOGCMs) respond differently to forcing. This study focuses on changes in the Atlantic Meridional Overturning Circulation (AMOC), ocean heat content (\(\Delta\)OHC), and the spatial pattern of ocean dynamic sea level (\(\Delta \zeta\)). We analyse experiments following the FAFMIP protocol, in which AOGCMs are forced at the ocean surface with standardised heat, freshwater and momentum flux perturbations, typical of those produced by doubling \(\hbox {CO}_{{2}}\). Using two new heat-flux-forced experiments, we find that the AMOC weakening is mainly caused by and linearly related to the North Atlantic heat flux perturbation, and further weakened by a positive coupled heat flux feedback. The quantitative relationships are model-dependent, but few models show significant AMOC change due to freshwater or momentum forcing, or to heat flux forcing outside the North Atlantic. AMOC decline causes warming at the South Atlantic-Southern Ocean interface. It does not strongly affect the global-mean vertical distribution of \(\Delta\)OHC, which is dominated by the Southern Ocean. AMOC decline strongly affects \(\Delta \zeta\) in the North Atlantic, with smaller effects in the Southern Ocean and North Pacific. The ensemble-mean \(\Delta \zeta\) and \(\Delta\)OHC patterns are mostly attributable to the heat added by the flux perturbation, with smaller effects from ocean heat and salinity redistribution. The ensemble spread, on the other hand, is largely due to redistribution, with pronounced disagreement among the AOGCMs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Knowledge of anthropogenically forced climate change in the ocean is vitally important for humanity, but projections are limited by uncertainties in key aspects, including change in the Atlantic Meridional Overturning Circulation (AMOC) (Weijer et al. 2020), and the geographical pattern of change in sea-level worldwide (Slangen et al. 2014). These two aspects and the relationship between them are the subjects of this study.
Atmosphere-ocean coupled general circulation models (AOGCMs) are standard tools used to project future climate and sea level. The sixth phase of the Coupled Model Intercomparison Project (CMIP6) provides a common framework to run experiments that start from a near-equilibrium (or ‘well spun-up’) preindustrial control state (piControl) and integrate forward in time, applying time-varying forcing agents for the past and future. While numerous forcing agents, including various greenhouse gases and anthropogenic aerosols, are expected to alter future climate in the real world, for mechanistic analysis it is useful to study the effects of idealised scenarios of carbon dioxide (\(\hbox {CO}_2\)) alone, which gives the dominant anthropogenic forcing. One standard scenario forces AOGCMs with \(\hbox {CO}_2\) concentrations that rise from preindustrial levels at 1% \(\hbox {year}^{-1}\), called ‘1pctCO2’ (Eyring et al. 2016).
Even though 1pctCO2 is an idealised and simplified scenario of climate change, it is challenging to unpick the reasons why models give different responses. There are both atmospheric and oceanic causes of model diversity in ocean climate change. The global surface temperature increase that restores the top of atmosphere radiative balance given an instantaneous doubling of \(\hbox {CO}_2\) (the so-called ‘effective climate sensitivity’) differs across models. Cloud feedbacks are thought to be a key cause of differing climate sensitivities of models (e.g. Zelinka et al. 2020). The ocean component of each AOGCM has a unique sensitivity to changes in surface fluxes of heat, freshwater or momentum (i.e. wind stress). The unique sensitivity could arise from biases in preindustrial state, differing representations of ocean transport processes and other technical factors.
In addition, the different control climates of models (Bouttes and Gregory 2014), especially sea surface temperature (SST) biases (He and Soden 2016) and wind field biases (Lyu et al. 2020) are also thought to play a role in causing the spread of surface flux changes and hence sea-level projections in particular. This line of thinking has been investigated with sets of experiments in which a single ocean model is forced with multiple choices of surface boundary conditions like SST (Huber and Zanna 2017) or surface fluxes (Bouttes and Gregory 2014). These studies find that it is possible to mimic aspects of the across-model diversity of ocean circulation by forcing a single model with a range of boundary conditions.
A complementary approach was proposed through the Flux Anomaly Forced Model Intercomparison Project (FAFMIP), which applies consistent flux perturbations to a variety of AOGCMs (Gregory et al. 2016; Couldrey et al. 2021) or ocean-only general circulation models (OGCMs) (Todd et al. 2020). FAFMIP forcing emulates 1pctCO2 forcing, except that the oceans are forced directly with flux perturbations rather than changing greenhouse concentrations. The FAFMIP design comprises five experiments: one steady-state control experiment with an extra passive tracer, three experiments with individually applied flux perturbations, and one experiment with all perturbations applied simultaneously (Gregory et al. 2016). (Further details are discussed in Sect. 2.2.)
FAFMIP experiments are able to account for the role of ocean model diversity in causing ensemble spread in a more consistent way than was previously possible. Results from these experiments have shown that applying the same flux perturbations to different models reproduces an ensemble spread similar to that of 1pctCO2 runs, suggesting that diversity in ocean models is (at least part of) the cause (Todd et al. 2020; Couldrey et al. 2021). In the present paper, we analyse FAFMIP experiments with a wider set of AOGCMs than was previously available to examine the relationship of heat flux forcing to sea-level change and AMOC change.
Global mean thermosteric sea level rise, due to thermal expansion of a warming ocean, makes up 21–43% of the total global mean sea-level rise (GMSLR) projected for the years 2081–2100 (Hermans et al. 2021) in a mid-range emissions scenario (SSP2/RCP4.5). Ocean heat content change (\(\Delta\)OHC) is therefore a crucial cause of sea-level rise. The melting of land ice (glaciers and ice sheets) adds mass to the ocean (as freshwater), and makes up most of the remainder of GMSLR.
Regional sea-level change is highly nonuniform and can be very different from the global mean because of a mixture of ocean and climate dynamics, and solid-Earth processes. Ocean dynamic sea level, \(\zeta\), is defined at each time and location in these experiments as
where \(\eta\) is the local sea-surface height relative to a surface of uniform geopotential (the geoid) and \({\overline{\eta }}\) is the area mean averaged over the global ocean. Under \(\hbox {CO}_{{2}}\) forcing, AOGCMs experience a radiative imbalance that warms the climate and causes sea-level changes. The dynamic sea-level change (\(\Delta \zeta\)) is
which is the local \(\eta\) change with its global area mean change subtracted. Even in moderate emissions scenarios like RCP 4.5, by the period 2081–2100 the spatial variability of \(\Delta \eta\) is large, such that some locations experience a local sea-level change greater than double the global mean change (Gregory et al. 2016). These strong deviations from the global mean change are brought about by the distribution of surface flux changes and by changes in ocean currents (and consequently perturbed ocean transports of heat and salinity), including the AMOC.
The AMOC is a key process of the climate system because of its role in converting warm and saline low-latitude surface waters into cold, dense deep waters. The representation of the AMOC, in terms of its strength and structure, differs markedly in climate models, as well as its projected weakening by the end of the \(21^{{\mathrm{st}}}\) Century (Weijer et al. 2020). An anticorrelation between the preindustrial, steady state AMOC strength and its future change under anthropogenic climate change was noted in earlier AOGCMs (Gregory et al. 2005) that still holds for the current generation (Weijer et al. 2020), a relationship that remains to be explained. The diversity in projected AMOC decline is a leading-order cause of uncertainty in future sea-level change in the North Atlantic (NA) (Yin et al. 2009; Bouttes and Gregory 2014). Efforts to understand the functioning of the AMOC are therefore vital to constrain projections of the effects of future climate change.
In the North Atlantic, northward flowing surface waters experience intense evaporation in the low latitudes followed by intense cooling at high latitudes and thereby become dense North Atlantic Deepwater (NADW), which sinks and flows south in the oceanic abyss. While deep waters are formed in the North Atlantic, they are thought to be partly returned to the upper ocean diffusively into the low-latitude thermocline (Munk and Wunsch 1998; Kuhlbrodt et al. 2007) and mostly in the Southern Ocean, where strong westerly winds tilt isopycnals upwards (Gnanadesikan 1999; Nikurashin and Vallis 2012). AMOC changes have the potential to be forced under future anthropogenic climate change via several avenues.
Previous studies have examined the sensitivity of the AMOC to these different forcings in individual models (e.g. Bouttes and Gregory 2014; Garuba and Klinger 2018; Dias et al. 2020b; Cael and Jansen 2020), the small original FAFMIP ensemble (Gregory et al. 2016) and pairs of models (Todd et al. 2020; Jin et al. 2021a). Such studies suggest that the anomalous heat flux is the main driver of AMOC change under greenhouse gas forcing (in the absence of large freshwater additions via glacial melt, which is beyond the scope of this study). While models agree that heat flux forcing weakens the AMOC, the degree of the decline is uncertain across models (Gregory et al. 2016; Todd et al. 2020). In addition, the AMOC response to freshwater and wind stress forcing is also unclear. Gregory et al. (2016) noted no significant AMOC changes in response to freshwater and momentum flux perturbations using the original AOGCM ensemble, but Todd et al. (2020) found some small changes using a different suite of models.
Freshwater and momentum flux forcing experiments have produced a variety of AMOC responses, owing to differences in the types of models used, details of the forcing, and other factors. Some studies find that freshwater cycle amplification strengthens the AMOC (e.g. Cael and Jansen 2020; Todd et al. 2020). While Garuba and Klinger (2018) found evidence of weakening in an ocean-only model study, subsequent work using coupled simulations found that heat fluxes rather than freshwater fluxes drive AMOC weakening (Garuba and Rasch 2020). Recent studies employing an idealised doubling of southern hemisphere westerly wind stress magnitude have shown AMOC strengthening (Lüschow et al. 2021), as well as a transient AMOC strengthening and subsequent return to a weakened state (Lohmann et al. 2021). Using less intense momentum forcing, Todd et al. (2020) found that the AMOC response to wind stress perturbation was generally weak, showing changes of inconsistent sign across their AOGCM ensemble. In this work, we compare the magnitude of AMOC responses to heat, freshwater and momentum flux forcing. We focus much of our analysis on the response to heat flux forcing, since we expect it to produce the strongest ocean responses; in terms of AMOC strength, ocean heat content and sea level (Gregory et al. 2016; Couldrey et al. 2021).
To investigate the sensitivity of the AMOC to heat flux perturbation in more detail, with more models, in this paper we propose and demonstrate two further FAFMIP experiments. These modify the heat flux forcing in the North Atlantic only, as described in Sect. 2.2. In this work, we use the both original and the new FAFMIP experiments to address the following questions: (1) How does the AMOC respond to perturbations to fluxes of heat, freshwater and momentum? (2) To what extent is the AMOC sensitive to heat flux forcing in the North Atlantic versus elsewhere? (3) Is the spread of AMOC weakening across different models related to the spread of the heat input into the North Atlantic or to interior processes? (4) How does a weakened AMOC affect the global distribution of ocean heat content change? (5) How does a weakened AMOC affect patterns of regional dynamic sea-level change?
A description of the experimental setup, analytical methods and models is given in Sect. 2. Then, we assess the ensemble’s AMOC responses to the different atmosphere-ocean flux perturbations in Sect. 3. Some possible causes of the ensemble spread of AMOC weakening are explored in Sect. 4. The global distribution of ocean heat content change (\(\Delta\)OHC) is described in Sect. 5. The connection between the AMOC change and regional dynamic sea-level change in three key regions (the North Atlantic, North Pacific and Southern Ocean) is described in Sect. 6, and its contributions from heat addition, heat redistribution, salinity redistribution and changes in ocean mass loading are determined. The conclusions are laid out in Sect. 7.
2 Methods
2.1 Dynamic sea level
Following recent naming conventions, \(\eta\) in (1) is ‘sterodynamic sea level’ (Gregory et al. 2019). Dynamic sea level, \(\zeta\), reveals local deviations of sea level (that may be positive or negative) relative to the global mean, because it has an area mean of zero by definition. Nonzero values of \(\zeta\) are caused by ocean circulation and horizontal density gradients. \(\zeta\) is the variable ‘zos’ in CMIP terminology (Griffies et al. 2016).
In CMIP6 1pctCO2 experiments, the addition of freshwater into the ocean from melting land ice is not modelled and so \(\overline{\Delta \eta }\) in (2) is purely due to global mean thermosteric sea-level change. Note that because the global mean of \(\Delta \zeta\) is zero by definition, local \(\Delta \zeta\) is negative wherever \(\Delta \eta\) is smaller than the global-mean thermosteric sea level rise \(\overline{\Delta \eta }\), even if local \(\Delta \eta\) is zero or positive. The dynamic sea-level anomaly \(\Delta \zeta\) can readily be calculated in CMIP experiments by subtracting the ‘zos’ field in a transient experiment (like 1pctCO2) from a steady-state control run (like piControl).
2.2 Experiments
The FAFMIP protocol (Gregory et al. 2016) recreates certain effects of 1pctCO2 forcing by applying perturbations that are common across models directly to the ocean surface. The surface flux perturbations are derived from the multi-model mean changes in atmosphere-ocean fluxes of heat, freshwater and momentum, averaged over years 61–80 (covering the time of atmospheric \(\hbox {CO}_2\) doubling relative to preindustrial levels at year 70) in 1pctCO2 experiments. Since the perturbations are applied to the sea-water surface, the atmosphere and sea ice are not directly affected by the perturbations, but indirect effects can result from the redistribution of heat and freshwater. In all the FAFMIP forced experiments (freshwater and wind stress as well as the heat flux forced varieties), changes to all the surface fluxes (of heat, freshwater and momentum) can result from SST change caused by the imposed perturbation. The redistribution feedback (described later in this section) is such a phenomenon.
The present study analyses output from seven FAFMIP experiments, described below, in Table 1 and in Appendix A.1. Five of these experiments constitute the original FAFMIP protocol (Gregory et al. 2016). We hereby define the other two as additions to the FAFMIP protocol, namely faf-heat-NA50pct in Tier 1, and faf-heat-NA0pct in Tier 2.
Experiment 1: faf-passiveheat This experiment functions as a control (like piControl) because its climate is not forced and it experiences only internally generated variability. However, it also features a passive tracer, \(T_A\), that is initially zero everywhere in the ocean and passive heat is added at the ocean surface via a flux, F, whose annual mean is shown in Fig. 1a. The tracer is advected and diffused around the ocean via the same schemes that each model uses to transport temperature, T. The tracer does not affect ocean density and therefore does not change ocean transports, so it is called ‘passive heat’. Although the tracer surface flux is applied in the same way to each model, the \(T_A\) distribution in the ocean will be different across models because of each model’s unique unperturbed ocean transport.
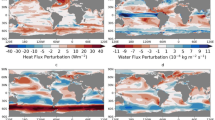
Annual mean of the heat flux perturbation in 100pct, with the North Atlantic (NA) box region denoted within the black dashed line (80 \(^\circ \hbox {W}\)–10 \(^\circ \hbox {E}\), 30–65 \(^\circ \hbox {N}\)). a In the 50pct and 0pct experiments the heat flux perturbation within the NA box is reduced by half (b) and to zero (c), relative to the 100pct experiment, while being unchanged elsewhere. Annual means of the perturbations to freshwater (d), eastward momentum (e) and northward momentum fluxes (f)
Experiment 2: faf-heat, or 100pct In this experiment, the perturbation heat flux, F (Fig. 1a), is added to ocean temperature, T. It is applied directly to the ocean water surface as an external heat flux forcing (rather than a radiative forcing, as in greenhouse gas experiments). The perturbation is strongly positive (downward, i.e. heating the ocean) in the North Atlantic and Southern Ocean. To prevent the atmosphere from absorbing the heat imposed by F, it is decoupled from T and instead sees the surface field of a redistributed temperature tracer (\(T_R\)) to calculate the interactive atmosphere-ocean heat flux (Q). This second tracer is initially equal to T and does not feel the added heat from F, but is otherwise transported around the ocean like T. The perturbation flux causes T (and therefore ocean density) to change, which changes ocean heat transports, which in turn change the distribution of \(T_R\). Coupling with an interactive atmosphere is maintained because the heat flux Q (calculated using \(T_R\)) is applied to both T and \(T_R\). The coupling with sea ice is modified in the same way as for the atmosphere. Further details about F and \(T_R\) are included in Appendix A.1.
This experiment also features the added temperature tracer, \(T_A\), whose initial value is zero everywhere and whose surface boundary condition is F, as in faf-passiveheat. The total temperature T is the sum of added and redistributed temperature,
The distribution of \(T_A\) in faf-heat will differ from that of faf-passiveheat because the former experiences transient climate change (and changing ocean heat transports) while the latter does not. The difference of \(T_A\) between the two experiments therefore reflects the part of oceanic added heat storage that is not passive, i.e. the ‘active’ redistribution of added heat.
The use of \(T_A\) and \(T_R\) creates three main advantages over conventional radiative forcing experiments. First, the atmosphere can be decoupled from the imposed perturbation allowing for common heat flux forcing to be directed straight into the ocean. Second, the ocean heat content that was already in the system prior to the perturbation can be discriminated from the heat added to the system by the perturbation. Third, the same surface heat flux perturbation is applied in all AOGCMs, rather than being determined by individual AOGCMs’ responses to atmospheric radiative forcing. This experiment is faf-heat in CMIP6 terminology, but is also called 100pct in this study for conciseness and to reflect the strength of the forcing in the North Atlantic relative to the other two heat flux experiments, described later in the section.
Coupling the atmosphere to \(T_R\) instead of T and applying a strong heat flux F into the North Atlantic has the expected effect of weakening the AMOC, but also creates an unintended feedback. The perturbation increases T in the subpolar North Atlantic by increasing \(T_A\), which reduces deepwater formation by convection and weakens the overturning. The weakened overturning reduces the northward transport of heat from the tropics to the subpolar North Atlantic. This causes \(T_R\) to increase in low latitudes with a corresponding decrease in subpolar latitudes because the weakened overturning transports less tropical water northward. At steady state, the subpolar North Atlantic ocean is warmer than the atmosphere and so the downward heat flux, Q, is negative i.e. the ocean warms the atmosphere. In 100pct, the atmosphere sees only the cold anomalies of \(T_R\) and not the added heat of \(T_A\) at high latitudes. Because the air temperature has not changed, there is reduced heat loss by the subpolar Atlantic ocean and a positive heat flux anomaly, \(\Delta Q\), results. Crucially, the extra heat input by \(\Delta Q\) further weakens the AMOC and the northward heat transport, which further drives down \(T_R\), creating a positive feedback and causing \(\Delta Q\) to grow.
This so-called ‘redistribution feedback’ likely occurs in conventionally coupled experiments like 1pctCO2, although in 100pct it may be double counted because its effect is already included in F (Gregory et al. 2016). The result is that AMOC weakening is more intense in 100pct than in 1pctCO2 because \(F + \Delta Q\) is greater than the intended F in the North Atlantic. Gregory et al. (2016) note that the feedback approximately doubled the intended heat input into the North Atlantic in their four-model ensemble and that \(\Delta Q\) may be specific to each model. Nevertheless, the forcing strategy is still valuable because (1) it enables models to be forced with standardised flux forcing, (2) the effects of the redistribution feedback are mostly confined to the North Atlantic, (3) the feedback, although unintended, constitutes one type of model-specific response to common forcing that FAFMIP seeks to examine, and (4) it makes little difference to global \(\Delta\)OHC although it can be regionally important (Gregory et al. 2016). The diversity of \(F + \Delta Q\) will be examined in this work.
Experiment 3: faf-heat-NA50pct, or 50pct A modified version of the 100pct heat flux perturbation is applied in this experiment, wherein the heat input into North Atlantic is halved relative to the 100pct experiment. A rescaling region is defined as the area 80 \(^\circ \hbox {W}\)–10 \(^\circ \hbox {E}\), 30–65 \(^\circ \hbox {N}\) (the ‘NA box’ enclosed by black dashed lines in Fig. 1a–c). For this experiment, the flux perturbation inside the rescaling region is multiplied by 0.5 (Fig. 1b). The perturbation outside the rescaling region is unchanged relative to the 100pct experiment. The purpose of this experiment is to test whether the Atlantic Meridional Overturning Circulation responds linearly to North Atlantic heat input. In addition, given that the redistribution feedback described earlier is thought to double the North Atlantic heat input intended via F, the 50pct experiment may offer a way to apply a total heat flux similar to what was intended in 100pct. This experiment is faf-heat-NA50pct in CMIP6 terminology, but is also called 50pct in this study.
Experiment 4: faf-heat-NA0pct, or 0pct This experiment modifies the 100pct flux perturbation by applying zero flux in the region between 80 \(^\circ \hbox {W}\)–10 \(^\circ \hbox {E}\), 30–65 \(^\circ \hbox {N}\) (enclosed by black dashed lines in Fig. 1a–c). This experiment is faf-heat-NA0pct in CMIP6 terminology, but is also called 0pct in this study.
Experiment 5: faf-water The freshwater flux perturbation is derived from the ‘wfo’ CMIP diagnostic, which includes water fluxes due to precipitation, evaporation, river inflow and sea-ice/seawater exchange (and does not include land ice melt). The perturbation mainly intensifies the climatological fields of evaporation-minus-precipitation, consistent with the “wet gets wetter, dry gets drier” pattern (Held and Soden 2006). The mid latitudes feel increased evaporation (by about 10%), while freshwater input is enhanced elsewhere (also by about 10%), in the equatorial Pacific, the Southern Ocean, the Arctic Ocean and the high latitudes of the North Pacific and Atlantic Oceans (Fig. 1d). The perturbation has a very small global annual average and mainly redistributes freshwater.
Experiment 6: faf-stress The main characteristic of the wind stress perturbation is the enhancement and southward shift of the Southern Ocean westerlies (Fig. 1e, f). The perturbation increases the eastward wind stress between 45 and 65 \(^{\circ }\hbox {S}\) by approximately 10%. There are smaller effects in the mid latitudes in both eastward and northward wind stress (Fig. 1e, f). The perturbation does not affect sub-grid scale parameterisation schemes that depend on wind or ice stress, and is only applied to the ocean surface.
Experiment 7: faf-all The 100pct, faf-water and faf-stress perturbations are all applied simultaneously in this experiment. This experiment is used to investigate whether the perturbations interact with each other. The ocean response to faf-all can be judged to be linear if it is statistically indistinguishable from the linear sum of the responses to 100pct, faf-water and faf-stress.
2.3 Calculation of forced changes
This study seeks to describe and account for climatic changes in the ocean expected at the end of the current century. FAFMIP experiments aim to explore the unequilibrated state of the climate under steadily increasing \(\hbox {CO}_2\) in 1pctCO2 experiments. The 1pctCO2 scenario (exponentially rising greenhouse gas concentration) creates radiative forcing that increases approximately linearly in time, whereas FAFMIP forcing is time invariant. Forced changes are calculated here as the difference between the final decade mean (averaged over years 61–70) of a perturbation experiment relative to the final decade mean of the control (faf-passiveheat). The time-integral of 100 years of 1pctCO2 forcing is roughly equivalent to 70 years of FAFMIP forcing. These anomalies relative to the control are denoted using \(\Delta\), e.g. \(\Delta \zeta\) for the dynamic sea-level change.
Decadal averages are calculated to smooth out the effects of unforced natural variability, since the object of this study is the change in the climate state. A forced change is considered significant if the difference between an experiment and control decade is larger than double the decadal standard deviation of the control experiment. A range of \(\pm 2\) standard deviations represents approximately a 95\(\%\) interval for normal distributions. Locations with insignificant \(\Delta \zeta\) are set to zero for plotting purposes (i.e. assumed equal to the global mean thermosteric sea-level change). This step is performed before the ensemble mean is calculated. Where linear regressions and correlations are calculated, a relationship is taken to be significant if the p value is less than 0.05 (i.e. a 95% confidence level).
Fields of ‘zos’ by definition have zero global area mean, and in cases where the field was provided with a nonzero area mean, the mean was removed. Following recent conventions (Gregory et al. 2019; Couldrey et al. 2021), we decompose the dynamic sea-level change, \(\Delta \zeta\), into three components
where \(\Delta \zeta _T\) is the thermosteric part (due to temperature change), \(\Delta \zeta _S\) is the halosteric part (due to salinity change) and \(\Delta \zeta _M\) is the manometric part (due to the local time-mean change in mass per unit area of the ocean). Together, the sum of \(\Delta \zeta _T\) and \(\Delta \zeta _S\) is the steric part of the dynamic sea-level change, i.e. due to the change in seawater column density. \(\Delta \zeta _T\) is calculated using
as the depth integral (from the surface, \(\eta\), to the full ocean depth, H with a layer thickness, dz, all in units of metres), of the temperature change (\(\Delta T\), \(^{\circ }C\)) multiplied by the seawater thermal expansion coefficient (\(\alpha\), \(^{\circ }C^{-1}\)) with the global mean thermosteric change, \(l_{\theta }\), subtracted. Different temperature tracers (i.e. the total temperature T, or its added and redistributed components \(T_A\) and \(T_R\)) may also be used in (5) to partition the thermosteric change into parts due to temperature addition and redistribution. Similarly, \(\Delta \zeta _S\) is calculated using
where \(\beta\) is the dimensionless haline contraction coefficient, \(\Delta S\) is the salinity change, a minus sign converts contraction to expansion for comparability with \(\Delta \zeta\) and \(\Delta \zeta _T\) with the global mean halosteric change, \(l_{S}\), subtracted. Unlike \(\Delta \zeta _T\), subtracting the global area mean halosteric change has only a negligible effect on \(\Delta \zeta _S\) because the total ocean salinity change is negligible in these experiments for all AOGCMs. \(\alpha\) and \(\beta\) were calculated using the decade mean fields of temperature and salinity from the final decade of the control experiment.
The manometric component, \(\Delta \zeta _M\), is found by rearranging (4) and subtracting the two steric components (\(\Delta \zeta _T\) and \(\Delta \zeta _S\)) from \(\Delta \zeta\). This solution is satisfactory for AOGCMs, but in the real world other components of dynamic sea level are important. Real world effects that are not modelled in these experiments are the changes due the inverse barometer effect, the addition of ocean mass due to land ice melt, and gravitational, rotational and deformational effects due to the rearrangement of the planet’s mass (see Couldrey et al. 2021, their Section 2.3, for more details). The manometric component would have a nonzero global area mean if there were a substantial change in the global ocean mass, but most ocean GCMs do not simulate the global ocean mass balance (in particular, because they are Boussinesq, and because they do not include ice sheets). Since this study is focused on the spatial patterns of sea-level change, not its global mean, \(\Delta \zeta _M\) is shown here with its area mean removed throughout. In practice, this step makes a negligible difference to plots of \(\Delta \zeta _M\).
2.4 Decomposition of thermosteric sea-level change
Dynamic sea-level change can be conceptually decomposed into ‘added’ and ‘redistributed’ components. The combined action of all processes that affect heat transport, including resolved and parameterised advection, diffusion and convection, is symbolically denoted as \(\mathrm {\Phi }\), the transport operator, following Gregory et al. (2016) and Couldrey et al. (2021). The convergence of temperature due to the three-dimensional resolved velocity field, \({\textbf {u}}\), and parameterised subgrid-scale transport processes, \({\textbf {P}}\), is represented symbolically using the transport operator acting on the temperature enclosed within parentheses as \(\mathrm {\Phi }(T)=-\nabla \cdot ({\textbf {u}}T+{\textbf {P}})\). The unperturbed, steady-state ocean temperature, \({\overline{T}}\), and transport, \(\overline{\mathrm {\Phi }}\), are calculated as long term averages (denoted by overlines) over a quasi-steady state simulation such as faf-passiveheat. At steady state, the interior ocean temperature and transport only fluctuate through stationary, internally generated variability and so the time mean convergence of subsurface unperturbed temperature, \(\overline{\mathrm {\Phi }}({\overline{T}})\), is zero.
Transient climate change experienced by forced climate simulations causes the atmosphere-ocean fluxes to change, which cause anomalies in ocean temperature, \(T'\), and transport, \(\mathrm {\Phi }'\), relative to the unperturbed state, denoted with primes. Consequently, the convergence of heat, \(\mathrm {\Phi }(T)\) changes and becomes nonzero, causing ocean temperature to change by
where \([\overline{\mathrm {\Phi }}+\mathrm {\Phi }']({\overline{T}}+T')\) represents the action of both the unperturbed and perturbed transport on the unperturbed and perturbed temperature. The term \(\overline{\mathrm {\Phi }}({\overline{T}})\) does not appear because it is zero.
Five causes of temperature change are revealed in (7): F, the surface heat flux perturbation, ΔQ, the redistribution feedback heat flux, \(\overline{\mathrm {\Phi }}(T')\), transport of anomalous temperature by unperturbed transport; \(\mathrm {\Phi }'({\overline{T}})\) ocean transport anomalies redistributing unperturbed temperature and \(\mathrm {\Phi }'(T')\), the anomalous transport acting on perturbed temperature. The temperature change T' is the sum of added and redistributed temperature changes, so \(\overline{\mathrm {\Phi }}(T')\) and \(\mathrm {\Phi }'(T')\) each have an added and a redistributed component. Initially, the added components of these terms are dominant (appendix of Couldrey et al. 2021). We perform this decomposition only in the experiments where the heat fluxes are perturbed directly (100pct, 50pct and 0pct, Sect. 2.2).
The added and redistributed temperature diagnostics allow for the three contributions from (7) to dynamic sea-level change to be diagnosed. The total thermosteric sea-level change due to all three convergences of temperature in (7) is calculated using ocean temperature, as in (5). The sea-level change due to the storage of passive temperature, \(\Delta \zeta _{TP} \: (\mathrm{from} \: F+\overline{\mathrm{\Phi}}(T_A))\), is
where \(T_A\) is the added temperature in faf-passiveheat and the global area-mean passive thermosteric change, \(l_{\theta P}\), is subtracted. Since added temperature is initialised from zero, its anomaly is simply the time mean of the \(T_{A}\) field in the final decade of faf-passiveheat.
The sea-level change due to redistribution of unperturbed temperature by perturbed transports, \(\Delta \zeta _{TR} \: (\mathrm{from} \: \Delta Q+\overline{\mathrm{\Phi}}(T_R)+\mathrm{\Phi}'(\overline{T})+\mathrm{\Phi}'(T_R))\), is
where \(\Delta {T_{R}}\) is the anomaly of \(T_{R}\) from one of the climate change runs (100pct, 50pct or 0pct) and T from faf-passiveheat (i.e. \(\Delta T_{R}=T_R-T\)). The global area-mean redistributed thermosteric change, \(l_{\theta R}\), is subtracted although it is negligibly small.
The effect of the perturbed transport redistributing added (or ‘active added’) temperature on sea level, \(\Delta \zeta _{TAA} \: (\mathrm{from} \: \mathrm{\Phi}'(T_A))\), is
where \(\Delta {T_{A}}\) is the difference between the added heat in 100pct and faf-passiveheat, and the global area-mean active added thermosteric change, \(l_{\theta AA}\), is subtracted. Note that this quantity can only be evaluated for the 100pct experiment, because faf-passiveheat was run with the 100pct heat flux as the added heat boundary condition. There are no passive runs equivalent to faf-passiveheat that use the 50pct and 0pct boundary conditions for passive tracers. It is useful to consider the active and passive contributions to added thermosteric sea-level changes together as the added sea-level change, \(\Delta \zeta _{TA}\), given by
where \(T_A\) is the added temperature in 100pct, 50pct or 0pct and the global area-mean added thermosteric change, \(l_{\theta A}\), is subtracted. As in \(\Delta \zeta _{TP}\), the added anomaly is simply the time mean \(T_{A}\) field in the final decade of 100pct, 50pct or 0pct.
2.5 Description of models used
This study analyses output from coupled atmosphere-ocean general circulation models, and different ensembles are used depending on the availability of output fields. Three models did not complete all seven experiments (FGOALS-g3, GISS-E2-R-CC, MPI-ESM1-2-HR).
Before being run as part of the 6th phase of CMIP, the FAFMIP experimental design was tested with four CMIP5-era models (CanESM2, GFDL-ESM2M, GISS-E2-R-CC, MPI-ESM-LR) and one CMIP3-era model (HadCM3) (Gregory et al. 2016). To date, one further CMIP5-era model (HadGEM2-ES) and 9 CMIP6-era models have performed FAFMIP experiments (ACCESS-CM2, CanESM5, CAS-ESM2-0, CESM2, FGOALS-g3, HadGEM3-GC31-LL, MPI-ESM1-2-HR, MIROC6 and MRI-ESM2-0). Previous analysis shows that there are no obvious systematic differences between the regional patterns of dynamic sea-level change across model eras (Couldrey et al. 2021), suggesting that output from all participant models can be analysed together as a single ensemble. The original purpose of the first FAFMIP simulations described by (Gregory et al. 2016) was to demonstrate the viability of the experimental design. Having fulfilled that purpose, we derive added value from those experiments by including them in this analysis, since the use of a large ensemble serves FAFMIP’s goal of explaining AOGCM diversity. A detailed comparison of the eras of AOGCMs is included in Sect. A.4.
While the spatial resolution of AOGCM ocean components varies across the ensemble, they all share the functional similarity that mesoscale activity, O(\(<100 \,\hbox {km}\)), is not fully resolved. The ocean components are relatively coarse resolution with an approximately 1-by-1 degree grid, O(\(\sim 110\)-by-110 km), and so mesoscale and finer-scale activity is parameterised. The finest resolution model (MPI-ESM1-2-HR) uses a 0.4-by-0.4 degree grid that can resolve some large eddies, in addition to an eddy flux parameterisation to capture unresolved activity. The number of vertical levels used by each model varies widely, with HadCM3 having the fewest (20) and HadGEM3-GC31-LL the most (75). Eddy-parameterising AOGCMs (i.e. those used here) often feature unrealistically weak boundary currents and gyre circulations which can lead to cold surface temperature biases (Roberts et al. 2019; Hewitt et al. 2020). These models are too coarse to resolve processes like convection and features like eddies, dense overflows and plumes, the actions of which must be represented by parameterisation schemes, which differ markedly across AOGCMs. Different choices about subgrid-scale parameterisations and parameter values are thought to cause diverse representations of ocean transports and phenomena like the AMOC (Danabasoglu et al. 2014).
3 AMOC weakening
The AMOC strength is calculated as the maximum of the time mean mass overturning streamfunction in the Atlantic between 500 and 2000 m depth and north of 30 \(^{\circ }\hbox {N}\). This is calculated from the CMIP variables ‘msftmz’ or ‘msftyz’ meridional-depth or y direction-depth overturning mass streamfunction (dependant on model grid), which is the depth and zonal/x-direction integral of the meridional/y direction ocean mass transport (see (Griffies et al. 2016), their Sect. I6 for more details). All ensemble members showed significant AMOC weakening in response to the 100pct forcing, whereas the faf-water and faf-stress forcing produced significant changes in only some of the models (Fig. 2a–c). The test for significance is described in Sect. 2.3. This ensemble reproduces the well-known relationship between control AMOC strength and AMOC weakening in response to greenhouse gas forcing (Gregory et al. 2005) (Fig. 2a). The slope of the linear fit (m) and correlation (r, see Appendix A.2 for details) between AMOC and \(\Delta\)AMOC from the 100pct heat flux perturbation experiment (\(m=\) \(-\)0.539 and \(r=\) \(-\)0.653, respectively) are similar to those found by Gregory et al. (2005) in response to \(\hbox {CO}_2\) forcing (\(m=-0.45\) and \(r=-0.74\)). Recent analysis of 16 AOGCMs (4 of which were excluded as outliers) found slightly stronger anticorrelations between AMOC and \(\Delta\)AMOC forced under various emissions scenarios (r between \(-0.80\) and \(-0.76\)) and a weaker relationship under abrupt greenhouse gas forcing (\(r=-0.51\), \(p=0.09\)) (Weijer et al. 2020). Clearly the anticorrelation appears across a range of types of twenty-first century forcing, with some small variations in statistical strength. It is interesting to note that the AMOC-versus-\(\Delta\)AMOC relationship (and the spread across the ensemble) has persisted across CMIP eras, despite continuous model development.
AMOC change versus control AMOC strength for 100pct a, faf-stress b, and faf-water c. AMOC change from 100pct versus AMOC change from faf-all d, with linear fit (purple line) and a 1–1 line (black dashed line). The AMOC change for models circled in red is not significantly outside internal variability. Linear fits and descriptive statistics are shown where a significant linear regression exists. n: number of models, m: slope, c: y intercept, r: correlation coefficient, p: p-value, e: standard error
Additionally, some models (MPI-ESM1-2-HR and MRI-ESM2-0) show continuous AMOC decline over the heat flux experiments, while the rest saturate and stabilise after the first decades (Fig. 3). There is a tendency for models with stronger control overturning to show more temporal variability, (Fig. 4d) which may be related to the AMOC-versus-\(\Delta\)AMOC relationship.
The wind stress and freshwater flux perturbations cause small AMOC changes that are not significant for most models (Figs. 2b, c and 3). This result agrees with the previous findings of Gregory et al. (2016) and Todd et al. (2020), and is reproduced across a larger ensemble of AOGCMs.
The wind stress perturbation slightly strengthens the AMOC in MPI-ESM1-2-HR and CESM2 (by 1.5 Sv and 2.0 Sv respectively), while it weakens the overturning in CanESM5 by 0.8 Sv (Fig. 2b). The faf-stress forcing is much weaker (Southern Ocean westerly wind stress increases by about 10%) than the idealised momentum perturbation (doubling of wind stress magnitude) applied to MPI-ESM1-2-HR by Lohmann et al. (2021). The difference of forcing probably explains why they obtained a larger strengthening, which proved transient on longer timescales. While the more intense wind stress perturbations studied in the literature tend to produce AMOC strengthening (Delworth and Zeng 2008; Lohmann et al. 2021; Lüschow et al. 2021), the faf-stress results from our 15-AOGCM ensemble highlight that weaker forcing, of the magnitude expected for \(\hbox {CO}_{{2}}\)-induced climate change during this century, produces mostly insignificant responses.
The freshwater perturbation produced moderate weakening (\(\simeq -\)4 Sv) in MIROC6 and GFDL-ESM2M, slight weakening (\(\simeq -\)1 Sv) in CanESM2 and HadCM3, and slight strengthening (\(\simeq +\)1 Sv) in HadGEM2-ES and HadGEM3-GC31-LL (Fig. 2c). Cael and Jansen (2020) argued that, all other things being equal, the equilibrium response of the AMOC to an intensification of the freshwater cycle will be a strengthening. The reason they gave was that intensified freshwater fluxes amplify the salinity contrasts that drive the AMOC. Our results echo previous findings that freshwater cycle amplification produces AMOC strengthening in some models and weakening in others (Todd et al. 2020). While we cannot account for these diverse responses fully, we highlight two possible factors: (1) the presence of coupled feedbacks in our AOGCMs that are absent from ocean only models used by Cael and Jansen (2020), Todd et al. (2020). (2) the short duration of our experiments is designed to emulate the expected transient response of the climate toward the end of the current century, which may differ from the responses at longer timescales (Cael and Jansen 2020; Lohmann et al. 2021).
The diverse responses to forcing highlight varying sensitivity of the models that is not well understood. Nevertheless, the key result is that the models show greater sensitivity to the heat flux forcing than to the other two fluxes. Crucially, the models lie close to a 1–1 line when the AMOC weakening in 100pct is plotted against the change in faf-all (Fig. 2d). This indicates that the AMOC change in faf-all, where all perturbations are applied simultaneously, results mostly from the heat flux perturbation and that the perturbations do not produce nonlinear interactions. This can also be seen by the similarity of the time series of AMOC anomalies in 100pct and faf-all (Fig. 3). Gregory et al. (2016) and Couldrey et al. (2021) inferred this result based on the similarity of the North Atlantic dynamic sea-level change in 100pct and 1pctCO2 experiments, and we are able to confirm it directly because we now have available the faf-all experiment. Clearly, the main action of greenhouse-gas forcing on the AMOC is via the heat flux rather than the other two fluxes. The rest of this study will therefore focus on the effects of heat flux forcing on the AMOC and ocean transports generally.
AMOC strength relative to the time mean control strength for 15 models (a–o) for different perturbations: wind stress only (black), freshwater only (blue), heat 100pct only (red solid), all three perturbations applied simultaneously (thick purple), heat 50pct only (red dashed) and heat 0pct (red dotted). Grey envelope indicates \(\pm 2SD\) where SD is the temporal standard deviation of annual mean AMOC strength from the control
The 50pct forcing, like the 100pct, produces significant weakening in all 13 models (Figs. 3, 4a). The regression slope of \(\Delta\)AMOC against AMOC in 50pct is not significant at the 95% confidence level (\(p=0.182\)), possibly because the decade average period was not sufficient to remove enough scatter from temporal variability. When the AMOC anomaly is calculated using the entire 70 year experiment duration, the relationship becomes significant (\(r=-0.607\), \(p=0.0278\)), but we focus our analysis using final decade mean differences for consistency with the FAFMIP aim of investigating the climate state at (rather than up to) the time of \(\hbox {CO}_2\) doubling (Gregory et al. 2016). The weakening in 50pct is slightly more than half the weakening in 100pct, indicated by the slope of 0.539 in Fig. 4b and the multi-model ensemble mean weakening (\(-5.1\,\hbox {Sv}\) for 50pct and \(-9.0\,\hbox {Sv}\) for 100pct, Fig. 5a). This shows that for this magnitude of heat flux forcing, the AMOC weakening is approximately linearly related to the heat input in the North Atlantic.
The 0pct heat flux perturbation causes significant, slight AMOC weakening (between \(-0.5\) and \(-3 \,\hbox {Sv}\)) in six models and AMOC strengthening in two models, CESM2 and HadGEM3-GC31-LL (by 1.9 and 3.5 Sv, Fig. 4c). In the strengthening models, it seems that the action of the perturbation in the high latitude Barents-Kara sea (Fig. 1d and Appendix A.1) stimulates an anomalous upward heat flux (out of the ocean) that spins up the overturning slightly (not shown). The ensemble as a whole shows that the AMOC is more sensitive to heat flux perturbations directed inside the NA box than outside, since the 0pct AMOC responses are either insignificant or smaller than the 50pct and 100pct responses. Taken together, the 100pct, 50pct and 0pct experiments show that AMOC change is approximately proportional to the heat flux perturbation applied within the (80 \(^\circ \hbox {W}\)–10 \(^\circ \hbox {E}\), 30–65 \(^\circ \hbox {N}\)) North Atlantic region, and the AMOC is comparatively little affected by heat flux perturbations elsewhere.
AMOC change versus control AMOC strength for 100pct in black and 50pct in red (a), \(\Delta\)AMOC from 100pct versus 50pct (with linear fit, black dashed line, and 0.5 gradient, red dashed line), AMOC change versus control AMOC strength for 0pct, (c) and AMOC strength versus control variability as the temporal standard deviation of annual averages, (d). Red circles in a, c indicate models with no significant change. Linear fits and descriptive statistics are shown. n: number of models, m: slope, c: y intercept, r: correlation coefficient, p: p-value, e: standard error
Next, we explore \(F+\Delta Q\) in these experiments and investigate whether \(\Delta Q \simeq F\) in 100pct, as suggested by Gregory et al. (2016). The imposed forcing in the North Atlantic stimulates a feedback that fluxes extra heat into the ocean from the atmosphere (the redistribution feedback, see Sect. 2.2). The result is that the total heat received by the ocean is not purely what is provided by F, the perturbation flux, but \(F+\Delta Q\), which includes the nonzero atmosphere-ocean heat flux change, \(\Delta Q\). Note that instead of averaging over the final decade (as in the rest of the analysis), \(\Delta Q\) is found by averaging over the full 70 year integration. This is justified because the state of the ocean (i.e. the AMOC change) in the final decade results from the cumulative effects of \(\Delta Q\) over the whole experiment, not just the \(\Delta Q\) in the final decade. Results are qualitatively similar if the final decade is used (not shown).
Total heat flux into the North Atlantic box (perturbation plus atmosphere-ocean heat-flux change, \(F+\Delta Q\)) versus the change in AMOC across the three heat flux experiments where \(\Delta Q\) is averaged over the full 70 years. a Each \(+\), \(\times\) and \(\bullet\) denotes an AOGCM, and different symbols denote experiments (100pct, 50pct, 0pct respectively). Bold magenta symbols show the multi-model ensemble mean for each experiment. Comparison of control AMOC strength and the slope of linear regression of \(\Delta\)AMOC versus \(F+\Delta Q\) from a, calculated for each model, b (left axis). Correlation between \(F+\Delta Q\) and \(\Delta\)AMOC for each model with insignificant correlations (\(p>\) 0.05) circled in red, b (right axis). Ratio of \(\Delta Q\) from 100pct and 50pct, horizontal dashed line indicates a ratio of 2, c. Ratio of \(\Delta Q_{50}\) and \(F_{50}\), horizontal dashed line indicates \(\Delta Q_{50}=F_{50}\). Horizontal dotted lines in c and d show the Model Ensemble Mean (MEM)
Looking at all three heat flux experiments together, we see that larger heat fluxes into the North Atlantic cause stronger AMOC weakening (Fig. 5a). The ensemble average of \((F+\Delta Q)/F\) is 2.0 for 100pct and 2.1 for 50pct, indicating that the feedback approximately doubles the intended heat input, as suggested by Gregory et al. (2016). For the majority of models, \(F_{50}+\Delta Q_{50}\) (subscripts indicate experiments) is closer than \(F_{100}+\Delta Q_{100}\) to \(F_{100}\) i.e. the red crosses lie closer than the black plus signs to the black dashed line in Fig. 5a. Therefore, the 50pct forcing may provide a total heat flux into the Atlantic that is more similar in magnitude to 1pctCO2 forcing than the 100pct forcing. This was the motivation for the 50pct experiment.
Regressing \(\Delta\)AMOC against \(F+\Delta Q\) from the three experiments for each model individually reveals an AOCGM-dependent slope of AMOC weakening per area-average North Atlantic heat input, i.e. the models’ AMOCs differ in their sensitivity to heat flux input (Fig. 5b, black symbols, left axis). There is a considerable spread in this sensitivity across the ensemble, with the most sensitive model, MRI-ESM2-0, having a sensitivity more than twice as large as the least, HadCM3 (\(-0.66\) and \(-0.25\) respectively, ensemble average \(-\)0.39 Sv \(\hbox {m}^{2}\,\hbox {W}^{-1}\)). Whereas the magnitude of the weakening (in Sv) correlates with the control AMOC strength (\(r=-0.65\) for 100pct, Fig. 4a), this metric of sensitivity (in Sv \(\hbox {m}^{2}\) \(\hbox {W}^{-1}\)) does not correlate significantly with control AMOC strength (\(r=-0.36, p=0.22\), Fig. 5b, left axis).
There is a strong anticorrelation between \(F+\Delta Q\) and \(\Delta\)AMOC, both in the multi-model ensemble mean (\(r=-0.99, p=0.031\) and Fig. 5a, magenta symbols) and for individual models (Fig. 5b, red symbols, right axis, \(r<-0.98\) for most models). Although the anticorrelation is insignificant (with only three points, \(p>0.05\)) for most models, the AMOC weakening of each model is nevertheless closely related to the North Atlantic heat input.
The heat flux due to the redistribution feedback differs in strength across models and between experiments. The ratio \(\Delta Q_{100}/\Delta Q_{50}\) indicates whether the redistribution feedback increases linearly with F in the North Atlantic box (Fig. 5c). For individual models, this ratio can differ from 2.0, indicating that the feedback is not a linear response to the forcing (Fig. 5c). For some models the ratio is greater than 2 (CanESM2: 2.6, CAS-ESM2-0: 2.9, CESM2: 3.0, ACCESS-CM2: 5.6), while for others it is less than 2 (MIROC6: 1.3, HadGEM3-GC31-LL: 1.4, HadGEM2-ES and MRI-ESM2-0: both 1.6). The ensemble mean of \(\Delta Q_{100}/\Delta Q_{50}\) is 2.24. Differences in the strength of the feedback do not appear to be correlated with whether or not the models AMOC weakening saturates or shows continuous decline (as in MPI-ESM1-2-HR and MRI-ESM2-0, Fig. 3).
The ratio \(\Delta Q_{50}/F_{50}=\Delta Q_{50}/(\frac{1}{2}F_{100})\) indicates how closely the heat flux perturbation \(F_{50}+\Delta Q_{50}\) in the 50pct experiment approximates the intended perturbation \(F_{100}\). If the ratio is unity, \(F_{50}+\Delta Q_{50}=F_{100}\). Although \(F_{50}+\Delta Q_{50}\) is closer than \(F_{100}+\Delta Q_{100}\) to \(F_{100}\), there is considerable spread in \(\Delta Q_{50}/F_{50}\) among models (Fig. 5d). Five of the 13 models show a \(\Delta Q_{50}/F_{50}\) that is either smaller than 0.5 or larger than 1.5. Therefore, halving the perturbation does not accurately compensate for the redistribution feedback in individual models, although it is quite close in the ensemble mean (\(\Delta Q_{50}/F_{50}=1.16\)).
4 Causes of diversity of forced AMOC change
The diversity of AMOC weakening in response to heat flux forcing remains to be understood, although these experiments shed some new light. In particular, there are no significant correlations between the strength of the redistribution feedback averaged within the NA box and the AMOC weakening in either 100pct or 50pct, indicating that the feedback is not the source of the spread (Fig. 6a, \(\Delta Q\) is the redistribution feedback and F is the same in all models). There is a significant (\(p<0.05\)) anti-correlation (\(r=-0.734\)) between the control atmosphere-ocean heat flux averaged over the NA box and the models’ control AMOC strength (Fig. 6b). Given this relationship and the correlation between control AMOC strength and AMOC weakening, one might expect a relationship between the total heat flux change in the NA box (\(F+\Delta Q\)) and the control AMOC strength or the control NA box heat flux, but none is apparent (Fig. 6c, d). Although the change in the heat flux clearly affects the AMOC strength, it is not the cause of spread of AMOC weakening. In these experiments, \(F+\Delta Q\) and \(\Delta\)AMOC are transient responses and it may be that a new equilibrium state is necessary for a correlation to arise.
Relationships between total heat input into NA box and AMOC change for 100pct (black), 50pct (red) and 0pct (blue) for 13 models. a Descriptive statistics are shown for 100pct and 50pct but the relationships are not significant (\(p>0.05\)). Control heat flux averaged over the NA box versus control AMOC strength, with descriptive statistics, (b). Control AMOC strength versus total heat input into NA box for the three experiments, where no significant relationship exists, (c). Control heat flux averaged over the NA box versus total heat input into NA box for the three experiments, where no significant relationship exists, (d)
If the spread of surface heat fluxes cannot explain the diversity of AMOC weakening, then likely the cause is an interior ocean process (or processes). Temperature tendency diagnostics allow for ocean heat content change to be attributed to specific processes in a consistent manner across models (Griffies et al. 2016). Away from the ocean surface (i.e. below 100 m), the temperature tendency of ocean grid cells can be attributed to the action of (1) the resolved advection, (2) the parameterised advection by mesoscale and submesoscale eddies (3) the parameterised along-isopycnal eddy diffusion and (4) the combined action of all vertical and dianeutral diffusive processes such as convection, boundary layer mixing, shear instability and more. The diagnostics and their calculation are described further in Appendix A.5, and much more detail can be found in (Griffies et al. 2016), their Appendix L. The resolved and parameterised advection are often summed together and called the ‘residual mean advection’, which can itself be combined with the isopycnal eddy diffusion to give the ‘super-residual transport’ (Kuhlbrodt et al. 2015). Some models may include other processes in their heat budget (e.g. geothermal heating), but for our purposes, the total ocean grid cell temperature tendency is very close to the sum of these four processes. This partitioning framework has been used to study ocean heat budgets in several recent studies (Dias et al. 2020a, b; Savita et al. 2021) including model intercomparison work (Exarchou et al. 2015; Todd et al. 2020; Saenko et al. 2021). Note that a full, process-based analysis of temperature tendencies of these models is beyond the scope of this work, and the analysis here aims to serve as a starting point for future investigation.
In most models, the quasi-steady state (i.e. unperturbed, preindustrial) heat budget of the NA box region below 100 m is maintained through a first order balance between the warming by the resolved advection (due to downwelling warm waters brought from low latitudes) and cooling via the vertical and dianeutral processes (which flux heat upward into the mixed layer where it can be lost to the atmosphere) (Fig. 7a, b, e). In GFDL-ESM2M only (model G), the NA box is warmed by vertical and dianeutral processes, and strongly cooled by parameterised eddy advection. In other models, there are small roles for the parameterised eddy advection and isopycnal diffusion (which both weakly cool the region). The relative contributions of these processes differ across the models; no individual process is correlated with the control AMOC strength.
Area-mean heat budget in faf-passiveheat in the NA box summed from 100 m to bottom with control AMOC strength for 9 models. The total tendency (a) and its contributions from resolved advection (b), parameterised eddy advection (c), isopycnal eddy diffusion (d), and the vertical and dianeutral diffusion processes (e), SRT is the sum of the resolved advection, eddy advection and isopycnal diffusion, (f)
In 100pct, the heat budget is perturbed, and the warming by the resolved advection becomes less positive while the cooling by vertical and dianeutral processes becomes less negative (Fig. 8a, b, e). This can be interpreted as a reduction in northward heat transport by the large scale transports alongside a reduction of convection and deepwater formation. In most models, the warming effect is larger and the NA box region below 100 m warms, but in HadGEM3-GC31-LL (model K) there is net cooling. Most models show very little change due to mesoscale advection or isopycnal diffusion (exceptions being GFDL-ESM2M and MIROC6, models G and L, which show warming anomalies, and HadGEM2-E, model J, which shows cooling by isopycnal diffusion). Overall, there is no significant correlation between the change in AMOC strength and any of the heat budget components. The spread of AMOC weakening cannot be readily attributed to any particular component of the local heat budget.
Area-mean heat budget anomalies in 100pct in the NA box summed from 100 m to bottom with the change in AMOC strength for 9 models. The total tendency (a) and its contributions from resolved advection (b), parameterised eddy advection (c), isopycnal eddy diffusion (d), and the vertical and dianeutral diffusion processes (e), SRT is the sum of the resolved advection, eddy advection and isopycnal diffusion, (f)
The spread of AMOC weakening and its connection with the mean, unperturbed state remains to be explained (Weijer et al. 2020). The simple heat budget analysis presented here indicates no clear ocean heat transport process that is responsible for the \(\Delta\)AMOC spread. Instead, it may be that the diverse AMOC responses are connected to across-AOGCM differences in mean state, which can have many causes. Biases in the latitudinal positioning atmospheric circulation (such as the mid-latitude westerlies and Inter-tropical Convergence Zone) have been connected to mean AMOC strength biases, and hence also its weakening (Lyu et al. 2020). Errors in North Atlantic sea ice extent can adversely affect the representation of the AMOC (Heuzé 2017). Biases in the layout and intensity of ocean circulation features like the North Atlantic Current and subpolar gyre affect seawater properties in the subpolar North Atlantic and, hence, AMOC strength; this becomes especially important when comparing AOGCMs of various resolutions (Jackson et al. 2020). The interconnection between the atmosphere, ocean and sea ice makes it difficult to attribute model differences to particular causes, and further investigation into all these connections is needed.
5 Global distribution of \(\Delta\)OHC
Having examined the surface heat flux change and ocean heat transport processes in the previous sections, we next compare patterns of \(\Delta\)OHC across the heat flux experiments. The horizontal distribution of \(\Delta\)OHC in 100pct is characterised by large column integrals of \(\Delta\)OHC per unit area in the Arctic, Atlantic, and Southern Ocean (Fig. 9). In the 50pct and 0pct experiments, the smaller perturbation in the North Atlantic means there is much less \(\Delta\)OHC across the entire Atlantic and in the Arctic (Fig. 9b, c). This mostly reflects that much of the \(\Delta\)OHC in the subpolar North Atlantic results from the local heat input. In the tropical Atlantic, there is much less accumulation in 50pct than in 100pct, and less still in 0pct. This could be due directly to the smaller heat addition in 50pct and 0pct, but could also be due to less redistributed warming. Previous work shows that much of the warming at low latitudes results from tropical heat convergence and reduced northward heat transport in response to a weakened AMOC (Gregory et al. 2016; Dias et al. 2020b; Couldrey et al. 2021). The regional importance of redistribution and addition will be shown later.
Well away from the North Atlantic, there are small \(\Delta\)OHC differences in the reduced heat flux experiments relative to 100pct (Fig. 9b, c). The positive 50pct–100pct and 0pct–100pct difference in the North Pacific indicates that AMOC weakening is associated with a decrease in the high latitude North Pacific heat content. On the other hand, AMOC weakening tends to increase the heat content of the Northern Indian Ocean and low latitude Indian-sector Southern Ocean. These locations appear to respond remotely to the forcing in the subpolar North Atlantic.
The depth profile of the global area integral \(\Delta\)OHC from 100pct reveals that the majority of heat is stored in the upper 1.5 km; a typical distribution for greenhouse gas forcing experiments (Saenko et al. 2021). The global total area integrals of the 0pct and 50pct forcing as proportions of the 100pct forcing are 0.7 and 0.85, respectively. To compare whether the heat input into the North Atlantic has a strong effect on vertical distribution of heat, the vertical profiles of \(\Delta\)OHC 0pct and 50pct are rescaled (i.e. divided by 0.7 and 0.85 respectively), and plotted with the profile from 100pct (Fig. 10b). The vertical distribution of \(\Delta\)OHC is largely the same across the three experiments. This result is somewhat surprising, since one might expect weaker deep \(\Delta\)OHC in experiments with larger AMOC weakening. Instead, Fig. 10b reveals that the depth of global \(\Delta\)OHC is largely independent of the heat input into the North Atlantic and the degree of AMOC weakening. This reflects that the Atlantic Meridional Overturning is not the main mechanism that conveys excess heat into the deep ocean. Instead, the result implies that excess heat is mostly transported into the deep ocean in other locations, likely the Southern Ocean.
Depth distribution of \(\Delta\)OHC from 100pct, showing the model ensemble mean (MEM) of 12 models (solid black line) and ensemble spread (MES, ± 2 standard deviations, dashed black lines), a. MEM depth distribution of \(\Delta\)OHC in 100pct (black solid), 50pct (red dashed) and 0pct (cyan dotted) respectively, where 50pct and 0pct have been rescaled to have the same global integral as 100pct, b. Depth distribution of ensemble standard deviation of \(\Delta\)OHC, c
\(\Delta\)OHC per latitude in the final decade of 100pct relative to faf-passiveheat showing the model ensemble mean (MEM) of 12 models (solid black line) and ensemble spread (MES, ± 2 standard deviations, dashed black lines), (a). MEM zonal distribution of \(\Delta\)OHC in 100pct (solid black), 50pct (dashed red) and 0pct (dotted cyan) respectively, (b). Zonal distributions of \(\Delta\)OHC as in (b), except 50pct and 0pct are rescaled to give the same global integral as 100pct, (c). Ensemble standard deviation of rescaled zonal \(\Delta\)OHC (i.e. ensemble spread of c), (d)
The zonal distribution of \(\Delta\)OHC is highly uneven, with more heat accumulating in the Southern Ocean between 60 and 30 \(^{\circ }\hbox {S}\) than at any other latitude for all heat flux experiments (Fig. 11a, b). The small \(\Delta\)OHC in the northern hemisphere relative to the southern reflects that although the heat flux per unit area into the North Atlantic is strong (Fig. 1a), that region’s area is small enough that it does not dominate the global picture. \(\Delta\)OHC is moderate between 30 \(^{\circ }\hbox {S}\) and 30 \(^{\circ }\hbox {N}\), and reduces northward of 15 \(^{\circ }\hbox {N}\). The \(\Delta\)OHC between 30 \(^{\circ }\hbox {S}\) and 30 \(^{\circ }\hbox {N}\) in 0pct is about 60% of 100pct, indicating that the heat input into the North Atlantic box (and the heat redistribution that it causes) is responsible for \(\sim\)40% of the \(\Delta\)OHC at these latitudes (Fig. 11b). North of 30 \(^{\circ }\hbox {N}\), the \(\Delta\)OHC in 0pct is just one quarter of that of 100pct, indicating that three quarters of the heat stored in the global northern mid- to high latitudes is caused by the heat input into the Atlantic between 30–65 \(^\circ \hbox {N}\).
Rescaling the zonal distribution of \(\Delta\)OHC from the 50pct and 0pct experiments to match the global integral of 100pct reveals how the spatial structure of \(\Delta\)OHC varies for the different heat inputs (Fig. 11c). As expected, the reduced heat input into the North Atlantic in 50pct and 0pct causes there to be relatively more heat storage in the southern hemisphere than in the northern. Interestingly, the across-experiment differences between the rescaled distributions (Fig. 11c) are much less pronounced than the absolute distributions (Fig. 11b). This implies that the heat redistribution due to AMOC weakening has a smaller effect than the added heat on the ensemble mean global zonal distribution of \(\Delta\)OHC. The 50pct distribution is generally halfway between that of 0pct and 100pct, indicating a linearity of the response to the intensity of the forcing.
The across-model standard deviation of the rescaled \(\Delta\)OHC is similar in size across the experiments at most latitudes (Fig. 11d). This indicates that the ensemble spread of the zonal distribution of \(\Delta\)OHC is mostly a response to the heat input outside the NA box, rather than within. Therefore, the uncertainty in the zonal distribution of \(\Delta\)OHC is mostly due to the uncertain response to local forcing, rather than the spread of AMOC weakening. Note that because the scaling factors are based on the perturbations’ global integrals, the rescaling in the Southern hemisphere excessively amplifies the patterns of 50pct and 0pct (where the local perturbations are identical). The spread of the absolute zonal \(\Delta\)OHC distributions (i.e. the spread of Fig. 11b rather than c) is not shown because the difference across experiments mostly reflects the difference in global integrals of the forcing: the unscaled spread is largest for 100pct, the smallest for 0pct and with 50pct in between. In the spread of the absolute zonal \(\Delta\)OHC distributions, the values south of 20 \(^{\circ }\hbox {S}\) are very similar (not shown).
6 Regional sea-level change
6.1 Connection between AMOC change and sea-level change
The 100pct heat flux perturbation causes widespread sea-level change (Fig. 12a), with spatial characteristics similar to those noted previously in greenhouse-gas forced experiments (Yin et al. 2009; Gregory et al. 2016). Key features include strong rise in the North Atlantic larger than the global area mean (i.e. positive \(\Delta \zeta\) values), a North Atlantic dipole (positive \(\Delta \zeta\) northward of the North Atlantic current, and neutral values southward), a North Pacific dipole (negative \(\Delta \zeta\) northward of the Kuroshio Extension current, and positive values southward) and a meridional gradient of sea-level change across the Southern Ocean (positive \(\Delta \zeta\) at low latitudes, becoming neutral to negative further southward).
Ensemble mean dynamic sea level change (\(\Delta \zeta\)) in 100pct for 13 models, (a). Correlation between gridpoint \(\Delta \zeta\) and the AMOC change of each model for 100pct, where insignificant correlations (\(p>0.05\)) have been masked out, (b). Relationship between the amplitude of the global pattern of dynamic sea level change, \(\Delta \zeta _G\) (defined in the text), and \(\Delta\)AMOC, (c)
Greenhouse-gas forced sea-level change in the North Atlantic is closely associated with the weakening AMOC (Yin et al. 2009; Sigmond et al. 2020). To investigate whether the model ensemble spread of \(\Delta \zeta\) is linked to the spread of \(\Delta\)AMOC, the dynamic sea-level change in 100pct at each gridpoint is correlated with the change in AMOC strength for each model (Fig. 12b).
The spread of \(\Delta \zeta\) shows a strong anticorrelation with \(\Delta\)AMOC in the GIN Sea (Fig. 12b). The GIN Sea is an important site of deepwater formation in coarse-resolution AOGCMs, and so models that show more AMOC weakening (more negative \(\Delta\)AMOC) also tend to show more positive \(\Delta \zeta\) here (i.e. an anticorrelation, Fig. 12b). This connection was noted by Saenko et al. (2017), but unlike in that work, these models show no correlation between \(\Delta \zeta\) in the Labrador Sea and \(\Delta\)AMOC. This difference may be because higher resolution models like the one used by Saenko et al. (2017) tend to host more vigorous convection and deepwater formation in the Labrador Sea than coarser AOGCMs like the ones used here (Hewitt et al. 2020).
Elsewhere, in the Arctic Ocean and near the Northwest European and Northeast American coasts \(\Delta \zeta\) and \(\Delta\)AMOC are anticorrelated (Fig. 12b). These areas of anticorrelation highlight regions where the spread of AMOC weakening represents a major uncertainty in the projection of future sea level. In the low-latitude Indian sector of Southern Ocean (north of the subtropical front), western tropical Pacific and subtropical Pacific, \(\Delta \zeta\) and \(\Delta\)AMOC show a positive correlation. In these locations, the sea-level change is larger in models with less negative (i.e. nearer zero) AMOC change. Possible mechanisms behind the correlation in the low latitude Southern Ocean are explored later in Sect. 6.4 (Table 2).
While Fig. 12 reveals the connections between \(\Delta \zeta\) and \(\Delta\)AMOC at the gridpoint scale, the connections at the basin scale can be found by averaging \(\Delta \zeta\) over each ocean area (Table 3). The basins are defined according to the standard CMIP6 basin masks (Griffies et al. 2016). The area-mean \(\Delta \zeta\) is significantly anticorrelated with \(\Delta\)AMOC only in the Arctic. Even when the Atlantic area average is restricted to the North Atlantic north of 45 \(^{\circ }\hbox {N}\), where \(\Delta \zeta\) is strongest, the anticorrelation is insignificant. The anticorrelations in the Arctic and Atlantic (even though the latter is insignificant) likely reflect a similar relationship to the one described earlier: more positive \(\Delta \zeta\) co-occurs in models with more negative \(\Delta\)AMOC. \(\Delta \zeta\) has a zero global area mean by definition, so strongly positive values in the Arctic and Atlantic associated with strong AMOC decline must be compensated by negative values elsewhere (note that the Atlantic \(\Delta\)AMOC-\(\Delta \zeta\) anticorrelation is not significant). This property creates the insignificant weakly positive correlations elsewhere; in the Pacific, Indian and Southern Oceans where models with stronger (more negative) AMOC change also more negative \(\Delta \zeta\) in these oceans. The spread of AMOC weakening across AOGCMs is clearly important for the spread of Arctic sea level change and the high latitudes of the North Atlantic, but elsewhere the association is weaker.
It is useful to consider a metric of the strength of the global pattern of \(\Delta \zeta\) for each model: \(\Delta \zeta _G\). Regions of strong positive and negative \(\Delta \zeta\) are defined using the ensemble mean field: the positive region is defined where \(\Delta \zeta >0.05\) m (reds in Fig. 12a) and the negative region is where \(\Delta \zeta <-0.05\) m (blues in Fig. 12a). For each model, the difference between the area mean \(\Delta \zeta\) of the positive region and the area mean of the negative region reflects the absolute amplitude of the pattern. The metric \(\Delta \zeta _G\) anticorrelates with the AMOC change: models that show more negative AMOC change are also models with a more intense absolute pattern of \(\Delta \zeta\) (\(r=-0.55\), \(p=0.049\), Fig. 12c). Hence, there is a model independent pattern of \(\Delta \zeta\) whose amplitude is related to \(\Delta\)AMOC. This anticorrelation highlights that differences in ocean model structure cause diverse patterns of \(\Delta\)OHC and sea-level rise, even when all AOGCMs are forced with an identical heat flux perturbation. Note that the anticorrelation does not imply that the spread of AMOC weakening causes the spread of sea-level rise intensity. Instead, it is likely that the AMOC correlates with the processes that cause \(\Delta\)OHC and sea-level rise, like a proxy for ocean model sensitivity generally.
6.2 North Atlantic and neighbouring Arctic
The pattern of dynamic sea-level change in the North Atlantic in 100pct shows that much of the region experiences local changes that are larger than the global average (i.e. positive \(\Delta \zeta\), Fig. 13a). The main features that have been noted previously are evident, including the dipole in the western basin between 30–55 \(^{\circ }\hbox {N}\), positive values around much of coast north of 40 \(^{\circ }\hbox {N}\), and the tongue of positive values extending westward from West Africa (Gregory et al. 2016; Todd et al. 2020; Couldrey et al. 2021). The thermosteric component is large along the path of the western boundary current (Fig. 13b). The steric change due to the combined redistribution of temperature and salinity causes negative \(\Delta \zeta\) (Fig. 13c), which incompletely opposes the strongly positive added thermosteric change (Fig. 13d). Water mass redistribution tends to cause opposing thermosteric and halosteric effects, but the temperature effect is larger (Fig. 13e) and so the total redistributed steric change resembles a weakened version of the redistributed thermosteric change (Fig. 13c,e). Close to the coast, especially around North America, Greenland and northwestern Europe, the manometric component is large (Fig. 13f), consistent with increased mass loading on the continental shelves (Lowe and Gregory 2006; Landerer et al. 2007; Yin et al. 2010).
Multi model ensemble mean North Atlantic dynamic sea-level change and its components for 11 models for 100pct, a–f and 0pct, h–m. The total change (a) and thermosteric (b), redistributed steric (c) and manometric (f) parts. The thermosteric part is further partitioned into added (d) and redistributed (e) parts. The total (a) is the sum of c, d and f. Redistributed steric is the sum of redistributed thermosteric and halosteric parts
The thermosteric part of sea-level change has important contributions from both added and redistributed heat (Fig. 13d,e). The 100pct heat flux perturbation causes large amounts of thermosteric rise due to the accumulation of added heat north of 10 \(^{\circ }\hbox {N}\), concentrating in the subpolar latitudes and extending along the path of the deep western boundary current and eastern side of the subtropical gyre (Fig. 13d). The input of heat weakens the meridional overturning, inhibiting the northward movement of warm waters from low latitudes. This redistribution of heat causes a warming (and thermosteric rise) in the tropics, the Gulf of Mexico and along the western boundary current path, while simultaneously cooling the subpolar and subtropical gyres (causing negative thermosteric \(\Delta \zeta\), Fig. 13e). There is relatively little thermosteric change in the Atlantic-Arctic interface, owing to a lack of both added and redistributed change.
In contrast to 100pct, there is very little sea-level response in the North Atlantic and Eurasian Arctic under 0pct forcing, Fig. 13h-m. The multi model mean ensemble mean (MEM) dynamic sea-level absolute change does not exceed 0.15 m and in most parts of the region is smaller than 0.05 m (Fig. 13h). This reveals that almost all the local changes in 100pct (i.e. Figure 13a) result from the forcing directed into the NA box. Note that because each component of \(\Delta \zeta\) is calculated relative to its global-area mean, the weakly negative values of \(\Delta \zeta\) due to added heat signify regions where there is less added heat than average, not necessarily absolute sea-level fall (Fig. 13k). For a similar reason, the redistributed thermosteric \(\Delta \zeta\) is weakly negative in the subpolar North Atlantic: since there is no forcing here, there is less sea-level change due to redistribution than the global average (Fig. 13l). The manometric term is weakly positive on the North Atlantic shelves in 0pct (Fig. 13m) because the nonzero forcing elsewhere causes global mean thermosteric sea-level rise, which drives ocean mass onto shelves everywhere.
Multi model ensemble standard deviation of North Atlantic dynamic sea-level change and its components for 11 models for 100pct, a–f and 0pct, h–m. The spread of the total change (a) and spread of various parts: thermosteric (b), redistributed steric, (c) added thermosteric (d), redistributed thermosteric (e) and manometric (f)
There is substantial spread across the model ensemble in spatial pattern of dynamic sea-level change in 100pct (Fig. 14a). Across much of the North Atlantic, the ensemble standard deviation is greater than 0.05 m, which represents a spread of at least 50% of the ensemble mean change (Fig. 13a). The standard deviation exceeds 0.1 m in the subpolar gyre east of Greenland, which is of the same order as the ensemble mean change. The spread is not attributable to a single component of sea level. Rather, both steric (Fig. 14b, c) and manometric effects (Fig. 14f) are uncertain across models. Further, there is much more spread in the individual components (Fig. 14b–f) than in the total dynamic change (Fig. 14a). In other words, the models disagree more on how the spatial pattern of sea-level change is produced than on the pattern of total dynamic sea-level change itself. Nevertheless, the redistribution of heat and salt by perturbed transports stands out as especially uncertain (Fig. 14e, c).
The models tend to agree that the total dynamic change in response to 0pct forcing is small (Fig. 13h and Fig. 14h). Since there is very little added heat in the region, the small spread in \(\Delta \zeta\) arises due to redistributed steric spread (Fig. 14j).
To summarise, the 100pct and 0pct experiments highlight that in the North Atlantic and neighbouring Arctic,
-
The heat flux directed into the NA box region (80 \(^\circ \hbox {W}\)–10 \(^\circ \hbox {E}\), 30–65 \(^\circ \hbox {N}\)) is responsible for local changes to ocean transports of heat and salt that are highly uncertain across models.
-
While the transport of added heat contributes part of the ensemble uncertainty, the diversity across models of the patterns of redistribution of climatological heat and salt is a major driver of uncertainty in the projection of sea-level change.
-
The uncertainty in the model response to forcing outside the 80 \(^\circ \hbox {W}\)–10 \(^\circ \hbox {E}\), 30–65 \(^\circ \hbox {N}\) box (i.e. in 0pct) is smaller than the uncertainty in the response to heat fluxes within the box.
-
The North Atlantic and Arctic are therefore especially sensitive to the heat fluxes supplied locally, and the next sections will explore the extent to which other parts of the ocean are remotely affected.
6.3 North Pacific and Amerasian Arctic
The dynamic sea-level change in the North Pacific and Arctic is smaller in magnitude than in the North Atlantic (note that the scale bar in Fig 15 is half that in Fig. 13). The main characteristic in the North Pacific is a dipole switching sign from positive south of 40 \(^{\circ }\hbox {N}\) to negative further north (Fig. 15a). It is thought that the perturbed heat fluxes steepen the across-current sea-level slope and intensify the Kuroshio extension current (Chen et al. 2019b) as well as the Kuroshio Extension recirculation gyre (Suzuki and Tatebe 2020).
Multi model ensemble mean North Pacific dynamic sea-level change and its components for 11 models for 100pct, a–f and for 100pct with 0pct subtracted out, h–m. The total change (a) and thermosteric (b), redistributed steric (c) and manometric (f) parts. The thermosteric part is further partitioned into added (d) and redistributed (e) parts. The total (a) is the sum of c, d and f. Redistributed steric is the sum of redistributed thermosteric and halosteric parts
The North Pacific pattern is mostly a result of added heat accumulating more in the subtropical than the subpolar gyre (Fig. 15d) particularly within the subtropical mode water (Suzuki and Tatebe 2020). The redistribution of salt and heat by the intensified Kuroshio extension and recirculation gyre partly weakens the pattern set by the added heat (Fig. 15c,e). Evidently, these perturbed transports of heat and salt are not density compensated, as the redistributed steric pattern is mostly thermosteric (Fig. 15c,e).
Although the manometric change is positive along the entire western coastal margin of the Pacific (Fig. 15f), there are also clear steric changes that contribute to the total pattern (Fig. 15b,c). The North Pacific coastal changes are therefore unlike the changes in the coastal North Atlantic, where the manometric component is the largest (Fig. 13f). Finer scale modelling would be necessary to properly resolve the details of coastal sea-level change, but even these relatively coarse AOGCMs highlight the importance of different sea-level components in different regions.
In the Arctic, \(\Delta \zeta\) is positive near the Eurasian and North American coasts and negative toward the pole. The regions of positive dynamic sea-level change have a strong manometric component (Fig. 15f) that is modified to second order by steric effects (Fig. 15b,c). The redistributed steric pattern is quite different from the thermosteric (Fig. 15c,e), indicating that freshening dominates. The thermosteric effects are dominated by widespread redistributive cooling (Fig. 15b,e) and a relative deficit of added heat around the Bering Strait and the Russian Far East (Fig. 15d).
Showing the difference between the 100pct and 0pct experiments reveals the remote effects of the heat flux into the NA box on the North Pacific and Arctic. Note that Fig. 15h-m shows the pattern of 100pct with the pattern of 0pct removed, unlike Fig. 13h-m which simply shows the pattern of 0pct. Part of the negativity of the subpolar North Pacific dipole is a remote response to the forcing in the Atlantic (Fig. 15h). The forcing into the NA box causes a small redistributed cooling north of 45 \(^{\circ }\hbox {N}\) (Fig. 15l) that is mostly density-compensated by the salinity change, giving very little steric redistribution (Fig. 15j). This response may be a rapid adjustment of the pycnocline in response to the changes in the North Atlantic (but we have not studied the mechanism).
The Arctic south of about 80\(^{\circ }\hbox {N}\) is profoundly affected by the heat input into the NA box (Fig. 15h). Much of the added heat that accumulates in Arctic originates from the North Atlantic (Fig. 15k). The total thermosteric change (Fig. 15i) is smaller than the added part alone, because of the redistributive cooling that results from the weakened AMOC (Fig. 15l).
Most of the manometric change (which is responsible for the positive \(\Delta \zeta\) on the Eurasian and North American Arctic coasts) is a result of the North Atlantic heat flux (Fig. 15m) and so is the Arctic freshening and halosteric rise (visible as redistributed steric change, Fig. 15j). The redistributed steric and manometric changes are of opposite sign because the sea-level gradient between coast and open ocean caused by the reduced salinity of the open ocean is opposed by movement of mass onto the shelf. Note that the pronounced halosteric changes (inferred from the difference between Fig. 15j and l) must be the result of a redistribution of ocean salinity due to AMOC weakening, because the freshwater input into the ocean is not perturbed in these simulations. Arctic sea-level rise can be caused by increased freshwater input from precipitation, reduced evaporation, river runoff or melting glacial; these processes, apart from the last, are represented by the freshwater flux perturbation of faf-water, but not in the faf-heat simulations.
Multi model ensemble standard deviation of North Pacific dynamic sea-level change and its components for 11 models for 100pct, a–f and 0pct, h–m. The spread of the total change (a) and spread of various parts: thermosteric (b), redistributed steric (c), added thermosteric (d), redistributed thermosteric (e) and manometric (f)
Added thermosteric \(\Delta \zeta\) in the Amerasian Arctic is more positive in 0pct than 100pct (Fig. 15k). This is not because there is more heat added in the Pacific sector in 0pct, but because there is no heat added in the NA box. Hence the global mean is less positive in 0pct, and anywhere outside the NA box is more positive with respect to the global mean.
The across-ensemble standard deviation of \(\Delta \zeta\) in the North Pacific in 100pct is mostly in the range 0.025–0.05 m (Fig. 16a), and sizable compared with \(\Delta \zeta\), which is locally within \(\pm 0.075\) m (Fig. 15a). This uncertainty mostly arises via the redistribution of salt and heat (Fig. 16c,e) whereas the distribution of added heat is relatively consistent across the models (Fig. 16d). In the Arctic, the uncertainty is much larger, especially away from the coast (Fig. 16a) mostly from the opposed halosteric and manometric contributions (Fig. 16c,f).
The patterns of the spread in the North Pacific 0pct are quite similar to those of 100pct, (i.e. comparing Fig. 16a–f with h–m). Just as the halosteric and manometric components contribute the most to the Arctic mean change, these components also show the most spread across models (Fig. 16c,f) although the thermosteric component is also uncertain (Fig. 16b). In the Arctic, the spread in 100pct is larger than that of 0pct. Therefore part of the uncertainty in the dynamic change is due to the forcing in the North Atlantic box via the halosteric and manometric components (Fig. 16c,f), with the rest attributable to forcing directed elsewhere (Fig. 16j,m).
To summarise, in the North Pacific and Eurasian Arctic, the 100pct and 0pct experiments show that:
-
Part of the North Pacific \(\Delta \zeta\) is remotely forced by the heat flux in the 80 \(^\circ \hbox {W}\)–10 \(^\circ \hbox {E}\), 30–65 \(^\circ \hbox {N}\) North Atlantic box.
-
The remote forcing causes a small redistributed cooling in the subpolar North Pacific. Since this cooling is not density compensated by salinity redistribution, it causes a small negative \(\Delta \zeta\).
-
The Eurasian Arctic dynamic sea-level change is largely a product of the heat flux into the NA box, which results from all of the sea-level components: added thermosteric, redistributed thermosteric, halosteric, and manometric.
-
The redistribution of heat and salt contributes markedly to the overall uncertainty in local \(\Delta \zeta\); the uncertainty in \(\Delta \zeta\) due to added heat is secondary.
-
The across-ensemble uncertainty in the Eurasian Arctic is especially large, and is due in a large part to the diverse patterns of salinity redistribution and manometric change resulting from the North Atlantic heat input.
6.4 Southern Ocean
The 100pct sea-level change in the Southern Ocean is characterised by a strong meridional gradient, with positive \(\Delta \zeta\) in the north (especially around the South African coast), switching to neutral values in the mid-latitudes (40–50 \(^{\circ }\hbox {S}\)), with negative values further south (Fig. 17a). To first order, the \(\Delta \zeta\) meridional gradient is set by the thermosteric change (Fig. 17b) where more added heat accumulates at lower latitudes than higher (Fig. 17d). Perturbed transports cause heat from the low-latitude Atlantic and Indian sectors to be redistributed southward into a band at approximately 45 \(^{\circ }\hbox {S}\) (Fig. 17e). The neutrality of the redistributed steric change in the Atlantic sector north of 45 \(^{\circ }\hbox {S}\) reflects that the halosteric change completely compensates the thermosteric redistribution (Fig. 17c), and so \(\Delta \zeta\) is neutral in this sector. The manometric component is unimportant except on the continental shelf, which is only a small fraction of the ocean area (Fig. 17f).
Multi model ensemble mean Southern Ocean dynamic sea-level change and its components for 11 models for 100pct, a–f and for 100pct with 0pct subtracted out, h–m. The total change (a) and thermosteric (b), redistributed steric (c) and manometric (f) parts. The thermosteric part is further partitioned into added (d) and redistributed (e) parts. The total (a) is the sum of c, d and f. Redistributed steric is the sum of redistributed thermosteric and halosteric parts
The remote effects of heat input into the NA box are revealed by subtracting the 0pct pattern from the 100pct (Fig. 17h). The perturbed transports redistribute the unperturbed heat and salt content differently in 100pct and 0pct. The heat flux into the NA box causes the redistributive warming around 30–45 \(^{\circ }\hbox {S}\) (Fig. 17l). This redistribution enhances the band of low-latitude warming by added heat (Fig. 17d). At the same time, the redistribution of salinity that compensates the redistributed thermosteric change in the Atlantic sector is also caused by the North Atlantic heat input (inferred from the difference between Fig. 17j and l). The correlation between \(\Delta \zeta\) and \(\Delta\)AMOC (Fig. 12b) north of 40 \(^{\circ }\hbox {S}\) in the Indian sector (north of the subtropical front) corresponds to a region of negative redistributive \(\Delta \zeta\) (Fig. 17e,l). The correlation may arise because models with stronger AMOC weakening also show more redistributive cooling here. As noted earlier, the AMOC weakening itself may not be the sole cause of the correlation; it may be a proxy for more sensitive ocean transports generally.
The pattern of \(\Delta \zeta\) is more positive in 0pct than 100pct across much of the region because there is a larger change due added heat relative to the global-area mean across the Southern Ocean (Fig. 17k). This is the same kind of reason as for the widespread, weak negative values of 100pct-minus-0pct in the North Pacific (Fig. 15k).
Multi model ensemble standard deviation Southern Ocean dynamic sea-level change and its components for 11 models for 100pct, a–f and for 100pct with 0pct subtracted out, h–m. The spread of the total change (a) and spread of various parts: thermosteric (b), redistributed steric (c), added thermosteric (d), redistributed thermosteric (e) and manometric (f)
The spread of \(\Delta \zeta\) in the Southern Ocean (Fig. 18a) is mostly due to the redistribution of heat (Fig. 18e). The similarity of patterns in 100pct and 0pct indicates that model spread of redistribution forced by the heat flux outside the NA box (included in both 100pct and 0pct, Fig. 18e,l) has similar patterns to the model spread of redistribution in heat flux forced by heat flux within NA box (included only in 100pct, Fig. 18e). While the patterns of spread are similar in the two experiments, the intensity is slightly larger in 100pct (e.g. in the low latitude Atlantic sector) indicating that the forcing in the NA box causes part of the spread.
In summary, the Southern Ocean responses to 100pct and 0pct forcing reveal that:
-
The heat flux into the NA box causes a redistribution of heat around \(30-45\) \(^\circ \hbox {S}\) in the Atlantic and Indian sectors which contributes part of the band of positive \(\Delta \zeta\). The opposing redistribution of salinity is large enough to compensate the effect of heat in the Atlantic sector, but not in the Indian.
-
The spread of \(\Delta \zeta\) mostly corresponds to the spread due to redistribution, which is partly attributed mostly to the local forcing and partly to the remote forcing from the North Atlantic. To probe the heat redistribution in more detail, heat content change in the Southern Ocean will be explored in the next section.
6.5 Heat redistribution and addition in the Southern Ocean
The models tend to agree that the low latitude, Atlantic- and Indian-sector band of redistributed warming in 100pct corresponds to a southward translation of warm surface waters from further north (Fig. 17e). This redistributive warming occurs within the upper 1.5 km (Fig. 19, above the horizontal grey dotted line). At the same time, the cooling immediately north (in the Indian Sector) is caused by shoaling (rising) isotherms (Fig. 19, north of the right vertical grey dotted line at 40 \(^{\circ }\hbox {S}\)). The overall intensity and details of the spatial structure of this redistribution pattern centred on 40 \(^{\circ }\hbox {S}\) vary across models, but the ensemble mean picture highlights the common features (Fig. 19a). When the 0pct pattern is removed from 100pct, a similar pattern of warming exists, indicating that heat input into the NA box is the dominant cause (Fig. 19b). However, in some models (CanESM2, CAS-ESM2-0, HadCM3, HadGEM3-GC31-LL, MRI-ESM2-0) the warming pattern is clearer and stronger in 100pct-minus-0pct, indicating that the local forcing causes changes in transports that partly dampen the remote warming effect of the weakened AMOC (Fig. 19b, f, j, p, t, x).
Depth-Latitude sections of redistributed temperature change in the Atlantic and Indian Sector Southern Ocean (longitudinally averaged 60 \(^{\circ }\hbox {W}\)–180 \(^{\circ }\hbox {E}\)) between 0–3 km depth. Pairs of plots for each model compare 100pct (left and inner right panels) and 100pct with the 0pct pattern (inner left and right panels). Multi-model ensemble mean (MEM) for 11 models (a, b) and individual models (c–x). Solid black lines in a and b show climatological mean positions of the 1, 3, 5, 10 \(^{\circ }\)C isotherms from faf-passiveheat and dashed lines show the perturbed \(T_R\) isotherms in 100pct (a) and 100pct-0pct (b). Horizontal dotted grey line indicates 1.5 km depth, above which most of the redistributed temperature changes occur. Vertical left and right dotted grey line indicate 55 and 40 \(^{\circ }\hbox {S}\) respectively, which distinguish zones with different characteristic redistributed temperature change
The AMOC weakening causes a southward redistribution of warm, low latitude waters in the uppermost 1.5 km (Morrison et al. 2016) which shifts the subtropical front southwards. This response has been described before (Winton et al. 2013; Marshall et al. 2015; Dias et al. 2020b; Shi et al. 2020), and we now show that it is reproduced in all the models of our ensemble partly because of the forcing in the NA box. Dias et al. (2020b) describe how an intensified Brazil current alongside a positive poleward heat transport anomaly due to reduced southward transport of cold water by the deep western boundary current, cause heat to converge north of the subtropical front. The 100pct and 0pct experiments now clearly demonstrate this link across several models.
Chen et al. (2019a) describe an atmospheric mechanism that causes enhanced heat storage north of 50 \(^{\circ }\hbox {S}\) and reduced storage further south. In that work, a weakened AMOC was shown to reduce northward heat transport, which caused tropospheric cooling in the northern hemisphere and tropospheric warming centred on 50 \(^{\circ }\hbox {S}\). The southern hemisphere warming enhances the poleward temperature gradient south of 50 \(^{\circ }\hbox {S}\) and weakens the gradient to the north. This displaces the westerlies further southward and creates a wind stress curl anomaly that causes anomalous downwelling (heat convergence) north of 50 \(^{\circ }\hbox {S}\) and anomalous upwelling of cold waters further south. The effects of the weakened AMOC on Southern Ocean sea level in 100pct and 0pct are consistent with those described by Chen et al. (2019a) (even though different methods of forcing the AMOC are used in the two studies). The broad similarity between the Southern Ocean patterns of \(\Delta \zeta\) in 100pct, 0pct and their weakened AMOC experiment (their Fig. 3a) implies that these patterns are caused by the surface heat and momentum flux anomalies associated with the atmospheric adjustment to AMOC weakening. The present work shows how that pattern arises mostly due to the addition of heat via the perturbed surface flux (Fig. 17d), but also secondarily through oceanic heat redistribution caused directly by the AMOC weakening (Fig. 17l).
South of 55 \(^{\circ }\hbox {S}\) (southward of the left vertical dotted line in Fig. 19), the models disagree on the pattern of redistributed warming in both 100pct and 0pct. Four models (CanESM2, CAS-ESM2-0, HadGEM3-GC31-LL and MPI-ESM-LR) show warming extending down below 1.5 km depth (below the horizontal dotted grey line), corresponding to southward shifts of sloped isotherms (rather than deepening of flat isotherms) in 100pct. These differences between model responses are quite substantial, and we have not further investigated them. The encroachment of warm circumpolar deep waters onto the Antarctic continental slope has the potential to enhance the melt of ice shelves (Kusahara and Hasumi 2013) and can warm descending plumes of newly formed bottom waters (Couldrey et al. 2013). The cause for these diverse model responses is not clear, and yet it is a key uncertainty for future sea-level projection.
Southern Ocean \(\Delta\)OHC (full depth, south of 30 \(^{\circ }\hbox {S}\)) in 100pct, showing the total (blue bars) and added component (orange bars) arranged by increasing added heat storage in 100pct for 11 models, (a). Southern Ocean \(\Delta\)OHC as in a, for 0pct, (b). Comparison of added \(\Delta\)OHC in 100pct (orange filled bars) and 0pct (orange unfilled bars), (c). Comparison of \(\Delta\)OHC due to heat redistribution in 100pct (green filled bars) and 0pct (green unfilled bars) with error sticks indicating the range of unforced Southern Ocean heat content variability, \(\pm 2\sigma (OHC)\), double the detrended temporal standard deviation of the decadal variability of OHC south of 30 \(^{\circ }\hbox {S}\) in faf-passiveheat, (d)
To see the effect of changes in Atlantic heat transport, we compare the full-depth \(\Delta\)OHC south of 30 \(^{\circ }\hbox {S}\) between the 100pct and 0pct experiments, and its contribution from added and redistributed heat (Fig. 20). The multi-model ensemble mean total \(\Delta\)OHC in 100pct is 447 ZJ (\(1 \,\hbox {ZJ} \equiv 10^{21}\hbox {J}\)), with a spread (standard deviation) of 32 ZJ. The vast majority of this heat is added via the perturbation flux (\(\hbox {MEM} = 406 \,\hbox {ZJ}\), Fig. 20a–c), while redistribution increases the \(\Delta\)OHC (\(MEM = +45 \,\hbox {ZJ}\)) in most models (Fig. 20d). The added \(\Delta\)OHC is similar in 100pct and 0pct for most models except CESM2 (Fig. 20c). The differences in added \(\Delta\)OHC between experiments for CESM2 have not been explored, but may relate to the sea-ice coupling (see Appendix A.1). In the Southern Ocean, \(\Delta\)OHC can be compared directly between 100pct and 0pct without accounting for the different global integrals by rescaling (as in Figs. 10, 11). Heat added in the North Atlantic is not able to reach the Southern Ocean within the 70 years simulated.
Crucially, in every model (except CESM2) the redistribution is more positive (or less negative) in 100pct than in 0pct, indicating that AMOC decline increases the \(\Delta\)OHC of the Southern Ocean (Fig. 20d) although the size of Southern Ocean \(\Delta\)OHC by heat redistribution does not correlate with the strength of AMOC weakening (not shown). In CESM2, the difference in redistribution \(\Delta\)OHC is similar between 100pct and 0pct, given the internal variability. Evidently, the effect of Southern Ocean warming via redistribution in response to a weakened AMOC described earlier imprints on the \(\Delta\)OHC of the entire basin.
However, the models do not all have positive redistribution in 100pct; it is weakly negative in MRI-ESM2-0 (-13 ZJ) and GFDL-ESM2M (-21 ZJ). In these models, although the weakened AMOC causes the low latitude redistributed warming (Fig. 19j, t), there are other redistributive effects of opposite sign. The spread of redistribution (34 ZJ) is slightly smaller than the spread in added heat (41 ZJ) or total \(\Delta\)OHC (32 ZJ). That the spread in each of the two components is larger than in the total indicates some degree of compensation between, i.e. that models with larger added \(\Delta\)OHC have less redistribution, but the anticorrelation between heat addition and redistribution insignificant in 100pct (\(r=-0.53\), \(p=0.09\)) and significant in 0pct: (\(r=-0.67\), \(p=0.02\)). Removing CESM2 as an outlier (given its unique sea ice coupling, see Appendix A.1) makes the anticorrelation for 0pct become insignificant. Like Morrison et al. (2016), we also note that the balance of passive and perturbed transport processes is spatially variable, making spatially integrated results sensitive to the choice of domain.
7 Discussion and conclusions
The FAFMIP protocol provides a consistent way to force AOGCMs with common perturbations to the atmosphere-ocean fluxes of heat, freshwater and momentum (wind stress). The FAFMIP experiments are designed to reproduce typical ocean climate change after about 100 years of atmospheric \(\hbox {CO}_2\) increasing at 1% \(\hbox {year}^{-1}\). In this paper we have presented new results from existing FAFMIP simulations with an enlarged set of AOGCMs, as well as two new FAFMIP experiments. The new results from the original FAFMIP experiments with an ensemble of 15 AOGCMs show that:
-
The AMOC weakening under \(\hbox {CO}_{{2}}\) increase is almost entirely the result of the perturbed heat fluxes, rather than the changes in freshwater flux or wind stress; there are no non-linear interactions between forcings when applied simultaneously.
-
The AMOC responses to freshwater and wind stress perturbation are inconsistent across models, with most showing no significant change, some showing weak strengthening and some showing weak decline.
-
An unintended consequence of the experimental design means that the ‘redistribution feedback’ is double-counted in FAFMIP experiments, which increases the total heat flux into the North Atlantic beyond what was intended by the perturbation. The strength of this feedback differs across models, but it is not the cause of the diversity in AMOC weakening.
-
The spread of AMOC weakening is a major source of uncertainty for projections of future sea level in the North Atlantic and Arctic. This spread is associated mainly with diverse patterns of heat redistribution, although added heat also plays a role.
-
The spread of AMOC weakening across models and its correlation with control AMOC strength remain unaccounted for; further process-based analyses of model heat and salt budgets with FAFMIP experiments might shed more light.
The new experiments are modified versions of the heat flux experiment, wherein the perturbation is reduced to 50% and 0% in the North Atlantic between 80 \(^\circ \hbox {W}\)–10 \(^\circ \hbox {E}\), 30–65 \(^\circ \hbox {N}\) while remaining unchanged elsewhere. The new experiments, performed using 13 models, demonstrate that
-
The AMOC weakening is approximately linearly related to the magnitude of the anomalous heat flux directed into the North Atlantic.
-
The AMOC is primarily sensitive to the heat input in the North Atlantic; it is relatively insensitive to heat input elsewhere.
-
Reducing the perturbation in the North Atlantic 50pct experiment may provide a total forcing (the sum of the perturbation and the redistribution feedback) that is more similar to the perturbation intended by the original 100pct. However, since the strength of the redistribution feedback varies across models, the total heat input varies across models.
-
To first order, the vertical distribution of the global-area integral heat content change is unaffected by the AMOC decline, highlighting that this pattern is mostly set by the Southern Ocean (which is the other region of deep heat storage).
-
The heat content of the North Pacific and Southern Ocean are remotely affected by the heat input into the North Atlantic. The AMOC decline causes a weak but quantifiable global redistribution of ocean heat.
-
In particular, the weakening of the AMOC causes warming at the interface of the Southern Ocean and South Atlantic, due to reduced northward heat transport.
Differences in the fluxes of heat, freshwater and momentum have been invoked to explain the diverse AMOC responses forcing noted in the literature (e.g. Huber and Zanna 2017; Cael and Jansen 2020; Jochum and Eden 2015). Here, we demonstrate that even when consistent forcing is applied, our large ensemble of 15 AOGCMs produces inconsistent AMOC responses. For freshwater and momentum, most AMOC changes are small or insignificant. For heat, the ensemble shows a large spread of AMOC weakening. These results suggest that differences in ocean model structure or control state give each AOGCM a unique sensitivity to forcing.
Differences in the distributions of temperature and salinity (i.e. model state biases) may be a cause of the diverse responses. While it is understood that ocean buoyancy contrasts underpin the AMOC, it is unclear exactly which buoyancy contrasts are relevant; whether between the NADW and the low latitude thermocline waters or Southern Ocean intermediate waters (Gnanadesikan 1999; Nikurashin and Vallis 2012). Temperature and salinity play different roles in setting buoyancy contrasts that support the AMOC (Wolfe and Cessi 2014), and the relative importance of the two tracers is likely to differ across models. Further, details of the surface balance between evaporation and precipitation are also likely to be key determinants of the overturning (Wolfe and Cessi 2014). It is possible that the buoyancy contrasts that drive the AMOC are specific to each model, and so perturbations to those contrasts may produce diverse responses. The FAFMIP common forcing framework will be useful to probe these diverse responses in future investigation.
Unlike in ocean-only studies, our study permits coupled feedbacks to influence the AMOC response, which may explain the apparent inconsistencies between the AOGCMs studies here and the OGCM responses studied previously (Garuba and Klinger 2018; Todd et al. 2020). In particular, further studies examining ocean-only models alongside their coupled AOGCM configurations would be insightful to eliminate the redistribution feedback and identify other feedbacks (Todd et al. 2020).
This work adds to others in finding that the processes that cause heat content change differ markedly across models, and the reasons are unclear (Exarchou et al. 2015; Todd et al. 2020; Saenko et al. 2021). The ocean process diagnostics likely contain a wealth of insight that has yet to be fully realised. In particular, a detailed intercomparison of AOGCMs’ salinity and buoyancy budgets using these diagnostics has yet to be undertaken, but is highly warranted. Previous work has shown that salinity biases and diverse freshwater transports in AOGCMs can have important consequences for the representation of the AMOC (Mecking et al. 2017).
Data Availability Statement
The CMIP6 model output analysed in this study is made available via the Earth System Grid Federation (ESGF) and can be found at https://esgf-node.llnl.gov/search/cmip6/ or one of the other ESGF nodes. The pre-CMIP6 output can be shared upon reasonable request.
References
Bi D, Dix M, Marsland S et al (2020) Configuration and spin-up of ACCESS-CM2, the new generation Australian Community Climate and Earth System Simulator Coupled Model. J Southern Hemisphere Earth Syst Sci 70(1):225–251
Bouttes N, Gregory JM (2014) Attribution of the spatial pattern of CO2-forced sea level change to ocean surface flux changes. Environ Res Lett 9(3):34004
Cael BB, Jansen MF (2020) On freshwater fluxes and the Atlantic meridional overturning circulation. Limnol Oceanogr Lett 5(2):185–192
Chen C, Liu W, Wang G (2019) Understanding the uncertainty in the 21st century dynamic sea level projections: the role of the AMOC. Geophys Res Lett 46(1):210–217
Chen C, Wang G, Xie SP et al (2019) Why Does Global Warming Weaken the Gulf Stream but Intensify the Kuroshio? J Clim 32(21):7437–7451
Colella P, Woodward PR (1984) The piecewise parabolic method (PPM) for gas-dynamical simulations. J Comput Phys 54(1):174–201
Couldrey M, Jullion L, Naveira Garabato A et al (2013) Remotely induced warming of Antarctic Bottom Water in the eastern Weddell gyre. Geophys Res Lett 40(11). https://doi.org/10.1002/grl.50526
Couldrey MP, Gregory JM, Dias FB et al (2021) What causes the spread of model projections of ocean dynamic sea-level change in response to greenhouse gas forcing? Clim Dyn 56(1):155–187
Cox MD (1984) A primitive equation, 3-dimensional model of the ocean. GFDL Ocean Group Tech. Rep. 1. Geophysical Fluid Dynamica Laboratory/NOAA. Princeton University, Princeton
Danabasoglu G, Yeager SG, Bailey D et al (2014) North Atlantic simulations in Coordinated Ocean-ice Reference Experiments phase II (CORE-II). Part I: Mean states. Ocean Modell 73:76–107. https://doi.org/10.1016/j.ocemod.2013.10.005
Danabasoglu G, Lamarque J, Bacmeister J et al (2020) The community earth system model version 2 (CESM2). J Adv Model Earth Syst 12(2):e2019MS001,916
Delworth TL, Zeng F (2008) Simulated impact of altered Southern Hemisphere winds on the Atlantic meridional overturning circulation. Geophys Res Lett 35(20)
Dias F, Domingues CM, Marsland SJ et al (2020) On the superposition of mean advective and eddy-induced transports in global ocean heat and salt budgets. J Clim 33:1121–1140. https://doi.org/10.1175/JCLI-D-19-0418.1
Dias F, Fiedler R, Marsland S et al (2020) Ocean heat storage in response to changing ocean circulation processes. J Clim 33(21):9065–9082. https://doi.org/10.1175/JCLI-D-19-1016.1
Dunne JP, John JG, Adcroft AJ et al (2012) GFDL’s ESM2 global coupled climate-carbon earth system models. Part I: Physical formulation and baseline simulation characteristics. J Clim 25(19):6646–6665
Exarchou E, Kuhlbrodt T, Gregory JM et al (2015) Ocean heat uptake processes: a model intercomparison. J Clim 28(2):887–908
Eyring V, Bony S, Meehl GA et al (2016) Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization. Geosci Model Dev 9:1937–1958. https://doi.org/10.5194/gmd-9-1937-2016
Ferreira D, Marshall J, Heimbach P (2005) Estimating eddy stresses by fitting dynamics to observations using a residual-mean ocean circulation model and its adjoint. J Phys Oceanogr 35(10):1891–1910
Garuba OA, Klinger BA (2018) The role of individual surface flux components in the passive and active ocean heat uptake. J Clim 31(15):6157–6173
Garuba OA, Rasch PJ (2020) A partial coupling method to isolate the roles of the atmosphere and ocean in coupled climate simulations. J Adv Model Earth Syst 12(9):e2019MS002,016. https://doi.org/10.1029/2019MS002016
Gent PR, McWilliams JC (1990) Isopycnal mixing in ocean circulation models. J Phys Oceanogr 20(1):150–155
Giorgetta MA, Jungclaus J, Reick CH et al (2013) Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the Coupled Model Intercomparison Project phase 5. J Adv Model Earth Syst 5(3):572–597
Gnanadesikan A (1999) A simple predictive model for the structure of the oceanic pycnocline. Science 283(5410):2077–2079
Gordon C, Cooper C, Senior CA et al (2000) The simulation of SST, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled model without flux adjustments. Clim Dyn 16:147–168. https://doi.org/10.1007/s003820050010
Gregory JM, Dixon KW, Stouffer RJ, et al (2005) A model intercomparison of changes in the Atlantic thermohaline circulation in response to increasing atmospheric CO2 concentration. Geophys Res Lett 32(12)
Gregory JM, Bouttes N, Griffies SM et al (2016) The Flux-Anomaly-Forced Model Intercomparison Project (FAFMIP) contribution to CMIP6: investigation of sea-level and ocean climate change in response to CO2 forcing. Geosci Model Dev 9(11):3993–4017. https://doi.org/10.5194/gmd-9-3993-2016
Gregory JM, Griffies SM, Hughes CW, et al (2019) Concepts and terminology for sea level: mean, variability and change, both local and global. Surv Geophys 1–39
Griffies SM (1998) The Gent-McWilliams Skew Flux. J Phys Oceanogr 28(5):831–841
Griffies SM, Danabasoglu G, Durack PJ et al (2016) OMIP contribution to CMIP6: experimental and diagnostic protocol for the physical component of the Ocean Model Intercomparison Project. Geosci Model Dev 9(9):3231–3296. https://doi.org/10.5194/gmd-9-3231-2016
Gutjahr O, Putrasahan D, Lohmann K et al (2019) Max Planck Institute Earth System Model (MPI-ESM1. 2) for High-Resolution Model Intercomparison Project (HighResMIP). Geophys Model Dev 12:3241–3281
He J, Soden BJ (2016) The impact of SST biases on projections of anthropogenic climate change: a greater role for atmosphere-only models? Geophys Res Lett 43(14):7745–7750. https://doi.org/10.1002/2016GL069803
Held IM, Soden BJ (2006) Robust responses of the hydrological cycle to global warming. J Clim 19(21):5686–5699
Hermans THJ, Gregory JM, Palmer MD et al (2021) Projecting global mean sea-level change using CMIP6 models. Geophys Res Lett 48(5):e2020GL092,064
Heuzé C (2017) North Atlantic deep water formation and AMOC in CMIP5 models. Ocean Sci 13(4):609–622
Hewitt HT, Roberts M, Mathiot P et al (2020) Resolving and parameterising the ocean mesoscale in earth system models. Current Clim Chang Rep 6:137–152. https://doi.org/10.1007/s40641-020-00164-w
Holland WR, Chow JC, Bryan FO (1998) Application of a third-order upwind scheme in the NCAR ocean model. J Clim 11(6):1487–1493
Huber MB, Zanna L (2017) Drivers of uncertainty in simulated ocean circulation and heat uptake. Geophys Res Lett 44(3):1402–1413
Jackson LC, Roberts MJ, Hewitt HT et al (2020) Impact of ocean resolution and mean state on the rate of AMOC weakening. Clim Dyn 55(7):1711–1732
Jin J, Dong X, He J et al (2021) Ocean response to a climate change heat-flux perturbation in an ocean model and its corresponding coupled model. Adv Atmos Sci 39(1):55–66. https://doi.org/10.1007/s00376-021-1167-y
Jin J, Zhang H, Dong X et al (2021) CAS-ESM2. 0 Model datasets for the CMIP6 flux-anomaly-forced model intercomparison project (FAFMIP). Adv Atmos Sci 38(2):296–306
Jochum M, Eden C (2015) The connection between Southern Ocean winds, the Atlantic meridional overturning circulation, and Indo-Pacific upwelling. J Clim 28(23):9250–9257
Kiss AE, Hogg AM, Hannah N et al (2020) ACCESS-OM2 v1. 0: a global ocean-sea ice model at three resolutions. Geosci Model Dev 13(2):401–442
Kuhlbrodt T, Griesel A, Montoya M, et al (2007) On the driving processes of the Atlantic meridional overturning circulation. Rev Geophys 45(2)
Kuhlbrodt T, Gregory JM, Shaffrey LC (2015) A process-based analysis of ocean heat uptake in an AOGCM with an eddy-permitting ocean component. Clim Dyn 45(11–12):3205–3226. https://doi.org/10.1007/s00382-015-2534-0
Kuhlbrodt T, Jones CG, Sellar A et al (2018) The low-resolution version of HadGEM3 GC3. 1: development and evaluation for global climate. J Adv Model Earth Syst 10(11):2865–2888
Kusahara K, Hasumi H (2013) Modeling Antarctic ice shelf responses to future climate changes and impacts on the ocean. J Geophys Res Ocean 118(5):2454–2475
Landerer FW, Jungclaus JH, Marotzke J (2007) Regional dynamic and steric sea level change in response to the IPCC-A1B scenario. J Phys Oceanogr 37(2):296–312
Li L, Yu Y, Tang Y et al (2020) The flexible global ocean-atmosphere-land system model grid-point version 3 (FGOALS-g3): description and evaluation. J Adv Model Earth Syst 12(9):e2019MS002,012. https://doi.org/10.1029/2019MS002012
Lohmann K, Putrasahan DA, von Storch J et al (2021) Response of northern North Atlantic and Atlantic meridional overturning circulation to reduced and enhanced wind stress forcing. J Geophys Res Oceans 126(11):e2021JC017,902. https://doi.org/10.1029/2021JC017902
Lowe JA, Gregory JM (2006) Understanding projections of sea level rise in a Hadley Centre coupled climate model. J Geophys Res Oceans 111(11):1–12. https://doi.org/10.1029/2005JC003421
Lüschow V, Marotzke J, von Storch JS (2021) Overturning response to a surface wind stress doubling in an eddying and a non-eddying ocean. J Phys Oceanogr 51(4):1007–1020
Lyu K, Zhang X, Church JA (2020) Regional dynamic sea level simulated in the CMIP5 and CMIP6 models: mean biases, future projections, and their linkages. J Clim 33(15):6377–6398. https://doi.org/10.1175/JCLI-D-19-1029.1
Marshall J, Scott JR, Armour KC et al (2015) The ocean’s role in the transient response of climate to abrupt greenhouse gas forcing. Clim Dyn 44(7–8):2287–2299
Marsland SJ, Haak H, Jungclaus JH et al (2003) The Max-Planck-Institute global ocean/sea ice model with orthogonal curvilinear coordinates. Ocean Model 5(2):91–127
Martin GM, Bellouin N, Collins WJ et al (2011) The HadGEM2 family of Met Office Unified Model climate configurations. Geosci Model Dev 4(3):723–757. https://doi.org/10.5194/gmd-4-723-2011
Mauritsen T, Bader J, Becker T et al (2019) Developments in the MPI-M earth system model version 1.2 (MPI-ESM1. 2) and its response to increasing CO2. J Adv Model Earth Syst 11(4):998–1038
Mecking JV, Drijfhout SS, Jackson LC et al (2017) The effect of model bias on Atlantic freshwater transport and implications for AMOC bi-stability. Tellus A: Dyn Meteorol Oceanogr 69(1). https://doi.org/10.1080/16000870.2017.1299910
Morrison AK, Griffies SM, Winton M et al (2016) Mechanisms of Southern Ocean heat uptake and transport in a global eddying climate model. J Clim 29(6):2059–2075
Munk W, Wunsch C (1998) Abyssal recipes II: Energetics of tidal and wind mixing. Deep Sea Res Part I 45(12):1977–2010
Nikurashin M, Vallis G (2012) A theory of the interhemispheric meridional overturning circulation and associated stratification. J Phys Oceanogr 42(10):1652–1667
Prather MJ (1986) Numerical advection by conservation of second-order moments. J Geophys Res Atmos 91(D6):6671–6681
Redi MH (1982) Oceanic isopycnal mixing by coordinate rotation. J Phys Oceanogr 12(10):1154–1158
Roberts MJ, Baker A, Blockley EW et al (2019) Description of the resolution hierarchy of the global coupled HadGEM3-GC3. 1 model as used in CMIP6 HighResMIP experiments. Geosci Model Dev 12(12):4999–5028
Saenko OA, Yang D, Myers PG (2017) Response of the North Atlantic dynamic sea level and circulation to Greenland meltwater and climate change in an eddy-permitting ocean model. Clim Dyn 49(7):2895–2910
Saenko OA, Gregory JM, Griffies SM et al (2021) Contribution of ocean physics and dynamics at different scales to heat uptake in low-resolution AOGCMs. J Clim 34(6):2017–2035
Savita A, Zika JD, Domingues CM et al (2021) Super residual circulation: A new perspective on ocean vertical heat transport. J Phys Oceanogr 51(8):2443–2462
Schmidt GA, Kelley M, Nazarenko L et al (2014) Configuration and assessment of the GISS ModelE2 contributions to the CMIP5 archive. J Adv Model Earth Syst 6(1):141–184
Shi JR, Talley LD, Xie SP et al (2020) Effects of buoyancy and wind forcing on Southern Ocean climate change. J Clim 33(23):10003–10020
Sigmond M, Fyfe JC, Saenko OA et al (2020) Ongoing AMOC and related sea-level and temperature changes after achieving the Paris targets. Nat Clim Chang 10(7):672–677
Slangen ABA, Carson M, Katsman CA et al (2014) Projecting twenty-first century regional sea-level changes. Clim Chang 124(1–2):317–332
Suzuki T, Tatebe H (2020) Future dynamic sea level change in the western subtropical North Pacific associated with ocean heat uptake and heat redistribution by ocean circulation under global warming. Prog Earth Planet Sci 7(1):1–10. https://doi.org/10.1186/s40645-020-00381-9
Swart NC, Cole JNS, Kharin VV et al (2019) The Canadian Earth System Model version 5 (CanESM5.0.3). Geosci Model Dev Discuss. https://doi.org/10.5194/gmd-2019-177
Tatebe H, Ogura T, Nitta T et al (2019) Description and basic evaluation of simulated mean state, internal variability, and climate sensitivity in MIROC6. Geosci Model Dev 12(7):2727–2765
Todd A, Zanna L, Couldrey M, et al (2020) Ocean-only FAFMIP: understanding regional patterns of ocean heat content and dynamic sea level change. J Adv Model Earth Syst e2019MS002027
Weijer W, Cheng W, Garuba OA et al (2020) CMIP6 models predict significant 21st century decline of the Atlantic Meridional Overturning Circulation. Geophys Res Lett 47(12):e2019GL086,075. https://doi.org/10.1029/2019GL086075
Winton M, Griffies SM, Samuels BL et al (2013) Connecting changing ocean circulation with changing climate. J Clim 26(7):2268–2278
Wolfe CL, Cessi P (2014) Salt feedback in the adiabatic overturning circulation. J Phys Oceanogr 44(4):1175–1194
Yang D, Saenko OA (2012) Ocean heat transport and its projected change in CanESM2. J Clim. https://doi.org/10.1175/JCLI-D-11-00715.1
Yin J, Schlesinger ME, Stouffer RJ (2009) Model projections of rapid sea-level rise on the northeast coast of the United States. Nat Geosci 2(4):262–266
Yin J, Griffies SM, Stouffer RJ (2010) Spatial variability of sea level rise in twenty-first century projections. J Clim 23(17):4585–4607
Yu R (1994) A two–step shape–preserving advection scheme. Adv Atmos Sci 11(4):479–490
Yukimoto S, Kawai H, Koshiro T et al (2019) The Meteorological Research Institute Earth System Model Version 2.0, MRI-ESM2. 0: description and basic evaluation of the physical component. J Meteorol Soc Jpn Ser II 97(5):931–965
Zelinka MD, Myers TA, McCoy DT et al (2020) Causes of higher climate sensitivity in CMIP6 models. Geophys Res Lett 47(1):e2019GL085,782. https://doi.org/10.1029/2019GL085782
Zhang H, Zhang M, Jin J et al (2020) Description and climate simulation performance of CAS-ESM Version 2. J Adv Model Earth Syst 12(12):e2020MS002,210. https://doi.org/10.1029/2020MS002210
Acknowledgements
We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modelling groups for producing and making available their model output. We thank the Earth System Grid Federation (ESGF) for archiving the data and providing access, and the multiple funding agencies who support CMIP6 and ESGF. This work was supported in part by Grant NE/R000727/1 from the UK Natural Environment Research Council as a contribution to the WCRP’s Grand Challenge on Regional Sea Level Change and Coastal Impacts. XD and J. Jin were supported by Grant 41991282 from the National Natural Science Foundation of China. OG was supported by the DOE Office of Science Biological and Environmental Research (BER), as a contribution to the HiLAT-RASM project. Contribution from HH was supported by Max Planck Society for the Advancement of Science. AH was supported by the Regional and Global Model Analysis (RGMA) component of the Earth and Environmental System Modeling (EESM) program of the U.S. Department of Energy’s Office of Science Biological and Environmental Research (BER), as a contribution to the CATALYST project. Contributions from J. Jungclaus, AK and SO were supported in part through the Deutsche Forschungs Gemeinschaft (DFG) as part of the SPP 1889 on “Regional sea level change and society”. HL and ZY were supported by Grant 41931183 from the National Natural Science Foundation of China. ACCESS-CM2 simulations were supported by NCMAS and NCI-STRESS2020 grants through the National Computing Infrastructure National Facility at the Australian National University. AS was supported by a Tasmanian Graduate Research Scholarship and CSIRO-UTAS Quantitative Marine Science top-up and by the Australian Research Council (ARC) (CE170100023; DP160103130) and by projects jointly funded through CSIRO and the Earth Systems and Climate Change Hub of the Australian Government’s National Environmental Science Programme. AS is thankful for the support from the Consortium for Ocean-Sea Ice Modelling in Australia (COSIMA). TS was supported by the Integrated Research Program for Advancing Climate Models (TOUGOU) Grant Number JPMXD0717935457. LZ was supported by the Natural Environment Research Council (NERC) Grant NE/R000727/1 (UKFAFMIP), NE/P019218/1 (TICTOC), and NSF GEO 2048576. The authors gratefully acknowledge the input of the anonymous reviewers and Quran Wu, whose feedback improved the quality and clarity of this work.
Funding
This work was supported in part by Grant NE/R000727/1 from the UK Natural Environment Research Council as a contribution to the WCRP’s Grand Challenge on Regional Sea Level Change and Coastal Impacts. XD and J. Jin were supported by Grant 41991282 from the National Natural Science Foundation of China. OG was supported by the DOE Office of Science Biological and Environmental Research (BER), as a contribution to the HiLAT-RASM project. Contribution from HH was supported by Max Planck Society for the Advancement of Science. AH was supported by the Regional and Global Model Analysis (RGMA) component of the Earth and Environmental System Modeling (EESM) program of the U.S. Department of Energy’s Office of Science Biological and Environmental Research (BER), as a contribution to the CATALYST project. Contributions from J. Jungclaus, AK and SO were supported in part through the Deutsche Forschungs Gemeinschaft (DFG) as part of the SPP 1889 on “Regional sea level change and society”. HL and ZY were supported by Grant 41931183 from the National Natural Science Foundation of China. ACCESS-CM2 simulations were supported by NCMAS and NCI-STRESS2020 grants through the National Computing Infrastructure National Facility at the Australian National University. AS was supported by a Tasmanian Graduate Research Scholarship and CSIRO-UTAS Quantitative Marine Science top-up and by the Australian Research Council (ARC) (CE170100023; DP160103130) and by projects jointly funded through CSIRO and the Earth Systems and Climate Change Hub of the Australian Government’s National Environmental Science Programme. TS was supported by the Integrated Research Program for Advancing Climate Models (TOUGOU) Grant Number JPMXD0717935457. LZ was supported by the Natural Environment Research Council (NERC) Grant NE/R000727/1 (UKFAFMIP), NE/P019218/1 (TICTOC), and NSF GEO 2048576.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflicts of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
1.1 Treatment of surface flux perturbations and extra tracers
The heat flux perturbation F is applied like a surface heat flux; it does not penetrate below the surface like shortwave radiation does. The 100pct heat flux perturbation supplies about 196 TW (\(1 \mathrm {TW} = 1\times 10^{12} W\)) of heat into the North Atlantic between 80 \(^\circ \hbox {W}\)–10 \(^\circ \hbox {E}\), 30–65 \(^\circ \hbox {N}\) (the ‘NA box’, enclosed by black dashed lines in Fig. 1a–c), or about 208 TW into the wider region including the Greenland-Iceland-Norwegian (GIN) Sea and Barents-Kara (BK) Sea between 80 \(^\circ \hbox {W}\)–100 \(^\circ \hbox {E}\) and 30–85 \(^\circ \hbox {N}\).
Note that because the perturbation in 50pct and 0pct outside the NA box is the same as in the 100pct experiment, there is still some forcing applied to the high latitude North Atlantic: about 23 TW into the GIN Sea and 11 TW out of the BK sea (Fig. 1c), for a total of 12 TW or about 5.7% of the 100pct experiment. A more complex rescaling region could have been devised, but the simplicity of a square latitude-longitude box was appealing and found to be sufficient to capture \(>90\%\) of the North Atlantic perturbation heat flux in preliminary testing of the experimental design.
If the atmosphere were coupled to the surface field of T in the typical way, then an opposing air-sea heat flux would tend to remove the SST anomaly created by F. Similarly, if the sea-ice were coupled to T as usual, the added heat would tend to melt the sea-ice. To prevent such effects, the atmosphere and sea-ice are decoupled from T and instead coupled to the surface field of another passive tracer, called the redistributed temperature, \(T_R\). \(T_R\) is initialised equal to T at the start, is transported in the ocean using the same schemes as T, receives the air-sea heat flux Q like T, but is not forced by the surface heat flux perturbation.
In the case of CESM2 only, technical difficulties meant that it was not possible to run any heat flux experiments (faf-all, 100pct, 50pct, 0pct) with the sea ice heat flux coupled to \(T_R\). Instead, the sea ice heat flux is computed using T. In this case, this deviation from the FAFMIP protocol was deemed acceptable, since the model’s forced responses are qualitatively similar to the other AOGCMs’, especially in terms of AMOC weakening and sea-level change. As a result of the unique coupling, it is possible for added heat to be removed from the ocean in the melting of sea-ice. This may be the cause of the unusually small accumulation of added heat in the Southern Ocean (Fig 20c), but the details of the mechanism have not been explored fully.
1.2 Calculation of the correlation coefficient
The correlation between n pairs of paired data x and y, is calculated using the sample correlation coefficient, r, defined as
where i is the index and an overline indicates the mean.
1.3 Descriptions of AOGCMS
1.4 Notes on the use of AOGCMs from different CMIP eras
The full ensemble of AOGCMs that have performed FAFMIP simulations to date comprises 15 members: 9 of which are the latest generation CMIP6 models, 5 are previous generation CMIP5 models, and one is from the CMIP3-era. (Tables 2, 4). Some of the AOGCMs have undergone considerable structural changes between the fifth and sixth CMIP era. In addition to developments of their other submodels, the ocean components of CanESM2 and HadGEM2-ES were replaced with the NEMO ocean to create their CMIP6 counterparts, CanESM5 and HadGEM3-GC31-LL. These two models are therefore substantially different across the two generations. Nevertheless, we have included these older AOGCMs (CanESM2, HadCM3 and HadGEM2-ES) because they constitute part of the ensemble that FAFMIP was intended to probe. On the other hand, the two other models CMIP5-era models (MPI-ESM-LR and GFDL-ESM2M) are still in use performing CMIP6 experiments, reflecting their continued utility and relevance as tools for climate study. In what follows, we investigate whether there are substantial differences in the ocean responses to forcing between the AOGCMs of different eras.
Ensemble mean dynamic sea level change (\(\overline{\Delta \zeta }\)) in 100pct for the 6 pre-CMIP6 AOGCMs, (a), and the 9 CMIP6 AOGCMS, (b). Ensemble spread (standard deviation) dynamic sea level change (\(\sigma (\Delta \zeta )\)) in 100pct for the 6 pre-CMIP6 AOGCMs, (c), and the 9 CMIP6 AOGCMS, (d)
In the analyses described in the main body, all of the AOGCMs are analysed together as a single ensemble. Aggregating the AOGCMs into a single ensemble is justified by the similarity of the spatial patterns of the sea level responses between the CMIP6 and pre-CMIP6 eras. Here, the main ensemble is subdivided into a pre-CMIP6 ensemble and a CMIP6 ensemble, and the dynamic sea-level change Model Ensemble Mean (MEM, \(\overline{\Delta \zeta }\)) and Spread (MES, \(\sigma (\Delta \zeta )\)) are compared. The same qualitative features are apparent (the dipoles in the North Atlantic and North Pacific, the gradient across the Southern Ocean) (Fig. 21a, b). The patterns of \(\overline{\Delta \zeta }\) are highly correlated between the two sub-ensembles: \(r=0.757, p<0.05\). The ‘intensity’ of the spatial pattern can be quantified as the spatial standard deviation of \(\overline{\Delta \zeta }\). This metric reveals that the spatial pattern of \(\overline{\Delta \zeta }\) is stronger (i.e. the highs are higher, the lows lower) for the CMIP6 ensemble than the pre-CMIP6 ensemble (0.0896 m and 0.0652 m respectively).
The Model Ensemble Spread (MES) of \(\Delta \zeta\) is similar for both the CMIP6 and the pre-CMIP6 AOGCMs (Fig. 21c, d). The main regions showing large ensemble spread are similar for the two eras: the North Atlantic, the Arctic, the Southern Ocean and the North Pacific. Indeed, the patterns of \(\sigma (\Delta \zeta )\) are highly correlated between the two sub-ensembles: \(r=0.722, p<0.05\). The area means of the maps of \(\sigma (\Delta \zeta )\) are similar for the two eras: 0.0383 m and 0.0354 m for pre-CMIP6 and CMIP6 respectively. The similarity of the sub-ensembles’ means and spreads therefore justifies treating them together as a single ensemble.
As for Fig. 2, except using only CMIP6-era AOGCMS. AMOC change versus control AMOC strength for 100pct a, faf-stress b, and faf-water c. AMOC change from 100pct versus AMOC change from faf-all d, with linear fit (purple line) and a 1–1 line (black dashed line). The AMOC change for models circled in red is not significantly outside internal variability. Linear fits and descriptive statistics are shown, n: number of models, m: slope, c: y intercept, r: correlation coefficient, p: p-value, e: standard error
The differences of the AMOC strength and its weakening are compared between the full ensemble and the CMIP6-only subset. Alternate version of Figs. 2 and 4 using only CMIP6-era AOGCMs reveal that similar AMOC-vs-\(\Delta\)AMOC relationships exist using only the latest generation ensemble, although the relationships are less robust (Fig. 22 and 23). While the 100pct and 50pct forcing is sufficient to produce AMOC weakening in all 8 CMIP6 AOGCMs, the AMOC-vs-\(\Delta\)AMOC relationships are insignificant, given a threshold of \(p<0.05\) (Fig. 22a and 23a). For 100pct, the AMOC-vs-\(\Delta\)AMOC gradient (Full: \(m=-0.539\), CMIP6: \(m=-0.638\)) and correlation (Full: \(r=-0.653\), CMIP6: \(r=-0.640\)) are similar, in spite of the CMIP6-only relationships being formally insignificant. The standard error of the regression is also poorer for the CMIP6-only ensemble (\(e=0.313\) versus \(e=0.188\) for the full ensemble).
The faf-stress and faf-water perturbations did not produce significant AMOC change in most CMIP6 AOGCMs (Fig. 22b, c). Only 2 of the 9 CMIP6 AOGCMs showed significant change in response to momentum and water flux perturbation. This finding is qualitatively consistent with the larger ensemble: a majority of models show no signficant AMOC change. Further, of the CMIP6 models showing significant change, the AOGCMs disagree on the sign of the change. Finally, the weakening in faf-all-vs-100pct plot very close to a 1-to-1 line, indicating strong similarity between the weakening of the two experiments, and a lack of non-linear effects of the perturbations on AMOC weakening (Fig. 22d). This regression gradient is closer to 1 for the CMIP6-only ensemble (\(m=1.04\)) than the full (\(m=1.12\)).
As for Fig. 4 except using only CMIP6-era AOGCMS. AMOC change versus control AMOC strength for 100pct in black and 50pct in red (a), \(\Delta\)AMOC from 100pct versus 50pct (with linear fit, black dashed line, and 0.5 gradient, red dashed line), AMOC change versus control AMOC strength for 0pct, (c) and AMOC strength versus control variability as the temporal standard deviation of annual averages, (d). Red circles in a indicate models with no significant change. Linear fits and descriptive statistics are shown m: slope, c: y intercept, r: correlation coefficient, p: p-value, e: standard error
The effect of restricting the ensemble to only CMIP6 AOGCMs does not strongly affect the ratio of AMOC weakening between 100pct and 50pct, although the relationship between the two is rendered insignificant (Fig. 4b). The slope itself is relatively little changed (\(m=0.479\) for CMIP6, \(m=0.539\) for the full ensemble), but the correlation is weaker (\(r=0.670\) for CMIP6, \(r=0.762\) for the full ensemble), and the p value rises above 0.05 when the ensemble is restricted. The 0pct AMOC-vs-\(\Delta\)AMOC relationship is insignificant using either the restricted CMIP6 ensemble or the full. The relationship between the control AMOC strength and control AMOC variability for the CMIP6 ensemble is very similar to the full ensemble, both in terms of the gradient (\(m=0.051\) for CMIP6 only, \(m=0.055\) for the full ensemble) and the correlation (\(r=0.819\) for CMIP6 only, \(r=0.779\) for the full ensemble).
In summary, the dynamic sea level responses of the CMIP6 and pre-CMIP6 AOGCMs are quantitatively and qualitatively similar, both in terms of ensemble mean and spread. The responses of the CMIP6-only subset to the faf-stress and faf-water forcing are qualitatively similar to the full ensemble. The main consideration in using the full ensemble or restricting the analysis to only CMIP6 models using the small subset degrades the significance of the AMOC-vs-\(\Delta\)AMOC anticorrelations. This may be due to the considerable random error of this type of relationship, requiring many members to generate robust statistics. The more usual and robust method of averaging random temporal variability involves performing multiple realisations of each experiment, but this incurs computational costs that were prohibitive for FAFMIP. Instead, the decadal averaging approach of this study will likely leave some random temporal noise. Another possibility could be that the AMOC-vs-\(\Delta\)AMOC relationship noted in previous generations of AOGCMs (e.g. Gregory et al. 2005) no longer applies to the sixth generation. The latter explanation seems unlikely, given that Weijer et al. (2020) also note that AMOC-vs-\(\Delta\)AMOC anticorrelation exists for the majority of CMIP6 models under projected 21st Century climate forcing. Therefore, we include all available FAFMIP AOGCMs, regardless of their era, to maximise the ensemble size.
1.5 Temperature tendency diagnostics
Heat budget tendency terms (described in Sect. 4) can be found by calculating the heat convergence (i.e. the volume integrated heating rate per horizontal area, in \(\hbox {Wm}^{-2}\)) of each model grid cell that results from the various advective or diffusive processes. The total temperature time tendency of an ocean grid cell is
where T is the model temperature, the product of seawater density and gridcell thickness \(\rho dz\) is the seawater mass per horizontal area, u is the three-dimensional resolved velocity field and P is the parameterised subgrid-scale transport processes. This tendency is the variable called ‘opottemptend’ in CMIP6 terminology (Griffies et al. 2016), for models which use potential temperature (the variable is ‘ocontemptend’, for models which use conservative temperature). The tendency due to the parameterised eddy advection (the CMIP6 variable called ‘opottemppadvect’) is
where v* is the parameterised eddy-induced velocity (e.g. Gent and McWilliams 1990; Griffies 1998).
The tendency due to the resolved advection is
There is no specific CMIP6 variable for this tendency, but it is calculated by subtracting the tendency due to parameterised eddy advection (‘opottemppadvect’) from the tendency due to residual mean advection (‘opottemprmadvect’). The tendency due to the parameterised along-isopycnal diffusion (the CMIP6 variable called ‘opottemppmdiff’) is
where P\(_I\) is the parameterised diffusive heat transport caused the mixing action of mesoscale eddies (e.g. Redi 1982; Griffies 1998). The tendency due to the parameterised dianeutral or diapycnal fluxes (i.e. acting vertically, across neutral or density surfaces, the CMIP6 variable called ‘opottempdiff’) is
where P\(_V\) is the parameterised diffusive heat transport associated with all vertical and dianeutral processes. The precise composition of this term depends on the schemes used in each model and may include convection, boundary layer mixing, interior shear-driven mixing, gravity wave-induced mixing, background diffusion and others.
Depending on model formulation, P may include other parameterisation schemes that affect the ocean model heat flux, such that
These other processes are neglected in this study, since the main terms are the ones described above.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Couldrey, M.P., Gregory, J.M., Dong, X. et al. Greenhouse-gas forced changes in the Atlantic meridional overturning circulation and related worldwide sea-level change. Clim Dyn 60, 2003–2039 (2023). https://doi.org/10.1007/s00382-022-06386-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-022-06386-y