1 Introduction

Climate change influences global and regional hydrological variabilities and affects water resource supplies, and thus is essential for the environment and human development (Immerzeel et al. 2010; Vörösmarty et al. 2000). High-resolution regional climate modeling has shown the distinct capability in addressing research issues related to climate and hydrological applications. Regional climate models (RCMs) not only produce reliable added value at higher temporal-spatial resolution (Knist et al. 2018; Qiu et al. 2019; Solman and Blázquez, 2019), but also incorporate internally consistent water and energy exchanges throughout the land–atmosphere interface (Campbell et al. 2019; Knist et al. 2017; Smirnova et al. 2016).

It has been pointed out that the land surface processes require a precise description in numerical weather and climate modeling (Betts and Silva Dias 2010; Koster et al. 2010; Ma et al. 2017; Santanello et al. 2018; Senatore et al. 2015). As land surface models (LSMs) integrated in RCMs usually have a crude representation of terrestrial water movements (Clark et al. 2015), one state-of-the-art focus in recent years has arisen on fully coupled atmospheric-hydrological modeling systems (Butts et al. 2014; Davison et al. 2018; Lahmer et al. 2020; Larsen et al. 2014; Ning et al. 2019; Rummler et al. 2019; Senatore et al. 2015; Zhang et al. 2019). Shrestha et al. (2014) employed the coupled Terrestrial Systems Modeling Platform (Gasper et al. 2014) for the North Rhine-Westphalia region in Germany. They found that the surface and groundwater processes enhanced the redistribution of moisture to dry soils, thereby influencing the exchange fluxes distribution and atmospheric boundary layer development. By coupling the hydrological model PROMET with Mesoscale Model version 5 (MM5), Zabel et al. (2012) noticed that the surface hydrological processes can influence evapotranspiration and precipitation either positively or negatively in central Europe, depending on prevailing hydrological conditions. Later on, Zabel and Mauser (2013) indicated that the coupled modeling improved near-surface temperature simulation in the Upper Danube catchment. By using the Weather Research and Forecasting (WRF) model and its coupled hydrological model system WRF-Hydro, many studies illustrated that the near-surface lateral hydrological processes including overland flow and subsurface flow influence the regional climate, water cycle, and land–atmosphere feedbacks. In southern Italy, Senatore et al. (2015) investigated the impact of lateral terrestrial flow on surface hydrometeorological variables, and found that the latent heat fluxes were increased and the precipitation was influenced modestly. Arnault et al. (2016b) concluded that the impact on precipitation depends on the size of the analyzed area. Gao et al. (2006) and Zhang et al. (2019) performed the coupled simulations for short-term and long-term scale over high-elevation and complex terrain region in the northeastern Tibet Plateau. Their results demonstrated the influence of the lateral hydrological processes not only on the near-surface atmosphere, but also on the joint atmospheric-terrestrial water balance. Over the central Europe, Arnault et al. (2018) and Rummler et al. (2019) employed ensemble simulations during the summer season, and confirmed the importance of lateral flow description in regional atmospheric modeling via precipitation spread and regional local recycling. All of the above studies demonstrated the capability of fully coupled models in representing complex interaction between climate and land surface processes.

Uncertainties broadly exist in regional climate modeling related to model physics parameterization, internal variabilities, and external forcing (e.g., Braun and Tao 2000; Crétat et al. 2012; Klein et al. 2015; Laux et al. 2017). Multiple planetary boundary layer (PBL) parameterization schemes are available in numerical models, which are known to have a broad impact on RCM applications. In India, Gunwani and Mohan (2017) found that the PBL scheme is sensitive to downscaled meteorological fields over different climatic zones in WRF simulations. Likewise, many studies compared different PBL parameterization in meteorological condition prediction, by aiming to ascertain an appropriate PBL scheme for specific geographical regions (e.g., Avolio et al. 2017; García-Díez et al. 2013; Hu et al. 2010). Over a coastal mountainous region in Canada, Onwukwe and Jackson (2020) conducted yearlong WRF simulations and found that the disparities in mixing strengths among PBL schemes were more considerable in summer than in winter, depending on moist stable conditions and airflow direction. Given that the PBL scheme adopts assumptions concerning mass, moisture, and energy transport from the land surface to the low atmosphere, uncertainties associated with the PBL parameterization could directly relate to land–atmosphere interactions. In the framework of fully coupled atmospheric-hydrological model systems, studies on the effects of different PBL parameterization schemes are usually lacking.

Precipitation originating from local evapotranspiration source is known as precipitation recycling, which has been actively used as a diagnostic measure of land–atmosphere interaction (Eltahir and Bras 1996; Trenberth 1999; van der Ent et al. 2013). The E-tagging method initially ‘tags’ the water vapor evaporated from the land surface, then treats the tagged moisture in the same way as all moisture does in the RCMs, and follows it in space and time until it precipitates. It considers the source-sink relations through all physical processes and relaxes the vertical-mixing assumption of other precipitation recycling measures (Arnault et al. 2016a; Insua-Costa and Miguez-Macho, 2018). Therefore, it is thought to be the most physically realistic way to access the recycled precipitation quantity, thus allowing for detecting small perturbation-induced changes at the land–atmosphere interface (Arnault et al. 2019; Dominguez et al. 2016; Zhang et al. 2019). For example, by incorporating the E-tagging method with MM5, Wei et al. (2015) investigated the annual cycle of the contribution of evaporation to precipitation for the Poyang Lake region in China, emphasizing the importance of land surface characteristics in the atmospheric hydrological cycle. Knoche and Kunstmann (2013) and Arnault et al. (2016a) traced the evaporated moisture pathways in West Africa, and they revealed the effect of vertical wind shear to regional precipitation recycling. On a large scale, Yang and Dominguez (2019) and Gao et al. (2020) employed a tagging-enabled WRF model for South America and Tibetan Plateau respectively, highlighting the effects of land surface conditions on recycled precipitation. These studies confirmed the ability of the E-tagging method to quantitatively assess land–atmosphere interactions.

Understanding the interactions between the atmospheric, land surface and hydrological processes is of great importance in complex mountain terrain. This is particularly true for the high mountain environment, which is considered as the nature’s water tower while is experiencing more rapid climate change (Immerzeel et al. 2010; Pepin et al. 2015). The Heihe River Basin (HRB) is such an environment. It is located in Northwestern China, stretching from Tibetan Plateau to Mongolia, and suffering from water shortage and ecosystem deterioration problems (Cheng et al. 2014). In the upper reach of HRB, where the mountain elevation is particularly high, the water availability has been declared to be significantly sensitive to climate change (Li et al. 2020; Luo et al. 2016; Ma et al. 2019; Zhang et al. 2016). The hydrological cycle in this arid alpine area and its connection to climate change still needs to be further understood, which requires a joint assessment of land–atmosphere interaction processes with a complex coupled modeling system (Zhang et al. 2019). Therefore, within the context of improving terrestrial hydrological processes in regional climate modeling, it is important to further understand the role of terrestrial water flow on land–atmosphere interactions in such an arid, high mountain environment area like HRB. An improved understanding can be achieved with the above-mentioned fully coupled atmospheric-hydrological modeling, by considering physics parameterization uncertainties and the quantification of the interactions strengthen with the E-tagging approach.

For this purpose, we use the newly developed E-tagging method embedded in the standard WRF and fully coupled WRF-Hydro model, and carry out ensemble simulations for the HRB region by varying PBL parameterizations. The main goals of this study are: (1) to assess the impact of lateral terrestrial flow on the simulation of surface hydrometeorological variables and land–atmosphere interactions, (2) to evaluate to what extent the PBL parameterization influences land–atmosphere interactions, and (3) to identify the respective impact of lateral terrestrial flow and the PBL parameterization uncertainties in a fully coupled modeling approach. The analyses of land surface-precipitation feedback processes (Asharaf et al. 2012; Schär et al. 1999) and precipitation recycling based on E-tagging are used as quantitative measures. To our knowledge, this is the first effort performed in regional climate modeling to consider uncertainties in the evaporated water tracing method originating from model physics parameterizations.

In the following, Sect. 2 briefly describes the study region and used datasets. In Sect. 3, the model descriptions and setup, as well as the ensemble strategy and quantitative methods are addressed. The results of ensemble modeling are discussed in Sect. 4, and the conclusions are summarized in Sect. 5.

2 Study region and dataset

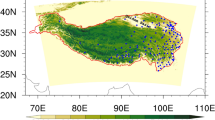
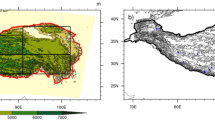
The Heihe River Basin (HRB) is the second-largest inland river basin in China, covering an area of approximately 143,000 km2. The river starts from the Qilian Mountain in the northern Tibetan Plateau and disappears at two terminal lakes in the Gobi Desert. From the upstream mountains to the desert in downstream, the elevation decreases from 5500 to 1000 m (Fig. 1b), and the annual precipitation decreases from 550 to 50 mm. The water vapor transport over HRB is mainly controlled by the middle-latitude westerly wind and polar north wind, with the weakened East Asian summer monsoon obstructed by the Qilian Mountains in the upstream (Wang et al. 2004; Wang et al. 2018a, b). Therefore, the precipitation in HRB shows large seasonal and spatial variability, with more than 80% precipitation occurring from May to September and 70% precipitation over the upper mountains (Li et al. 2018a). Due to the steep terrain gradients (Fig. 1b) and climate characteristics, the natural landscape and hydrological conditions show an obvious spatial heterogeneity (Cheng et al. 2014). The upper reach of HRB is a typical alpine environment, where the main landscape is covered by alpine meadow, with the annual air temperature between − 3 °C and 0 °C. The middle reach of HRB is spatially fragmentarily covered with lower oasis and dryland cropland. In this area, the river water and groundwater are largely consumed by irrigation water withdrawal. The downstream of HRB is vastly covered by the sand and gravel deserts plus certain riparian ecosystems. The climate is extremely dry, with annual precipitation less than 50 mm and potential evapotranspiration greater than 1000 mm (Ma et al. 2014). The ecological system over the middle and downstream of HRB is threatened by an increase of water consumption, and is significantly dependent on upstream hydrological variability under rapid climate change (Cheng et al. 2014; Zhang et al. 2016). Therefore, this study particularly focuses on the upper reach of HRB (upper HRB) outlet at the Yingluoxia hydrological gauge (1634 m a.s.l.). The upper HRB is entirely situated within the Qilian Mountains, with a drainage area of 10,009 km2. Two additional hydrological gauges, located at Qilian (2590 m a.s.l.) and Zhamashike (2635 m a.s.l), measure the streamflow of eastern and western tributaries in the upper HRB (Fig. 1c).

Fig. 1
figure 1

a Geographic location of the Heihe River Basin and the location of WRF/WRF-Hydro model domain. b Terrain topography and river network of the drainage of Heihe River Basin, with nearby meteorological stations shown in red cycles. c Zoom of the topography, stream channels and the discharge gauges (orange rectangles) described in the 300-m high resolution WRF-Hydro routing subgrid for the upper Heihe River Basin

Full size image

The China Meteorological Forcing Dataset (CMFD), the Global Land Evaporation Amsterdam Methodology (GLEAM) dataset, and soil moisture dataset of European Space Agency’s Climate Change Initiative (ESA CCI) are used for evaluating the modeling results. The CMFD data was constructed by merging 740 in-situ China Meteorological Administration (CMA) stations with various advanced retrospective analyses data resources (He et al. 2020). This product provides gridded meteorological analysis over China with spatial and temporal resolutions of 0.1° and 3 h, respectively. Extensive studies suggested that CMFD accurately represents the meteorological conditions within and surrounding the HRB region (Pan et al. 2014; Yang et al. 2017b). In this study, CMFD is used for the validation of air temperature and precipitation, and for offline hydrological model driving (see Sect. 3.1). The GLEAM dataset (Martens et al. 2017) is the global evapotranspiration product based on remote sensing observation, with a spatial resolution of 0.25°. Based on the point-validation of GLEAM dataset across China via eddy covariance measurements, Yang et al. (2017a) confirmed the capability of GLEAM in representing monthly and spatial variations of evapotranspiration around upper HRB. The soil moisture from ESA CCI is the remotely sensed surface soil moisture combined from active and passive microwave sensors measurements, with a spatial resolution of 0.25° (Gruber et al. 2019). For the site-based measurements, 18 meteorological stations within and surrounding the HRB (Fig. 1b) collected by CMA stations and Heihe Watershed Allied Telemetry Experimental Research project (Li et al. 2013) are used for further verifying air temperature and precipitation. Daily streamflow observation records from 3 hydrological gauges in upper HRB, shown in Fig. 1c, are provided by the Hydrological Bureau of Gansu Province. The missing records from meteorological stations are linearly interpolated with the nearby stations. The streamflow records affected by dry season dam operation at Yingluoxia gauge are reconstructed using linear-line fit with two upstream gauge records.

3 Modeling experiments and methods

3.1 WRF and WRF-Hydro setup

The advanced research WRF model (Skamarock and Klemp 2008) version 3.7 and its Hydrological modeling system WRF-Hydro (Gochis et al. 2015) are employed for regional atmosphere-hydrology simulations to address the research objectives of this study. WRF is a numerical meteorological and climate model that is widely used in weather and climate research as well as operational applications (Powers et al. 2017). WRF-Hydro affords a set of supplementary hydrological components to the WRF model, which enables the capability of lateral redistribution of the hydrological condition at the land surface (Gochis et al. 2015). All WRF and WRF-Hydro simulations are run in a single-domain configuration, covering the whole HRB and centering at the upper HRB (Fig. 1a). Acknowledging that the refined model grid improves orography representation over highly complex terrain, thereby offering added values in simulated surface fields (e.g., Fosser et al. 2014; Karki et al. 2017; Woodhams et al. 2018), all simulations are performed at a convection-permitting resolution of 3 km with 350 × 350 grid points. This high resolution excludes the uncertainties from cumulus parameterization, thus allowing for a more realistic simulated soil moisture-precipitation feedback (Prein et al. 2015; Taylor et al. 2013). The vertical coordinate is a hybrid terrain-following coordinate with 40 levels and pressure top at 20 hPa. The atmospheric lateral boundary conditions are provided by the operational analysis from the European Center for Medium-Range Weather Forecasts (ECMWF), with 0.125° spatial resolution and 6-h intervals. The model physics adopted in this study includes the WRF single-moment 6-class (WSM6) microphysics scheme (Hong and Lim 2006), the Rapid Radiative Transfer Model longwave radiation scheme (Mlawer et al. 1997), and the Dudhia shortwave radiation scheme (Dudhia 1989). The different PBL schemes used for turbulence parameterization are described in Sect. 3.2

The land surface static characteristics are replaced with the accurate localized dataset, acknowledging their noticeable impact on atmospheric modeling in the study area (Gao et al. 2008; Meng et al. 2009; Wen et al. 2012). The land cover map is updated with the Multi-source Integrated Chinese Land Cover Map (Ran et al. 2012), and the soil texture map is adapted from the Chinese 1: 1,000,000 scale Soil Map and Harmonized World Soil Database (HWSD) version 1.2. The Noah-LSM scheme is used for parameterizing lower boundary interactions in the land surface (Chen and Dudhia 2001). In the WRF model, Noah-LSM only considers vertical water and energy exchanges in a 4-layer soil column within a 2-m soil depth.

The above model configurations are the same in WRF and coupled WRF-Hydro simulations. In WRF-Hydro, a separated 300-m hyper-resolution subgrid is prepared with WRF-Hydro Pre-processing Tool using the hydrological data and maps based on Shuttle Elevation Derivatives at multiple Scales (HydroSHEDS; Lehner et al. 2008). At each WRF model timestep, hydrological variables including surface water amount and soil moisture are disaggregated from the 3-km WRF grid to the 300-m hydro subgrid. Afterward, additional hydrological processes including lateral subsurface flow routing, overland flow routing, and channel water routing are resolved in this hydro subgrid, resulting in an updated surface state variable. The drainage water from the soil bottom is collected in a groundwater bucket for each basin area, and is used for baseflow calculation via an exponential function. We note that the water routed in the channel and collected in the bucket has no further feedback to the land surface modeling. A detailed description of the water routing schemes and baseflow routine in WRF-Hydro is available in Gochis et al. (2015). Succeeding the above hydrological procedures, surface water amount and soil moisture content on the fine hydro subgrid are linearly averaged back to the coarse WRF grid. Therefore, the land surface condition modulated by lateral terrestrial flow feeds back to WRF atmospheric processes at the next iteration of the Noah-LSM.

Calibrating the hydrological parameters is relevant to the realistic representation of terrestrial water processes in hydrological modeling. Driven by the observational-based CMFD dataset, the WRF-Hydro model is calibrated in its offline mode using observed daily streamflow at the Yingluoxia gauge. After model calibration, the Nash–Sutcliffe efficiency and Kling-Gupta efficiency (Gupta et al. 2009) of the simulated streamflow reach the values of 0.6 and 0.79, respectively. The calibration procedure has been elaborated in Yucel et al. (2015) and detail of calibration results has been discussed in Zhang et al. (2019). The calibrated parameter set is therefore used in fully coupled WRF-Hydro simulations.

3.2 PBL schemes and experimental strategy

Three PBL schemes in WRF and WRF-Hydro are used for investigating modeling sensitivity to turbulence parameterization: the Yonsei University (YSU) scheme, the Mellor-Yamada-Janjic (MYJ) scheme, and the Asymmetrical Convective Model version 2 (ACM2) scheme. These three PBL schemes are chosen as they have been extensively considered in turbulence parameterization uncertainty studies (Arnault et al. 2018; García-Díez et al. 2013; Gómez-Navarro et al. 2015; Gunwani and Mohan, 2017; Hu et al. 2010). The YSU scheme is a first-order scheme that uses the nonlocal eddy diffusivity coefficient to explicate turbulent fluxes (Hong et al. 2006). The MYJ scheme is a local closure scheme and it uses a 1.5-order turbulence model with a prognostic equation for the turbulent kinetic energy (Janjić 1994). ACM2 uses a combination of nonlocal upward convective mixing and local downward mixing, and treats nonlocal fluxes using a transilient matrix (Pleim 2007). In this study, all the WRF and coupled WRF-Hydro simulations are configured with the model setups in Sect. 3.1 and run three times, one for each of these three PBL schemes. This gives a model ensemble of six members, that are three WRF members and three WRF-Hydro members (Table 1).

Table 1 List of the six WRF and WRF-Hydro experiments, along with the used PBL scheme, brief description of the PBL scheme, and the LSM parameterizations
Full size table

A schematic view of model ensemble members is provided in Fig. S1. When intercomparing the ensemble members in Fig. S1, the comparisons in horizontal (orange line) indicate the model uncertainties related to PBL schemes, and the comparisons in vertical (blue line) express the influences related to lateral terrestrial flow. In the following, we call Hydro-ensembles the ones which use only WRF members (WRFS) or WRF-Hydro members (WRFH). Then, we call PBL-ensembles the ones which use only one PBL scheme.

For all ensemble simulations, the initial soil conditions is spun-up by the 2-year WRF simulation with the ACM2 PBL scheme, ensuring their comparability in the following analyses. All the simulations are performed from 2008 to 2010, which allows to account for the interannual modeling variabilities.

3.3 Evaporated water tagging method

The physically realistic method to trace online the water originating from evapotranspiration, known as E-tagging, is used for diagnosing and quantifying the land–atmosphere interactions in the study. This method was firstly technically realized in the German Weather Service’s hydrostatic high-resolution model (HRM) by Sodemann et al. (2009) for a regional application. Later on, this E-tagging method has been implemented and verified with MM5 (Knoche and Kunstmann 2013) and WRF (Arnault et al. 2016a; Insua-Costa and Miguez-Macho 2018).

The E-tagging method developed by Arnault et al. (2016a) is used in this study. It has been incorporated in both standard WRF and coupled WRF-Hydro, and is compatible with the physics parameterizations selected for model setups in Sects. 3.1 and 3.2. The following tagging procedure is employed: (1) Define the upper HRB as the source region for water tracing, the evapotranspiration from the upper HRB (red outline in Fig. 1b) being labeled as the tagged evapotranspiration (ETtag); (2) Analogously replicate the numerical formulations related to the advection and turbulent transport of the original water species (qn) for the tagged water species (qn,tag); (3) Introduce a weighting coefficient (qn,tag/qn) for the computation of tagged water phase transitions. Following this procedure, tagged water species are traced until tagged precipitation at the surface (Ptag) or tagged advection outside of the domain’s boundaries. It is noted that the tagged water species which leave the lateral boundaries of the model domain are set to zero, which means that the returning of tagged water species from outside of the domain is neglected.

3.4 Quantitative measures of land–atmosphere interactions

To quantify the interactions between land surface and atmosphere, we firstly use the analysis framework of land surface-precipitation feedback processes proposed by Schär et al. (1999) and advanced by Asharaf et al. (2012). This analysis is based on the atmospheric water balance, and assumes that the water vapor transported through a region and from the local evapotranspiration is well mixed.

For a control experiment, the relationship of precipitation (P), evapotranspiration (ET), and the atmospheric water vapor transport in a specific region is described as:

$$P = \chi { }\left( {ET + Q_{in} } \right).$$
(1)

Qin is the atmospheric water inflow calculated by integration of water vapor fluxes through the boundary of the selected area. χ is called precipitation efficiency, which is defined as the fraction of the water vapor entering a certain region, either by evapotranspiration or atmospheric water transport, that falls as precipitation within the same region afterward.

For a perturbation experiment, Eq. (1) can be rewritten as:

$$P^{\prime} = \chi^{\prime}{ }\left( {ET^{\prime} + Q^{\prime}_{in} } \right),$$
(2)

where dashed variables stand for the conditions in the perturbation experiment. Subtracting Eq. (1) from Eq. (2), the precipitation difference ΔP is written as:

$$\Delta P = P^{\prime} - P = \chi^{\prime}\left( {ET^{\prime} + Q^{\prime}_{in} } \right) - \chi { }\left( {ET + Q_{in} } \right),$$
(3)

where Δ denotes the differences between the perturbation experiment and control experiment. Rearranging the right-hand terms according to Schär et al. (1999) and Asharaf et al. (2012), ΔP can be expressed as:

$$\Delta P = \underbrace {{\Delta \chi \left( {{\text{ET}} + Q_{{{\text{in}}}} } \right)}}_{{\text{Efficiency effect}}} + \underbrace {{\chi \Delta {\text{ET}}}}_{{\text{Surface effect}}} + \underbrace {{\chi \Delta Q_{{{\text{in}}}} }}_{{\text{Remote effect}}} + \underbrace {{\Delta \chi \left( {\Delta {\text{ET}} + \Delta Q_{{{\text{in}}}} } \right)}}_{{{\text{Residual}}}}.$$
(4)

In Eq. (4), the precipitation difference ΔP is separated into three terms and residual. The first term reflects the processes affecting the transformation of available atmospheric water into precipitation. It is the indirect contribution through the changes in precipitation efficiency Δχ, referred to as efficiency effect. The second and the third terms reflect the precipitation change by direct contribution through the changes in surface evapotranspiration ΔET and changes in atmospheric water vapor inflow ΔQin, referred to as surface effect and remote effect, respectively. The residual term is very small and can be neglected. Therefore, this analysis allows distinguishing between the direct and indirect processes of lateral terrestrial flow on the simulated precipitation from the model simulations. In this study, the coupled WRF-Hydro ensemble is considered as the perturbation experiment which additionally depicts the lateral terrestrial flow. The feedback analysis based on Eq. (4) is conducted with WRF and coupled WRF-Hydro simulations which use the same PBL scheme (blue line in Fig. S1).

Precipitation recycling ratio is used as another measure for quantifying land surface-atmosphere interactions strength. Precipitation recycling ratio is defined as the fraction of evaporation-originated precipitation in the total precipitation, in this case for the upper HRB area. Based on the E-tagging method, the precipitation recycling ratio is calculated as:

$$\beta = P_{tag} /P.$$
(5)

The higher value of \(\beta\) stands for a higher contribution of locally evaporated water to local precipitation.

4 Results and discussion

The quantification measures of land–atmosphere interactions depend on the performance of modeling results in reproducing the hydrometeorological fields, i.e., precipitation, temperature, evapotranspiration, and discharge. Therefore, the simulated hydrometeorological fields from model ensembles are evaluated and discussed at first, then followed by discussions on quantified land–atmosphere interactions.

4.1 Hydrometeorological fields

4.1.1 Precipitation

The annual precipitation from model ensembles is spatially compared with the CMFD gridded precipitation and ground measurements in Fig. 2. As illustrated in Fig. 2a, the observational reference shows a precipitation band along with the Qilian Mountain, with a decrease of precipitation from southeast to the northwest. The heavy precipitation is centered to the south of HRB, while the minimal precipitation is spread over the lowland area in the north. All the considered ensemble members capture the above spatial pattern of precipitation, and are consistent with the ground measurements (Fig. 2b–f). The monthly averaged precipitation in the upper HRB from Hydro-ensembles WRFS and WRFH, is temporally compared with CMFD in Fig. 3a. It shows that all the simulations skillfully reproduce the monthly and seasonal variation of precipitation. Similar to many RCM simulations (e.g., Pan et al. 2014; Xiong and Yan 2013; Yang et al. 2017b; Zhang et al. 2018), all the model ensembles overestimate precipitation over the high mountains from May to August (Fig. 3a). In comparison to CMFD precipitation for the upper HRB, the Hydro-ensembles WRFS and WRFH overestimate precipitation by 221 mm/year and 231 mm/year respectively, and the PBL-ensembles simulate 201–254 mm/year more precipitation, in which the ACM2 ensemble shows the smallest bias and MYJ ensemble shows the highest. Taking into account the fact that CMFD merges sparse ground observations over flat valley area around the study area (Fig. 1b), the wet bias of precipitation in the upper HRB could be partially attributed to the fact that high mountain precipitation is not well represented in the gridded reference dataset (Chen et al. 2015; Pan et al. 2014; Yang et al. 2017b).

Fig. 2
figure 2

Annual accumulated precipitation derived from a CMFD, and the Hydro-ensembles of b WRFS-ENS and c WRFH-ENS for the period 2008–2010. d–f are for the PBL-ensembles of d YSU-ENS, e MYJ-ENS and f ACM2-ENS. Colored circles represent the ground-observed precipitation from in-situ stations

Full size image
Fig. 3
figure 3

Monthly variation of a precipitation, b 2-m air temperature, c evapotranspiration and d soil water content averaged in the upper HRB from reference datasets (CMFD, GLEAM, ESA CCI), and the Hydro-ensemble (WRFS-ENS, WRFH-ENS) in the period of 2008–2010

Full size image

Spatially, all the WRF and coupled WRF-Hydro experiments show much more spatial details in comparison to the reference data, in relation to the high resolution employed for the simulation. In the high mountains to the south, the precipitation distribution is highly associated with elevation, and shows more precipitation on the northern flank of the Qilian Mountains (Chen et al. 2018a; Wang et al. 2018a). As an important component of precipitation, snowfall is primarily distributed over high-altitude mountains, accounting for approximate 23% of total precipitation in the upper HRB. This spatial distributions of simulated snowfall and snow water equivalent from ensemble simulations (Fig. S2) are comparable and similar to that of Pan et al. (2017). These localized spatial patterns of orographic precipitation and snowfall prove the trustworthy of ensemble simulations in representing precipitation quantities.

4.1.2 Near-surface temperature

The comparisons of 2-m air temperature between CMFD and the Hydro-ensembles are displayed in Figs. 3b and 4. Both model ensembles simulate monthly averaged temperature variations in good agreement with the reference dataset (Fig. 3b), with statistically significant correlation coefficients above 0.98. As shown in Fig. 4, the spatial variations of annual mean temperature are also realistically reproduced, with a spatial correlation of 0.96 for the whole HRB and 0.81 for the upper HRB. Comparing with CMFD reference, the simulated near-surface temperature from all ensemble members is slightly lower during the summertime and higher during the wintertime (Fig. 3b), with a warm bias ranging from 0.3 to 0.9 °C. This model performance is fairly comparable to that obtained with other RCM simulations (e.g., Gao et al. 2015; Pan et al. 2012).

Fig. 4
figure 4

Annual mean 2-m air temperature derived from a CMFD, and the Hydro-ensemble of b WRFS-ENS and c WRFH-ENS for the period 2008–2010. Colored circles represent the ground-observed 2-m air temperature from in-situ stations

Full size image

4.1.3 Evapotranspiration and soil moisture

Evapotranspiration (ET) and surface soil water content from the Hydro-ensembles are evaluated with the GLEAM and ESA CCI datasets as time series for the upper HRB in Fig. 3c, d. Soil water content comparison is only available during summertime due to the general missing values in the wintertime. In general, simulated monthly ET in the upper HRB shows good agreement with GLEAM with correlation coefficients above 0.84 (p < 0.01) and the simulated soil water content is also quite comparable with ESA CCI observations. Overall, the Hydro-ensemble WRFH overestimates ET by about 61 mm/year while WRFS underestimates ET by about 11 mm/year. As shown in Fig. 3c, d, WRFH overestimates the peak value of ET in the summertime, which is associated with the higher soil moisture in the WRFH ensemble. All simulations slightly underestimate ET during March and April in the upper HRB where elevation is high. As the air temperature is below 0 °C (Fig. 3b) and the precipitation is low (Fig. 3a) during this springtime, the underestimated ET could be largely attributed to an inaccurate specification of the frozen soil thawing mechanism in land surface modeling (Duan et al. 2018; Zhang et al. 2019; Zheng et al. 2017). In Fig. 5, the spatial pattern of ET in GLEAM is fairly represented in the model ensembles, with a maximum in the southeast, and declining values from the southern to the northern HRB. It is noted that simulation results additionally represent spatial variations of ET according to local vegetation conditions and precipitation distribution (Fig. 2). These high-resolution features of ET, which cannot be detected in the GLEAM dataset, are similar to those shown by satellite data-derived results (Wu et al. 2020).

Fig. 5
figure 5

Annual mean accumulated evapotranspiration derived from a GLEAM, and the Hydro-ensembles of b WRFS-ENS and c WRFH-ENS for the period 2008–2010

Full size image

4.1.4 Impact of lateral terrestrial flow on hydrometeorological fields

The role of lateral terrestrial flow on simulated hydrometeorological variables is inspected by intercomparing the Hydro-ensembles WRFH and WRFS (Sect. 3.2). Displayed in Fig. 3, the monthly time series of precipitation from the two Hydro-ensembles show similar variations, with small differences in the monthly amounts, while the ET and soil moisture is distinctly higher in WRFH, with around 0.5 mm/day more ET and 0.03 m3/m3 higher soil water content than those in WRFS during the summertime. Furthermore, the range of ET in each Hydro-ensemble is generally less than 0.18 mm/day (Fig. 3c). This robustly indicates that the increase of evapotranspiration in WRFH corresponds to the description of lateral terrestrial flow, regardless of the precipitation uncertainties. Since lateral flow does not directly affect the snowpack, the snow melting process is related to the simulated air temperature, which is comparably similar in all ensemble simulations (Fig. 3b). Slight differences in snowmelt are associated with the differences in snowfall between WRFS and WRFH ensembles (Fig. S3).

The spatial differences of related hydrometeorological variables are explored for the months from May to September (Fig. 6), which is defined as the rainy-season (Su et al. 2017; Zhang et al. 2018). By enabling lateral terrestrial hydrological processes within atmosphere modeling, the land surface in turn is affected according to the terrain complexity. Regardless of the precipitation differences, Fig. 6c shows that ET systematically increased over the areas with high elevation gradients in the Qilian Mountains, and with small differences in the northern flat regions and flat valleys. The increase of ET is consistent with the increase of soil moisture, which is caused by laterally moved and re-infiltrated surface runoff. Temperatures between the two Hydro-ensembles are rather similar. WRFH shows slightly lower near-surface temperature than WRFS alongside the mountains, within − 0.2 °C, as a consequence of a more evaporative cooling effect. These wetting and cooling results in mountainous areas are consistent with findings in the Eastern Alps area (Rummler et al. 2019).

Fig. 6
figure 6

Differences in a accumulated precipitation, b mean 2-m air temperature, c accumulated evapotranspiration, and d surface soil moisture between the Hydro-ensembles (WRFH-ENS minus WRFS-ENS) for the rainy-season (May–September) in 2008–2010

Full size image

4.2 Streamflow

Simulated streamflow hydrographs from the coupled WRF-Hydro ensemble are compared with gauge observations in Fig. 7. In general, the timing of hydrograph peaks and the flow recession are well captured by all ensemble members. The temporal variations of streamflow are comparable with observed streamflow, except for the baseflow amount during the dry period, which is mostly underestimated. Apart from the fact that WRF-Hydro explicitly describes the subsurface flow in a soil layer of 2 m depth only and oversimplifies deeper groundwater processes with a simple bucket baseflow parameterization (Gochis et al. 2015; Li et al. 2017; Rummler et al. 2019; Yucel et al. 2015), streamflow underestimation during low flow period could be further attributed to a lack of glacier wastage modeling in the current model framework.

Fig. 7
figure 7

Range of daily time series of simulated streamflow by the coupled WRF-Hydro ensemble at the outlets of the gauges a Yingluoxia, b Qilian and c Zhamashike for the period 2008–2009. The observed streamflow is shown as black solid lines

Full size image

As indicated in previous coupled WRF-Hydro applications (Arnault et al. 2016b; Kerandi et al. 2018; Rummler et al. 2019; Senatore et al. 2015), our results similarly underline the impact of simulated precipitation on streamflow simulation. Related to the overrated precipitation amount, the peak flows are mostly overestimated during the rainy-season, resulting in low KGE coefficient values spanning from 0.02 to 0.21. With respect to different PBL schemes used in the coupled modeling, the simulated hydrographs in all members are similar, however, distinguishable ranges are obtained at flow peaks during the rainy period. This behavior is quite comparable to the ensemble simulations over central Europe and Alps catchments (Arnault et al. 2018; Rummler et al. 2019). The uncertainties in the peak flows can be justified by the simulated precipitation differences, which not only rely on the amounts and spatial distributions, but also on the intensity and duration of heavy precipitation events (Kokkonen et al. 2004; Rasmussen et al. 2012). Nevertheless, the ratios of total streamflow to precipitation are reasonably reproduced at all three gauges. The calculated streamflow ratios show values of 0.38–0.40 at Qilian gauge, 0.40–0.41 at Zhamashike gauge, and 0.36–0.38 at Yingluoxia gauge, respectively, and these are quite comparable with various pure hydrological modeling results (Chen et al. 2018b; Gao et al. 2016; Li et al. 2018b; Ruan et al. 2017; Yang et al. 2015).

4.3 Land surface-precipitation feedback processes

As the precipitation amount during the dry season is quite small and similar among all ensemble members (Fig. 3a), the land surface-precipitation feedback analysis focuses on the rainy-season from May to September. Figure 8 displays the quantified effect terms of lateral terrestrial flow on precipitation in the upper HRB with each PBL scheme. The results among different PBL schemes are quite consistent. The direct contribution of evapotranspiration changes to precipitation changes is small and positive in all months, in relation to the higher evapotranspiration in coupled WRF-Hydro. Since the soil moisture conditions can modify mesoscale moisture convergence thereby affect atmospheric water inflow (e.g., Cook et al. 2006; Koster et al. 2016; Schär et al. 1999), the remote effect reaches its maximum value in July when the water transport is the strongest. The positive or negative remote effects are related to the atmospheric moisture convergence differences and the relative location of the study area (Fig. S5j–l). The efficiency effect shows the dominant contribution to the change of precipitation, with the largest absolute value throughout the rainy-season. In the model system, this efficiency effect corresponds to the convection organization triggered by moisture convergence and model physical processes. Being influenced by lateral terrestrial flow, the modeled specific humidity and latent heating (i.e., evapotranspiration) increase at the land surface (Fig. S4j–l), in association with a shallower boundary layer, a decrease in lifting condensation level, and an increase of most unstable convective available potential energy across southern mountains (Fig. S5a–j). These results suggest that the lateral terrestrial flow potentially affects the spatial distribution and strength of convection through a change in atmosphere stability, similar to the study cases of direct perturbation of wetter soil moisture conditions (e.g., Asharaf et al. 2012; Froidevaux et al. 2014; Wei et al. 2016). Therefore, although the lateral terrestrial flow has a relatively small direct impact on precipitation, it promotes much larger indirect impact on precipitation through atmospheric moisture convergence and convective processes.

Fig. 8
figure 8

Monthly quantified change of precipitation (WRFH-PBL minus WRFS-PBL) in the upper HRB for the rainy-season in 2008–2010

Full size image

As atmospheric moisture convergence and convection formation are both influenced by model physical parameterization schemes, the precipitation changes and the quantified effects are varying from month to month among three PBL-ensembles. The effect of different PBL schemes will be investigated using E-tagging method in the following section.

4.4 Evapotranspiration tagging and precipitation recycling

4.4.1 Distribution of tagged precipitation and precipitation recycling

The tagged evaporated water which precipitates at the ground, namely the tagged precipitation (Ptag), and the precipitation recycling ratio are spatially displayed in Fig. 9 for the standard WRF simulations with the three PBL schemes. The results from coupled WRF-Hydro simulations are similar and are displayed in Figure S6. The tagged precipitation is mainly distributed around the source region, the upper HRB, and alongside the mountain range stretching from southeast to northwest. Besides, the higher amount of tagged precipitation falls at the mountain peaks within and to the south of the upper HRB, which confirms the role of the Qilian Mountain blocking the atmospheric water transport to the Tibet Plateau (Li et al. 2015; Wang et al. 2018b).

Fig. 9
figure 9

Spatial pattern of a–c annual tagged precipitation amount and precipitation recycling d–f from the WRF standalone simulations (WRFS) with respect to 3 PBL schemes for the period 2008–2010

Full size image

Only a small portion of evaporated water falls back to the source area, resulting in an annual precipitation recycling ratio less than 2.2% (Table 2), whereas the predominant portion flows outside the domain boundaries. In Fig. 10, the calculated monthly precipitation recycling ratio ranges from 0.05 to 3.9%, which is comparable to that obtained in a previous study (Zhang et al. 2019). This low precipitation recycling feature in the study area is confirmed by all ensemble members, and it is mainly related to the fact that the source area is small. The precipitation recycling ratio is scale-dependent, explaining that it tends to zero at the point-scale and reaches 1 at the global-scale (Arnault et al. 2016a; Burde and Zangvil 2001; Trenberth 1999). In the following, we compare the E-tagging results among ensemble members to investigate the PBL-related and lateral terrestrial flow-induced changes in local recycled precipitation.

Table 2 Annual precipitation recycling of the upper HRB for each model ensemble member
Full size table
Fig. 10
figure 10

Monthly precipitation recycling ratio calculated from all WRF standalone and coupled WRF-Hydro ensemble members

Full size image

4.4.2 Impact of PBL scheme on precipitation recycling

As shown in Figs. 9, S6 and Table 2, it is found that the annual tagged precipitation and precipitation recycling show differences among the PBL schemes. For the WRFS ensemble, the MYJ scheme has the largest amount of tagged precipitation around 15.5 mm/year, and the highest precipitation recycling ratio of 1.76%. The ACM2 scheme has the lowest amount of tagged precipitation of 11.9 mm/year, with a precipitation recycling ratio of 1.28%. A similar difference among the PBL schemes is also found in the case of the WRFH ensemble (Table 2).

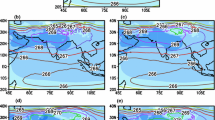
The calculated monthly precipitation recycling ratios for all ensemble members are displayed in Fig. 10. The precipitation recycling ratio shows a distinct seasonal cycle, which is quite comparable among all PBL schemes, showing the lowest values during the winter season and higher values in the summer season. For the magnitude, again, the highest precipitation recycling ratio is found in the PBL scheme of MYJ throughout the whole period, and the ACM2 scheme shows the lowest values. These differences in precipitation recycling could be explained by the local closure difference in the PBL parameterization. The local closure schemes (i.e., MYJ) usually produce insufficient mixing in the convective boundary layer (Brown 1996; Cohen et al. 2015; Xie et al. 2012), and this weaker vertical mixing tends to transfer less surface water vapor to higher atmospheric levels (Hu et al. 2010). However, the nonlocal schemes (i.e., YSU, ACM2) usually transport more moisture away from the surface and deposit more moisture at a higher atmospheric level (Hong and Pan 1996; Hu et al. 2010; Srinivas et al. 2007). These differences in moisture mixing are exemplified in the vertical profile shown in Fig. 11. The MYJ scheme exhibits more moisture in the low atmosphere below the height of 5500 m, whereas the ACM2 scheme displays the lowest moisture. In the higher atmosphere, the ACM2 scheme is inversely showing the higher moisture mixing ratio with respect to the YSU and MYJ schemes. As the moisture particles in the higher atmosphere levels can be transported farther away to remote regions, the precipitation recycling ratio from the ACM2 scheme is accordingly low.

Fig. 11
figure 11

Vertical profiles of the difference in a total water vapor mixing ratio and b tagged water vapor mixing ratio between three PBL parameterization schemes for June and August in 2008. Differences are respectively calculated from each PBL ensemble and their ensemble mean

Full size image

4.4.3 Impact of lateral terrestrial flow on precipitation recycling

Figures 12 and 13 illustrate the precipitation recycling differences between the Hydro-ensemble WRFH and WRFS as spatial maps and monthly time series, respectively. Concerning the impact of lateral terrestrial flow, spatial precipitation recycling increases in the northwestern upper HRB, with a total increased ratio of 0.47% and up to 0.93% in mountain peaks (Fig. 12). Despite the uncertainties introduced by the PBL schemes, lateral terrestrial flow systematically increases the monthly precipitation recycling ratios, up to 1.2% more in the summertime (Fig. 13).

Fig. 12
figure 12

Spatial pattern of precipitation recycling from Hydro-ensembles of a WRFS, b WRFH and c their difference (WRFH minus WRFS)

Full size image
Fig. 13
figure 13

Monthly precipitation recycling ratio differences with respect to lateral terrestrial flow. Differences are respectively calculated from WRFH- and WRFS- for each PBL scheme

Full size image

Differential vertical profiles of moisture mixing ratio between the WRFH and WRFS are shown in Fig. 14, one for June 2008 when the recycling ratio differences is the largest, and the other for August 2008 when the differences display the widest range. For both months, WRFH enhances the moisture in the lower atmosphere and decreases moisture in the higher atmosphere up to the height of 9000 m. The tagged moisture in WRFH is comparatively higher below the height of 7000 m. The vertical change of moisture mixing ratio robustly illustrates that the enriched evapotranspiration in WRFH intensifies the wetting in the lower atmosphere and reduces the mixing ratio in the free convection level above. This lateral terrestrial flow-induced feedback mechanism is comparable to the results of positive feedbacks obtained by directly perturbating soil moisture fields to a wetter condition (Schär et al. 1999). As such an intensified wetting in the low atmosphere causes convective instability and increases the possibility of moist convection (Derbyshire et al. 2004; Yin et al. 2015), thereby increasing the local precipitation recycling. However, as shown in Figs. 6a and 8, the increase of precipitation recycling ratio is not necessarily associated with an increase of precipitation, as the precipitation in the study area is dominated by remote water sources through atmospheric water transport. In particular, this ensemble result confirms the blocking effect of topography in the weakened East Asian summer monsoon environment, and endorses the positive feedback of local land–atmosphere interactions in the study area.

Fig. 14
figure 14

Vertical profiles of the differences in a total water vapor mixing ratio and b tagged water vapor mixing ratio between WRFH- and WRF- for June and August in 2008. Differences are respectively calculated from WRFH- and WRFS- for each PBL scheme

Full size image

5 Summary and conclusions

In this study, we have addressed the sensitivity of simulated land–atmosphere interactions to model physics parameterization and lateral terrestrial flow description over a high mountainous area, the Heihe River Basin in Northwest China. Two ensembles of convection-permitting simulations with the fully coupled atmosphere-hydrology model WRF-Hydro and the standalone WRF model are generated by varying turbulence parameterization with three PBL schemes (YSU, MYJ, and ACM2), which allows for assessing the robustness of results. All the simulations are set up for three consecutive years from 2008 to 2010, using 3-km high horizontal resolution. To assess the strength of land–atmosphere interactions, the advanced evaporated water tagging method is embedded with both WRF-Hydro and WRF to quantify the contribution of local evaporated water to precipitation in the study area. Our main findings are summarized in the following.

Ensemble results show that spatial patterns and monthly variations of air temperature, precipitation, and evapotranspiration are similarly simulated by changing the PBL scheme and terrestrial flow description. PBL schemes show a modest impact on the simulated monthly basin-averaged precipitation and evapotranspiration. By considering lateral terrestrial flow movement in coupled WRF-Hydro, evapotranspiration is distinctly increased with surface soil moisture regardless of different PBL parameterization, whereas the precipitation is not much affected.

Driven by atmospheric lateral boundary forcing only, the coupled WRF-Hydro ensemble reasonably reproduces the daily streamflow in its seasonal cycle and variabilities. Different PBL parameterizations induce a spread in simulated streamflow during the rainy and peak flow period, but not during the dry and recession period. This highlights the sensitivity of simulated streamflow to modeled precipitation in fully coupled modeling.

The results of land surface-precipitation feedback analysis and evaporated water tagging demonstrate the positive feedback and the non-neglectable role of lateral terrestrial flow on land–atmosphere interactions in the study area. Despite the relatively small precipitation recycling values less than 2.2%, which is related to the small-scale analysis area, PBL parameterization and lateral terrestrial flow are found to both affect the regional precipitation recycling. A reduced vertical mixing is associated with a higher precipitation recycling.

Overall, this joint investigation demonstrates the simulated land–atmosphere interactions strength in dependency of the parameterized model physics in regional climate modeling. Most importantly, the presented ensemble results highlight that the precipitation recycling ratio increases spatially and temporally due to the consideration of the lateral water flow, irrespective of how the PBL scheme parameterizes vertical mixing. This result reinforces the noteworthy role of lateral terrestrial flow components in the modeled hydrology–land surface–atmosphere earth systems (e.g., Fan et al. 2019; Prein et al. 2015; Santanello et al. 2018). We conclude that further studies targeting land–atmosphere interactions by applying a climate modeling approach should be conducted by accounting for the description of the terrestrial hydrological compartment.