A low order dynamical model for runoff predictability

Abstract

Recent work has identified potential multi-year predictability in soil moisture (Chikamoto et al. in Clim Dyn 45(7–8):2213–2235, 2015). Whether this long-term predictability translates into an extended predictability of runoff still remains an open question. To address this question we develop a physically-based zero-dimensional stochastical dynamical model. The model extends previous work of Dolgonosov and Korchagin (Water Resour 34(6):624–634, 2007) by including a runoff-generating soil moisture threshold. We consider several assumptions on the input rainfall noise. We analyze the applicability of analytical solutions for the stationary probability density functions (pdfs) and for waiting times for runoff under different assumptions. Our results suggest that knowing soil moisture provides important information on the waiting time for runoff. In addition, we fit the simple model to daily NCEP1 reanalysis output on a near-global scale, and analyze fitted model performance. Over many tropical regions, the model reproduces the simulated runoff in NCEP1 reasonably well. More detailed analysis over a single gridpoint illustrates that the model, despite its simplicity, is able to capture some key features of the runoff time series and pdfs of a more complex model. Our model exhibits runoff predictability of up to two months in advance. Our results suggest that there is an optimal predictability “window” in the transition zone between runoff-generating and dry conditions. Our model can serve as a “null hypothesis” model reference against more complex models for runoff predictability.

1 Introduction

There are several approaches to modelling and predicting water runoff (Nash and Sutcliffe 1970). The first approach is numerically simulating it using physical models (Chikamoto et al. 2015; Ajami et al. 2016; Kanamitsu et al. 2002; Nakaegwa 2008; Manabe 1969; Dai 2016; Beck et al. 2017, and others). The advantages of this approach is that these models are physically-based, and that they allow the runoff to be efficiently incorporated as a component of a complex climate model, or reanalysis. The disadvantage is that numerical models are too complex to provide theoretical probability distributions for the runoff, or analytic expressions relevant for its predictability.

The second approach is using statistical models (Mandelbrot and Wallis 1968; Bunde et al. 2013; Lehner et al. 2017; Kundzewicz et al. 2014; Kirono et al. 2010). This approach is computationally simpler, and can exploit empirical relationships that the physical models can not yet simulate well. In addition, sometimes a particular statistical model can directly result from an assumed form of the physical model (Klemes 1978). Moreover, a statistical model can be used to complement a physical model in a so-called “statistical–dynamical approach” (e.g., Slater and Villarini 2018). However, usually statistical models do not provide insights into the governing physical processes responsible for the relationships found in the observations. Moreover, it may be difficult to extrapolate empirical relationships found in limited observations to more extreme unobserved situations, to ungauged basins, or to future climate conditions (Nash and Sutcliffe 1970).

A third modelling approach is based on stochastic dynamical models. They combine computational simplicity with a physically-based framework (Naidenov and Sveikina 2002; Dolgonosov and Korchagin 2007; Bartlett et al. 2015; Zielinski 1984). Despite advances in this area, such models have not been sufficiently tested against more complex climate models which represent both atmospheric dynamics and land surface processes. In addition, some studies (Naidenov and Sveikina 2002; Dolgonosov and Korchagin 2007) do not consider a hydrologic threshold—a value of the system state at which the system exhibits sudden changes in dynamics (James and Roulet 2009; Penna et al. 2011; McMillan et al. 2014, and others). An example of such a threshold is runoff that abruptly increases above a certain soil moisture value. It is important to consider hydrologic thresholds because they occur in field observations (e.g., James and Roulet 2009; Penna et al. 2011). Bartlett et al. (2015) break important new ground by introducing a threshold that depends on two variables: rainfall and antecedent soil moisture. On the other hand, a piecewise constant soil-moisture-runoff threshold is analysed in Zielinski (1984).

Overall, the advantage of stochastic dynamical models is that they are both physically-based, and computationally efficient. Moreover, it may allow us to directly relate the probability density function (pdf) of runoff to the physical parameters of the hydrologic system. This may be very useful if one wants to understand how changes in these parameters (due to, for example, land use change or anthropogenic climate change) may affect the hydrologic pdfs. In addition, these pdfs can be compared to output of more complex models such as global climate models (GCMs).

We adopt the stochastic dynamical modeling approach since our goal is to analyze runoff predictability and to directly relate runoff pdfs and return waiting times to the properties of the hydrologic system. In contrast to some previous work, here we aim to develop the simplest possible representation of the underlying system, while accounting for the potential non-linearity in the soil moisture-runoff relationship. We also incorporate a hydrologic threshold previously found in observations (James and Roulet 2009; Penna et al. 2011; Meyles et al. 2003; McMillan et al. 2014, and others). We hence adopt the simple nonlinear runoff model of Dolgonosov and Korchagin (2007) (hereafter DK2007), which has been derived from first principles, and augment it by adding a soil moisture threshold, and by explicitly including evapotranspiration. Notably, in this model runoff depends just on soil moisture, but not on rainfall, which simplifies some analytic formulations.

A central notion of this paper is predictability. Here we broadly define predictability using the philosophy of DelSole (2004): a variable is considered predictable in a given model on a given time scale if and only if its probabilistic forecasts (conditional on some initial conditions) at that lead time are different from the climatological distribution for at least some values of initial conditions. A necessary and sufficient condition for predictability as thus defined is the dependence of forecast pdf on the initial conditions. Qualitatively, this dependence may be visualized through plotting bivariate pdfs of future forecast and initial condition (to be shown later), or by a simple scatterplot of modelled values on themselves at some time lag. Quantitatively, linear dependence can be estimated using autocorrelation function (ACF). A limit of linear predictability is then a lag time when the ACF crosses a given threshold (e.g., a threshold of statistical significance). A variable that has no linear predictability on a given time scale may still be non-linearly predictable.

The purpose of this study is to construct a low-order dynamical model of runoff, and to analyze its predictability using these methods. This work centers on the derivation of the analytical pdfs for soil moisture and runoff, and of the waiting time for runoff occurrence (Sect. 2), as well as on the sensitivity analysis of the model (Sect. 3). We conclude our analysis by comparing the model to NCEP1 reanalysis output (Sect. 4) and to the original model of DK2007, discuss some model caveats (Sect. 5) and provide a future outlook (Sect. 6).

2 Model formulation and analytical expressions for some metrics

2.1 Model formulation

The original zero dimensional water balance model for a single location (Dolgonosov and Korchagin 2007) reads (in a slightly different notation):

$$\begin{aligned} \frac{dy}{dt} = \mu + b \xi _1 - r(y), \end{aligned}$$

(1)

with

$$\begin{aligned} r(y) = k y^q (1 + b_2 \xi _2). \end{aligned}$$

(2)

Here y is soil moisture, t is time, $\mu$ is low-frequency deterministic effective rainfall (rainfall minus evapotranspiration), b is effective rainfall standard deviation, and r is runoff. Note, that $\mu$ can in principle also include a seasonal climatology of rainfall variations. Parameters k and q define the non-linear relationship between soil moisture and runoff. The model uses two standard Gaussian noises $\xi _1$ and $\xi _2$. The former is the rainfall noise, and the latter models the stochastic fluctuations in the watershed characteristics.

We modify this model by including an explicit threshold, a simple linear representation of evapotranspiration, and by also considering a more realistic rainfall noise structure. On the other hand, we neglect the fluctuations in watershed characteristics. The revised model, which we use on a daily time scale, reads:

$$\begin{aligned} \frac{dy}{dt} = -\lambda y + \mu + b \xi - r(y), \end{aligned}$$

(3)

where $\lambda y$ represents evapotranspiration, and $\mu + b\xi$ is precipitation with a low-frequency deterministic (e.g. long-term mean or climatology) and a stochastic component (to be discussed later). Note that the mean seasonal cycle can be easily included into $\mu$. For our analytical calculations, however, we will use time-independent long-term mean values. The linear dependence of evapotranspiration on soil moisture is, of course, a crude approximation. Linear relationship of evapotranspiration ratio (evapotranspiration over net radiation) has been previously considered by Koster and Suarez (2001) based on empirical relationships in July output of an atmospheric general circulation model. When seasonality in net radiation is not considered, this implies a linear relationship between soil moisture and evapotranspiration. Neglecting the impacts of runoff, such linear relationship is also implicit in autoregressive models of order 1 (AR1) for soil moisture (Yu and Cruise 1982; Delworth and Manabe 1988; Chikamoto et al. 2015). Finally, r(y) represents runoff, which is given by the following:

$$\left\{ \begin{aligned} r(y) = & \;0\quad if\quad y < y_{c} \quad \quad \quad \quad \quad \quad \;\;(4) \\ r(y) = & \;k(y - y_{c} )^{q} \quad {\text{otherwise}},\quad \quad \quad (5) \\ \end{aligned} \right.$$

Thus, $y_c$ is the threshold value of soil moisture, above which runoff is generated. We formulate runoff as a function of soil moisture alone, not rainfall, because of (1) consistency with the physically-derived formulation of DK2007 and other previous work (e.g., Klemes 1978; Meyles et al. 2003; McMillan et al. 2014), (2) the presence of travel time of water between throughfall and streamflow at measurement sites (McMillan et al. 2014), (3) the tendency of the new water to be a minor fraction of runoff across a range of studies (e.g., James and Roulet 2009) and (4) computational advantages, since in this case runoff is a function of one random variable only (soil moisture). Specifically, the latter will allow us to derive useful analytical formulae for stationary pdfs and runoff waiting times (Sects. 2.2, 2.3, 2.4).

The model equation can be also rewritten in the following form:

$$\begin{aligned} dy = [-\lambda y + \mu - r(y)] dt + b \Delta p, \end{aligned}$$

(6)

where dy is the soil moisture change over a time period dt and $b \Delta p$ are precipitation anomalies. Here we use $dt=1$ day. In addition, $\Delta p$ are the normalized precipitation anomalies, and b is the standard deviation of the final precipitation anomalies. We consider two different formulations for the precipitation anomalies. In the first formulation (A) we assume that $\Delta p = dW \sim N(0, dt)$, e.g., standard Wiener process increments.

In the second case (B), we take $\Delta p$ from high-frequency rainfall anomalies identified in daily rainfall data from the NCEP1 reanalysis (Kalnay et al. 1996, to be discussed in detail later). Finally, in the third case (C), the model is forced by the actual NCEP1 daily rainfall. We discuss advantages and disadvantages of the simplifying assumption used in (A) throughout the paper.

2.2 Fokker–Planck equation and its stationary solution

In this section we present the solution of the stationary Fokker–Planck equation (FPE) describing the pdf p(y) of the soil moisture y for the formulation A with the idealized Gaussian rainfall noise. We provide the full derivation in “Appendix 1”. The steady-state FPE on $y \in (0, \infty )$ reads:

$$\begin{aligned}&\frac{\partial }{\partial y}\left[ a(y)p(y) \right] - \frac{1}{2} \frac{\partial ^2}{\partial y^2} \left[ \sigma p(y) \right] =0, \nonumber \\&\quad a(y)=-\lambda y + \mu - r(y) \end{aligned}$$

(7)

with $\sigma =b^2$. Solving this equation we obtain the stationary pdf for y as:

$$\left\{ \begin{aligned} p(y) = & \;N_{1} \exp \left\{ {\frac{2}{\sigma }(\mu y - \frac{1}{2}\lambda y^{2} )} \right\}\quad if\quad 0 < y < y_{c} \quad \quad \quad \quad \quad \quad \quad \quad (8) \\ p(y) = & \;N_{1} \exp \left\{ {\frac{2}{\sigma }\left[ { - \frac{{\lambda y^{2} }}{2} + \mu y - \frac{k}{{q + 1}}(y - y_{c} )^{{q + 1}} } \right]} \right\} \qquad \quad \quad \quad \quad \quad (9) \\ & \quad if \quad y \geq y_{c}, \quad \end{aligned} \right.$$

where $N_1$ is a constant chosen so that the pdf integrates to 1 over all $y>0$. In practice, an upper limit for the integration interval is chosen where p(y) becomes sufficiently small. Using Eqs. (4) and (5). the corresponding pdf for runoff p(r) above the soil moisture threshold can be calculated as

$$\begin{aligned} p(r)=\ & {} N_2 r^{\frac{1-q}{q}} \exp \left\{ \frac{2k^{-\frac{1}{q}}(\mu - \lambda y_c) r^{\frac{1}{q}}}{\sigma } - \frac{\lambda k^{-\frac{2}{q}}r^{\frac{2}{q}}}{\sigma } \nonumber \right. \\&\left. - \frac{2k^{-\frac{1}{q}}r^{\frac{q+1}{q}}}{\sigma (q+1)} \right\} , \end{aligned}$$

(10)

where

$$\begin{aligned} N_2 = N_1 \frac{k^{-\frac{1}{q}}}{q} \exp \left\{ \frac{2 \mu y_c}{\sigma } - \frac{\lambda y_c^2}{\sigma } \right\} \end{aligned}$$

(11)

is a constant.

2.3 Analytical expression for waiting time for runoff

The goal of our study is to estimate the predictability of runoff in a simple zero-dimensional stochastic null hypothesis model. In this model, runoff is a nonlinear function of soil moisture. Previous work suggested that the latter can be represented as red noise obtained by the integration of stochastic forcing by rainfall (Delworth and Manabe 1988; Chikamoto et al. 2015), which leads to long-term predictability. We are interested in quantifying to which extent this predictability translates into predictability for runoff. We focus first on the average waiting time between runoff events and its uncertainty. This quantity can be useful to quantify and assess the risk of flooding in riparian regions (Langill and Abizaid 2020; Marchetti et al. 2020).

More specifically, here we calculate the mean waiting time until runoff r exceeds a particular value v. This problem is equivalent to finding the mean waiting time until the soil moisture, originally at y, hits a corresponding value u, necessary to generate runoff v. This value can be easily calculated by solving Eq. 5 for y. This is a problem known in stochastical dynamical systems’ analysis as the “first passage time” problem (Gardiner 1985). It can be shown that the mean passage time T(y) before soil moisture first hits level u satisfies the ordinary differential equation (see Gardiner 1985):

$$\begin{aligned} a(y) \frac{\partial T(y)}{\partial y} + \frac{1}{2} \sigma \frac{\partial ^2 T(y)}{\partial y^2} = -1 \end{aligned}$$

(12)

with boundary conditions in our particular case as (see Gardiner 1985):

$$\begin{aligned} \begin{aligned} \frac{\partial T(y)}{\partial y} \Bigr |_0&= 0 \\ T(u)&= 0. \end{aligned} \end{aligned}$$

(13)

In “Appendix 2” we show that T(y) can be calculated as:

$$\begin{aligned} T(y) = \frac{2}{\sigma } \int _y^u \frac{1}{p(y')} \left[ \int _0^{y'} p(z) dz \right] dy'. \end{aligned}$$

(14)

This property is interesting on its own from the point of view of time series theory. It states that for a process with an additive independent Gaussian noise, it is sufficient to know just the stationary pdf and the magnitude of the noise to calculate the mean waiting time to cross from one value to another. In other words, knowing the underlying dynamics is not required.

2.4 Standard deviation of waiting time for runoff

This section describes the derivation of the standard deviation of waiting time for runoff that exceeds a particular value. The second moment of passage time $T_2(y)$ satisfies the following equation (Gardiner 1985):

$$\begin{aligned} a(y) \frac{\partial T_2(y)}{\partial y} + \frac{1}{2} \sigma \frac{\partial ^2 T_2(y)}{\partial y^2} = -2 T(y) \end{aligned}$$

(15)

The boundary conditions in our case are:

$$\begin{aligned} \begin{aligned} \frac{\partial T_2(y)}{\partial y}\Bigr |_0&= 0 \\ T_2(u)&= 0. \end{aligned} \end{aligned}$$

(16)

It can be shown (“Appendix 3”) that the solution is:

$$\begin{aligned} T_2(y) = \frac{4}{\sigma } \int _y^u \frac{1}{p(y')} \left[ \int _0^{y'} p(z) T(z) dz \right] dy'. \end{aligned}$$

(17)

The mean and the second moment can be used to find the standard deviation of waiting time $\sigma _T$ as follows:

$$\begin{aligned} \begin{aligned} \sigma _T(y) = \sqrt{T_2(y) - T(y)^2}. \end{aligned} \end{aligned}$$

(18)

3 Model output and sensitivity analysis

3.1 Model output for “standard” parameter settings

This section presents some model output for a set of “standard” parameters (Table 1). These settings are chosen based on a fit to daily 1970–2002 NCEP1 reanalysis output (Kalnay et al. 1996) for a Malaysia data point (lon = 101.25$^\circ$, lat = 4.76$^\circ$). The parameter fitting procedure is described in detail in Sect. 4. We choose this location as it exhibits a relatively weak seasonal cycle, and a prominent runoff-generating threshold. More detailed analysis of model simulations forced with actual rainfall is provided in Sect. 4.

In contrast to Sect. 4, b is chosen as the standard deviation of just the high-frequency rainfall anomalies. These are rainfall deviations from a LOWESS fit trend with a span of 1 month (Cleveland 1979). We show the autocorrelation function (ACF) of this noise in Fig. 1, and pdf in Fig. 5 (top left). The anomalies are characterized by a mild positive autocorrelations for lags up to two days, and mild negative autocorrelation for lags of four to twelve days. The pdf is reasonably close to a normal distribution (Fig. 5, top left), but it is positively skewed (Table 1). Table 1 enumerates differences in key statistics between original NCEP1 rainfall anomalies and high-frequency NCEP1 rainfall anomalies. Naturally, the original rainfall is more variable than the high-frequency part, however, it is also less skewed because of the addition of the more symmetric annual cycle (e.g., Fig. 16).

Moreover, b and $\mu$ are then scaled by an equal factor so that runoff is generated only some of the time. Since our model includes the runoff-generating threshold, we are interested in simulations where this threshold is being crossed. This scaling is required to compensate for the effect of removing the seasonal cycle (as it will be shown later, no rainfall scaling is required to simulate intermittent runoff when actual NCEP1 rainfall is used). The final settings are summarized in Table 2.

Figure 2 shows the time series output of the last 20,000-day period of a run that was ran for one million daily time steps, with a spin-up of 300,000 time steps. We use the strong order 1.5 Taylor scheme (Kloeden and Platen 1999) for the model integration. The soil moisture keeps alternating between the values below the 670 mm threshold (corresponding to no runoff), and above the threshold (corresponding to runoff). Sometimes random variability in rainfall creates prolonged excursions of soil moisture away from the threshold, on the order of years. This results in extended high-flow or no runoff conditions. This indicates runoff predictability, which we analyze in more detail in the following sections.

Table 1 Some key statistics of scaled high-frequency NCEP1 rainfall noise, compared with the original high-frequency NCEP1 rainfall noise, and to the original NCEP1 rainfall anomalies

Table 2 Standard parameter settings for the simple nonlinear runoff model with a threshold

Fig. 1

Autocorrelation function of daily high-frequency rainfall anomalies of NCEP1 reanalysis for years 1970–2002 for a Malaysia location (lon = 101.25$^\circ$, lat = 4.76$^\circ$)

Fig. 2

Simulated time series of soil moisture (upper panel), and runoff rates (lower panel) from last 20,000 days of the simulation (at 1 day time step resolution) of the simple runoff model with standard parameter settings. Red line: soil moisture threshold of 670 mm

Figure 3 displays the pairs plot for the the full model output (excluding the spin-up): soil moisture, runoff, and waiting time for runoff (top row to bottom row). Waiting time for runoff for a time step $t_0$ is the difference between the minimum $t_r \ge t_0$ at which runoff occurs, and $t_0$. Here, diagonal panels display marginal pdfs of key model output, such that ith output variable corresponds to the ith diagonal panel. Panels in the lower left show a bivariate joint pdfs of model output. Specifically a panel in the ith row and the jth column displays the bivariate pdf of the ith and jth variables. Upper right panels display correlations. Specifically, a panel in the ith row and the jth column displays the correlation between the ith and the jth variable.

The distribution of soil moisture (1st row, 1st column) is roughly symmetric. This indicates that at these parameter settings the stabilizing effect of the runoff that pulls the soil moisture down to the soil moisture threshold is relatively small. Negative soil moisture skewness been found in another model (Bartlett et al. 2015) for a particular parameter setting, yet in that model soil moisture is actually bound by a hard upper threshold which it can not exceed. Soil moisture has a moderate positive correlation with runoff (1st row, 2rd column), and a moderate negative correlation (1st row, 3rd column) with the waiting time for runoff. Here, runoff is a deterministic function of soil moisture. Yet, the correlation between the two is considerably less than one, because of the nonlinearity of their relationship. The drier it is, the longer the waiting time for runoff, because it takes longer for random fluctuations in rainfall to bring soil moisture up to the runoff-generating threshold. The runoff pdf (2nd row and 2nd column) is a positively skewed distribution. This pdf compares reasonably well with prior work that considers runoff a function of both soil moisture and rainfall (Bartlett et al. 2015). We note that these pdfs are sensitive to model parameter settings (to be discussed later). Runoff has a weak negative correlation with the waiting time for runoff (2nd row, 3rd column), because at positive runoff this time is zero, while at zero runoff this time is positive. The soil moisture and conditional runoff pdfs (for non-zero runoff) are in excellent agreement with the analytical solutions (Fig. 4) from the Fokker–Planck equation.

The assumption of normally distributed rainfall used so far needs to be evaluated in more detail. Figure 5 compares the pdfs obtained using numerical model runs forced with realistic high-frequency noise structure (formulation B) to the analytical pdfs assuming Gaussian noise. Three locations are considered so that they sample different climatic regimes, and model parameters are fit to daily NCEP1 data for each location. Standard deviation b is the one corresponding to standard deviation of the high-frequency precipitation anomalies. Here, the numerical model was integrated using the second order weak explicit Platen numerical method (Kloeden and Platen 1999). We do not use the order 1.5 Taylor method as it requires two different random variables as a forcing. The high-frequency rainfall anomalies from the 33-year long reanalysis period are simply recycled to fit one million daily time steps. The first 300,000 time steps are discarded. Even though the realistic rainfall noise can be substantially skewed, the analytical pdfs capture the mean and standard deviation of the realistic noise case relatively well.

Furthermore, we provide an additional check of the viability of the independent noise assumption. Specifically, we compare pdfs from the numerical model forced with actual NCEP1 1970-2002 daily rainfall for the Malaysia location (formulation C) to another simulation where the high-frequency rainfall anomalies were reshuffled so that they become serially independent (blue and green lines in Fig. 6). Both simulations are run for 15,053 days, with the first 3000 days discarded as spinup. Analysis of the soil moisture time series indicates that such spin-up time is reasonable. Precipitation has been recycled beyond the length of the 1970–2002 period to fill in the 15,053 days. In the case of reshuffled high-frequency precipitation, final precipitation has been limited to positive values, resulting in some differences in the rainfall pdf. The soil moisture and runoff results show almost no difference between the two simulations. This further suggests that the assumption of independent daily rainfall may be reasonable.

Overall, the results suggest that the assumption of Gaussian precipitation noise at a daily time scale may be appropriate to model some aspects of the soil moisture and runoff pdfs. The assumption is also expected to be correct at longer time scales as real-world precipitation tends to become more independent and normal with time averaging (Storch and Zwiers 1999).

Fig. 3

“Pairs plot” for the output of the simple runoff model. Diagonal panels display histograms of soil moisture, runoff, and waiting time for runoff, with red lines showing the means, blue dashed lines showing the medians, and blue dotted lines showing the 95% confidence intervals. Top right panels display correlations between variable pairs, with the font size proportional to the correlation coefficient. Bottom left panels show scatterplots of variable pairs. See text for more information

Fig. 4

Comparison of analytical (red) and numerical (blue) pdfs for soil moisture (all time steps), and runoff (nonzero runoff time steps) for the run of the simple runoff model with standard parameter settings

Fig. 5

Comparison of numerical pdfs for rainfall anomalies, soil moisture and runoff from simulations forced with realistic noise structure (blue) to the analytical pdf with Gaussian rainfall noise (red). (Left): Malaysia (lon = 101.25$^\circ$, lat = 4.76$^\circ$), (center): Northern Europe (lon = 15.00$^\circ$, lat = 60.00$^\circ$), and (right): Novaya Zemlya (lon = 99.38$^\circ$, lat = 79.04$^\circ$)

Fig. 6

Comparison of pdfs for rainfall, soil moisture, and runoff for the Malaysia location for a simulation forced with original NCEP1 rainfall (blue), and the one forced with reshuffled high-frequency rainfall with independent residuals (green). Also shown are the pdfs from the NCEP1 reanalysis (orange). The box in the box-and-whisker plots represents the interquartile range, the vertical black line represents the median, and the whiskers extends to the most exreme data points which are no more than 1.5 interquartile ranges away from the box

Figure 7 demonstrates runoff waiting times, and their uncertainty from the analytic expressions, derived in Sects. 2.3 and 2.4 (orange lines), compared with results from the numerical model integrations (blue lines and black contours). For this plot, the model is integrated for 10 million time steps (with the initial 300,000 time steps discarded) in order to better sample different soil moisture states. We use the order 1.5 strong Taylor method. Both the mean waiting time, and its spread, appear to match relatively well, although the analytical results tend to be slightly smaller compared to the numerical ones. The higher the soil moisture the less, on average, is the waiting time for runoff, since it takes less time for random fluctuations in rainfall to bring the soil moisture up to the level necessary to generate runoff of that magnitude. The standard deviation of the waiting time decreases with soil moisture, as well. For the “any runoff” case the mean and the standard deviation converge to zero at the threshold value of soil moisture (670 mm). For a given soil moisture the waiting times are higher for runoff > 0.05 mm day$^{-1}$, compared to any runoff.

These results are compared to the realistic high-frequency precipitation noise case (grey lines). We do not perform any time reshuffling of the high-frequency noise. For this case, for the reasons previously outlined we use the weak explicit second order Platen numerical method. As “Appendix 4” suggests, both numerical methods are appropriate for the daily time step. In the realistic noise simulation, when the soil moisture is relatively high, the waiting time mean and standard deviation are similar to the Gaussian noise case. However, during dry periods it takes considerably longer, on average, to wait for runoff in the realistic forcing case. We thus conclude for the analysis of waiting time statistics that the Gaussian noise assumption is not valid at the daily time scale. We henceforth adopt the formulation B (realistic high-frequency noise) to model path-dependent metrics.

The dependence of the waiting times on initial soil moisture provides a clear indication of predictability. For instance, in the realistic noise case if the soil moisture attains values around 660 mm, it takes on average less than 100 days to get the first runoff event. However, it takes on average around 300 days if soil moisture is around 640 mm. The reasons for the difference in the waiting times between the Gaussian and the more realistic noise case need to be studied further. Our results pave the way for construction of conditional pdfs for runoff exceedance times given the soil moisture. Our approach can then be seen as an improvement over the frequentist pdfs derived from the observations alone, as there may simply be a lack of observations to derive such pdfs. In future studies this framework could be expanded to include other parameters such as, for example, soil water at various depth, season, soil type, air temperature, etc. However, to be useful to policy-makers any relevant runoff models will need to be calibrated with field measurements, not reanalysis output as it was done here.

We further demonstrate (“Appendix 5”) that the slope of the waiting time to runoff relationship is independent of the runoff exceedance value. This indicates that waiting time predictability extends to other runoff exceedance values.

Fig. 7

Kernel density estimates of the joint probability density function for waiting times for any runoff (left) and runoff > 0.05 mm day$^{-1}$ (right) as well as soil moisture for time steps without runoff from the numerical model simulation with standard parameter values (black contour lines). The contour lines are equidistant between 1 and 95% of the maximum of the kernel density estimate. Also shown are the waiting time means ± standard deviations conditional on binned soil moisture values from the numerical model with the Gaussian precipitation noise (blue lines), with realistic precipitation noise (grey lines), and from the analytic expressions (orange lines). Parameters as in Fig. 5

3.2 Sensitivity analysis of the simple model

In this subsection, we present a sensitivity analysis of the simple model, with the goal of investigating the effect of changing the parameters on the output of the model.

Fig. 8

Sensitivity analysis of natural logarithm of soil moisture (y-axis) stationary pdf (color) (using equations (8), (9)) as a function of simple model parameters which are varied individually away from their standard settings (x-axes), whilst keeping other parameters at their standard values. Parameter units are: q [unitless], k [mm$^{1-q}$ day$^{-1}$], $\mu$ [mm day$^{-1}$], $\lambda$ [day$^{-1}$], $y_c$ [mm], and b [mm day$^{-1}$]. Red lines indicate soil moisture values at which corresponding pdfs reach about 10% of their maximum values

First, we explore the sensitivity of the analytical soil moisture y pdf to the model parameters in Fig. 8. The figure indicates relative importance of the precipitation mean $\mu$, the evapotranspiration constant $\lambda$, and the runoff threshold $y_c$ for the pdf of the soil moisture, whereas the nonlinear generation parameter k and exponent q, as well as the rainfall standard deviation b appear to be less critical. Decreasing the runoff exponent decreases the negative feedback on the soil moisture at very high level of soil moistures, thereby allowing the upper tail of the soil moisture pdf to extend to higher values. When precipitation mean is increased, or evapotranspiration constant $\lambda$ is decreased, mean soil moisture increases less than linearly as the parameters change. This is because soil moisture has a soft cap of 670 mm (e.g., any soil moisture in excess of 670 mm goes into runoff which pulls soil moisture down towards the threshold value). Yet, no such stabilizing effect exists below the soil moisture threshold. Thus, any changes in the hydrological parameters in our model which lead to drier conditions in this case tend to be more critical in terms of their effects on soil moisture pdf, than the changes that lead to wetter conditions. Increasing the soil moisture threshold from 335 to 1340 mm first leads to linear changes (as a function of the threshold) of the soil moisture pdf mode, while later the mode converges to a constant value considerably below the threshold. As the threshold increases, soil moisture can attain progressively greater values without running off. As it does so, evapotranspiration also increases, as it is a linear function of soil moisture in our model. Eventually the evapotranspiration becomes so strong that it hinders the further accumulation of soil moisture to the extent that the latter almost never rises to the threshold value. The major effect of the rainfall standard deviation b is on the width of the soil moisture pdf.

Fig. 9

Same as Fig. 8 but for the natural logarithm of runoff pdf (from equations (9), (10)) and without the 10% pdf guidance lines

We present the sensitivity analysis of the natural log of the analytical runoff pdf in Fig. 9. Note that this is not a conditional pdf, and does not integrate to one for each parameter value, but rather to the overall runoff probability. Thus, the point probability mass at zero runoff is omitted from the plot. We see that at low values of q runoff events tend to become weaker. At these q values as soil moisture increases beyond the threshold, runoff increases as a low power of soil moisture. This is expected to draw the soil moisture back to its threshold value via prolonged sluggish runoff, as opposed to rapid intense runoff. Rainfall mean $\mu$ appears to have a fundamental impact on runoff. Lowering the mean even slightly below the standard value of 5.1 mm day$^{-1}$ leads to continuously dry conditions (Fig. 9). Naturally, runoff also appears to increase at lower evapotranspiration, and lower runoff thresholds. At the threshold of 400 mm runoff becomes essentially continuous.

It is noteworthy to examine the probability density of extreme runoff events from the analytic expressions. As Fig. 9 indicates, extreme runoff events (e.g., 5 mm day$^{-1}$) are possible at large q values. The parameter q is related to the dominant regime of runoff over the watershed (turbulent vs. laminar) in the original model of DK2007. The corresponding parameter in our model may be also related to watershed characteristics. Caution should be exercised, however, in translating these results to the real world as the Gaussian noise assumption may lead to inaccuracies in simulating tails of the pdfs (Fig. 5).

Fig. 10

Sensitivity analysis of the natural logarithm of mean waiting time for runoff (color) from numerical experiments for different initial soil moisture values (y-axis) as a function of simple model parameters which are varied away from their standard settings (x-axes). Parameter units are: $\mu$ [mm day$^{-1}$], $\lambda$ [day$^{-1}$], and b [mm day$^{-1}$]. Omitted parameters use standard parameter settings. White regions are soil moisture conditions which happen too infrequently to make a robust average. The models runs use realistic high-frequency precipitation noise input

Figure 10 (left) shows the sensitivity of waiting time for runoff incidence (expressed as a natural log) to some model parameter settings. Since the analytic expressions were found to be inadequate to simulate path-dependent metrics (Sect. 3.1), we extract the waiting times from numerical simulations. We run the model for 1 million time steps with the initial 300,000 days discarded as equilibration, using the weak second order explicit Platen numerical method and realistic precipitation noise structure as previously described. Since varying parameters away from standard values shifts the soil moisture pdf, and since we need a large number of soil moisture samples to calculate the mean waiting time, we are restricted to limited parameter ranges. Runoff generation parameters are excluded from this analysis, as they only affect the output of the model at values above the threshold of 670 mm. The figure illustrates that the waiting time, as expected, increases at low soil moistures. Yet, the most profound increases in the waiting time are achieved by ramping up evapotranspiration parameter $\lambda$ or by decreasing the mean rainfall $\mu$. The influence of rainfall standard deviation on the waiting time is relatively mild.

Fig. 11

Sensitivity analysis of autocorrelation function (ACF) of runoff as the simple model parameters are varied away from their standard settings (x-axes). Parameter units are: q [unitless], k [mm$^{1-q}$ day$^{-1}$], $\mu$ [mm day$^{-1}$], $\lambda$ [day$^{-1}$], $y_c$ [mm], and b [mm day$^{-1}$]. The results are based on numerical model simulations which use realistic high-frequency precipitation noise forcing

A measure of runoff predictability can be obtained from the structure of the autocorrelation function (ACF) of runoff. Fig. 11 shows the sensitivity of the runoff ACF to varying model parameters. The ACF results are based on numerical model integrations with same specifications as the ones used for the mean waiting times sensitivity analysis. Note that in the white regions the model generates no runoff. Runoff generation exponent q is of fundamental importance for the runoff ACF, with smaller exponents generating more autocorrelated runoff, which is potentially more predictable. The first reason for this is as follows. Theoretically, soil moisture behavior can be approximated by red noise (Delworth and Manabe 1988). Statistical simulations suggest that a power of a red noise process is not as autocorrelated as the original process (Fig. 12). In our model q is the exponent by which soil moisture anomalies away from the threshold are raised to obtain runoff. This is expected to lead to larger runoff autocorrelations at low q close to one, and lower autocorrelation at high q. In addition, everything else being equal, higher q is expected to lead to a steeper slope of runoff as a function of soil moisture. As explained in previous work (Koster and Suarez 2001), this can break the autocorrelation in soil moisture. As runoff is a function of soil moisture, this can thus contribute to lower autocorrelation in runoff.

Parameters k and b impart a considerably smaller effect on the ACF. The reduction of the ACF at higher b can be seen as the consequence of increasing random noise in the system. An interesting effect can be seen for the parameters affecting runoff probability $\mu$, $\lambda$ and $y_c$. During the transition to the completely dry regime, ACF first increases, and than rapidly decreases before no runoff is generated. A similar effect has been observed under very different parameter values, and using Gaussian rainfall noise (not shown). Lower runoff autocorrelation in wetter regimes may be due to the fact that increase in runoff with soil moisture in these regimes can break the autocorrelation of soil moisture itself (Koster and Suarez 2001). Since runoff is a function of soil moisture, lower soil moisture autocorrelation can then lead to decreased autocorrelation in runoff. At the parameter values of the highly autocorrelated runoff (transitions to dry regimes), it occurs in prolonged rare events (not shown). The reasons for higher autocorrelation at the transition parameter values need to be analysed in more detail in further studies.

Fig. 12

ACF of simulated AR(1) noise time series with standard deviation of 50 and length = 100,000; as well as of the cubic power of the same time series. Units are arbitrary

4 Comparison with NCEP1 reanalysis output

The model presented here captures some key physical features of runoff. Whether it has any fidelity in representing the dynamics and statistics of more complex climate models shall be addressed in this section. We compare the results of our zero-dimensional null hypothesis model with the simulated daily soil moisture and runoff data from the NCEP1 reanalysis (Kalnay et al. 1996) for years 1970–2002. NCEP1 is chosen over NCEP2 reanalysis and GFDL-ESM2M model due to the fact that NCEP1 data are consistent with a runoff generating soil moisture threshold for some locations. Later years were not used due to an intermittent bug affecting runoff output (Ebisuzaki, Pers. Comm., 2020). NCEP1 reanalysis uses the soil model of Mahrt and Pan (1984) and Pan and Mahrt (1987). This model has two layers. Hydraulic diffusivity and conductivity are parametrized as functions of soil volumetric water content. Evaporation is obtained using a two-step approach. When the soil is relatively wet it is equal to potential evaporation from the modified Penman relationship. This relationship includes atmospheric stability, moisture deficit, wind speed, and radiative fluxes. If potential evaporation demands can not be met, the evaporation instead depends on the soil moisture gradient in the upper soil layer (Mahrt and Pan 1984; Pan and Mahrt 1987). In addition, the NCEP1 soil model includes transpiration based on the simple biosphere (SiB) model (Ebisuzaki, Pers. Comm., 2019).

The parameters of our simplified model are estimated grid-point-wise from the reanalysis dataset in the following way. First, the runoff threshold $y_c$ is found from soil moisture ${\mathbf {y}} = (y_1, y_2, \ldots , y_l)$ and runoff ${\mathbf {r}} = (r_1, r_2, \ldots , r_l)$ time series of length l according to an algorithm that is similar to a bisection method. Besides the soil moisture and runoff, the altorithm also takes in a bandwidth c and a threshold tolerance parameter tol [mm]. First, the algorithm sorts soil moisture values in increasing order. Then, it considers the lowest c soil moisture values, which are centered on rank $n_0$. If more than 50% of these values generate runoff, then soil moisture associated with index $n_0$ becomes the threshold and the algorithm stops. Otherwise, top c soil moistures are considered, with $n_1$ as the median index. If less than 50% of these datapoints generate runoff then threshold is set to the soil moisture associated with index $n_1$. Thus, when there is too little or too much runoff, the threshold is set directly, without invoking the bisection-like method. Otherwise, we calculate $n_f$ rank as the mean of $n_0$ and $n_1$. The 50% threshold condition is checked again for $n_f$. If less then 50% of the c sorted soil moistures centered on $n_f$ are runoff-generating then $n_f$ becomes the new $n_0$. Otherwise, it becomes the new $n_1$. The new $n_f$ is calculated again as the mean of $n_0$ and $n_1$ and the procedure is repeated. Next iterations are generated in the same way. The algorithm stops when the difference between soil moistures associated with $n_0$ and $n_1$ drops below $tol \times range({\mathbf {y}})$, at which point the threshold is set to the soil moisture corresponding to the final $n_f$, which is the mean of the final $n_0$ and $n_1$. We use $tol=0.02$ and $c=51$ because these values result in both efficient and reasonable algorithm performance.

We illustrate the performance of the threshold estimation method for a single grid point (lon = 185.62$^{\circ }$, lat = 65.71$^{\circ }$ in Fig. 13. We choose this point because it exhibits a pronounced threshold, so that the algorithm performance can be checked by a simple visual inspection. In the NCEP1 reanalysis, there is a marked threshold above which runoff tends to non-linearly increase with soil moisture away from zero. Our threshold algorithm correctly identifies the location of this threshold $y_c$. Similar algorithm results have been found for a range of diverse locations (not shown).

Fig. 13

Illustration of the dexterity of the soil moisture threshold algorithm. Scatterplot of NCEP1 reanalysis runoff and soil moistures for a single grid point (lon = 185.62$^{\circ }$, lat = 65.71$^{\circ }$; gray circles). Red line: soil moisture threshold estimated by our threshold identification algorithm. Around the threshold there is a transition from a predominantly dry regime, to a runoff-generating regime. Black line: fitted power relationship between soil moisture excess above the threshold and runoff

An initial estimate of our simplified model parameters k and q is provided by the linear regression of $\ln ({\mathbf {r}})$ on $\ln ({\mathbf {y}}-y_c)$ for soil moisture above the threshold in NCEP1 reanalysis (Fig. 13). This initial estimate is then used as a starting value for a non-linear regression to obtain better estimates of k and q. The fitted runoff - soil moisture curve $r(y)=k(y-y_c)^q$ is shown in black in Fig. 13.

We then diagnose the theoretical evapotranspiration in NCEP1 using changes in soil moisture, rainfall and runoff (Eq. 6). Zero-intercept linear regression of the diagnosed evapotranspiration on soil moisture provides an estimate of $\lambda$ (see Eq. 6). We optimize different parameters separately in accordance with previous work (Nash and Sutcliffe 1970).

To obtain a forward simulation, we force the simple runoff model with daily rainfall from the NCEP1 reanalysis, which includes the seasonal cycle (formulation C). We use explicit weak second order Platen numerical scheme, which only requires a single random variable as a forcing, whereas the order 1.5 strong Taylor scheme requires two random variables. We use the time step of 1 day, to match the reanalysis time resolution.

Fig. 14

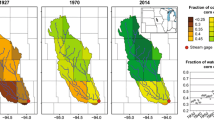
Maps of model parameters fitted to daily NCEP1 reanalysis output for years 1970–2002. See Table 2 for parameter description and their units. $dr/dy^*$ parameter is described in text. The lower left panel shows the Nash-Sutcliffe Efficiency (NSE, Nash and Sutcliffe 1970) as a measure of model fidelity relative to the complex NCEP1 dataset over years 1988–2002. NSE = 1 corresponds to a perfect match of simulated runoff in simple model forced with NCEP1 precipitation and the reanalysed NCEP1 runoff. Lower right: map of decorrelation time scale [day] of runoff for years 1988–2002 as modelled using the simple model with fitted parameters and forced with a location-specific constant mean rainfall plus high-frequency NCEP1 rainfall anomalies (see text for more information)

4.1 Spatial maps of model parameters and model performance

We first analyze maps of fitted model parameters, and model performance compared to NCEP1 daily reanalysis as a reference in Fig. 14. We discard regions with no or almost no runoff (five or less days with runoff) from the analysis as the results of the parameter fits may be difficult to interpret in those cases. In addition, once the threshold is fitted, if there are again five or less days with runoff when the soil moisture is above the threshold, the parameters k and q are not estimated. Furthermore, those locations are also excluded from the model performance evaluation.

Mean (upper left) and standard deviation (upper right) of daily precipitation are determined directly from NCEP1 daily precipitation (Fig. 14). The pattern of the runoff exponent q estimates shows a range of values from 2 to 4 for most areas that are generating substantial runoff. This exponent characterizes the non-linearity in the relationship between the runoff and the excess soil moisture $y^* = y - y_c$. The most nonlinear response can be found in many tropical regions, such as the Amazon, parts of Africa, India and southeast Asia, but also eastern United States and west coast of North America. According to Fig. 11, high q values may correspond to a rapid loss of auto-correlation and a reduced level of predictability. On the other hand, there are minima over the Tibetian plateau, southern USA, Greenland, and some other regions in transition zones between dry and wet areas. The values over Greenland and the Tibetan Plateau are clearly related to the presence of snow, which is not properly captured in our simplified null hypothesis model. The low values over southern USA are observed in the transition area bordering on dry areas with limited runoff, and are related to insufficient runoff data used to fit this exponent. Previous work has related parameter q to the dominant nature of flow over the watershed, e.g, laminar vs. turbulent (Dolgonosov and Korchagin 2007). However, because our parameterization uses not soil moisture, but rather its anomaly above a threshold, these are different parameters, and are not intercomparable. We do not discuss parameter k here, as its units depend on q, resulting in limited interpretability. Instead, we estimate the effect changing y above the threshold has on runoff r by $dr/dy^*$, the slope in the relationship between runoff above the threshold and excess soil moisture. The pattern of this slope has some association with the overall magnitude of rainfall. Specifically, this slope attains high values over Amazonia, as well as parts of southeast Asia and central Africa. The maxima over the Tibetian plateau and Greenland are again linked to the presence of snow and land ice over these areas.

Estimated evapotranspiration constant $\lambda$ exhibits pronounced maxima over the tropical regions and is smallest in the polar regions and over Tibet (Fig. 14). Previously, Delworth and Manabe (1988) have estimated an inverse of $\lambda$, which they call “evaporative damping time scale” using output from GFDL atmospheric climate model. There are some qualitative similarities between the spatial patterns of $\lambda$ in the two studies. The general pattern of smaller evapotranspiration constant values over higher latitudes results from the lower net radiation balance at the surface at these latitudes, as discussed in Delworth and Manabe (1988). The smooth latitudinal gradient of the net radiation field can not, however, explain the minimum over Tibet (Delworth and Manabe 1988). In their work, this minimum is formed because that area is snow covered. Thus, some fraction of the mean net radiation surplus there is used to melt snow, which decreases potential evaporation and thus $\lambda$ in their analysis. Overall, our values of $\lambda$ are smaller compared to the values deduced from Delworth and Manabe (1988). This may be because they use a constant small soil field capacity (parameter similar to soil moisture threshold) of 150 mm. Since $\lambda$ is the ratio of potential evaporation to soil field capacity, this may result in higher values of $\lambda$ in their study.

The pattern of critical soil moisture derived by fitting our zero-dimensional null-hypothesis model to the NCEP1 data highlights a remarkably similar $y_c$ for most areas. This may be due the simplicity of the soil moisture model used in NCEP1 (Mahrt and Pan 1984). Furthermore, uniform soil type with a uniform top layer soil moisture capacity is used across the globe (Ebisuzaki, Pers. Comm., 2020). In addition, as is with some other parameters, anomalous $y_c$ values occur in ice-covered areas of Greenland and Tibet. Note that our analytical model solutions have been calculated under the assumptions that neither the mean rainfall nor the model parameters are seasonally modulated. This assumption can affect some of the interpretations of the key patterns.

We also show the map of Nash-Sutcliffe Efficiency (NSE, Nash and Sutcliffe 1970) of the fitted model over years 1988–2002 (Fig. 14). NSE is defined as (Nash and Sutcliffe 1970):

$$\begin{aligned} NSE = \frac{F_0^2-F^2}{F_0^2}, \end{aligned}$$

(19)

where $F_0^2$ is the sum of the observed squared deviations from the observed mean (in this case, NCEP1 reanalysis), and $F^2$ is the sum of squared errors (SSE) of the simple model with respect to the reanalysis. The maximum value of NSE (representing the perfect model) is 1, while decreases below this value indicate deterioration of model performance. At values below 0 the model SSE becomes larger than the sum of the observed squared deviations from the mean. For daily data, NSE values over 0.40 have been reported in literature as satisfactory for daily simulations (e.g., Moriasi et al. 2007). Based on this cutoff, our calibrated model can be considered satisfactory for Central America, parts of South America, of Africa, and of southeast Asia. In addition, reasonable performance is found for the west coast of the United States. These tend to be tropical regions with high precipitation, absence of hard snow cover, and a weaker seasonal cycle compared to polar regions. On the other hand, the NSE is low in polar regions, even after calibration (Fig. 14). This is because these regions include snow, which is poorly represented in NCEP1 (W. Ebizuaki, personal communication), and not represented at all in our model. In addition, polar regions experience a strong seasonal cycle. This may require different values of model parameters for different seasons. However, we use the same parameter values for all seasons, which may also be an additional caveat of our approach.

The reasonable performance compared to NCEP1 over many tropical areas, suggest that our simple null hypothesis model can be useful for studying runoff and its predictability in multi-basin studies over the tropics. Deviations in observed and simulated dynamics from our simplified zero-dimensional model may indicate the presence of more complicated processes, including effects of runoff from other gridpoints, strong seasonality, urbanization, land-use change, presence of irrigation and rivers and other factors affecting the nonlinear relationship between runoff and excess soil moisture (equations (4) and (5)).

Finally, we also provide the map of ACF decorrelation time of the simple model (lower right panel of Fig. 14). For this analysis we use location-specific mean rainfall plus location-specific high-frequency rainfall anomalies (other settings are the same as in other panels). Thus, high-frequency rainfall structure is the same as in NCEP1 but rainfall loses its seasonality. We do not use the actual NCEP1 rainfall due to complex effects of seasonality in the forcing. We also do not use a normally distributed rainfall with mean and standard deviation of the NCEP1 rainfall because using such a distribution has resulted in many points without runoff. We note that using high-frequency rainfall from NCEP1 also to some extent expands the dry areas without runoff (displayed in white). This is because there are no dry and wet seasons in the this rainfall time series. This means there is less chance for prolonged rainfall events.

The decorrelation time map shows distinct minima over the Amazon basin, west coast of North America, parts of southeast Asia and eastern USA. These regions are associated with higher precipitation (Fig. 14, upper left). Because the soil moisture threshold is similar across most areas in our analysis, it is reasonable to expect more runoff in areas with more precipitation. As it has been discussed previously, higher dependence of runoff of soil moisture in the wet regimes can break the autocorrelation of soil moisture (Koster and Suarez 2001). This, in turn, can decrease runoff autocorrelation itself, as runoff in our model is a direct function of soil moisture. Moreover, same regions tend to be associated with higher q estimates, suggesting a more nonlinear runoff as a function of soil moisture above the threshold (cf. Fig. 14). This may cause decreased autocorrelation as discussed before (cf. Sect. 3.2). Other areas of decreased autocorrelation are Tibet and parts of Greenland. As stipulated before, these areas are not well-represented in our model as we do not consider ice or snow. Central North America, and most of continental mid- and high-latitude Eurasia are associated with longer decorrelation times. These areas tend to be drier and have lower q estimates compared to the fast decorrelated areas. We note that decorrelation times in these areas can be as high as 2 months long. There are also areas with high decorrelation times over Africa and South America, but these areas are much smaller. Runoff predictability on a time scale of two months may be important from the water management perspective.

Overall, our analysis suggests that there may be an optimal predictability window for runoff at relatively dry yet runoff-generating conditions. Furthermore, in this window runoff predictability may extend to at least two months.

4.2 Comparison to the original DK2007 model

In this section we compare the performance of the new model with the original DK2007 model. To remind the reader, our model differs by (1) the absence of noise in the k parameter, (2) presence of the runoff threshold and (3) incorporation of evaporation into the model structure. As a consequence, the model needs rainfall as a forcing. The original model, on the other hand, is forced by effective rainfall (i.e., rainfall minus evaporation).

The parameters of the original DK2007 model are estimated from the NCEP1 data in the similar way to the model developed here, but with some differences. Specifically $\mu$ and b are associated with the effective precipitation. This results in many points with negative $\mu$; they are excluded from further analysis. Both the runoff-generating threshold and $\lambda$ are set to 0. In the estimates of k and q, generation of starting values for the nonlinear regression works somewhat differently. Specifically, only data points with soil moistures above the $y_c$ of the corresponding new model are used for the linear regression to generate these starting values. This modification results in more stable parameter estimates. The final nonlinear regression procedure is unchanged (except, of course, for employing the zero-threshold for runoff). Finally, for simplification, we do not use any noise on the k parameter in the DK2007 model. The reason is that we do not have any forcing time series for that noise.

We generate the NSE field of the DK2007 model in the same way as for the new model. Figure 15 shows the difference (our model minus the DK2007 model) of the NSE. Our model generally shows as improvement over the tropical regions, some mid- and high-latitude coastal regions, and Greenland. On the other hand, DK2007 model appears to be better at simulating most mid- and high-latitude continental areas. There are several reasons for improvement of our model in some regions. First, transpiration data is not available from NCEP1. Excluding transpiration from the forcing may degrade the DK2007 model performance. In addition, DK2007 forcing comes from the difference in rainfall and evaporation. Both of these have associated errors. Subtracting one uncertain variable from another is expected to result in increase in error, if errors in two variables are independent. Furthermore, there is a clear threshold in the NCEP1 reanalysis data between 650 and 680 mm. Thus, a zero-threshold model is a mis-specified model for such data. Using a mis-specified model can lead to a poorer fit of the soil-moisture-runoff curve, and contribute to worse performance. There is also a reason for the degradation of performance in our model in some regions. We model evaporation as a linear function of precipitation, whereas it is a forcing in the DK2007 model. In the regions where the linear season-independent approximation is poor, we can thus expect degraded performance. It is not surprising then that our model tends to perform worse in regions with strong seasonality.

Overall, the main advantages of our model seem to be less requirements on the forcing data. Our model is particularly useful when evapotranspiration forcing data or forecasts are not available. In addition, for locations with a runoff generating threshold, this model is the only correctly specified model.

Fig. 15

Nash–Sutcliffe efficiency difference between the original DK2007 model over years 1988–2002 and the new model used here (new minus original)

4.3 Performance comparison for a single grid point

For the more detailed performance analysis, we choose a point over Malaysia (lon = 101.25$^{\circ }$, lat = 4.76$^{\circ }$) because of the weak seasonal cycle, relative to the noise level, and presence of a strong runoff-generating threshold. Again, the zero-dimensional null hypothesis model is forced with the daily reanalyzed precipitation from NCEP1 (formulation C). We discard the first 3000 days of the forward simulation, and keep running the model for 12,053 days, to exactly match the length of the NCEP1 period. After the end of year 2002, NCEP1 precipitation is recycled for another 3000 days, i.e., precipitation time-series re-starts again from year 1970. Model parameters are the same as the ones used for the standard model integration in Sect. 3.1, except the precipitation mean and std. are those of the reanalysis-derived rainfall. We note that $\lambda$ is found to be significant (p< 0.001) based on simple zero-intercept linear regression not accounting for dependence.

Figure 16 compares NCEP1 reanalysis with the output of the fitted simple model for years 1980–1987. The NCEP1 precipitation reveals a double wet season with peaks in boreal spring and autumn. There is a dry period at the beginning of the year. Rainfall is characterised by day-to-day persistence, with no dry days during the peaks of the wet periods. Soil moisture tends to stay above the runoff-generating threshold most of the time. The deep trough in the soil moisture occurs during the beginning of the year, whereas the second trough between the peaks of the wet seasons is much less pronounced (Fig. 16). The second wet season is associated with higher soil moisture. The time series of runoff follows the soil moisture, with markedly higher runoff during the second wet season. There can be long dry periods without any substantial runoff during the dry season. These are the periods when soil moisture consistently stays below the runoff-generating threshold. Runoff, as soil moisture, is characterised by profound serial dependence. The two extreme rainfall events at the end of years 1981 and 1987 are associated with extreme precipitation events. Yet, there are no pronounced soil moisture peaks during those events, indicating that for those cases excess rainfall runs off as opposed to replenishing the water storage in the soil.

The empirically-optimized simple runoff model is able to effectively capture many aspects of the reanalysis output (Fig. 16). For example, the model also exhibits sharp troughs in soil moisture with associated cessation of runoff at the beginning of the year. Yet, the model tends to underestimate the depth of these troughs. Moreover, the return of the soil moisture to its maximum level during the beginning of the spring wet season appears to happen earlier in the model. This may simply be in part because there is more soil moisture in the simple model to start with at the end of the dry season. The behavior during the double wet season is captured relatively well. Yet, in the model, the two soil moisture peaks during the double wet season are of similar magnitude, which is in contrast to the larger peak in the fall in NCEP1. Similarly, the simple model cannot capture the magnitude of the second peak in runoff, as well as the extreme rainfall/runoff events. In the NCEP1 reanalysis soil moisture model, infiltration rate is equal to the precipitation up to the so-called maximum infiltration rate, and any excesses which can not evaporate turn into runoff (Mahrt and Pan 1984). There is no such maximum infiltration rate in our model. This may explain its inability to capture the runoff extremes in NCEP1.

We compare the relevant pdfs for this location in Fig. 6 (orange and blue lines). Rainfall exhibits a bimodal distribution, with the largest peak between 10 and 15 mm day$^{-1}$, and a long upper tail. The probability density for soil moisture is negatively skewed. The fitted model overestimates the height of the mode of the soil moisture pdf and underestimates the lower tail, but captures the shape of the pdf relatively well. When the soil is sufficiently wet (which is most of the time in our case, see the bottom panel of Fig. 16), the NCEP1 evaporation is determined using a modified Penman relationship which includes wind speed, radiative fluxes, atmospheric stability, and moisture deficit. Hence, at the same soil moisture values, evaporation will be different depending on the variety of atmospheric conditions, which in turn is expected to increase the variability in the soil moisture itself. Yet, in our simple runoff model, evapotranspiration is simply a linear function of soil moisture. This is consistent with the broader soil moisture pdf found in the reanalysis. In addition NCEP1 includes transpiration that uses SiB model (Ebisuzaki, Pers. Comm., 2019), as well as nudging of soil moisture to climatology, which may explain part of the differences between the pdfs. Some aspects of the runoff pdf are also captured, such as the long upper tail. Yet, the model exhibits a mild bimodality in the pdf. There is no such pronounced bimodality in the reanalysed runoff pdf. The model captures the interquartile range particularly well. Overall, the fitted simple model captures some aspects of the time series and pdf of the reanalysed soil moisture and runoff. Using realistic rainfall structure as a forcing, it can therefore be used as an appropriate null-hypothesis model to study aspects of runoff predictability.

Fig. 16

Comparison of daily NCEP1 reanalysis output (orange) with the tuned simple precipitation-forced model (blue) for years 1980–1987 for a point over Malaysia (lon = 101.25$^{\circ }$, lat = 4.76$^{\circ }$). Tick labels on the x-axes mark the start of the corresponding years. Red horizontal line is the runoff-generating soil moisture threshold

5 Caveats

Our study is subject to important caveats. Our model is a zero-dimensional bucket model. Thus, it does not explicitly include processes that occur on the vertical or spatial scale in reality, such as diffusion of soil water and inflowing runoff from other grid points in the watershed. Moreover, McMillan et al. (2014) find that even across just one catchment more than one model may be needed, due to substantial spatial variability in hydrological processes. Transpiration and snow are not included.

In a landmark study, Koster and Suarez (2001) show analytically that soil moisture autocorrelation (which influences runoff autocorrelation in our study) depends on, among other things, the seasonality of the atmospheric forcing, as well as on the feedback between soil moisture and atmospheric forcing. Only the formulation C considers the seasonal forcing. Seasonally-varying catchment parameters (McMillan et al. 2014), and the feedback between soil moisture and rainfall can be subject of future work.

Modelled evapotranspiration in our model is a simple linear function of soil moisture. Inclusion of more realistic evapotranspiration should be considered in future work. One potential avenue to is to parametrize variations in atmospheric conditions that modify the evaporation as an additional noise term. The magnitude of this term can be, for example, be proportional to soil moisture, indicating the larger influence of the stochastic atmospheric conditions on the actual evaporation in wetter conditions that is found in the more complex model of Mahrt and Pan (1984) and Pan and Mahrt (1987). The power law relationship between soil moisture and runoff, although stemming from physical considerations (Dolgonosov and Korchagin 2007), does not explain why soil moisture may lag after runoff during storm events in dry conditions (Penna et al. 2011) leading to a switch in the hysteretic loop in the streamflow-soil-moisture space depending on the antecedent soil moisture conditions.

6 Conclusions and future work

We develop a physically-based stochastic–dynamical low order model of soil moisture and runoff motivated by the previous work of Dolgonosov and Korchagin (2007). The model includes a simple parameterization for evapotranspiration, a soil-moisture-runoff threshold, and a nonlinear runoff (as a function of soil moisture) above the runoff threshold. Because the model requires only rainfall as a forcing it can be applied in conditions when evaporation hindcasts or forecasts are not readily available.

We consider an idealized model formulation with an independent Gaussian rainfall forcing, as well two formulations with more realistic noise forcings. The idealized Gaussian formulation is able to capture some aspects of stationary pdf of system state that is found in a more complex formulation. The Gaussian formulation can be used to derive analytic expressions for the pdfs of soil moisture and runoff, and for the waiting times for runoff above any value. However, the simple formulation can not well represent path-dependent metrics (e.g., waiting times for runoff) that are found in a more complex model formulation.

Comparison of fitted model to NCEP1 reanalysis reveals its skill in reproducing daily NCEP1 runoff output over many tropical areas. When forced with high-frequency rainfall anomalies derived from NCEP1, our simple model indicates areas over North America and Eurasia where runoff may be predictable for up to 2-months. More detailed analysis at a location with a relatively weak seasonal cycle and a pronounced threshold shows that the model can also capture the negatively skewed soil moisture distribution, and positively skewed runoff distribution found in NCEP1.

In our model the drier it is, the longer it takes to wait for runoff above a given level, suggesting a fundamental state-dependent predictability relationship for runoff. We prove that for the Gaussian noise case the slope of the waiting time vs. soil moisture curve is independent of the particular runoff exceedance value. We explore the sensitivity of the pdfs, and the time series properties of soil moisture and runoff to model parameters. When moving from wet (runoff-generating) to dry (no runoff) regimes in the parameter space, an interesting behavior is observed in the autocorrelation function of runoff (ACF). Specifically, it first increases, and then rapidly decreases before the parameters enter into a dry regime, therefore highlighting possible windows of optimal predictability, especially in semi-arid regions.

The model, and its analytical formulae can be useful in future theoretical studies exploring the effects of global climate or land-use changes. The model can be utilized to quantify effects of these changes on hydrological pdfs, and on runoff predictability. The study of Chikamoto et al. (2015), explores the long-term potential predictability of soil moisture in a coupled general circulation model and compares the results to the Delworth and Manabe (1988) zero dimensional null hypothesis model of soil moisture. This method enabled Chikamoto et al. (2015) to identify processes that deviate from the simple Ornstein-Uhlenbeck integration of white precipitation noise, thereby improving our understanding of sources of potential predictability in key hydrological variables. Our study is an extension of this approach to a new hydrological variable – runoff, and presents a new null hypothesis model for runoff predictability.

Appendices

Appendix 1

In this appendix, we present the derivation of the solution of stationary Fokker–Planck equation (FPE) describing the pdf of the soil moisture y and runoff r for the formulation A with the Gaussian noise. The steady-state FPE on $y \in (0, \infty )$ reads:

$$\begin{aligned}&\frac{\partial }{\partial y}\left[ a(y)p(y) \right] - \frac{1}{2} \frac{\partial ^2}{\partial y^2} \left[ \sigma p(y) \right] =0, \nonumber \\&\quad a(y)=-\lambda y + \mu - r(y) \end{aligned}$$

(20)

with $\sigma =b^2$. The general solution on an interval $(0, \infty )$, slightly modified to account for constant $\sigma$ is (Gardiner 1985)

$$\begin{aligned} p(y) = \frac{N}{\sigma } \exp \left\{ \frac{2}{\sigma } \int _0^y a(x) dx \right\} , \end{aligned}$$

(21)

where N is a normalization constant that ensures that the pdf integrated to 1 over the interval. In practice, we formulate two separate Fokker–Planck equations above and below the threshold, and solve them separately for the unnormalized stationary probability density functions p(y), each of which is then scaled so that the pdf is continuous at $y=y_c$ (Gardiner 1985). In our case, the stationary pdf of y is:

$$\left\{ \begin{aligned} p(y) = & \;N_{1} \exp \left\{ {\frac{2}{\sigma }\left( {\mu y - \frac{1}{2}\lambda y^{2} } \right)} \right\}\quad if\quad 0 < y < y_{c} \quad \quad \quad \quad \quad \quad \quad \quad (22) \\ p(y) = & \;N_{1} \exp \left\{ {\frac{2}{\sigma }\left[ { - \frac{{\lambda y^{2} }}{2} + \mu y - \frac{k}{{q + 1}}(y - y_{c} )^{{q + 1}} } \right]} \right\}\quad if\quad y \ge y_{c} ,\quad \quad (23) \\ \end{aligned} \right.$$

where $N_1$ is a constant chosen so that the pdf integrates to 1 over all $y>0$. In practice, an upper limit for the integration interval is chosen where p(y) becomes sufficiently small.

The corresponding pdf for runoff g(r(y)) above the threshold can be obtained using the change of variables technique (Klemes 1978):

$$\begin{aligned} g(r)= & {} N_2 r^{\frac{1-q}{q}} \exp \left\{ \frac{2k^{-\frac{1}{q}}(\mu - \lambda y_c) r^{\frac{1}{q}}}{\sigma } - \frac{\lambda k^{-\frac{2}{q}}r^{\frac{2}{q}}}{\sigma } \nonumber \right. \\&\left. - \frac{2k^{-\frac{1}{q}}r^{\frac{q+1}{q}}}{\sigma (q+1)} \right\} \end{aligned}$$

(24)

where

$$\begin{aligned} N_2 = N_1 \frac{k^{-\frac{1}{q}}}{q} \exp \left\{ \frac{2 \mu y_c}{\sigma } - \frac{\lambda y_c^2}{\sigma } \right\} \end{aligned}$$

(25)

is a constant. To simplify the notation we will refer to this pdf as p(r) in the main text of the paper.

Appendix 2

In this appendix, we derive the mean waiting time before soil moisture, originally at y, reaches level u, necessary to generate runoff of magnitude v. We restrict the analysis to the interval (0, u), where the lower barrier at 0 is reflecting, and upper boundary at u is absorbing (the reflecting assumption on the lower boundary is of no importance since we assume there is no probability density there). We define G(y, t) as the probability that soil moisture is still in the interval (0, u) at time t. It can be shown that the mean passage time T(y) before soil moisture first hits level u, $T(y)=\int _0^{\infty } G(y,t) dt$ satisfies the ordinary differential equation (see Gardiner (1985)):

$$\begin{aligned} a(y) \frac{\partial T(y)}{\partial y} + \frac{1}{2} \sigma \frac{\partial ^2 T(y)}{\partial y^2} = -1 \end{aligned}$$

(26)

The boundary conditions are (see Gardiner 1985):

$$\begin{aligned} \begin{aligned} \frac{\partial G(0,t)}{\partial y}&= 0 \\ G(u, t)&= 0 \end{aligned} \end{aligned}$$

(27)

which means that:

$$\begin{aligned} \begin{aligned} \frac{\partial T(y)}{\partial y} \Bigr |_0&= \int _0^\infty \frac{\partial G(0,t)}{\partial y} dt = 0 \\ T(u)&= \int _0^\infty G(u,t) dt = 0 \end{aligned} \end{aligned}$$

(28)

The quantity T(y) obeys the following general solution (see Gardiner (1985), note that in our case $\sigma$ is constant):

$$\begin{aligned} T(y) = 2\int _y^u \frac{1}{\psi (y')} \left[ \int _0^{y'} \frac{\psi (z)}{\sigma } dz \right] dy', \end{aligned}$$

(29)

where

$$\begin{aligned} \psi (y) = \exp \left( \int _0^y 2\frac{a(x)}{\sigma }dx \right) \end{aligned}$$

(30)

and a(x) is obtained from the stationary Fokker–Planck equation (Eq. 7). This expression can be simplified further noting that in our case $\psi (y) \propto p(y)$. Thus, in practice, T(y) is calculated as:

$$\begin{aligned} T(y) = \frac{2}{\sigma } \int _y^u \frac{1}{p(y')} \left[ \int _0^{y'} p(z) dz \right] dy'. \end{aligned}$$

(31)

Appendix 3

This section describes the derivation of the standard deviation of waiting time for runoff that exceeds a particular value. We first find the expression for the second moment of waiting time, and then use it to find the standard deviation. The second moment of passage time $T_2(y) = \int _0^\infty t G(y,t)dt$ satisfies the following equation (Gardiner 1985):

$$\begin{aligned} a(y) \frac{\partial T_2(y)}{\partial y} + \frac{1}{2} \sigma \frac{\partial ^2 T_2(y)}{\partial y^2} = -2 T(y) \end{aligned}$$

(32)

The first boundary condition is:

$$\begin{aligned} \begin{aligned} w_2(0)&= \frac{\partial T_2(y)}{\partial y}\Bigr |_0 = \int _0^\infty \frac{\partial }{\partial y}[t G(0,t)] dt \\&= \int _0^{\infty } \left[ \frac{\partial t}{\partial y}G(0,t) + t \frac{\partial G(0,t)}{\partial y} \right] dt = 0 \\ \end{aligned} \end{aligned}$$

(33)

by using the boundary conditions on G (Eq. 27), considering that t is not a function of y, and representing the second part of the integral as a limit:

$$\begin{aligned}&\int _0^{\infty } t \frac{\partial G(0,t)}{\partial y} dt = \lim _{g \rightarrow \infty } \int _0^g t \frac{\partial G(0,t)}{\partial y} dt \nonumber \\&\quad = \lim _{g \rightarrow \infty } \int _0^g 0 dt = 0 \end{aligned}$$

(34)

The second boundary condition is:

$$\begin{aligned} T_2(u) = \int _0^\infty t G(u,t) dt = 0. \end{aligned}$$

(35)

We first modify Eq. (32) by multiplying by $\frac{2}{\sigma (y)}$ and re-arranging:

$$\begin{aligned} \frac{\partial ^2 T_2(y)}{\partial y^2} + 2 \frac{a(y)}{\sigma } \frac{\partial T_2(y)}{\partial y} = -\frac{4T(y)}{\sigma }. \end{aligned}$$

(36)

This is a first-order ODE in $w_2$:

$$\begin{aligned} \frac{\partial w_2(y)}{\partial y} + 2\frac{a(y)}{\sigma } w_2(y) = -\frac{4T(y)}{\sigma }. \end{aligned}$$

(37)

The solution of this equation is:

$$\begin{aligned} w_2(y) = -\frac{4}{\psi (y)} \int _0^y \frac{\psi (z)T(z)}{\sigma }dz. \end{aligned}$$

(38)

Now,

$$\begin{aligned} T_2(u) - T_2(y) = \int _y^u w_2(y') dy'. \end{aligned}$$

(39)

Thus,

$$\begin{aligned}T_2(y) & = -\int _y^u w_2(y') dy' \\ &= 4 \int _y^u \frac{1}{\psi (y')}\nonumber \left[ \int _0^{y'} \frac{\psi (z)T(z)}{\sigma }dz \right] dy'. \end{aligned}$$

(40)

Using $\psi (y) \propto p(y)$ the result becomes:

$$\begin{aligned} T_2(y) = \frac{4}{\sigma } \int _y^u \frac{1}{p(y')} \left[ \int _0^{y'} p(z) T(z) dz \right] dy'. \end{aligned}$$

(41)

The mean and the second moment can be used to find the standard deviation of waiting time $\sigma _T$ as follows:

$$\begin{aligned} \begin{aligned} \sigma _T(y) = \sqrt{T_2(y) - T(y)^2}. \end{aligned} \end{aligned}$$

(42)

Appendix 4

In this appendix, we evaluate the performance of the second order explicit weak Platen numerical integration method. We integrate the model at standard parameter settings using the Platen numerical method, using the 10 million daily time steps of which the first 300,000 are discarded. As Fig. 17 indicates, two different methods generate nearly identical waiting times that are similar to the analytical results. This indicates that time step of 1 day is reasonable, and justifies the use of the Platen numerical method for some simulations.

Fig. 17

Same as Fig. 7 (left), but the gray lines are conditional means ± standard deviations from the numerical model run with Gaussian noise integrated using explicit second-order weak Platen numerical method. The gray lines almost completely overlap with blue lines (1.5 order strong Taylor numerical method)

Appendix 5

In this appendix, we prove that the slope of the waiting time to runoff is independent of the runoff exceedance value v (corresponding to exceedance soil moisture value u) . First, we derive a result which will be needed for the computation. If f(x) is continuous on (x, b) then:

$$\begin{aligned} \int _x^b f(x) dx = F(b) - F(x), \end{aligned}$$

(43)

where F is an antiderivative of f. Thus,

$$\begin{aligned} \frac{\partial }{\partial x} \left( \int _x^b f(t) dt \right) = F'(b) - F'(x) = -f(x) \end{aligned}$$

(44)

From Eq. (31),

$$\begin{aligned} \frac{\partial T(y)}{\partial y} &= \frac{2}{\sigma } \frac{\partial }{\partial y} \nonumber \quad \left\{ \int _y^u \frac{1}{p(y')} \left[ \int _0^{y'} p(z) dz \right] dy' \right\} \\ &= -\frac{2}{\sigma p(y)} \int _0^y p(z) dz. \end{aligned}$$

(45)

Because soil moisture cannot be negative this is equal to:

$$\begin{aligned} -\frac{2 \times \text {cdf(y)}}{\sigma p(y)} \propto -\frac{\text {cdf(y)}}{p(y)} = g(y) \perp v. \end{aligned}$$

(46)

Equation (46) shows a fundamental result: the slope of the mean waiting time curve is independent of the runoff exceedance threshold. This means if we know just a single point on this curve for a given runoff threshold, we may be able to reconstruct a large portion of the curve if we know a curve for a different threshold. This may seem obvious, but this mathematically proves that runoff waiting times are predictable not just for the two exceedance values analyzed, but for essentially all exceedance values (at least for the parameter values considered).