Abstract
Changes in ocean properties and circulation lead to a spatially non-uniform pattern of ocean dynamic sea-level change (DSLC). The projections of ocean dynamic sea level presented in the IPCC AR5 were constructed with global climate models (GCMs) from the Coupled Model Intercomparison Project 5 (CMIP5). Since CMIP5 GCMs have a relatively coarse resolution and exclude tides and surges it is unclear whether they are suitable for providing DSLC projections in shallow coastal regions such as the Northwestern European Shelf (NWES). One approach to addressing these shortcomings is dynamical downscaling – i.e. using a high-resolution regional model forced with output from GCMs. Here we use the regional shelf seas model AMM7 to show that, depending on the driving CMIP5 GCM, dynamical downscaling can have a large impact on DSLC simulations in the NWES region. For a business-as-usual greenhouse gas concentration scenario, we find that downscaled simulations of twenty-first century DSLC can be up to 15.5 cm smaller than DSLC in the GCM simulations along the North Sea coastline owing to unresolved processes in the GCM. Furthermore, dynamical downscaling affects the simulated time of emergence of sea-level change (SLC) above sea-level variability, and can result in differences in the projected change of the amplitude of the seasonal cycle of sea level of over 0.3 mm/yr. We find that the difference between GCM and downscaled results is of similar magnitude to the uncertainty of CMIP5 ensembles used for previous DSLC projections. Our results support a role for dynamical downscaling in future regional sea-level projections to aid coastal decision makers.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
An increase in coastal sea level has major socioeconomic impacts as it can lead to, for instance, flooding, erosion, saltwater intrusion and the decline of coastal wetlands (Nicholls and Cazenave 2010). However, the magnitude of sea-level change (SLC) varies for different locations (Church et al. 2013). Regionally, projected SLC can deviate up to 50% from the global mean (Kopp et al. 2014; Slangen et al. 2014). This spatially non-uniform pattern of relative SLC is the result of different contributions, such as changes in the ocean and atmosphere, land ice mass change, vertical land motion (VLM), glacial isostatic adjustment (GIA) and terrestrial water storage (TWS) (Church et al. 2013). Here, we focus on ocean dynamic sea-level change (DSLC) due to local changes in sea-water density and local convergence or divergence of mass (steric and manometric SLC respectively, Gregory et al. 2019).
Projections of DSLC driven by climate change scenarios are commonly made with the output of coupled global climate models (GCMs, e.g. Slangen et al. 2012, 2014; Church et al 2013; de Vries et al. 2014; Kopp et al. 2014; Palmer et al. 2018). Simulations of these models can be obtained from the Coupled Model Intercomparison Project Phase 5 (CMIP5) database (Taylor et al. 2012). At the time of writing CMIP6 models are being released (Eyring et al. 2016). Computational constraints limit the horizontal ocean resolution of CMIP5 GCMs to about 100 by 100 km, but horizontal resolution varies considerably across the CMIP5 model ensemble. The vertical resolution of most GCMs is limited in shallow regions due to their unevenly spaced vertical levels at fixed depths (z-coordinates). Additionally, GCMs omit tides and storm surges. However, in shallow shelf seas such as the North Sea, small-scale bathymetric features and hydrodynamical processes such as tidal mixing can be important for simulating DSLC. Furthermore, an increased horizontal ocean resolution can give enhanced eddy activity (Suzuki et al. 2005; Penduff et al. 2010), which affects simulated sea-level variability. Thus, GCMs may not be the most appropriate means for providing DSLC projections in coastal regions. For local stakeholders and impact studies projections at a finer spatial resolution are also desired.
Sea-level projections at a finer spatial resolution can be obtained by downscaling, which is a technique to obtain regional to local detail from larger scale information (Rummukainen 2010). Here, we focus on dynamical downscaling by using a high-resolution regional climate model (RCM). Dynamical downscaling has previously been applied to study present-day hydrodynamics and the regional impact of future climate change for the North Sea and the Northwestern European Shelf (NWES) region (see Schrum et al. (2016) for a comprehensive review). These studies have mainly focused on future changes in ocean temperature, salinity and circulation (e.g. Ådlandsvik 2008; Holt et al. 2010, 2018; Mathis et al. 2013; Mathis 2013; Tinker et al. 2015, 2016, Mathis et al. 2017) and primary production and biochemistry (e.g. Wakelin et al. 2015; Holt et al. 2016). Extreme sea levels and tides have mainly been studied with barotropic models (e.g. Sterl et al. 2009; Howard et al. 2010; Pickering et al. 2012; Ward et al. 2012; Pelling et al. 2013; Pelling and Green 2014; Cannaby et al. 2016; Idier et al. 2017; Palmer et al. 2018; Howard et al. 2019). DSLC on the NWES however, has not extensively been studied with RCMs, with the exception of Mathis (2013) who analyzed the seasonal variation of 100-yr sea-level trends in the North Sea with the HAMSOM model. Consequently, the effects of downscaling DSLC projections for this region have not been fully quantified.
In other geographic regions dynamical downscaling is known to affect DSLC projections substantially. Zhang et al. (2017) used a 1/10° near-global ocean model (75°S to 75°N) driven by the atmospheric forcing of an ensemble of 17 CMIP5 GCMs for Australia. The downscaled DSLC was found to differ 1–3 cm from the original projections along the Australian coast, and was up to 20 cm larger further offshore. For the North Pacific, downscaled DSLC was computed with the regional ocean model ROMS (¼° by ¼°) for three different driving CMIP5 GCMs (Liu et al. 2016). Along the coast of Japan, downscaled DSLC can differ up to 10 cm from the original DSLC depending on the driving GCM.
In this study we assess the importance of dynamical downscaling for the NWES region and quantify the uncertainties related to constructing regional DSLC projections with CMIP5 GCMs. We do this by downscaling the simulations of two CMIP5 GCMs with a regional shelf seas model (the Atlantic Margin Model (AMM7), O’Dea et al. 2017) and comparing the results with the original simulations for two different representative concentration pathways (RCPs, Meinshausen et al. 2011). In addition, we discuss projected changes in the seasonal cycle of sea level in our simulations, which appears to be a gap in the current literature (e.g. Slangen et al. 2014; Kopp et al. 2014; Meyssignac et al. 2017; Palmer et al. 2018) but is an important aspect of extreme sea levels and tides (Pugh 1987). We assess whether the increased spatial and temporal resolution of our downscaled simulations leads to more realistic simulations of sea level on subannual timescales.
We start by presenting our downscaling setup and the methods and observational data used to evaluate our simulations in Sect. 2. Next, we show in Sect. 3 that dynamical downscaling improves historical GCM simulations compared to observations of sea surface temperature (SST), sea surface salinity (SSS), mean dynamic topography (MDT) and sea-level variability on seasonal-to-interannual timescales. We will discuss the large differences that dynamical downscaling can introduce in terms of annual mean DSLC and its different components in Sect. 4, and how these differences depend on the driving GCM and climate change scenario. In Sect. 5 we focus on subannual timescales and analyze the projected changes in the seasonal sea-level cycle of the GCM and downscaled simulations. We end with a discussion and our conclusions in Sect. 6.
2 Data and methods
Here, we introduce the RCM and GCMs (Sect. 2.1) followed by our downscaling set-up (Sect. 2.2). Next, we discuss how we decompose DSLC in our analysis (Sect. 2.3). Finally, we present our framework to compare the sea surface height (SSH) output of the different models (Sect. 2.4) and to compare to observational data (Sect. 2.5).
2.1 NEMO AMM7 and the CMIP5 GCMs
We use the AMM7 (Coastal Ocean version 6) configuration of the primitive-equation modeling framework Nucleus for European Modelling of the Ocean (NEMO) V3.6 (Madec and NEMO Team 2016) to downscale long-term simulations of two CMIP5 GCMs. AMM7 is a hydrodynamic model of the NWES region that has been extensively described and validated, and is being used for operational ocean forecasting (O’Dea et al. 2012, 2017) and marine reanalyses (Renshaw et al. 2019). Its domain (henceforth the NWES region) extends from 20°W to 13°E and from 40°N to 65°N (Fig. 1a), allowing to internally resolve the exchange of water across the shelf break. The horizontal resolution is 1/15° latitude by 1/9° longitude, or nominally 7 by 7 km. Thus, on the shelf AMM7 does not resolve the internal Rossby radius (~ 4 km) (O’Dea et al. 2012) and is not eddy-resolving, but can capture small-scale topographical features that GCMs cannot. AMM7 has 50 vertical levels with hybrid z-\({\varvec{\sigma}}\) coordinates (Siddorn and Furner 2013; see O’Dea et al. 2012 and Madec 2016 for details on handling horizontal pressure gradient errors). As a result, processes such as vertical mixing and bottom boundary layers will be handled better than in CMIP5 GCMs, in which the mean depth of the North Sea (~ 80 m) is represented by only 7–8 vertical levels.
We downscale the simulations of two example CMIP5 GCMs (Taylor et al. 2012) commonly used for sea-level projections, namely HadGEM2-ES (Collins et al. 2011) and MPI-ESM-LR (Giorgetta et al. 2013). Up to 2005, the CMIP5 GCMs are forced by observed greenhouse gas concentrations, and from 2006 to 2099 by the RCP4.5 (intermediate) or RCP8.5 (business-as-usual) scenario (Meinshausen et al. 2011). These simulations are used to force AMM7 from 1972–2099. AMM7 is spun up from 1972 to 1979; analyses are done for 1980–2099. Here we only show results for RCP8.5, whereas we show results for RCP4.5 in the Supplementary Information, as DSLC for RCP4.5 is spatially similar to that for RCP8.5 but smaller in magnitude.
The ocean component of HadGEM2-ES has 40 vertical z-levels (maximum of 17 on the shelf) and a horizontal resolution of 1° by 1° (~ 85 km) on the NWES. The ocean component of MPI-ESM-LR also has 40 vertical z-levels (maximum of 12 on the shelf) and a bipolar grid with poles on Greenland and in the Weddell Sea. The curvilinear grid has an approximate resolution of 0.45° latitude by 0.82° longitude (~ 50 km) in the central North Sea, with increasing horizontal resolution toward Greenland. As a result, MPI-ESM-LR includes several topographical features which are not captured in HadGEM2-ES, such as the Norwegian Trench, the English Channel and the Irish Sea (Fig. 1b, c).
2.2 Downscaling setup
The GCM simulations are prescribed to AMM7 as boundary conditions at the lateral ocean boundaries and at the surface in a “one-way nesting” approach. For clarity, from now on we will refer to the simulations of HadGEM2-ES and MPI-ESM-LR as GCM-HAD and GCM-MPI, respectively. The downscaled simulations from AMM7, driven by HadGEM2-ES and MPI-ESM-LR, will be referred to as RCM-HAD and RCM-MPI, respectively.
2.2.1 Atmospheric forcing
The atmospheric surface forcing is obtained from simulations of the Rossby Centre regional atmospheric model RCA4 (Strandberg et al. 2014). RCA4 has been used to dynamically downscale the atmosphere component of GCM-HAD and MPI-HAD for the European Coordinated Regional Downscaling Experiment (CORDEX) domain (Giorgi et al. 2009). Direct fluxes are used rather than bulk formulae: atmospheric pressure, precipitation minus evaporation and long-wave radiation are prescribed daily and 10 m wind and short-wave radiation 6-hourly.
Since no downscaled preindustrial atmospheric forcing is available from RCA4, we did not downscale the preindustrial control runs of HadGEM2-ES and MPI-ESM-LR. Control runs can be used to correct SSH for spurious model drift (Sen Gupta et al. 2013). As model drift is small compared to forced trends especially on the shallow continental shelf (Sen Gupta et al. 2013), we expect that dedrifting will not significantly impact our findings, in particular not the comparison between GCM and downscaled simulations.
2.2.2 Lateral boundary conditions
The lateral boundary conditions consist of monthly mean temperature and salinity, barotropic currents and SSH, which are derived from the GCMs and interpolated onto the AMM7 grid. Temperature, salinity and barotropic currents are directly prescribed, and a relaxation zone of 10 grid points with a tanh-shaped relaxation parameter relaxes the internal solution to the prescribed boundary values (Madec and NEMO Team 2016). SSH, and additionally 15 tidal constituents, are indirectly prescribed: a Flather radiation condition (Flather 1976) corrects the depth-mean velocity normal to the lateral boundaries based on the SSH gradients between the internal solution and the lateral boundaries (Madec and NEMO Team 2016). Directly prescribing SSH and prescribing barotropic currents through radiation conditions instead was found to be detrimental to the simulation of tides. SSH is derived from the ‘zos’ field of the driving CMIP5 GCMs, which gives SSH anomalies with respect to a time-invariant geoid. We ensured that global mean ‘zos’ is 0 m by removing the global mean at each timestep prior to generating the boundary conditions. The SSH boundary conditions were anomalized with respect to their spatial and temporal mean and for reasons of numerical stability an offset of 0.5 m was added.
2.2.3 River run-off and Baltic outflow
We simulate river run-off with the Total Runoff Integration Pathways (TRIP) river routing model (Oki and Sud 1998) using the daily run-off from RCA4. Exchange with the Baltic Sea through the Danish Straits and the Kattegat occurs at too small scales to resolve in AMM7. Instead, a climatology is used for temperature, salinity and barotropic currents for the Baltic inflow to the North Sea following O’Dea et al. (2017). As a consequence, downscaled DSLC along the Norwegian coast will be biased to present-day conditions.
2.3 Computing changes in bottom and atmospheric pressure and the local steric effect
To analyze the drivers of DSLC (Sect. 4.2), we decompose simulated DSLC into changes due to manometric change (local convergence/divergence of mass, which is related to bottom pressure change) and due to the local steric effect (depth-integrated density changes of the water column) as follows (Ponte 1999; Gregory et al. 2019):
where \({\varvec{\eta}}\) refers to SSH, \({\varvec{t}}\) to time, \({\varvec{g}}\) is the gravitational acceleration, \({\varvec{\rho}}\) the density and \({{\varvec{\rho}}}_{\varvec{0}}\) a constant reference density at sea level, \({{\varvec{p}}}_{{\varvec{b}}}\) the bottom pressure, \({{\varvec{p}}}_{{\varvec{a}}}\) the atmospheric pressure and \({\varvec{H}}\) the local ocean depth.
Bottom pressure changes (r.h.s. of Eq. (1), first term) and local steric changes (r.h.s. of Eq. (1), second term) are directly available from AMM7 output, but not for both GCMs. For the GCMs we therefore compute local steric change from the 3D fields of temperature and salinity, using the Gibbs SeaWater (GSW) toolbox (McDougall and Barker 2011) of the Thermodynamic Equation of SeaWater 2010 (TEOS-10). Thermosteric and halosteric SLC can be computed similarly, keeping respectively salinity and temperature constant. We subsequently compute bottom pressure change from Eq. (1). Differences in twenty-first century local steric SLC on the NWES between the direct AMM7 output and the GSW computation are less than 4 mm, so the methods are comparable.
Atmospheric pressure changes (\({{\varvec{p}}}_{{\varvec{a}}})\) also contribute to bottom pressure changes (\({{\varvec{p}}}_{{\varvec{b}}})\). Their effect on sea level, referred to as the inverse barometer (IB) effect \({{\varvec{\eta}}}_{{\varvec{I}}{\varvec{B}}}\), is computed as follows (Stammer and Huttemann 2008):
where \({{\varvec{p}}}_{{\varvec{a}}}^{\boldsymbol{^{\prime}}}\) is defined as the local pressure anomaly with respect to the global area-weighted mean atmospheric pressure \(\stackrel{-}{{{\varvec{p}}}_{{\varvec{a}}}}\) as a function of location \({\varvec{x}}\) and \({\varvec{y}}\), and time \({\varvec{t}}\). Here, for both the GCMs and downscaled simulations we compute \({{\varvec{p}}}_{{\varvec{a}}}^{\boldsymbol{^{\prime}}}\) in Eq. (2) with respect to the global mean (\(\stackrel{-}{{{\varvec{p}}}_{{\varvec{a}}}}\)) obtained from the GCM simulations. We include the IB effect in the presented sea-level results unless stated otherwise.
2.4 Comparing DSLC in the GCMs with DSLC in AMM7
Both the CMIP5 GCMs and AMM7 apply the Boussinesq approximation. The Boussinesq approximation refers to replacing in-situ density by a reference density in all equations except the vertical momentum equation and the equation of state (Gill 1983). As a result, Boussinesq models conserve volume rather than mass, and for global Boussinesq models the global-mean thermosteric sea-level change (‘zostoga’ in CMIP5 models) needs to be diagnosed. Boussinesq models are still influenced by a local steric effect (Griffies et al. 2014). Since we use one-way dynamical downscaling in a relatively small domain, we neglect the effect that refining the GCM regionally has on ‘zostoga’.
Since the spatial mean density changes in Boussinesq models while volume is conserved, the bottom pressure shows a physically spurious change (Griffies and Greatbatch 2012) following Eq. (1) (Sect. 2.3). AMM7 has Boussinesq dynamics like the GCMs, but only covers a limited region. Consequently, AMM7 does not conserve the same volume as the GCMs, leading to a different regional mean DSLC and a different (spurious) bottom pressure change.
Additionally, discrepancies in mass transport across the boundaries of the NWES region between the GCMs and AMM7 can result from the interpolation of the lateral boundary conditions (e.g. barotropic currents) from the parent grid onto the AMM7 grid and from the different representations of bathymetry, atmosphere and river run-off.
To directly compare DSLC in the GCMs with DSLC in AMM7, we correct the DSLC output of AMM7 for the differences in regional mean DSLC resulting from the Boussinesq approximation and from discrepancies in mass transport due to artefacts of the downscaling setup. A spatially uniform correction to prognostic Boussinesq SSH can be made a posteriori based on the spatial mean density change, but only for models with closed boundaries (Greatbatch 1994). This applies to CMIP5 GCMs, but not to a nested regional model. Instead, we apply a spatially uniform correction to the DSLC simulations of AMM7 by enforcing global mass conservation. To this end, we replace the area-weighted mean manometric SLC of AMM7 (regional mean DSLC due to bottom pressure change only, or equivalently, the total regional mass change) with the regional mean manometric SLC in the driving GCMs:
where \({\Delta{\varvec{\eta}}}_{{\varvec{A}}{\varvec{M}}{\varvec{M}}{\varvec{7}}}^{\boldsymbol{*}}\) and \(\Delta {{\varvec{\eta}}}_{{\varvec{A}}{\varvec{M}}{\varvec{M}}{\varvec{7}}}\) refer to corrected and uncorrected DSLC of AMM7, respectively, as a function of location and time. \(\Delta {{\stackrel{-}{{\varvec{\eta}}}}^{{{\varvec{P}}}_{{\varvec{b}}}}}_{{\varvec{A}}{\varvec{M}}{\varvec{M}}{\varvec{7}}}\) and \(\Delta {{\stackrel{-}{{\varvec{\eta}}}}^{{{\varvec{P}}}_{{\varvec{b}}}}}_{{\varvec{G}}{\varvec{C}}{\varvec{M}}}\) refer to the area-weighted mean DSLC due to bottom pressure changes only (first term on the l.h.s. of Eq. (1), excluding atmospheric pressure changes) in the NWES region, as simulated by AMM7 and the GCMs, respectively.
2.5 Observational data for model evaluation
AMM7 has been extensively tested and downscaling setups similar to ours have been validated against observations in previous studies (e.g. Tinker et al. 2015). When forced by a preindustrial control run of HadGEM3, AMM7 reproduces interannual sea-level variability observed with satellite altimetry and tide gauges well (Tinker et al. submitted). As different forcing introduces different biases, we will evaluate our historical simulations against observations in Sect. 3.
Model evaluation is complicated by internal variability: although the historical part of CMIP5 simulations is forced by observed changes in atmospheric composition (Taylor et al. 2012), the timing of internal variability in the models is not expected to match the timing of observed variability. Therefore, we focus on the capability of our models to reproduce the observations in a statistical sense. We extend the historical period 1980–2005 of our simulations to 2017 using RCP8.5. The time periods used within this window depend on the availability of each observational dataset.
Richter et al. (2017) compared 20-yr sliding windows of historical CMIP5 simulations (1850–2005) with satellite altimetry (1993–2012) in the Northern North Atlantic. They found little effect of internal variability on the correlation between simulated and observed mean dynamic topography (MDT), a measure of the average strength of geostrophic circulation. However, internal variability had a larger effect on the correlation with observed interannual sea-level variability and linear trends. Therefore, we compare satellite altimetry to simulated MDT, but use the longer records that tide gauges (TGs) provide to compare to simulated sea-level variability. A comprehensive comparison of TG records with simulated sea-level trends including the contributions of VLM, GIA, TWS and land ice mass change is beyond the scope of this study.
For MDT, we use the MDT CNES CLS18 product (Rio et al. 2014), which provides the mean SSH above the GOCO05S geoid model for the period 1993–2012. The CNES MDT is based on a combination of GRACE and GOCE data, satellite altimetry and in-situ data, and is provided on a 1/8° by 1/8° grid.
Observations of SST are obtained from the Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) (Donlon et al. 2012; Roberts-Jones et al. 2012), which combines satellite data and in-situ data. It is available at a resolution of 1/20° by 1/20° for the period 1992–2010.
Observations of SSS for 1980–2017 are derived from the EN4.2.0 dataset (Good et al. 2013), which provides quality-controlled subsurface temperature and salinity measurements from profiling instruments and Argo floats. As the spatial and temporal resolution of EN4 in the NWES region are limited, we use EN4 only qualitatively. Similarly to Tinker et al. (2015), we do not use the optimally interpolated dataset. Instead, we average salinity observations within the first 10 m below the surface over winter (DJF) and summer (JJA) months and assign them to the nearest grid cell of a 1/4° by 1/4° grid. Mean salinity values computed from less than 4 years of data are rejected.
We use monthly and annual TG records from the revised local reference (RLR) dataset obtained from the Permanent Service for Mean Sea Level (PSMSL) website (Holgate et al. 2013; PSMSL 2018). We select TGs (Supplementary Fig. 1) on the NWES with a series length of over 50 years and with data coverage of at least 28 years during 1980–2017 (\(\ge\) 75%). Stations in near proximity of the Baltic outflow are excluded, because exchange with the Baltic Sea is not resolved in any of our models (Sect. 2.2.3). Simulated annual mean SSH nearest to the TGs is subsampled based on the temporal coverage of each individual TG record.
The comparison of the GCM simulations with the AMM7 simulations, and of simulations with observations, involves datasets provided at different grids and resolutions. Throughout the paper, we will show all data on their original grids, as this best shows their spatial characteristics. When analyzing the differences between models, and between models and observations, computations are made and presented on the AMM7 grid to avoid losing the high-resolution information of AMM7. To this end, data with a different resolution and/or land mask are bilinearly interpolated and ocean grid cells that were originally land are filled with nearest neighbor interpolation.
3 The impact of dynamical downscaling on historical simulations
In the following sections we compare the historical GCM and downscaled simulations of MDT (Sect. 3.1), SST and SSS (Sect. 3.2) and sea-level variability (Sect. 3.3) to observations and investigate the information that dynamical downscaling with AMM7 adds.
3.1 Mean dynamic topography
The observed MDT CNES CLS18 anomalies (w.r.t. the regional mean) for 1993–2012 show a northwest to southeast gradient (Fig. 2a) perpendicular to the North Atlantic Current that flows along the shelf break. This slope current is driven by the combination of a horizontal density gradient and a sloping bathymetry (Huthnance 1984). Along the southeastern North Sea coastline and in the Kattegat, observed MDT is higher than elsewhere on the shelf.
MDT anomalies (1993–2012), observed: a MDT CNES CLS18 and simulated: b GCM-HAD, c RCM-HAD, d GCM-MPI and e RCM-MPI. Simulated MDT is the time-mean of annual mean sea level, excluding the IB effect. The historical simulations are extended with the RCP8.5 scenario for 2006–2012. The regional mean MDT was removed from all fields. The PCCs and RMSEs of simulations vs observations are indicated in the panels
Simulated MDT generally agrees well with the observations: we find pattern correlation coefficients (PCCs) with the observations of 0.86 and 0.90 for respectively GCM-HAD and GCM-MPI in the NWES region (Fig. 2b and d). The accuracy of satellite altimetry is lower near the coasts than in the deep ocean due to land contamination (e.g. Deng et al. 2002), while we expect downscaling to provide added value especially on the shelf. Additionally, the across-track resolution of satellite altimetry is much lower than the resolution of AMM7. Despite these limitations, we find that after downscaling the PCCs of GCM-HAD and GCM-MPI improve to 0.94 and 0.94, respectively (Fig. 2c and e). The MDT of GCM-HAD is improved most. The root mean square error (RMSE) changes slightly after downscaling (0.07 m for GCM-HAD and RCM-HAD, and 0.08 and 0.06 m for GCM-MPI and RCM-MPI, respectively).
All models reproduce the observed northwest to southeast MDT gradient reflecting the slope current, but this is captured only crudely by GCM-HAD (Fig. 2b). The gradient of high to low MDT off the coast of Norway, perpendicular to the Norwegian Coastal Current and Atlantic inflow through the Norwegian Trench, is present in all models except GCM-HAD (Fig. 2c–e). These topographically-steered currents cannot be resolved by GCM-HAD since its horizontal resolution is insufficient for a realistic bathymetry. However, the high MDT along the Norwegian coast is not clearly present in the MDT CNES CLS18 product either (Fig. 2a), most likely due to insufficient resolution and land contamination (Ophaug et al. 2015; Idžanovic and Ophaug 2017).
Along the southeastern North Sea coastline all models show elevated MDT similar to the observations, but for GCM-HAD this is obscured by a checkerboard pattern (Fig. 2b). Such a checkerboard pattern may be related to numerical instabilities in horizontal diffusivity. Along the western boundary of the NWES region, simulated MDT is lower than observed MDT for all models. In the Norwegian Sea, simulated MDT is too low in GCM-MPI, RCM-HAD and RCM-MPI, and does not agree spatially with the observations in GCM-HAD.
Overall, dynamical downscaling with AMM7 adds value to the CMIP5 GCM simulations of MDT. The spatial improvement is largest for GCM-HAD, which has a coarser horizontal resolution than GCM-MPI. Horizontal resolution is important to resolve the North Atlantic Current and Norwegian Coastal Current. This is in line with previous findings on the impact of dynamical downscaling of GCMs on the simulation of ocean circulation in the NWES region (e.g. Ådlandsvik and Bentsen 2007). Resolving these currents is important for the exchange of heat and salt between the deep ocean and the shelf (Huthnance 1995) and therefore likely to impact the emergent patterns of DSLC in climate change simulations.
3.2 Sea surface temperature and sea surface salinity
Next, we assess model skill at resolving the lateral transport and surface fluxes of heat and freshwater in the NWES region by comparing the historical simulations to observations of climatological SST and SSS. In winter, observed SST from OSTIA is relatively warm in the southwest of the NWES region (Fig. 3a). The warm Atlantic water flows northward following the shelf break and enters the North Sea via its southern and northern entrances. SST is colder in the east of the North Sea, along Norway and in the Norwegian Sea. In summer, observed SST is relatively high in the east of the North Sea (Fig. 3b) and the SST of the slope current is less pronounced.
Climatological SST (1992–2010) in winter (DJF) and summer (JJA) from a–b the observational dataset OSTIA, and simulated for c–d GCM-HAD, e–f RCM-HAD, g–h GCM-MPI and i–j RCM-MPI. Note the different scales used for winter and summer. The historical simulations are extended with the RCP8.5 scenario for 2006–2010. The PCCs and RMSEs of simulations vs observations on the shelf are indicated in the panels. Biases relative to the observations are shown in Supplementary Fig. 2
Compared to OSTIA, GCM-HAD is around 0.5–1.5 °C too warm at the surface on the shelf in winter (Fig. 3c). Along the coasts, biases are larger and can reach up to 3 °C near the Danish coast (see Supplementary Fig. 2 for anomalies w.r.t. observations). The SST of the slope current and the inflow of Atlantic water into the North Sea are not well reproduced by GCM-HAD. The English Channel in GCM-HAD is closed and we find cold biases of channel water of up to 0.9 °C with respect to the observations. In summer, GCM-HAD (Fig. 3d) is around 2.5 °C colder than OSTIA near the Danish coast, and up to 5.2 °C warmer around the coast of the UK. Evaluated on the shelf, the PCCs and RMSEs of GCM-HAD with observations are 0.92 and 1.09 °C in winter, and 0.50 and 2.13 °C in summer, respectively. Dynamical downscaling of GCM-HAD clearly improves the representation of SST (Fig. 3e and f). Similar to previous downscaled simulations (Holt et al. 2010; Tinker et al. 2015), RCM-HAD spatially reproduces the observed SST pattern in winter of the warm North Atlantic Current flowing along the shelf break and into the North Sea (Fig. 3e). The biases in summer SST around the UK of RCM-HAD are reduced compared to GCM-HAD (Fig. 3f). The PCCs increase and RMSEs reduce to 0.97 and 0.88 °C in winter, and to 0.88 and 1.16 °C in summer, respectively.
In winter, GCM-MPI is mostly around 0.3–1.4 °C warmer than observations in the northern North Sea and north of Scotland, and around 0.6–1.1 °C colder west of the UK (Fig. 3g). Like GCM-HAD, GCM-MPI is also too warm along the southeastern coasts of the North Sea (up to 2.6 °C) in winter compared to OSTIA. GCM-MPI resolves the SST of the slope current and the SST in the English Channel in winter better than GCM-HAD. In summer, GCM-MPI is around 1 °C warmer than observations north of the UK and in the English Channel, and around 0.8–2.2 °C colder in the central and eastern North Sea (Fig. 3h). On the shelf, GCM-MPI has PCCs and RMSEs of 0.91 and 0.69 °C in winter, and 0.82 and 0.86 °C in summer, respectively, so has smaller biases than GCM-HAD. Dynamical downscaling adds more spatial information and reduces biases with respect to the observations in both seasons (Fig. 3i and j). The PCCs increase and RMSEs reduce to 0.96 and 0.54 °C in winter, and 0.90 and 0.66 °C in summer, respectively.
Similar to MDT, the biases of simulated SST with respect to the observations are larger for GCM-HAD than for GCM-MPI, and the improvement for GCM-HAD after downscaling is also larger. Part of this might be explained by the more realistic bathymetry and land mask of GCM-MPI. Near the boundaries of the NWES region, biases of RCM-HAD and RCM-MPI with observations are larger than in the interior, and the downscaled simulations are closer to their driving GCMs due to the applied boundary conditions.
The observed climatological SSS is low in the German Bight, along part of the Dutch coast, in the Skagerrak and around Norway, owing to the freshwater outflow of rivers and the Baltic Sea (Huthnance 1991), with moderate seasonal variation (Fig. 4a and b). In contrast to the observations, in GCM-HAD low SSS is not confined to the coasts but spread out through most of the southeastern North Sea (Fig. 4c and d). Simulated SSS there is around 1.5–2 PSU lower than EN4 (see also Supplementary Fig. 3). The observed low SSS around Norway is not reproduced by GCM-HAD, pointing to the misrepresentation of the Norwegian Coastal Current and/or Baltic outflow. RCM-HAD (Fig. 4e and f) is more similar to the observations than GCM-HAD, but is fresher than EN4 in the German Bight, and more saline around Norway.
Climatological SSS (1980–2017) in winter (DJF) and summer (JJA) for a–b the observational dataset EN4, and simulated for c–d GCM-HAD, e–f RCM-HAD, g–h GCM-MPI and i–j RCM-MPI. The historical simulations are extended with the RCP8.5 scenario for 2006–2017. Biases relative to the observations are shown in Supplementary Fig. 3
GCM-MPI displays low SSS around Norway like the EN4 observations, but does not reproduce the low SSS confined to the southeastern coast of the North Sea (Fig. 4g and h). GCM-MPI is 4–6 psu too fresh in the Skagerrak compared to EN4. Downscaling also improves GCM-MPI, but like RCM-HAD, RCM-MPI (Fig. 4i and j) is too fresh in the German Bight and too saline around Norway. The SSS of RCM-HAD and RCM-MPI are similar. This indicates that SSS on the shelf is controlled more strongly by freshwater input from E-P, river run-off, Baltic outflow and the circulation on the shelf than by dynamics outside of the domain. Compared to the GCMs, AMM7 also simulates lower SSS around the UK and west of France near freshwater input from river run-off. However, EN4 observations are too sparse to facilitate a meaningful evaluation in those regions.
3.3 Interannual and seasonal sea-level variability
In addition to MDT (geostrophic circulation), SST and SSS, which have been used to evaluate downscaled simulations before (e.g. Ådlandsvik and Bentsen 2007; Holt et al. 2010; Mathis et al. 2013; Tinker et al. 2015), we also evaluate the historical simulations of seasonal and interannual sea-level variability. Here, we take historical interannual variability as the standard deviation of the detrended annual mean SSH during 1980–2017, and seasonal variability as the mean amplitude of the seasonal cycle of SSH.
The observed TG data (colored circles) show a relatively large interannual variability in the German Bight and north of the Netherlands (Fig. 5a), and slightly increased variability around the north of Norway. The large variability in the German Bight is also observed with satellite altimetry and can be explained well with a regression with local wind, SST and sea-level pressure (Sterlini et al. 2016).
Simulated interannual sea-level variability (1980–2017) calculated as the standard deviation (std.) of detrended annual mean SSH for a GCM-HAD, b RCM-HAD, d GCM-MPI and e RCM-MPI, with colored circles depicting observed interannual variability at TGs. The historical simulations are extended with the RCP8.5 scenario for 2006–2017. The PCCs and RMSEs of simulations vs observations are indicated in the panels. Scatter plots of simulated vs observed interannual variability at TGs for (c) GCM-HAD and RCM-HAD and for (f) GCM-MPI and RCM-MPI
GCM-HAD displays a relatively large interannual variability in the German Bight (Fig. 5a), but in contrast to the observations this extends to the coast of Norway as well. In the deep ocean, GCM-HAD simulates a large interannual variability, especially near the western boundary of the NWES region. Comparing simulated interannual variability near TG stations to the observed TG data, GCM-HAD has a PCC of 0.7 and RMSE of 1.12 cm. Dynamical downscaling improves the interannual sea-level variability of GCM-HAD compared to the TG records (Fig. 5c), mainly along the Norwegian coast. Indeed, RCM-HAD (Fig. 5b) has an increased PCC of 0.90 and a decreased RMSE of 0.84 cm.
The observed interannual variability is better reproduced by GCM-MPI (Fig. 5d) than by GCM-HAD, which is reflected by a PCC of 0.83 and a RMSE of 0.55 cm with respect to the observations. Similar to GCM-HAD, the interannual variability in GCM-MPI is larger in parts of the deep ocean than on the shelf. In contrast to GCM-HAD, the skill of GCM-MPI at reproducing observed variability is only marginally affected by downscaling (Fig. 5e and f). The PCC remains unchanged after downscaling, and the RMSE decreases from 0.55 to 0.52 cm for RCM-MPI. The comparison suggests that the impact of dynamical downscaling on simulations of interannual sea-level variability along the coast depends strongly on the driving GCM. The patterns of large interannual variability in the deep ocean are roughly similar between GCMs and downscaled simulations. The transition near the shelf break from small variability on the shelf to large variability in the deep ocean is more pronounced in the downscaled simulations, likely because the shelf break is better resolved in AMM7.
TGs in the German Bight and along the north coast of Norway show the highest seasonal variability (Fig. 6, colored circles). The observed seasonal amplitude gradually increases northward along the Dutch coast. The simulated seasonal amplitude is typically smaller in the southwest of the NWES region and increases toward the north and northeast for all models (Fig. 6a, b, d and e). Although GCM-HAD simulates high variability in the German Bight and around Norway, it has little spatial coherency in the North Sea and along the Norwegian coast (Fig. 6a) and does not compare well with the TGs (Fig. 6c). The PCC and RMSE of GCM-HAD with the observations are 0.84 and 2.18 cm, respectively. Dynamical downscaling strongly improves the fit with observations: RCM-HAD has a PCC of 0.94 and an RMSE of 1.57 cm (Fig. 6b and c). Especially in the central North Sea, the seasonal amplitude is larger for RCM-HAD than for GCM-HAD.
Simulated amplitude of the seasonal cycle of sea level \({S}_{A}\) (1980–2017) calculated as half of the difference between annual minimum and maximum SSH and averaged for all years for a GCM-HAD, b RCM-HAD, d GCM-MPI and e RCM-MPI, with colored circles depicting the observed seasonal amplitude at TGs. The historical simulations are extended with the RCP8.5 scenario for 2006–2017. The PCCs and RMSEs of simulations vs observations are indicated in the panels. Scatter plots of the simulated vs observed seasonal amplitude at TGs for (c) GCM-HAD and RCM-HAD and for (f) GCM-MPI and RCM-MPI
GCM-MPI also displays high seasonal variability in the German Bight, but this variability extends too far south along the Dutch and Belgian coasts (Fig. 6d). This leads to a poor fit with the observations: the PCC and RMSE of GCM-MPI are 0.67 and 2.99 cm, respectively. Around Norway, the simulation agrees with the observations better. Again, dynamical downscaling leads to a much better fit (Fig. 6e and f), especially along the southeastern coast of the North Sea. The PCC and RMSE of RCM-MPI are 0.95 and 0.94 cm, respectively.
The improved model skill likely results from the increased ocean resolution and downscaled atmospheric forcing in our setup. However, the seasonal cycle is also affected by river run-off and tides (Tsimplis and Woodworth 1994), of which the latter is not included in the GCMs. Seasonal variability in RCM-HAD and RCM-MPI (Fig. 6b and d) is remarkably similar (PCC of 0.82 over the NWES region, and similar biases w.r.t. TGs) despite the different driving GCMs, indicating that the boundary conditions have a lesser influence. Comparing Figs. 5 and 6 shows that particularly along the coasts, the seasonal cycle benefits more from dynamical downscaling than interannual variability, which has a larger dependency on the lateral boundary conditions.
Summarizing, dynamical downscaling generally improves the historical GCM simulations with respect to observations (i.e. reduces biases). We expect that dynamical downscaling will improve the simulations of other CMIP5 GCMs as well, especially since most CMIP5 GCMs have a lower horizontal resolution than MPI-ESM-LR in the NWES region. The evaluation shows that the bathymetry and land mask of GCM-HAD is too coarse to resolve the circulation on and along the shelf. This can influence sea-level projections as well.
4 The impact of dynamical downscaling on projected DSLC
In this section we assess the effect of dynamical downscaling on simulations of future DSLC (Sect. 4.1) and its different components (Sect. 4.2). Additionally, we investigate the time of emergence (Hawkins and Sutton 2012; Lyu et al. 2014) of SLC above background variability (Sect. 4.3).
4.1 DSLC projections for the twenty-first century
We compute twenty-first century DSLC as the difference between time-mean sea level in the historical period (1980–2005) and at the end of the century (2074–2099). The global-mean thermosteric SLC ‘zostoga’ (see Sect. 2.4) is excluded. For RCP8.5, all models project a relative sea-level rise on the NWES (Fig. 7), with the strongest increase for GCM-HAD (Fig. 7a). The results for RCP4.5 are spatially similar to the results for RCP8.5, but have smaller magnitudes (Supplementary Fig. 4).
The differences in DSLC between GCM-HAD and RCM-HAD (Fig. 7a and b) are large, especially in the North Sea (Fig. 7c): DSLC is up to 15.5 cm larger in GCM-HAD than in RCM-HAD along the southeastern coast (up to 8 cm larger for RCP4.5). This difference is approximately 30% of the sterodynamic SLC (DSLC plus ‘zostoga’, Gregory et al. 2019) simulated by GCM-HAD for the North Sea. It is of similar magnitude to the uncertainty of CMIP5 ensembles used for previous regional sea-level projections (e.g. Slangen et al. 2012, 2014; de Vries et al. 2014; Kopp et al. 2014; Palmer et al. 2018). DSLC in GCM-HAD is 5–7 cm larger than in RCM-HAD north of the UK, 3–4 cm larger along the coastline of France and Spain, and 2–4 cm smaller along parts of the Irish coast. In the Irish Sea differences in DSLC between GCM-HAD and RCM-HAD are also large, since the Irish Sea is not resolved in GCM-HAD and interpolated values are used instead. Unlike GCM-HAD, RCM-HAD simulates a distinct sea-level rise in the Norwegian Trench despite the climatology used for the Baltic outflow. This points toward changes in shelf circulation or in the Atlantic inflow into the North Sea (Holt et al. 2018).
In contrast to GCM-HAD and RCM-HAD, the spatial patterns of DSLC in GCM-MPI (Fig. 7d) and RCM-MPI (Fig. 7e) generally agree well. DSLC in GCM-MPI is up to 3.5 cm smaller than in RCM-MPI in the Bay of Biscay (Fig. 7f). In the North Sea, GCM-MPI simulates slightly larger DSLC, but differences with RCM-MPI do not exceed 2.5 cm (7% of the sterodynamic SLC simulated by GCM-MPI). The differences are much smaller than for GCM-HAD, which points to the importance of a realistic bathymetry and land mask for sea-level projections.
In the deep ocean, differences with the downscaled simulations in the deep ocean can exceed differences on the shelf for both GCMs (Fig. 7c and f). The currents east of Iceland and along the Faroe Islands show a sea-level fall relative to the global mean in RCM-HAD, but not in GCM-HAD. DSLC in GCM-MPI around the Faroe Islands is smaller than on the shelf, but in RCM-MPI it is larger. Near the western boundary of the NWES region, GCM-HAD (Fig. 7a) shows a large sea-level rise, whereas in GCM-MPI (Fig. 7d) sea level falls relative to the global mean change. This is likely caused by changes in the gyre circulation west of the region, which are inherited in the downscaled simulations through the lateral boundary conditions (Fig. 7b and e).
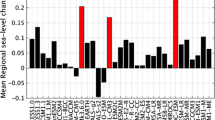
In GCM-HAD there is a large contrast (~ 18 cm) between DSLC northeast and southwest of the English Channel (Fig. 7a). Apparently, the closed English Channel in GCM-HAD prohibits circulation into the North Sea via its southern entrance. The DSLC gradient across the closed English Channel reduces by approximately 13 cm after dynamically downscaling (Fig. 7b). For GCM-MPI, which has an open English Channel, dynamical downscaling hardly affects the SLC gradient. To explore the effect of a closed English Channel on DSLC further, we assess the difference between DSLC on either side of the English Channel in 18 additional CMIP5 GCMs (Fig. 8). For all 20 GCMs and the downscaled simulations, twenty-first century DSLC is larger near Vlissingen (northeast of the channel) than near Brest (southwest of the channel). The difference is largest for HadGEM2-ES (~ 18 cm, closed English Channel) and smallest for EC-EARTH (~ 0.55 cm, open English Channel). On average, the difference between DSLC near Vlissingen and Brest is 4.2 cm for the 10 CMIP5 models with an open English Channel (squares), and 8.5 cm for the 10 CMIP5 models with a closed English Channel (circles). Like HadGEM2-ES, other CMIP5 models with a closed English Channel and a large gradient in DSLC across the channel might benefit substantially from dynamical downscaling.
Simulated DSLC (excluding the IB effect) between 1980–2005 and 2074–2099 (RCP8.5) near Vlissingen vs near Brest for 20 CMIP5 models with a closed English Channel (circles) or open English Channel (squares), and for our downscaled simulations (asterisks). The models downscaled in this study are indicated in red (HadGEM2-ES) and blue (MPI-ESM-LR). The solid 1:1 line denotes equal DSLC in Vlissingen and Brest
4.2 Drivers of projected DSLC
To better understand which processes drive the DSLC differences between the GCM and downscaled simulations (Fig. 7), we decompose DSLC into local steric SLC (Fig. 9) and SLC related to bottom pressure changes (manometric SLC, Fig. 10) following Eq. (1) (Sect. 2.3). We exclude the IB effect here, since it is small on centennial timescales (Church et al. 2013) and differences in DSLC due to the IB effect between our models are less than 0.5 cm.
Local steric SLC (derived in Sect. 2.3) between 1980–2005 and 2074–2099 (RCP8.5) for a GCM-HAD b RCM-HAD, c RCM-HAD minus GCM-HAD, d GCM-MPI, e RCM-MPI and f RCM-MPI minus GCM-MPI. The differences in (c) and (f) are computed on the AMM7 grid; black crosses indicate the original GCM coastline
Manometric SLC (SLC related to bottom pressure changes, as derived in Sect. 2.3) between 1980–2005 and 2074–2099 (RCP8.5) for a GCM-HAD b RCM-HAD, c RCM-HAD minus GCM-HAD, d GCM-MPI, e RCM-MPI and f RCM-MPI minus GCM-MPI. The differences in (c) and (f) are computed on the AMM7 grid; black crosses indicate the original GCM coastline. The global-mean thermosteric change ‘zostoga’ has been added to all fields to correct for the spurious bottom pressure change of the GCMs due to the Boussinesq approximation (Sect. 2.4)
All models project the largest steric change in the deep ocean (Fig. 9a, b, d and e), because when heated a deeper water column expands more than a shallow one. If no other forces balance the resulting SSH gradient, these volume anomalies are redistributed from the deep ocean toward the shelf (Landerer et al. 2007). This mass redistribution leads to a slight bottom pressure decrease in the deep ocean and to a sea-level rise on the shelf (Fig. 10a, b, d and e). The dependency of local steric and bottom pressure change on water column depth means that differences between models will depend partially on differences in bathymetry. The imprint of bathymetry is indeed visible in Fig. 9c and f and Fig. 10c and f, for example in the North Sea, the Norwegian Trench and along the shelf break. Note that these steric and bottom pressure change differences often have opposite signs.
On the shelf, the differences in local steric and manometric SLC between GCM-HAD and RCM-HAD are large (Figs. 9c and 10c). The local steric change in GCM-HAD can be over 15 cm larger than in RCM-HAD in the northern North Sea. GCM-HAD also simulates a much larger local steric change north of Scotland, where the representation of the shelf break is crude (Fig. 1b). SLC due to bottom pressure changes is up to 13 cm larger in GCM-HAD than in RCM-HAD in the North Sea. These effects combined lead to the large DSLC differences in the North Sea between GCM-HAD and RCM-HAD (Fig. 7c). The DSLC differences between GCM-MPI and RCM-MPI (Fig. 7f) on the shelf are the result of a slightly larger local steric change on the Armorican and Aquitaine shelfs (Fig. 9f), and a slightly smaller bottom pressure change mainly in the North Sea and Irish Sea in RCM-MPI (Fig. 10f).
Off the shelf, differences in local steric and manometric SLC display a complex spatial pattern and partially cancel out. Differences in the local steric change between the GCM and downscaled simulations are largest in the north and northwest of the domain. The decrease in sea level with respect to the global mean change in RCM-HAD and the increase in RCM-MPI east of Iceland and around the Faroe Islands (Fig. 7b and e), and the resulting differences with the GCMs, are mainly driven by local steric changes (Fig. 9c and f).
Despite the shallow depth of the North Sea, the differences in local steric changes between GCM-HAD and RCM-HAD (Fig. 9c) in the North Sea are large (10–17 cm). To see if this is the result of differences in temperature change or differences in salinity change, we further decompose steric change into thermosteric (Fig. 11) and halosteric (Fig. 12) SLC (explained in Sect. 2.3). All models simulate large thermosteric sea-level rise in the deep ocean, except RCM-HAD southeast of Iceland (Fig. 11a, b, d and e). Halosteric SLC partially cancels out thermosteric SLC and is negative in the southwest of the NWES region and positive elsewhere in all models (Fig. 12a, b, d and e). On the shelf, thermosteric SLC is in the order of a few cm, and differences between GCM-HAD and RCM-HAD (Fig. 11c) and between GCM-MPI and RCM-MPI (Fig. 11f) are mostly below 1 cm.
The differences in halosteric SLC between GCM-HAD and RCM-HAD are up to 15 cm (Fig. 12c) on the shelf. This indicates that DSLC in the northern North Sea in GCM-HAD is larger than in RCM-HAD (Fig. 7c) mainly because of differences in depth-integrated salinity change. This can be the result of (a combination of) differences in the projected changes in river run-off, evaporation minus precipitation, Atlantic inflow and shelf circulation that are introduced by dynamical downscaling. Halosteric SLC is also larger in RCM-MPI than in GCM-MPI, especially in the Bay of Biscay (Fig. 12f). As shown in Sect. 3, the bathymetry and land mask of GCM-HAD are too coarse to model the Atlantic inflow through the Norwegian Trench and English Channel, affecting salinity on the shelf (Fig. 4) and thus DSLC.
4.3 Time of emergence of sea-level change
In addition to the DSLC over the twenty-first century, we investigate the time of emergence (ToE) of sterodynamic SLC (Hawkins and Sutton 2012; Lyu et al. 2014), which is a measure of the magnitude of forced SLC relative to internal sea-level variability. The detection of SLC relative to background noise is useful for impact assessments and adaption planning (Kirtman et al. 2013). We calculate the ToE of sterodynamic SLC relative to the simulated historical time-mean sea level (1980–2005). ToE is defined as the time in the middle of a 26-yr window following the 26-yr historical period in which the change in time-mean sea level relative to the historical window exceeds and remains outside the bands of one standard deviation of detrended annual-mean SSH in both this and the historical window.
For all models sterodynamic SLC has emerged above variability on most of the shelf after 2020 (Fig. 13a, b, d and e). Emergence in the German Bight is later than elsewhere in the North Sea because of the high local interannual variability (Fig. 5). Compared to RCM-HAD, ToE in GCM-HAD is up to 6 years earlier in the North Sea and along the coast of France and Scotland, 3 years later south of the UK and up to 8 years later in the Norwegian Trench (Fig. 13c). These differences are relatively small despite the large differences in DSLC between GCM-HAD and RCM-HAD by the end of the twenty-first century (Fig. 7c). Since the differences in historical interannual variability on the shelf between both models are not very large (Fig. 5a and b), this indicates that DSLC in the North Sea in RCM-HAD starts to diverge from DSLC in GCM-HAD mainly after the ToE. In the deep ocean, sterodynamic SLC emerges later than on the shelf for both models since interannual variability in the deep ocean is larger (Fig. 5a and b). The sea-level fall east of Iceland and around the Faroe Islands in RCM-HAD (Fig. 7b) is not detectable above sea-level variability before the end of the twenty-first century (Fig. 13b).
ToE of sterodynamic SLC (RCP8.5) relative to the historical period 1980–2005 for a GCM-HAD, b RCM-HAD, c RCM-HAD minus GCM-HAD, d GCM-MPI, e RCM-MPI and f RCM-MPI minus GCM-MPI. The differences in (c) and (f) are computed on the AMM7 grid; black crosses indicate the original GCM coastline. Yellow grid cells indicate no emergence before the end of the century. For these grid cells we use the value 2099 in (c) and (f)
On the shelf, differences in ToE between GCM-MPI and RCM-MPI (Fig. 13f) are larger than between GCM-HAD and RCM-HAD, especially along the coasts of the UK and Norway. For example, the ToE in the Irish Sea in GCM-MPI is up to 12 years earlier than in RCM-MPI, despite differences in twenty-first century DSLC between GCM-MPI and RCM-MPI of less than 2.5 cm (Fig. 7f). Since sea-level variability and the timing of SLC differ between GCM and RCM, the effect of dynamical downscaling on ToE on the NWES can be large, even if differences in DSLC by the end of the twenty-first century are relatively small. The ToE on the shelf is similar for RCP4.5 and RCP8.5 since emergence occurs mostly before the RCPs start to significantly diverge. Emergence for RCP4.5 is somewhat earlier in RCM-HAD than in GCM-HAD in the German Bight and south of the UK (Supplementary Fig. 5). Similar to GCM-HAD and RCM-HAD, emergence in GCM-MPI and RCM-MPI is later in the deep ocean than on the shelf. West of the shelf sterodynamic SLC does not emerge before the end of the twenty-first century, indicating that the projection of sea-level fall (Fig. 7d and e) is strongly affected by interannual variability.
5 Projected changes in the seasonal sea-level cycle
In Sect. 3.3 it was shown that dynamical downscaling improved the fit with the observed amplitude of the seasonal sea-level cycle at TGs. Therefore, we also analyze the impact of dynamical downscaling on the projected changes in seasonal amplitude. Changes in the seasonal sea-level cycle may heighten the risk associated to sea-level rise on subannual timescales. In most of the domain, the linear trends of the seasonal amplitude over the twenty-first century are not significantly different from 0 (yellow) for any of the models (Fig. 14a, b, d and e). For RCP4.5 an even smaller part of the NWES region displays significant trends (Supplementary Fig. 6). In locations with significant trends, differences between GCM-HAD and RCM-HAD can be as large as the trends themselves (Fig. 14c). The trends in GCM-HAD are up to 0.33 mm/yr smaller than in RCM-HAD in the southern North Sea, which is a large difference compared to the observed historical seasonal amplitude of around 7 cm (Fig. 5). For GCM-MPI and RCM-MPI, the trends are mostly significant and positive around the north of the UK (Fig. 14d and e). A large difference in trends is displayed in the southwest of the NWES region. In the northern North Sea, trends in GCM-MPI can be up to 0.19 mm/yr smaller than in RCM-MPI (Fig. 14f). The large differences in trends between the GCM and downscaled simulations suggest that RCMs should be used for accurate projections of the change in seasonal amplitude in the NWES region.
Linear trends in the amplitude of the seasonal cycle of sea level \({S}_{A}\) (1980–2099, RCP8.5) for a GCM-HAD, b RCM-HAD, c RCM-HAD minus GCM-HAD, d GCM-MPI, e RCM-MPI and f RCM-MPI minus GCM-MPI. Yellow grid cells indicate linear regression coefficients that are not significantly different from 0 (2 standard errors; 95% confidence). The differences in (c) and (f) are computed on the AMM7 grid; black crosses indicate the original GCM coastline. Differences are yellow when both simulations have insignificant trends
Next, we use the linear trends in Fig. 14 to detrend the amplitude of the seasonal sea-level cycle. The interannual variability of the seasonal amplitude over the twenty-first century can be calculated by taking the standard deviation of the detrended signal (Fig. 15). The seasonal amplitude shows substantial interannual variability for all models (Fig. 15a, b, d and e), especially when compared to the linear trends in Fig. 14. The variability is largest in the German Bight, and smaller at the British coast of the North Sea. This is in line with the twentieth century observations at TG stations around the North Sea (Dangendorf et al. 2013; Frederikse and Gerkema 2018). The results are similar for RCP4.5 (Supplementary Fig. 7).
Interannual variability of the amplitude of the seasonal cycle of sea level \({S}_{A}\) (1980–2099) calculated as the standard deviation of the detrended timeseries of \({S}_{A}\) (RCP8.5), for a GCM-HAD, b RCM-HAD, c RCM-HAD minus GCM-HAD, d GCM-MPI, e RCM-MPI and f RCM-MPI minus GCM-MPI. The differences in (c) and (f) are computed on the AMM7 grid; black crosses indicate the original GCM coastline
On the shelf, differences in the interannual variability of the seasonal amplitude between GCM-HAD and RCM-HAD (Fig. 15c) can be up to 1.6 cm (~ 40% of the standard deviation in GCM-HAD), and up to 2.6 cm (~ 32% of the standard deviation in GCM-MPI) between GCM-MPI and RCM-MPI (Fig. 15f). The high variability in the German Bight simulated by GCM-MPI extends further along the southeastern coast of the North Sea than in RCM-MPI, similar to the bias of its historical mean seasonal amplitude relative to observations (Fig. 5). Hence, dynamical downscaling is important to better project the variability of the amplitude of the seasonal sea-level cycle in the NWES region.
6 Discussion and Conclusions
Previous projections of regional sea level have been constructed with the output of CMIP5 GCMs (e.g. Slangen et al. 2012, 2014; Church et al. 2013; de Vries et al. 2014; Kopp et al. 2014; Palmer et al. 2018). However, such GCMs have a horizontal ocean resolution in the order of 100 km and exclude some of the key processes relevant to shelf seas. Therefore, GCMs might not be the most appropriate means of providing sea-level projections for coastal regions. The objective of this study was to explore the use of dynamical downscaling with the regional model AMM7 to refine the CMIP5 GCM simulations of the ocean dynamic component of sea-level variability and long-term change for the NWES region.
In agreement with previous dynamical downscaling studies for the NWES (e.g. Ådlandsvik and Bentsen 2007), we find that dynamical downscaling improves historical GCM simulations with respect to observations of SST, SSS and MDT. Additionally, we show that dynamical downscaling provides a better representation of sea-level variability on seasonal-to-interannual timescales (Sect. 3). The improvement reflects the importance of a realistic bathymetry and land mask to resolve important topographically-steered currents along and on the shelf, which requires a sufficient horizontal and vertical resolution. MPI-ESM-LR has a relatively high horizontal resolution and reproduces observations better than HadGEM2-ES. Related to this, we find that the improvement after dynamical downscaling is generally larger for HadGEM2-ES than for MPI-ESM-LR.
The inclusion of key processes for the NWES and the improvement in reproducing observed ocean properties and sea-level characteristics that was demonstrated in Sect. 3 promotes greater confidence in the emergent patterns of DSLC in our dynamically downscaled simulations. Depending on the driving GCM, the impact of dynamical downscaling on twenty-first century DSLC can be substantial (Sect. 4). For MPI-ESM-LR, differences between the GCM and downscaled simulations are in the order of a few cm on the shelf. For HadGEM2-ES the downscaled DSLC is up to 15.5 cm (RCP8.5) smaller along the North Sea coastline than in the original GCM simulations (up to 8 cm for RCP4.5). This is of comparable magnitude to the uncertainty in CMIP5 ensembles used for previous regional sea-level projections (e.g. Church et al. 2013; Slangen et al. 2014). To draw more general conclusions additional CMIP5 models need to be dynamically downscaled. However, since the horizontal resolution of HadGEM2-ES is more typical for the CMIP5 ensemble than the horizontal resolution of MPI-ESM-LR, we expect the results of dynamical downscaling for HadGEM2-ES to be representative of other CMIP5 models as well.
Part of the differences in projected twenty-first century DSLC between the GCM and downscaled simulations are caused by the differences in bathymetry and land mask between the models. Our results show that it is important for DSLC projections that models resolve the main topographic features such as the English Channel, the Norwegian Trench and the transition from the deep ocean to the shelf. This is further supported by the finding that the impact of dynamical downscaling is larger for HadGEM2-ES than for MPI-ESM-LR. Therefore, sea-level projections for the NWES constructed with an ensemble of GCMs could be improved by weighting or excluding models based on their bathymetry and land mask or skill at reproducing observations regionally (e.g. McSweeney et al. 2015). This can have a substantial effect on model spread (Little et al. 2015).
Besides the magnitude of simulated DSLC, dynamical downscaling also affects the projected time of emergence of sterodynamic SLC. When including the global-mean thermosteric change, the SLC signal emerges above internal variability after 2020 for most of the NWES in all of our models. The ToE is later in the deep ocean. Spatially, this compares well with the results of Lyu et al. (2014) obtained with CMIP5 GCMs. However, dynamical downscaling of HadGEM2-ES and MPI-ESM-LR can delay the emergence of sterodynamic SLC on the shelf by up to 12 years (Sect. 4.3). Instead of using preindustrial control runs to estimate (unforced) internal sea-level variability (Lyu et al. 2014), dynamical downscaling can be used to estimate the ToE of SLC more realistically, accounting for both the mean state and the variability around the mean state that can both evolve over time.
We have also shown that historical GCM simulations of the amplitude of the seasonal cycle of sea level strongly improve after dynamical downscaling (Sect. 3.3). The projected trends and interannual variability of the seasonal amplitude over the twenty-first century can differ substantially between the GCM and downscaled simulations (Sect. 5). This means that dynamical downscaling offers the ability to investigate DSLC on subannual timescales. The primary driver for sea-level projections is coastal flood risk. A stronger seasonal cycle of sea level, or for instance of tidal amplitudes, may exacerbate the in-year risk associated with the annual-mean increase in sea level. This can be relevant to sediment transport and the recoverability of ecological systems in coastal wetlands.
Our dynamical downscaling setup does not include a two-way coupling between AMM7 and the atmosphere nor between AMM7 and the ocean of the driving GCMs, which would allow the RCM to influence the global solution. Although we find that dynamical downscaling improves the SST simulations of the GCMs relative to the observations (Sect. 3.2), a two-way atmosphere–ocean coupling was found to be important for downscaled SST to evolve more independently from the atmospheric forcing provided by the parent model (Mathis et al. 2017). Future studies could investigate the sensitivity of the results of dynamical downscaling to two-way coupling, to the implementation of the boundary conditions and to using different RCMs, or isolate the role of tides in the simulations. The DSLC output can be combined with other SLC contributors to construct comprehensive downscaled sea-level projections. Monte Carlo approaches such as used by Palmer et al. (2018) can readily accommodate this new information.
Several CMIP6 models will have an increased horizontal ocean resolution of 1/4° (Haarsma et al. 2016) and are expected to better resolve the topographic scales in the NWES region. Despite these advancements, the vertical resolution of most GCMs remains limited in shallow shelf seas. Additionally, to fully resolve eddy-induced sea-level variability horizontal ocean resolution needs to be increased beyond the first baroclinic Rossby radius on the shelf (~ 4 km). GCMs operating at such small scales are decades away in terms of computational feasibility (Holt et al. 2017), while the latest generation of 3D regional ocean models can resolve these scales already (e.g. Graham et al. 2018). Our results show the importance of improving the representation of coastal regions in GCMs for regional sea-level projections for the NWES, and support a role for dynamical downscaling in improving projections for coastal regions.
References
Ådlandsvik B (2008) Marine downscaling of a future climate scenario for the North Sea. Tellus, Series A Dynam Meteorol Oceanogr 60A(3):451–458. https://doi.org/10.1111/j.1600-0870.2008.00311.x
Ådlandsvik B, Bentsen M (2007) Downscaling a twentieth century global climate simulation to the North Sea. Ocean Dyn 57(4–5):453–466. https://doi.org/10.1007/s10236-007-0125-2
Cannaby H, Palmer MD, Howard T, Bricheno L, Calvert D, Krijnen J, Wood R, Tinker J, Bunney C, Harle J, Saulter A, Neill CO, Bellingham C, Lowe J (2016) Projected sea level rise and changes in extreme storm surge and wave events during the 21st century in the region of Singapore. Ocean Sci 12:613–632. https://doi.org/10.5194/os-12-613-2016
Church JA, Clark PU, Cazenave A, Gregory JM, Jevrejeva S, Levermann A, Merrifield MA, Milne GA, Nerem RS, Nunn PD, Payne AJ, Pfeffer WT, Stammer D, Unnikrishnan AS (2013) Sea level change. In Stocker TF, Qin D, Plattner GK, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (Eds.), In: climate change 2013: the physical science basis. contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, United Kingdom and New York, USA
Collins WJ, Bellouin N, Gedney N, Halloran P, Hinton T, Hughes J, Jones CD (2011) Development and evaluation of an Earth-System model – HadGEM2. Geoscient Model Dev 4:1051–1075. https://doi.org/10.5194/gmd-4-1051-2011
Dangendorf S, Wahl T, Mudersbach C, Jensen J (2013) The seasonal mean sea level cycle in the Southeastern North Sea. J Coastal Res 65:1915–1920. https://doi.org/10.2112/SI65-324.1
de Vries H, Katsman C, Drijfhout S (2014) Constructing scenarios of regional sea level change using global temperature pathways. Environm Res Lett. https://doi.org/10.1088/1748-9326/9/11/115007
Deng X, Featherstone WE, Hwang C, Berry PAM (2002) Estimation of contamination of ERS-2 and POSEIDON satellite radar altimetry close to the coasts of Australia. Mar Geodesy 25(4):249–271. https://doi.org/10.1080/01490410214990
Donlon CJ, Martin M, Stark J, Roberts-jones J, Fiedler E, Wimmer W (2012) Remote sensing of environment the operational sea surface temperature and sea ice analysis ( OSTIA ) system. Remote Sens Environ 116:140–158. https://doi.org/10.1016/j.rse.2010.10.017
Eyring V, Bony S, Meehl GA, Senior CA, Stevens B, Stouffer RJ, Taylor KE, Dynamique DM, Pierre I, Laplace S, Ipsl LMD (2016) Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization. Geoscient Model Dev 9:1937–1958. https://doi.org/10.5194/gmd-9-1937-2016
Flather RA (1976) A tidal model for the northwest European shelf. Mem Soc R Sci Liege 10:141–164
Frederikse T, Gerkema T (2018) Multi-decadal variability in seasonal mean sea level along the North Sea coast. Ocean Sci 14: 1491–1501. https://doi.org/https://doi.org/10.5194/os-14-1491-2018
Gill AE (1983) Atmosphere-ocean dynamics. Applied Ocean Research (1st ed.). Academic Press. https://doi.org/10.1016/0141-1187(83)90039-1
Giorgetta MA, Jungclaus J, Reick CH, Legutke S, Bo M, Brovkin V, Claussen M (2013) Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the coupled model intercomparison project phase 5. J Adv Model Earth Syst 5:572–597. https://doi.org/10.1002/jame.20038
Giorgi F, Jones C, Asrar GR (2009) Addressing climate information needs at the regional level: the CORDEX framework. WMO Bull 58(3)
Good SA, Martin MJ, Rayner NA (2013) EN4: Quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J Geophys Res Oceans 118(12):6704–6716. https://doi.org/10.1002/2013JC009067
Graham JA, Dea EO, Holt J, Polton J, Hewitt HT, Furner R, Guihou K, Brereton A, Arnold A, Wakelin S, Manuel J, Sanchez C, Adame CGM (2018) AMM15: A new high resolution NEMO configuration for operational simulation of the European North West Shelf. Geoscient Model Dev Discuss 11(2), 1–23. https://doi.org/https://doi.org/10.5194/gmd-11-681-2018
Greatbatch J (1994) A note on the representation of steric sea level in models that conserve volume rather than mass. J Geophys Res Oceans 99(3):767–771. https://doi.org/10.1029/94JC00847
Gregory JM, Griffies SM, Hughes CW, Lowe JA, Church JA, Fukimori I, Gomez N, Kopp RE, Landerer F, Le Cozannet G, Ponte RM, Stammer D, Tamisiea ME, van de Wal RSW (2019) Concepts and terminology for sea level: mean variability and change, both local and global. Surv Geophys 9:9–10. https://doi.org/10.1007/s10712-019-09525-z
Griffies SM, Greatbatch RJ (2012) Physical processes that impact the evolution of global mean sea level in ocean climate models. Ocean Model 51:37–72. https://doi.org/10.1016/j.ocemod.2012.04.003
Griffies SM, Yin J, Durack PJ, Goddard P, Bates SC, Behrens E, Zhang X (2014) CORE-II virtual special issue an assessment of global and regional sea level for years 1993–2007 in a suite of interannual CORE-II simulations. Ocean Modell 78:35–89. https://doi.org/10.1016/j.ocemod.2014.03.004
Haarsma RJ, Roberts MJ, Vidale PL, Senior CA, Bellucci A, Bao Q, Chang P, Corti S, Fuˇ NS (2016) High resolution model intercomparison project (HighResMIP v1 .0) for CMIP6, (April), 4185–4208. https://doi.org/10.5194/gmd-9-4185-2016
Hawkins E, Sutton R (2012) Time of emergence of climate signals. Geophys Res Lett 39(L01702):1–6. https://doi.org/10.1029/2011GL050087
Holgate SJ, Matthews A, Woodworth PL, Rickards LJ, Tamisiea E, Bradshaw E, Foden PR, Gordon KM, Jevrejeva S, Pugh J, Journal S, May N, Holgate SJ, Lesley LW, Proudman J (2013) New Data Systems and products at the permanent service for mean sea level. J Coastal Res 29(3):493–504. https://doi.org/10.2112/JCOASTRES-D-12-00175.1
Holt J, Wakelin S, Lowe J, Tinker J (2010) The potential impacts of climate change on the hydrography of the northwest European continental shelf. Prog Oceanogr 86(3–4):361–379. https://doi.org/10.1016/j.pocean.2010.05.003
Holt J, Schrum C, Cannaby H, Daewel U, Allen I, Artioli Y, Bopp L, Butenschon M, Fach BA, Harle J, Pushpadas D, Salihoglu B, Wakelin S (2016) Potential impacts of climate change on the primary production of regional seas: a comparative analysis of five European seas. Prog Oceanogr 140:91–115. https://doi.org/10.1016/j.pocean.2015.11.004
Holt J, Hyder P, Ashworth M, Harle J, Hewitt HT, Liu H, New AL, Pickles S, Porter A, Popova E, Icarus Allen J, Siddorn J, Wood R (2017) Prospects for improving the representation of coastal and shelf seas in global ocean models. Geosci Model Dev 10(1):499–523. https://doi.org/10.5194/gmd-10-499-2017
Holt J, Polton J, Huthnance J, Wakelin S, O’Dea E, Harle J, Yool A, Artioli Y, Blackford J, Siddorn J, Inall M (2018) Climate-driven change in the North Atlantic and Arctic Oceans can greatly reduce the circulation of the North Sea. Geophys Res Lett. https://doi.org/10.1029/2018GL078878
Howard T, Lowe J, Horsburgh K (2010) Interpreting century-scale changes in southern north sea storm surge climate derived from coupled model simulations. J Climate 23(23):6234–6247. https://doi.org/10.1175/2010JCLI3520.1
Howard T, Palmer MD, Bricheno LM (2019) Contributions to 21st century projections of extreme sea-level change around the UK. Environ Res Lett 1(9) https://doi.org/https://doi.org/10.1088/2515-7620/ab42d7
Huthnance JM (1984) Slope Currents and “JEBAR”. J Phys Oceanogr https://doi.org/https://doi.org/10.1175/1520-0485(1984) 014%3c0795:SCA%3e2.0.CO;2
Huthnance JM (1991) Physical oceanography of the North Sea. Ocean Shorel Manag 16(3–4):199–231. https://doi.org/10.1016/0951-8312(91)90005-M
Huthnance JM (1995) Circulation, exchange and water masses at the ocean margin: the role of physical processes at the shelf edge. Progress Oceanogr 35(95), 353–431 https://doi.org/https://doi.org/10.1016/0079-6611(95)80003-C
Idier D, Paris F, Cozannet GL, Boulahya F, Dumas F (2017) Sea-level rise impacts on the tides of the European Shelf. Cont Shelf Res 137:56–71. https://doi.org/10.1016/j.csr.2017.01.007
Idžanovic M, Ophaug V (2017) The coastal mean dynamic topography in Norway observed by CryoSat-2 and GOCE. Geophys Res Lett 44:5609–5617. https://doi.org/10.1002/2017GL073777
Kirtman B, Power SB, Adedoyin JA, Boer GJ, Bojariu R, Camilloni I, Doblas-Reyes FJ, Fiore AM, Kimoto M, Meehl GA, Prather M, Sarr A, Kimoto M, Schär C, Sutton R, van Oldenborgh GJ, Vecchi G, Wang HJ (2013) Near-term Climate Change: projections and predictability. In: Climate change 2013: the physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change
Kopp RE, Horton RM, Little CM, Mitrovica JX, Oppenheimer M, Rasmussen DJ, Strauss BH, Tebaldi C (2014) Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earth’s Future 2(8):383–406. https://doi.org/10.1002/2014EF000239
Landerer FW, Jungclaus JH, Marotzke J (2007) Ocean bottom pressure changes lead to a decreasing length-of-day in a warming climate. Geophys Res Lett. https://doi.org/10.1029/2006GL029106
Little CM, Horton RM, Kopp RE, Oppenheimer M, Yip S (2015) Uncertainty in twenty-first-century CMIP5 sea level projections. J Clim 28(2):838–852. https://doi.org/10.1175/JCLI-D-14-00453.1
Liu ZJ, Minobe S, Sasaki YN, Terada M (2016) Dynamical downscaling of future sea level change in the western North Pacific using ROMS. J Oceanogr 72(6):905–922. https://doi.org/10.1007/s10872-016-0390-0
Lyu K, Zhang X, Church JA, Slangen ABA, Hu J (2014) Time of emergence for regional sea-level change. Nature Climate Change 4:1006–1010. https://doi.org/10.1038/nclimate2397
Madec G, NEMO Team (2016) NEMO ocean engine. doi: 10.5281/zenodo.1472492.
Mathis M (2013) Projected forecast of hydrodynamic conditions in the North Sea for the 21st century. University of Hamburg. https://doi.org/http://doi.acm.org/10.1145/958491.958523
Mathis M, Elizalde A, Mikolajewicz U (2017) Which complexity of regional climate system models is essential for downscaling anthropogenic climate change in the Northwest European Shelf? Clim Dyn 50(7–8):2637–2659. https://doi.org/10.1007/s00382-017-3761-3
Mathis M, Mayer B, Pohlmann T (2013) An uncoupled dynamical downscaling for the North Sea: Method and evaluation. Ocean Model 72:153–166. https://doi.org/10.1016/j.ocemod.2013.09.004
McDougall TJ, Barker PM (2011) Getting started with the TEOS-10 and the Gibbs Seawater (GSW) Oceanographic Toolbox. SCOR/IAPSO WG127.
McSweeney CF, Jones RG, Lee RW, Rowell DP (2015) Selecting CMIP5 GCMs for downscaling over multiple regions. Clim Dyn 44:3237–3260. https://doi.org/10.1007/s00382-014-2418-8
Meinshausen M, Smith SJ, Calvin K, Daniel JS, Kainuma MLT, Lamarque J-F, Matsumoto K, Montzka SA, Raper SCB, Riahi K, Thomson A, Velders GJM, van Vuuren DPP (2011) The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim Change 109:210–241. https://doi.org/10.1007/s10584-011-0156-z
Meyssignac B, Slangen ABA, Agosta C, Champollion N, Church JA, Fettweis X, Ligtenberg SRM, Marzeion B, Melet A, Palmer MD, Richter K, Roberts CD, Spada G (2017) Evaluating model simulations of twentieth-century sea level rise. Part I: Global mean sea level change. J Climate 30(21), 8539–8563. doi: 10.1175/JCLI-D-17-0110.1.
Nicholls RJ, Cazenave A (2010) Sea-Level rise and its impact on coastal zones. Science 328(5985):1517–1520. https://doi.org/10.1126/science.1185782
O’Dea E, Furner R, Wakelin S, Siddorn J, While J, Sykes P, King R, Holt J, Hewitt H (2017) The CO5 configuration of the 7km Atlantic margin model: large-scale biases and sensitivity to forcing, physics options and vertical resolution. Geosci Model Dev 10(8):2947–2969. https://doi.org/10.5194/gmd-10-2947-2017
O’Dea EJ, Arnold AK, Edwards KP, Furner R, Hyder P, Martin MJ, Siddorn JR, Storkey D, While J, Holt JT, Liu H (2012) An operational ocean forecast system incorporating NEMO and SST data assimilation for the tidally driven European North-West shelf. J Operati Oceanogr 5(1):3–17. https://doi.org/10.1080/1755876X.2012.11020128
Oki T, Sud YC (1998) Design of total runoff integrating pathways (TRIP)-a global river channel network. Earth Interact 2(1), 7–22. https://doi.org/https://doi.org/10.1175/1087-3562(1998) 002%3c0001:DOTRIP%3e2.3.CO;2
Ophaug V, Breili K, Gerlach C (2015) A comparative assessment of coastal mean dynamic topography in Norway by geodetic and ocean approaches. J Geophys Res 120:7807–7826. https://doi.org/10.1002/2015JC011145
Palmer M, Howard T, Tinker J, Lowe J, Bricheno L, Calvert D, Gregory J, Harris G, Krijnen J, Pickering M, Roberts C, Wolf J (2018) UKCP18 Marine report
Pelling HE, Mattias Green JA (2014) Impact of flood defences and sea-level rise on the European shelf tidal regime. Cont Shelf Res 85:96–105. https://doi.org/10.1016/j.csr.2014.04.011
Pelling HE, Mattias Green JA, Ward SL (2013) Modelling tides and sea-level rise: to flood or not to flood. Ocean Model 63:21–29. https://doi.org/10.1016/j.ocemod.2012.12.004
Penduff T, Juza M, Brodeau L, Smith GC, Barnier B, Molines JM, Treguier AM, Madec G (2010) Impact of global ocean model resolution on sea-level variability with emphasis on interannual time scales. Ocean Sci 6(1):269–284. https://doi.org/10.5194/os-6-269-2010
Permanent service for mean sea level (PSMSL) (2018) Tide Gauge Data. Retrieved March 15, 2018, from https://www.psmsl.org/data/obtaining/
Pickering MD, Wells NC, Horsburgh KJ, Green JAM (2012) The impact of future sea-level rise on the European shelf tides. Cont Shelf Res 35:1–15. https://doi.org/10.1016/j.csr.2017.02.004
Ponte RM (1999) A preliminary model study of the largerscale seasonal cycle in bottom pressure over the global ocean. J Geophys Res 104(1998), 1289–1300. https://doi.org/https://doi.org/10.1029/1998JC900028
Pugh DT (1987) Tides. John Wiley & Sons Ltd, Surges and Mean Sea-Level
Renshaw CR, Wakelin S, Mahdon R, O’Dea E, Tinker J (2019) North West European Shelf Production Centre NORTHWESTSHELF_REANALYSIS_PHY_004_009. Retrieved from https://resources.marine.copernicus.eu/documents/QUID/CMEMS-NWS-QUID-004-009.pdf
Richter K, Nilsen JEO, Raj P, Bethke I, Johannessen JA, Slangen A, Marzeion B (2017) Northern North Atlantic Sea level in CMIP5 climate models : evaluation of mean state, variability, and trends against altimetric observations. J Clim 30:9383–9398. https://doi.org/10.1175/JCLI-D-17-0310.1
Rio M, Mulet S, Picot N (2014) Beyond GOCE for the ocean circulation estimate: Synergetic use of altimetry, gravimetry, and in situ data provides new insight into geostrophic and Ekman currents. Geophys Res Lett 41:8918–8925. https://doi.org/10.1002/2014GL061773
Roberts-Jones J, Fiedler EK, Martin MJ (2012) Daily, global, high-resolution SST and sea ice reanalysis for 1985–2007 using the OSTIA system. J Clim 25(18):6215–6232. https://doi.org/10.1175/JCLI-D-11-00648.1
Rummukainen M (2010) State-of-the-art with regional climate models. WIREs Climate Change 1(1), 82–96. https://doi.org/https://doi.org/10.1002/wcc.8
Schrum C, Lowe J, Markus Meier HE, Grabemann I, Holt J, Mathis M (2016) Projected change—North sea. In Q. M. & C. F. (Eds.), North Sea Region Climate Change Assessment (pp. 175–217). Springer, Cham. https://doi.org/https://doi.org/10.1007/978-3-319-39745-0_6
Sen Gupta A, Jourdain NC, Brown JN, Monselesan D (2013) Climate Drift in CMIP5 Models. J Clim 26:8597–8615. https://doi.org/10.1175/JCLI-D-12-00521.1
Siddorn JR, Furner R (2013) An analytical stretching function that combines the best attributes of geopotential and terrain-following vertical coordinates. Ocean Model 66:1–13. https://doi.org/10.1016/j.ocemod.2013.02.001
Slangen ABA, Carson M, Katsman CA, van de Wal RSW, Koehl A, Vermeersen LLA, Stammer D (2014) Projecting twenty-first century regional sea-level changes. Climat Change 124:317–332. https://doi.org/10.1007/s10584-014-1080-9
Slangen ABA, Katsman CA, van de Wal RSW, Vermeersen LLA, Riva REM (2012) Towards regional projections of twenty-first century sea-level change based on IPCC SRES scenarios. Clim Dyn 38(5–6):1191–1209. https://doi.org/10.1007/s00382-011-1057-6
Stammer D, Huttemann S (2008) Response of regional sea level to atmospheric pressure loading in a climate change scenario. J Clim 21:2093–2101. https://doi.org/10.1175/2007JCLI1803.1
Sterl A, van den Brink H, de Vries H, Haarsma R, van Meijgaard E (2009) An ensemble study of extreme storm surge related water levels in the North Sea in a changing climate. Ocean Sci 5:369–378. https://doi.org/10.5194/os-5-369-2009
Sterlini P, de Vries H, Katsman C (2016) Sea surface height variability in the North East Atlantic from satellite altimetry. Clim Dyn 47(3–4):1285–1302. https://doi.org/10.1007/s00382-015-2901-x
Strandberg G, Bärring L, Hansson U, Jansson C, Jones C (2014) CORDEX scenarios for Europe from the Rossby Centre regional climate model RCA4.
Suzuki T, Hasumi H, Sakamoto TT, Nishimura T, Abe-Ouchi A, Segawa T, Okada N, Oka A, Emori S (2005) Projection of future sea level and its variability in a high-resolution climate model: ocean processes and greenland and antarctic ice-melt contributions. Geophys Res Lett. https://doi.org/10.1029/2005GL023677
Taylor K, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93(4):485–498. https://doi.org/10.1175/BAMS-D-11-00094.1
Tinker J, Lowe J, Holt J, Pardaens A, Wiltshire A (2015) Validation of an ensemble modelling system for climate projections for the northwest European shelf seas. Prog Oceanogr 138:211–237. https://doi.org/10.1016/j.pocean.2015.07.002
Tinker J, Lowe J, Pardaens A, Holt J, Barciela R (2016) Uncertainty in climate projections for the 21st century northwest European shelf seas. Prog Oceanogr 148:56–73. https://doi.org/10.1016/j.pocean.2016.09.003
Tsimplis MN, Woodworth PL (1994) The global distribution of the seasonal sea level cycle calculated from coastal tide gauge data. J Geophys Res Atmos 991(C8):16031–16040. https://doi.org/10.1029/94JC01115
Wakelin SL, Artioli Y, Butenschön M, Allen JI, Holt JT (2015) Modelling the combined impacts of climate change and direct anthropogenic drivers on the ecosystem of the northwest European continental shelf. J Mar Syst 152:51–63. https://doi.org/10.1016/j.jmarsys.2015.07.006
Ward SL, Green JAM, Pelling HE (2012) Tides, sea-level rise and tidal power extraction on the European shelf. Ocean Dyn 62(8):1153–1167. https://doi.org/10.1007/s10236-012-0552-6
Zhang X, Church JA, Monselesan D, McInnes KL (2017) Sea level projections for the Australian region in the 21st century. Geophys Res Lett 44(16):8481–8491. https://doi.org/10.1002/2017GL074176
Acknowledgements
We thank Thomas Frederikse, Stephen Griffies and Theo Gerkema for their input to this study. We used colorbrewer 2.0 and cmocean colormaps for our figures. The dynamically downscaled datafields underlying the figures are available at the 4TU repository (https://doi.org/10.4121/uuid:ef1c5cca-3900-49f3-9049-6719598a128d). JT and MP were supported by the Met Office Hadley Centre Climate Programme funded by BEIS and Defra. CK was supported by NWO (Netherlands Organisation for Scientific Research), VIDI grant 864.13.011. We acknowledge the World Climate Research Programme’s Working Group on Coupled Modeling, which is responsible for CMIP, and thank the associated climate modeling groups for producing and making available their model output used in this study. For CMIP5 the U.S. Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals. MDT CNES CLS18 was produced by CLS and distributed by Aviso + , with support from Cnes (https://www.aviso.altimetry.fr/).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hermans, T.H.J., Tinker, J., Palmer, M.D. et al. Improving sea-level projections on the Northwestern European shelf using dynamical downscaling. Clim Dyn 54, 1987–2011 (2020). https://doi.org/10.1007/s00382-019-05104-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-019-05104-5