Mechanisms of decadal variability in the Labrador Sea and the wider North Atlantic in a high-resolution climate model

Abstract

A necessary step before assessing the performance of decadal predictions is the evaluation of the processes that bring memory to the climate system, both in climate models and observations. These mechanisms are particularly relevant in the North Atlantic, where the ocean circulation, related to both the Subpolar Gyre and the Meridional Overturning Circulation (AMOC), is thought to be important for driving significant heat content anomalies. Recently, a rapid decline in observed densities in the deep Labrador Sea has pointed to an ongoing slowdown of the AMOC strength taking place since the mid 90s, a decline also hinted by in-situ observations from the RAPID array. This study explores the use of Labrador Sea densities as a precursor of the ocean circulation changes, by analysing a 300-year long simulation with the state-of-the-art coupled model HadGEM3-GC2. The major drivers of Labrador Sea density variability are investigated, and are characterised by three major contributions. First, the integrated effect of local surface heat fluxes, mainly driven by year-to-year changes in the North Atlantic Oscillation, which accounts for 62% of the total variance. Additionally, two multidecadal-to-centennial contributions from the Greenland–Scotland Ridge outflows are quantified; the first associated with freshwater exports via the East Greenland Current, and the second with density changes in the Denmark Strait Overflow. Finally, evidence is shown that decadal trends in Labrador Sea densities are followed by important atmospheric impacts. In particular, a positive winter NAO response appears to follow the negative Labrador Sea density trends, and provides a phase reversal mechanism.

1 Introduction

The North Atlantic ocean is a major source of decadal variability (e.g. Kerr 2000; Frankcombe et al. 2008; Vianna and Menezes 2013) with reported widespread climate impacts (Knight et al. 2006; Zhang and Delworth 2006; Sutton and Dong 2012). Predicting the North Atlantic therefore has a great importance for decadal prediction (e.g. Collins et al. 2006). One of the key locations to explain this decadal variability is the Labrador Sea, which is an important region of deep convection that contributes significantly to the formation of North Atlantic Deep Water (NADW; Haine et al. 2008), and thus also to the intensity of the deep western boundary current (DWBC; Hodson and Sutton 2012). Modelling studies (e.g. Delworth et al. 1993; Eden and Willebrand 2001) suggest that Labrador Sea waters¹ can influence both the Atlantic Meridional Overturning Circulation (AMOC) and the subpolar gyre (SPG) strength and in this way affect decadal variability in the wider North Atlantic. Understanding precisely the drivers of these Labrador Sea changes, and how exactly these later relate to the large-scale ocean circulation is of critical importance to better predict future decadal changes in the North Atlantic sector.

Observations suggest that the ocean circulation has played a key role in recent climate variability in the North Atlantic. The first decade of direct measurements from the RAPID array shows a significant decrease in AMOC strength at 26°N since 2004 AD (Smeed et al. 2014). A decline is also reported in float-derived estimates of the subsurface circulation (Palter et al. 2016) and altimetry-inferred estimates of the upper subpolar gyre strength (Häkkinen and Rhines 2004; Hakkinen and Rhines 2009). Other observational records, such as the deep densities in the Labrador Sea or the wider subpolar gyre, can offer invaluable indirect information on changes in ocean dynamics, as suggested by model outputs (Robson et al. 2014a; Hermanson et al. 2014). In particular, recent observed changes of water mass properties in the deep (i.e. 1000–2500 m) Labrador Sea suggest that the AMOC weakening started in the mid 1990s (Robson et al. 2014a), leading to an important reduction in the meridional heat transport that is most probably responsible for the observed cooling in the eastern SPG ocean heat content since 2005 AD (Robson et al. 2016). The lagged relationship between deep Labrador Sea density and upper ocean trends would suggest that the cooling could continue and extend to the whole North Atlantic, as indicated by the MetOffice’s decadal prediction systems (Hermanson et al. 2014). Thus, it could give rise to a negative phase of the Atlantic Multidecadal Variability (AMV), which is an ocean state associated with important climate impacts.

Climate models are a useful tool to quantify and attribute these impacts, and further explore the recent ocean changes. Different studies with models demonstrate, in particular, that the AMV—defined as a coherent pattern of sea surface temperature (SST) anomalies in the North Atlantic most probably linked to the variability of the AMOC (Knight et al. 2005)—induces multidecadal changes in, e.g., the frequency of occurrence of Atlantic hurricanes (Knight et al. 2006), the drought conditions in the Sahel (Zhang and Delworth 2006) and summer precipitation in southwestern North America and western Europe (Sutton and Hodson 2005). The relative contribution of stochastic atmospheric forcing and ocean dynamics to AMV variability remains to be clarified (e.g. Clement et al. 2015; Zhang et al. 2016). However, models do suggest that the ocean circulation played a decisive role in the observed rapid warming of the North Atlantic SPG (Robson et al. 2012a) and probably contributed to the previous cooling during the 1960s and 1970s (Hodson et al. 2014). In addition, initialised decadal hindcasts based on climate models show high predictability for these large SPG temperature changes (Robson et al. 2012b, 2014b; Yeager et al. 2012) and have been able, in particular, to anticipate the on-going eastern SPG cooling trend (Hermanson et al. 2014). The initialisation of the ocean, including the overturning circulation, is essential to explain the good prediction skill in the SPG (Robson et al. 2014b).

However, the most important drivers of the ocean circulation variability remain largely unknown due to the limited availability of direct observations. This problem can be partly circumvented by using AMOC proxies, like the deep Labrador Sea densities. Unlike the AMOC, this later quantity has been observed since 1950 AD, allowing more robust relationships to be established at the decadal time scale. Also, the AMV is a less reliable AMOC fingerprint to track its past variability as, being based on SSTs, it is strongly affected by a variety of external factors (Roberts et al. 2013), such as volcanic and anthropogenic aerosols (Otterå et al. 2010; Booth et al. 2012). Many studies, based both in models (e.g. Eden and Willebrand 2001; Getzlaff et al. 2005; Yeager et al. 2012; Danabasoglu et al. 2016) and observations (e.g. Dickson et al. 1996; Curry et al. 1998; Kieke and Yashayaev 2015), show a direct connection between the winter North Atlantic Oscillation (NAO; Hurrell 1995) and Labrador Sea water properties, explained through the cooling effect that NAO-driven westerly winds exert on Labrador Sea surface. Modelling studies also show that this buoyancy signal, integrated over time, can explain at least half of the total AMOC variance (Ortega et al. 2011; Mecking et al. 2014). Yet, the exact contribution of the NAO to AMOC variability in the real world is still to be quantified. Advective processes are also relevant to understand the recent Labrador Sea water changes. Following the passage of the Great Salinity Anomalies (GSA) in the 1960–1970s (Dickson et al. 1988), 1980s (Belkin et al. 1998) and 1990s (Häkkinen 2002)—three major events of freshwater inflows in the North Atlantic with different origins, magnitude and extent (Houghton and Visbeck 2002)—Labrador Sea waters have experienced subsequent freshenings affecting the rate of deep water formation (Kieke and Yashayaev 2015). Since the 1970s, a deep long-term freshening of the Labrador Sea is observed (Robson et al. 2016), which could be related to a change in the overflows feeding the Labrador Sea from the Arctic (Dickson et al. 2002). Other potential influences to Labrador Sea density relate to the transport of heat content anomalies from the eastern subpolar gyre, linked themselves to changes in the strength and position of the North Atlantic Current (NAC; Sutton and Allen 1997; Menary et al. 2015).

Labrador Sea water signals have been reported to influence other remote regions of the North Atlantic. For instance, they lead by 6 years the changes in the deep waters near Bermuda (Curry et al. 1998). Through their contribution to the NADW, Labrador Sea waters are also important to understand the southward propagation of AMOC anomalies observed in models, although the propagation timescale appears to be dependent on the region (Zhang 2010) and the model resolution (Getzlaff et al. 2005). Eddy-permitting models, as opposed to non-eddy resolving ones, show a fast (almost in-phase) southward propagation of the AMOC signals consistent with the speed of boundary waves (Getzlaff et al. 2005). Longer lead times between the Labrador Sea and the subtropics are explained through the existence of interior pathways different than the DWBC (Bower et al. 2009), in which advection processes dominate (Zhang 2010). It is, however, still unclear how Labrador Sea waters relate to these latitudinal AMOC changes, and the two distinct propagation timescales.

In this study we assess the link of Labrador Sea densities with the ocean circulation and their relationship with the climate in the wider North Atlantic. In particular, we address the following questions:

• 1. How do Labrador Sea waters affect the AMOC and associated northward salt/heat transport?

• 2. What is the chain of events leading to the development of prolonged Labrador Sea density trends, such as the one recently observed (Robson et al. 2014a)?

• 3. Is there any impact on the atmosphere as a result of the broader ocean response to the Labrador Sea changes?

• 4. Are there any feedback mechanisms at play?

The analysis is based on a control run with the state-of-the-art coupled climate model HadGEM3-GC2 (hereafter referred to as GC2; Williams et al. 2015). This model has an eddy-permitting ocean resolution and a highly resolved stratosphere, two key aspects that have been shown, respectively, to improve the representation of the Gulf Stream extension (Williams et al. 2015), and reproduce more realistic atmospheric teleconnections and interactions (Ineson and Scaife 2009) as compared to models with lower resolution. This is the same model configuration used in the operational seasonal and decadal forecast systems of the Met Office (GloSea5-GC2 and DEPRESYS3, respectively). Note that an earlier version of GloSea5, based on a slightly different model configuration, has produced the first skilful long-range predictions of the NAO (Scaife et al. 2014), suggesting that the model has a good representation of the relevant processes in the North Atlantic.

The article is organized as follows: Sect. 2 describes the model and its climatology. Sect. 3 presents the main results, which include a characterisation of Labrador Sea density variability in the model, its link with the ocean circulations, and the identification of the associated drivers and atmospheric impacts. A final discussion and conclusions are presented in Sects. 4 and 5.

2 Model description and mean climatology

2.1 Model configuration

GC2 (Williams et al. 2015) is a high-resolution version of the Met Office HadGEM3 coupled model, including ocean, atmosphere, sea-ice and land-surface components. The atmosphere component is the Global Atmosphere version 6.0 of the Met Office Unified Model (UM; Walters et al. 2011), with a horizontal resolution of N216 (92 km at the equator and 60 in mid latitudes) and 85 levels in the vertical (with a top at 85 km). It is coupled with the land-surface model, corresponding to the Global Land version 6.0 of the Joint UK Land Environment Simulator (JULES; Best et al. 2011), which shares the same grid and is part of the same model executable as the atmospheric component. The ocean model is the Global Ocean 5.0 (Megann et al. 2014) version of the v3.4 NEMO model (Madec 2008) under the ORCA025 tripolar grid configuration. It comprises 75 vertical levels (24 of them in the top 100 m) and runs with a nominal horizontal resolution of 0.25°, the same used by the Sea Ice component, that corresponds to version 4.1 of the Los Alamos Sea Ice Model (CICE; Hunke and Lipscomb 2010). This version of CICE includes five sea-ice thickness categories and has improved the representation of Arctic sea ice concentration and extent with respect to the previous coarser configurations (Rae et al. 2015). For further details on the different components of the model please refer to Megann et al. (2014), Rae et al. (2015) and Walters et al. (2016). Likewise, a detailed description of the coupling and the systematic errors can be found in Williams et al. (2015).

Note that GC2 is an updated version of HadGEM3 (hereafter referred to as HG3), also run at the same resolution but using the NEMO version 3.2 and lacking some additional developments. HG3 presents a prominent mode of bi-decadal variability in the Subpolar Gyre region (Menary et al. 2015), a periodicity that is not present in GC2, thus pointing to differences in the key processes and interactions. In the North Atlantic, the most important difference between the two model versions arises from a correction to the treatment of convective mixing in the turbulent kinetic energy (TKE) scheme in NEMO v3.4 (used in GC2), leading to substantially lower winter mixed layer depth biases (Megann et al. 2014). At the end of the paper, we discuss conjointly the new findings in GC2 and the previous results with HG3.

2.2 Experiment description

We examine a 310-year long preindustrial control simulation with GC2. This differs from the present day control simulation analysed in Jackson et al. (2015) as it uses CMIP5 forcings appropriate to 1850 (Jones et al. 2011). They consist of well-mixed greenhouse gases (CO₂, CH₄, N₂O, chlorofluorocarbons, and hydrofluorocarbons), tropospheric aerosols (including sulfates, soot, biomass aerosols and organic carbon from fossil fuels), monthly-varying climatological tropospheric and stratospheric ozone concentrations, solar irradiance fixed as the average of the two solar cycles within 1850–1882 (from http://solarisheppa.geomar.de/solarisheppa/sites/default/files/data/Calculations_of_Solar_Irradiance.pdf), and stratospheric volcanic aerosol at background levels (Sato et al. 1993). This preindustrial control simulation was initialised from the end of previous preindustrial control simulations produced during the development period of GC2, totaling 132 years, with the aim of minimising the spin-up period and maximising the useable period of the GC2 preindustrial control examined in this paper. A small and constant drift, mostly notable in the deep ocean, is still present in temperature and salinity. Since our interest is on decadal and multidecadal variability, all variables are linearly detrended at the grid point scale prior to analysis. Note that this is the same model simulation analysed in Robson et al. (2016) to investigate the causes of the recent cooling trend in the North Atlantic.

2.3 Model climatology

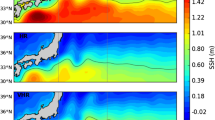
We now describe the mean state in GC2 of the relevant ocean variables for North Atlantic climate. The long-term climatology of the AMOC streamfunction in depth coordinates (AMOC-z; Fig. 1a) shows an overturning cell with a maximum value of 16.8 Sv at 30°N. At 26°N—the latitude of the RAPID array—the climatological maximum is 15.3 Sv and occurs at 650 m, too shallow and about 2 Sv weaker than for the RAPID measurements (17.2 Sv at 1000 m; McCarthy et al. 2015). The largest variance is found in the subtropics, with a standard deviation (SD) of 1.4 Sv at 33°N. There is no notable change in the intensity and vertical extent of the AMOC cell with respect to the climatology in the GC2 present day control run (Fig. 2 in Jackson et al. 2015), suggesting a negligible effect of the changes in radiative forcing since the preindustrial period on the mean AMOC state. The important role of subpolar latitudes emerges more clearly when the AMOC streamfunction is calculated in σ₂ density space (AMOC-σ; Fig. 1b), which highlights the major contribution of water mass transformation in the North Atlantic. Indeed, its climatological maximum value (i.e. 17.3 Sv) occurs at 58°N, where the Labrador Sea is located. The AMOC-σ streamfunction is fairly uniform with latitude, a feature that is particularly true for the denser waters associated with NADW formation, as seen in previous studies with other models (Zhang 2010; Talandier et al. 2014; Kwon and Frankignoul 2014). Besides this closer representation of NADW variability, another advantage of the AMOC-σ over the AMOC-z streamfunction, highlighted first in Kwon and Frankignoul (2014) for the CCSM3 model, is a stronger relationship with the meridional ocean heat transport, especially in the subpolar gyre region.

Fig. 1

a Time mean (in shaded colours) and standard deviation (in contours) of the Atlantic Meridional Overturning Circulation (AMOC) streamfunction expressed in depth coordinates in GC2. b–d The same but for the AMOC streamfunction in σ₂ density space, the Atlantic barotropic streamfunction and the mixed layer depth in march, respectively. The red box in c, d highlights the Labrador Interior region used in subsequent analyses. Likewise, the yellow and blue lines in c indicate the location of the Denmark Strait and the Faroe-Scotland Ridge, respectively. e Time mean temperature (in shaded colors) and salinity (in contours) fields in a section across the Denmark Strait. Green and magenta boxes delimit where the East Greenland Current (EGC) and Denmark Strait Overflow (DSO) indices are defined, respectively. f Time mean of the vertically averaged 1000 m ocean current velocity (in vectors) and speed (in shaded colours)

Figure 1c describes the mean state of the barotropic streamfunction, and therefore the main characteristics of the subtropical and subpolar gyres in the model. The Labrador Sea appears as a key region for the subpolar gyre, as it is there that the anticlockwise gyre circulation strength attains both its maximum climatological mean (42 Sv) and standard deviation (5 Sv). The mean value is comparable with observed transport estimates of 37–42 Sv for the DWBC strength at the exit of Labrador (53°N), obtained from a compilation of moored current meters, hydrographic surveys and sections, and 0.08° eddy-resolving forced simulations (Fischer et al. 2004, 2010; Xu et al. 2013). There is also a particularly large variance in the region of the Gulf Stream and the NAC, up to four time larger than for the subpolar gyre. The deepest convection in the model is observed in the Labrador Sea (Fig. 1d), with other key regions like the Irminger and Nordic Seas also showing winter mixed layer depths greater than 1000 m. However, the region exhibiting largest variability is in the Nordic Seas, possibly due to a higher role of sea ice interactions.

We now look in Fig. 1e at the mean temperature and salinity profiles in a section accross the Denmark Strait (yellow transect in Fig. 1c). The Denmark Strait is a key place to understand Labrador Sea variability if we consider its proximity, and the presence of two distinct major currents. First, the East Greenland Current (EGC, green box in Fig. 1e), which is located at the surface and along the western boundary and associated with the export of anomalously fresh and cold waters. And second, the Denmark Strait Overflow (DSO, purple box in Fig. 1e), which provides the densest contribution to the NADW (Swift et al. 1980) and is associated with cold and relatively fresh waters from the subsurface. Other Greenland-Scotland outflows can also potentially impact the Labrador Sea density changes. In particular, GC2 presents a major branch of cold and fresh waters coming through the Faroe-Scotland ridge (blue thick line in Fig. 1c), which feeds directly into the Eastern SPG. The role of these different flows will be further discussed in Sect. 3.3. Finally, Fig. 1f describes the speed and direction of the mean ocean currents in the top 1000 m. Boundary currents are particularly intense along the Greenland coast (south of the ridge) and also near Newfoundland, the passage regions of the EGC and the exiting Labrador current, respectively.

2.4 Computation of the density components

All density values in this study are computed using the International Equation of State of seawater (EOS-80) referred to the level of 2000 dbar (σ₂), to give more emphasis to the deep water properties. Temperature and salinity contributions to density are calculated using the thermal expansion and haline contraction coefficients. These are themselves estimated as the σ₂ change (in the EOS-80 equation) associated with a small increase in temperature (0.02 °C) and salinity (0.01 psu), respectively.

3 Results

3.1 Characteristics of density variability in the interior Labrador Sea

We first characterise how Labrador Sea densities evolve with time and depth (Fig. 2). To separate the Labrador Sea contributions to the AMOC from those of the boundary currents our analysis is focused on the Interior Labrador Sea (ILS; red box in Fig. 1f), a region with no direct influence of the boundary currents. Interestingly, this is also a region with both enhanced variability in the subpolar gyre strength and anomalously deep winter convection (Fig. 1c, d). Figure 2a shows hints of decadal variability in the ILS densities, with upper ocean signals penetrating downward and generally reaching the 3000 m depth. Both temperature and salinity seem to play an active role in driving these density changes (Fig. 2b–d), with temperature dominating at all depths except 2000–3000 m (Fig. 2e). The stronger influence of salinity at deeper levels, together with the particularly long (almost centennial) timescale associated, suggest a potential contribution of Arctic discharges, as reproduced in other climate models exhibiting enhanced multi-decadal variability (approx. 70–80 years) in the North Atlantic (Jungclaus et al. 2005; Hawkins and Sutton 2007).

Fig. 2

a–c Hovmoller plot (depth vs. time) of the standardised anomalies of the spatially averaged Interior Labrador Sea densities and the related thermal and haline components, respectively. Anomalies are computed with respect to the long-term mean. d Vertically averaged (0–3000 m) relative contributions of the thermal and haline components to density, respectively. These relative contributions are computed as the percentage of levels in a given time step for which the haline (or alternatively thermal) contribution to density represents more than half of the full density anomaly. For clarity, both timeseries are smothed using 11-year moving averages. e The same but for the temporally averaged contributions. In this case, the percentage refers to a given depth level and counts how many time steps are dominated by each one of the density components

The leading mode as described by the first Empirical Orthogonal Function (EOF) of the spatially averaged ILS densities is illustrated in Fig. 3, and explains 67% of the total variance. Its corresponding Principal Component (PC1-ILS, Fig. 3a) shows smooth multidecadal variations, with a similar timescale as for the observed 1000–2500 m Labrador Sea densities (Robson et al. 2014a). Figure 3a also shows the variations in the maximum AMOC-z strength at 45°N after the Ekman transport is removed (AMOC-45N-noek), in order to isolate the thermo-haline driven component. 45°N is the latitude where the AMOC is more strongly correlated with PC1-ILS (Fig. 4b). To remove the Ekman signal, we integrate vertically the Ekman velocities (after introducing a depth-uniform return flow to ensure no net meridional mass transport) following Eq. 6 in Baehr et al. (2004), an approach only valid in depth space. AMOC-45N-noek shares a large part of the slow modulations in PC1-ILS, but also includes higher frequency variations (blue line in Fig. 3a). A similar result, with Atlantic midocean densities showing smoother changes than the AMOC is reported in Roberts et al. (2013). In their study this difference relates to the fact that subsurface hydrographic properties are less exposed than the AMOC to high-frequency surface fluctuations, which can be a major advantage for the detection of low-frequency forced changes (Vellinga and Wood 2004). In GC2, the leading EOF of ILS densities describes a coherent vertical profile (Fig. 3b), with maximum values in the upper 2000 m that decrease slowly with depth and become almost zero below 3000 m. Most of this density structure is thermally driven, except for the deeper ocean where salinity dominates.

Fig. 3

a Evolution of the first PC of the spatially averaged standardised Labrador Interior densities (PC1-ILS; red box in Fig. 1c) and the maximum AMOC streamfunction at 45°N after the Ekman transport is removed (AMOC-45N-noek). b Vertical structure of the EOF associated with the first PC (black line), re-scaled to density units by multiplying by the standard deviation at each depth level. The contributions of salinity and temperature to this density profile (purple and blue lines, respectively) are computed by regressing PC1-ILS onto their corresponding spatially averaged fields. c Time-lag correlations between PC1 and a selection of North Atlantic climate indices: the AMOC-45N-noek, a subpolar gyre strength index (SPGSI), the averaged heat fluxes in the Labrador Interior (HFL) and the North Atlantic Oscillation (NAO). Dots denote correlation values exceeding a 95% confidence level based on a t-test that takes into account the series autocorrelation. Positive lags correspond to PC1 leading the changes in the other variables

Fig. 4

a In-phase correlation between PC1-ILS and the barotropic streamfunction. The blue box encloses the region where the SPGSI is defined. b The same but between PC1-ILS and the AMOC streamfunction in depth coordinates. Stippling highlights the correlation values exceeding the 95% confidence level

Figure 3c describes the cross-correlations between PC1-ILS and other relevant variables. A persistent NAO influence (via related local surface heat fluxes) precedes the changes in PC1-ILS by up to 9 years. PC1-ILS mode is therefore associated with the cumulative (instead of instantaneous) cooling effect of these NAO-driven atmospheric heat fluxes, which can themselves explain the dominant contribution of temperatures in the upper levels. Note that similar prolonged periods with predominant positive NAO phases have been observed in the real world (e.g. 1980s to mid 1990s), and are associated with major changes in the subpolar gyre region (Robson et al. 2012a). The link with ocean dynamics is explored in Fig. 4, describing the in-phase spatial correlations between PC1-ILS and both the barotropic and meridional overturning streamfunctions. PC1-ILS variations are strongly linked with changes in the strength of the western SPG, and also with changes in the AMOC at subpolar latitudes. Maximum correlations occur in phase with PC1-ILS (Fig. 3c) and are stronger for an index of the SPG strength (SPGSI, here defined as the spatially averaged barotropic streamfunction over the blue box in Fig. 4a) than for the AMOC-45N-noek.

We have characterised and described the dominant mode of ILS variability in the model, identifying a significant statistical link with both the horizontal and meridional circulations. The next sub-section explores the relationships between these three variables (i.e. PC1-ISL, SPGSI and AMOC-45N-noek) and density changes across the western boundary current, and also their respective contributions to the meridional ocean heat transport.

3.2 Labrador Sea density link with the ocean circulation and transports

Western boundary densities are an important driver of AMOC variability as a direct consequence of the thermal wind equation (Tulloch and Marshall 2012), which relates the meridional mass transport to the zonal density gradients (Hirschi and Marotzke 2007).

Here we look first at the link between Labrador Sea densities and changes along the western margin of the Atlantic, and explore their particular relationship with the AMOC and the SPG (Fig. 5). Figure 5d–l shows the correlations at different lead times between the AMOC-45N-noek and the density profiles on different latitudinal sections near the North American continental margin. The focus is first set on a section across 57°N (Fig. 5d–f), covering both the coast and the Interior Labrador Sea (red box). In this region, an upper ocean signal (top 1500 m) appears in phase with the AMOC (Fig. 5e), with maximum values near the continent and also in the ILS. Two years later (Fig. 5f), maximum correlations occur below 1500 m, suggesting some downward penetration of the previous surface signal. A further look at other zonal sections (Fig. 5g–l) shows that, in GC2, only the densities in the upper 1500 m correlate coherently across all latitudes with the AMOC. These are therefore the key levels contributing to intensify the AMOC strength and enhance the northward heat transport. By contrast, it appears also that the deep Labrador densities do not contribute directly to the AMOC variability in this model.

Fig. 5

a–c Correlation between the SPG strength index (SPGSI) and density across a zonal section at 57 N near the western Atlantic boundary, with the SPGSI leading by 2 years, in phase with, and lagging by 2 years the changes in density, respectively. Thin black contours enclose areas with correlation values exceeding the 95% confidence level established as in Fig. 3c. The red box denotes the longitudes of the Interior Labrador Sea over which PC1-ILS is calculated. The dashed horizontal line highlights the 1500 m depth level. d–f The same as in a–c but between the AMOC-45N-noek and the density profiles. g–i and j–l The same as in d–f but for zonal sections at 45°N and 35°N

In contrast to the AMOC, SPG variability is associated with more deeply reaching density signals at 57°N (Fig. 5a, c). Note that the cyclonic geostrophic flow associated with these vertically uniform positive density anomalies is indeed consistent with a SPG strengthening. Maximum in-phase correlations with the SPGSI index are seen below 1500 m and over the ILS region, thus involving deeper levels than previously found for the AMOC-45N-noek (Fig. 5e). Similar depths are reached when the AMOC lags the changes in density by two years (Fig. 5f). This lag is because SPG changes tend to follow those in the AMOC by 1–2 years, as supported by a cross-correlation analysis between both indices (not shown). This particular lag represents the typical time required for the upper density anomalies to penetrate downward.

The latitudinal coherence of the AMOC signals related to PC1-ILS is now explored in Fig. 6. In-phase with PC1-ILS, the full AMOC-z shows a large-scale intensification (Fig. 6a) from midlatitudes to the Equator, with maximum values between 40–45°N. This is consistent with results from coarser models (Lohmann et al. 2014), showing a strong link between North Atlantic deep water formation and AMOC variability between 40–50°N. Part of the subtropical AMOC-z signal precedes the changes in PC1-ILS and is associated with the local effect of the Ekman transport (Fig. 6b), which is ultimately driven by the NAO (that leads PC1-ILS for up to a decade). The NAO establishes a well-known dipolar wind pattern between subtropical and subpolar latitudes, inducing northward Ekman transport in the first region and southward in the second (see e.g. Fig. 7a in Ortega et al. 2012). Besides this instantaneous Ekman-driven response, the NAO also induces a slow delayed AMOC response, due to the effect of westerly wind variability in driving Labrador Sea deep water formation. This slow effect is more evident once the Ekman signal has been removed from the AMOC-z streamfunction (AMOC-z-noek; Fig. 6c), which now shows a strengthened AMOC at northern latitudes (50–60°N) that propagates southward in 2–3 years time. This southward propagation, however, is disrupted again around 30°N, which is probably due to limitations of the AMOC-z streamfunction to represent the meridional connectivity with the subtropics (Zhang 2010). In fact, an uninterrupted intensification across all latitudes is observed when the AMOC-σ streamfunction is considered (Fig. 6d). Two apparent propagation timescales for the AMOC-σ signal are seen, the first being almost instantaneous and in phase with PC1-ILS, and the second developing slowly (~8 years) after the PC1-ILS intensifies and being more restricted to mid-latitudes. This later timescale is consistent with the delayed baroclinic oceanic response to the NAO, identified in Eden and Willebrand (2001).

Fig. 6

Time-lag correlations between PC1-ILS and a the maximum AMOC-z streamfunction, b the zonally averaged Ekman transport, c the maximum AMOC-z after the Ekman component has been removed, and d the maximum AMOC-σ streamfunction, at each latitude. Only correlation values exceeding the 95% confidence level as established in Fig. 3c, are shown

Now we look at the lead-lag relationships of Labrador Sea densities and the different circulation indices with the meridional ocean heat transport (OHT). Consistently with the associated AMOC changes in Fig. 6, PC1-ILS also represents a general OHT strengthening that is particularly evident north of 40°N (Fig. 7a). This strengthening is preceded by an OHT increase in the subtropics, which cannot be explained through changes in the AMOC-z-noek streamfunction (Fig. 6c). These local OHT changes are most probably wind-driven, as they appear in the same latitudes and lead times in which the northward Ekman transport is intensified (Fig. 6b), and coincide also with predominant positive NAO phases (Fig. 3c). The latitudinal OHT variations specific to AMOC-45N-noek are shown in Fig. 7b. Consistent with Fig. 6d, two different propagation timescales for the AMOC-driven OHT changes are hinted. First, an almost instantaneous response that is most probably associated with the propagation speed of boundary waves, as evidenced in other eddy-permitting models (Getzlaff et al. 2005). And second, a slowly developing response that might involve a signal propagation through interior pathways (Zhang 2010). The SPGSI-driven OHT changes are described in Fig. 7c. As expected from the strong correlation between SPGSI and PC1-ILS in Fig. 3c, they are largely consistent with the changes described above for PC1-ILS (Fig. 7a). The main difference is seen for the in-phase correlations, that in SPGSI are characterised by large positive values at mid-latitudes, probably associated with rapid responses of both the ocean heat content and the SPG to NAO fluctuations. Much weaker relationships are obtained between the previous indices (PC1-ILS, SPGSI, AMOC-45N-noek) and the meridional ocean salinity transport (not shown). In this case, all the three circulation indices relate to a local in-phase increase of salinity at midlatitudes, but show no consistent changes over the Tropics.

Fig. 7

Time-lag correlations between the OHT at different latitudes and a PC1-ILS, b AMOC-45N-noek and c SPGSI. Only correlation values exceeding the 95% confidence level as established in Fig. 3c are shown. Positive lags indicate that the OHT is lagging the changes in the other indices

This subsection has demonstrated the close link between the ILS densities and both the North Atlantic overturning and barotropic circulations in GC2, all of them influencing the northward OHT. It has also highlighted the important role in the model of the top 1500 m west boundary densities to induce coherent AMOC changes across latitudes. We now move on to examine the processes responsible for Labrador Sea density variability in GC2.

3.3 Drivers of Labrador Sea density variability

Labrador Sea density changes can respond to both atmospheric and oceanic influences. The above analysis has highlighted a persistent leading relationship of NAO variability on PC1-ILS (Fig. 3c), with the accumulation of the associated surface heat fluxes playing a key role. Here we quantify its total contribution to PC1-ILS variability. To do so, a least-squares regression model for PC1-ILS is defined, using the local heat fluxes at different lead times as the only predictor. Note that no significant contribution of the local surface freshwater fluxes (precipitation minus evaporation) on PC1-ILS variability is remarked (not shown). This is an equivalent approach to the one employed in Ortega et al. (2011) for the AMOC. The equation is as follows:

$$\text{PC1}-\text{ILS}\left( t \right)=\underset{i=0}{\overset{L}{\mathop \sum }}\,{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{i}}}\text{HFL}\left( t-i \right)+\text{ }\!\!\xi\!\!\text{ }$$

where α_i is the regression coefficient for lead-time i, HFL the timeseries of surface heat fluxes in the ILS region, ξ the residuals of the regression model, and L the maximum lead-time.

This atmospheric influence is accounted for in the regression model presented in Fig. 8, which considers a maximum lead-time between the heat fluxes and PC1-ILS of 12 years. This is the shortest L for which the HFL timeseries becomes uncorrelated with the residuals at all lead-times, thus guaranteeing that all PC1-ILS variability associated to the ILS heat fluxes is accounted for in the regression model (noted as PC1-ILS-HFL from now on). This model explains 62% of the total PC1-ILS variance. A linear regression of PC1-ILS-HFL with the ILS density components at all depths (not shown) reproduces most of the distinct features in Fig. 3b, such as the uniform contribution of salinity across the whole water column, as well as a maximum temperature signal in the top 50 m, decreasing first sharply (from 50 to 100 m) and later on smoothly with depth. The upper maximum is related to the instantaneous effect of heat fluxes, while the slowly decreasing signal likely results from the downward propagation of heat fluxes accumulated from previous lead times. The residuals of PC1-ILS-HFL show a pronounced nearly centennial modulation (Fig. 8a) and correlate strongly (R = 0.61, p value <0.05) with PC1-ILS (Fig. 8b). This correlation is difficult to explain if the residuals were composed by pure stochastic noise and thus suggests that additional contributions, e.g. from the Greenland–Scotland overflows, are at play. PC1-ILS-HFL residuals relate to maximum salinity-driven density changes in the upper ocean (top 400 m) and thermally-driven changes in the subsurface (between 1500 and 2500 m; Fig. 8c). The first maxima could be potentially explained by changes in the EGC while the second probably relates to variations in the dense water overflows (i.e. from the Denmark Strait and Faroe-Scotland Ridge).

Fig. 8

a Evolution of PC1-ILS, a regression model of its variability based on ILS heat fluxes (PC1-ILS-HFL), and the associated residuals. b Scatterplot of PC1-ILS against the residuals of the regression model. c Regression of the standardised residuals onto the spatially averaged ILS density components. Depths with the largest thermal (1800 m) and haline (50 m) signals are highlighted with dashed horizontal lines

Let’s first focus on the shallow contribution. Figure 9a compares the evolution of the PC1-ILS-HFL residuals with the density components of the EGC. Despite some differences at the decadal time-scale, particularly evident during the period 2160–2270, two of the four major maxima in the residuals (occurring in 2280 and 2395) are clearly preceded by large salty and dense anomalies in the EGC (Fig. 9a). This suggests that the influence of the EGC on Labrador Sea density is related to the occurrence of extreme salinity events. A four-box conceptual model by Born and Stocker (2014) supports the importance of salt fluxes from the boundary currents to drive convection in the Interior Labrador, and the SPG variability. The cross-correlations in Fig. 10a describe the average lead-lag relationship between the PC1-ILS-HFL residuals and the EGC indices. The associated density signals (black lines) lead by 1 year the changes in the residuals. It becomes also evident that these density changes are salinity driven, with temperature just playing a compensating role.

Fig. 9

a Evolution of the PC1-ILS-HFL residuals and three standardised EGC indices, defined as the total, thermal and haline density components averaged over the green box in Fig. 1e. All timeseries are smoothed using 11-year running averages. The dotted vertical lines denote a period of poor agreement between the PC1-ILS-HFL residuals and the full EGC density. b The same but for a selection of DSO indices (computed as averages over the purple box in Fig. 1e). c Evolution of the standardised DSO haline density component (DSO-RHOS), and a standardised index of deep ILS salinity, computed as the vertically averaged salinity between 2000 and 3000 m

Fig. 10

a, b Time-lag correlations between the PC1-ILS-HFL residuals and the density components of EGC and DSO, respectively. Correlation values exceeding the 95% confidence level are highlighted with symbols. Negative lags stand for the EGC and DSO indices leading the PC1-ILS-HFL residuals. c The same as in a but between the DSO density components, and those of the deep ILS waters. In this case, negative lags stand for the DSO indices leading

Likewise, other ocean signals, such as the DSO, might be at the origin of the multidecadal variability and the other maxima in the PC1-ILS-HFL residuals. Figure 9b confirms that DSO density variations describe reasonably well the multidecadal modulations in the PC1-ILS-HFL residuals, in particular during the highlighted period from 2160 to 2270 where the EGC shows a rather different evolution. Furthermore, in the first part of this period, DSO densities experience a sustained increasing trend anticipating the occurrence of the maximum seen in the residuals in year 2215, which is not attributable to the EGC. Volume transport and density changes across the Faroe-Scotland Ridge (FSR) also exhibit important multidecadal and centennial modulations (not shown) in line with the timescales recently reported in paleocurrent proxy data from the Icelandic basin (Mjell et al. 2016). The influence of the FSR overflow is, however, not independent from that of the DSO. In particular, the changes in both their flow speed and salinity exports are strongly correlated, with in-phase correlation coefficients larger than 0.6. For simplicity, the rest of this analysis will be focused on the DSO.

Over the whole simulation, PC1-ILS-HFL residuals lag by about 2 years the changes in the DSO densities (Fig. 10b), but unlike for the EGC, these density DSO signals result from combined contributions of temperature and salinity. The DSO influence on the PC1-ILS-HFL residuals appears to be first thermally driven (for leading times from 12 to 3 years), and explained through the combined effect of both DSO salinity and temperature for shorter lead times. Note also the particularly large correlations found when the PC1-ILS-HFL residuals lead the DSO components by 10 years (positive lags in Fig. 10b). These probably represent a delayed DSO response to changes in the meridional transports at lower latitudes, which follow in turn the changes in the ILS densities. A cross-correlation analysis between the DSO density components and the ILS densities at different levels (not shown) locates the leading temperature signal in the upper ocean (top 2000 m), while the salinity-leading contribution takes place at deeper levels (2000–3000 m). Note that these coincide with the same levels at which salinity dominates the ILS density evolution in Fig. 2e. This important role of DSO exports in leading by about a decade the centennial changes in deep ILS salinity is illustrated in Figs. 9c and 10c.

We have identified above the major drivers of ILS density variability. These include the accumulation of atmospheric heat fluxes at the surface, episodic inflows of large salinity anomalies by the EGC, and slowly varying modulations in the DSO and FSR exports (both temperature and salinity driven). In light of the long-timescales involved in most of these ILS density changes, which might imply potential for climate predictability, the next subsection looks at the associated atmospheric impacts.

3.4 Atmospheric impacts

To explore the potential impacts associated with the recent observed Labrador Sea density weakening (Robson et al. 2014a), we perform a composite analysis on a selection of analogous events in GC2. This focus on strong trends is expected to increase the signal-to-noise ratio of the atmospheric responses, which may not be necessarily appreciable in regression analyses based on interannual timescales (Allison et al. 2014). In particular, we compute the composite atmospheric trends following by 5 years the 9 largest non-overlapping 15-year decreasing trends in PC1-ILS (Fig. 11a). This particular lead time is selected after the analysis in (Robson et al. 2016), that identifies, in the same simulation, a trend towards more positive NAO phases 5 years after the strongest decreasing trends in the deep Labrador Sea densities (1000–2500 m). Here, we look at the composite delayed winter (DJF) and summer (JJA) trends on SLP and other surface variables with high socioeconomic impacts, like temperature and precipitation.

Fig. 11

a Occurrence of the nine largest non-overlapping 15-year long decreasing trends in PC1-ILS. b Composite of 15-year linear trends in DJF SLP following the nine events above, where SLP trends are offset by 5 years (i.e. for each event the first year used to compute the SST trend lags the first year used to calculate the PC1-ILS trend by 5 years). Stippling shows where trends are significant at the 95% confidence level according to a Monte-Carlo test based on 1000 random draws of nine independent 15-year trends from PC1-ILS. c–e The same as in b but for DJF trends in air temperature at 1.5 m (T1.5 m), SST and total rainfall. f–i The same as in b–e but for JJA trends

The delayed winter impacts are described in Fig. 11b–e. Consistent with Robson et al. (2016), trends in PC1-ILS give rise to a positive NAO-like trend pattern in winter (Fig. 11b). Likewise, trends in surface air temperature at 1.5 m (SAT; Fig. 11c) describe the canonical quadrupole structure associated with the NAO (Hurrell et al. 1997), with positive values over Northern Europe and the United States and negative values over Eastern Canada and North Africa. In the ocean (Fig. 11d), there is a large warming along the Gulf Stream Extension and a widespread cooling in the SPG region, both also present in the spatial SAT trends. The location southeast of Greenland where the maximum cooling occurs coincides with the North Atlantic “warming hole” region, which is related in several studies to an AMOC decline (Drijfhout et al. 2012; Rahmstorf et al. 2015), thus further supporting the close association between PC1-ILS and the AMOC. Only small winter precipitation trends are observed over the continents (Fig. 11e), the largest changes being a zonal dipole in the mid-latitude North Atlantic, with increased rainfall in the Grand Banks and decreased rainfall west of Europe. Previous studies with different coupled models (Gastineau and Frankignoul 2012; Frankignoul et al. 2013) highlight the key role of AMOC-driven SST anomalies in the Gulf Stream and NAC region in the generation of winter NAO responses, triggered through changes in local surface heat fluxes that affect eddy activity in the North Atlantic storm track. These studies, based on lagged linear regressions with the annual AMOC strength, report a typical warming over the SPG region of 0.4 °C and a negative NAO-like dipole of the order of −0.6 hPa for AMOC increases of 1 Sv. That is, a 1.5 hPa north-to-south gradient in SLP when the Gulf Stream Extension warms by 1 °C. Our composite analyses, following instead the strong decreasing trends in the Labrador Sea densities—which are themselves linked to AMOC decreases—, describe an equivalent SLP gradient and SST change of 7.2 hPa and −1.1 °C, respectively. The sign of the response is consistent in both analyses, but the magnitude of the changes is larger in GC2. This could be due to the fact that our study is specifically focused on large extreme events and is therefore more adequate to identify potentially non-linear atmospheric responses.

Interestingly, different impacts appear for the summer atmospheric circulation (Fig. 11f), mainly characterised by a blocking situation over Scandinavia. Enhanced blocking activity, but more located over the eastern SPG, has been previously associated with the development of abrupt cooling events over the region (Drijfhout et al. 2013). A strong local warming is now noticed east of Greenland, possibly linked to summer ocean-ice interactions. Due to the different atmospheric circulation, the associated summer inland T1.5 trends (Fig. 11g) are also different than for winter, in particular over Western Europe and northeastern North America where a cooling is now established. As in winter, no noteworthy summer precipitation impacts are observed over the continents, although a southward migration of the Intertropical Convergence Zone (ITCZ) is seen in the Equatorial Atlantic and Eastern Pacific. This is a well-known equatorial response caused by a southward expansion of the northward Hadley cell that compensates for the reduced ocean northward heat transport following the AMOC declines (Kageyama et al. 2009). It is furthermore possible that part of the anomalous summer atmospheric circulation in the mid-latitudes described above is forced by ITCZ-driven SST changes (via latent heat fluxes) in the Tropics. Other dynamical extratropical atmospheric responses to low-latitude SST forcing have been previously identified both for the winter (e.g. Sutton et al. 2000) and summer seasons (e.g. Cassou et al. 2005).

An analogous composite analysis based on the PC1-ILS increasing trends (not shown) identifies nearly opposite atmospheric impacts to those described above. In particular, a clear negative NAO-like pattern is established in winter, and the SPG and Gulf Stream regions experience a warming and a cooling, respectively. Also worth noting is a northward shift in the ITCZ position, now present both during winter and summer. These and the above results are consistent with Allison et al. (2014), that explored the sensitivity of climate impacts to the polarity of rapid decadal AMOC changes in a variety of climate models, and concluded that the associated atmospheric and surface ocean changes are approximately symmetric.

In conclusion, by focusing on a selection of large events characterised by rapid decadal changes in the ILS densities, we have identified two major atmospheric impacts. First, a delayed winter NAO response that furthermore provides a negative feedback to the initial ILS changes. And second, a meridional displacement in the ITCZ—mainly visible in summer—that responds to changes in the ocean circulation. These two atmospheric signals lead to important climate impacts over the continents.

3.5 Summary of the interactions

A schematic of the different processes and interactions described for GC2 throughout the article is represented in Fig. 12. Positive density anomalies in the Interior Labrador Sea appear in response to a combination of different factors, including the accumulation of cooling surface heat fluxes driven by the NAO for up to a decade, the delayed influence of salinity exports by the EGC, as well as slow changes in the Denmark Strait overflows inducing first a cooling and later on a salinification of the deep Labrador Sea waters. Almost concomitant anomalously dense waters are seen in the upper 1500 m of the Labrador Sea and all along the western boundary, where they contribute to speed up the AMOC. Such coherent structure across latitudes is not clear for the deeper ILS waters, which instead induce a local acceleration of the SPG strength. It is therefore through this combined effect on both the meridional and horizontal ocean circulations that positive ILS density anomalies increase the northward heat and salinity transports. These transports provide a first feedback mechanism on the ILS densities. Yet, the associated temperature and salinity changes produce competing effects, the first (i.e. arrival of warmer waters) contributing to reverse, while the second (i.e. arrival of saltier waters) contributing to maintain the initial ILS density anomalies. An additional feedback mechanism through the atmosphere is also present. Negative NAO phases appear 5 years after the increased AMOC conditions, thus establishing a mechanism of phase reversal for the ILS densities.

Fig. 12

Schematic diagram of the Labrador Sea interactions in GC2

In the following section we discuss the associated uncertainties and how they affect the relevance of these findings for the real world.

4 Discussion

Before making any inferences for the real world, some of the previous findings merit further discussion. This includes the degree of realism of the key drivers identified in the model, the impact of the major model biases and misrepresented processes on our results, and some limitations inherent to our analysis.

The major role of the NAO in driving Labrador Sea variability in GC2 appears consistent with observations (Dickson et al. 1996; Visbeck et al. 2003) and other model studies (Eden and Willebrand 2001; Guemas and Salas 2008; Ortega et al. 2012; Yeager et al. 2012; Danabasoglu et al. 2016). During positive NAO phases, strengthened westerly winds increase surface heat loss in the Labrador region, and this signal propagates downward contributing to cool the whole water column. Thus, the observed decline in the NAO from the 1950s to 1970 was followed by a warming in the Labrador Sea, and the predominant positive NAO phases in the early 1990s gave rise to a remarkable Labrador Sea cooling (Curry et al. 1998). Also, episodes of persistently high (or low) NAO phases have been linked to anomalously deep (or shallow) Labrador Sea convection (e.g. Pickart et al. 2002; Kieke and Yashayaev 2015), an influence that can explain the vertical homogeneity of the Labrador Sea signals in GC2. Other atmospheric conditions than the canonical NAO might exert an influence on Labrador convection in the real world. For instance, a recent analysis with reanalysis data and forced-ocean sensitivity experiments (Kim et al. 2016) has identified a somewhat different dipole structure, with a mid-latitude high occupying the western (instead of the eastern) North Atlantic, that explains half of the episodes of strong heat loss in the Labrador Sea. This atmospheric pattern appears to be accompanied by La Niña conditions, suggesting some remote influence from the Pacific on Labrador convection.

As for the other ocean influences, the degree of realism of the simulated Arctic contributions is probably limited by model deficiencies in the representation of the Denmark Strait overflows, which are too strong when compared to observational estimates (Megann et al. 2014). Some differences are also noted regarding the associated time scale and origin of salinity signals influencing the Labrador Sea. Thus, while our model shows centennial modulations in the DSO discharges, three major GSA events have been observed in the real world since the 1960s. Two of them (early 1980s and early 1990s) are associated with the effect of severe winters on the Labrador Sea waters. Additionally, the 1980s and 1970s GSA events are influenced by remote freshwater exports from the Arctic (via the Fram Strait) and the Canadian Archipelago, respectively (Belkin et al. 1998).

In light of these differences, two important model biases to keep in mind are the anomalously strong winter convection and the relatively shallow NADW return flow in GC2 as compared to observations. The simulated climatological winter mixed layer depth is deeper than 2000 m in some areas of the Labrador Sea, which is in stark contrast with reported values of 500–1000 m inferred from observations (de Boyer Montégut et al. 2004). This overestimation of convection can thus affect how realistically upper ocean signals penetrate downward in the model. The overly shallow NADW return flow in GC2 is due to excess entrainment in the representation of the overflows (Megann et al. 2014). This issue might explain why while previous works (Hodson and Sutton 2012; Robson et al. 2014a; Menary et al. 2015) report a close link between the deep Labrador Sea densities (typically between 1000 and 3000 m) and the AMOC, in GC2 this link is only found for the upper Labrador Sea densities (top 1500 m). But, which one of these relationships is more realistic? The answer is not clear. Other results both with profiling floats released at 700 and 1500 m (e.g. Fischer and Schott 2002; Bower et al. 2009) and high-resolution models (Spence et al. 2012) suggest that subsurface Labrador Sea waters are often advected into the North Atlantic Interior instead of following the DWBC toward the subtropics, thus reducing the direct role of these waters on the AMOC at lower latitudes. These studies also provide evidence for the existence of interior pathways, which could explain the slow timescale observed in GC2 for the southward propagation of AMOC anomalies, contrasting with the additional almost instantaneous timescale related to fast wave adjustments along the western boundary.

Finally, it is important to remark that our previous analysis does not account for the total contribution of the SPG strength to the net OHT. The SPG strength index defined in this study accounts broadly for the advection of mean temperatures by the anomalous gyre circulation (v′T₀). Therefore, this index mostly describes the increased (or decreased) advection of relatively warm and salty waters entering the SPG in the region downstream of the NAC (Fig. 7c). The contribution of anomalous temperatures transported by the mean flow (v₀T′) has not been considered in this study, and can potentially be of the same order than the v′T₀ component, as previously shown for HG3 (Menary et al 2015). This v₀T′ component is responsible for the westward transport of heat content anomalies from the eastern SPG, which can potentially feed back onto the Labrador Sea waters. To properly quantify the importance of this contribution would require a detailed heat budget breakdown, which is out of the scope of this paper.

5 Conclusions

Water mass properties in the Labrador Sea exhibit large decadal variability, which is believed to play an important role in the decadal variability of the wider North Atlantic Ocean. This study has investigated Labrador Sea density variability on decadal to multi-decadal timescales in a 310-year control simulation with the high-resolution coupled climate model HadGEM3-GC2 (GC2). In particular, we have explored the chain of events leading to changes in Interior Labrador Sea (ILS) density, and the links between ILS density and large-scale ocean circulation and transports.

To do so we first evaluated the leading mode of ILS densities (PC1-ILS; accounting for 67% of the total variance), which exhibits strong multi-decadal variability. PC1-ILS is characterised by a fairly uniform vertical profile, with maximum density values in the top 2000 m, followed by a slow decrease with depth down to 4000 m. Both temperature and salinity contribute to the vertical structure of density anomalies associated with PC1-ILS. The major drivers of PC1-ILS variability can be summarised as follows:

• The largest contribution is due to the temporal integration of local surface heat fluxes, primarily driven by changes in the North Atlantic Oscillation (NAO). A univariate regression model of PC1-ILS, which uses as a predictor surface heat fluxes averaged over the interior Labrador Sea and accumulated for 12 consecutive years, explains 62% of the PC1-ILS variance. This result is consistent with previous works with other models, supporting a dominant role of NAO forcing on Labrador Sea deep water formation (Ortega et al. 2011), the Atlantic Meridional Overturning Circulation (AMOC) and the subpolar gyre strength (Mecking et al. 2014).

• The residual variability of PC1-ILS (i.e. the variability of PC1-ILS not explained by the regression model) exhibits coherent variations on centennial timescales, highlighted particularly by the occurrence of three major density maxima in the 310 year time series. This residual variance has two distinct density components: a salinity-driven component in the upper ocean and a thermally-driven component in the subsurface.

• The upper ocean salinity variability is related to variations in the East Greenland Current (EGC). Large anomalous salinity exports by the EGC are found to precede two of the three density maxima in the residuals of PC1-ILS. This is consistent with other models, which support a role of similar Arctic salinity outflows in driving bidecadal (Escudier et al. 2013) to multidecadal (Jungclaus et al. 2005; Hawkins and Sutton 2007) changes in the AMOC.

• An additional Arctic contribution comes from the influence of dense Greenland-Scotland overflows on the Labrador Sea densities. In particular, the strongest influence comes from the Denmark Strait Overflow waters (DSO). Analysis of the PC1-ILS residuals reveals that these waters first influence the subsurface temperature changes in the Labrador Sea, and also – after a delay of 9 years – induce salinity changes at the deepest levels. The role of DSO is also consistent with rapid AMOC changes in the HadCM3 model (Hawkins and Sutton 2008), which are explained by a flow of anomalous dense waters through the Denmark Strait.

Regarding the relationship between variability in Labrador Sea densities and variability in ocean circulation and transports, the major findings are as follows:

• In GC2, AMOC variability is most closely linked to Labrador Sea density variability in the upper 1500 m, mediated by propagation of signals along the western boundary. The lack of a strong relationship to density variability at deeper levels is likely related to a shallow bias in the mean AMOC in this particular model.

• The PC1-ILS index is found to be a good proxy of the AMOC strength (R = 0.6) due to its strong link with upper ocean Labrador Sea densities. Our analysis also supports using the AMOC streamfunction calculated in density space (AMOC_σ) to track how the associated signals propagate from high to low latitudes, as in Zhang (2010). Indeed, the link of PC1-ILS with the circulation in the subtropics can only be observed when the AMOC_σ streamfunction is considered. The analysis is also suggestive of two distinct speeds for the AMOC changes to propagate from high to low latitudes (Fig. 6d), characterised by a fast (almost instantaneous) and a slow time scale (i.e. 5–7 years), which is more evident for the AMOC_σ streamfunction. Two similar AMOC propagation time scales have been identified in the model GFDL-CM2.1 (Zhang 2010), associated with fast-propagating boundary waves and slow advection through interior pathways, respectively.

• By contrast, the SPG strength is strongly linked with in-phase Labrador Sea density anomalies that extend over the whole water column, and are largest at mid depths (i.e. 1000–1500 m). Changes in the strength of the SPG are consistent with the geostrophic response induced by these Labrador Sea density anomalies.

• Since PC1-ILS is connected with both the shallow and deep ILS densities, it provides an even better proxy of the SPG (R = 0.8) than for the AMOC strength in this model. This analysis therefore refines the previous interpretation of Labrador Sea densities as a precursor of AMOC variability (Robson et al. 2014a, 2016), by highlighting that Labrador Sea densities might also affect the SPG strength, and thus provide a link between the variability of both the gyre and the overturning circulations.

• PC1-ILS is also a good indicator (R > 0.5 at mid-latitudes) of ocean heat transport (OHT) changes across the Atlantic. A few years before the changes in PC1-ILS there is an intensification of the northward heat transport between 10–40°N, which is explained by local changes in the Ekman transport (the Ekman transport itself is ultimately driven by the NAO and concomitant with the NAO-driven surface heat fluxes giving rise to the Labrador density anomalies). Once the density anomalies are formed their subsequent influence on the ocean circulation leads to an intensification of the OHT, this time starting at high latitudes and propagating southward. In phase with PC1-ILS, there is a coherent OHT intensification at all latitudes, which is consistent with the effect of the fast propagating boundary waves on the AMOC. In subsequent years, the OHT intensification continues, but almost exclusively at subpolar latitudes.

The link with the OHT (and related ocean salt transport; OST) provides a negative feedback (positive for OST) on the Labrador Sea densities. Although it is the same sign, the feedback is weaker than for the previous version of the HadGEM3 model (HG3; Menary et al. 2015), which exhibits a strong 17-year periodicity that is not present in the version analysed in this study. In HG3, the phase reversal is instead related to a strong negative feedback between Labrador Sea densities and those in the North Atlantic Current (NAC). However, a similar mechanism is not found in GC2.

The interaction with the atmosphere also seems to be different in GC2 compared to HG3. In HG3 the NAO plays an intensifying role on the Labrador Sea/NAC feedback, which is most effective at inter-annual timescales. In particular, the NAO forces an anomalous geostrophic current response contributing significantly to the NAC changes that first feed onto the SPG temperatures, and eventually onto the Labrador Sea. However, in GC2, the mechanism is different. We identify a delayed NAO response that contributes to phase reversal in Labrador Sea densities through surface flux changes. This response is particularly clear after large sustained trends in ILS densities. A positive NAO signal emerges, overall, 5 years after the strongest decadal decreasing trends in PC1-ILS, most likely driven by the ocean surface temperature changes following the weakened OHT associated with these events. Note that by selecting these rapid large amplitude transitions, the signal-to-noise ratio is improved, and the atmospheric signal is better detected.

Finally, it is also important to highlight the similar timescales between the simulated PC1-ILS changes and those of the observed deep Labrador Sea densities (Robson et al. 2014a), suggesting that similar drivers to the ones identified in this study might be at play in the real world. Our results with GC2 support a major role of NAO-driven ocean heat fluxes on Labrador Sea densities, and thus on the evolution of the SPG as well as the AMOC, a result that is consistent with previous studies exploring the reasons for the rapid warming in the North Atlantic during the 90s (Robson et al. 2012a, b; Yeager et al. 2012). GC2 also suggests that changes in the water exports through the Denmark Strait may play a role in the observed anomalously low densities in the deep Labrador Sea following 2000 AD (Robson et al. 2016). In the last few years, coinciding with this minimum in Labrador Sea densities, there seems to be a new tendency towards positive winter NAO phases (observed in 2012, 2014, 2015 and 2016). This might as well suggest that the delayed negative NAO feedback identified in GC2, and also reported for the AMOC in other models (Gastineau and Frankignoul 2012), is potentially present in the real world. Understanding the processes and mechanisms behind this atmospheric response is beyond the scope of this paper, and will be the subject of a follow-up study.