Projections of extreme storm surge levels along Europe

Abstract

Storm surges are an important coastal hazard component and it is unknown how they will evolve along Europe’s coastline in view of climate change. In the present contribution, the hydrodynamic model Delft3D-Flow was forced by surface wind and atmospheric pressure fields from a 8-member climate model ensemble in order to evaluate dynamics in storm surge levels (SSL) along the European coastline (1) for the baseline period 1970–2000; and (2) during this century under the Representative Concentration Pathways RCP4.5 and RCP8.5. Validation simulations, spanning from 2008 to 2014 and driven by ERA-Interim atmospheric forcing, indicated good predictive skill (0.06 m < RMSE < 0.29 m and 10 % < RMSE < 29 % for 110 tidal gauge stations across Europe). Peak-over-threshold extreme value analysis was applied to estimate SSL values for different return periods, and changes of future SSL were obtained from all models to obtain the final ensemble. Values for most scenarios and return periods indicate a projected increase in SSL at several locations along the North European coastline, which is more prominent for RCP8.5 and shows an increasing tendency towards the end of the century for both RCP4.5 and RCP8.5. Projected SSL changes along the European coastal areas south of 50°N show minimal change or even a small decrease, with the exception of RCP8.5 under which a moderate increase is projected towards the end of the century. The present findings indicate that the anticipated increase in extreme total water levels due to relative sea level rise (RSLR), can be further enforced by an increase of the extreme SSL, which can exceed 30 % of the RSLR, especially for the high return periods and pathway RCP8.5. This implies that the combined effect could increase even further anticipated impacts of climate change for certain European areas and highlights the necessity for timely coastal adaptation and protection measures. The dataset is publicly available under this link: http://data.jrc.ec.europa.eu/collection/LISCOAST.

Introduction

The coastal zone is an area of high interest, characterized by increased population density, hosting important commercial activities and constituting habitats of high socioeconomic value (Costanza 1999). Sea level rise (SLR) in view of climate change poses a serious threat to coastal areas and as a consequence, much research effort has focused on this aspect of coastal hazard (Church and White 2011; Hinkel et al. 2014; Hogarth 2014; Hoggart et al. 2014; Jevrejeva et al. 2014; Losada et al. 2013; Tol 2009). Extreme events, however, determine an additional hazard component. Some studies report an increased intensity and frequency of extreme water levels along several coastal regions in the world (Izaguirre et al. 2013; Ullmann and Monbaliu 2010; Wang et al. 2014; Weisse et al. 2014). However, the majority of the observed changes are related to changes in mean sea level (Menéndez and Woodworth 2010), while there is a lack of significant trends in storminess (Dangendorf et al. 2014a; Woodworth and Blackman 2002). The latter is in agreement to the conclusions of Ferreira et al. (2009), who found no statistically significant increasing.

Storm surges, also referred to as meteorological residuals or meteorological tide, constitute along with the waves and the tidal oscillations the main components of extreme water levels along the coastal zone (Losada et al. 2013; Lowe et al. 2010). Storm surges are forced by wind driven water circulation towards or away from the coast and by atmospheric pressure driven changes of the water level; i.e. the inverse barometric effect (WMO 2011). The magnitude of the storm surge depends on a number of factors including the size, track, speed and intensity of the storm system, the nearshore local bathymetry (water depth) and the shape of the coastline (Arns et al. 2015).

Recently, a number of studies evaluated the potential dynamics of future extreme storm surge levels (SSL) in view of climate change. In particular, regional projections of SSL have been generated along the Mediterranean (Conte and Lionello 2013; Jordà et al. 2012; Marcos et al. 2011), North Sea (Debernard and Røed 2008; Gaslikova et al. 2013; Howard et al. 2010; Woth et al. 2006), as well as the Atlantic coast of Europe (Lowe et al. 2001, 2009, 2010; Marcos et al. 2012) and Baltic Sea (Gräwe and Burchard 2012; Meier 2006; Meier et al. 2004) (Table 1).

Table 1 Examples of previous efforts to generate projections of extreme SSL under climate change scenarios; next to the reference, information is provided related to the time period and the spatial extent of the study, the climate change scenarios assessed, the climate, atmospheric and ocean circulation models used, as well as the spatial resolution of the models used in the calculations (values in parentheses and the last column; unit: degrees)

Despite the urgency of preparing for the anticipated changes in extreme water levels along Europe, there is still limited, if any, information on SSL projections under the Representative Concentration Pathways (RCPs) (IPCC 2013). Moreover, most previous studies are at local/regional scale and there has been no effort at European scale (Table 1) which implies that (1) there are several European regions for which there is no information on projected SSL in view of climate change; (2) the use of different greenhouse gas emission scenarios, climate and ocean models, as well as the diversity of the European coastal environments make it difficult to draw some general conclusions at a European scale.

Against the foregoing background, the present study uses a hydrodynamic model forced by CMIP5 climate model wind and pressure fields (Taylor et al. 2011) to generate projections of extreme storm surge levels (SSL) along the European coastline, for a baseline ‘historical’ period and two RCPs scenarios: RCP4.5 and RCP8.5 (Meinshausen et al. 2011). The RCP4.5 and RCP8.5 scenario correspond to a likely global mean temperature increase of 2.0–3.6 °C and 3.2–5.4 °C in 2081–2100 above the 1850–1900 levels (IPCC 2013) respectively, where RCP4.5 may be viewed as a moderate–emission–mitigation-policy scenario and RCP8.5 as a high-end, business-as-usual scenario. The authors are confident that the results of the study, including a public-access dataset of extreme SSL (available from this URL: http://data.jrc.ec.europa.eu/collection/LISCOAST), can be beneficial for research and policy-making efforts towards the timely response to the climate impacts along the European coastline (alternative URLs: http://data.europa.eu/89h/0026aa70-cc6d-4f6f-8c2f-554a2f9b17f2; http://data.europa.eu/89h/deff5a62-074c-4175-bce4-f8f13e0437a3; http://data.europa.eu/89h/a25677b7-2296-4eeb-82f2-70c78690ae10).

Methods

Numerical model setup

The Delft3D-Flow module of the open source model Delft3D (Deltares 2014) has been applied to estimate the propagation of the SSL due to the combined effect of the wind and the atmospheric pressure gradient. The model has been used successfully in similar applications in the past (Sembiring et al. 2015). The Delft3D-Flow module set-up that has been adopted solves the 2D non-linear shallow water equations on a staggered Arakawa C-grid, according to an implicit finite difference approximation on a vertical σ—coordinate system.

After extensive model optimization and validation tests, the numerical grid setup that was finally selected was a regular grid of 0.2° resolution (Table 2), including Europe and a large extent of the N. Atlantic (spanning from 40°W to 47°E and from 26°N to 73°N; Fig. 2); as it proved to be the best compromise in terms of data quality, model stability and computational times. Water level model output was obtained every 3 h and every 25 km along the coastline.

Table 2 Information about the model setup and the simulations

Model validation

A hindcast run spanning from 01/01/1979 to 01/06/2014 was forced by hindcast atmospheric pressure and wind fields obtained from the ERA-Interim database (Dee et al. 2011) and the resulting storm surge values were validated against water level time series available from the JRC Sea Level Database (http://webcritech.jrc.ec.europa.eu/SeaLevelsDb). The temporal resolution of the measurements is typically in the order of few hours and the temporal extent of the validation dataset varies among stations (Fig. 1), covering the period from 2008 and on; a period characterized by an increased marine storm activity including high impact events (e.g. Bertin et al. 2014; Breilh et al. 2013; Met Office and Centre for Ecology and Hydrology 2014; Vousdoukas et al. 2012). After identifying and excluding gaps or periods with rogue data, a tidal harmonic analysis was applied with the widely used t-tide package (Pawlowicz et al. 2002) in order to obtain the residual storm surge water levels η _s. The latter were then compared directly with the model output and evaluated in terms of the root mean square error (RMSE):

$$RMSE = \sqrt {\frac{{\sum\nolimits_{i}^{n} {\left( {\eta_{{s,{\text{measured}}}}^{i} - \eta_{{s,{\text{model}}}}^{i} } \right)^{2} } }}{n}}$$

(1)

where n is the number of measurements in the storm surge time series at a given location. The relative RMSE error (%RMSE) was also estimated in order to take into account spatial variations in the range of the SSL:

Fig. 1

Temporal availability of sea level data used for model validation. Each line corresponds to a different station, while colors correspond to the 10 different European regions

$$\% RMSE = \frac{{\sqrt {\frac{{\sum\limits_{i}^{n} {\left( {\eta_{{s,{\text{measured}}}}^{i} - \eta_{{s,{\text{model}}}}^{i} } \right)^{2} } }}{n}} }}{{\hbox{max} \left( {\eta_{{s,{\text{measured}}}}^{{}} } \right)}} \times 100$$

(2)

Agreement in terms of the probability density function of the values was assessed after applying the Kolmogorov–Smirnov test (K–S), considering a 5 % significance level. Given that the study focuses on the extreme SSL, we evaluated the monthly maxima SSL of the model output and the tidal gauge measurements with the K–S test rather than considering the complete measured and simulated time series.

Climate scenarios

The period 1970–2000 was considered as baseline period, while 2010–2040 and 2070–2100 were considered as the short and long term future scenarios for RCP4.5 and RCP8.5, respectively. The two time slices will be mentioned as 2040 and 2100 hereinafter for reasons of brevity (e.g. RCP8.5₂₀₄₀).

The model was forced by the 6-h output of 8 climate models available at the CMIP5 database, namely the ACCESS1-0, ACCESS1-3, (CSIRO-BOM Australia), CSIRO-Mk3.6.0 (CSIRO-QCCCE, Australia), EC-EARTH (EC-EARTH consortium), GFDL-ESM2M (NOAA Geophysical Fluid Dynamics Laboratory USA), HadGEM2-CC (Met Office Hadley Centre UK), and MPI-ESM-LR, MPI-ESM-MR (Max-Planck-Institut für Meteorologie Germany). The specific models were selected as previous studies have shown (Perez et al. 2014) that they have good skill to reproduce the synoptic climatologies and the inter-annual variations across Europe.

In order to additionally evaluate the performance of the modelling strategy (i.e. combination of the CMIP5 atmospheric forcing with Delft3D model) in reproducing the SSL conditions along the European shoreline the obtained SSL time series for the baseline period were compared with the ones of the previously validated ERA-INTERIM forced SSL reanalysis (see Sect. 3.1), before and after applying Bias correction following the approach proposed by Haerter et al. (2011) and used by later studies (e.g. see Grillakis et al. 2013).

$$\eta_{s,BIAS{\text{-}}CORRECTED}^{{}} = \left( {\frac{{\eta_{s,ORIGINAL} - \overline{{\eta_{s,ORIGINAL} }} }}{{\sigma (\eta_{s,ORIGINAL} )}}} \right) \cdot \sigma (\eta_{s,ERA - INTERIM} ) + \overline{{\eta_{s,ERA{\text{-}}INTERIM} }}$$

(3)

For better analysis of the model performance and the storm surge scenarios, the European coastal zone was divided into 10 regions on the grounds of the geographical and physical setting: Black Sea, East, Central and West Mediterranean, South- and North-North Atlantic, Bay of Biscay, as well as North, Baltic and Norwegian Sea (Fig. 2).

Fig. 2

Map of Europe showing the overall Delft3D model domain (black, dashed line) and the 10 different coastal regions defined for the analysis of the model results (color continuous lines)

Extreme value statistical analysis

The peak-over threshold (POT) approach was applied to identify extreme events for each 30-year time slice, according to a certain SSL threshold parameter u. Given that the peaks need to be independent observations and not the result of the same extreme event, it is common to apply de-clustering of events using a minimum time difference between peaks varying from 34 h to 5 days (Lowe and Gregory 2005). At the present study, the value selected for the time window was 72 h in agreement to previous studies (Marcos et al. 2011; Serafin and Ruggiero 2014), while the threshold parameter u was different for each location ensuring that the average number of events per year in the baseline period was ~5 at each studied point. Considering an average of 5 events per year for extreme values statistical analysis is also common for such studies, given that such analyses are sensitive to u. The selected exceedance events per year were pooled and modelled according to the Generalized Pareto Distribution (GPD) (Coles 2001):

$$F(y) = \left\{ {\begin{array}{*{20}l} {1 - \left( {1 + \frac{\xi y}{\sigma }} \right)^{{ - \frac{1}{\xi }}} ,} & {\xi \ne 0,y > 0} \\ {1 - \exp \left( { - \frac{y}{\sigma }} \right),} & {\xi = 0,y > 0} \\ \end{array} } \right.$$

(4)

where y is the time-series of SSL above the threshold u such as y = η _s  − u, σ is the scale parameter and ξ is the shape parameter. The scale parameter σ of the GPD is related with the scale parameter ψ and the location parameter μ of the generalized extreme value distribution according to:

$$\sigma = \psi + \xi (u - \mu )$$

(5)

Τhe parameters of the GPD are estimated using the maximum likelihood method and subsequently the N-year return SSL is estimated as follows (Coles 2001):

$$\eta_{s,N} = \left\{ {\begin{array}{*{20}l} {u + \frac{\sigma }{\xi }[({\rm N}n_{y} \zeta_{u} )^{\xi } - 1],} & {\xi \ne 0} \\ {u + \sigma \log ({\rm N}n_{y} \zeta_{u} ),} & {\xi = 0} \\ \end{array} } \right.$$

(6)

where n _y is the number of annual exceedances per year in each time slice and ζ _u the probability that an empirical value exceeds the threshold u. Extreme SSL values were calculated for different return periods and T _r  = [5, 10, 50, 100] years are discussed in the present manuscript.

Seasonal variations

In order to assess the seasonal dynamics of SSL and potential changes therein, the monthly maxima SSL were grouped into seasons, with winter spanning from December to February, spring from March to May, summer from June to August and autumn from September to November and average maximum seasonal values were estimated. The grouped monthly maxima were averaged to obtain a characteristic value for each climate model, time slice and season in order to give insight into the seasonal variations of the extreme SSL; while the standard deviation σ _SSL of the monthly maxima was used as a proxy of inter-annual variability.

Projected changes, ensemble averaging and statistical significance

The 8-member model ensemble implies that the above analysis resulted, for each model output point, in a set of SSL values for the different simulations, return periods and seasons; and for each of the above cases ensemble means were calculated from all different climate models. Apart from the actual SSL values, absolute and percentage changes (Δη _s and %Δη _s , respectively) for each return period were obtained by subtracting the baseline values (η _{s, baseline}) from the RCP4.5 and RCP8.5 ones (η _{s, RCP}), from each climate model:

$$\Delta \eta_{s} = \eta_{{s,{\text{RCP}}}} - \eta_{{s,{\text{baseline}}}}$$

(7)

$$\%\Delta \eta_{s} = \frac{{\eta_{{s,{\text{RCP}}}} - \eta_{{s,{\text{baseline}}}} }}{{\eta_{{s,{\text{baseline}}}} }} \times 100$$

(8)

All the above are applied for each model output location; while ensemble averages were estimated also for the absolute and relative SSL changes in order to reduce the uncertainty of the projections and model agreement was evaluated on the grounds of the coefficient of variation CV (Alfieri et al. 2015; Knutti and Sedlacek 2013):

$$CV_{{}} = \frac{{\sigma_{{\Delta \eta_{s} }} }}{{\overline{{\Delta \eta_{s} }} }}$$

(9)

The coefficient of variation CV is defined as the ratio between the standard deviation of the model ensemble σ and the ensemble mean value, and decreases as intra-model variability becomes a smaller fraction of the ensemble mean; implying stronger model agreement and statistical significance of the ensemble mean. In the present case, values with |CV| > 1 were not considered, which roughly corresponds to an average agreement of five out of six models (i.e. 84 % probability), If one assumes that relative changes are normally distributed (Alfieri et al. 2015). Additionally, the CV was also utilized in order to evaluate model agreement for all the ensemble mean estimations; i.e. SSL for the different return periods, as well as seasonal mean.

Results

Model validation

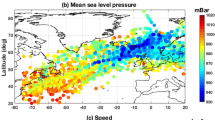
Data from 184 tidal gauge stations were processed in order to identify data gaps or to mask periods with low-quality data, resulting in a set of 110 stations with periods of valid ground-truth residual water level data coinciding with the simulation period. Following the initial filtering of the tide gauge records, the region with the largest number of acceptable quality tidal gauge records was the North Atlantic (36), followed by Central Mediterranean (21), the North Sea (14) and East/West Mediterranean (9); while only one station was found in the West Iberia and 2 in the Black Sea (Table 3). It is also important to underline that the temporal availability (Fig. 1) and data quality was poorer along the Black Sea and East Mediterranean. Overall, the model showed to reproduce satisfactory the measurements (Fig. 3) and spatial variations in the model performance were observed (Fig. 4), with RMSE values ranging from 0.06 to 0.29 m, while  %RMSE varied between 10 and 29 % (Table 3).

Table 3 Overview of model performance along the 10 defined European regions: number of tidal gauge stations, percentage of stations with the same distribution of monthly maxima according to the Kolmogorov–Smirnov test, as well as mean, maximum and minimum values of the RMS error in m and as a percentage of the SSL range

Fig. 3

Examples of storm surge time series generated from the model (red dashed line) versus measurements from four of the tidal gauge stations

Fig. 4

Model validation performance: scatter plot showing RMS error in m (a) and as a percentage of the SSL range (b) for all the available tidal gauge stations

Most of the Mediterranean, the Atlantic coast and the Norwegian Sea were characterized by absolute RMSE values below 0.1 m, while RMSE > 0.15 m were observed along the North Adriatic and the North Sea (Fig. 4a). The latter high RMSE values appeared to be related to the higher η _s range, as implied by the relatively low %RMSE values in the same areas (Fig. 4b). The highest %RMSE values were observed along the Aegean Sea (%RMSE > 0.2), while overall model performance was poorer along the Black and Mediterranean Sea (mean %RMSE ranging from 18 to 25 %). On the contrary, the lowest  %RMSE was observed in the Norwegian Sea (mean  %RMSE = 13 %, see Table 3).

Q–Q plots indicate that the model was capable of reproducing the probability distribution function of the measured SSL (Fig. 5), which was the crucial skill given the extreme value statistical analysis to follow. The model overestimated the lower values at some locations in S. Europe (e.g. Fig. 5a–f), while the opposite was observed in the North, Baltic and Norwegian Sea (e.g. Fig. 5g–j); however the lower values are of minor interest for the scope of the present study. On the other hand, the extremes were underestimated at some stations (see Fig. 5a–c, e, f), a possible artifact of the coarse atmospheric forcing and numerical grid. However, the model’s capacity to simulate SSL is considered satisfactory given that the scope of the study is to project trends under climate change scenarios and not to provide accurate operational forecasts. This is also confirmed by the results of the Kolmogorov–Smirnov test (Table 3), which showed agreement in the monthly maxima distributions for almost all validation points along North Europe, and at least for 80 % of the points along South Europe.

Fig. 5

Model validation performance: scatter plots comparing measured and simulated SSL for each tidal gauge location. The colors express point density (increasing from blue to red), the red dashed line expresses the perfect fit, while the black dots show the q–q plots of the two time series. The inset map (k) shows the location of the displayed tide gauge records, one from each of the 10 European regions; while the RMSE and Kolmogorov–Smirnov test results are shown, with 0 indicating same monthly maxima distributions

The monthly maxima SSL values from the ERA-INTERIM forced reanalysis run were compared with the values obtained from the baseline period runs forced by the 8-member ensemble and the estimated average  %RMSE values per model varied from 28.1 % (EC-EARTH; see also Table 4) to 33.6 % (GFDL-ESM2M) around a mean of 30.4 %, before applying the Bias correction. As expected, the coarser CMIP5 models resulted in lower SSL values with mean normalized Bias around −12 % and the biggest deviations observed for ACCESS1-3, CSIRO-Mk3-6-0, and HadGEM2-CC (Table 4). After applying the BIAS correction and repeating the extreme value analysis, the agreement with the reanalysis values improved substantially to a mean %RMSE of 10.8 % (Table 4), with Kolmogorov–Smirnov test results indicating the same probability distributions between the Bias corrected CMIP5 and ERA-INTERIM runs. Overall, the monthly maxima values were similar among models and the biggest deviations from the reanalysis were found along the North and Baltic Sea (Fig. 6). The reported accuracy is considered satisfactory given that %RMSE was estimated from monthly maxima and the CMIP5 models are reproducing climate in a stochastic manner and thus the time domains are approximately matching with the reanalysis.

Table 4 Results from the baseline runs validation using the 8-member climate model ensemble vs the ERA-INTERIM forced reanalysis: normalized RMSE (%RMSE), Normalized Bias (NBI) before Bias correction and  %RMSE after Bias correction (%RMSE-BC)

Fig. 6

Normalized RMSE (%RMSE) comparing monthly maxima from the baseline runs validation using the ERA-INTERIM forced reanalysis vs the 8-member climate model ensemble after Bias correction (%RMSE-BC)

Storm surge projections

The estimated extreme SSL obtained by the 8-member model ensemble appeared to follow similar spatial patterns among the different scenarios and return periods (Fig. 7); with SSL values along the North Sea increasing eastwards, and being substantially higher than the ones along the rest of Europe. Another area characterized by higher SSL values was the UK coastline of the Irish Sea, followed by marginal areas of the Baltic Sea (e.g. Kattegat, Gulf of Finland and the North Gulf of Bothnia; see Fig. 7) and the Norwegian Sea. Anticipated extreme SSL appeared to be η _s  < 2 m for most of South Europe with higher values observed along parts of the North Adriatic and of the North Black Sea.

Fig. 7

Ensemble mean of extreme SSL (m) along the European coastline obtained for 5, 10, 50, and 100 years return periods (shown in different columns), for the baseline period (a–d), as well as their projected relative changes under RCP4.5₂₀₄₀ (e–h), RCP8.5₂₀₄₀ (i–l), RCP4.5₂₁₀₀ (m–p), RCP8.5₂₁₀₀ (q–t) scenarios (shown in different lines). Warm/cold colors express increase/decrease, respectively; while points with high model disagreement are shown with gray (|CV| > 1)

The spatial variations of the relative changes in extreme SSL for all the studied RCPs are shown in Fig. 7, while an overview of the general tendencies per European region is provided by the mean frequency curves (Fig. 8). The reader should note that hereinafter changes which are shown and discussed concern only the ones for which strong model agreement has been found among the 8-member ensemble (CV < 1).

Fig. 8

Overview of changes in the extreme SSL along the 10 defined European regions (a–j): horizontal axis expresses return period in years and the vertical the corresponding SSL, while each curve corresponds to a different RCP scenario and time slice: baseline (red), RCP4.5₂₀₄₀ (blue), RCP8.5₂₀₄₀ (green), RCP4.5₂₁₀₀ (purple), RCP8.5₂₁₀₀ (orange). The inset map (k) shows the limits of the 10 European regions

An increasing tendency was shown for the Black Sea, especially under RCP8.5 (Fig. 8a), with the current 100-year event expected to occur every 90.2 and 85 years under RCP8.5₂₀₄₀ and RCP8.5₂₁₀₀, respectively. While the projected increase of the extreme η _s is estimated especially at the east part of the Black Sea, the overall values are small and the changes are not significant in terms of absolute values (Fig. 7; see also “Appendix”).

Minor changes are projected for the extreme SSL projections at the Mediterranean Sea, with the most prominent increase projected along the West Mediterranean under RCP8.5₂₁₀₀ indicating a 29 year reduction in the return period of the present 100-year event (Fig. 8d). Projected increase in SSL was also found along the East Mediterranean; indicatively the present 100-year event was projected to occur every 75, 95.2 and 95.3 years under RCP8.5₂₀₄₀, RCP4.5₂₁₀₀ and RCP8.5₂₁₀₀, respectively (Fig. 8b). Along the Central and West Mediterranean the frequency of the present-day 100-year event was shown decrease in 2040 and to decrease towards the end of the century (Fig. 8c,d).

Projected SSL change along the South Atlantic coast of Europe and the Bay of Biscay was small (Figs. 7, 8e, f), as changes became more prominent at latitudes above 50°N. The present 100-year event at the South Atlantic coast was projected to occur every 143.5 and 130.8 years under RCP4.5₂₁₀₀ and RCP8.5₂₁₀₀, respectively (Fig. 8e), while a mild increase was projected for the Bay of Biscay for most scenarios (Fig. 8f). An increase was projected under all the studied RCPs along the Atlantic coast of North Europe (Figs. 7, 8g), with the present 100-year event projected to occur every T _r  = 82.4, 89.5, 89.2 and 83.8 under RCP4.5₂₀₄₀, RCP8.5₂₀₄₀, RCP4.5₂₁₀₀, and RCP8.5₂₁₀₀, respectively (Fig. 8g); even though the projected frequency of the 10-year event remained relatively stable for all RCPs but RCP8.5₂₁₀₀.

The North Sea was projected to experience increased storm surge activity (Fig. 8h), especially towards the end of the century, i.e. the present 100-year event was projected to occur every 80.2 and 81.3 years under RCP4.5₂₁₀₀ and RCP8.5₂₁₀₀, respectively. The relative change in extreme SSL was shown to increase eastwards, as most of the UK east coast showed small decrease or no change (Fig. 7). Strong projected increase in frequency was also observed for the Baltic Sea, for all scenarios apart from RCP4.5₂₀₄₀; with the present day 100-year event projected to take place every 44, 72, and 51 years under RCP8.5₂₀₄₀, RCP4.5₂₁₀₀, and RCP8.5₂₁₀₀, respectively (Fig. 8i). Finally an increase in storm surge intensity was projected for the Norwegian Sea for all RCPs, with the present day 100-year event projected to take place every 79.4, 51, 63.5, and 47.7 years under RCP4.5₂₀₄₀,RCP8.5₂₀₄₀, RCP4.5₂₁₀₀, and RCP8.5₂₁₀₀, respectively (Fig. 8j).

Seasonal analysis

Monthly maxima were grouped into seasons and were averaged in order to give insight to the seasonal variations of the extreme SSL (Fig. 9); as expected, the spatial variations were similar to the ones of the extreme values. For all scenarios the season with the highest SSL was winter, followed by autumn; while summer was typically the season characterized by the lowest SSL extremes. The standard deviation σ _SSL was used as a proxy of inter-annual variability and its spatial variations followed the ones of the actual values; e.g. areas like the North and the Baltic Sea where the higher SSL occur, were also characterized by high standard deviation values (Fig. 9).

Fig. 9

Mean seasonal maxima along the European coastline and their relative changes; columns correspond to the Winter, Spring, Summer, Autumn, and the standard deviation (σ) while lines different runs: values for the baseline run (a, e); and their relative changes under RCP4.5₂₀₄₀ (f–j), RCP8.5₂₀₄₀ (k–o), RCP4.5₂₁₀₀ (p–t), RCP8.5₂₁₀₀ (u–y). Warm/cold colors express increase/decrease, respectively; while points with high model disagreement are shown with gray (|CV| > 1)

The projected relative changes of the mean seasonal SSL maxima were grouped and averaged for each studied region along with the corresponding inter-annual variability, standard deviation σ _SSL (Fig. 10). Overall the seasonal SSL values appeared intensified towards the end of the century, which was also relevant for the inter-annual variability. The Baltic Sea was the area with the highest increase in the seasonal maxima %Δη _s , with an increasing tendency for all seasons especially towards the end of the century, and under RCP8.5 (Fig. 10d). The second highest increase was shown along the North Sea, and especially towards the end of the century, with the projected increase exceeding 2 % in most cases. The general trend for the Norwegian Sea shows a decrease in the inter-annual variability, driven by decreasing or stable winter and spring SSL values and increase summer and autumn ones, especially towards the end of the century.

Fig. 10

Projected changes in the inter-annual variability of extreme SSL averaged for each of the 10 European regions expressed as percentage of change of the mean seasonal maxima from the baseline run values and of their stand deviation for the different RCP scenarios and time slices: RCP4.5₂₀₄₀ (a), RCP8.5₂₀₄₀ (b), RCP4.5₂₁₀₀ (c), RCP8.5₂₁₀₀ (d)

On the contrary, for both RCPs and more significantly for the last period of the century, the seasonal mean maximum SSL at the European Atlantic coast appeared to decrease; a pattern that was more obvious along the Bay of Biscay (up to 3 %); while the projected changes in the remaining areas were very limited. The projected decrease of the seasonal maxima does not appear to be of similar intensity on a year-long basis, and as a result the inter-annual variability is projected to increase along all the areas found south of 50°N, except from the East Mediterranean.

Discussion

General remarks

Previous studies have shown that the uncertainties introduced by the ocean models are small compared to the ones related to the accuracy and resolution of the atmospheric forcing (e.g. Jordà et al. 2012). Moreover, in the case of SSL projections in view of climate change additional uncertainty is introduced by: (A) the future socio-economic development and policy actions (manifested as RCPs); (B) knowledge gaps in understanding and predicting the climate system, expressed as differences among climate models; (C) the skill of the hydrodynamic model to reproduce short duration/high energy, extreme events over large spatial domains (Calafat et al. 2014; Conte and Lionello 2013), especially given the limitations in the spatial resolution of both the meteorological forcing and ocean model, which are inevitable due to the spatial and temporal extent of the projections; and (D) the extreme value statistical analysis, affected by the selected frequency analysis approach and distribution shape, as well as the return period curve fitting (Hamdi et al. 2014). All the above points are discussed in the following paragraphs, apart from point A which is considered beyond the scope of the present study.

Climate model uncertainties (point B) were reduced to the greatest possible extent by (1) ensuring the skill of the circulation model to reproduce extreme SSL values along Europe through validation against tidal gauge data (Sect. 3.1); (2) selecting the CMIP5 climate models which according to Perez et al. (2014) are ranked with high skill in reproducing the synoptic climatologies and inter-annual variations along Europe; (3) using the validated SSL reanalysis, forced by more detailed atmospheric forcing, to apply BIAS correction on the SSL values generated from the atmospheric forcing of each climate model, in order to further ensure that the validity of the SSL projections; and (4) using a 8-member climate model ensemble and considering the ensemble mean only when model agreement is acceptable through a threshold in the coefficient of variation.

Regarding point C, recent efforts to simulate extreme storm surge events along large domains, such as the Mediterranean Sea, have shown that models often underestimate the extremes and in particular the ones related to short duration/high energy events (Calafat et al. 2014; Conte and Lionello 2013); something that could also apply for some locations at the present study. The latter might be related to processes which take place in finer temporal and spatial scales than the ones presently considered, where the quality of the output is directly affected by the resolution of both the meteorological (Cavaleri and Bertotti 2004) and ocean model (Cid et al. 2014). For example, it has been shown that along shallow areas storm surge is practically wind driven and detailed representation of the wind field is important; for that reason many regional/local scale studies apply a downscaling of the wind/pressure input using a finer atmospheric model (see Table 1 and references therein); which was not feasible in the present case due to the size of the computational domain and the related computational cost. Overall the approach followed appears to be valid since model validation showed that the model could reproduce satisfactorily the measured SSL, and the RMSE errors were at similar levels with previous efforts (Cid et al. 2014). This is also in agreement to previous studies which have demonstrated that global driven simulations are capable of predicting changes in extreme SSL without previous downscaling (Howard et al. 2010).

Water level variations are important for SSL, as the depth modulates the bottom friction, and thus the circulation patterns (Arns et al. 2015); while tidal currents interact with the wind-driven circulation applying an additional non-linear effect on the extreme η _s levels (Bernier and Thompson 2007; Zijl et al. 2013). As also shown by the validation results, the errors related to omitting the tidal circulation in the simulations are low and well below the uncertainty introduced by other components such as the atmospheric forcing. Moreover, tidal contributions on total water levels have their own probability density functions and thus they would affect also the SSL ones, therefore it was decided to run storm surge simulations without a tidal sea level signal; since the increased complexity and computational times from considering the tidal component in the simulations outweigh the potential gains in data quality. The same applies to the benefits of considering projections of relative sea level rise (RSLR) instead of running all simulations at the present day sea levels, since there is consensus in previous studies that to a first order approximation changes in mean sea level and SSL can be added linearly (Howard et al. 2010; Lowe and Gregory 2005; Sterl et al. 2009; Weisse et al. 2012).

Finally, an important factor of uncertainty in generating SSL projections is the extreme value statistical analysis, mainly related to (1) the selected frequency analysis approach; (2) the selected distribution shape; and (3) the fact that sometimes the return period considered can be even 2 orders of magnitude higher than the duration of the analyzed time series. The latter is a common limitation in similar studies and it has be to highlighted that while projected SSL changes for higher return periods >100 years carry an increased level of uncertainty and therefore should be considered without caution; despite compensation efforts compensated by the use of the model ensemble, and the coefficient of variation as proxy of model agreement. The frequency analysis approach along with the distribution shape have been shown to affect the projected SSL values (Hamdi et al. 2014), and there is certain variety in the approach selected in previous similar studies; i.e. r-largest (Marcos et al. 2011), GEV (Gaslikova et al. 2013) and non-stationary methods (Méndez et al. 2007; Serafin and Ruggiero 2014).

Regarding this study, several extreme value statistical approaches were tested and the extreme SSL values estimated for the baseline run were compared with values available in the literature; and the present implementation of the GPD was chosen as the most reliable approach. Overall, the effect of all the discussed potential limitations on data quality becomes even less critical since the present study focuses on assessing relative changes in extreme SSL, rather than presenting accurate η _s predictions or operational forecasts. Still, it is important to remind the reader and potential user of the dataset that the relative accuracy of the absolute SSL values should be considered in the 10–20 % range. Moreover, the subtraction between baseline and scenario values cancels out most possible shortcomings in the SSL simulations.

Storm surge projections

Given that, according to the authors’ knowledge, there are no previous studies on projected SSL values at European scale, the obtained results will be discussed against findings from existing regional studies. For the case of the Baltic Sea, earlier studies in historical storm surge trends have reported no statistically significant increasing trend (Baerens and Hupfer 1999; Menéndez and Woodworth 2010; Suursaar et al. 2015), while previous studies report a projected increase under SRES scenarios (Debernard and Røed 2008; Gräwe and Burchard 2012; Meier 2006; Weisse et al. 2009; Woth et al. 2006); in agreement with the present findings. The area shows some of the highest increases in projected extreme SSL in Europe and the seasonal values (Fig. 10) indicate increased storm surge activity during all the seasons of the year, but especially during spring and summer.

At the same time while some studies on SLR trends along the Baltic Sea have indicated a decreasing trend, also shown in the dataset produced by Pardaens et al. (2011); Johansson et al. (2014) concluded that the past negative trend in mean sea level in the Gulf of Finland will not continue in the future, because an accelerated global average SLR will offset the land uplift. Therefore, the presently projected increase in SSL could balance a potential decrease in future sea levels, resulting in comparable levels of coastal hazard in the future. However, in the case of positive RSLR supported by several studies (Johansson et al. 2014; Meier 2006) the Baltic Sea will experience even higher pressure by extreme coastal events, in agreement to results from Gräwe and Burchard (2012) for the West Baltic Sea.

Given that there are limited, if any, sources of information on storm surge projections along the Norwegian Sea, the present projections can be compared mostly with observations based on historical data. The results obtained project small or no increase in SSL, and when there is it is mostly restricted to the summer and autumn values for most scenarios (Fig. 10). This is partially contradicting with the findings of Menéndez and Woodworth (2010) who found a statistically significant increase for the historical data for both the total water level and the SSL. Overall the Norwegian coastline appears to be at low-risk in terms of coastal inundation as it is characterized by (1) a steep topography, providing a natural protection against increased water levels; and (2) sophisticated coastal protection schemes for low-lying areas of high socio-economic value; e.g. port facilities.

The North Sea is an area subject to some of the highest SSL in Europe (Fig. 7), with the projections indicating a future increase in the extremes, especially along the eastern part. The latter is in agreement with previous projections based on SRES scenarios (Debernard and Røed 2008; Woth et al. 2006), which also indicated an increase in strong westerly winds (Gaslikova et al. 2013), but also of the inter-annual variability (Dangendorf et al. 2014b). Furthermore, previous studies report results relatively similar to the present patterns along the south east coast of UK, i.e. small, or no projected storm surge change (Debernard and Røed 2008; Gaslikova et al. 2013; Howard et al. 2014; Lowe et al. 2009; Woth et al. 2006); as well as along the Dutch coast (Howard et al. 2014; Sterl et al. 2009).

The storm surge projections showed an increase along the Atlantic coast of the UK and Ireland, which was related to a consistent increase of the winter extremes, as well as of the inter-annual variability among the scenarios studied (Fig. 10); in line with previous studies predicting that the projected RSLR in the area will be combined with an increase in wind speeds and consequently in extreme SSL (Brown et al. 2010, 2012; Debernard and Røed 2008; Lowe et al. 2009). Lowe et al. (2009) found the highest projected increase in η _s values along the Bristol Channel and the Severn Estuary, which was also shown by the present dataset for some scenarios.

The Atlantic coast of France, Spain and Portugal is exposed to very energetic waves generated along the North Atlantic (Pérez et al. 2014), which constitute the dominant coastal hazard component (Almeida et al. 2012; Ciavola et al. 2011); with the latter potentially justifying the limited number of previous efforts to generate regional storm surge projections. The present findings indicate relatively stable or even decreasing η _s levels along most of the Bay of Biscay, being in agreement with the results of Marcos et al. (2012), who also reported a decrease towards the end of the century for both A1B and A2 SRES scenarios. The above are also in agreement with the observations of Menéndez and Woodworth (2010) on historical data.

The Mediterranean Sea has been studied extensively in terms of projected storm surge dynamics and there is consensus among studies based on SRES scenarios for no changes, or even a decrease in the frequency and intensity of extreme events (Androulidakis et al. 2015; Conte and Lionello 2013; Jordà et al. 2012; Marcos et al. 2011). This comes in agreement with the reported historical trends (Menéndez and Woodworth 2010), as well as with the present findings, projecting changes mostly in the ±5 % band, either positive or negative.

The North Adriatic is a region which has been studied more thoroughly due to the highly vulnerable, and socio-economically important Venice area, with most previous projections reporting no statistically significant change, or even decrease (Mel et al. 2013; Troccoli et al. 2012), even though Lionello et al. (2012) report a projected increase in frequency of extreme events around Venice, under a B2 SRES scenario. The latter is in agreement with the present projections which indicate weakly increasing extreme η _s values for certain RCPs along parts of the North Adriatic, with the latter not always including the Venice area (Fig. 7).

The present dataset presents projections of changes in extreme SLL values during this century, as well as of their seasonal variations; while previous studies have provided evidence of variability also on intermediate time scales, e.g. controlled by the North Atlantic Oscillation (NAO) (Dangendorf et al. 2014b; Marcos et al. 2011). Gillett and Fyfe (2013) report no significant increase in the NAO under RCP4.5 projected by CMIP5 models, which is contradicting to the projected increase in SSL values; on the other hand could be justified by the inability of some climate models to correctly simulate the physical processes connected to the NAO (Davini and Cagnazzo 2014). Therefore, analyzing further the patterns and controls of SLL variability is a very interesting direction for further research.

Implications for coastal management and adaptation in view of climate change

The projections presented here only concern the storm surge (atmospheric) contribution to sea level, which is one of the main components of extreme water levels along the coast and therefore, they are complementary to other studies focusing on RSLR attributed to other causes, such as thermal expansion or ocean mass variations (Nicholls et al. 2014; Pardaens et al. 2011). The mean projected increase in extreme SSL along Europe in 2100 and for a moderate ice-sheet behavior scenario is around 46 and 67 cm for RCP4.5 and RCP 8.5, respectively (based on data available by Hinkel et al. 2014). Even though, some storm surge attenuation is likely to happen due to the increased sea levels (e.g. Arns et al. 2015), the projected increase in SSL reaches 30 cm at certain locations and especially for the high return period events.

For example, the mean contribution of the projected increase in the 100 year storm surge event to the projected increase in the corresponding TWL for the entire European coastline, under RCP8.5 and towards the end of the century was shown to be around 18 %; with the latter exceeding 30 % for 14 % of the studied coastal location. As a result the contribution of extreme SSL to anticipated increasing total water levels is not negligible and implies an additional stress to several coastal locations in Europe due the combined effect of the intensified extreme events and RSLR. At the same time, increasing extreme SSL values could even result in similar risk levels even under negative projections of RSLR; e,g. in areas with anticipated uplift (Johansson et al. 2014).

An additional coastal hazard component are the waves, which during extreme events result in an increase in water level and energy flux towards the coast, accelerating sediment transport processes and thus driving coastal erosion, dune breaching and inundation (Bertin et al. 2012; Ciavola et al. 2011; Roelvink et al. 2009). Wave heights can exceed 10 m along exposed coasts, such as the Atlantic ones, and in order to obtain a complete idea of future coastal hazards it is essential to include projections of extreme wave events; a work currently in progress. There is no doubt that waves are drivers of long term morphological changes on the coast which should not be underestimated, however the waves have the smallest temporal scales and coastal morphology tends to be in a state of dynamic equilibrium with wave-driven processes (Dean 1991; Yates et al. 2009). Therefore, the water level remains a very critical parameter for coastal erosion and impact, since even a small increase in SSL could enhance the consequences of extreme events, despite the fact that the SSL amplitude could be even an order of magnitude lower than the wave height (e.g. Vousdoukas et al. 2012).

Finally, significant increase of extreme η _s was projected for both RCP4.5 and RCP8.5 scenarios towards the end of the century and for both time slices under RCP8.5. The latter implies that even if moderate emission mitigation policies will be enacted, coastal adaptation and protection measures should appear as high priority in the European policy agenda, since for many regions the increase in total water levels from the combined effect of RSLR and SSL, by the end of the century, is projected to exceed 1 m with respect to the actual water levels. This increase can be above the limits of most present coastal protection measures (Burcharth et al. 2014; Hunter et al. 2013; Weisse et al. 2014). The indications are even stronger for the business-as-usual RCP8.5 scenario, under which most Northern Europe coasts were projected to experience a significant increase in storm surge extremes.

Conclusions

The effect of climate change on extreme SSL along the European coastline has been studied by forcing a hydro-dynamic model with meteorological wind and atmospheric pressure fields derived from a 8-member model ensemble and covering the baseline 1970–2000 period, as well as the 2010–2040 and 2070–2100 periods under the RCP4.5 and RCP8.5 emission scenarios.

Model simulations have been validated comparing output from a hindcast run forced by ERA-INTERIM wind and pressure fields, with data from 110 tide gauges. Spatial variations of SSL were well reproduced by the model, with the relative RMSEs being <20 % for more than 105 stations and <15 % for more than 60 stations. In some cases extreme SSL were underestimated, but the overall model performance was satisfactory given that the scope of the study is to project relative changes under climate change scenarios and not to result in accurate operational forecasts.

The estimated extreme SSL along the North Sea was the highest along Europe and increased eastwards, while higher SSL values were also projected along the west-facing coastline of the Irish Sea, followed by marginal areas of the Baltic Sea and the Norwegian Sea. Anticipated extreme SSL values were substantially lower for most of the South Europe with the exception of the North Adriatic and some parts of the North Black Sea.

Ensemble mean changes of future SSL were estimated after comparing the baseline with the RCP runs and for most scenarios and return periods the projections indicated an increase in SSL along the North European coastline, which was more prominent under RCP8.5 pointing to an increasing tendency towards the end of the century for both RCPs. Projected changes in extreme SSL along the European coastal regions below 50°N showed minimal change or even a small decrease, with the exception of RCP8.5₂₁₀₀ for which a moderate increase was often projected.

Seasonal mean monthly maxima along North Europe showed a projected increasing tendency overall and an increase in the inter-annual variability especially under RCP8.5₂₁₀₀, while projected SSL changes along South Europe being in most cases one order of magnitude lower.

The present findings indicate that for many European coastal locations the projected increase in extreme SSL can be around 15 %, but can even reach 40 % of the projected RSLR, implying that the combined effect could have serious consequences. The significant increase of extreme SSL projected for both RCPs towards the end of the century implies that even if moderate emission mitigation policies will be enacted, coastal adaptation and protection measures should appear as high priorities in the European policy agenda. The indications are even stronger for in the case of the business-as-usual RCP8.5, under which most of the Northern Europe coastline is projected to experience a significant increase in storm surge extremes.

Appendix

See Figs. 11 and 12.

Fig. 11

Ensemble mean of extreme SSL (m) along the European coastline obtained for 5, 10, 50, and 100 years return periods (shown in different columns), for the baseline period (a–d), as well as their projected changes under RCP4.5₂₀₄₀ (e–h), RCP8.5₂₀₄₀ (i–l), RCP4.5₂₁₀₀ (m–p), RCP8.5₂₁₀₀ (q–t) scenarios (shown in different lines). Warm/cold colors express increase/decrease, respectively; while points with high model disagreement are shown with gray (|CV| > 1)

Fig. 12

Mean seasonal maxima along the European coastline and their relative changes; columns correspond to the Winter, Spring, Summer, Autumn, and the standard deviation (σ) while lines different runs: values for the baseline run (a, e);and their changes under RCP4.5₂₀₄₀ (f–j), RCP8.5₂₀₄₀ (k–o), RCP4.5₂₁₀₀ (p–t), RCP8.5₂₁₀₀ (u–y). Warm/cold colors express increase/decrease, respectively; while points with high model disagreement are shown with gray (|CV| > 1)