Abstract
Despite being a well-established research field, the detection and attribution of observed climate change to anthropogenic forcing is not yet provided as a climate service. One reason for this is the lack of a methodology for performing tailored detection and attribution assessments on a rapid time scale. Here we develop such an approach, based on the translation of quantitative analysis into the “confidence” language employed in recent Assessment Reports of the Intergovernmental Panel on Climate Change. While its systematic nature necessarily ignores some nuances examined in detailed expert assessments, the approach nevertheless goes beyond most detection and attribution studies in considering contributors to building confidence such as errors in observational data products arising from sparse monitoring networks. When compared against recent expert assessments, the results of this approach closely match those of the existing assessments. Where there are small discrepancies, these variously reflect ambiguities in the details of what is being assessed, reveal nuances or limitations of the expert assessments, or indicate limitations of the accuracy of the sort of systematic approach employed here. Deployment of the method on 116 regional assessments of recent temperature and precipitation changes indicates that existing rules of thumb concerning the detectability of climate change ignore the full range of sources of uncertainty, most particularly the importance of adequate observational monitoring.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As a research field, the detection and attribution (D&A) of climate change is at least a quarter of a century old (Wigley and Barnett 1990), with pioneering studies going back to at least the 1970s (Chervin et al. 1974; Chervin and Schneider 1976; Hasselmann 1979). Despite this healthy age (at least in climate change research terms), D&A remains solely a research field and has yet to make the transition to also being a service. This contrasts with projections (and even predictions) of future climate change, for instance, which are readily available in various tailored formats through a number of internet sites. In this paper we attempt to lay some of the groundwork for making such a transition by developing and testing an algorithm for rapid assessment of the degree to which a response to anthropogenic emissions is detectable for a specified climate variable, spatial domain, season, and historical period. In particular, the algorithm assesses the quality of data sources entering into a comparison against expected (historical) and observed climate change, performs the comparison, and examines the robustness of the comparison to uncertainties in the input data. Its output is a description of confidence (Mastrandrea et al. 2010) concerning the existence and magnitude of the role of anthropogenic emissions in observed regional climate change.
Possible interest in a rapid D&A service is emerging on a number of fronts. One is still within scientific research itself. For instance, the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC AR5) assessed the role of observed changes in climate on observed impacts in natural and human systems, and the role of anthropogenic emissions on observed changes in climate, but generally did not consider the relevance of one for the other: i.e. whether the observed attributed climate changes have any observed impacts, or whether the attributed impacts are related to anthropogenic climate change (Bindoff et al. 2013; Cramer et al. 2014). A primary reason was the lack in the available literature documenting D&A studies that could support such an assessment, coupled with the lack of an established methodology for efficient estimation that could have been implemented by the chapter authors. With the algorithm developed in this paper, Hansen and Stone (2015) explore this gap by evaluating the role of anthropogenic climate change in the observed climate changes noted to have observed impacts in the IPCC AR5 (Cramer et al. 2014).
Another source of interest is within the wider private and public policy-making community, who are increasingly considering detection and attribution evidence when making policy and adaptation decisions. For this reason, attribution is a recurring component of the World Meteorological Organisation’s Global Framework for Climate Services, for instance (World Meteorological Organization 2014). However, recent developments have tended to focus on understanding extreme weather within the context of anthropogenic climate change (Stott et al. 2013; James et al. 2014) due to the highly visible impacts of such events, with less attention on describing longer-term changes within a service setting.
Some efforts have been made to produce a large set of D&A information on long-term climate change for a variety of regions, domain sizes, seasons, and/or periods (e.g. Karoly and Wu 2005; Jones et al. 2013). Such efforts fall short of a service, not least because any region-season-period-variable combination of interest to someone (e.g. because of a government agency’s remit) are unlikely to align well with any amongst the limited number that can possibly be examined in a research paper. There is of course a philosophical point here: if we have studies attributing observed global warming to emissions, and that warming is expected to be broadly uniform across the globe, do we really need local, seasonal, and/or shorter-period analyses too? Indeed, Christidis et al. (2012) estimate distributions of regional annual mean temperatures for recent years under actual and hypothetical natural (i.e. no human influence on the climate) scenarios by using results of analyses conducted at larger spatial scales to infer the more local information (Christidis et al. 2010). The relevant assumptions break down for climate variables with more heterogeneous trends, however, such as the timing of the rain season onset. And in any case many stakeholders see a necessity for local information: climate services are under continual demand to provide explicitly local predictions of future warming. Thus while current attribution products are useful for scientific understanding, it is not clear that they provide an accurate source of information for making policy decisions.
The information content of most D&A studies exploring the role of anthropogenic emissions on historical climate change is also incomplete. Their analyses are generally expressed in strictly quantitative terms (usually a statistical significance level or confidence interval on some metric like a regression coefficient), without an explicit assessment of the relevance of unquantified factors, such as the accuracy of the observational data product (Jones and Stott 2011). The IPCC assessment reports differ in this respect, using a calibrated “confidence” language to characterise the total effect of all contributors, quantifiable or not, to building confidence in assessments (Mastrandrea et al. 2010). This confidence language will form the basic output of the algorithm developed in this paper. With the intention that it can be implemented on a large number of cases on a rapid time scale, this algorithm is necessarily generic in nature, and thus ignores additional possible worthy inputs, such as local observational data products. Such issues are discussed further in Sect. 5. As such, the output from this algorithm might be better described as estimates of what more focused and comprehensive analyses would conclude, with this algorithm implemented specifically because resource constraints preclude the detailed analyses for now.
2 The confidence estimation algorithm
2.1 The confidence metric
The desired output of this attribution assessment is a description of confidence concerning the attribution of a major role of anthropogenic emissions in an observed change in regional climate (with attribution of at least a minor role being another output obtained along the way). The algorithm is centred around the comparison of observed variations in the climate against our expectations of how the climate should have changed, with the latter developed through some sort of understanding of how the climate might respond to external drivers (Hegerl et al. 2010; Hegerl and Zwiers 2011). Around that comparison we must also consider the adequacy of our understanding, of the implementation of our understanding, and of the inputs to the analysis.
Mastrandrea et al. (2010) formulate two qualitative descriptors for use in assessments conducted by the Intergovernmental Panel on Climate Change for summarising current understanding of various statements with regards to climate change. The intention of the algorithm being developed in this paper is to estimate belief in whether a statement of attribution is accurate based on direct evidence, so we adopt the confidence descriptor here. This confidence descriptor merges evaluation of the quality and quantity of evidence (Sect. 2.3) and of the degree of agreement across sources of evidence (Sect. 2.4) into a single qualitative assessment. It has been adopted in the D&A chapters of all recent IPCC assessment reports (Seneviratne et al. 2012; Bindoff et al. 2013; Cramer et al. 2014), allowing direct comparison in Sect. 3 between results estimated here and in two of those reports.
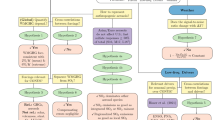
While the output is qualitative, the algorithm itself is quantitative, with the mapping from the latter to the former described in Sect. 2.5. It uses a numerical metric, c, to characterise confidence (Fig. 1). The metric is assigned an initial value which depends on the number of input data sources (Sect. 2.3.1). This value is then left unchanged or reduced based on a series of tests which examine our belief in the adequacy of the input data sources and our understanding of the relevent processes (Sect. 2.3). It is then further left unchanged or modified based on a series of tests which evaluate the agreement between observed changes and our expectations based on process-based modelling (Sect. 2.4). All of these tests output a confidence-reduction factor, \(\gamma\), by which the confidence metric is multiplied. Because reduction of the metric is always by multiplication, the order of the tests does not in fact matter.
Schematic of the algorithm for estimating the confidence in the detection and attribution of a climate response to anthropogenic drivers. An initial metric based on the availability of data products is degraded according to tests against various criteria. These tests are described in Sects. 2.3 through 2.4
2.2 Ingredients
The steps of the algorithm for estimating confidence for a given aspect of climate change use various combinations of the following inputs:
-
Information about the climate change of interest, specifically identification of the climate variable, specification of the seasonal extent, and specification of the spatial extent.
-
\(N_{obs}\) gridded observational products. The usage of multiple data sets allows some (albeit likely incomplete) inclusion of measurement error and the uncertainty in calculating a regionally and seasonally averaged estimate from instantaneous point measurements.
-
Simulations of the climate system from \(N_{mod}\) models which have been driven with all known possible important drivers of climate change, including both anthropogenic and natural drivers. For dynamical climate models, averaging across multiple simulations which produce different possible weather trajectories for each model provides a more accurate estimate of the model’s response signal.
-
Simulations of the climate system from the same \(N_{mod}\) climate models but which have been driven with natural drivers only.
-
A large number of years of simulations of dynamical climate models with no variations in external drivers beyond the annual cycle. While in practice it would be preferable to have these for each of the above \(N_{mod}\) climate models, in practice the sampling requirement of a large ensemble dictates that we will assume that in general data will be borrowed from available simulations of these and other models.
2.3 Assessment of data sources (evidence)
2.3.1 Diversity of data sources
The observational and (after-the-fact) prediction products comprise our ultimate sources of evidence, so having more numerous independent products available should increase the robustness of the evidence base. We consider the predictions of response signals to come solely from simulations of dynamical climate models (e.g. Taylor et al. 2012), generally of about the same generation (note however that having models of different generations, for instance “state-of-the-art” dynamical models and “back-of-the-envelope” zero-dimensional models, could add substantially to confidence by indicating a lack of sensitivity of conclusions to climate model design). If the errors in the variability and response signals of climate models were independent, then we would expect the information content to scale as \(\sqrt{N_{mod}}\). However, because climate models have not been developed in isolation, it might be expected that they share errors, and indeed recent studies suggest that ad hoc collections of climate models of similar levels of complexity have an effective sample size only about one half the total number of models (Jun et al. 2008; Pennell and Reichler 2010) in terms of the errors in their mean climatology. In the absence more relevant studies, we assume that a similar property holds for interannual variability.
Similarly, observational data products are not independent of each other, most particularly in sharing most of the measurements they use as input. Studies of the effective sample size of observational products are currently lacking, but in any case would likely be variable- and region-dependent. Through analogy, we suppose a similar scaling as for climate models. In research-grade assessments, it may be possible to better characterise these effective sample sizes, for instance noting the degree with which the observational products share the input data. The important assumption here is that the information content scales as \(\sqrt{N}\). The mapping of the metric to the qualitative levels described in Sect. 2.5 includes a calibration that would override any multiplicative constant added here, so we take the initial confidence as
While in theory this allows an infinite initial confidence, in practice only reasonable values of \(\gamma _{sources}\) are possible with the current diversity of data sources (e.g. Table 3).
2.3.2 Observational measurement density
The spatial distribution of observational measurements is not uniform, and in some areas may be insufficient for accurate representation of the regional climate. To estimate the adequacy of measurement density, we estimate the fraction of the variance of the time series of a regional climate variable that is accounted for by the given measurement density using a method building on that employed in New et al. (2000). For the land-based variables, we consider the number of stations reporting in the month for each grid cell. Sea surface temperature products instead report the total number of individual measurements taken from moving ships so, following the analysis of Jones et al. (1997), we divide by 5 to get an effective number of stations.
The stations in each grid cell (or “effective stations” in the case of ocean data) are assigned random locations within that grid cell, subject to land/sea definitions. Stations are considered to only become active or inactive in a specific order (e.g. while there is a single station in the cell it is always station A, it never moves or changes identity, and if a second station is then added, later on that station will be deactivated before station A). Stations that are active for less than 90 % of the total period examined are discarded. This threshold is fairly strict, but it serves the purpose of ensuring that the first and last 5-year segments of a 50-year period (as examined in later sections) both have data. Moreover, because the lowest station coverage occurs during the final decade of this period, results should be insensitive to relaxation of this threshold to values as low as 75 % or to even lower values when accompanied with additional thresholds for coverage at the ends of the period. We then estimate the fraction of the variability accounted for by the available active stations at each point within the region on a higher resolution (\(0.1^{\circ }\times 0.1^{\circ }\) longitude-latitude) grid. Only stations within the decorrelation radius, \(r_{decorr}\), of the grid cell are considered (New et al. 2000). It is assumed that differences between two stations separated by distance \(r_{stat}\) can be represented as random noise that is correlated in space with fractional variance \(1-e^{-2\cdot \frac{r_{stat}}{r_{decorr}}}\). The fractional variance accounted for by the station coverage, \(\gamma _{density}\), is then provided by the integral on the high-resolution grid of the product of the variance unaccounted for by the given stations:
where \(a_{cell}\) and \(a_{region}\) are the spatial area of the cell on the high-resolution grid and of the region respectively, \(N_{year}\) is the number of years in the period, and the stations being considered (stat(cell, year)) varies with location and year.
In practice, measurement density is not available for most observational products, so for the evaluation conducted in Sect. 3 we only obtain this information from one product for each climate variable (Table 1). For the land-based variables these observation counts are for a relatively high-spatial-resolution product, while for sea surface temperature the information is only available for the relatively coarse resolution (200,000 km2) HadSST3.1.1.0. The HadSST3.1.1.0 density data, which consider in situ data only, will furthermore be an underestimate for higher resolution products that also use satellite data in more recent decades, such as those used in the analysis of Sect. 3; this could produce a bias toward lower confidence in regions with a small number of in situ measurements, such as the Antarctic Ocean.
2.3.3 Region size
Dynamical climate models have a limited spatial resolution, meaning they are better at reproducing variations in large-scale mechanisms than ones closer to the resolution size. Furthermore, the smaller scale characteristics of the anthropogenic drivers of climate change (particularly aerosol emissions) are less well understood than the larger scale properties. This means we are a priori less confident in analyses of climate model predictions for smaller regions. Similarly, the accuracy of observational products becomes more sensitive to the interpolation method used at scales around or smaller than the station separation. To account for this, the confidence metric is reduced by an amount related to the region’s size. If \(a_{region}\) is the area covered by the region in units of \(10^{6}\, \hbox {km}^{2}\), then the confidence metric is multiplied by
The functional form is such that \(\gamma \sim 1\) at continental scales (Jones et al. 2013), and such that \(\gamma \sim 0.5\) at scales around the smallest dynamical resolution of the current generation of climate models (about \(4^{2}\) times larger than the grid cell size) (Fig. 2). The lower value of 0.5 is a balance between acknowledging that the modelling and observational products may retain some skill even if they are not fully resolving processes and features and realising that size-related inaccuracies are also likely to emerge as penalties in the tests described in Sect. 2.4 which we do not want to double count.
The functional forms of two of the confidence multipliers underlying the algorithm. Left the multplication factor relating to region size, with representative countries listed. Right the multiplication factor relating to whether the predicted magnitude of the response to anthropogenic emissions matches the observed magnitude, as estimated by linear regression, for the case of 21 combinations of observational and model data products. The point at which the p value of the comparison of the number of matches against the binomial distribution is 0.1 is marked
2.3.4 Physical representation
The basic physical processes behind some aspects of the climate are both well understood and mostly resolved in dynamical models, but this is not the case for some variables. For instance, the microphysical processes that generate precipitation are not simulated in climate models, but rather are approximated by somewhat heuristic algorithms. In recognition of this, the confidence metric is multiplied by a constant that depends only on the climate-variable:
The general effect on confidence for precipitation is a reduction of one of the Mastrandrea et al. (2010) levels.
It would be preferable if this factor could be informed by more developed empirical or process-based methods. A relevant question is whether the climate model is reliable, but this is essentially considered by the steps described in Sects. 2.4.2 through 2.4.5. Unfortunately, understanding of what additional qualities of a climate model are required to make it more accurate in the D&A context remain poorly understood (Santer et al. 2009; Flato et al. 2013). Therefore, in the interest of not introducing complexity which does not clearly add information, for now Eq. 4 seems the most parsimonious option.
2.4 Comparison between the data sources (agreement)
2.4.1 Comparison of observed and predicted climate change
The analysis method behind much research into the detection and attribution of climate change in recent years applies a linear regression model to compare output from climate model simulations against observed climate changes (Bindoff et al. 2013). The central idea is to separate aspects of the climate response that we consider to be known (i.e. tightly constrained by external parameters) from those that we consider to be less well known (i.e. not tightly constrained). The pattern by which the climate system is expected to respond to a particular external driver is generally considered robust and well estimated by past and current dynamical climate models; thus the pattern can act as a fingerprint for that response. For instance, both the climate system and models of the climate system should respond to a large volcanic eruption soon after that eruption, a feature that distinguishes its response from other drivers. In contrast, the magnitude of the response may not be something that is particularly well estimated by current climate models, because this depends on feedback processes within the climate system, such as how cloud microphysics interact with the larger scale climate, whose effects are not so directly constrained.
With this in mind, if \(X_{obs}(t)\) represents variations in an observed climate variable as a function of time t, \(X_{ant,mod}(t)\) represents the expected climate response to anthropogenic external drivers according to climate model mod, and \(X_{nat,mod}(t)\) represents the expected climate response to natural external drivers, then the regression can be written as (Allen and Tett 1999):
Note that all X are all taken as anomalies with zero mean over the full \(N_{year}\) period. \(R_{obs,mod}(t)\) is the residual of the regression and \(\beta _{ant,obs,mod}\) and \(\beta _{nat,obs,mod}\) are the regression coefficients estimated such that the variance of \(R_{obs,mod}(t)\) is minimised. This formulation of the regression assumes that we can perfectly estimate the \(X_{ant,mod}(t)\) and \(X_{nat,mod}(t)\) responses (Allen and Stott 2003). In the test cases examined in Sects. 3 and 4 this assumption is important because the estimates will be derived from a small number of climate model simulations. However, the resulting underestimate in the uncertainty from the regression will be compensated by repetitive estimation (and solving of the regression equation) using multiple (\(N_{obs}\cdot N_{mod}\)) combinations of observational and climate model data sources. An option for further development would be to utilise regression approaches that explicitly permit multiple estimates of both the dependent and independent variables, thus considering all observational and climate model data sources in a single calculation (Hannart et al. 2014).
The regression assumes that responses to climate change are linearly additive, which has yet to be strongly tested at subcontinental scales, but which nevertheless appears reasonable for the magnitude of the temperature and precipitation responses considered here as well as given the statistical power afforded by the available data sets (Shiogama et al. 2012). Available climate model data (Sect. 3.1) generally only cover the \(X_{nat,mod}(t)\) response signal and the \(X_{all,mod}(t)=X_{ant,mod}(t)+X_{nat,mod}(t)\) response to the full combination of anthropogenic and natural drivers. Substituting into Eq. 5 we get:
The regression coefficients \(\beta _{ant,obs,mod}\) and \(\beta _{nat,obs_mod}+\beta _{ant,obs,mod}\) and their uncertainty due to the limited sampling of the observed climate response against the noise of natural internally generated variability of the climate system are estimated using the code available at http://www.csag.uct.ac.za/~daithi/idl_lib/detect/ (Allen and Tett 1999). Traditionally, a response to anthropogenic forcing is considered to be detected if \(\beta _{ant,obs,mod}\) is positive and inconsistent with zero at some level of statistical significance given this sampling uncertainty.
The regression is performed separately for each combination of the \(N_{obs}\) observation data products and the \(N_{mod}\) climate model products. The translation of these regression analyses into modification of the confidence metric is described in Sects. 2.4.2 through 2.4.5.
2.4.2 Matching signals
This test addresses the question whether the fingerprint of the anthropogenic response expected by the climate models is indeed found in the observational data. In terms of the regression, the question is whether \(\beta _{ant,obs,mod}>0\). This step is the critical test for a climate change detection analysis. If we suppose that each of the climate models and observational products represent random samples of the probability distributions of possible models and observations respectively, then we can add the probability distributions for each of the \(N_{obs}\cdot N_{mod}\) observation-model combinations and calculate the fraction of the combined distribution that is greater than zero, \(f_{signal}\). The confidence metric is then multiplied by \(\gamma _{signal}=f_{signal}\).
2.4.3 Match of magnitude of anthropogenic climate change
Whether the magnitude of the observed signal matches the predicted magnitude is often considered a component of attribution rather than detection (Hegerl et al. 2010). However, a match in magnitude can be considered an indication that the observed signal analysed in the regression is indeed the predicted signal, rather than, for instance, a response to an ignored driver that happens to closely resemble the predicted response to anthropogenic drivers. In this sense a match of magnitudes helps to build confidence.
Within the regression formulation used here, the question is whether any of the regression coefficients for the anthropogenic response, \(\beta _{ant,obs,mod}\) are inconsistent with 1. This is a two-sided problem so we cannot use a similar approach as in Sect. 2.4.2. Instead, we consider the number, \(n_{fail}\), of the \(N_{obs}\cdot N_{mod}\) estimates of the \(\beta _{ant,obs,mod}\) regression coefficients that are inconsistent with 1 at the \(\alpha =0.1\) significance level, i.e. whether 1 lies outside of the 90 % (statistical) confidence range. The choice of \(\alpha =0.1\) simply follows the standard of most regression-based climate change studies (e.g. Bindoff et al. 2013). The p value, \(p_{ant}\), of obtaining \(n_{fail}\) failures in a binomial distribution centred on probability \(\alpha =0.1\) is then used to calculate the multiplication factor of
where the exponent is defined such that the factor is halfway to its lowest value at \(p_{ant}=\alpha\) (Fig. 2). The one-sided nature reflects that our confidence is not diminished if fewer estimates of \(\beta _{ant,obs,mod}\) are inconsistent with 1 than would be expected by chance (even though that could reflect an overestimation of uncertainty). The maximum penalty of 40 % reflects a view that while a mismatch of magnitudes does indicate an inconsistency between predicted and observed responses, it does not necessarily interfere with detection (e.g. Gillett et al. 2005).
2.4.4 Match of magnitude of natural climate change
The above test only concerns the response to anthropogenic drivers. While they are less directly connected to the conclusions of the analysis, it would also help build confidence (or not reduce it) if the observed response to natural drivers is also not inconsistent with the predicted response. The step described in Sect. 2.4.3 is repeated here but for the estimates of \(\beta _{nat,obs,mod}\) and with a smaller maximum reduction, such that
The maximum 10 % reduction reflects that this test is less relevant for conclusions regarding anthropogenic forcing. For instance, climate models predict short cool periods following large explosive volcanic eruptions, but the observed cooling is significantly smaller than predicted. While it seems current climate models have a problem in representing relevant feedbacks, the detection of a response to volcanic eruptions is nevertheless generally considered robust (Bindoff et al. 2013).
2.4.5 Consistency of autonomous variability
As an extremely nonlinear system, the climate generates variability autonomously whether it is being influenced by external factors or not. If the assumptions behind the regression hold and all the important external drivers have been included in the \(X_{all,mod}(t)\) and \(X_{nat,mod}(t)\) pair, then the residual \(R_{obs,mod}(t)\) from the regression should be indistinguishable from this autonomous variability. Simulations of climate models whose external drivers do not vary from year to year (labeled “unforced preindustrial simulations” in Table 4) provide an estimate of what that variability should be on the multi-decadal time scale that is relevant here. A comparison of the \(R_{obs,mod}(t)\) arising from the regression and the variability in these unforced simulations is performed following (Allen and Tett 1999).
In many cases the residual is inconsistent with the unforced simulations at the \(\alpha =0.1\) significance level. Following the same approach as in Sect. 2.4.4, the multiplication factor is defined as
If the residuals from all \(N_{obs}\cdot N_{mod}\) combinations fail the test, then this can have the effect of lowering by up to three Mastrandrea et al. (2010) confidence levels. As with inconsistencies in the regression coefficients, gross failure of the residual test is a major concern (especially as it is a weak test, Allen and Tett 1999), and could reflect missing drivers, amongst other possibilities.
2.4.6 Major role
Assessment of the attribution of observed climate change to anthropogenic emissions requires a description of the magnitude of that role relative to other factors (Hegerl et al. 2010). For this algorithm we assess whether emissions have had a “major role” in the behaviour of the observed climate (Stone et al. 2013). This is interpreted as asking whether the anthropogenic response accounts for at least one third of the temporal variance; other possible contributors to the variance would be the response to natural drivers, autonomous variability, or possible neglected drivers. This is calculated by integrating the variance of the adjusted anthropogenic response (\(\beta _{ant,obs,mod}\cdot X_{ant,mod}(t)\)) across the calculated probability distribution of the regression coefficient \(\beta _{ant,obs,mod}\):
where
The dq are the quantiles of the probability distribution of the \(\beta _{ant,obs,mod}\) regression coefficient, and \(\sigma _{obs}^{2}\) and \(\sigma _{obs,mod}^{2}(q)\) are the variances of the observed data \(X_{obs}(t)\) and the adjusted model data \(\beta _{ant,obs,mod}(q){\cdot }X_{ant,mod}(t)\), respectively. Note that without this test of the relative role, this algorithm is assessing the detection of an anthropogenic response in observed climate change (Hegerl et al. 2010; Stone et al. 2013).
2.5 Mapping the quantitative metric to the qualitative levels
The multiplication factors described in Sects. 2.3 through 2.4 are multiplied together to produce the confidence metric:
This metric is then mapped to the confidence levels listed in Table 2 which include the five levels of Mastrandrea et al. (2010) as well as a further level of no confidence (\(c_{map}=0\)) for cases where no evidence is available or the algorithm reveals a fundamental disagreement between expected and observed responses. The mapping is performed according to
The logarithmic nature of this mapping function reflects the multiplicative nature in which the tests modify the initial \(\gamma _{sources}\) value. The constants serve two purposes. First, if \(N_{obs}=N_{mod}=1\) and all \(\gamma\) multipliers are equal to 1 (i.e. all tests are passed perfectly, then \(c_{map}=2.5\) and we have medium confidence of a major anthropogenic contribution. Second, adding one within the logarithm provides a lower bound of no confidence, but it distorts the logarithmic interpretation, which the factor of 3 within the logarithm alleviates for larger values.
3 Comparison against detailed assessments
3.1 Data
In this section we compare attribution results from the algorithm described above against assessments in the IPCC AR5. The data required by the algorithm can be divided into observationally-based data (\(X_{obs}\)) and climate model-based data. The observational data sets used are listed in Table 3, selected on the basis of having global (terrestrial or marine) coverage, covering the 1951–2010 period, and having a spatial resolution finer than \(250^{2} \text {km}^{2}\). All of the terrestrial air temperature and precipitation data sets are based on in situ station monitoring, while the two marine data sets analyse both in situ measurements and, in more recent decades, remote sensing data. The Hurrell sea surface temperature data set adopts HadISST1 values through to October 1981, then NOAA OI.v2 values (Reynolds and Smith 1994) thereafter. Because not all products report the monitoring density, only the data sets listed in Table 1 are used for that purpose.
The response signals \(X_{all,mod}(t)\) and \(X_{nat,mod}(t)\), as well as the autonomous unforced variability \(X_{noise}\), can be estimated from simulations of dynamical climate models driven with only the respective external drivers. For this analysis, we take simulations from the CMIP5 database (Taylor et al. 2012) listed in Table 4. The spatial resolution lists the average box size on the grid used to output the data. This is the same grid or approximates the scale used in the model’s dynamical calculations. Because of the nature of simulation numerics, models effectively only resolve features several times this scale; in this sense the listed spatial resolution is not directly comparable against the resolution listed for the observational data sets. For each of the models with multiple available simulations for estimating the response signals \(X_{all,mod}\) and \(X_{nat,mod}\), the sampling noise is reduced by averaging across the 3 to 10 simulations available in each case. The regression model (Sect. 2.4.1) is estimated for each combination of the \(N_{mod}=7\) climate models with available simulations and the \(N_{obs}\) observational products, resulting in 21 regression models for 2-m air temperature over land, 14 for sea surface temperature, and 28 for precipitation. Data for estimating the autonomous unforced variability \(X_{noise}\) is taken from these and additional climate models in order to allow a more precise estimate of the expected covariance of the residual \(R_{obs,mod}(t)\).
3.2 IPCC AR5 WGI chapter 10 assessments
A first comparison can be made against the assessments of regional warming from the climate change detection and attribution chapter of the IPCC AR5 (Bindoff et al. 2013). The statements were intended to be robust for the regional domain and time period. We assume that all statements:
-
refer exclusively to land territory (including the Arctic statement, due to the paucity of marine monitoring in the Arctic);
-
are relevant to the 1951–2010 period (except for the Arctic for which the 1961–2010 period more closely matches the statement);
-
apply to the IPCC regional definitions used in the IPCC AR5 (Hewitson et al. 2014);
-
apply to annual mean values averaged evenly over the region.
Table 5 compares confidence assessments made with the algorithm developed in Sect. 2 against assessments for statements made in the IPCC AR5.
The algorithm agrees with the IPCC AR5 assessments for the attribution assessments for all of the populated regions except Africa, where the confidence metric falls just shy of the border between medium and high confidence. The station density step is the dominant difference between the African result and those for the other populated regions (not shown). The difference for the Antarctica conclusion similarly arises because the CRU TS 3.22 product used for estimating station density does not cover Antarctica. In contrast, the discrepancy for the Arctic conclusion arises mostly from the test of the residual variability after the regression.
3.3 IPCC AR5 WGII chapter 22 assessments
A further comparison can be made against the subcontinental detection and attribution assessments made in the African chapter of the IPCC AR5 (Niang et al. 2014). An interesting aspect of this comparison is that one of the authors of this paper led the compilation of these African assessments in the IPCC AR5, and thus differences in calibration of confidence levels should not be an issue (inasmuch as this paper’s algorithm reflects the author’s calibration). Niang et al. (2014) provide assessments for both precipitation and temperature, both of detection and of attribution of a major role for five regions based on the Regional Economic Communities. Because there were no available studies that directly performed D&A analysis for these regions, the assessments were performed through expert judgement by considering the combination of results from studies investigating various components of the emissions-to-climate-change chain, plots comparing observations and model simulations prepared for the report, evaluation of our level of understanding of the relevant processes, and evaluation of the adequacy of the observational network. While no time period is specified, the assessments are heavily influenced by the time series plots of observed and simulated change shown in the chapter (which happen to share a large number of data sources with this paper); given these plots and that monitoring density improves markedly in the 1960s, we take the relevant period to be 1961–2010. Additionally, while the IPCC AR5 precipitation assessments are for land areas only, the temperature assessments apply to the combined terrestrial and Exclusive Economic Zone (EEZ) territories. Because of the lack of high spatial resolution observational products of combined terrestrial and marine near-surface air temperature, we must treat the terrestrial and marine areas separately, and thus we assume that the assessments apply equally to these two components of the overall region.
The comparison is listed in Table 6. Unlike for the comparison in Sect. 3.2, there are more numerous discrepancies for the African regions. Precipitation assessments are all the same or less confident than in the IPCC AR5. For major-role attribution, the inconsistency for four regions could arise simply from the lack of a no confidence level in the IPCC AR5. The only two-level discrepancy is for rainfall over ECOWAS (the Economic Community of West African States). In Niang et al. (2014) the ECOWAS assessment was based on a number of detailed studies which considered the underlying data sources and processes in more detail than in our algorithm, for instance by evaluating the ability of climate models to adequately represent the West African monsoon and rejecting models which did not pass a certain benchmark. However, many of these studies specifically examined the drying and partial recovery of rainfall over the Sahel, which only partly overlaps with the ECOWAS region (note that the spatial averaging of precipitation performed here is based on fractional anomalies, so a 30 % reduction in some part of the Sahel would be considered equivalent to a 30 % reduction in a corresponding area on the much wetter coast). This case may therefore be illustrating both the relative strength of detailed targeted analysis in comparison to this paper’s algorithm, and the relative strength of the algorithm in being easily tailored to the specific requirement of an assessment (in this case the ECOWAS territorial area).
Marine temperature detection and major-role attribution assessments both tend to be assigned higher confidence by the algorithm, whereas discrepancies tend to balance for terrestrial temperature. In part this is a reflection of the separation of the joint terrestrial-marine assessments: some of the terrestrial assessments suffer from poor station coverage, so when the better-monitored marine areas are separated they are freed from this penalty. ECCAS (the Economic Community of Central African States) suffers especially from poor monitoring coverage over land, but not over its EEZ.
4 Application to nation-scale regions
In this section we deploy the algorithm on precipitation and temperature changes over a large number of regions. We adopt the regions developed for an operational system linking changes in the chance of extreme weather to anthropogenic emissions (http://www.csag.uct.ac.za/~daithi/forecast, Angélil et al. 2014). These regions are based on political/economic groupings and are all approximately \(2\,\hbox {million}\,\hbox {km}^{2}\) in size. Because of limitations in the modelling technique used by that system, all regions are terrestrial and exclude countries dominated by archipelagos (e.g. Indonesia) as well as Antarctica. The limited political/economic links of some countries also impose limits within the \(2\,\hbox {million}\,\hbox {km}^{2}\) size criterion (e.g. Suriname and Ukraine). For the sake of simplicity we maintain those omissions. The algorithm is run on annual total precipitation and annual mean 2 m air temperature over these regions. (As in Sect. 3.3, the spatial averaging of precipitation is on the fractional anomaly, so arid and wet areas contribute equally to a region’s variability.) The data sources are the same as listed in Tables 3 and 4.
The results for detection of an anthropogenic influence and for attribution of a major anthropogenic role (differing through the exclusion/inclusion of \(\gamma _{major}\) from the “major role” test) are shown in Fig. 3. An anthropogenic influence on precipitation variations is only detected with a reasonable confidence in some northern mid and high latitude regions, and with one exception (consistent with the recent assessment report for part of that region (Bhend 2015)) there is at most very low confidence that that role is substantial. The reason for this is apparent in Fig. 4, which shows how the estimate of confidence is affected by the various steps of the algorithm, and in Fig. 5, which maps selected multiplication factors (specifically those that vary noticeably from region to region). For a large number of the regions, inadequate station density in the monitoring networks is a major restriction on confidence in detection. Note that because of the smaller decorrelation scale the network density must be considerably higher for precipitation than for temperature (Table 1), meaning that for temperature station density is only a large constraint in central Africa and the Western Arctic (Fig. 6). Unlike for temperature, all of the steps in the algorithm contribute to a notable decrease in the confidence metric for detection of precipitation changes over almost all regions. The magnitude of any potentially detected signal is always very small in relation to the autonomous year-to-year variability of the climate system, leading to consistently large decreases (\(\gamma _{major}\le 0.25\)) in confidence at the “major role” step distinguishing detection of an anthropogenic influence from attribution of a major role.
Assessments of the detection of an influence (top row) and attribution of a major role (bottom role) for anthropogenic emissions in observed climate variations during the 1961–2010 period over various political/economic regions of the world. All regions are terrestrial and approximately \(2\,\hbox {million}\,\hbox {km}^{2}\); land areas not included in any regions are shown in white. All assessments are for annual averages
Calculation of the confidence metric for the assessments shown in Fig. 3 of the detection and attribution of observed climate variations during the 1961–2010 period for various \({\sim }2\,\hbox {million}\,\hbox {km}^{2}\) political/economic regions of the world
Maps of the multiplication factors contributing to the calculation of the confidence metrics for the precipitation assessments shown in Fig. 3 for various \({\sim }2\,\hbox {million}\,\hbox {km}^{2}\) political/economic regions of the world. Colour levels are the same for all of the pink maps, with the range of the colour bar reflecting the range of possible values of the multiplication factor. Maps are not show for the “diversity of data sources”, “region size”, or “physical representation” steps because these are set to be identical or near-identical across these regions, nor for the “major role” step, for which all multiplication factor values are \(\gamma _{major}\le 0.25\)
Maps of the multiplication factors contributing to the calculation of the confidence metrics for the temperature assessments shown in Fig. 3 for various \({\sim } 2\,\hbox {million}\,\hbox {km}^{2}\) political/economic regions of the world. Colour levels are the same for all of the pink maps, with the range of the colour bar reflecting the range of possible values of the multiplication factor. Maps are not show for the “diversity of data sources”, “region size”, or “physical representation” steps because these are set to be identical or near-identical across these regions, nor for the “matching signals” step, for which all multiplication factor values are close to 1
Not surprisingly, confidence is much higher for temperature changes, with at least high confidence in detection of an anthropogenic influence over most regions outside of Africa (Fig. 3). The attribution of a major role is assigned slightly less confidence, with only three high-latitude regions with large warming signals retaining very high confidence. The spatial pattern of confidence in detection (and attribution) differs from the expected signal-to-noise ratio (Mahlstein et al. 2011; Bindoff et al. 2013). The reason for this is apparent by looking at the lowest-confidence case in Fig. 4. While all four regions with low or very low confidence in detection are located in an area of the tropics with an expected high signal-to-noise ratio, they are also regions with poor monitoring station coverage; monitoring coverage tends to be a major factor for regions with medium confidence in detection as well. This illustrates that the current rule-of-thumb of stronger detectability of warming in the tropics (Bindoff et al. 2013) ignores the full set of sources of uncertainty, and in particular the role of adequate long-term monitoring.
5 Discussion
This paper has both developed a framework for assessing the detection and attribution of climate change on a large scale and developed a specific implementation. The framework is simply an explicit quantification of the framework developed and applied in recent IPCC Assessment Reports (Seneviratne et al. 2012; Bindoff et al. 2013; Cramer et al. 2014), based on the confidence level formulation of Mastrandrea et al. (2010). This considers not only the result of a single comparison of expected responses to climate change with observed trends, but also examines the agreement between comparisons using different data sources, as well as the underlying appropriateness and accuracy of those data sources. In terms of implementation in the IPCC reports, it has generally been assumed that the components of confidence are separable. What is new in the algorithm developed in this paper is the concept that the components are also quantifiable and multiplicative. The degree to which both these assumptions are justifiable is open to discussion, but for this algorithm the assumptions only need to hold approximately, because the algorithm is not intended for use as an expert “final word” but rather a more general tool.
In terms of the specific implementation developed in this paper, it is centred around the popular multiple linear regression approach underlying much climate change detection and attribution research (Bindoff et al. 2013), but other options exist. Indeed, exploration of multiple methods should really be considered in establishing confidence. Similarly the division of the components of confidence could probably be chosen differently, according to the exact nature of the detection and attribution study. For instance, in some cases (e.g. because an impact has been observed) there may be a required direction of climate change, and so an additional test will be needed to ensure that the required trend exists in the observational products being used (Hansen and Stone 2015).
There are three specific areas of the implementation that require consideration. First, the algorithm operates within a realm of well-behaving inputs. For instance, while it is plausible, as stipulated in Sect. 2.3.1, that the maximum possible confidence should be the same when \([N_{obs}=3, N_{mod}=6]\) as when \([N_{obs}=6, N_{mod}=3]\), it is less obvious that the situation \([N_{obs}=36, N_{mod}=1]\) or \([N_{obs}=1, N_{mod}=36]\) should also have the same maximum confidence. Modifications may be warranted for such extreme situations.
Second, the quality of the development of the various steps in the algorithm varies considerably. For instance, confidence in detection must depend directly on the station density as well as the distribution of those stations, and there must be no confidence when there are no observations at all (Hegerl et al. 2010). While the method used here makes simple assumptions about the spatial correlation of climatic variability, these same assumptions are well tested and have also been used in the development of respected observational products. However, the way in which a statistical failure of the “variability match” step in the regression analysis should be translated into a quantitative modification of the confidence metric is less obvious. While selection of the maximum possible reduction in confidence by this step has been informed by experience with regression analysis, the value is still a subjective choice based on the authors’ experience and intuition. Fortunately, some of the steps that seem to have the greatest bearing on the final confidence (monitoring density, signal match, and major role) are also the steps with the highest quality translation from analysis to confidence metric. Nevertheless, a decision to give substantially more weight to some of the other steps (particularly “match of magnitude of anthropogenic climate change”) could be important for some regions, for both precipitation and temperature (Figs. 5, 6).
Finally, the output of this algorithm is qualitative in nature, and the relation between qualitative terms like “major role” and quantitative metrics remains at least partly subjective. Fortunately, results here do not appear to have been that sensitive to choice of “major role” threshold. However, the mapping from the quantitative confidence metric, c, through \(c_{map}\) into the qualitative Mastrandrea et al. (2010) levels can lead to systematic shifts of a full confidence level. In that sense the comparisons performed in Sect. 3 against existing expert assessments served an important role to check on the calibration of the algorithm.
Ultimately, this algorithm is no substitute for detailed expert detection and attribution analysis. For instance, the “physical representation” step (Sect. 2.3.4) is the only step in the algorithm responsible for evaluating whether the climate models are capable of representing the processes required in order to adequately represent the regional and seasonal climate of interest. Currently that step consists of a simple binary function depending only on the climate variable. Future development of the algorithm could add some evaluation of, for instance, the spatial pattern of the mean annual climatology and the annual cycle, but it is hard to envisage a systematic approach that could ever be as nuanced and detailed as an expert evaluation whilst remaining generalisable.
Despite these disadvantages relative to detailed expert assessments, this algorithm has some important strengths that mean it can serve as a complementary tool. Most particularly, it can be deployed simply and straightforwardly on a large scale, as illustrated in Sect. 4. Performing those 116 assessments in 116 separate detailed papers would require unobtainable resources; in contrast, the main performance bottleneck in conducting the calculations presented in Sect. 4 was simply the extraction of the regional and seasonal data from the various data products. While there were some discrepancies between the algorithm’s results and those of existing expert assessments, these did not necessarily point to a fault in the algorithm: some of the expert assessments were based on fewer data sources, for instance. Given these points, this algorithm, or approaches similar to it, could provide an important tool toward the inclusion of detection and attribution analysis within the provision of climate services.
References
Allen MR, Stott PA (2003) Estimating signal amplitudes in optical fingerprinting, part I: theory. Clim Dyn 21:477–491
Allen MR, Tett SFB (1999) Checking for model consistency in optimal fingerprinting. Clim Dyn 15:419–434
Angélil O, Stone DA, Tadross M, Tummon F, Wehner M, Knutti R (2014) Attribution of extreme weather to anthropogenic greenhouse gas emissions: sensitivity to spatial and temporal scales. Geophys Res Lett 41:2150–2155. doi:10.1002/2014GL059234
Bhend J (2015) Regional evidence of global warming. In: BACC II Author Team (ed) Second assessment of climate change for the Baltic Sea basin, Regional Climate Studies. Springer, pp 427–439. doi:10.1007/978-3-319-16006-1_23
Bindoff NL, Stott PA, AchutaRao KM, Allen MR, Gillett N, Gutzler D, Hansingo K, Hegerl G, Hu Y, Jain S, Mokhov II, Overland J, Perlwitz J, Sebbari R, Zhang X, et al (2013) Detection and attribution of climate change: from global to regional. In: Stocker TF, Qin D, Plattner GK, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate Change 2013: The physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, pp 867–952
Chen M, Xie P, Janowiak JE, Arkin PA (2002) Global land precipitation: a 50-yr monthly analysis based on gauge observations. J Hydrometeorol 3:249–266
Chervin RM, Schneider SH (1976) On determining the statistical significance of climate experiments with general circulation models. J Atmos Sci 33:405–412
Chervin RM, Gates WL, Schneider SH (1974) The effect of time averaging on the noise level of climatological statistics generated by atmospheric general circulation models. J Atmos Sci 31:2216–2219
Christidis N, Stott PA, Zwiers FW, Shiogama H, Nozawa T (2010) Probabilistic estimates of recent changes in temperature: a multi-scale attribution analysis. Clim Dyn 34:1139–1156
Christidis N, Stott PA, Zwiers FW, Shiogama H, Nozawa T (2012) The contribution of anthropogenic forcings to regional changes in temperature during the last decade. Clim Dyn 39:1259–1274
Cramer W, Yohe GW, Auffhammer M, Huggel C, Molau U, da Silva Dias MAF, Solow A, Stone DA, Tibig L, et al (2014) Detection and attribution of observed impacts. In: Field CB, Barros VR, et al (eds) Climate change 2014: impacts, adaptation, and vulnerability. Part A: global and sectoral aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, pp 979–1037
Flato G, Marotzke J, Abiodun B, Braconnot P, Chou SC, Collins W, Cox P, Driouech F, Emori S, Eyring V, Forest C, Gleckler P, Guilyardi E, Jakob C, Kattsov V, Reason C, Rummukainen M, et al (2013) Evaluation of climate models. In: Stocker TF, Qin D, Plattner GK, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, pp 741–866
Gillett NP, Allan RJ, Ansell TJ (2005) Detection of external influence on sea level pressure with a multi-model ensemble. Geophys Res Lett 32:L19714. doi:10.1029/2005GL023640
Hannart A, Ribes A, Naveau P (2014) Optimal fingerprinting under multiple sources of uncertainty. Geophys Res Lett 41:1261–1268. doi:10.1002/2013GL058653
Hansen G, Stone DA (2015) Attributing observed climate change impacts to human influence. Nat Clim Change (in press)
Hansen J, Ruedy R, Sato M, Lo K (2010) Global surface temperature change. Rev Geophys 48:RG4004. doi:10.1029/2010RG000345
Harris I, Jones PD, Osborn TJ, Lister DH (2014) Updated high-resolution grids of monthly climatic observations—the CRU TS3.10 dataset. Int J Climatol 34:623–642
Hasselmann K (1979) On the signal-to-noise problem in atmospheric response studies. In: Shaw DB (ed) Meteorology of tropical oceans. Royal Meteorological Society of London, London, pp 251–259
Hegerl G, Zwiers F (2011) Use of models in detection and attribution of climate change. WIREs Clim Change 2:570–591
Hegerl GC, Hoegh-Guldberg O, Casassa G, Hoerling MP, Kovats RS, Parmesan C, Pierce DW, Stott PA (2010) Good practice guidance paper on detection and attribution related to anthropogenic climate change. In: Stocker TF, Field CB, Qin D, Barros V, Plattner GK, Tignor M, Midgley PM, Ebi KL (eds) Meeting report of the Intergovernmental Panel on Climate Change expert meeting on detection and attribution of anthropogenic climate change. IPCC Working Group I Technical Support Unit, University of Bern, Bern, Switzerland
Hewitson B, Janetos AC, Carter TR, Giorgi F, Jones RG, Kwon WT, Mearns LO, Schipper ELF, van Aalst MKea (2014) Regional context. In: Barros VR, Field CB, et al (eds) Climate change 2014: impacts, adaptation, and vulnerability. Part B: regional aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, pp 1133–1197
Hurrell JW, Hack JJ, Shea D, Caron JM, Rosinski J (2008) A new sea surface temperature and sea ice boundary dataset for the Community Atmosphere Model. J Clim 21:5145–5153
James R, Otto F, Parker H, Boyd E, Cornforth R, Mitchell D, Allen M (2014) Characterizing loss and damage from climate change. Nat Clim Change 4:938–939
Jones GS, Stott PA (2011) Sensitivity of the attribution of near surface temperature warming to the choice of observational dataset. Geophys Res Lett 38:L21702. doi:10.1029/2011GL049324
Jones GS, Stott PA, Christidis N (2013) Attribution of observed historical near-surface temperature variations to anthropogenic and natural causes using CMIP5 simulations. J Geophys Res 118:4001–4024. doi:10.1002/jgrd.50239
Jones PD, Osborn TJ, Briffa KR (1997) Sampling errors in large-scale temperature averages. J Clim 10:2548–2568
Jun M, Knutti R, Nychka DW (2008) Spatial analysis to quantify numerical model bias and dependence: how many climate models are there. J Am Stat Assoc 103:934–947
Karoly DJ, Wu Q (2005) Detection of regional surface temperature trends. J Clim 18:4337–4343
Kennedy JJ, Rayner NA, Smith RO, Saunby M, Parker DE (2011a) Reassessing biases and other uncertainties in sea-surface temperature observations since 1850 part 1: measurement and sampling errors. J Geophys Res 116:D14103. doi:10.1029/2010JD015218
Kennedy JJ, Rayner NA, Smith RO, Saunby M, Parker DE (2011b) Reassessing biases and other uncertainties in sea-surface temperature observations since 1850 part 2: biases and homogenisation. J Geophys Res 116:D14104. doi:10.1029/2010JD015220
Mahlstein I, Knutti R, Solomon S, Portmann RW (2011) Early onset of significant local warming in low latitude countries. Environ Res Lett 6:034009
Mastrandrea MD, Field CB, Stocker TF, Edenhofer O, Ebi KL, Frame DJ, Held H, Kriegler E, Mach KJ, Matschoss PR, Plattner GK, Yohe GW, Zwiers FW (2010) Guidance note for Lead Authors of the IPCC Fifth Assessment Report on consistent treatment of uncertainties. Intergovernmental Panel on Climate Change (IPCC). http://www.ipcc.ch
Matsuura K, Willmott CJ (2012) Terrestrial air temperature and precipitation: 1900–2010 gridded monthly time series (v3.01). Tech. rep., University of Delaware. http://climate.geog.udel.edu/~climate/html_pages/Global2011/index.html
New M, Hulme M, Jones P (2000) Representing twentieth-century space-time climate variability. Part II: development of 1901–96 monthly grids of terrestrial surface climate. J Clim 13:2217–2238
Niang I, Ruppel OC, Abdrabo MA, Essel A, Lennard C, Padgham J, Urquhart P, et al (2014) Africa. In: Barros VR, Field CB, et al (eds) Climate change 2014: impacts, adaptation, and vulnerability. Part B: regional aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, pp 1199–1265
Pennell C, Reichler T (2010) On the effective number of climate models. J Clim 24:2358–2367
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res 108:4407. doi:10.1029/2002JD002670
Reynolds RW, Smith TM (1994) Improved global sea surface temperature analysis using optimum interpolation. J Clim 7:929–948
Santer BD, Taylor KE, Gleckler P, Bonfils C, Barnett TP, Pierce DW, Wigley TML, Mears C, Wentz FJ, Brüggemann W, Gillett NP, Klein SA, Solomon S, Stott PA, Wehner MF (2009) Incorporating model quality information in climate change detection and attribution studies. Proc Natl Acad Sci 106:14778–14783
Schneider U, Becker A, Finger P, Meyer-Christoffer A, Ziese M, Rudolf B (2014) GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor Appl Climatol 115:15–40
Seneviratne SI, Nicholls N, Easterling D, Goodess CM, Kanae S, Kossin J, Luo Y, Marengo J, McInnes K, Rahimi M, Reichstein M, Sorteberg A, Vera C, Zhang X et al (2012) Changes in climate extremes and their impacts on the natural physical environment. In: Field CB, Barros V, Stocker TF, Qin D, Dokken DJ, Ebi KL, Mastrandrea MD, Mach KJ, Plattner GK, Allen SK, Tignor M, Midgley PM (eds) Managing the risks of extreme events and disasters to advance climate change adaptation. Cambridge University Press, Cambridge, pp 109–230
Shiogama H, Stone DA, Nagashima T, Nozawa T, Emori S (2012) On the linear additivity of climate forcing-response relationships at global and continental scales. Int J Climatol 33:2542–2550
Stone D, Auffhammer M, Carey M, Hansen G, Huggel C, Cramer W, Lobell D, Molau U, Solow A, Tibig L, Yohe G (2013) The challenge to detect and attribute effects of climate change on human and natural systems. Clim Change 121:381–395
Stott PA, Allen MR, Christidis N, Dole R, Hoerling M, Huntingford C, Pall P, Perlwitz J, Stone DA (2013) Attribution of weather and climate-related extreme events. In: Asrar GR, Hurrell JW (eds) Climate science for serving society: research, modelling and prediction priorities. Springer, Berlin, pp 307–337
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:485–498
Wigley TML, Barnett TP et al (1990) Detection of the greenhouse effect in the observations. In: Houghton JT, Jenkins GJ, Ephraums JJ (eds) Climate change. The IPCC scientific assessment. Cambridge University Press, Cambridge, pp 241–255
World Meteorological Organization (2014) Annex to the implementation plan of the global framework for climate services—climate services information system component. Switzerland, Geneva
Acknowledgments
The authors wish to thank members of the International Detection and Attribution Group and an anonymous reviewer for useful comments. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research, under contract number DE-AC02-05CH11231. GH was supported by a grant from the German Ministry for Education and Research. We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modeling groups for producing and making available their model output. We also thank the groups listed in Tables 1 and 3 for producing and making available their observational climate products.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Stone, D.A., Hansen, G. Rapid systematic assessment of the detection and attribution of regional anthropogenic climate change. Clim Dyn 47, 1399–1415 (2016). https://doi.org/10.1007/s00382-015-2909-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-015-2909-2