Extinction of the northern oceanic deep convection in an ensemble of climate model simulations of the 20th and 21st centuries

Abstract

We study the variability and the evolution of oceanic deep convection in the northern North Atlantic and the Nordic Seas from 1850 to 2100 using an ensemble of 12 climate model simulations with EC-Earth. During the historical period, the model shows a realistic localization of the main sites of deep convection, with the Labrador Sea accounting for most of the deep convective mixing in the northern hemisphere. Labrador convection is partly driven by the NAO (correlation of 0.6) and controls part of the variability of the AMOC at the decadal time scale (correlation of 0.6 when convection leads by 3–4 years). Deep convective activity in the Labrador Sea starts to decline and to become shallower in the beginning of the twentieth century. The decline is primarily caused by a decrease of the sensible heat loss to the atmosphere in winter resulting from increasingly warm atmospheric conditions. It occurs stepwise and is mainly the consequence of two severe drops in deep convective activity during the 1920s and the 1990s. These two events can both be linked to the low-frequency variability of the NAO. A warming of the sub-surface, resulting from reduced convective mixing, combines with an increasing influx of freshwater from the Nordic Seas to rapidly strengthen the surface stratification and prevent any possible resurgence of deep convection in the Labrador Sea after the 2020s. Deep convection in the Greenland Sea starts to decline in the 2020s, until complete extinction in 2100. As a response to the extinction of deep convection in the Labrador and Greenland Seas, the AMOC undergoes a linear decline at a rate of about −0.3 Sv per decade during the twenty-first century.

1 Introduction

During the past decades, the idea of a weakening and even collapsing Atlantic Meridional Overturning Circulation (AMOC) as a response to global warming, and its possible impact on the climate of Western Europe (Manabe and Stouffer 1999), has been a recurrent and heated debate within the climate community (Bryden et al. 2005). The main argument for a possible decline of the AMOC is the reduction of deep wintertime convective mixing in the northern North Atlantic. Without this deep convective mixing, the renewal of the North Atlantic Deep Water (NADW) is compromised (Dickson and Brown 1994), which, as a result, compromises the sustainment of the northern bottom branch of the thermohaline circulation (THC). This branch of the THC acts as the buoyancy-driven contributor to the AMOC but is not its main driver. Indeed, the AMOC is primarily sustained by mechanical energy input through wind-driven upwelling, gyre circulation, and wind and tidal vertical mixing (Kuhlbrodt et al. 2007; Medhaug and Furevik 2011). Therefore, it is likely that the potential extinction of deep convection in the northern hemisphere would not necessarily lead to a collapse of the AMOC (Marotzke and Scott 1999; Kuhlbrodt et al. 2007; Gelderloos et al. 2012). However, many studies show the important role of deep water formation in setting the strength and the variability of the AMOC, primarily through deep convective mixing in the Labrador Sea (Jungclaus et al. 2005; Kuhlbrodt et al. 2007; Gelderloos et al. 2012). Deep convection in the Nordic Seas is also reported to play a significant role, for instance, Langehaug et al. (2012) could link the variability of the AMOC to the variability of the overflows across the Greenland-Scotland Ridge. Moreover, models show a high degree of correlation between convection in the Labrador Sea and the variability of the AMOC at different time scales (Eden and Willebrand 2001; Biastoch et al. 2008).

In present-day climate conditions, it has been shown that the variability of deep convection in the Labrador Sea is largely driven by the North Atlantic Oscillation (NAO); through its influence on the wintertime buoyancy loss to the atmosphere (Latif et al. 2006; Frankignoul et al. 2009) (with positive NAO conditions promoting convective mixing). Furthermore, the transport of freshwater from the Fram Strait along the Greenland coast into the Labrador Sea is also known as a contributing factor to deep convection (Holland et al. 2001; Jungclaus et al. 2005; Koenigk et al. 2006). In a warmer climate, however, the deep convective mixing that occurs in the Labrador Sea and the Irminger Sea is expected to decline due to a warming and a freshening of the surface (Latif et al. 2006; Deshayes et al. 2007; Koenigk et al. 2007; Frankignoul et al. 2009).

Therefore, it is important to understand how the frequency and the intensity of episodes of deep convection will respond to global warming. Because of the coupled nature of the involved mechanisms, coupled climate models are well suited to study the interactions between deep convection and other climate-related processes. We address these issues by analyzing the data from a 12-member ensemble of historical and future climate simulations. These simulations were carried out with EC-Earth following the CMIP5 protocol. This paper is organized as follow. The model, the simulations and the method used to monitor oceanic deep convection are described in Sect. 2. Our results are presented in Sect. 3. We study the spatial distribution, the evolution, and the variability of north-hemispheric deep convection in our ensemble of simulations. A focus is given to the Labrador Sea convection, in particular to its link with the NAO and the causes of the extinction. The link between the Labrador Sea deep convection and the AMOC is also studied, as well as the fate of the AMOC in the twenty-first century. A summary and a conclusion are given in Sect. 4.

2 Model, simulations and convection indices

2.1 The EC-Earth model

The EC-Earth project is a multinational effort to develop a comprehensive earth system model. In this study we analyze simulations that were performed with version 2.3 of the model. EC-Earth comprises an atmosphere-land surface module coupled to an ocean-sea ice module (Hazeleger et al. 2010, 2012). The atmospheric component of EC-Earth is based on the Integrated Forecasting System (IFS) cycle 31r1 of the European Centre for Medium Range Weather Forecasts (ECMWF) with some improvements from later cycles, such as the land surface scheme H-TESSEL (Balsamo et al. 2009). IFS is used at a T159 spectral resolution (corresponding to 1.125°) with 62 vertical levels up to 5 hPa. The ocean component is the Nucleus for European Modeling of the Ocean (NEMO) version 2 (Madec 2008). NEMO uses the so-called ORCA1 configuration, which consists of a tri-polar grid with poles over northern North America, Siberia and Antarctica at a resolution of about 1°. A higher resolution of a third of a degree is applied close to the equator, and due to the definition of the poles, the resolution around the North Pole is slightly higher than 1°. 42 z-coordinates vertical levels are defined together with a partial-step representation of the bottom topography. The effects of the subgridscale processes (mainly the mesoscale eddies) are represented by an isopycnal mixing/advection parametrization as proposed by Gent and McWilliams (1990). The vertical mixing is parametrized according to a local turbulent kinetic energy (TKE) closure scheme (Blanke and Delecluse 1993). A bottom boundary layer scheme, similar to that of Beckmann and Döscher (1997), is used to improve the representation of dense water spreading. The Louvain-la-Neuve Sea Ice Model version 2, LIM2, (Fichefet and Maqueda 1997; Bouillon et al. 2009) is included in NEMO, with dynamics based on Hibler (1979) and thermodynamics based on Semtner (1976). The atmosphere-land surface module and the ocean-sea ice module are coupled through the Ocean Atmosphere Sea Ice Soil coupler (OASIS) version 3 ( Valcke 2006); the coupling frequency is 3 h.

In the present context of deep convection, it is important to note that the ocean components of state-of-the-art coupled earth systems like EC-Earth lack the ability to resolve convection due to their coarse horizontal resolution (Marshall et al. 1997; Marshall and Schott 1999). In order to mimic the effect of convection, and suppress static instabilities, parametrizations are used to artificially mix sea water properties vertically in the statically unstable portion of the water column (Cox 1984; Marotzke 1991). In NEMO, this is done by locally enhancing the vertical eddy diffusivity by a few orders of magnitude ($k_z=10\,\hbox {m}^{2}/\hbox {s}$). The mixed-layer depth is then estimated at each time step using the so-called turbocline depth criterion. The turbocline depth is the depth at which the vertical eddy diffusivity coefficient (resulting from the vertical physics alone, not the isopycnal part) falls below a given value (taken equal to 0.05 m²/s in NEMO). Moreover, note that since this version of EC-Earth lacks a continental ice-sheet component, the extra surface freshwater influx resulting from the melting of the Greenland ice-sheet is simply omitted.

2.2 Model simulations

The results presented in this paper are based on an ensemble of 12 numerical simulations of the climate. These simulations span the historical period and the twenty-first century and were performed with EC-Earth following the guidelines for the Coupled Model Intercomparison Project 5 (CMIP5, Taylor et al. 2012). The historical simulations were initialized in 1850 from different time slices taken 15 years apart over the last 200 years of a 600 year long pre-industrial control simulation (hereafter PI simulation). This PI simulation used 1850 greenhouse gas concentrations and aerosol forcing, and was the continuation of an initial spin-up simulation that was run for 440 years with present-day forcing. Following the CMIP5 protocol, these historical simulations were forced by observed greenhouse gas and aerosol concentrations until 2005. They were then extended until 2100, forced by both the RCP4.5 and the RCP8.5 anthropogenic greenhouse gas emission scenarios. RCP4.5 is a relatively low emission scenario while RCP8.5 is a strong emission scenario (Moss et al. 2010). They correspond to an increase (relative to the pre-industrial period) of the radiative forcing by $+4.5\,\hbox {W/m}^{2}$ and $+8.5\,\hbox {W/m}^{2}$ respectively by the year 2100. Note that for a few members, technical problems were encountered during the upload of some atmospheric fields to the ESGF¹ CMIP5 database. Consequently, sea-level pressure is only available for eight members, and the surface latent and sensible heat fluxes for nine members.

The climate of the model in present-day and in the PI simulation is described in more details by Hazeleger et al. (2012) and Sterl et al. (2012) for the ocean. An overview of the Arctic climate of the twentieth and twenty-first century as simulated by EC-Earth in these CMIP5 simulation is presented by Koenigk et al. (2013). Moreover, the evolution of the oceanic heat transport into the Arctic has been studied by Koenigk and Brodeau (2014).

2.3 Monitoring deep convection in a climate model

In the literature, different approaches have been used to monitor deep convection in ocean and climate models. They usually rely entirely on the mixed-layer depth (hereafter MLD) in winter. Some studies have used the deepest MLD in the convection region of interest (Schott et al. 2009; Yashayaev and Loder 2009), while others have used the surface area of the region where the MLD exceeds a reference depth (Lavergne et al. 2014). L’Hévéder et al. (2012) used both the vertical and horizontal extent of the convectively-mixed region as indices (but still as single indices). Oka et al. (2006) defined a convection index as the spatially-averaged MLD over the convection region of interest; which is equivalent to considering the whole mixed volume, as done by Koenigk et al. (2007). This mixed volume approach, while taking into account both the horizontal and the vertical extent of the mixed region, has the shortcoming that it does not exclude convective events with too shallow mixing to contribute to the formation of deep water. Therefore, in this study, we refine this mixed volume approach by only considering the convective mixing that occurs below a specific depth that we refer to as the depth criterion ($z_{crit}$). With other words, $z_{crit}$ is the minimum depth that convection has to reach to be considered as deep. We define an index for deep convection, hereafter referred to as the DMV (Deep Mixed Volume) index, as the mean mixed volume in March restricted to the points of the convection region located below $z_{crit}$ (Fig. 1). Therefore, the DMV is equal to zero when the mixed-layer in March is shallower than $z_{crit}$ in the entire box. For convenience, the DMV is expressed in Sverdrups (Sv), as a mixed volume for a time period of 1 year. Note that because we use monthly averaged ocean fields, deep convection episodes that exceed $z_{crit}$ during a period shorter than 1 month can be missed since the monthly-averaged MLD might turn out to be shallower than $z_{crit}$. Moreover, the binary and strongly discontinuous nature of deep convection (periods of several consecutive years without deep convection are possible) might limit the usefulness of the DMV for some statistical analysis such as correlations. To overcome this problem, we also use the mixed volume approach by defining the MV index, which is equivalent to the DMV based on a depth criterion equal to zero. Contrarily to the DMV, the MV index cannot be equal to zero during winters with shallow convective mixing, which ensures the continuous behavior of the index.

There is no clear consensus in the literature on the actual depth that convective mixing has to reach to be considered as deep. Therefore, the choice of the depth criterion for the DMV has to be somewhat arbitrary. In our study, we follow a definition of deep convection by Marshall and Schott (1999): violent and deep-reaching convection that mixes surface waters to great depth, setting and maintaining the properties of the abyss. This definition is consistent with the topic of this study, namely the response of the THC to global warming and its impact on the AMOC. The choice of $z_{crit}$ should therefore be dependent on the convection region, because the deep water masses to be renewed are not necessarily found at the same depth.

In the Labrador Sea, the convection should reach a depth at which it is able to sustain the renewal of Labrador Sea Water (LSW) that will eventually become NADW after traveling eastward and southward and being mixed with denser and deeper water masses originating from the overflows (Greenland-Scotland Ridge). Based on observations, Yashayaev (2007) mentions that this process is possible if convection in the Labrador Sea reaches a minimum depth of 1000 m. Therefore, we define $z_{crit}$ as 1000 m in the Labrador Sea. Note that this is consistent with EC-Earth, in which the maximum of the AMOC is found slightly above 900 m.

In the Nordic Seas, however, and more generally in any convection site located north of the Greenland-Scotland Ridge, the depth at which dense water is found is controlled by the depth of the overflows at the Denmark Strait and Faroe Banks Channel. Therefore, the minimum depth requirement would be that convection has to exceed the depth of the Denmark Strait sill, which is about 600 m in the model (slightly deeper in reality). Based on the last 100 years of the PI simulation, we find that the mean potential density of the seawater overflowing at the Denmark Strait is $\sigma _0=27.98$. In observations this value is slightly higher, between 28 and 28.05 (Nikolopoulos et al. 2003). The depth of the sill of the Faroe Banks Channel is 880 m in EC-Earth, and the simulated potential density of overflowing seawater reaches $\sigma _0=28.02$. Now, because the enhanced vertical diffusivity approach used to parametrize convection in the model is non-penetrative, the potential density of seawater inside a convective chimney (assuming a uniform $\sigma _0$ in the whole chimney) that extends down to the isopycne $\sigma _0$, is denser or at least equal to $\sigma _0$ and is therefore able to sustain the renewal of the deep water mass of density $\sigma _0$. Therefore, as a compromise between the potential density of seawater overflowing at the Denmark Strait and Faroe Banks Channel sills in the model, we will consider convection in the Nordic Seas to be deep if it exceeds the depth at which the isopycne $\sigma _0=28.0$ is found. Technically, we choose $z_{crit}$ as the depth of the model grid point that is the closest to the isopycne $\sigma _0=28.0$ inside the Greenland-Iceland-Norway Seas (GIN box in Fig. 2). Based on the last-100-year mean of the PI simulation, this depth is $z_{crit}=725\,\hbox {m}$ ($\sigma _0=27.997$). Note that the sensitivity of our results to the choice of $z_{crit}$ will be discussed whenever possible.

3 Variability and fate of north-hemispheric deep convection in EC-Earth

In this section we discuss the spatial distribution, the temporal evolution and the variability of deep convection in the sub-polar gyre and the Nordic Seas. Then, we focus on Labrador Sea deep convection (hereafter referred to as LSDC). We first study the implication of the NAO and the surface heat flux on the variability of LSDC before analyzing the cause of the decline and extinction of LSDC. Finally, the link between LSDC and the AMOC, as well as the response of the AMOC to the decline and the extinction of north-hemispheric deep convection is discussed. Note that we chose 1850–1990 as the reference period for the historical simulations because the final collapse of LSDC occurs during the 1990s (this will be discussed in this section).

3.1 Comparison of deep convection in EC-Earth and observations

Analysis of the winter MLD in the 12 historical simulations shows that episodes of deep convection occur in the following regions: Labrador Sea, Irminger Sea, Iceland basin, northwest of Scotland and in the Greenland Sea (Fig. 2). In these regions, the mixed-layer is typically deepest during March. On average, based on the historical mean, the March MLD reaches almost 1400 m in the Labrador Sea, about 1000 m in the Irminger Sea, and slightly less than 800 m in the Greenland Sea. These simulated sites of deep convection coincide relatively well with observations (Dickson et al. 1996; Marshall and Schott 1999; Bacon et al. 2003; Pickart et al. 2003), but the deep-mixing that occurs north-west of Scotland in the model seems to be somewhat overestimated. Figure 3 compares the ensemble mean of the model MLD in March and observations from Argo² profiles (Holte et al. 2010), and shows that the convection site in the Labrador Sea is slightly misplaced to the southeast. This shift in the location of LSDC is a common feature of coarse resolution models (Jungclaus et al. 2005; Oka et al. 2006). Note that the observational data need to be used with some care since they cover a short period of time and are based only on a single or just a few Argo profiles at each grid point. From an analysis of the individual ensemble members, we find that during years with enhanced deep convection, and regardless of the convection site, convective mixing tends to go unrealistically deep and often reaches the bottom (see Fig. 13 for LSDC); which is also a common feature of ocean GCMs (Treguier et al. 2005; Oka et al. 2006). Together with the MLD, Fig. 3 also shows the ice edge in March in observations from the NSIDC³ (Cavalieri et al. 1996) and model simulations. The deepest mixed-layer occurs relatively near to the ice edge in both observations and EC-Earth. However, EC-Earth simulates too much ice in the Labrador and Nordic Seas, which can be related to the misplacement of deep convection compared to observations. It remains unclear, particularly for the Labrador Sea area, if the excessive eastward extent of sea-ice in EC-Earth is the cause or the consequence of the shift of the convection site. Results from Koenigk et al. (2013) showed that the Arctic atmospheric two-meter air temperature is generally about one to two degrees colder in EC-Earth than in ERA-interim reanalysis data, which might indicate that the southward shift of the ice edge is related to this cold bias. On the other hand, a study by Deser et al. (2002) indicated the importance of deep water formation for the position of the ice edge in the Labrador Sea.

3.2 Temporal evolution of deep convection in the twentieth and the twenty-first century

Based on the historical ensemble mean of the simulated MLD in March (Fig. 2), we define the horizontal boxes used to monitor deep convection with the DMV and MV indices defined in Sect. 2.3. First, located south of Greenland, the Labrador box includes the simulated LSDC area. The Ice-Scot box includes the convection sites of the Irminger Sea, Iceland basin and west of Scotland. The GIN box includes most of the Greenland-Iceland-Norway Seas. A fourth box, labeled Nansen, centered north-east of Franz Josef Land is added to monitor the onset of deep convection over the Nansen basin in the second half of the twenty-first century (Fig. 4e). As discussed in Sect. 2.3, we chose the depth criterion of 1000 m for the Labrador and Ice-Scot boxes and 725 m in the GIN and Nansen boxes.

As shown in Figs. 4 and 5, in EC-Earth, the Labrador Sea is by far the largest contributor to deep convective mixing in the northern hemisphere during the historical period, with a mean deep mixed volume of about 3.5 Sv, which is three times more than in the GIN Seas. This is due to both deeper convective mixing and a typically larger horizontal extent of the convection area. This is in good agreement with observations, which indicate that the largest amount of dense water in the North Atlantic is formed in the Labrador Sea (Talley and McCartney 1982; Dickson and Brown 1994; Rhein et al. 2002; Yashayaev 2007; Schott et al. 2009). During the early historical period, it is also the region where deep convection is more likely to occur in a given winter as shown in Table 1. Figure 5 shows that convection is most intense between 1850 and 1920 in all three main convection sites of the North Atlantic. After 1920, the convection in the Labrador and the Ice-Scot areas shows a marked drop until 1930. Thereafter, the ensemble mean of the deep convection is rather constant until about 1990 and 1970 in the Labrador Sea and Ice-Scot areas, respectively. This is followed by further decrease and a total extinction at about 2030 in the Labrador Sea and slightly earlier in the Ice-Scot region. In contrast to this, convection is relatively stable in the GIN Seas until the 2020s. Thereafter, a steady decline occurs and convection disappears totally in RCP8.5 at the end of the twenty-first century; however, in the RCP4.5, GIN Seas deep convection (hereafter GSDC) stabilizes on a lower level. Figure 4 shows that the areas of strongest convection in the Labrador Sea and Ice-Scot area are spatially robust. This is different in the GIN Seas, where the convection area moves northward together with the northward moving ice edge. At the end of the twenty-first century, as a consequence of sea-ice-free winters, a new convection site appears in the Nansen Basin in RCP8.5 (Figs. 4e, 5d). During the period of enhanced convective activity (1850–1920), the probability of occurrence for convection in a given winter is 70 % for the Labrador Sea and about 60 % in the GIN Seas and the Ice-Scot area (Table 1). In the Labrador Sea and the Ice-Scot area, this is also to the period with the deepest convective mixing, with a mean depth of about 1500 m in the Labrador Sea (Fig. 4a). During this period, the shutdowns of LSDC are short, they typically do not last longer than one winter and never exceed four consecutive winters (Fig. 6). Following the 1920s’ drop, the probability of deep convection in the Labrador Sea and the Ice-Scot area decreases substantially. The duration of the shutdowns of LSDC is also slightly increased and shutdowns of almost one decade become possible (Fig. 6). In the GIN Seas, however, the probability of deep convection remains rather stable and even increases in the first half of the twenty-first century, but goes along with a northward shift of the convection site and deeper mixing (compare Fig. 4b, d). With the RCP8.5 scenario, in the end of the twenty-first century, deep convective activity only subsists north of 75°N, mostly in the Nansen basin and very weakly in the GIN Seas (Figs. 4, 5).

Note that these results are almost independent of the depth criterion for the LSDC (see the DMV’ index in Fig. 5a). However, the analysis of the duration of the shutdowns, shown in Fig. 6, turns out to depend on the depth criterion used. Their duration is shortened when using a shallower depth criterion, but we found a similar trend towards longer shutdowns (not shown). The use of a deeper criterion to monitor GSDC also leads to slightly different results (see the DMV’ index in Fig. 5b). For instance, the resurgence of GSDC in the 2000s is not captured with the deeper criterion of 1000 m.

3.3 Variability of deep convection in the historical simulation

In EC-Earth, just as observations suggest, LSDC is subject to unpredictable and strong variability, with the resumption of deep convection after shutdowns of sometimes several years. Note that the likelihood of shutdowns of about one decade in the model increases with global warming (Fig. 6), but seems to be underestimated with regards to observations. For example, Yashayaev and Loder (2009) showed that 2008 was the first year with deep convection in the Labrador Sea since 1994. As a consequence of this strong year-to-year variability, and due to the binary nature of deep convection, the ensemble mean of the DMV exhibits a very strong interannual to interdecadal variability despite the reasonable size of the ensemble. The spread of the ensemble is very large, typically of the same order as the DMV itself (Fig. 5). 12 members are clearly not enough to smooth out the natural variability and only retain the forced variability of deep convection. Interestingly, the ensemble mean of the Labrador DMV exhibits pronounced decadal fluctuations during the first five decades of the historical simulations (Fig. 5a). To investigate if this is due to noise or to an artifact of the initialization of the ensemble members from the PI simulation, each historical member was extended back in time with the relevant slice of the PI simulation. We did not find any initial discontinuity at the start of the historical members. However, it turns out that the 200-year long slice of the PI simulation used to initialize the historical members shows a peak in the spectrum of the Labrador DMV at 15 years (Fig. 7a). Since the historical simulations started exactly every 15 years from the PI simulation, most historical members initiated during a similar phase of the Labrador DMV at year 1850. After a few decades, noise and maybe also the impact of changing the external forcing degrade these variations of the ensemble mean Labrador DMV. Note that the 15-year oscillation is not robust when using not only the last 200 years but the last 500 years of the PI simulation. This peak at 15 years is in good agreement with the peak at 13 years that Oka et al. (2006) found for the MLD in the Labrador Sea in a 600-year long coupled simulation. During the historical period, LSDC undergoes a significant decadal oscillation with a peak at 15–18 years (Fig. 7b). These timescales fit relatively well to the 20-year variability of the sub-polar gyre found in a recent study by Escudier et al. (2013). Also Langehaug et al. (2012) showed a link between decadal variations in the sub-polar gyre and decadal variability in the Labrador Sea Water, as well as in atmospheric patterns, such as the East Atlantic Pattern and the NAO. The link between the NAO index, the related surface heat fluxes, and the Labrador Sea convection in our model, will be analyzed in detail in the next section.

When it comes to GSDC, the only significant decadal oscillation found during the last 200 years of the PI simulation corresponds to a period of 20 years (Fig. 7c). During the historical period, based on the ensemble, GSDC shows two distinct peaks at respectively 13 and 20 years, but nothing significant at 18 years where LSDC shows its main peak (Fig. 7b, d). This suggests that the correlation between convection in the two sites is low. This is confirmed by correlation analysis: with a 95 % confidence level of roughly 0.1 (a reduced sample size which takes into account the lag-1 auto-correlation of the convection indices is assumed) we find that the correlation between Labrador and GIN convection indices (using both the DMV and MV indices) is negative albeit barely significant. Typically, the ensemble mean of the anti-correlation never exceeds 1.5 regardless of the time slice of the historical period used. In contrast to our results, Dickson et al. (1996) showed that a strengthening of the convective activity in the Labrador Sea can be related to a weakening of the convective activity in the Greenland Sea (from the 1970s to the 1990s). Indeed, Oka et al. (2006) found a seesaw relationship between the convection in the Labrador Sea and in the GIN Seas in their coupled model. There does not seem to be such a seesaw relationship in EC-Earth.

3.4 Influence of surface heat flux and NAO in the Labrador Sea

NAO is the dominant pattern of climate variability in the North Atlantic (Hurrell 1995; Visbeck et al. 2003). Positive NAO winter conditions enhance northerly winds over the Labrador Sea and the southward transport of cold air; this leads to enhanced heat release from the ocean, and by densifying surface water, to enhanced convection. During negative phases of the NAO, however, winter conditions in the Labrador Sea are anomalously warm since less cold air is advected from the ice-covered Arctic. Consequently, the upper ocean is not sufficiently cooled and the surface stratification remains too pronounced, which tends to suppress LSDC (Dickson et al. 1996; Curry et al. 1998; Visbeck et al. 2003; Latif et al. 2006; Yashayaev 2007). In some models, it has also been shown that the NAO is the dominant atmospheric mode that forces the AMOC (Eden and Willebrand 2001; Deshayes and Frankignoul 2008; Kwon and Frankignoul 2011).

Here, the NAO index is constructed as the difference between the mean wintertime (JFM) sea-level pressure anomalies between the Azores (Portugal) and Reykjavik (Iceland) (Hurrell 1995) (Fig. 8a). The pressure anomalies are standardized about 1850–1990 [Hurrell (1995) normalized about 1864–1994].

In EC-Earth, the wintertime heat loss to the atmosphere over the Labrador Sea is significantly correlated with the NAO (Table 2). Nevertheless, the correlation of roughly 0.75 indicates that winter heat loss is not entirely controlled by the NAO and that the stratification of the surface might also play a significant role. For example, following a freshening of the surface in the convection site, the temporary shutdown of convection will promote the stagnation of a relatively fresh and cold surface layer in winter, which, will limit the heat loss to the atmosphere, even though this occurs during a period of high NAO. As expected, the convective mixing (as monitored by the MV index), is also positively correlated with the surface heat loss (Table 3). Here too, the correlation, slightly larger than 0.7, indicates that convection is not entirely driven by the surface heat loss. In Sect. 3.5 we will show that the late autumn stratification of the water column in the convection site is important as well. Consequently, we find a positive, yet weaker correlation between the convective mixing (MV) and the NAO (Table 2) with values ranging from 0.5 up to 0.6 during the historical period and the early twenty-first century (Table 2). This correlation also emerges over the decadal time scale in Fig. 8a, in which, at least before the twenty-first century, periods of high NAO generally coincide with periods of increased convective activity. The correlation between LSDC and NAO is found to be relatively stable across ensemble members. The same correlation is lower when using the DMV rather than the MV, but remains significant (about 0.45).

In the twenty-first century, winters with a positive NAO index become more frequent in EC-Earth, and the mean NAO index increases to 0.2 and 0.4 until 2000–2050 and 2050–2100, respectively (Fig. 8a). Cattiaux et al. (2013) showed, that the frequency of both NAO+ and NAO- winter weather regimes increases in future simulations with CMIP5 models. However, in contrast to our model, about two third of the analyzed CMIP5 models in Cattiaux et al. (2013) show a trend towards a more negative winter mean NAO index in the twenty-first century. Therefore, EC-Earth, by simulating winters with an increased probability for positive NAO in the twenty-first century, tends to generate conditions more conductive to LSDC than some other CMIP5 models do. However, this does not prevent the extinction of LSDC, which is discussed in Sect. 3.5. At some point, in the early twenty-first century, the surface warming over the Labrador Sea has become such, that even winters with a very high NAO index are unable to trigger the onset of deep convection.

3.5 Extinction of Labrador Sea deep convection

There are two main mechanisms that can prevent deep convection from occurring during a given winter. The first mechanism is what we will refer to as bad preconditioning: the stratification of the water column is so pronounced in autumn that it compromises the onset of convection and its potential deepening during the winter to come. In this case, the presence of the anomalously buoyant surface layer can have two origins: insufficient buoyancy loss to the atmosphere during the past year(s) or a lateral influx of buoyant water converging into the convection site at the surface (Straneo 2006). Another possible cause for bad preconditioning is the absence of so-called remnant convected Labrador Sea Water below the surface layer due to the absence of convection during the previous winter(s) (Våge et al. 2009). The lack of vertical mixing during these winters without deep convection prevents the subsurface from being cooled. As a result, the subsurface warms up, which further undermines the preconditioning. Therefore, once deep convection has stopped, its resumption becomes increasingly more difficult. We will refer to this positive feedback as the shutdown feedback.

The second mechanism that can prevent deep convection from occurring is what we will refer to as mild winter conditions: the surface heat loss to the atmosphere in autumn and winter, which is supposed to first destabilize the water column and then sustain convection, is too weak due to insufficiently cold surface atmospheric conditions. As discussed in the previous section, this can be the case in the Labrador Sea during winters with a negative NAO index, or as a result of severe global warming.

Ultimately, the actual cause of a shutdown of deep convection often turns out to be a combination of these two mechanisms. Such a combination has been reported by Lazier (1980) to have caused the shutdown of LSDC in the late 1960s and early 1970s, and which coincided with both a freshwater anomaly and low NAO winter conditions. Indeed, many authors have linked past and present-day shutdowns of LSDC to pronounced freshwater anomalies and persisting low NAO winter conditions (Gelderloos et al. 2012), but it remains unclear to what extent each of these two mechanisms actually contribute.

As shown in Fig. 5a, the decline and the extinction of LSDC in EC-Earth occur stepwise, mainly during two relatively short periods of roughly one decade each: the 1920s and the 1990s. During each of these two decades, the DMV index drops by almost 2 Sv.

The 1920s’ drop of deep convective activity in the Labrador Sea follows a transition (in the 1910s) from two decades with positive winter NAO conditions to four decades with negative conditions (Fig. 8a). Over the Labrador Sea, this switch in the sign of the mean winter NAO state leads to an increase of winter surface air temperature by 1 °C between 1910 and the early 1920s (Fig. 9a). These milder winter conditions limit the heat loss to the atmosphere, mostly by reducing the sensible heat flux (Fig. 9a, b). Due to a relatively cold and saline surface layer during the 1910s (Figs. 10, 11), it takes several years for these milder winters to have a negative impact on convection. In the early 1920s, though, with the persisting negative NAO conditions, the shutdown feedback is eventually triggered, leading to a drop in deep convective activity and a warming of the surface layer. Between 1930 and the mid-1950s, a freshening of the surface layer helps maintain a pronounced stratification, even though the surface layer is not warming anymore (Fig. 10), which limits convective activity until the mid-1950s. This freshening is caused by an increase in the surface lateral freshwater import from the East-Greenland Current (hereafter EGC) in the Labrador Sea (transect LNE 0–104 m in Fig. 12c). In EC-Earth, this period with relatively weak LSDC and negative NAO also coincides with a warming of the North Atlantic region (0–60°N, 7.5–75°W, not shown). A similar warming period has been found by Booth et al. (2012) in the HadGEM-model, followed by a cooling after 1955, and can also be seen in observations. Booth et al. (2012) related these variations in the North Atlantic to the observed varying aerosol forcing. However, the warming in EC-Earth starts a few years earlier, and the cooling slightly later, and is less pronounced in EC-Earth than in HadGEM and observations. Thus, it is unclear if the same mechanism is working in EC-Earth or if this period is purely due to natural variations in the model. During this period, strong episodes of convection have already become half as likely as in the late nineteenth century, while their depth has been remaining relatively stable (Fig. 13). In the mid-1950s, the return of winters with positive NAO, together with a salinification of the surface, are able to overcome the ongoing warming of the surface layer, and allows a brief resurgence of LSDC during the 1960s.

The 1990s’ collapse of LSDC coincides with an increase of the buoyancy of the surface layer in late autumn (Fig. 10), which indicates that bad preconditioning is involved. Figures 10 and 11 show that this increase of the surface buoyancy is mainly caused by a warming as no anomalous freshening of the surface has yet occurred. Prior to the collapse of LSDC, during the 1980s, winters with unusually strong positive NAO conditions (Fig. 8a) maintain the winter heat loss to the atmosphere at a value sufficiently high to sustain convection, despite the ongoing surface warming. During the 1980s, LSDC also benefits from a deficit in the lateral flux of heat (Fig. 12a), which is due to a cooling of the EGC initiated in the mid 1970s and is maximal in the mid-1980s (not shown). In the late 1980s, the NAO index returns to more neutral and slightly negative values for two decades. As a result, due to milder winters, the heat loss to the atmosphere, that had overcome the ongoing warming and remained more or less constant during the 5 previous decades, is decreased by almost $20\,\hbox {W/m}^{2}$ in a few years (Fig. 9a). Between 1989 and 1991, the resulting heat gain for the Labrador box is $+0.01\,\hbox {PW}$. Meanwhile, the EGC has started to recover from its mid-1980s cold anomaly and is warming up at high rate. This is seen as positive lateral flux of heat for the Labrador box (increase of $+0.015\,\hbox {PW}$ between 1986 and 1990). These milder winter conditions, together with the momentary increase of the lateral influx of heat, trigger the shutdown feedback in the early 1990s, which leads to the shutdown of deep convection and a rapid warming of the surface layer (Figs. 10, 11b). This period coincides with the overall warming of the Labrador Sea that begins in 1990 (see $\varDelta HC/\varDelta t$ in Fig. 12a). The sea surface is warming but the surface air is warming at an even higher rate (Fig. 9a, c). This causes the winter heat loss to the atmosphere to continuously decrease at a rate of almost $1\,\hbox {W/m}^{2}$ per year, mainly due to the decrease of the sensible heat flux (Fig. 9b). Meanwhile, due to the absence of deep convective mixing in winter, the subsurface also starts to warm up from the late 1990s onward (see below 100 m in Fig. 11b), making the resumption of LSDC more and more unlikely. Indeed, the warming of the subsurface, which occurs below 100 m, coincides with the quasi-disappearance of LSDC that follows the collapse. In the mid-2000s, the warming can already be felt under 1000 m.

The steady decrease in the difference between the SST and the two-meter air temperature in winter (Fig. 9a), which continuously reduces the sensible heat loss to the atmosphere (Fig. 9b), plays an important role in preventing the resumption of deep convection from the end of the twentieth century onward. There are two main reasons behind this decrease of the winter air-sea temperature gradient. First, the arctic amplification leads to a warming of the air masses that are advected from the north into the Labrador Sea region. Second, in the future simulations, due to the northward retreat of the sea ice edge, the same air masses have to travel a longer distance over the relatively warm ocean, and are thus warmer when they enter the Labrador Sea area. The ocean surface, in contrast, is warming at a much lower rate, partly due to the absence of convective mixing that tends to promote the stagnation of a thin, cold, and fresh surface layer in winter. Also, it has been shown that the oceans are generally warming at a lower rate than the Arctic and land areas (Stocker et al. 2013).

Following the 1990s’ collapse, and according to the DMV index, the total extinction of LSDC occurs in the 2020s (Fig. 5a). With regards to the historical period, this post-collapse period is characterized by longer shutdowns of LSDC (Fig. 6), the quasi-absence of strong convection episodes, and shallower convective mixing (about 400 m shallower than in the early historical period, Fig. 13). By defining the year of extinction as the last year of the RCP8.5 simulation with a DMV index larger than 0.1 Sv, we find that the complete extinction of LSDC occurs in 2022, with a standard deviation of 8 years between members. When the shallower depth criterion of 725 m is used, the extinction is delayed to 2040 with a standard deviation of 8.5 years. The extinction is partly caused by the rapid freshening of the surface layer initiated in the early twenty-first century (Figs. 10, 11c). This freshening adds up to the ongoing warming of the surface to strongly increase the surface buoyancy throughout the twenty-first century, preventing any possible resurgence of LSDC. The same absence of convective mixing that causes the warming of the subsurface prevents the excess of freshwater in surface layer to be mixed downwards, restricting the freshening to the first few hundred meters (Fig. 11c), which further enhances the surface stratification. Between 2020 and the mid-2060s, the freshening of the first 100 m of the Labrador Sea corresponds to an increase of the influx of freshwater of 0.02 Sv. During the same period, the increase in the term P-E only accounts for one fifth of this (increase by <0.004 Sv, see Fig. 9c), suggesting that the freshening is mainly caused by lateral advection of freshwater from the surrounding seas. As shown in Fig. 12b, the Labrador box renews much of its water via the EGC (transect LNE) and its western boundary (transect LW). Between the 2020s and the 2060s, the freshening of the EGC causes a doubling of the lateral influx of liquid freshwater through the transect LNE (from 0.05 Sv to almost 0.11 Sv, see Fig. 12c). This is also true for the first 100 m, even though the freshwater import is only increased by a factor of 1.6. Also, the freshwater influx through the western boundary slightly increases. The decrease in the term P-E (Fig. 9c) is caused by both an increase of the evaporation and a decrease in precipitation (the increase of evaporation contributes to two third to the decrease of P-E).

3.6 Implications for the AMOC

In EC-Earth, the AMOC is weaker than observation-based estimates. The ensemble mean of the AMOC and the inter-member spread in EC-Earth is compared to observations from the RAPID array at 26°N (Duchez et al. 2014) between 2005 and 2013 in Fig. 8b. The mean value for RAPID is 16.9 Sv while it is 14.7 Sv in EC-Earth. At 24°N, both Ganachaud (2003) and Lumpkin and Speer (2007) give estimates of 18.5 Sv ($\pm 2\,\hbox {Sv}$). At 48°N, the estimate of Ganachaud (2003) is $16\pm 2\,\hbox {Sv}$ against roughly 13 Sv for EC-Earth in the 1990s. The AMOC in EC-Earth is slightly outside the error interval found in the literature but is in the range of estimates from coupled GCMs (Drijfhout et al. 2011; Weaver et al. 2012).

During the historical period, the interdecadal variability of the AMOC suggests a delayed response to LSDC (Figs. 8b, 5a). For example, the fingerprints of both the initial oscillatory pattern (1850–1900) and the resumption of LSDC in the 1960s can be identified in the AMOC, particularly at 48°N. Eden and Willebrand (2001) and Biastoch et al. (2008) found strong correlations between LSDC and the interannual to decadal variability of the AMOC with their respective models. Koenigk et al. (2006) found no significant correlation between surface salinity in the Labrador Sea (which affects the density of the surface waters and thus ocean stratification and deep water formation in the Labrador Sea) and the AMOC in ECHAM5/MPI-OM at interannual time scales. Häkkinen (1999), instead, argues that there is also such a relation on interannual time scales. The basic understanding is that there is a high correlation at longer timescales because it takes several years to consume the reservoir of deep water in the Labrador Sea, which is formed during winters with strong convection. Thus, a single winter with or without convection does not necessarily have a strong impact on the AMOC. However, episodes of several years with or without deep convection can strongly affect the AMOC (Jungclaus et al. 2005; Mikolajewicz et al. 2005). Spectral analysis shows that the variability of the model AMOC in mid-latitudes is dominated by low-frequency (interdecadal) oscillations (Fig. 7e, f), with a signal somewhere between white noise ($A(f)=cst$) and pink noise ($A(f)=1/f$). During the last 200 years of the PI simulation, the significant peak at 15 years is in excellent agreement with what we found for LSDC (Fig. 7a). For the ensemble historical mean, just as for LSDC, this timescale is extended by a few years with a peak centered at 18 years (Fig. 7b, f). These spectral similarities between LSDC and the AMOC highlight a link at the decadal time scale in the model. Therefore, we study the cross-correlation between the maximum of the AMOC at different latitudes and the Labrador DMV using smoothed time series (Fig. 14). The positive and significant correlations (at the 95 % confidence level) when convection leads by a few years, confirms that in EC-Earth, LSDC has a positive and delayed impact on the AMOC. For the historical period, the highest correlation is 0.6 and is found between 45 and 50°N when convection leads by 3 or 4 years. This correlation depends weakly on the choice of the depth criterion. Indeed, correlations using the MV index show a similar pattern as in Fig. 14, with comparable and slightly lower values (0.58 at 45° when AMOC leads by 5 years). Correlations at the interannual time scale (using non smoothed time-series), however, are lower but still significant, with a maximum value of 0.39 at 50°N when the convection is leading by 1 year (not shown). Thus, in EC-Earth, LSDC has a significant impact on the strength of the AMOC, with a delay ranging from a couple of years up to a decade. Interestingly, it also suggests that this delay increases linearly as the latitude decreases: the further away from the latitudes of the Labrador Sea (i.e. the closer to the Equator) the longer the delay. Note that the same correlations calculated for the last 200 years of the PI simulation do not show higher values.

The negative correlation shown in the negative lag domain of Fig. 14 is barely significant at the 95 % confidence level, but it suggests that the AMOC also applies a negative feedback on LSDC. A strong AMOC tends to enhance the poleward transport of warm surface waters towards the sites of convection, which, in return, hinders the onset of deep convection by increasing the stratification (Danabasoglu 2008; Delworth and Zeng 2012). This anti-correlation is only significant at 55°N when AMOC leads convection by 9 years: −0.34 and is not higher in the last 200 years of the PI simulation.

In response to the warming caused by an increasing atmospheric CO2 concentration, most climate models predict a decline of the AMOC (Gregory et al. 2005), often linked to a reduction in the rate of formation of LSW (Stouffer et al. 2006). In EC-Earth, following the 1990s’ collapse and the extinction of LSDC, the AMOC undergoes a steady decline during the whole twenty-first century at a rate of about 0.3 and 0.4 Sv per decade at respectively 26 and 48°N (Fig. 8b). With the RCP4.5 emission scenario, however, the decline of the AMOC is halted around 2050 and slightly recovers during the second half of the 21st century.

4 Summary and conclusion

This study focused on the variability and the possible future development of oceanic deep convection in the northern North Atlantic using an ensemble of 12 historical and future emission scenarios simulations with EC-Earth.

A new index, that only takes into account the deep part of the convectively-mixed volume in March, was defined in order to study the evolution and the possible extinction of deep convection in the main convection sites of our model, namely Labrador Sea, GIN Seas and Scotland-Iceland region. The definition of this index is based on deep water renewal considerations and is thought to be more consistent with the requirement of a sustainment of the northern branch of the thermohaline circulation.

During the historical period, convection in the Labrador Sea accounts for most of the deep water formed in the northern hemisphere, while the GIN Seas and the Iceland-Scotland area contribute to a much lesser extent. The interannual variability among ensemble members is large in all regions and the probability for deep convection in a random year at the end of the nineteenth century is 59 % in the Iceland–Scotland area, 63 % in the GIN Seas, and 70 % in the Labrador Sea. Throughout the twentieth century, and except for the GIN Seas deep convection, this probability is substantially reduced, particularly from the late twentieth century onward. Also the convection depth of individual events is reduced, but less rapidly than the occurrence.

The decline of deep convection in the Labrador Sea starts in the early twentieth century and is mainly the consequence of two successive one-decade-long drops that occur in the 1920s and the 1990s. The typical duration of shutdowns of Labrador Sea deep convection increase from 1.6 years in the early historical period to 4 years during the early twenty-first century, and implies a maximum of 4 and 12 consecutive years without deep convection, respectively. Following the 1990s’ collapse, deep convection in the Labrador Sea almost completely ceases but remains possible until the complete extinction that occurs in the early 2020s with the RCP8.5 forcing. In the Iceland–Scotland area, the decline and extinction of deep convection follows a very similar pattern with a complete extinction by 2020. In the GIN Seas, however, the convection site is displaced poleward and deep convection starts to decline steadily from the 2020s onward, until its extinction at the very end of the twenty-first century. Around 2060, a new area with deep convection forms in the Nansen Basin with the high emission scenario RCP8.5, made possible by a year-round loss of sea ice in this area. However, this deep convection area only exists for about 20–30 years before increased surface temperatures lead to an extinction of convection again. Under the assumption of the RCP4.5 emission scenario, the complete extinction of deep convection in the Labrador Sea and the Iceland–Scotland area is only delayed by a few years, while it is prevented in the GIN Seas, with a convective activity remaining at about half of its early historical level. The main reason for the very limited impact of the RCP4.5 forcing with regards to RCP8.5 is that greenhouse gas concentrations do not differ much between the different RCP-scenarios in the first decades of the twenty-first century. Thus, deep convection already collapsed before a possible stabilization effect in the lower emission scenario RCP4.5 could begin. The deep convection in the Nansen Basin does not occur in the RCP4.5 simulations, probably due to the slower retreat of sea ice.

In the historical period, the NAO and the related surface heat flux over the Labrador Sea are the main driver of the interannual variability of deep convection. The positive and significant correlation between NAO and Labrador Sea convection remains constant throughout the simulations as long as convection exists. Our study also suggests that the interdecadal variability of the NAO index plays an important role in controlling the extinction pattern of the Labrador Sea deep convection. Indeed, both the 1920s and the 1990s’ drops of deep convective activity can be linked to a switch from a period with relatively high winter NAO conditions to a period with negative conditions.

When it comes to interdecadal variability, Labrador Sea convection is found to be dominated by oscillations with a period ranging from 13 to 20 years, with a peak in the spectrum at 18 years. GIN Seas convection has a more bi-modal distribution, with two significant peaks at 13 and 20 years. Deep convection in the Labrador Sea is not significantly correlated to its GIN Seas counterpart. Cross-correlation and spectral analysis suggest that the interdecadal variability of the AMOC is partly driven by deep convection in the Labrador Sea, particularly between 40° and 50°, with a lag of 3–5 years. Under slight attenuation, this signal propagates southward and the convection leads the AMOC by about 7 years at 20°N.

The collapse of Labrador Sea deep convection during the 1990s is triggered by a combination of milder winter conditions, linked to a negative switch of the winter NAO index, and a brief excess of lateral influx of heat from the East-Greenland current. It is the unusually high NAO conditions of the 1980s in the model that seem to postpone the collapse to the 1990s, and possibly makes it more abrupt. The collapse itself, and the extinction that follows, are the result of an amplification of the warming of the upper layer caused by reduced sensible heat loss to the atmosphere in winter, and the absence of deep convective mixing. The reduction of the sensible heat loss is the consequence of a reduction of the air-sea temperature gradient at the surface, which results from a more rapid warming of near surface atmospheric temperatures compared to the ocean surface.

The complete extinction of Labrador Sea deep convection in the early 2020s coincides with the development of a severe freshening of the surface, which is primarily caused by a freshening of the East-Greenland current. This freshening of the surface adds up to the ongoing warming of the upper layer to further strengthen the surface stratification, preventing any possible resumption of deep convection. The melting of the Greenland ice-sheet, which is not taken into account in our simulations, could likely contribute to an even earlier extinction of deep convection. Following the deficit of North Atlantic deep water formation implied by the extinction of Labrador Sea deep convection and the weakening of GIN Seas deep convection, the AMOC undergoes a nearly linear reduction of 3–4 Sv from the end of the twentieth to the end of the twenty-first century. As suggested by previous studies, this stresses the importance of other processes, such as the wind, in driving the AMOC.

Table 1 Probability (%) for the occurrence of winter deep convection in each of the four convection boxes during different periods

Table 2 Ensemble mean (N = 8) of the correlations between the JFM NAO index and the JFM net heat loss to the atmosphere in the Labrador box ($-Q_{net}$), and between the JFM NAO index and the Labrador MV index (mixed volume in March)

Table 3 Same as in Table 2 but for the correlation between the JFM net heat loss to the atmosphere in the Labrador box ($-Q_{net}$) and the Labrador MV index (mixed volume in March), and the ensemble size $(\hbox {N}\,=\,12)$

Fig. 1

Idealized oceanic section illustrating how the DMV index (Deep Mixed Volume, gray shaded area) is calculated based on the mixed-layer depth in March and a depth criterion $z_{crit}$

Fig. 2

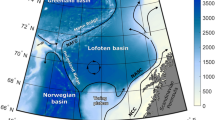
Ensemble mean $(\hbox {N}\,=\,12)$ of the mixed-layer depth (color-bar) and the sea-ice extent (50 % sea-ice concentration contour, blue line) in EC-Earth in March; averaged over the period 1850–1990 (shown on the native NEMO/ORCA1 grid). Four rectangular boxes (dashed black lines) are defined to include the main areas of deep convection and are labeled as follow: Labrador (1), Ice-Scot (2), GIN (3) and Nansen (4). These boxes are used to build the deep convection indices defined in Sect. 2.3. The five transects that form the Labrador box are labeled anti-clockwise according to their geographical position: LS, LE, LNE, LNW and LW

Fig. 3

Mixed-layer depth (color-bar) and sea-ice extent (50 % sea-ice concentration contour, purple line) in March. a Observations: Mixed-layer depth based on Argo-profiles collected between 2000 and 2013 (Holte et al. 2010) and sea-ice extent from NSIDC for the period 2000–2013 (Cavalieri et al. 1996). b EC-Earth, ensemble mean $(\hbox {N}\,=\,12)$ for the period 2000–2013, for easier comparison with observations the MLD and the sea-ice concentration of the model are interpolated on the same grid as the observations. Note that this figure is primarily intended to be used for comparing the locations of convection sites since depth values in (a) are only derived from a single to a few in-situ profiles, and are therefore not comparable to the model mean

Fig. 4

Ensemble mean $(\hbox {N}\,=\,12)$ of the model mixed-layer depth (color-bar) and sea-ice extent (50 % concentration, white area) in March for five different periods, a 1850–1920, b 1930–1990, c 1990–2013, d 2025–2050 and e 2075–2100. For the present-day period (c, 1990–2013), the red contour shows the observed 50 % sea-ice concentration from the NSIDC (Cavalieri et al. 1996)

Fig. 5

Ensemble mean $(\hbox {N}\,=\,12)$ of the deep mixed volume index (DMV, thin blue line) and its 11-year running mean (thick blue line) for the historical period extended with the RCP8.5 (solid lines) and the RCP4.5 (dashed lines) emission scenarios. Also the 11-year running mean of the DMV built with an alternative $z_{crit}$ (thin gray lines). The gray shading shows the 11-year running mean of the inter-member standard deviation about the mean

Fig. 6

Probability (%, y-axis) for the occurrence of a shutdown of Labrador Sea deep convection of a given duration (consecutive years with DMV = 0, x-axis), for three different time slices of the historical period extended with the RCP8.5 scenario. The ensemble mean and the standard deviation of the duration of the shutdowns is given in the legend

Fig. 7

Amplitude spectrum of: a DMV in the Labrador box, c DMV in the GIN box, and e annually-averaged maximum of the AMOC between 45°N and 50°N, for the 200-year long period of the pre-industrial control simulation that was used to provide the initial conditions of the 12 members. Same but for the ensemble mean $(\hbox {N}\,=\,12)$ of the amplitude spectrum during the historical period (1850–1990) in (b, d, f). Black dotted lines indicate the white (or pink) noise spectrum and gray lines the 95 % significance levels about the white (or pink) noise spectrum (based on 5000 randomly generated time-series with the same distribution as the relevant time-series)

Fig. 8

Ensemble mean (thin black lines), its 11-year running mean (thick black lines) $\pm$ the inter-member standard deviation (gray shading) of: a Wintertime NAO index (left axis) and Labrador mixed volume index (MV, only 11-year running mean, dashed lines, right axis). b Annually-averaged maximum of the AMOC at 48°N and 24°, black dots show the AMOC as estimated from the RAPID array at 26°N (Duchez et al. 2014). All curves are for the historical period, extended with the RCP8.5 scenario, except for the medium and thick dark gray curves that show the RCP4.5 scenario for the AMOC

Fig. 9

11-year running-mean of the ensemble mean $(\hbox {N}\,=\,9)$ of various surface variables spatially-averaged over the Labrador box. a Surface net heat flux and the temperature difference between the sea and the air at 2 m. b Turbulent (latent and sensible) and long-wave components of the surface heat flux. c Downward freshwater flux (precipitation minus evaporation) and sea surface temperature. JFM mean (thick lines) and annual mean (thin lines)

Fig. 10

11-year running average of the ensemble mean of the $\sigma _0$ potential density in the first 104 m of the Labrador box in November (black line) and the year-to-year standard deviation about the mean for the period 1850–1990 period (thin gray dashed line). To show the contribution of temperature, the $\sigma _0$ density is calculated using the actual temperature and a constant value of salinity taken as the 1850–1990 mean (red line). The same is done using a constant temperature and the actual salinity to show the contribution of salinity (blue line)

Fig. 11

11-year running average of the ensemble mean $(\hbox {N}\,=\,12)$ of (a) the $\sigma _0$-density in the Labrador box in November as a function of depth. Same for the anomaly of b potential temperature and c salinity. Anomaly is calculated as the difference from the 1850–1990 mean. Historical simulations extended with the RCP8.5 scenario

Fig. 12

Ensemble mean $(\hbox {N}\,=\,12)$ of the following annually-averaged fluxes. a Lateral and surface net heat fluxes, and the year-to-year variation of the 3D-integrated heat content (HC). The residual term (sum) is not zero because the contribution of the diapycnal mixing, w-velocity, eddy induced fluxes and sea-ice melting/formation has been omitted; and because of some approximations in the calculation of the lateral flux of heat (see the “Appendix”). Thick lines show the 11-year running mean. b 11-year running mean of the lateral flux of volume. c 11-year running mean of of the lateral flux of liquid freshwater. The reference temperature and salinity used to calculate the lateral fluxes of heat and freshwater are taken as the ensemble mean of the 3D-averaged value in the Labrador box during 1850–1990: 3.185 °C and 34.963 PSU (for 0-bottom) and 34.627 PSU (for 0–104 m). Lateral fluxes are calculated through the vertical transects defined in Fig. 2 using the method described in the “Appendix”. A positive flux means a gain for the box

Fig. 13

Probability for the occurrence of strong wintertime deep convection in the Labrador Sea (in %, bars and left axis). Here, strong means that the DMV exceeds the long-term ensemble mean (1850–1990, N = 12) of the DMV by at least one inter-member standard deviation (long-term ensemble mean, given in the figure). Mean depth of the deep mixed-layer in March during these winters with strong convection, restricted to the area of the box where the MLD exceeds the depth criterion ${z_{crit}}$ (black lines and stars, right axis)

Fig. 14

Ensemble mean ($\hbox {N}\,=\,12$) of the cross-correlation between the Labrador DMV and the annually-averaged maximum of the AMOC at a given latitude (y-axis) during the period 1850–1990, based on smoothed time-series (11-year running mean). The linear trend is subtracted from all time-series prior to calculating the correlation. The 95 % confidence level is shown as dashed white contours and takes into account the strong auto-correlation introduced by the smoothing process by assuming a reduced sample size $N_s = 12\, N_y(1-\rho _1)/(1+\rho _1)$, where $N_y$ is the number of years considered and $\rho _1$ the lag-1 auto-correlation of the smoothed predictor time-series (DMV)

Appendix

Lateral transports of volume, heat, and liquid freshwater across a vertical transect collinear to the plane defined by the axes l (horizontal) and z (vertical), are calculated as follows:

$$\begin{aligned} F_{volume}= & {} \int _{l}\int _{z} \mathbf {U}_H \cdot \mathbf {n} ~dl~dz \nonumber \\ F_{heat}=\, & {} \rho _0 C_{P} \int _{l}\int _{z} \left( \theta - T_0 \right) \mathbf {U}_H \cdot \mathbf {n} ~dl~dz \nonumber \\ F_{freshwater}=\,& {} F_{volume} -\frac{1}{S_0} \int _{l}\int _{z} S\,\mathbf {U}_H \cdot \mathbf {n} ~dl~dz \end{aligned}$$

(1)

n is the unit vector normal to the section (i.e. normal to the plane defined by l and z). $\mathbf {U}_H$ is the horizontal component of the velocity, $\theta$ the potential temperature and S the salinity. $T_0$ and ${S_0}$ are a reference mean of the temperature and salinity, respectively, inside the domain. $\rho _0$ is a rough estimate of the density of sea-water and is taken equal to 1025 kg/m³. The specific heat of sea-water $C_P$ is 3990 J/kg/K.