Abstract
Despite the spatially homogenous summer temperature pattern in Fennoscandia, there are large spreads among the many existing reconstructions, resulting in an uncertainty in the timing and amplitude of past changes. Also, there has been a general bias towards northernmost Fennoscandia. In an attempt to provide a more spatially coherent view of summer (June–August, JJA) temperature variability within the last millennium, we utilized seven density and three blue intensity Scots pine (Pinus sylvestris L.) chronologies collected from the altitudinal (Scandinavian Mountains) and latitudinal (northernmost part) treeline. To attain a JJA temperature signal as strong as possible, as well as preserving multicentury-scale variability, we used a new tree-ring parameter, where the earlywood information is removed from the maximum density and blue intensity, and a modified signal-free standardization method. Two skilful reconstructions for the period 1100–2006 CE were made, one regional reconstruction based on an average of the chronologies, and one field (gridded) reconstruction. The new reconstructions were shown to have much improved spatial representations compared to those based on data from only northern sites, thus making it more valid for the whole region. An examination of some of the forcings of JJA mean temperatures in the region shows an association with sea-surface temperature over the eastern North Atlantic, but also the subpolar and subtropical gyres. Moreover, using Superposed Epoch Analysis, a significant cooling in the year following a volcanic eruption was noted, and for the largest explosive eruptions, the effect could remain for up to 4 years. This new improved reconstruction provides a mean to reinforce our understanding of forcings on summer temperatures in the North European sector.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Understanding past climate change and variability allows us to quantify the impact of the recent anthropogenic influence on the climate system by quantifying its natural behaviour and variability (Frank et al. 2010). Moreover, using proxy-data to increase the understanding of past climate changes, such as extreme events and abrupt changes, provides, together with historical sources, tools to understand how climate has affected societies in the past (e.g. Büntgen et al. 2011a). Since the first high-resolution reconstruction of Northern Hemisphere temperatures (Mann et al. 1999) was introduced, an increasing number of attempts to reconstruct global or hemispheric climate has been made (e.g. Masson-Delmotte et al. 2013). Although they all display their own characteristics, depending on methods used and proxies included, in general they provide a broadly coherent picture of the climate evolution over the last two millennia. Still, since global change has a strong regional expression, it is vital that we can provide information also on these spatial scales. The efforts of the PAGES 2K consortium (2013) is an excellent example of looking at regional climate change through time.
When it comes to reconstructing mid-to-high latitude climate variability with high (annual) resolution, tree rings are the most widely used climate proxy. This is because of the relative ease of creating well replicated, accurately dated chronologies with annual resolution that can be calibrated against meteorological observations. Over time the discipline of dendroclimatology has evolved from providing local (site) climate information, to regional (combining several sites within a region), and finally hemispheric and global averages. With an ever increasing number of sampled sites across the world, an increasing number of tree-ring based field (gridded) reconstructions of temperature (Gouirand et al. 2008, hereafter G08; Cook et al. 2012) and drought (e.g. Cook et al. 2004, 2010; Touchan et al. 2011; Seftigen et al. 2014a) have been produced within the last decade. Field reconstructions have the obvious advantage of providing information of past climate with a high spatiotemporal resolution, yielding means to study contemporary climate variability among sub-regions.
Fennoscandia, being located in the high-latitude boreal zone, is well suited for dendroclimatological studies, and consequently has a long tradition of climate and environmental research using tree-ring data (see Linderholm et al. 2010a for a review). Fennoscandia is also the home of several of the worlds’ longest tree-ring chronologies: Finnish Lapland (Helama et al. 2002), Torneträsk (Grudd et al. 2002) and Jämtland (Gunnarson 2008), covering large parts of the Holocene. Data from the latter two has also been used to represent Fennoscandia in several hemispheric and global temperature reconstructions (Jones et al. 1998; Mann et al. 1999; Esper et al. 2002; Briffa et al. 2002; Moberg et al. 2005; D’Arrigo et al. 2006; Ljungqvist 2010).
Over the last few years several new chronologies spanning the last millennium have been produced in Fennoscandia, mainly in the far north. In addition to providing reconstructions of local warm-season temperature variability (Grudd 2008; Gunnarson et al. 2011; Melvin et al. 2013) and past changes in cloud cover and sunshine (Young et al. 2012; Loader et al. 2013) from single-site data, some of these chronologies have been included in multi-site studies to infer past regional climates (Büntgen et al. 2011b; Esper et al. 2012; McCarroll et al. 2013). Still, looking at the spatial expression of the above mentioned “supra long” chronologies as well as regional reconstructions based on trees from northernmost Sweden, it is evident that they mainly represent their own regions and not the whole of Fennoscandia. Previous gridded multi-proxy reconstructions of Pan-European temperatures (Luterbacher et al. 2004, hereafter L04; Guiot et al. 2010, hereafter G10) have mainly been based on proxy data from continental Europe, making them less reliable for Fennoscandia. Focusing only on Fennoscandia, G08 showed that it is possible to provide a reliable reconstruction of summer temperatures for the whole of this region provided that also data from its central parts is included. However, it was evident that the lengths of most of the records then available were insufficient to provide a spatially coherent reconstruction beyond the mid-seventeenth century.
The aim of this paper is to provide a spatiotemporally coherent summer temperature history of Fennoscandia for most of the last millennium. The motivation is the statement from Esper et al. (2012), that despite the high number of high-resolution proxy records in northern Fennoscandia, which are individually well calibrated against observations, the summer temperature evolution during the last millennium is still not well understood. This is due to the large difference among the records, despite this being a region characterised by spatially homogeneous summer temperature patterns. To reach our aim, we used density and blue intensity (McCarroll et al. 2002) data from northernmost Fennoscandia (Esper et al. 2012; Forfjorddalen from McCarroll et al. 2013) as well as from a north–south transect along the Scandinavian Mountains (Björklund et al. 2013), including previously unpublished data. In Sect. 2, we describe the density and blue intensity data, as well as how it is transformed into the newly developed “Δ parameter” that has been shown to contain a high-quality summer temperature signal (Björklund 2014; Björklund et al. 2014a, see a more detailed description below). After the transformation, the data is standardised using a modified hybrid of the RCS and signal-free standardisation methods (Melvin and Briffa 2008; Björklund et al. 2013, see below) intended to preserve as much of the common low-frequency variability in the resulting chronologies as possible. In Sect. 3 we describe the reconstruction used to derive a more spatially representative view of summer temperature variability for the last 900 years. We use a similar method to McCarroll et al. (2013), combining ten chronologies into a Fennoscandian average. Descriptions of the new reconstruction, as well as comparisons with previous ones are given in Sect. 4. In Sect. 5, we present a tentative field reconstruction for the region using the ten chronologies, and compare the results to previous gridded reconstructions focusing on or including Fennoscandia (L04, G08 and G10). In Sect. 6, we briefly examine the influence of two forcings on Fennoscandian summer temperatures, where volcanic eruptions represent short term, and North Atlantic sea-surface temperatures (SST) long-term forcing. Finally, we summarise our findings in Sect. 7.
2 Tree-ring data
2.1 Tree-ring data
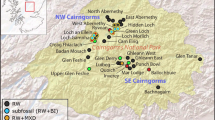
We used seven Δ Density and three Δ blue intensity (ΔBI) chronologies derived from Pinus sylvestris (Scots pine) increment cores and cross sections collected from eight sites in Fennoscandia (Fig. 1; Table 1). All density data was produced using an ITRAX multiscanner (www.coxsys.se) (see Gunnarson et al. (2011) for a detailed description of the process), except for the density data we used from the Esper et al. (2012) network, which was produced using DENDRO2003 (Eschbach et al. 1995). The density samples were prepared according to standard techniques (Schweingruber et al. 1978). The optical BI data was produced following the protocols developed by Campbell et al. (2011) and Björklund et al. (2014a). Digital images were produced with a flatbed scanner at 1,600 dpi resolution (Epson Perfection V600 Series) calibrated with SilverFast Ai professional scan software using the Calibration Target (IT8.7/2). All density and optical images were analysed with the commercial software WinDendro™.
Map of the studied domain showing the locations of the chronologies used in this study. a Forfjorddalen, b Tjeggelvas, c Arjeplog, d Ammarnäs, e Kittelfjäll, f Jämtland and g Rogen. Data was also used from the NSCAN (Esper et al. 2012) region (blue box). Also indicated are the location of the Torneträsk chronology (Melvin et al. 2013, grey filled box) and the NFEN (McCarroll et al. 2013) region (open grey box). The smaller red box corresponds to the target domain for the regional average reconstruction (see Sect. 4) and larger open red box to the target domain for the field reconstruction (see Sect. 5)
Several works have shown that MXD from Fennoscandian Scots pines contain high-quality temperature information for an extended growing season spanning from April/May to August/September (Briffa et al. 2001; Grudd 2008; Linderholm et al. 2010b; Gunnarson et al. 2011; Björklund et al. 2013; Melvin et al. 2013). However, here we utilise the new ΔDensity and ΔBI parameters (Björklund et al. 2014a), which is defined as the MXD (MXBI) value for each annual increment minus the earlywood density (BI). Since the earlywood will contain some information of the spring (April–May) conditions, removing this from the maximum density (BI) will provide a more focused summer (June through August, JJA) temperature signal in the remaining ΔDensity (ΔBI). The motivation to use ΔDensity and ΔBI in this study was that, although they comprise information from shorter target seasons, they contain stronger temperature signals than their MXD and MXBI counterparts (Björklund et al. 2014a), and can in some cases alleviate biases caused by “modern sampling” (Melvin 2004). Furthermore, it is critical for the BI proxy which cannot function as a component in an RCS based climate reconstruction without this transformation. Actually, additional adjustments need to be made. Björklund et al. (2014a) showed that transforming BI data into ΔBI yields a marked improvement compared to only using MXBI, but ΔBI is systematically biased in the lowermost frequencies, because the sample with the highest (lowest) mean BI values display a lowered (raised) contrast between the earlywood and latewood elements that are used to calculate ΔBI. Consequently, ΔBI chronologies have a systematic bias in them if the older samples in a chronology are dark, which is usually the case. To overcome this, we performed a contrast adjustment on the BI data using the method described in Björklund (2014) and Björklund et al. (2014b), yielding ΔBIadj.
2.2 Standardisation
To remove the age-related trend and other non-climatological variance in the tree-ring data, while trying to preserve as much low-frequency (centennial and longer) information as possible, we standardised the data using a regionally constrained individual signal-free standardisation method (termed RSFi), introduced by Björklund et al. (2013). This is a modified version of the signal-free method by Melvin and Briffa (2008), combining the individual signal free (ISF) and RCS signal free (RSF) approaches (we refer to Björklund et al. (2013) for a detailed description of the method). Briefly, in addition to retain long-term variability similar to RCS, RSFi also attempts to remove noise from local “random” disturbances in the decadal time-frame, such as stand dynamics, and also obvious miss-estimations of growth trends, by using a signal-free data-adaptive curve-fitting approach where the detrending functions subsequently are forced to the same mean as the local average of the regional curve (RC). By respecting the mean value of each tree-ring measurement it is possible to alleviate the segment length-curse (Cook et al. 1995) and retain climatic information on centennial timescales, if life spans of included trees are of this age. However, similar to RCS, RSFi cannot distinguish between variability in mean values that is climatically induced from ones that is only a function of microsite circumstances.
Due to the homogeneity of JJA temperatures in the studied region, all tree-ring data was loaded in the same signal-free run. This was done to remove the effects of external disturbances that may affect a sub-region (e.g. human impacts, insect outbreaks and fires) but which are unrelated to climate. Since such impacts rarely are randomly distributed among the trees at a site, they may be misinterpreted as a climate signal in a chronology. The tree-ring datasets for each site was subsequently averaged separately, to retain a purer temperature signal from each individual chronology. This has the benefit of reducing the uncertainties around the mean values in subsequent composite chronologies. Consequently, the chronologies can also be used in sub-regional to local interpretations of temperature with greater accuracy in the high frequency domain, as well a better estimations of local low-frequency variability.
3 Reconstruction methods
3.1 The making of a regional average reconstruction
The reliable parts of each chronology were evaluated using the expressed population signal (EPS; Wigley et al. 1984), where the EPS value quantifies how well the samples represent the whole population of trees. EPS was calculated over 50-year moving windows with a 1-year lag, and when EPS values fell below 0.85 the chronologies were truncated. To reconstruct regional JJA temperatures, we used the same approach as McCarroll et al. (2013), viz. normalising (z-scoring) all the ten chronologies over successively longer periods back in time depending on their timespans (see Table 1), and then averaging them, giving equal weight to each series using the same parsimony logic as McCarroll et al. (2013), into a composite chronology over the full 1100–2006 CE period. The target temperature data for the reconstruction was the global land surface 5° × 5° resolution CRUTEM.4.2.0.0 data set covering the period 1850–2006 (Jones et al. 2012), averaged over the grid points covering the 10–30°E, and 60–70°N region (Fig. 1). The reason for choosing this coarse gridded dataset was to get an as long as possible calibration period. A transfer model was developed, using simple linear regression, to reconstruct temperature back in time, where JJA temperature anomalies (deviations from the 1971–2000 mean) were set as predictand and the averaged regional tree-ring index (in year t) as the predictor. To test the temporal stability and quality of the model, we employed a split sample calibration/verification procedure (Gordon 1982), where the common period of instrumental and tree-ring data was split into two periods of equal length (1855–1930 and 1931–2006 respectively). The first sub-period was used for calibration, and the second withdrawn for validation. Calibration and verification periods were then exchanged and the process repeated. The final model was built over the full 1855–2006 period. The skill of the transfer function was assessed in the calibration period with the coefficient of multiple determination (R2) statistic, and in the verification period by means of the reduction of error (RE) and coefficient of efficiency (CE), root mean square error (RMSE) and R2 statistics (see Cook et al. 1999 for a full explanation). Uncertainties in the form of ±1 RMSE were added to the regression-based and rescaled final reconstruction. The RMSE was computed between observed and rescaled estimates of past temperatures, thus reflecting the added variance associated with rescaling.
3.2 A field reconstruction based on the ten chronologies
A point-by-point regression approach (PPR) (Cook et al. 1999) was used to generate fields of JJA temperature anomalies from the tree-ring network. The method has previously been used to reconstruct “atlases” of both hydroclimatic metrics (e.g. Cook et al. 1999, 2004, 2010; Touchan et al. 2011; Seftigen et al. 2014a, b) and temperature (Cook et al. 2012). Although the PPR approach is not explicitly spatial, the underlying spatial patterns in the gridded data can be well preserved using this method (Cook et al. 1999). The PPR was performed in the MATLAB (Release 2013a) environment. A search radius of 1,500 km, previously used by Cook et al. (2012), was used to locate potential tree-ring predictors for each grid point reconstruction. This search radius is roughly corresponding to the spatial decorrelation pattern of instrumental data (i.e. decorrelation decay distance CDD, see Jones et al. 1997) in Fennoscandia (results not shown). All tree-ring chronologies within the search radius were screened to eliminate tree-ring data poorly correlated with temperature at a given grid point. The screening was performed over the calibration period by means of correlation analysis using a two-tailed screening probability of α = 0.05, testing the association between tree-ring data and temperature in current year (t) only. This screening method is quite conservative, and we only used tree-ring data that was positive correlated with temperatures. Retained tree-ring chronologies were transformed into orthogonal eigenvectors through Principal Component Analysis (PCA). The lower order eigenvectors (>1.0) were used as potential predictors in a stepwise regression. An initial model was first fit, and then the explanatory power of incrementally larger and smaller models was assessed. For each iteration the p value of an F-statistic was computed, to test the model with and without the potential predictor. The predictor was added (removed) from the model if the p value was <0.05 (<0.1). The stepwise regression was terminated when no predictors were added or removed from the model. For each grid point, regression models were built for nests to account for the changing chronology coverage back in time (see Cook et al. 1999 for a detailed method description). The calibration period mean and standard deviation of each individual reconstruction nest was scaled to have the same mean and standard deviation as the instrumental temperature data over the calibration period. The nests were then put together to produce a complete full-length reconstruction for each grid point.
The instrumental temperature data used for the field reconstruction was a Fennoscandian subset of the global monthly 0.5° × 0.5° gridded CRU TS3.21 dataset (this is an update of the CRU TS3.10 version described in Harris et al. 2014), spanning over the 1901–2012 interval. The target area covered the 4.5–30.0°E and 54.5–70.0°N region (Fig. 1), consisting of a total of 1,355 grid points. This is the same domain previously reconstructed by G8, although they used a different approach. Temperature anomalies (relative to the 1971–2000 average) for JJA were used as the target for the reconstruction. The calibration and verification procedure was the same as the one described in 3.1, although with different sub-periods (1901–1953 and 1954–2006), and the final model was built over the full 1901–2006 period. Only grid points that produced significant calibration regression models (p value of the F-statistic <0.05), and where CE or RE values exceeded a zero threshold value in the most recent nest were used to produce the final full-period calibration models.
4 New estimates of Fennoscandian summer temperatures
4.1 The new regional average reconstruction
The RSFi standardised ΔDensity and ΔBIadj chronologies are shown in Fig. 2a–j. It is clear that they share common variability on both short and long timescales, and compared to the multi-proxy data used in McCarroll et al. (2013, see their Fig. 3), they display more coherent variance and long-term evolution. The higher coherency among our data is partly due to the choice of proxies. The McCarroll et al. (2013) regional northern Fennoscandian reconstruction (hereafter NFEN) was truly a multi tree-ring proxy reconstruction, including tree-ring widths, MXD, MXBI and height increment, all having slightly different target seasons and temperature responses. By using only two (highly related) proxies as well as utilizing the Δ parameters, we were able to get a higher agreement among the chronologies. Perhaps the largest improvement in chronology coherence is due to the novel standardization, that efficiently removes random and non-random non-temperature noise from individual chronologies.
Top right time-series plots of observed and reconstructed JJA temperature anomalies from nest 1. Shown below is the full Fennoscandian JJA temperature anomaly (from 1971–2000 average) reconstruction, based on the 1855–2006 reconstruction models and smoothed with a 50-year cubic smoothing spline with a 50 % frequency response cutoff. The dashed horizontal line is the long-term (1100–2006 CE) mean. Also shown is the ± 1 root mean square error (RMSE) uncertainties (light blue lines)
Due to the varying lengths of the ten chronologies, we used a nested approach (Meko 1997) to reconstruct JJA temperatures. The first nest, containing all chronologies, spans over the period 1550–2006, the second 1300–2006 (seven chronologies), the third 1200–2006 (five chronologies) and the fourth 1100–2006 (three chronologies). The calibration/verification procedure was applied to those chronologies included in respective nest to assess the change in reconstruction skill with decreasing number of chronologies. Based on the high CE and RE and R2 values, which were highly similar for all the nests (Table 2), we can conclude that (1) using our data we can provide a very skilful estimate of JJA temperatures, and (2) the skill does not change with decreasing number of chronologies, showing that the strong JJA tree-ring association is temporally stable in the calibration period. In fact, the slight increase in \({\text{R}}_{\text{adj}}^{2}\) for the full calibration period from nest 1–4 indicates that only a few key may adequately represent average regional (10–30°E, 60–70°N) temperatures, as previously proposed by G08. However, to get a more robust reconstruction for a larger region, we advocate the use of as many high-quality sites as possible, especially to ensure a sound spatial representation in the distant past. The full reconstruction of Fennoscandian JJA temperatures was obtained by combining the five individual reconstructions into a single one (Fig. 3). The reconstruction was scaled to the instrumental data over the calibration period, and uncertainties in the form of ±1 RMSE (of the calibration model) was added to each reconstructed value (see above).
4.2 The new field reconstruction
Figure 4 shows maps of the calibration (R2) and verification (R2 and CE) statistics for the PPR derived temperature field reconstruction. As a rule of thumb, a CE value >0 indicates that the reconstruction has some skill in excess of the verification period climatology of the instrumental data (Cook et al. 1999). From the calibration/validation maps it is clear that the regions where the tree-ring data originates from exhibits the greatest amount of model skill. However, the spatial pattern of the RE and CE differs between the two verification periods, displaying slightly lower score, but for a larger region, in the early verification (late calibration) period, and slightly higher scores more centred to the north in the late verification (early calibration period). So, even though the reconstruction captures more than 50 % of the variance in temperature variability over a large part of this region, and CE is well above the zero threshold in both the best and worst replicated nests, a shift in the spatial association between the tree-ring data and JJA temperatures can be noted during the twentieth century. The nature of this shift is unclear, but possibly it is a reflection of changes in the timing of the growing season in Fennoscandia during last century (e.g. Linderholm et al. 2007), affecting the target season for the trees in the central and southern parts of the network. A slight shift in the JJA temperature sensitivity of these chronologies is also seen between the early and late calibration periods of the regional average reconstruction (Table 2).
Averaging together all grid point reconstruction for which calibration R2 >0.5 (632 grid points in total) produces a regional mean reconstruction (not shown here) that is virtually identical to the regional average reconstruction provided in Fig. 3. This is not surprising, since the large search radius (1,500 km) in the PPR approach will result in all chronologies being chosen as predictors in the regressions for each of the grid points in the target region. The implication of this is that, even though the region has a homogenous JJA temperature pattern, the representation in the grid points where the correlation is low will not truly reflect the local conditions. To overcome this bias, an improved spatial distribution of data is needed from the presently unrepresented regions (e.g. southern Norway and Sweden, and eastern Finland). An increased network would allow us to extract the local “flavours” in temperatures, which would be more meaningful when studying sub-regional variability.
5 Comparison with other Fennoscandian reconstructions
5.1 Temporal comparison
Next we compared our new summer temperature reconstruction to a set of previously published reconstructions, based totally or in part on MXD data, which have been shown to be good representations of northern Fennoscandian warm-season temperatures. For this comparison we choose the well-known Torneträsk record (recently adjusted by Melvin et al. 2013), the “northern Scandinavia” (northernmost Sweden and Finland) reconstruction by Esper et al. (2012, hereafter NSCAN), and NFEN where the latter two targeted JJA, but Melvin et al. (2013) targeted May–August. Although Esper et al. (2012, Fig. 6) pointed out notable differences in temperature levels among various regional reconstructions, we did not expect large deviations among the selected reconstructions since part of the data used in NSCAN and NFEN was also included in our reconstruction.
Figure 5 shows the temporal evolution of the four above mentioned reconstructions. In general, there is a good agreement among them, all displaying similar distinct variability in the twelfth century, the cold periods in the mid-fifteenth century and around 1600 (the latter being by far the coldest period during the last 900 years in our new reconstruction) as well as the twentieth century warming. However, there are also periods where the records disagree. One such period is the thirteenth century, which corresponds to the transition from the Medieval Climate Anomaly (Medieval warm epoch, Lamb 1965) into the Little Ice Age (LIA, ibid.). While our new reconstruction and NFEN suggest a recovery after the rather abrupt temperature decline in the late 1200s in the latter part of the thirteenth century, such a recovery is less conspicuous in NSCAN, and the evolution of Torneträsk is the opposite of the others in the thirteenth century. Compared to the others, our new reconstruction suggests an earlier transition to the fifteenth century warming peak and also that this peak occurred slightly earlier. Another period of deviation among the records is found between the mid-1600s and 1900. Our new reconstruction suggests less multidecadal temperature variability during this period compared to the others, where one example is the temperature peak in the last half of the eighteenth century seen in Torneträsk and NFEN, which is much less pronounced in NSCAN and our new reconstruction. The large heterogeneity among the reconstructions during this period is surprising since most chronologies are quite well replicated. A deviation of the NFEN is reasonable, since it contains a range of tree-ring proxies with differing expressions of summer temperatures, but the other reconstructions are derived from MXD, including common data, and was thus expected to be more coherent. Likely this issue can be solved with a more coherent and careful approach to both choice of standardisation method, data selection and parameters used (see Frank et al. 2010). The results presented here and, perhaps more convincingly those of Björklund (2014), who showed that a set ΔDensity chronologies standardised with the RSFi method were far more coherent compared to their RCS standardised MXD counterparts which displayed more of a “spaghetti plot”, suggests that our method could solve at least some of the discrepancies observed among current data.
Comparison of a the new regional Fennoscandian JJA temperature reconstruction, b Torneträsk (Melvin et al. 2013), c the NSCAN (Esper et al. 2012), and d the NFEN (McCarroll et al. 2013). All chronologies have been normalised over the 1100–2005 period and smoothed with a 50-year spline with a 50 % frequency cut off to facilitate comparisons
Possibly some of these discrepancies are due to different sub-regional expressions of temperature variability. Despite the overall homogenous summer temperature pattern, temporal and spatial changes likely occur. As an example, climate in Fennoscandia is closely linked with the atmospheric circulation, e.g. the North Atlantic Oscillation (NAO, e.g. Visbeck et al. 2001), and circulation patterns are not spatially stable through time, partly due to shifts in the position of the polar jet stream (Hudson 2012). This is particularly noticeable during summer where the southern node of the summer NAO, variability of which is closely linked to climate in Fennoscandia (Folland et al. 2009), has shifted in position through time. Consequently, changes in the average positions of circulation patterns over Fennoscandia could cause contrasting or differing temperature responses across the synoptic-scale boundaries within a region (e.g. between the central Scandinavian Mountains and northernmost Sweden). Using tree-ring isotope records, long-term changes in the large-scale atmospheric circulation over northernmost Scandinavia, associated with the Arctic Oscillation, have been inferred for the last millennium, (Young et al. 2012; Loader et al. 2013), and ongoing work targeting the summer NAO (Salo et al. in prep.) will provide possibilities to investigate this further. Additionally, detailed studies of periods of deviance among local-to-regional reconstructions could help us detect sub-regional climate variability and better understand the spatial variability of the atmospheric circulation and its impacts. Thus, efforts should also be made to analyse sub-regional differences in addition to reconstructing large-scale means.
Looking at the spatial representation of the four reconstructions over the 1901–2005 period (Fig. 6), obvious differences among the patterns can be seen. Note that here we only highlight correlations >0.71, corresponding to an explained variance of the observed JJA temperatures of 50 % or above. Of the three old reconstructions, the one from Torneträsk, where the data comes from a confined region, has the best spatial representation for northern Fennoscandia. Correlations above 0.71 are found down into central Norway and Sweden, and along the west coast of Finland, and a correlation “hot spot, with values exceeding 0.8, is found over and south of the sampled region. This again confirms that MXD data from Torneträsk has an unusually strong warm-season temperature signal representing a wide region. Of the two multi-site reconstructions, NSCAN displays a slightly larger area with correlations above 0.71, displaying a spatial pattern quite similar to that of Torneträsk, albeit a bit weaker and more northerly confined. This is not surprising since data from Torneträsk (living trees) were included in NSCAN. The spatial pattern of the multi-proxy and multi-site NFEN reconstruction resembles that of NSCAN, although it is slightly weaker and centred over the northernmost part of Fennoscandia. The highest correlations are found in northern Norway and over north-westernmost Sweden, which partly includes the Torneträsk region.
Field-correlation between average JJA temperatures from the CRU TS 3.21 dataset (Harris et al. 2014) and: top left the new regional Fennoscandian summer temperature reconstruction, top right Torneträsk (Melvin et al. 2013), bottom left NFEN (McCarroll et al. 2013) and bottom right NSCAN (Esper et al. 2012), during the period 1901–2005. Note that only correlations >0.70 are shown in this figure
Turning to our new reconstruction, it is evident that including data from more southerly sites along the Scandinavian Mountains yields a much stronger and spatially larger correlation pattern. Correlations >0.71 are found over most of Fennoscandia except for southern Norway and Sweden and the northernmost tip of Finland. The strongest correlations are found over much of northern Sweden and also across the Gulf of Bothnia in western Finland. Compared to the best nest of G08 (see their Fig. 8), the spatial correlations are slightly weaker using the present chronology, but it should be noted that the best nest in G08 was based on 30 chronologies, and only extending back to 1893, and also that the calibration period was shorter (1901–1970). Actually, the correlation pattern of the new reconstruction corresponds quite well with that of nest 4 in G08, which contained 12 chronologies from 9 sites (extending back to 1696). However, contrary to G08, where there is a progressive decrease in the spatial correlation values with decreasing number of chronologies, the correlation patterns show only very marginal changes from nest 1 to nest 4 (see supplementary figure S1). Thus, even though we cannot attain a reconstruction that represents summer temperatures for the whole of Fennoscandia with high fidelity using the present data, we have shown that it is possible to provide a robust and reliable reconstruction for large parts of this region for the last 900 years.
The added value of the RSFi standardisation method used here is that it will provide mean chronologies with larger variability because of reduced noise levels in the included chronologies compared to those produced with RCS. Since the temperature variation where the included chronologies are located is very similar, our assumption is that the increase in coherence among the chronologies is due to the standardisation. One important achievement with this new method is that the coherence among RSFi standardised chronologies is significantly higher on frequencies lower than decadal timescales compared to those standardised using the classic RCS method (Björklund 2014).
5.2 Spatial comparison
The new field reconstruction was compared with two previously published multi-proxy gridded temperature reconstructions: (1) the 0.5° × 0.5° resolved JJA temperature fields provided by L04 covering 1500–2004 CE, and (2) the 5° × 5° gridded reconstruction of April-September temperatures reconstructed by G10 for the 600–2007 CE interval. Both datasets cover the European domain, and are based on a range of climate proxies, including tree-ring data. Figure 7 shows point-by-point correlation maps between our new reconstructed temperature field and the two datasets. Because of the coarser grid of G10, we averaged the grid-points within each 5° grid in our reconstruction in the comparison with G10.
Top plot point-by-point correlation fields between the new Fennoscandian JJA spatial temperature reconstruction and reconstructed gridded warm-season temperatures produced by Luterbacher et al. (2004). The correlations have been derived over two periods, 1500–1700 CE (left) and 1700–1900 CE (right), and are significant at p < 0.05. Lower plot: same as the top plot, but between the new Fennosandian reconstruction and gridded multi-proxy spring-summer temperature reconstruction provided by Guiot et al. (2010). All of the correlations, which are calculated over the 1100–2006 CE interval, are close to zero and do not reach the 0.05 significance level
L04 shows high spatial coherency with our reconstruction in the period 1700–1900, which is a period when L04 includes observational data from Fennoscandia. Prior to that, when L04 is mainly based on proxies from continental Europe, except for Baltic and Icelandic sea-ice data, Greenland Ice core data and tree-ring width data from northwestern Norway and Siberia (see supplementary material in L04), the correlation trails off considerably. Turning to the comparison with G10, the spatial correlation is very low (<0.20) for the entire domain during the whole 1100–2006 period, with no centuries showing much higher associations between the two (not shown). This is rather surprising, since G10 utilized several tree-ring chronologies from Fennoscandia (see table S1 in G10), where our reconstruction and G10 both include Forfjorddalen. However, G10 only used tree-ring width data from this region, which contains a much weaker temperature signal than MXD (e.g. Briffa et al. 2001). Moreover, G10 reconstructs a longer season (April–September) which may have an influence on the result. Still, it is obvious the two “whole Europe” reconstructions are of very limited relevance for Fennoscandia, and clearly show that more local data from the northernmost region of Europe is needed to fully represent the entire region.
6 A brief look at some forcings of Fennoscandian JJA temperatures
In this section, we briefly examine the influence of two forcings on Fennoscandian JJA temperatures over the last 900 years. We focus on SST variability representing long-term forcing, and volcanic eruptions representing short-term forcing. We do not discuss solar influences since this was already sufficiently done in McCarroll et al. (2013). In addition to the influence of the NAO (e.g. Chen and Hellström 1999; Hurrell et al. 2003), climate variability in Fennoscandia is related to the large-scale circulation in the North Atlantic Ocean, where the multidecadal variability of North Atlantic SST (the Atlantic Multidecadal Oscillation, AMO), has been linked to temperature and precipitation in the North Atlantic region, including Fennoscandia (Knight et al. 2005; Sutton and Hodson 2005). Moreover, McCarroll et al. (2013) found a positive correlation between NFEN and observed North Atlantic SST during JJA, being strongest to the north of Fennoscandia. As expected, our new reconstruction showed similar, but spatially wider, correlation patterns with significant (p < 0.05) positive correlations found over the Norwegian Sea and the Barents Sea (Fig. 8). In addition, significant correlations are found over the sub-polar gyre (negative) and the subtropical gyre (positive), suggesting a link between Fennoscandian summer temperatures and the thermohaline circulation. This will be investigated in a further study.
Spatial field correlations between the new Fennoscandian JAA temperature reconstruction and gridded sea surface temperature (HadlSST1, Rayner et al. 2003) during the period 1870–2006
Large explosive volcanic eruptions can have significant impacts on regional to global temperatures, depending on the amount of volcanic aerosols emitted into the lower troposphere on temperatures (Robock 2000). In winter, volcanic eruptions are associated with slightly increased temperatures, particularly the year after the eruption (Robock and Mao 1992). In summer, individual large eruptions may cause large-scale cooling, lasting for 2–3 years after the event, with a maximum effect usually occurring 1 year after the eruption (Jones et al. 2003). Due to the importance of volcanic eruptions as short-term forcings on global temperatures, efforts have been made to locate, date and estimate the impact of eruptions in the pre-instrumental era (Gao et al. 2012; Crowley and Unterman 2013). Also, using high-resolution paleoclimate data (mainly tree-ring data), studies of the impacts of known (or inferred) past volcanic eruptions on temperature have been made (e.g. Briffa et al. 1998; Fischer et al. 2007). In general, these studies have shown that anomalous growth depressions, interpreted as low temperatures, are in many cases associated with volcanic eruptions.
Here we further investigated the link between volcanic eruptions and inferred summer cooling in Fennoscandia which has previously been shown (Jones et al. 2013; McCarroll et al. 2013). Temporal relationship between anomalously cold summers and known past explosive volcanic eruptions was assessed through Superposed Epoch Analysis (SEA, Lough and Fritts 1987). By using this technique, we evaluated whether the mean value of reconstructed temperature is significantly different during the eruption year compared to 1–5 years immediately before/after the event. SEA was performed in dplR (Bunn et al. 2014), where the significance of the departure from the mean temperature was estimated trough bootstrap resampling. We used the dataset from Gao et al. (2008), available at the NOAA World Data Center for Paloclimatology (Gao et al. 2009), of past volcanic eruption to set the key years for running SEA. The results indicate a statistically cooling effect 1 year after the eruption (Fig. 9). For especially large eruptions, where the annual stratospheric volcanic sulphate aerosol injections were 20 Tg or more, the cooling seems to have persisted for up to 4 years after the event, which roughly corresponds to the 3-year lifetime of volcanic aerosols (Oman et al. 2005). Hence, frequent volcanic activity in the latter half of the fifteenth, seventeenth and late eighteenth– early nineteenth centuries might be responsible for some of the persistent temperature decline as seen in the reconstruction during these periods. These results are generally consistent with previous studies (e.g. Briffa et al. 1998; Fischer et al. 2007; Jones et al. 2013; McCarroll et al. 2013) highlighting the importance of explosive volcanisms as an external driver of North European climate variability.
Top plot reconstructed temperature anomalies compared with the Northern Hemispheric sulphate loadings series from ice core data (Gao et al. 2008, 2009) since the 1100 CE. Dashed lines indicate the 20 and 40 Tg thresholds, respectively. Bottom plot results of the Superposed Epoch Analysis (SEA), used to detect the presence or absence of a volcanic forcing signal in the reconstructed temperature series. The analysis was conducted using (left plot) all known eruptions over the past nine centuries (43 key years), and only those eruptions where the annual stratospheric volcanic sulfate aerosol injections exceeded (middle plot) 20 Tg (15 key years) and (right plot) 40 Tg (7 key years), respectively
7 Summary and concluding remarks
Based on 10 ΔDensity and ΔBI chronologies from 8 sites from along the Scandinavian Mountains and the northern treeline, we provided a new skilful (based on calibration/verification statistics) reconstruction of Fennoscandian summer (JJA) temperatures for the last 900 years. We showed that, compared to previous reconstructions, our reconstruction has a larger spatial expression, representing not only the northern part of Fennoscandia, but also its central parts. However, the southern region remains elusive due to the present lack of ΔDensity and ΔBI from those parts. Based on the data we used, where the Δ parameter strengthens the JJA temperature signal, and the geographical spread of the chronologies, we argue that our reconstruction is presently the best representation for a wider Fennoscandian region. Moreover, using our chronology network, we showed that it is possible to make a skilful field reconstruction for the region. It should be noted that due to the limited spatial distribution of the data, the utilized method does not allow us to fully estimate small scale variability within the grid. To improve the spatial representation as well as constraining the estimates of past summer temperature variability, we advocate that the method described is used and that additional efforts are made to utilize the new BI proxy, which is an affordable complement to density with possibilities to yield similarly excellent temperature information.
References
Björklund JA (2014) Tree-rings and climate: standardization, proxy-development, and Scandinavian summer temperature history. PhD thesis. Department of Earth Sciences, University of Gothenburg. http://www.gvc.gu.se/forskning/klimat/paleoklimat/GULD/Publications/thesises-and-reports/
Björklund JA, Gunnarson BE, Krusic PJ, Grudd H, Josefsson T, Östlund L, Linderholm HW (2013) Advances towards improved low-frequency tree-ring reconstructions, using an updated Pinus sylvestris L. MXD network from the Scandinavian Mountains. Theor Appl Climatol 113:697–710
Björklund JA, Gunnarson BE, Seftigen K, Esper J, Linderholm HW (2014a) Blue intensity and density from Northern Fennoscandian tree rings: using earlywood information to improve reconstructions of summer temperature. Clim Past 10:877–885
Björklund JA, Gunnarson BE, Seftigen K, Peng Z, Linderholm HW (2014b) The merit of using adjusted blue intensity data to attain high-quality summer temperature information: a case study from Central Scandinavia. Holocene (in press)
Briffa KR, Jones PD, Schweingruber FH, Osborn TJ (1998) Influence of volcanic eruptions on Northern Hemisphere summer temperature over the last 600 years. Nature 393:450–455
Briffa KR, Osborn TJ, Schweingruber FH, Harris IC, Jones PD, Shiyatov SG, Vaganov EA (2001) Low-frequency temperature variations from a northern tree-ring density network. J Geophys Res 106:2929–2941
Briffa KR, Osborn TJ, Schweingruber FH, Jones PD, Shiyatov SG, Vaganov EA (2002) Tree-ring width and density around the Northern Hemisphere: part 1, local and regional climate signals. Holocene 12:737–757
Bunn A, Korpela M, Biondi F, Campelo F, Mérian P, Mudelsee M, Qeadan F, Schulz M, Zang C (2014) dplR: dendrochronology program library in R. R package version 1.6.0. http://huxley.wwu.edu/trl/htrl-dplr, http://R-Forge.R-project.org/projects/dplr/
Büntgen U, Tegel W, Nicolussi K, McCormick M, Frank D, Trouet V, Kaplan JO, Herzig F, Heussner K-U, Wanner H, Luterbacher J, Esper J (2011a) 2500 Years of European climate variability and human susceptibility. Science 331:578–582
Büntgen U, Raible C, Frank D, Helama S, Cunningham L, Hofer D, Nievergelt D, Verstege A, Stenseth N, Esper J (2011b) Causes and consequences of past and projected Scandinavian summer temperatures, 500–2100 AD. PLoS One 6:e25133
Campbell R, McCarroll D, Robertson I, Loader NJ, Grudd H, Gunnarson B (2011) Blue intensity in Pinus sylvestris tree-rings: a manual for a new palaeclimate proxy. Tree Ring Res 67:127–134
Chen D, Hellström C (1999) The influence of the North Atlantic oscillation on the regional temperature variability in Sweden: spatial and temporal variations. Tellus A 51:505–516
Cook ER, Briffa KR, Jacoby G (1995) The segment length curse in long tree-ring chronology development for paleoclimatic studies. Holocene 5:229–237
Cook ER, Meko DM, Stahle DW, Cleaveland MK (1999) Drought reconstructions for the continental United States. J Clim 12:1145–1162
Cook ER, Woodhouse CA, Eakin CM, Meko DM, Stahle DW (2004) Long-term aridity changes in the western United States. Science 306:1015–1018
Cook ER, Anchukaitis KJ, Buckley M, D’Arrigo RD, Jacoby JC, Wright WE (2010) Asian monsoon failure and megadrought during the lastmillennium. Science 328:486–489
Cook ER, Krusic PJ, Anchukaitis KJ, Buckley BM, Nakatsuka T, Sano M, PAGES Asia2 k Members (2012) Tree-ring reconstructed summer temperature anomalies for temperate East Asia since 800 CE. Clim Dyn 41:2957–2972
Crowley TJ, Unterman MB (2013) Technical details concerning development of a 1200–year proxy index for global volcanism. Earth Syst Sci Data 5:187–197
D’Arrigo R, Wilson R, Jacoby G (2006) On the long-term context for late twentieth century warming. J Geophys Res 111:D03103
Eschbach W, Nogler P, Schär E, Schweingruber F (1995) Technical advances in the radiodensitometrical determination of wood density. Dendrochronologia 13:155–168
Esper J, Cook ER, Schweingruber FH (2002) Low-frequency signals in long tree-ring chronologies for reconstructing past temperature variability. Science 295:2250–2253
Esper J, Büntgen U, Timonen M, Frank DC (2012) Variability and extremes of Northern Scandinavian summer temperatures over the past two millennia. Glob Planet Change 88–89:1–9
Fischer EM, Luterbacher J, Zorita E, Tett SFB, Casty C, Wanner H (2007) European climate response to tropical volcanic eruptions over the last half millennium. Geophys Res Lett 34:L05707
Folland CK, Knight J, Linderholm HW, Fereday D, Ineson S, Hurrell JW (2009) The summer north Atlantic oscillation: past, present and future. J Clim 22:1082–1103
Frank D, Esper J, Zorita E, Wilson R (2010) A noodle, hockey stick, and spaghetti plate: a perspective on high-resolution paleoclimatology. Wiley Interdiscip Rev: Clim Change 1:507–516
Gao C, Robock A, Ammann C (2008) Volcanic forcing of climate over the past 1500 years: an improved ice core-based index for climate models. J Geophys Res 113:D23111
Gao C, Robock A, Ammann C (2009) A 1500 year ice core-based stratospheric volcanic sulfate data. IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series # 2009-098. NOAA/NCDC Paleoclimatology Program, Boulder CO, USA
Gao C, Robock A, Ammann C (2012) Correction to Volcanic forcing of climate over the past 1500 years: an improved ice core-based index for climate models. J Geophys Res 117:D16112
Gordon G (1982) Verification of dendroclimatic reconstructions. In: Hughes MK, Kelly PM, Pilcher JR, LaMarche VC Jr (eds) Climate from tree rings. Cambridge University Press, Cambridge, pp 58–61
Gouirand I, Linderholm HW, Moberg A, Wolfarth B (2008) On the spatiotemporal characteristics of Fennoscandian tree-ring based summer temperature reconstructions. Theor Appl Climatol 91:1–25
Grudd H (2008) Torneträsk tree-ring width and density AD 500–2004: a test of climatic sensitivity and a new 1500-year reconstruction of north Fennoscandian summers. Clim Dyn 31:843–857
Grudd H, Briffa KR, Karlen W, Bartholin TS, Jones PD, Kromer B (2002) A 7400-year tree-ring chronology in northern Swedish Lapland: natural climate variability expressed on annual to millennial timescales. Holocene 12:657–665
Guiot J, Corona C, ESCARSEL members (2010) Growing season temperatures in Europe and climate forcings over the past 1400 years. PLoS One 5:e9972
Gunnarson BE (2008) Temporal distribution pattern of subfossil pines in central Sweden: perspective on holocene humidity fluctuations. Holocene 18:569–577
Gunnarson BE, Linderholm HW, Moberg A (2011) Improving a tree-ring reconstruction from west-central Scandinavia: 900 years of warm-season temperatures. Clim Dyn 36:97–108
Harris I, Jones PD, Osborn TJ, Lister DH (2014) Updated high-resolution grids of monthly climatic observations: the CRU TS3.10 Dataset. Int J Climatol 34:623–642
Helama S, Lindholm M, Timonen M, Meriläinen J, Eronen M (2002) The supra-long Scots pine tree-ring record for Finnish Lapland: part 2, interannual to centennial variability in summer temperatures for 7500 years. Holocene 12:681–687
Hudson RD (2012) Measurements of the movement of the jet streams at mid-latitudes, in the Northern and Southern Hemispheres, 1979–2010. Atmos Chem Phys 12:7797–7808
Hurrell JW, Kushnir Y, Ottersen G, Visbeck M (2003) An overview of the North Atlantic oscillation. Geophys Monogr Ser 134:1–35
Jones PD, Osborn TJ, Briffa KR (1997) Estimating sampling errors in large scale temperature averages. J Clim 10:2548–2568
Jones PD, Briffa KR, Barnett TP, Tett SFB (1998) High resolution palaeoclimatic records for the last millennium: interpretation, integration and comparison with general circulation model control-run temperatures. Holocene 8:455–471
Jones PD, Moberg A, Osborn TJ, Briffa KR (2003) Surface climate responses to explosive volcanic eruptions seen in long European temperature records and mid-to-high latitude tree-ring density around the Northern Hemisphere, in Volcanism and the earth’s atmosphere. Geophys Monogr Ser 139:239–254
Jones PD, Lister DH, Osborn TJ, Harpham C, Salmon M, Morice CP (2012) Hemispheric and large-scale land-surface air temperature variations: an extensive revision and an update to 2010. J Geophys Res Atmos 117:D05127
Jones PD, Melvin TM, Harpham C, Grudd H, Helama S (2013) Cool North European summers and possible links to explosive volcanic eruptions. J Geophys Res 118:6259–6265
Knight JR, Allan RJ, Folland CK, Vellinga M, Mann ME (2005) A signature of persistent natural thermohaline circulation cycles in observed climate. Geophys Res Lett 32:L20708
Lamb HH (1965) The early medieval warm epoch and its sequel. Palaeogeogr Palaeoclimatol Palaeoecol 1:13–37
Linderholm HW, Walther A, Chen D (2007) Twentieth-century trends in the thermal growing season in the Greater Baltic Area. Clim Change 87:405–419
Linderholm HW, Björklund JA, Seftigen K, Gunnarson BE, Grudd H, Jeong J-H, Drobyshev I, Liu Y (2010a) Dendroclimatology in Fennoscandia: from past accomplishments to future potential. Clim Past 6:93–114
Linderholm HW, Gunnarson BE, Liu Y (2010b) A comparison of two Scots pine tree-ring proxies and standardization methods: examples from the central Scandinavian Mountains. Dendrochronologia 28:239–249
Ljungqvist FC (2010) A new reconstruction of temperature variability in the extratropical Northern Hemisphere during the last two millennia. Geogr Ann 92(A):339–351
Loader N, Young G, Grudd H, McCarroll D (2013) Stable carbon isotopes from Torneträsk, northern Sweden provide a millennial length reconstruction of summer sunshine and its relationship to Arctic circulation. Quat Sci Rev 62:97–113
Lough JM, Fritts HC (1987) An assessment of the possible effects of volcanic eruptions on North American climate using tree-ring data, 1602–1900 AD. Clim Change 10:219–239
Luterbacher J, Dietrich D, Xoplaki E, Grosjean M, Wanner H (2004) European seasonal and annual temperature variability, trends, and extremes since 1500. Science 303:1499–1503
Mann ME, Bradley RS, Hughes MK (1999) Northern hemisphere temperatures during the past millennium: inferences, uncertainties and limitations. Geophys Res Lett 26:759–762
Masson-Delmotte V, Schulz M, Abe-Ouchi A, Beer J, Ganopolski A, González Rouco JF, Jansen E, Lambeck K, Luterbacher J, Naish T, Osborn T, Otto-Bliesner B, Quinn T, Ramesh R, Rojas M, Shao X, Timmermann A (2013) Information from paleoclimate archives. In: Stocker, TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA
McCarroll D, Pettigrew E, Luckman A, Guibal F, Edouard JL (2002) Blue reflectance provides a surrogate for latewood density of high-latitude pine tree-rings. Arct Antarct Alp Res 34:450–453
McCarroll D, Loader NJ, Jalkanen R, Gagen MH, Grudd H, Gunnarson BE, Kirchhefer AJ, Friedrich M, Linderholm HW, Lindholm M, Boettger T, Los SO, Remmele S, Kononov YM, Yamazaki YH, Young GHF, Zorita E (2013) A 1200-year multiproxy record of tree growth and summer temperature at the northern pine forest limit of Europe. Holocene 23:471–484
Meko DM (1997) Dendroclimatic reconstruction with time varying subsets of tree indices. J Clim 10:687–696
Melvin TM (2004) Historical growth rates and changing climatic sensitivity of boreal conifers. Dissertation, University of East Anglia, Norwich, UK
Melvin TM, Briffa KR (2008) A “signal-free” approach to dendroclimatic standardisation. Dendrochronologia 26:71–86
Melvin T, Grudd H, Briffa KR (2013) Potential bias in ‘updating’ tree-ring chronologies using regional curve standardisation: re-processing 1500 years of Torneträsk density and ring-width data. The Holocene 23:364–373
Moberg A, Sonechkin DM, Holmgren K, Datsenko NM, Karlén W (2005) Highly variable Northern hemisphere temperatures reconstructed from low- and high-resolution proxy data. Nature 433:613–617
Oman L, Robock A, Stenchikov G, Schmidt GA, Ruedy R (2005) Climatic response to high latitude volcanic eruptions. J Geophys Res 110:D13103
PAGES 2 k consortium (2013) Continental-scale temperature variability during the past two millennia. Nat Geosci 6:339–346
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res 108(D14):4407
Robock A (2000) Volcanic eruptions and climate. Rev Geophys 38:191–219
Robock A, Mao J (1992) Winter warming from large volcanic eruptions. Geophys Res Lett 19:2405–2408
Schweingruber FH, Fritts HC, Bräker OU, Drew LG, Schär E (1978) The X-ray technique as applied to dendrochronology. Tree Ring Bull 38:61–91
Seftigen K, Björklund J, Cook ER, Linderholm HW (2014a) A field reconstruction of Fennoscandian summer hydroclimate variability for the last millennium. Clim Dyn. doi:10.1007/s00382-014-2191-8
Seftigen K, Cook ER, Linderholm HW, Fuentes M, Björklund J (2014b) The potential of deriving tree-ring based field reconstructions of droughts and pluvials over Fennoscandia. J Clim (in press)
Sutton RT, Hodson DLR (2005) Atlantic Ocean forcing of the North American and European summer climate. Science 309:115–118
Touchan R, Anchukaitis KJ, Meko DM, Sabir M, Attalah S, Aloui A (2011) Spatiotemporal drought variability in northwestern Africa over the last nine centuries. Clim Dyn 37:237–253
Visbeck MH, Hurrell JW, Polvani L, Cullen HM (2001) The North Atlantic oscillation: past, present, and future. Proc Natl Acad Sci 98:12876–12877
Wigley TML, Briffa KR, Jones DP (1984) On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J Clim Appl Meteorol 23:201–213
Young G, McCarroll D, Loader N, Gagen M, Kirchhefer A, Demmler J (2012) Changes in atmospheric circulation and the Arctic oscillation preserved within a millennial length reconstruction of summer cloud cover from northern Fennoscandia. Clim Dyn 39:495–507
Acknowledgments
First of all we would like to thank the County Administrative Boards of Jämtland, Norrbotten and Västerbotten for giving permissions to conduct dendrochronological sampling along the Scandinavian Mountains. We also thank Jan Esper for sharing the NSCAN MXD data, and Danny McCarroll and one anonymous reviewer for their helpful comments and suggestions which helped to improve this manuscript. This work was supported by Grants from the two Swedish research councils (Vetenskapsrådet and Formas, Grants to Hans Linderholm). This research contributes to the Swedish strategic research areas Modelling the Regional and Global Earth system (MERGE), and Biodiversity and Ecosystem services in a Changing Climate (BECC) and to the PAGES2K initiative. This is contribution # 30 from the Sino-Swedish Centre for Tree-Ring Research (SISTRR).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Linderholm, H.W., Björklund, J., Seftigen, K. et al. Fennoscandia revisited: a spatially improved tree-ring reconstruction of summer temperatures for the last 900 years. Clim Dyn 45, 933–947 (2015). https://doi.org/10.1007/s00382-014-2328-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-014-2328-9