Abstract
For the construction of regional climate change scenarios spanning a relevant fraction of the spread in climate model projections, an inventory of major drivers of regional climate change is needed. For the Netherlands, a previous set of regional climate change scenarios was based on the decomposition of local temperature/precipitation changes into components directly linked to the level of global warming, and components related to changes in the regional atmospheric circulation. In this study this decomposition is revisited utilizing the extensive modelling results from the CMIP5 model ensemble in support for the 5th IPCC assessment. Rather than selecting a number of GCMs based on performance metrics or relevant response features, a regression technique was developed to utilize all available model projections. The large number of projections allows a quantification of the separate contributions of emission scenarios, systematic model responses and natural variability to the total likelihood range. Natural variability plays a minor role in modelled differences in the global mean temperature response, but contributes for up to 50 % to the range of mean sea level pressure responses and local precipitation. Using key indicators (“steering variables”) for the temperature and circulation response, the range in local seasonal mean temperature and precipitation responses can be fairly well reproduced.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For many places in the world, climate change projections are an important source of information about changes in the characteristics of the local climate. In the low-lying delta of the Netherlands the impacts of climate variability and change are receiving continued attention, as it is the ability to cope with these varying environmental conditions that partly explains the success of this country. For this a frequent update on the scientific insights concerning climate change and its impacts is required. The construction of regional climate change scenarios is used as a practical tool to carry these scientific insights forward into various sectors in society, including the sectors involved with water management and safety issues (Van den Hurk et al. 2013).
A description of changes in the characteristics of regional climate variables can be facilitated by a systematic analysis of the main drivers of local change. In a previous set of regional climate change scenarios for the Netherlands (Van den Hurk et al. 2007), labelled KNMI’06, uncertainty in the response of two major drivers of regional climate change to altered greenhouse gas and aerosol concentrations was identified: the change of the global mean temperature, and the response of the regional atmospheric circulation. For each of these two drivers indicators were defined that were used as “steering variable” controlling the range of the local response. The steering variables were used to construct 2 × 2 discrete regional climate change scenarios, contrasting the probabilistic approach as pioneered in the UK (Murphy et al. 2009). KNMI’06 was based on an assessment and selection of a set of Global Climate Model (GCM) simulations used in the preparation of the Fourth IPCC assessment report (AR4; IPCC 2007) (Van Ulden and Van Oldenborgh 2006). In addition, a regional downscaling procedure using an ensemble of Regional Climate Models (RCMs) (Lenderink et al. 2007), statistical downscaling using local observations (e.g., Bakker et al. 2011) and regional sea level scenarios (Katsman et al. 2008) were constructed.
Recently, results from the GCM projections from the 5th Coupled Model Intercomparison Project CMIP5 (Taylor et al. 2011) driven by 4 different Representative Concentration Pathways (RCPs) were released. This large ensemble of projections is used to reassess the degree to which uncertainty in local responses can be described by a combination of only two steering variables. This assessment supports the construction of a new set of regional climate change scenarios, based on the updated information from the new climate model projections. Given the inertia in the climate change effect assessment chain, the structure of the scenarios should preferably be consistent with the previous generation, KNMI’06 (Haasnoot and Middelkoop 2012). The scenarios should be conditioned on external drivers that explain a relevant fraction of the projected spread in local temperature and precipitation responses.
The CMIP5 range of projected change in temperature and precipitation in Western Europe is analysed and related to variability in the projected global mean temperature and the regional atmospheric circulation. First the rationale and basic methodology will be explained, followed by the main results. In a final results section the new steering variables are presented and briefly compared to KNMI’06, and we conclude with some final remarks on the use of the steering variables.
2 Method and data
2.1 Rationale and basic methodology
GCM projections of future climate in response to changes in climate forcings—such as greenhouse gas and aerosol concentrations, land use change and solar forcings—display a pronounced range of outcomes due to a combination of differences between model formulation and—structure, internal (natural) variability, and differences in the initialization of climate states (Cox and Stephenson 2007). The magnitude of the variance explained by natural fluctuations varies with the averaging period considered, although natural variability is manifest at all relevant time scales up to multiple decades. At the regional scale (where “regional” refers to areas of sub-continental size) the projected range has a different magnitude and origin than the global mean range of responses. Local feedbacks, advection from remote areas, and a larger amplitude of natural climate variability all contribute to pronounced spatial patterns of climate responses (Hawkins and Sutton 2009).
The condensation of the many possible manifestations of climate change at the regional scale into a limited number of scenarios requires a drastic simplification of the governing interactions while retaining as much of the spread as possible. Hence we focus on the most important processes contributing to the spread in projected response in the regional seasonal mean temperature and precipitation considering a climatic time scale of several decades.
The dominant response to a change in the climate forcings is a change in the global mean temperature. The equilibrium magnitude of this temperature change is given by the product of the strength of the forcing and the climate sensitivity. A second-order response is a change of the spatial pattern of this temperature change, which depends on spatially variable feedbacks and responses. One of these responses is the change in the (surface) pressure patterns governing the atmospheric circulation. Changes in the frequency distribution of patterns of atmospheric circulation can give rise to systematic alterations of the mean temperature and precipitation climate for areas near land–ocean transitions with a strong circulation variability, such as Western Europe (e.g. De Vries et al. 2012). Being situated in a strong climatic gradient over the land-sea transition, the local climate in the environment of the Netherlands is strongly related to advection and convergence of moisture and heat. Increased frequency of westerlies leads to a regional warming and wetter conditions in winter, and relatively cool and wet summer conditions.
Appreciating the fact that other responses or forcings may impose substantial effects on the regional temperature or precipitation climate in Western Europe, we derive only two steering variables for regional climate change scenarios: the global mean temperature change, and the atmospheric circulation response. Usage of the global mean temperature change as driver combines the range in climate forcing, the range in (model specific) climate sensitivity and the varying spatial temperature patterns into a single variable, explaining a large fraction of the variability of local temperature response. The quantity expressing the range in circulation response is chosen in order to optimize the explained variance in the local precipitation response across the large ensemble of GCM projections. This method implies a strong link between the steering variables and the local expression of seasonal mean temperature and precipitation change. This is different from an a priori ranking of major response patterns for different subregions, as is applied for instance for Australian climate change scenarios by Whetton et al. (2012). In our case, the target domain is sufficiently small to define fairly robust large scale climate patterns that are optimised to maximise the explained variance in the target region across models (Watterson 2012).
The method is designed to disentangle the circulation effects on regional temperature and precipitation change from changes imposed by the first order global mean temperature increase. This is achieved by a two-step approach: the first step establishes a relation between modelled responses in regional climate variables and global mean temperature, while in the second step circulation induced anomalies of this regional response to global mean temperature change are derived. In step one we express the response of all quantities as a change per unit global warming, obtained from transient climate projections. These so-called normalized responses are used to find deviations from the first order linear response to the global warming, related to anomalies in the atmospheric circulation response (step two).
2.2 Available model data
The response range is deduced from 245 transient CMIP5 climate integrations (1950–2100) distributed over four RCPs, provided by up to 37 modelling systems per RCP. A total number of 110 GCM/RCP combinations were used (see “Appendix” for an overview). Many modelling systems provided multiple realizations for a given RCP, allowing to distinguish between forced and unforced (“natural”) climate variability. The included simulations matched all CMIP5 integrations that are used to prepare the AR5 Working Group 1 Annex I “Atlas” (Collins et al. 2013) except FIO-ESM. This model simulated a strong regional cooling in Western Europe, probably related to a strong decline of the Atlantic Meridional Overturning Circulation (AMOC). It is a strong outlier in the CMIP5 ensemble, thereby violating many assumptions of linearity in the statistical analysis executed here. The model generates an interesting future scenario for Western Europe, but a collapse of the AMOC is explicitly not included in the updated climate change scenarios. FIO-ESM is excluded from the analysis presented here.
The four RCPs have been covered by a variable number of models, and the models have used a variable number of ensemble members for each projection. From each run temperature, precipitation and mean sea level pressure have been gridded to a common 2.5 × 2.5° grid (without considering land/sea contrasts explicitly), averaged to monthly values, and split into seasonal archives following the normal midlatitude meteorological convention (DJF = December–January–February, MAM = March–April–May, JJA = June–July–August and SON = September–October–November). From these simulations, a transient response is derived by subtracting (temperature, pressure) or dividing by (precipitation) the climatology of a reference period (1976–2005) from any (future) time slice average. The choice of the reference period allows comparison of the results to the KNMI’06 scenarios released earlier.
The response of local temperature (ΔT loc ) and precipitation (ΔP loc ) that is analysed here concerns the projected response in an area roughly encompassing the Rhine basin (6°–9°E, 47°–52°N). Model results interpolated to the four 2.5 × 2.5° grid points within this domain are spatially averaged. The use of this averaged sample of grid points in this area suppresses spatial noise induced by for instance the nearby land-sea gradient, and reflects climate variability in an area that is relevant for the Netherlands, which is situated in the Rhine discharge area.
3 Response patterns from the model ensemble
In this section we will first analyse the patterns of response in temperature and mean sea level pressure for the 110 GCM/RCP combinations, followed by exploring mean sea level pressure (MSLP) patterns that are optimally related to the variability of the projected temperature or precipitation in the Rhine area. From these analyses the temperature and circulation steering variables will be derived. Finally, an analysis of the degree to which natural variability contributes to the range in projected steering variables will be presented.
3.1 Global and regional temperature response
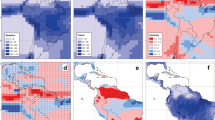
Considerable spread in calculated global mean temperature response can be expected when a common climate forcing is provided to a range of GCMs (Rogelj et al. 2012). This spread represents differences in the modelled climate response and its spatial structure, and internal variability of the climate system. However, the spatial structure of the temperature response between the reference period and any future time slice during the twenty-first century is fairly robust among the models. For each season Fig. 1 shows this average warming pattern. It is a weighted average of the slope of the best-fit regression for each GCM/RCP combination between the ensemble mean projected temperature response at a given location and the global mean temperature (∂T/∂T glob ) for all years in the 1976–2100 period. For this slope of the regression of a variable X against global mean temperature we use the notation ΔT X in the following. The weights are inversely proportional to the number of GCMs running a particular RCP (see “Appendix”), giving equal weights to each RCP. However, the patterns are rather similar across the different RCPs (not shown), hence the response scales to a good approximation linearly with the global mean temperature (Giorgi 2005; Mitchell 2003). For the Atlantic sector of the Northern Hemisphere land areas warm faster than the ocean in all seasons, and high latitudes warm much faster than the global mean outside the summer season, due to among other factors the feedbacks involving sea ice and snow. The Southern and Western European continents warm stronger in JJA and SON than in the winter/spring seasons (Haarsma et al. 2009). A muted response is evident in the Northwest Atlantic, corresponding to the subpolar gyre, which warms up less due to a reduction of the Atlantic Meridional Overturning Circulation (AMOC) (Drijfhout et al. 2013).
Colour shading: Seasonal mean 2 m temperature response as fraction of the global mean temperature response [−] (ΔTT) averaged for 110 ensemble mean GCM/RCP combinations, obtained by regression between time series of local temperature on global mean temperature. In the averaging of the GCM/RCP combinations every RCP is given equal weight. Contour lines: RMSE [K] of the regression, averaged over the GCM/RCP combinations. The red box indicates the area for which the temperature pattern strength PT is calculated
The warming pattern in a large zone encompassing the Western European continent and the North Atlantic sector varies quasi-linearly with ΔT glob across the GCM/RCP ensemble. For each individual GCM simulation the strength of the regional warming Pattern of Temperature, PT, is expressed as a projection on the weighted mean response:
where the subscript i refers to the GCM simulation, the overbar denotes the weighted mean of all GCM/RCP combinations (Fig. 1), and the summation takes place of all grid points in the area indicated in Fig. 1. The fraction of explained variance of the relationship between PT and ΔT glob (calculated by the squared correlation coefficient) ranges between 86 % in DJF and 94 % in SON (Table 1).
The strong relationship between the global mean temperature response and the warming pattern strength does also reflect a robust relationship between the modelled global mean warming and the temperature response in a small area as the Rhine basin. 75 to 91 % of the variance of the temperature response in the Rhine basin (ΔT loc ) across the GCM ensemble is explained by the variance in ΔT glob , depending on the season (Table 1; see Fig. 2). This fraction of explained variance is increased slightly to 93–96 % when variability in the strength of the warming pattern is taken into account (regression between PT and ΔT loc ). This would be a reason to use PT is a steering variable for the regional climate change scenarios. However, the slightly higher fraction of explained variance compared to ΔT glob was not considered to be enough to compensate for the increased complexity resulting from the addition of the inter-model variations of the warming pattern. Therefore we proceed using ΔT glob as our first steering variable.
Local temperature response per GCM/RCP combination in 2071–2100 relative to 1976–2005 as function of ΔTglob over the same period. Numbers refer to the GCM system (see “Appendix”), color code refers to the RCP. Also shown is the best linear fit (solid lines) and the 1:1 slope (dotted lines)
The relation between ΔT loc and ΔT glob varies considerably over the seasons (Fig. 2). In DJF and MAM the projected local temperature increase corresponds closely to the global mean temperature increase. However, in summer and autumn local feedback processes (such as continental drying, or cloud responses to surface warming) amplify the warming in the Rhine basin, up to 1.6 times the global mean temperature increase. This seasonal signature is only partially consistent with the findings of Van Oldenborgh et al. (2009), who explored the seasonality in modelled and observed regional warming trends using several model ensembles, including phase 3 of the Coupled Model Intercomparison Project. In their analysis also MAM showed a relatively strong regional warming. However, their main conclusion is that the observed warming trends (1950–2008) exceed the projected regional anomalies strongly, also in the winter season. Apparently also for this extensive CMIP5 ensemble a bias in the projected regional warming trend needs to be interpreted carefully in order to determine the (near-term) local temperature trend projections.
3.2 Response in surface pressure
The distinct warming pattern can lead to a systematic change in the mean sea level pressure. Figure 3 shows the MSLP response per unit global warming across the collection of GCMs and RCPs, obtained by the slope of the best-fit regression between T glob and MSLP over the 1976–2100 period and weighted across the 110 GCM/RCP combinations as for the temperature response (Fig. 1). This normalized MSLP response shows a marked seasonal pattern, with opposite responses in the Mediterranean area for DJF and JJA, and generally high pressure anomalies West of the British Isles. The Mediterranean response in JJA represents a typical surface heat low response related to the strong Mediterranean warming (Haarsma et al. 2009). The East Atlantic high pressure response in the warm seasons projects well on the Summer North Atlantic Oscillation (SNAO) (Bladé et al. 2012) and may be related to the relative cooling in the Northwest Atlantic.
As Fig. 1 for the normalized MSLP response (ΔTMSLP, [hPa/K] computed over the period 1976–2100). Contour lines indicate one standard deviation of normalized MSLP responses across the GCM ensemble [hPa/K]. The red box indicates the area for which the pattern strength PSmean is calculated
3.3 Pressure fields related to local temperature and precipitation response
Variations across the model ensemble of the pressure response will lead to deviations in local temperature and precipitation responses (e.g. Rodwell et al. 1999). This sensitivity of the local climate to the regional atmospheric circulation makes it relevant to consider variations in the MSLP response within the large CMIP5 GCM/RCP ensemble. In the following we will explore a number of indicators for atmospheric circulation response.
An efficient way to define pressure patterns whose variability is well correlated to the variability in ΔT loc or ΔP loc is linear regression between MSLP and the local climate variables across the ensemble of all 110 GCM/RCP combinations. Wallace and Gutzler (1981) applied this technique to find teleconnection patterns involving the dynamics of geopotential height. However, all quantities involved (ΔMSLP, ΔT loc and ΔP loc ) are strongly related to global mean temperature response, which makes a pattern obtained by a straight regression between ΔMSLP and ΔT loc or ΔP loc not a suitable independent steering variable. This can be avoided by looking for patterns in normalized MSLP response (ΔT MSLP) that explain large fractions of variance in normalized local responses, ΔT T loc and ΔT P loc . Using normalized values for both variables removes a possible strong correlation to ΔT glob , and expresses the degree to which regional atmospheric circulation changes will result in local responses that are largely independent from ΔT glob .
In the KNMI’06 climate change scenarios variations in the response of the regional atmospheric circulation were evaluated by the zonal component of the geostrophic wind speed, G west . Here we evaluate this circulation variable for our GCM/RCP ensemble, by calculating it from ΔT MSLP (Fig. 3) in a 20 × 20° area centred at (10°E, 50°N). The quantity thus obtained the response in Eastward geostrophic wind per degree global mean warming. In order to assess the degree to which model variations in G west response can explain variations in local temperature or precipitation responses, the fraction of explained variance (squared correlation coefficient) of the regression between ΔT G west and the normalized local temperature/precipitation responses ΔT T loc and ΔT P loc is shown in Table 2. Lenderink et al. (2007) explored this relation for DJF and JJA for a selection of regional climate model integrations. The results from our study demonstrate that G west is to some extent related to variations in the precipitation response in SON and DJF, and to the JJA temperature response, but the fractions of variance explained are relatively low. G west ignores variations in meridional pressure gradients or vorticity, which are circulation characteristics that are considered important for the local temperature and precipitation climate (Van Ulden and van Oldenborgh 2006).
Another way to quantify model spread in the MSLP response is to diagnose the projection of the individual model response on the ensemble mean response, as shown in Fig. 3. This projection is limited to an area of influence to P loc and T loc . Trial and error experimentation with the size and position of this area revealed that using (30°W–40°E) to (30°N–65°N) is optimally correlated to these local climate characteristics. The quantity of interest, labelled PS mean then is defined as
where the overbar denotes the weighted mean response, σ(ΔT MSLP)i is the spatial standard deviation of the normalized MSLP response of model i within the defined area, and the correlation is applied across all grid points within this area. PS mean is high for models with a pressure response that has a similar spatial structure as the mean response, and for which the spatial variability (the pattern amplitude) is strong. Table 2 shows that this expression of regional pressure response does not outperform G west , although more circulation characteristics are incorporated. This can be compared to a study by Cattiaux et al. (2012), who explored the contribution of changes in the variability of the regional surface pressure distribution to the European mean temperature using analogues. In their analysis changes in the variability of the atmospheric circulation did not lead to systematic changes in the European mean temperature. Although our temperature metric is different since it is limited to the Rhine basin area, and we explore variations of seasonal means, the low fraction of explained variance reported in Table 2 is consistent with their results.
The MSLP response pattern that is optimally correlated to variations in ΔT loc , obtained by linear regression between the fields of ΔT MSLP and the normalized temperature response in the Rhine area (ΔT T loc ) across the GCM/RCP ensemble, is shown in Fig. 4. For DJF and JJA the patterns show a similarity with the mean MSLP response (Fig. 3) with a high and low MSLP response in the Mediterranean area for DJF and JJA respectively, implying that local temperature anomalies are to some extent governed by relatively strong or weak regional pressure response anomalies. Note however that the Summer NAO pattern does not project strongly on temperature in the Rhine basin. For the transition seasons, e.g. MAM, the local temperature anomalies are affected by quite different pressure anomalies than the mean pressure response. In SON the local temperature response is hardly correlated to pressure response anomalies in a large surrounding domain. In DJF high temperatures in the Rhine basin are associated with South-westerly flows. In JJA warm easterlies set up by a relatively low pressure response in Southern Europe is favourable for above average temperature conditions.
Normalized MSLP response pattern [hPa/K] related to the normalized Rhine basin temperature response Tloc [K/K], derived from linear regression across the sample of GCM/RCP combinations. Areas where the fraction of explained variance of the regression between Tloc and MSLP (indicated by contour lines) <0.05 are blanked. The red box indicates the area where the pattern strength PST is defined
A similar procedure aimed at finding MSLP anomalies that co-vary with precipitation anomalies in the Rhine area leads to different spatial MSLP response distributions (Fig. 5). In all seasons except MAM a dipole pattern with a relatively low MSLP response in the Baltic area and a high pressure anomaly in the Southwest leads to relatively wet responses in the Rhine area. This relative pressure distribution sets up a north-westerly flow bringing relatively warm and moist air into the NW European area, which explains its coincidence with a positive local precipitation response. For MAM the best fit pattern is a low pressure area overlying the Rhine basin. Note that the MSLP anomalies per percent of precipitation change vary strongly over the seasons. During JJA the relation between ΔT P loc and ΔT MSLP is very sensitive (and in fact explains a relatively low fraction of variance; Table 2): small pressure anomalies are related to large relative precipitation responses.
As Fig. 4 for the normalized pressure response related to Rhine basin precipitation response [hPa/%]. Note the different color scale for each season
A quantitative relationship between the patterns depicted in Figs. 4 and 5 and the local climate characteristics can again be obtained by utilizing Eq. 2 to express the correspondence between the normalized pressure response in any given GCM projection and the target patterns. Similar to the definition of PS mean we can define a temperature related pressure response index PS T by
where MSLP T denotes the best fit value of ΔT MSLP versus ΔT T loc shown in Fig. 4, and σ and ρ are calculated over all grid points within the denoted area with a fraction of explained variance >0.05. Equivalently, a precipitation related pressure response index PS P is
with MSLP P equal to the best fit value of ΔT MSLP versus ΔT P loc shown in Fig. 5.
Table 2 shows the fraction of explained variance of local temperature and precipitation responses when using PS T or PS P as predictor. Not surprisingly, precipitation anomalies co-vary much better with PS P than with G west or PS mean , while for temperature PS T gives the best correspondence in DJF and JJA. The poor relationship between ΔT loc and PS P can well be understood from comparing the patterns shown in Figs. 4 and 5. In DJF, for instance, positive temperature anomalies require South-western flow regimes while relatively high precipitation responses are associated with North-westerly flows. Although these North-westerlies do transport maritime air masses into the Western European domain, they have a cooler area of origin than South-western flow directions (Sepp and Jaagus 2002). It will thus be impossible to define an indicator for atmospheric circulation responses that explains a fair amount of intermodal variability for both temperature and precipitation response in the area of interest. The consequences of this will be explored below.
3.4 Natural variability
The modelled response to the RCP radiative forcing varies across the ensemble of projections due to a combination of differences in model formulation and inherent natural variability. This is clearly illustrated in Fig. 6, where the evolution of the projected PS p and T glob , averaged using a running mean filter of 30 years, is shown. The monotonic increase in T glob with time is employed by considering T glob as the independent variable, plotted on the horizontal axes. In these plots, the time dependence of PS p is expressed by defining MSLP i in Eq. (4) as the (time varying) MSLP response relative to the mean MSLP in the 1976–2005 reference period. Shown are the results from the 110 ensemble mean GCM/RCP combinations, together with individual ensemble members from a single GCM (EC-Earth). The spread in PS p from the collection of GCM/RCP models (which includes different RCPs) is substantially reproduced by the ensemble members of this single GCM. EC-Earth appears to have a relatively low response in global mean temperature, reflecting a moderate climate sensitivity (Hazeleger et al. 2012). Its MSLP response varies around small values for all seasons except JJA and MAM, where it follows the GCM ensemble towards a negative expression of the pattern shown in Fig. 5 as ΔT glob increases. This gradual decrease of PS p is associated with a systematic warming and drying in the Mediterranean area (see Fig. 3) that imposes dry conditions at higher latitudes (Haarsma et al. 2009). The small systematic MSLP response in DJF suggests that EC-Earth is a relative outlier in the ensemble of GCMs. In this season a persistent MSLP response is apparent, since some individual time series diverge and don’t rejoin the ensemble plume anymore. However, this is an artefact of the expression of the MSLP response relative to a reference value which is diagnosed from the very same ensemble member.
Time series projection covering 1976–2100 of PSP as function of global mean temperature response filtered with a 30 year running mean averaging window for the four seasons. PSP is defined using the time-varying MSLP response relative to the mean in the 1976–2005 reference period. Grey lines indicate the ensemble mean GCM experiments for all RCPs, while the coloured lines show results from individual ensemble members from two RCP-experiments carried out with the EC-Earth GCM (model ID 13 and 14 in “Appendix”). Note the different scales of the vertical axes
The presence of GCMs running multiple ensemble members per RCP (see “Appendix”) allows an estimate of the contribution of natural variability to the overall spread in the response. The ratio between the signal and total variance is estimated from a comparison between the ensemble spread of the group of models with ≥3 members to the ensemble spread for all members in the entire ensemble. A weighted estimate of the total variance σ 2e across the collection of individual model ensemble members running a particular RCP is given by
where n i is the number of ensemble members for model i, n GCM is the total number of models running a particular RCP scenario, and the overbar denotes the average of all GCMs participating in a particular RCP. x ij is the response in a given time slice of member j from model i, and n i is the total number of ensemble members for model i. In this expression every GCM gets an equal weight, regardless its number of ensemble members. The natural variability σ 2n was estimated as the ensemble spread averaged for all models with at least 3 ensemble members for a given RCP projection:
where n ni≥3 indicates the GCMs with ≥3 ensemble members, and the overbar refers to the ensemble mean of GCM i participating in the given RCP. The signal/total variance ratio S/T can then be written as
where “signal” refers to the systematic difference in temperature or MSLP response across the sample of GCM/RCP combinations. The results are slightly sensitive to the minimum number of members per model used to define σ 2n .
Figure 7 shows the signal to total variance ratio for both steering variables ΔT glob and PS p and the local temperature and precipitation responses for the four different scenarios. For the global mean temperature in all seasons the variance is dominated by the difference between the ensemble mean model responses, S/T ≈ 1. For the pressure pattern response the situation is quite different. For instance, in all seasons except JJA the variance across the model mean responses is 40–60 % of the total variance across the individual members with a tendency to increase as the climate forcing increases over the scenarios. Natural variability thus accounts for nearly half of the overall variance. In JJA the variance across the models is significantly larger than in the other seasons. The natural variability adds a similar absolute amount of variance to the spread across the model mean responses, but the relative contribution is smaller than in the other seasons.
Fraction of variance in global mean temperature response Tglob pressure response index PSp and local temperature and precipitation response Tloc and Ploc in the time slice 2071–2100 for each RCP arising from a systematic difference between ensemble mean GCM projections (signal/total variance). Values <<1 imply a strong contribution of natural variability diagnosed from the spread between individual ensemble members from a GCM experiment. RCPs are colour-coded as in Fig. 2
The S/T ratio of local responses in temperature and precipitation generally increase as the climate forcing (RCP) becomes stronger. Natural variability is not a dominant factor explaining variability in ΔT loc , but for precipitation it contributes stronger to the spread in model results. Estimates of contributions of natural variability to the overall response are broadly consistent with the findings of Deser et al. (2012).
4 Regional mean temperature and precipitation response
In order to reconstruct the local temperature and precipitation response from the steering variables ΔT glob and PS p explored above a simple multivariate regression equation is used (Van Ulden and Van Oldenborgh 2006):
where ΔX loc is the local response (either temperature or precipitation), and a x and b x describe the relationship between the large scale steering variables and the local responses, which vary seasonally. a x and b x are found from the multivariate regression between ΔX loc , ΔT glob and PS p across the ensemble of GCM/RCP projections. Selecting representative values of ΔT glob and PS p allows to derive scenario values of ΔT loc and ΔP loc .
Figure 8 shows a condensation of the results illustrated in Fig. 6, by plotting the mean responses of ΔT glob and PS p for the 2071–2100 period for each GCM/RCP combination compared to the reference period. Except at low values of ΔT glob (particularly for RCP2.6 with its highly non-linear trend in ΔT glob ), the pressure response index PS p of most models can be found within a range that is linearly increasing with ΔT glob , as indicated by the dotted lines in Fig. 8. This range is quantified by taking the 1 and 99 percentile value of the ensemble of ΔPS p /ΔT glob values from all model projections except RCP2.6.
Scatter plot of projected change in Tglob and PSp over the time slice 2071–2100 relative to the reference period 1976–2005 for each GCM/RCP combination. Dotted lines denote the assumed range of PSp values for a given global mean temperature increase (see text). Colors and labels as in Fig. 2. Note the different scale of the vertical axes
In KNMI’06 the global mean temperature steering variables for the end of the twenty first century were chosen to be 2 and 4 K increase relative to the reference period 1976–2005. From the present study the matching values of the circulation steering variable PS p are chosen to span the range marked by the dotted lines shown in Fig. 8 (see Table 3).
Figure 9 shows the estimated local precipitation and temperature response for all projections using Eq. 8 and the values corresponding to the steering variables based on the KNMI’06 values (Table 3). This demonstrates the range of the local climate change scenarios generated by applying the steering variable values in Table 3, and allows a comparison with the previous KNMI’06 scenarios for local responses in temperature and precipitation.
Mean response in local temperature and precipitation between the reference period and 2071–2100 for each GCM/RCP combination (colour-coded and labelled as in Fig. 2). The four corner points of the grey shapes mark the results obtained from the regression Eq. (8) and using steering variable values indicated in Table 3. Blue dots connected by dashed lines show the results obtained from the previous climate change scenarios KNMI06
The selection of ΔT glob = 2 K as the lowest value is clearly inconsistent with the modelled response to the RCP2.6 scenario. Simultaneously, quite some models project higher local temperature responses than generated by our scenario procedure using ΔT glob = 4 K. For most seasons except JJA the range in local precipitation response, induced mainly by assumed variations in circulation patterns, is larger than in KNMI’06. Also, the new regressions span the projected range in local precipitation responses better than the old scenarios, which is consistent with the improved fraction of explained variance compared to the use of G west (Table 2). Note that we only purport to span the model uncertainty by the choice of steering parameters, which is about half the total variability (Fig. 7). Natural variability in the 30-year time slices causes the models to fall outside the grey areas, especially for models with only a single realisation. For JJA the local warming anomaly relative to ΔT glob is quite a bit stronger than assumed in KNMI’06 (cf. Fig. 2), while a positive precipitation response is not generated by the current procedure, in contrast with earlier results. Precipitation response in both MAM and especially SON remain to be very uncertain, with both scenario procedures leading to positive and negative response values.
5 Discussion and conclusions
An extensive set of GCM projections has been used to analyse main drivers of regional climate change in the Rhine basin area and the Netherlands. Unlike the previous set of KNMI climate scenarios, no selection of the available GCM projections has been applied based on a metric such as the one proposed by Reichler and Kim (2008). Common model biases in mean, variability and trends that make the raw model data unrealistic are thus not explicitly dealt with. 245 ensemble members of up to 37 modelling systems simulating 4 transient RCP scenarios were used to generate a set of robust patterns of regional temperature response relative to the global mean warming. Similarly, a regression between local precipitation response and MSLP yields physically plausible pressure distributions that are well related to the local response.
We find warming patterns in the region of Western Europe that support earlier findings of larger than average warming of the land area (particularly in boreal summer) and a strong Arctic amplification (in boreal winter). The surface pressure response to this warming varies stronger over the model ensemble than the spatial temperature response fields, but show clear patterns of high pressure anomalies in the Mediterranean (DJF) and west of the British Isles (JJA). This pressure response does not necessarily lead to uniform responses in temperature or precipitation in the Rhine basin: pressure response patterns that lead to strong temperature anomalies are different from the response patterns that generate large precipitation anomalies. Since temperature variance is largely explained by differences in projected global mean temperature, we have selected the pressure response pattern that explains local precipitation responses optimally as a second steering variable. With these steering variables we are able to span a considerable fraction of the CMIP5 range in local temperature and precipitation responses.
Natural variability (calculated for 30 year averages) gives a minor contribution to the global mean temperature response. However, it does account for approximately 50 % of the range projected by the different GCM and RCP combinations for all seasons except JJA. This large fraction of natural variability in the total variance leads to lower fractions of explained variance of local precipitation response, but can generally be used to select time slices of individual ensemble members from a given GCM projection that is representative for a particular scenario steering variable value, even if the full output of GCMs that show this behaviour is unavailable. Downscaling of these time slices will enable the construction of scenario values of other relevant local weather variables, such as higher quantiles of (daily) temperature and precipitation, or quantities like evaporation, wind speed, radiation or atmospheric humidity.
The steering variables serve their purpose of collapsing most of the scenario and model uncertainty of climate change in a small spatial domain onto a two-dimensional space that is sampled by 2 × 2 discrete scenarios. As such it is conceptually very different from approaches where ensembles of GCM projections are downscaled using dynamical or statistical methods. Our approach ensures that a wide ensemble of projections can be analysed in a singular framework. Although the ensemble of downscaled model projections rapidly increases for many regions including Europe (Giorgi et al. 2009), it is still a considerable effort to generate an ensemble as large as the one that is used here. In addition, our method is particularly useful for regimes for which a limited number of external factors can be identified that explain a fair amount of variance across the ensemble of projections in the area of interest. This applies to small areas like the Rhine basin here, or areas subject to a strong forcing from for instance the North Atlantic Oscillation or the El Niño Southern Oscillation (ENSO).
Since our method mainly quantifies modes of uncertainty that can be related to large scale external drivers, local implications of variability of these drivers still need to be assessed with methods that are able to resolve processes at finer spatial or temporal scales. Our method generates boundary conditions from which a set of suitable GCM projections or time slices can be selected in the clouds of Fig. 9 that are further downscaled dynamically (see e.g. Lenderink et al. 2007). Dynamical or This downscaling allows generating the spatially consistent high-resolution numerical fields required by impact models. Methods to deal with common model biases before or after downscaling are subject of on-going research.
References
Bakker AMR, Van den Hurk BJJM, Bessembinder JJE, Kroon T (2011) Reduced climate forcings for large-scale hydrological scenario calculations. Environ Model Softw 26:797–803
Bladé I, Liebmann B, Fortuny D, van Oldenborgh GJ (2012) Observed and simulated impacts of the summer NAO (SNAO) in the Southern Europe/Mediterranean region: connections to projected drying in this region. Clim Dyn 39:709–727. doi:10.1007/s00382-011-1195-x
Cattiaux J, Yiou P, Vautard R (2012) Dynamics of future seasonal temperature trends and extremes in Europe: a multi-model analysis from CMIP3. Clim Dyn 38:1949–1964. doi:10.1007/s00382-011-1211-1
Collins M, Arblaster J, Hesselbjerg Christensen J, Marozke J, van Oldenborgh GJ, Power S, Rummukainen M, Zhou T (2013) Annex I: Atlas of global and regional climate projections. In Stocker, Qin (eds), Fifth assessment report of the IPCC, WG1: the physical basis (to appear)
Cox P, Stephenson D (2007) Climate change—a changing climate for prediction. Science 317:207–208
De Vries H, Haarsma R, Hazeleger W (2012) Western European cold spells in current and future climate. Geophys Res Lett 39:L04706. doi:10.1029/2011GL050665
Deser C, Phillips A, Bourdette V, Teng H (2012) Uncertainty in climate change projections: the role of internal variability. Clim Dyn 38:527–546
Drijfhout S, van Oldenborgh GJ, Cimatoribus A (2013) Is a decline of AMOC causing the warming hole above the North Atlantic in observed and modeled warming patterns? J Clim. doi:10.1175/JCLI-D-12-00490.1
Giorgi F (2005) Interdecadal variability of regional climate change: implications for the development of regional climate change scenarios. Meteorol Atmos Phys 89:1–15
Giorgi F, Jones C, Asrar GR (2009) Addressing climate information needs at the regional level: the CORDEX framework. WMO Bull 58:175–183
Haarsma RJ, Selten FM, van den Hurk BJJM, Hazeleger W, Wang X (2009) Drier Mediterranean soils due to greenhouse warming bring easterly winds over summertime central Europe. Geophys Res Lett 36:L04705. doi:10.1029/2008GL036617
Haasnoot M, Middelkoop H (2012) A history of futures: a review of scenario use in water policy studies in the Netherlands. Environ Sci Policy 19:108–120
Hawkins E, Sutton R (2009) The potential to narrow uncertainty in regional climate predictions. Bull Am Meteorol Soc 90:1095–1107
Hazeleger W, Wang X, Severijns C, Ştefănescu S, Bintanja R, Sterl A, Wyser K, Semmler T, Yang S, van den Hurk B, van Noije T, van der Linden E, van der Wiel K (2012) EC-Earth V2.2: description and validation of a new seamless Earth system prediction model. Clim Dyn 39:2611–2629. doi:10.1007/s00382-011-1228-5
IPCC (2007) Climate Change 2007: the physical science basis. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL (eds) Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Katsman CA, Hazeleger W, Drijfhout SS, van Oldenborgh GJ, Burgers GJH (2008) Climate scenarios of sea level rise for the northeast Atlantic Ocean: a study including the effects of ocean dynamics and gravity changes induced by ice melt. Clim Change 91:351–370. doi:10.1007/s10584-008-9442-9
Lenderink G, van Ulden A, van den Hurk B, Keller F (2007) A study on combining global and regional climate model results for generating climate scenarios of temperature and precipitation for the Netherlands. Clim Dyn 29:157–176
Mitchell TD (2003) Pattern Scaling—an examination of the accuracy of the technique for describing future climates. Clim Change 60:217–242
Murphy JM, Sexton DMH, Jenkins GJ, Booth BBB, Brown CC, Clark RT, Collins M, Harris GR, Kendon EJ, Betts RA, Brown SJ, Humphrey KA, McCarthy MP, McDonald RE, Stephens A, Wallace C, Warren R, Wilby R, Wood R (2009) UK climate projections science report: climate change projections. Met Office Hadley Centre, Exeter
Reichler T, Kim J (2008) How well do coupled models simulate today’s climate? Bull Am Meteorol Soc 89:303–311
Rodwell MJ, Rowell DP, Folland CK (1999) Oceanic forcing of the wintertime North Atlantic Oscillation and European climate. Nature 398:320–323
Rogelj J, Meinshausen M, Knutti R (2012) Global warming under old and new scenarios using IPCC climate sensitivity range estimates. Nat Clim Change 2:248–253. doi:10.1038/nclimate1385
Sepp M, Jaagus J (2002) Frequency of circulation patterns and air temperature variations in Europe. Boreal Environ Res 7:273–279
Taylor KE, Stouffer RJ, Meehl GA (2011) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:485–498. doi:10.1175/BAMS-D-11-00094.1
Van den Hurk BJJM, Klein Tank AMG, Lenderink G, van Ulden A, van Oldenborgh GJ, Katsman C, van den Brink H, Keller F, Bessembinder J, Burgers G, Komen G, Hazeleger W, Drijfhout S (2007) New climate change scenarios for the Netherlands. Water Sci Technol 56:27–33. doi:10.2166/wst.2007.533
Van den Hurk B, Klein Tank A, Katsman C, Lenderink G, te Linde A (2013) Tailored climate change scenarios for vulnerable sectors in the Netherlands. In: Roger A, Pielke Sr (eds) Climate vulnerability. Academic Press, San Diego (in press)
Van Oldenborgh GJ, Drijfhout SS, van Ulden A, Haarsma R, Sterl A, Severijns C, Hazeleger W, Dijkstra H (2009) Western Europe is warming much faster than expected. Clim Past 5:1–12. doi:10.5194/cp-5-1-2009
Van Ulden AP, van Oldenborgh GJ (2006) Large-scale atmospheric circulation biases and changes in global climate model simulations and their importance for climate change in Central Europe. Atmos Chem Phys 6:863–881
Wallace JM, Gutzler DS (1981) Teleconnections in the Geopotential Height Field during the Northern Hemisphere Winter. Mon Weather Rev 109:784–812
Watterson IG (2012) Understanding and partitioning future climates for Australian regions from CMIP3 using ocean warming indices. Clim Change 111:903–922
Whetton P, Hennessy K, Clarke J, McInnes K, Kent D (2012) Use of Representative Climate Futures in impact and adaptation assessment. Clim Change 115:433–442
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
See Table 4.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
van den Hurk, B., van Oldenborgh, G.J., Lenderink, G. et al. Drivers of mean climate change around the Netherlands derived from CMIP5. Clim Dyn 42, 1683–1697 (2014). https://doi.org/10.1007/s00382-013-1707-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-013-1707-y