1 Introduction

Low-frequency climate variability is important because it may mask the greenhouse-warming signal in the present climate record (Knight et al. 2005). It is also the main contributor to low-frequency variations of regional climate (Sutton and Hodson 2005).

Variability on time scales from decadal to centennial scales has been detected in a large number of observations (e.g., Bjerknes 1964; Levitus 1989; Kushnir 1994; Minobe 1997; Gray et al. 2003, 2004). Studies with numerical models suggest that this low-frequency variability may originate from the variation of the meridional overturning circulation (MOC) (e.g., Delworth et al. 1993; Häkkinen 1999, 2000).

However, the mechanisms of the low-frequency MOC variability, particularly the role of ocean–atmosphere coupling and ocean dynamics, are not fully understood. On the one hand, the low-frequency variability may arise as an ocean self-sustained mode (e.g., Weaver and Sarachik 1991; Weaver et al. 1991; Huck et al. 1999, 2001; Te Raa and Dijkstra 2002, 2003). This variability relates to a phase difference between changes in the meridional heat transport and a zonal redistribution of density anomalies, and is linked to weakening and strengthening of the deep water formation in the high latitudes and the subsequent generation and removal of east–west steric height gradients.

On the other hand, an interplay between the atmosphere and the ocean, through either ‘one-way’ (the ocean responds to the atmospheric forcing passively) or ‘two-way’ coupling (the ocean does not only respond to the atmospheric forcing, but also feeds back to the atmosphere) can also cause low-frequency climate variability (e.g., Mikolajewicz and Maier-Reimer 1990; Timmerman et al. 1998; Delworth and Greatbatch 2000; Wu and Liu 2005).

The purpose of this work is to investigate the low frequency variability of the MOC using the coupled atmosphere–ocean general circulation model ECHAM5/MPIOM. One advantage of using this model is that it does not employ flux adjustment. The coupled model exhibits variability at periods of near 30 years and about 60 years. This paper focuses on the 30-year variability, which is named interdecadal variability (IDV), and shows that it is an ocean self-sustained mode; the 60-year variability, referred to as multidecadal variability (MDV), is an air-sea coupled mode, and is discussed in detail in a forthcoming paper.

The paper is organized as follows: Sect. 2 describes the coupled model and the experiment design; Sect. 3 presents the simulated low frequency variability; Sect. 4 describes mechanism of the IDV; Sect. 5 shows evidence indicating the influence of the newly formed deep water on the upper ocean; and a summary and discussion is given in Sect. 6.

2 Model description and experiments

The ECHAM5/MPIOM model has undergone significant development in recent years. The technical details of these developments are described in Roeckner et al. (2003) and Marsland et al. (2003) for the atmosphere and ocean component respectively. The atmosphere model is run at T31 resolution and has 19 vertical (hybrid) levels. The ocean has 3° × 3° average horizontal grid spacing with 40 unevenly spaced vertical levels. An orthogonal curvilinear grid allows for an arbitrary placement of the grid poles. In the current set-up, the ocean model’s North Pole is shifted to Greenland and the South Pole to the center of the Antarctic continent. This approach not only removes the numerical singularity associated with the convergence of meridians at the geographical North Pole, but also produces higher resolution in the deep water formation regions in both hemispheres and gives a realistic representation of overflow water (Jungclaus et al. 2008). Interactive runoff and glacier calving schemes are used. Various aspects of the mean state and internal variability of a model version with higher resolution are discussed by Jungclaus et al. (2005, 2006) and Zhu et al. (2006). Note that no flux adjustment is deployed in all experiments in our studies.

Since all processes are inherently coupled within the context of a fully coupled model, it is difficult to confirm the speculations about the mechanisms responsible for the low-frequency variability. Following the experiment strategy of Delworth and Greatbatch (2000), we conduct a suite of experiments using the ocean component of the coupled model, MPIOM, driven by suitably chosen time series of surface flux forcing. All model parameters in the ocean-only experiments are identical to those in the fully coupled model. Monthly surface fluxes (heat, water and momentum) from the coupled model integration are interpolated to daily data, which are then used to drive the ocean model. In some experiments, climatological mean surface fluxes taken from the coupled integration are used instead. This design excludes forcing variability at time scales longer than the seasonal cycle and allows us to evaluate the role of the respective atmospheric forcing. In all experiments, sea ice thickness is restored to climatology calculated from the coupled run. This constraint helps to reduce model drift. The suite of experiments is listed in Table 1.

Table 1  List of experiments
Full size table

The coupled model (CPL, refer to Table 1 for abbreviations) is in total 1099 years long. We derive the climatological atmospheric forcing from the coupled model years 700–750. All other simulations are ocean-only experiments, which start from the oceanic condition at the coupled model year 709:

  1. (1)

    In experiment CTR, the ocean model is forced by surface fluxes taken from the coupled model output between year 709 and year 1099.

  2. (2)

    In experiment RAND, for each year of the integration, the flux forcing from a randomly selected year from the coupled model output (from year 709 to year 1099) is applied. In this manner, there is no feedback from the ocean to the atmosphere.

  3. (3)

    In experiment CLIM, the ocean model is driven by climatological month-to-month surface fluxes, thus the variability of the atmospheric forcing longer than the seasonal cycle is excluded. Both CLIM and RAND are in total 1700 years long. The last 1100 years are analyzed.

All ocean-only experiments are without substantial model drift, although the surface heat fluxes are specified independently of sea surface temperature (SST) and there is no damping of SST anomalies through the surface heat flux term. This is because the restoring of the sea-ice thickness to a climatological seasonal cycle provides a large scale damping on the system. In a realistic situation, negative (positive) SST anomalies at higher latitudes will create positive (negative) anomalies of sea-ice thickness. As the sea-ice thickness is restored to climatology, heat was effectively added to (removed from) the system. Additionally, explicit diffusion and the advection of heat by the time-varying three-dimensional oceanic circulation also serve to effectively damp the locally generated heat anomalies (Delworth and Greatbatch 2000).

3 Simulated low-frequency variability

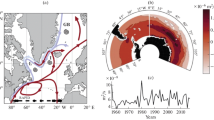
We define the MOC index as the zonally averaged streamfunction at 30°N, 960 m. In the coupled model the MOC index has a mean of about 18 Sv (1 Sv = 106 m3/s) and exhibits substantial variations through the entire time series (Fig. 1a). Its wavelet analysis shows a local maximum near 60 years between year 250 and 600, which then smoothly moves to near 30 years at around year 700 and 800, and moves again to near 50–60 years at year 900 (Fig. 1b). The MOC index also exhibits variability with a period between 130 and 200 years (Fig. 1b). The existence of this centennial modulation of the climate variability is crucial for trend detection issues; however, it is not within the scope of this paper and we focus only on time scales between 30 and 100 years. The separation of the 30- and 60-year variability in time suggests that they may originate from different dynamics, which is also suggested by the following ocean-only experiments.

Fig. 1
figure 1

a Time series and b wavelet of the zonally averaged streamfunction in the Atlantic at 30°N, 960 m in the fully coupled run. The thick line in a is the 11-year running mean of the original time series (in gray). In b, the hatched area denotes the cone of influence due to zero padding and should not be considered. The contour line denotes the 5% significance level against red-noise background

Full size image

To evaluate what is responsible for the low frequency variability on the scale of decades, a suite of experiments using the ocean component of the coupled model were conducted (refer to Table 1 for experiment set-ups) showing the following results:

  1. (1)

    CTR (Fig. 2a): For the first 100 years, CTR almost fully reproduces the variability of CPL. Afterwards, the MOC gradually weakens by about 1 Sv, but it still captures to a large extent the low-frequency oscillatory behavior of the CPL. The weaker mean state of the MOC in CTR is likely due to the reduced noise level in the atmospheric forcing (Balan 2006). The similar oscillatory behavior in CPL and CTR confirms that the framework of using only the ocean component of the coupled model is appropriate for analyzing the MOC fluctuations.

  2. (ii)

    RAND and CLIM: The mean strength of MOC indices in both RAND and CLIM are 15 Sv (Fig. 2b) and exhibit considerable low frequency variability, with smaller amplitude in CLIM (0.8 Sv, Fig. 2c). While RAND and CLIM represent clearly the 30-year variability as in CPL, spectral energy is damped between 50 and 80 years in both cases, different from in CPL (Fig. 2d).

Therefore, the 30-year variability, referred to as Interdecadal Variability (IDV), can exist under climatological atmospheric forcing; the variability between 50 and 80 years, comparable to the 60-year variability in Fig. 1b and referred to as multidecadal variability (MDV), is damped out when the two-way atmosphere–ocean coupling (at time scales longer than the seasonal cycle) is partly (RAND, in which the ocean does not influence the atmosphere) or completely (CLIM) inhibited.

Fig. 2
figure 2

Time series (a–c) and their spectrum (d) of the MOC index (units: Sv) from all experiments listed in Table 1. Thin lines in a denote original MOC index and the corresponding thick lines denote those filtered with an 11-year running mean (CTR in solid line and CPL in dashed line); in b, CLIM is denoted as the black line and RAND as the gray line; in d, lines denote the spectrum of CPL (gray dashed line), RAND (gray solid line), and CLIM (black solid line). The spectrum of CPL is obtained from the last 700 years of the MOC time series (Fig. 1a). An AR (1) process is fitted to RAND and CLIM, respectively, shown as the solid lines with the same color as the corresponding spectrum. The dash-dotted gray lines denote the upper limit of the 95% confidence level for RAND and CLIM. The IDV and MDV band are highlighted by the gray boxes

Full size image

The rest of the paper focuses on the IDV based on the experiment in which the ocean model is forced by climatological atmospheric forcing (CLIM); a forthcoming paper will focus on the 60-year multidecadal variability.

4 Physics of the interdecadal variability

Fluctuations of the MOC are related to changes in the density structure of the North Atlantic; consequently, this density redistribution, according to geostrophy, will lead to the adjustment of the ocean circulation. In this section, we first investigate the relation between horizontal density gradients and the ocean circulation (Sect. 4.1) before we discuss the relative contribution of temperature and salinity to the density variation (Sect. 4.2).

4.1 Horizontal density gradients and ocean circulation

The ocean interior is in geostrophic balance at first order. In the north-south direction, surface density increases from equator to pole, driving an eastward surface flow along the mutual boundary between the subpolar gyre and the subtropical gyre, i.e., the Gulf Stream and North Atlantic Current (NAC) system. In the east-west direction, if we look at the subpolar frontal zone, water near the British Islands is warmer and hence lighter than in the western part where colder (denser) water from the subpolar basin prevails. This east-west density gradient sustains the pressure gradient for the northward mass transport in the upper ocean. This geostrophic relation has been shown as the maintaining mechanism of the interdecadal mode in a simple ocean model (Te Raa and Dijkstra 2002). The purpose of this section is to revisit the relation between the horizontal density gradients and the meridional and zonal streamfunctions within a more complex ocean model. The related terms are defined as follows:

  1. (1)

    The east-west and north-south density gradients are determined by four density indices computed in the following selected areas: near the British Islands, in the Labrador basin, near Newfoundland (denoted as A, B, and C in Fig. 3), and near the zonal band centered at 30°S in the South Atlantic (about 28–31°S, not shown). Density indices are averaged over each of the selected areas and in the vertical over the upper 2,000 m. Zonal and meridional density differences are formed: the east-west difference D ew between A and C and the north-south difference D ns between B and the southern region. D ew describes the density difference formed by warm subtropical water flowing through area A and the cold subpolar water flowing through area C (Fig. 3a); if we assume the density in the southern region is constant, D ns describes mainly the density variation in the Labrador Sea basin.

  2. (2)

    The zonal streamfunction is approximated by the mass transport of the NAC through section D (Fig. 3). The NAC is characterized by temperature higher than 8°C and by strong eastward velocity (Fig. 3b). The northern part of the section is almost occupied by cold water from the subpolar basin, mainly the deep water formed in the Labrador Sea basin, with homogeneous temperature ranging from 6 to 7°C. The warm NAC is separated from the cold subpolar water by the subpolar front, which is near the maximum u-velocity (10 cm/s) at the surface (Fig. 3b). Below 2,000 m lies the well-stratified lower North Atlantic Deep Water. The mass transport by the NAC through section D (mass transport through the dashed box in Fig. 3b) is calculated to indicate the NAC strength.

  3. (3)

    The meridional streamfunction is taken directly from the zonally averaged streamfunction in the North Atlantic.

The linear time-lag regression analysis is performed between zonal and meridional mass transport and the density differences (only the period between lag −15 and lag 0 is shown). The following results are noted:

  1. (1)

    The east-west density difference (D ew) is almost out of phase with the MOC; and the north-south density gradient (D ns) leads the MOC by about 2 years (Fig. 4); The NAC mass transport has a maximum correlation with D ns of about 0.6, when D ns leads 3 years (Fig. 4).

  2. (2)

    The D ew variation is closely related to the variation of the meridional streamfunction (Fig. 5a): the MOC has its minimum near lag −15 and its maximum near lag 0, and its transition from negative to positive phase takes place between lag −10 and lag −5. This process is in correspondence with the transition of D ew from its maximum to its minimum (Fig. 4).

  3. (3)

    The anomalous mass transport through section D is shown in Fig. 5b: between lag −15 and lag 0, NAC evolves from its minimum to maximum, corresponding to the recovery of D ns from its minimum to maximum during this period (Fig. 4).

  4. (4)

    We also note that at section D the NAC mass transport is out-of-phase with the eastward LSW transport. For example, at lag −15, when NAC transport is weaker, the eastward LSW transport is stronger. Meanwhile, the current anomalies in the upper ocean are out of phase with those beneath. For instance, at lag 0 the NAC is stronger (with a positive sign) and the eastward LSW is weaker (with a negative sign), the current anomalies beneath them are with negative and positive signs respectively. As is shown later, these current anomalies at greater depth reflect the response of the ocean current field to the varying LSW thickness.

Fig. 3
figure 3

a Locations where horizontal density gradients are calculated. They are denoted by the red dots, marked as A, B and C. Red squares denote the location of the cross-NAC section (D). The mean sea surface temperature (shaded, °C) and mean velocity at 57 m (vector, with double scales, in gray and black respectively) are also shown. b Mean potential temperature (shaded, °C) and mean zonal velocity (contours, cm/s) at section D. The grid points are labeled from 1 to 8 going from north to south. Real distances between two neighboring grid points are not equal but here plotted with the same interval. The dashed box is where the NAC mass transport is calculated, covering the upper 1,085 m and horizontally from point 5 to point 8

Full size image
Fig. 4
figure 4

Time–lag correlation coefficients between the east-west density gradient (D ew) with the MOC (dash dotted), between the north-south density gradient (D ns) with the MOC index (solid line), and between the north-south density gradient (D ns) and the NAC transport (dashed circled). An 11-year running mean is applied to all time series before the correlation calculation. Negative lags mean that the former term in each case is leading, in the case of D ns correlated to NAC, meaning D ns leading the NAC

Full size image
Fig. 5
figure 5

a Regression coefficients of the Atlantic zonally averaged streamfunction onto the MOC index (Units: Sv/Sv). Positive lags mean the MOC leading. The interval for the shaded area is 0.1. Values between −0.2 and 0.2 are not shown. b Regression coefficients of mass transport through section D in Fig. 3b onto the MOC index (shaded, units: Sv /Sv). Values between −1 and 1 are not shown. Positive lags mean the MOC leading. Point 1–8 goes from north to south. The x-axis does not correspond to the real distance between the selected points

Full size image

4.2 The role of temperature and salinity for density variation

In order to determine the relative contribution of temperature and salinity to the density changes (shown above), the density and its thermal- and haline-components are taken from the Labrador Sea where the mean March mixed layer depth (MLD) exceeds 1,200 m (identical to region B in Fig. 3a). These time series from the upper 2,000 m are regressed onto the MOC index at various time lags and the regression coefficients are averaged horizontally and vertically over the selected ocean domain (Fig. 6).

Fig. 6
figure 6

Regression coefficients between various quantities and the time series of the MOC index at 30°N in CLIM (kg/m3/Sv). The solid line with circles, the dashed line, and the dash-dotted line denote the regression of potential density, its haline and thermal part onto the MOC index. The reference depth is at 2,000 m. The regression coefficients were averaged vertically and horizontally over the region where the mean March MLD in the Labrador Sea is larger than 1200 m

Full size image

The density anomalies lead the maximum MOC by 4 years, suggesting that the variation of the density induces changes in the MOC. The density fluctuation attributable to temperature anomalies are almost in phase with the density variation, whereas the density anomalies attributable to salinity anomalies vary out of phase, counteracting the thermal effects. Therefore, temperature dominates the density fluctuation and salinity plays an opposite but secondary role.

5 Influence of Labrador sea water (LSW) on the upper ocean

Observational evidence shows that the deep-water formation in the Labrador Sea varies on a scale of decades (Bersch et al. 2007; Yashayaev 2007). Moreover, this varying deep-water production has a potential of influencing the upper ocean (Curry and McCartney 2001; Cooper and Gordon 2002). In this section, we look into the variability of the newly formed deep water and its interaction with the upper ocean.

The data are taken from each March every year in order to capture the maximum deep-water formation. We define the LSW with potential density between 1027.32 and 1027.5 kg/m3. Note that in experiment CLIM, climatological atmospheric forcing is applied, therefore, the characteristics of the simulated deep water are not meant to match those in the real world (e.g., Pickart et al. 2002).

The LSW occupies the entire subpolar basin and leaves the basin through two pathways (Fig. 7): one along the deep western boundary from east of Newfoundland and the other entering the eastern North Atlantic basin and traveling southward from both sides of the Mid-Atlantic Ridge, which is more clear in the integrated mass transport by the LSW (not shown). These two simulated pathways are consistent with observational data (e. g., Schott et al. 2004). However, it may also be a feature of coarse-resolution models.

Fig. 7
figure 7

Mean thickness (shaded, m) of LSW. Vectors shown are mean velocity field at 1,525 m (units: cm/s). Note that double scales are used

Full size image

Linear time-lag regression of the near-surface temperature, LSW thickness and current fields with the MOC shows the following results (Fig. 8, only the period between lag -15 and lag 0):

  1. (1)

    Strong LSW thickness variations occur in the Labrador Sea basin and along the NAC path. The former region is also where most of the LSW is formed (Fig. 7). The LSW formation center shifts between the Labrador Sea center and its boundary region (Fig. 8a): during a weak MOC phase, more LSW is formed in the center and less along the boundary (at lag -15 in Fig. 8a); and vice versa (at lag 0 in Fig. 8a).

  2. (2)

    When the MOC is near its minimum (at lag -15), weak warm anomalies occupy the Labrador Sea basin and along the NAC path. Meanwhile, cold near-surface anomalies occur in the eastern subpolar basin and the subtropics (Fig. 8b). The subsequent recovery of the MOC is accompanied by the advection of cold near-surface temperature anomalies from the subtropics into the subpolar basin (Fig. 8b).

  3. (3)

    The near-surface temperature anomalies along the NAC path are in close correspondence to the LSW thickness field: warm anomalies appear east of Newfoundland at lag -15 (Fig. 8b) and are advected eastward accumulating in the eastern subtropical basin (from lag -15 to lag 0, Fig. 8b), in correspondence to the simultaneous development of the negative LSW thickness anomalies (Fig. 8a).

  4. (4)

    Moreover, the current anomalies surrounding the temperature anomalies along the NAC path are likely directly linked to the warming and cooling in the subpolar basin (Fig. 8b): at lag -15, warm anomalies occur along the NAC path and partly extend southward into the eastern subtropical basin. These warm anomalies are accompanied by anticyclonic current anomalies, which direct southward southwest to the British Islands leading to reduced northward heat transport and account for the large-scale cooling in the subpolar basin. The situation is reversed at lag 0: cold anomalies occur along the NAC path and are accompanied by cyclonic current anomalies, which direct northward southwest to the British Islands and correspond to the warming in the subpolar basin.

We also note that the corresponding current anomalies show that the LSW prefers different paths passing the Mid-Atlantic Ridge depending on the MOC state: when the MOC is near its minimum, more LSW goes from the eastern side and less from the western side (lag -15 in Fig. 8a); during strong MOC phase, more LSW directs to the western side instead.

Fig. 8
figure 8

Regression coefficients of a the LSW thickness (shaded) and velocity at 1,525 m (vector), b the temperature averaged over the upper 150 m (shaded, °C) and velocity at 47 m (vector, cm/s) onto the MOC index. The units are all in reference to per standard deviation of the MOC index in CLIM. Lags are in years and positive lags mean the MOC leading

Full size image

6 Summary and discussions

This study presents an attempt to understand the mechanisms that generate inter-to-multi-decadal variability of the MOC by using ECHAM5/MPIOM. The MOC exhibits variability of a 30-year period (IDV), which exists under climatological atmospheric forcing, is therefore an ocean internal mode. The MOC also shows concentrated spectral energy near 60 years (MDV), which is much damped when there is no two-way atmosphere–ocean coupling (Fig. 2d). Therefore, it is most likely an atmosphere–ocean coupled mode. Therefore, different dynamics may be at work in different frequency range, which is also indicated by the separation of the 30- and 60-year variability in time, as shown in the wavelet analysis (Fig. 2b). The coexistence of several physical modes provides a possible explanation for the multi-time-scales observed in sea surface temperature field (see Fig. 1a, Knight et al. 2005).

The 30-year interdecadal variability is related to the interplay between the horizontal density gradients and the ocean circulation. Advection of temperature anomalies changes the horizontal density gradients, which in turn induce changes in the zonal and meridional circulation. Our results agree well with that suggested by Te Raa and Dijkstra (2002, 2003); besides, their simple model is forced only by heat fluxes and salinity variation is not considered, thus the density changes in their model are mainly determined by temperature anomalies, consistent with the dominating role of temperature in our model. The agreement between two models with different complexity suggests that the IDV is a robust mode.

Delworth et al. (1993) find pronounced variability in the MOC index with an average period about 50 years in GFDL model. Although it is not clearly pointed out, the 50-year oscillation shows also a geostrophic character: the east-west temperature anomalies are related geotropically to the meridional transport of density anomalies (see their Fig. 18 and 19); the close relation between the north-south density gradient and the zonal circulation can also be derived from their Fig. 12 and Fig 18. Therefore, the physical mechanisms in our studies are basically very similar. One difference is that in their studies, salinity dominates the density fluctuation in the subpolar basin while it is temperature in our model (Fig. 6). This difference suggests that the simulated feedbacks between the atmosphere and the ocean are probably different in these two models, which may explain why their 50-year is an oceanic response to the atmospheric low frequency variability (Delworth and Greatbatch 2000) and the IDV in our model is ocean self-sustained.

Hátún et al. (2005) argue that the subpolar gyre modulates the northward transport of heat and salt and therefore with subsequent consequences for deep-water formation and the MOC. This is consistent with our findings: during times of enhanced subpolar gyre strength (Fig. 8b, lag -10, lag -5) warm (and salty, not shown) water accumulates to the west of the Iberian Peninsula. On the other hand, we demonstrate that the LSW, an important component of the MOC, penetrates into the basin, strongly influencing the gyre circulation by modulating the circulation in the Subtropical–Subpolar boundary region, namely the NAC system.

Along the NAC path, the LSW thickness anomalies influence the near-surface temperature anomalies and their speed, which can be derived from the following facts:

  1. (1)

    The LSW thickness anomalies are not generated locally; instead, they reflect the variability of the LSW formation in the sinking region. These LSW thickness anomalies are advected to the NAC path, which takes 2–3 years, suggested by the time by which the maximum D ns leads the minimum D ew (Fig. 4).

  2. (2)

    By lowering (lifting) the upper LSW boundary, the reduced (enhanced) LSW thickness, on the one hand, induces cyclonic (anticyclonic) current anomalies; on the other hand, according to thermal wind relation, the LSW thickness anomalies generate anticyclonic (cyclonic) current anomalies in the upper ocean (Fig. 8a, b), accounting for the opposite signs of the eastward mass transport by the NAC and the LSW through section D and the vertical out-of-phase current anomalies (Fig. 5b).

  3. (3)

    These surface current anomalies account for the simultaneous reduced (enhanced) eastward NAC mass transport (Fig. 5b) and the consequent warming (cooling) along the subpolar front (Fig. 8b).

Therefore, the speed of the near surface temperature anomalies along the NAC path is influenced by the slow LSW advection at the intermediate depth. The influence of the deep LSW on the upper ocean has been noted in the HadCM2 model (Cooper and Gordon 2002) and also in the observational data (Curry and McCartney 2001). The 3-year advection time of the LSW to move out of the Labrador basin and reach east of Newfoundland is also consistent with the estimate by Cooper and Gordon (2002).

The LSW can also influence the upper ocean along the NAC path through the so-called ‘obduction’ process in which the water from the permanent pycnocline is irreversibly transferred into the mixed layer above (Qiu and Huang 1995; Haines and Old 2005). This communication between the LSW and the mixed layer is manifested in the model by persistent upwelling between the winter mixed layer and the upper LSW boundary (not shown). The quantification of the obduction rate is not done in this paper and is planned for subsequent studies.

The close relation between the near-surface temperature along the NAC path and the underlying LSW motivates us to gain insight into the state of the MOC and the LSW through knowledge of the near-surface ocean temperature near the subpolar front where the LSW flows beneath the NAC; moreover, it may also provide information on the preferred path of the southward LSW branch reaching the eastern Atlantic: reduced (enhanced) LSW thickness is associated with cyclonic (anticyclonic) current anomalies which direct more (less) LSW to the eastern side of the Mid-Atlantic Ridge but less (more) to the western side (Fig. 8a). Although the simulated pathway of the LSW in our model is far too eastward, the same mechanism may also hold in more realistic circumstances, such as near the Grand Banks where the deep water splits into two branches, one moving southward along the western boundary and the other entering the eastern North Atlantic basin (Fischer and Schott 2002).

Our analyses also show that strong variation of the LSW takes place in the Labrador Sea basin where most of the LSW is formed (Fig. 7) and intensive winter mixing takes place (not shown). We further find the maximum standard deviation of the winter MLD also occurs in the boundary region (not shown), suggesting that reduced (increased) LSW formation in this region is directly caused by the weakened (enhanced) winter mixing. The area of maximum convection shows also considerable spatial variation. The reason for the spatial shift is still unclear but could be related to changes in the strength of the deep boundary current that is fed by the overflows (Wood et al. 1999).

We acknowledge that the results presented above are from the ocean model MPIOM driven by climatological surface forcing. We conduct analyses in a similar way to experiment RAND and similar results are obtained. Therefore, the mechanism of the IDV is quite robust. On the other hand, how the IDV interacts with other physical modes, such as the 60-year multidecadal variability resulting from the atmosphere–ocean coupling, when dynamic air-sea coupling is considered, remains open for further studies.