Abstract
Mud is a cohesive material which contains predominantly clay minerals, water, organic matter and some amounts of silt and sand. Mud samples can have complex rheological behaviour, displaying viscoelasticity, shear-thinning, thixotropy and yield stress. In this study, influence of organic matter on the rheological behaviour of different mud samples having similar densities is investigated. Four samples, collected from different locations and depths of Port of Hamburg (Germany) were selected. Two samples with the density of about 1210 kg/m3 and two samples with the density of about 1090 kg/m3 were analysed by different rheological tests, including stress ramp-up tests, flow curves, thixotropic tests, oscillatory amplitude and frequency sweep tests. Two yield stress regions (with two yield stress values stated as “static” and “fluidic” yield stresses) were identified for all the samples, and these regions, corresponding to a structural change of the samples were significantly different from sample to sample due to the differences in organic matter content. For lower density samples, the ratio of fluidic to static yield stress increased from 3 to 4.4 while it increased from 4.4 to 5.2 in case of higher density samples, by increasing the organic matter content. The thixotropic studies showed that the mud samples having lowest organic matter content (VH and KBZ) exhibit a combination of thixotropic and anti-thixotropic behaviours. The results of frequency sweep tests revealed the solid-like character of the mud within the linear viscoelastic regime. Mud samples having higher organic matter content (RV and RT) had a higher complex modulus (417 Pa and 7909 Pa) than the ones with lower organic matter content (13 Pa and 1774 Pa), for a given density. This study demonstrated that the density only is not a sufficient criterion to predict the rheology of different mud. Furthermore, even small amounts of organic matter content change significantly the mud rheological behaviour.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Mud, found in lake beds, river beds, or coastal seabed, is a cohesive material which contains predominantly clay minerals, water, organic content and some amounts of silt and sand. Estuarine mud beds are continuously disturbed by wave motion leading to the formation of different mud layers which can be classified as suspended mud, fluid mud, pre-consolidated/stationary mud and consolidated cohesive bed (Ross and Mehta 1989; Mehta 2013). Fluid mud is usually defined as a fluid having a density within the range of 1030–1300 kg/m3 and concentrations about 10–100 g/L, in which settling is considerably hindered by the presence of flocs (Inglis and Allen 1957; Whitehouse et al. 2000; McAnally et al. 2007). Extensive research has been done on the floc size measurements in the laboratory for muddy sediments (Manning and Dyer 2002; Gratiot and Manning 2004; Manning et al. 2007; Spencer et al. 2010). The hindered settling behaviour was also observed for the sand/mud mixtures (Whitehouse and Manning 2007; Manning et al. 2010; Manning et al. 2011; Spearman et al. 2011; Spearman and Manning 2017). The presence of fluid mud makes the navigation in ports and waterways and the maintenance of dredging channels more difficult (May 1973; Parker and Kirby 1982; Kirichek et al. 2018). Mud samples are known to exhibit complex rheological behaviours like viscoelasticity, shear-thinning, thixotropy and yield stress (Coussot 1997; Van Kessel and Blom 1998). The presence of yield stress in mud results from the presence of aggregate networks, for particles volume concentration above 8% (Kranenburg 1994).
In literature, correlation between density or volume fraction of natural sediments and the yield stresses has been extensively reported. Xu and Huhe presented the rheological studies of natural mud at Lianyungang, China using a RS 6000 rheometer with the help of both steady and dynamic measurements (Xu and Huhe 2016). They correlated the yield stress values with the mud volume concentration and fitted the experimental data with an exponential empirical relation. Soltanpour and Samsami compared the rheology of kaolinite and Hendijan mud, northwest part of Persian Gulf (Soltanpour and Samsami 2011). They linked the rheological parameters with the water content in the natural and artificial sediments using exponential relations. Similarly, the relation between Bingham yield stress and the density of the natural mud sediments was also reported in the literature using empirical exponential relations (Carneiro et al. 2017; Fonseca et al. 2019).
As it is already reported in the literature, the cohesion and rheological properties of muddy sediments are strongly dependent on the presence of organic matter/biopolymer (Paterson et al. 1990; Paterson and Hagerthey 2001; Tolhurst et al. 2002; Wurpts 2005; Malarkey et al. 2015; Schindler et al. 2015; Parsons et al. 2016). However, a systematic analysis of the influence of organic matter on the rheological properties of mud samples and a quantification thereof is still missing. Therefore, in this study, we aim to answer the question “is the density or volume fraction of solids enough to predict/link the rheology of the natural sediments?” by studying the rheological behaviour of mud samples with similar densities, but different organic matter content. Four samples, collected from different locations at different state of consolidation from Port of Hamburg (Germany) were selected. Two of the samples had a similar density of about 1210 kg/m3, whereas the two others had a similar density of about 1090 kg/m3. Rheological analysis was performed by conducting stress ramp-up tests, flow curves, thixotropic tests, oscillatory amplitude and frequency sweep tests.
Experimental
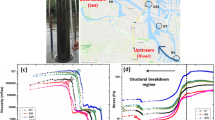
In this study, the mud samples were collected from different locations (Vorhafen (VH), Köhlbrand (KBZ), Rethe (RT) and Reiherstieg Vorhafen (RV)) of Port of Hamburg, Germany using a 1-m core sampler (Fig. 1b). Figure 1a shows the selected locations at the port. These locations were chosen on the basis of a preliminary analysis, which showed that the selected locations have different amounts of organic matter content with significantly different rheological fingerprint. The collected samples were then divided into different layers based on the differences in their visual consistency such as fluid mud (FM), pre-consolidated (PS), pre-consolidated to consolidated (PS/CS) and consolidated (CS) sediments (Fig. 1c). Four different samples were then selected having similar densities, but with different organic matter content. The samples were packed in sealed containers and transported to the laboratory. The dry density of the minerals was assumed to be 2650 kg/m3 (Coussot 1997). The bulk density of the mud samples was determined by the method reported in (Coussot 2017). Particle size distributions within the different mud layers were measured using static light scattering (Malvern MasterSizer 2000MU). There are several limitations of this instrument which need to be considered such as (i) it is based on the Mie theory which basically assumes the spherical shape of all the particles which can be inappropriate for mud sediments; (ii) only a certain concentration range is practically possible to measure, if it is too low or too high, a warning message will appear; and (iii) for samples with higher sand fractions, this techniques gives higher average particle diameter (D90) due to the smoothing of the dataset by the software (Ibanez Sanz 2018). However, this technique was used in this study because it is very easy and fast to use. The organic matter content of the sediments was determined using an ISO standard 10694:1996-08 (ISO. 1995). The characteristics of the chosen mud samples are summarised in Table 1. Before the rheological experiments, all the mud samples were homogenized by mild hand stirring.
Rheological experiments were performed using a HAAKE MARS I rheometer (Thermo Scientific, Germany) with concentric cylinder (Couette) geometry (CC25DIN, gap width = 2 mm, distance from the bottom of cup = 5.3 mm, and sample volume = 16 ml). A waiting time of 3–5 min was used to eliminate the disturbance created by the bob after attaining its measurement position. The temperature was maintained at 20 °C during each experiment using a Peltier controller system. Each experiment was carried out in duplicate to check the repeatability of the measurements. Stress ramp-up tests were performed using the stress-controlled mode of the rheometer. An increasing stress was applied from 0 to 500 Pa at a rate of 1 Pa/s, depending upon the consistency of the sample. The corresponding motor dispalcement was measured, and the shear rate and viscosity were then determined. The flow curve experiments were carried out using a shear rate–controlled mode of the rheometer by linearly incrasing the shear rate from 0 to 25 s−1 in 170 s and from 25 to 300 s−1 in 100 s without giving enough time between each point of measurement to reach steady state. The steady state was not achieved in the flow curves to reduce the experimental time, in order to minimise the settling phenomenon which is very significant for fluid mud samples. Thixotropic experiments were performed by increasing the shear rate from 0 to 100 s−1 followed by shearing at 100 s−1 for 30 s and then decreasing from 100 to 0 s−1. The dynamic experiments were executed either as a function of oscillation amplitude or frequency. Preliminary amplitude sweep tests were carried out at a constant frequency of 1 Hz to estimate the linear viscoelastic regimes. Frequency sweep tests were then performed from 0.1 to 100 Hz within the linear viscoelastic regimes. The storage modulus (G′), and loss modulus (G″) were recorded as a function of frequency. The complex modulus, G∗ and the phase angle, δ can then be calculated as follows:
Results and discussion
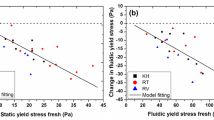
Figure 2a and b presents the results of stress ramp-up tests for sediments having similar densities in the form of apparent viscosity as a function of stress. From these viscosity curves, two yield regions were identified from the decline in viscosity. However, to compare the yield stress values of different samples, the approach reported by (Zhu et al. 2001) was used to obtain the yield stress values by extrapolation. The stress values associated with the first decline are referred to as “static” yield stress, \( {\tau}_y^s \), while the second decline stress values are termed as “fluidic” yield stress, \( {\tau}_y^f \) (Shakeel et al. 2019a). The static yield stress value is most probably associated with the relaxation of the sample structure, including the breakage of large flocs into smaller flocs, as already suggested by Nosrati et al. 2011. The further breakdown of smaller flocs into very small flocs or individual particles can be linked with the fluidic yield stress values. Table 1 shows the results of stress ramp-up tests, where the mud samples with similar densities display markedly different static and fluidic yield stress values.
Apparent viscosity as a function of stress for mud sediments having a similar lower and b similar higher densities. The boxes with dotted lines represent the yield regions and the circles represent the static (\( {\tau}_y^s \)) and fluidic (\( {\tau}_y^f \)) yield stress values obtained by linear slope extrapolation
Italicized entries show the samples with similar higher densities and the bold entries represent the samples with similar lower densities
The samples from RV and RT revealed higher yield stress values, both static (9 Pa and 60 Pa) and fluidic (40 Pa and 312 Pa), as compared to the static (0.8 Pa and 18 Pa) and fluidic (2.44 Pa and 79 Pa) yield stress values of samples from locations VH and KBZ. This shows that, for lower density samples, the ratio of fluidic to static yield stress increased from 3 to 4.4 while it increased from 4.4 to 5.2 in case of higher density samples, by increasing the organic matter content. Higher yield stresses, at a given density, can be linked with higher organic matter content as a large number of flocs are strongly interconnected at high organic matter content (see Fig. 2). Increasing shear rate sweeps were also performed to obtain the flow curves. Each displayed measuring point was recorded 0.4-7 sec after the corresponding shear stress was applied. This time was too short to enable the system to reach steady state. The resultant flow curves are shown in Fig. 3a, b. The behaviour of the samples from RV and RT locations was again quite different from their corresponding location with same density, with higher stress values in response to the applied shear rate, which may be linked with their higher organic matter content.
Thixotropic behaviour of mud samples was systematically studied by increasing and decreasing the shear rate between 0 and 100 s−1. The shape of the hysteresis loop depends upon various factors including the nature of the material, shear history prior to the analysis, level and rate of shearing. Comprehensive reviews have been made on thixotropy by (Barnes 1997) and (Mewis and Wagner 2009). Figure 4a, b shows the results of thixotropic experiments for the sediments having similar densities. Mud samples from RV and RT locations displayed a typical thixotropic behaviour (decrease in viscosity with shearing action), whereas anti-thixotropy or negative thixotropy behaviour was evident at lower shear rates for the sediments collected from VH and KBZ locations.
The similar combination of thixotropy and anti-thixotropy was also reported by (Nosrati et al. 2011) for muscovite dispersions. This peculiar combination of thixotropy and anti-thixotropy could be linked with the existence of shear thickening phenomenon, which was observed for these samples in stress weep tests at higher stresses. However, it could also be due to the slippage between the bob and the sample. The mud samples from RV location showed a typical thixotropic behaviour for the entire investigated shear rate range by having lower viscosity/stresses in the ramp down curve. This behaviour may again be associated with their high organic content: a large number of flocs have been disrupted which require long times to reform. These results confirm that the thixotropic behaviour of natural sediments is a strong function of organic matter content.
In the oscillatory mode of analysis, amplitude sweep tests at a constant frequency were performed prior to the frequency sweep experiments in order to identify the linear viscoelastic regime for selecting suitable stress values. The results of frequency sweep tests within linear regime are shown in Fig. 5a, b, c, d. These tests are suitable for analysing the mechanical properties of the material without affecting the structure of the system. It was observed that the complex modulus of all the samples displayed a very weak frequency dependency. Furthermore, the phase angle values were very small (no cross-over), which confirmed the solid-like behaviour of the samples over the entire range of investigated frequencies. A similar solid-like behaviour of the natural sediments as a function of frequency, within the linear regime, was previously reported in the literature (Van Kessel and Blom 1998; Soltanpour and Samsami 2011; Xu and Huhe 2016).
The complex modulus values were considerably different for the mud samples with similar densities, whereas the phase angle values were not markedly different from each other (see Table 1). Mud samples having higher organic matter content (RV and RT) had a higher complex modulus (417 Pa and 7909 Pa) than the ones with lower organic matter content (13 Pa and 1774 Pa), for a given density. The complex modulus is a measure of the consistency of the system, while the phase angle is representative of the degree of structuration (Lupi et al. 2016; Shakeel et al. 2018; Shakeel et al. 2019b; Shakeel et al. 2019c). The results showed that the consistency of the mud samples can be varied by changing the OM content or density, whereas the degree of structuration remains the same for all the samples. This also means that the density of all investigated samples is higher than the one required to form a structured system. At high frequencies, an increase in complex modulus and a decrease in phase angle was observed, which was due to the rheometer head inertial effects at such higher frequencies. Additionally, this head inertial effect was less evident for the sample with higher organic matter content (RV) because this sample was more consistent, as shown by higher moduli (Fig. 5a). This experimental data obtained due to the head inertial effects was removed from the figures to eliminate the misconception.
The values of the rheological properties of mud samples from different locations were also compared with the rheological parameters of the mud samples investigated in this study (Table 2). The mud samples from the Port of Rotterdam, the Port of Santos and the Port of Hamburg have similar rheological parameters values for similar density ranges. However, the samples from Eckernförde Bay exhibited significantly lower yield stresses values for comparable density ranges. This might be due to the differences in organic matter content, measuring technique or analysis of rheological data. The samples from other sources displayed considerably higher rheological parameters values but their densities were much higher than the densities of the three ports mentioned above.
In literature, it is mentioned that the rheological properties particularly yield stress can be used as a criterion to define the nautical bottom (i.e. navigable fluid mud layer). For example, 100 Pa yield stress value is being used for Port of Emden, Germany as a criterion for the nautical bottom approach (Wurpts 2005). However, as the results of this study clearly indicate, for the Port of Hamburg, one yield stress value as criterion for nautical bottom, for the whole Port, would be misleading. As shown in the article, totally different rheological behaviours are observed in different regions of the Port of Hamburg, primarily because of their different content of organic matter. The definition of a critical yield stress value is therefore to be studied more into details, for different mud sample compositions to be found in a given port.
Conclusions
The mud samples analysed in the article exhibit complex rheological behaviours like viscoelasticity, shear-thinning, (anti-)thixotropy and yield stress. These rheological behaviours, and in particular, the two yield stresses found in the mud systems, are strong functions of density or volume fraction of solids. It was shown that even a few percent of organic matter affects significantly the rheological fingerprint of the mud. Mud samples having similar densities were significantly rheologically dissimilar from each other due to the presence of organic matter. The ratio of fluidic to static yield stress displayed an increase from 3 to 4.4 for samples with the density of about 1090 kg/m3, while for higher density samples (about 1210 kg/m3) it increased from 4.4 to 5.2, by increasing the organic matter content. From frequency sweep tests, it was shown that the complex modulus of samples with higher organic matter content (RV and RT) displayed higher values (417 Pa and 7909 Pa) than the samples with lower organic matter content (13 Pa and 1774 Pa), for a given density. This is coherent with the viscoelastic properties of organic matter/polysaccharides, already reported in literature (Baravian et al. 2007), which clearly plays a dominant role in clay-organic matter systems, even at low organic matter content. The presented analysis shows that the rheological properties of mud samples are strongly correlated with the density and organic matter of the samples. Furthermore, even small amounts of organic matter content change significantly the mud rheological behaviour. A further quantification of the effect of the type of organic matter/polyelectrolyte at different ionic strengths or pH on the rheological fingerprint of mud samples can help to link rheology to the mud density and organic matter.
References
Baravian C, Benbelkacem G, Caton F (2007) Unsteady rheometry: can we characterize weak gels with a controlled stress rheometer? Rheol Acta 46:577–581. https://doi.org/10.1007/s00397-006-0135-x
Barnes HA (1997) Thixotropy—a review. J Non-Newtonian fluid Mechanics 70:1–33. https://doi.org/10.1016/S0377-0257(97)00004-9
Carneiro JC, Fonseca DL, Vinzon SB, Gallo MN (2017) Strategies for measuring fluid mud layers and their rheological properties in ports. J Waterw Port Coast Ocean Eng 143:04017008. https://doi.org/10.1061/(ASCE)WW.1943-5460.0000396
Coussot P (1997) Mudflow rheology and dynamics. CRC Press, Rotterdam
Fass RW, Wartel SI (2006) Rheological properties of sediment suspensions from Eckernforde and Kieler Forde Bays, Western Baltic Sea. Int J Sediment Res 21:24–41
Fonseca DL, Marroig PC, Carneiro JC, Gallo MN, Vinzón SB (2019) Assessing rheological properties of fluid mud samples through tuning fork data. Ocean Dyn 69:51–57. https://doi.org/10.1007/s10236-018-1226-9
Gratiot N, Manning AJ (2004) An experimental investigation of floc characteristics in a diffusive turbulent flow. J Coast Res:105–113
Huang Z, Aode H (2009) A laboratory study of rheological properties of mudflows in Hangzhou Bay, China. Int J Sed Res 24:410–424. https://doi.org/10.1016/S1001-6279(10)60014-5
Ibanez Sanz M (2018) Flocculation and consolidation of cohesive sediments under the influence of coagulant and flocculant. In: Delft University of Technology
Inglis C, Allen F (1957) The regimen of the thames estuary as affected by currents, salinities, and river flow. Pro Inst Civ Eng 7:827–868. https://doi.org/10.1680/iicep.1957.2705
ISO. (1995) Soil quality: Determination of organic and total carbon after dry combustion (elementary analysis). ISO
Kirichek A, C Chassagne, H Winterwerp, A Noordijk, R Rutgers, C Schot, K Nipius, Vellinga T (2018) How navigable are fluid mud layers? Terra et Aqua: International Journal on Public Works, Ports and Waterways Developments
Kranenburg C (1994) The fractal structure of cohesive sediment aggregates. Estuar Coast Shelf Sci 39:451–460. https://doi.org/10.1016/S0272-7714(06)80002-8
Lupi FR, Shakeel A, Greco V, Oliviero Rossi C, Baldino N, Gabriele D (2016) A rheological and microstructural characterisation of bigels for cosmetic and pharmaceutical uses. Mater Sci Eng C 69:358–365. https://doi.org/10.1016/j.msec.2016.06.098
Malarkey J, Baas JH, Hope JA, Aspden RJ, Parsons DR, Peakall J, Paterson DM, Schindler RJ, Ye L, Lichtman ID, Bass SJ, Davies AG, Manning AJ, Thorne PD (2015) The pervasive role of biological cohesion in bedform development. Nat Commun 6:6257. https://doi.org/10.1038/ncomms7257
Manning AJ, Dyer KR (2002) The use of optics for the in situ determination of flocculated mud characteristics. J Opt A Pure Appl Opt 4:S71–S81. https://doi.org/10.1088/1464-4258/4/4/366
Manning AJ, Friend PL, Prowse N, Amos CL (2007) Estuarine mud flocculation properties determined using an annular mini-flume and the LabSFLOC system. Cont Shelf Res 27:1080–1095. https://doi.org/10.1016/j.csr.2006.04.011
Manning AJ, Baugh JV, Spearman JR, Whitehouse RJS (2010) Flocculation settling characteristics of mud: sand mixtures. Ocean Dyn 60:237–253. https://doi.org/10.1007/s10236-009-0251-0
Manning AJ, Baugh JV, Spearman JR, Pidduck EL, Whitehouse RJS (2011) The settling dynamics of flocculating mud-sand mixtures: Part 1—Empirical algorithm development. Ocean Dyn 61:311–350. https://doi.org/10.1007/s10236-011-0394-7
May EB (1973) Environmental effects of hydraulic dredging in estuaries. Alabama Marine Resources Laboratory
McAnally WH, Friedrichs C, Hamilton D, Hayter E, Shrestha P, Rodriguez H, Sheremet A, Teeter A (2007) Management of fluid mud in estuaries, bays, and lakes. I: Present state of understanding on character and behavior. J Hydr Eng 133:9–22. https://doi.org/10.1061/(ASCE)0733-9429(2007)133:1(9)
Mehta AJ (2013) An introduction to hydraulics of fine sediment transport. World Scientific Publishing Company
Mewis J, Wagner NJ (2009) Thixotropy. Adv Colloid Interf Sci 147:214–227. https://doi.org/10.1016/j.cis.2008.09.005
Nosrati A, Addai-Mensah J, Skinner W (2011) Rheology of aging aqueous muscovite clay dispersions. Chem Eng Sci 66:119–127. https://doi.org/10.1016/j.ces.2010.06.028
Parker WR, Kirby R (1982) Time dependent properties of cohesive sediment relevant to sedimentation management-European experience. In: Estuarine Comparisons. Academic Press, pp 573-589
Parsons DR, Schindler RJ, Hope JA, Malarkey J, Baas JH, Peakall J, Manning AJ, Ye L, Simmons S, Paterson DM, Aspden RJ, Bass SJ, Davies AG, Lichtman ID, Thorne PD (2016) The role of biophysical cohesion on subaqueous bed form size. Geophys Res Lett 43:1566–1573. https://doi.org/10.1002/2016GL067667
Paterson DM, Hagerthey SE (2001) Microphytobenthos in constrasting coastal ecosystems: biology and dynamics. In: Reise K (ed) Ecological Comparisons of Sedimentary Shores. Springer Berlin Heidelberg, Berlin, pp 105–125
Paterson DM, Crawford RM, Little C (1990) Subaerial exposure and changes in the stability of intertidal estuarine sediments. Estuar Coast Shelf Sci 30:541–556. https://doi.org/10.1016/0272-7714(90)90091-5
Ross MA, Mehta AJ (1989) On the Mechanics of Lutoclines and Fluid Mud. J Coast Res:51–62
Schindler RJ, Parsons DR, Ye L, Hope JA, Baas JH, Peakall J, Manning AJ, Aspden RJ, Malarkey J, Simmons S, Paterson DM, Lichtman ID, Davies AG, Thorne PD, Bass SJ (2015) Sticky stuff: redefining bedform prediction in modern and ancient environments. Geology 43:399–402. https://doi.org/10.1130/G36262.1
Shakeel A, Lupi FR, Gabriele D, Baldino N, De Cindio B (2018) Bigels: A unique class of materials for drug delivery applications. Soft Materials 16(2):77–93
Shakeel A, Kirichek A, Chassagne C (2019a) Rheological analysis of mud from Port of Hamburg, Germany. J Soils Sediments 1–10. https://doi.org/10.1007/s11368-019-02448-7
Shakeel A, Farooq U, Iqbal T, Yasin S, Lupi FR, Gabriele D (2019b) Key characteristics and modelling of bigels systems: A review. Materials Science and Engineering: C 97:932–953
Shakeel A, Mahmood H, Farooq U, Ullah Z, Yasin S, Iqbal T, Chassagne C, Moniruzzaman M (2019c) Rheology of Pure Ionic Liquids and Their Complex Fluids: A Review. ACS Sustainable Chemistry & Engineering 7(16):13586–13626
Soltanpour M, Samsami F (2011) A comparative study on the rheology and wave dissipation of kaolinite and natural Hendijan Coast mud, the Persian Gulf. Ocean Dyn 61:295–309. https://doi.org/10.1007/s10236-011-0378-7
Spearman J, Manning AJ (2017) On the hindered settling of sand-mud suspensions. Ocean Dyn 67:465–483. https://doi.org/10.1007/s10236-017-1034-7
Spearman JR, Manning AJ, Whitehouse RJS (2011) The settling dynamics of flocculating mud and sand mixtures: part 2—numerical modelling. Ocean Dyn 61:351–370. https://doi.org/10.1007/s10236-011-0385-8
Spencer KL, Manning AJ, Droppo IG, Leppard GG, Benson T (2010) Dynamic interactions between cohesive sediment tracers and natural mud. J Soils Sediments 10:1401–1414. https://doi.org/10.1007/s11368-010-0291-6
Tolhurst TJ, Gust G, Paterson DM (2002) The influence of an extracellular polymeric substance (EPS) on cohesive sediment stability. In: Winterwerp JC, Kranenburg C (eds) Proceedings in Marine Science. Elsevier, pp 409-425
Van Kessel T, Blom C (1998) Rheology of cohesive sediments: comparison between a natural and an artificial mud. J Hydraul Res 36:591–612. https://doi.org/10.1080/00221689809498611
Whitehouse R, Manning A (2007) Mixing it: how marine mud and sand interact. Innovation & Research Focus, Institution of Civil Engineering, London, Thomas Telford Services Ltd 71
Whitehouse R, Soulsby R, Roberts W, Mitchener H (2000) Dynamics of Estuarine Muds: A Manual for Practical Applications. Thomas Telford
Wurpts R (2005) 15 years experience with fluid mud: definition of the nautical bottom with rheological parameters. Terra et Aqua: International Journal on Public Works, Ports and Waterways Developments
Xu J, Huhe A (2016) Rheological study of mudflows at Lianyungang in China. Int J Sediment Res 31:71–78. https://doi.org/10.1016/j.ijsrc.2014.06.002
Yang W, Yu G-l, Tan S, Wang H-k (2014) Rheological properties of dense natural cohesive sediments subject to shear loadings. Int J Sediment Res 29:454–470. https://doi.org/10.1016/S1001-6279(14)60059-7
Zhu L, Sun N, Papadopoulos K, Kee DD (2001) A slotted plate device for measuring static yield stress. J Rheol 45:1105–1122. https://doi.org/10.1122/1.1392299
Funding
This study is funded by the Hamburg Port Authority and carried out within the framework of the MUDNET academic network. https://www.tudelft.nl/mudnet/.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shakeel, A., Kirichek, A. & Chassagne, C. Is density enough to predict the rheology of natural sediments?. Geo-Mar Lett 39, 427–434 (2019). https://doi.org/10.1007/s00367-019-00601-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00367-019-00601-2