On the numerical and mesh-dependent parameters in a computationally enhanced phase-field fracture model coupled with a novel mesh refinement strategy

Abstract

The phase-field method has been proven as a robust and computationally efficient approach to model the propagation of fractures in brittle solids. However, the performance of this technique in the context of finite element method can be questioned due to restrictions in the mesh structure and the element size to capture the fracture as a diffusive damaged region. This study is dedicated to developing a methodology for finding an appropriate length-scale parameter to model the fracturing process in a way that matches the physical character of failure in materials. The fracture process zone is chosen as the key feature in this study to propose relationships for estimating the length-scale parameter based on the tensile strength and cracking properties, and the robustness of the method is verified using experimental data. To employ the phase-field method in modelling large-scale domains and complex geometries, a novel mesh refinement strategy is developed to increase the computational efficiency based on predicting a corrected tensile strength limit depending on the element size to capture the crack-tip effectively. The proposed mesh refinement strategy reduces the computational effort significantly. Reliability and robustness of the developed relationships are successfully examined by simulating benchmark cases and comparisons with physically measured data.

1 Introduction

Modelling fracture propagation and nucleation have been of interest among the community of the computational mechanics for the past few decades. Several methods have been developed in the context of the finite element method (FEM) to trace the fracture pathways in solids. Some of these methods such as adaptive remeshing [1] and the cohesive zone element method [2] are highly dependent on the mesh structure. Therefore, size and type of the elements play important roles in the accuracy and reliability of the crack-path predictions [3]. The well-known extended finite element method (XFEM) can be categorised separately as it models the fractures by adding the enrichment functions to the elements [4]. Using XFEM, the fracture propagation can be modelled based on the principles of the Linear Elastic Fracture Mechanics (LEFM) and does not require mesh refinement as long as the element size is satisfactory for a reliable calculation of the field variables. The other approach in the context of FEM is the phase-field method, an energy-based approach for modelling fractures which is conceptually aligned with Griffith’s hypothesis [5].

Along with the concept of the phase-field method, various formulations have been proposed to calculate how the contribution of the mobilised strain energy is considered for breaking down the solid [6]. The calculation of crack driving force can be strain-dependent [7,8,9] or stress-dependent [10, 11] functionals, depending on the physics of rupture in the material. A formulation was introduced by Miehe et al. [7] who hypothesised that the crack only forms through the elements under tension, so the tensile part of the strain energy is only considered via spectral decomposition of the strain tensor. Amor et al. [8] formulated the crack driving force based on separating the deviatoric and volumetric parts of the strain energy. Later, stress-based formulations were introduced to the community based on various failure criteria. The choice of stress-based formulations restricts the degradation to only the regions where the maximum principal stresses exceed the tensile strength of the material [10], requiring considerations with regard to the construction of an appropriate computational mesh.

In the strain-based approach of Miehe et al. in 2010 [7], changing the value of the length-scale parameter (l₀) was found to have a significant impact on the cracking response. The dependency of the phase-field method on the user-defined value of l₀ was later resolved by Miehe et al. in 2015 [10] calculating the critical energy release rate as a function of the length-scale parameter and tensile strength of the material. This proposed relationship was not verified against experimental data. It has been proved mathematically that the response of the phase-field fracture model becomes identical to that of the discrete fracture when ${l}_{0}\to 0$ [12]. From a physical perspective, Bažant correlated the length-scale parameter to the maximum aggregate size in concrete material by comparing the failure response of damage models to the relevant experimental data [13]. In another study [14], ${l}_{0}$ has been recommended to be 2–3 times larger than the microstructural cell size in cellular materials. Calibrating input parameters, especially length-scale parameter, with micro- and meso-scale characteristics of cracking such as the fracture process zone (FPZ) and tensile failure in materials is one of the major contributions of this study.

In the phase-field fracture modelling, the finite element (FE) mesh must be fine enough to capture the width of the diffusive fracture effectively [15]. It has been recommended by Miehe et al. [7] that the maximum size of quadrilateral elements must be limited to ${l}_{0}/2$ for the fully damaged region. Choice of the element size has a significant effect on the error and convergence rate of the results of the phase-field fracture model [16]. In relatively large geometries and heterogeneous media, using a fine-mesh structure makes the computations too expensive, so including mesh refinement can be a feasible solution to keep the computational effort low while maintaining the reliability of the simulations [17]. In modelling the phase-field fracture in heterogeneous and non-isotropic materials, having a robust mesh refinement unit becomes vital to capture the possible tortuosity in the crack-path and reducing the uncertainties in predicting crack-paths [18,19,20,21]. Several studies have been conducted on developing adaptive mesh refinement techniques which are mainly concerned with the implementation and increasing the efficiency of the computations [22,23,24]. The magnitude of the load increments can also affect the accuracy and stability of the FE analysis during the fracture propagation because of the stiffness degradation due to cracking [25]. In subsequent load-steps, there exists a critical stage when the tensile stress in the element exceeds the strength of the material, which must be predicted by the computational mesh in fracture modelling tools. Previous studies on the phase-field fracture models coupled with the mesh refinement technique have not explicitly addressed the details of this critical stage, so we try to introduce controlling limits in our proposed mesh refinement strategy as well as the recommendations regarding its implementation to reliably predict the stage of tensile failure and the fracture propagation response independent from the mesh characteristics, specifically the element size.

In this paper, we aim to improve the reliability and performance of the phase-field fracture modelling, respectively, by introducing: (i) a set of relationships based on the principles of LEFM, allowing one to select the model input parameters according to the physical nature of failure in the material, and (ii) a mesh refinement strategy capable of capturing the FPZ at the right stage of the deformation history (when tensile failure occurs) to model the phase-field fracture with the least computational effort. For this purpose, we use two strain- and stress-based formulations introduced by Miehe et al. [7, 10] for calculating the crack driving force so that our recommendations cover different formulations in calculating the contribution of the strain energy in the damage evolution model. The numerical model is coupled with a predictive h-refinement algorithm, which can track the crack-tip effectively by estimating the extent of the FPZ throughout the mesh. The mesh refinement strategy proposed in this work is verified through a comparative assessment between the results taken from the refined mesh and a well-built fine-mesh structure for the simulations of mode-I fracture propagation. As for the first purpose of this work, we develop practical relationships for determining the inputs of the phase-field fracture model based on the LEFM. To do so, we relate the length-scale parameter to the material properties, including the critical tensile strength, fracture toughness, and the size of the FPZ. The proposed relationships are tested with regard to a set of experimental data to confirm their applicability in the phase-field fracture model. Our results demonstrate that using the stress-based formulation of Miehe et al. [10] for defining the crack driving force requires the use of a corrected value for the fracture energy and length-scale parameter based on the critical tensile strength and the size of the FPZ.

2 Phase-field fracture modelling

In this section, mathematical formulations for modelling brittle diffusive fractures under quasi-static loading condition are given in both linear and geometrically nonlinear FE analyses.

2.1 Energy minimisation approach

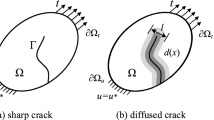
The ratio of the change of internal energy $\delta {\Pi }$ to the change of newly formed surface area $\delta A$ (due to fracture propagation) is known as critical energy release rate $G_{c} = \delta {\Pi }/\delta A$ and is recognised as a material property. Francfort and Marigo [5] proposed a novel approach for tracking the fracture propagation based on the variational theory by minimising the total energy functional ($\Pi$), consisting of bulk strain energy ($W_{{{\text{bulk}}}}$) and the surface energy ($W_{{{\text{crack}}}} = \mathop \int \limits_{\Gamma } G_{c} dA$). By introducing a phase-field parameter ($d$) to represent the fracture boundary ($\Gamma$) and the surface energy density function $\gamma \left( {d,\nabla d} \right)$, the internal potential energy functional can be formulated over the volume (${\Omega }$) as [26]

$$ {\Pi } = \mathop \int \limits_{{\Omega }} {\text{W}}_{{{\text{bulk}}}} {\text{dV}} + \underbrace {{{\text{G}}_{{{\rm c}}} \mathop \int \limits_{{\Omega }} \left[ {\frac{{{\text{l}}_{0} }}{2}\left| {\nabla {\text{d}}} \right|^{2} + \frac{1}{{2{\text{l}}_{0} }}\left( {1 - {\text{d}}} \right)^{2} } \right]{\text{dV}}}}_{{{\text{W}}_{{{\text{crack}}}} }} $$

(1)

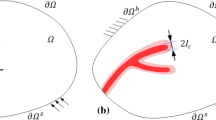
where the critical energy release rate $G_{c} = \delta {\Pi }/\delta A$ is a material property. Variation of the phase-field (damage) parameter is governed by a Dirac-type function as $d\left( {x{\prime}} \right) = 1 - e^{{ - \left| {x{\prime}} \right|/l_{0} }}$, where values $d = 0$ and $d = 1$ represent fully damaged and intact materials, respectively, and $l_{0}$ is so-called the length-scale parameter which governs how wide the diffusive fracture is considered. Equation (1) is re-written by affecting a degradation function $g\left( d \right) = d^{2} + k_{\varepsilon }$ on the tensile part of the bulk strain energy [7] as

$$ {\Pi } = \mathop \int \limits_{{\Omega }} \left( {{\text{d}}^{2} + {\text{k}}_{{\upvarepsilon }} { }} \right)\left[ {{\text{W}}_{{{\text{bulk}}}}^{ + } } \right]{\text{dV}} + \mathop \int \limits_{{\Omega }} \left[ {{\text{W}}_{{{\text{bulk}}}}^{ - } } \right]{\text{dV}} + {\text{G}}_{{{\rm c}}} \mathop \int \limits_{{\Omega }} \left[ {\frac{{{\text{l}}_{0} }}{2}\left| {\nabla {\text{d}}} \right|^{2} + \frac{1}{{2{\text{l}}_{0} }}\left( {1 - {\text{d}}} \right)^{2} } \right]{\text{dV}} $$

(2)

where $k_{\varepsilon } \ll 1$ is a regularisation parameter to maintain numerical stability [7], and $W_{{{\text{bulk}}}}^{ \pm }$ will be defined in the following section based on the spectral decomposition of strain and stress tensors.

2.2 Geometrically nonlinear framework

In the context of kinematics of large deformations, an updated Lagrangian FE framework is chosen to derive the weak forms from the internal energy functional of a fracturing body. The undeformed body in Euclidean space is defined in the reference (undeformed) configuration ${\Omega 0}$ and can undergo deformations in subsequent load steps. The relative position of two adjacent points in the current configuration (${\Omega }_{{{\rm t}}}$) can be mapped over the reference configuration (${\Omega 0}$) using a mapping function as ${\varvec{x}}_{{{\rm i}}} = \phi \left( {{\varvec{X}}_{{{\rm i}}} ,t} \right)$, see Fig. 1. The Green–Lagrange strains are defined as ${\varvec{E}} = 0.5\left( {{\varvec{C}} - {\varvec{I}}} \right)$, where ${\varvec{F}}\left( {{\varvec{X}},t} \right) = \nabla_{{{\rm X}}} \left( \phi \right)$ is the deformation gradient and ${\varvec{C}} = {\varvec{F}}^{{{\rm T}}} \cdot {\varvec{F}}$ is the right Cauchy–Green deformation tensor [27]. For the system to remain in equilibrium, the variation of ${\Pi }$, assuming a fixed state of damage ($\overline{d}$), with respect to arbitrary displacements ${\varvec{\zeta}}$ must vanish as

$$ \begin{aligned} \delta {\Pi }\left( {{\varvec{C}},\overline{d}} \right)\left[ {\varvec{\zeta}} \right]{\kern 1pt} & = \mathop \int \limits_{{{\Omega 0} }} g\left( {\overline{d}} \right) \cdot \frac{{\partial W_{{{\text{bulk}}}}^{ + } \left( {{\varvec{C}},\overline{d}} \right)}}{{\partial {\varvec{C}}}}{ \sim }D{\varvec{C}}\left[ {\varvec{\zeta}} \right] dV + \mathop \int \limits_{{{\Omega 0} }} \frac{{\partial W_{{{\text{bulk}}}}^{ - } \left( {{\varvec{C}},\overline{d}} \right)}}{{\partial {\varvec{C}}}}{ \sim }D{\varvec{C}}\left[ {\varvec{\zeta}} \right] dV \\ & \quad - \delta W_{{{\text{ext}}}} = \mathop \int \limits_{{{\Omega 0} }} \left( {g\left( {\overline{d}} \right)\left[ {\varvec{S}} \right]^{ + } + \left[ {\varvec{S}} \right]^{ - } } \right){ \sim }D{\varvec{E}}\left[ {\varvec{\zeta}} \right] dV - \delta W_{{{\text{ext}}}} = 0 \\ \end{aligned} $$

(3)

where $W_{{{\text{bulk}}}} \left( {{\varvec{C}},\overline{d}} \right) = g\left( {\overline{d}} \right)W_{{{\text{bulk}}}}^{ + } + W_{{{\text{bulk}}}}^{ - }$ is the degraded bulk energy, and $\left[ {\varvec{S}} \right]^{ \pm } = 2\partial W_{{{\text{bulk}}}}^{ \pm } \left( {\varvec{C}} \right)/\partial {\varvec{C}}$ is the tensile and compressive parts of the second Piola–Kirchhoff stress defined in the reference configuration [27]. The bulk strain energy contributions $W_{{{\text{bulk}}}}^{ \pm } \left( {\varvec{C}} \right)$ for a compressible Neo–Hookean material are defined as

$$ W_{{{\text{bulk}}}}^{ \pm } \left( {\varvec{C}} \right){ } = \mu \left[ {\left( {\ln {\mathcal{S}}_{1}^{ \pm } } \right)^{2} + \left( {\ln {\mathcal{S}}_{2}^{ \pm } } \right)^{2} + \left( {\ln {\mathcal{S}}_{3}^{ \pm } } \right)^{2} } \right] + \frac{\lambda }{2}\left( {\ln J_{ + } } \right)^{2} $$

(4)

where $\mu$ and ${\uplambda }$ are Lame parameters. Tensile and compressive stretches ${\mathcal{S}}_{{{\rm i}}}^{ \pm }$ are formulated as

$$ \left\{ {\begin{array}{*{20}c} {{\mathcal{S}}_{{{\rm i}}}^{ + } = {\mathcal{S}}_{{{\rm i}}} - 1_{ + } + 1} \\ {{\mathcal{S}}_{{{\rm i}}}^{ - } = {\mathcal{S}}_{{{\rm i}}} - 1_{ - } + 1} \\ \end{array} } \right. $$

(5)

where ${\mathcal{S}}_{{{\rm i}}}^{2}$ are the eigenvalues of the spectral decomposition of tensor ${\varvec{C}}$ [27]. Cauchy stress tensors in the current configuration ${\Omega }_{t}$ can be reached via the mapping function $\left[ {\varvec{\sigma}} \right]^{ \pm } { } = J^{ - 1} {\varvec{F}} \cdot \left[ {\varvec{S}} \right]^{ \pm } { } \cdot {\varvec{F}}^{{{\rm T}}}$, where $J = \left| {\varvec{F}} \right|$ is the Jacobian of the deformation tensor [27]. In an updated Lagrangian FE framework, the linearised form of Eq. (3) in the direction of $\delta {\varvec{u}}$ is constructed over ${\Omega 0}$, while ${\varvec{u}}_{{{\text{n}} + 1}} = {\varvec{u}}_{{{\rm n}}} + \delta {\varvec{u}}$.

$$ \begin{aligned} \mathop \int \limits_{{{\Omega 0} }} \nabla_{{{\rm x}}} \left( {\varvec{\zeta}} \right) & { \sim }\left[ {{\mathbf{\mathcal{C}}}\left( {{\varvec{u}}_{{{\rm n}}} ,\overline{d}} \right)} \right]{ \sim }\nabla_{{{\rm x}}} \left( {\delta {\varvec{u}}} \right){ }dV + \mathop \int \limits_{{{\Omega 0} }} \left[ {g\left( {\overline{d}} \right)\left[ {\varvec{\sigma}} \right]_{{{\rm n}}}^{ + } + \left[ {\varvec{\sigma}} \right]_{{{\rm n}}}^{ - } } \right]{ \sim }\left[ {\nabla_{{{\rm x}}}^{T} \left( {\delta {\varvec{u}}} \right) \cdot \nabla_{{{\rm x}}} \left( {\varvec{\zeta}} \right)} \right] J_{{{\rm n}}} dV \\ & \quad - \mathop \int \limits_{{{\Omega 0} }} {\varvec{b}} \cdot {\varvec{\zeta}} \cdot J_{{{\rm n}}} \left( {\nabla_{{{\rm x}}} \cdot \delta {\varvec{u}}} \right)d{\text{V}} - \mathop \int \limits_{{\partial {\Omega 0}_{{\varvec{\sigma}}} }} {\varvec{\zeta}} \cdot \delta {\varvec{T}}d{\text{A}} = 0 \\ \end{aligned} $$

(6)

where $\nabla_{{{\rm x}}}$ is taken with respect to the moving spatial coordinates ${\varvec{x}}_{{{\rm i}}}$ at step $t_{{{\rm n}}}$, ${\varvec{b}}$ is the body forces, and ${\varvec{T}}$ are the traction forces on the Neumann boundaries $\partial {\Omega 0}_{{\varvec{\sigma}}}$. In the nonlinear analysis, the elasticity tensor ${\mathbf{\mathcal{C}}}\left( {{\varvec{u}}_{{{\rm n}}} ,\overline{d}} \right)$ is updated iteratively to account for the variation of stiffness due to geometrical deformations, further details are provided in Appendix B.

Fig. 1

Kinematics of large deformation and the definition of mapping function (${\varvec{\phi}}$) in two-dimensional Euclidean space

2.3 Linear elastic framework

In the linear analysis, the evolution of stiffness due to geometrical deformations is not of interest since the computational domain remains unchanged. Assuming a fixed state of damage ($\overline{d}$), the principle of virtual work in a linear elastic FE framework is reached by finding a stationary position of $\delta {\Pi } = 0$ with respect to arbitrary displacements ${\varvec{\zeta}}$.

$$ \begin{aligned} \delta {\Pi }\left( {{\varvec{u}},\overline{d}} \right)\left[ {\varvec{\zeta}} \right] & = \mathop \int \limits_{{{\Omega 0} }} g\left( {\overline{d}} \right) \cdot \frac{{\partial W_{{{\text{bulk}}}}^{ + } \left( {\varvec{\varepsilon}} \right)}}{{\partial {\varvec{\varepsilon}}}}{ \sim }\delta {\varvec{\varepsilon}}\left[ {\varvec{\zeta}} \right] dV + \mathop \int \limits_{{{\Omega 0} }} \frac{{\partial W_{{{\text{bulk}}}}^{ - } \left( {\varvec{\varepsilon}} \right)}}{{\partial {\varvec{\varepsilon}}}}{ \sim }\delta {\varvec{\varepsilon}}\left[ {\varvec{\zeta}} \right] dV - \delta W_{{{\text{ext}}}} \\ = \mathop \int \limits_{{{\Omega 0} }} \left( {g\left( {\overline{d}} \right)\left[ {\varvec{\sigma}} \right]^{ + } + \left[ {\varvec{\sigma}} \right]^{ - } } \right){ \sim }\delta {\varvec{\varepsilon}}\left[ {\varvec{\zeta}} \right] dV - \delta W_{{{\text{ext}}}} = 0 \\ \end{aligned} $$

(7)

where ${\varvec{\varepsilon}} = 0.5\left( {\nabla_{{{\rm X}}} {\varvec{u}} + \nabla_{{{\rm X}}}^{{{\rm T}}} {\varvec{u}}} \right)$ is the infinitesimal strain tensor and the energy contributions are defined below.

$$ W_{{{\text{bulk}}}}^{ \pm } \left( {\varvec{\varepsilon}} \right){ } = \frac{\lambda }{2}\left\langle {{\text{tr}}\left[ {\varvec{\varepsilon}} \right]_{ \pm }^{2} } \right\rangle + \mu {\text{tr}}\left\langle {{\varvec{\varepsilon}}^{2} } \right\rangle_{ \pm } $$

(8)

The principle of virtual work for the linear elastic setting is constructed as

$$ \mathop \int \limits_{{{\Omega 0} }} \nabla_{{{\rm X}}} \left( {\varvec{\zeta}} \right){ \sim }g\left( {\overline{d}} \right) [ {\mathbb{C}} ]{ \sim }\nabla_{{{\rm X}}} \left( {\delta {\varvec{u}}} \right){ }dV - \mathop \int \limits_{{{\Omega 0} }} {\varvec{\zeta}} \cdot {\varvec{b}}d{\text{V}} - \mathop \int \limits_{{\partial {\Omega }{0}_{{\varvec{\sigma}}} }} {\varvec{\zeta}} \cdot {\varvec{T}}d{\text{A}} = 0 $$

(9)

where ${\mathbb{C}}$ is the unchanged fourth-order elasticity tensor for linear elastic material.

2.4 Damage evolution model

The internal potential energy of the system (${\Pi }$) is minimised with respect to the phase-field parameter $\left( d \right)$ to obtain the weak form of the damage evolution model. Hiring a staggered approach for the energy minimisation, a fixed state of the displacements ($\overline{\boldsymbol{u}}$) is considered, and a stationary position of $\delta {\Pi } = 0$ with respect to arbitrary damage $\omega$ is searched using the weak form of the damage evolution model as

$$ \begin{aligned} \delta {\Pi }\left( {\overline{\boldsymbol{u}},d} \right)\left[ \omega \right] & = \mathop \int \limits_{{{\Omega 0} }} 2\frac{H}{{G_{c} }}\left( d \right)\left[ \omega \right] d{\text{V}} + l_{0} \mathop \int \limits_{{{\Omega 0} }} \left( {\nabla_{{{\rm X}}} \omega \cdot \nabla_{{{\rm X}}} d} \right) d{\text{V}} - \mathop \int \limits_{{{\Omega 0} }} \frac{{\left( {1 - d} \right)}}{{l_{0} }}\left[ \omega \right]d{\text{V}} \\ & \quad - l_{0} \mathop \int \limits_{{\partial {\Omega 0} }} \left[ \omega \right]\nabla_{{{\rm X}}} d \cdot {\varvec{N}}dA = 0 \\ \end{aligned} $$

(10)

where Neumann boundary conditions $\nabla_{{{\rm X}}} d \cdot {\varvec{N}} = 0$ are applied on all the boundaries $\partial {\Omega 0}$, and $H$ is a history field defined in the following to ensure the irreversibility of fracture [7].

$$ H = \mathop {\max }\limits_{{{\mathcal{T}} \in \left[ {0,t} \right]}} W_{{{\text{bulk}}}}^{ + } \left( {\overline{\boldsymbol{u}},{\mathcal{T}}} \right) $$

(11)

In this study, we consider two formulations, namely the strain-based $H_{1}$ and the stress-based $H_{2}$ criteria, to form the crack driving force ($H/G_{c}$) to be used in the crack evolution weak form (Eq. 10). The $H_{1}$ criterion, proposed by Miehe et al. in 2010 [7], is defined for both cases of nonlinear and linear elasticity as

$$ H_{1}^{{{\text{Nonlinear}}}} = \mathop {\max }\limits_{{{\mathcal{T}} \in \left[ {0,t} \right]}} \left( {\mu \mathop \sum \limits_{{{\text{i}} = 1}}^{3} \left( {\ln {\mathcal{S}}_{{{\rm i}}}^{ + } \left( {\mathcal{T}} \right)} \right)^{2} + \frac{\lambda }{2}\left( {\ln J\left( {\mathcal{T}} \right)_{ + } } \right)^{2} } \right) $$

(12)

$$ H_{1}^{{{\text{linear}}}} = \mathop {\max }\limits_{{{\mathcal{T}} \in \left[ {0,t} \right]}} \left( {\frac{\lambda }{2}{\text{tr}}\left[ {{\varvec{\varepsilon}}\left( {\mathcal{T}} \right)} \right]_{ + }^{2} + \mu {\text{tr}}{\varvec{\varepsilon}}^{2} \left( {\mathcal{T}} \right)_{ + } } \right) $$

(13)

The second criterion $H_{2}$ is the stress-based one, proposed by Miehe et al. in 2015 [10], which is defined in the following. Cracking occurs if and only if the condition $\sum {{\sigma_{{{\rm i}}}}_{ + }^{2}} > \sigma_{c}^{2}$ is satisfied for the element, where $\sigma_{c}$ is the critical tensile stress of the material.

$$ H_{2} = \mathop {\max }\limits_{{{\mathcal{T}} \in \left[ {0,t} \right]}} \left( {\mathop \sum \limits_{i = 1}^{3} \frac{{\sigma_{{{\rm i}}} \left( {\mathcal{T}} \right)_{ + }^{2} }}{{\sigma_{c}^{2} }} - 1_{ + } \times \frac{{\sigma_{c}^{2} }}{{2E{\prime}}}} \right) $$

(14)

In the above equation, $\sigma_{{{\rm i}}} \left( {\mathcal{T}} \right)$ are the principal Cauchy stresses in time (obtained via spectral decomposition of the undegraded Cauchy stress tensor ${\varvec{\sigma}}$), and $E{\prime} = \mu{\prime}\left( {2\mu{\prime} + 3\lambda{\prime}} \right)/\left( {\lambda{\prime} + \mu{\prime}} \right)$ is the effective young modulus in plane-strain condition. Note that $\mu{\prime} = \mu - \lambda \left( {\ln J} \right)$ and $\lambda{\prime} = \lambda$ in the case of finite elasticity, while $\lambda{\prime} = \lambda$ and $\mu{\prime} = \mu$ in the linear elasticity case.

2.5 Numerical algorithm

The FE formulations presented previously have been implemented in MATLAB for modelling phase-field fracture propagation. In this study, the PDE-toolbox in MATLAB has been used for mesh generation and refinement [27]; the built-in function “generateMesh” is used to construct two-dimensional FE mesh structures using first-order 3-noded elements, and “refinemesh” is used to perform h-refinement on the coarse elements, see Sect. 4 for further details on the refinement strategy. Matrix forms of the damage evolution model and the mechanical equilibrium in both linear and geometrically nonlinear FE analyses are implemented in MATLAB, and the global system of equations is solved using the built-in function “mldivide”. Employing a staggered approach [7], displacement and damage fields are solved in an iterative manner, where $i$ is the iteration counter (for convergence in the damage field $d_{{{\text{n}} + 1}}^{{\left( {\text{i}} \right)}}$) in each load-step: ($n + 1$). The problem is solved for displacements and damage (${\varvec{u}},d$) in the following algorithm:

• 1. Set the initial values for damage and displacements from the converged results of the previous load-step: ($n$), i.e. ${\varvec{u}}_{{{\text{n}} + 1}}^{{\left( {{\text{i}} = 0} \right)}} = {\varvec{u}}_{{{\rm n}}}$ and $d_{{{\text{n}} + 1}}^{{\left( {{\text{i}} = 0} \right)}} = d_{{{\rm n}}}$.

• 2. Applying Dirichlet and Neumann boundary conditions and forming the vector of external forces.

• 3. Starting the iterative solver: $i = i + 1$

• 4. Set $d_{{{\text{n}} + 1}}^{{\left( {\text{i}} \right)}} = d_{{{\text{n}} + 1}}^{{\left( {{\text{i}} - 1} \right)}}$ fixed and solve for ${\varvec{u}}_{{{\text{n}} + 1}}^{{\left( {\text{i}} \right)}}$ via satisfying weak forms of the principle of virtual work: Eqs. (6) or (9), depending on having nonlinear or linear analyses, respectively. Note that an internal iterative approach in solving for displacements ${\varvec{u}}_{{{\text{n}} + 1}}^{{\left( {\text{i}} \right)}}$ is required for the case of nonlinear FE analysis [29].

• 5. Set ${\varvec{u}}_{{{\text{n}} + 1}}^{{\left( {\text{i}} \right)}}$ fixed and solve for $d_{{{\text{n}} + 1}}^{{\left( {\text{i}} \right)}}$ via satisfying the weak form of damage evolution model, Eq. (10).

• 6. Check whether the mesh refinement is required (details are provided in Sect. 4). For each element in every iteration ($i$), if $\sigma_{p1} > \sigma_{c}^{{{\text{eq}}}}$:

  • a. Yes: perform h-refinement and go to 3.

  • b. No: go to 7.

• 7. Check the convergence in the damage field in two subsequent iterations using the absolute convergence criterion [29]. If $\left| {d_{{{\text{n}} + 1}}^{{\left( {\text{i}} \right)}} - d_{{{\text{n}} + 1}}^{{\left( {{\text{i}} - 1} \right)}} } \right| < \epsilon_{{{\rm d}}}$:

  • a. Yes: exit.

  • b. No: go to 3.

In all the simulations performed in this paper, the acceptable tolerance in the damage field, denoted as ϵ_d, has been chosen as ϵ_d = 10^–7. Additionally, to prevent the risk of an endless loop when using an extremely small tolerance value, a maximum limit for the number of iterations (i) is set. The mesh refinement is performed for the critical coarse element (identified as explained in Sect. 4) by adding an extra node (extra degrees of freedom) on the longest boundary of the targeted element. Nodal values of damage and displacements for the newly added degrees of freedom are calculated using a linear interpolation of the nodal values between which the added node is placed, (h-refinement approach) [29]. The mesh refinement is implemented in each iteration, and the mechanical equilibrium is satisfied after each cycle of refinement, ensuring the stability of the new mesh structure.

3 Setting up the input parameters in the phase-field method

Calculation of strain- and stress-based history fields ($H_{1}$ and $H_{2,}$ respectively) depends on the elemental quantities (i.e. strain and stress values over the Gauss integration points) and can be affected by the size and order of the element. In this section, a formulation will be proposed that relates the length-scale parameter ($l_{0}$) to the material properties and the micro-mechanical behaviour of the cracking in brittle materials. The length-scale parameter ($l_{0}$) is correlated with the FPZ such that the boundary of which can be captured by the diffusive phase-field fracture over the elements. We rely on the principles of LEFM that define the maximum and minimum principal stresses around the crack-tip in plane-strain condition, respectively, as [30]

$$ \sigma_{{{\text{p}}1}} = \frac{{K_{I} }}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left( {1 + \sin \frac{\theta }{2}} \right) $$

(15)

$$ \sigma_{{{\text{p}}2}} = \frac{{K_{I} }}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left( {1 - \sin \frac{\theta }{2}} \right) $$

(16)

where $K_{I}$ is the stress intensity factor for mode-I fracture, and ($r,\theta$) are polar coordinates, origin of which is set on the crack-tip. As $r \to 0$, the principal stresses become singular, and the material enters a plastic state around the crack-tip, so-called the FPZ, the boundaries of which can be formulated using Von Mises yield criterion.

$$ \left\{ {\begin{array}{*{20}c} {\sqrt {\left( {\sigma_{{{\text{p}}1}} - \sigma_{{{\text{p}}2}} } \right)^{2} + \left( {\sigma_{{{\text{p}}3}} - \sigma_{{{\text{p}}2}} } \right)^{2} + \left( {\sigma_{{{\text{p}}3}} - \sigma_{{{\text{p}}1}} } \right)^{2} } < \sigma_{c} } & {\forall r > r_{c} } \\ {\sqrt {\left( {\sigma_{{{\text{p}}1}} - \sigma_{{{\text{p}}2}} } \right)^{2} + \left( {\sigma_{{{\text{p}}3}} - \sigma_{{{\text{p}}2}} } \right)^{2} + \left( {\sigma_{{{\text{p}}3}} - \sigma_{{{\text{p}}1}} } \right)^{2} } \ge \sigma_{c} } & {\forall r \le r_{c} } \\ \end{array} } \right. $$

(17)

The critical radius $r_{c}$, defined below, separates the plastic region inside the FPZ from the elastic stress regime [30].

$$ r_{c} \left( \theta \right) = \frac{{K_{Ic}^{2} }}{{4\pi \sigma_{c}^{2} }}\left[ {\frac{3}{2}\sin^{2} \theta + \left( {1 - 2\nu } \right)^{2} \left( {1 + \cos \theta } \right)} \right] $$

(18)

In the above equation, $K_{Ic}$ is the mode-I critical stress intensity factor (fracture toughness) and $G_{c} = K_{Ic}^{2} /E{\prime}$ [30]. It can be understood from the above relationship that a material with higher tensile strength implies a smaller size for the FPZ, equally meaning the requirement for a smaller value of $l_{0}$ in modelling the phase-field fracture. In order to visualise the dependency of $r_{c} \left( \theta \right)$ on $\sigma_{c}$, the boundary of $r_{c} \left( \theta \right)$ associated with different values of $\sigma_{c}$ is plotted in polar coordinates in Fig. 2, assuming constant values of $E$ = 210 GPa, $\nu$ = 0.3, and $G_{c}$ = 2.7E−3 kN/mm. The maximum value of the FPZ’s half-width is recognised by $r_{{{\text{FPZ}}}} = \left| {r_{c} \left( { \pm \pi /2{ }} \right)} \right|$.

Fig. 2

Demonstration of the FPZ boundary for different values of the critical tensile strength ${\sigma }_{c}$ in polar coordinates ($r,\theta$)

On the one hand, there must exist Gauss integration points (equivalent to one element for the case of the first-order 3-noded elements in this study) inside the imaginary FPZ around the crack-tip to capture the maximum principal stresses $\sigma_{{{\text{p}}1}}$ that are higher than the tensile strength of the material (i.e. tensile failure). On the other hand, the maximum acceptable size for the crack-tip element must be kept as $h_{{{\text{el}}}} = l_{0} /4$ to ensure the independency of the solution from the computational mesh. In Appendix A, we have shown that setting the element size to $h_{{{\text{el}}}} = l_{0} /4$ guarantees the independency of the solution from the mesh while keeping the computational cost at an optimum level. Therefore, we hypothesise that $l_{0}$ can be chosen based on the size of FPZ ($r_{{{\text{FPZ}}}}$). To ensure capturing high stresses ($\sigma_{{{\text{p}}1}} > \sigma_{c}$) in the FPZ, $r_{c} \left( \theta \right) = l_{0} /4$ is substituted into Eq. (18). The re-arranged form of Eq. (18) is written below as a recommendation to calculate the length-scale parameter as

$$ l_{0} = G_{c} E{\prime}\left[ {1.5\sin^{2} \beta + \left( {1 - 2\nu } \right)^{2} \left( {1 + \cos \beta } \right)} \right]/\left( {\pi \sigma_{c}^{2} } \right) $$

(19)

where $\beta$ depends on the element shape (e.g. $\beta$ = $60^\circ$ for the first-order 3-noded element) ensuring that the whole area of the element fits inside the FPZ, see Fig. 2. Equation (19) is recommended to be used in setting up the value of $l_{0}$ in the phase-field model when employing $H_{2}$-criterion in calculating the crack driving force in the damage model. If the length-scale parameter is decided to be chosen regardless of the material properties, due to computational limitations, a corrected value of the tensile strength ($\sigma_{c}^{{{\text{PF}}}}$), that is calculated using Eq. (20), must be implemented into Eq. (14) for calculating $H_{2}$ in the damage model to avoid errors in the cracking response of the body.

$$ \sigma_{c}^{{{\text{PF}}}} = \sqrt {\frac{{G_{c} E{\prime}}}{{\pi l_{0} }}\left[ {1.5\sin^{2} \beta + \left( {1 - 2\nu } \right)^{2} \left( {1 + \cos \beta } \right)} \right]} $$

(20)

It is evident that ${\sigma }_{c}^{\mathrm{PF}}={\sigma }_{c}$ if the length-scale parameter is selected using Eq. (19).

By re-arranging Eq. (20), we also recommend using the following relationship to calculate the fracture energy $G_{c}^{{{\text{PF}}}}$ based on the experimentally measured value of the tensile strength $\sigma_{c}$, while using $H_{2}$ criterion in the damage evolution model.

$$ G_{c}^{{{\text{PF}}}} = \frac{{\pi \sigma_{c}^{2} l_{0} }}{{E{\prime}\left[ {1.5\sin^{2} \beta + \left( {1 - 2\nu } \right)^{2} \left( {1 + \cos \beta } \right)} \right]}} $$

(21)

The above equation can be used in the phase-field model if the length-scale parameter is chosen with regard to the size of FPZ (i.e. $l_{0} = 4r_{FPZ}$). The FPZ’s half-width ($r_{FPZ}$) can be estimated using techniques such as the acoustic emission (AE) tomography and laser holography [31].

The applicability of the proposed relationships, Eqs. (19–21) are tested with regard to experimental data in Sect. 5.2.

4 Mesh refinement strategy

The refinement strategy is built upon two obligations: (i) tracking the FPZ to provide satisfactory element size around the crack-tip, and (ii) minimising the computational cost while maintaining the reliability.

4.1 Refinement due to the maximum principal stresses in the FPZ

First, we consider the results achieved from the reference element size $h_{{{\text{el}}}}^{{{\text{Ref}}}} = l_{0} /4$ as the reliable acceptable answer. In Fig. 3a, it is seen that the maximum principal stress $\sigma_{p1}$ for the reference-size ($h_{{{\text{el}}}}^{{{\text{Ref}}}}$) crack-tip element grows with the increase of the crack-mouth opening displacement (CMOD) and exceeds the tensile strength $\sigma_{c}$ at a point that is named “the critical stage”. The rate of growth of $\sigma_{p1}$ decreases as the size of the crack-tip element increases, so the maximum principal stress can be underestimated in the elements with the size greater than $h_{{{\text{el}}}}^{{{\text{Ref}}}} = l_{0} /4$. Hence, we assign a corrected value of the tensile strength limit to any element whose size is larger than $h_{{{\text{el}}}}^{{{\text{Ref}}}}$. To calculate the corrected tensile strength limit, we must find out to what extent the element size $h_{{{\text{el}}}}$ would affect the stress $\sigma_{p1}$ in the coarse-sized element. In Fig. 3a, the evolution of the maximum principal stress taken from the simulations in which the size of the crack-tip element is coarser than $h_{{{\text{el}}}}^{{{\text{Ref}}}}$ is plotted with respect to CMOD. The resulted values of the maximum principal stress from coarse-size elements equivalent to the actual tensile strength $\sigma_{c}$ on the reference-size element curve are found for multiple cases of $h_{{{\text{el}}}}$ in Fig. 3a. The analyses are repeated for different values of $l_{0}$, and scattering the results of $\sigma_{c}^{{{\text{eq}}}} /\sigma_{c}$ with respect to dimensionless values $h_{{{\text{el}}}} /l_{0}$ results in the curve presented in Fig. 3b. The formulation on the curve fitted to the results in Fig. 3b gives us the relationship between $c_{\sigma }^{{{\text{predict}}}} = \sigma_{c}^{{{\text{eq}}}} /\sigma_{c}$ and $h_{{{\text{el}}}} /l_{0}$ as

$$ c_{\sigma }^{{{\text{predict}}}} = e^{{ - 4\left( {h_{{{\text{el}}}} /l_{0} } \right)}} + 0.7e^{{ - 0.35\left( {h_{{{\text{el}}}} /l_{0} } \right),}} $$

(22)

allowing one to estimate the equivalent tensile strength limit in the elements whose sizes are larger than $h_{{{\text{el}}}}^{{{\text{Ref}}}}$. Thus, the mesh refinement takes place in those elements, in which $\sigma_{p1} > c_{\sigma }^{{{\text{predict}}}} \times \sigma_{c}$.

Fig. 3

a shows the stress history of the crack-tip element with respect to CMOD to find the equivalent tensile strength limit $\sigma_{c}^{{{\text{eq}}}}$ for different element sizes (red circles); b shows the function $c_{\sigma }^{{{\text{predict}}}}$ with respect to $h_{{{\text{el}}}} /l_{0}$

4.2 Refinement due to the increase of the surface energy

Accumulation of the elastic strain energy in the element causes the surface energy to grow and reach the maximum possible value $G_{c} /2l_{0}$, which is equivalent to when damage is $d$ = 0. For the crack-tip element, the evolution of $\gamma \left( {d,\nabla d} \right)$ with respect to CMOD is plotted in Fig. 4 for both criteria $H_{1}$ and $H_{2}$ for formulating the history field in the damage evolution model. The evolution of $\gamma \left( {d,\nabla d} \right)$ is calculated incrementally in subsequent steps that can be divided into two states, which we call sub-critical and super-critical. In super-critical state, full degradation of the element is potentially inevitable, and an acceptable size for the element is mandatory to allow for the full degradation of the element. The critical values of damage ($d_{{{\text{critical}}}}$) are equal to 0.65 and 0.78 for $H_{1}$ and $H_{2}$ criteria, respectively, according to Fig. 4. The mesh refinement must be performed to satisfy the condition $h_{el} \le l_{0} /4$ for those elements in which $d < d_{{{\text{critical}}}}$.

Fig. 4

The evolution of the crack surface energy density and damage parameter for $H_{1}$ and $H_{2}$ criteria for the crack-tip element having the reference size $h_{{{\text{el}}}}^{{{\text{Ref}}}} = l_{0} /4$

4.3 Reliability of the mesh refinement strategy

In Fig. 5a, the load–displacement responses of various coarse mesh structures under refinement are compared to that of the reference mesh structure with no refinement, indicating an acceptable compatibility and the capability of the mesh refinement strategy in generating response curves close to the reference result. The evolution of damage, surface energy density, and principal stresses for the crack-tip element in various mesh structures with different initial element sizes with respect to CMOD are plotted in Fig. 6. The proposed refinement strategy can effectively match the elemental responses of the refined mesh structures with that of the reference fine-mesh ($h_{{{\text{el}}}}^{{{\text{Ref}}}} = l_{0} /4$). It is seen in Fig. 6a that lowering the element size further than $l_{0} /4$ would result in capturing higher stresses; however, the point of failure (fully degradation) is of our interest for a reliable prediction of the start of fracture propagation. This critical point of failure is the same for the mesh structures with element size lower than $h_{{{\text{el}}}}^{{{\text{Ref}}}} = l_{0} /4$. As mentioned in the introduction, some refinement strategies suggest limits only based on the increase of the surface energy $\gamma$ (e.g. performing the refinement when $\gamma$ in an element exceeds a certain limit [24]). The results of damage evolution and load–displacement curves are shown in Fig. 7 for the case where a $\gamma$-limit is set for identifying the elements that require refinement. Having $\gamma$-limit only can result in unnecessary remeshing in regions far away from the crack-tip delaying the fracture nucleation, especially when the initial coarse element is too larger than the targeted element size. Comparing the results taken from the refinement method proposed in this study (Figs. 5 and 6) to the case of $\gamma$-limit only (Fig. 7) confirms the reliability of our mesh refinement strategy in simulating the fracture propagation with no delay.

Fig. 5

a shows the load–displacement response for the coarse mesh structures undergoing mesh refinement. b–d show three mesh structures before and after cracking with different initial element size

Fig. 6

a shows the effect of mesh refinement on the prediction of the maximum principal stress at the crack-tip. b elucidates the role of mesh refinement on the evolution of surface energy density at the crack-tip element. c and d are the damage evolution history at the crack-tip element related to $H_{1}$ and $H_{2,}$ respectively

Fig. 7

The results when the mesh refinement is performed when $\gamma > 3G_{c} /8l_{0}$, as proposed by [24]. a shows the load–displacement response, and b depicts the delay in damage evolution in this case

4.4 CPU runtime and performance of the method

To demonstrate the computational efficiency of the proposed mesh refinement algorithm, we present the information on the CPU runtime for shear and tensile benchmark examples in Fig. 8a (the relevant information of the boundary value problems are presented in Appendix A for brevity). The numerical model has been implemented and run in MATLAB, and the CPU core used by the machine is Intel i7-9800 3.00 GHz processor. The simulations are once done for the ideal fine-mesh structures with no refinement involved (see Fig. 8c, e), and the same problem is solved for coarse mesh structures undergoing multiple cycles of mesh refinement (see Figs. 8d, f) assuming different sizes for the initial element ($h_{{{\text{el}}}}^{{{\text{initial}}}}$). Figure 8a shows that applying the proposed mesh refinement strategy reduces the CPU runtime by 65–85% depending on the initial element size used in the domain. As a general recommendation, the initial element size in the range $3l_{0} < h_{{{\text{el}}}}^{{{\text{initial}}}} < 9l_{0}$ could be taken as an optimum choice because the final number of degrees of freedom do not change significantly by choosing element size larger than $4l_{0}$, although the number of calls for the refinement unit would increase by choosing the initial element size larger than $9l_{0}$ for the modelled benchmark examples, see Fig. 8b.

Fig. 8

a and b shows the effect of choosing the initial element size $h_{{{\text{el}}}}^{{{\text{initial}}}}$ on the performance and compares the runtime, the total DOFs, and the number of times calling the mesh refinement unit. c, e are the ideal mesh structures; d, f are the refined coarse mesh structures for tensile and shear tests, respectively.

5 Numerical simulations and comparisons

Several illustrative examples are presented to test the validity and capabilities of the presented numerical framework for modelling fractures. The presented methodology for setting up the input parameters is verified by comparing the ensuing numerical results to the experimental data of the fracture toughness.

5.1 Symmetric and asymmetric bending tests

We first setup the symmetric bending test to compare the load–displacement response curves resulted from the nonlinear FE analysis to the results provided by Miehe et al. [7] and Ambati et al. [32]. The geometry, as shown in Fig. 9, is built using the same dimensions used in [7], and the material properties $\lambda$ = 12 GPa, $\mu$ = 8 GPa, $G_{c}$ = 0.5 N/mm, and $l_{0}$ = 0.06 mm are chosen same as the values presented in [7, 32]. The initial geometry and the final deformed mesh structure are illustrated in Figs. 9a, b. As can be seen, the displacement-controlled loading ($u_{{{\rm y}}}$) is applied on the top boundary of the beam. The state of damage (fracture pattern) is depicted in Fig. 9c, and the refined mesh in the vicinity of the initial notch is magnified, where the stretched elements in the Lagrangian mesh can be seen. The vertical reaction forces obtained from nonlinear analyses are plotted with respect to the imposed vertical displacement on top of the beam in Fig. 10 for the case analyses of using $H_{1}$ and $H_{2}$ criteria, where an acceptable agreement can be seen between our results and those in the literature [7, 32]. We acknowledge that our results show a small discrepancy from the results of Ambati et al. [32] because of the consideration of geometrical nonlinearity in this study during the application of incremental loading, compared to the linear FE analysis (kinematics of small strains) in [32]. The response curve of the case analysis where $H_{2}$ criterion is used shows a higher peak value compared to that of $H_{1}$ criterion. When employing $H_{2}$ criterion in the damage model, the damaged zone becomes restricted to evolve over the elements in which the maximum principal stress exceeds the tensile strength limit. In the analysis case of using $H_{1}$ criterion, the damage parameter can potentially evolve in every element when the level of strain energy increases, so the captured peak load is generally lower than that of the $H_{2}$ criterion, as a greater region in the continuum has been damaged. It is also seen in Fig. 10 that Miehe et al. [7] have reported a significantly lower peak load because of the consideration of dissipation energy (e.g. dissipation in the form of heat) in their model, which is neither considered in the work of Ambati et al. [32] nor in our formulations.

Fig. 9

a, b depicts the beam bending boundary value problem (BVP) and the initial and deformed mesh structures after refinement (geometry dimensions in mm), and c is the crack pattern (damage state)

Fig. 10

The vertical reaction forces with respect to the imposed displacements ${u}_{y}$, taken from our nonlinear FE analysis

For illustrative purposes and testing the accuracy of the proposed mesh refinement algorithm, we simulate the cracking of an asymmetric bending test where the beam includes circular imperfections as experimentally introduced by Bittencourt et al. [33] and numerically simulated by [7, 32] using phase-field method, while setting $\lambda$ = 12 GPa, $\mu$ = 8 GPa, $G_{c}$ = 1 N/mm, and $l_{0}$ = 0.01 mm. In the experiment [33], two configurations are considered for the length of the initial notch ($a$) and its distance from the centre of the beam ($b$), see Fig. 11a, and the experimental observations are depicted in Figs. 11b, c. Using our developed numerical model, the experimental observations of crack patterns can be acceptably reproduced in the simulations as depicted in Fig. 12. The crack pattern observed in the experiments (Fig. 11b) has been replicated successfully using the $H_{2}$ criterion in the damage evolution model as demonstrated in Fig. 12b. According to Fig. 12c, it is found that moving the notch towards the centre and extending its length has caused a significant reduction in the peak load resisted by the structure before rupture (failure due to cracking).

Fig. 11

a is the geometry used for asymmetric bending test with holes [7] (dimensions in mm). b, c show the experimental observations by [34] for two different configurations of notch length and notch distance from the centre of the beam

Fig. 12

Our numerical results of the simulations of asymmetric bending test with holes next the notch. a, b depict the crack-paths for the notch configurations (a = 1.5 mm and b = 5 mm) and (a = 1 mm and b = 6 mm), respectively; c is a comparison between load–displacement responses of these two configurations

5.2 Setting up the input parameters with regard to the experimental measurements

To verify the applicability of the relationships proposed in Sect. 3 regarding selecting the input parameters to be used in the phase-field fracture modelling, we use experimental data of Brazilian disk, cracked chevron-notched Brazilian disk (CCNBD) and semi-circular bending (SCB) tests of rock specimens. We particularly benefit from the SCB test in the simulations to re-calculate mode-I fracture toughness ($K_{Ic}$) to be compared with the experimentally measured value of $K_{Ic}$. The SCB test is initially introduced by Chong and Kuruppu in 1984 to determine the fracture toughness in rock materials based on the maximum load capacity $P_{{{\text{max}}}}$ of the semi-circular specimen and geometrical characteristics as [34]

$$ K_{Ic} = \frac{{Y{\prime}P_{{{\text{max}}}} \sqrt {\pi a} }}{BD} $$

(23)

$$ Y{\prime} = - 1.297 + 9.516\frac{S}{D} - \left( {0.47 + 16.457\frac{S}{D}} \right)\beta + \left( {1.071 + 34.401\frac{S}{D}} \right)\beta^{2} $$

(24)

where $B$ is the width of the specimen, $D = 2R$, $\beta = a/R$ and $S$ is the distance between two supports. To test the proposed relationship in Eq. (21) on defining the fracture energy based on the FPZ size and the tensile strength of the material, we set up the SCB-test simulations using the experimental data provided by Dutler et al. [35], listed in Table 1. We investigate whether our simulations would output similar $P_{{{\text{max}}}}$ if the relationships in Sect. 3 are employed. Therefore, the values of $G_{c}^{{{\text{PF}}}}$ = 0.01034 N/mm, calculated using Eq. (21), and $l_{0} = 4r_{{{\text{FPZ}}}} = 9$ mm are given to the model as inputs. The load–displacement response curves are plotted in Fig. 13a, and the crack-pattern is shown in Fig. 13b, noticing that our simulation is in plane strain condition ($B$ = 1 mm). The peak load taken from Fig. 13a for the $H_{2}$ criterion is $P_{{{\text{max}}}}$ = 36.13 N, which is very close to the experimental measurement $P_{{{\text{max}}}} /B{ }$ = 35.87 N/mm, ($B$ = 39.3 mm in the experiment). This comparison can confirm that our recommendation for estimating $G_{c}^{{{\text{PF}}}}$ and using the FPZ size for the length-scale parameter ($l_{0} = 4r_{{{\text{FPZ}}}}$) when hiring $H_{2}$ criterion is meaningful and can be used in engineering applications.

Table 1 Material properties of granodiorite SCB samples [35]

Fig. 13

Load–displacement response of SCB specimen using $H_{1}$ and $H_{2}$ criteria in the context of the phase-field method, and the crack-pattern (dimensions in mm)

CCNBD tests are conducted on five cores with different diameters taken from Aberpergwm and Dove’s Nest shale formations, for which the experimental load–displacement curves are shown in Fig. 14c. These response curves are used to estimate the elastic material properties ($E,\nu$) using FE simulations. Experimentally measured values of mode-I fracture toughness from CCNBD tests, using the ISRM method [36], are listed in Table 2 for all samples. The experimental data ($E,\nu ,{ }K_{IC}$) in Table 2 are then used as inputs for modelling the phase-field cracking of the SCB-test simulations. We use the $H_{2}$ criterion in the model and vary the user-defined length-scale parameter. Having user-defined values for $l_{0}$, Eq. (20) is employed to set an appropriate value for the tensile strength limit to be used in the phase-field model ($\sigma_{c}^{{{\text{PF}}}}$), while the fracture energy is calculated as $G_{c} = K_{Ic}^{2} /E{\prime}$. We then simulate the SCB-test models and re-calculate $K_{Ic}$ based on the numerical results of the peak load ($P_{{{\text{max}}}}$). Numerically calculated values of $K_{Ic}$, from Eq. (23), are then compared to the experimental values in Fig. 15 for different values of $l_{0}$. It is concluded that Eq. (20) provides an appropriate value for $\sigma_{c}^{{{\text{PF}}}}$ to be used as a reliable input in the model. These results confirm the applicability of the proposed method and the relationships in Eqs. (19–21) in practical engineering problems to calibrate the input parameters in the presented phase-field fracture modelling framework [37].

Fig. 14

a shows CCNBD test setup, b is the boundary value problem (BVP) used for calculating elastic properties, and c shows the load–displacement curves from CCNBD tests

Table 2 Material properties of the shale samples for CCNBD tests

Fig. 15

The values of fracture toughness calculated from the simulations of the SCB test compared with experimental values (scattered)

6 Conclusion

In this study, we used the principles of LEFM and proposed practical relationships for setting up the input parameters in the phase-field fracture model such as the length-scale parameter and fracture energy based on the physically measurable material properties. Characteristics of the fracture process zone. The proposed method on choosing the input parameters was tested by comparing the results of the SCB-test simulations to the experimental data on the fracture toughness of shale rock specimens, showing a strong compatibility and confirming the reliability of the proposed relationships. The proposed method of selecting the input parameters can be employed in modelling diffusive fracture propagation and damage nucleation in engineering applications such as hydraulic fracturing in unconventional reservoirs.

Second, a novel mesh refinement strategy for detecting the elements around the crack-tip which are close to their tensile failure limit was developed to be used in the phase-field fracture models to increase the reliability and reduce the computational cost of the simulations. The refinement strategy relies on capturing the FPZ by predicting the critical stresses in coarse-size elements. According to the numerical results, refinement is critical elements must be done to reduce the element size to $l_{0} /4$ for having a reliable simulation. Due to the large dimension and possible complexities of the real-world engineering problems, it would be computationally more efficient to use a coarse mesh structure initially and to constantly perform mesh refinement as the fracture propagates. Depending on the boundary value problem and the size of the geometry, and the initial element size, the proposed mesh refinement algorithm can reduce the computational effort by 50–70 percent. Based on the analysis done for evaluating the performance, increasing the initial element size can contribute to reducing the computational cost up to a certain level, and the optimum recommended element size for the initial coarse mesh structure is recommended to be 3–9 times larger than the length-scale parameter. Reliability of the mesh refinement strategy and correctness of the implementation have been tested successfully by simulating complex cracking scenarios, the results of which are compatible with the experimental observations.

Appendices

Appendix A

Two benchmark examples, which are originally presented by Miehe et al. [7], are presented here for the purpose of model verification as well as for conducting the mesh sensitivity analysis.

1.1 Tensile test benchmark example

A single-notch square domain is subjected to the imposed tensile displacements on the top boundary while fixed at the bottom, as shown in Fig. 16. By increasing the displacements, the elastic strain energy is being mobilised, and the phase-field fracture starts propagating at the crack-tip towards the right boundary. In this example, we use the material properties $E$ = 210 GPa, Poisson’s ratio $\nu$ = 0.3, and the fracture energy $G_{c}$ = 2.7E-3 kN/mm and choose the length-scale parameter $l_{0}$ = 15E-3 mm. The element size along the expected crack-path is set as $h_{{{\text{el}}}}$ and is smaller than everywhere else in the domain to capture the diffusive fracture effectively. The load–displacement response curves for two different sizes of $h_{{{\text{el}}}}$ are plotted in Fig. 17. Increasing the element size $h_{{{\text{el}}}}$ results in an overestimation of the load capacity (i.e. the peak value of the load–displacement curve) as well as a delay in the crack nucleation stage (the rupture of the domain). The captured load capacity is sensitive to the element size $h_{{{\text{el}}}}$, so the problem is solved for different sizes, and the mesh sensitivity analysis is plotted in Fig. 18. According to this, the maximum acceptable element size is identified to be $h_{{{\text{el}}}} = l_{0} /4$ to ensure the mesh-independency condition. It is also seen from Fig. 18 that the maximum principal stress of the crack-tip element keeps increasing with reducing $h_{{{\text{el}}}}$ following a rate of $\sqrt {1/h_{{{\text{el}}}} }$, which is also compatible with the theory of LEFM on appearing singular stresses by getting closer to the crack-tip [30], see Eq. (15).

Fig. 16

a shows the boundary value problem defined in [7] (dimensions in mm); b is the final crack pattern developed in the body; c is the mesh structure in the region where the crack is expected to form; d, e depict the geometry around the crack-tip before and after formation of the crack. The length of the initial notch is $a_{0}$ = 0.5 mm

Fig. 17

The load–displacement responses for a specific case of length-scale $l_{0}$ = 15E-3 mm and different mesh sizes $h_{{{\text{el}}}}$ (both linear and nonlinear results are shown). The response curves are compared to results of [7, 37]

Fig. 18

Variation of the load capacity and the captured maximum principal stress due to the crack-tip element size $h_{{{\text{el}}}}$ for a fixed length-scale parameter $l_{0}$ = 15E-3 mm

1.2 Shear test benchmark example

Setting the material properties to those used in the tensile test, the same single-notch square domain is modelled here while subjected to shearing lateral displacements (${\varvec{u}}_{{{\rm x}}}$) on the top boundary. The purpose of simulating the shear test is to examine the capability of the developed model and the mesh refinement strategy. We also investigate the effect of the crack driving force formulation on the failure response of the domain. The lateral load–displacement response curves related to $H_{1}$ and $H_{2}$ criteria on defining the crack driving force are plotted and compared to the results of Miehe et al. [7] as well as to the results of the ideal fine-mesh structures having the element size ($h_{{{\text{el}}}} = l_{0} /4$), see Fig. 19. Setting a lower limit for the maximum allowable iteration ${\text{iter}}_{{{\text{max}}}}$ in the simulation reduces the propagation speed because the energy minimisation cannot be done completely (no complete convergence in the damage field) in a single load–step, and the load–displacement curve drops in a smoother manner. Using the $H_{2}$ criterion results in a sharper decrease of the tolerated load after the nucleation stage (see Fig. 19b), while employing $H_{1}$ criterion causes a smoother reduction of the load, as shown in Fig. 19a. The crack patterns are the same for both cases, although a larger area of the domain is affected by damage when using $H_{1}$ criterion (see Fig. 19c, d).

Fig. 19

a, b show the horizontal reaction forces at the bottom of the domain with respect to ${{\varvec{u}}}_{\mathrm{x}}$ applied on the top boundary for criteria ${H}_{1}$ and ${H}_{2}$. c, d depict the crack pattern and affected region by damage for criteria ${H}_{1}$ and ${H}_{2}$, respectively.

Appendix B

Weak forms are linearised to be numerically implemented for the case of two-dimensional plane-strain finite element analysis.

2.1 Finite element matrix form of the principle of virtual work (finite strains)

The principle of virtual work (Eq. 6) is adapted to an updated Lagrangian nonlinear finite element framework by approximating the displacements and weighting functions over iso-parametric elements as ${\varvec{u}}^{{{\rm h}}} = {\varvec{N}}_{{\mathbf{u}}} \left\{ {\varvec{u}} \right\}$ and ${\varvec{\zeta}}^{{{\rm h}}} = {\varvec{N}}_{{\mathbf{u}}} \left\{ {c_{{\mathbf{u}}} } \right\},$ respectively, where $\left\{ {\varvec{u}} \right\} = \left\{ {\begin{array}{*{20}c} {u_{{{\text{x}}_{1} }}^{1} } & {u_{{{\text{x}}_{2} }}^{1} } & {u_{{{\text{x}}_{1} }}^{2} } & {u_{{{\text{x}}_{2} }}^{2} } & {u_{{{\text{x}}_{1} }}^{3} } & {u_{{{\text{x}}_{2} }}^{3} } \\ \end{array} } \right\}^{{{\rm T}}}$ are the vector of nodal displacements and ${\varvec{N}}_{{\mathbf{u}}}$ is the matrix of shape functions for the first-order 3-noded element. In the nonlinear finite element analysis, the elasticity tensor of the element is affected by the deformations in the Lagrangian mesh. Hence, the system of equations is solved in an iterative manner by updating the global stiffness matrix with respect to the updated nodal coordinates ${\varvec{x}}_{{{\rm i}}}$. The finalised displacement field ${\varvec{u}}_{{{\text{n}} + 1}}$ is resulted from the displacements of the previous step ${\varvec{u}}_{{{\rm n}}}$ and incremental displacements $\Delta {\varvec{u}}_{{{\text{n}} + 1}}^{{\left( {\text{k}} \right)}}$ of the subsequent iterations at the step ($n + 1$) as [29]

$$ {\varvec{u}}_{{{\text{n}} + 1}} = {\varvec{u}}_{{{\rm n}}} + \mathop \sum \limits_{k = 1}^{{k_{{{\text{max}}}} }} \Delta {\varvec{u}}_{{{\text{n}} + 1}}^{{\left( {\text{k}} \right)}} $$

(B-1)

where $k$ is the number of iterations satisfying for the convergence of $\Delta {\varvec{u}}_{{{\text{n}} + 1}}^{{\left( {\text{k}} \right)}}$. The matrix form of Eq. (6) is derived in the following to solve for $\Delta {\varvec{u}}_{{{\text{n}} + 1}}^{{\left( {\text{k}} \right)}}$ iteratively [29], given a fixed state of damage $\overline{d}_{{{\text{n}} + 1}}.$

$$\begin{array}{l}{\left\{ {{{{\rm c}}_u}} \right\}^T}\mathop \int \limits_{{\Omega _0}}^{{~}} {{\bf B}}_u^T{\mathcal C}_{n + 1}^{\left( {k - 1} \right)}{{{\bf B}}_u}\left\{ {\Delta {{\bf u}}_{n + 1}^{\left( k \right)}} \right\}{{\rm d}}V + {\left\{ {{{{\rm c}}_u}} \right\}^T}\mathop \int \limits_{{\Omega _0}}^{{~}} {{\bf B}}_u^T\left[ {{{\left[ {{{\boldsymbol{\sigma} }}_{n + 1}^{\left( {k - 1} \right)}} \right]}^T} \oplus {{\bf I}}} \right]{{{\bf B}}_u}\left\{ {\Delta {{\bf u}}_{n + 1}^{\left( k \right)}} \right\}{{\rm J}}_{n + 1}^{\left( {k - 1} \right)}{{\rm d}}V = \\ \underbrace {{{\left\{ {{{{\rm c}}_u}} \right\}}^T}\mathop \int \limits_{{\Omega _0}}^{{~}} {{\bf N}}_u^T{{{\rho }}_0}{{\bf G}}~{{{\rm J}}_n}{{\rm d}}V + {{\left\{ {{{{\rm c}}_u}} \right\}}^{{\rm T}}}\mathop \int \limits_{\partial {\Omega _0}_{{\boldsymbol{\sigma} }}}^{{~}} {{\bf N}}_u^T\left\{ {{{{\bf T}}_{n + 1}}} \right\}~{{\rm d}}A}_{{{\rm external~forces}}~:{{~}}{{{\bf R}}_{n + 1}}} - \underbrace {{{\left\{ {{{{\rm c}}_u}} \right\}}^T}\mathop \int \limits_{{\Omega _0}}^{{~}} {{\bf B}}_u^T\left\{ {{{\boldsymbol{\sigma} }}_{n + 1}^{\left( {k - 1} \right)}} \right\}{{\rm J}}_{n + 1}^{\left( {k - 1} \right)}{{\rm d}}V}_{{{\rm internal~forces}}~:{{~}}{{\bf F}}_{n + 1}^{\left( {k - 1} \right)}} \end{array}$$

(B-2)

The test function is ${\varvec{\zeta}} = {\varvec{N}}_{{\mathbf{u}}} \left\{ {c_{{\mathbf{u}}} } \right\}$, $\left[ {{\varvec{\sigma}}^{{{\rm T}}} \oplus {\varvec{I}}} \right]_{{{\text{mnpq}}}} = \sigma_{{{\text{qn}}}} \delta_{{{\text{mp}}}}$, and the fourth-order tensor ${\mathbf{\mathcal{C}}}_{{{\text{n}} + 1}}^{{\left( {{\text{k}} - 1} \right)}}$ is defined as [27]

$$ {\mathbf{\mathcal{C}}}_{{{\text{mnpq}}}} = g\left( {\overline{d}_{{{\text{n}} + 1}} } \right)\left[ {\frac{\lambda }{{J_{{{\text{n}} + 1}}^{{\left( {{\text{k}} - 1} \right)}} }}\delta_{{{\text{mn}}}} \delta_{{{\text{pq}}}} + \frac{{\left( {\mu - \lambda \ln J_{{{\text{n}} + 1}}^{{\left( {{\text{k}} - 1} \right)}} } \right)}}{{J_{{{\text{n}} + 1}}^{{\left( {{\text{k}} - 1} \right)}} }}\left( {\delta_{{{\text{mp}}}} \delta_{{{\text{nq}}}} + \delta_{{{\text{mq}}}} \delta_{{{\text{np}}}} } \right)} \right] $$

(B-3)

where ${\text{m}},{\text{n}},{\text{p}},{\text{q}} = 1,2,3$, $\delta$ is the Kronecker delta, and $\kappa_{\varepsilon } \ll 1$ is set to avoid the numerical instability caused by ${\mathbf{\mathcal{C}}}_{{{\text{mnpq}}}} = \left[ 0 \right]$ in fully damaged elements. Matrix ${\varvec{B}}_{{\mathbf{u}}}$ is the derivative of the shape function matrix ${\varvec{N}}_{{\mathbf{u}}}$ with respect to the current coordinates, defined in the following [28].

$$ \left[ {{\varvec{N}}_{{\mathbf{u}}} { }} \right]_{2 \times 6} = \left[ {\begin{array}{*{20}c} {N_{1} } & 0 & {N_{2} } & 0 & {N_{3} } & 0 \\ 0 & {N_{1} } & 0 & {N_{2} } & 0 & {N_{3} } \\ \end{array} } \right] $$

(B-4)

$$ \left[ {{\varvec{B}}_{{\mathbf{u}}} } \right]_{4 \times 6} = \left[ {\begin{array}{*{20}c} {\partial N_{1} /\partial x_{1} } & 0 & {\partial N_{2} /\partial x_{1} } & 0 & {\partial N_{2} /\partial x_{1} } & 0 \\ 0 & {\partial N_{1} /\partial x_{2} } & 0 & {\partial N_{2} /\partial x_{2} } & 0 & {\partial N_{3} /\partial x_{2} } \\ {\partial N_{1} /\partial x_{2} } & 0 & {\partial N_{2} /\partial x_{2} } & 0 & {\partial N_{3} /\partial x_{2} } & 0 \\ 0 & {\partial N_{1} /\partial x_{1} } & 0 & {\partial N_{2} /\partial x_{1} } & 0 & {\partial N_{3} /\partial x_{1} } \\ \end{array} } \right] $$

(B-5)

2.2 Finite element matrix form of the principle of virtual work (small strains)

For the linear elastic analysis, the problem can be solved in one iteration, and the matrix form of Eq. (9) can be derived as [28]

$$ \left\{ {c_{{\mathbf{u}}} } \right\}^{{{\rm T}}} \mathop \int \limits_{{{\Omega 0} }} {\varvec{B}}_{{\mathbf{s}}}^{{{\rm T}}} \left[ {\mathbb{C}} \right]{\varvec{B}}_{{\mathbf{s}}} \left\{ {{\varvec{u}}_{{{\text{n}} + 1}} } \right\}d{\text{V}} = \left\{ {c_{{\mathbf{u}}} } \right\}^{{{\rm T}}} \mathop \int \limits_{{{\Omega 0} }} {\varvec{N}}_{{\mathbf{u}}}^{{{\rm T}}} \rho \boldsymbol{G }d{\text{V}} + \left\{ {c_{{\mathbf{u}}} } \right\}^{T} \mathop \int \limits_{{\partial {\Omega 0}_{{\varvec{\sigma}}} }} {\varvec{N}}_{{\mathbf{u}}}^{{{\rm T}}} \left\{ {{\varvec{T}}_{{{\text{n}} + 1}} } \right\} d{\text{A}} $$

(B-6)

where ${\mathbb{C}}$ is the fourth-order tensor of elasticity, and ${\varvec{B}}_{{\mathbf{s}}}$ is the derivative of shape function matrix ${\varvec{N}}_{{\mathbf{u}}}$ in the small strain framework [28].

$$ \left[ {\mathbb{C}} \right] = g\left( {\overline{d}_{{{\text{n}} + 1}} } \right)\left[ {\begin{array}{*{20}c} {\lambda + 2\mu } & \lambda & 0 \\ \lambda & {\lambda + 2\mu } & 0 \\ 0 & 0 & \mu \\ \end{array} } \right] $$

(B-7)

$$ \left[ {{\varvec{B}}_{{{\rm s}}} { }} \right]_{3 \times 6} = \left[ {\begin{array}{*{20}c} {\partial N_{1} /\partial X_{1} } & 0 & {\partial N_{2} /\partial X_{1} } & 0 & {\partial N_{3} /\partial X_{2} } & 0 \\ 0 & {\partial N_{1} /\partial X_{2} } & 0 & {\partial N_{2} /\partial X_{2} } & 0 & {\partial N_{3} /\partial X_{2} } \\ {\partial N_{1} /\partial X_{2} } & {\partial N_{1} /\partial X_{1} } & {\partial N_{2} /\partial X_{2} } & {\partial N_{2} /\partial X_{1} } & {\partial N_{3} /\partial X_{2} } & {\partial N_{3} /\partial X_{1} } \\ \end{array} } \right] $$

(B-8)