Reliability index based strategy for the probability-damage approach in fail-safe design optimization (β-PDFSO)

Abstract

This research proposes a new formulation for fail-safe size optimization, considering the probability of occurrence of each failure scenario and the random structural parameters as sources of uncertainty. Essentially, the fail-safe reliability-based design optimization is reformulated, where the term “damaged structure” coalesces information of the whole set of damaged configurations. Thus, a single random reliability index is defined, representing the reliability of a limit-state of the damaged structure, which accounts for the safety level of the entire set of damaged configurations. The method provides the optimum design for which the reliability indices of the damaged structure are achieved at the confidence level the designer demands. The first application example corresponds to an academic analytical problem. The second and third application examples correspond to practical engineering cases: a 2D truss structure with stress constraints as well as the tail section of an aircraft fuselage with stress and buckling constraints. Results show a considerable reduction of the objective function compared to the fail-safe RBDO, which could lead to oversized designs. In this sense, mass savings up to 13.6% are achieved for the industrial-like application example.

1 Introduction

Structural design in several engineering fields must consider failure scenarios that are unlikely, but could occur over the service life, causing damage to the structure. An example of this can be found in the design of cable-stayed bridges, where regulations contemplate the possibility that the impact of a vehicle may break a cable. Thus, the recommendations for stay cable design, testing, and installation developed by the Post-Tensioning Institute [38] define the load combination that the bridge must withstand in the absence of the damaged cable after the accident. In aerospace, there are a huge variety of accidental situations that could lead to a loss of structural performance as a result of an object striking the aircraft. Some examples are bird strikes, runway debris, or hail, as well as the detachment of a rotating engine part and subsequent impact on the aircraft (engine blade loss, uncontained engine rotor failure, propeller blade failure, etc.). These scenarios are covered by extensive regulations that apply to aircraft design. Thus, requirements specified by the Federal Aviation Administration in FAR 25.571(e) [21] establish that “The airplane must be capable of successfully completing a flight during which likely structural damage occurs as a result of: uncontained fan blade impacts, uncontained engine failures or uncontained high energy rotating machinery failure”. More specifically, the Advisory Circulars AC 20-128A [17] and AC 25.905-1 [19] provide design recommendations for these events, establishing the set of load combinations that the damaged structure must withstand, known as Get Home Loads.

Fail-safety is a structural design philosophy that considers that a structure must be able to sustain possible damage. This damage could be of different nature, and can be classified into two categories: deterioration and accidental damages. Deterioration damage refers to the degradation of the material properties during normal operation, e.g., fatigue or corrosion effects. On the other hand, accidental damage is related to occasional events prompted by discrete sources, e.g., uncontained engine rotor failure or bird strikes. Niu [36] established fail-safe design practices for fatigue-related damages, where crack propagation may lead to “a failure of a single member in redundant structure or partial failure of a monolithic structure”. Therefore, the situation must be studied “one instance at a time”. This makes sense, because fatigue failure does not generally incur in several members failed at the same time. In contrast, when a structure is damaged by a discrete source, multiple failures can occur simultaneously at different locations. As aviation regulations contemplate this discrete source of damage, the simultaneous collapse of several members in an aircraft represents a real design practice.

Guaranteeing structural safety in damage scenarios will inevitably require an increase in the structural weight. The final design should provide alternative resistant structural schemes to sustain the stresses when partial damage occurs, hence redistributing the internal forces in the remaining structure. From the designer’s perspective, it is of interest to ascertain the minimum weight increase that will ensure the required safety. In that sense, several investigations were carried out by combining optimization techniques with the fail-safe strategy. They could be classified into fail-safe topology optimization and fail-safe size optimization.

Topology optimization is particularly attractive when the physical size, shape, and connectivity of the structure are not previously defined. Only some quantities in the problem are known, such as the design domain, applied loads, and boundary conditions. Due to its general approach, this type of structural optimization brings the best chance to find groundbreaking designs, making it appropriate for preliminary stages in a structural design process. Generally, fail-safe topology optimization pursues to minimize the compliance of a conceptual design that can sustain damage.

Some researchers have analyzed the local failure in topology optimization for truss structures, where the local failure can be modeled straightforwardly by removing one bar from the truss, since a clear definition of a structural member exists. Achtziger and Bendsøe  [2] studied the optimal topology of a truss, so that stiffness after degradation is maximized. Mohr et al.  [33] proposed a redundant robust topology optimization of truss. Stolpe [40] modeled failure as either a complete damage of some predefined number of members or by degradation of the member areas, and concluded that the optimal topology can change drastically even in the situation that only one member is partially degraded. Based on this idea, Pollini [37] performed the fail-safe optimization of viscous dampers.

Another research line is focused on the fail-safe topology optimization of continuum structures. In this case, the first limitation is the absence of discrete structural elements to be eliminated, as members emerge after performing the optimization process. Jansen et al. [24] were the first to address this aspect by defining damage scenarios in the continuum design domain, eliminating areas or patches of a given size. In this approach, the fail-safe optimization problem was formulated as minimizing the compliance of the worst-case damage scenario. As a consequence of eliminating part of the design domain, the original bar could not be generated; hence, robust optimization introduced redundant members into the design to replace the non-existing bar. Results showed that the designs obtained contain a number of redundant bars which leads to an increased robustness with respect to local removal of material. One of the major shortcomings of Jansen et al. [24] was that it involves a very large number of finite-element analyses (FEA) models at the scale equal to the number of elements. To overcome this difficulty, Zhou and Fleury [43] established a computationally viable solution for this problem, significantly reducing the computational burden. Nevertheless, some of these patches could be empty, containing only void regions instead of structural parts. To improve this aspect, Ambrozkiewicz and Kriegesmann  [3] proposed strategies to determine the placement of the damaged zones. The first approach stated that a patch can be considered empty if the maximum value of the densities in the patch is below a certain threshold. The second one was based on a load-path identification. As a result, the computational cost was reduced significantly. Wang et al. [42] proposed an efficient optimization strategy to obtain the designs which are insensitive to the occurrence of local failure, introducing the von Mises failure criterion to evaluate the patches to be damaged or undamaged. By defining the failure coefficient, the material properties of a given patch was regarded as degenerated if its von Mises stress exceeded an allowable stress. Furthermore, Ambrozkiewicz and Kriegesmann [4] presented a sequential topology and shape optimization for fail-safe design, consisting of three steps: (1) minimizing the compliance subject to volume constraints to get a preliminary design, (2) identifying the load-bearing members of the optimal design and creation of damage scenarios, and (3) performing a density-based shape optimization using the damage scenarios. Smith and Norato [39] introduced a topology optimization technique for the design of fail-safe structures made of geometric components. It was concluded that the methodology was significantly more efficient than density-based techniques, since the number of analyses required is proportional to the number of geometric components and independent from the mesh. Kranz et al. [26] proposed load-path-based evaluation scheme for fail-safe topology optimization, where redundant structures are obtained at much less computational cost. Hederberg and Thore [23] combined density-based topology optimization with a moving morphable component representation of structural damage, obtaining more robust fail-safe designs.

As already discussed, topology optimization approaches have enormous potential in the early stages of the design process of a structure. However, in advanced stages of the design, there are numerous features of the structure that are already frozen and cannot be modified. Generally, shape and geometry of the structure are not considered variable at this stage and topology optimization methods cannot be used. It is at this point that size optimization methods gain prominence. Often, the industry requires fail-safe designs, which can be obtained by reinforcing the original structure, i.e., without adding additional structural elements. Thus, an industrial example known to the authors is the optimization of the tail-cone structure of an aircraft taking into account possible structural failures. Some of the possible failures that the aircraft company contemplates are the release of an unducted blade from open rotor engines or an uncontained auxiliary power unit (APU) rotor failure, generating debris that strike the aircraft. Alternatively, other types of partial damage are the collapse of one of the bars supporting the APU, a failure of a fitting in the interface between the tail-section and the forward section, or a fire event in the APU compartment, which may cause damage in the skin or firewalls. Optimization of this structure with these failure scenarios cannot be tackled with fail-safe topology optimization, but can be addressed with fail-safe size optimization methods.

One of the first works in fail-safe size optimization of structures was presented by Sun et al. [41]. In their work, stress, displacement, buckling, and natural frequency constraints were applied for each failure case. Arora et al. [5] and Nguyen and Arora [35] proposed an optimization strategy to perform fail-safe structural optimization of large structures. Feng and Moses [22] explored several criteria for optimizing size components in a structure to consider both extreme and accident conditions. Marhadi et al. [29] proposed an optimization strategy that attempts to maximize the energy absorption by considering the possible damage to the members that integrate the structure. Recent research  considers finite-element models of the intact structure and a set of possible partial collapses into the optimization process. Fail-safe deterministic size optimization was first applied to shell structures by Baldomir et al. [6]. This multi-model approach aimed to obtain a minimum penalty weight over the intact structure while guaranteeing the fulfillment of several limit-states in both the intact and damaged configurations. As a result, the final optimum design would be safe under all the damaged scenarios considered. Lüdeker and Kriegesmann [27] performed a fail-safe optimization of beam structures, aiming for the mass minimization of lattice structures subjected to stress constraints, proposing strategies to reduce the number of constraints in the optimization problem. Considering local degradation of member properties, recent observations by Dou and Stolpe [12] show that the degradation of one arbitrary member may yield to a worse objective function than the complete removal of the member. In the same trend, Dou and Stolpe [13] characterized local thickness degradation in a part of a member by combining different damaged models into the fail-safe design problem.

One of the main shortcomings of the previous fail-safe techniques was that their formulations did not contemplate the quantification of reliability in the final optimal design when there is uncertainty in any parameter. The only way of increasing the reliability in those approaches is by the use of partial safety factors. Thus, Cid et al. [8, 9], made a further step by proposing a fail-safe probabilistic approach, in which these uncertainty data were taken into account in the fail-safe design. In that research, the reliability index associated with each limit-state had to be guaranteed in the intact model and all damaged scenarios simultaneously. By applying this technique, it was possible to guarantee a specific target reliability index on each limit-state.

The fail-safe approaches described in the paragraph above aim to simultaneously meet all limit-states in the whole set of damaged configurations. Admittedly, this strategy may seem too conservative and could lead to oversized designs, since the accidental situation will be a single event and it is unknown which partial collapse will occur. In addition, it should be taken into consideration that some damaged configurations may have different probability of occurrence than others. These values of probability of occurrence of each damaged configuration can be grounded in historical evidence of accidents. For instance, in the aerospace field, the Federal Aviation Administration conducted several studies [18], characterizing uncontained engine rotor failures from historical accidents occurred from 1962 to 1989. In the civil engineering field, companies have reported accidental situations applied to cable-stayed bridges, in which the accidental situation where three adjacent cables break due to an impact of a vehicle is less probable than the breakage of a single cable. To address this aspect, a new methodology, denoted as probability-damage approach for fail-safe design optimization (PDFSO) was proposed by Cid et al. [10], where the probability of occurrence of each damage scenario was contemplated as a new source of uncertainty into the deterministic fail-safe optimization problem. In that strategy, the main novelty was to define a new probabilistic formulation where the set of responses from the damaged configurations associated with the same limit-state are transformed into a single probabilistic constraint. That probabilistic constraint represents a limit-state in the damaged structure. Thus, the fulfillment of the limit-states associated with the damaged structure are guaranteed for a specific confidence level $R^\mathrm{{T}}$ imposed by the designer. That confidence level takes into account the risk that designer is willing to admit in case an accidental situation happens. As a result, the optimum design would be an intermediate solution between the deterministic optimization of the intact model and the fail-safe deterministic optimization. In the same trend, Martínez-Frutos and Ortigosa [30] incorporated the probability of occurrence of each damage situation into a risk-averse approach for fail-safe topology optimization, using level-set-based optimization techniques. More recently, Martínez-Frutos and Ortigosa [31] consider the probability of occurrence at a specified location and failure size as sources of uncertainty in a robust fail-safe topology optimization.

Although the PDFSO approach considerably improved the fail-safe formulation, the main shortcoming was that the aleatory uncertainty in parameters affecting the structure was not integrated in that approach. Thus, a preliminary work addressing this problem was presented by the authors [11]. Therefore, the purpose of this research is to extend that work by fully describing and formulating a new fail-safe optimization strategy, taking into account the two sources of uncertainty. The fundamental idea behind the new multi-model approach is that the reliability index ($\beta$) associated with a limit-state of the damaged structure is not a single value. On the contrary, there will be as many values of $\beta$ as damaged configurations with their associated probability of occurrence. Therefore, it is possible to construct a new discrete random distribution function of $\beta$ to define the reliability index associated with a limit-state of the damaged structure. The new constraint is then formulated as the probability of the reliability index being lower than the target reliability index, with the confidence level demanded by the designer. It is important to emphasize that if the effect of having different probabilities of occurrence for each damaged model was disregarded, a damaged configuration very harmful to the structure but with a low probability of occurrence compared to others could lead to an oversized design, as the target reliability index ($\beta ^\mathrm{{T}}$) of each limit-state would have to be guaranteed in all the damaged configurations simultaneously.

Since the fail-safe RBDO provides a conservative design by guaranteeing the reliability indices in all the damaged scenarios, the $\beta$-PDFSO approach improves that methodology by including the probability of occurrence of each damaged configuration into the problem statement. As a result, the main advantage of this method is that lighter fail-safe designs can be obtained with the confidence level required by the designer. This formulation applies to any size optimization problem that contemplates multiple failure scenarios and inherent random uncertainty in the parameters.

The remainder of the paper is organized as follows. Section 2 describes the theoretical background, summarizing previous fail-safe techniques relevant for this research. In Sect. 3, the $\beta$-PDFSO approach is formulated, providing a detailed description of the method. Then, Sect. 4 presents three application examples of increasing complexity to demonstrate the capabilities of the proposed approach: the first example corresponds to an academic problem, with analytical expressions to simulate the structural responses in the intact and damaged models. The second example represents a steel lattice truss bridge, where the structure must resist accidental scenarios where some bars break due to a vehicle impact. The third example corresponds to a industrial-like application example for airplanes with open rotor engines, where two types of accidental situations can occur: debris released from the engine striking the fuselage or the detachment of fittings that connect the fuselage section with the VTP/HTP or with the rear tail cone section. Section 5 compares the computational cost in terms of iterations and function calls. Section 6 offers concluding remarks and suggests future research lines. Section 7 provides the link of a GitHub repository with the source code of the $\beta$-PDFSO method applied to the analytical example presented in Sect. 4.1.

2 Theoretical background

2.1 Fail-safe deterministic optimization

Baldomir et al. [6] presented a fail-safe deterministic optimization approach to achieve minimal weight structures that are safe in the event of partial collapse. The methodology defines a model of the complete structure and D incomplete configurations of the structure (Fig. 1). An identification label $M_{i}$ is assigned to each model, where $M_{0}$ corresponds to the intact model and $M_{i}$ ($i=1,\ldots ,D$) is associated with the damaged configurations.

Fig. 1

General definition of the intact model and damaged configurations

The basis of this method requires the definition of a group of damaged versions of the structure where design conditions are imposed. The modifications that the algorithm performs during the optimization process on the intact structure are also applied to the damaged models simultaneously. The compact formulation of the fail-safe deterministic optimization is presented in Eq. (1), where F is the objective function that only affects the intact structure and depends on the set of design variables d, and g is the set of constraints affecting both intact and incomplete structures $M_i.$

$$\begin{aligned}&\mathrm {min}\;F(\mathbf{d} ) \end{aligned}$$

(1a)

$$\begin{aligned} &\mathrm {s.t.} \nonumber \\ & g_{j}^{M_{i}}(\mathbf{d} ) \ge 0 \quad j=1, \ldots ,m^{M_{i}} \quad i=0,\ldots ,D \end{aligned}$$

(1b)

2.2 Fail-safe RBDO

Subsequently, the previous approach was completed by introducing the hypothesis that some parameters affecting the structural responses of intact and damaged models were random in nature, leading to a probabilistic approach, denoted as fail-safe RBDO. Cid et al. [8, 9] formulated this method where it is necessary to solve the reliability analyses on the intact structure and the damaged configurations simultaneously at each iteration of the optimization process. The formulation of the fail-safe RBDO is shown in Eq. (2):

$$\begin{aligned}&\mathrm {min}\;F(\mathbf{d} ) \end{aligned}$$

(2a)

$$\begin{aligned}&\mathrm {s.t.} \nonumber \\ & P[G_{j}^{M_i}(\mathbf{d} ,\mathbf{x} )<0] \le \Phi (-\beta _j^\mathrm{{T}}) \quad j=1,\ldots ,m^{M_i} \quad i=0,\ldots ,D \end{aligned}$$

(2b)

where P[–] is the probability operator, G represents the limit-state in the whole set of models $M_i$, which now also depends on the random variables x, $\Phi$ is the CDF of a standard normal distribution, and $\beta ^\mathrm{{T}}$ is the target reliability index. Equation (2b) means that the probability of overcoming the limit-state $G_{j}^{M_i}$ has to be lower than or equal to the target probability of failure, $\Phi (-\beta _j^\mathrm{{T}})$. If the problem in Eq. (2) is solved through the reliability index approach (RIA) [14], Eq. (2b) can be rewritten as $\beta _{j}^{M_i}(\mathbf{d} ,\mathbf{x} ) \ge \beta _j^\mathrm{{T}}$, where the reliability index of each limit-state $\beta _{j}^{M_i}$ must be greater than the target reliability index $\beta _{j}^\mathrm{{T}}$. Normalizing this equation, the multi-model RBDO problem can be reformulated as in Eq. (3):

$$\begin{aligned}&\mathrm {min}\;F(\mathbf{d} ) \end{aligned}$$

(3a)

$$\begin{aligned} &\mathrm {s.t.} \nonumber \\ & H_j^{M_{i}}(\mathbf{d} ,\mathbf{x} ) = \beta _{j}^{M_i}(\mathbf{d} ,\mathbf{x} )/\beta _j^\mathrm{{T}} - 1 \ge 0 \quad j=1,\ldots ,m^{M_i} \quad i=0,\ldots ,D \end{aligned}$$

(3b)

2.3 Probability-damage approach for fail-safe design optimization (PDFSO)

Finally, Cid et al. [10] formulated the probability-damage approach for fail-safe design optimization (PDFSO). That research incorporates a source of uncertainty that had not been taken into account in fail-safe optimization approaches until then. It involves the consideration that each damaged configuration has its own probability of occurrence. That is, accidental situations that can lead to partial collapse of the structure do not necessarily have the same probability of occurrence. This information can be introduced into the optimization problem in such a way that each damaged configuration affects the final design based on its probability of occurrence.

To illustrate this concept, we consider as an example of structural response $g_{j}$ the limit-state of stress $\sigma$ in a generic element j as $g_{j}:\sigma _{j}-\sigma _{\mathrm {max}}$. Figure 2 shows the limit-state g in the element j in each damaged configuration $M_i$ ($g_j^{M_1}, g_j^{M_2}, g_j^{M_i}, \ldots , g_j^{M_D}$). As each limit-state $g_j$ is influenced by the probability of occurrence of the damaged configurations $P_{M_i}$, a source of uncertainty is included in the problem. Thus, a probabilistic formulation is defined where the values of the structural response $g_{j}^{M_{i}}$ in all damaged models are used to construct a single random response $\hat{G}_{j}$ per limit-state. The probability mass function of the new random limit-state $\hat{G}_{j}$ is presented in Fig. 3. The PDFSO approach is formulated in Eq. (4). A deeper explanation of this methodology can be found in Cid et al. [10].

$$\begin{aligned}&\mathrm {min}\;F(\mathbf{d} ) \end{aligned}$$

(4a)

$$\begin{aligned} & \mathrm {s.t.} \nonumber \\ & g_{j}^{M_{0}}(\mathbf{d} ) \ge 0&j=1,\ldots ,m^{M_{0}} \end{aligned}$$

(4b)

$$\begin{aligned}&P[\hat{G}_{j}(\mathbf{d} ) < 0] \le p_{f_{j}}^\mathrm{{T}} \quad&j=1,\ldots ,m^{M_{0}} \end{aligned}$$

(4c)

Equation (4c) means that the probability of overcoming the limit-state in the damaged structure ($\hat{G}_{j}$) has to be lower than or equal to a specific target probability of failure $p_{f_{j}}^\mathrm{{T}}$. This means that in case of an accidental situation, the fulfillment of all the limit-states is guaranteed with at least a confidence level of $R_j^\mathrm{{T}}=1-p_{f_{j}}^\mathrm{{T}}$.

Fig. 2

Limit-state in the element j (in black color) in each incomplete configuration $M_{i} \rightarrow g_{j}^{M_{i}}$, $i \in$ [1,D]

Fig. 3

Probability mass function of $\hat{G}_{j}$ obtained through the values in each incomplete configuration $M_{i} \rightarrow g_{j}^{M_{i}}$, $i \in$ [1,D]

3 Reliability index strategy into PDFSO ($\beta$-PDFSO)

3.1 Introduction

The fail-safe strategy presented in this paper merges the two methodologies described in Eqs. (2) and (4) to obtain an unified approach which simultaneously considers the uncertainty due to the probability of occurrence of each damaged model and the inherent uncertainty in parameters that affect the structural response. The main idea is to formulate a PDFSO problem under aleatory uncertainty, where the reliability index associated with a limit-state of the damaged structure is defined by a probability mass function. The reason is that there is no certainty concerning which damaged configuration of the whole set may occur; hence, it is not possible to give a unique value of $\beta$ for a limit-state referring to the damaged structure. This strategy, denoted as $\beta$-PDFSO, is described in detail in the following section.

3.2 Description and formulation

The fundamental assumption in the $\beta$-PDFSO is that a partial collapse will occur, causing damage to the structure. Therefore, simultaneously guaranteeing a target reliability index over all possible damaged configurations seems a very restrictive approach. In addition, each failure scenario should contribute to the final design according its probability of occurrence $P_{M_i}$. It is important to note that the probability of a given damaged configuration $P_{M_i}$ is defined here as the following conditional probability: $P[M_i|A]$, where A is the accidental event that produces a partial collapse of the structure. Thus, an initial premise to satisfy is that $\sum _{i=1}^{D} P_{M_{i}}=1$, since we assume in the optimization problem that an accidental situation will occur and that the events $M_i$ are independent of each other.

The AC 25.1309-1B [20] defines these events as “hazardous failure conditions” and must be considered as “extreme remote events”, having an average probability per flight hour of the order of $10^{-7}$ (one accident per 10 million hour of flight). Thus, the actual probability of occurrence of a specific damaged configuration will be given by the value $P_{M_i}$ multiplied by the probability of having an accident of this type P[A].

Generally, RBDO problems are formulated with the aim to minimize a function subject to the reliability index associated with each limit-state j being greater than a target reliability index. However, applying this approach over the intact and all the damaged configurations simultaneously might be too conservative, as only one of them will happen. Given that $\beta _j$ (reliability index with respect to the limit-state $G_j$) can be calculated at each damaged configuration ($M_i$), there would be as many reliability indices ($\beta _j$) as damaged configurations with their associated probability occurrence, resulting in pairs of values [$\beta _j^{M_i}$, $P_{M_i}$]. Therefore, the $\beta$-PDFSO approach coalesces all the $\beta _j^{M_i}$ into a single random reliability index, denoted as $\hat{\beta }_j$, using the probability of occurrence of each damaged configuration $P_{M_i}$. This idea is illustrated in Figs. 4 and 5. The sketch presented in Fig. 4 shows the reliability index in the generic element j in each damaged configuration $M_i$ ($\beta _j^{M_1}, \beta _j^{M_2},\ldots ,\beta _j^{M_i},\ldots ,\beta _j^{M_D}$) with the values of probability of occurrence $P_{M_i}$. Using this information, the scheme presented in Fig. 5 can be created, where the horizontal coordinate of each point represents the values of the reliability index in each damaged configuration, $\beta _j^{M_i}$ ($i=1,\ldots ,D$), and the vertical coordinate indicates the value of the probability of occurrence of the associated damaged configuration, $P_{M_i}$. Thus, this representation can be understood as the probability mass function, $f_{\hat{\beta }_j}$, of the discrete random variable $\hat{\beta }_j=\beta _{j}^{M_{1}}, \beta _{j}^{M_{2}}, \ldots, \beta _{j}^{M_{D}}$.

Fig. 4

Reliability index in the element j (in black color) in each incomplete configuration $M_{i} \rightarrow \beta _{j}^{M_{i}}$, $i \in$ [1,D]

Fig. 5

Probability mass function of $\hat{\beta }_{j}$ obtained through the values in each incomplete configuration $M_{i} \rightarrow \beta _{j}^{M_{i}}$, $i \in$ [1,D]

As a result, a single design constraint per limit-state can be generated using this new random variable $\hat{\beta }_j$ that represents the reliability of the damaged structure in the limit-state $G_j$. The idea is to define the design constraint to ensure that $\beta _j^\mathrm{{T}}$ will be achieved with the certainty the designer demands. Then, a new RBDO problem can be defined ($\beta$-PDFSO) as presented in Eq. (5)

$$\begin{aligned}&\mathrm {min}\;F(\mathbf{d} ) \end{aligned}$$

(5a)

$$\begin{aligned}&\mathrm {s.t.} \nonumber \\ & \beta _{j}^{M_{0}}(\mathbf{d} ,\mathbf{x} ) \ge \beta _j^\mathrm{{T}} \quad&j=1,\ldots ,m^{M_{0}} \end{aligned}$$

(5b)

$$\begin{aligned}&P[\hat{\beta }_{j}(\mathbf{d} ,\mathbf{x} ) < \beta _j^\mathrm{{T}}] \le p_{f_{j}}^\mathrm{{T}} \quad&j=1,\ldots ,m^{M_{0}} \end{aligned}$$

(5c)

Equation (5b) guarantees the specified target reliability index $\beta ^\mathrm{{T}}$ over the limit-states associated with the intact model $M_0$. Furthermore, Eq. (5c) denotes that the probability of not guaranteeing the safety level in the damaged structure $\hat{\beta }_{j}$ must be lower than the target probability of failure $p_{f_{j}}^\mathrm{{T}}$ accepted by the designer. The complementary value of $p_{f_{j}}^\mathrm{{T}}$ is denoted as target reliability level, $R_{j}^\mathrm{{T}}=1-p_{f_{j}}^\mathrm{{T}}$, understood as the confidence level of the structure when an accidental collision occurs.

The $\beta$-PDFSO problem when $p_{f_j}^\mathrm{{T}}$ = 0 provides an optimum solution that matches the result of solving the fail-safe RBDO [9], where the reliability indices for the whole set of damaged configurations are simultaneously greater than or equal to the target reliability index ($\beta _j^{M_i} \ge \beta _j^\mathrm{{T}},\; \forall \;i,j$). However, as stated above, guaranteeing $\beta _j^\mathrm{{T}}$ in all damaged configurations seems a rather restrictive approach. When adopting a value of $p_{f_j}^\mathrm{{T}} \ne 0$, $\beta _j^\mathrm{{T}}$ would not be satisfied in some limit-states, but the final design must comply with Eq. (6)

$$\begin{aligned} \sum _{\beta _j^{M_i} < \beta _j^\mathrm{{T}}} P_{M_i}\le p_{f_j}^\mathrm{{T}} \end{aligned}$$

(6)

To clarify this point, Fig. 6 shows a simplified case with only four damaged configurations indicating how the design constraints are checked at the optimum solution for a generic limit-state j.

Fig. 6

Graphical example to check constraints at the optimum design (simplified case with only four damaged configurations)

As can be seen, the reliability index $\beta _j$ is below the target reliability index $\beta _j^\mathrm{{T}}$ in the damaged configurations $M_2$ and $M_4$. Thus, the probability of not guaranteeing $\beta _j^\mathrm{{T}}$ in the damaged structure for that limit-state will be the probability of $M_2$ or $M_4$ occurring, i.e., the sum of their probabilities of occurrence. Consequently, at the optimum design, $P_{M_2}+P_{M_4}$ must be lower than or equal to $p_{f_j}^\mathrm{{T}}$, as stated in Eq. (5c).

After normalizing the probabilistic constraints (5b) and (5c), the $\beta$-PDFSO can be reformulated as in Eq. (7). The probability mass function of $\hat{H}_j$ is defined through the pair of values [$H_{j}^{M_{i}}$, $P_{M_i}$] $\forall$ i, which gives rise to a piecewise discontinuous cumulative distribution function $F_{\hat{H}_{j}}$. Figure 7 shows the flowchart of the $\beta$-PDFSO problem formulated in Eq. (7)

$$\begin{aligned}&\mathrm {min}\;F(\mathbf{d} ) \end{aligned}$$

(7a)

$$\begin{aligned} &\mathrm {s.t.} \nonumber \\ &H_{j}^{M_{0}}(\mathbf{d} ,\mathbf{x} ) = \beta _j^{M_0}/\beta _j^\mathrm{{T}} - 1 \ge 0 \quad&j=1,\ldots ,m^{M_{0}} \end{aligned}$$

(7b)

$$\begin{aligned}&P[\hat{H}_{j}(\mathbf{d} ,\mathbf{x} ) < 0] \le p_{f_{j}}^\mathrm{{T}} \quad&j=1,\ldots ,m^{M_{0}} \end{aligned}$$

(7c)

The optimization code was developed in MATLAB [32], using the SQP algorithm implemented in the fmincon function. The algorithm modifies the design variables at each finite difference step, where the input data of the FE models are automatically updated. An HPC cluster is used to simultaneously calculate the reliability indices in all the configurations, what greatly accelerates the iterative procedure. The following steps need to be performed in a loop until convergence:

• 1. The set of damaged FE meshes representing the damaged configurations must be defined prior to initiating the optimization procedure ($M_i$, $i=0,\ldots ,D$).

• 2. The value for the design variables $\mathbf{d} ^k$ is established for the initial design, $k=0$.

• 3. The objective function $F(\mathbf{d} ^k)$ is evaluated in the intact model $M_0$.

• 4. The reliability indices $\beta _j^{M_i}$ are calculated through the First-Order Reliability Method (FORM) at each limit-state j in all the models $M_i$. This is done by performing a parallel analysis of the whole set of models, since it is a computationally expensive task.

• 5. Once the reliability indices $\beta _j^{M_i}$ are obtained, the design constraints of the intact and damaged structure need to be evaluated:

  • 5.1 The constraints associated with the intact model can be directly evaluated with the normalized form of the reliability indices, $H_j^{M_0}=\beta _j^{M_0}/\beta _j^\mathrm{{T}}-1$. Then, Eq. (7b) can be evaluated.

  • 5.2 To evaluate each constraint associated with the damaged structure (which is unknown), the CDF of the normalized random reliability index in the damaged structure ($F_{\hat{H}_{j}}$) has to be built for each limit-state j. The single random response ($\hat{H}_{j}$) represents the reliability of the damaged structure and contains the information of the reliability indices $\beta _j^{M_i}$ in all damaged configurations as well as their probability of occurrence $P_{M_i}$. Since $\hat{H}_j$ is a discrete random response, it must be interpolated over the entire domain to apply gradient-based optimization. Furthermore, $F_{\hat{H}_j}$ has to be continuous and differentiable to compute its gradients. For this reason, the Piecewise Cubic Hermite Interpolating Polynomial (PCHIP) from Matlab was adopted to evaluate Eq. (7c). As a result, by evaluating $F_{\hat{H}_j}$(0) at different values of design variables, different values of the constraints are obtained, allowing the algorithm to progress.

• 6 If F converged and the design constraints are satisfied, the final design is achieved. Otherwise, the design variables are updated.

• 7 The iterative process continues ($k=k+1$) going back to step 3 until the convergence criteria are satisfied. The first criterion is the one based on Karush–Kuhn–Tucker (KKT) conditions, that is, the objective function has to be non-decreasing in feasible directions, within the value of the optimality tolerance. This value is established in the fmincon solver through the parameter OptimalityTolerance, set to $10^{-3}$. The second criterion refers to the fulfillment of design constraints, which have to be satisfied within the value of the constraint tolerance. This value is established in the fmincon solver through the parameter ConstraintTolerance, also set to $10^{-3}$

Fig. 7

Flowchart of $\beta$-PDFSO

4 Case studies

Three examples of structural optimization using the $\beta$-PDFSO formulated in Eq. (7) are presented below. In all of them, the same target reliability index $\beta _j^\mathrm{{T}}=\beta ^\mathrm{{T}}=3.7190$ is adopted for all limit-states j, which corresponds to a target probability of failure of $10^{-4}$.

4.1 Analytical problem

This section introduces a simple analytical example to illustrate the application of the $\beta$-PDFSO. The main objective is to provide the reader with a simple example to facilitate the understanding of the method. The idea is to define a fail-safe optimization problem using mathematical expressions to simulate the objective function F and the structural responses $R_j$. These structural responses do not have any physical meaning. They are only analytical expressions that simulate the behavior of a structural system. That is, an increase in the value of the design variables leads to an increase in the value of the objective function and reduces the value of the structural responses. These structural responses depend on the design variables $\mathbf{d} =[d_1, d_2]$, the random variables $\mathbf{x} =[x_1, x_2]$ and a vector of coefficients $\mathbf{c} =[c_1, c_2, c_3, c_4, c_5, c_6]$, as shown in Eq. (8)

$$\begin{aligned}&R_1^{M_{i}}(\mathbf{d} ,\mathbf{x} ,\mathbf{c} ) = \frac{1 + x_1}{c_1 + c_2 \cdot d_{1} + c_3 \cdot d_{2} + c_4 \cdot d_{1}d_{2} + c_6 \cdot d_{2}^{2} + x_2} \end{aligned}$$

(8a)

$$\begin{aligned}&R_2^{M_{i}}(\mathbf{d} ,\mathbf{x} ,\mathbf{c} ) = \frac{1 + x_1}{c_1 + c_2 \cdot d_{1} + c_3 \cdot d_{2} + c_5 \cdot d_{1}^{2} + c_6 \cdot d_{2}^{2} + x_2} \end{aligned}$$

(8b)

By varying the vector c, the structural responses are modified, being possible to obtain different values for the intact and damaged configurations: the vector c is taken as the unit vector to represent the structural responses in the intact model ($R_j^{M_0}$), while values between 0 and 1 are used to simulate the responses in the damaged configurations ($R_j^{M_i},\;i=1,\ldots ,D$). In this example, a different vector c $=[c_1, c_2, c_3, c_4, c_5, c_6]$, is set for each response $R_j^{M_i}$, expressed as $\mathbf{c} _j^{M_{i}}$. Only some values of these coefficients are summarized in the arrays presented in Eq. (9). The full-length matrices are available in a GitHub repository at link: https://github.com/claracbengoa/betaPDFSO

$$\begin{aligned} \mathbf{c} _1^{M_0} \quad&= \begin{pmatrix} 1&1&1&1&1&1 \end{pmatrix} \end{aligned}$$

(9a)

$$\begin{aligned} \begin{pmatrix} \mathbf{c} _1^{M_1} \\ \vdots \\ \mathbf{c} _1^{M_i} \\ \vdots \\ \mathbf{c} _1^{M_{60}} \end{pmatrix}&= \begin{pmatrix} 0.1541 &{} 0.9090 &{} 0.6027 &{} 0.8211 &{} 0.9190 &{} 0.5018 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ c_1 &{} c_2 &{} c_3 &{} c_4 &{} c_5 &{} c_6 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0.4975 &{} 0.9755 &{} 0.9560 &{} 0.5210 &{} 0.3379 &{} 0.8228 \end{pmatrix} \end{aligned}$$

(9b)

$$\begin{aligned} \mathbf{c} _2^{M_0} \quad&= \begin{pmatrix} 1&1&1&1&1&1 \end{pmatrix} \end{aligned}$$

(9c)

$$\begin{aligned} \begin{pmatrix} \mathbf{c} _2^{M_1} \\ \vdots \\ \mathbf{c} _2^{M_i} \\ \vdots \\ \mathbf{c} _2^{M_{60}} \end{pmatrix}&= \begin{pmatrix} 0.0171 &{} 0.6790 &{} 0.5531 &{} 0.5832 &{} 0.3742 &{} 0.9777 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ c_1 &{} c_2 &{} c_3 &{} c_4 &{} c_5 &{} c_6 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0.4150 &{} 0.3916 &{} 0.8286 &{} 0.3054 &{} 0.9518 &{} 0.9177 \end{pmatrix} \end{aligned}$$

(9d)

By adopting this approach, the structural responses defined in Eq. (8) (which could represent stresses, displacements, ...) increase for values of c lower than 1, being possible to simulate a loss of structural capacity in the damaged configurations. In this problem, $D=60$ was taken as the number of damaged configurations. The probability of occurrence $P_{M_i}$ of each damaged configuration is shown in Table 1.

Table 1 Probability of occurrence of the partial collapses shown in Fig. 8

The objective is to minimize the objective function F, defined as the sum of the design variables d = [$d_1$, $d_2$]. In a deterministic approach without any source of uncertainty, the design constraint would simply be that the response $R_j$ is less than the allowed response $R_{\max }$. However, two sources of uncertainty are taken into account in this problem: the aleatory uncertainty in the random parameters x = [$x_1$, $x_2$] affecting the structural response and the uncertainty due to the probability of occurrence of each partial collapse.

The formulation of the $\beta$-PDFSO problem is presented in Eq. (10), with the probabilistic constraints of the intact (Eq. 10b) and damaged configurations (Eq. 10c). The random variables are defined as normally distributed with mean $\varvec{\mu }_\mathbf{x }$ = (0.25, 1) and standard deviation $\varvec{\sigma }_\mathbf{x }$ = (0.025, 0.1). As there are two structural responses ($R_j$, with $j=1,2$), the problem has a total of four design constraints (two for the intact model and two for the damaged structure)

$$\begin{aligned}&\mathrm {min}\;F(\mathbf{d} ) \; = \; \mathrm {min}\;(d_{1} + d_{2}) \end{aligned}$$

(10a)

$$\begin{aligned} &\mathrm {s.t.} \nonumber \\ & H_j^{M_{0}} = \frac{\beta _j^{M_0}}{\beta ^\mathrm{{T}}} - 1 \ge 0&\quad j=1,2 \end{aligned}$$

(10b)

$$\begin{aligned}&P[\hat{H}_j < 0] \le p_{f}^\mathrm{{T}}&\quad j=1,2 \end{aligned}$$

(10c)

$$\begin{aligned}&\mathrm {being} \; \beta _j^{M_i} \; \text {the reliability index associated with } \nonumber \\&G_j^{M_i} = 1 - \frac{R_j^{M_i}}{R_{\mathrm {max}}} \ge 0 \quad i=0,\ldots ,60 \\&\mathrm {with} \quad R_{\mathrm {max}} = 1/4 \nonumber \end{aligned}$$

(10d)

Equation (10b) guarantees the specified target reliability index $\beta ^\mathrm{{T}}$ over the limit-state associated with the intact model, $G_j^{M_{0}}$. Equation (10c) refers to the design constraints associated with the damaged structure, meaning that the probability of not guaranteeing $\beta ^\mathrm{{T}}$ when a partial collapse occurs has to be lower than or equal to the admissible probability of failure $p_{f}^\mathrm{{T}}$. To evaluate this constraint, the probability mass function of $\hat{H}_j$ is built through the pair of values [$H_j^{M_{i}}$,$P_{M_i}$] in all the damaged configurations. The responses $H_j^{M_{i}}$ are obtained by performing a FORM, calculating the reliability index $\beta _j^{M_i}$ associated with the limit-state $G_j^{M_i}$. This limit-state is defined in its normalized form, so that the structural response $R_j^{M_i}$ is lower than the maximum value of the response $R_{\mathrm {max}}$. The definition of the probabilistic constraints is summarized in Fig. 8.

Fig. 8

Definition of the probabilistic constraints from the reliability indices

The optimization problem presented in Eq. (10) was solved for a target reliability index $\beta ^\mathrm{{T}} = 3.7190$ and target probabilities of failure $p_{f}^\mathrm{{T}}$ equal to 0.02, 0.05, and 0.10, which correspond to a confidence level, $R^\mathrm{{T}}$, of 0.98, 0.95, and 0.90, respectively. This means that the optimum design obtained from the $\beta$-PDFSO approach guarantees a target reliability index of 3.7190 when a partial collapse occurs with at least certainties of survival of 98, 95, and 90%, respectively.

The results are presented in Table 2, along with the results of the intact and fail-safe RBDO. As can be seen, $\beta$-PDFSO result is bounded between the intact (F = 1.8376) and fail-safe (F = 6.5941) RBDO designs, leading to a reduction in the objective function of 7.51%, 22.09% and 35.88% for $p_f^\mathrm{{T}}$ = 0.02, 0.05, and 0.10, respectively. Analyzing for example the case with $p_f^\mathrm{{T}}$ = 0.05, it means that when a partial collapse occurs, $\beta _j \ge \beta ^\mathrm{{T}}$ is satisfied with at least 95% probability. Thus, the objective function can be reduced by 22.09% with respect to the fail-safe RBDO, where $\beta ^\mathrm{{T}}$ is guaranteed with a reliability level of 100%.

Table 2 Comparison of the $\beta$-PDFSO, fail-safe, and intact RBDO optima

The active constraints for the intact model and fail-safe RBDO designs are summarized in Table 3. In these formulations, the target reliability index is guaranteed in all configurations, having exactly the value $\beta =3.7190$ for the active limit-states. The active constraints for the $\beta$-PDFSO problem appear in Table 4. It can be drawn from this table that the sum of $P_{M_{i}}$ associated with those damaged configurations where the target reliability index is not guaranteed is always below the value of $p_{f}^\mathrm{{T}}$ imposed by the designer in the optimization problem, as stated in Eq. (6). In addition, Figs. 9, 10 and 11 show the CDFs associated with active constraints in the $\beta$-PDFSO for $p_{f}^\mathrm{{T}}$ = 0.02, 0.05, and 0.10, respectively.

Table 3 Active constraints ($\beta _j=3.7190$) at the intact and fail-safe RBDO optima

Table 4 Active constraints ($P[\hat{H}_j<0] \le p_f^\mathrm{{T}}$) at the $\beta$-PDFSO optima for $p_{f}^\mathrm{{T}}$ = 0.02, 0.05, and 0.10. Damaged configurations $M_i$ where $\beta _j < 3.7190$

Fig. 9

CDF of $\hat{H}_2$ at the $\beta$-PDFSO optima for $p_{f}^\mathrm{{T}}$ = 0.02

Fig. 10

CDF of $\hat{H}_2$ at the $\beta$-PDFSO optima for $p_{f}^\mathrm{{T}}$ = 0.05

Fig. 11

CDFs at the $\beta$-PDFSO optima for $p_{f}^\mathrm{{T}}$ = 0.10

4.2 Two-dimensional truss structure

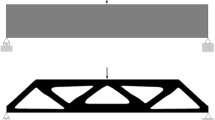
This example corresponds to a practical engineering case of a 125-bar truss structure, with elements supporting axial and bending forces. The structure represents a 160 m long and 10 m high bridge, with a spacing of 5 m between vertical bars. The load case considered corresponds to the application of concentrated forces of 200 kN in the nodes of the bottom cord, as presented in Fig. 12. It is assumed that an accident causing loss of some bars will occur as a result of a vehicle impact. Recent civil engineering codes [7] contemplate that “structural schemes must ensure that the accidental removal of a limited part of the structure does not compromise its integrity”. The FE model was defined in Abaqus [1], with bars modeled through the B21 element type and solid circular section. The bar IDs appear in Fig. 12, where only the left part is shown due to the symmetry of the structure. Uncertainty is present in the concentrated forces applied in nodes of the bottom chord, taking the load value as a normal random variable with mean $\mu _P$ = 200 kN and standard deviation $\sigma _P$ = 20 kN.

Fig. 12

Two-dimensional truss structure with 125 bars

Fig. 13

46 partial collapses of the structure

Figure 13 shows the set of 46 damaged models considered in the problem. It is assumed that only the inner bars can be damaged and the likelihood of simultaneously breaking two bars will be less than breaking only one. Scenarios where more than two bars are damaged simultaneously are not taken into account. Three types of partial collapses were considered, whose probabilities of occurrence are summarized in Table 5.

Table 5 Probability of occurrence for each damaged model

The design variables are the cross-sectional radius of the members. The structure has been divided into 12 zones with one design variable each. Table 6 lists the members that have the same design variable, as well as their initial values.

Table 6 Definition of the 12 design variables (DV)

The complete formulation of the problem is presented in Eq. (11), where the volume V of the intact structure is considered as the objective function. Probabilistic design constraints of normal stress in the members are established. As discussed in Sect. 3, two types of constraints are defined: the first one affects only the limit-states of the intact structure and the second one affects the damaged structure, which is unknown. Therefore, it is necessary to define the confidence level required over these restrictions.

$$\begin{aligned}&\mathrm {min\;}V =\sum _{i=1}^{125} (\pi \cdot r_{i}^{2}) \cdot l_{i} \;&\end{aligned}$$

(11a)

$$\begin{aligned} &\mathrm {s.t.} \nonumber \\ & H_{j}^{M_{0}} = \beta _j^{M_0}/\beta ^\mathrm{{T}} - 1 \ge 0 \quad&j=1,\ldots ,125 \end{aligned}$$

(11b)

$$\begin{aligned}&P[\hat{H}_{j} < 0] \le p_{f}^\mathrm{{T}} \quad&j=1,\ldots ,125 \end{aligned}$$

(11c)

$$\begin{aligned}&\mathrm {with} \quad G_j^{M_i} = \sigma _{\mathrm {max}} - \sigma _j^{M_i} \ge 0 \;&(\mathrm {tension\;bars}) \nonumber \\&G_j^{M_i} = \sigma _j^{M_i} - \sigma _{\mathrm {min}} \ge 0 \;&(\mathrm {compression\;bars}) \nonumber \\&\sigma _{\mathrm {min}}=-104\;\mathrm {MPa}, \; \sigma _{\mathrm {max}}=130\;\mathrm {MPa}. \nonumber \end{aligned}$$

In this example, a minimum reliability index of $\beta ^\mathrm{{T}}$ = 3.719 is imposed and three confidence levels have been considered: $R_{j}^\mathrm{{T}}$ = 0.98, 0.95 and 0.9 which correspond to a probability of failure of $p_{f}^\mathrm{{T}}$ = 0.02, 0.05 and 0.1, respectively. Table 7 shows the optimum values of the bar radius in the intact structure that minimizes its weight satisfying the probabilistic constraints. The results show that the final volume of the design is always between the intact (V = 52.1511 m$^3$) and fail-safe (V = 102.1052 m$^3$) RBDO designs. We can appreciate that if the designer increases the confidence level close to the maximum ($R_{j}^\mathrm{{T}}$ = 1), the design leads to the fail-safe RBDO. On the contrary, if the confidence level decreases, the solution leads to the RBDO optimum when only the intact structure is considered. With this approach, the savings obtained for each $R_{j}^\mathrm{{T}}$ are the following: 0.79%, 3.66%, and 17.93% for $R_{j}^\mathrm{{T}}$ of 0.98, 0.95, and 0.9, respectively.

Table 7 Comparison of the $\beta$-PDFSO, fail-safe, and intact RBDO optima

Furthermore, it was found that the decrease in the value of $R^\mathrm{{T}}$ is not linear with the decrease achieved in the objective function. Also, it is observed that although the $\beta$-PDFSO provides designs with values of the objective function bounded between the intact RBDO and fail-safe RBDO results, the design variables do not necessarily follow this rule. For instance, for $R^\mathrm{{T}}$ = 0.98, the bottom chord in zones 1 and 3 are higher than the values in the fail-safe RBDO.

Bars with active stress constraints for the intact and fail-safe RBDO designs are shown in Fig. 14, all of them with a reliability index equal to 3.719. Figure 15 and Table 8 show the active limit-states for the $\beta$-PDFSO designs ($p_{f}^\mathrm{{T}}$ = 0.02, 0.05 and 0.10). Particularly, the damaged configurations where the reliability indices are not guaranteed are shown. Thus, although $\beta ^\mathrm{{T}}$ is not achieved in some damaged configurations, the addition of their probabilities of occurrence is less than the $p_{f}^\mathrm{{T}}$ set by the designer.

Fig. 14

Limit-states of stress ($\sigma _j^{M_i}$) associated with active constraints ($\beta _j=3.7190$) at the intact (a) and fail-safe (b) RBDO optima

Fig. 15

Limit-states of stress ($\hat{\sigma }_j$) associated with active constraints ($P[\hat{H}_j<0] \le p_f^\mathrm{{T}}$) at the $\beta$-PDFSO optima

Table 8 Limit-states of stress ($\hat{\sigma }_j$) associated with active constraints ($P[\hat{H}_j<0] \le p_f^\mathrm{{T}}$) at the $\beta$-PDFSO optima for $p_{f}^\mathrm{{T}}$ = 0.02, 0.05, and 0.10

Thus, in the case $p_{f}^\mathrm{{T}}$ = 0.10, the stress in bar 43 ($\sigma _{43}$) is an active limit-state in the damaged structure, since $P[\hat{H}_{43}\le 0]$ = 0.099963 as can be seen in Fig. 16, satisfying the probabilistic constraint shown in Eq. (11c). This can also be checked by the sum of the values of $P_{M_{i}}$ where $\beta ^\mathrm{{T}}$ is not achieved, $M_{10}$, $M_{12}$, $M_{25}$, $M_{40}$, and $M_{42}$, being lower that the target value of 0.1. This slightly difference is due to the use of the polynomial interpolation to evaluate the piecewise CDF, as can be seen in the zoom presented in Fig. 16. The same behavior can be observed in Table 8 for the remaining limit-states and different values of $p_f^\mathrm{{T}}$.

Fig. 16

CDF of stress constraint in bar 43 at the $\beta$-PDFSO optima for $p_{f}^\mathrm{{T}}$ = 0.10

4.3 Aircraft-tail fuselage

The motivation for this industrial-type example comes from the demands of the aviation sector. One of the designs considered for the new generation of single-aisle aircraft includes two open rotor engines with two blade planes. This configuration must account for incidents produced by unleashed debris striking the fuselage, such as the release of unducted blades or debris originated by uncontained engine failures. Thus, the proposed failure cases correspond to a representative sample of the damage scenarios contemplated by the industry in modern aircraft (Table 11). The 3D model presented in Fig. 17 represents the rear part of a commercial aircraft. The propulsion system consists of two open rotor engines, which are mounted in section 19 of the aircraft. This section is 6100 mm long, with a frontal interface frame 3300 mm wide and 3500 mm high, and a rear frame 1200 mm wide and 1400 mm high connecting to the tail cone. Section 19 consists of a fuselage skin stiffened by frames, stringers, and a torsion box; whose purpose is to absorb the VTP and HTP loads. These engines contain big unducted blades that could be released in the event of failure, as well as other rotating components inside the nacelle that could lead to an uncontained rotor failure [25, 28].

Fig. 17

Position of section 19 in the airplane (left) and FE model (right)

The FE model of section 19 was defined using Nastran [34]. It has a total of 4044 degrees of freedom, comprising 570 shell elements (CQUAD4 and CTRIA3), 543 bar elements (CBAR and CBEAM), and 280 truss elements (CROD), to represent the fuselage skin, frames, stringers, and the torsion box. Rigid connections (RBE3) are used to simulate the load transmission of the vertical and horizontal tail plane (VTP and HTP). Another RBE3 is defined to constrain the nodes of the interface frame, as shown in Fig. 17. Loads from the VTP, HTP, and tail cone are applied in section 19, as shown in Fig. 17. The load cases used in this example are defined in Table 9. Young moduli of the materials used in skin and stiffeners are considered as normal random variables whose mean and standard deviations are shown in Table 10. Uncertainty in load values is contemplated through the definition of a multiplication factor $\phi$, defined as a new normal random variable as presented in Table 10.

Table 9 Definition of load cases

Table 10 Definition of random variables

Essentially, two types of failure scenarios associated with discrete events were considered in this research. The first one represents the accidental situations that generate debris striking the aircraft fuselage, such as the release of broken blades or uncontained engine failures. Examples of real accidents of this type can be found in reports by the Federal Aviation Administration [15, 16, 18]. The damaged models related to these events correspond to those presented in Fig. 18, going from $M_1$ to $M_{54}$. The second failure scenario is associated with the fitting failure in the VTP/HTP or rear tail cone joints. These situations are commonly studied in the aerospace industry when analyzing airframe assemblies, where a failure of the lugs and bolts can lead to the detachment of two assembled sections. In this case, the damaged models are presented in Fig. 19, with labels from $M_{55}$ through $M_{66}$, where one of the fittings fails.

Fig. 18

Partial collapses ($M_{1}$ – $M_{54}$) in example 3

Fig. 19

One fitting failure ($M_{55}$ – $M_{66}$) in example 3

The aerospace industry agrees upon different probabilities of occurrence for damage scenarios of different nature. In this example, as the real values should be obtained from confidential aircraft reports, approximate values were adopted to simulate a realistic probability assignment of the failure events. Table 11 shows each type of failure considered as well as their probability of occurrence.

Table 11 Probability of occurrence of the damaged configurations presented in Figs. 18 and 19

The aim is to obtain the minimum mass of the skin and frames in the intact structure due to the consideration of the probability of occurrence of the set of 66 partial collapses and the uncertainty in the random parameters presented in Table 10. The skin was divided in five zones, and frames were organized into two groups, corresponding to a different channel profile. Thus, the skin thickness of each zone and the dimensions of each frame profile amount to a total number of 13 design variables. All of them are presented in Fig. 20. The skin thicknesses ($Sk_i$) are bounded between 0.4 and 5 mm. The dimensions of each frame profile are the web length ($Fh_i$), bounded between 50 and 150 mm, the flange length ($Fb_i$) bounded between 20 and 100 mm, and the web thickness and flange thickness ($Fth_i$, $Ftb_i$) bounded between 3 and 12 mm.

Fig. 20

Design variables: frame section (left), side view (center), and top view (right)

The $\beta$-PDFSO problem is formulated in Eq. (12). Von mises stress constraints over each skin zone, normal stress constraints over each frame, and buckling constraints over the first eigenvalue are considered. For the CQUAD4 elements, von Mises stresses are evaluated at the centroid of the element. Then, the stresses are calculated at the top and bottom faces of the element. For the design constraints, the maximum value is taken. For the CBAR elements, stresses are evaluated at both ends in the outer vertices of the transversal cross section. The minimum and maximum values are taken for the design constraints. Equation (12b) refers to the design constraints of the intact model, in which $\beta ^\mathrm{{T}}$ = 3.719 is guaranteed for all the limit-states. Equation (12c) corresponds to the design constraints of the damaged structure, where $\beta ^\mathrm{{T}}$ is guaranteed with a confidence level $R^\mathrm{{T}}=1-p_{f}^\mathrm{{T}}$. Two problems were solved, using $p_{f}^\mathrm{{T}}$ values of 0.05 and 0.10.

$$\begin{aligned}&\mathrm {min}\;M = M_{Sk} + M_{F} \; [\mathrm {kg}] \end{aligned}$$

(12a)

$$\begin{aligned}&\mathrm {s.t.} \nonumber \\&\left. \begin{array}{llll} H_{\sigma _{Sk\;\mathrm {zone}\;k}}^{M_0,\;\mathrm {LC}\;j} &{} = &{} \beta _{\sigma _{Sk\;\mathrm {zone}\;k}}^{M_0,\;\mathrm {LC}\;j}/\beta ^\mathrm{{T}} - 1 \ge 0 &{} \quad k=1,\ldots ,5 \\ H_{\sigma _{\mathrm {max},\;\mathrm {frame}\;k}}^{M_0,\;\mathrm {LC}\;j} &{} = &{} \beta _{\sigma _{\mathrm {max},\;\mathrm {frame}\;k}}^{M_0,\;\mathrm {LC}\;j}/\beta ^\mathrm{{T}} - 1 \ge 0 &{} \quad k=1,\ldots ,8 \\ H_{\sigma _{\mathrm {min},\;\mathrm {frame}\;k}}^{M_0,\;\mathrm {LC}\;j} &{} = &{} \beta _{\sigma _{\mathrm {min},\;\mathrm {frame}\;k}}^{M_0,\;\mathrm {LC}\;j}/\beta ^\mathrm{{T}} - 1 \ge 0 &{} \quad k=1,\ldots ,8 \\ H_{\lambda _1}^{M_0,\;\mathrm {LC}\;j} &{} = &{} \beta _{\lambda _1}^{M_0,\;\mathrm {LC}\;j}/\beta ^\mathrm{{T}} - 1 \ge 0 \\ \end{array}\right\} \; j=1,\ldots ,6 \end{aligned}$$

(12b)

$$\begin{aligned}&\left. \begin{array}{llll} P[\hat{H}_{\sigma _{Sk\;\mathrm {zone}\;k}}^{\mathrm {LC}\;j} &{}< 0] \le p_{f}^\mathrm{{T}} &{} \quad k=1,\ldots ,5 \\ P[\hat{H}_{\sigma _{\mathrm {max},\;\mathrm {frame}\;k}}^{\mathrm {LC}\;j} &{}< 0] \le p_{f}^\mathrm{{T}} &{} \quad k=1,\ldots ,8 \\ P[\hat{H}_{\sigma _{\mathrm {min},\;\mathrm {frame}\;k}}^{\mathrm {LC}\;j} &{}< 0] \le p_{f}^\mathrm{{T}} &{} \quad k=1,\ldots ,8 \\ P[\hat{H}_{\lambda _1}^{\mathrm {LC}\;j} &{} < 0] \le p_{f}^\mathrm{{T}} \\ \end{array}\right\} \; j=1,\ldots ,6 \end{aligned}$$

(12c)

$$\begin{aligned} 11.2799 \le \frac{F_{hk}}{F_{thk}} \le 15.5099 \quad k=1,2 \end{aligned}$$

(12d)

$$\begin{aligned} 3.1725 \le \frac{F_{bk}}{F_{tbk}} \le 4.23 \quad k=1,2 \end{aligned}$$

(12e)

$$\begin{aligned} & \begin{array}{llll} \mathrm {with} \quad & G_{\sigma _{Sk\;\mathrm {zone}\;k}}^{M_i,\;\mathrm {LC}\;j} & = & \sigma _{\mathrm {max}}^{\mathrm {VON}} - \sigma _{Sk\;\mathrm {zone}\;k}^{M_i,\;\mathrm {LC}\;j} \ge 0 \nonumber \\ & G_{\sigma _{\mathrm {max},\;\mathrm {frame}\;k}}^{M_i,\;\mathrm {LC}\;j} & = & \sigma _{\mathrm {max}}^{\mathrm {normal}} - \sigma _{\mathrm {max},\;\mathrm {frame}\;k}^{M_i,\;\mathrm {LC}\;j} \ge 0 \nonumber \\ & G_{\sigma _{\mathrm {min},\;\mathrm {frame}\;k}}^{M_i,\;\mathrm {LC}\;j} &= & \sigma _{\mathrm {min},\;\mathrm {frame}\;k}^{M_i,\;\mathrm {LC}\;j} - \sigma _{\mathrm {min}}^{\mathrm {normal}} \ge 0 \nonumber \\ & G_{\lambda _1}^{M_i,\;\mathrm {LC}\;j} & = & \lambda _1^{M_i,\;\mathrm {LC}\;j} - 1.2 \ge 0 \nonumber \\ & {\sigma _{\mathrm {max}}^{\mathrm {VON}}=300\mathrm {MPa}, \sigma _{\mathrm {min}}^{\mathrm {normal}}=-180\mathrm {MPa}, \sigma _{\mathrm {max}}^{\mathrm {normal}}=300\mathrm {MPa}} \nonumber \end{array} \end{aligned}$$

Table 12 shows the optimum values of skin thicknesses and dimensions of frame profiles. It can be concluded that the final mass of the design is always between the intact (M = 230.6758 kg) and fail-safe (M = 514.8307 kg) RBDO designs. Mass savings increase up to 5.30% for a confidence level of 0.95 and 13.56% for a confidence level of 0.90. As in the previous example, the design variables are not bounded between the lower and upper bounds provided by the intact and fail-safe RBDO designs. In this case, the flange length in the type 2 frame ($Fb_2$) is not bounded between 32.6178 and 34.3031, having values for $R^\mathrm{{T}}$ = 0.95 and 0.90 of 29.7569 and 27.4679 mm. This means that that the optimum design resulted in a different load-path structure compared with the fail-safe RBDO.

Table 12 Comparison of the $\beta$-PDFSO, fail-safe, and intact RBDO optima

By assuming the confidence level of $R^\mathrm{{T}}$ =0.90, the mass of the design is considerably reduced compared to the fail-safe RBDO, while still yielding acceptable safety levels. The reason is that an accidental scenario leading to a partial collapse of the structure is an event categorized in the AC 25.1309-1B [20] as extremely remote, that corresponds to a probability less than $10^{-7}$. Therefore, considering a $p_f^\mathrm{{T}}$ = 0.10 implies that only in the 10% of the accidents of this type that occur, the reliability index of some limit-states will not reach the desired $\beta ^\mathrm{{T}}$ in some of the damaged configurations. Active constraints for the optimum designs shown in Table 12 are summarized in Tables 13 and 14. As in the example presented in Sect. 4.2, there are some damaged configurations where $\beta ^\mathrm{{T}}$ is not guaranteed in some limit-states. However, the addition of the probability of occurrence associated with these constraints is less than the $p_{f}^\mathrm{{T}}$ set by the designer. In addition, Figs. 21 and 22 show the CDF of the limit-states associated with active constraints in the $\beta$-PDFSO for $p_{f}^\mathrm{{T}}$ = 0.05 and 0.10, respectively.

Table 13 Limit-states associated with active constraints ($\beta =3.7190$) at the intact and fail-safe RBDO optima

Table 14 Limit-states associated with active constraints ($P[\hat{H}_j<0] \le p_f^\mathrm{{T}}$) at the $\beta$-PDFSO optima for $p_{f}^\mathrm{{T}}$ = 0.05 and 0.10. Damaged configurations $M_i$ where $\beta < 3.7190$

Fig. 21

CDF of the first buckling eigenvalue constraint for LC6 at the $\beta$-PDFSO optima for $p_{f}^\mathrm{{T}}$ = 0.05

Fig. 22

CDF of the minimum normal stress constraint in frame 5 for LC6 at the $\beta$-PDFSO optima for $p_{f}^\mathrm{{T}}$ = 0.10

5 Computing facilities

The examples developed have been solved in a high-performance cluster (HPC) with 1504 computing cores, a theoretical peak performance of 32.5 TFLOP’s and a physical memory of 4 TB. Table 15 shows a summary of the computational effort in terms of iterations and number of analyses for all examples. All the cases have been run employing 1 core of the HPC and assigning a physical memory of 2 GB to each.

A summary of the computational burden for all the examples is presented in Table 15. The number of iterations and function evaluations is compared for the intact model RBDO, fail-safe RBDO, and $\beta$-PDFSO. As can be seen, the number of function evaluations in the intact model RBDO is considerably lower than the other approaches. The reason is that the set of design constraints is greatly reduced, because there are no damaged configurations in the optimization problem; hence, the final structure is not fail-safe. In the fail-safe RBDO and $\beta$-PDFSO, the reliability indices in all the damaged configurations need to be calculated. The difference is that in fail-safe RBDO each constraint refers to the reliability index $\beta _j$ of one damaged model. In contrast, $\beta$-PDFSO requires the construction of a new constraint that groups the values of $\beta _j$ from different damaged models, which complicates convergence.

Table 15 Summary of the computational effort (iterations and function evaluations)

6 Conclusions

The $\beta$-PDFSO is a new fail-safe optimization strategy to obtain minimum weight structures that takes into account the probability of occurrence of each accidental scenario, as well as uncertainty in parameters affecting structural responses. The results show that it is possible to avoid oversized designs compared to those obtained using a standard fail-safe RBDO approach, in which the probability of occurrence of each damaged configuration is disregarded.

The advantages provided by the proposed method can be clearly seen in example 1, where a reduction of 8.92% is achieved for a confidence level of $R^\mathrm{{T}}$ = 0.98 compared to the result given by the fail-safe RBDO. Furthermore, for $R^\mathrm{{T}}$ equal to 0.95 and 0.90, the methodology achieves reductions of the objective function up to a 20.99% and 32.60%, respectively. In structural application example 2, savings achieved are 0.79%, 3.66%, and 17.93% for the same $R^\mathrm{{T}}$ values as in example 1. Finally, in example 3, the objective function is reduced by up to 5.30% for $R^\mathrm{{T}}$ = 0.95 and a 13.56% for $R^\mathrm{{T}}$ = 0.90.

It is worth mentioning that an accident leading to a partial collapse of a structure is an event categorized by the regulations as extremely remote. In the case of an aeronautical structure, a probability of less than $10^{-7}$ is established. In this context, it seems appropriate to establish a confidence level on the constraints affecting the damaged structure. The $\beta$-PDFSO has demonstrated to be a promising approach for achieving optimum designs under fail-safe conditions for industrial application in which specific probability of occurrence of each damaged configuration is available. Nevertheless, authors are aware that the method is computationally expensive due to having to calculate the reliability indices of all limit-states for all damaged configurations. Further research concerning strategies to alleviate the computational cost are currently under development. They are oriented to reduce the set of reliability indices to calculate for each iteration of the optimization process. Other future work is aimed at including not only random uncertainty but also epistemic uncertainty.

7 Replication of results

MATLAB code with the $\beta$-PDFSO method applied to the analytical example presented in Sect. 4.1 is available at link: https://github.com/claracbengoa/betaPDFSO.