A further study comparing forward search multivariate outlier methods including ATLA with an application to clustering

Abstract

This paper makes comparisons of automated procedures for robust multivariate outlier detection through discussion and simulation. In particular, automated procedures that use the forward search along with Mahalanobis distances to identify and classify multivariate outliers subject to predefined criteria are examined. Procedures utilizing a parametric model criterion based on a $\chi ^2$-distribution are among these, whereas the multivariate Adaptive Trimmed Likelihood Algorithm (ATLA) identifies outliers based on an objective function that is derived from the asymptotics of the location estimator assuming a multivariate normal distribution. Several criterion including size (false positive rate), sensitivity, and relative efficiency are canvassed. To illustrate relative efficiency in a multivariate setting in a new way, measures of variability of the multivariate location parameter when the underlying distribution is chosen from a multivariate generalization of the Tukey–Huber $\epsilon$-contamination model are used. Mean slippage models are also entertained. The simulation results here are illuminating and demonstrate there is no broadly accepted procedure that outperforms in all situations, albeit one may ascertain circumstances for which a particular method may be best if implemented. Finally the paper explores graphical monitoring for existence of clusters and the potential of classification through occurrence of multiple minima in the objective function using ATLA.

1 Introduction

Outlier detection methods in multivariate data analysis that use the forward search begin with Hadi (1992, 1994) and have gained much publicity with a book and subsequent articles of Atkinson et al (2003), Riani et al (2009), Cerioli et al (2014, 2018, 2019). These articles show that multivariate outlier detection methods exist in a wide variety of settings effectively using different adopted techniques and methodology, with varying intended applications albeit with the same ultimate objective to detect and classify outliers. Riani et al (2009) and Cerioli et al (2019) cite an adaptive trimmed likelihood algorithm (ATLA) published in Clarke and Schubert (2006) which is the multivariate culmination of adaptive methods of trimming discussed in earlier settings including Clarke (1994, 2000), and Bednarski and Clarke (2002). This is a natural extension of the trimmed likelihood estimator countenanced in the univariate and multivariate discussion in Bednarski and Clarke (1993), Butler (1982), Butler et al (1993), Hadi and Luceno (1997), and Clarke et al (2017). See chapters 7 and 8 of Clarke (2018) for a panoramic discussion linking the estimators to the minimum covariance determinant (MCD) estimator of Rousseeuw (1983). The performance of the multivariate ATLA algorithm of Clarke and Schubert (2006) was not previously considered in comparisons even though it was cited. The aim of this paper is to highlight the performance of the original methods of Hadi (1992, 1994) and also the methods of Riani et al (2009) which are all based on the forward search, albeit in different ways, along with ATLA. Other algorithms are briefly considered such as the Blocked Adaptive Computationally Efficient Outlier Nominators method (BACON) (Billor et al , 2000) but only on an intermittent/ad-hoc basis.

Measures of performance indicated by earlier authors vary. This combined with the wide variety of classification techniques made under various assumptions can make comparisons difficult. The importance of this paper is to show empirically at least that there is no universally superior method in outlier detection and subsequent multivariate estimation. There is no single all-encompassing measure or statistic for the performance of an outlier method for any given situation or simulation. For example, a single univariate observation that is known to be outlying may not explicitly imply that of a multivariate outlier with the addition of new variate(s) and the opposite may apply for a single multivariate outlier not necessarily implying that of a univariate one when considering one of its components. Therefore it is important that one defines what constitutes an outlier in the context of the above methods and, in-turn derive and outline a motivation for such methods. Briefly summarizing, an outlier in this context, constitutes an observation that lies at a sufficient distance away from the [centroid of the] majority of the data. By using the word majority it is acknowledged that the methods rely on an initial robust calculation to derive a subset of size $h=\lfloor (n+p+1)/2\rfloor$ that is assumed to be outlier free, in order to maximize what is termed the finite sample breakdown point (see Rousseeuw (1983) and Clarke (2018)). Here n is the sample size and p is the dimension of the multivariate data in question. Furthermore, regarding the magnitude distance, this may be dependent on the underlying algorithm and its inherent methodology involving a chosen metric. Unlike the Euclidean distance which does not account for correlated variates, the scale-invariant Mahalanobis distance has been shown to be a useful measure of a multivariate observation’s outlyingness and thus has led to its continued use in outlier detection, cluster analysis and classification techniques (Mahalanobis 1936; Wilks 1963). However, it is common knowledge that even a single outlier is able to distort measures of multivariate location and scale which can cause an obvious disconnect between the value of Mahalanobis distance that a given observation takes on and whether or not it is outlying. Such perturbations can often result in instances of masking and swamping. See Barnett and Lewis (1994). While it may be possible to overcome these issues through consideration of all possible subsets by way of exhaustive enumeration, this would be precluded due to the combinatorial explosion for large n and p in sorting out all cases. The forward search procedure is a commonly adopted technique that aims to rectify such issues through iterative exploration of subsets by way of a computationally simple algorithm. The method partitions the observations to form what is called a basic subset. This basic subset is assumed to be outlier free and is based on an initial robust calculation. It is then iteratively redefined by inflating this subset based on Mahalanobis distances calculated with respect to this subset. Subsequently one arrives at a final classification subject to a predefined criterion.

It could be said the above should only be treated as a simplified explanation of this procedure as there exists a number of variations which employ different methodology.

In an alternative development Cabana et al (2021) and Leys et al (2018) use robust Mahalanobis distances. While these have assisted in overcoming issues of masking and swamping, they may not be entirely appropriate when used iteratively in the forward search due to computational burden. Should the data size and dimension permit it, the opportunity to utilise such developments are possible yet these will not be exercised in the context of this paper. See also Filzmoser et al (2014).

A principal motivation for this study is the focus on an adaptive procedure known as the multivariate adaptive trimmed likelihood algorithm (ATLA); described in Clarke and Schubert (2006) and Clarke (2018). This numerical routine serves as a multivariate outlier detection method based on the use of the forward search to locate a subset which minimizes a measure of the asymptotic variance of the multivariate location estimator. This method utilizes the minimum covariance determinant (MCD) (Rousseeuw , 1983) based on the Fast-MCD algorithm (Rousseeuw and Driessen , 1999) to obtain a robust initial starting subset preceding the forward search. Hubert et al (2012) proposed an improved MCD algorithm which came as a later development to the initial realization of the ATLA algorithm in Clarke and Schubert (2006). Hubert et al (2012) and Garciga and Verbrugge (2021) demonstrate the improved performance of this deterministic algorithm which serves as motivation for its inclusion in the ATLA algorithm used in this paper.

The use of sample covariance correction factors in the calculation of Mahalanobis Distances, as in Hadi (1992, 1994), for example, that are designed to achieve consistency under the multivariate normal distribution in order to combat bias, do prevent application to certain combinations of n and p. This also brings into question the possible over-reliance on an assumed distribution such as the $\chi ^2$ shown by Krazanowski (1988).

2 Simulation study

2.1 Size

In order to demonstrate the adaptive nature of the multivariate ATLA, estimates of size are given based on Monte Carlo Simulation of $N=1,000$ samples of size n and variables p generated from the multivariate distribution $\mathcal {N}_{p}(\mathbf {0}, I _{p})$. Here $\mathbf {0}$ is the $p\times 1$ mean vector of zeroes and $I _{p}$ is the assumed $p\times p$ identity covariance matrix. The size is the proportion of samples where at least one outlier is detected. There may be more than one outlier detected in any one sample for example. In addition we will also incorporate size estimates of three similar multivariate outlier detection methods that utilise the forward search in some capacity. These include the Blocked Adaptive Computationally Efficient Outlier Nominators (BACON) method by Billor et al (2000), an automatic multivariate outlier detection procedure by Riani et al (2009) (we will refer to as FSM) and the original forward search procedure (referred to here as FS) proposed by Hadi (1992, 1994). The method BACON is available in the R package robustX (Stahel and Maechler , 2019) and the method FSM is in the package fsdaR (Todorov and Sordini , 2020). The results from these simulations are presented in Table 1.

Table 1 Estimated size and total number of false positives for simulations of $N=1,000$ randomly generated samples of size n from $\mathcal {N}_{p}(\mathbf {0}, I _{p})$

For this simulation two variations of ATLA have been presented. Each pertain to different initial robust estimates based on the aforementioned MCD algorithms; FASTMCD and Deterministic MCD respectively. The FASTMCD algorithm was originally utilized in the ATLA in order to achieve a robust initial starting subset of size $h=\lfloor (n+p+1)/2 \rfloor$ out of $n_{h}=\text {log}(0.05)/\text {log}(1- {\left( {\begin{array}{c}(n+p)/2\\ p+1\end{array}}\right) } / {\left( {\begin{array}{c}n\\ p+1\end{array}}\right) } )$ possible subsets. Unlike the FASTMCD algorithm which initially considers random subsets, the proposal of Hubert et al (2012) arrives at a subset with the smallest MCD based on six estimators computed in a deterministic way. For the simulations presented in this paper use is made of the ‘Deterministic MCD’, that is ATLA$^{b}$, algorithm due to reasons that will become known.

It is worth mentioning here that unlike the ATLA, these procedures utilize a fixed simultaneous significance level for an assumed parametric distribution which we have chosen to set at $\alpha =0.01$. The BACON algorithm also requires the user to define the initial subset size, m. As per recommendation in the literature we have chosen to use the default of $m=4\cdot p$ for these simulations. It is noted that while BACON and FS cannot be used when $n=25$ and $p=10$, see footnotes c and d, this does not preclude use of ATLA and FSM. Here ATLA$^b$ has a smaller average size of $1\%$ while FSM has a size of $10.6\%$. Also note the decrease in average size between ATLA$^{a}$ and ATLA$^b$ for these particular parameters.

The adaptive nature of the ATLA method in this analysis demonstrates that if the data are multivariate normal the method soon with sample size of $n\ge 100$ shows almost no unnecessary rejection of outliers under the assumed model.

While other methods than ATLA use a nominal fixed size $\alpha$ with $\alpha =0.01$ recommended, the maximum average size for ATLA$^b$ is $1.9\%$ in Table 1 and often is much lower. Yet the ATLA$^b$ technique works powerfully to identify outliers in the tabulations below. This is so much so that it is thought not to be a disadvantage to not be able to set the size specifically.

2.2 Average power and performance measures

In order to assess and compare the performance of ATLA in situations involving contaminated data we will be generating $N=1,000$ samples of size n for which $n-k$ observations are generated from $\mathcal {N}_{p}(\mathbf {0}, I _{p})$ and k observations from the mean shifted distribution $\mathcal {N}_{p}(4\cdot \mathbf {J}, I _{p})$ representing the contaminated distribution. Here $\mathbf {J}$ is a $p\times 1$ vector of ones. The parameter k will be chosen in accordance with varying levels of contamination $\epsilon =k/n$ up to a maximum of say, $\epsilon =0.4$. The following measures of performance are considered:

• Average power $=$ For each sample one calculates the proportion of the k planted outliers that are identified as such and then takes the average over all samples of all such proportions.

• $p_1 =$ Proportion with which exactly the k outlying observations are identified as outliers.

• $p_2 =$ Proportion with which at least one planted outlier is identified.

• $p_3 =$ Proportion with which there is false identification.

• $p_4 =$ Proportion with which at least all the k outliers are trimmed.

• $p_5 =$ Proportion with which observations are identified.

The results from these simulations are presented in Tables 2 and 3 respectively. Note for simplicity we have chosen to omit the performance measures $p_{2}, p_{4}$ and $p_{5}$, however, these are available in the Supplementary Materials.

Table 2 Performance measures of respective outlier methods through simulations of $N=1,000$ spherically symmetric data $[n\le 100]$ generated from the mean slippage model

Table 3 Performance measures of outlier detection methods through simulations of $N=1,000$ spherically symmetric data $[n>100]$ generated from the mean slippage model

In response to referees’ request we have included in Tables 2 and 3 smaller proportions of contamination $\epsilon = 0.02$ and 0.04 where possible, to illustrate what can happen with just one or a few outliers for $n=25,\; 50$ or 100 as this may be typical in practice.

In those instances that have resulted in a violation in the breakdown point for the respective algorithm, data have been omitted. Due to such restrictions, values for $n=25$, $p=10$ and $\epsilon =0.4$ have been omitted. It is as a result of achieving inconsistent results and in order to ensure brevity that we have chosen not to include BACON in this comparison . One can argue that for the parameters used in this investigation this would not be a fair comparison due to BACON’s comparatively low breakdown point. It can also be noted that BACON may be preferred in the case of very large data sets including those of higher dimension because of its computational efficiency.

In terms of the average power it appears that ATLA consistently achieves the highest probability out of the four tested methods with FSM equalling or falling closely behind in most circumstances. It is only in some simulations where the average power of FSM exceeds that of ATLA albeit only by a slight margin. In particular, simulations involving lower contamination ($\epsilon =0.04$) FSM achieves a higher average power. Unlike the average power, the results for $p_1$ are not as clearly defined, with all four methods demonstrating differing optimal situations. In some instances of particularly high contamination FSM and also FS perform extremely poorly. This can be explained since the default breakdown point of FSM, for example, is chosen to be 0.4, whereas the nominal percent of contamination is set at $\epsilon =0.4$. This may be “corrected” by resetting the default breakdown point for large amounts of contamination to 0.5 in FSM, whereupon a better result for FSM ensues, for example the “Average power” $n=50,\;p=10,\;\epsilon =0.4,\;k=20$ is 0.964, which compares with the reported value of Table 2 of 0.028. However, it is the default value of 0.4 that is given in the use of the algorithm, and one is not to know in the case of $p=10$ dimensions whether or not there will be large amounts of contamination in order to adjust the FSM algorithm. ATLA does not have this problem.

On the other hand ATLA remains stable in this event, given that ATLA is the multivariate extension of its univariate estimation algorithm developed in Clarke (1994) which was shown to have breakdown point of near one half.

One will also note that ATLA has a propensity to over-trim for larger n and small p through false identification demonstrated in $p_3$; a trait which is consistent with the influence of swamping.

2.2.1 Correlated data

The previous section dealt with spherically symmetric ($\Sigma = I _{p}$) multivariate distributions generated out of the mean slippage model. While algorithms presented here are based on affine equivariant statistics which are accounted for by linear transformations, it is interesting to examine empirical performance under a correlated error structure. Briefly here we consider examples where both distributions are correlated and this is done for $p=2$.

For each distribution we have chosen to use a simple first order autoregressive covariance structure to generate bivariate ($p=2$) samples with correlation coefficient $\rho =0.5$ and 0.9 respectively. That is,

$$\begin{aligned} \Sigma = \begin{bmatrix} 1 &{} \rho \\ \rho &{} 1 \end{bmatrix}, \quad \rho =0.5, 0.9. \end{aligned}$$

(1)

Due to the proximity of the distributions for $\rho =0.9$, as seen in Fig. 1b), we have chosen to let the contaminating distribution have shifted mean $5\cdot \mathbf {J}$. Simulations have been limited to bivariate samples for illustration purposes. Results from these simulations are presented in Tables 4 and 5 respectively.

Ostensibly, comparing performances with previous simulations one is able to gauge an apparent decrease in performance across all methods. Although this may not be an indication of their inadequacy but rather a by-product of the selected simulation framework. As the proximity of the two distributions grow closer for increasing $\rho$, the distinction between which distribution a particular observation comes from, becomes difficult (See Fig. 1). Again, the supplementary performance measures can be found in the Supplementary Materials. In terms of the average power, in the majority of cases ATLA performs better in comparison to other methods. A similar but inherently different approach based on regression can be found in Riani et al (2014).

Table 4 Performance measures of outlier detection methods through simulations of $N=1,000$ bivariate data generated through the mean slippage model with correlation $[\rho =0.5]$

Table 5 Performance measures of outlier detection methods through simulations of $N=1,000$ bivariate data generated through the mean slippage model with correlation $[\rho =0.9]$

2.3 Further discussion of supplementary performance measures

In the Supplementary Materials from the mean slippage model there are some notable advantages of ATLA in that it performs well in identifying at least one outlier, $p_2$, and at least the k planted outliers, $p_4$ in comparison to FSM and FS for such cases involving $\epsilon \ge 0.08$. The latter two methods appear to falter with large 40% proportions of contamination for sample sizes n greater than or equal 50. This is as explained in previous discussion of the breakdown point of FSM.

For the mean slippage model with correlation $\rho = 0.5$ or $\rho =0.9$, again in the Supplementary Materials show that ATLA consistently trims all k outliers, at a greater rate than FSM or FS, considering the reported values for $p_4$.

Values for $p_2$ and $p_5$ are included for completeness.

2.4 Relative efficiency of outlier trimmed location estimates

Another way we might assess the performance of an outlier detection algorithm is through the relative efficiency of the outlier-trimmed location estimates.

By results of the Cramér Rao Lower Bound a measure of efficiency of a unbiased multivariate estimator say $\mathbf {T}$ is as follows,

$$\begin{aligned} \text {Eff}(\mathbf {T})= \frac{|\varvec{\mathcal {I}}\left( \varvec{\theta }\right) ^{-1}|}{|\text {Var}(\mathbf {T})|} \end{aligned}$$

(2)

Noting here that $|\text {Var}(\mathbf {T})|$ corresponds to the generalized variance which in this case is the determinant of the covariance matrix of the estimator $\mathbf {T}$, call it $|\varvec{\Sigma _T}|$. The matrix $\varvec{\mathcal {I}}\left( \varvec{\theta }\right) ^{-1}$ is the inverse of Fisher Information of the unknown parameter vector $\varvec{\theta }$. See Rao (1973) for further information on these arguments.

Hence if one were to compare the efficiencies of two multivariate location estimates, $\mathbf {T}_{2}$ relative to $\mathbf {T}_{1}$ for example, then this would involve the following calculation,

$$\begin{aligned} \text {RelEff}(\mathbf {T}_{1}, \mathbf {T}_{2}) = \frac{\text {Eff}\left( \mathbf {T}_{2}\right) }{\text {Eff}\left( \mathbf {T}_{1}\right) } = \frac{|{\varvec{\Sigma }}_{\mathbf {T}_{1}}|}{|{\varvec{\Sigma }}_{\mathbf {T}_{2}}|}, \end{aligned}$$

(3)

where $|\cdot |$ denotes the determinant of the associated covariance matrix of location estimates. For example, the efficiency of ATLA relative to FSM would show ATLA as the better estimate for relative efficiencies greater than one.

Now for simulations of data generated through the Tukey–Huber

$\epsilon$-contamination model,

$$\begin{aligned} f(\varvec{\mu },\varvec{\Sigma },\epsilon ) = (1-\epsilon )\cdot \mathcal {N}_{p}(\varvec{\mu },\varvec{\Sigma })+\epsilon \cdot \mathcal {N}_{p}(\varvec{\mu },\varvec{\Sigma }\cdot \sigma ^2) \end{aligned}$$

(4)

we choose to fix $\varvec{\mu }=\varvec{0}$, $\varvec{\Sigma }= I _{p}$ and $\sigma ^{2}=9$ for simplicity.

Here we will produce estimates of the relative efficiencies of the respective algorithms with respect to ATLA. That is we identify $\mathbf {T}_2$ in equation (3) as the ATLA estimate for location and a scaled estimate of the denominator in the second part of the equation is the determinant of the variance covariance matrix of the ATLA trimmed location estimates. For example, if we calculate the relative efficiency of FSM, then the numerator in equation (3) would be the the determinant of the variance covariance matrix of the estimates of location achieved using FSM. Note with the underlying model (4) the estimates of location are unbiased and consistent estimates of $\varvec{\mu }$. Since according to Cator et al (2012) the estimators are asymptotically normal even at the distribution (4), it follows the ratio of the generalized variances can be estimated as we have done here.

The results from simulations of $N=1,000$ for various levels of contamination $\epsilon$, sample sizes n and variables p are presented in Table 6 where covMCD and DetMCD are explained below.

Table 6 Relative Efficiencies of ATLA to the respective outlier algorithms for the trimmed multivariate location estimates through simulations of $N=1,000$ samples generated from the Tukey–Huber Model

Fig. 1

Scatterplot matrix of a simulation of bivariate data with correlation of $\rho =0.5$ [a)] and $\rho =0.9$ [b)] respectively. The ellipses here represent the $95\%$ bivariate normal density contours

In discussing efficiency we allude to two well known methods of estimating multivariate location. For these simulations we have included for comparison the R function covMcd available from the robustbase package (Maechler et al , 2019) which is a robust location estimation method that utilizes the MCD. This function contains arguments that allow use of two possible MCD proposals; the Fast MCD algorithm spawned out of Rousseeuw and Driessen (1999) as well as the “Deterministic MCD” algorithm proposed by Hubert et al (2012). In the case of FASTMCD this algorithm searches through $n_{h}$ possible subsets of size $h=\alpha \cdot n$ for some predefined $0.5\le \alpha <1$, whose covariance matrix yields the lowest determinant. Both of these procedures are known to have a particularly high breakdown point and have been included in this simulation to highlight what to expect in performance given data that consists of a high percentage of contamination. Here the name “DetMCD” is used to denote the deterministic MCD algorithm and “covMCD” is used to denote the initial Fast MCD algorithm. The relative efficiencies of these algorithms are compared to ATLA where just the Det MCD is employed in both cases for the initial start of the forward search algorithm.

In consideration of the two MCD methods there is an apparent lack of efficiency of the high breakdown point estimators of location, ATLA performing remarkably well in simulations with lower proportions of contamination. One will also notice the Deterministic MCD algorithm consistently produces a higher efficiency in comparison with the FASTMCD; one of the motivating factors for its substitution in ATLA. It is only in a few such cases where covMCD is the more efficient estimator but mostly by a small margin. ATLA beats FS generally for $n\ge 50$ and is not as efficient for $n=25$. There are mixed results for relative efficiencies of FSM and ATLA. There is no clear winner. ATLA appears to be better in cases when the dimension, p, is higher.

3 Cluster monitoring and detection

Due to the ability to detect outliers, the use-case of the forward search has shown that it can be further extended into the area of cluster analysis. It has been explored in a number of circumstances including Atkinson and Riani (2004), and Cerioli et al (2019).

However most notably graphical techniques can be employed to aid in monitoring successive iterations of the forward search in an attempt to divulge the structure of the data and assist in possible outlier or cluster identification. This includes forward-plots to enable monitoring of the subset inflations by displaying the minimum Mahalanobis distance among units in the non-basic subset. Examples of this for parametric cases are in Atkinson et al (2003), Atkinson and Riani (2004), Atkinson et al (2018) and Riani et al (2009).

Utilizing multiple minima for a chosen objective function is not necessarily a new finding. Examples are given in say Rocke and Woodruff (1999). It is intuitively reasonable to justify that the majority of works in a solution to classification/clustering problems are simply those of optimization; with techniques such as k-means, Gaussian mixture models, Mean-shift or perhaps support-vector machines that utilize this in some capacity. In the case of ATLA, the employed objective function, which is optimally chosen based on the sample size, is evaluated based on the occurrence (or lack there-of) of minima. That is, observations are deemed as outlying based on the minimum of any minima occuring for an $\alpha >0$ corresponding to the proportion of trimming. Otherwise if no such minima exist then the data set may be considered outlier free. Here we argue the benefit of incorporating plots of the objective function to assist in divulging the structure of the data, which may be clustered (based on occurrence of multiple minima), and by monitoring the search.

3.1 Objective functions of ATLA

Now one of the by-products of not utilizing a particular stopping criteria, as in ATLA, is that the entire search must be conducted. While this results in a slight increase in computational cost, it on the other hand opens the possibility for graphical monitoring and also mitigates the possibility for erroneous miss-classifications that may be a result of type II error; an inevitable characteristic for large samples. For instance, algorithms BACON, and FS when including a good observation, leave no path for that observation to leave once included. The FSM procedure which is contained within the FSDA Toolbox for MATLAB also contains similar routines which allow for the entire search to be conducted and thus monitored.

Moreover the procedure utilized in ATLA allows observations to leave the basic subset which enables spurious subset inflations to be “corrected” in subsequent iterations. This also minimizes over-reliance on the initial robust location/scale estimate facilitating the path of dividing the basic subset and the non basic subset. It can be remarked here that an observation may leave the basic subset at any point in the FSM algorithm.

Through existence of multiple minima (for an $\alpha >0$) in the objective function, one is able to discern the possible existence of multiple contaminating distributions/clusters. It is possible to demonstrate this with a simulation of clustered data composed of a total of five clustered samples with $n=500$ generated as follows:

• Cluster 1: $\mathcal {N}_{3}(\mathbf {0}, I _{3})$ of size $n_{1}=275$ representing the majority population.

• Cluster 2: $\mathcal {N}_{3}(\mathbf {1}\cdot \sqrt{\chi ^{2}_{0.975,3}}, 0.1\cdot I _{3})$ of size $n_{2}=50$.

• Cluster 3: $\mathcal {N}_{3}([0,0,-2.5\cdot \sqrt{\chi ^{2}_{0.975,3}}], I _{3})$ of size $n_{3}=75$.

• Cluster 4: $\mathcal {N}_{3}([0,0,5\cdot \sqrt{\chi ^{2}_{0.975,3}}], I _{3})$ of size $n_{4}=75$.

• Cluster 5: $\mathcal {N}_{3}([0,4\cdot \sqrt{\chi ^{2}_{0.975,3}},1.5\cdot \sqrt{\chi ^{2}_{0.975,3}}],\varvec{\Sigma })$ of size $n_{5}=25$ where $\varvec{\Sigma }=\text {diag}(1,0.1,0.1)$.

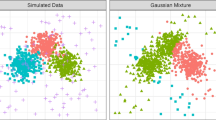
Figure 2 shows the pairwise scatterplot matrix for simulated data generated from these distributions. As one can gauge from such plots, Cluster 2 with points shown as yellow $\triangle$-symbols are representative of what is referred to as a point mass cluster while points in Cluster 5 shown as purple $\boxtimes$-symbols follow a line mass cluster.

Fig. 2

Scatterplot matrix of simulated data containing 5 sample clusters generated out of different distributions with point coloring and symbols to highlight the cluster whence it belongs to

Fig. 3

Objective Functions of ATLA based on $N=100$ simulated datasets generated from the clustered distributions highlighted above. The darker shaded line corresponds to the dataset shown in Fig. 2 with labels to demonstrate the occurrence of minima at basic subsets containing the exact associated cluster(s)

Now performing the multivariate ATLA procedure on this simulated data it is possible to plot the objective function over successive basic subsets. Looking at Fig. 3 one is able to discern the existence of five minima at relative basic subset sizes of 275, 325, 400, 475 and 500 respectively. The latter four minima correspond to subsets classifications that contain the exact cumulative cluster distributions whence they were originally generated from.

By allowing the original ATLA procedure to iteratively classify and trim each of the subsets based on the objective function criterion (Fig. 4) than this results in a similar final cluster classification. Doing so also ensures the optimal objective function proposal is used for a given application upholding the adaptive nature of the algorithm. Although this methodology would not be recommended for large data sets due to computational expense, it does present the procedure and motivation behind the optimization criteria for the objective function proposals.

In addition to the classification of these clusters, either through multiple application trimmings or minima subset comparisons, one is able to identify intra-cluster outliers. This can be observed in the simulated data shown in Fig. 5 which presents four identified intra-cluster outliers and the exact classification of clusters whence they originally belong to.

Here it is important to emphasize that the T1 and T2 proposals of Clarke and Schubert (2006) assume samples are taken from populations which follow a multivariate normal distribution, hence departures from such distribution will not guarantee results. It can be noted that this is an ad-hoc feature of the algorithm and not the sole intended purpose. Due to its construction of finding an initial subset of size $h=\lfloor (n+p+1)/2\rfloor$, successful cluster discrimination may only be possible for clusters which are smaller than this value. Nevertheless, relaxation of these restrictions are elementary yet come at the cost of increased probability of breakdown. Further research will benefit in the context of clustering and use of the forward search. Perhaps utilization of soft-trimming through weights in the ATLA procedure may prove useful for better cluster discrimination and monitoring.

Fig. 4

Objective functions for successive applications of ATLA based on a continuation of the trimming of $N=100$ simulated datasets as shown in Fig. 3. The solid lines denote the approximate minima which yields the final outlier classification/trimming (if any). Note the positioning of the vertical lines are consistent with cluster locations shown previously with each application imposing trimmings of size approximately 50, 75, 75 and 25 respectively

Fig. 5

Scatterplot matrix of a simulated dataset with point coloring to denote the cluster designation obtained through multiple applications of ATLA. Four points shown as $\boxtimes$, $\times$, $\triangledown$ and $\oplus$-respectively, correspond to outliers found when performing ATLA on trimming subsets discovered after each application

4 Conclusion

The comparison and discussion of outliers here is limited to the case of the multivariate normal distribution. We do not entertain here the multivariate t-distribution, for example, which was also adequately explained in Clarke and Schubert (2006). Outliers are usually modelled at the multivariate normal distribution because of the central limit theorem. Further improvements in the ATLA algorithm were implemented based on developments in multivariate estimation in particular MCD and subsequently demonstrated in simulation results. We have explained the power of the three methods that use the forward search and there are varying terms of performance, with no outright winner. ATLA has a good all-round performance, vindicating its introduction in Clarke and Schubert (2006). To illustrate further the ATLA approach we apply it to clustering, albeit in an elementary dataset simulated out of predefined cluster distributions.