Multivariate Outlier Detection in Applied Data Analysis: Global, Local, Compositional and Cellwise Outliers

Abstract

Outliers are encountered in all practical situations of data analysis, regardless of the discipline of application. However, the term outlier is not uniformly defined across all these fields since the differentiation between regular and irregular behaviour is naturally embedded in the subject area under consideration. Generalized approaches for outlier identification have to be modified to allow the diligent search for potential outliers. Therefore, an overview of different techniques for multivariate outlier detection is presented within the scope of selected kinds of data frequently found in the field of geosciences. In particular, three common types of data in geological studies are explored: spatial, compositional and flat data. All of these formats motivate new outlier concepts, such as local outlyingness, where the spatial information of the data is used to define a neighbourhood structure. Another type are compositional data, which nicely illustrate the fact that some kinds of data require not only adaptations to standard outlier approaches, but also transformations of the data itself before conducting the outlier search. Finally, the very recently developed concept of cellwise outlyingness, typically used for high-dimensional data, allows one to identify atypical cells in a data matrix. In practice, the different data formats can be mixed, and it is demonstrated in various examples how to proceed in such situations.

1 Introduction

In practice, it is not uncommon that the underlying assumptions of classical statistical methods are not met, as these approaches only reflect a rough approximation of reality. This can have far-reaching effects on classical estimation methods and yield questionable results. That is why robust statistics aims at the detection of outliers and the development of robust estimation procedures. In this context, an outlier refers to an experimentally found observation that differs considerably from the underlying data structure, and does not match the hypothetical distribution describing the remaining set of regular data points. However, these irregular observations do not have to be erroneous artefacts able to adversely affect the subsequent statistical procedures, but can convey valuable information regarding the data behaviour. Nevertheless, it is necessary to identify these particular irregularities before conducting subsequent data analysis. In the univariate domain, these observations are typically associated with extreme values; this may be different in the multivariate case, where outliers are not necessarily extreme in one dimension but deviate in several dimensions from the main data structure. In this case, outlier identification becomes more challenging.

It is important to note that in statistics, outliers always refer to an underlying model. For instance, in linear regression analysis, a linear relationship between the response and the predictor variables is assumed, and there are also quite strict model assumptions for the error term (homogeneity, independence, normal distribution). In robust statistics these strict model assumptions may be violated, and outliers refer to observations which cause such deviations (Maronna et al. 2006).

Reliable outlier detection can only be done based on robust statistical estimators which are not affected by those outliers. For example, it is well known that the least-squares estimator in linear regression is sensitive to outlying observations. Diagnostics based on scaled residuals could thus be misleading, because the parameter estimates could already be biased. Also, an iterative procedure which removes one outlier at a time based on residual diagnostics, and re-estimates the regression parameters, can be misleading. The reason is the so-called swamping and masking effect: Swamping can be observed when a regular data point is falsely classified as an outlier, because the chosen measure of outlyingness is affected by the contamination. Masking also refers to a wrong judgment due to contamination, but here the outliers would not be identified, because they appear as regular observations. Hence, methods quantifying the degree of outlyingness of an observation have to be robust against a considerable fraction of outliers themselves.

Even if the practitioner is not employing a statistical model, it may be of interest if the data at hand have inconsistencies in terms of outliers. Those outliers could in fact be the most interesting observations, because they refer to atypical phenomena, and thus they should be flagged. Also in this case, a statistical outlier detection procedure usually uses a model. Most often it is assumed that the data are generated from a multivariate normal distribution, with a certain centre and covariance. Multivariate outliers deviate from this model.

In general, statistical theory of multivariate outlier detection is based either on univariate projection of the multivariate data or on the estimation of the empirical covariance structure to obtain distance estimates of outlyingness (Filzmoser and Hron 2008). The intuitive idea behind the former methodology is to project the concept of a multivariate outlier into the one-dimensional space as exemplified by Peña and Prieto (2001) and Maronna and Zamar (2002). In the latter approach, the underlying covariance structure of the data is used to define an outlyingness distance measure that can unambiguously assign to each multidimensional data point a distance to the centre of the bulk of the data. More formally, consider a p-dimensional data matrix $\mathbf {X} \in \mathbb {R}^{(nxp)}$ with n observations denoted by $\mathbf {x}_{i}=(x_{i1},\ldots ,x_{ip})$, for $i=1,\ldots ,n$. A standard approach for quantifying the outlyingness of an observation $\mathbf {x}_i$ in the multivariate domain is the Mahalanobis distance

$$\begin{aligned} \text{ MD }_i := \text{ MD }(\mathbf {x}_i,\mathbf {m},\mathbf {C})=\sqrt{(\mathbf {x}_i-\mathbf {m})' \mathbf {C}^{-1}(\mathbf {x}_i-\mathbf {m})} , \end{aligned}$$

(1)

where $\mathbf {m}=\mathbf {m}(\mathbf {x}_1,\ldots ,\mathbf {x}_n)$ and $\mathbf {C}=\mathbf {C}(\mathbf {x}_1,\ldots ,\mathbf {x}_n)$ represent estimators of multivariate location and covariance, respectively (Mahalanobis 1936). In the simplest case, the estimates $\mathbf {m}$ and $\mathbf {C}$ are given by the arithmetic mean and the empirical covariance matrix, which, however, can adversely affect the MD measure due to their inherent sensitivity in the case of outlying behaviour. Alternatively, the Mahalanobis distance can be modified to add robustness by exchanging the classical measures of multivariate location and scatter with more robust estimates such as the minimum covariance determinant (MCD). The MCD estimators are given by the centre and scatter of the subset of those h points (with $\frac{n}{2} \le h \le n$) which yield the smallest determinant of the empirical covariance matrix (Rousseeuw and Driessen 1999). For data coming from a multivariate normal distribution, the classical squared Mahalanobis distance approximately follows a chi-square distribution with p degrees of freedom ($\chi ^2_p$) (Maronna et al. 2006). Since large values of the (squared) Mahalanobis distance tend to correspond to outlying observations, either a quantile of the chi-square distribution (e.g., $\chi ^2_{p;0.975}$) can be defined as a lower cut-off limit for classifying data points as outliers, or an adaptive approach for finding an appropriate cut-off value can be considered, taking into account the dimensionality and sample size of the data (Filzmoser et al. 2005).

A key strength of the robust MCD estimator is the property of affine equivariance, so that the multivariate location $\mathbf {m}$ and scatter $\mathbf {C}$ estimators fulfill

$$\begin{aligned}&\mathbf {m}(\mathbf {Ax}_1+\mathbf {b},\ldots ,\mathbf {Ax}_n+\mathbf {b})= \mathbf {Am}(\mathbf {x}_1,\ldots ,\mathbf {x}_n)+\mathbf {b}, \end{aligned}$$

(2)

$$\begin{aligned}&\mathbf {C}(\mathbf {Ax}_1+\mathbf {b},\ldots ,\mathbf {Ax}_n+\mathbf {b})=\mathbf {AC}(\mathbf {x}_1,\ldots ,\mathbf {x}_n)\mathbf {A}' , \end{aligned}$$

(3)

for any non-singular matrix $\mathbf {A} \in \mathbb {R}^{(pxp)}$ and for any vector $\mathbf {b} \in \mathbb {R}^p$. As a result of this property, the robust Mahalanobis distance remains unaffected under affine transformations,

$$\begin{aligned} \text{ MD }(\mathbf {Ax}_i+\mathbf {b})=\text{ MD }(\mathbf {x}_i)\quad \text {for} ~i=1,\ldots ,n, \end{aligned}$$

(4)

and the detection of outlying observations does not rely on the choice of $\mathbf {A}$ and $\mathbf {b}$ (Filzmoser and Hron 2008). Therefore, the potential outliers will remain identical, no matter which matrix $\mathbf {A}$ and vector $\mathbf {b}$ are chosen for the transformation used.

While at first sight outlier detection by means of the presented methods gives the impression of being universally applicable, it is important to emphasize that the term outlyingness must always be seen in relation to the field of application. Further, each discipline of application collects distinctive data types that are characterized by individual traits relevant to its subject area. Thus, specific needs usually arise depending on the type of data, such as spatial, compositional or flat data (more variables than observations). For instance, the robust Mahalanobis distance as presented above is restricted to the detection of “global” outliers; these are observations deviating from the data majority. However, in the case of spatial data with defined geographical coordinates, the identification and handling of local outliers, which are points that significantly deviate from their spatially defined neighbourhood, has to be considered in the preliminary stages of data analysis as well. Compositional data—characterized by contributions on a whole—are often given in relative form such as proportions and percentages, and they require particular preprocessing before classical detection techniques can properly identify data anomalies. In this context, the property of affine equivariance of the MCD estimator allows for an appropriate representation of the information in an unconstrained Euclidean space in order to apply outlier diagnostic tools. A rather new approach to outlier detection is presented in cellwise outlier detection, since row-wise elimination of outliers can be detrimental in data consisting of large sets of variables and a relatively small number of observations. Nevertheless, one should keep in mind that outlier detection is not a fully automatic procedure which follows certain predefined steps. Rather, subject matter knowledge should be considered, but the statistical needs and questions to be answered for the problem at hand are essential as well.

In the following, a variety of multivariate outlier detection approaches will be demonstrated in selected kinds of data that originate from real-world studies in the discipline of geosciences. Our aim is to illustrate how these types of data can be analysed using existing outlier detection methodology with software already available in standard statistical packages (e.g., R package mvoutlier). As the literature on applied outlier detection is so extensive, a comprehensive description of all the methodologies is not feasible. Instead, a number of methods and areas of application have been selected based on the availability of software, with the intention to give the applied practitioner a broad overview and an understanding of specific needs in applied multivariate outlier detection. The paper is organized as follows. Section 2 will focus on data whose observations are associated with spatial positions. It will be shown how the robust Mahalanobis distance estimator can be extended to identify both global and local outliers in spatial data. The notion of compositional data and its requirements prior to conducting data analysis are presented in Sect. 3. In Sect. 4, the recently proposed independent contamination framework is introduced to motivate the concept of cellwise outlier detection. Further, a graphical outlier diagnostic tool on the basis of logratios is presented to visualize the estimated cellwise outlyingness information. Finally, Sect. 5 is devoted to a brief synopsis of the concepts introduced.

2 Local Versus Global Outlyingness

Spatial data consist of empirical (multivariate) attribute values associated with geographical coordinates. While global outliers are data points that are located away from the bulk of the data in the multivariate space, local outliers differ in their non-spatial attributes from observations within a locally restricted neighbourhood (Filzmoser et al. 2014). Thus, in order to properly introduce the concept of a spatial outlier, it requires a precise definition of a spatial neighbourhood. One common option is to define the local neighbourhood, $\mathscr {N}_i$, in the spatial domain through a maximum distance $d_{\max }$ around an observation $\mathbf {x}_i$, for $i \in \{1,\ldots ,n\}$, representing the ith row of the $(n\times p)$ data matrix $\mathbf {X}$. Data points $\mathbf {x}_j \in \mathscr {N}_i$ for $j \in \{1,\ldots ,i-1,i+1,\ldots ,n\}$ are then considered neighbours of $\mathbf {x}_i$ with $d_{i,j} < d_{\max }$, where $d_{i,j}$ denotes the distance between $\mathbf {x}_i$ and $\mathbf {x}_j$. However, following this approach, issues may arise at the border area, as they are rather sparsely populated by neighbouring data points and the size of the neighbourhood population can vary widely. Alternatively, it may be of interest to consider a fixed number k of neighbours which can be achieved by the k-nearest neighbours (kNN) approach. The pairwise distances between $\mathbf {x}_i$ and all remaining $\mathbf {x}_j$ are sorted as $d_{i,(1)} \le d_{i,(2)}\le \cdots \le d_{i,(n-1)}$, and the local neighbourhood of $\mathbf {x}_i$ is then formally defined as $\mathscr {N}_i=\{\mathbf {x}_j \in \mathbf {X}: d_{i,(j)} \le d_{i,(k)}\}$. The data points associated with the k smallest distances will then form the restricted neighbourhood, see Filzmoser et al. (2014) for more detailed explanations.

The concepts of global and local outlyingness are not mutually exclusive. On the contrary, techniques of outlier detection should be able to adequately identify and differentiate between global outliers, local outliers, deviating points that exhibit both, and of course regular observations. In the past, there has been a great amount of research devoted to issues in local outlier detection, see, for example, Haslett et al. (1991), Breunig et al. (2000), Chawla and Sun (2006), or Schubert et al. (2014). However, further research is still needed in the context of multivariate outlier detection dealing with spatial dependence. One approach by Filzmoser et al. (2014) considers the so-called degree of isolation of an observation $\mathbf {x}_i$ from a pre-specified proportion $(1-\beta )$ of its neighbourhood $\mathscr {N}_i$,

$$\begin{aligned} \chi ^2_{p;\alpha (i)}\left( \text{ MD }^2(\mathbf {x}_i)\right) = \text{ MD }^2\left( \mathbf {x}_i,\mathbf {x}_{(\lceil n(i)\beta \rceil )}\right) \quad \text {for}~ i=1,\ldots ,n , \end{aligned}$$

(5)

where the measure $\alpha (i)$ is indicative of the local outlyingness of $\mathbf {x}_i$. The fraction $\lceil n(i)\beta \rceil$ expresses the number of similar data points $\mathbf {x}_j$ within $\mathscr {N}_i$. The remainder must be sufficiently different. The strictness of the methodology can be regulated by the adaptive control of the local neighbourhood size and the fraction of neighbours an observation should be similar to in regard to its multivariate, non-spatial characteristics (Filzmoser et al. 2014).

An adaptation of Filzmoser et al. (2014) was presented by Ernst and Haesbroeck (2017) through the inclusion of the local neighbourhood structure for the computation of the covariance matrix and the restriction of the local outlier search to observations within a homogeneous neighbourhood. According to Chawla and Sun (2006), unstable areas are characterized by strong heterogeneous behaviour of the observations, which is why outlier detection within these regions is meaningless. The measure of local outlyingness is obtained through the definition of the following: (1) a local neighbourhood restricted through a homogeneity condition of the multivariate non-spatial attributes, (2) locally estimated covariance matrices using the regularized MCD estimator and lastly, (3) an outlyingness distance within the neighbourhood obtained by pairwise robust Mahalanobis distances in the non-spatial space using the local covariance matrices. The modified version of Filzmoser et al. (2014) is called the regularized spatial detection technique by the authors Ernst and Haesbroeck (2017).

Note that, even though the approach introduced by Filzmoser et al. (2014) enables the search for homogeneous neighbourhoods by setting the fraction parameter $0.5 \le \beta \le 1$, the local outlier search is not restricted to data points with sufficiently concentrated non-spatial characteristics. In the following example, the local outlier technique of Filzmoser et al. (2014) will be demonstrated. For a thorough comparison of the approach by Filzmoser et al. (2014) and the regularized spatial detection technique, see Ernst and Haesbroeck (2017).

2.1 Example 1

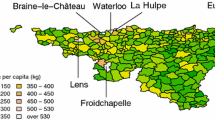
The first example makes use of the GEMAS data set, originating from the GEMAS project, a large-scale geochemical mapping project carried out in most of the European countries (Reimann et al. 2012). Here, the focus is on just two measurements, the mean temperature and the annual precipitation at the sample locations. Figure 1(right) shows the scatter plot of the data. There are many observations which clearly deviate from the majority, and those would refer to global multivariate outliers. In order to identify local outliers, the neighbourhood size is fixed to $k=10$ next neighbours. Moreover, $\beta =0.1$ and the 10 most extreme local outliers are computed according to the measure of Eq. (5). These observations are indicated with blue circles in Fig. 1, and the left plot also shows the 10 corresponding neighbours. These observations are not necessarily extreme in the data cloud. For example, there are local outliers in the north of Spain, where it is known that the humidity and temperature have a strong local variability. It is also not surprising that these measurements might differ greatly on the island of Crete when compared with locations at the neighbouring Greek islands, which are in fact quite distant.

Fig. 1

Local outlier detection for two variables of the GEMAS data set. Left: 10 most extreme local outliers, together with their 10 nearest neighbours; right: scatter plot of the two variables, with 10 most extreme local outliers indicated

3 Outlier Detection in Compositional Data

Compositional data are observations which consist of multivariate attributes where the interest is on analysing relative contributions of some whole, see, for example, Aitchison (1982) or Filzmoser et al. (2018). Thus, the relevant information of compositional data is contained in the ratios of the variables rather than in the variables themselves. This has implications for outlier detection procedures, which need to be adapted to this type of data. For instance, in the field of geochemistry, the statistical analysis of the mineral composition of geological samples or the chemical composition of rock may be of interest, and information about the presence of outliers could be important to the practitioner.

Although compositional data are repeatedly characterized exclusively by a constant sum constraint, the data distinguish themselves from simply constrained data by two additional requirements. On the one hand, the information given in the variables must not be dependent on the unit scale (scale invariance), and on the other hand, results of subcompositions should be consistent with the results obtained from the full composition (subcompositional coherence). Further, compositional data do not comply with Euclidean geometry, but induce their own geometry commonly referred to as the Aitchison geometry on the simplex. In this space, the variables can only obtain values ranging from 0 up to a fixed constant $\kappa$ (e.g., in the case of percentages $\kappa =100$). Another shortcoming of the relative nature of the variables is its biased covariance structure given the fact that the raw values of a composition are dependent on each other (Pawlowsky-Glahn and Buccianti 2011). Indeed, the increase in one variable of a single observation may yield a decrease in another variable. On the whole, the closed form and natural interdependencies within compositional data prevent the proper application of standard statistical techniques for data analysis, see Filzmoser and Hron (2008) or Filzmoser et al. (2009).

To tackle these shortcomings, the family of logratio transformations of the data from the simplex to the real space was introduced in order to express the compositional data points in orthonormal coordinates (Hron et al. 2010). Each composition $\mathbf {x}$ represents a random vector consisting of strictly positive components in the D-part simplex space

$$\begin{aligned} S^D = \left\{ \mathbf {x}=(x_1,\ldots ,x_D) \in \mathbb {R}^D: x_i>0, i=1,\ldots ,D, \sum _{i=1}^{D} x_i= \kappa \right\} , \end{aligned}$$

(6)

where again $\kappa$ denotes a fixed constant. A component of a composition is called a part, which must fulfill the condition of not being zero, since naturally only the ratios between the parts are informative in compositional data analysis. At this juncture, it has to be noted that appropriate approaches exist in the case of zero parts ($x_i=0$ for $i \in \{1,\ldots ,D\}$ in Eq. (6) caused, for example, by measurements below a certain detection limit or missing information, see Martín-Fernández et al. (2003), Pawlowsky-Glahn and Buccianti (2011), Templ et al. (2017) and in the high-dimensional case Templ et al. (2016), but this issue will not be considered in this article.

The logratio transformation approach allows the preprocessing of the original data by mapping them from the constrained simplex space, $S^D$, into the Euclidean real space $\mathbb {R}^{D-1}$. It is then possible to adapt standard statistical procedures for data analysis to the transformed data and obtain well-founded results. The main family members of logratio transformations highlighted in the literature are the additive logratio (alr), the centred logratio (clr) and the isometric logratio (ilr) transformation. They are all bijections, but only the last two are isometric. Both the alr and the clr transformation were introduced by Aitchison (1982) but later replaced by the ilr transformation proposed by Egozcue et al. (2003). The alr is not distance-preserving, and although the clr is isometric, it yields a singular covariance structure. The ilr-transformed data form an orthonormal basis in the ($D-1$)-dimensional hyperplane spanned by clr coefficients. More formally, the ilr transformation is an isometric and bijective mapping, $\hbox {ilr}: S^D \rightarrow \mathbb {R}^{D-1}$. One particular proposal of the chosen basis is

$$\begin{aligned} \mathbf {z}= \hbox {ilr}(\mathbf {x}) = (z_1,\ldots ,z_{D-1}) , \end{aligned}$$

(7)

with

$$\begin{aligned} z_j=\sqrt{\frac{D-j}{D-j+1}}\ln \frac{x_{j}}{\root D-j \of {\prod _{k=j+1}^D x_k}} \quad \text {for}~ j=1,\ldots ,D-1 , \end{aligned}$$

(8)

(Fišerová and Hron 2011). From this definition it follows that the non-collinear data point $\mathbf {z}$ is now the representation of $\mathbf {x} \in S^D$ in the $(D-1)$-dimensional hyperplane. The suggested ilr coordinates are referred to as pivot (logratio) coordinates, since one part of the composition is set as the pivot (in this case $x_1$). In applications, the pivot is not chosen at random, since only the pivot can be interpreted straightforwardly in terms of its relative dominance compared with all other parts of the composition. The corresponding coordinate, here $z_1$, expresses all relative information about part $x_1$ in the composition, since $x_1$ is not involved in any of the other coordinates (Filzmoser et al. 2018). This is particularly useful for the interpretation, because $z_1$ can now be explained in terms of $x_1$.

Robust methods of outlier detection in compositional data analysis can work with the data expressed in (ilr) coordinates, but applying them to the raw compositions directly would lead to misleading results. As mentioned in Sect. 1, quantitative assessment of outlyingness either depends on univariate projections or makes use of the empirical covariance structure. In the latter approach, the clr transformation leading to covariance singularity as mentioned before cannot be considered for the means of outlier detection. However, the suggested ilr coordinates do not yield data singularity, which is why the robust Mahalanobis distance can be applied. The affine equivariant MCD estimator ensures the invariance of the identified irregularities from the choice of transformation used (Filzmoser and Hron 2008). Note that in the case of violations of the transformed data from elliptical symmetry, again adequate data transformations such as the Box–Cox transformation can be performed when using the Mahalanobis distance measure for outlyingness (Barceló et al. 1996).

3.1 Example 2

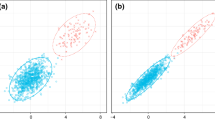
Consider geochemical concentration data from the O-horizon of the Kola project (Reimann et al. 1998), a geochemical mapping project carried out on the Kola Peninsula. For illustration purposes, a composition consisting of the elements As, Cd, Co, Cu, Mg, Pb and Zn is selected. The composition is expressed in pivot coordinates, see Eq. (8), and Mahalanobis distances based on the MCD estimator are computed. These are shown in the left plot of Fig. 2 together with the outlier threshold (horizontal line). The right plot shows the observations with specific symbols in the map of the Kola region. Large $+$ refers to a multivariate outlier, while a large circle refers to “inliers”, which are data points in the data centre. Red colour means that the average element concentration is high, and blue colour is for low average concentration. For more detailed explanations see Filzmoser et al. (2005). One can see two locations with several multivariate outliers with high concentrations: the area around Nikel (in the north, close to the Barents Sea), and that around Monchegorsk (in the east), where large smelters are located.

Fig. 2

Multivariate outlier detection of a composition of the Kola O-horizon data. Left: Mahalanobis distances with outlier threshold; right: outlyingness information in the map of the sampling area

Figure 3 uses the same symbols as in Fig. 2(right). The single plots show univariate scatter plots of the first pivot coordinates, when the corresponding part is moved to the first position in Eqs. (7) and (8). Thus, they present all relative information of these variables in the considered composition. For instance, it can be seen that multivariate outlyingness is caused mainly by dominance of Co and Cu.

Fig. 3

Interpretation of the multivariate outliers shown in Fig. 2 by pivot coordinates

3.2 Example 3

A further geochemical data set considered here is the Baltic Soil Survey (BSS) data set (Reimann et al. 2000). The topsoil measurements are used, and the composition of the oxides SiO$_2$, TiO$_2$, Al$_2$O$_3$, Fe$_2$O$_3$, MnO, MgO, CaO, Na$_2$O, K$_2$O and P$_2$O$_5$. For this 10-part composition, local multivariate outlier detection is carried out. A first step is to express the data in ilr coordinates, see Eq. (8), and then the method of Filzmoser et al. (2014) is applied. Figure 4(left) shows the local (left part) and global (right part) outliers, sorted according to their outlyingness value. The 20 most extreme local outliers are selected in this plot, together with their 10 nearest neighbours, and this information is shown in the map in the right plot. In this plot, two observations are marked by blue circles. Now the spatial coordinates for these compositions are exchanged, and the local outlier detection procedure is applied again. The resulting 20 most extreme local outliers are shown in Fig. 5. The two marked observations now appear as local outliers. Note that it is not unusual that samples are exchanged by improper sample handling.

Fig. 4

Local outlier detection for the BSS data. Left: sorted local and global outliers with neighbours, and 20 most extreme local outliers selected; right: those outliers are shown in the map with their 10 nearest neighbours

Fig. 5

Local outlier detection for the modified BSS data

4 Cellwise Outlier Detection for High-Dimensional Data

In the past, traditional robust procedures have assumed the entire observation to be erroneous or irregular in the case of a single faulty variable entry. However, row-wise downweighting or omission of observations associated with outlying behaviour can further impair the existing information and thus should be avoided. This is particularly relevant in the context of flat data consisting of a large set of variables and a relatively low number of observations. Therefore, the focus of robust statistics has increasingly shifted in recent years to the identification of cellwise outliers in high-dimensional data. The cellwise paradigm was demonstrated by Alqallaf et al. (2009) through the introduction of a new contamination framework called the independent contamination model (ICM). This includes independently contaminated cells that can cause conventional robust methods to fail. Given a data matrix $\mathbf {X} \in \mathbb {R}^{(nxp)}$ with sample size n, a set of variables of size p, and the probability $\varepsilon$ of a single cell being contaminated, the probability $\varepsilon ^*$ of an observation being contaminated is then given by

$$\begin{aligned} \varepsilon ^* = 1 - (1-\varepsilon )^p . \end{aligned}$$

(9)

It follows that $\varepsilon ^*$ can quickly exceed the breakdown point of 50% with increasing $\varepsilon$ and fixed p, but also with small $\varepsilon$ and increasing p. Consequently, rather small proportions of independent single-cell contamination, in combination with high dimensionality, can lead to the failure of row-wise robust and affine equivariant estimators, which generally require at least half of the observations to be uncontaminated. Furthermore, single-cell contamination does not necessarily have to be simply indicated by irregular entries of the affected cells, but may also be characterized by an unusual relationship between the contaminated variable and its correlated ones (Rousseeuw and Bossche 2018).

Of course, both types of outliers can be present in application. As a result, identification of cellwise outlyingness requires modern approaches to multivariate outlier detection that are able to handle both cellwise and casewise (row-wise) outliers. Recent approaches to cellwise outlier detection are based on the adapted Stahel–Donoho estimator (Van Aelst 2016), the generalized S-estimator (Agostinelli et al. 2015), cellwise prediction models (Rousseeuw and Bossche 2018), and the pairwise logratios of the variables (Walach et al. 2019). Here, the focus is on the cellwise outlier detection techniques presented in Rousseeuw and Bossche (2018) and Walach et al. (2019).

Note also that tools for cellwise outlier detection have been developed in the case of zeros in compositional data (Beisteine 2016).

The approach introduced by Rousseeuw and Bossche (2018) is based on the prediction of each cell and the subsequent comparison with the actual entries. However, the technique is currently limited to numeric values, binary and nominal variables are sorted out in the preprocessing step. Since correlated variables serve as predictors, the presented method depends on the size of the set of variables and the existence of correlated information which might not be the case for every single variable. Sparse data sets might pose a problem as well. An alternative cellwise-outlier detection algorithm called cell-rPLR is presented by Walach et al. (2019). Information regarding the cellwise outlyingness of an observation is obtained through the robustly centred and scaled logratio of pairs of its variables and the use of a weight function called the outlyingness function. Once again, consider the data matrix $\mathbf {X} \in \mathbb {R}^{(nxp)}$ with sample size n and observations defined by $\mathbf {x}_{i}=(x_{i1},\ldots ,x_{ip})$, but this time each observation is associated with one of G groups of samples arranged together in blocks which are denoted by $\mathbf {X}^{(g)}$, with $g = \{1,\ldots ,G\}$ and are of size $n_g$, with $n=n_1+\cdots +n_g$ such that $\mathbf {X}=(\mathbf {X}^{(1)},\ldots , \mathbf {X}^{(G)})'$. An element of the submatrix $\mathbf {X}^{(g)}$ will be denoted by $x_{ij}^{(g)}$ with $i = \{1,\ldots ,n_g\}$ and $j = \{1,\ldots ,p\}$.

The logratios of two variables $j,k \in \{1,\ldots ,p\}$ can then be obtained through

$$\begin{aligned} y_{ijk} := \ln \left( \frac{x_{ij}^{(g)}}{x_{ik}^{(g)}}\right) . \end{aligned}$$

(10)

It follows that a total of $p^2$ logratios is obtained for each observation i with p variables, where $y_{ijk} = 0$ if $j = k$ and $y_{ijk} = -y_{ijk}$. Subsequently, the outlyingness values $w^*_{ijk}$ are obtained through a weight function $\omega ^*(\tilde{y}_{ijk})$ which is applied to the $p^2$ (robustly) standardized logratios $\tilde{y}_{ijk}$. To obtain outlyingness values for each cell respectively, the $w^*_{ijk}$ are accumulated robustly through

$$\begin{aligned} w_{ij}=\text {median}\left( w^*_{ij1}, w^*_{ij2},\ldots , w^*_{ijd}\right) \quad \text {for}~i,j=1,\ldots ,p. \end{aligned}$$

(11)

The aggregation over the j indices would only lead to a reversed sign but would not affect the outlyingness value of the cell, due to the property that $\omega ^*(u)=-\omega ^*(-u)$ and $y_{ijk} = -y_{ijk}$. In the case of a monotone outlyingness function, the standardized logratios can be aggregated first before applying the outlyingness function.

The algorithm for cell-rPLR is mainly a graphical outlier diagnostic tool that can (depending on the choice of the weight function) indicate the outlyingness of an observation on the basis of two approaches: labelling and scoring. The labelling technique allows for a binary classification into regular observations and potential outliers. Scoring approaches are closer to the natural idea that robust methods of outlier detection should only indicate suspicion by means of an outlyingness spectrum but leave it up to the user to make the final decision. Therefore, the outlyingness information is visualized in cell-rPLR using different colours and colour intensities if the scoring approach to outlier detection is chosen. For the labelling approach, observations associated with an outlyingness value close to zero represent regular data points, whereas a value close to the limits of the specified weight function can indicate a potential outlier. Note that the visualized colour scheme and outlier approach depends mainly on the chosen outlyingness function. In the simulation study described in Walach et al. (2019), the DDC method and cell-rPLR were compared, and it was found that cell-rPLR had superior performance in terms of accuracy and misclassification of regular observations. However, it must be mentioned that DDC does not make use of grouping information, while cell-rPLR does.

4.1 Example 4

The same composition from the Kola data as in Example 2 is used. The interest here is in a more detailed interpretation of the element contributions to outlyingness of the region around Monchegorsk when compared with the background. For this reason, samples on an east–west transect through Monchegorsk are selected, see Fig. 6(left). This is of course not a high-dimensional data problem, but cellwise outlier detection can still be informative and useful.

The right plot of Fig. 6 shows the values of the centred logratio coefficients of Cu (they are proportional to the pivot coordinate for Cu) along the transect, together with a smoothed line. It can be seen that in the area of Monchegorsk (distance zero), Cu is very dominant in the composition, and these values reach the background at a distance of about 100 km. The cellwise outlier procedure of Walach et al. (2019) is applied, and the result is shown in Fig. 7. The outlyingness values are scaled in $[-1,1]$, with the colour coding shown in the plot. Almost all elements show extreme logratios in the area around Monchegorsk—the ratios with As, Co and Cu are very high, those with Mg, Pb, Zn are exceptionally low. One can also see that for Cu and Co, a much bigger area around Monchegorsk is affected, compared with the other elements.

Fig. 6

Kola data set; left: selected samples (dark blue) on an east–west transect through Monchegorsk (large pink symbol); right: values of the centred logratio coefficients of Cu along the transect, with smoothed line

Fig. 7

Cellwise outlier detection for the selected Kola data along the transect through Monchegorsk

4.2 Example 5

The Gjøvik data set, considered here for cellwise outlier detection, consists of mineral soil samples sampled along a linear transect in Norway (Flem et al. 2018). In total, 40 samples are available, taken from 15 different sample media. Here, just two media are used and compared: cowberry leaves (CLE) and cowberry twigs (COW). In total, 20 chemical element concentrations are considered, see Fig. 8. The purpose of this study was the identification of new mineral deposits. There are known mineral deposits (Mo and Pb), which are indicated on the horizontal axis (distance in this linear transect) in Fig. 8. This plot uses the same colour coding as in Fig. 7, and it shows the cellwise outlyingness information. Exceptionally high logratios with Mo and Pb are visible exactly at the known mineralizations in both sampling media. At a distance of about 23 km, several elements show unusual logratios with high values for Ni. This could be an interesting location for exploration.

Fig. 8

Cellwise outlier detection for the Gjøvik data set

5 Conclusions

The purpose of this paper was to illustrate the individual particularities of different kinds of data in the context of multivariate outlier detection in the area of geosciences. Depending on the application case and the question raised, amendments of the traditional outlier techniques to these particular needs are required.

The diversity of both the data sets and the outlier detection methods described has demonstrated that multivariate outlier detection is much more than just a preprocessing step for data cleaning. Multivariate outliers can indicate whether single observations differ substantially from most other observations (global outliers) or from most of the neighbouring observations (local outliers). They can reveal whether a whole connected region is “special”, and can inform as to the size of this area. Using specific coordinate presentations, it may be determined how the outliers differ from the regular observations. Cellwise outlier detection can be used to identify mineralization, or to monitor how the variable information changes locally in an area.

The methods presented are aimed solely at identifying potential outliers—data points that deviate from the majority of the data cloud. These flagged outliers may often be the most interesting observations for the interpretation, and usually they are not erroneous measurements, but simply inconsistent due to some underlying phenomenon. If such measurements are indeed incorrectly recorded, they should in the worst case be removed, or if possible, corrected. Subject matter knowledge is helpful for this step in order to determine the reasonability of irregularity. If they are kept as they are, it is recommended that robust statistical techniques be applied for subsequent analysis, since such methods automatically downweight outlying observations (according to the statistical model) due to their degree of outlyingness.

The outlier detection methods employed here were based on the assumption that the data majority is originating from a multivariate normal distribution—after they have been expressed in coordinates in the case of compositional data. Moreover, these methods require data on a continuous scale, and they would not work for categorical or binary variables. There are outlier detection methods which also cope with deviations from normality and mixed data types, mainly originating from the field of computer science. For an overview, see for example Zimek and Filzmoser (2018).

In the era of “big data”, there is an increased need for procedures which are helpful for inspecting the quality and consistency of the data. As the volume of data continues to grow, there is greater potential for outliers, and thus a greater need for outlier identification to ensure the validity of the findings. More data also implies that new outlier detection routines need to be investigated and assessed for their ability to handle large amounts of information. Such methods should be able to identify structural breaks in the data, and they should be applicable to (automatically) selected data subsets. In other words, there are many future challenges for adapting and developing outlier detection methods.

Finally, a brief (possibly subjective) overview is provided of R packages (R Development Core Team 2019) which include functionality for robust statistical estimation and outlier detection (Table 1).

Table 1 Overview of R packages including tools for robustness and outlier detection