Abstract
The main contribution of Davies and Hoy (Am Econ Rev 85:980–986, 1995) was a “necessary and sufficient” condition for comparing inequality between income distributions according to the principle of transfer sensitivity (PTS). Chiu (Soc Choice Welf 28:375–399, 2007) showed that although the condition is sufficient, it is not necessary. In this paper, we provide the correct necessary and sufficient condition, and demonstrate with a simple example how the corrected condition allows for more pairs of distributions to be ranked by PTS. The correction clarifies the connection between Lorenz curve comparisons and inequality rankings when the curves intersect.
Similar content being viewed by others
Notes
In the favourable composite transfer defined by Shorrocks and Foster (1987), the progressive transfer occurs in a lower range of incomes than does the regressive transfer, although the two transfers may occur over intersecting income ranges. See Davies and Hoy (1995) for a discussion of the normative appeal of placing greater emphasis on inequality that occurs for relatively lower incomes within the distribution.
In the literature, Proposition 2 of Davies and Hoy (1995) is usually cited as an equivalence between PTS and the comparison of variances for appropriately truncated subpopulations of a pair of income distributions. See, for example, Davies and Shorrocks (2000) and Cowell (2011) for citations in monographs, and Aaberge (2009), Gajdos and Weymark (2012) and Ibragimov et al. (2018) for citations in other publications.
This is clear upon comparing his Lemma 2 and Footnote 11 with our Proposition 1 here.
Theorem 5.2.3 in Athreya and Lahiri (2006, p.155) states integration by parts under mild conditions. Since cumulative distribution functions are always nondecreasing right-continuous and the quadratic function in our derivations never has any point of discontinuity, it follows as a corollary of Theorem 5.2.3 that in our situation, integration by parts is workable for general distributions including discontinuities.
It can be shown that \(z_i^*\) is also the unique zero root of S(y) on \([G^{-1}(P_i),F^{-1}(P_i)]\). Indeed, applying integration by parts to (2) yields \(P_iG^{-1}(P_i)+\int _{(G^{-1}(P_i),z_i^*]}G(y)dy=P_iF^{-1}(P_i)-\int _{(z_i^*,F^{-1}(P_i)]}F(y)dy\), and to \(\int _{[\underline{y},G^{-1}(P_i)]}ydG(y)=\int _{[\underline{y},F^{-1}(P_i)]}ydF(y)\) yields \(\int _{[\underline{y},G^{-1}(P_i)]}G(y)dy-P_iG^{-1}(P_i)=\int _{[\underline{y},F^{-1}(P_i)]}F(y)dy-P_iF^{-1}(P_i)\). Summing up the two equations results in \(S(z_i^*)=0\).
References
Aaberge R (2009) Ranking intersecting Lorenz curves. Soc Choice Welf 33:235–259
Athreya KB, Lahiri SN (2006) Measure theory and probability theory. Springer Texts in Statistics, 1st edn. Springer, New York, NY. https://doi.org/10.1007/978-0-387-35434-7
Atkinson AB (1970) On the measurement of inequality. J Econ Theory 2:244–263
Atkinson AB (2008) More on the measurement of inequality. J Econ Inequal 6:277–283
Blackorby C, Donaldson D (1978) Measures of relative equality and their meaning in terms of social welfare. J Econ Theory 18:59–80
Chiu WH (2007) Intersecting Lorenz curves, the degree of downside inequality aversion, and tax reforms. Soc Choice Welf 28:375–399
Cowell F (2011) Measuring inequality. Oxford University Press, Oxford
Davies J, Hoy M (1995) Making inequality comparisons when Lorenz curves intersect. Am Econ Rev 85:980–986
Davies J, Shorrocks AF (2000) The distribution of wealth. In: Atkinson A, Bourguignon F (eds) Handbook of income distribution, vol 1. North-Holland, Amsterdam
Gajdos T, Weymark JA (2012) Introduction to inequality and risk. J Econ Theory 147:1313–1330
Ibragimov M, Ibragimov R, Kattuman P, Ma J (2018) Income inequality and price elasticity of market demand: the case of crossing Lorenz curves. Econ Theor 65:729–750
Menezes C, Geiss C, Tressler J (1980) Increasing downside risk. Am Econ Rev 70:921–932
Shorrocks AF, Foster JE (1987) Transfer sensitive inequality measures. Rev Econ Stud 54:485–497
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Michael Hoy acknowledges financial support from Social Sciences and Humanities Research Council (SSHRC) (Grant 430407). Lin Zhao acknowledges financial support from the National Natural Science Foundation of China (Grant 71871212)
Appendix: Proof of the Claim
Appendix: Proof of the Claim
Decompose the population into \((n+1)\) disjoint subpopulations defined by \((P_{i-1},P_i]\). Denote the cumulative distribution function of income for the ith subpopulation under F by \(F_i\). Mathematically, \(F_i(y)\) equals 0 for \(y<F^{-1}(P_{i-1})\), equals \([F(y)-P_{i-1}]/[P_i-P_{i-1}]\) for \(y\in [F^{-1}(P_{i-1}),F^{-1}(P_i)]\), and equals 1 for \(y>F^{-1}(P_i)\). Then, \(F(y)=\sum _{i=1}^{n+1}(P_i-P_{i-1})F_i(y)\). Similarly, we define \(G_i\) and have \(G(y)=\sum _{i=1}^{n+1}(P_i-P_{i-1})G_i(y)\). Let \(L(F;P)=\int _{\underline{y}}^{F^{-1}(P)}ydF(y)/E(F)\) denote the Lorenz curve coordinate corresponding to the lowest 100P percent of income recipients. Similar notation applies to G. Under \(E(F)=E(G)\), we have: \(E(F_i)=E(G_i)\) for all \(i=1,\ldots ,n+1\); \(L(F_i;P)\ge L(G_i;P)\) for all \(P\in [0,1]\) for i odd; and \(L(F_i;P)\le L(G_i;P)\) for all \(P\in [0,1]\) for i even. The change from \(G_i\) to \(F_i\) consists of a series of MPCs if i is odd, and a series of MPSs if i is even.
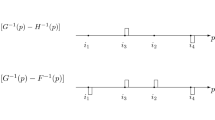
Let \(S_i(y)=\int _{\underline{y}}^y[G_i(x)-F_i(x)]dx\). Due to \(dL(F;P)/dP=F^{-1}(P)/E(F)\) and \(dL(G;P)/dP=G^{-1}(P)/E(G)\), we have \(F^{-1}(P_i)\le G^{-1}(P_i)\) for i odd and \(G^{-1}(P_i)\le F^{-1}(P_i)\) for i even. Thus, \(S_i(y)\ge 0\) on \([G^{-1}(P_{i-1}),G^{-1}(P_i)]\) for i odd, and \(S_i(y)\le 0\) on \([F^{-1}(P_{i-1}),F^{-1}(P_i)]\) for i even. Figure 1 provides a graphical illustration of \(S_i(y)\) for \(n=3\). Observing \(S(y)=\int _{\underline{y}}^y[G(x)-F(x)]dx=\sum _{i=1}^{n+1}(P_i-P_{i-1})S_i(y)\), we have \(S(y)=(P_i-P_{i-1})S_i(y)\ge 0\) on \([F^{-1}(P_{i-1}),F^{-1}(P_i)]\) for i odd and \(S(y)\le 0\) on \([G^{-1}(P_{i-1}),G^{-1}(P_i)]\) for i even. Thus, to check (3) for all \(z\in [\underline{y},\overline{y}]\), we only need to check it on \([G^{-1}(P_i),F^{-1}(P_i)]\) with i even. \(\square \)
Rights and permissions
About this article
Cite this article
Davies, J., Hoy, M. & Zhao, L. Revisiting comparisons of income inequality when Lorenz curves intersect. Soc Choice Welf 58, 101–109 (2022). https://doi.org/10.1007/s00355-021-01343-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-021-01343-w