The political economy of (De)centralization with complementary public goods

Abstract

This paper provides a political economy analysis of (de)centralization when local public goods—with spillovers effects—can be substitutes or complements. Depending on the degree of complementarity between local public goods, median voters strategically delegate policy to either ‘conservative’ or to ‘liberal’ representatives under decentralized decision-making. In the first case, it accentuates the free-rider problem in public good provision, while it mitigates it in the second case. Under centralized decision-making, the process of strategic delegation results in either too low or too much public spending, with the outcome crucially depending on the sharing of the costs of local public spending relative to the size of the spillover effects. Hence, with a common financing rule, centralization is welfare improving if and only if both public good externalities and the degree of complementarity between local public goods are both relatively large.

Appendix

1.1 Proof of Lemma 1

The first derivative of $v_{j}\left( \mathbf {e}\right)$ given by (3) with respect to $e_{j}$ is given by

$$\begin{aligned} \dfrac{\partial v_{j}\left( \mathbf {e}\right) }{\partial e_{j}}=\theta _{j}F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \dfrac{\partial G_{j}\left( \mathbf {e}\right) }{\partial e_{j}}-1. \end{aligned}$$

(19)

From (1), we have that $\partial G_{j}\left( \mathbf {e}\right) /\partial e_{j}=\left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma }e_{j}^{-\sigma }$, and hence

$$\begin{aligned} \dfrac{\partial v_{j}\left( \mathbf {e}\right) }{\partial e_{j}}=\theta _{j}F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma }e_{j}^{-\sigma }-1. \end{aligned}$$

(20)

Now, calculating the derivative of (20) with respect to $e_{-j}$, we have

$$\begin{aligned} \dfrac{\partial ^{2}v_{j}\left( \mathbf {e}\right) }{\partial e_{j}\partial e_{-j}}= & {} \theta _{j}e_{j}^{-\sigma }\left\{ F^{\prime \prime }\left( G_{j}\left( \mathbf {e}\right) \right) \dfrac{\partial G_{j}\left( \mathbf {e} \right) }{\partial e_{-j}}\left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma }\right. \nonumber \\&\left. +\sigma F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma -1}\dfrac{\partial G_{j}\left( \mathbf {e}\right) }{\partial e_{-j}}\right\} , \end{aligned}$$

(21)

which can be rewritten as

$$\begin{aligned} \dfrac{\partial ^{2}v_{j}\left( \mathbf {e}\right) }{\partial e_{j}\partial e_{-j}}=\theta _{j}e_{j}^{-\sigma }\dfrac{\partial G_{j}\left( \mathbf {e} \right) }{\partial e_{-j}}\left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma -1}\left\{ F^{\prime \prime }\left( G_{j}\left( \mathbf {e}\right) \right) G_{j}\left( \mathbf {e}\right) +\sigma F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \right\} .\nonumber \\ \end{aligned}$$

(22)

Now, let $\mu \equiv -[F^{^{\prime \prime }}\left( G_{j}\left( \mathbf {e} \right) \right) .G_{j}\left( \mathbf {e}\right) ]/F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right)$ be the elasticity of the marginal utility for public good consumption and factorizing by $F^{\prime }\left( G_{j}\right)$, we obtain

$$\begin{aligned} \dfrac{\partial ^{2}v_{j}\left( \mathbf {e}\right) }{\partial e_{j}\partial e_{-j}}=\theta _{j}e_{j}^{-\sigma }\dfrac{\partial G_{j}\left( \mathbf {e} \right) }{\partial e_{-j}}\left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma -1}F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ \sigma -\mu \right] , \end{aligned}$$

(23)

We also have $\partial G_{j}\left( \mathbf {e}\right) /\partial e_{-j}=\beta \left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma }e_{-j}^{-\sigma }$. Hence, (23) can be rewritten as

$$\begin{aligned} \dfrac{\partial ^{2}v_{j}\left( \mathbf {e}\right) }{\partial e_{j}\partial e_{-j}}=\beta \theta _{j}e_{j}^{-\sigma }e_{-j}^{-\sigma }\left[ G_{j}\left( \mathbf {e}\right) \right] ^{2\sigma -1}F^{\prime }\left( G_{j}\left( \mathbf { e}\right) \right) \left[ \sigma -\mu \right] , \end{aligned}$$

(24)

Therefore, $\partial ^{2}v_{j}(\mathbf {e)/\partial }e_{j}\mathbf {\partial } e_{-j}$ is positive (respectively negative) and local public investments are strategic complements (respectively substitutes) for $\sigma$ larger (respectively lower) than $\mu$.

1.2 Proof of Lemma 2

(i) Existence We first show that the game of public good provision admits a pure strategy Nash equilibrium. First, each region’s representative can at most invest its private endowment, y, in the public good so that the strategy space of each representative is a compact interval, $S=[0,y]$. We now show that the maximization problem of each representative is strictly concave. Using (19), the second derivative of $v_{j}(\mathbf {e)}$ with respect to $e_{j}$ is given by

$$\begin{aligned} \dfrac{\partial ^{2}v_{j}\left( \mathbf {e}\right) }{\partial e_{j}^{2}} =\theta _{j}\left\{ F^{\prime \prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ \dfrac{\partial G_{j}\left( \mathbf {e}\right) }{\partial e_{j} }\right] ^{2}+F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \dfrac{ \partial ^{2}G_{j}\left( \mathbf {e}\right) }{\partial e_{j}^{2}}\right\} . \end{aligned}$$

(25)

The first term in $\left\{ .\right\}$ is negative since $F^{\prime \prime }\left( .\right) <0$. The sign of the second term is the same as the sign of $\partial ^{2}G_{j}\left( \mathbf {e}\right) /\partial e_{j}^{2}$ since $F^{\prime }\left( .\right) >0$. We have $\partial G_{j}\left( \mathbf {e} \right) /\partial e_{j}=\left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma }e_{j}^{-\sigma }$ and hence

$$\begin{aligned} \dfrac{\partial ^{2}G_{j}\left( \mathbf {e}\right) }{\partial e_{j}^{2}} =\sigma \left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma -1}\dfrac{ \partial G_{j}\left( \mathbf {e}\right) }{\partial e_{j}}e_{j}^{-\sigma }-\sigma \left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma }e_{j}^{-\sigma -1}. \end{aligned}$$

(26)

Again, $\partial G_{j}\left( \mathbf {e}\right) /\partial e_{j}=\left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma }e_{j}^{-\sigma }$, so that (26) can be rewritten as follows

$$\begin{aligned} \dfrac{\partial ^{2}G_{j}\left( \mathbf {e}\right) }{\partial e_{j}^{2}} =\sigma \left[ G_{j}\left( \mathbf {e}\right) \right] ^{2\sigma -1}e_{j}^{-2\sigma }\left[ 1-\left[ G_{j}\left( \mathbf {e}\right) \right] ^{1-\sigma }e_{j}^{-(1-\sigma )}\right] . \end{aligned}$$

(27)

This (second) derivative is strictly negative since $\left[ G_{j}\left( \mathbf {e}\right) \right] ^{1-\sigma }e_{j}^{-(1-\sigma )}=1+\beta (e_{-j}/e_{j})^{1-\sigma }>1$. It follows that $\partial ^{2}v_{j}\left( \mathbf {e}\right) /\partial e_{j}^{2}$ given by (25) is strictly negative. Specifically (and for future use), substituting $\partial ^{2}G_{j}\left( \mathbf {e}\right) /\partial e_{j}^{2}=-\sigma \beta \left[ G_{j}\left( \mathbf {e}\right) \right] ^{2\sigma -1}e_{j}^{-2\sigma }(e_{-j}/e_{j})^{1-\sigma }$ into (25) yields

$$\begin{aligned} \dfrac{\partial ^{2}v_{j}\left( \mathbf {e}\right) }{\partial e_{j}^{2}}= & {} \theta _{j}\left\{ F^{\prime \prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ G_{j}\left( \mathbf {e}\right) \right] ^{2\sigma }e_{j}^{-2\sigma }\right. \nonumber \\&\left. -\sigma \beta F^{\prime }\left( G_{j}\left( \mathbf {e} \right) \right) \left[ G_{j}\left( \mathbf {e}\right) \right] ^{2\sigma -1}e_{j}^{-2\sigma }(e_{-j}/e_{j})^{1-\sigma }\right\} . \end{aligned}$$

(28)

Factorizing by $F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ G_{j}\left( \mathbf {e}\right) \right] ^{2\sigma -1}e_{j}^{-2\sigma }$ and using $\mu =-[F^{^{\prime \prime }}\left( G_{j}\left( \mathbf {e}\right) \right) .G_{j}\left( \mathbf {e}\right) ]/F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right)$, (28) can be rewritten as

$$\begin{aligned} \dfrac{\partial ^{2}v_{j}\left( \mathbf {e}\right) }{\partial e_{j}^{2}} =-\theta _{j}F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ G_{j}\left( \mathbf {e}\right) \right] ^{2\sigma -1}e_{j}^{-2\sigma }\left[ \mu +\sigma \beta (e_{-j}/e_{j})^{1-\sigma }\right] <0.\nonumber \\ \end{aligned}$$

(29)

As a result $v_{j}\left( \mathbf {e}\right)$ is strictly concave and continuous in $e_{j}$ for $\sigma \in \left[ 0,1\right)$ or $\sigma \in (1,+\infty )$, which guarantees the existence of a pure strategy Nash equilibrium. In this equilibrium, the first-order condition given by (4) is both necessary and sufficient for characterizing the best-response function of region j’s representative.

(ii) Uniqueness We first observe that there does not exist an equilibrium in which for one region a corner solution at zero public investments is obtained while an interior solution holds for the other region for any $\sigma \in \left\{ \left[ 0,1\right) \cup (1,+\infty )\right\}$. First, for $\sigma \in \left[ 0,1\right)$, the first-order condition (4) cannot be satisfied for $e_{j}=0$ and $e_{-j}>0$ because in that case $G_{j}\left( \mathbf {e}\right) >0$ and the left-hand term of (4) approaches infinity. Second, if $\sigma \in (1,+\infty )$ and $e_{j}=0$ then, as mentioned in the text, we take the limit of (1), i.e. $G_{j}\left( \mathbf {e}\right) =0$ and $G_{-j}\left( \mathbf {e}\right) =0$. Hence, $v_{-j}\left( \mathbf {e}\right)$ is strictly decreasing in $e_{-j}$, and so $e_{j}=0$ and $e_{-j}=0$ are mutually best responses.

Next, we show that there exists a unique equilibrium with $e_{j}^{*}>0$, for $j=A,B$, when local public investments are strategic substitutes—i.e. $\sigma \in \left[ 0,\mu \right)$—and when they are strategic complements—i.e. $\sigma \in (\mu ,+\infty )$. For $\sigma \in \left[ 0,\mu \right)$, the proof proceeds by contradiction (in the spirit of Bloch and Zenginobuz 2007). Suppose that there exists two distinct equilibria $\mathbf {e\equiv }\left( e_{j},e_{-j}\right) \in \mathfrak {R}_{+}^{*2}$ and $\mathbf {e}^{\prime }\mathbf {\equiv }\left( e_{j}^{\prime },e_{-j}^{\prime }\right) \in \mathfrak {R}_{+}^{*2}$. Suppose further, without loss of generality, that $e_{j}^{\prime }<e_{j}$. We first show that this implies $G_{j}\left( \mathbf {e}^{\prime }\right) >G_{j}\left( \mathbf {e}\right)$. From the first-order condition (4), we have $\theta _{j}F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma }=e_{j}^{\sigma }$. The right-hand term (RHT) is lower with $e_{j}^{\prime }$ than with $e_{j}$, which implies that the left-hand term (LHT) must also be lower with $e_{j}^{\prime }$. The derivative of this term with respect to $G_{j}\left( \mathbf {e}\right)$ is given by $\partial \left( LHT\right) /\partial G_{j}\left( \mathbf {e}\right) =\theta _{j}F^{\prime \prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma }+\sigma \theta _{j}F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ G_{j}\left( \mathbf {e} \right) \right] ^{\sigma -1}$. This can be rewritten as $\partial \left( LHT\right) /\partial G_{j}\left( \mathbf {e}\right) =\theta _{j}\left[ G_{j}\left( \mathbf {e}\right) \right] ^{\sigma -1}F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ \sigma -\mu \right]$, which is negative for $\sigma <\mu$ (so that the LHT is decreasing in $G_{j}\left( \mathbf {e}\right)$). Hence, we must have $G_{j}\left( \mathbf {e}^{\prime }\right) >G_{j}\left( \mathbf {e}\right)$ for satisfying the first-order condition in region j when $e_{j}^{\prime }<e_{j}$. However, $G_{j}\left( \mathbf {e}^{\prime }\right) >G_{j}\left( \mathbf {e}\right)$ and $e_{j}^{\prime }<e_{j}$ necessarily imply $e_{-j}^{\prime }>e_{-j}$ and $G_{-j}\left( \mathbf {e}^{\prime }\right) >G_{-j}\left( \mathbf {e}\right)$. But for region $-j$, the RHT of the first-order condition is (also) increasing in $e_{-j}$ and the LHT is (also) decreasing $G_{-j}\left( \mathbf {e}\right)$. Therefore, one cannot have another equilibrium $\mathbf { e}^{\prime }\ne \mathbf {e}$, which satisfies the two first-order conditions. To summarize, there is a unique equilibrium which involves $e_{A}^{*}>0$ and $e_{B}^{*}>0$ for $\sigma \in \left[ 0,\mu \right)$ .

Suppose now that $\sigma \in (\mu ,+\infty )$. In an interior equilibrium, public good provision is still characterized by the first-order condition (4) with equality. This equation implicitly defines $e_{j}=\varphi \left( \theta _{j},e_{-j}\right)$. By the implicit function theorem, $\varphi (.)$ is continuous and furthermore $\partial e_{j}/\partial e_{-j}=-\left[ \partial ^{2}v_{j}\left( \mathbf {e}\right) \mathbf {/}\partial e_{j}\partial e_{-j}\right] /[\partial ^{2}v_{j}\left( \mathbf {e}\right) /\partial e_{j}^{2}]$, with $\partial ^{2}v_{j}\left( \mathbf {e}\right) /\partial e_{j}^{2}$ being strictly negative (from Lemma 2). Using (24) and (29), we have

$$\begin{aligned} \dfrac{\partial e_{j}}{\partial e_{-j}}=\dfrac{\beta \left( \sigma -\mu \right) }{\mu \left[ e_{-j}/e_{j}\right] ^{\sigma }+\sigma \beta \left[ e_{-j}/e_{j}\right] }, \end{aligned}$$

(30)

which is positive for $\sigma >\mu$ (and negative for $\sigma <\mu$). When $\sigma >\mu$, one can also observe that $\partial ^{2}e_{j}/\partial e_{-j}^{2}<0$, so that best-response functions are increasing at a decreasing rate. We also have that $\left( \partial e_{j}/\partial e_{-j}\right) _{\left| e_{-j}\rightarrow 0\right. }=+\infty$, which means that near the origin, each best-response function must be on the upper side of the $45{{}^\circ }$ line. At the other extreme, we have $\left( \partial e_{j}/\partial e_{-j}\right) _{\left| e_{-j}\rightarrow +\infty \right. }=0$, so that each best-response function must cross the $45{{}^\circ }$ line. Since its slope is always decreasing, each best-response function crosses the $45{{}^\circ }$ line only once. There is thus a unique equilibrium which involves $e_{A}^{*}>0$ and $e_{B}^{*}>0$ for $\sigma \in (\mu ,+\infty )$.

For $\sigma =\mu$—which corresponds to the analysis of Besley and Coate (2003)—there is a unique equilibrium in dominant strategies, and best-response functions are two straight lines with 0 slope.

1.3 Proof of Lemma 3

We first show that $e_{j}$ and $G_{j}\left( \mathbf {e}\right)$ are increasing in $\theta _{j}$. Equilibrium public good provision is characterized by the first-order condition (4). Again, this equation implicitly defines $e_{j}=\varphi \left( \theta _{j},e_{-j}\right)$. By the implicit function theorem, $\partial e_{j}/\partial \theta _{j}=-\left[ \partial ^{2}v_{j}\left( \mathbf {e}\right) \mathbf {/}\partial e_{j}\mathbf { \partial }\theta _{j}\right] /[\partial ^{2}v_{j}\left( \mathbf {e}\right) /\partial e_{j}^{2}]$. Using (20), we have $\partial ^{2}v_{j}\left( \mathbf { e}\right) \mathbf {/}\partial e_{j}\mathbf {\partial }\theta _{j}=F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right) \left[ G_{j}\left( \mathbf {e} \right) \right] ^{\sigma }e_{j}^{-\sigma }>0$. Again, we also have $\partial ^{2}v_{j}\left( \mathbf {e}\right) /\partial e_{j}^{2}<0$ (Lemma 2). It follows that $\partial e_{j}/\partial \theta _{j}>0$. This also implies that $\partial G_{j}\left( \mathbf {e}\right) /\partial \theta _{j}>0$ since $G_{j}\left( \mathbf {e}\right)$ is increasing in $e_{j}$.

Next suppose that $\theta ^{\prime }>\theta$ and $\theta _{j}>\theta _{j}^{^{\prime }}$. The inequality $w_{j}(\theta ,\theta _{j},\theta _{-j} \mathbf {)}\ge w_{j}(\theta ,\theta _{j}^{\prime },\theta _{-j}\mathbf {)}$ can be rewritten as $\theta \left[ F\left( G_{j}\left( \theta _{j},\theta _{-j}\right) \right) -F(G_{j}(\theta _{j}^{\prime },\theta _{-j}))\right] \ge e_{j}\left( \theta _{j},\theta _{-j}\right) -e_{j}(\theta _{j}^{\prime },\theta _{-j})$. The right-hand term and the term in $\left[ .\right]$ in the left-hand side are both strictly positive (since F(.) is also an increasing function). So, if this inequality is verified for a type $\theta$ citizen in region j, it is also obviously verified for a type $\theta ^{\prime }$ citizen with $\theta ^{\prime }>\theta$, i.e., $w_{j}(\theta ^{\prime },\theta _{j},\theta _{-j}\mathbf {)}\ge w_{j}(\theta ^{\prime },\theta _{j}^{\prime },\theta _{-j}\mathbf {)}$. Suppose now that $\theta ^{\prime }<\theta$ and $\theta _{j}<\theta _{j}^{^{\prime }}$. The inequality $w_{j}(\theta ,\theta _{j},\theta _{-j}\mathbf {)}\ge w_{j}(\theta ,\theta _{j}^{\prime },\theta _{-j}\mathbf {)}$ can be rewritten as $\theta \left[ F(G_{j}(\theta _{j}^{\prime },\theta _{-j}))-F\left( G_{j}\left( \theta _{j},\theta _{-j}\right) \right) \right] \le e_{j}(\theta _{j}^{\prime },\theta _{-j})-e_{j}(\theta _{j},\theta _{-j})$. Again, the right-hand term and the term in $\left[ .\right]$ in the left-hand side are both strictly positive. So if this inequality is verified for a type $\theta$ citizen in region j, it is also obviously verified for a type $\theta ^{\prime }$ citizen with $\theta ^{\prime }<\theta$, i.e., $w_{j}(\theta ^{\prime },\theta _{j},\theta _{-j}\mathbf {)}\ge w_{j}(\theta ^{\prime },\theta _{j}^{\prime },\theta _{-j}\mathbf {)}$.

1.4 Proof of Proposition 1

Here, we just assume the existence of a LNSPE (under the sufficient condition that $\sigma \ge \bar{\sigma }$) and characterize the properties of this equilibrium. We also show that if a symmetric LNSPE exists, then this equilibrium is unique. The proof of the existence of such an equilibrium under decentralization is given in a separate appendix. In this second appendix, we also show that, in the case of a decentralized system, there exists a SPNE for $\sigma =0$ and $\sigma \in \left[ \mu ,1\right)$. This additional appendix is available upon request.

(i) in a LNSPE, the preferred representative of region j’s median voter is given by the first-order condition (6). We first derive the expression for $\partial e_{-j}^{*}/\partial \theta _{j}$. For expositional convenience only let $j\equiv A$ and $-j\equiv B$, so that we first determine $\partial e_{-B}^{*}/\partial \theta _{A}$. Using (4), $e_{B}^{*}$ must satisfy

$$\begin{aligned} \theta _{B}F^{\prime }\left( G_{B}\left( \mathbf {e}^{*}\right) \right) \left[ G_{B}\left( \mathbf {e}^{*}\right) \right] ^{\sigma }e_{B}^{*-\sigma }-1=0. \end{aligned}$$

(31)

Differentiating this expression with respect to $\theta _{A}$ yields

$$\begin{aligned}&-\;\theta _{B}\sigma e_{B}^{*-\sigma -1}F^{\prime }\left( G_{B}\left( \mathbf {e}^{*}\right) \right) \left[ G_{B}\left( \mathbf {e}^{*}\right) \right] ^{\sigma }\dfrac{\partial e_{B}^{*}}{\partial \theta _{A}}\nonumber \\&\quad +\;\theta _{B}e_{B}^{*-\sigma }\sigma \left[ G_{B}\left( \mathbf {e}^{*}\right) \right] ^{\sigma -1}F^{\prime }\left( G_{B}\left( \mathbf {e}^{*}\right) \right) \dfrac{\partial G_{B}\left( \mathbf {e}^{*}\right) }{ \partial \theta _{A}}\nonumber \\&\quad +\;\theta _{B}e_{B}^{*-\sigma }\left[ G_{B}\left( \mathbf {e}^{*}\right) \right] ^{\sigma }F^{^{\prime \prime }}\left( G_{B}\left( \mathbf {e} ^{*}\right) \right) \dfrac{\partial G_{B}\left( \mathbf {e}^{*}\right) }{\partial \theta _{A}}=0. \end{aligned}$$

(32)

Factorizing by $\theta _{B}e_{B}^{*-\sigma -1}\left[ G_{B}\left( \mathbf { e}^{*}\right) \right] ^{\sigma -1}$, the equality (32) reduces to

$$\begin{aligned}&-\sigma F^{\prime }\left( G_{B}\left( \mathbf {e}^{*}\right) \right) \left[ G_{B}\left( \mathbf {e}^{*}\right) \right] \dfrac{\partial e_{B}^{*}}{\partial \theta _{A}}\nonumber \\&\quad +\sigma e_{B}^{*}F^{\prime }\left( G_{B}\left( \mathbf {e}^{*}\right) \right) \dfrac{\partial G_{B}\left( \mathbf {e}^{*}\right) }{ \partial \theta _{A}}\nonumber \\&\quad +e_{B}^{*}\left[ G_{B}\left( \mathbf {e}^{*}\right) \right] F^{^{\prime \prime }}\left( G_{B}\left( \mathbf {e}^{*}\right) \right) \dfrac{\partial G_{B}\left( \mathbf {e}^{*}\right) }{\partial \theta _{A}} =0 \end{aligned}$$

(33)

Now, factorizing by $F^{\prime }\left( G_{B}\left( \mathbf {e}^{*}\right) \right)$ and use $\mu =-[F^{^{\prime \prime }}\left( G_{j}\left( \mathbf {e} \right) \right) .G_{j}\left( \mathbf {e}\right) ]/F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right)$, then the equality (33) reduces to

$$\begin{aligned} -\sigma \left[ G_{B}\left( \mathbf {e}^{*}\right) \right] \dfrac{ \partial e_{B}^{*}}{\partial \theta _{A}}+\sigma e_{B}^{*}\dfrac{ \partial G_{B}\left( \mathbf {e}^{*}\right) }{\partial \theta _{A}}-\mu e_{B}^{*}\dfrac{\partial G_{B}\left( \mathbf {e}^{*}\right) }{ \partial \theta _{A}}=0. \end{aligned}$$

(34)

We also have $G_{B}\left( \mathbf {e}^{*}\right) =\left[ e_{B}^{*1-\sigma }+\beta e_{A}^{*1-\sigma }\right] ^{\frac{1}{1-\sigma }}$ and hence

$$\begin{aligned} \dfrac{\partial G_{B}\left( \mathbf {e}^{*}\right) }{\partial \theta _{A} }=\left[ G_{B}\left( \mathbf {e}^{*}\right) \right] ^{\sigma }\left( e_{B}^{*-\sigma }\dfrac{\partial e_{B}^{*}}{\partial \theta _{A}} +\beta e_{A}^{*-\sigma }\dfrac{\partial e_{A}^{*}}{\partial \theta _{A}}\right) . \end{aligned}$$

(35)

Substituting this expression into (34), we have

$$\begin{aligned} -\sigma \left[ G_{B}\left( \mathbf {e}^{*}\right) \right] \dfrac{ \partial e_{B}^{*}}{\partial \theta _{A}}+e_{B}^{*}\left[ G_{B}\left( \mathbf {e}^{*}\right) \right] ^{\sigma }\left( e_{B}^{*-\sigma }\dfrac{\partial e_{B}^{*}}{\partial \theta _{A}}+\beta e_{A}^{*-\sigma }\dfrac{\partial e_{A}^{*}}{\partial \theta _{A}} \right) \left( \sigma -\mu \right) =0.\nonumber \\ \end{aligned}$$

(36)

Factorizing by $\left[ G_{B}\left( \mathbf {e}^{*}\right) \right] ^{\sigma }$ and observing that $\left[ G_{B}\left( \mathbf {e}^{*}\right) \right] ^{1-\sigma }=\left[ e_{B}^{*1-\sigma }+\beta e_{A}^{*1-\sigma }\right]$, the equality (36) reduces to

$$\begin{aligned} -\sigma \left( e_{B}^{*1-\sigma }+\beta e_{A}^{*1-\sigma }\right) \dfrac{\partial e_{B}^{*}}{\partial \theta _{A}}+e_{B}^{*}\left( e_{B}^{*-\sigma }\dfrac{\partial e_{B}^{*}}{\partial \theta _{A}} +\beta e_{A}^{*-\sigma }\dfrac{\partial e_{A}^{*}}{\partial \theta _{A}}\right) \left( \sigma -\mu \right) =0.\nonumber \\ \end{aligned}$$

(37)

This implies

$$\begin{aligned} \dfrac{\partial e_{B}^{*}}{\partial \theta _{A}}=\left[ \dfrac{\beta \left( \sigma -\mu \right) e_{B}^{*}e_{A}^{*-\sigma }}{\mu e_{B}^{*1-\sigma }+\sigma \beta e_{A}^{*1-\sigma }}\right] \dfrac{ \partial e_{A}^{*}}{\partial \theta _{A}}. \end{aligned}$$

(38)

Now, assuming that the median voters in both regions have the same taste parameter m , this implies that $\theta _{A}=\theta _{B}=\theta$ and $e_{A}^{*}=e_{B}^{*}=e^{*}$. In a symmetric equilibrium, (38) then reduces to

$$\begin{aligned} \dfrac{\partial e_{B}^{*}}{\partial \theta _{A}}\left| _{e_{B}^{*}=e_{A}^{*}}\right. =\dfrac{\beta \left( \sigma -\mu \right) }{\mu +\sigma \beta }\dfrac{\partial e_{A}^{*}}{\partial \theta _{A}}\left| _{e_{A}^{*}=e_{B}^{*}}\right. . \end{aligned}$$

(39)

Substituting into the first-order condition (6) then yields

$$\begin{aligned} \left( \dfrac{m}{\theta }-1\right) +\dfrac{m\beta }{\theta }\dfrac{\left( \sigma -\mu \right) \beta }{\mu +\sigma \beta }=0. \end{aligned}$$

(40)

The solution of this equation is thus given by (7) in Proposition 1.

(ii) We have $\theta ^{*}\gtreqqless m$, if $\left( 1+\beta \right) \left[ \mu \left( 1-\beta \right) +\sigma \beta \right] \gtreqqless \mu +\sigma \beta$, which reduces to $\beta ^{2}(\sigma -\mu )\gtreqqless 0$ or $\sigma \gtreqqless \mu$.

1.5 Proof of Lemma 4

We show that aggregated payoff given by (12) is strictly concave, so that a unique solutions results. From Lemma 2—Equation (29)—we have that $\partial ^{2}v_{j}\left( \mathbf {e}\right) /\partial e_{j}^{2}<0$. It is then sufficient to show that $\partial ^{2}v_{-j}\left( \mathbf {e}\right) /\partial e_{j}^{2}<0$. We have

$$\begin{aligned} \dfrac{\partial v_{-j}\left( \mathbf {e}\right) }{\partial e_{j}}=\theta _{-j}F^{\prime }\left( G_{-j}\left( \mathbf {e}\right) \right) \dfrac{ \partial G_{-j}\left( \mathbf {e}\right) }{\partial e_{j}}-1. \end{aligned}$$

(41)

Now, calculating the second derivative of $v_{-j}(\mathbf {e)}$ with respect to $e_{j}$, we obtain

$$\begin{aligned} \dfrac{\partial ^{2}v_{-j}\left( \mathbf {e}\right) }{\partial e_{j}^{2}} =\theta _{-j}\left\{ F^{\prime \prime }\left( G_{-j}\left( \mathbf {e} \right) \right) \left[ \dfrac{\partial G_{-j}\left( \mathbf {e}\right) }{ \partial e_{j}}\right] ^{2}+F^{\prime }\left( G_{-j}\left( \mathbf {e}\right) \right) \dfrac{\partial ^{2}G_{-j}\left( \mathbf {e}\right) }{\partial e_{j}^{2}}\right\} .\nonumber \\ \end{aligned}$$

(42)

The first term in $\left\{ .\right\}$ is negative since $F^{\prime \prime }\left( .\right) <0$. The sign of the second term in $\left\{ .\right\}$ is the same as the sign of $\partial ^{2}G_{-j}\left( \mathbf {e}\right) /\partial e_{j}^{2}$ since $F^{\prime }\left( .\right) >0$. We have $\partial G_{-j}\left( \mathbf {e}\right) /\partial e_{j}=\beta \left[ G_{-j}\left( \mathbf {e}\right) \right] ^{\sigma }e_{j}^{-\sigma }$, and hence

$$\begin{aligned} \dfrac{\partial ^{2}G_{-j}\left( \mathbf {e}\right) }{\partial e_{j}^{2}} =\beta \left\{ \sigma \left[ G_{-j}\left( \mathbf {e}\right) \right] ^{\sigma -1}\dfrac{\partial G_{-j}\left( \mathbf {e}\right) }{\partial e_{j}} e_{j}^{-\sigma }-\sigma \left[ G_{-j}\left( \mathbf {e}\right) \right] ^{\sigma }e_{j}^{-\sigma -1}\right\} . \end{aligned}$$

(43)

Again, $\partial G_{-j}\left( \mathbf {e}\right) /\partial e_{j}=\beta \left[ G_{-j}\left( \mathbf {e}\right) \right] ^{\sigma }e_{j}^{-\sigma }$ so that (43) can be rewritten as follows

$$\begin{aligned} \dfrac{\partial ^{2}G_{-j}\left( \mathbf {e}\right) }{\partial e_{j}^{2}} =\beta \sigma \left[ G_{-j}\left( \mathbf {e}\right) \right] ^{2\sigma -1}e_{j}^{-2\sigma }\left[ \beta -\left[ G_{-j}\left( \mathbf {e}\right) \right] ^{1-\sigma }e_{j}^{-(1-\sigma )}\right] , \end{aligned}$$

(44)

which is strictly negative since $\left[ G_{-j}\left( \mathbf {e}\right) \right] ^{1-\sigma }e_{j}^{-(1-\sigma )}=\beta +(e_{-j}/e_{j})^{1-\sigma }>\beta$. It follows that $\partial ^{2}v_{-j}\left( \mathbf {e}\right) /\partial e_{j}^{2}<0$. Together with Lemma 2, we have that $v_{j}\left( \mathbf {e}\right) +v_{-j}\left( \mathbf {e}\right)$ is strictly concave in $e_{j}$. There is thus a unique solution which is given by the (necessary and sufficient) first-order condition (13).

1.6 Proof of Proposition 2

Again for this proof, we just assume the existence of a LNSPE (under the sufficient condition that $\mu \ge 0.5$) and characterize the properties of this equilibrium. The proof of existence of such an equilibrium under centralization is given in a separate appendix, which is available upon request.

In a LNSPE, the preferred representative of region j’s median voter is given by the first-order condition (14). We then need to derive the expression of $\partial \tilde{e}_{-j}/\partial \theta _{j}$. Again, for expositional convenience only, we derive the outcome of the delegation stage for region A keeping in mind that the same reasoning will apply for region B. Hence, we first characterize $\partial \tilde{e}_{B}/\partial \theta _{A}$.

Using (13), $\tilde{e}_{A}$ and $\tilde{e}_{B}$ are such that

$$\begin{aligned}&\dfrac{\theta _{A}F^{\prime }\left( G_{A}\left( {\tilde{\mathbf{e}}}\right) \right) \left[ G_{A}\left( {\tilde{\mathbf{e}}}\right) \right] ^{\sigma }+\beta \theta _{B}F^{\prime }\left( G_{B}\left( {\tilde{\mathbf{e}}}\right) \right) \left[ G_{B}\left( {\tilde{\mathbf{e}}}\right) \right] ^{\sigma }}{ \tilde{e}_{A}^{\sigma }}\nonumber \\&\quad =\dfrac{\theta _{B}F^{\prime }\left( G_{B}\left( {\tilde{\mathbf{e}}}\right) \right) \left[ G_{B}\left( {\tilde{\mathbf{e}}}\right) \right] ^{\sigma }+\beta \theta _{A}F^{\prime }\left( G_{A}\left( {\tilde{\mathbf{e}}}\right) \right) \left[ G_{A}\left( {\tilde{\mathbf{e}}}\right) \right] ^{\sigma }}{ \tilde{e}_{B}^{\sigma }}. \end{aligned}$$

(45)

We then obtain

$$\begin{aligned} \theta _{A}F^{\prime }\left( G_{A}\left( {\tilde{\mathbf{e}}}\right) \right) \left[ G_{A}\left( {\tilde{\mathbf{e}}}\right) \right] ^{\sigma }=\dfrac{ \theta _{B}F^{\prime }\left( G_{B}\left( {\tilde{\mathbf{e}}}\right) \right) \left[ G_{B}\left( {\tilde{\mathbf{e}}}\right) \right] ^{\sigma }\left( \tilde{ e}_{A}^{\sigma }-\beta \tilde{e}_{B}^{\sigma }\right) }{\left( \tilde{e} _{B}^{\sigma }-\beta \tilde{e}_{A}^{\sigma }\right) }. \end{aligned}$$

(46)

Substituting into (13)—with $j\equiv B$ and $-j\equiv A$—and simplifying, we have

$$\begin{aligned} \theta _{B}F^{\prime }\left( G_{B}\left( {\tilde{\mathbf{e}}}\right) \right) \left[ G_{B}\left( {\tilde{\mathbf{e}}}\right) \right] ^{\sigma }(1-\beta ^{2})=\tilde{e}_{B}^{\sigma }-\beta \tilde{e}_{A}^{\sigma }. \end{aligned}$$

(47)

Differentiating this expression with respect to $\theta _{A}$ yields

$$\begin{aligned}&\theta _{B}(1-\beta ^{2})\left[ \left[ G_{B}\left( {\tilde{\mathbf{e}}} \right) \right] ^{\sigma }F^{\prime \prime }\left( G_{B}\left( {\tilde{\mathbf{e}}}\right) \right) \dfrac{\partial G_{B}\left( {\tilde{\mathbf{e}}} \right) }{\partial \theta _{A}}+\sigma \left[ G_{B}\left( {\tilde{\mathbf{e}}} \right) \right] ^{\sigma -1}\dfrac{\partial G_{B}\left( {\tilde{\mathbf{e}}} \right) }{\partial \theta _{A}}F^{\prime }\left( G_{B}\left( {\tilde{\mathbf{e }}}\right) \right) \right] \nonumber \\&\quad =\sigma \tilde{e}_{B}^{\sigma -1}\dfrac{\partial \tilde{e}_{B}}{\partial \theta _{A}}-\sigma \beta \tilde{e}_{A}^{\sigma -1}\dfrac{\partial \tilde{e} _{A}}{\partial \theta _{A}}. \end{aligned}$$

(48)

We also have

$$\begin{aligned} \dfrac{\partial G_{B}\left( {\tilde{\mathbf{e}}}\right) }{\partial \theta _{A} }=\left[ G_{B}\left( {\tilde{\mathbf{e}}}\right) \right] ^{\sigma }\left( \tilde{e}_{B}^{-\sigma }\dfrac{\partial \tilde{e}_{B}}{\partial \theta _{A}} +\beta \tilde{e}_{A}^{-\sigma }\dfrac{\partial \tilde{e}_{A}}{\partial \theta _{A}}\right) . \end{aligned}$$

(49)

Substituting into (48) and factorizing by $\left[ G_{B}\left( {\tilde{\mathbf{e}}}\right) \right] ^{2\sigma -1}$, we have

$$\begin{aligned}&\theta _{B}(1-\beta ^{2})\left[ G_{B}\left( {\tilde{\mathbf{e}}}\right) \right] ^{2\sigma -1}\left[ F^{\prime \prime }\left( G_{B}\left( {\tilde{\mathbf{e}}}\right) \right) G_{B}\left( {\tilde{\mathbf{e}}}\right) +\sigma F^{\prime }\left( G_{B}\left( {\tilde{\mathbf{e}}}\right) \right) \right] \nonumber \\&\quad \left( \tilde{e}_{B}^{-\sigma }\dfrac{\partial \tilde{e}_{B}}{\partial \theta _{A}}+\beta \tilde{e}_{A}^{-\sigma }\dfrac{\partial \tilde{e}_{A}}{ \partial \theta _{A}}\right) =\sigma \tilde{e}_{B}^{\sigma -1}\dfrac{\partial \tilde{e}_{B}}{\partial \theta _{A}}-\sigma \beta \tilde{e}_{A}^{\sigma -1}\dfrac{\partial \tilde{e} _{A}}{\partial \theta _{A}}. \end{aligned}$$

(50)

Now, factorizing by $F^{\prime }\left( G_{B}\left( {\tilde{\mathbf{e}}}\right) \right)$ and using $\mu =-[F^{^{\prime \prime }}\left( G_{j}\left( \mathbf { e}\right) \right) .G_{j}\left( \mathbf {e}\right) ]/F^{\prime }\left( G_{j}\left( \mathbf {e}\right) \right)$ gives

$$\begin{aligned}&\theta _{B}(1-\beta ^{2})\left[ G_{B}\left( {\tilde{\mathbf{e}}}\right) \right] ^{2\sigma -1}F^{\prime }\left( G_{B}\left( {\tilde{\mathbf{e}}}\right) \right) \left[ \sigma -\mu \right] \left( \tilde{e}_{B}^{-\sigma }\dfrac{ \partial \tilde{e}_{B}}{\partial \theta _{A}}+\beta \tilde{e}_{A}^{-\sigma } \dfrac{\partial \tilde{e}_{A}}{\partial \theta _{A}}\right) \nonumber \\&\quad =\sigma \tilde{e}_{B}^{\sigma -1}\dfrac{\partial \tilde{e}_{B}}{\partial \theta _{A}}-\sigma \beta \tilde{e}_{A}^{\sigma -1}\dfrac{\partial \tilde{e} _{A}}{\partial \theta _{A}}. \end{aligned}$$

(51)

Now, using (47), we have

$$\begin{aligned}&\left( \tilde{e}_{B}^{\sigma }-\beta \tilde{e}_{A}^{\sigma }\right) \left[ G_{B}\left( {\tilde{\mathbf{e}}}\right) \right] ^{\sigma -1}\left[ \sigma -\mu \right] \left( \tilde{e}_{B}^{-\sigma }\dfrac{\partial \tilde{e}_{B}}{ \partial \theta _{A}}+\beta \tilde{e}_{A}^{-\sigma }\dfrac{\partial \tilde{e} _{A}}{\partial \theta _{A}}\right) \nonumber \\&\quad =\sigma \tilde{e}_{B}^{\sigma -1}\dfrac{\partial \tilde{e}_{B}}{\partial \theta _{A}}-\sigma \beta \tilde{e}_{A}^{\sigma -1}\dfrac{\partial \tilde{e} _{A}}{\partial \theta _{A}}. \end{aligned}$$

(52)

Observing that $\left[ G_{B}\left( {\tilde{\mathbf{e}}}\right) \right] ^{\sigma -1}=1/\left[ \tilde{e}_{B}^{1-\sigma }+\beta \tilde{e} _{A}^{1-\sigma }\right]$, we have

$$\begin{aligned}&\left( \tilde{e}_{B}^{\sigma }-\beta \tilde{e}_{A}^{\sigma }\right) \left( \sigma -\mu \right) \left( \tilde{e}_{B}^{-\sigma }\dfrac{\partial \tilde{e} _{B}}{\partial \theta _{A}}+\beta \tilde{e}_{A}^{-\sigma }\dfrac{\partial \tilde{e}_{A}}{\partial \theta _{A}}\right) \nonumber \\&\quad =\left( \tilde{e}_{B}^{1-\sigma }+\beta \tilde{e}_{A}^{1-\sigma }\right) \left( \sigma \tilde{e}_{B}^{\sigma -1}\dfrac{\partial \tilde{e}_{B}}{\partial \theta _{A}}-\sigma \beta \tilde{e }_{A}^{\sigma -1}\dfrac{\partial \tilde{e}_{A}}{\partial \theta _{A}}\right) . \end{aligned}$$

(53)

We then have

$$\begin{aligned} \dfrac{\partial \tilde{e}_{B}}{\partial \theta _{A}}=\left[ \dfrac{\sigma \beta \left( \tilde{e}_{B}^{1-\sigma }\tilde{e}_{A}^{\sigma -1}+\beta \right) +\beta \left( \sigma -\mu \right) \left( \tilde{e}_{B}^{\sigma } \tilde{e}_{A}^{-\sigma }-\beta \right) }{\left( \sigma -\mu \right) \left( \beta \tilde{e}_{A}^{\sigma }\tilde{e}_{B}^{-\sigma }-1\right) +\sigma \left( 1+\beta \tilde{e}_{A}^{1-\sigma }\tilde{e}_{B}^{\sigma -1}\right) } \right] \dfrac{\partial \tilde{e}_{A}}{\partial \theta _{A}}. \end{aligned}$$

(54)

As for the decentralization system, we focus on a symmetric equilibrium i.e. $m_{A}=m_{B}=m$, which implies $\theta _{A}=\theta _{B}=\theta$ and $\tilde{e}_{A}=\tilde{e}_{B}=\tilde{e}$. The above expression then reduces to

$$\begin{aligned} \dfrac{\partial \tilde{e}_{B}}{\partial \theta _{A}}\left| _{\tilde{e} _{B}=\tilde{e}_{A}}\right. =\dfrac{\beta \left[ 2\sigma -\mu \left( 1-\beta \right) \right] }{2\sigma \beta +\mu \left( 1-\beta \right) }\dfrac{\partial \tilde{e}_{A}}{\partial \theta _{A}}\left| _{\tilde{e}_{A}=\tilde{e} _{B}}\right. . \end{aligned}$$

(55)

In addition, from (13), we also have in a symmetric equilibrium $F^{\prime }\left( G\left( {\tilde{\mathbf{e}}}\right) \right) \left[ G\left( {\tilde{\mathbf{e}}}\right) \right] ^{\sigma }\tilde{e}^{-\sigma }=1/\left[ \theta \left( 1+\beta \right) \right]$. Substituting this last expression into (14) (with $m_{j}=m$) yields

$$\begin{aligned} \left( \dfrac{m}{\theta \left( 1+\beta \right) }-\dfrac{2-\lambda }{2} \right) \dfrac{\partial \tilde{e}_{A}}{\partial \theta _{A}}\left| _{ \tilde{e}_{A}=\tilde{e}_{B}}\right. +\left( \dfrac{\beta m}{\theta \left( 1+\beta \right) }-\dfrac{\lambda }{2}\right) \dfrac{\partial \tilde{e}_{B}}{ \partial \theta _{A}}\left| _{\tilde{e}_{B}=\tilde{e}_{A}}\right. =0. \end{aligned}$$

(56)

Finally, substituting (55) into (56) yields

$$\begin{aligned}&\left[ 2m-\theta \left( 1+\beta \right) \left( 2-\lambda \right) \right] \left[ 2\sigma \beta +\mu \left( 1-\beta \right) \right] \nonumber \\&\quad + \; \beta \left[ 2\beta m-\theta \left( 1+\beta \right) \lambda \right] \left[ 2\sigma -\mu \left( 1-\beta \right) \right] =0. \end{aligned}$$

(57)

The solution of this equation in $\theta$ is thus given by (15) in Proposition 2.

(ii) It is immediately verified that $\tilde{\theta }\gtreqqless m$ if $\lambda \gtreqqless \tilde{\lambda }$ with $\tilde{\lambda }\equiv 2\beta /\left( 1+\beta \right)$.

1.7 Welfare under decentralization and centralization

From (4) with $F(G)=G^{1-\mu }$, we can obtain the level of public investment in each region in the symmetric equilibrium of a decentralized system, that is $e^{*}=\left[ \theta ^{*}\left( 1-\mu \right) \left( 1+\beta \right) ^{\frac{\sigma -\mu }{1-\sigma }}\right] ^{\frac{1}{\mu }}$. Substituting (7) into this expression, we then obtain

$$\begin{aligned} e^{*}=\left[ \dfrac{\left( 1-\mu \right) \left[ \mu \left( 1-\beta \right) +\sigma \beta \right] \left( 1+\beta \right) ^{\frac{1-\mu }{ 1-\sigma }}}{\mu +\sigma \beta }m\right] ^{\frac{1}{\mu }}. \end{aligned}$$

(58)

We then obtain the following level of welfare for the median voter under a decentralized system,

$$\begin{aligned} \upsilon ^{*}=\mu \left[ \beta (1+\sigma )+\mu (1-\beta )\right] \left[ \dfrac{\left[ \left( 1-\mu \right) \left[ \mu \left( 1-\beta \right) +\sigma \beta \right] \right] ^{1-\mu }\left( 1+\beta \right) ^{\frac{1-\mu }{ 1-\sigma }}}{\mu +\sigma \beta }m\right] ^{\frac{1}{\mu }}.\nonumber \\ \end{aligned}$$

(59)

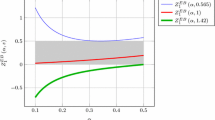
Assuming that $\mu =0.5$, we obtain (17) in the text.

Using (13) with $F(G)=G^{1-\mu }$, we obtain the level of public investment in each region in the symmetric equilibrium of a centralized system, that is $\tilde{e}=\left[ \tilde{\theta }\left( 1-\mu \right) \left( 1+\beta \right) ^{\frac{1-\mu }{1-\sigma }}\right] ^{\frac{1}{\mu }}$. Using (15), we then have

$$\begin{aligned} \tilde{e}=\left[ \dfrac{2\left( 1-\mu \right) \left[ 2\sigma \beta +\mu \left( 1-\beta \right) ^{2}\right] \left( 1+\beta \right) ^{\frac{1-\mu }{ 1-\sigma }}}{4\sigma \beta +\mu \left( 1-\beta \right) \left[ 2-\lambda (1+\beta )\right] }m\right] ^{\frac{1}{\mu }}. \end{aligned}$$

(60)

We then obtain the following level of welfare for the median voter under a centralized system.

$$\begin{aligned} \tilde{\upsilon }= & {} \mu \left[ 4\sigma \beta +2(1-\beta )\left[ \beta +\mu \left( 1-\beta \right) \right] -\lambda \left( 1-\beta ^{2}\right) \right] \nonumber \\&\quad \times \left[ \dfrac{\left[ 2\left( 1-\mu \right) \left[ 2\sigma \beta +\mu \left( 1-\beta \right) ^{2}\right] \right] ^{1-\mu }\left( 1+\beta \right) ^{\frac{ 1-\mu }{1-\sigma }}}{4\sigma \beta +\mu \left( 1-\beta \right) \left[ 2-\lambda (1+\beta )\right] }m\right] ^{\frac{1}{\mu }}. \end{aligned}$$

(61)

Assuming that $\mu =0.5$, we obtain (18) in the text.

1.8 Proof of Proposition 3

(i) When $\lambda =0$, we have under a centralized system

$$\begin{aligned} \tilde{\upsilon }_{\left| \lambda =0\right. }=\dfrac{\left[ 4\sigma \beta +(1-\beta )^{2}\right] \left[ 4\sigma \beta +(1-\beta ^{2})\right] \left( 1+\beta \right) ^{\frac{1}{1-\sigma }}}{4\left[ 4\sigma \beta +\left( 1-\beta \right) \right] ^{2}}m^{2}, \end{aligned}$$

(62)

while for $\lambda =1$, we have

$$\begin{aligned} \tilde{\upsilon }_{\left| \lambda =1\right. }=\dfrac{4\sigma \beta \left[ 4\sigma \beta +(1-\beta )^{2}\right] \left( 1+\beta \right) ^{\frac{1 }{1-\sigma }}}{\left[ 8\sigma \beta +(1-\beta )^{2}\right] ^{2}}m^{2}. \end{aligned}$$

(63)

The welfare of each region under a decentralized system is still given by (17).

Hence, when $\lambda =0$, the welfare difference between a centralized and a decentralized system is given by

$$\begin{aligned} \tilde{\upsilon }_{\left| \lambda =0\right. }-\upsilon ^{*}=\dfrac{ \sigma \beta ^{3}\left[ \sigma \beta \left( 3+2\beta -\beta ^{2}\right) +(1-\beta ^{2})\right] \left( 1+\beta \right) ^{\frac{1}{1-\sigma }}}{\left[ 4\sigma \beta +\left( 1-\beta \right) \right] ^{2}\left[ 1+2\sigma \beta \right] ^{2}}m^{2}. \end{aligned}$$

(64)

This expression is clearly positive for any $\sigma \in \left\{ \left[ 0,1\right) \cup (1,+\infty )\right\}$ and $\beta \in \left[ 0,1\right]$.

When $\lambda =1$, the welfare difference between a centralized and a decentralized system is given by

$$\begin{aligned} \tilde{\upsilon }_{\left| \lambda =1\right. }-\upsilon ^{*}=\dfrac{ \left[ 4\sigma ^{2}\beta ^{2}(1+\beta )(6\beta -\beta ^{2}-1)+4\sigma \beta (1-\beta )^{2}(3\beta -1)-(1-\beta )^{5}\right] \left( 1+\beta \right) ^{ \frac{2-\sigma }{1-\sigma }}}{4\left[ 8\sigma \beta +\left( 1-\beta \right) ^{2}\right] ^{2}\left[ 1+2\sigma \beta \right] ^{2}}m^{2}.\nonumber \\ \end{aligned}$$

(65)

The sign of $\tilde{\upsilon }_{\left| \lambda =1\right. }-\upsilon ^{*}$ is the same as the sign of

$$\begin{aligned} \Gamma \left( \sigma ,\beta \right) =4\sigma ^{2}\beta ^{2}(1+\beta )(6\beta -\beta ^{2}-1)+4\sigma \beta (1-\beta )^{2}(3\beta -1)-(1-\beta )^{5},\nonumber \\ \end{aligned}$$

(66)

which is quadratic in $\sigma$. Thus $\Gamma \left( \sigma ,\beta \right) =0$ has two solutions given by

$$\begin{aligned} \hat{\sigma }=-\dfrac{(1-\beta )^{2}}{2\beta (1+\beta )} \quad \hbox { and } \quad \tilde{\sigma } =\dfrac{(1-\beta )^{3}}{2\beta (6\beta -\beta ^{2}-1)}. \end{aligned}$$

(67)

Clearly, $\hat{\sigma }$ is negative while $\tilde{\sigma }$ is positive if only if $6\beta -\beta ^{2}-1\ge 0$ or $\beta \ge 3-2\sqrt{2}$.

Furthermore, the second derivative of $\Gamma \left( \sigma ,\beta \right)$ with respect to $\sigma$ is also positive if $\beta \ge 3-2\sqrt{2}$ and negative if $\beta \le 3-2\sqrt{2}$. Then, for $\beta \le 3-2\sqrt{2}$, $\Gamma \left( \sigma ,\beta \right)$ reaches a global maximum and furthermore $0\ge \tilde{\sigma }\ge \hat{\sigma }$, which necessarily implies that $\Gamma \left( \sigma ,\beta \right) <0$ for any $\sigma \ge 0$. When $\beta \ge 3-2\sqrt{2}$, $\Gamma \left( \sigma ,\beta \right)$ reaches a global minimum and hence $\Gamma \left( \sigma ,\beta \right)$ is positive only if $\sigma \ge \tilde{\sigma }\ge 0\ge \hat{\sigma }$.