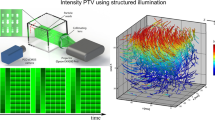
Abstract
Many problems in fluid mechanics require single-shot 3D measurements of fluid flows, but are limited by available techniques. Here, we design and build a novel flexible high-speed two-color scanning volumetric laser-induced fluorescence (H2C-SVLIF) technique. The technique is readily adaptable to a range of temporal and spatial resolutions, rendering it easily applicable to a wide spectrum of experiments. The core equipment consists of a single monochrome high-speed camera and a pair of ND: YAG lasers pulsing at different wavelengths. The use of a single camera for direct 3D imaging eliminates the need for complex volume reconstruction algorithms and easily allows for the correction of distortion defects. Motivated by the large data loads that result from high-speed imaging techniques, we develop a custom, open-source, software package, which allows for real time playback with correction of perspective defects while simultaneously overlaying arbitrary 3D data. The technique is capable of simultaneous measurement of 3D velocity fields and a secondary tracer in the flow. To showcase the flexibility and adaptability of our technique, we present a set of experiments: (1) the flow past a sphere, and (2) vortices embedded in laminar pipe flow. In the first experiment, two channel measurements are taken at a resolution of 512 × 512 × 512 with volume rates of 65.1 Hz. In the second experiment, a single-color SVLIF system is integrated on a moving stage, providing imaging at 1280 × 304 × 256 with volume rates of 34.8 Hz. Although this second experiment is only single channel, it uses identical software and much of the same hardware to demonstrate the extraction of multiple information channels from single channel volumetric images.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Progress in experimental fluid mechanics is often limited by techniques for measuring flow fields (Tropea et al. 2007). This is especially true for chaotic flows-such as turbulence—which necessitate single-shot 3D measurements (Wu et al. 2015; Ma et al. 2017). In recent decades, high-speed imaging has been made possible through the development of low light high-speed cameras, high-speed scanning mirrors and the development of mass data processing techniques (Versluis 2013). The development of the digital camera resulted in experimental two-dimensional imaging techniques such as planar laser-induced fluorescence (PLIF), particle imaging velocimetry (PIV), and particle tracking velocimetry (PTV). PLIF works by shining a laser sheet through a fluid sample that is embedded with a fluorescent tracer (Hammack et al. 2018; Zhu et al. 2019). The fluorescent signal that arises from the laser sheet exciting the tracer is then captured by a camera. PIV and PTV rely on imaging a fluid sample that is embedded with particle tracers (Bryanston-Cross and Epstein 1990; Palafox et al. 2007; Adamczyk and Rimai 1988; Brücker and Althaus 1992).
Traditionally, imaging of fluid dynamics has been restricted to planar investigations. However, fluids flows are intrinsically three-dimensional, and hence to experimentally capture the full dynamics volumetric imaging is necessary. For example, planar imaging techniques have been widely applied to study the flow dynamics of animals (Katija et al. 2015; Pepper et al. 2015; Samson et al. 2019). In one study, volumetric PIV imaging was applied to study hydrodynamics of a shark tail (Flammang et al. 2011), leading to qualitatively different results than previous work using planar PIV on the wake structures (Wilga and Lauder 2002, 2004). In this particular case a dual-ring vortex structure shed from the tails could not be fully resolved from the planar measurements alone, leading to an incorrect interpretation of the overall flow structure. Similarly, in the study of turbulence intrinsically 3D mechanisms like vortex stretching cannot be resolved from planar measurements alone (Ouellette 2012).
PIV, PTV and PLIF can be extended to three-dimensional imaging. One approach is to integrate a system of multiple cameras, or stereoscopes, to capture unique viewing angles enabling the reconstruction of volumes from the various viewing perspectives. This approach is implemented in tomographic particle image velocimetry (TPIV) (Ortiz-Dueñas et al. 2010), tomographic particle tracking velocimetry (TPTV) (Cornic et al. 2020) and tomographic laser-induced fluorescence (TLIF) (Meyer et al. 2016). An alternative is to image volumes of the fluid by sectioning slices of the sample with a laser sheet that is scanned in time (Krug et al. 2014). This approach is used in scanning volumetric laser-induced fluorescence (SVLIF); it has the benefit of simpler hardware (i.e., a single camera) and much simpler post-processing of the resulting data. Recent technological developments—e.g., imaging hardware and mass data processing techniques—now make it possible to achieve high spatial and temporal resolutions in volumetric imaging (Osborne et al. 2016; Shi et al. 2018).
Here, we present a novel high-speed two-color scanning volumetric laser-induced fluorescence (H2C-SVLIF) technique. The core equipment of the imaging system consists of a single high-speed camera and a scanning laser sheet produced by pair of pulsed ND: YAG lasers which enable two-color imaging. The system is designed such that it can be easily adaptable to a diverse array of experimental set-ups by readily tuning its temporal and spatial resolutions. Notably, our implementation includes open-source software which corrects for perspective and other distortion effects when the recorded volumes are displayed or analyzed, removing the need for telecentric lenses or other complicated optical systems. As a result, the system is incredibly versatile, able to adapt to a wide range of scales and image deep (cubic) volumes if desired. This system operates at the limit of fundamental and practical limits to volumetric imaging in terms of both speed and resolution.
Although other volumetric two-color techniques have been showcased, e.g., Halls et al. (2018) and Kashanj and Nobes (2023), these approaches have been constrained to small volume of interests (VOIs) with dimensions 14 × 14 × 24 mm3 and 5 × 5 × 50 mm3, respectively. The method presented here is not subject to these limitations; for example, in Sect. 7.1 we present volumetric imaging with dimensions of 159 × 159 × 168 mm3. We conduct measurements with data throughput of 1.7 × 1010 voxels/second, which is of order 10–104 times more data throughput than previous two-color volumetric imaging approaches.
The apparatus described here is also the first to demonstrate high-speed two-color scans for the simultaneous acquisition of LIF and PTV data. Moreover, our technique operates at video rates or faster--greater than 60 Hz-with the use of a single high-speed camera which operates at frame rates greater than 70 kHz. Our imaging demonstrates a notable advancement over existing techniques due to its enhanced imaging capabilities, flexibility and adaptability, rendering it well suited to a wide range of problems in fluids that necessitate high-speed single-shot volumetric imaging.
As a proof of concept, we conduct H2C-SVLIF measurements for a set of experiments: (1) flow past a sphere, and (2) vortices embedded in pipe flow. In the first of the experiments, we use two separate fluorescent dyes excited by a pair of pulsed lasers to simultaneously track small tracer particles and dyed volumes of fluid. In the second case we extract two separate data channels-a velocity field reconstructed from tracer particles and the high resolution dyed vortex lines-using geometric identification of these two features. The set of experiments use identical software and nearly identical hardware, demonstrating the flexibility of our technique. While the focus of this paper is primarily the imaging system itself, we also provide the demonstrated data processing and visualization techniques that are easily expedited using our own novel custom open-source software (Kleckner 2021b). This software has the ability to correct for spatial distortion defects in real time while simultaneously overlaying arbitrary 3D data (e.g., the location of tracked particle or dyed lines). Moreover, non-uniform illumination defects, present in the volumes acquired, are also corrected for in the pre-processing stage
The outline of this paper is as follows: Sect. 2 presents the basic design and experimental hardware used in our imaging system, Sect. 3 discusses the fundamental and practical limits to H2C-SVLIF, Sect. 4 addresses challenges posed by processing large data sets and how our open-source in-house viewing software is adapted to handle these data sets. In Sect. 5, we discuss the post-processing for distortion correction, calibration for the captured volumes, and correction of illumination defects. In Sect. 6, we discuss the process for the tracking of the particles and the interpolation method for the reconstruction of a Eulerian velocity field. In Sect. 7, we present results from our example systems, followed up by the conclusion in Sect. 8.
2 Imaging hardware
The H2C-SVLIF system includes a laser sheet generator, a high-speed camera (Phantom V2512), and a custom-designed synchronization board. This board-which is controlled through a visualization workstation-synchronizes the camera and laser sheet generator (Fig. 1). To image in three dimensions, the laser sheet is swept across the sample while the high-speed camera records the fluorescent emission slices of the sample. The system is designed to be highly adjustable: the scan width and height are adjustable to image systems at a variety of scales. The scanning laser sheet is generated by a mobile integrated platform, allowing the position and height of the laser sheet to be easily adjusted (Fig. 2). The laser sources for the sheet are a pair of diode-pumped lasers (Spectra Physics Explorer One XP 355-2 and One XP 532-5). The beams are first expanded to 3 mm, and then combined on a dichroic mirror and directed upward to the scanning head platform. The head has a manually adjustable height; the 3 mm width of the lasers in the vertical beam section ensures that the divergence of the beams is small enough that this does not significantly affect the beam size over the range of accessible heights. The beams are then de-expanded to the appropriate diameter for the Powell lens (1 mm), which spreads the laser into a uniform vertical sheet. (If needed, the collimation adjustment on the final beam expander can be used to adjust the focus of the final sheet.) Finally, the laser is reflected off a galvanometer mirror (Thorlabs GVS002) and directed to the sample.
A schematic of the H2C-SVLIF control system. The entire setup is synchronized using a custom-designed board controlled through a GUI in the visualization workstation. The synchronization board generates signals which are sent to the lasers triggering them on alternating frames (purple and green), the galvanometer (blue), and high-speed camera (yellow and red). Details of the laser sheet generator are given in Fig. 2
A schematic of the laser sheet generator. The laser sheet is produced via a pair of pulsed ND: YAG lasers of wavelengths 355 nm and 532 nm. The laser beams pass through a pair of beam expanders (BE). The beams then travel to a dichroic mirror (DM) which combines the beams. From there, the beams get deflected up to a scanning-head platform and pass through a beam de-expander (BD). The scanning-head platform can be manually translated to adjust to a variety of sample heights. Finally, the beams get deflected into the Powell lens (PL) and into the scanning mirror (SM). The resulting laser sheet is then swept across a sample
The high-speed camera, galvanometer, and the lasers are synchronized using the custom-designed synchronization board; schematics for this board are publicly available on GitHub (Kleckner 2021a). This board sends an analog sawtooth signal to the galvanometer controller to define the scanned volume; this can be adjusted in software as needed. Two digital pulse signals are dispatched to the pulsed lasers, inducing fluorescence at distinct wavelengths during alternate frames. This allows a monochrome camera to be used, improving both effective resolution and signal-to-noise ratio as compared to cameras with color chips. A digital frame sync signal is sent to the camera to trigger synchronized acquisition. A second trigger signal is sent to the camera to designate the start of the first recorded volume. This entire setup is controlled through a visualization workstation connected to the synchronization board through a USB connection. The camera is also connected to the workstation through a 10 Gb ethernet port, allowing for fast download of large data sets.
3 Fundamental and practical limits to high-speed volumetric imaging
Volumetric imaging systems are subject to constraints in resolution, speed and signal-to-noise ratio. These limits may either be fundamental physical constraints (diffraction and shot noise) or practical hardware limitations (camera speed, sensitivity, and data storage). We discuss each of these below, and arrive at practical limits for high-speed volumetric imaging with the currently available hardware. This discussion is tailored to guide those involved in high-speed volumetric imaging techniques as the same constraints are applicable to their systems.
3.1 Image resolution
Ideally, the laser sheet would maintain the same thickness throughout the sample, but in practice this is limited by diffraction. Although we are only focusing the laser sheet along a single axis, the beam parameters can still be computed with standard Gaussian optics (Siegman Anthony 1986), assuming the source laser has a Gaussian profile (as is the case for the lasers used in our sheet generator). A reasonable balance between the thickness of the sheet and the distance over which it is focused can be obtained by setting the Rayleigh length, \(z_R = \frac{n_s \pi w ^2_0}{\lambda }\), to be half of the sample size in the direction of laser travel, \(L_x\) (Fig. 2), where \(n_s\) is the index of refraction of the sample, \(w_0\) is the waist of the Gaussian beam, and \(\lambda\) is the vacuum wavelength of the laser.
To ensure uniform sampling, we set the depth of a single voxel to be equal to the full width half maximum (FWHM) of the laser sheet. This results in a voxel size \(h_{z,dl} = w_0 \sqrt{2 \ln 2} = \sqrt{\frac{\lambda \ln 2}{\pi n_s L_x}}\). This should be regarded as the maximum useful resolution; higher resolutions would result in a negligible increase in information in the measured volume. Although the resolution limits above were based on the laser sheet, the same fundamental limits apply to the camera system and corresponding lens, i.e., \(h_{x,dl} = h_{y,dl} = \sqrt{\frac{\lambda \ln 2}{\pi n_s L_z}}\). Table 1 shows the diffraction limited resolutions as a function of sample size.
For large volume sizes, \(L_z \gtrapprox 100\) mm, the diffraction limited resolution, \(N_{x,dl}\), exceeds the image resolutions of commonly available high-speed cameras. As a result, it is sometimes desirable to under-resolve the image. This brings additional benefits as it allows for an increase in the physical size of the aperture in the camera, which corresponds to a brighter image for the same amount of laser power. Provided our desired image resolution, \(N_{x}\), is lower than the diffracted limited resolution \(N_{x, dl}\), we can approximate the defocusing with a ray optics approach (Ward and Jacobson 2000). Here we define an F-number for the lens aperture: \(F = f/a\), where a is the aperture diameter and f is the focal length. (Note that per our definition, \(F=8\) corresponds to ‘f/8’, as it is usually specified on camera lenses.) To compute the acceptable lens aperture, we will set the ‘circle of confusion’ (the size of a defocused spot at the edge of the volume) to \(c=2p\), where p is the pixel pitch on the camera sensor (\(p =\) 28 \(\mu\)m for the Phantom V2512). If we then require that the depth of field be equal to \(L_z\), we can obtain:
where \(M=p/h\) is the image magnification, and h is the size of a voxel along the x or y axis at the center of the imaged volume. The correction due to the sample index of refraction, \(n_s\), can be computed using a ray transfer matrix (Gerrard and Burch 1994).
3.2 Image intensity
In order to obtain an image with good signal-to-noise ratio, we need to ensure a sufficient amount of light reaches the image sensor. Electronic camera sensors work by converting incoming photons to electrons, which are then amplified and digitized. The number of electrons per pixel read by the sensor is given by \(n_e = \eta n_\gamma\), where \(\eta\) is the quantum efficiency (\(\eta \approx 0.4-0.95\) for modern sensors (Janesick 2007) and \(n_\gamma\) is the number of photons which reach a single pixel in each image exposure. In practice the two relevant sources of noise are technical readout noise and shot noise which comes from the fact that electrons are quantized. The technical readout noise is typically referred to as the dark noise and measured in terms of number of electrons, \(n_d\), and the quantum mechanical shot noise is due to relative fluctuations of photons hitting the sensor and has an amplitude of \(\sqrt{n_e}\) (Janesick 2007). Assuming these are the only sources of noise, the signal-to-noise ratio is given by \(\text {SNR} = n_e/\sqrt{n_d^2 + n_e}\). Although \(n_d\) can be as low as 1 electron for high sensitivity SCMOS or CCD cameras, it is approximately of order \(n_d \approx 10-20\) electrons for high-speed cameras (Gilroy and Lucatorto 2019). If we assume \(\eta = 0.5\) and \(n_\gamma = 1000\) photons/pixel, \(\text {SNR} \approx 20\). Note that this is primarily limited by quantum efficiency and shot noise, and so a lower noise camera would produce only marginally better results (a perfect camera with \(\eta =1\) and no excess noise would produce \(\text {SNR} \approx 30\)). In the following discussion we will use \(n_\gamma = 1000\) photons/pixel as the reference level of intensity; in practice this produces satisfactory images for later analysis.
We image samples by seeding them with a fluorescent dye which is excited by the laser sheet. If we wish to produce \(n_\gamma\) photons per pixel, the required energy in a single laser pulse, assuming the small angle approximation, is given by,
where \(E_{pulse}\) is the laser pulse energy, \(E_{\gamma }=h_p c / \lambda \approx 4 \times 10^{-19}\) J is the energy of a single photon (\(h_p\) is the Planck constant, c is the speed of light, and we have computed the energy for \(\lambda =\) 500 nm), \(\eta _{opt} \approx 0.5\) is the overall optical efficiency of the system (including the quantum yield of the dye and any other optical sources of loss), \(\theta = \frac{M}{2 n_s F}\) is the sample half-angle (see Fig. 3), \(\gamma\) is the extinction coefficient of a single voxel which is fully dyed, and \(N_{y}\) is the image resolution in the vertical direction. The term in parentheses is the fractional solid angle of light collected by the camera lens. For situations where the majority of the sample is dyed, we require \(\gamma \ll 1/N_{x}\) to prevent significant shadowing effects.
Schematic of the focusing optics of the camera. The defocused spot size occurs for distances outside the depth of field. The permissible circle of confusion, c, occurs at the rear and at the front depth of field. The maximum lens aperture size, a, depends on the sample angle, \(\theta\). Here, \(d_o\) and \(d_i\) are the distance to object and distance to image, respectively
Let us consider a reference case, where we are imaging a cubic volume of size \(L_x = L_y = L_z=100\) mm, filled with water (\(n_s=1.33\)), and pumped with a 532 nm laser. If we use the diffraction limited resolution (\(N_{dl} = 1060\)) for the image resolution and have a pixel size of \(p=28\) \(\mu\)m, we obtain \(M = 0.297\). The corresponding aperture size per (Eq. 1) is \(F \approx 59\) (assuming \(n=1.33\)). If we assume an extinction coefficient of \(\gamma = 0.1/N_{x} \approx 10^{-4}\), and a peak imaging brightness of \(n_\gamma \approx\) 1000, the required pulse energy is \(\approx 10\) mJ, which is around 100 times more power than is produced by common pulsed lasers with a sufficiently high repetition rate of \(\approx 10^4-10^5\) Hz (Hong et al. 2001).
This reference case suggests a practical limitation: when imaging macro-scale objects, the resulting large F-number and small magnification will necessitate a large energy per pulse. In this case, a significant improvement can be made by under-resolving the image, and increasing the camera aperture so that the resolution is limited by the depth-of-field of the lens, as described in Sect. 3.1. A decrease in the resolution will result in bigger spot sizes of the permissible circle of confusion, and will in turn correspond to a larger half-angle of the imaging sample, scaling as \(\theta \propto 1/N_{z}\).
As an example, suppose we reduce the resolution to \(N_x = N_y = N_z = 500\). In this case we can decrease the magnification to \(M = 0.140\), and increase the aperture size so that \(F \approx 15\). Furthermore, let us assume that only a small fraction of the sample is dyed, then we can increase the dye density so that \(\gamma =1/N_{x}\). Taking into account all of these modifications, the resulting energy required per pulse is \(E_{pulse} \approx\) 65 \(\mu\)J. If we are recording volumes at a rate of 60 Hz, this is an average power of 2 W, which is achievable with commonly available lasers.
3.3 Volumetric recording rate
The volumetric acquisition rate of our H2C-SVLIF imaging system is limited by the sweeping rate of the galvanometer and the resolution of the high-speed camera. At low resolutions, the volumetric acquisition rate will approach the maximum sweeping rate of the galvanometer motor. For a sawtooth signal the maximum sweeping rate at full scale bandwidth for our galvanometer is 175 Hz. Our volumetric acquisition rates, ~ 60 Hz (see Table 2), are the fastest for deep (cubic) volumetric imaging, faster than reported two-color volumetric imaging techniques, e.g., Halls et al. (2018); Kashanj and Nobes (2023).
At high resolutions, the volumetric acquisition rate is limited by the throughput of the high-speed camera. Due to the finite speed of the galvanometer, it will produce a smooth linear ramp during a fraction of the total scan time, known as the duty cycle, \(\eta _{d}\). The duty cycle depends on the volume scan rate and the speed at which the galvanometer can reset and stabilize. The camera recording signal is synchronized with the effective scan period to only record during this period. The following equation is used to compute the volume rate of the system when limited by the throughput of the camera,
where \(r_v\) is the volumetric acquisition rate, \(r_f\) is the frame rate of the camera, and \(N_z\) is the resolution in the scanning depth direction, and \(N_c\) is the number of channels.
4 File formats and viewing software
One of the challenges presented by volumetric imaging is the large data sets produced by the method. For example, 10 s of 5123 volumes recorded at 100 vol/s results in a 134 GB of data (assuming 8-bit data storage). This data can be compressed, though for scientific analysis it should be done using a lossless method. Also, ideally the data would be capable of being decompressed fast enough for real-time viewing. This is a difficult constraint: playback at 30 volumes per second would require a decompression speed of 4 GB/s (as measured in the decompressed data).
In a typical experiment, a large fraction of the image volume is empty (i.e., containing no dye). In practice, this can range from 50 to 95% of the image voxels. In order to facilitate compression, we clip all pixel values below a certain threshold, chosen to eliminate the dark noise but have minimal impact on the collected data. After this clipping, the image volumes contain large contiguous regions of zeros which can be easily compressed using an LZ4 algorithm, supported by the widely used VTK data format (Schroeder 2006). Using this data format, we are also able to include perspective correction metadata in these files. This allows for acquired videos, corrected for volume distortions, to be played back at high rates by our open-source multi-scale ultra-fast volumetric imaging (MUVI) software (Kleckner 2021b) on standard desktop or laptop computers. This software is also capable of dynamically displaying other 3D data, including derived flow fields (see, for example, Fig. 9) (Schroeder 2006; Ahrens et al. 2005).
5 Post-processing
The volume imaged by the high-speed camera and scanning system is subject to distortion due to the viewing angle of the camera and the scan as seen in Fig. 1. Thus, the raw data obtained by our 3D imaging system includes distortion and non-uniform illumination due to the varying angle of the laser sheet and perspective foreshortening from the imaging system. Since we employ the use of prime lenses (Mikro-Nikkor AF 105 mm f/2.8 D), distortion effects are negligible as these prime lenses have extremely low distortion (Reznicek 2014). Although in principle the perspective effects could be eliminated optically (i.e., using a telecentric lens), this significantly complicates the experimental design and, in practice, limits the volume size. Moreover, non-uniformity in the illumination provide additional variations of order 10–20%. We have developed methods for correcting the resulting distortion in real-time display of the volumes, and for correcting the non-uniform illumination in the pre-processing. This is enabled through our customized viewing software (MUVI) presented in Sect. 4.
By employing the use of a single high-speed camera and imaging directly in 3D, the post-processing task for the reconstruction of volumes is streamlined when compared to tomographic imaging techniques such as TPIV and TPTV. Tomographic imaging techniques necessitate multiple distinct viewing angles typically achieved through camera systems or reflecting mirrors (Ortiz-Dueñas et al. 2010; Halls et al. 2018). These techniques result in intricate imaging system designs, complex volume reconstruction algorithms and distortion correction procedures particularly when imaging deeper volumes. As a result, these techniques are often constrained to VOIs which are shallow in at least one dimension, e.g., Wu et al. (2015); Eshbal et al. (2019); Lv et al. (2022). In contrast, our technique utilizes a straightforward geometric approach that directly maps raw space coordinates (the position of each voxel in the recorded data) to physical space coordinates. The implementation of single-camera H2C-SVLIF also enables the imaging of complete 3D structures and deep VOIs (see Tables 3, 4), extending beyond particle imaging. This kind of imaging is not readily achievable with systems reliant on only a few distinct viewing angles or cameras.
5.1 Distortion correction
To correct the perspective, we use the following coordinate systems and transformations between them (Fig. 4):
-
Raw space coordinates Each point is assigned a coordinate (\(u'\), \(v'\), and \(w'\)) in the range of 0–1, based on the relative position of each voxel along each axis in the raw recorded data. These voxels will be subject to distortion due to the scan angle of the laser sheet and the viewing angle of the high-speed camera.
-
Slope space coordinates Due to the nature of the imaging system, \(u'\), \(v'\), and \(w'\) correspond to slopes (\(m_x\), \(m_y\) and \(m_z\)) in physical space, rather than displacements. Note that, in the case of the laser scanner this ‘slope’ actually refers to an angle, but the difference is negligible (less than 1%) if the maximum angle is less than \(\approx 10^\circ\). At the maximum scan angle of our scanner (12.5°), voxels will appear \(\approx\) 20% larger at the edges but in practice we maintain the scan angle relatively low (\(\approx 8^\circ\)) to mitigate this effect. The relationship between raw coordinates and the slopes is given by:
$$\begin{aligned} u'&= \left( \frac{d_z}{L_x} m_x + \frac{1}{2}\right) \end{aligned}$$(4)$$\begin{aligned} v'&= \left( \frac{d_z}{L_y} m_y + \frac{1}{2}\right) \end{aligned}$$(5)$$\begin{aligned} w'&= \left( \frac{d_x}{L_z} m_z + \frac{1}{2}\right) . \end{aligned}$$(6) -
Physical space coordinates We can compute the slope space coordinates in relation to physical space coordinates (x, y, and z) using the equations:
$$\begin{aligned} m_x&= \frac{x}{d_z - z} \end{aligned}$$(7)$$\begin{aligned} m_y&= \frac{y}{d_z - z} \end{aligned}$$(8)$$\begin{aligned} \tan (m_z)&\approx m_z = \frac{z}{d_x - x}. \end{aligned}$$(9) -
Idealized image coordinates It is also useful to define idealized image coordinates (u, v, and w) in an undistorted space:
$$\begin{aligned} x = \left( u - \frac{1}{2}\right) L_x \end{aligned}$$(10)$$\begin{aligned} y = \left( v - \frac{1}{2}\right) L_y \end{aligned}$$(11)$$\begin{aligned} z = \left( w - \frac{1}{2}\right) L_z. \end{aligned}$$(12)The limits of these coordinates extend slightly beyond the range 0 to 1 because of the mismatch between the non-rectilinear imaged space and the rectilinear idealized space (i.e., the extent to which the purple box in Fig. 4 extends beyond the black outline).
From these definitions, we can relate the raw image coordinates to the idealized image coordinates:
where:
It is also possible to reverse this transformation:
where:
Although in principle the volumes could be perspective corrected before viewing and analysis, this would either result in image degradation or require up-scaling of the data. Both are highly undesirable. As a result, we have developed viewing software which corrects the perspective as it is being displayed. This works by converting the raw image coordinates into the idealized image coordinates using the equations above. As the transformation is relatively simple, this can be done at a low level in the display pipeline with minimal impact on performance.
The distortion also needs to be corrected for any features extracted from the raw volume data. For example, consider the problem of particle tracking: if the raw volumes are sent to particle identification software, it will return their positions in the raw image space. These positions can then be converted to the idealized image space after the particle identification. The software library also provides built-in functions for this coordinate transformation.
5.2 Effective distance
The distortion correction discussed in the previous section assumes that the imaged volume has the same index of refraction as medium surrounding the scanning head and camera. For typical experiments, however, the imaged volume will be in a fluid, and so the deflection of the light rays by the dielectric interfaces needs to be accounted for. In practice, this means that the distances, \(d_x\) and \(d_z\), from the sample center to the scanner head and from the sample center to the camera needs to be replaced with an effective distance, \(d_\text {eff}\), accounting for the changing index of refraction, see Fig. 5.
The relationship between the maximum ray slopes, \(m_i\), in different layers (e.g., air, glass, and water) is given by Snell’s law, and applying the small angle approximation results in,
where \(n_i\) is the index of each layer. This relationship can be derived from Snell’s law assuming the light rays are nearly perpendicular to all surfaces.
Thus, for a total of K interfaces,
and therefore,
where \(n_K\) is the index of the final layer (i.e., \(n_K = n_s\) is the index of the imaged volume). This effective distance can be used if layers are measured directly. Note this correction is applied to both the distance from the scanner to the sample center, \(d_x\), and the distance from the camera to the sample center, \(d_z\), for both the spatial calibration and intensity correction.
5.3 Spatial calibration
We have also developed a process for automating the determination of parameters, \(L_{x}\), \(L_{y}\), \(L_{z}\) and \(d_{x}\), \(d_{z}\), using a calibration target. The determination of these parameters allow us to map the raw distorted space coordinates to physical space coordinates. The target is composed of a regular grid of fluorescent spots, spaced by 5 mm, on a flat sheet of acrylic. The target is created from a sheet of 6 mm thick orange fluorescent acrylic, painted black on one side. A laser engraving system is used to engrave a rectangular grid of 1 mm spots, removing the black paint in these areas and exposing the fluorescent plastic underneath.
The distortion correction parameters, \(L_{x}\), \(L_{y}\), \(L_{z}\) and \(d_{x}\), \(d_{z}\), can be obtained directly from the raw distorted volumes of the grid captured by the camera. The process of obtaining the distortion correction parameters is as follows:
-
1.
Image the target in the sample fluid, placed at an approximately 45° angle with respect to the camera so that the laser scanner can illuminate it entirely while also being fully visible to the camera.
-
2.
Locate the centers of each spot in raw space coordinates using a particle tracking algorithm (see Sect. 6).
-
3.
Construct a model which transforms from the positions on the target to the raw space coordinates, including distortion corrections. This model incorporates \(L_{x}\), \(L_{y}\), \(L_{z}\) and \(d_{x}\), \(d_{z}\) as well as arbitrary displacements and rotations of the target (modeled as Euler angles). Eqns. 18–22 return the idealized image coordinates (u, v and w) from the raw distorted space coordinates (\(u'\), \(v'\), and \(w'\)). Then, we transform the idealized image coordinates to physical space coordinates (x, y and z) by applying Eqns. 10–12. Finally, the calibration target is rotated and displaced to lie flat and centered on the Z = 0 plane. The model first takes a 3 \(\times\) 3 grid near the center of the volume and fits the grid onto the plane by optimizing the distortion parameters discussed in the next step.
-
4.
Optimize the parameters of this model using the Broyden–Fletcher–Goldfarb–Shanno algorithm (Nocedal and Wright 2006). We minimize the following egg-crate fitness function:
$$\begin{aligned} U&= -\cos ^2 \left( \frac{\pi x'}{s}\right) \cos ^2 \left( \frac{\pi y'}{s}\right) + \left( \frac{\pi z'}{s}\right) ^2, \end{aligned}$$(26)where s = 5 mm is the known distance between target points, and \(x'\), \(y'\), and \(z'\) are physical space coordinates of the tracked points after applying the transformation model in the previous step. The optimizer returns the distortion parameters, displacements and rotations.
-
5.
The entire image target is calibrated by repeating Step 3 and Step 4 and using initial guesses (the approximate distortion parameters, displacements, and rotations) returned by Step 4.
Figure 6 shows an actual captured image of a calibration target before and after the perspective correction. We compute the RMS between the tracked points and the reconstructed points of our model, and find it to be within subvoxel accuracy, RMS ~ 0.23 voxels.
5.4 LIF calibration
For many LIF applications, it is necessary to produce a signal which is proportional to the local dye density. In the weak excitation limit, the fluorescence intensity of the dye is proportional to the local dye concentration (Krug et al. 2014), and in turn the digital signal recorded on the camera is also proportional to the fluorescence intensity (Manin et al. 2018). However, due to the optical configuration of our laser scanning system, the intensity of the laser sheet systematically varies by 10% or more across the volume. To correct this, we obtain a correction field which compensates for several experimental imperfections using a solution of uniform dye intensity. We image the uniform dye with the 3D scanning system to obtain an intensity field, \(c_u\), measured in units of digital counts on the camera sensor. We then fit this to a reference model:
where b is the black level of the camera. \(f_y\) is a piece-wise cubic spline correction function in \(s_y\) fitted with 20 points. \(f_z\) is also a piece-wise cubic spline correction function in \(l_z\) fitted with 5 points. \(\ell _x\) and \(\ell _z\) are the lengths of light ray from the inside of the tank to a point in the imaged volume (see Fig. 7), and \(s_y\) corresponds to the slope along the laser sheet (used to correct the non-uniform sheet profile). \(\eta\) is a decay constant with units of 1/m, used to model the absorption of the excitation by the uniform dye.
Schematic showing the intra-tank distances, \(\ell _x\), \(t_x\) and \(t_z\) used for the LIF reference model, Eqn. 27
This complete model is fit using a least squares minimization routine, which obtains optimal values for \(\eta\) and the parameters defining the cubic splines for \(f_y\) and \(f_z\). All other values are have been obtained previously using the volume calibration procedure (see Sect. 5.3). A corrected digital signal value, \(c'\), proportional to the dye intensity is then given by:
where c is an experimentally recorded intensity field. Note that the exponential decay of the illumination is not included, as this is only relevant for the uniformly dyed reference sample, \(c_u\). In other words, this neglects dye shadowing effects in experimentally relevant samples (Mayer et al. 2018). The performance of this correction is limited by camera readout noise, shot noise, and intensity noise of the laser sheet (stated by the manufacturer to be 4% for 355 nm excitation and 3% for 532 nm), each of which produces random fluctuations that cannot be corrected. To reduce the impact of these sources of noise on the reference intensity, \(c_r\), we optimize our correction parameters using a temporal average of 19 volumes, \({\bar{c}}_u = \sum \nolimits _{t_i} \frac{c_u}{T}\).
The magnitude of uncorrectable noise can be obtained directly from fluctuations in \(c_u\) for different volumes: \(\sigma _u^2 = \langle \overline{({\bar{c}}_u - c_u)^2} \rangle\), where \(\langle \cdot \rangle\) represents a spatial average, e.g., \(\langle c \rangle = \sum _{x_i, y_i, z_i} \frac{c}{N_x N_y N_z}\). In practice the fit of \(c_r\) will always have some noise; this can be characterized by \(\sigma _r^2 = \langle ({\bar{c}}_u - c_r)^2 \rangle\). Experimentally, we obtain \(\sigma _r \approx \frac{1}{2}\sigma _u\). Thus, variations in the corrected intensity for experimental data sets are dominated by random fluctuations rather than imperfections in the reference model. In practice, we obtain signal-to-noise ratios of ~ 17 dB for the UV channel and ~ 30 dB for the Green channel. Note, for the Green channel, the noise is computed after cropping 10% of the volume from each edges before analysis to avoid edge effects.
6 Velocity measurements
In order to measure the velocity of the fluid, we use a particle tracking velocimetry (PTV) approach which locates individual tracer particles in the 3D volumes and links them into tracks over time. We then use a resampling algorithm to interpolate these tracks into smooth particle velocities, and a second algorithm to interpolate these discrete velocities onto an arbitrary regular grid, giving an effective velocity resolution on the order of particle spacing. We note that if desired, it would also be possible to perform 3D PIV to obtain a velocity field (for example using OpenPIV; Liberzon et al. (2020)). However, for the example cases presented below, it is possible to resolve individual tracer particles, so a particle tracking method is preferred.
We use an open-source library, Trackpy (Allan et al. 2016) for particle identification and tracking from volume to volume. Trackpy is an implementation of the Crocker–Grier algorithm (Crocker and Grier 1996), which works by finding local peak intensities in the volumes. After localizing the peak intensities, the algorithm finds the positions of the particles by taking the average position of the pixels for which the particles spans and weights them by the brightness to locate their center of mass. After recovering the positions of the particles, we update the image coordinates of the particles to physical space coordinates using the distortion parameters, as discussed in Sect. 5.3. More advanced Lagrangian particle tracking (LPT) methods are discussed in Schanz et al. (2013) and Schröder and Schanz (2023) for high number of particle identification and the corresponding tracking of particles over extensive periods of time.
Under optimal scenarios the Crocker–Grier algorithm can return particle locations with sub-voxel accuracy, although in practice this is not always the case. Sub-voxel tracking requires that the tracer particles are well resolved, in other words that they span at least several pixels in the recorded image. Tracking a large number of particles would require a much high resolution data set, with a correspondingly lower recording rate. Given the inherent data rate limitations of volumetric imaging with current technology (as opposed to 2D imaging), in most cases it will be preferable to use sub-voxel tracer particles at high density.
To smooth out the resulting trajectories, we implement a modified Savitzky–Golay (SG) filter (Abraham and Golay 1964). An average of ~ 22,000–70,000 particles were present in each frame for the experiments outlined in Sect. 7. The filter requires a minimum track length and fits a 15 point window around each measurement to a second order polynomial. After the fit, ~ 20,000–55,000 trajectories are yielded, which allows us to resolve ~ 4 times as many trajectories than in other studies (Janke et al. 2017; Krug et al. 2014), depending on the experimental configuration. The “modified" part of the filter includes the ability to smooth trajectories of particle tracks with a small number of missing frames. This filter returns a new list of particle locations and velocities, giving us a randomly spaced velocity field measurement of the fluid. The complete implementation of this method is included in the MUVI software (Kleckner 2021b).
Given the inherent resolution limits of H2C-SVLIF—and the desire to minimize the Stokes number of the tracer particles—it is typically the case that the tracer particles are smaller than an individual voxel. As a result, sub-pixel tracking is typically not feasible, and the resulting discretization of the particle position provides the largest source of noise in the velocity reconstruction. To estimate the noise in the worst case scenario, we implement our SG filter on 5,000 virtual particles moving at assigned random velocities, with positions discretized onto a grid. The error between assigned velocities and the ones computed using the filter was found to have an uncertainty (standard deviation) of \(\sigma _t = 0.016\ hr_v\), where h is the voxel size along the specified axis and \(r_v\) is the volumetric acquisition rate. The exact Stokes number in our example data in Sect. 7 depends on the water temperature and particle size used, but is of order 10−3.
To resample the velocity obtained at our randomly seeded particle locations to a regular grid, we implement a second order windowed polynomial fit in three spatial coordinates (Parviz and Moin 2008). One advantage of this method is one can also compute the strain tensor or vorticity from the derivatives of the polynomial fit (Kambe 2007). In practice, we select a radial cosine window as the weight function, \(w(r) = \frac{1}{2}(1 + \cos \frac{\pi r}{a_0})\), and apply a least squares fit for smoothing (Geçkinli and Yavuz 1981). The size of the interrogation window is set to \(a_{0} = 3 {\overline{r}}\), where \({\overline{r}}\) is the median particle spacing; \({\bar{r}} =\) 3–5 mm 7. Higher particle concentrations are achievable in order to increase the resolution, however, attenuation effects and shadowing effects due to high particle concentration must be considered. To resolve features in our flow field we seed particles resulting in concentrations of \(\approx\) 12–20 particles per cm3 which is \(\approx\) 28 times higher than in the study by Schneiders et al. (2016), for the case of our highest seeded particle concentration. The window size is selected such that, on average, there are 3.6 times more measured particle velocities than fit parameters. If desired, this size can be reduced to improve the spatial resolution of the results at the expense of an increase in noise sensitivity. The noise associated with the resampler, \(\sigma _p\), will be less than the noise for individual particle trajectories due to the inherent smoothing associated with the interpolation method. The resampler noise depends on the size of the interrogation window and the uncertainty of the trajectories. For an interrogation window of size \(a_0 = 3 {\bar{r}}\) the noise was found to be \(\sigma _p\) \(= 0.005\ hr_v\). This was determined by calculating the standard deviation from a resampled volume containing randomly seeded trajectories of standard deviation \(\sigma _t\).
To eliminate the effect of spurious trajectories that sometimes result from errors in the linking stage, we first implement the windowed polynomial interpolation scheme on the sparse grid and interpolate the data back onto itself. This allows us to calculate the relative error between the interpolated velocities and the data; we then discard the worst 5% of particles. From the remaining trajectories, we reapply the windowed polynomial interpolation scheme to compute the velocity and vorticity on a regular grid.
Without modification, the effectiveness of this interpolation scheme is diminished near physical boundaries which reduces the number of measured particles in the fit window. In situations where these boundaries are at known locations and speeds-as in the experimental examples described below-this can be mitigated by inserting artificial tracer particles on the boundary which move at the boundary speed. In order to avoid biasing the resampling algorithm, we set the spacing of particles on the surface equal to the mean particle spacing. This scheme significantly improves the quality of the velocity measurements near the boundaries.
7 Results
We present two different sets of experiments to demonstrate our H2C-SVLIF imaging technique: (1) flow past a sphere with simultaneous measurement of tracer particles and a passive tracer and (2) laminar pipe flow with streamwise vortices embedded with dye. Although the second experiment only uses a single fluorescent channel, it uses most of the same hardware and identical software to extract two types of data from a single channel. In both cases, we collect PTV data and present flow analysis by reconstructing the velocity and vorticity field. Dye is used to reveal different flow patterns in each of the experiments.
7.1 H2C-SVLIF
To validate our novel H2C-SVLIF technique, we designed a pair of test experiments consisting of a 50 mm sphere pulled through a tank of water using a linear actuator (Fig. 8 and Supplementary Movie S1) for two different derivatives of Coumarin dye (Thermo Scientific Chemicals Coumarin 2 and Thermo Scientific Chemicals Coumarin 120). The solute of the dyes is water and the resulting molarity of the solutions are 25–140 μmol/L. . The fluid is randomly seeded with neutrally buoyant tracer particles (Cospheric Orange Polyethylene Micro-spheres with 106–125 μm diameter); the number density is chosen so that they have an average spacing of \({\bar{r}} =\) 3–5 mm. Their fluorescent absorption is well matched to the 532 nm laser (peak absorption: 525 nm, peak emission: 548 nm). A 532 nm dielectric laser notch filter is placed in front of the camera lens to block any light directly reflected from the sphere or other parts of the apparatus (i.e., so that we only image the fluorescent light).
The sphere is accelerated from rest and is suspended vertically by a 9 mm diameter stainless steel tube which also acts as a feeding channel for the dye. The dye is then ejected from a system of escape channels that lie along the equator of the sphere. We conduct measurements at \(Re =\) 400 and 950 for the respective UV dyes. The absorption maxima of the dyes are well matched to the 355 nm laser. Coumarin 2, while commonly available, exhibits lower water solubility compared to Coumarin 120. Additionally, its absorption peak is slightly further from the UV laser pulse, making Coumarin 120 a preferable choice for achieving a better signal-to-noise ratio. We implement the intensity correction method outlined in Sect. 5.4 for datasets acquired using Coumarin 120 as the dye for ejection. Note that to further improve the SNR of the UV excited dyes we use a larger aperture of f/2.8. Although this sacrifices some resolution near the edges of the sample, these regions primarily contain only tracer particles. Fortunately, spreading the intensity of a single tracer particle over several pixels should actually improve the particle tracking accuracy (Crocker and Grier 1996).
The reconstructed 3D images illustrate dye shedding from the sphere alongside the PTV velocities in Fig. 9. The intensity shown in Fig. 9 is corrected as described in Sect. 5.4 so one can retrieve quantitative concentration data from the images shown here, if needed. Our study aligns with previous research (Spietz et al. 2017; Sansica et al. 2018), which predict the emergence of vortex rings within the range of \(400 \le Re \le 950\). The presence of these rings is visualized through the circulation of dye around them (refer to Fig. 9 and Supplementary Movie S2). Moreover, our analysis identifies a boundary layer near the sphere where vorticity flips sign, and the core of the vortex rings, as evidenced in Figs. 10 and 11. In a similar experimental investigation conducted by Eshbal et al. (2019), these features were absent. They reported an error estimate of 1% to 2% for their reconstructed velocities after applying a 3 × 3 smoothing Gaussian filter, and report a velocity field of size 32 × 32 × 5 voxels. Our investigation yields a comparable noise estimate, utilizing the Savitzky–Golay filter outlined in Sect. 6, of approximately 1.4% and a velocity field of size ~ 40 × 40 × 40 voxels for deep VOIs.
Raw and processed data for flow past a sphere, taken at \(Re = 400\), visualized in the MUVI software. (a) A volume of the UV dye channel, showing the sphere and the fluid shed from the dye injection points which lie along the equator of the sphere. (b) An overlay of the 3D tracer particle data (teal, obtained from the green excited dye channel). (c) An overlay of some of the velocities measured from tracer particles (purple to yellow arrows)
(a) The out-of-plane velocity field, (b) the in-plane-velocity field, and (c) the in-plane vorticity field are plotted for a horizontal slice near the bottom of the sphere at \(L_y = -18\). Measurements are taken at \(Re = 950\). The in-plane velocity field reveals the core of a vortex ring, and the in-plane vorticity field reveals the corresponding vortex ring that is shed from the surface of the sphere
7.2 One-Color SVLIF
In situations where image features are sufficiently different in geometry or brightness, multiple data streams can be obtained from a single fluorescent channel. This is desirable because it drastically reduces the complexity and size of the setup, and is adequate for many flows of interest. As an example to demonstrate this technique, we present high-speed volumetric imaging of stream-wise vortices embedded in laminar pipe flow.
Although the same H2C-SVLIF laser scanning head can be used in single channel mode, here we use a smaller, cheaper, and lighter system which can easily be integrated onto the moving carriage (Fig. 12). We note, however, that this system uses an identical camera and synchronization board as well as the same software to control the scanner and image the resulting data. All the optics for this experiment are mounted onto a breadboard that is itself mounted onto a moving carriage that follows the flow in the pipe. The laser used is a diode-pumped pulsed laser (Spectra Physics Explorer One HE 532-200).
(a) Experimental setup investigating vortex line instabilities in transitional pipe flow using single-color SVLIF. (b) The region of interest is contained in an acrylic box in order to submerge the quartz pipe in index-matched fluid. (c) Within the pipe, the wing is held in place with stainless steel tubes that inject Rhodamine 6 G dye into channels to image vortex cores downstream
The flow under investigation is created by injecting two counter-rotating vortices into a laminar background pipe flow. Experimental parameters are listed in Table 5. The vortices are generated by a small hydrofoil placed in the pipe; the resulting vortices are made visible by injecting dilute Rhodamine 6 G through slots in the leading edge (Fig. 12c). The pipe is held in place by an acrylic box for the purpose of submerging the pipe in index-matched fluid (water), and providing stability to the tube (Fig. 12b). The qualitative appearance of these dyed vortex cores appears as two bright lines spanning the frame, allowing us to track them precisely using the Fast Marching Method (Fig. 13a–b; (Sethian 1999; Kleckner and Irvine 2013)).
One minor modification compared to the previous results is that the laser sheet generator is displaced along the y-axis as opposed to the x-axis as described above. As a result, the distortion correction uses a modified formula where \(x \leftrightarrow y\), but which is otherwise identical. This imaging configuration was chosen to minimize the distance light travels through the sample for both the laser sheet and camera, improving imaging quality for this particular experiment.
In addition to the dyed vortices, we also include small tracer particles in the flow (Cospheric Orange Polyethylene Micro-spheres size 106–125 μm), with a mean particle spacing of \({\bar{r}} \approx 3.0\) mm. This allows for simultaneous measurement of the velocity field in the pipe (Fig. 13b–e). The combined reconstruction technique allows for coarse resolution velocity fields (~ 3 mm) to be measured at the same time as high resolution (~ 1 mm) vortex line geometry (Supplementary Movie S3).
(a) Example of raw data in MUVI volumetric viewer. (b) Vortex line tracking is used in conjunction with particle tracking to find vortex location and reconstruct trajectories around vortex lines superimposed onto raw data. These trajectories are used to resample select measurements onto a regular grid using a second-order polynomial fit, and are displayed in conjunction with vortex line locations, shown as white and black points outlined in red. (c) Streamwise velocity profile makes a distinct shape as vortices move slower moving fluid inward and faster moving fluid outward. (d) Streamwise vorticity profile shows vortices seeded by wing. (e) Cross stream velocity also follows vortex cores, shown as regions of higher velocity around vortex cores
8 Conclusion
We have presented a novel H2C-SVLIF imaging technique which permits flexible high-speed volumetric imaging of multiple data channels in a fluid flow. This system is considerably faster than existing multi-channel volumetric imaging techniques; is capable of two channel speeds of up to 65 volumes per second at a resolution of 512 × 512 × 512. For demonstration purposes, we have employed the technique to image two different experiments using similar techniques and hardware. In addition to demonstrating the flexibility of our novel H2C-SVLIF technique, we provide a comprehensive discussion of the practical limits of the technique, including laser intensity, sample size/resolution, and camera and scanning speed. We have also described fundamental limits to volumetric imaging, including both diffraction limits to resolution and the effects of shot noise to the SNR of the resulting images. All of these limits should apply not only to our experiments, but to any high-speed volumetric imaging using similar techniques.
Our system also includes open-source software and hardware which simplifies and automates much of the data gathering, imaging, and processing. This includes automated correction of perspective distortion effects using a calibration target, correction of non-uniform illumination, and real time playback and manipulation of the resulting data which incorporates these corrections. By integrating the ability to correct for distortion effects we considerably simplify the experiment setup, which would otherwise require large and complicated optics to produce rectilinear imaging.
The test experiments presented in this manuscript demonstrate simultaneous visualization of the reconstructed velocity tracks and dyed regions of fluid. This demonstrates the ability to reconstruct multiple high-speed data streams in 3D from a single experiment, using either 2 channel imaging or by reconstruction of geometrically distinct features in a single channel. The flexibility of the technique allows it to be applied to a wide range of systems for high-speed single-shot measurements.
References
Adamczyk AA, Rimai L (1988) 2-Dimensional particle tracking velocimetry (PTV): technique and image processing algorithms. Exp Fluids 6(6):373–380. https://doi.org/10.1007/BF00196482
Ahrens J, Geveci B, Law C (2005) Paraview: an end-user tool for large data visualization
Allan D, Caswell T, Keim N et al (2016) trackpy: Trackpy v0.3.2. https://doi.org/10.5281/zenodo.60550,
Brücker C, Althaus W (1992) Study of vortex breakdown by particle tracking velocimetry (PTV). Exp Fluids 13(5):339–349. https://doi.org/10.1007/BF00209508
Bryanston-Cross P, Epstein A (1990) The application of sub-micron particle visualisation for PIV (Particle Image Velocimetry) at transonic and supersonic speeds. Prog Aerosp Sci 27(3):237–265. https://doi.org/10.1016/0376-0421(90)90008-8
Cornic P, Leclaire B, Champagnat F et al (2020) Double-frame tomographic PTV at high seeding densities. Exp Fluids 61(2):23. https://doi.org/10.1007/s00348-019-2859-2
Crocker JC, Grier DG (1996) Methods of digital video microscopy for colloidal studies. J Colloid Interface Sci 179(1):298–310
Eshbal L, Rinsky V, David T et al (2019) Measurement of vortex shedding in the wake of a sphere at \(Re=465\). J Fluid Mech 870:290–315. https://doi.org/10.1017/jfm.2019.250
Flammang BE, Lauder GV, Troolin DR et al (2011) Volumetric imaging of shark tail hydrodynamics reveals a three-dimensional dual-ring vortex wake structure. Proc R Soc B Biol Sci 278(1725):3670–3678. https://doi.org/10.1098/rspb.2011.0489
Geçkinli NC, Yavuz D (1981) A set of optimal discrete linear smoothers. Signal Process 3(1):49–62. https://doi.org/10.1016/0165-1684(81)90064-5
Gerrard A, Burch JM (1994) Introduction to matrix methods in optics. Courier Corporation, London
Gilroy K, Lucatorto T (2019) Overcoming shot noise limitations in high speed imaging with bright field mode
Halls BR, Hsu PS, Roy S et al (2018) Two-color volumetric laser-induced fluorescence for 3D OH and temperature fields in turbulent reacting flows. Opt Lett 43(12):2961. https://doi.org/10.1364/OL.43.002961
Hammack SD, Carter CD, Skiba AW et al (2018) 20 kHz CH \({^{2}}\) O and OH PLIF with stereo PIV. Opt Lett 43(5):1115. https://doi.org/10.1364/OL.43.001115
Hong Z, Zheng H, Chen J et al (2001) Laser-diode-pumped Cr4+, Nd3+:YAG self-Q-switched laser with high repetition rate and high stability. Appl Phys B 73(3):205–207. https://doi.org/10.1007/s003400100641
Janesick JR (2007) Photon transfer. SPIE, Bloomington
Janke T, Schwarze R, Bauer K (2017) Measuring three-dimensional flow structures in the conductive airways using 3D-PTV. Exp Fluids 58(10):133. https://doi.org/10.1007/s00348-017-2407-x
Kambe T (2007) Elementary fluid mechanics. World Scientific, London
Kashanj S, Nobes DS (2023) Application of 4D two-colour LIF to explore the temperature field of laterally confined turbulent Rayleigh-Bénard convection. Exp Fluids 64(3):52. https://doi.org/10.1007/s00348-023-03589-9
Katija K, Colin SP, Costello JH et al (2015) Ontogenetic propulsive transitions by Sarsia tubulosa medusae. J Exp Biol 218(15):2333–2343. https://doi.org/10.1242/jeb.115832
Kleckner D (2021a) Kleckner lab github repository: analog-digital synchronization board schematics. https://github.com/klecknerlab/ad_sync
Kleckner D (2021b) Kleckner lab github repository: Muvi lab 3d imaging library. https://github.com/klecknerlab/muvi
Kleckner D, Irvine WTM (2013) Creation and dynamics of knotted vortices. Nat Phys 9(4):253–258. https://doi.org/10.1038/nphys2560
Krug D, Holzner M, Lüthi B et al (2014) A combined scanning PTV/LIF technique to simultaneously measure the full velocity gradient tensor and the 3D density field. Measur Sci Technol 25(6):5065
Liberzon A, Lasagna D, Aubert M, et al (2020) OpenPIV/openpiv-python: OpenPIV - Python (v0.22.2) with a new extended search PIV grid option. https://doi.org/10.5281/zenodo.3930343,
Lv M, Chen S, Xu W (2022) 3D spatial resolution characterization for volumetric computed tomography. AIP Adv 12(3):035,322
Ma L, Lei Q, Ikeda J et al (2017) Single-shot 3D flame diagnostic based on volumetric laser induced fluorescence (VLIF). Proc Combust Inst 36(3):4575–4583. https://doi.org/10.1016/j.proci.2016.07.050
Manin J, Skeen SA, Pickett LM (2018) Performance comparison of state-of-the-art high-speed video cameras for scientific applications. Opt Eng 57(12):1. https://doi.org/10.1117/1.OE.57.12.124105
Mayer J, Robert-Moreno A, Sharpe J et al (2018) Attenuation artifacts in light sheet fluorescence microscopy corrected by OPTiSPIM. Light Sci Appl 7(1):70. https://doi.org/10.1038/s41377-018-0068-z
Meyer TR, Halls BR, Jiang N et al (2016) High-speed, three-dimensional tomographic laser-induced incandescence imaging of soot volume fraction in turbulent flames. Opt Express 24(26):29547–29555. https://doi.org/10.1364/OE.24.029547
Nocedal J, Wright SJ (2006) Numerical optimization. Springer, New York
Ortiz-Dueñas C, Kim J, Longmire EK (2010) Investigation of liquid-liquid drop coalescence using tomographic PIV. Exp Fluids 49(1):111–129. https://doi.org/10.1007/s00348-009-0810-7
Osborne JR, Ramji SA, Carter CD et al (2016) Simultaneous 10 kHz TPIV, OH PLIF, and CH2O PLIF measurements of turbulent flame structure and dynamics. Exp Fluids 57(5):65. https://doi.org/10.1007/s00348-016-2151-7
Ouellette NT (2012) Turbulence in two dimensions. Phys Today 65(5):68–69. https://doi.org/10.1063/PT.3.1570
Palafox P, Oldfield MLG, LaGraff JE et al (2007) PIV maps of tip leakage and secondary flow fields on a low-speed turbine blade cascade with moving end wall. J Turbomach 130(1):52. https://doi.org/10.1115/1.2437218
Parviz M, Moin MS (2008) Multivariate polynomials estimation based on gradientboost in multimodal biometrics. In: Advanced intelligent computing theories and applications with aspects of contemporary intelligent computing techniques. Communications in Computer and Information Science, Springer Berlin Heidelberg, Berlin, Heidelberg, pp 471–477, https://doi.org/10.1007/978-3-540-85930-7_60
Pepper RE, Jaffe JS, Variano E et al (2015) Zooplankton in flowing water near benthic communities encounter rapidly fluctuating velocity gradients and accelerations. Mar Biol 162(10):1939–1954. https://doi.org/10.1007/s00227-015-2713-x
Reznicek J (2014) Method for measuring lens distortion by using pinhole lens. Int Arch Photogramm Remote Sens Spatial Inf Sci XL-5(5):509–515. https://doi.org/10.5194/isprsarchives-XL-5-509-2014
Samson JE, Miller LA, Ray D et al (2019) A novel mechanism of mixing by pulsing corals. J Exper Biol 222(15):52
Sansica A, Robinet JC, Alizard F et al (2018) Three-dimensional instability of a flow past a sphere: mach evolution of the regular and Hopf bifurcations. J Fluid Mech 855:1088–1115. https://doi.org/10.1017/jfm.2018.664
Abraham S, Golay MJE (1964) Smoothing and differentiation of data by simplified least squares procedures. Anal Chem 36(8):1627–1639. https://doi.org/10.1021/ac60214a047
Schanz D, Schröder A, Gesemann S et al (2013) ‘Shake The Box’: a highly efficient and accurate Tomographic Particle Tracking Velocimetry (TOMO-PTV) method using prediction of particle positions
Schneiders JFG, Caridi GCA, Sciacchitano A et al (2016) Large-scale volumetric pressure from tomographic PTV with HFSB tracers. Exp Fluids 57(11):164. https://doi.org/10.1007/s00348-016-2258-x
Schröder A, Schanz D (2023) 3D Lagrangian particle tracking in fluid mechanics. Annu Rev Fluid Mech 55(1):511–540. https://doi.org/10.1146/annurev-fluid-031822-041721
Schroeder W (2006) The visualization toolkit: an object-oriented approach to 3D graphics, 4th edn. New York, Kitware
Sethian JA (1999) Fast marching methods. SIAM Rev 41(2):199–235. https://doi.org/10.1137/S0036144598347059
Shi S, Ding J, Atkinson C et al (2018) A detailed comparison of single-camera light-field PIV and tomographic PIV. Exp Fluids 59(3):46. https://doi.org/10.1007/s00348-018-2500-9
Siegman Anthony E (1986) Physical Properties of Gaussian Beams. In: Lasers. University Science Books, p 1–1
Spietz HJ, Hejlesen MM, Walther JH (2017) Iterative Brinkman penalization for simulation of impulsively started flow past a sphere and a circular disc. J Comput Phys 336:261–274. https://doi.org/10.1016/j.jcp.2017.01.064
Tropea C, Yarin AL, Foss JF (2007) Springer handbook of experimental fluid mechanics. Gale Virtual Reference Library. Springer, Berlin
Versluis M (2013) High-speed imaging in fluids. Exp Fluids 54(2):1458. https://doi.org/10.1007/s00348-013-1458-x
Ward P, Jacobson E (2000) Manual of photography, 9th edn. Focal Press, Burlington
Wilga CD, Lauder GV (2002) Function of the heterocercal tail in sharks: quantitative wake dynamics during steady horizontal swimming and vertical maneuvering. J Exp Biol 205(16):2365–2374. https://doi.org/10.1242/jeb.205.16.2365
Wilga CD, Lauder GV (2004) Hydrodynamic function of the shark’s tail. Nature (London) 430(7002):850–850. https://doi.org/10.1038/430850a
Wu Y, Xu W, Lei Q et al (2015) Single-shot volumetric laser induced fluorescence (VLIF) measurements in turbulent flows seeded with iodine. Opt Express 23(26):33408. https://doi.org/10.1364/OE.23.033408
Zhu X, Sabatino DR, Rossman T (2019) 3D planar laser-induced fluorescence (PLIF) reconstruction of a hairpin vortex. In: AIAA
Funding
Funding for this research was provided by the Department of Defense (Defense University Research Instrumentation Program awarded by the Army Research Office, Award Number W911NF-19-1-0215), the National Science Foundation under Grant CBET-2330349, and the UC Merced Academic Senate Faculty Research Grants program.
Author information
Authors and Affiliations
Contributions
D.K. and S.K. conceived the 3D imaging concept, acquired funding, and advised D.T.S., T.M., and C.C. on its implementation. D.T.S., C.C., T.M. and D.K. designed and constructed the imaging apparatus and wrote the associated imaging software. D.T.S. and C.C. conducted the demonstration experiments and data analysis. D.T.S., S.K., D.K., and C.C. wrote the main manuscript text. D.K. prepared Fig. 1. D.T.S. prepared Fig. 2, 3, 4, 5, 6, 7, 8, 9, 10. C.C. prepared Figs. 11, 12. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing financial interests.
Ethical approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary file 1 (mp4 41885 KB)
Supplementary file 2 (mp4 56037 KB)
Supplementary file 3 (mp4 14663 KB)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tapia Silva, D., Cooper, C.J., Mandel, T.L. et al. High-speed two-color scanning volumetric laser-induced fluorescence. Exp Fluids 65, 100 (2024). https://doi.org/10.1007/s00348-024-03831-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-024-03831-y