1 Introduction

The flow above and within the interstices of rough river beds has significant implications on hyporheic transport processes, sediment transport and bed resistance (Rickenmann and Recking 2011; Boano et al. 2014; Raus et al. 2019). With the aim of unraveling these near-bed hydrodynamic processes, non-intrusive measurement techniques, such as planar or stereo particle image velocimetry (PIV), have been successfully applied to study the flow above the roughness elements (e.g., Detert and Nikora 2010; Mohajeri et al. 2015; Akutina et al. 2019). However, impaired optical access due to roughness elements or laser reflections hamper the investigation of the flow within the bed interstices. Solutions to overcome these shortcomings have been found for relatively simple bed configurations composed of cubes. Florens et al. (2013) used a planar-PIV system with “spy cubes” with embedded mirrors to visualize the flow in the obscured canopy region, while Chagot et al. (2020) used a telecentric optical arrangement with transparent cubes. Beside being a simplification of natural river beds, such approaches are not feasible when the immobile bed matrix is filled with mobile sediments, which represents our long-term goal. In this case, planar-PIV measurements associated with refractive index matching (RIM) of the bed elements and the fluid can be an option (e.g., Voermans et al. 2017; Rousseau and Ancey 2020). Yet, while RIM has been used for the analysis of sediment transport in laminar flows (Mouilleron et al. 2009; Aussillous et al. 2013), it remains a challenge for the proper modeling of fully turbulent flows due to complexity and costs. In order to avoid this, a PIV-based solution without index matching was sought. The solution consists in viewing the flow from above through the water surface with an angle steep enough to access the canopy region down to the bottom of the bed interstices. However, the necessarily steep viewing angle raises three main issues which need to be resolved or validated. First, the nonzero viewing angle, being non-perpendicular to the flow, implies significant projection errors so that in-plane displacements cannot be accurately resolved with just one PIV camera. A second view from a different angle is necessary, i.e., a stereoscopic view, with the added benefit of yielding the third velocity component normal to the laser sheet. Steep viewing stereo PIV systems have been used in situ for flow measurements in rivers through the water surface (Cameron et al. 2013; Rouzès 2018). In these cases, symmetrical PIV setups are sufficient with the cameras positioned symmetrically to the laser sheet. Here, however, a symmetrical setup would not allow the measurement of the flow close to an obstacle within the bed interstices as the view of one of the two cameras would be impaired by the obstacle itself. Thus, a stereo-PIV setup with both cameras positioned on one side of the laser sheet is adopted to guarantee a similar optical access to the bed interstices for both cameras. The second issue related to the steep viewing angle is represented by laser light reflections at the bed. These need to be filtered out, accomplished here via fluorescent particles. Finally, random free surface perturbations distort the images. This implies the need of a transparent cover on the free surface, such as a glass plate.

The use of surface glass plates to reduce the influence of surface waves on PIV measurements is quite widespread (Detert and Nikora 2010; Mohajeri et al. 2015; Cameron et al. 2013). Their size and shape vary according to the application from narrow streamlined ones used to stabilize the laser sheet (e.g., Hofland and Booij 2004; Nikora et al. 2019) to wide-area-covering ones for the camera optical access (e.g., Detert and Nikora 2010; Cameron et al. 2013). However, only theoretical approaches for turbulent boundary layer development over smooth plates have been used until now to predict the boundary layer growth under the glass plate and its influence on the flow (Cameron et al. 2013; Mohajeri et al. 2015).

To our knowledge, neither the effect of a steep viewing angle (not to be confused with the angle between the two cameras, i.e., the stereo angle) on stereo-PIV measurements nor the effect of glass plates on the flow has been investigated experimentally. To address these two issues, flow measurements over a rough bed composed of spheres were performed simultaneously with two measurement systems: the top-viewing steep-angle stereo PIV and a standard planar side-viewing PIV. The new experimental setup and methodology are described in Sect. 2. The validation of the stereo-PIV system is presented in Sect. 3, and the influence of the glass plate on the flow is analyzed in Sect. 4.

2 Experimental methods

2.1 Flume and rough bed

The experiments are performed in a 9.2 m long, 30 cm wide and 32 cm-high tilting flume of the Institute of Hydromechanics at the Karlsruhe Institute of Technology (KIT). A set of two vertical grids with an open area of 65% with a distance of 5 cm from each other are installed at the inlet of the flume to reduce the turbulence intensity and uniformize the flow. See Trevisson (2022) for a drawing of the flume. Water levels are measured with two ultrasonic sensors with a vertical resolution of 0.5 mm located 2 m and 5.45 m downstream of the inlet and used to ensure flow uniformity. The flow rate is measured with a calibrated venturimeter.

Two layers of spheres with a radius \(R=1\) cm are glued over the whole length of the flume in a staggered symmetric pattern of length \(l_{x}=4.54\) cm and width \(l_{y}=2.62\) cm (Fig. 1a–c). The rough immobile bed thus formed has a total thickness \(k=3.3\) cm and a porosity \(\phi =0.57\) and is similar to the one used by Trevisson and Eiff (2022) composed of one layer of spheres to model a natural gravel bed.

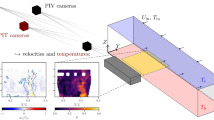
The stereo-PIV system is installed 5.7 m downstream of the inlet, where the origin of the local coordinate system is located (Fig. 1b). The origin of the streamwise oriented x-axis corresponds to the leading edge of the glass plate, described in Sect. 2.2. The vertical z-axis originates at the top of the spheres (Fig. 1b) and the transverse y-axis at the center of the channel (Fig. 1a).

2.2 Stereo-PIV system setup

The stereo-PIV system is composed of two high-frequency iDS cameras with a resolution of \(1936 \times 1216\) pixels (model UI-3060CP-M-GL Rev.2 iDS) and of a 4 W continuous laser with a wavelength of 445 nm (Fig. 1a, b). The cameras are equipped with LaVision Mount Version 3 Scheimpflug adapters on which AF DC-Nikkor 105 mm f/2 D lenses are mounted. The cameras are installed 50 cm away from the laser and at a height of 125 cm above the top of the spheres looking down with a steep viewing angle \(\zeta \approx 70^{\circ }\) to the horizontal axis (Fig. 1a, b). This steep viewing angle allows access to the bed interstices down to \(z = -2.3R\) without optical blocking by the spheres out of the laser plane (For yet higher sphere densities, the viewing angle would need to be increased further). A horizontal stereo angle \(\gamma \approx 26^{\circ }\) between the lens planes (Fig. 1c) is chosen within the optimal stereo-angle range of 20\(^{\circ }\)–30\(^{\circ }\) recommended by Lawson and Wu (1997) to optimize the resolution of the in- and out-of-plane velocity components. In order to ensure a uniform focus on the whole measurement plane, the camera sensor is tilted according to the Scheimpflug criterion (Prasad and Jensen 1995).

Fig. 1
figure 1

Experimental setup: a transverse, b longitudinal and c top view. In b, the red and green areas are the measurement regions of the stereo and planar PIV, respectively. For the validation of the stereo PIV, the measurement area of the planar PIV is restricted to the green area above the spheres’ top. The vertical dashed lines identify the five patterns of spheres below the boat. The insert in b highlights the boat submergence compared to the undisturbed water surface \(\Delta _{s}^w\) and the boat submergence compared to the water level at the leading edge \(\Delta _s^L\). In c, a characteristic pattern of spheres is highlighted with \(l_{x}=4.54\) cm and \(l_{y}=2.62\) cm

Full size image

A glass plate (called “boat” hereafter) with a length \(L=25\) cm and a width of 29.5 cm, rounded at the leading and trailing edges with a radius of curvature of 2 cm, is fixed flush with the water surface (Fig. 1a–c). The flow stagnation at the leading edge leads to a slight local increase in the water surface (Fig. 1b), which inhibits the formation of air pockets below the boat. Before installing the boat, uniform flow conditions are established. The boat is then fixed to the flume and levelled to match the undisturbed water surface within \(\pm 0.5\) mm (the submergence \(\Delta _s^w\) in Fig. 1b) and with a slope difference error less than 1/500.

The laser is installed in the center of the channel at a height of 105 cm from the top of the spheres (Fig. 1a). The laser beam is expanded through a cylindrical diverging lens to a laser sheet parallel to the streamwise direction with a thickness of 1 mm and a longitudinal extension of 26 cm to illuminate the whole flow region beneath the boat (Fig. 1b). The field of view of the stereo-PIV cameras spans the second pattern of spheres downstream of the leading edge of the boat (the green area in Fig. 1b).

The flow is seeded with in-house-made yellow fluorescent particles. These have a mean diameter of 10 \({\upmu }\)m and a density of 1.09 \(\text {g/cm}^3\), guaranteeing almost neutrally buoyant conditions. The particles are not perfectly spherical with a mean aspect ratio (ratio between the major and minor axis of a particle) of 1.4 with only 10% of the particles having an aspect ratio larger than 2. By equipping the cameras with long-pass filters with a cut-off wavelength of 475 nm, the laser reflections at the bed in the blue spectral region are filtered out, while the particle signal in the yellow-red spectral region is retained.

The stereo-PIV cameras are calibrated with a two-level calibration plate to account for perspective distortions and the non-uniform magnification factor. The calibration plate is aligned with the laser sheet below the boat in submerged conditions. For the image-world mapping, the camera pinhole model by Tsai (1986) implemented in the Davis PIV software version 8.4.0 is used. The image distortions induced by the refraction of the optical rays at the water surface are corrected through the radial distortion parameters included in the pinhole model. The PIV image pairs are first dewarped in the laser sheet plane (resulting in a resolution of 14.4 pixel/mm) and then correlated to yield the 2D-2C velocity field for each camera (Wieneke 2005). A self-calibration is then performed to correct small misalignments between the calibration plate and the laser sheet on the basis of the algorithm by Wieneke (2005). The in- and out-of-plane velocity components are computed by combining the planar velocity measurements of each camera.

2.3 Setup for the validation of the stereo-PIV system

The stereo-PIV system is validated with a planar-PIV system installed on the side of the flume. It is composed of an iDS high-frequency camera, UI-3060CP-M-GL Rev.2, equipped with a Nikkor 50 mm f/1.2 lens and a 475-nm-long-pass filter. The camera is aligned perpendicularly to the laser sheet at a distance of 90 cm from the flume wall (Fig. 1a), yielding an image resolution of 10.5 pixel/mm. The camera is centered over the second pattern of spheres sharing the same measurement region above the top of the spheres with the stereo-PIV cameras (green area above the horizontal dotted line in Fig. 1b). The stereo- and planar-PIV systems are triggered simultaneously.

Two experiments, presented in Table 1, are performed under uniform flow conditions with two different water depths H (defined with respect to the sphere’s top Fig. 1b). In this manner, the influence of the optical path, which depends on the water depth, is assessed. In Table 1, the experiments are given acronyms with H referring to the water depth and low (l) and high (h) to \(H=5.9\) cm and \(H=10.8\) cm, respectively. The shear stress conditions, defined by the shear velocity \(u_{*}=\sqrt{gHi}\) with i the bed slope, are chosen to test the stereo PIV in the presence of strong velocity gradients in the near-bed region.

For each experiment, 4500 PIV bursts are recorded simultaneously by each PIV system at a time interval equivalent to a bulk time unit (H/U) to guarantee statistically independent samples and good time convergence of the flow statistics. Two images per burst are recorded at a frequency adjusted for each PIV system and each flow to yield particle displacements of about 10 pixels. The bursts are processed with the Davis-PIV software version 8.4.0 based on a multipass iterative PIV algorithm with universal outlier detection by Westerweel and Scarano (2005). A final correlation size of 32 \(\times\) 32 pixels and of 24\(\times\) 24 pixels with 50% overlap is chosen for the stereo- and planar-PIV systems, respectively, to yield the same grid resolution of \(1.1 \times 1.1\) \(\text {mm}^2\).

Table 1 Flow parameters for the validation of the stereo-PIV system
Full size table

2.4 Setup for the analysis of the boat’s influence

The influence of the boat on the flow is investigated with the planar-PIV system (Sect. 2.3). The flow field measured with and without the boat is compared for the same flow conditions. The measurement area covers, in this case, the whole region between the boat and the top of the spheres as highlighted in red in Fig. 1b.

A total of three experiments are performed under uniform flow conditions by varying the Reynolds number \(Re=UH/\nu\), which affects the boundary layer development, and the water depth H (Table 2) with values similar to the ones adopted for the validation of the stereo-PIV system: a low and high \(\text {Re}=[15000,30000]\) and a low and high \(H=[5.8,10.8]\) cm. Accordingly, in Table 2, the experiments are given acronyms with \(R-\) and \(H-\) referring to the Reynolds number and the water depth, respectively.

For each experiment in Table 2, two PIV runs are performed one with and one without boat. During each PIV run, a total number of bursts equivalent to 5000 bulk time units are recorded. The PIV bursts are processed with the PIV algorithm described in Sect. 2.3 with a final correlation window of \(12 \times 12\) pixels with 50 % overlap. A ruler is positioned at the leading edge of the boat and attached to the flume wall to assess the influence of the boat on the local water levels.

Table 2 Flow parameters for the analysis of the influence of the boat
Full size table

3 Validation of the stereo-PIV system

3.1 Time-averaged flow fields

Fig. 2
figure 2

Normalized time-averaged streamwise and vertical velocity fields, \(\overline{u}/U_e\) and \(\overline{w}/U_e\), and normalized Reynolds-shear-stress fields \(\tau _{uw}/\rho _fu_*^2\) for Exp. Hl: a–c 2D2C-planar and d–f 2D3C-stereo-PIV measurements. The striped sphere is positioned out of plane

Full size image

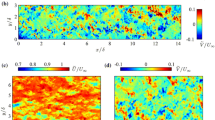
In Fig. 2, the time-averaged streamwise and vertical velocities, \(\overline{u}\) and \(\overline{w}\), and the Reynolds shear stress, \(\tau _{uw}\) (= \(-\rho _{f}\overline{u'w'}\)), obtained with both the planar (2D2C) and stereo (2D3C) PIV system are compared for the Hl case (see Table 1). \(\overline{u}\) and \(\overline{w}\) are normalized by the effective bulk velocity \(U_{e}\) = \(Q/(WH_{e})\), where the effective water depth \(H_{e}=H+\phi k\) takes into account the volumetric displacement induced by the spheres (Akutina et al. 2019). \(\tau _{uw}\) is normalized by the bed shear stress \(\rho _f u_{*}^2\). Figures 2a–c show that the planar PIV is able to capture the flow only above the spheres. The sphere (striped) in the out-of-plane position impairs the view within the canopy. The stereo PIV, on the other hand, captures the flow down to the bottom layer of spheres (Fig. 2d–f).

The streamwise velocity field \(\overline{u}(x,z)\) obtained from the stereo PIV in Fig. 2d shows good agreement with the one obtained from the planar PIV in Fig. 2a, both in the bulk and in the near-bed region.

The vertical velocity fields \(\overline{w}(x,z)\) in Fig. 2b and 2e also show good agreement. Only the positive vertical velocity region extends also to the lee side of the spheres for the stereo PIV, while it is confined above the spheres for the planar PIV.

Finally, the Reynolds-shear-stress fields in Fig. 2c and 2f show also good agreement, notably with a region of higher shear stress near the top of the spheres, i.e., the shear layer. The shear layers have a similar vertical extent. Yet, the center of the shear layer is slightly shifted upwards in the stereo-PIV data. Similar considerations can be drawn also for the Hh case (not shown here).

Overall, the stereo-PIV system with the steep viewing angle is able to properly reconstruct the flow field above the spheres. The slight misalignments in the vertical velocity and Reynolds-shear-stress field patterns are discussed further in Sect. 3.4.

3.2 Flow topology within the bed interstices

Since in the bed interstices (\(z < 0\)), a direct validation with the planar PIV is not possible, the integrity of the vector field was evaluated on the basis of topological principles following the method developed by Foss (2004). It allows to assess if a measured flow pattern overlaid to a surface (e.g., a PIV plane) is kinematically possible on the basis of the critical points present in the surface. Critical points are nodes (N) where infinite streamlines converge or diverge, and saddles (S) through which only two streamlines pass in opposite directions (Perry et al. 1969). Given a PIV vector field overlaid to a planar surface, the admissible number of nodes and of saddles must satisfy the Euler characteristic of the surface \(\chi _{E}\) (Foss et al. 2016):

$$\begin{aligned} \chi _{E}=2\sum N +\sum N'- 2\sum S -\sum S' - \sum OA \end{aligned}$$
(1)

where \(N'\) is the number of half nodes, \(S'\) of half saddles and OA the number of obtuse angles found along the surface’s perimeter. Considering that any surface can be obtained from the continuous deformation of a sphere “through which holes have been punched and to which handles have been attached” (Foss et al. 2016), the Euler characteristic of the surface is given a priori by this formation process (Foss 2004):

$$\begin{aligned} \chi _{A}=\chi _{\text {sphere}} -2 \sum \text {Handles} - \sum \text {Holes} \end{aligned}$$
(2)

where \(\chi _{\text {sphere}}\) = 2. The edges of the surface where the velocity vectors point inward or outward of the surface identify holes, while edges tangential to the velocity vectors are called seams. The integrity of a PIV vector field is verified if \(\chi _{E}\) = \(\chi _{A}\).

Fig. 3
figure 3

Time-averaged velocity vector field in the x–z plane. The perimeter of the surface for the topological characterization of the vector field is highlighted with the seams in red and the holes in blue. The half-saddles \(S'\) are marked with a red dot. The lines in red within the surface are streamlines

Full size image

Figure 3 shows the time-averaged velocity vector field in the x–z plane within the bed interstices. For the topological characterization, the surface of interest is chosen such that it encompasses the flow field in between the spheres up to z/H = 0.08. The red perimeter lines in Fig. 3 identify seams and the blue ones holes. It can be seen that the surface is characterized by five holes and no handles, so that \(\chi _{A} = -3\). Three half saddles \(S'\) can be identified, so that Eq. 1 yields \(\chi _{E} = -3\). The flow field integrity in between the spheres is thus verified.

The flow pattern in Fig. 3 does not show the presence of a recirculation region in the lee side of the upstream sphere, as observed for flows around submerged spheres over planar rough beds (Papanicolaou et al. 2011; Dey et al. 2011). Instead, it is characterized by an upwelling region originating below the first layer of spheres. It is surmised that this upwelling flow leads to vorticity annihilation, usually associated with the convergence of streamlines (Hunt and Eames 2002; Sau et al. 2003).

3.3 Time- and spatially-averaged flow statistics

Fig. 4
figure 4

Comparison of the vertical profiles of the normalized double-averaged streamwise and vertical velocities, \(\langle \overline{u}\rangle _{x}/U_e\) and \(\langle \overline{w}\rangle _{x}/U_e\), of the normalized longitudinally-averaged streamwise, vertical and transverse stresses, \(\langle \overline{u'^{2}}\rangle _{x}/u_{*,2C}^2\), \(\langle \overline{w'^{2}}\rangle _{x}/u_{*,2C}^2\) and \(\langle \overline{v'^{2}}\rangle _{x}/u_{*,2C}^2\) and of the normalized longitudinally-averaged Reynolds shear stresses \(-\langle \overline{u'w'}\rangle _{x}/u_{*,2C}^2\) obtained with the planar (2D2C) and stereo (2D3C)-PIV for Exp. Hl (a–f) and Exp. Hh (g–n). The dashed lines represent the 95% confidence interval of time convergence

Full size image

To assess the capability of the stereo PIV to reconstruct the flow, Fig. 4 presents a comparison between the longitudinally-averaged vertical profiles of the first and second order moments obtained with the planar and stereo PIV for Exp. Hl and Exp. Hh. The longitudinal average is performed over the second pattern of spheres below the boat (Fig. 1b). The first order moments, i.e., the double-averaged streamwise and vertical velocities, \(\langle \overline{u}\rangle _{x}\) and \(\langle \overline{w}\rangle _{x}\), are normalized by the effective bulk velocity. The second-order moments, i.e., the longitudinally-averaged streamwise, vertical and transverse normal stresses, \(\rho _{f}\langle \overline{u'^{2}}\rangle _{x}\), \(\rho _{f}\langle \overline{w'^{2}}\rangle _{x}\) and \(\rho _{f}\langle \overline{v'^{2}}\rangle _{x}\), and the longitudinally-averaged Reynolds shear stresses \(-\rho _{f}\langle \overline{u'w'}\rangle _{x}\) are normalized by the shear velocity \(u_{*,2C}\) obtained from the extrapolation of the shear-stress profile, obtained from the planar PIV, to the top of the spheres (Table 3).

Figures 4a and 4g show that the streamwise velocity profiles of the planar and stereo PIV overlap well within the measurement error for both experiments over the whole water depth. The vertical velocity profiles in Figs. 4b and 4h also show good agreement. Differences between the two profiles are close to 0.05 pixels, i.e., in the range of the subpixel interpolation error.

In the case of the second-order moments, while the streamwise normal stresses \(\langle \overline{u^{'2}}\rangle _x\) match over the whole water depth (Figs. 4c and 4i), the vertical normal stresses \(\langle \overline{w^{'2}}\rangle _x\) obtained with the stereo PIV are higher than the ones obtained with the planar PIV (Figs. 4d and 4l). These differ by a factor of 1.4 in the bulk flow (\(0.2<z/H<0.95\)) and by a factor of 2 near the top of the spheres (\(z/H\approx 0\)) as well as near the boat (\(z/H\approx 1\)). The reason why \(\langle \overline{w^{'2}}\rangle _x\) is over-estimated by the stereo PIV is investigated in the next section.

The Reynolds-shear-stress profiles in Figs. 4f and 4n show good agreement between the stereo- and planar-PIV data over the whole water depth. Yet, in the case of Exp. Hl (Fig. 4f), the shear stress peak is slightly misaligned by the stereo PIV at the boat and at the top of the spheres, as also shown in Fig. 2. Nevertheless, the extrapolation of the shear stress profiles to the top of the spheres yields similar shear velocities within the measurement uncertainty, as Table 3 shows.

The transverse normal stresses \(\langle \overline{v^{'2}}\rangle _x\) available only through the stereo PIV (Figures 4e and 4m) can be considered reliable as the transverse velocities are determined during the stereo reconstruction on the basis of the streamwise velocities (Raffel et al. 2018), which are very well represented by the stereo PIV.

The comparison between the stereo and planar PIV has led to similar results for the low and high water depth. Thus, the length of optical path, different for the high and low water depth, does not affect the reconstruction of the flow field by the stereo-PIV system.

Table 3 Shear velocities obtained from the extrapolation of the Reynolds-shear-stress profiles to the top of the spheres for the planar \(u_{*,2C}\) and stereo PIV \(u_{*,3C}\). The errors are derived from the extrapolation of the time-convergence confidence intervals of the Reynolds shear stresses
Full size table

3.4 Steep-viewing-angle impact on the vertical velocities

Fig. 5
figure 5

Comparison of the time series of the instantaneous signal of the streamwise turbulent intensity \(u'u'\) (a), of the vertical turbulent intensity \(w'w'\) (b) and of the turbulent stresses \(-u'w'\) (c) sampled with the planar (2D2C) and stereo (2D3C) PIV at \(x/\lambda _x=1.6\) and \(z/H=0.23\) in Exp. Hl. d Average difference in vertical particle displacement between the stereo and planar PIV as a function of the vertical velocity signal obtained with the planar PIV at \(x/\lambda _x=1.6\) and \(z/H=0.23\). The vertical whiskers represent one standard deviation around the average difference in particle displacement and the dotted line the average difference in particle displacement

Full size image

In this section, the overestimation of \(\langle \overline{w'^{2}}\rangle _{x}\) by the stereo PIV is investigated. Since the planar and stereo PIV are triggered simultaneously, a direct comparison of the temporal signals of the velocities is possible. Figure 5 shows the comparison of the instantaneous products of \(u'u'\), \(w'w'\) and \(-u'w'\) for Exp. Hl. The analysis is performed at \(x/l_{x}\) = 0.6 and z/H = 0.23, corresponding to the center of the planar-PIV camera sensor, where the perspective error is absent.

Figure 5a shows that both \(u'u'\)-signals are in almost perfect agreement. Figure 5b shows, however, that the stereo PIV tends to overestimate the \(w'w'\)-signal. This instantaneous discrepancy in vertical velocity fluctuations does not affect \(-u'w'\) though (Fig. 5c), which shows good agreement between the two signals. Thus, the turbulent events are properly represented by the stereo PIV.

No phase shift between the stereo- and planar-PIV signals is detected in Fig. 5a–c. This shows that not only the stereo- and planar-PIV signals are aligned in time, as expected, but they are also aligned in space.

Figure 5d shows the distribution of the difference in vertical particle displacement between the stereo-PIV \(\Delta z_{[3C]}\) and planar-PIV \(\Delta z_{[2C]}\), over 100 bins of the vertical velocity \(w_{2C}\). In each bin, the average difference \(\Delta z_{[3C]}\)-\(\Delta z_{[2C]}\) is computed as well as the standard deviation of this difference (the vertical whiskers). It can be seen that the difference in vertical particle displacement does not depend on the magnitude of the vertical velocity and is close to 0.1 pixel on average, comparable to the precision of the PIV-measurement (Raffel et al. 2018). However, the standard deviation of the vertical-velocity difference shows that the stereo PIV tends to over- or underestimate the vertical particle displacements of the planar PIV by approximately 1 pixel. This error is effectively a peak-locking (bias) error, which does not affect the time-averaged vertical velocities. It affects instead the normal stresses (Christensen 2004), in this case the vertical ones, leading to their overestimation, as seen here.

The reason for this peak-locking error is very likely due to the steep vertical viewing angle of the stereo PIV, compressing the projection of the seeding particles onto the image plane by a factor of 3.3 in the vertical direction. Image dewarping performed during the stereo-PIV processing leads to particles of bigger size and higher vertical stretching compared to the undistorted planar-PIV particles, as a visual comparison of the stereo- and planar-PIV images (not shown) reveals. The dewarping should not affect the particle displacement, if the shape of the dewarped particles does not change between two PIV-frames. Unfortunately, changes in the shape of the dewarped particles between the first and second frame can be caused by changes in the light intensity reflected by the particles (due to transverse movements through the Gaussian-shaped laser sheet) and of their orientation (not perfectly spherical particles). As a result, the particle centroid is displaced from its actual location, introducing an error in the particle displacement. An alternative could consist in calculating the velocity field on the undistorted stereo-PIV images, reconstructing the velocity field in the world coordinate system on the basis of the camera calibration, thus avoiding the dewarping step. Also, the use of more spherical particles could help.

4 The influence of the boat on the flow

Figures 6a–d show the normalized time-averaged streamwise velocity fields \(\overline{u}/U_e\) and the normalized Reynolds-shear-stress fields \(-\overline{u'w'}/u_{*}^2\) with boat (B) and without (NB) for Exp. RhHh. Most of the flow does not appear to be affected by the boat, except just below (compare Fig. 6a with b and 6c with d). Below the boat, the decreased streamwise velocities and negative shear stresses reveal the boundary layer developing along the boat. Closer inspection reveals that the boundary layer induces just a slight increase in the streamwise velocities and a reduction of the shear stress in the bulk flow region for \(0.2\lesssim z/H\lesssim 0.8\), consistent with accelerated flow conditions (Song and Chiew 2001). The near-bed region for \(z/H\lesssim 0.1-0.2\) is indistinguishable with and without the boat. Both are characterized by similar and equally intense periodic flow disturbances in the roughness sublayer (see the flow acceleration and deceleration above and behind the spheres, respectively, in Fig. 6a, b and the shear layers in the spheres’ lee in Fig. 6c, d). Thus, the boundary layer below the boat does not measurably affect the flow region near the spheres.

Fig. 6
figure 6

Normalized time-averaged streamwise velocity fields \(\overline{u}/U_e\) (a, b) and Reynolds-shear-stress fields \(- \overline{u'w'}/u_{*}^{2}\) (c, d) for Exp. RhHh. The plots on the left refer to the case without boat (NB) and on the right to the case with the boat (B), respectively. The red continuous line in plots (b) and (d) corresponds to the isostress line \(-\rho _f \overline{u'w'}=0\) identifying the boundary layer

Full size image

The development of the bulk-flow statistics in the longitudinal direction in the presence of the boat is investigated in Fig. 7 by comparing the normalized first- and second-order moments spatially-averaged over each of the five patterns of spheres below the boat (Fig. 1b) for Exp. RhHh. No significant differences in the bulk flow below the boundary layer are observed between the flow statistics of the different patterns except for the vertical velocities \(\langle \overline{w}\rangle _x/U_e\) (Fig. 7b). However, these differences are only about twice the subpixel interpolation error of about 0.05 pixel and thus negligible. In summary, the acceleration of the flow in the longitudinal direction induced by the increasing boundary layer below the boat can be neglected. Similar results were also obtained for Exp. RlHl and RlHh (not shown).

Fig. 7
figure 7

Vertical profiles of the normalized first- and second-order statistics spatially-averaged over each of the five patterns of spheres in the presence of the boat for Exp. RhHh

Full size image

The influence of the boat on the bulk flow is investigated in Fig. 8 by comparing the normalized first and second order moments for the B- and NB-case in Exp. RlHl, RlHh and RhHh. Given the negligible flow non-uniformity seen in Fig. 7, the statistics are spatially averaged over the second pattern of spheres, already used as a reference for the validation of the stereo-PIV system (Sect. 3). The Reynolds and normal stresses, \(-\rho _{f}\langle \overline{u'w'}\rangle _{x}\), \(\rho _{f}\langle \overline{u'u'}\rangle _{x}\) and \(\rho _{f}\langle \overline{w'w'}\rangle _{x}\), are normalized by the shear velocity \(u_{*_{,NB}}\) obtained from the extrapolation of the Reynolds-shear-stress profile of the NB-case to the top of the spheres (Table 4).

Figures 8a, f, k show a very slight increase in streamwise velocity in the presence of the boat. The velocity increases by 1% in Exp. RlHl and RhHl with a low water depth and by 0.6% in Exp. RhHh with a high water depth. No significant difference is observed for the vertical velocities \(\langle \overline{w}\rangle _{x}\) (Fig. 8b, g, l), which overlap within the 95% time-convergence error.

Fig. 8
figure 8

Comparison of the vertical profiles of the normalized double-averaged streamwise and vertical velocities, \(\langle \overline{u}\rangle _{x}/U_e\) and \(\langle \overline{w}\rangle _{x}/U_e\), of the longitudinally-averaged Reynolds shear stresses \(-\rho _{f}\langle \overline{u'w'}\rangle _{x}/u_{*,NB}^2\) and of the longitudinally-averaged streamwise and vertical normal stresses, \(\rho _{f}\langle \overline{u'u'}\rangle _{x}\) and \(\rho _{f}\langle \overline{w'w'}\rangle _{x}\), for the case with (B) and without boat (NB) for all experiments. The spatial average is performed over the second pattern of spheres. The dashed lines represent the 95% confidence interval of time-convergence. The horizontal dot–dashed line identifies the edge of the boat’s boundary layer

Full size image

The Reynolds and normal stresses are damped in the presence of the boat (see the three columns on the right in Fig. 8). The level of damping does not exceed 15% for the low water depth (Exp. RlHl and RhHl) and 5% for the high water depth (Exp. RhHh). The turbulence damping in the presence of the boat is consistent with previous results on accelerated open-channel flows where the turbulence levels are dampened compared to a uniform flow (Kironoto and Graf 1996; Song and Chiew 2001). However, near the top of the spheres (\(z/H\lesssim 0.1\)), the Reynolds and normal stresses with and without the boat collapse in all experiments. This confirms that the near-bed region is dominated by the shear layers developing in the lee side of the spheres (Fig. 6c, d). The values of shear velocity obtained from the extrapolation of the Reynolds shear stress to the top of the spheres for the B- and the NB-case are indeed the same within the measurement error, as Table 4 shows.

Table 4 Shear velocities obtained from the extrapolation of the Reynolds-shear-stress profiles to the top of the spheres with \(u_{*,B}\) and without the boat \(u_{*,NB}\). The errors are derived from the extrapolation of the time-convergence confidence intervals of the Reynolds shear stresses
Full size table
Fig. 9
figure 9

Longitudinal evolution of the boundary layer thickness \(\delta\) along the boat. The red continuous lines are the best fit of Eq. 3. The blue profiles represent the prediction of \(\delta\) based on the scaling law for a turbulent boundary layer developing along a smooth plate (Schlichting and Gersten 2017)

Full size image

For all flow statistics investigated, the bulk Reynolds number does not affect the difference between the case with and without the boat (compare Exp. RlHl with Exp. RhHl in Fig. 8). Thus, the water depth appears to have the strongest influence with a higher increase in streamwise velocity and a higher damping of the turbulent statistics for lower water depths. This can be explained on the basis of the development of the normalized boundary layer thickness \(\delta /H\) in Fig. 9. \(\delta\) is identified here as the elevation for which the Reynolds shear stress \(-\rho _f\overline{u'w'}(x,z)=0\), since the outer flow is not vertically homogeneous and no free-stream velocity can be defined. Figure 9 shows that \(\delta\) covers in relative terms a higher portion of the water depth in experiments with lower H. The small flow acceleration induced by the boundary layers on the bulk flow can be related to the displacement thickness \(\delta ^*\), which describes the vertical displacement of the streamlines outside of the boundary layer. Assuming that the relationship \(\delta ^*=\delta /8\) developed for turbulent boundary layers on smooth plates (Schlichting and Gersten 2017) holds, \(\delta ^*\) causes a higher contraction of the bulk flow for lower water depths, resulting in higher flow acceleration for Exp. RhHl and RhHl than for Exp. RhHh as observed in Fig. 8. The streamwise velocity profiles in the presence of the boat in Fig. 8a, f, k can be indeed obtained from the undisturbed flow by reducing the cross section by \(\delta ^*/H\approx 1\)% for Exp. RhHl and RhHl and by \(\delta ^*/H\approx 0.6\)% for Exp. RhHh (with \(\delta ^*\) estimated on the basis of the average \(\delta\) in the range \(0.23<x/L<0.4\), i.e., the second pattern of spheres, in Fig. 9).

For prediction purposes, the measured boundary layers are compared in Fig. 9 with the traditional scaling law for turbulent boundary layers developing on a smooth plate, \(\delta =0.36 x \text {Re}_{x}^{1/5}\) (Schlichting and Gersten 2017) with \(\text {Re}_{x}=U_{H}x/\nu\) (blue symbols). To predict \(\delta\), \(U_{H}\) is approximated by the velocity at the water surface in the absence of the boat. The measured \(\delta\) deviate from the smooth plate predictions, being not only higher but also displaying nonzero values at the leading edge. The latter suggests flow separation at the leading edge of the boat possibly caused by a recirculation bubble triggering an early detachment of the boundary layer, as observed in previous studies on boundary layers over smooth plates (Ota et al. 1981; Stevenson et al. 2016). Thus, the prediction of the boundary layer based on traditional scaling laws originating at the leading edge tends to under-predict the actual boundary layer thickness.

To assess whether the measured boundary layers nevertheless follow a 1/5-power law with shifted origin, the measured \(\delta\)-profiles are fitted as follows:

$$\begin{aligned} \delta =a_{\delta }(x-X_o)\text {Re}_{x-X_o}^{-1/5} \end{aligned}$$
(3)

where \(a_{\delta }\) is a proportionality factor, \(X_o\) a virtual origin to account for the non-zero \(\delta\) at the leading edge, and \(\text {Re}_{x-X_o}\) = \(U_{\delta }(x-X_o)/\nu\) (where \(U_{\delta }\) is here the velocity measured at the boundary layer depth). \(a_{\delta }\) and \(X_o\) are determined by minimizing the root mean square error between \(\delta\) and Eq. 3. Figure 9 shows that the measured boundary layers scale with a power law of 1/5. Table 5 lists the fitting parameters of Eq. 3 along with the boat submergence at the leading edge \(\Delta _s^L\), i.e., the difference between the water level at the leading edge induced by the local flow stagnation and the boat elevation (Fig. 1b). \(a_{\delta }\) deviates from the theoretical values of 0.37, with lower values observed for a higher submergence \(\Delta _s^L\). The virtual origin \(X_o\) appears to increase with \(\Delta _s^L\). This suggests that even when accurate positioning of the boat to the water surface is performed and a rounded leading edge is used, the developing boundary layer is very sensitive to the water level conditions at the leading edge.

Table 5 Boat submergence at the leading edge \(\Delta _s^L\) and fitting parameters of Eq. 3 for the boundary layer thickness \(\delta\)
Full size table

5 Conclusions

A novel stereo-PIV setup with a steep vertical viewing angle of 70\(^{\circ }\) was developed to measure the flow region in between roughness elements with the aid of a glass plate on the water surface (“boat”) and fluorescent seeding particles. The stereo-PIV measurements are validated with planar-PIV measurements above the roughness elements. The comparison shows that the stereo-PIV system can be used to measure accurately all flow statistics involving the streamwise and transverse velocity components. However, while the average vertical velocity component is also measured accurately, the vertical normal stresses are overestimated by a factor of 1.4. The overestimation is due to peak-locking errors resulting from the lower vertical resolution induced by the steep viewing angles. To reduce the impact of the vertical resolution, it is advised to compute the velocity field on the undistorted PIV images before the projection onto the world coordinate system and not after, thereby avoiding detrimental image deformations.

Comparing the flow field in the streamwise wall-normal plane with and without the boat via planar PIV, it is shown that a boat has a limited impact on the bulk flow which is slightly accelerated (max 1% for the cases investigated). The turbulent shear stresses are instead slightly attenuated (max 15%). The flow acceleration is proportional to a contraction of the flow cross section equal to the displacement thickness of the boundary layer developing along the boat. Thus, the higher the water depth, the lower the flow acceleration. For all water depths and Reynolds numbers investigated, no impact of the boat is attested in the near-bed region, where the flow is dominated by the shear layers developing behind the spheres.

When using a boat, particular care should be taken to level it accurately with the water surface (\(\pm 0.5\) mm). For the type of boat used with a rounded leading edge, the boundary layer developing along the boat is sensitive to the boat submergence at the leading edge which affects the boundary-layer development. Thus, traditional scaling laws for turbulent boundary layers over smooth plates with origin at the leading edge tend to underestimate the developing boundary layer.