Measurement of the turbulent heat fluxes in mixed convection using combined stereoscopic PIV and PIT

Abstract

The results of simultaneous measurements of velocity and temperature fields in a turbulent mixed convection airflow are analyzed and discussed. To access local temperature and velocity fields in airflows, we present a combination of stereoscopic particle image velocimetry and particle image thermometry. The obtained flow fields make it possible to determine the local convective heat fluxes, thus giving insight into the dynamics of plumes and Taylor–Görtler-like vortices. The evaluated mean local heat fluxes further reveal that the main convection roll transports a substantial amount of heat along the cooling plate and back to the heated bottom plate. Yet, the associated mean turbulent heat fluxes remain positive as they are dominated by the correlation of the temperature and the vertical velocity component. More specifically, a statistical analysis of the local heat flux distribution reveals that Taylor–Görtler-like vortices lead to more skewed distributions of the turbulent convective heat fluxes than plumes.

Graphical abstract

1 Introduction

Mixed convection occurs whenever buoyancy and forces induced by external pressure gradients of similar strength drive a flow. Such flows are found on a large range of length scales in both nature and technical applications. One example is the interaction between the heat generated by passengers and the forced convective flow originating from an air-conditioning system inside aircraft (Kühn et al. 2009) and trains (Suárez et al. 2017). Recently, the flow patterns of mixed convection have been under scrutiny, since they determine the transport of pathogens (Bourouiba 2021). Due to the complex dynamics and instabilities observed in the context of mixed convection, previous studies were frequently carried out in generic setups (Westhoff et al. 2010; Kühn et al. 2011; Bailon-Cuba et al. 2012; Wu et al. 2021) to improve the understanding of the formation of the salient structures at reduced geometric complexity.

The flow structures in the sample investigated in this work have previously been studied by Mommert et al. (2020) by means of tomographic particle image velocimetry. They identified a flow also exhibiting Taylor–Görtler-like (TG) vortices, driving the dynamic behavior. TG vortices are coherent structures also known from lid-driven cavity flow (Rhee et al. 1984), which can be observed during wild fires, where forest aisles remain intact, while adjacent areas burn down (Finney et al. 2015).

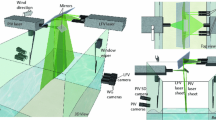
Figure 1 sketches an arrangement of these structures in the investigated experimental setup for a certain parameter range. Between the heated bottom plate (red) and the cold top plate (blue), a longitudinal (along X) convection roll (gray shade) is driven by the forced flow entering the convection cell through the openings at the long rear edges. This convection roll resembles the most dominant structure of the flow (cf. Schmeling et al. 2011). It is one of the prerequisites for the formation of TG vortices (circular arrows) above the heated bottom plate as its streamlines are curved in the vicinity of the sample’s edges. The second prerequisite is represented by the friction forces introduced by the nearby walls.

Fig. 1

Sketch of the mixed convection setup heated at the bottom (red) and cooled at the top (blue) with openings at the long rear edges to introduce a forced flow component. A longitudinal convection roll is highlighted in gray. The arrows below this region reflect the arrangement of TG vortices

TG vortices are of particular interest, since they induce a longitudinal transport component to the flow and are also able to travel in longitudinal direction (Mommert et al. 2020). Further, the characteristics of the heat transport provided by these vortices are of interest, since they are formed above the heated bottom plate like plumes but are driven by inertial forces and should therefore behave differently compared to purely buoyancy-driven plumes. While Direct Numerical Simulations provide the complete three-dimensional velocity and temperature fields allowing to determine the local heat fluxes (Shishkina and Wagner 2007; Emran and Schumacher 2012), acquiring the latter as measured data is still challenging. In principle, combined temperature and velocity measurements are possible using instrumented (Liot et al. 2016), luminescent (Abram et al. 2018) or thermochromic (Dabiri 2008) tracer particles. For the application, the type and size of the tracer particles had to be chosen with regard to a sufficiently strong signal and a negligible sinking rate. In this respect, we decided to use finely dispersed unencapsulated, thermochromic liquid crystals (TLCs) which had already been successfully applied by Schmeling et al. (2014, 2015) for a mono-particle image velocimetry setup. We extended the latter to a stereoscopic setup, which was used in the past for liquid flows (Funatani and Fujisawa 2002; Fujisawa et al. 2008; Moller et al. 2021). To our knowledge, the here presented measurement is the first to combine stereoscopic particle image velocimetry (stereo PIV) and particle image thermometry (PIT) for airflows. By providing temperatures and three velocity components within a horizontal plane, it further allows for the calculation of the vertical convective heat flux required to resolve the contribution of TG vortices to the total vertical heat transport.

Before analyzing the acquired data by discussing the developing flow structures and the induced heat transport, details of the setup including the PIV and PIT installation as well as the pre- and post-processing of the data are presented.

2 Experimental setup

Figure 2 presents a sketch of the mixed convection sample with the setup for the newly developed combination of PIT and stereo PIV. These measurement techniques are further described in Sects. 2.1 and 2.2, covering PIV and its combination with PIT. The mixed convection sample resembles a ventilated, rectangular Rayleigh-Bénard experiment with the height $H=0.5\,{\textrm{m}}$ and the aspect ratios $\Gamma _{XY}=\frac{L}{H}=5$ and $\Gamma _{YZ}=\frac{W}{H}=1$, to which air is supplied and removed through in- and outlets at the top and bottom. Both orifices are situated at the rear wall and extend over the entire cell width with heights of 0.05H (top) and 0.03H (bottom).

As the velocities of the inlet jet are significantly higher than those of the rising air at the rear wall (Schmeling et al. 2011), the cooling plate is effectively shielded by the inlet jet. Therefore, the relevant temperature difference $\Delta T = T_{{\textrm{h}}} - T_{{\textrm{in}}}$ includes the temperatures of the heated bottom plate $T_{{\textrm{h}}}$ and of the inflowing air $T_{{\textrm{in}}}$. Subsequently, the Rayleigh number is $\text {Ra}=\frac{g\beta \Delta T H^3}{\nu \alpha }$, the Reynolds number equals $\text {Re}=\frac{U_{{\textrm{in}}}H}{\nu }$, and the constant Prandtl number is given by $\text {Pr}=\frac{\nu }{\alpha }$. Here, g is the gravitational acceleration, $\beta$ the thermal expansion coefficient, $\nu$ the kinematic viscosity, $\alpha$ the thermal diffusivity, and $U_{{\textrm{in}}}$ the average absolute velocity at the inlet. Additionally, the Richardson number $\text {Ri}= \frac{\text {Ra}}{\text {Pr}\text {Re}^2}$ displays whether natural convection $(\text {Ri}\gg 1)$ or forced convection $(\text {Ri}\ll 1)$ is dominant, while ${\mathcal {O}}(\text {Ri}) = 1$ is associated with a mixed convective flow. The sample is bounded by double walls made of polycarbonate to minimize the heat exchange with the surroundings while preserving optical accessibility. To optimize contrast, the faces of the top, bottom, and rear wall are blackened.

In this work, the relevant parameters were $U_{{\textrm{in}}}=0.4\,{\mathrm {m/s}}$, $T_{{\textrm{in}}}=23.9\,^\circ {\textrm{C}}$, $T_{{\textrm{h}}}=40.2\,^\circ{\textrm{C}}$ and $T_{{\textrm{c}}}=25.4\,^\circ{\textrm{C}}$, while the flow leaving the sample, i.e., the velocity and temperature in the outlet, developed according to the flow in the sample. This leads to the dimensionless numbers $\text {Ra}=1.72\times 10^8$, $\text {Re}=1.22\times 10^4$, $\text {Pr}=0.71$ and $\text {Ri}=1.6$, which were chosen to replicate the flow regime which is driven by TG vortices (Mommert et al. 2020).

Fig. 2

Sketch of the convection sample with the combined PIV-PIT setup. A LED light source. B PIV cameras. C PIT cameras. Yellow plane: Light sheet. Red dots: Thermistor positions during the dynamic calibration

2.1 PIV setup

The light sheet for the combined PIV and PIT measurement was positioned at $Z=H/8$, in accordance with earlier measurements in this sample conducted by Niehaus et al. (2020) in a vertical section parallel to the X-Z plane. They showed that vortex pairs bound to the bottom plate have a height of up to H/5. As these structures were probably TG vortices, we expect them to be cut by the measurement domain.

For the measurement presented in the following, a white light LED array (A in Fig. 2) was used to illuminate the tracer particles. Images were taken by two cameras (B). A list of instruments and stereo PIV parameters is compiled in Table 1.

Table 1 Parameters of the stereoscopic PIV setup

To ensure the best overlap of the dewarped particle images, a self-calibration (Wieneke 2005) based on the particle images was conducted. Moreover, velocity vectors with immoderately large magnitudes ($\vert {\textbf{u}}\vert > 5\,U_{{\textrm{in}}}$), deviations larger than 50% of the mean magnitude of the surrounding vectors or stereoscopic reconstruction residua larger than $0.5\,{\textrm{px}}$ were marked as outliers and subsequently interpolated. These criteria resulted in $1.3\%$ of all vectors to be treated as outliers. Additionally, the region of $Y > 0.8\,H$ and certain areas at $Y \approx 0.65\,H$ had to be masked due to reflections of the bottom plate and the rear wall.

2.2 PIT setup

Analogous to the PIV setup, two color-sensitive cameras (C in Fig. 2) were used for the image acquisition. Thereby, the second camera mainly serves to improve the accuracy, since in principle one camera is sufficient for conducting PIT. Details on the PIT camera configuration and the resulting field of view are listed in Table 2.

Table 2 Parameters of the PIT setup

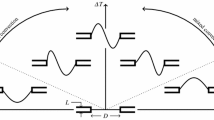
It was crucial to ensure spatial and temporal correspondence of both camera systems. Hence, a central sequencing device was employed in accordance with the scheme presented in Fig. 3. The trigger source provided individual delays, a, b and c, in response to the component-specific camera delays, $\tau _{\alpha }$ and $\tau _{\beta }$. In contrast to the cameras, the reaction of the LED light sources is approximated as instant for the time scales considered here (Schmeling et al. 2014). This sequencing ensures that light-source-controlled exposures lie within the camera exposure intervals. While the PIV system requires two light pulses with a delay of $\tau$, the exposure time of the PIT system was chosen long enough to cover both pulses in order to achieve a higher signal-to-noise ratio.

Fig. 3

Trigger sequence for the combined PIV-PIT measurement

The spatial correspondence of both systems was achieved by applying a direct linear transformation (DLT) using the same calibration target for both systems. A detailed overview of the calibration procedure is presented in Fig. 4.

Fig. 4

Calibration workflow for both stereoscopic PIV and PIT

Since there is no neutrally buoyant thermosensitive seeding material for the investigation of airflows, it was not possible to let the fluid temperatures converge to iso-thermal states for the temperature calibration, as it is common practice for TLCs in liquids (e.g., Moller et al. 2019; Schiepel et al. 2021). Hence, the dynamic calibration concept suggested by Schmeling et al. (2014) was applied. This workflow is shown in the bottom part of Fig. 4, and its details are described in the following paragraphs, which refer to the single steps of the flow chart set in italics.

For the dynamic calibration, four pre-calibrated negative-temperature coefficient (NTC) thermistors were used, which were positioned within the sample to reach into the light sheet during the calibration measurement. The red dots in Fig. 2 highlight their locations. For the measurement domain, the variation of the viewing angle was below $2\,^\circ$ and, hence, no local color shifts, as reported by Schiepel et al. (2021) and Moller et al. (2019), were to be expected. In order to conduct the calibration in similar conditions with regard to the measurements, TLC particles were introduced into the flow via the inlet which was operated at the identical $\text {Re}$ number as during the measurement. For this purpose, the used TLC mixture (see Table 2) was chosen based on preliminary tests with temperature sensors considering the reduced color play range when the material is present as droplets (Ciofalo et al. 2003).

To save seeding material while covering the complete temperature range, the temperature of the bottom plate was slowly raised and an automated system (Mommert et al. 2019) was used to selectively trigger calibration measurements at different bottom plate temperatures.

The subtraction of minimum images is common practice for PIV. However, this step is more complex for PIT since the use of a Bayer filter offers different options to subtract a minimum image. Here, the minimum images were not calculated from image series with present TLC seeding but from the empty sample to avoid a color-cast. Nevertheless, minimum images created this way still carry color information affecting the calibration. Accordingly, the same minimum images were used for the calibration and measurement image series. The subtraction of the minimum image also took place on the raw-image level. That means values of physical sensor pixels, representing either red, green or blue in the Bayer matrix, were subtracted.

In the demosaicing step, these raw pixel values associated with the Bayer matrix are mapped onto a new grid. The red, green, and blue values of each point of the new grid were determined by the surrounding raw values. Therefore, the $4 \times 4$ kernel recommended by the camera manufacturer PCO AG (2006) was used. Compared to a smaller kernel, this one suppressed noise, whereas the associated loss of resolution was insignificant since the TLC particles appeared as mist in the lower-resolution PIT images for both kernels.

For generating a calibration data set, the $20 \times 20$ pixel kernels around the thermistors' image positions were taken into account and color values were converted from the RGB (red: $C_R$, green: $C_G$, blue: $C_B$) to the HSV (hue: $C_H$, saturation: $C_S$, value: $C_V$) color space (Smith 1978). The kernels were then masked, so that only pixels that were bright and saturated enough were kept. Also oversaturated pixels were excluded, since they are associated with increased image noise. Specifically, $C_V \ge 0.035$ and $0.1 \le C_S \le 0.99$ must be satisfied. The same masking conditions were also applied to the measurements. For the calibration, kernel averages with a hue standard deviation of $\sqrt{\textrm{Var}({C_H})}>5\%$ or less than $5\%$ unmasked pixels were also omitted. These restrictions reduced the calibration data set to $69\%$ of its original size. The calibration values were gathered in $0.14\,{\textrm{K}}$-wide bins. In addition, the data of the different cameras and thermistor positions were combined in these bins as an angle dependency was not observed.

Before the binned data was finally mapped onto the hue values, the white balance was modified in the RGB color space to optimize the linearity of the calibration function.

Fig. 5

Calibration function (red) based on the averages of the $0.14\,{\textrm{K}}$ bins (black). The error bars indicate the hue standard deviation of the values in one bin (horizontal) and the uncertainty ($0.08\,{\textrm{K}}$) of the thermistor pre-calibration (vertical). The gray area reflects the uncertainty of the calibration function

Figure 5 displays the calibration result (black dots) with bars indicating $1\sigma$ measurement uncertainties. The regression result of the calibration function suggested by Schiepel et al. (2021)

$$\begin{aligned} T(C_H)=-\frac{p_0}{C_H-p_1}+p_2+p_3\cdot (C_H-p_1) \end{aligned}$$

(1)

is presented as a red line, with the $1\sigma$ regression uncertainty indicated in gray. It combines a linear relation and the typical asymptotic behavior as the temperatures approach the upper limit of the TLC’s range ($p_1$). The regression results with the associated uncertainties are listed in Table 3.

Table 3 Parameter values of the PIT calibration function

In agreement with the findings of Ciofalo et al. (2003), the usable temperature range of TLC droplets was significantly smaller than the nominal temperature range ($25\,^\circ{\mathrm{C}}$...$45\,^\circ {\textrm{C}}$) for the used mixture.

Figure 5 further reveals that the $1\sigma$ margin is relatively narrow for the calibration function due to the high number of calibration values. In contrast, the hue uncertainty of a single pixel amounted to $\sigma _{C_H}=3.4\,{\textrm{deg}}$ based on the hue fluctuations observed during the dynamic calibration. To estimate the temperature uncertainty of one pixel, the Gaussian error propagation of Eq. 1 yields

$$\begin{aligned} \sigma _{T_{\textrm{px}}}^2=\, & {} \frac{\sigma _{p_0}^2}{(C_H-p_1)^2} + \sigma _{p_2}^2 + \frac{p_0^2(\sigma _{p_1}^2+\sigma _{C_H}^2)}{(C_H-p_1)^4} \nonumber \\{} & {} + p_3^2(\sigma _{p_1}^2+\sigma _{C_H}^2) + (C_H-p_1)^2\sigma _{p_3}^2. \end{aligned}$$

(2)

For the measurements, this uncertainty was mitigated using $n_{\textrm{px}}=8 \times 8$ pixels to calculate the temperature of an interrogation window which resulted in a final uncertainty of $\sigma _T={\sigma _{T_{\textrm{px}}}}\big /{\sqrt{n_{\textrm{px}}}}$. Figure 6 shows that this leads to uncertainties of $\sigma _{T}< 0.1\,\textrm{K}$ for the vast majority of the temperature range. More specifically, $5.4\%$ of the measured values are below and $2.0\%$ are above the limits in which the TLC produce results with low uncertainties.

Fig. 6

Uncertainties of the temperature (black line) together with the temperature distribution of the measurement (gray histogram)

2.3 Heat flux calculation

The acquired fields of both velocity and temperature data were subsequently mapped onto a common grid using the respective camera calibration functions in order to allow the calculation of convective heat fluxes. Therefore, a normalized temperature $\theta$ is defined as

$$\begin{aligned} \theta =\frac{T-T_{{\textrm{in}}}}{\Delta T}. \end{aligned}$$

(3)

The local Nusselt number associated with a vertical heat transfer is

$$\begin{aligned} \text {Nu}_Z=\frac{H}{\alpha } u_Z \theta . \end{aligned}$$

(4)

In order to assess the correlation of vertical velocity and temperature, the local turbulent heat flux is expressed via

$$\begin{aligned} \text {Nu}_{\textrm{turb},\,Z}=\frac{H}{\alpha } u'_Z \theta '. \end{aligned}$$

(5)

The Reynolds decomposition was used to obtain the fluctuations of the vertical velocity and the temperature,

$$\begin{aligned} u'_Z = u_Z-\langle u_Z\rangle _t \quad \text {and}\quad \theta ' = \theta -\langle \theta \rangle _t, \end{aligned}$$

(6)

with $\langle \cdot \rangle _t$ being the time average over the entire measurement duration ($N_t=2427$ time steps).

To estimate the uncertainty of $\text {Nu}$, the values of $T_{{\textrm{in}}}$, $\Delta T$, H, and $\alpha$ are assumed to be without uncertainty. Then, the uncertainty of the normalized temperature is simply scaled by the temperature difference, $\sigma _{\theta }={\sigma _T}\big /{\vert \Delta T\vert }\approx 0.006$. In a similar stereo PIV setup, the uncertainty of the out-of-plane component was estimated to be $\sigma _{u_Z}\approx 0.003\,{\mathrm{m/s}}$ (Mommert 2022). As the stereoscopic viewing angles for the system used in Mommert (2022) were narrower than in the here presented setup, the value is a high estimation (Bhattacharya et al. 2016). Under these assumptions, the uncertainty of the local Nusselt numbers is

$$\begin{aligned} \sigma _{\text {Nu}_Z}^2 = \frac{H^2}{\alpha ^2} \left( {u_Z}^2 \sigma _{\theta }^2 + \theta ^2\sigma _{u_Z}^2 \right) . \end{aligned}$$

(7)

The resulting uncertainties are displayed in Fig. 7. In the top row, the resulting $\text {Nu}_Z$ (left) and $\sigma _{\text {Nu}_Z}$ (right) depending on possible vertical velocities $u_Z$ and temperatures $\theta$ are shown. In the bottom row, scatter plots reveal the dependency of the absolute (left) and relative uncertainties (right) for the calculated $\text {Nu}_Z$ based on the velocity and temperature ranges. These calculations show that the absolute uncertainties are limited to $\sigma _{\text {Nu}_Z}\lesssim 100$ implying decaying relative uncertainties for larger $\text {Nu}_Z$.

Fig. 7

Top left: Local Nusselt number $\text {Nu}_Z$ for possible velocities $u_Z$ and temperatures $\theta$. Top right: Uncertainties of the local Nusselt number $\sigma _{\text {Nu}_Z}$ for possible $u_Z$ and $\theta$. Bottom left: Uncertainties of the local Nusselt number $\sigma _{\text {Nu}_Z}$ for possible $\text {Nu}_Z$. Bottom right: Relative uncertainties $\sigma _{\text {Nu}_Z}/\vert \text {Nu}_Z\vert$ for possible $\vert \text {Nu}_Z\vert$

Assuming that all instantaneous $u_Z$ and $\theta$ contributing to the respective time average are subject to the same uncertainty, $\sigma _{u'_Z}\approx \sigma _{u_Z}$ and $\sigma _{\theta '}\approx \sigma _{\theta }$ apply for large $N_t$.

Therefore, the uncertainties for $\text {Nu}_{\textrm{turb},\,Z}$ are similar to those of $\text {Nu}_Z$.

In addition to the uncertainties, the turbulent heat fluxes are also subject to spatial resolution effects, which are examined in Appendix A.

3 Results and discussion

3.1 Flow structures

To present examples of the flow structures developing in the considered convection cell, Fig. 8 displays four uncorrelated instantaneous velocity and temperature fields. On the left side, the vectors represent the planar components of the velocities and the color of the vectors displays the out-of-plane component ($u_Z$). On the right side, the dimensionless temperatures $\theta$ are color-coded. The isotherms of $\theta =\left\{ 0.2;0.4\right\}$ are additionally plotted together with the velocity vectors on the left side in order to trace possible correlations. The masked areas at $Y \approx 0.65\,H$ were not considered in the following analysis as the respective values were distorted by the influence of light reflected from sensors at the rear wall. In addition to the masked regions, another artifact in the form of a slight temperature offset at $Y\approx 0.45\,H$ became apparent in the instantaneous fields. In this region, no mask was applied because the further analysis, including the temperature fluctuations, yielded smooth fields, confirming the offset nature.

Fig. 8

Snapshots of instantaneous velocity and temperature fields measured at $218.5\,\textrm{s}$, $240.5\,\textrm{s}$, $260.75\,\textrm{s}$ and $363\,\textrm{s}$ (top to bottom) displayed as vectors (left) and color contours (right). In the left column, every second vector is plotted along both axes. The out-of-plane velocity component is reflected by the color of the vectors. The isotherms $\theta =\left\{ 0.2; 0.4 \right\}$ are included in the left row

The fields of the different times shown in Fig. 8 consistently display a predominantly down-welling fluid motion, i.e., negative $u_Z$, in the front part of the sample ($0.1\,W \le Y \le 0.4\,W$) and larger proportions of up-welling fluid, i.e., positive $u_Z$, for larger Y. These are the footprints of the main longitudinal convection roll in the measurement plane. The temperatures remain mainly in the range of $0 \le \theta \le 0.4$ since the continuous inflow of cold air has a stronger influence on the surveyed region than the nearby heating at the bottom plate.

Besides, there are two types of recurring structures: The first are plumes reflected by regions of rising, warm ($\theta \ge 0.25$) fluid located in the front part of the sample ($0\le Y \le 0.1\,H$) extending up to $0.075\,L$ in X-direction. Since these plumes are characterized by higher temperatures than their surroundings, they most likely originate from the edge vortex between the heated bottom plate and the front wall where heat is accumulated. The second type of recurring structures are regions of rising fluid, which are elongated in Y-direction with a limited extension in X-direction with $0.05\,L$. They also reach into the front regions where the main convection roll induces a down-welling flow. Examples of this can be observed in Fig. 8 at $t=240.5\,\textrm{s}$ and $X=0.33\,L$ or at $t=363\,\textrm{s}$ and $X=0.28\,L$. Further, these examples only partially exhibit elevated temperatures in combination with their positive $u_Z$. Based on their elongated shape and independence from the occurrence of elevated temperatures, we classify these structures as the footprints of TG vortices.

3.2 Vertical heat fluxes

In order to gain deeper insight into these structures, we investigate the vertical transport of heat. As a first step, the time-averaged fields of $\text {Nu}_Z$ and $\text {Nu}_{\textrm{turb},\,Z}$ are displayed in Fig. 9. The field of mean convective heat flux values $\langle \text {Nu}_Z \rangle _t$ reflects a clear separation of negative values for the front part ($Y\le 0.5\,H$) and positive values at the rear. This arrangement differs from pure thermal convection, where negative heat fluxes occur only temporally and spatially limited (Shishkina and Wagner 2007; Moller et al. 2022). Since the dimensionless temperature is bound by $0\le \theta \le 1$, the sign of $\text {Nu}_Z$ solely depends on $u_Z$. While this normalization is not intuitive for Rayleigh–Bénard convection, it is suitable for this mixed convection flow, since a clearly defined mean temperature is not observed in the considered flow. Based on this normalization, the field of the local heat flux reflects that a large amount of heat transferred from the bottom plate to the air is transported in a complete cycle of the main convection roll, confirming the shielding effect of the inlet jet which prevents a heat transfer to the cooled top plate. This and the fact that the forced flow induces higher velocities in the main convection roll than buoyancy leads to local $\vert \text {Nu}_Z\vert$, which are several times higher than those obtained in Rayleigh–Bénard convection (Shishkina and Wagner 2007; Moller et al. 2022).

Fig. 9

Fields of the temporally averaged vertical heat fluxes $\langle \text {Nu}_{Z}\rangle _t$ (left) and turbulent heat fluxes $\langle \text {Nu}_{\textrm{turb},\,Z}\rangle _t$ (right)

Moreover, the mean field of the turbulent heat flux $\langle \text {Nu}_{\textrm{turb},\,Z} \rangle _t$ is displayed on the right side of Fig. 9. It exhibits positive values for the complete measurement domain indicating that $u_Z$ and $\theta$ are well correlated. The field of $\langle \text {Nu}_{\textrm{turb},\,Z} \rangle _t$ further contains a clear gradient in Y-direction with the largest mean turbulent heat flux around $Y\approx 0.1H$. Overall, this indicates that the proposed measurement method is suited for the quantification of local heat fluxes.

3.3 Turbulent heat flux statistics

To improve the understanding of the origin of the positive values of the time-averaged turbulent heat fluxes, a histogram of $\text {Nu}_{\textrm{turb},\,Z}$—covering the complete spatial and temporal extent of the measurement—is displayed in Fig. 10 with a bin width of 20. This histogram exhibits a mode value of zero. Hence, the positive mean values of $\text {Nu}_{\textrm{turb},\,Z}$ are attributed to a positive skewness of the distribution.

Fig. 10

Distribution of the vertical turbulent heat fluxes $\text {Nu}_{\textrm{turb},\,Z}$ with regard to the entire measurement domain

To further quantify the skewness, we define it as

$$\begin{aligned} \gamma = \frac{M_3(\text {Nu}_{\textrm{turb},\,Z})}{M_2(\text {Nu}_{\textrm{turb},\,Z})^\frac{3}{2}}, \end{aligned}$$

(8)

with $M_i$ as the central moment of order i. For the global distribution displayed in Fig. 10, this yields $\gamma \approx 3.3$.

Since the turbulent heat fluxes proved to be strongly dependent on Y, the skewness $\gamma$ is subsequently investigated for each Y-grid coordinate. For this purpose, the left side of Fig. 11 reflects the mean turbulent heat flux ($\langle \text {Nu}_{\textrm{turb},\,Z} \rangle _{X,t}$) and the skewness of the distributions of individual Y. Further, three of these heat flux distributions are shown on the right side of Fig. 11 for positions marked on the left side.

Fig. 11

Left side: Dependence of the skewness $\gamma$ and the mean value $\langle \text {Nu}_{\textrm{turb},\,Z} \rangle _{X,t}$ on Y. Right side: Exemplary distributions of $\text {Nu}_{\textrm{turb},\,Z}$ for the Y positions marked on left side

The Y-dependency of the mean values $\langle \text {Nu}_{\textrm{turb},\,Z} \rangle _{X,t}$ reflects the 2-dimensional distribution shown in Fig. 9 and exhibits a maximum at $Y \approx 0.1\,H$. However, the maximum of the skewness is located further away from the wall ($Y \approx 0.25\,H$). This allows to differentiate between the two different types of structures mentioned before: The plumes rising near the front wall are associated with the maximum of $\langle \text {Nu}_{\textrm{turb},\,Z} \rangle _{X,t}$ while exhibiting only a relatively low positive skewness. The corresponding turbulent heat flux histogram (green) of Fig. 11 reveals that the high mean values are associated with a large variance in combination with a moderate skewness.

In contrast, high skewness values and moderate mean values of the turbulent heat flux can be observed in the region of larger Y, where TG vortices develop. The significance of the skewness can be traced by the red and purple histograms in Fig. 11. While the left tail of both distributions is almost identical, the red distribution exhibits significantly more extreme events on the right side. This leads to a larger right tail and ultimately an increased skewness and mean value compared to the purple distribution.

A connection between the high skewness values and TG vortices is supported by earlier research based on the Rayleigh stability criterion (Mommert et al. 2020). These investigations showed that—for similar dimensionless numbers as in the present case—TG vortices are generated at wall distances of $0.15\,H \le Y \le 0.25\,H$. This corresponds to the increase in the skewness values. This increase is followed by a less steep decline as the vortices decay while they are transported in Y-direction by the main convection roll. Therefore, we regard high skewness values as a statistical footprint of TG vortices.

4 Conclusion

We successfully applied a new measurement method combining stereoscopic particle image velocimetry with dynamically calibrated particle image thermometry to mixed convection of air. The simultaneously available velocity and temperature fields were successfully used to calculate local vertical heat fluxes. The analysis of the absolute vertical heat fluxes revealed the accumulation of heat in the large-scale circulation present in the investigated setup including a downward directed heat transfer. The investigation of the corresponding turbulent heat fluxes showed that the vertical velocity component and the temperature are well correlated in all regions of the measurement domain. A more profound statistical analysis of the vertical turbulent heat fluxes further revealed two flow regimes: The first includes plumes at the front wall, where rising air is associated with the maximum of the turbulent heat flux. This manifests itself in a high variance and moderate skewness in the statistical distributions at the respective Y-values. The second regime corresponds to Taylor–Görtler-like vortices, which are characterized by elevated skewness values and moderate mean values as statistical footprints.

While this study showed that the heat transport in mixed convection is driven by processes clearly different from those of purely thermal convection, like Rayleigh-Bénard convection, questions regarding a quantitative comparison still remain unanswered. For such a comparative study, a unified temperature normalization is needed to determine how the contribution of forced convection enhances or suppresses the heat transport.

Appendix A: Spatial resolution effects

Both PIV and PIT rely on spatial averaging within the respective interrogation windows. Therefore, the size of the interrogation windows affects the turbulent heat fluxes, since they are the product of both temperature and velocity fluctuations. To investigate this influence, we coarsened the raw velocity and temperature grids by downsampling. Specifically, regions of $2\times 2$, $4\times 4$ and $8\times 8$ grid points were combined by averaging.

Figure 12 adds histograms of $\text {Nu}_{\textrm{turb},\,Z}$ for the different resolutions to the one originally shown in Fig. 10. It shows that the distributions are narrower for coarser grids. However, this effect is more pronounced for the left tail of the distribution, implying that regions of negative turbulent heat fluxes are more likely to be small and require high spatial resolutions to be mapped correctly.

Fig. 12

Distribution of the vertical turbulent heat fluxes $\text {Nu}_{\textrm{turb},\,Z}$ with respect to the whole measurement domain for different grid resolutions

To see how this affects the skewness, Fig. 13 shows the results for the coarsened grids in the context of Fig. 11. With respect to the mean values $\langle \text {Nu}_{\textrm{turb},\,Z} \rangle _{X,t}$, all grid sizes up to $4\times 4$ consistently cover the peak at $Y\approx 0.1\,H$ and its slopes. Only the $8\times 8$ grid is to coarse to sufficiently cover the peak.

For the Y-dependence of the skewness values $\gamma$, the stronger effect on the negative turbulent heat fluxes leads to increased skewness values for coarser grids. Accordingly, the results of the spatial resolution achieved here may still overestimate the skewness values, since not all scales of the flow were fully resolved. However, we are confident that the results presented here, which define the characteristics of the flow structures, are universal with respect to grid size, since the shape and maximum locations of the $\gamma$-graphs remain the same for all grids studied.

Fig. 13

Dependence of the skewness $\gamma$ and the mean value $\langle \text {Nu}_{\textrm{turb},\,Z} \rangle _{X,t}$ on Y for different grid resolutions