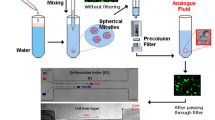
Abstract
The reduction of blood damage is still a big challenge in blood-carrying medical devices. In vitro experiments are performed to investigate the damage-causing effects, but due to the opaqueness of blood cells, only near-wall flows can be observed. Thus, several transparent blood models to visualize the rheologic behavior of blood have been proposed and examined. Nevertheless, two-phase blood models with added particles still represent the properties of blood inadequately or are very expensive and complex to produce. In this in vitro study, the viscosity, the flow behavior and the cell deformation of human red blood cells have been compared to a novel, easy-to-produce, two-phase blood model fluid with deformable alginate microspheres. The comparison has been performed in a cone-plate rheometer, a straight and a hyperbolic converging microchannel. The viscosity of the blood model fluid with a particle fraction of 30% showed a shear-thinning behavior, comparable to that of blood at room and human body temperature within shear rates from 7 to \(2000\,\hbox {s}^{-1}\). The alginate microspheres were deformable in an extensional flow and formed a cell free layer comparable to that of blood in a straight microchannel. The experiments showed a good optical accessibility of the two-phase flow with traceable movements of individual microspheres in the center of the microchannel. It could be shown that our proposed blood model fluid is a promising tool for the analysis of two-phase flows in complex flow geometries.
Graphical Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Blood damage in blood-carrying medical devices like cardiac assist devices, oxygenators or artificial heart valves continue to be challenges that need to be addressed. Therefore, in vitro experiments are mostly performed to investigate predetermined areas of these devices and to measure hemolysis and thrombogenicity. However, the hemolysis measurement in particular is then only related to the whole system as a black box, and it is not possible to identify particularly hemolytic areas. Especially due to the two-phase character and non-Newtonian behavior of blood, there are numerous effects that influence hemolysis. Specifics of the theoretical motion of the RBCs in various types of flows have yet to be experimentally analyzed. (Faghih and Sharp 2019) Nevertheless, the analysis of the fluid dynamics of in vivo human blood samples is difficult due to cost, safety, and ethical reasons. Another important disadvantage of using whole blood is the degradation of blood samples over time and the variability of properties in different samples from different donors (Baskurt et al. 2009; Sadek et al. 2021; Sousa et al. 2011). Additionally, due to the opaque RBCs, flow can only be visualized in areas close to the wall. Therefore, in vitro studies with blood-analogous fluids are a common alternative to visualize the flow with repeatable experiments (Wickramasinghe et al. 2002; Lerche et al. 1993; Campo-Deaño et al. 2013; Li et al. 2010; Deplano et al. 2014).
Thus, there has been an increasing interest in developing transparent fluids with similar flow behaviors to blood, which have the added advantage of not involving ethical and safety difficulties and behave in the identical way in each experiment (Sousa et al. 2011; Sadek et al. 2021). The most commonly used blood model fluid is a water-glycerol mixture (Buchmann et al. 2011; Deplano et al. 2014; Doutel et al. 2015; Geoghegan et al. 2012; Gray et al. 2007; Yousif et al. 2011; Li et al. 2010). This Newtonian single-phase fluid can be sufficient under flow conditions with high shear rates (Sadek et al. 2021), because the blood viscosity is often regarded as Newtonian at shear rates higher than \(1000\hbox { s}^{-1}\) (Baskurt et al. 2007). It is often used to validate numerical flow simulations in experimental setups (Su et al. 2012; Schüle et al. 2016). However, investigations have shown that a non-Newtonian flow can only be represented insufficiently by a Newtonian fluid. The wall shear stresses and occurring eddy sizes differ greatly from each other (Gray et al. 2007; Zhang et al. 2008; Pohl et al. 2000; Mann et al. 1987).
Further additives like polyacrylamide or xanthan gum are therefore used to mimic the shear-thinning behavior of blood (Brindise et al. 2018; Campo-Deaño et al. 2011; Completo et al. 2014; Najjari et al. 2016; Sousa et al. 2011). Nevertheless, blood is a two-phase fluid containing 36–50% (physiological hematocrit) of deformable cells (Baskurt et al. 2007). The mechanical properties and interaction of red blood cells highly influence the blood rheology, as they account for 99% of all cells in the blood. RBCs have a density of \(1.125\hbox { g mL}^{-1}\), whereas the plasma has a density of \(1.025\hbox { g mL}^{-1}\) (Baskurt et al. 2007). This leads to a density deviation of 0.1 g/ml and sedimentation of the cells in low velocities. The axial migration of RBCs in small vessels leads to a shear-thinning effect that lowers the viscosity of blood by forming a cell free layer (CFL). It is observed in vessels below \(300\,\upmu \hbox {m}\) and is even greater in smaller vessels from 10 to \(100\,\upmu \hbox {m}\), known as the Fåhræus-Lindqvist effect. Moreover, it results in a decreased hematocrit in smaller vessels because the cellular content of the smaller side vessels is mainly fed by the marginal stream of the originating vessel (plasma skimming). (Baskurt et al. 2007; Sadek et al. 2021) These effects have a huge influence and determine where hemolysis can occur (Murashige et al. 2016; Kink and Reul 2004; Leslie et al. 2013).
There are several approaches to model RBCs in transparent fluids. Rigid particles like polymethylmethacrylate (PMMA) have been used (Calejo et al. 2016; Pinho et al. 2017), but the rheologic behavior of blood is highly influenced by the deformabilty and flexibility of RBCs (Baskurt et al. 2007). Thus, deformable microspheres of polydimethylsiloxane (PDMS) (Muñoz-Sánchez et al. 2016; Anes et al. 2018; Pinho et al. 2019), surfactant micelles (Lima et al. 2020) or so called ghost cells (erythrocytes deprived of hemoglobin) (Jansen 2018; Schöps et al. 2020) have been examined (for a full review see also Sadek et al. (2021)).
Although these models come much closer to mimicking the rheology of blood than Newtonian fluids, they still have significant differences and limitations. The model particles are too rigid, have different sedimentation or aggregation effects, are not suitable for hematocrits close to the physiological magnitude, or they are costly, time-consuming or difficult to produce on a large scale (Sousa et al. 2011; Calejo et al. 2016; Pinho et al. 2017, 2019; Lima et al. 2020; Schöps et al. 2020; Sadek et al. 2021). Despite numerous advances, the development of a reliable blood model fluid with a particle fraction comparable to a physiological hematocrit remains a major challenge (Sadek et al. 2021).
The objective of this work was to examine an easy-to-produce, transparent, two-phase blood model fluid with deformable alginate microspheres as RBC models. They have already been used with larger diameter as sufficient tracer particles with a small particle fraction to investigate near wall flows (wall Particle Image Velocimetry (PIV)) (Kertzscher et al. 2008). Ertürk et al. (2013) used approximately \(20\,\upmu \hbox {m}\) alginate microspheres with fluorescein as tracer particles in oil and air flow and Varela et al. (2016) functionalized them with Rhodamin B and showed the applicability in PIV and Planar Laser-Induced Fluorescence (PLIF). The microspheres are suitable to follow the flow in a liquid as their porous structure allows them to take on the density of the surrounding fluid (Ertürk et al. 2013). Since alginate spheres have already been used in PIV measurement, and we observed a suitable transparency and traceability a further investigation of their capability of modeling RBCs was the aim of this study. Moreover, the microspheres are deformable but stable in density, size and dimensions.
The here proposed alginate microspheres are produced with a water-in-oil emulsion method, that is well suited for up-scaling (Poncelet et al. 1992; Heng et al. 2003) and then dispersed in a water-calcium-chloride suspension (7%\(_{m/V}\)) with a particle fraction of up to 30%. It is hypothesized that the novel transparent two-phase blood model fluid can mimic important blood rheology parameters. Therefore the shear thinning effect in a cone-plate rheometer and the flow behavior and visual properties of human blood in a straight microchannel as well as the cell deformation of human RBCs in a microchannel with a hyperbolic contraction have been compared to the blood model.
2 Methods
2.1 Blood samples
To compare the two-phase blood model fluid with human blood, each experiment was performed with both fluids. The samples have been obtained by venipuncture of healthy male or female volunteers with hematological profiles in a physiological range. Citrate phosphate dextrose adenine (CPDA-1) was used as an anticoagulant solution [S-Monovette, CPDA1, 5.6mL, Sarstedt, Nümbrecht, Germany]. The samples were stored at \(7^{\circ }\hbox {C}\) and used within 12 hours after the venipuncture. The hematocrit of the blood sample was determined directly after the venipuncture [XP300, Sysmex America, Inc., Lincolnshire, U.S.A.]. If hemodilution was necessary for the comparison with the blood model, the sample was weighed and diluted with phosphate buffered saline solution (DPBS) (Dulbecco’s Phosphate Buffered Saline (1x), Life Technologies, Carlsbad, USA) to the desired hematocrit. This standard practice is recommended by the American Society of Testing and Materials for blood experiments (ASTM F1841-19 2019; ASTM F1841-97 2017).
2.2 Two-phase blood model
Alginate is the structural component of brown algae. As a salt (e.g., sodium alginate), it can be dissolved in water and gelled by adding drops into calcium chloride (CaCl\(_2\)) to form an elastic and transparent bead. In this study, the water in oil emulsion method was used to produce a sufficiently large number of microspheres. (Poncelet et al. 1992; Heng et al. 2003)
An emulsion of paraffin oil [Paraffin oil high viscosity, Art. No. 8904.1, Carl Roth, Karlsruhe, Germany] (continuous phase) and a 3%\(_{m/V}\) alginate solution [Sodium alginate, technical, SLR, S/2160/53, Fisher Chemical, Leicestershire, U.K.] (disperse phase) was prepared: 100 mL oil was filled in a 300 mL glass container and 0.2 mL of Span 80 [Span 80, Art. No. 9426.1, Carl Roth, Karlsruhe, Germany] (2%\(_{V}\) of the alginate solution) was added as an emulsifier. The mixture was then stirred for two hours while 10 mL of the alginate solution was added continuously. To cross-link the droplets, 150 mL calcium chloride solution (7%\(_{m/V}\)) [Calcium chloride dihydrate, C7902, BioReagent, Sigma-Aldrich, Darmstadt, Germany] was then added to the emulsion by a syringe pump [PHD ULTRA, Item 70-3007, Harvard Apparatus, Massachusetts, U.S.] while stirring continuously. Cured alginate microspheres were formed. In the last step, the stirring was stopped and the oil separates from the rest. The alginate microspheres sink to the bottom in the aqueous phase and were separated from the oil.
Afterward, the microspheres were sorted by size with a sedimentation method, to be in the same order of magnitude as the average RBC diameter of \(8.5\,\upmu \hbox {m}\) (Baskurt et al. 2007). A roller pump [Reglo Digital MS-4/12 ISM 597, Ismatec, Opfikon, Switzerland] generates a volume flow in a tube with a conical taper that leads vertically into a beaker with the alginate microspheres in a calcium chloride solution The fluid moves upwards in the tube with a pump velocity of \(0.003\,\hbox {mm s}^{-1}\). The sedimentation velocity of the particles depends on their diameter. So, particles whose sedimentation velocity is greater than the velocity in the tube are not transported upwards. This makes it possible to determine a threshold diameter that can be sucked in. The resulting size distribution of the microspheres is \(8.37\,\upmu \hbox {m}\) \(\pm 1.87\,\upmu \hbox {m}\) and has been measured microscopically [Digital Microscope VHX-970F, Keyence, Milton Keynes, U.K.].
The density of alginate microspheres was determined by comparing their sedimentation behavior in different water-glycerol mixtures [Glycerol (Certified ACS), Fisher Chemical, Leicestershire, U.K.] of known density. No sedimentation or flotation could be detected in a solution with a density of \(1.116\hbox { g mL}^{-1}\).
For the plasma model, calcium chloride has to be added as a stabilizing factor for the microspheres. In preliminary studies, different water-CaCl\(_2\)-glycerol mixtures were tested as plasma models, but resulted in too high viscosities at high shear rates. Thus, a plasma model with a Newtonian solution of 7%\(_{m/V}\) calcium chloride in distilled water with a density of 1.044 \(\hbox {g mL}^{-1}\) was chosen for this study. The particle fraction of the model was 30%, 5% or 1% depending on the measurement and the hematocrit of the compared blood sample. To adjust the particle fraction, the alginate microspheres in the storage fluid (7% CaCl\(_2\)-solution) are centrifuged at 4000 rcf for 5 min. The fluid is pipetted off and the sample is weighed. To estimate the remaining 7% CaCl\(_2\)-solution with a density of 1.044 g/ml in between the microspheres, the packing factor was estimated. For microspheres with an equal radius it lies between 0.52 (cubical packing) and 0.74 (pyramidal or tetrahedral packing) (White and Walton 1937). Because of the deformability of the alginate microspheres and the variation in size, a high packing density of 0.7 was selected. Thus, the particle fraction of the microspheres can be calculated and diluted with the calcium chloride solution to the desired particle fraction.
2.3 Viscosity measurement
To measure the viscosity of the two-phase blood model fluid in dependence of shear rates rheometer measurements [mcr-502-wesp, Anton Paar, Graz, Austria] were performed. The cone-plate shearing plane with a gap of 100 \(\upmu \hbox {m}\) was used. The particle fraction of the model and hematocrit of the blood was 30%. All measurements were performed at 22\(^{\circ }\hbox {C}\) (room temperature) as well as 37\(^{\circ }\hbox {C}\) (body temperature). At both temperatures, the instrument measured the data points at equal intervals with logarithmic scaling from 6.69 to 2000 \({\hbox {sec}^{-1}}\). The progression of the viscosity curve was compared with viscosity values found in the literature. Chien (1975) and Thurston and Henderson (2007) measured the viscosity of human blood in a concentric cylinder couette viscometer at a temperature of 37\(^{\circ }\hbox {C}\) from 0.1 to 230 \(\hbox {s}^{-1}\) and at a temperature of 22\(^{\circ }\hbox {C}\) and from 0.02 to 130 \(\hbox {s}^{-1}\) respectively. Cokelet and Meiselman (2007) used the same method and measured the shear-dependent blood viscosity from 0.02 to 130 \(\hbox {s}^{-1}\) (the temperature was not provided).
2.4 Microfluidic setup
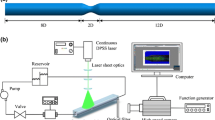
The experimental setup for the investigation of the flow inside the microchannels consists of a digital microscope [Digital Microscope VHX-970F, Keyence, Milton Keynes, U.K.] and an objective lens, combined with a high-speed camera [MotionXtra N4-S3, IDT, Newark, New Jersey, U.S.]. The different microchannels were placed on the stage of the microscope and the working fluids were drawn from a reservoir by a syringe pump [PHD ULTRA, Item 70-3007, Harvard Apparatus, Massachusetts, U.S.]. The blood was placed on a mixer plate [MS1 Minishaker, IKA, Staufen, Germany] to avoid the segregation of the cells and the plasma. The blood model fluid was continuously mixed by a magnetic stirrer [BenchMate VM-D, Variomag, Daytona Beach, U.S.] (see Fig. 1).
2.5 Visibility and cell free layer
For the analysis of the flow behavior in a straight microchannel, a circular microchannel with a diameter of 306 \(\upmu \hbox {m}\) was used. The working fluids were pumped through the microchannel at room temperature with a constant flow rate of \(12\,\hbox {mL h}^{-1}\). The volume flow was chosen to be of the same order of magnitude as the volume flow of blood in arterioles of similar size (Fåhraeus 1929; Fahraeus and Lindqvist 1931). For the measurement of the CFL, the blood had a hematocrit of 7% and the blood model fluid a particle fraction of 5%. For the comparison of the flow visibility, the undiluted blood had a hematocrit of 42% and the blood model fluid a particle fraction of 30%. Images of the flowing blood, or blood model, were taken at a frame rate of 3000 \(\hbox {s}^{-1}\). A sequence of 500 greyscale images was taken at a resolution of \(1016\times 720\) pixels. All images show a cross section of the microfluidic channel that was focused on the widest part of the microchannel.
2.6 Deformation measurement
For the observation of the cell deformation a microchannel in fused silica was produced by selective laser-induced etching and welding [LightFab GmbH, Aachen]. In the microchannel, a hyperbolic constriction is followed by a sudden expansion. As shown in Fig. 2, the width (w) and constriction length (l) of the microchannel are both 400 \(\upmu \hbox {m}\) with a minimum gap in the microchannel (g) and total depth of 20 \(\upmu \hbox {m}\). This defined geometry allows strong extensional flows with a homogeneous expansion rate to be generated near the center line (Sousa et al. 2011; Campo-Deaño et al. 2011). The Hencky strain (see equation 1) (Feigl et al. 2003) of the microchannel corresponds to the Hencky strains used in other studies to analyze the deformation of RBC models (Pinho et al. 2017, 2019; Carneiro et al. 2021):
To observe individual microspheres or RBCs, the working fluids have been adjusted to a particle fraction or hematocrit of 1% and were withdrawn from the beaker with a velocity of \(10\,\upmu \hbox {L}/\hbox {min}\) at room temperature (Lee et al. 2009). This results in a laminar flow with a Reynolds number of \(Re =8.2\) for the RBCs in DPBS (dynamic viscosity of \(1.02\,\hbox {mPa s}\), density of \(1.0053\hbox { g mL}^{-1}\)) and \(Re = 8.6\) for the alginate microspheres in CaCl\(_2\)-solution (dynamic viscosity of \({1.003}\,\hbox {mPa s}\), density of \(1.044\hbox { g mL}^{-1}\)). The average velocity is 0.417 m/s and the maximum velocity is 0.833 m/s. This results in an average shear rate in the investigated area of 83 330 \(\hbox {s}^{-1}\) and thus a flow in the linear range of the shear-thinning viscosity curve. The average shear stress is in the range of 83.8 Pa to 85 Pa.
The flow induced deformation has been quantified by the Deformation Index (DI) that ranges from zero (no deformation) to one (maximal deformation):
Where x is the major and y the minor axis length of an ellipsoidal cell or microsphere. The DI was determined in two regions of interest (ROIs) (see Fig. 3): one in the narrowest region of the hyperbolic constriction with a size of 20 \(\upmu \hbox {m} \times {50}\,\upmu \hbox {m}\) and one in the abrupt expansion after the constriction with 50 \(\upmu \hbox {m} \times {50}\,\upmu \hbox {m}\).
The two ROIs in the hyperbolic converging microchannel with a 20 \(\upmu \hbox {m}\) constriction. Region 1 (R1) with a size of 20 \(\upmu \hbox {m} \times {50}\,\upmu \hbox {m}\) and Region 2 (R2) in the abrupt expansion behind the constriction with 50 \(\upmu \hbox {m} \times {50}\,\upmu \hbox {m}\)
A set of 500 greyscale images was taken at 10 000 frames per second and imported into an image processing software [ImageJ, NIH, U.S.] (Schneider et al. 2012). The images were converted to a binary picture using a chosen threshold and the flowing RBCs / alginate microspheres were measured frame by frame automatically by the Analyze Particles function. The output results of this measurement were the major and minor axis lengths of the fitted ellipse of the particles, and the x-y coordinates of their centroid. The data of the DI of all particles in R1 and R2 were determined, and then averaged for each region separately. To exclude overlapping particles in the ROIs, only particle sizes with a major value of 25 \(\upmu \hbox {m}\), an area from 10 to \(150\,\upmu \hbox {m}^{2}\) and with a DI less than 0.7 were considered (Dobbe et al. 2002; Lee et al. 2009; Carneiro et al. 2021; Yaginuma et al. 2013).
3 Results
3.1 Viscosity
The cone-plate rheometer measurement showed a shear-thinning viscosity of the blood model fluid at 22\(^{\circ }\hbox {C}\) as well as 37\(^{\circ }\hbox {C}\) (see Fig. 4). Compared to the measured viscosity values of human blood from the studies by Chien (1975); Thurston and Henderson (2007) as well as Cokelet and Meiselman (2007), the blood model fluid behaves similar to blood. From 1000 to 2000 \(\hbox {s}^{-1}\), the curve of the blood model fluid reached an almost constant value of 0.0046 \(\hbox {Pa s}\) at 22\(^{\circ }\hbox {C}\) and 0.0037 \(\hbox {Pa s}\) at 37\(^{\circ }\hbox {C}\). It is well-established that at high shear rates above 100 \(\hbox {s}^{-1}\), the viscosity of healthy human blood with 40–47% hematocrit asymptotically approaches values of 0.004 \(\hbox {Pa s}\) to 0.006 \(\hbox {Pa s}\) at room temperature and of 0.0035 \(\hbox {Pa s}\) to 0.004 \(\hbox {Pa s}\) at body temperature (Brooks et al. 1970; Arora 2006; Thurston and Henderson 2007; Chien 1975; Cokelet and Meiselman 2007). Thus, the viscosity of the blood model fluid with a particle fraction of 30% is in the same order of magnitude as the viscosity of human blood at 40–47% hematocrit for shear rates between 6.69 to 2000 \(\hbox {s}^{-1}\).
Rheometer measurement in a cone-plate rheometer [mcr-502-wesp, Anton Paar, Graz, Austria] at temperatures of 22\(^{\circ }\hbox {C}\) and 37\(^{\circ }\hbox {C}\) of the blood model fluid with a particle fraction of 30% in comparison with the viscosity of blood at a hematocrit of 40–45% . The viscosity of the blood model fluid was measured at shear rates from 6.69 to 2000 \(\hbox {s}^{-1}\). The viscosity of human blood was found in previous studies. Chien (1975) measured the viscosity of human blood at a temperature of 37\(^{\circ }\hbox {C}\) from 0.1 to 230 \(\hbox {s}^{-1}\), Thurston and Henderson (2007) at a temperature of 22\(^{\circ }\hbox {C}\) and from 0.02 to 130 \(\hbox {s}^{-1}\) and Cokelet and Meiselman (2007) from 0.05 to 1500 \(\hbox {s}^{-1}\) (the temperature was not provided (n.p.)). All three studies used a concentric cylinder couette viscometer
3.2 Visibility and CFL in a straight microchannel
In the straight microchannel two different hematocrits were compared to a particle fraction that was in proportion to that detected in the viscosity measurement (30–42%). Comparing the blood model fluid with a particle fraction of 5%, a blood sample was diluted to a hematocrit of 7%. The 30% particle fraction was compared to an undiluted blood sample with 42% hematocrit (see Fig. 5). In the experiments with 7% blood and 5% alginate microspheres, the alginate microspheres were clearly distinguishable from each other. Single RBCs were only differentiable in the flow near the wall. Whereas in the flow of the blood model, individual alginate microspheres could be differentiated from each other due to their transparency and their movement could even be followed in the center of the microchannel. In both fluids, a similar cell-free layer (CFL) of 22 \(\upmu \hbox {m} \pm 3\,\upmu \hbox {m}\) occurred. Within the blood model, faster aggregate formation in the tubes and microchannel were observed when stopping the syringe pump.
In the comparison of 30% particle fraction to 42% hematocrit, no CFL and no individual RBCs were visible. The alginate microspheres were still distinguishable from each other in the focus plane at the center of the microchannel.
3.3 Deformation
To measure the deformation index, n = 175 RBCs and n = 48 alginate microspheres were detected in region 1. In region 2, n = 804 RBCs and n = 348 microspheres were evaluated. The qualitative observation (see Fig. 6) of the images already showed a considerable deformation of the alginate microspheres as well as the RBCs. The average DI of the alginate microspheres in the maximal constriction region R1 was 0.44 ±0.14 and in the abrupt expansion region R2 it was 0.19 ±0.11 (see Fig. 7). The mean DI of the RBCs in region 1 was 0.51 ±0.14 and in region 2 a deformation of 0.31 ±0.17 occurred. The mean value of the DI of the alginate microspheres in R1 is statistically significantly lower from that of the RBC (\(p = 4.8288*e^{-4}\), Mann–Whitney-U-test) with a mean difference of 14%. In R2, the DI of the alginate microspheres is 40% lower in mean (\(p = 8.345*e^{-36}\), Mann–Whitney-U-test).
Evaluation of the deformation index of the alginate microspheres and RBCs in the constriction region (1) and expansion region (2). In region 1 the RBCs (n = 175) show a mean DI of 0.51 ±0.14 and the alginate microspheres (n = 48) show a DI of 0.44 ±0.14. In region 2 the RBCs (n = 804) have a DI of 0.31 ±0.17 and the alginate microspheres (n = 348) of 0.19 ±0.11
4 Discussion
The properties of the proposed blood model fluid were analyzed and compared to human blood successfully. The described production process is easy to apply, and an upscaling of the produced quantity can be achieved with a few adjustments to the setup. The transparency, deformability and ease of manufacture of the microspheres support the use of alginate. Another advantage for future adaptations could be that other substances can be embedded in the microspheres during the manufacturing process. In this way, the optical but also magnetic or electrical properties of the model can be further adapted. The size of the alginate microspheres used in this study was 8.37 \(\upmu \hbox {m}\) \({\pm 1.87}\,\upmu \hbox {m}\) in diameter. Compared to RBCs with a biconcave disk shape of 2.4 \(\upmu \hbox {m}\) thickness, a diameter of 8.5 \(\upmu \hbox {m}\) (Baskurt et al. 2007), the size of the microspheres corresponds very well, but the spherical shape differs to the disk shape of the RBCs. However, if one takes into account that almost all two-phase blood models use spherical particles as RBC substitutes and in PIV measurements spherical particles are also commonly used, this limitation is not a specific disadvantage of the here proposed model. Ghost cells (Jansen 2018; Schöps et al. 2020) offer an advantage here, but it remains to be investigated whether the processing has a negative effect on the deformability and flow behavior of the former RBCs. The density of RBCs is 1.125 \(\hbox {g mL}^{-1}\) and that of alginate microspheres is 1.116 \(\hbox {g mL}^{-1}\). The surrounding plasma or calcium-chloride solution has a density of 1.025 \(\hbox {g mL}^{-1}\) and 1.044 \(\hbox {g mL}^{-1}\) respectively. Thus, the density deviation of the blood model with 7% is in the same order of magnitude as that of blood with 10%. This should lead to a similar behavior in sedimentation.
The viscosity of blood varies greatly depending on hematocrit, temperature and donor. The viscosity of the blood model fluid lies within this physiological deviation range at temperatures of 22\(^{\circ }\hbox {C}\) and 37\(^{\circ }\hbox {C}\) and hematocrits of 40–47%. Even though the plasma model (calcium chloride solution) is a Newtonian fluid, the blood model fluid showed a shear-thinning non-Newtonian viscosity. At low shear rates of 6.69 \(\hbox {s}^{-1}\) to 12 \(\hbox {s}^{-1}\) at 37\(^{\circ }\hbox {C}\) the viscosity of the blood model fluid varied slightly. One reason could be aggregation and sedimentation effects during the measurement, but even more likely the measuring method, the cone-plate rheometer, used here. The geometry of cone-plate rotational rheometers can accelerate cell sedimentation during rotation at very low shear rates and is thus not that reliable in this range (Schmid-Schönbein et al. 1968; Cokelet and Meiselman 2007). The viscosity values taken from the literature and compared to the blood model fluid were obtained from cylindrical couette rheometers. Further measurements of the blood model fluid in an equal device should therefore be carried out in future.
The slope of the viscosity of the blood model fluid in low shear rates is higher than in the measurements with blood. This can be caused by aggregate formation of the alginate microspheres. This formation of rouleaux is physiological in blood and causes a thixotropic (time-dependent) behavior at low shear rates up to about 10 \(\hbox {s}^{-1}\). It is due to the process of breaking up rouleaux into individual erythrocytes. (Baskurt et al. 2007; Huang et al. 1987) The binding of alginate microspheres to each other appears to be more pronounced than in RBCs. This effect has also been observed in other blood substitute models (Carneiro et al. 2021). A future improvement could be to add Dextran 40 to improve the shear-thinning effect and decrease aggregation (Brooks et al. 1970; Flormann et al. 2016; Pinho et al. 2019; Lima et al. 2020). Nevertheless, the measurement proved that the blood model fluid with a particle fraction of 30% is suitable to model blood at room and body temperature with a 40–47% hematocrit in shear rates of 6.69 \(\hbox {s}^{-1}\) to 2000 \(\hbox {s}^{-1}\).
In the straight microchannel, the advantages resulting from the transparency of the blood model fluid were shown. It was possible to detect the movements of individual microspheres at a particle fraction of 5% and 30% in the center of the microchannel. Within the 7% and 42% samples no individual RBC was visible, due to the opaqueness of blood. It has already been shown, that the alginate microspheres are well suited as tracer particles in PIV and PLIF at low particle fractions and even fluorescein or other dyes can be added to further improve the traceability (Kertzscher et al. 2008; Ertürk et al. 2013; Varela et al. 2016). By using deformable microspheres, the results would be more comparable to the actual cell movement. In future studies, PIV measurements with alginate microspheres could focus on higher particle fractions to study the two-phase flow with microsphere interactions in laser light sections in the center of the flow.
Within the straight microchannel, the CFL of the blood model fluid at a particle fraction of 5% and blood sample at a hematocrit of 7% is comparable and can be further investigated for additional hematocrits in microchannels with a hyperbolic constriction as used in the deformation section (see Fig. 2, Pinho et al. (2017, 2019) and Carneiro et al. (2021)).
In order to achieve better comparability with other blood models, the microchannel used for the deformation investigations was based on previous studies (Sousa et al. 2011; Campo-Deaño et al. 2011; Pinho et al. 2017, 2019; Carneiro et al. 2021). In both regions of interest (R1 and R2), the DI of the alginate microspheres was smaller than that of the RBCs with a percentage deviation of 14% and 40%, respectively. Nevertheless, they reached a considerable deformation that also explains the shear-thinning viscosity of the whole blood model. The average deformation of RBCs in the narrowest part of the microchannel was 0.51 ± 0.14. The average shear stress is in the range of 83.8 Pa to 85 Pa. According to the formula of (Faghih and Sharp 2020), this results in an aspect ratio of 3.1 and therefore a theoretical deformation index of 0.52. This is also in line with experimental studies using the same method to measure the DI as in this study (Lee et al. 2009; Pinho et al. 2019; Zhao et al. 2006; Yaginuma et al. 2013).
Behind the constriction in R2, the RBCs remain in the ellipsoidal shape for a longer time while the alginate microspheres return to their original shape more quickly so their DI was 40% lower. Thus, the relaxation time of the RBCs, that depends on the viscoelasticity (Faghih and Sharp 2019), is longer than that of alginate microspheres. The viscoelasticity of the alginate microspheres has not yet been examined further. It is planned as a future step.
N = 48 was the lowest number of measurable results for the alginate microspheres in the small constriction and was found to be a sufficiently high number since standard deviation and deformation index converged. The same image sequence with the same evaluation method was chosen for the alginate microspheres in R2 and the RBCs in R1 and R2, resulting in higher numbers of measurable results.
Compared with another blood model fluid consisting of PDMS particles in Dextran 40, that showed the best agreement in modeling the deformation of RBCs so far (Sadek et al. 2021; Pinho et al. 2019; Carneiro et al. 2021), the average percentage deviation of the deformation compared to RBCs in R1 and R2 is lower: By examining the same regions of interest, Pinho et al. (2019) detected a deviation of approximately 20% in R1 and >50% in R2. In the study of Carneiro et al. (2021) a percentage deviation of the DI of approximately 25% in R1 and >50% in R2 were measured. Nevertheless, the standard deviation of the DIs of the alginate microspheres is higher than that of the 6:4 PDMS particles in Dextran 40 (Pinho et al. 2019; Carneiro et al. 2021).
5 Conclusion
We proposed a novel two-phase blood model fluid with alginate microspheres modeling the RBCs and calcium chloride solution modeling the blood plasma. To validate the model, the shear rate dependent viscosity, the flow behavior of the blood model fluid in a straight microchannel and the deformation of single alginate microspheres in a hyperbolic converging microchannel have been examined. Considering the shear-thinning properties of the blood model fluid viscosity, the flow behavior in the straight microchannel with formation of a CFL, the possibility to track the movement of individual microspheres in the center of the flow and the deformability of the individual alginate microspheres in the extensional flow, promising results are revealed. With this study it could be shown that our novel blood model fluid is well suited to be used in experimental setups to mimic the two-phase flow behavior of blood. The future work will focus on decreasing the aggregational effects of the alginate microspheres and implement a PIV analysis with a particle fraction close to the physiological hematocrit. Investigations in more complex microchannels are planned to further validate the blood model.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Anes CF, Pinho D, Muñoz-Sánchez BN, Vega EJ, Lima R (2018) Shrinkage and colour in the production of micro-sized PDMS particles for microfluidic applications. J Micromech Microeng 28(7):075002
Arora D (2006) Computational hemodynamics: hemolysis and viscoelasticity. Rice University
ASTM F1841-19 (2019) Standard practice for assessment of hemolysis in continuous flow blood pumps. Standard f1841-19, American Society for Testing and Materials - ASTM International
ASTM F1841-97 (2017) Standard practice for assessment of hemolysis in continuous flow blood pumps. Standard f1841-97(reapproved 2017), American Society for Testing and Materials - ASTM International
Baskurt O, Boynard M, Cokelet G, Connes P, Cooke BM, Forconi S, Liao F, Hardeman M, Jung F, Meiselman H et al (2009) New guidelines for hemorheological laboratory techniques. Clin Hemorheol Microcirc 42(2):75–97
Baskurt OK, Hardeman MR, Rampling MW, Meiselman HJ (2007) Handbook of hemorheology and hemodynamics, vol 69. IOS press, Amsterdam
Brindise MC, Busse MM, Vlachos PP (2018) Density- and viscosity-matched Newtonian and non-Newtonian blood-analog solutions with PDMS refractive index. Exp Fluids 59(11):1–8
Brooks DE, Goodwin JW, Seaman GV (1970) Interactions among erythrocytes under shear. J Appl Physiol 28(2):172–177 (PMID: 5413303)
Buchmann NA, Atkinson C, Jeremy MC, Soria J (2011) Tomographic particle image velocimetry investigation of the flow in a modeled human carotid artery bifurcation. Exp Fluids 50(4):1131–1151
Calejo J, Pinho D, Galindo-Rosales F, Lima R, Campo-Deaño L (2016) Particulate blood analogues reproducing the erythrocytes cell-free layer in a microfluidic device containing a hyperbolic contraction. Micromachines 7(1):4
Campo-Deaño L, Dullens RP, Aarts DG, Pinho FT, Oliveira MS (2013) Viscoelasticity of blood and viscoelastic blood analogues for use in polydymethylsiloxane in vitro models of the circulatory system. Biomicrofluidics 7(3):034102
Campo-Deaño L, Galindo-Rosales FJ, Pinho FT, Alves MA, Oliveira MS (2011) Flow of low viscosity Boger fluids through a microfluidic hyperbolic contraction. J Nonnewton Fluid Mech 166(21–22):1286–1296
Carneiro J, Lima R, Campos JB, Miranda JM (2021) A microparticle blood analogue suspension matching blood rheology. Soft Matter 17(14):3963–3974
Chien S (1975) Biophysical behavior of red cells in suspensions. Red Blood Cell 2:1031–1133
Cokelet GR, Meiselman HJ (2007) Macro-and micro-rheological properties of blood. In: Biomedical and Health Research-Commission of the European Communities, IOS Press, vol 69, p 45
Completo C, Geraldes V, Semiao V (2014) Rheological and dynamical characterization of blood analogue flows in a slit. Int J Heat Fluid Flow 46:17–28
Deplano V, Knapp Y, Bailly L, Bertrand E (2014) Flow of a blood analogue fluid in a compliant abdominal aortic aneurysm model: Experimental modelling. J Biomech 47(6):1262–1269
Dobbe J, Streekstra G, Hardeman M, Ince C, Grimbergen C (2002) Measurement of the distribution of red blood cell deformability using an automated rheoscope. Cytom J Int Soc Anal Cytol 50(6):313–325
Doutel E, Carneiro J, Oliveira MSN, Campos JBLM, Miranda JM (2015) Fabrication of 3d mili-scale channels for hemodynamic studies. J Mech Med Biol 15(01):1550004
Ertürk N, Düzgün A, Ferrè J, Varela S, Vernet A (2013) Alginate flow seeding microparticles for use in particle image velocimetry (piv). Delft University of Technology, Faculty of Mechanical, Maritime and Materials Engineering, and Faculty of Aerospace Engineering
Faghih MM, Sharp MK (2019) Modeling and prediction of flow-induced hemolysis: a review, vol 18. Springer, Berlin Heidelberg
Faghih MM, Sharp MK (2020) Deformation of human red blood cells in extensional flow through a hyperbolic contraction. Biomech Model Mechanobiol 19(1):251–261
Fåhraeus R (1929) The suspension stability of the blood. Physiol Rev 9(2):241–274
Fahraeus R, Lindqvist T (1931) The viscosity of the blood in narrow capillary tubes. Am J Physiology-Leg Content 96(3):562–568
Feigl K, Tanner F, Edwards B, Collier J (2003) A numerical study of the measurement of elongational viscosity of polymeric fluids in a semihyperbolically converging die. J Nonnewton Fluid Mech 115(2):191–215
Flormann D, Schirra K, Podgorski T, Wagner C (2016) On the rheology of red blood cell suspensions with different amounts of dextran: separating the effect of aggregation and increase in viscosity of the suspending phase. Rheol Acta 55(6):477–483
Geoghegan PH, Buchmann NA, Spence CJT, Moore S, Jermy M (2012) Fabrication of rigid and flexible refractive-index-matched flow phantoms for flow visualisation and optical flow measurements. Exp Fluids 52(5):1331–1347
Gray JD, Owen I, Escudier MP (2007) Dynamic scaling of unsteady shear-thinning non-Newtonian fluid flows in a large-scale model of a distal anastomosis. Exp Fluids 43(4):535–546
Heng PWS, Chan LW, Wong TW (2003) Formation of alginate microspheres produced using emulsification technique. J Microencapsul 20(3):401–413 (PMID: 12881119)
Huang C, Chen H, Pan W, Shih T, Kristol D, Copley A (1987) Effects of hematocrit on thixotropic properties of human blood. Biorheology 24(6):803–810
Jansen SV (2018) Development of an in-vitro fluorescent haemolysis detection method using ghost cells. PhD thesis, Dissertation, RWTH Aachen University, 2017
Kertzscher U, Berthe A, Goubergrits L, Affeld K (2008) Particle image velocimetry of a flow at a vaulted wall. Proc Inst Mech Eng [H] 222(4):465–473
Kink T, Reul H (2004) Concept for a new hydrodynamic blood bearing for miniature blood pumps. Artif Organs 28(10):916–920
Lee SS, Yim Y, Ahn KH, Lee SJ (2009) Extensional flow-based assessment of red blood cell deformability using hyperbolic converging microchannel. Biomed Microdevice 11(5):1021–1027
Lerche D, Vlastos G, Koch B, Pohl M, Affeld K (1993) Viscoelastic behaviour of human blood and polyacrylamide model fluids for heart valve testing. J Phys III 3(6):1283–1289
Leslie LJ, Marshall LJ, Devitt A, Hilton A, Tansley GD (2013) Cell exclusion in couette flow: evaluation through flow visualization and mechanical forces. Artif Organs 37(3):267–275
Li C-P, Lo C-W, Lu P-C (2010) Estimation of viscous dissipative stresses induced by a mechanical heart valve using piv data. Ann Biomed Eng 38(3):903–916
Lima R, Vega EJ, Moita AS, Miranda JM, Pinho D, Moreira AL (2020) Fast, flexible and low-cost multiphase blood analogue for biomedical and energy applications. Exp Fluids 61(11):231
Mann KA, Deutsch S, Tarbell JM, Geselowitz DB, Rosenberg G, Pierce WS (1987) An experimental study of newtonian and non-newtonian flow dynamics in a ventricular assist device. J Biomech Eng 109(2):139–147
Murashige T, Sakota D, Kosaka R, Nishida M, Kawaguchi Y, Yamane T, Maruyama O (2016) Plasma skimming in a spiral groove bearing of a centrifugal blood pump. Artif Organs 40(9):856–866
Muñoz-Sánchez BN, Silva SF, Pinho D, Vega EJ, Lima R (2016) Generation of micro-sized pdms particles by a flow focusing technique for biomicrofluidics applications. Biomicrofluidics 10(1):014122
Najjari MR, Hinke J, Bulusu K, Plesniak M (2016) On the rheology of refractive-index-matched, non-newtonian blood-analog fluids for piv experiments. Exp Fluids 57(6):1–6
Pinho D, Campo-Deaño L, Lima R, Pinho FT (2017) In vitro particulate analogue fluids for experimental studies of rheological and hemorheological behavior of glucose-rich rbc suspensions. Biomicrofluidics 11(5):054105
Pinho D, Muñoz-Sánchez B, Anes C, Vega E, Lima R (2019) Flexible pdms microparticles to mimic rbcs in blood particulate analogue fluids. Mech Res Commun 100:103399
Pohl M, Wendt MO, Koch B, Vlastos GA (2000) Mechanical degradation of polyacrylamide solutions as a model for flow induced blood damage in artificial organs. Biorheology 37(4):313–324
Poncelet D, Lencki R, Beaulieu C, Halle J, Neufeld R, Fournier A (1992) Production of alginate beads by emulsification/internal gelation. i. methodology. Appl Microbiol Biotechnol 38(1):39–45
Sadek SH, Rubio M, Lima R, Vega EJ (2021) Blood particulate analogue fluids: a review. Materials 14(9):2451
Schmid-Schönbein H, Gaehtgens P, Hirsch H et al (1968) On the shear rate dependence of red cell aggregation in vitro. J Clin Investig 47(6):1447–1454
Schneider CA, Rasband WS, Eliceiri KW (2012) NIH Image to ImageJ: 25 years of image analysis. Technical report
Schöps M, Clauser JC, Menne MF, Faßbänder D, SchmitzRode T, Steinseifer U, Arens J (2020) Ghost cells for mechanical circulatory support in-vitro testing: a novel large volume production. Biotechnol J 1900239:1900239
Schüle CY, Thamsen B, Blümel B, Lommel M, Karakaya T, Paschereit CO, Affeld K, Kertzscher U (2016) Experimental and numerical investigation of an axial rotary blood pump. Artif Organs 40(11):E192–E202
Sousa PC, Pinho FT, Oliveira MS, Alves MA (2011) Extensional flow of blood analog solutions in microfluidic devices. Biomicrofluidics 5(1):014108
Su B, Chua LP, Wang X (2012) Validation of an axial flow blood pump: computational fluid dynamics results using particle image velocimetry. Artif Organs 36(4):359–367
Thurston GB, Henderson NM (2007) Viscoelasticity of human blood. In: Biomedical and Health Research-Commission Of The European Communities, IOS Press, vol 69, p 72
Varela S, Balagué I, Sancho I, Ertürk N, Ferrando M, Vernet A (2016) Functionalised alginate flow seeding microparticles for use in particle image velocimetry (piv). J Microencapsul 33(2):153–161
White H, Walton S (1937) Particle packing and particle shape. J Am Ceram Soc 20(1–12):155–166
Wickramasinghe SR, Kahr CM, Han B (2002) Mass transfer in blood oxygenators using blood analogue fluids. Biotechnol Prog 18(4):867–873
Yaginuma T, Oliveira MS, Lima R, Ishikawa T, Yamaguchi T (2013) Human red blood cell behavior under homogeneous extensional flow in a hyperbolic-shaped microchannel. Biomicrofluidics 7(5):054110
Yousif MY, Holdsworth DW, Poepping TL (2011) A blood-mimicking fluid for particle image velocimetry with silicone vascular models. Exp Fluids 50(3):769–774
Zhang G, Zhang M, Yang W, Zhu X, Hu Q (2008) Effects of non-newtonian fluid on centrifugal blood pump performance. Int Commun Heat Mass Transfer 35(5):613–617
Zhao R, Antaki JF, Naik T, Bachman TN, Kameneva MV, Wu ZJ (2006) Microscopic investigation of erythrocyte deformation dynamics. Biorheology 43(6):747–765
Acknowledgments
The authors pay great tribute to Prof. Dr.-Ing. Klaus Affeld, on whose ideas the development of this model is based. We also would like to thank Prof. Dr. Michael Gradzielski for providing the rheometer and for his input on this study.
Funding
Open Access funding enabled and organized by Projekt DEAL. This study was supported by the Investitions bank Berlin and the European Regional Development Fund (funding code: 10168084).
Author information
Authors and Affiliations
Contributions
Conceptualization was contributed by VF, GG, ML; data curation was contributed by VF, JP; formal analysis was contributed by VF; investigation was contributed by VF, JP, AP; methodology was contributed by VF, JP; VF, GG contributed to supervision; VF contributed to validation; VF contributed to visualization; writing—original draft, was contributed by VF; writing—review and editing, was contributed by GG, ML, UK; project administration was contributed by ML; funding acquisition was contributed by UK; resources were contributed by UK
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts to disclose.
Ethics approval
The study was approved as a part of the vote of the ethics committee of the Charité - Universitätsmedizin Berlin (EA2/279/20, 9.12.2020).
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Froese, V., Gabel, G., Parnell, J. et al. Flow study on a transparent two-phase blood model fluid based on alginate microspheres. Exp Fluids 63, 188 (2022). https://doi.org/10.1007/s00348-022-03538-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-022-03538-y