Abstract
The application of a compact pulsed fiber laser for high-speed time-resolved particle image velocimetry (TR-PIV) measurements in the potential core of a turbulent round jet is presented at repetition rates of up to \(500\,\hbox {kHz}\). The master oscillator power amplifier laser architecture consists of a pulsable seed diode whose emission is amplified in a Yb-doped fiber. The pulsed laser is operated continuously at repetition rates ranging from \(10\,\hbox {kHz}\) to \(1\,\hbox {MHz}\) with adjustable pulse widths at an output power of 50 W. The maximum rated pulse energy of \(486\,\upmu \hbox {J}\) is reached at \(100\,\hbox {kHz}\), making the laser suitable for measurements of turbulent flows and highly transient phenomena. To demonstrate the feasibility of the laser for flow velocimetry, TR-PIV is conducted in a turbulent round jet. Two different high-speed camera systems are employed: a high-speed CMOS camera running at \(200\,\hbox {kHz}\) and \(400\,\hbox {kHz}\) and an in situ storage CCD camera for burst-mode PIV measurements at \(500\,\hbox {kHz}\). For the CMOS system, the capability of measuring several characteristic quantities of turbulent flows is discussed with regard to the effects of uncertainty and spatial resolution. The presented system extends the range of suitable laser systems for high-speed PIV measurements offering continuous pulsing at repetition rates of up to \(1\,\hbox {MHz}\) at a compact footprint. The amount of consecutive images is solely limited by the onboard storage of the camera, which enables unprecedented temporal dynamic ranges.
Graphical Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Particle image velocimetry (PIV) has become a widely used experimental method to measure flow fields in various applications (Raffel et al. 2018; Westerweel et al. 2013). For the investigation of transient phenomena as they appear in turbulent flows, high-speed PIV (HS-PIV) systems with kilohertz repetition rates have become an established standard. Typically, nanosecond-pulsed high-power lasers are needed to generate images with sufficient signal-to-noise ratio and low motion blur caused by particle movement during illumination. Within this work, we use the term high-speed for repetition rates beyond \(1\,\hbox {kHz}\) and ultra-high-speed for repetition rates beyond \(100\,\hbox {kHz}\) given that these terms have been defined loosely within the context of PIV or imaging methods.
Generally, two different approaches exist to generate time-resolved high-speed PIV (TR-PIV) recordings depending on the temporal recording scheme (Beresh 2021). The first option, employed within this work, is to operate both laser and camera systems continuously, creating a set of temporally equidistant images. The second approach, high-speed double-pulse PIV (DP-PIV), is commonly used when the maximum desirable particle shift between two consecutive images dictated by the interrogation window (IW) size requires an inter-frame time \(\varDelta t\) smaller than the minimally possible duration between two laser pulses of one cavity or the minimally possible inter-frame recording duration of the camera at a given amount of utilized pixels. This recording scheme has been enabled by the introduction of high-speed dual-cavity lasers in combination with double-frame recording modes on modern high-speed camera sensors. As both laser cavities can be triggered individually, the particle shift of high-speed flows can be captured without the limitation of the repetition rate of a single laser cavity, which, however, still dictates the effective temporal resolution of the high-speed time series. TR-PIV data can be used to derive both statistical properties of turbulent flows and quantities only computable from time series of velocities such as integral time scales or spectra (Willert 2015; Beresh 2021). The latter makes TR-PIV suitable for replacing single-point hot-wire measurements with the additional benefit of local spatial information suitable for space–time correlation measurements (Wernet 2007). In the following, a brief summary of current high-speed camera and laser technologies for PIV applications is given including representative examples of investigations in the literature. Eventually, continuously pulsing fiber lasers are introduced in the context of flow velocimetry.
A multitude of digital high-speed imaging sensor technologies has emerged over the course of the last decades, which has enabled diagnostics of turbulent and highly transient flow phenomena. For high-speed PIV, three main technological approaches are worth noting: complementary metal-oxide-semiconductor (CMOS) sensors, burst image sensors including in situ storage image sensors (ISIS), and multi-sensor camera arrays. An overview on high-speed imaging technologies is found in Tsuji (2018) and Thurow et al. (2013). Continuous readout CMOS cameras are the most common category of imaging sensors found in high-speed PIV as they offer relatively small pixel sizes in the order of \(20\,\upmu \hbox {m}/\hbox {px}\) enabling high spatial resolutions for optimized particle imaging when coupled to high-quality lenses. Temporally, they offer frame rates of several \(10\,\hbox {kHz}\) at megapixel sensor sizes and can be run faster when the amount of active pixels is decreased. For instance, TR-PIV at \(400\,\hbox {kHz}\) for spectra measurements is possible when a small field of view (FOV) is chosen as exemplified by Beresh et al. (2018). The dual-frame exposure capabilities of such sensors can as well be utilized to perform DP-PIV given that a higher amount of active pixels is preferred over a desired temporal resolution. State-of-the-art ISIS sensors can be operated in burst-mode at full sensor size at repetition rates of up to \(100\,\hbox {MHz}\) (Suzuki et al. 2020). As the charge of each acquired image is stored on memory arrays on the sensor itself, the sensor size limits the number of acquired frames to a few hundred images. Due to the need of space for the in situ storage, however, the ratio of the photoactive area to the total sensor size for conventional CCD sensors is small, resulting in relatively large effective pixel sizes (e.g., \(66.3\,\upmu \hbox {m}/\hbox {px}\) for the chip developed by Etoh et al. (2003) of the Shimadzu HPV-2 used within this study) and distortions of small imaged objects (Rossi et al. 2014), which imposes a challenge for the imaging of small tracer particles. Recently, CMOS burst image sensors, which make use of a spatial separation between the photosensitive pixels and their corresponding memory, have been developed to achieve an improved sensor array design for high-resolution imaging (Tochigi et al. 2013; Suzuki et al. 2020). When the amount of active pixels at a given frame rate is too small, multiple cameras can be optically combined in an array such that every sensor only images one or two frames (in dual-frame exposure mode) of the time series. Such systems have enabled full-frame megahertz PIV measurements (Wernet and Opalski 2004; Murphy and Adrian 2010; Brock et al. 2014) but obviously come at the cost of a very limited amount of consecutive recordings.
As of yet, three main laser architectures have been used for high-speed PIV measurements: clustered multi-channel (CMC) laser systems, diode-pumped solid state (DPSS) bulk lasers, and burst-mode lasers (Thurow et al. 2013; Slipchenko et al. 2020). CMC laser systems are used when high pulse energies at repetition rates much higher than individual laser cavities can provide are needed, such that each cavity corresponds to a single frame in the final PIV recording. Similar to multi-sensor camera arrays, the amount of consecutive pulses is limited by the amount of laser cavities, making CMC lasers only suitable for the observation of single events like flows close to propagating shock waves (Murphy and Adrian 2010). High-speed Q-switched DPSS lasers offer continuous pulsing operation at single-cavity repetition rates up to 150 kHz (Edgewave IS and GX series) and have been used extensively in fluid mechanics and combustion research applications (Böhm et al. 2011). In DP-PIV systems, dual-cavity DPSS lasers offer flexible transient adjustment of the inter-frame pulse duration \(\varDelta t\), which, for instance, has enabled high-speed PIV in statistically unsteady turbulent flows in running combustion engines (Baum et al. 2014). Operation of DPSS laser systems is, however, challenging due to the limitations imposed by high thermal loads at high repetition rates and the optical beam overlap needed for flexible DP-PIV pulsing. In order to overcome the thermal limitations at higher repetition rates, burst-mode lasers operate at a limited duty cycle and are therefore able to reach sufficient energy output for operation in the megahertz range (Slipchenko et al. 2020). Modern systems rely on the master oscillator power amplifier (MOPA) architecture pioneered by Lempert et al. (1996) in which a low-power seed laser is guided through several amplification stages. Recent advancements have allowed for the development of compact doublet pulse systems incorporating fiber seed lasers utilized for DP-PIV at repetition rates of \(100\,\hbox {kHz}\) yielding pulse energies of \(800\,\upmu \hbox {J}\) at burst durations of 10 ms (Smyser et al. 2018). Longer burst durations of up to 100 ms have been enabled by dual-wavelength diode pumping (Slipchenko et al. 2014) utilized for spatio-temporal correlation measurements from DP-PIV at \(100\,\hbox {kHz}\) in the intermediate region of a turbulent jet (Miller et al. 2016). The data were subsequently analyzed to demonstrate deviations from Taylor’s hypothesis of frozen turbulence by showing that the mean convective velocity is larger than the actual velocity of the time-delayed cross-correlation function (Roy et al. 2021). Other notable recent investigations using pulse-burst lasers include PIV measurements of supersonic jets emerging into a transonic wind tunnel (Beresh et al. 2015) and subsequent spectra measurements at \(400\,\hbox {kHz}\) (Beresh et al. 2018) and \(1\,\hbox {MHz}\) (Beresh et al. 2020) using a limited amount of active pixels on CMOS sensors. In reactive flows, pulse-burst lasers have been recently applied for \(100\,\hbox {kHz}\) PIV in a gas turbine swirl combustor simultaneously with OH* chemiluminescence imaging (Philo et al. 2021). While pulse-burst lasers have facilitated the majority of recent investigations with a focus on ultra-high-speed laser diagnostics, they suffer from limited burst durations due to overheating of the amplifier stages and a complicated optical architecture that demands high investment and maintenance costs and explains their almost exclusive usage within research applications.
As is apparent from the presented state-of-the-art laser systems for HS-PIV, several technological and practical limitations have to be dealt with when scaling laser systems up for ultra-high repetition rate PIV applications. First, thermal stress within the laser cavity limits the continuously available output power and repetition rate of DPSS systems, while the high pulse energy output of pulse-burst lasers is temporally limited by thermal constraints in the amplifiers. Thermal lensing changes the beam profile for increasing pump energies in both systems, too. Hence, neither laser architecture can currently provide a continuously pulsing high-energy output at repetition rates beyond \(150\,\hbox {kHz}\) with unchanged beam profile characteristics over all power set points. Second, both DPSS and pulse burst lasers require the full laser system to be mounted rigidly onto a balanced surface for stable operation, which might be challenging for test environments with limited optical access and possible vibrations as they, e.g., appear in optically accessible engines. Third, the financial investment and maintenance costs of DPSS bulk lasers, and especially pulse-burst lasers, are high as they are often custom-built and not aimed toward a larger industrial market, limiting their usage to specific research applications in aerodynamics and combustion. This limitation might impede the wide-spread application of HS-PIV outside of these research communities.
Within this work, we introduce fiber lasers as an alternative laser architecture suitable for HS-PIV, which show an improved performance on all of the three discussed limitations. In the following, a brief introduction into the characteristics of fiber lasers is given. Fiber lasers have become a widespread variant among solid-state lasers within the last decades, frequently used in materials processing applications such as silicon scribing (Yang et al. 2016), milling (Williams et al. 2014), and marking (Gabzdyl 2008). Comprehensive information of fiber laser technology is provided by Samson and Dong (2013) and Ter-Mikirtychev (2019). The distinctive feature of fiber lasers and amplifiers is the fiber resonator design consisting of a core fiber doped with rare earth ions such as Nd3+, Yb3+, Er3+, or Tm3+ covered in an undoped fiber through which the diode-laser pump beam is led. The center core design of such double-clad fibers is optimized such that the pump radiation always passes the doped center core, leading to an excitation of the laser crystal. In contrast with DPSS resonators or pulse-burst amplifiers, the ratio of the surface area to the volume of the crystal is large in optical fibers, leading to an efficient heat transfer to the outside of the fiber diminishing the need for active water cooling entirely. However, other loss mechanisms peculiar to fiber optics such as stimulated Brillouin scattering, stimulated Raman scattering, and Kerr nonlinearity have to be considered (Samson and Dong 2013).
Nanosecond-pulsed fiber lasers suitable for HS-PIV can either be realized by Q-switching or amplification of a diode laser seed pulse within a MOPA configuration. The latter approach allows for a flexible setting of the laser pulse width combined with a diffraction-limited beam quality at high fiber amplifier gains. As will be demonstrated with the fiber laser unit used within this work, pulsed MOPA configurations can be operated continuously at repetition rates of \(1\,\hbox {MHz}\) for average power outputs of 50 W with excellent beam quality factors. As the output laser beam is already led through a fiber, collimated output fibers can be directly mounted to fiber lasers enabling flexible output beam coupling in challenging environments. The fiber-based beam path allows compact footprints and the use of standard components, enabling relatively low costs of ownership compared to DPSS and pulse-burst systems.
In this work, we systematically explore the feasibility of a state-of-the-art pulsed Yb:YAG fiber laser for ultra-high-speed TR-PIV measurements up to repetition rates of \(500\,\hbox {kHz}\). Two camera systems, a high-speed CMOS camera and an in situ storage CCD camera, are used to capture the particle images taken in the potential core of a turbulent round jet.
The paper is structured as follows. Section 2 describes the basic properties of the utilized fiber laser system followed by a description of the experimental methodology in Sect. 3. Initial analysis of the investigations includes the assessment of the raw PIV images in Sect. 4.1 and the mitigation of peak locking in Sect. 4.2. Further, the computation of statistical turbulent moments based on an analysis of the measurement uncertainty is presented in Sect. 4.3, followed by a discussion of turbulent scales derived from correlation measurements in Sect. 4.4. The computation of temporal power spectral density measurements is discussed in Sect. 4.5, and the applicability of Taylor’s hypothesis through an analysis of space–time correlations is presented in Sect. 4.6. The main findings are summarized in Sect. 5.
2 Fiber laser system
The laser system utilized for PIV within this study is a commercial nanosecond-pulsed Yb:YAG fiber laser (GLPN-500-1-50-M, IPG Photonics) depicted in Fig. 1a. The nanosecond-pulsed Yb:YAG fiber laser is based on the master oscillator power amplifier (MOPA) architecture in which a low-power seed laser is amplified by guiding the seed pulse through a pumped gain medium in which stimulated emission increases the final output power significantly. Here, a pulsed seed diode laser operated at 1030 nm is amplified within a Yb-doped double-clad fiber as depicted in Fig. 1b. The linear s-polarization of the seed laser beam is maintained within the single-mode fiber. Energy-efficient diode laser pumping of the fiber gain medium enables a compact footprint of the laser module of \(0.07\,\hbox {m}^2\) (\(0.27\,\hbox {m} \times 0.26\,\hbox {m}\)), which is solely cooled through fans. The amplified laser pulse is guided into a water-cooled laser head by a 1.7-m-long delivery fiber, resulting in second-harmonic generation (SHG) to the final output wavelength of 515 nm. Table 1 summarizes the main technical properties of the fiber laser system.
Continuous operation of the laser is possible at pulse repetition rates (PRR) of \(10\,\hbox {kHz}\) to 1 MHz with a nominal average output power of 50 W. The MOPA architecture allows for a direct control of the seed laser pulse width. The maximum pulse energy of approx. \(500\,\upmu \hbox {J}\) is kept constant between 10 kHz and \(100\,\hbox {kHz}\) and further decreases with repetition rate such that the output power is kept constant at 50 W.
A measurement of the output laser beam profile at a PRR of \(100\,\hbox {kHz}\) using a beam-profiling CMOS camera (WinCamD-LCM, Dataray) is shown in Fig. 2. As is apparent, the beam shows a symmetric Gaussian profile with only minor deviations, indicating the diffraction-limited beam quality obtained through the laser architecture. In fact, a fit of a 2D Gaussian profile described by \(I(x,y) = \mathrm {exp}(-(x^2+y^2)/\sigma ^2)\) to the normalized profile yields a standard deviation of \(\sigma = 0.67\,\hbox {mm}\) with a coefficient of determination of \(R^2 = 0.987\). The beam diameter, calculated at a normalized intensity of \(1/e^2\) is 2.68 mm. The measured beam quality factor of \(M^2 = 1.43\) underlines the great potential of the laser to be focused to small beam waists, which is important for precise material processing applications. This is as well beneficial for PIV as thin laser sheets are needed to reach high spatial resolutions, although the bell-shaped laser profile has to be expanded wide enough in the perpendicular dimension to guarantee a homogeneous particle scattering intensity throughout the whole field of view. It has to be noted that the size and shape of the beam profile remain unchanged when the output intensity is varied which underlines the advantage of the laser architecture in contrast with thermal lensing occurring in bulk lasers and amplifiers of pulse-burst lasers.
3 Experimental methodology
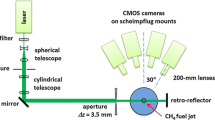
To demonstrate the feasibility of the fiber laser system for the diagnostics of turbulent flows, TR-PIV was conducted within the potential core of an axisymmetric turbulent jet exiting as a fully developed pipe flow, which is a well-investigated generic configuration (Papadopoulos and Pitts 1998; Xu and Antonia 2002; Mi et al. 2001). The experimental setup is displayed in Fig. 3a.
A pipe of diameter \(D = 2.8\,\hbox {mm}\) was mounted horizontally within the burner head of the microwave plasma heater test stand at TU Darmstadt (Eitel et al. 2015). The stainless steel pipe can be used for fuel injection into hot co-flows and was therefore coated with a ceramic insulation, which increased the size of the tip to an outer diameter of 6 mm as depicted in Fig. 3b. It was bent \(90^{\circ }\) upwards to facilitate injection of the jet flow from above. The straight part of the pipe from the bending to the jet exit had a length of 185D to ensure a fully developed turbulent pipe flow as boundary condition. Particle seeding was provided by an aerosol generator (AGF 10, Palas) generating di-ethylhexyl sebacate (DEHS) droplets with a mean size of \(0.5\,\upmu \hbox {m}\). The seeder was placed directly in front of the pipe connection to mitigate the influence of agglomeration on the particle size distribution. The air flow through the aerosol generator and pipe was regulated by mass flow controllers (EL-Flow Prestige, Bronkhorst) which were connected to a pressurized dried air supply system. The co-flow did not run during the experiments such that the ambient can be approximated as quiescent. As the near-field potential core region of the jet was analyzed within this study, the ambient air was not seeded with tracer particles. The jet flow was operated isothermally at ambient conditions of \(T = 295\,\hbox {K}\) and \(p = 1\,\hbox {bar}\). The operating points chosen for the experimental investigation at bulk flow Reynolds numbers \(Re\) of 10,000 and 18,200 are displayed with the respective laser and camera configuration in Table 2.
The output head of the fiber laser was mounted directly on a traversable beam delivery system including all additional optics as shown in Fig. 3a. The high-speed cameras were rigidly connected to the traversing system as well (not shown) to fix the relative position of the laser beam and the field of view. The laser sheet was created by a set of cylindrical lenses (effective focal lengths of \(f_1 = -50\,\hbox {mm}\), \(f_2 = 300\,\hbox {mm}\), and \(f_3 = 1000\,\hbox {mm}\)), which resulted in a beam thickness in the probe volume of 290 mm (FWHM) while being laterally expanded to a length of 35 mm. The laser sheet thickness was optimized as a compromise between high fluence resulting in sufficient Mie scattering signal from the DEHS particles and high spatial resolution on the one side, and the prevention of out-of-plane motion of the quickly moving particles in the turbulent flow on the other side.
Two high-speed camera systems were utilized in the TR-PIV analysis, a continuous readout CMOS camera (Photron FASTCAM SA-X2) and an in situ storage CCD camera (Shimadzu HPV-2), to evaluate their performance for UHS-TR-PIV measurements at different frame rates. The lens configurations and pixel calibration values are displayed in Table 2. Although the apertures of the camera lenses were fully open causing a limited depth of field, the small laser beam thickness resulted in a uniform size distribution of the particle images, which was verified by defocussing the lens and simultaneously observing changes in the imaged particle sizes throughout the frame. The fields of view of all three configurations are shown in Fig. 3b including an instantaneous vector field measured in configuration C. The SA-X2 recordings were used to capture the flow field directly at the jet exit at \(200\,\hbox {kHz}\) and for higher-resolved measurements in the centerline region starting at \(x = 0.9D\) using a repetition rate of \(400\,\hbox {kHz}\). The characteristic temporal and spatial turbulent scales of a round jet are smallest within its potential core, which therefore serves as an ideal target to highlight the capabilities of an ultra high-speed repetition rate system at a finite spatial resolution, whose effect on measured turbulence properties will be discussed in Sect. 4. For the HPV-2 measurements, the flow velocity was increased and the measurement position was traversed slightly downstream to optimize the particle shift for the lower spatial resolution and higher repetition rate of the imaging system. The spatial resolution of correlation-based PIV algorithms was thoroughly investigated by Kähler et al. (2012) and is around the size of the interrogation window as long as particle images do not exceed more than 3 px.
The PIV images were captured and processed in the software Davis 10 (LaVision). The data acquisition system, laser, and camera were synchronized using an external timing unit (9520 Series, Quantum Composers). The length of each recording was solely limited by the on-board storage of the cameras, which resulted in over 1.2 million vector fields at \(400\,\hbox {kHz}\) for the SA-X2. Theoretically, this setting would allow for a temporal dynamic range (TDR), defined as the ratio of the highest to the lowest resolvable frequency, of over 600,000. However, as shown in Sect. 4.5 in the frequency domain, this value is limited by multiple other factors like noise, spatial resolution, and the variance of the power spectral density estimation (Beresh 2021) and will be evaluated based on the experimental results. For PIV processing, a correlation-based multi-pass algorithm with a window overlap of 75% was used. The final four passes at the smallest interrogation window size w were performed with a Gaussian weighting. This ensures better spatial resolution as the local information around the IW centroid is weighted higher and is commonly used in state-of-the-art PIV codes. The vectors were subsequently validated using the universal outlier detection method of Westerweel and Scarano (2005) using a \(5\times 5\) median filter kernel. No additional denoising (as proposed by Oxlade et al. (2012) for TR-PIV spectra measurement) was performed to sincerely assess the quality of the PIV data set for further analysis.
4 Results and discussion
4.1 Assessment of raw particle images
As an initial step of analysis, the data quality of the raw images is assessed. Figure 4 shows representative single-shot particle images and their associated computed vector fields for every configuration. Recordings obtained with the SA-X2 CMOS camera show clearly distinguishable spherical particle shapes with sufficient signal-to-noise ratio to reliably compute a vector field. The single-shot raw images of the HPV-2 CCD in situ storage camera (Fig. 4e) were obtained at a similar pixel resolution than those at \(200\,\hbox {kHz}\) of the SA-X2 but could only be properly processed when defocussing the image slightly such that single particles have merged into a continuous structure. This was necessary as the large pixel size of the HPV-2 (\(66.3\,\upmu \hbox {m} \times 66.3\,\upmu \hbox {m}\)) is mainly needed for storage gates, which limits the ratio of the photoactive area to the entire pixel area (also referred to as fill factor) to only 0.6%. This poses a problem to accurate imaging of small-scale structures as it was reported by Rossi et al. (2014) for the same camera chip model. When small moving structures like particles are imaged in focus at the given magnification, the particle image does not span more than one pixel and even disappears completely when a particle position between two neighboring photoactive CCD areas is imaged. Subsequently, the particle image flashes and disappears as particles are moving from frame to frame which can only be avoided by defocusing the image slightly. Still, the mean correlation value of the PIV processing was 0.84 for the adjusted imaging system of the HPV-2, which underlines the validity of the data for an ultra-high-speed flow analysis. It can be expected that the next generation of in situ storage cameras with smaller pixel pitch values based on CMOS technology can further improve the metrological performance of such a setup when high repetition rates are preferred over the amount of consecutively recorded frames (Suzuki et al. 2020).
It should be noted that at a repetition rate of \(1\,\hbox {MHz}\), the PIV system was capable of capturing images with sufficient signal-to-noise ratio such that PIV processing would have been possible. However, due to the large pixel size and hence poor spatial resolution of the ISIS-CCD chip in combination with the limited flow rates dictated by the maximum throughput of the used seeder, all particle shifts were below 2 px such that the dynamic range of the computed vector field was poor.
4.2 Peak locking
A common systematic error introduced in PIV measurements is peak locking (Michaelis et al. 2016). This effect is relevant when the Mie scattering signal of a single particle is imaged smaller than one pixel, leading to a loss of sub-pixel accuracy resulting in preferential particle displacements to integer multiples of the imaged pixel resolution. Figure 5 displays the velocity histograms of the entire field of view of all vector fields of one measurement in units of pixel displacements together with the associated modulo plots for the two worst-resolved camera configurations. For the HPV-2, a total of 808 vector fields from eight camera bursts are included. Instead of comparing the velocity histograms at a fixed point, the display of velocities within the entire camera frame increases the amount of data points for the HPV-2 in comparison to the high amount of consecutively recorded vector fields of the SA-X2 CMOS camera. Hence, as the measurements encompass different fields of view, the histograms contain a wide range of velocities depending on their position within the jet (i.e., lower velocities in the shear layer and higher velocities in the centerline region of the potential core). As is apparent, the distributions show no clear sign of a preferential displacement toward integer multiples, demonstrating the negligible effect of peak locking for all presented measurements. Previously conducted high-speed TR-PIV measurements by Wernet (2007) (\(25\,\hbox {kHz}\)) and Beresh et al. (2018) (\(400\,\hbox {kHz}\)) both had to mitigate the effect of peak locking through the use of either special PIV processing algorithms or diffusion filters to spread out the particle image over several pixels. In this investigation, no additional filtering or post-processing was necessary as the pixel magnification was high enough to image particle scattering images larger than 1.5 pixels on average.
a–f Velocity histograms within the entire FOV of the respective configurations displayed as pixel shifts \(\varDelta x\) and \(\varDelta y\) for all employed measurement setups. g–h Normalized histograms of the sub-pixel shift for the streamwise velocity component of measurements at \(200\,\hbox {kHz}\) using the SA-X2 and \(500\,\hbox {kHz}\) using the HPV-2 highlighting the suppression of peak locking of the presented PIV measurements
4.3 Measurement uncertainty and turbulence statistics measurement
Apart from the systematic errors introduced by peak locking, PIV measurements suffer from additional sources of uncertainty, whose quantification is important to reach accurate estimations of the local turbulence statistics. Generally, the measurement of statistical moments does not require time-resolved PIV but is usually performed using low-speed DP-PIV systems with statistically independent single shots of the flow field (as recently exemplified by Scharnowski et al. (2019) in a high-speed wind tunnel). However, as has been pointed out by Willert (2015) for the example of wall-bounded flows, TR-PIV offers the capability of efficiently extracting statistical measurements and quantities, which require a time series of the flow field like temporal correlations and spectra from the same measurement. For the CMOS camera, the large number of samples (in the case of \(400\,\hbox {kHz}\) over 1.2 mio. consecutively recorded vectors) is made possible by the continuously pulsing fiber laser and is solely limited by the on-board memory size of the camera. It should be noted, however, that the effective number of statistically independent samples \(N_{e}\) is lower and will be computed using the temporal autocorrelation of fluctuating velocities in Sect. 4.4.
As the camera noise level is increased substantially for measurements at repetition rates of several \(100\,\hbox {kHz}\) compared to the full frame operation at max. \(12.5\,\hbox {kHz}\), the following section explores the PIV measurement uncertainty with respect to the size of the chosen interrogation window at a fixed position on the jet centerline and how the turbulence level and higher-order statistics are affected by the spatial filtering effect associated with an increase in the interrogation window size.
For the streamwise velocity component u, the turbulence level is computed by the ratio of the standard deviation \(\sigma _{u}\), also referred to as the root-mean-square of the velocity fluctuations \(\sqrt{\langle u^{\prime ^2} \rangle }\), and the mean velocity \(\langle u \rangle\) as is shown in Equation (1).
Generally, all measurement systems introduce errors to instantaneously measured velocities, whereby the apparent standard deviation of the measured velocity distribution \(\sigma _{u,m}\) is a superposition of the true velocity fluctuations caused by turbulent motion of the flow \(\sigma _{u,turb}\) and the measurement error \(\sigma _{u,err}\) and can be expressed as Equation (2).
This relationship implies that accurate turbulence level measurements should be conducted such that the error variance \(\sigma ^2_{u,err}\) is small compared to the actual fluctuations \(\sigma ^2_{u,turb}\). Otherwise, it is necessary to quantify the measurement error reliably such that the true velocity fluctuations \(\sigma ^2_{u,turb}\) can be extracted from the measured standard deviation of the velocity fluctuations. As the true error variance \(\sigma ^2_{u,err}\) is unknown, it will be approximated by the mean-square of the uncertainty of instantaneous velocities \(\sigma ^2_{U_u}\) which holds true for accurate uncertainty quantification methods as the number of independent observations approaches infinity (Sciacchitano et al. 2015; Sciacchitano and Wieneke 2016).
In the literature, several methods have been proposed to directly determine the measurement uncertainty from PIV recordings as was collaboratively explored by Sciacchitano et al. (2015). Alternatively, Scharnowski et al. (2019) have presented a method with which the measurement uncertainty and turbulence level can be extracted simultaneously through a variation in the particle shift \(\varDelta x\) by altering the inter-frame time \(\varDelta t\) of a DP-PIV system. Although this method is promising for accurate turbulence level measurements using DP-PIV systems, it has drawbacks with regard to the presented TR-PIV measurements in this study: a variation in the inter-frame time is not feasible for ultra-high repetition rates as a further decrease in \(\varDelta t\) simultaneously increases the measurement uncertainty due to an increase in camera noise at higher recording speeds and a decreased signal-to-noise ratio due to a decrease in the laser pulse energy resulting in a lower Mie scattering intensity of individual tracer particles. Therefore, the correlation statistics (CS) method of Wieneke (2015) was chosen to quantify the random uncertainty of the PIV measurements discussed within this study. As current uncertainty quantification methods including CS do not account for the error bias introduced through peak locking (Sciacchitano et al. 2015), the prevention of small particle images resulting in distorted velocity histograms as discussed in Sect. 4.2 is an important prerequisite for a reliable quantification of the random error.
To exemplify a turbulence level correction based on the uncertainty estimation, configurations A and B including measurements at \(400\,\hbox {kHz}\) and \(200\,\hbox {kHz}\) with varying interrogation window sizes are used in the following analysis at a fixed position of \(x = 1.2D\) on the centerline. For configuration B, Fig. 6a shows the distribution of the instantaneous uncertainty of the streamwise velocity \(U_u\) both in units of meters per second and pixel shifts per image pair.
The uncertainty distributions reveal that an increase in the interrogation window size lowers the uncertainty (also expressed as the mean uncertainty \(\langle U_u \rangle\) in Table 3). The uncertainty from the CS method takes the individual contribution of each pixel within the IW to the correlation calculation into account. Thus, as the IW size is increased, a larger number of particles is included in the correlation computation which mitigates the influence of noise that is overemphasized for smaller IW sizes and leads to an overall lower uncertainty value. Hence, a higher spatial resolution comes at the cost of higher individual velocity measurement uncertainties. This is especially evident when comparing the largest and smallest IW sizes in Fig. 6a. However, when observing the uncertainties for IW lengths of 24 px and 32 px, both distributions show similar uncertainties. This discontinuity from the previously identified trend might be explained when observing the distribution of the correlation values in Fig. 6b. As the IW size increases, the correlation values for the PIV vector calculation decrease, which is contrary to the trend of the uncertainty distributions. A reason for this could be the inhomogeneous nature of the turbulent shear flow in which these particles move: although the number of particles per IW increases with w, additionally included particles are differently positioned in the inhomogeneous flow field and therefore behave differently, lowering the correlation value. Besides, Westerweel (2008) has presented a theoretical analysis of how gradients within the correlation window correlation window lower the peak correlation values. Hence, for an increase in the IW size from 24 px and 32 px, the correlation values are decreased, which outweighs the decreased amount of noise in the correlation calculation for the uncertainty calculation.
As shown in Table 3, the mean absolute uncertainty ranges between 0.14 px and 0.16 px, which is equal to mean relative uncertainties between 1.63% and 2% of individually measured velocities. For the correction of the streamwise turbulence level, the ratio of the variance of the measurement uncertainty and the measured variance of the velocity fluctuations \(\sigma ^2_{U_u}/\sigma ^2_{u,m}\) provides a measure of the amount of uncertainty contained in the measured velocity fluctuations. For the measurements taken at \(400\,\hbox {kHz}\), this ratio increases as the IW size decreases, which results in a higher relative correction of the turbulence level from the measured value \(\mathrm {Tu}_{u,m}\) to the corrected value \(\mathrm {Tu}_{u,corr}\). At \(200\,\hbox {kHz}\), an additional temporal filtering of the turbulent fluctuations results in a significantly smaller measured turbulence level, which translates into an increased ratio between measurement uncertainty and measured fluctuations. The results of the corrected turbulence levels finally show that as the repetition rate is increased and the IW size is decreased, the extent of temporal and spatial filtering of turbulent structures decreases leading to higher measured turbulence levels. The measured turbulence levels are similar to previously conducted measurements of the exit conditions of turbulent jets performed by Papadopoulos and Pitts (1998) (\(\approx 4\%\) at \(x/D = 0.16\)), Xu and Antonia (2002) (4%), and Mi et al. (2001) (\(\approx 3\%\) at \(x/D = 0.05\)) which used velocity measurements based on hot wire anemometry. Given that the measurements presented in Table 3 are located further downstream at \(x/D = 1.2\), a slightly increased value to the literature references is reasonable.
Two additional rows in Table 3 show results for elliptically weighted interrogation windows with weighting factors \(w_x \times w_y\) of \(32\,\hbox {px} \times 16\,\hbox {px}\) (axially aligned) and \(16\,\hbox {px} \times 32\,\hbox {px}\) (radially aligned). As both IWs have the same size, they should include a similar amount of noise. Still, the uncertainty of u of the radially aligned IW is on average higher than that of the axially aligned IW, further explaining the trends observed in Fig. 6 based on the inclusion of differently moving particles in the inhomogeneous flow as interrogation windows are increased in sized radially. It is interesting to note that \(\sigma ^2_{U_u}/\sigma ^2_{u,m}\) for the axially aligned elliptically weighted IW is even lower than that of the square window of size \(w = 48\,\hbox {px}\), underlining the additional benefit of IWs with adapted shapes in shear flows.
The increasing measured turbulence level with decreasing IW size can be directly seen from the widths of the velocity histograms of configuration B in Fig. 7. Apart from the width of the distribution, which is associated with the standard deviation or magnitude of measured velocity fluctuations, it can be observed that the shape of the distribution functions are affected by a change of IW size, too. Namely, the smaller the size of the IW is set, the larger is the deviation of the skewness S and kurtosis K from the Gaussian reference values of \(S = 0\) and \(K = 3\) as is shown in Table 4. A similar trend is observed for elliptically weighted IWs with different orientations but equal size: the axially aligned IW displays a stronger departure from a Gaussian distribution than the radially aligned counterpart. Interestingly, former investigations in the exit region of a turbulent pipe jet have shown similar values to those measured with the smallest IW size of 16 px: Figure 1 of Papadopoulos and Pitts (1998) shows a measured skewness of –0.5 and a kurtosis of 3.4 at the jet exit (read from plot) and distributions of the scalar fluctuations show similar values in Fig. 21 of Mi et al. (2001). Both experiments were conducted with wire probes, which were smaller than the majority of turbulent structures of the respective flows and only minimally filtered the measured quantities spatially. It can therefore be concluded that the larger the IW size is chosen, the higher will be the low-pass filtering effect resulting in a closer-to-Gaussian distribution shape quantified by higher-order statistics such as skewness and kurtosis.
To conclude, in an inhomogeneous flow as discussed herein, an increase in the IW size results in more particles being taken into account during vector calculations that are further away from the centerline and therefore exhibit different conditions in the shear flow of the turbulent jet. Filtering over a multitude of such differently moving particles results in a distribution closer to a normal distribution, suppressing the underlying probability distribution of turbulence structures. Similar to the measurement of turbulence intensities, the effect of spatial filtering of the IW needs to be considered when computing higher-order statistics in turbulent shear flows.
4.4 Measurement of turbulent scales using autocorrelations
Apart from the statistical analysis performed in Sect. 4.3, the high imaging rate and large sample size of the presented PIV data sets enable a high-resolution analysis of velocity time series for correlations and power spectral density estimates. As the repetition rate is increased to \(400\,\hbox {kHz}\) for the highest temporal dynamic range, an IW length of 16 px only yields 32 vectors to be extracted along the axial coordinate (128 px window length with 75% IW overlap), limiting the spatial dynamic range. Therefore, this postage-stamp approach (Beresh et al. 2018) serves as a promising tool to extract temporally resolved data but lacks at providing simultaneous spatial information over larger spatial displacements.
First, the longitudinal integral turbulent scales are extracted at a planar spatial position \(\mathbf {x} = (x,y)\) based on the Eulerian autocorrelation function
where the spatial lag in two dimensions is denoted by \(\mathbf {\xi } = (\xi , \eta )\) and the temporal lag is expressed by \(\tau\). From this definition as the most general form of a space–time correlation in the Eulerian sense, the temporal autocorrelation can be calculated by setting \(\mathbf {\xi } = \mathbf {0}\), whereas the spatial autocorrelation is computed along the axial direction using \(\mathbf {\xi } = (\xi , 0)\) and \(\tau = 0\). Figure 8a shows the results of the temporal autocorrelation at a position of \(x = 1.2D\) on the centerline (\(y = 0D\)) and Fig. 8b displays the spatial autocorrelation at a position of \(x = 0.9D\) on the centerline (\(y = 0D\)), such that the full field of view of the \(400\,\hbox {kHz}\) measurements (until \(x = 1.6D\)) is encompassed by the spatial lag.
For both the spatial and temporal autocorrelations, a decrease in the IW size leads to an earlier decorrelation of the turbulent fluctuations. This observation can be explained by two superimposed effects. First, larger IW sizes lead to increased spatial filtering of small turbulent structures. These smaller structures will however decay quicker (according to the energy cascade) and are therefore not taken into account leading to an increased value of the correlation coefficient compared to smaller interrogation windows, which resolve smaller turbulent structures. Second, velocity vectors calculated within smaller interrogation windows are computed at higher noise levels, as less particles contribute to the overall correlation calculation. Consequently, a correlation of noisier velocity signals leads to a decreased value of the correlation coefficient as both the temporal and spatial lag increase (Nobach 2015).
Based on the correlation functions calculated, the integral scales (Eqs. (4) and (5)) are listed in Table 5. For the temporal autocorrelation, the computation of the integral time scale \(T_{uu}\) is realized by numerically integrating the correlation function until the first zero-crossing using the trapezoidal rule. Due to the limited spatial range, the integral length scale \(L_{uu}\) is only evaluated for the smallest IW of 16 px by integrating over all available data points. The correlation value at the highest spatial lag is 0.028 and therefore close to the zero-crossing such that the left out area under the correlation curve is small and the computed integral length scale is slightly underestimated. As the computed values show, an accurate measurement of the integral time scale requires high repetition rates (beyond \(200\,\hbox {kHz}\) to at least acquire 10 samples before the zero-crossing), which has been previously only achieved by pulse-burst lasers at significantly lower amounts of consecutively recorded samples (Miller et al. 2016).
Additionally, the effective number of statistically independent samples \(N_e\) can be computed using Equation (6), where \(T_{t}\) is the total observation time of the time-resolved measurement (Sciacchitano and Wieneke 2016). For an IW size of 16 px, \(N_e\) is 137,831, showing that even though the temporal autocorrelation function is well-resolved, a large number of statistically independent samples for the robust computation of statistical moments remain.
To put the measurements of statistical quantities into perspective, the standard measurement uncertainty of the mean axial velocity can be computed as \(U_{\langle u \rangle } = \sigma _{u}/\sqrt{N_e} = 0.01\,\hbox {m/s}\) (Sciacchitano and Wieneke 2016). This small value truly shows the advantage of a TR-PIV measurement equipped with a continuously pulsing laser in combination with a large on-board memory of the camera to achieve a high value of \(N_e\). In comparison to state-of-the-art low-speed PIV systems, it should be concluded that despite the lower amounts of \(N_e\) of these systems (typically around 1000), they still offer superior spatial resolution and lower measurement noise leading to lower uncertainties of individually measured vectors. For instance, Scharnowski et al. (2019) report a value of \(\langle U_u \rangle = 0.05\,\hbox {px}\) for an interrogation window length of 16 px compared to our measured value at the same IW size of \(\langle U_u \rangle = 0.16\,\hbox {px}\).
Based on the calculation of the integral scales, further characteristic turbulent scales can be determined. In isotropic turbulence, the Taylor microscale is defined as
where the dissipation rate of turbulent kinectic energy is given by \(\varepsilon\) and the kinematic viscosity is denoted by \(\nu\). A direct experimental determination of the Taylor microscale without the need of assuming isotropic turbulence requires a highly resolved measurement of the transverse autocorrelation \(R_{vv}\), at which an osculating parabola is fitted, whose zero-crossing determines \(\lambda\) (Pope 2012). Due to the limited spatial resolution of the given measurements, this direct approach is unfortunately not feasible and equation (7) will be used instead. The smallest dissipative length scale is the Kolmogorov length scale \(\eta _k\), which is given by equation (8).
As is apparent from the definitions of \(\lambda\) and \(\eta _k\), the dissipation rate of turbulent kinectic energy \(\varepsilon\) is required for the computation of both values. The determination of \(\varepsilon\) is, however, strongly affected by a limited spatial resolution, as \(\varepsilon\) is defined through the gradient tensor of fluctuating velocities, instead of the velocity fluctuations themselves (Pope 2012). A number of investigations have developed methods to improve the accuracy of dissipation rate measurements from PIV to extract \(\varepsilon\) from, e.g., curve fitting of energy spectra (Xu and Chen 2013) or using a large-eddy approach to correct for the filtering of the IW size (Bertens et al. 2015), but the results of these methods are dependent on the individual flow boundary conditions and further assumptions. Hence, we will employ a simple dimensional analysis to roughly estimate the turbulent dissipation rate using the integral length scale \(L_{uu}\) and the standard deviation of the axial velocity component \(\sigma _{u}\) (Batchelor 1953):
Unfortunately, as discussed by Burattini et al. (2005), the constant \(C_\varepsilon\) is dependent on the boundary conditions of the flow and can not be assumed to be a universal constant. Available data in the literature ranges from values of \(C_\varepsilon =\) 0.5–2.5 depending on flow type and turbulent Reynolds numbers (Burattini et al. 2005), which is why we estimate \(C_\varepsilon\) as unity in Equation (9). This approach at least guarantees an estimation of the order of magnitude of the derived turbulent scales. The results of the estimation of turbulent scales are \(199\,\upmu \hbox {m}\) for the Taylor microscale and \(15\,\upmu \hbox {m}\) for the Kolmogorov scale. The spatial resolutions of the PIV system estimated to be around \(314\,\upmu \hbox {m}\) for the smallest IW size is in the order of the Taylor microscale and much larger than the Kolmogorov length.
4.5 Power spectral density estimation
Turbulence spectra provide detailed knowledge on the scales through which turbulent kinetic energy is transported in the energy cascade. Therefore, they offer the capability to compare differently resolved PIV measurements and their low-pass filtering characteristics on the small-scale portion of the turbulent structures. Their computation from time-resolved data is usually performed by a periodogram, which represents the Fourier transform of the biased estimate of the temporal autocorrelation. As 1242 298 consecutive time-resolved samples could be obtained at a repetition rate of \(400\,\hbox {kHz}\), a periodogram spanning a frequency range of 0.32 Hz to \(200\,\hbox {kHz}\) (given by the sampling theorem) could theoretically be computed. However, the variance of the periodogram does not approach zero as the number of samples N is increased, making the periodogram an inconsistent estimate of the power spectrum (Hayes 1996). The widely used method of Welch solves this issue by intruducing a windowing scheme, such that the time series is separated into smaller overlapping portions for which a periodogram is computed. Subsequently, the individually computed periodograms are averaged, which results in a variance of zero as N approaches infinity, leading to a consistent estimate of the power spectrum (Welch 1967). Thus, a lower variance of the power spectral density is achieved by effectively lowering the spectral resolution, which is determined by the amount of samples in each window. This underlines the need for large amounts of continuously recorded velocity samples enabled by the fiber laser system to achieve low-variance high-resolution power spectrum estimates.
Figure 9 displays the temporal power spectral density estimations calculated using Welch’s method on the centerline of the potential core at an axial distance of \(x = 1.2D\). The signal was divided into portions of 6200 consecutive velocity samples and the overlap was chosen to be 50%. A Hann window function was applied to each periodogram calculation to minimize spectral leakage occuring during the discrete Fourier transform of the data sets. The chosen parameters lead to an increase in the minimally resolvable frequency to 64 Hz, which is still much lower than the relevant frequency scales of the turbulence decay.
The power spectral density curves all start to decay around a frequency of \(10\,\hbox {kHz}\), marking the onset of the inertial subrange. This again shows that repetition rates beyond \(100\,\hbox {kHz}\) are necessary to capture large amounts of the turbulence decay. However, the maximum resolvable frequency is not only dependent on the sampling rate but also on several other factors:
-
The spatial filtering of the finite interrogation window size also translates into a temporal filter through the convection of particles with the mean streamwise velocity \(\langle u \rangle\). According to the sampling theorem and Taylor’s hypothesis, the highest resolvable frequency through spatial filtering is computed through \(\langle u \rangle /(2w)\) and highlighted by dashed lines for each IW size in Fig. 9. Beyond this limit, all curves but the smallest IW size of 16 px show a steeper slope of decay due to the spatial low-pass filtering, which seems to be the main limiting factor of the highest resolvable frequency for the given flow configuration and TR-PIV system. It is however interesting to note that the curves are already slightly separated before reaching the respective resolution limits. This behavior could be the result of the shear flow characteristics (similar to the changes observed in the velocity histograms) or the increased amount of noise for smaller IW sizes that increases the amplitude of the power spectral density.
-
The frequency response of tracer particles is another factor that determines the maximum resolvable frequency of turbulent fluctuations. Following the analysis of Melling (1997), the used DEHS particles with a mean diameter of \(0.5\,\upmu \hbox {m}\) have a response time \(\tau _p\) of \(0.8\,\upmu \hbox {m}\), which is calculated as \(\rho _p d_p^2/(18 \mu )\). This can be used to derive the ratio between the kinetic energies of the particle velocity fluctuations and the fluid velocity fluctuations for high density ratios between particles and fluid as
$$\begin{aligned} \dfrac{\overline{u_p^2}}{\overline{u_f^2}} = (1 + 2\pi f \tau _p)^{-1}. \end{aligned}$$(10)This ratio gradually decreases with the sampling frequency f such that a ratio of 0.5 (as suggested by Mei (1996)) is reached at a frequency of \(190\,\hbox {kHz}\). Beresh et al. (2020) argues that this ratio can be further lowered to still resolve smaller velocity fluctuations as these contain a smaller amount of kinetic energy than large scales which is supported by in situ measurements of the particle response time. Hence, the particle response should not be the limiting factor in the presented TR-PIV measurements in this work.
-
As was already observed earlier, velocity time series calculated from smaller IW sizes are subject to higher amounts of noise, which adds to the overall spectral density estimation. Although the spatial low-pass filtering effect is less pronounced for smaller interrogation windows, the amplitude of the high-frequency noise floor is increased compared to larger IW lengths. Again, the trade-off between noise (or uncertainty of velocity measurements) and spatial resolution is apparent and has to be considered when performing turbulence analysis using PIV data.
It should be noted that multi-frame correlation algorithms could decrease the high-frequency correlation noise level as was recently assessed (Beresh et al. 2021). However, the particle shift per image pair of the presented measurements at \(400\,\hbox {kHz}\) was too large such that a multi-frame correlation algorithm could not improve the noise level of the high-frequency content of the measurements.
The results show that several factors have to be considered when assessing the temporal dynamic range of spectral density estimations. Despite these limitations however, the continuously pulsing fiber laser architecture enables unprecedented amounts of consecutively recorded samples at similar repetition rates to pulse-burst laser systems (Beresh et al. 2018; Miller et al. 2016) enabling a detailed analysis of small-scale turbulent flow structures.
4.6 Space–time correlations and applicability of Taylor’s hypothesis
Due to the decreased amount of active pixels of the CMOS camera at high repetition rates, the computation of spatial spectra relies on the transformation of temporal to spatial quantities. This is classically performed using Taylor’s hypothesis of frozen turbulence (Taylor 1938), which relies on the assumption that turbulent structures are convected by the mean velocity such that a straightforward transformation of temporal to spatial frequencies is performed as \(\kappa = f/\langle u \rangle\). This hypothesis is, however, only applicable in flows with low turbulence levels and is known to fail in free shear flows (Pope 2012; Del Álamo and Jiménez 2009). One option to experimentally test the applicability of Taylor’s hypothesis is an analysis of the space–time correlation \(\rho _{uu}(\xi ,\tau )\) (Wallace 2014; He et al. 2017). As TR-PIV offers the extraction of space–time correlations from a single measurement (Wernet 2007), it has been recently applied to analyze the deviations from Taylor’s hypothesis in the intermediate regions of a turbulent jet at a repetition rate of \(100\,\hbox {kHz}\) (Roy et al. 2021). It is therefore interesting to test if a deviation is observable on the centerline of the potential core, which shows a much lower turbulence level (\(\mathrm {Tu}_u \approx 5\%\)) than the fully developed region of the turbulent jet (\(\mathrm {Tu}_u \approx 25\%\)) (Xu and Antonia 2002; Mi et al. 2001). Although the spatial extent of the TR-PIV measurements of this work is fairly limited, a calculation of the space–time correlation \(\rho _{uu}(\xi ,\tau )\) according to equation (3) at moderate spatials lags is possible and was performed for both \(200\,\hbox {kHz}\) and \(400\,\hbox {kHz}\) as is shown in Fig. 10.
Space–time correlations of the streamwise velocity fluctuations \(\rho _{uu}(\xi ,\tau )\) on the centerline: a \(200\,\hbox {kHz}\) TR-PIV centered around \(x = 1.2D\), b \(400\,\hbox {kHz}\) TR-PIV encompassing \(x = 0.9D\) to \(x = 1.6D\). Convection of fluid elements through the mean streamwise velocity \(\langle u \rangle\) is shown by a dashed line, while the convection of the correlation peak is shown by circles
The isocorrelations, which are displayed by filled contours, represent elongated ellipses, as both numerical and experimental investigations of turbulent shear flows have shown before (Wernet 2007; Wallace 2014; Del Álamo and Jiménez 2009). If Taylor’s hypothesis would hold true, the isocorrelation contours were straight lines, whose slope represent the convection velocity with which turbulent structures are transported through the flow field (Zhao and He 2009; He et al. 2017). In the limited field of view of the \(400\,\hbox {kHz}\) measurements in Fig. 10b, this assumption is met with minor deviations. However, due to the decay of turbulence, the value of the correlation decreases from 1 at zero temporal and spatial lag as turbulent structures are convected downstream. The space–time correlations at \(200\,\hbox {kHz}\) in Fig. 10a provide a more complete view of the isocorrelation shapes, which become more asymmetric as the spatial and temporal lags increase.
A direct measure of this deviation can be given by comparing the convection of fluid elements by the mean axial velocity \(\langle u \rangle\) (dashed line) with the location of the correlation peak over several time lags (circles) in Fig. 10. It should be noted that the change in mean velocity over spatial lags was taken into account when calculating the convection of fluid elements. While the convection of turbulent structures is initially matching the mean velocity of the flow field, it deviates significantly at large lags. The decreased axial turbulent convection speed on the centerline is in parts a direct consequence of the local magnitude and direction of turbulent fluctuations, as fluid elements, which are radially transported away from the centerline through fluctuations are subject to lower mean velocities and will hence be convected more slowly in the axial direction. Further detailed investigations are, however, necessary to quantify the contributions of different influences to this phenomenon, especially considering the coupling between Eulerian and Lagrangian space–time correlations (He et al. 2017; Viggiano et al. 2021). While the differences are much smaller than those observed in the intermediate region by Roy et al. (2021), they show that a high-resolution TR-PIV system equipped with a fiber laser is capable of reliably measuring deviations from Taylor’s hypothesis in a region of relatively low turbulence intensity.
5 Conclusion
The application of a Yb:YAG fiber laser for ultra-high-speed time-resolved particle image velocimetry was demonstrated in the potential core of a turbulent round jet. The system provides sufficient pulse energy and excellent beam profile characteristics at repetition rates up to 1 MHz for the velocimetry of highly transient turbulent flows. Two different high-speed cameras, a CMOS and an in situ storage CCD camera, were employed to demonstrate turbulence measurements at repetition rates up to \(500\,\hbox {kHz}\).
The continuously pulsing laser enables the recording of large time series, which can be used to derive statistical quantities of turbulence, space–time correlations, and turbulence spectra. The quality of the PIV recordings was assessed in terms of their spatial resolution and measurement uncertainty, whose dependence on the interrogation window size was quantified. The computation of turbulent scales was demonstrated at a repetition rate of \(400\,\hbox {kHz}\), which was necessary to resolve the autocorrelations reasonably well. The influence of the interrogation window size on the power spectral density was investigated, which showed that the spatial resolution was the limiting factor of the frequency resolution of the presented TR-PIV measurements. Finally, space–time correlations revealed the deviations from Taylor’s hypothesis of frozen turbulence through a comparison of the convection velocity of the correlation peak with the mean axial flow velocity.
The demonstrated measurements show that the recent development of pulsed fiber laser technology can provide new insights into turbulent flows at a compact footprint and high flexibility. Future high-speed PIV investigations will strongly benefit from this advancement as unprecedented temporal dynamic ranges are possible, which challenge existing laser solutions for high-speed flow velocimetry.
References
Batchelor GK (1953) The theory of homogeneous turbulence. Cambridge science classics. Cambridge University Press, Cambridge
Baum E, Peterson B, Böhm B, Dreizler A (2014) On the validation of LES applied to internal combustion engine flows: Part 1: Comprehensive experimental database. Flow Turbul Combust 92(1–2):269–297. https://doi.org/10.1007/s10494-013-9468-6
Beresh SJ (2021) Time-resolved particle image velocimetry. Meas Sci Technol 32(10):102003. https://doi.org/10.1088/1361-6501/ac08c5
Beresh S, Kearney S, Wagner J, Guildenbecher D, Henfling J, Spillers R, Pruett B, Jiang N, Slipchenko M, Mance J, Roy S (2015) Pulse-burst PIV in a high-speed wind tunnel. Meas Sci Technol 26(9):095305. https://doi.org/10.1088/0957-0233/26/9/095305
Beresh SJ, Henfling JF, Spillers RW, Spitzer SM (2018) ‘Postage-stamp PIV’: small velocity fields at 400 kHz for turbulence spectra measurements. Meas Sci Technol 29(3):034011. https://doi.org/10.1088/1361-6501/aa9f79
Beresh SJ, Spillers R, Soehnel M, Spitzer S (2020) Extending the frequency limits of postage-stamp PIV to MHz rates. In: AIAA Scitech 2020 Forum, American Institute of Aeronautics and Astronautics, Reston, Virginia. https://doi.org/10.2514/6.2020-1018
Beresh SJ, Neal D, Sciacchitano A (2021) Validation of multi-frame PIV image interrogation algorithms in the spectral domain. In: AIAA Scitech 2021 Forum, American Institute of Aeronautics and Astronautics, Reston, Virginia. https://doi.org/10.2514/6.2021-0019
Bertens G, van der Voort D, Bocanegra-Evans H, van de Water W (2015) Large-eddy estimate of the turbulent dissipation rate using PIV. Exp Fluids. https://doi.org/10.1007/s00348-015-1945-3
Böhm B, Heeger C, Gordon RL, Dreizler A (2011) New perspectives on turbulent combustion: multi-parameter high-speed planar laser diagnostics. Flow Turbul Combust 86(3–4):313–341. https://doi.org/10.1007/s10494-010-9291-2
Brock B, Haynes RH, Thurow BS, Lyons GW, Murray NE (2014) An examination of MHz rate PIV in a heated supersonic jet. In: 52nd Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics, Reston, Virginia. https://doi.org/10.2514/6.2014-1102
Burattini P, Lavoie P, Antonia RA (2005) On the normalized turbulent energy dissipation rate. Phys Fluids 17(9):098103. https://doi.org/10.1063/1.2055529
Del Álamo JC, Jiménez J (2009) Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J Fluid Mech 640:5–26. https://doi.org/10.1017/S0022112009991029
Eitel F, Pareja J, Geyer D, Johchi A, Michel F, Elsäßer W, Dreizler A (2015) A novel plasma heater for auto-ignition studies of turbulent non-premixed flows. Exp Fluids. https://doi.org/10.1007/s00348-015-2059-7
Etoh TG, Poggemann D, Kreider G, Mutoh H, Theuwissen A, Ruckelshausen A, Kondo Y, Maruno H, Takubo K, Soya H, Takehara K, Okinaka T, Takano Y (2003) An image sensor which captures 100 consecutive frames at 1 000 000 frames/s. IEEE Trans Electron Dev 50(1):144–151. https://doi.org/10.1109/TED.2002.806474
Gabzdyl J (2008) Fibre lasers make their mark. Nature Photon 2(1):21–23. https://doi.org/10.1038/nphoton.2007.268
Hayes MH (1996) Statistical digital signal processing and modeling. Wiley, New York, NY
He G, Jin G, Yang Y (2017) Space-time correlations and dynamic coupling in turbulent flows. Ann Rev Fluid Mech 49(1):51–70. https://doi.org/10.1146/annurev-fluid-010816-060309
Kähler CJ, Scharnowski S, Cierpka C (2012) On the resolution limit of digital particle image velocimetry. Exp Fluids 52(6):1629–1639. https://doi.org/10.1007/s00348-012-1280-x
Lempert W, Wu PF, Miles R, Zhang B, Lowrance J, Mastrocola V, Kosonocky W (1996) Pulse-burst laser system for high-speed flow diagnostics. In: 34th Aerospace Sciences Meeting and Exhibit, American Institute of Aeronautics and Astronautics, Reston, Virigina
Mei R (1996) Velocity fidelity of flow tracer particles. Exp Fluids 22(1):1–13. https://doi.org/10.1007/BF01893300
Melling A (1997) Tracer particles and seeding for particle image velocimetry. Meas Sci Technol 8(12):1406–1416. https://doi.org/10.1088/0957-0233/8/12/005
Mi J, Nobes DS, Nathan GJ (2001) Influence of jet exit conditions on the passive scalar field of an axisymmetric free jet. J Fluid Mech 432:91–125. https://doi.org/10.1017/S0022112000003384
Michaelis D, Neal DR, Wieneke B (2016) Peak-locking reduction for particle image velocimetry. Meas Sci Technol 27(10):104005. https://doi.org/10.1088/0957-0233/27/10/104005
Miller JD, Jiang N, Slipchenko MN, Mance JG, Meyer TR, Roy S, Gord JR (2016) Spatiotemporal analysis of turbulent jets enabled by 100-kHz, 100-ms burst-mode particle image velocimetry. Exp Fluids. https://doi.org/10.1007/s00348-016-2279-5
Murphy MJ, Adrian RJ (2010) PIV space-time resolution of flow behind blast waves. Exp Fluids 49(1):193–202. https://doi.org/10.1007/s00348-010-0843-y
Nobach H (2015) A model-free noise removal for the interpolation method of correlation and spectral estimation from laser Doppler data. Exp Fluids. https://doi.org/10.1007/s00348-015-1975-x
Oxlade AR, Valente PC, Ganapathisubramani B, Morrison JF (2012) Denoising of time-resolved PIV for accurate measurement of turbulence spectra and reduced error in derivatives. Exp Fluids 53(5):1561–1575. https://doi.org/10.1007/s00348-012-1375-4
Papadopoulos G, Pitts WM (1998) Scaling the near-Field centerline mixing behavior of axisymmetric turbulent jets. AIAA J 36(9):1635–1642. https://doi.org/10.2514/2.565
Philo JJ, Frederick MD, Slabaugh CD (2021) 100 kHz PIV in a liquid-fueled gas turbine swirl combustor at 1 MPa. Proc Combust Inst 38(1):1571–1578. https://doi.org/10.1016/j.proci.2020.06.066
Pope SB (2012) Turbulent flows. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511840531
Raffel M, Willert CE, Scarano F, Kähler CJ, Wereley ST, Kompenhans J (2018) Particle image velocimetry. Springer International Publishing, Cham. https://doi.org/10.1007/978-3-319-68852-7
Rossi M, Pierron F, Forquin P (2014) Assessment of the metrological performance of an in situ storage image sensor ultra-high speed camera for full-field deformation measurements. Meas Sci Technol 25(2):025401. https://doi.org/10.1088/0957-0233/25/2/025401
Roy S, Miller JD, Gunaratne GH (2021) Deviations from Taylor’s frozen hypothesis and scaling laws in inhomogeneous jet flows. Commun Phys. https://doi.org/10.1038/s42005-021-00528-0
Samson B, Dong L (2013) Fiber lasers. In: Handbook of solid-state lasers, Elsevier, pp 403–462, https://doi.org/10.1533/9780857097507.2.403
Scharnowski S, Bross M, Kähler CJ (2019) Accurate turbulence level estimations using PIV/PTV. Exp Fluids. https://doi.org/10.1007/s00348-018-2646-5
Sciacchitano A, Wieneke B (2016) PIV uncertainty propagation. Meas Sci Technol 27(8):084006. https://doi.org/10.1088/0957-0233/27/8/084006
Sciacchitano A, Neal DR, Smith BL, Warner SO, Vlachos PP, Wieneke B, Scarano F (2015) Collaborative framework for PIV uncertainty quantification: comparative assessment of methods. Meas Sci Technol 26(7):074004. https://doi.org/10.1088/0957-0233/26/7/074004
Slipchenko MN, Miller JD, Roy S, Meyer TR, Mance JG, Gord JR (2014) 100 kHz, 100 ms, 400 J burst-mode laser with dual-wavelength diode-pumped amplifiers. Opt Lett 39(16):4735–4738. https://doi.org/10.1364/OL.39.004735
Slipchenko MN, Meyer TR, Roy S (2020) Advances in burst-mode laser diagnostics for reacting and nonreacting flows. Proc Combust Inst 38(1):1533-1560. https://doi.org/10.1016/j.proci.2020.07.024
Smyser ME, Rahman KA, Slipchenko MN, Roy S, Meyer TR (2018) Compact burst-mode Nd:YAG laser for kHz-MHz bandwidth velocity and species measurements. Opt Lett 43(4):735–738. https://doi.org/10.1364/OL.43.000735
Suzuki M, Sugama Y, Kuroda R, Sugawa S (2020) Over 100 Million Frames per Second 368 Frames Global Shutter Burst CMOS Image Sensor with Pixel-wise Trench Capacitor Memory Array. Sensors. https://doi.org/10.3390/s20041086
Taylor GI (1938) The Spectrum of Turbulence. Proc Royal Soc London Series A - Math Phys Sci 164(919):476–490. https://doi.org/10.1098/rspa.1938.0032
Ter-Mikirtychev VV (2019) Fundamentals of fiber lasers and fiber amplifiers, vol 181. Springer International Publishing, Cham. https://doi.org/10.1007/978-3-030-33890-9
Thurow B, Jiang N, Lempert W (2013) Review of ultra-high repetition rate laser diagnostics for fluid dynamic measurements. Meas Sci Technol 24(1):012002. https://doi.org/10.1088/0957-0233/24/1/012002
Tochigi Y, Hanzawa K, Kato Y, Kuroda R, Mutoh H, Hirose R, Tominaga H, Takubo K, Kondo Y, Sugawa S (2013) A global-shutter CMOS image sensor with readout speed of 1-Tpixel/s burst and 780-Mpixel/s continuous. IEEE J Solid-State Circuits 48(1):329–338. https://doi.org/10.1109/JSSC.2012.2219685
Tsuji K (2018) The micro-world observed by ultra high-speed cameras. Springer International Publishing, Cham. https://doi.org/10.1007/978-3-319-61491-5
Viggiano B, Basset T, Solovitz S, Barois T, Gibert M, Mordant N, Chevillard L, Volk R, Bourgoin M, Cal RB (2021) Lagrangian diffusion properties of a free shear turbulent jet. J Fluid Mech. https://doi.org/10.1017/jfm.2021.325
Wallace JM (2014) Space-time correlations in turbulent flow: a review. Theo Appl Mech Lett 4(2):022003. https://doi.org/10.1063/2.1402203
Welch P (1967) The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans Audio Electroacous 15(2):70–73. https://doi.org/10.1109/TAU.1967.1161901
Wernet M, Opalski A (2004) Development and application of a MHZ frame rate digital particle image velocimetry system. In: 24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, American Institute of Aeronautics and Astronautics, Reston, Virigina. https://doi.org/10.2514/6.2004-2184
Wernet MP (2007) Temporally resolved PIV for space-time correlations in both cold and hot jet flows. Meas Sci Technol 18(5):1387–1403. https://doi.org/10.1088/0957-0233/18/5/027
Westerweel J (2008) On velocity gradients in PIV interrogation. Exp Fluids 44(5):831–842. https://doi.org/10.1007/s00348-007-0439-3
Westerweel J, Scarano F (2005) Universal outlier detection for PIV data. Exp Fluids 39(6):1096–1100. https://doi.org/10.1007/s00348-005-0016-6
Westerweel J, Elsinga GE, Adrian RJ (2013) Particle image velocimetry for complex and turbulent flows. Ann Rev Fluid Mech 45(1):409–436. https://doi.org/10.1146/annurev-fluid-120710-101204
Wieneke B (2015) PIV uncertainty quantification from correlation statistics. Meas Sci Technol 26(7):074002. https://doi.org/10.1088/0957-0233/26/7/074002
Willert CE (2015) High-speed particle image velocimetry for the efficient measurement of turbulence statistics. Exp Fluids. https://doi.org/10.1007/s00348-014-1892-4
Williams E, Brousseau EB, Rees A (2014) Nanosecond Yb fibre laser milling of aluminium: effect of process parameters on the achievable surface finish and machining efficiency. Int J Adv Manuf Technol 74(5–8):769–780. https://doi.org/10.1007/s00170-014-6038-6
Xu D, Chen J (2013) Accurate estimate of turbulent dissipation rate using PIV data. Exp Therm Fluid Sci 44:662–672. https://doi.org/10.1016/j.expthermflusci.2012.09.006
Xu G, Antonia R (2002) Effect of different initial conditions on a turbulent round free jet. Exp Fluids 33(5):677–683. https://doi.org/10.1007/s00348-002-0523-7
Yang L, Huang W, Deng M, Li F (2016) MOPA pulsed fiber laser for silicon scribing. Opt Laser Technol 80:67–71. https://doi.org/10.1016/j.optlastec.2016.01.006
Zhao X, He GW (2009) Space-time correlations of fluctuating velocities in turbulent shear flows. Phys Rev E Stat Nonlinear Soft Matter Phys 79(4 Pt 2):046316. https://doi.org/10.1103/PhysRevE.79.046316
Acknowledgements
The authors would like to thank the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG, Projektnummer 237267381–TRR 150) for its support through CRC/Transregio 150 “Turbulent, chemically reactive, multi-phase flows near walls.” Andreas Dreizler is grateful for support by the Gottfried Wilhelm Leibniz program of the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG). We would like to express our gratitude toward Michael Lee, Michael Stark, and Tim Westphäling of IPG Laser GmbH for discussions regarding the operation of the fiber laser system. Finally, we would like to thank Cameron Tropea for providing the Shimadzu HPV-2 high-speed camera.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Geschwindner, C., Westrup, K., Dreizler, A. et al. Ultra-high-speed time-resolved PIV of turbulent flows using a continuously pulsing fiber laser. Exp Fluids 63, 75 (2022). https://doi.org/10.1007/s00348-022-03424-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-022-03424-7