Instantaneous flame front identification by Mie scattering vs. OH PLIF in low turbulence Bunsen flame

Abstract

Simultaneous OH-PLIF and Mie scatter imaging were used to investigate turbulent premixed flame edge detection under a range of turbulence characteristics on a stabilised piloted Bunsen burner. A 527 nm wavelength laser beam is used to generate a Mie scattering sheet at 500 Hz, and a 283 nm wavelength laser sheet is created using 355 nm wavelength laser to pump an optical parametric oscillator to induce florescence from OH radicals at 5 Hz. A phase-locking technique is applied to synchronize and lock the two laser systems. The number density method has been used to detect flame edges in Mie scattering images, and three algorithms were applied to OH-PLIF images as a reference. A comparison of the methods and different parameter setting is made by using the metrics of location difference, flame surface density and curvature of flame edges. The processed data show that once a well-tuned window size is determined by applying the number density method, averaged spatial differences between Mie scattering images and OH-PLIF images are of the order of or smaller than the laminar flame thickness, demonstrating that under these conditions, high frequency Mie scatter measurements can be used as well as OH-PLIF images to define the flame edge at that spatial resolution. The positive result confirms that double-frame Mie scattering allows the measurement of high frequency conditional velocity distributions and flame properties simultaneously using solely Mie scattering, provided that the particle density is suitably designed to be around 16 px$^2$ per particle.

Graphic Abstract

1 Introduction

In the study of turbulent premixed flames, it is essential to identify the flame edge and associated local velocities, particularly in the context of flame thicknesses much thinner than the characteristic turbulent length scales. A typical way to detect the flame edge location is to apply planar laser-induced fluorescence (PLIF) to detect characteristic flame species, such as formaldehyde (Wabel et al. 2017; Wang et al. 2019), or OH radicals (Kobayashi et al. 2005; Troiani et al. 2013; Wang et al. 2015). Mie scattering using droplets can also be used for the same purpose, as droplets evaporate through the flame front (Smallwood et al. 1995; Cheng et al. 1989; Cheng and Shepherd 1991; Filatyev et al. 2005). When solid particles are used as tracers, the flame edge can be defined by the change of the particle number density, as the heat release changes the gas density, leading to a corresponding change in particle number density Pfadler et al. (2007). For images acquired in a double-frame mode, velocity measurements can be simultaneously acquired via autocorrelation to yield the local conditional velocity via particle image velocimetry (PIV). Under these conditions, the flame edge location and spatial velocity distribution can be obtained simultaneously, allowing the investigation of the instantaneous flame displacement speed (Kerl et al. 2013) and flame-vortex dynamics (Geikie et al. 2021).

Simultaneous PIV and PLIF measurements have previously been conducted in many experiments, for example (Carter et al. 1998; Löffler et al. 2008; Tanahashi et al. 2005; Böhm et al. 2009; Boxx et al. 2012), in which often Mie scattering images are used to derive only the local velocity rather than the flame edge and conditional velocities (Petersson et al. 2011, 2012). As an example, Petersson et al. (2011, 2012) conducted PIV and PLIF measurements in a methane low-swirl burner to investigate the flame-flow interaction by using acetone as flow tracer. The flame edge was detected based on the maximum gradient of the OH signal, but the probability of finding the flame edge based on the acetone signal was not discussed. A detailed comparison between the flame edge derived from Mie scattering images and OH-PLIF was performed by Pfadler et al. (2007), and a flame front detection method based on the particle number density was applied to find the flame front location in a PIV measurement. However, no details of this method were reported, such as the effect of spatial resolution and corresponding thresholding algorithms. Filatyev et al. also produced simultaneous stereo-PIV and CH PLIF measurements in premixed turbulent flames (Filatyev et al. 2005), images from which were further analysed by Steinberg et al. (2008). However, the studies do not discuss how the flame edge was determined from the particle density, and how the results compare to edges obtained from CH PLIF measurements.

In this paper, we compare the outcome of methods for flame surface determination using detection by Mie scattering and OH-PLIF, and determine the sensitivity of key statistical quantities to algorithms and their parameters, using a Bunsen flame as a platform. The motivation for the comparison is to quantify the differences in the location of the edge and 2D metrics of flame behavior, so that the uncertainties in the determination of flame edges using high frequency Mie scatter (and thus particle-image velocimetry) on its own can be quantified.

2 Experimental methodology

2.1 Burner setup

The burner setup is shown in Fig. 1. The central flame was a turbulent methane/air Bunsen flame generated by a ID = 10 mm quartz tube. The pilot flame was generated by a porous ceramic plate surrounding the central tube. The equivalence ratio of the central flame and the pilot flame were set to be the same during the experiment. The central flame and the pilot flame were enclosed by a low velocity air flow in the outer range of the burner.

Fig. 1

Cutaway of the symmetry plane of the burner setup showing central quartz tube, pilot flame support and outer co-flow. Inset shows cross section of the perforated plate, with dimension of the diameter in mm

Figure 2 shows the flow path of the burner showing the relevant mass flow controllers (MFC). Only the central flow was seeded, and the seeding system was installed downstream of MFC2.

Fig. 2

Flow path diagram showing MFCs for inner flow (MFC1,2), pilot flow (MFC3,4) and co-flow (MCF5)

The turbulence in the central tube was generated by a mesh installed 40 mm upstream of the exit of the tube, consisting of a punched-hole pattern with holes measuring 1.2 mm in diameter, leaving an open area percentage of approximately 42 % (see inset in Fig. 1). A perforated ceramic plate (ID / OD = 14/140 mm, with 40.3 % open area) was used to generate a stabilized laminar pilot flame near the central flame.The surrounding pilot created a uniform product temperature which shielded the central flame from mixing with open air. The velocity field generated by the pilot flame depends on the mass flow rate of the methane/air mixture, which was tuned to ensure that a steady laminar flat flame was anchored immediately above the perforated plate, and was set to approximately half of the corresponding adiabatic flame mass flow rate.

2.2 Seeding system

Calcined aluminium oxide particle tracers were used for Mie scattering. The average size of the aluminium oxide powder was of the order of 1 $\mu$m, the seeding rate around 60–80 per mm$^3$, and the Stokes number below 0.01. Based on the heat capacity of Al$_2$O$_3$, the approximate particle heat loading was around 0.10–0.14 by mass for the solid particles, corresponding to a negligible effect to the overall heat release rate and product temperature.

A fluidized bed seeder was used to add solid particles into the air flow via a bypass valve. A needle valve was used to moderate the mass flow rate for the fluidization air, and thus the rate of particles emerging from the seeder. A short tube in the centre of the vessel served as the outlet of the chamber for the mixed flow. Measurements of the OH signal statistics with and without particles showed negligible difference in flame structure. Although seeding the pilot flow is possible, it would not improve on the edge measurement, as (a) there is sufficient seeding in the flammable mixture to allow identification of the density drop as a marker of the flame location, and (b) seeding the pilot flow with particle densities slightly different from the main flow would actually interfere with the detection of the flame location at the base, because the region containing flame expansion products near the base is thin, provided that the particle density is suitably chosen around 16 px$^2$ per particle.

2.3 Mie scatter

Mie scatter images were obtained by 527 nm wavelength pulses delivered by a Litron LDY 300 dual-head laser at 500 Hz. The laser beam was shaped into a sheet of 40 mm height $\times$ 0.5 mm thickness (as measured by burn paper) at the flame location by using one concave lens and two convex lenses. The beam exiting the laser head ($d~\approx$ 4 mm) was expanded by a plano-concave cylindrical lens ($f_1=-25$ mm) and reshaped by a plano-convex cylindrical lens ($f_2=50.8$ mm) into a 50 mm height$\times$4 mm thickness laser sheet. Finally, the laser sheet was focused by a plano-convex cylindrical lens ($f_3=500$ mm) into the desired laser sheet. The beam of 532 nm wavelength laser was clipped at the edges of 5 mm to create a near top-hat intensity profile with remaining height of 40 mm. A high speed Phantom V611 camera (LaVision) was used to record Mie scattering images using a visible lens objective with focal lens distance of 60 mm, which was doubled to 120 mm by adding a tele-converter, using a maximum aperture of f/2.8 mm.

The imaged region is $1280\times 800$ pixel$^2$ and covered $50\times 32$ mm ($H\times L$), with a spatial resolution of 39 $\mu$m/pixel. Mie scattering for each particle occupied around 2–3 pixels squared. The current seeding systems delivered 14–16 particles per $16\times 16$ pixel$^2$ interrogation window in the reactant side, corresponding to 0.047–0.062 particles per pixel$^2$ or about 16 pixels$^2$ per particle. This particle density was shown to be a good compromise between resolution for determining flame edge whilst providing sufficiently spaced particles for PIV interrogation. Five background images were taken and averaged to be subtracted by the Phantom V611 camera before recording Mie scattering images. The background noise is negligible compared to the fluctuation of the signal.

2.4 OH-PLIF

A laser beam from a single-pulse 355 nm wavelength Nd:YAG laser (Coherent Surelite-III) provided $\sim 165$ mJ/pulse was used to pump an OPO system (Coherent Horizon, tunable wavelength from 192 to 2750 nm) to deliver 2.5 ± 0.5 mJ/pulse at 283 nm at a fixed repetition rate of 10 Hz. The fluctuation in energy comes from the error on the pumping Nd:YAG laser (typically 5%) and temperature-sensitive crystals within the tunable OPO system, which have to be calibrated before every experiment. The energy fluctuation do not affect the results of flame edge detection, although a minimum value is required in order to measure a signal. The beam was firstly combined with the 527 nm laser beam with a 50 : 50 beam splitter (Thorlabs’ 50:50 UV Fused Silica Broadband Beamsplitters) and shaped into a laser sheet of $\sim$27$\times$0.1 mm thickness (as measured by sensitive paper) using the same three UV-transparent optical components for Mie scattering. The location of the last cylindrical concave lens is adjusted to ensure that the 283 nm laser sheet is at a minimum thickness through the sampling zone. The normal choice for OH PLIF is usually a dye laser, for higher energies within the spectral region. The energies provided by the OPO were sufficient to allow generate energies typical of high speed CMOS systems for OH PLIF, and is meanwhile sufficient to define the location of the flame edge with a spatial resolution slightly higher than that of the offered by the target test system using Mie scattering.

OH-PLIF signal images were recorded by a Nanostar intensified CCD (ICCD) camera at a recording frequency set to 5 Hz, using a UV lens with focal length 105 mm and a $320\pm 20$ nm pass-filter to cover the OH* chemiluminescence spectra (Zhao et al. 2018). The imaged region is $1280\times 1024$ pixels, with a pixel resolution of 36 $\mu$m/pixel. The limited spectral width of the OPO (5 cm$^{-1}$), compared with a Dye laser (typically 0.02 cm$^{-1}$), means that the OPO’s wider linewidth puts less energy into the wavelengths corresponding to the excitation wavelengths of OH compared with a narrower linewidth laser. However, the OPO produces a more uniform laser sheet (Tedder and Hicks 2012) and the intensity of the excitation in this experiment was in the linear range therefore image calibration was not necessary. The shutter time of the intensifier was set to 1 $\mu$s, which was sufficiently long to maximize signal but short enough to reduce interference from flame luminosity. The gain ratio of the intensifier was set to 60% so that the background noise is sufficiently low relatively to the signal. Five background images were taken and averaged to be subtracted by the ICCD camera before recording OH-PLIF images.

The signal-to-noise ratio (Sweeney and Hochgreb 2009) of the OH-PLIF image is defined as

$$\begin{aligned} {\mathrm{SNR}}={\frac{\mu _{S}-\mu _{N}}{\sigma _{S}}} \end{aligned}$$

(1)

where $\mu _{S}$ and $\sigma _{S}$ are the mean pixel intensity and standard deviation of the pixel intensity in the product gas side, respectively, and $\mu _{N}$ is the mean pixel intensity in the reactant side. For each OH-PLIF image, the SNR was calculated and averaged by selecting five 64 $\times$ 64 pixel$^2$ background regions in bottom regions of the product and reactant regions where flame is anchored by the tube and the OH signal are less affected the turbulence. The value of SNR in most OH-PLIF images in this paper was around 3, mainly because of a high $\sigma _{S}$ in the product side.

The large difference between the recording frequency of the OH PLIF and Mie scatter collection cameras was resolved by introducing a phase shift during the synchronization. A phase-locking circuit (Digilent Analog Discovery 2) was applied to synchronize the phase difference between the high- and low-speed systems. The phase-locking circuit continuously provides two signals, 10 and 500 Hz, with a constant phase difference. The 10 Hz signal triggers the ICCD camera and the Q-switch of the surelite, and the 500 Hz signal triggers the Phantom V611 camera and the 532 nm green laser. A trigger signal is given from the computer which controls the ICCD camera, and the Phantom V611 camera, simultaneously. Therefore, in each image-capturing step, 20 OH-PLIF images and 2000 Mie scattering images are collected, while the first OH PLIF image has no corresponding simultaneous Mie scattering image and was ignored.

2.5 Experimental conditions

The experimental conditions for the cases considered are listed in Table 1. The longitudinal integral time and length scales $\tau _0$ and $l_0$ were calculated along the central line of the burner from the longitudinal velocity correlations based on the definition of the spatial correlation using 1000 images. The turbulent Reynolds number $\text{Re}_T$ for the flow is defined as ${\text{Re}_T=\frac{u^{\prime }l_0}{\nu }}$, where $u^{\prime }$ is the measured free stream turbulence level, $l_0$ is the measured integral length scale and $\nu$ is the kinematic viscosity of the free stream mixture. The integral time scale is calculated as the auto-correlation of the velocity at the center line of the exit of the tube.

The Karlovitz number, $\text{Ka} = \tau _f/\tau _{\eta }$, is defined as the ratio of the flame time scale, $\tau _f$ , to the Kolmogorov or viscous time scale, $\tau _{\eta }$. The Kolmogorov time scale is estimated as $\tau _{\eta }=\tau _0 \text{Re}_T^{-1/2}$. The flame time scale is estimated as $\tau _f = \alpha /s_l^2$, where $\alpha$ is the thermal diffusivity in the fresh reactants, and $s_l$ is the corresponding laminar flame speed. The thermal diffusivity is estimated as $\alpha =\nu /\text{Pr}$, where Pr is the Prandtl Number taken as equal to 0.71 for the reactant mixtures considered in the present study.

Table 1 Experimental cases

2.6 Characteristics of the flame edge location

The procedure used for filtering and edging results of Mie scattering and OH PLIF images is discussed in Sect. 3. The results of the application of the algorithms consist of the 2D position $\mathbf{x}$ of the interface between reactants and products. The results were evaluated according to the following metrics.

Metric 1

Average minimum distance between coordinates (calculated pixelwise) of flame edges using different methods.

$$\begin{aligned} \overline{d}=\overline{\mid \mathbf{x}_{OH}-\mathbf{x}_{Mie}\mid } \end{aligned}$$

(2)

and $\mathbf{x}_{OH}$ and $\mathbf{x}_{Mie}$ are the 2D coordinates of the flame edges, $||(\cdot )||$ is the Euclidian minimum distance, and the average is over all images containing flame edges.

Metric 2

Local differences in 2D flame front curvature $\kappa$, defined as:

$$\begin{aligned} \kappa =\frac{{x}^{\prime }{y}^{\prime \prime }-{x}^{\prime \prime }{y}^{\prime }}{({x}^{{\prime }{2}}+{y}^{{\prime }{2}})^{3/2}} \end{aligned}$$

(3)

where coordinates $\mathbf{x} = (x(s),y (s))$ represent the two-dimensional parametric curve describing the flame location and where prime and double prime represent the first and second derivative with respect to the flame length parameter s.

Metric 3

Differences in the local flame surface density $\Sigma ^{\prime }$, which is defined as

$$\begin{aligned} \Sigma ^{\prime }&=\mid \nabla c\mid \delta (c-c^{*}) \end{aligned}$$

(4)

where $\delta (c)$ is the Kronecker delta function, $c^{*}$ corresponds to the flame front location.

3 Flame surface detection

The flame surface location in the projected 2D image is defined as an iso-surface that corresponds to the location of a representative scalar corresponding to the location of the flame. The scalar is often temperature or OH. In the case of temperature, the characteristic temperature rise distance is around 0.5 mm, and for OH, of the order of tens of micrometers. The choice of scalar and iso-scalar level can lead to small offsets between measured values. There have been few comparisons between temperature and OH measurements. At low turbulence levels, the OH and temperature profiles have been observed to match within a distance of the order of the laminar flame thickness (Kamal et al. 2017).

In the present case, we have used OH and Mie scatter to determine the flame edge. The algorithms used for either are discussed, and the sensitivity of the outcomes to the parameters chosen follows in results.

3.1 OH-PLIF processing: maximum gradient method

A flow chart of the processes used for determining the flame edge in OH-PLIF images is outlined in Fig. 3. Parameter sensitivity follows in Sect. 4.2.

Pre-processing operations of the images involve background subtraction, filtering the raw image with a moving mean filter and sharpening the contour of the intensity gradient. In this paper, the OH-PLIF images were firstly normalized by the maximum and minimum signals of pixel intensities and then denoised by a moving mean filter with a fixed size $\Delta _f$. The moving mean filter averages the signal in a local square of a given filter size.

The signal intensity is normalised to unity based on global image maxima and minima. The second step is to smooth the image using a suitably method and filter size such as a moving mean filter, with a size kernel associated from the estimated optical resolution of the system, which can also be dynamically or non-linearly adjusted for the location in the reactants or products (Kaiser and Frank 2007; Kamal et al. 2017; Malm et al. 2000). After normalisation, the choice of using maximum gradient of pixel intensity based on the Canny method (Canny 1986) to define the flame edge is used. Using the position of maximum gradient (Canny method) (Canny 1986) can be more sensitive to the presence of noise. Edge detection with gradients has been applied on CH$_2$O-PLIF or OH-PLIF images to define flame edges in a number of studies (Wang et al. 2019; Barlow et al. 2009; Malm et al. 2000; Hartung et al. 2008; Peterson et al. 2019; Ayoola et al. 2006).

Prior to application of the Canny method, anisotropic diffusion methods such as the one developed by Perona and Malik (1990) are used to minimise pixel noise without smearing the gradient of the signal, as previously applied to flame edge detection (Day et al. 2015). A Matlab toolbox for anisotropic diffusion (Lopes 2007) was directly used to conduct the process, using default parameters.

The flame edge was then determined by the maximum gradient of pixel intensity. The Matlab command of Canny edge detection (Canny 1986) was applied and the parameters were optimised as a compromise to remove noise yet detect an edge. There are three input parameters for the Canny edge detection command: a lower threshold, an upper threshold and the standard deviation of the filter, which were tuned to 0.05–0.1, 0.3–0.6 and 0.4–0.7, respectively, to avoid artificial unconnected edges. The final step for the maximum gradient method was to remove small misidentified bubbles for which the perimeter was smaller than 5% of the main flame contour, and connect the resulting sections to get a complete flame edge.

Fig. 3

Flowchart for OH-PLIF image processing

Fig. 4

Flowchart for Mie scattering image processing

3.2 Mie scatter processing: number density method

Images obtained using Mie scatter of particles are inherently noisier than corresponding images of continuous gaseous scalars, as they consist of discontinuities associated with the mean spacing between particles. However, it is possible to create a method to determine the location of the instantaneous flame front in such images via the location of the fluid density change, which is mirrored in the density of scattering particles (Pfadler et al. 2007; Tachibana et al. 2004). The procedure for determining the flame edge is outlined in Fig. 4 and described as follows.

In order to extract the local number density of particles, a local window size $w_d$ is chosen and the unconditional number density of particles is calculated over a square window of size $w_d$ as

$$\begin{aligned} \rho _{I,u}=N_I/w_d^2 \end{aligned}$$

(5)

where $N_I$ is the number of particles in a window determined by a counting algorithm that determines whether a pixel has the local maximum intensity. The counting algorithm consists of three steps: (i) filtering the background by setting a threshold $I_t$ which is slightly higher than the averaged pixel intensity of the background, (ii) finding the pixel with local maximum intensity and (iii) replacing the local maximum intensity pixel by a uniform intensity peak covering five pixels, with the center of a vertical cross symbol in the location of the original local maximum.

Fig. 5

Averaged measured local particle density $\rho _I$ over the whole image as a function of window size in a sample of Case 1. b Orange lines and light blue lines are averaged number densities in the pure product and pure reactant sides, respectively

Fig. 6

Sample illustration of the process for determination of the unconditioned threshold number density. a Sample Mie scatter image in Fig. 5a processed by selecting local maximum pixels and replaced local maximum pixels by ‘$+$’, with selected interrogation region enclosed by red rectangle. b Histogram of unconditional normalised number density within interrogation region selected in (a). c Histogram of conditional normalized number density in (a)

The latter step, which is equivalent of replacing the peak pixel with a Gaussian aggregate of sub-pixel width, helps the robustness of the algorithm as follows: when using only the local maximum pixel to calculate the number density in Eq. (5), the number density becomes small and discontinuous in the product side as the window size decreases. For typical product side particle area densities of order 8–10 particles per mm$^2$, a pixel with local maximum intensity makes the number density change dramatically when the edge of the window moves across this pixel. By replacing the original local maximum pixel by a cross symbol, the number density change is smooth as the number density changes step by step (from 1 to 4 to 5 and back to 1) as the edge of the window moves across the symbol. The replacement of the symbol also provides a suitable transition in the determination of the conditional number density.

In the final step, a Wiener filter is used to smooth the distribution of unconditional number density, followed by deriving a preliminary flame edge location based on the distribution of the unconditional number density. This is done by identifying the location of the minimum number density in the histogram of $\rho _{I}$, as discussed in Sect. 4.1. Following this step, a conditional particle density is defined as:

$$\begin{aligned} \begin{aligned} \rho _{I,c}=\left\{ \begin{array}{cc} N_I/N_p, &{} \rho _{I,u} \le \rho _{I,t} \\ N_I/N_r, &{} \rho _{I,u} > \rho _{I,t} \end{array} \right. \end{aligned} \end{aligned}$$

(6)

where $N_r$ and $N_p$ are numbers of pixels in the reactant and product side, respectively, which are separated by the preliminary flame edge, in the $w_d\times w_d$ window, respectively.

In one version of model (A), the flame edge is defined by setting a threshold or seeking the local maximum gradient of conditional number densities based on the distribution of conditional number density $\rho _{I,c}$. An alternative model uses an anisotropic diffusion filter before the determination of the maximum gradient. The spatial differences between the thresholding and maximum gradient methods are discussed in Sect. 4. The differences are limited to only a few pixels ($\sim 0.1$ mm).

Fig. 7

Result of the determination of the flame edge over a detail of image Fig. 6a with $w_d~=~40$, after conditioning the number density followed by a $4~\times ~4$ pixel Wiener filter and anisotropic diffusion filter using default parameters (gradient modulus threshold $\kappa =30$) a Colormap of $\rho _{I,c}$ and the flame edge defined by iso-contour of $\rho _{I,c}=0.35$. b Colormap of the gradient of $\rho _{I,c}$ and the flame edge defined by plotting the maximum $\mid \nabla \rho _{I,c}\mid$. c Comparison of flame edges derived in (a) and (b). Red line: flame edge defined by iso-contour of $\rho _{I,c}=0.35$ in (a); blue line: flame edge defined by maximum $\mid \nabla \rho _{I,c}\mid$

4 Results

4.1 Flame boundary definition using the number density method

Figure 5a shows a sample image of particle Mie scatter to illustrate the process, with locations of windows used for testing the number density. Number densities are calculated throughout the pure reactant side and the product side, which are averaged accordingly. The pure reactant side and the pure product side means windows are only selected in the region which is visibly in the reactant side and product side without covering the flame edge. Figure 5b compares values of the averaged $\rho _I$ for the sample image in either the product and or reactant side as a function of increasing window size. All windows in the pure reactant side and pure product side are averaged in Fig. 5b.

The value of the averaged number density converges very fast in either the product or reactant side, and there is a large difference between the values obtained for either side for the full range of $w_d$, suggesting the feasibility of separating the flame into the corresponding regions based on the number density. Although the averaged number density in the whole product and reactant side converges after $w_d~=~10$, the final value still needs further consideration, since the variance of the number density across the whole flame surface affects the quality of the result.

The raw Mie scatter image (1280 $\times$ 800 pixel$^2$) is divided into several sections from the bottom to the top of the image. The number of sections depends on the quality of seeding in each case; a total of four regions are used in cases 1 and 2. Figure 6a shows the spatial distribution of recognized local maximum pixel intensities in case 1, with one region highlighted by the red dashed lines. The raw image is processed by selecting pixels with local maximum intensity first and then expands selected pixels to a cross symbol, as described in Sect. 3.2.

Figure 6b shows the probability density function of unconditioned particle densities in the red region in Fig. 6a calculated by setting $w_d~=~40$. Values of number densities are normalized to unity so that different particle densities in different images can be analysed in the same scale, to make the post-processing program more robust.

The two easily recognised peaks represent the number density in reactant and product regions. The pdf appears to be continuous between these peaks in the region of 0.25–0.45 because the chosen window size of 40 $\times$ 40 spans across the physical flame edge where particles from both sides contribute to the local number density. The value of the number density between peaks, $\rho _{I,t}=0.35$ corresponds to a minimum probability in Fig. 6b, and is chosen as the threshold for the particle density for separating the product and reactant regions. For each separated region, such as the red region in Fig. 6a, the threshold $\rho _{I,t}$ is selected separately and defines the flame edge in this region. Following that step, the flame edge of the whole flame is defined by connecting these edges together as a preliminary flame edge. The unconditional number densities are analysed for each image to define the threshold $\rho _{I,t}$ based on the pdf of unconditional number density $\rho _{I,u}$, and thresholds $\rho _{I,t}$ are separately calculated by in each regions of every images by seeking the local minima in the pdf of unconditional number density.

After the unconditional number density is calculated, the distribution of the number density is smoothed by a $4~\times ~4$ Wiener filter before finding the iso-contour based on $\rho _{I,t}$. The use of the Wiener filter on the distribution of the number density reduces the interference of the error in the preliminary flame edge onto the final result, while the flame edge is not sensitive to the filter size here.

Once the threshold of the unconditioned number density is selected and the preliminary flame edge is defined, it is possible to refine the image analysis. Figure 6c shows the corresponding probability density function of the conditional number density where the product and reactant regions are calculated by Eq. (6) separately. The thresholds for the unconditional normalized number density in different zones are in general not equal but varied over a narrow range, leading to an offset of a few pixels in the detected flame edges between different zones. This offset is bridged by interpolating the threshold based on distances to centers of adjacent zones. After conditioning, a clear minimum arises close to zero, separated into two regions. Notice that the particle density is not entirely uniform in either product or reactant regions, due to imperfect distribution in the original seeding process.

After conditioning the images based on number densities, the flame edge can be defined by setting the threshold of the conditional number density again. Figure 7a shows a colormap of the conditional number density $\rho _{I,c}$, where the black line is the iso-contour of $\rho _{I,c}~=~0.35$, which corresponds to the minimum probability of $\rho _{I,c}$ in Fig. 6c, after conditioning the number density followed by a $4~\times ~4$ pixel Wiener filter.

Fig. 8

Variance of normalized OH signal and maximum gradient of normalized OH signal in product side after using movmean filter with an increasing filter size $\Delta _f$. The variance of the signal is dimensionless

Alternatively, the final flame edge can also be defined by the pixel location with the maximum gradient of the conditional number density. The anisotropic diffusion filter using default parameters (gradient modulus threshold $\kappa$=30) was applied to the distribution of the conditional number density to make the edge clear in space, so as to make it possible to determine the maximum gradient for the conditional number density as a criterion for binarizing the region into reactant or product. Figure 7b shows the corresponding colormap of the gradient of conditional number density $\mid \nabla \rho _{I,c}\mid$ and the black line is defined by the Canny method as the location of the local maximum gradient. Finally, Fig. 7c compares flame edges defined by the threshold $\rho _{I,c}=0.35$ in Fig. 7a and the maximum gradient of $\rho _{I,c}$ in Fig. 7b. The two criteria (number density threshold or its gradient) were found to give edge location results within 1–2 pixels. Because of the large difference between the product and reactant values of $\rho _{I}$ in Fig. 6c from $\rho _{I,c}~=~0.28$ to $\rho _{I,c}~=~0.42$, there is not a large spatial difference in the final flame edge location for a gradient selected in this range, as the threshold and maximum gradient coincide within a couple of pixels.

Fig. 9

Variance of the conditional number density and maximum gradient of the conditional number density in the reactant side with an increasing window size $w_d$ used for Mie scatter images. The variance is dimensionless

Fig. 10

Effect of window size $w_d$ on the flame edge detection in Particle Mie scattering for a given image for case 1

4.2 Parameter sensitivity

4.2.1 OH-PLIF images

In the maximum gradient method used for the OH images, the only effective factor is the filter size $\Delta _f$ of the moving filter, which simply averages the intensity of OH-signal in a certain square region.

Fig. 11

Single shot simultaneous images of particle Mie scattering (a) and OH PLIF (b) for case 1. a Particle Mie scattering image. The blue line indicates edge determined using threshold number density method using $w_d=40$ pixels. b OH-PLIF image. The red line was obtained using Canny method with movmean filter 16 $\times$ 16. c Overlay of flame location obtained as in (a) and (b)

Figure 8 shows how the variance of the normalized OH-PLIF signal decreases as the filter size $\Delta _f$ increases in the OH-PLIF sample image corresponding to Fig. 5a, where of course the OH-PLIF signal only exists in the product side, for cases 1 and 2. The variance of the signal drops to half of that of the the unfiltered signal at around $\Delta _f~=~16$ pixels, which corresponds to 0.56 mm, and further increases do not lead to significant change in variance, but of course correspond to distances larger than the laminar flame thickness.

Therefore, a filter of 16 $\times$ 16 pixels is chosen as the filter size $\Delta _f$ of the moving filter (movmean) for the maximum gradient method.

4.2.2 Mie scatter images

The number density bisection method using the pdf described in Sect. 4.1 resolves the selection of the threshold number density. However, the window size $w_d$ must still be selected, and the optimum value of the window size is discussed in this section.

The final position of the flame edge using the number density method in Mie scatter images is significantly affected by the choice of filter window size $w_d$. The main metrics affected are the prevalence of sharp corners as well as the local flame surface density.

Large window sizes lead to smoothing of sharp angles into filleted corners, the loss of flame curvature information, and lower estimates of flame surface density in cases when the flame edges are elongated. Conversely, too small a window is obviously unable to reveal the local number density.

Figure 9 presents the variance of the conditional number density and the maximum gradient of the conditional number density in the reactant side of the sample Mie scattering image in Fig. 5a as the window size $w_d$ increases. The variance of the number conditional density decreases from 0.14 to 0.8 between $w_d=2$–40, which ensures the flame edge can be easily detected when the window size $w_d=40$. The maximum gradient of the number density also starts to converge at $w_d=40$, which means the geometrical characteristics of the flame edge can be captured. Therefore, a window size $w_d$ for all images is chosen as $w_d=40$ pixels in this paper.

As an illustration of the consequences of the choice, Fig. 10 compares the effect of the window size $w_d$ on the determination of the flame edge defined by the number density method, for values of $w_d$ = 24, 40, 56 pixels, corresponding to 0.94, 1.57, 2.20 mm. Beyond $w_d$ = 20, the larger the window size, the smoother the flame edge becomes because of the reduction of the local variance. Figure 10 also shows that the spatial location of the flame edge does not change a lot when the window size $w_d$ increases from 24 to 56, while the local curvature decreases. The value chosen of $w_d~=~40$, or 1.57 mm balances the fidelity of the flame edge location and the smoothness of the curve. We note, however, that is of the order of three times the flame thickness.

A second parameter, the Wiener filter window of size $\Delta _f$ chosen for pre-filtering the number density before deriving the preliminary flame edge, was found not to affect the location of flame edge, so long as it is smaller than the window size $w_d$. The selected Wiener filter size here is 4 $\times$ 4 pixels, or 0.16 mm.

We conclude that the spatial resolution of the determination of the flame edge in the case of OH-PLIF is of the order of 0.5 mm, or the thermal thickness of the flame, whereas that of the Mie scatter particle density location may be of order 2–3 times higher. In the next section, we consider the accuracy of the metrics obtained for Mie scatter number density and OH-PLIF.

Fig. 12

Pdfs of the minimum distance d between two flame edges for 38 images analysed for Case 1 (light blue) and Case 2 (orange). The sign of d indicates the relative position of the Mie scattering edge relatively to OH-PLIF with respect to reactants, where positive means closer to the reactant side

Table 2 Fitted factors of P(d)

4.3 Metrics of particle Mie scattering compared with OH-PLIF

Figure 11 shows raw images of a particle Mie scattering image and its simultaneous OH-PLIF image with flame edges detected by the number density method and the maximum gradient method respectively, and compares them in the same plot. In Fig. 11a, the blue line is the flame edge detected by the number density method with $w_d$ = 40 and 4 $\times$ 4 Wiener filter in Model B. In Fig. 11b, the red line is the flame edge detected by the maximum gradient method based on the Canny method with 16 $\times$ 16 movmean filter. We observe an average overlap with mean differences of less than 0.16 mm, with a slight bias for the OH-PLIF image towards the product side relatively to the Mie scattering result.

4.3.1 Minimum absolute distance

Figure 12 presents the probability density functions of the minimum distance between flame edges detected for 38 simultaneous Mie scattering images and simultaneous OH-PLIF images for the two operating conditions considered. Positive values correspond to flame edges for Mie scattering images are closer to the reactant side, and conversely negative values corresponds to flame edges of OH-PLIF images closer to the reactant side, and the distances are normalised by the laminar flame thickness of 0.475 mm. The distributions of the minimum distances obtained for multiple images closely correspond to Gaussian curves in both case 1 and case 2, with only a slight degree of positive skew for both cases in Fig. 12. The Gaussian fitted factors are shown in Table 2. The right-skewness of case 2 appears to be slightly different with the case 1 at the top of the curve. The fitted Gaussian distribution, which is not symmetric at the small value of d.

The pdf P(d) shows that 4.6% of flame edges on the left side of Fig. 12a and 7.2% of flame edges on the right side corresponds to minimum distances larger than flame thickness in case 1. The distribution is physically understandable, given the filtering thicknesses used, and the convolution with the depth of the laser sheet thickness for the Mie-scatter case.

A similar behaviour is found for Case 2, which is found to yield a slightly narrower behavior when normalized by the flame thickness, given that the laminar flame thickness in case 2, 0.539 mm, is larger than Case 1, and the proportions of distances beyond the laminar flame thickness are 3.0% and 4.6% from zero, respectively. We conclude from the histograms that the number density method has a higher probability of detecting flame edges closer to the reactant side, but that the uncertainty is of the order of one third to one half of the flame thickness. Further analysis addresses the determination of curvature.

4.3.2 Curvature

Fig. 13

Local curvature of flame surface for particle Mie scattering and OH PLIF. Positive curvature corresponds to the center of the curvature in the product side and negative curvature corresponds to the center of curvature in the reactant side

Fig. 14

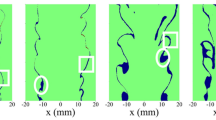
Behavior of number density in different types of flame edges. a Mie scatter image after first processing to detect maximum intensity points. Orange rectangle: center of curvature in the reactant side. Light blue rectangle: flat curvature. b Pdfs of unconditional number density in two sample regions in (a)

Figure 13 compares the local curvature of flame edges along the length of the curve s between the Mie scattering image and the OH-PLIF image corresponding to the same single image in Fig. 11. The local curvature is calculated by Eq. (3). The quantities $\dot{x}$, $\dot{y}$, $\ddot{x}$ and $\ddot{y}$ are derived based on the adjacent 16 pixels ($0.63 \times 0.63$ mm region). The noise under 0.63 mm is filtered in the curvature calculation, corresponding to $\kappa ~=~1.6$ mm$^{-1}$. Positive curvature corresponds to the centre of curvature in the product side. The x-axis represents the length of the curve s, with zero defined as the coordinate of the intersection point between the flame edge and the y-axis.

Figure 13 shows good but not perfect overlap between the two estimates. The absolute value of curvatures across the whole flame can still reach 1.6 mm$^{-1}$ which corresponds to a radius of curvature as small as 0.63 mm. In general, the nominal spatial resolution ($w_d=40$ pixel) of the number density method is in the order of 1.5 mm, and the spatial resolution of OH-PLIF is in order of 0.5 mm. The two curves in Fig. 13 show curvatures smaller than 2 mm$^{-1}$, which corresponds to the spatial resolution of OH-PLIF. Curvatures larger than 2 mm$^{-1}$ are therefore smeared in both methods. Figure 15 shows that the distribution of curvatures overlap for the two methods, as most of the curvature values are smaller than one reciprocal flame thickness. We conclude that the number density method can capture geometrical characteristics smaller than the window size (1.5 mm) but may not be fully able to resolve structures smaller than the flame thickness (0.47 mm in case 1)

At locations where the flame edge stretches into the product side, the maximum value of the curvature derived from Mie results is slightly higher than OH results, such as flame edges at $s=-8, -4, 4, 7, 13, 16$ and 20 mm. However, the reverse appears in locations where the flame edge stretches into the reactant side, where flame edges detected in OH-PLIF images tends to be sharper. This means flame edges are detected by the number density methods more sharply where the centre of curvature curvatures are in the reactant side, and the reverse for OH-PLIF.

The limitation cannot be simply explained by the over- and under-estimation of the number density where flame edge stretches, as discussed in the last section, because the under- and over-estimation should produce a symmetric effect when flame edge stretches into the reactant and product side. As an illustration, Fig. 14a highlights two regions in a sample Mie scatter image: the red region is a sample region which contains a part of flame edge which has a center of curvature in the reactant side, whilst the blue region is a sample region which consists of flat edges.

Fig. 15

Normalised pdf of local curvature scaled by the flame thickness for 38 pairs of Mie scattering and OH-PLIF images for each case

When calculating the unconditional number density, $\rho _I$ in the reactant side is underestimated when the flame edge curves into the product side (negative curvature), because the window covers both the reactant and product side. This makes the left peak of the pdf of the number density in Fig. 14 wider. The local minimum in the saddle between two peaks moves to the right (reactant) side because the reactant-side peak smaller than the left (product) side peak. As a consequence, the preliminary flame edge is recognised closer to where the unconditional number density is larger. The effect can only be reduced but not completely removed when the final flame edge is defined as a sharper curve stretching into the product side. In contrast, when the flame edge stretches into the reactant side (positive curvature), the number density in the product side is overestimated and the right peak in the pdf becomes higher and wider. However, unlike the case where reactants penetrate the product side, this change does not highly affect the value of local minimum between two peaks and the flame edge tends to remain smooth when the radius of curvature is smaller than the window size.

Figure 15 compares probability density functions of local curvature derived from flame edges detected in cases 1 as extracted from the same two groups of 38 images as before. The x-axis is normalised by the laminar flame thickness $\delta _L$. The distribution of curvature derived from OH flame edges in case 1 is close to a Gaussian distribution, representing the random stretching of the flame edge into product and reactant sides in the current tall flame, and such good consistency between Mie results and OH results also exists in case 2. The good consistency between two pdf curves in Fig. 15 shows that the number density method on Mie scattering images can generally detect most flame structures as the maximum gradient method used in OH-PLIF images. Two pdfs are not cut off at $\kappa =1/\delta _L$, which shows that two methods are still able to resolve some small-scale flame structures. Further investigation on the number density method of detecting small-scale structure with higher spatial resolution is necessary. Curves of Mie results in (a) and (b) have a mean close to zero and a width of $\sigma _{Mie}(\kappa )=0.62$ mm$^{-1}$ for case 1 and $\sigma _{Mie}(\kappa )=0.56$ mm$^{-1}$ for case 2, and that there is essentially no difference to the obtained curvature pdf using either technique.

4.3.3 Flame surface density

Figure 16a compares the local 2D FSD using particle Mie scattering and OH-PLIF along the length of the curve s. The FSD is calculated using Eq. (4), where the angles $\alpha$ and $\beta$ are calculated as $atan\{{\frac{dy}{ds}/\frac{dx}{ds}}\}$. The values of $\frac{dy}{ds}$ and $\frac{dx}{ds}$ are derived based on the adjacent 16 pixels so as to avoid zigzag from the pixelation.

Fig. 16

Local geometrical difference between Particle Mie scattering and OH-PLIF

Fig. 17

Probability density function of flame surface density $\Sigma ^{\prime }$ in Mie scattering and OH-PLIF images

The local FSD $\Sigma ^{\prime }$ represents the local normal direction of the flame edge in a 2D image. This means that small variations in the local direction are amplified in the comparison plot and accumulates on the value s. As an illustration, at $s=1$–7 mm, there are three peaks detected at edges obtained by two methods, while an offset of s exists between these three pairs of peaks because of the error accumulation on the value of s. As discussed with respect to Fig. 11c, the flame edge detected by the number density method tends to be located closer to the reactant side near the top of the flame, and this makes the value of $\Sigma ^{\prime }$ vs. s move to the left. The consistency of the $\Sigma ^{\prime }$ appears to be better on the left side of the flame where two flames edges are nearly overlapped. The integral of the local FSD $\Sigma ^{\prime }$ is proportional to the total length of the flame edge. The total lengths of flame edges in Mie scattering and OH-PLIF image by integrating $\Sigma ^{\prime }$ in Fig. 16a are 41.8 and 42.1 mm, so well in agreement.

Fig. 18

Problem sample images obtained in case 1: a Single image of Mie scattering and edge using number density method with $w_d=40$ pixels. b Single image of OH-PLIF using maximum gradient method with movmean filter 16$\times$16 pixels. c Comparison of flame edges between (a) and (b)

Figure 17 compares the probability density function of local flame surface density $\Sigma ^{\prime }$ derived from flame edges detected in 38 pairs of Mie scattering images and OH-PLIF images in case 1. The results using the two methods are shown to be essentially indistinguishable, and such consistency between two curves also shows up in case 2.

4.4 Singular difference cases

In a few cases, differences between the Mie scatter and OH-PLIF differences do appear. As an example, Fig. 18a shows a concave shadow product region in the Mie scatter region, corresponding to products, which is not present in the OH-PLIF signal in Fig. 18b, where the region indicates reactants. A reasonable guess is that the difference arises owing to the difference in the thickness of the laser sheets: if the flame surface in the featured region is nearly parallel with the thin OH-PLIF laser sheet ($\sim$ 100 $\mu$m thickness), the OH PLIF image would just graze the inside of the reactant zone, indicating mostly reactants, whereas the Mie scatter particle density is averaged over the 500 $\mu$m thickness, showing a lower particle density in the region. These inconsistencies clearly show some of the limitations of the PIV technique. As a suggestion for improving on the ambiguity, one possible way to resolve the uncertainty would be to add a flame edge measurement on the horizontal plane and observe whether the flame surface is overlapped with the vertical laser sheet.

5 Conclusions

This paper presents new data using simultaneous Mie scatter and OH PLIF images, details of algorithms for flame edge detection, and final comparison of measurements using Mie scatter and OH PLIF. Whereas previous studies had indicated that there were only a few differences between OH-PLIF or CH-PLIF and Mie scatter edge measurements (Steinberg et al. 2008; Pfadler et al. 2007), here we quantify these measurements statistically, and analyse the effect of image processing parameters on the comparisons.

By using a Wiener filter to de-noise the distribution of the number density and anisotropic diffusion method to make edges clear, the flame edge can be detected from particle Mie scattering images within an error of less than the laminar flame thickness. Using a previously number density thresholding method (Pfadler et al. 2007), the maximum gradient of the number density can be easily derived which corresponds to the maximum heat release and maximum density change of the flow. We show that there is an optimum size of the Mie averaging window which allows robust detection of edges with minimum variance, which is in the range of 32$\sim$48 pixels for the present setup, corresponding to 2.6$\sim$4.0 times of the laminar flame thickness. For images with densely distributed particles, smaller window sizes could be chosen.

Under these conditions, we demonstrate that there is very good agreement between the OH-PLIF and Mie scatter methods for flame location and curvature detection, with negligible differences in the probability density functions. Similarly, although there are visible local differences between the flame edges detected, there is negligible difference between the two methods in the measurements of 2D flame surface densities. A few pathological cases were detected in which the flame surface possibly aligns with the laser sheet, producing discrepancies in the Mie scatter images relatively to the OH, which was detected with a thinner laser sheet.

We conclude that Mie scatter detection of flame fronts are as robust as OH-PLIF would be at signal to noise levels for typical high frequency detection. However, it is clear that for methods using higher signal to noise for OH, and higher camera resolution, the latter method would offer superior spatial resolution. Therefore, based on the current evidence, it is possible to use high frequency Mie scatter methods for measurement of 2D flame properties within the resolution of one flame thickness.

Finally, we recognize that the current study spans only a limited range of turbulent conditions, and that it is possible that the agreement between the two techniques may be less favorable at higher turbulence levels. Future work on this matter is currently planned.