Abstract
Optical laser-based techniques and an extensive data analysis methodology have been developed to acquire flow and separation characteristics of concentrated liquid–liquid dispersions. A helical static mixer was used at the inlet of an acrylic 4 m long horizontal pipe to actuate the dispersed flows at low mixture velocities. The organic (913 kg m\(^{-3}\), 0.0046 Pa s) and aqueous phases (1146 kg m\(^{-3}\), 0.0084 Pa s) were chosen to have matched refractive indices. Measurements were conducted at 15 and 135 equivalent pipe diameters downstream the inlet. Planar laser induced fluorescence (PLIF) measurements illustrated the flow structures and provided the local in-situ holdup profiles. It was found that along the pipe the drops segregate and in some cases coalesce either with other drops or with the corresponding continuous phase. A multi-level threshold algorithm was developed to measure the drop sizes from the PLIF images. The velocity profiles in the aqueous phase were measured with particle image velocimetry (PIV), while the settling velocities of the organic dispersed drops were acquired with particle tracking velocimetry (PTV). It was also possible to capture coalescence events of a drop with an interface over time and to acquire the instantaneous velocity and vorticity fields in the coalescing drop.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Flows of two immiscible liquids in pipes are encountered in many industrial applications, including oil and gas production and processing, chemical and nuclear plants (Danielson 2012). Accurate characterisation of such flows is significant for predicting pressure drop together with hydrodynamic and heat and mass transfer properties, but has so far proved challenging, with mostly empirical formulations dominating the field. Detailed measurements in liquid-liquid flows are needed to improve fundamental understanding. In industrial scale systems, however, the information available is usually limited to phase holdup and pressure gradient measurements (Oddy and Pearson 2004), as the difficult thermodynamic conditions and opaque fluids restrict the implementation of several experimental techniques. These difficulties can be overcome in pilot scale research flow facilities, where detailed and local measurements of velocity fields, drop concentration and size distributions can be obtained, while interfacial phenomena such as drop break up and coalescence can be observed.
Two-phase liquid flows in pipes have been investigated considerably in the last half-century, with a wide range of experimental techniques applied. Visual observations and high speed imaging have been used extensively to obtain information on flow pattern characteristics, especially at low mixture velocities and in dilute dispersed flows. Typically, there is a large difference in the electrical properties of the two phases, which allows the application of impedance probes. Angeli and Hewitt (2000) and Hu and Angeli (2006) implemented a high frequency, alternating current, dual-electrode impedance probe to obtain local measurements in a pipe cross section of phase fractions, drop velocities and drop chord length distributions during dispersed flows. A similar probe working with direct current was later used by Voulgaropoulos et al. (2016). Barral and Angeli (2013) used a double-wire conductivity probe to describe the interfacial characteristics of the waves in stratified and dual-continuous flows. Tomography techniques, which can provide the phase fraction distribution in a pipe cross section, have also been used, based on conductivity (Ngan et al. 2009) or X-ray imaging (Schümann et al. 2016b), while Silva et al. (2007) developed a capacitance wire-mesh sensor to obtain the phase fractions.
For drop size measurements, Maaß et al. (2011) compared a focus beam reflectance instrument (FBRM), a two-dimensional optical reflectance instrument and a fibre optical focus beam reflectance sensor in a stirred vessel, and illustrated the limitations of the techniques based on the laser back-scatter principle. The FBRM probe has also been implemented during pipe flows (Schümann et al. 2016a), but with reported uncertainties of 50%. In recent years, further advances in optical/laser based techniques (Budwig 1994; Westerweel 1997) have allowed the application of Particle Image Velocimetry (PIV) (Kumara et al. 2010; Chinaud et al. 2017) and planar laser induced fluorescence (PLIF) (Liu et al. 2006; Wegmann and von Rohr 2006) to the pipe flow of immiscible liquids—in some cases with matching refractive index. From PIV measurements, the velocity profiles and subsequently the vorticity and the turbulence characteristics of the flow can be obtained during dispersed flow (Conan et al. 2007). Following a similar approach to PIV the dispersed drops can be tracked with particle tracking velocimetry (PTV) (Brevis et al. 2011). PLIF has been used to acquire information on the distribution of the phases, study the interface height and the drop size distributions (Morgan et al. 2012, 2017). PIV/PTV and PLIF usually resolve the flow characteristics on a plane in the flow, illuminated by a laser sheet. Measurements in all three dimensions are also possible with volumetric illumination and more than one camera (Maas et al. 1993; Kreizer and Liberzon 2011). A recent review by Wright et al. (2017) demonstrates previous works conducted in matched refractive index systems.
From the various patterns that form during the flow of two immiscible liquids, dispersed flows are very common. The stability of the dispersions and their tendency to separate will depend on the settling characteristics of the drops in the flow (Bourdillon et al. 2016). These systems are, however, very complex (Batchelor 1972; Balachandar and Eaton 2010) and models are often limited by the lack of detailed experimental data on the distribution of the phases, velocity profiles, drop sizes and their change along the pipe. To aid further studies of concentrated dispersed flows, a combination of PLIF and PIV/PTV techniques are developed in this work and are applied to liquid-liquid dispersions generated through a helical static mixer at low mixture velocities. The high speed PLIF technique enables measurements of flow distribution at two axial locations and helps to illustrate the transitions in flow patterns along the pipe. An image analysis method is proposed to acquire the respective drop size distributions. The velocity profiles in the aqueous phase and of the dispersed drops are measured using PIV and PTV, respectively. The experimental techniques used also allow coalescence events to be captured during flow.
2 Experimental methodology
2.1 Flow facility and instrumentation
The experiments were conducted in a liquid-liquid pilot scale flow facility that has an acrylic test section with 26 mm ID (Fig. 1). The test section comprises of a front and a back leg, each 4 m long, connected via a U-bend. Experiments were carried out at the front leg to avoid any changes to the flow due to the bend. The pipe consists of spools of various lengths to enable positioning of instrumentation at different axial locations. Each liquid is stored at a separate tank of 160 l capacity and is introduced by a centrifugal pump to a Y-shaped test section inlet, with the organic phase coming from the top and the aqueous from the bottom. The two liquids then pass through a 6-element helical static mixer (JLS International Ltd ®) that generates dispersed flows for a wide range of velocities and phase fractions. Each element is set perpendicularly at a 90\(^\circ\) angle to its adjacent elements, adding up to a total mixing length of 265 mm. After the test section, the liquids enter a gravity settler tank (220 l) and are left to separate, before they return to their respective storage tanks.
The test liquids were a low viscosity silicone oil and a \(\sim\)52% w/w water/glycerol mixture as shown in Table 1. Glycerol was added in the water to match the refractive index of the oil. It is important to match the refractive indices of the two liquids to avoid any light refraction at the interfaces, which limit laser-based measurements to only dilute dispersions. The refractive indices of the liquids were measured with an Abbe 5 by Bellingham & Stanley® refractometer, while their interfacial tension was measured with a Krüss® K100C Du Noüy ring instrument. The viscosities of the fluids were obtained with an Advanced Rheometric Expansion System (ARES TG-42, TA Instruments®). Experiments were carried out at ambient temperature of approximately 20 °C, which was periodically recorded. To avoid any overheating of the fluids, mainly by the pumps, the experimental runs were kept short.
A visualisation box was placed around the test section at two axial locations, \(x = 0.40\) and 3.50 m downstream the static mixer, or \(x^{+} = 15\) and 135, respectively, as shown in Fig. 2, where \(x^{+} = x/D\). The box was filled with glycerol, which closely matches the refractive index of the Perspex® acrylic pipe, and was used to minimise any optical distortions at the curved pipe wall. The setup for the PIV/PTV and PLIF experiments is shown schematically in Fig. 3. A DPSS green (532 nm) continuous laser system by Laserglow Technologies® was placed vertically below the pipe. The output of the laser was set at 3000 mW. A concave lens was used to generate a laser sheet in the transverse direction and at the middle of the pipe. The laser thickness was reduced to approximately \(\Delta l_{z} = 1\) mm at the focusing plane with a collimator. The laser sheet alignment was conducted with the help of a graticule target, with printed dots of known distances, placed inside an oil filled pipe section.
A small amount (\(\sim\,\) 0.02 ppm) of aqueous Rhodamine 6G dye was added in the aqueous phase to distinguish between the two liquids and better track the interface. Rhodamine B coated PMMA particles (\(\rho _{\mathrm{particles}}\) \(\sim\) 1200 kg m\(^{-3}\) with a particle size, \(d_{\mathrm{particles}}\), ranging from 1 to 20 µm) were used as tracers in the aqueous phase to acquire the corresponding velocity fields. Both the dye and the particles emit light at wavelengths above 590 nm. The particles Stokes number was below \(10^{-4}\) for all conditions investigated. A high speed camera (Phantom v1212 by Vision Research®) was placed on the side of the pipe, perpendicular to the visualisation box, to record the flow. A frequency ranging from 2 to 4 kHz was used at 1280 by 800 pixels2 with a spatial resolution of 16.9 px/mm, while the shutter speed was set at 95 µs, to allow enough light in the sensor, but at the same time avoid blurring caused by the displacement of the particles while the shutter is open. A Tokina® 100 mm macro lens was used together with a high pass filter (> 580 nm) to eliminate any spurious light or reflections of the laser on the pipe frame.
2.2 Image analysis
The PLIF experiments provide raw gray-scale images, where white regions denote the aqueous phase, which contains the fluorescent dye, while black regions represent the organic phase. A typical raw image is shown in Fig. 4a, with the oil droplets homogeneously dispersed in the aqueous phase. Brighter spots, of approximately one pixel size, correspond to the tracer particles in the aqueous phase. Each pixel has an intensity value, \(I_{p}\), ranging from 0 (black) to 255 (white) in the 8-bit images. The corresponding number probability to find a pixel with that intensity \(I_{p}\), \(P(I_{p})\), for this image is shown in the inset of Fig. 4a. The data are split in 51 bins with a width of \(I_{p} = 5\) each. Three peaks are clear. The highest peak is at \(I_{p} \sim\,\) 55 denoting the number of pixels in the continuous aqueous phase, while the secondary peak at \(I_{p} \sim\) 30 represents the region of the oil drops. The third smaller peak, with a probability of \(\sim\) \(10^{-4}\) present at \(I_{p} \sim\) 230, corresponds to the tracer particles on the image, which emit the most light. The images are pretreated with Matlab (Mathworks®) algorithms, developed in-house, to acquire information on the in-situ phase holdup distribution. The pre-treatment is also conducted to prepare the images for analysis with the PIV, PTV and drop size routines, that compute respectively the velocity field in the aqueous phase and the velocity and size of the dispersed phase.
Figure 4b illustrates the raw image after a median filter is applied. The filter is implemented to neighbourhoods of 5 by 5 pixels\(^{2}\) or \(q = 5\). Assuming a pixel neighbourhood matrix \([m_{i},n_{j}]\) with a size of \(q^{2}\) pixels\(^{2}\), its median value, \(\widetilde{[m_{i},n_{j}]}\), is obtained by taking the median of \([m_{i-q/2},\ldots ,m_{i+q/2-1},n_{j-q/2},\ldots ,n_{j+q/2-1}]\), where i and j are indices and denote the elements of the \([m_{i},n_{j}]\) matrix. It is clear that the histogram of Fig. 4b is smoother than that of Fig. 4a and the tracer particles are not shown. The images are binarised with an adaptive threshold algorithm (implemented in the adaptthresh function of Matlab) and are used to acquire the in-situ holdup values by averaging the instantaneous vertical intensity profiles over 4000 images. The uncertainty for these measurements stems mainly from the threshold sensitivity selection and is approximately \(\pm\,20\%\) at a 95% confidence level, even when altering the sensitivity by \(\pm\,50\%\) from the mean. To convert the two-dimensional measurements to volume fractions, it is assumed that that the same concentrations apply along the depth of the laser plane. This is a fair assumption considering that the depth of the laser plane is small. The phase fractions then recorded correspond to the middle plane of the pipe. The adaptive binarisation algorithm is based on the local mean intensity in the neighbourhood of each pixel, to take into consideration any noise coming from intensity fluctuations at dense drop regions. The images of Fig. 4b are also used for the PTV and drop size measurement routines. An in-house developed algorithm is implemented to capture the sizes of the drops as will be discussed in the next section (Sect. 3.2).
Image analysis during pre-treatment stage where a shows the raw image, b the image after a median filter is applied and c the image after a high-pass filter is applied. The scale bar is 5 mm long. The distributions in the insets display the probability of the pixel intensity on the corresponding image
The Matlab PTVlab toolbox by Brevis et al. (2011) is used to track the velocities of the drops. A combination of a cross-correlation (CC) and a relaxation algorithm (RM) is implemented. The CC algorithm cross-correlates a reference matrix of the initial frame, based on a drop signal, with the interrogation matrices centred at each of the candidate drops of the subsequent frame. The cross-correlation with the highest coefficient represents the drop motion. The RM, originally implemented by Baek and Lee (1996) for turbulent flows, is a statistical approach to find the largest displacement probability of a drop within a pre-select area around it. The drops tracked in this work have a wide size distribution, and thus not all of them can be detected on the same run. The drops under investigation are tracked by the detection algorithm of PTVlab with a correlation threshold of 0.5 and a drop detection area, \(a_{p}\).
By subtracting Fig. 4b from Fig. 4a, Fig. 4c is obtained, where the signal of the tracer particles is isolated. These images are binarised as well and then used to calculate the velocity fields in the aqueous phase, where the dye can no longer affect the correlations. Velocity profiles from the tracer displacement between consecutive frames with a \(\delta t =\) 250 to 500 µs were calculated using the Matlab PIVlab toolbox developed by Thielicke and Stamhuis (2014). A discrete Fourier transformation algorithm is used for the window deformation, starting from 64 by 64 pixels\(^2\) correlation windows with three iteration steps towards 16 by 16 pixels\(^2\) windows. A 50% vector interpolation overlap is used at each step giving a final grid with a spatial resolution of 82 pixels\(^2\). The correlation box at the first iteration needs to be larger than the maximum typical drop size (\(\sim\,\) 0.1D) so that enough tracers are present in each box to make possible the cross correlation (Augier et al. 2003). In addition, a large number of instantaneous velocity fields (about 4000) was acquired and statistical convergence was reached for all velocity profiles shown later. At regions of high drop concentration the uncertainties are higher; these cases will clearly be shown in the results. Similar procedures have been followed for correlations close to an interface (Chinaud et al. 2017). The correlation peak is fitted with a Gaussian function based on three points (Nobach and Honkanen 2005).
Several local and global vector validation methods have been used in PIV measurements (Westerweel and Scarano 2005). In this work, the axial, u, versus the vertical, v, velocity components from all correlation windows of all captured frames are plotted and appropriate limits are manually selected; outlier velocities are taken as false vectors typically caused by the presence of drops. In the second stage, each velocity component of each correlation box is compared with a lower and an upper threshold \(t_{l}\) and \(t_{h}\) as
respectively, where \(\bar{u}\) is the mean velocity, p is a parameter determining the strictness of the filter and \(\sigma _{\bar{u}}\) is the computed standard deviation of \(\bar{u}\) (Thielicke and Stamhuis 2014). The outliers are then replaced with the local mean values of the 3 by 3 neighbourhood correlation boxes. In most cases the mean velocities computed before and after the post-treatment deviated less than 1%, except for the first correlation box adjacent to the pipe walls, where the difference was about 30%. Since two-dimensional measurements are conducted, it is important to consider any effects from the out of plane transverse motion of the particles (Westerweel 1997, 2008). The gradient of the axial velocity in the depth of the laser plane (\(\Delta l_{z} = 1\) mm), \(\partial u/\partial z\), is estimated to be less than 5% of the maximum velocity, assuming a parabolic velocity profile in the transverse direction.
3 Results
3.1 Flow patterns and holdup
The PLIF images reveal important characteristics of the flow and its development in the middle plane of the pipe, which would not have been possible with standard imaging at the high dispersed phase fractions used. In Fig. 5a a typical image for mixture velocity \(u_{m} = 0.46\) m/s and input oil fraction \(\varphi _{o} = 0.12\) is illustrated at the two axial locations studied, \(x^{+} = 15\) and 135. The mixture velocity and the input oil fractions are calculated, respectively, as
where \(Q_{a}\) and \(Q_{o}\) are the input flow rate of the aqueous and organic phases, respectively, and A is the pipe cross-sectional area. At \(x^{+} = 15\), the organic phase is dispersed homogeneously in the continuous aqueous phase. In the static mixer, the organic phase, which is significantly less than the aqueous, breaks up into small drops. For the same conditions the flow without the static mixer is stratified. For this reason, it is expected that the dispersion will separate downstream the test section. As can be seen at \(x^{+} = 135\), the drops have segregated to the top of the pipe, driven by the difference in the density of the liquids. For dispersions formed by the flow in the pipe, this separation of drops does not occur, because the turbulence levels are high enough to generate the dispersions in the first place. Pérez (2005) also used a static mixer and observed significant stratification downstream the inlet at low mixture velocities. Conan et al. (2007) and Voulgaropoulos et al. (2016) employed different multi-nozzle inlet configurations to generate dispersions at low velocities and reported similar findings to those shown in Fig. 5a. This segregation under gravity is the first step towards the separation of the phases in pipes as discussed by Pereyra et al. (2013).
The evolution of the dispersion for \(u_{m}\) = 0.36 m/s and \(\varphi _{o} = 0.79\) is shown in Fig. 5b for the same two axial locations. At these conditions, the aqueous phase is now dispersed in the continuous organic phase, close to the inlet. For this low mixture velocity, the segregation due to gravity is already advanced even at \(x^{+} = 15\) compared to Fig. 5a. A very thin film of the aqueous phase can also be observed on the bottom right of the image. By comparing the initial to the last axial locations, it is clear that both drop–drop and drop-interface coalescence have taken place. The dispersed drops are larger and fewer at \(x^{+} = 135\), compared to \(x^{+} = 15\), while the aqueous film thickness has increased. Between the two locations, a transition in the flow pattern has also occurred from dispersed aqueous drops in an organic continuous phase to dual-continuous flow, where both phases are continuous, while aqueous drops are present at the interface. This illustrates the second stage of dispersion separation in a pipe, which is controlled by coalescence phenomena.
As discussed in Sect. 2, the images can be processed to acquire in-situ oil volume fraction (\(\varepsilon _{o}\)) profiles along the vertical direction at the middle plane of the pipe cross-section as shown in Fig. 6. The trends are illustrated by lines calculated by fitting low order polynomials to successive adjacent data points using a moving average filtering approach (Guest 2012). The vertical profiles for different conditions of oil in water o/w and water in oil w/o dispersions are shown, respectively, in Fig. 6a, b. There is good agreement with the visual observations of Fig. 5 for all conditions. For most conditions investigated, the o/w dispersions have a homogeneous concentration in a pipe cross section at 15D and segregate further downstream. The segregation is more prominent at high dispersed phase fractions and low mixture velocities. The high drop concentrations in the packed layer are possible because of the wide range of drop sizes observed for \(u_{m} = 0.24\) and \(\varphi _{o} = 0.50\) as discussed by Pouplin et al. (2011).
For the w/o dispersions (Fig. 6b), in all cases studied a continuous layer of the initial dispersed aqueous phase forms at the bottom of the pipe, while the thickness of the drop-free oil layer at the top of the pipe increases. The stratification of the flow is evident by the gradients of the volume fraction curves in the middle of the pipe. The final thickness of the aqueous phase layers was found to depend only on the input phase fraction rather than the mixture velocity. Similar trends were recorded by Morgan et al. 2012.
3.2 Drop size and data treating algorithms
Drop size distributions were measured at the same two axial locations to quantify any changes along the test section. The flow rates used correspond to relatively low Re numbers (based on the fluid properties of the continuous phase and the mixture velocity) as \(Re = \rho _{c} u_{m} D/\mu _{c}\) and any changes in the drop size are attributed to coalescence rather than breakage phenomena. An algorithm was developed to detect and capture the circular contours of the drops. The images confirmed that the drops were in the majority of cases circular. In addition, the Reynolds and Eötvös numbers based on a characteristic drop diameter and velocity are
both in the order of \(\mathcal {O}\{10^{-1}\}\), suggesting that the drops should be spherical (Clift et al. 1978), where \(d_{p}\) and \(u_{d}\) are the drop diameter and velocity respectively, g is the gravitational acceleration, while the subscripts c and d denote the properties of the continuous and dispersed phases, respectively.
There have been many efforts in the literature to develop algorithms that accurately detect the drop circumference in images. Blaisot and Yon (2005) suggested a method to measure drop sizes of fuel sprays from high-speed images. Due to the wide depth of field, many drops appeared blurred and a correction to the apparent size of the unfocused drops was employed. To handle non-spherical droplets they developed a computational method, which calculated the second derivative of the filtered gray level function to detect the boundaries of the drops. Castanet et al. (2013) developed an approach based on a Laplacian of the Gaussian method used in particular for blob structures (Acharya and Ray 2005), to detect the outline of the drops, measure their size and track their trajectories in time. The method was applied in the secondary drops generated from drops impacting onto a heated surface.
The detection method developed in this work is implemented within the imfindcircles function of Matlab, where a circular Hough transform (CHT) algorithm is used to find circles in an image based on the pixel intensity gradients (Atherton and Kerbyson 1999). The parametric circular equations are written as
where \(c_{x}\) and \(c_{y}\) are the respective x and y spatial coordinates of the center of the circle i, \(d_{p}\) is the circle diameter which corresponds to the drop chord length measured, while \(\theta\) is the angle sweeping through the full 360° range to trace the perimeter of the circle. The search function locates the pixels of an image that fall on the peripheries of the drops in the form of three parameter values, namely \(c_{x}\), \(c_{y}\), \(d_{p}\).
Figure 7 illustrates the drop detection algorithm for an image taken at \(u_{m} = 0.46\) m/s and \(\varphi _{o} = 0.12\) at \(x^{+} = 135\). Even though the laser plane had a thickness of \(\Delta l_{z} \cong 1\) mm, some drops appear brighter than the rest. To improve the accuracy of the detection algorithm, the post-treated images of Fig. 4b are binarised with two sensitivity levels to capture the highest number of drops in each frame. Figures 7a and b illustrate the detection from each binarisation result, while Fig. 7c presents the two combined. Since some drops are detected by both the high and the low sensitivity values, any duplicates need to be removed. This is done with an overlapping filter, where drops are removed from the low threshold population for \(\delta <k\) with
where \(\delta\) is the distance between the centres of the two circles and \(\beta\) is a tolerance parameter set equal to 2 pixels. The final image is shown in Fig. 7d. It must be mentioned that the diameters measured for these images correspond to the drop chord lengths rather than the drop diameters. The chord length distributions can be transformed into drop size distributions as discussed by Hu et al. (2006). The chord length and drop diameter terms will be used interchangeably herein.
The size distributions of the drops detected in Fig. 7d are further analysed in Fig. 8. To produce reliable statistics a sufficiently large number of drops needs to be measured. The Sauter mean diameter of the drops is calculated as
and plotted in Fig. 8 for different sample sizes (i.e. number of drops measured, \(N_{d}\)). The \(d_{32}\) changes less than 1% for \(N_{d}\) above 600. Similar results are found for the mean drop size, \(d_{10}\), and the standard deviation, \(\sigma _{d_{p}}\), of the population (see inset in Fig. 8). The drop number distributions (not shown here) followed the same trend, with no change recorded after \(N_{d}\) \(\, \sim \,\) 600. For that reason, \(N_{d}> 600\) was used in all measurements. Angeli and Hewitt (2000) underlined that at least 350 drops need to be measured to increase the possibility of capturing very large drops (with small probability).
The change in drop size along the vertical direction is shown in Fig. 9 for \(u_{m} = 0.46\) m/s and \(\varphi _{o} = 0.12\) at \(x^{+} = 135\). The images are split in equally spaced horizontal segments. The ratio of the number of drops in each segment over the total number of drops measured in the cross-section (\(N_{d}^{+}\)) are also shown. The number of segments is chosen so that in each segment at least 600 drops are averaged, in order to have statistically meaningful average drop sizes, as discussed previously. In Fig. 9 the sizes and number of the drops measured manually from the images is also shown; in this case the two axes of each drop were measured assuming an ellipsoidal shape. The two approaches agree very well and the results from the data processing algorithm have an average deviation of less than 10% from the manual measurements for both \(N_{d}^{+}\) and \(d_{32}\).
As discussed for \(x^{+} = 135\) conditions and o/w dispersions, a larger number of drops is found at the top of the pipe (Fig. 9). The results agree well with the visual observations of Fig. 5a. The average drop size increases with \(y^{+}\) and then reduces again close to the upper wall. The larger drops tend to concentrate to the upper part of the pipe due to gravity, where they may also coalesce more easily. For values of \(y^{+} \geqslant 0.8\) smaller drops are measured, which agree with the visual observations of Fig. 5a; the concentration values were also found to decrease close to the wall and are attributed to lift forces that increase with the drop size. Similar trends have been reported by Schümann et al. (2016b).
In a turbulent flow field, the average drop sizes are generally found to be proportional to the We number, \(d_{32} \propto We^{-0.6}\), where \(We = \rho _{c} u_{m}^{2} D/\gamma\) (Brauner 2001). While in the present work the Re are kept relatively low, the static mixer that has large friction factor can induce turbulence (Middleman 1974) At the first axial measuring location the drop size will be determined mainly by the mixer. As can be seen in Fig. 10 at this location the Sauter mean diameter is proportional to \(We^{-0.6}\).
The evolution and growth of drop size is important for designing pipe separators (Danielson 2012; Pereyra et al. 2013). For this work, the changes of the drop size number distributions (\(N_{d} = \mathcal {O}\{10^{3}\}\)) along the test section are illustrated with histograms in Fig. 11a, b for two typical flow conditions of o/w and w/o dispersions, respectively. Also shown are the log-normal probability density functions (PDFs), \(f(d_{p})\), between the two axial locations \(x^{+} = 15\) and 135. The PDFs are computed as
where \(\mu _{d_{p}}\) and \(\sigma _{d_{p}}\) are respectively the mean and standard deviation of the drop population. Log-normal distributions have shown to capture well the behaviour of liquid–liquid drop size distributions in pipes (Angeli and Hewitt 2000), as they usually have a positive skewness, which was found to be true in the current experiments as well.
The two distributions appear very similar for Fig. 11a, with a slight increase of the probability to find drops with size of 1 mm in the last axial location. This variation in the distribution causes also a small change in the Sauter mean diameter, from \(d_{32} = 0.775\) mm for \(x^{+} = 15\) to \(d_{32} = 0.786\) mm for \(x^{+} = 135\) (or 2%) which, however, falls within the 10% of experimental uncertainty of the algorithm. For \(u_{m} = 0.36\) m/s and \(\varphi _{o} = 0.79\) the distributions of the aqueous drops are plotted in Fig. 11b for a bin size of 0.5 mm at the two axial locations. As is also shown in 5b, segregation of the drops has already occurred at \(x^{+} = 15\) and it continues downstream the test section. The Sauter mean diameter changes from \(d_{32} = 1.693\) at \(x^{+} =\) 15 to 4.315 at \(x^{+} = 135\). However, the \(d_{32}\) at \(x^{+} = 135\) is significantly increased due to a few drops above 5 mm, that account for less than 1% of the drop number population. The arithmetic mean diameter, changes from \(d_{10} = 1.047\) mm to \(d_{10} = 1.373\) mm between \(x^{+} =\) 15 and 135, respectively, or by about 31\(\%\), which is significantly smaller than the 155\(\%\) change of the \(d_{32}\). A discussion on the characterisation issues of drop populations has been given by Tate (1982). For most cases the drop size did not vary significantly for the o/w dispersions, while the change was more pronounced for the w/o dispersions.
3.3 Aqueous phase velocity
Vertical velocity profiles of the time-averaged axial velocity of the aqueous phase for two flow conditions at the two axial measuring locations. Filled symbols are for measurements in pure aqueous phase, faded symbols for regions with drops, while the empty symbols denote regions of low concentration of tracers
The velocity fields in the aqueous phase were acquired following the analysis discussed previously and the vertical profiles of the time-averaged axial velocity component \(\langle u \rangle\) of the aqueous phase are shown in Fig. 12. The velocities measured in the pure aqueous phase are shown with filled symbols, in the regions with drops with faded symbols and in the regions of low concentration of tracers with empty symbols. The velocity profiles for \(u_{m} = 0.46\) m/s and \(\varphi _{o} = 0.12\) are shown in Fig. 12a. The Reynolds number, based on the fluid properties of the continuous phase and the mixture velocity is equal to \(Re \simeq 1700\), which indicates laminar flow conditions.
In the first axial position \(x^{+} = 15\), the drops are homogeneously dispersed along the vertical pipe diameter (see also Fig. 6a). The resulting velocity profile is almost flat in the middle of the pipe and indicates plug flow conditions. It is possible that the flow is not yet fully developed at this axial location. Two symmetrical peaks appear on each side of the profile, which are equal to \(\sim 1.5\,u_{m}\). In the intermediate regime (\(Re \sim\) 2000) of a homogeneous dispersed flow (Pouplin et al. 2011) also reported a similar velocity profile with the maxima close to the wall. Similar velocity profiles have been reported by Lečić et al. (2016) and Grosjean et al. (1997), indicating a weak swirling motion due to the static mixer. The profile for this flow condition at the last axial location, \(x^{+} = 135\), becomes asymmetric. In the drop free water layer at the bottom of the pipe a parabolic-type profile develops with maximum velocity equal to about \(\sim 2.5\,u_{m}\). A similar trend was also reported by Conan et al. (2007) for this type of flow but for turbulent flow conditions (\(Re \simeq 7500\)) and similar concentration of drops equal to \(\varphi = 0.10\).
The velocity profiles for the two axial measuring locations and for \(u_{m} = 0.36\) m/s and \(\varphi _{o} = 0.79\), are illustrated in Fig. 12b and correspond to the images of Fig. 5b. For this flow condition, the tracer particles are inside the aqueous drops, and thus the velocity of the dispersed phase is measured. At the first axial location, the drops are still moving freely within the continuous oil phase and the profile has a maximum (equal to about \(\simeq\) 1.6 \(u_{m}\)) close to the middle of the pipe. At the last axial location, \(x^{+} = 135\), two continuous layers are present and the velocity profile has two peaks. The first peak is located in the aqueous continuous phase, while the second one is within the layer of drops above the aqueous layer and near the middle of the pipe, where the velocity of the drops should be higher.
3.4 Organic phase drop velocity
The trajectories of the drops are computed in this section through the Matlab PTVlab function. The Gaussian mask technique (Takehara and Etoh 1998) was used for the particle detection, with an appropriate drop detection area, \(a_{p}\), according to the image and the drop size distribution measured at each flow condition. In Fig. 13 the different time-averaged velocity profiles acquired for \(u_{m} = 0.46\) m/s and \(\varphi _{o} = 0.12\) at the first axial location and for three drop detection areas, \(a_{p}\), based on the measured Sauter mean diameter of the drops (i.e. for \(a_{p} \simeq 0.5\,d_{32}\), \(d_{32}\) and \(1.5\,d_{32}\)) are plotted. Figure 13a illustrates the axial velocity component, u. The velocity of the aqueous continuous phase is also plotted. It can be seen that the velocity profiles of the continuous and dispersed phases are similar, which is in accordance with homogeneous dispersed flows as the slip in the axial direction is expected to be very low (Augier et al. 2003).
Vertical profiles of the two velocity components for \(u_{m} = 0.46\) m/s and \(\varphi _{o} = 0.12\) at \(x^{+} = 15\). Three different PTV drop detection areas are used and compared against the continuous phase velocity from PIV measurements of Fig. 12a.
In Fig. 13b the profiles of the time averaged vertical velocity component, \(\langle v \rangle\), are plotted for the same condition. The profiles of \(\langle v \rangle\) agree very well qualitatively with the trends illustrated by Conan et al. (2007) for the secondary flows present in homogeneous dispersed pipe flows. From Fig. 13b, as can be seen, the vertical velocity of the drops increases with the drop detection area and hence the drop size. Specifically, the floatation terminal velocity of a drop under the influence of gravity, \(v_{d,t}\), has been well established in the literature (Perry and Green 1999). For the three drop sizes equal to \(0.5\,d_{32}\), \(d_{32}\) and \(1.5\,d_{32}\) the respective drop Reynolds numbers, \(Re_{p}\), based on the fluid properties of the continuous phase and the drop size, are \(Re_{p} = \mathcal {O}\{10^{-1}\}\). For these Reynolds numbers the drag coefficients are computed as
For spherical drops the terminal velocity is
Finally, a correction to the velocity is applied to account for the interactions between the drops as
where c is a parameter depended on \(Re_{p}\) (Perry and Green 1999). The velocity computed for \(d_{p} = d_{32}\) is equal to \(\dot{v}_{d} = 4.5\) mm/s. The experimental mean vertical velocity across the pipe diameter from the time-averaged PTV measurements is \(\langle \bar{v}_{d} \rangle = 6.8\) mm/s.
Pilhofer and Mewes (1979) developed an empirical model that calculates the vertical velocity of the drops in batch settling/floatation experiments. The model was recently found by Pereyra et al. (2013) to predict well experimental data of drops settling in horizontal pipes. The model is valid for Archimedes numbers above 1 and dispersed phase fractions ranging between 0.06 and 0.55, with
The vertical velocity for a swarm of drops can be then computed as
where the two floatation/settling parameters are equal to
and the Hadamard–Rybczynski factor, \(K_{HR}\) , and the friction coefficient, \(C_{W}\) , are
with
Equation 12 gives for \(d_{p} = d_{32}\) a vertical velocity \(\dot{v}_{d} = 6.6\) mm/s, which is in excellent agreement with the experimental velocity from PTV, with a difference of less than 3
It must be noted that the effects of local concentration gradients or any flow fluctuations at the wake of the drop are not taken into consideration in the settling/floatation models described previously. Further investigations of these effects, as described in the review by Balachandar and Eaton (2010), need to be carried out using the experimental approaches and data processing algorithms developed here.
3.5 Coalescence dynamics
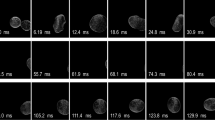
It was possible to capture some coalescence events of an aqueous drop with the aqueous-organic interface. One such event which lasted approximately 480 frames (120 ms) was captured at \(u_{m} = 0.46\) m/s, \(\varphi _{o} = 0.12\) and \(x^{+} = 135\), and is illustrated in Fig. 14. In the images, displayed for ten time steps, the relative instantaneous velocities are displayed, which were calculated by subtracting the mixture velocity from the local velocities. The vorticity is also shown in the z direction, which was computed by assuming two-dimensional flow on the measuring plane as
At \(t = 0\) ms the interface has ruptured on the right side of the drop. Under the effect of interfacial tension, the formed neck between the drop and the interface is expanding axially. The maximum velocity of the expanding neck occurs at \(t = 2.5\) ms. The axial velocities become symmetric on both sides of the drop at a later time step (\(t = 20\) ms). The same behaviour has been described by Mohamed-Kassim and Longmire (2004) for a confined system without a cross flow.
Gravity and Laplace pressure cause a strong downward motion of the aqueous phase from the drop to the bulk continuous phase (Weheliye et al. 2017). The combination of the axial and the vertical motions generates two counterrotating vortices in the drop. Similar velocity and vorticity patterns have also been observed in stationary systems (Mohamed-Kassim and Longmire 2004; Weheliye et al. 2017). The neck expansion velocities reported in stationary systems are also similar to the one observed in this work. The adjacent drops would have an effect on the film drainage rate and the local flow fields, as discussed by Bordoloi and Longmire (2012) on the effect of neighbouring particles on drop coalescence. Chinaud et al. (2016) showed that two more counteracting vortices form in the bulk coalescing phase. However, the spatial resolution in the current experiments is not high enough to capture these vortices. At time \(t \sim\) 40 ms the neck decreases until \(t \sim\) 60 ms. However, this does not lead to neck pinch off and partial coalescence, and thus after \(t \sim\) 80 ms the drop continues to drain in the bulk homophase. The rate of decay is similar for both the vertical velocity component and the vorticity.
(Colour online) The horizontal velocity and vorticity profiles at \(y^{+}= 0.2\) during coalescence. The same time steps are plotted as in Fig. 14 with t \(\in [2.5,110]\) milliseconds (light to dark)
The vertical velocity component, v, and the vorticity, \(\omega_{z}\), profiles are shown in Fig. 15a, b respectively, for the same time steps shown in Fig. 14, at the rupture location \(y^{+} = 0.20\) and after coalescence starts. As can be seen in Fig. 15a the absolute maximum of the vertical velocity increases as the coalescing drop moves along the pipe. The velocity v reaches the highest value for \(x^{+} = 134.9\) or \(t = 40\) ms. Once the formed neck between the drop and the interface starts decreasing, as shown for \(t = 60\) ms, the maximum v also temporarily decreases. At \(t = 80\) ms, when the neck starts expanding again, the vertical velocity increases again before finally the whole drop joins the continuous phase and the local vertical velocity peak decreases. A similar trend is observed in the vorticity shown in Fig. 15b. Two vorticity peaks, one negative (from the counterclockwise vortex) and one positive (from the clockwise vortex), form at each time step, which increase as the neck expands in the initial time steps. This is followed by a temporary decrease, an increase and then a final decay of the vorticity.
4 Conclusions and perspectives
The paper presents the experimental techniques and the data analysis methodology developed to study concentrated unstable liquid-liquid dispersions in a horizontal pipe. The experiments were carried out with a pair of liquids of matched refractive index and the dispersions were generated using a helical static mixer. With a continuous laser and a high speed camera, a combination of PLIF, PIV and PTV techniques were applied to obtain phase fraction, phase velocities and dispersed phase drop sizes. Measurements were taken at two axial locations to demonstrate the change in the flow patterns as the flow develops. From the PLIF measurements, information on the spatial configuration of the phases was acquired in a pipe cross section. Drops segregated downstream the pipe because of the density difference between the two phases, while the thickness of the drop-free continuous phase layer increased. A decrease in the concentration of the drops close to the top wall was recorded for most o/w cases. It was also found that when a layer of the dispersed phase was present in the pipe at the beginning of the test section, its thickness increased because of coalescence of drops with the layer.
A drop size measuring methodology from the PLIF images was developed. The Sauter mean drop sizes close to the mixer were found to be proportional to \(We^{-0.6}\). Comparisons between the beginning and end of the pipe showed an increase of drop size downstream the inlet, independent of the flow pattern, but higher rates were observed for the w/o dispersions. PIV measurements gave information on the velocity field of the aqueous phase. The profile had a plug-like shape in the fully dispersed flow cases, close to the inlet. At the downstream location, the shape of the profile depended on the flow pattern. PTV algorithms were applied to acquire the velocity fields of the dispersed phase drops. With the measurement techniques developed it was also possible to capture velocity fields in an aqueous drop coalescing with an interface in the presence of cross flow. The techniques developed will be used to study the evolution of liquid-liquid dispersed flows for a wide range of conditions and help understand the mechanism of phase separation in pipes.
References
Acharya T, Ray AK (2005) Image processing: principles and applications. Wiley, New York
Angeli P, Hewitt GF (2000) Flow structure in horizontal oil–water flow. Int J Multiph Flow 26(7):1117–1140
Atherton TJ, Kerbyson DJ (1999) Size invariant circle detection. Image Vis Comput 17(11):795–803
Augier F, Masbernat O, Guiraud P (2003) Slip velocity and drag law in a liquid–liquid homogeneous dispersed flow. AIChE J 49(9):2300–2316
Baek SJ, Lee SJ (1996) A new two-frame particle tracking algorithm using match probability. Exp Fluids 22(1):23–32
Balachandar S, Eaton JK (2010) Turbulent dispersed multiphase flow. Annual Rev Fluid Mech 42:111–133
Barral AH, Angeli P (2013) Interfacial characteristics of stratified liquid-liquid flows using a conductance probe. Experiments Fluids 54(10):1604
Batchelor GK (1972) Sedimentation in a dilute dispersion of spheres. J Fluid Mech 52(02):245–268
Blaisot JB, Yon J (2005) Droplet size and morphology characterization for dense sprays by image processing: application to the diesel spray. Experiments Fluids 39(6):977–994
Bordoloi AD, Longmire EK (2012) Effect of neighboring perturbations on drop coalescence at an interface. Phys Fluids 24(6):062106
Bourdillon AC, Verdin PG, Thompson CP (2016) Numerical simulations of drop size evolution in a horizontal pipeline. Int J Multiph Flow 78:44–58
Brauner N (2001) The prediction of dispersed flows boundaries in liquid–liquid and gas–liquid systems. Int J Multiph Flow 27(5):885–910
Brevis W, Niño Y, Jirka GH (2011) Integrating cross-correlation and relaxation algorithms for particle tracking velocimetry. Experiments Fluids 50(1):135–147
Budwig R (1994) Refractive index matching methods for liquid flow investigations. Exp Fluids 17(5):350–355
Castanet G, Dunand P, Caballina O, Lemoine F (2013) High-speed shadow imagery to characterize the size and velocity of the secondary droplets produced by drop impacts onto a heated surface. Experiments Fluids 54(3):1489–1505
Chinaud M, Voulgaropoulos V, Angeli P (2016) Surfactant effects on the coalescence of a drop in a Hele–Shaw cell. Phys Rev E 94(3):033101
Chinaud M, Park KH, Angeli P (2017) Flow pattern transition in liquid–liquid flows with a transverse cylinder. Int J Multiph Flow 90:1–12
Clift R, Grace JR, Weber ME (1978) Bubbles, drops, and particles. Dover Publications Inc, New York
Conan C, Masbernat O, Décarre S, Liné A (2007) Local hydrodynamics in a dispersedstratified liquid–liquid pipe flow. AIChE J 53(11):2754–2768
Danielson TJ (2012) Transient multiphase flow: past, present, and future with flow assurance perspective. Energy Fuels 26:4137–4144
Grosjean N, Graftieaux L, Michard M, Hübner W, Tropea C, Volkert J (1997) Combining LDA and PIV for turbulence measurements in unsteady swirling flows. Meas Sci Technol 8(12):1523
Guest PG (2012) Numerical methods of curve fitting. Cambridge University Press, Cambridge
Hu B, Angeli P (2006) Phase inversion and associated phenomena in oil–water vertical pipeline flow. Can J Chem Eng 84(1):94–94
Hu B, Angeli P, Matar OK, Lawrence CJ, Hewitt GF (2006) Evaluation of drop size distribution from chord length measurements. AIChE J 52(3):931–939
Kreizer M, Liberzon A (2011) Three-dimensional particle tracking method using FPGA-based real-time image processing and four-view image splitter. Experiments Fluids 50(3):613–620
Kumara WAS, Elseth G, Halvorsen BM, Melaaen MC (2010) Comparison of particle image velocimetry and laser Doppler anemometry measurement methods applied to the oil–water flow in horizontal pipe. Flow Meas Instrum 21(2):105–117
Lečić MR, Ćoćić AS, Burazer JM (2016) An experimental investigation and statistical analysis of turbulent swirl flow in a straight pipe. Therm Sci 00:191–191
Liu L, Matar OK, Hewitt GF (2006) An optical probe for liquid–liquid two-phase flows. Chem Eng Sci 61(12):40224026
Maas HG, Gruen A, Papantoniou D (1993) Particle tracking velocimetry in three-dimensional flows. Experiments Fluids 15(2):133–146
Maaß S, Wollny S, Voigt A, Kraume M (2011) Experimental comparison of measurement techniques for drop size distributions in liquid/liquid dispersions. Experiments Fluids 50(2):259–269
Middleman S (1974) Drop size distributions produced by turbulent pipe flow of immiscible fluids through a static mixer. Ind Eng Chem Process Des Dev 13(1):78–83
Mohamed-Kassim Z, Longmire EK (2004) Drop coalescence through a liquid/liquid interface. Phys Fluids 16(7):2170–2181
Morgan RG, Markides CN, Hale CP, Hewitt GF (2012) Horizontal liquidliquid flow characteristics at low superficial velocities using laser-induced fluorescence. Int J Multiph Flow 43:101–117
Morgan RG, Ibarra R, Zadrazil I, Matar OK, Hewitt GF, Markides CN (2017) On the role of buoyancy-driven instabilities in horizontal liquid–liquid flow. Int J Multiph Flow 89:123–135
Ngan KH, Ioannou K, Rhyne LD, Wang W, Angeli P (2009) A methodology for predicting phase inversion during liquid–liquid dispersed pipeline flow. Chem Eng Res Des 87(3):318–324
Nobach H, Honkanen M (2005) Two-dimensional Gaussian regression for sub-pixel displacement estimation in particle image velocimetry or particle position estimation in particle tracking velocimetry. Experiments Fluids 38(4):511–515
Oddy G, Pearson JRA (2004) Flow-rate measurement in two-phase flow. Annu Rev Fluid Mech 36:149–172
Pereyra E, Mohan RS, Shoham O (2013) A simplified mechanistic model for an oil/water horizontal pipe separator. Oil Gas Facil 2(3):40–46
Pérez CA (2005) Horizontal pipe separator (HPS\(^{\copyright }\)) experiments and modeling. PhD thesis, The University of Tulsa
Perry RH, Green DW (1999) Perry’s chemical engineers’ handbook. McGraw-Hill Professional, New York
Pilhofer T, Mewes D (1979) Siebboden-Extraktionskolonnen: Vorausberechnung unpulsierter Kolonnen. Verlag Chemie, New York
Pouplin A, Masbernat O, Décarre S, Liné A (2011) Wall friction and effective viscosity of a homogeneous dispersed liquid–liquid flow in a horizontal pipe. AIChE J 57(5):119–1131
Schümann H, Tutkun M, Nydal OJ (2016a) Experimental study of dispersed oil–water flow in a horizontal pipe with enhanced inlet mixing, Part 2: In-situ droplet measurements. J Pet Sci Eng 145:753–762
Schümann H, Tutkun M, Yang Z, Nydal OJ (2016b) Experimental study of dispersed oil–water flow in a horizontal pipe with enhanced inlet mixing, part 1: flow patterns, phase distributions and pressure gradients. J Pet Sci Eng 145:742–752
Silva MJD, Schleicher E, Hampel U (2007) Capacitance wire-mesh sensor for fast measurement of phase fraction distributions. Meas Sci Technol 18(7):2245–2251
Takehara K, Etoh T (1998) A study on particle identification in PTV particle mask correlation method. J Vis 1(3):313–323
Tate R (1982) Some problems associated with the accurate representation of droplet size distributions. In: Proceedings of the 2nd Iclass
Thielicke W, Stamhuis E (2014) PIVlab-towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J Open Res Softw 2(1):e30
Voulgaropoulos V, Zhai LS, Ioannou K, Angeli P (2016) Evolution of unstable liquid-liquid dispersions in horizontal pipes. In: Proceedings of the 10th North American conference on multiphase technology, Banff, Canada
Wegmann A, von Rohr PR (2006) Two phase liquid–liquid flows in pipes of small diameters. Int J Multiph Flow 32(8):1017–1028
Weheliye WH, Dong T, Angeli P (2017) On the effect of surfactants on drop coalescence at liquid/liquid interfaces. Chem Eng Sci 161:215–227
Westerweel J (1997) Fundamentals of digital particle image velocimetry. Meas Sci Technol 8:1379–1392
Westerweel J (2008) On velocity gradients in PIV interrogation. Experiments Fluids 44(5):831–842
Westerweel J, Scarano F (2005) Universal outlier detection for PIV data. Experiments Fluids 39(6):10961100
Wright SF, Zadrazil I, Markides CN (2017) A review of solid–fluid selection options for optical-based measurements in single-phase liquid, two-phase liquid–liquid and multiphase solid–liquid flows. Experiments Fluids 58(9):108
Acknowledgements
Victor Voulgaropoulos would like to acknowledge Chevron Corporation and UCL for his PhD studentship. Both authors would like to thank Karolina Ioannou, Carlos Avila and Lee Rhyne from Chevron Corporation for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Voulgaropoulos, V., Angeli, P. Optical measurements in evolving dispersed pipe flows. Exp Fluids 58, 170 (2017). https://doi.org/10.1007/s00348-017-2445-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-017-2445-4