Abstract
In modern drop-on-demand inkjet printing, the jetted droplets contain a mixture of solvents, pigments and surfactants. In order to accurately control the droplet formation process, its in-flight dynamics, and deposition characteristics upon impact at the underlying substrate, it is key to quantify the instantaneous liquid properties of the droplets during the entire inkjet-printing process. An analysis of shape oscillation dynamics is known to give direct information of the local liquid properties of millimeter-sized droplets and bubbles. Here, we apply this technique to measure the surface tension and viscosity of micrometer-sized inkjet droplets in flight by recording the droplet shape oscillations microseconds after pinch-off from the nozzle. From the damped oscillation amplitude and frequency we deduce the viscosity and surface tension, respectively. With this ultrafast imaging method, we study the role of surfactants in freshly made inkjet droplets in flight and compare to complementary techniques for dynamic surface tension measurements.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Inks used in inkjet printers are a complex mixture of solvents, co-solvents, pigments and one or more surfactants (Wijshoff 2010). The solvents carry the pigment particles to the medium and evaporate, solidify or crystallize, while the surfactants prevent wetting of the nozzle plate and promote spreading of the droplet after it impacts the underlying medium. In order to accurately control the droplet formation process, its in-flight dynamics, and subsequent interaction with the substrate, it is key to quantify the liquid properties of the droplet during the entire inkjet-printing process.
The surface tension of a surfactant solution is determined by the concentration of adsorbed surfactant molecules at the liquid–air interface. When a fresh interface is formed, the surface tension equals that of the solvent (Ohl et al. 2003) and it decreases while surfactants adsorb at the interface, until reaching an equilibrium surfactant concentration. The associated timescales of the adsorption process are governed by the diffusion time of the surfactant molecules to diffuse from the so-called adsorption depth h to the interface (Ferri and Stebe 2000). This depth depends on the bulk surfactant concentration, the critical micelle concentration and the surface concentration of surfactants at equilibrium surface tension (Ferri and Stebe 2000). The typical diffusion time then scales with the surfactant diffusion coefficient D as \(\tau _D \sim h^2/D\) and ranges from milliseconds to days, depending on the surfactant type and surfactant concentration (Chang and Franses 1995; Eastoe and Dalton 2000). As the surfactants in inkjet printing must act before the ink dries, it is required that they adsorb as fast as possible. Droplet formation, however, is an extremely fast process that takes in the order of \(10\,\upmu \hbox {s}\), which is shorter than the approximately \(100\,\upmu \hbox {s}\) that a droplet is typically in flight and much shorter than the time a droplet needs to evaporate, which is several seconds (Staat et al. 2016). A surfactant with a typical adsorption time scale of the order of milliseconds is considered a fast-adsorbing surfactant (Chang and Franses 1995; Eastoe and Dalton 2000); therefore, it is clear that the surface tension of an ink is higher during droplet formation and flight than during the later spreading and evaporation phases. Methods exist to measure the time-dependent dynamic surface tension; however, these measurement techniques require separate, off-line setups or are not fast enough to operate at the microseconds timescale of the inkjet process (Franses et al. 1996).
It was shown before that the surface tension and viscosity can be extracted directly from an analysis of the eigenfrequencies of shape modes of oscillating droplets (Loshak and Byers 1973; Stückrad et al. 1993; Brenn and Frohn 1993; Holt et al. 1997; Tian et al. 1997; Wang et al. 2006; González and García 2009; Yamada and Sakai 2012; Thoraval et al. 2013; Brenn and Teichtmeister 2013; Yang et al. 2014). Over the past decades, this method has also been proven to be very robust for various other systems, including jets (Ronay 1978a, b), bubbles (Leighton 1994; Brennen 1995), liquid samples of blood and biological tissues (Weiser and Apfel 1982; Weber et al. 2012) and soap bubbles (Kornek et al. 2010; Grinfeld 2012). The very early work of Rayleigh (1879) and Lamb (1881) showed that a liquid that is deformed from its equilibrium state can be treated as an oscillator (system), where surface tension provides the restoring force. The generalized system of a damped oscillator of an immiscible viscous fluid within another fluid was first described by Lamb (1932) and revisited by others (Reid 1959; Chandrasekhar 1959; Miller and Scriven 1968; Prosperetti 1980). However, the analysis up to now has focused on mm-sized droplets or has only measured the aspect ratio of \(\upmu \hbox {m}\)-sized droplets, instead of the full analysis.
a Schematic of a droplet that is symmetrical around the vertical axis showing the definitions of the distance from the center of mass to the liquid–air interface R, the polar angle \(\theta\) and the equilibrium radius \(R_0\) (dotted line). b The amplitude–time curve of the shape oscillation for a mode \(n=2\) of a droplet of equilibrium radius \(R_0 = 15\,\upmu \hbox {m}\). The damping rate \(\beta _2 = 22 \cdot 10^{3}\) \(\hbox {s}^{-1}\) is determined from the amplitude decay. c The corresponding Fourier transform of the amplitude–time curve, indicating the eigenfrequency of the shape mode \(f_2 = 57\) kHz
Here, we present an ultrafast imaging method to measure the surface tension and viscosity for \(\upmu {\hbox {m}}\)-sized inkjet droplets (corresponding to picoliters) in flight. We extend the well-known method to measure surface tension and viscosity from the eigenfrequencies of shape modes of oscillating droplets to the \(\upmu \hbox {m}\)-regime by employing ultrafast imaging. Ultrafast imaging is necessary as the microscopic length scale of picoliter droplets poses a few challenges. First, the eigenfrequencies of shape mode oscillations scale with the droplet radius as \(R_0^{-3/2}\), and thus high-speed imaging is not only required to capture droplets in flight moving at a speed near 10 m/s (\(\sim 10\,\upmu \hbox {m}/\upmu \hbox {s})\), but also to resolve the details of the surface mode oscillations. Secondly, the viscous effects become increasingly important, as can be evaluated from balancing the viscous forces and the capillary forces through the Ohnesorge number \({\text{ Oh }}={\mu /}\sqrt{{\sigma \rho R_0}}\), with \(\mu\) being the dynamic viscosity, \(\sigma\) the surface tension and \(\rho\) the density, especially for higher mode numbers n, since the Ohnesorge number scales with the mode number as \({\text{ Oh }}_n = \sqrt{2n}\,{\text{ Oh }}\) (Versluis et al. 2010). Thus, a decreasing droplet size leads to a faster decay of the oscillation amplitude due to damping.
The paper is organized as follows. In the next section, we revisit the background theory to extract the surface tension and viscosity from oscillating droplets. Then we present high-speed imaging experiments at two different timescales (\(\upmu \hbox {s}\) and ms) to vary the age of the freshly made droplet surface in Sect. 2 and describe the image analysis and requirements for obtaining sub-pixel accuracy in Sect. 3. The results are presented in Sect. 4 and compared to a complementary, off-line technique to measure the dynamic surface tension.
2 Shape mode oscillations
Here we briefly summarize Rayleigh’s original treatment (Rayleigh 1879), to express the shape of an axisymmetrically deformed drop at any moment in time t as a sum of Legendre polynomials \(P_n\)
with \(\theta\) the polar angle, \(a_n(t)\) the time-dependent surface mode amplitude coefficients and n the mode number (see Fig. 1a for the definitions of R and \(\theta\)). Assuming incompressibility of the liquid and no evaporation, we find that \(a_0(t) = R_0\), where \(R_0\) is the radius of a sphere with the volume of the drop, or the equilibrium radius. Since we place the origin of the coordinate system at the center of mass of the drop, it follows that \(a_1(t) = 0\), and Eq. (1) simplifies to
For a freely oscillating drop with small amplitude of oscillation the mode coefficients can be expressed as (Lamb 1881, 1932)
with eigenfrequency \(\omega _n\)
and
the damping rate of each mode n. The eigenfrequency depends on the liquid density \(\rho\) and the surface tension \(\sigma\), while the damping rate depends on \(\rho\) and the dynamic viscosity \(\mu\).
Figure 1b shows the amplitude–time curve of the shape oscillation for an \(R_0=15\) \(\upmu \hbox {m}\) droplet for a mode \(n=2\). Figure 1c shows the corresponding Fourier transform \(\tilde{a}_n\), indicating the eigenfrequency \(f_2\) of the shape mode. Thus, measuring \(\tilde{a}_n(t)\) while knowing n, \(\rho\) and \(R_0\) gives \(\sigma (t)\). Measuring \(\beta _n(t)\) from the decay rate, knowing n, \(\rho\) and \(R_0\), gives \(\mu (t)\). In the example of Fig. 1, we used pure water; the surface tension was chosen to be \(\sigma = 72\) mN/m, the viscosity was \(\mu =1\) mPas, and the density was \(\rho = 1000\) \(\hbox {kg/m}^3\), therefore the eigenfrequency of the mode \(n=2\) was \(f_2 = 57\) kHz with a damping rate of \(\beta _2 = 22 \times 10^3\) \(\hbox {s}^{-1}\). In order to record multiple frames of every oscillation cycle, ultrafast imaging at interframe times of 1–5 microseconds or up to 1 Mfps is required (Versluis 2013).
3 Droplet formation
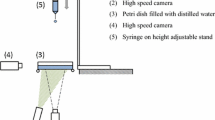
To test the dynamic effect of the surface tension and viscosity at different timescales, droplets of two different sizes were produced. In the first set of experiments, droplets were detached from the tip of a needle, where they were pendant for about five to ten seconds, i.e., enough time had passed for the concentration of surfactants at the interface to reach an equilibrium. The liquid was pushed out of a syringe (Hamilton Co.) by a syringe pump (PHD 2000, Harvard Apparatus) through a tube to a needle (19 gauge, flat tip, stainless steel, outer diameter 1.07 mm, Hamilton Co.). The flow-rate of the pump was kept low (\(\approx\) 0.05 mL/min) to ensure that the detachment was solely due to gravity and that we were in the regime where the surfactant adsorption at the liquid–air interface has reached an equilibrium. We used two different surfactants: 0.25% (w/w) sodium dodecyl sulfate (SDS, Fluka) in pure water and 0.1% (w/w) 1,2-hexanediol (HD, 98%, Aldrich) in pure water. To test the accuracy of the technique, we also performed experiments with pure water alone (18.2 \(\hbox {M}\Omega \,\hbox {cm}\), Milli-Q). The falling droplet was recorded with a high-speed camera (Fastcam SA-X2, Photron) running at a frame rate of 20 kHz in back illumination. A macro lens at a magnification of 1:1 was used to ensure sufficient spatial resolution. Figure 2 shows a representative recording of an oscillating water drop of \(R_0 = 1.5\) mm analyzed with this setup.
To investigate the surface tension and viscosity of the same liquid at a shorter timescale, we used a drop-on-demand printhead (MD-K-130, microdrop Technologies GmbH) that was actuated with a rectangular pulse from an arbitrary waveform generator (33220A, Agilent) via a wideband amplifier (model 7602M, Krohn-Hite) to generate a jet that breaks up into droplets about one hundred microseconds after actuation. The typical droplet size of a few tens of micrometers in radius, the velocity of a few meters per second and the corresponding eigenfrequency of shape oscillations of several tens of kHz dictate a requirement for spatial and temporal resolution that cannot easily be met with conventional high-speed imaging (Versluis 2013). The inkjet-printing process, however, is highly repeatable; therefore, we can record the shape oscillations of the droplets using stroboscopic imaging. The droplet is back illuminated, and its image is captured with a CCD camera (Sensicam QE, PCO AG) at a predetermined delay time after printhead actuation. By accurate control of the timing of the light source, camera and waveform generator with a pulse/delay generator (model 575-XC, Berkeley Nucleonics) the images obtained from many different droplets can be made into a sequence of the whole process. Motion blur in the images was reduced by using a pulsed laser (EverGreen, pulse width 7 ns, Quantel) for illumination. To also eliminate speckle and fringes due to interference and diffraction of the coherent laser light, the laser was projected on a fluorescent diffuser (Part number 1108417, LaVision) to produce broadband incoherent illumination while keeping the short exposure time (Van der Bos et al. 2011). Figure 3 shows a representative sequence of a jet that breaks up into droplets, generated and recorded with this setup.
Stroboscopic sequence of a drop-on-demand-printed jet that breaks up into droplets recorded using the iLIF method (Van der Bos et al. 2011). The head droplet of \(R_0 = 31\) \(\upmu \hbox {m}\) makes a shape oscillation as it travels through the field of view of the camera. The scale bar indicates a size of 100 \(\upmu \hbox {m}\) and the interframe time is 5 \(\upmu \hbox {s}\)
4 Image analysis
a Graph showing the detected boundary (orange markers) and the determination of the oscillation mode coefficients via the best fit of Eq. (2) up to \(n=20\) (black solid line) for one single frame of the recording in the sequence of Fig. 2 at \(t=12.5\) ms, see the enlargement in Fig. 2. The dotted line indicates the equilibrium radius \(R_0\). b The residual of the droplet boundary and its best fit to Eq. (2)
In each frame of every recording, we detected the position of the liquid–air interface by determining the inflection point of the intensity in the direction normal to the interface. In this way, we obtained a description for the drop boundary with sub-pixel accuracy. For a complete description of the technique on which this analysis is based, please see (Van der Bos et al. 2014).
The origin of the coordinate system was placed at the center of mass of the droplet, and the interface was divided in two parts along the axis of symmetry. The resulting halves were compared to check for axisymmetry and if this was not the case, the recording was not analyzed further. In the case of axisymmetry, the right halve was used for the remainder of the analysis. Then the interface was converted to polar coordinates and the distance from the center of mass to the droplet boundary R as function of the polar angle \(\theta\) was obtained. Figure 4 shows the detected drop boundary \(R(\theta )\) (orange markers) of the frame shown in the enlargement of Fig. 2. Please note that the smoothness of the curve is only due to the used inflection-point method, there has been no smoothing or averaging of the data. Equation (2) was then fitted to the data to find the equilibrium radius \(R_0\) and the mode coefficients \(a_2\ldots a_n\), up to \(n=20\). The black solid line in Fig. 4a is the best fit to Eq. (2) and is well within 0.1 pixels of the detected boundary (see the residue in Fig. 4b). By repeating this process for the subsequent frames of the recording, the time-dependent values of the mode coefficients \(a_n(t)\) were found. We can now determine the viscosity from the decay of the amplitude of the mode coefficients. Also the surface tension can be extracted directly, either from the Fourier transforms of \(a_n(t)\), or by fitting Eq. (3) to the experimental \(a_n(t)\). Both methods yield the same result and as we already perform the fitting procedure to obtain the damping, we opt to use the latter method to determine the surface tension. For pure water we obtain the mode coefficients shown in Fig. 5. The surface tension and viscosity that we find for a microliter drop (\(\sigma =72 \pm 1\) mN/m and \(\mu =1.1 \pm 0.2\) mPas) and a picoliter droplet (\(\sigma =73 \pm 2\) mN/m and \(\mu =1.0 \pm 0.5\) mPas) are both in good agreement with the expected values, which are \(\sigma =72.8\) mN/m and \(\mu =1.0\) mPas.
5 Results
Graphs showing the oscillation modes \(n=2\) (blue markers), \(n=3\) (green markers) and \(n=4\) (red markers) for pure water drops of two different sizes. The gaps in the data are discarded frames due to reflections at the drop boundary, resulting in unreliable edge detection. The surface tension \(\sigma\) and viscosity \(\mu\) are calculated from the best fits of Eq. 3 (dashed lines in a and b). a The water drop (\(R_0 = 1.5\) mm) depicted in Fig. 2, \(\sigma =72 \pm 1\) mN/m and \(\mu =1.1 \pm 0.2\) mPas. b An inkjet-printed water droplet (\(R_0=32\) \(\upmu \hbox {m}\)), \(\sigma =73 \pm 2\) mN/m and \(\mu =1.0 \pm 0.5\) mPas. c The residues of the oscillation modes in a and their best fit of Eq. (3). d The residues of the oscillation modes in b and their best fit of Eq. (3)
By adding the SDS as a surfactant solution, it is expected that there will be an influence of surface age on the surface tension and indeed Fig. 6a, b confirm this hypothesis. The surface tension of the microliter droplet (\(\sigma = 35 \pm 1\) mN/m) is much lower than that of the inkjet-printed picoliter droplet (\(\sigma = 63 \pm 1\) mN/m). The analysis shows that the surface tension remains constant in the analyzed range for both the microliter and picoliter droplets. In the case of the microliter droplet, the surfactant concentration at the liquid–air interface has reached an equilibrium before the droplet detached, while 150 \(\upmu \hbox {s}\) is apparently not enough time for the SDS molecules to significantly lower the surface tension of the freshly formed picoliter droplet.
Another interesting observation is that the measured viscosity of the large drop (\(\mu = 1.8 \pm 0.4\) mPas) is higher than that of the inkjet-printed drop (\(\mu = 1.0 \pm 0.2\) mPas), while the liquid is identical. We attribute this to the presence of adsorbed surfactant molecules at the interface. When the droplet is oscillating, the local surfactant concentration changes due to expansion and compression of the droplet surface. The resulting surface tension gradient gives rise to a redistribution of surfactant molecules over the droplet interface, which counteracts the droplet deformation. This additional resistance to deformation of the droplet increases the decay rate of the oscillation amplitude (Lu and Apfel 1991; Tian et al. 1995). This effect of surfactants is usually called the Gibbs elasticity, and its influence on the oscillation frequency and damping rate has been reported before for oscillating mm-sized droplets of surfactant solutions (Tian et al. 1997). Since the oscillation of the mm-sized SDS droplet is damped by the dynamic viscosity of the liquid and the surface viscosity caused by the surfactant, the value of \(\mu\) that we found from Eq. (5) does not represent the dynamic viscosity. In the case of \(\upmu \hbox {m}\)-sized droplets, we do not observe the effect of the Gibbs elasticity, because in this case fewer surfactant molecules are adsorbed at the liquid–air interface as shown by the much higher surface tension of 63 Nm/m. Therefore, the surface tension gradient due to droplet deformation is small.
Graphs showing the oscillation modes \(n=2\) (blue markers), \(n=3\) (green markers) and \(n=4\) (red markers) for drops of the SDS solution of two different sizes. The surface tension \(\sigma\) and viscosity \(\mu\) are calculated from the best fits of Eq. 3 (dashed lines in a and b). a A drop of the SDS solution (\(R_0 = 1.2\) mm), \(\sigma =35 \pm 1\) mN/m and \(\mu =1.8 \pm 0.4\) mPas. B An inkjet-printed SDS solution droplet (\(R_0 = 34\) \(\upmu \hbox {m}\)), \(\sigma = 63 \pm 1\) mN/m and \(\mu = 1.0 \pm 0.2\) mPas. c The residues of the oscillation modes in a and their best fit of Eq. 3. d The residues of the oscillation modes in b and their best fit of Eq. 3
The other surfactant that we studied, 1,2-hexanediol, is used in inks for inkjet printers, yet the influence of the surface age on the fluid properties of the HD solution is not known a priori. Although 1,2-hexanediol has surfactant-like properties due to its structure (Romero et al. 2007), the dynamic surface tension of a dilute HD solution has not been reported to our knowledge. Our experiments show that there is a significant effect of surface age on both the surface tension and the viscosity: The surface tension decreases from \(64 \pm 1\) mN/m for the \(\upmu \hbox {m}\)-sized droplet (surface age between \(\approx 200\) \(\upmu \hbox {s}\) and 10 ms) to \(58 \pm 1\) mN/m for the mm-sized droplet (surface age of \(\approx \,5\) s), and the viscosity increases from \(1.1 \pm 0.2\) mPas (\(\upmu \hbox {m}\)-sized droplet) to \(1.5 \pm 0.2\) mPas (mm-sized droplet). The surface age of the \(\upmu \hbox {m}\)-sized droplet is not known exactly because the liquid–air interface in the nozzle (i.e., the meniscus) is not a fresh interface at the moment a jet is ejected from the printhead. The surfactant concentration on the surface before droplet generation is determined by the jetting frequency, which in this experiment was 100 Hz, setting the upper bound of the surface age of the droplet. The lower bound of the surface age is set by the droplet formation time, which in this case was approximately 200 \(\upmu \hbox {s}\).
We have performed dynamic surface tension measurements of the very same HD solution using the maximum bubble pressure method (SITA online t60, SITA Messtechnik GmbH) and, as is seen in Fig. 7, both the surface tension measured from droplet oscillations at the longer timescale and the trend that a fresher surface has a higher surface tension are in agreement with the MBPM measurements (blue crosses).
Dynamic surface tension of the HD solution. The red circles give the values found from droplet oscillations, the blue crosses are the MBPM measurements, and the black dotted line is the best fit of Eq. (6) to the MBPM data with \(\sigma _{0}=72.8\) mN/m
We compare the values of the surface tension that we found from droplet oscillations to the empirical formula which was successfully used to describe the dynamic surface tension of various types of surfactant solutions (Hua and Rosen 1988; Gao and Rosen 1995)
in which \(\tau\) and k are fitting parameters, \(\sigma _0\) is the surface tension of a freshly formed interface at \(t=0\), and \(\sigma _{\mathrm{{eq}}}\) is the equilibrium surface tension. The surface tension of a freshly formed interface is equal to that of the solvent, so with \(\sigma _{0}=72.8\) mN/m we fit Eq. (6) to the MBPM data to find \(\sigma _{\mathrm{{eq}}} = 57.6\) mN/m, \(\tau =2.1\) ms, and \(k = 0.77\), see the black dotted line in Fig. 7. As is seen in Fig. 7, the values of the surface tension that were measured from the shape oscillations of both the mm- and \(\upmu \hbox {m}\)-sized droplets agree with this model, within the experimental uncertainty. A printhead with a higher jetting frequency is needed to reduce the uncertainty in the surface age, and this remains a topic for future research.
6 Conclusions
In conclusion, we have developed a technique based on the stroboscopic imaging of the shape oscillation of inkjet-printed droplets to measure in-line the surface tension and viscosity of a liquid during the process of inkjet printing. With this technique, we show that the surface tension of an ink that contains surfactants right after droplet formation is significantly higher compared to the equilibrium value. We attribute this to the surfactant adsorption process, which needs more time to reach an equilibrium than the droplet is in flight. On the other hand, the viscosity of the same surfactant solution is lower during droplet formation than it is when the surface is fully covered with surfactant molecules. We attribute this to the high surface coverage of surfactant molecules, which is accompanied by an increased resistance to interfacial deformation of the droplet due to the Gibbs elasticity.
References
Brenn G, Frohn A (1993) An experimental method for the investigation of droplet oscillations in a gaseous medium. Exp Fluids 15(2):85
Brenn G, Teichtmeister S (2013) Linear shape oscillations and polymeric time scales of viscoelastic drops. J Fluid Mech 733:504
Brennen CE (1995) Cavitation and bubble dynamics. Oxford University Press, Oxford
Chandrasekhar S (1959) The oscillations of a viscous liquid globe. Proc Lond Math Soc 3(1):141
Chang CH, Franses EI (1995) Adsorption dynamics of surfactants at the air/water interface: a critical review of mathematical models, data, and mechanisms. Colloid Surface A 100:1
Eastoe J, Dalton JS (2000) Dynamic surface tension and adsorption mechanisms of surfactants at the air-water interface. Adv Colloid Interface Sci 85:103
Ferri JK, Stebe KJ (2000) Which surfactants reduce surface tension faster? A scaling argument for diffusion-controlled adsorption. Adv Colloid Interface Sci 85(1):61
Franses EI, Basaran OA, Chang CH (1996) Techniques to measure dynamic surface tension. Curr Opin Colloid Interface 1(2):296
Gao T, Rosen MJ (1995) Dynamic surface tension of aqueous surfactant solutions. J Colloid Interface Sci 172(1):242
González H, García FJ (2009) The measurement of growth rates in capillary jets. J Fluid Mech 619:179
Grinfeld P (2012) Small oscillations of a soap bubble. Stud Appl Math 128(1):30
Holt RG, Tian Y, Jankovsky J, Apfel RE (1997) Surface-controlled drop oscillations in space. J Acoust Soc Am 102(6):3802
Hua XY, Rosen MJ (1988) Dynamic surface tension of aqueous surfactant solutions: I. basic paremeters. J Colloid Interface Sci 124(2):652
Kornek U, Müller F, Harth K, Hahn A, Ganesan S, Tobiska L, Stannarius R (2010) Oscillations of soap bubbles. New J Phys 12(7):073031
Lamb H (1881) On the oscillations of a viscous spheroid. Proc Lond Math Soc 1(1):51
Lamb H (1932) Hydrodynamics. Cambridge University Press, Cambridge
Leighton TG (1994) The acoustic bubble. Academic, London
Loshak J, Byers CH (1973) Forced oscillations of drops in a viscous medium. Chem Eng Sci 28(1):149
Lu HL, Apfel RE (1991) Shape oscillations of drops in the presence of surfactants. J Fluid Mech 222:351
Miller CA, Scriven LE (1968) The oscillations of a fluid droplet immersed in another fluid. J Fluid Mech 32(3):417
Ohl CD, Tijink A, Prosperetti A (2003) The added mass of an expanding bubble. J Fluid Mech 482:271
Prosperetti A (1980) Free oscillations of drops and bubbles: the initial-value problem. J Fluid Mech 100(2):333
Rayleigh L (1879) On the capillary phenomena of jets. Proc Royal Soc Lond 29(196–199):71
Reid WH (1959) The oscillations of a viscous liquid globe with a core. Proc Lond Math Soc 3(3):388
Romero CM, Páez MS, Miranda JA, Hernández DJ, Oviedo LE (2007) Effect of temperature on the surface tension of diluted aqueous solutions of 1,2-hexanediol, 1,5-hexanediol, 1,6-hexanediol and 2,5-hexanediol. Fluid Phase Equilib 258(1):67
Ronay M (1978a) Determination of the dynamic surface tension of inks from the capillary instability of jets. J Colloid Interface Sci 66(1):55
Ronay M (1978b) Determination of the dynamic surface tension of liquids from the instability of excited capillary jets and from the oscillation frequency of drops issued from such jets. Proc Royal Soc Lond A 361:181
Staat HJJ, Wijshoff H, Versluis M, Lohse D (2016) In preparation
Stückrad B, Hiller WJ, Kowalewski TA (1993) Measurement of dynamic surface-tension by the oscillating droplet method. Exp Fluids 15(4–5):332
Thoraval MJ, Takehara K, Etoh T, Thoroddsen S (2013) Drop impact entrapment of bubble rings. J Fluid Mech 724:234
Tian Y, Holt RG, Apfel RE (1995) Investigations of liquid surface rheology of surfactant solutions by droplet shape oscillations: theory. Phys Fluids 7(12):2938
Tian Y, Holt RG, Apfel RE (1997) Investigation of liquid surface rheology of surfactant solutions by droplet shape oscillations: experiments. J Colloid Interface Sci 187(1):1
van der Bos A, van der Meulen MJ, Driessen T, van den Berg M, Reinten H, Wijshoff H, Versluis M, Lohse D (2014) Velocity profile inside piezoacoustic inkjet droplets in flight: comparison between experiment and numerical simulation. Phys Rev Appl 1(1):014004
van der Bos A, Zijlstra A, Gelderblom E, Versluis M (2011) iLIF: illumination by Laser-Induced Fluorescence for single flash imaging on a nanoseconds timescale. Exp Fluids 51(5):1283
Versluis M (2013) High-speed imaging in fluids. Exp Fluids 54(2):1458
Versluis M, Goertz D, Palanchon P, Heitman I, van der Meer S, Dollet B, de Jong N, Lohse D (2010) Microbubble shape oscillations excited through ultrasonic parametric driving. Phys Rev E 82(2):026321
Wang TG, Anilkumar AV, Lee CP (2006) Oscillations of liquid drops: results from USML-1 experiments in space. J Fluid Mech 308:1
Weber RJK, Benmore CJ, Tumber SK, Tailor AN, Rey CA, Taylor LS, Byrn SR (2012) Acoustic levitation: recent developments and emerging opportunities in biomaterials research. Eur Biophys J 41(4):397
Weiser MAH, Apfel RE (1982) Extension of acoustic levitation to include the study of micron-size particles in a more compressible host liquid. J Acoust Soc Am 71(5):1261
Wijshoff H (2010) The dynamics of the piezo inkjet printhead operation. Phys Rep 491(4):77
Yamada T, Sakai K (2012) Observation of collision and oscillation of microdroplets with extremely large shear deformation. Phys Fluids 24(2):022103
Yang L, Kazmierski BK, Hoath SD, Jung S, Hsiao WK, Wang Y, Berson A, Harlen O, Kapur N, Bain CD (2014) Determination of dynamic surface tension and viscosity of non-Newtonian fluids from drop oscillations. Phys Fluids 26(11):113103
Acknowledgements
The authors would like to thank Eek Huisman for help with the MBPM measurements. This work is supported by NanoNextNL, a micro- and nanotechnology consortium of the Government of the Netherlands and 130 partners (Project No. 10B.07).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Staat, H.J.J., van der Bos, A., van den Berg, M. et al. Ultrafast imaging method to measure surface tension and viscosity of inkjet-printed droplets in flight. Exp Fluids 58, 2 (2017). https://doi.org/10.1007/s00348-016-2284-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-016-2284-8