Abstract
To take full advantage of recombinant Pichia pastoris (Komagataella phaffii) as a production system for heterologous proteins, the complex protein secretory process should be understood and optimised by circumventing bottlenecks. Typically, little or no attention has been paid to the fate of newly synthesised protein inside the cell, or its passage through the secretory pathway, and only the secreted product is measured. However, the system’s productivity (i.e. specific production rate qp), includes productivity of secreted (qp,extra) plus intracellularly accumulated (qp,intra) protein. In bioreactor cultivations with P. pastoris producing penicillin G acylase, we studied the dynamics of product formation, i.e. both the specific product secretion (qp,extra) and product retention (qp,intra) as functions of time, as well as the kinetics, i.e. productivity in relation to specific growth rate (μ). Within the time course, we distinguished (I) an initial phase with constant productivities, where the majority of product accumulated inside the cells, and qp,extra, which depended on μ in a bell-shaped manner; (II) a transition phase, in which intracellular product accumulation reached a maximum and productivities (intracellular, extracellular, overall) were changing; (III) a new phase with constant productivities, where secretion prevailed over intracellular accumulation, qp,extra was linearly related to μ and was up to three times higher than in initial phase (I), while qp,intra decreased 4–6-fold. We show that stress caused by heterologous protein production induces cellular imbalance leading to a secretory bottleneck that ultimately reaches equilibrium. This understanding may help to develop cultivation strategies for improving protein secretion from P. pastoris.
Key Points • A novel concept for industrial bioprocess development. • A Relationship between biomass growth and product formation in P. pastoris. • A Three (3) phases of protein production/secretion controlled by the AOX1-promoter. • A Proof of concept in production of industrially relevant penicillin G acylase. |
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Pichia pastoris (Komagataella phaffii) is one of the most effective and versatile host systems for the production of heterologous proteins. It has already been used for the production of more than five hundred different proteins, and the number is expected to increase (Baghban et al. 2019; Juturu and Wu 2018). This organism is advantageous compared to other yeast systems, especially through its ability to secrete a high-quality protein product with a lower basal secretion of its own proteins (Delic et al. 2013). Thus, downstream processing is reduced, having a substantial and beneficial impact on manufacturing costs.
Despite this growing acceptance and many successful applications, production of some recombinant proteins by this host has been hindered by several intracellular processes, where protein secretion ranks among the most commonly encountered bottlenecks (Delic et al. 2013). Expression strategies typically rely on the conventional methanol-inducible alcohol oxidase 1 promoter, pAOX1 (Vogl and Glieder 2013). Even though high titres are recorded occasionally when employing pAOX1 (Barrigon et al. 2015), generally the levels of gene expression and protein production are relatively poor, despite the evident strength of this promoter (Edwards-Jones et al. 2015). Moreover, secretion levels of proteins, whose genes are expressed from the pAOX1 promoter, are highly variable between different types of products. Detailed studies dealing with descriptions of the kinetics of product formation (i.e. specific productivity in relation to specific growth rate qp(μ)), reflecting an equilibrium between various steps involved in protein secretion, have already appeared (Barrigon et al. 2015; Looser et al. 2017; Raschmanova et al. 2018). A detailed description of dynamic changes in specific production and secretion rates during the cultivation time course qp(t) is however, still in demand.
It has been proven that production of more complex proteins, especially those of bacterial origin (Ahmad et al. 2014; Hesketh et al. 2013; Puxbaum et al. 2015), is hindered by the limited capacity of Pichia’s secretory machinery. To improve productivity of bioprocesses, discovering a physiological explanation for these secretion bottlenecks is of immense importance. Greatly improved efficiency in the development of new bioprocesses is expected when factors requiring investigation are reduced (Doran 1995; Reichelt et al. 2017).
Development of an efficient process for industrial production of penicillin G acylase (PGA) would be of great relevance, since this enzyme is used for kinetically controlled and environmentally friendly synthesis of β-lactam antibiotics (Srirangan et al. 2013). In addition, there is an emerging interest in leveraging the intrinsic versatility of this enzyme for multiple organic syntheses; the demand for PGA at an affordable price is growing rapidly (Grulich et al. 2013; Maresova et al. 2014). So far, PGA has not yet been produced efficiently by either Saccharomyces cerevisiae (Ljubijankic et al. 2002) or P. pastoris (Maresova et al. 2010; Senerovic et al. 2006; Sevo et al. 2002). Previous studies with P. pastoris strain X33 producing penicillin G acylase from Achromobacter sp. (ENS strain) showed that production of this enzyme in yeast hosts was significantly hindered and that the titres obtained were not satisfactory from an economic point of view (Ljubijankic et al. 2002; Maresova et al. 2010; Maresova et al. 2017; Senerovic et al. 2006). The majority of the enzyme produced remained inside the cells, while only a small proportion was secreted. Therefore, an in-depth description of secretion dynamics of PGA under different growth conditions, as well as a description of the associated physiological responses are imperative to overcome secretion bottlenecks, and thus to improve the efficiency of biotechnological production of PGA with P. pastoris.
In the present study, we quantified the time-dependent specific rate of PGA secretion from recombinant P. pastoris and its interdependence with intracellular PGA retention and biomass growth. The aim was to establish a general basis for the development of effective bioprocess strategies for Pichia-based protein production systems.
Material and methods
Strain
The recombinant strain P. pastoris X33 pENS2 (ENS) (Mut+ phenotype) producing penicillin G acylase (PGA; EC 3.5.1.11) from Achromobacter sp. was used in this study. Construction of the strain is described by Maresova et al. (2017). Briefly, plasmid pENS2, based on the vector pPICZαA (Invitrogen, CA, USA), contained a codon-optimised pga gene fused to the α-mating factor leader signal sequence from S. cerevisiae under the control of the pAOX1 promoter. The linearized plasmid was integrated into the AOX1 locus of P. pastoris X33. The gene encoding PGA was codon optimised and synthesised by GeneCust, Luxembourg. The strain has been deposited in the strain collection of the Institute of Microbiology of the Czech Academy of Sciences (Laboratory of Enzyme Technology) under the strain code ENS2.
Culture media
Pre-cultures were cultivated in buffered glycerol complex medium: 10 g glycerol, 10 g yeast extract, 20 g peptone, 100 mM potassium phosphate buffer (pH 6.0), 13.4 g yeast nitrogen base without amino acids and 0.4 mg biotin l−1. The inoculum and cultivation medium for bioreactor cultivations was adapted from (Hellwig et al. 2001). Defined mineral medium contained 2.86 g K2SO4, 0.17 g CaSO4·2H2O, 0.64 g KOH, 2.3 g MgSO4·7H2O, 0.2 g EDTA, 7.23 g H3PO4, 0.1 ml of polypropylene glycol, and, added separately, 4.35 ml of filter-sterilised PTM1 solution l−1 and 0.87 mg of biotin l−1. The PTM1 stock solution consisted of 5.0 ml of 69 % H2SO4, 3.84 g CuSO4, 0.08 g NaI, 3.0 g MnSO4·H2O, 0.2 g Na2MoO4·2H2O, 0.02 g H3BO3, 0.92 g CoCl2·6H2O, 20.0 g ZnCl2 and 65.0 g FeSO4·7H2O l−1. Batch cultures were typically performed at ≤ 30 g of glycerol l−1. The feed solution for fedbatch cultures contained 588 g of glycerol, 2.4 mg of biotin and 12 ml of PTM1 solution kg−1, or 792 g of methanol 2.4 mg of biotin and 12 ml of PTM1 solution kg−1, respectively. All chemicals used were of puriss grade p.a., purchased from Sigma-Aldrich (Switzerland), unless otherwise stated. Glycerol was purchased from Hänseler AG (Herisau, Switzerland).
Bioreactor cultivations
The fedbatch process comprised a phase of biomass growth in both batch and fedbatch modes and a production phase in fedbatch mode (see Table 1 for parameters’ nomenclature). The cultivation protocol was described previously (Hyka et al. 2010; Looser et al. 2017). All cultivations were performed at 30 °C, pH of 5.5, 3 l (l−1) min−1 aeration, and 1100 rpm agitation; for detailed description see Table S1. The process was initiated with a batch culture of 6-l working volume, containing 30 g of glycerol per litre. At the point of substrate depletion, the exponentially increasing feed of glycerol was initiated (growth fedbatch). A methanol feed was exponentially added during the subsequent production phase (production fedbatch). Feed rates, in g l−1 supporting a desired constant specific growth rate, were calculated based on equation 1. The value of initial feed rate F0 (equation 2) is given by the desired specific growth rate (μset), maximum biomass to substrate yield (Yx/s), specific maintenance rate of substrate per gram of biomass per hour (ms), initial concentration of cell dry weight (cdw) in gram per litre (x0) multiplied by the initial volume in litre (V0) and the mass fraction of substrate in the feed solution (win).
Samples from the bioreactor were taken every four (4) hours during the production phase and immediately centrifuged, analysed or cryopreserved. Data on the secretion of PGA in cultivation ENS-D (from the 50th hour onwards) were biased by the post harvesting treatment. Therefore, to avoid potential conflicts in the results, we decided not to consider these data.
Online analyses in bioreactors
The relative partial pressure of oxygen (pO2) in the medium, concentrations of both CO2 and O2 in the exhaust gas (extended process gas analyser; Biospectra AG, Schlieren, Switzerland), pH, temperature, reactor overpressure and reactor weight were all monitored online during bioreactor cultivations.
Gravimetric determination of biomass concentration
To determine the cell dry weight (cdw), 2 ml of the culture broth were transferred into a previously tared Eppendorf microtube (previously dried at 105 °C for ≥ 48 h) and centrifuged (4 °C, 12000 rpm, 5 min). The pellet was then washed with deionised water and was dried (48 h, 105 °C; Heraeus Instruments, Zurich, Switzerland) and weighed. All measurements of biomass were performed in duplicates.
Substrate and metabolite concentrations
The concentration of glucose, methanol and ethanol were determined by high-pressure liquid chromatography (HPLC) using an LC-20AB device equipped with a SIL-20A autosampler, CTO-20A thermostated column oven and RID-10A refractometer detector (Shimadzu). The Aminex HPX-87H column, with an inside diameter (i.d.) of 300 by 7.8 mm (Bio-Rad, Munich, Germany), was run at 40 °C, with a flow rate of 0.6 ml min−1 under isocratic conditions, with 2.5 mM H2SO4 and an injection volume of 25 μl; performed by the ZHAW analytical laboratory (Wädenswil, Switzerland).
DNA concentration in supernatant
Ten microlitres of the culture supernatant were mixed with 2 μl of 100× SYBR Green (Thermo Fisher Scientific, MA, USA) and 188 μl of TE buffer (10 mM Tris HCl, 1 mM EDTA, pH 8). Fluorescence of the samples was measured using a DTX 880 Multimode Detector with Multimode Analysis software (Beckman Coulter, CA, USA) at an excitation wavelength of 485 nm and an emission wavelength of 535 nm.
Penicillin G acylase activity assay
The biomass and supernatant of a culture were separated by centrifugation (4 °C, 5000 rpm, 8 min). The pellet was rinsed with 0.1 M sodium phosphate buffer pH 8.0 (SPB), frozen at − 80 °C for 2 h, resuspended in the original sampling volume with SPB, and cells were disrupted by glass beads (diameter 0.5 mm, Willy A. Bachofen AG. Basel, Switzerland). Cell debris was removed by centrifugation and the activity of PGA was measured in the supernatant. Separated culture supernatant was supplemented with SPB to the original sampling volume.
The activity of PGA was assayed in SPB supplemented with penicillin G (2% solution) using the method described in (Balasingham et al. 1972). The activity of one unit (U) is defined as the amount of PGA producing 1 μM of 6-aminopenicillanic acid min−1 at 37 °C. The activity was determined both in the cells (retained PGA) and in the supernatant (secreted PGA) using the described method, and the activities measured in the supernatant were corrected for the whole culture broth volume (Looser et al. 2015).
Data verification and fitting
For cultivation phases with a constant specific growth rate (which was controlled by an exponentially increasing substrate feed rate), integral values of specific growth rate and yield coefficients were estimated by linear regression. Specific product formation rate was calculated by multiplication of product-to-biomass yield by the corresponding specific growth rate.
In addition, all specific rates were computed using data interpolated into the off-line measurements. Using the calculated μ value, the theoretical biomass (x·V) at time t was determined according to equation 3.
The values of the theoretical biomass were compared to the measured values, and deviations between the measured and theoretical values did not exceed ± 10%.
Mathematical fitting
To describe PGA production as a function of time and biomass growth, a descriptive mathematical model was proposed and used to calculate the specific rate of product formation (qp) over the time course of the cultivation. The general trend of qp development over production time, which was observed in all cultivation processes, is schematically displayed in Fig. 1. From the experimental data, we determined the time range over which the shift in productivity occurred. This shift was characterised by the time point tk, which represents the time when qp equalled 0.5 Δqp. For the pre- and post-tk periods separately, Pearson product moment correlation coefficients were calculated through data points of total biomass and respective total product. Point tx, where the maximal R2 was determined as the point with the highest qp of the respective period, was calculated according to equation 4, where cp·V is the totally formed product. Using equation 4qp,max of the pre- tk period and qp,min of the post-tk period were calculated.
The qp at a given time point was modelled by a modified Weibull function (equation 5).
Here, α and β are constraints to be chosen such that the observed experimental product profile in fedbatch culture was closely approximated by numerical integration of the Luedeking–Piret equations (equations 6 and 7).
Coefficient m represents the slope of the qp time course at time point tk (Fig.1). m and tk were optimised for each process by the Solver-function of MS Excel in order to minimise the deviation between measured and simulated (cp·V) values.
The descriptive model developed was used to recreate the specific product formation rate of total enzyme produced (qp,total) and the fraction of enzyme retained inside the cell (qp,intra). The values for the specific rate of product secretion (qp,extra) were obtained by subtracting qp,intra from qp,total.
The adequacy of this model was determined by optimality criteria, i.e. by evaluating the closeness of fit, the residual sum of squares and consequently by the coefficient of determination (R2) and average deviation (Table S2). A p value lower than 0.05 was considered statistically significant. The R2 was above 0.98 for all data tested (Table S2), indicating that more than 98 % of the total variation could be described by the mathematical model. The calculated data were therefore well matched with the experimental data.
All correlation coefficients, R2 and p values were calculated using the analysis of variance (ANOVA) test (MS Excel software).
Results
Based on our experiments and previous results (Maresova et al. 2017), we observed that the PGA produced in P. pastoris (measured in enzyme activity units, U) was not secreted as intended; the majority of the enzyme was retained within the cells. The total enzyme produced was divided into two fractions that were measured separately: titre of enzyme secreted into the culture medium cp,extra (U l-1) and titre retained within the cells cp,intra (U l-1).
The specific rate of total product formation qp,total (U (gcdw)-1 h-1) was quantified as the amount of total active enzyme (i.e. intracellular plus secreted) produced per gram of cell dry weight (cdw) per hour. Using the same logic, qp,total was divided into the specific rate of product secretion qp,extra (U (gcdw)-1 h-1) (calculated from the enzyme concentration (titre) measured in the cultivation medium), and the specific rate of product retention within the cells qp,intra (U (gcdw)-1 h-1) (calculated from the enzyme concentration (titre) measured inside the cells) (Fig. 2). This result section refers only to the production phase of the performed processes and time 0 denotes the start of this phase (initiation of the methanol feed).
Quantification of intra- and extracellular recombinant protein. Recombinant protein (dark grey circles) folding and maturation takes place in the endoplasmic reticulum. Mature protein is then translocated into the Golgi apparatus and subsequently encapsulated in vesicles and secreted to the extracellular environment. Concentrations of the enzyme inside the cells cp,intra (U l−1) and in the supernatant cp,extra (U l−1) are quantified as enzyme activity per litre of culture volume. Specific rate of intracellular retention qp,intra (U (gcdw)−1 h−1) represents the activity of product per gram cdw per hour that is retained within the maturation and secretory machinery inside the cell. The specific rate qp,extra (U (gcdw)−1 h−1) corresponds to the activity of secreted product (extracellular enzyme) per gram of cdw per hour
Specific growth and production rates in fedbacth cultivation
To study PGA formation, five fedbatch cultures were performed using strain ENS (Table S1) with minimal, chemically well-defined medium at different set points determining different specific growth rates (μset) during the production phase. Both the evolution of specific productivity (qp) during the time course of cultivation and the relationship between production and growth were studied in detail.
The product formation kinetics of pAOX1-controlled protein production is usually bell-shaped, with an optimum specific growth rate with methanol (typically 10–25% of the maximum specific growth rate with methanol) that results in the highest specific productivity (Looser et al. 2015). Therefore, cultivations in the present study were performed at different specific growth rates μset, namely 7.3%, 11.5%, 15.4%, 17.5%, and 23% of μmax (cultivations ENS-A, B, C, D, E), which were maintained by exponentially increasing feeding of methanol.
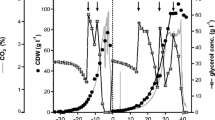
In order to study the evolution of qp over the time course of cultivation, the qp values were calculated with the descriptive mathematical tool, using theoretical values of PGA activity, and were plotted against time in order to visualise separately the time-dependent development of qp,total, qp,intra, qp,extra. The graphical validation of the mathematical data can be seen in Fig. 3a, where measured and calculated theoretical values of PGA activities were compared (process ENS-C was taken as an example, for comparison of all processes; see Figure S1).
Time course of PGA production with distinguished phases with respect to qp. The displayed data were acquired in the cultivation ENS-C and represent the typically observed trend in PGA formation in all cultivations enlisted within this work. a Amount of PGA (in kU) during the production phase of cultivation. The symbols represent measured enzyme: crossed squares, total amount; full squares, intracellular amount; empty squares, extracellular amount. The solid lines represent the calculated theoretical values for the respective measured enzyme (kU). b The coloured lines marked by respective square symbols represent calculated qp(t) values: green (crossed squares)—qp,total, blue (full squares)—qp,intra, red (empty squares)—qp,extra (U (gcdw)−1 h−1). The black bold line represents the time development of intracellular PGA activity per gram cdw (U (gcdw)−1), which indicates the saturation of the cell with product. The time course of the specific production rate of PGA qp(t) was divided into three phases as indicated by the vertical dotted lines: initial, transition and saturation phase. Production time 0 indicates the time, from which methanol was fed
Changes in specific rate of PGA production over time
In all cultivations, the following three phases of the qp(t) dependency were distinguished (Fig. 3b):
Initial phase (I): The first steady phase in which the specific rate of total product formation, qp,total, was maximal and remained unchanged. Specific rates of product secretion qp,extra and product retention qp,intra did not change significantly. The amount of intracellular PGA produced per gram of biomass (U (gcdw)−1) increased sharply from the beginning of the production phase.
Transition phase (II): In this dynamic phase, qp,total decreased. The intracellular enzyme produced per gram of biomass (cp, intra per biomass; U (gcdw) −1) stabilised and its maximum was reached towards the end of this phase. qp,intra decreased considerably, forming a sigmoidal curve, and qp,extra temporarily increased and then partially decreased to reach a new steady state in the saturation phase.
Saturation phase (III): The second equilibrium phase, in which the specific production rates reached a new steady state; qp,total and qp,intra were at their lowest, whereas a higher stable qp,extra was achieved than in the phase (I).
In each cultivation, the specific growth rate of biomass was maintained at a constant value by exponentially increasing the methanol feed (Table 2); therefore, changes in specific productivity rates within one process were independent of changes in growth.
Active enzyme (penicillin G acylase) retained inside the cells
For each cultivation, the average specific rate of product retention qp,intra was calculated from the steady-state initial and saturation phases (Fig. 4b).
Initial phase: The specific rate of protein retention did not differ significantly between cultivations with different μset (Fig. 4b). The average calculated value for ENS-B to ENS-E equalled (2.68 ± 0.18) U (gcdw)−1 h−1. The exception from the described trend was observed in culture ENS-A growing with a μ of 0.0031 h−1, where the specific product retention rate was lower, reaching a qp,intra of 1.74 U (gcdw)−1 h−1.
Transition phase: The maximum saturation of cells with active enzyme was highly dependent on the initial μset of the culture as it entered transition phase II. A strong negative correlation (R2 of 0.99) between the maximal intracellular concentration (U (gcdw) −1) and increasing μset was observed (Fig. 5). The maximal and minimal intracellular concentrations of active enzyme were measured for process ENS-B (μ = 11.4 % of μmax), equalling 122.06 U (gcdw) −1 and for process ENS-E (μ = 23% of μmax) equalling 97.86 U (gcdw)−1, respectively. The time points for maximal intracellular concentration and μset also followed the same negative correlation (R2 of 0.99). The faster the culture grew, the shorter the time needed to fully saturate the cells (Fig. 5). Culture ENS-E growing at 23% of μmax took 56 h to reach intracellular saturation, in comparison with culture ENS-B growing at 11.5% of μmax that took 106 h to reach this state, although the average number of generations until saturation was similar, in the range from 1.68 to 1.80 (values calculated using saturation time and specific growth rate of the culture).
Saturation phase: The specific productivity of intracellular protein was independent of the specific growth rate; all processes stabilised at a comparable rate equalling (0.558 ± 0.058) U (gcdw)−1 h−1 (Fig. 4).
Relationship between specific growth rate of biomass and the specific rates of product secretion and intracellular retention in different phases of the bioprocess a Specific rate of protein secretion (qp,extra, U (gcdw)−1 h−1) in initial phase (I) (full symbols) and saturation phase (III) (empty symbols) plotted against specific growth rate (μset). b Specific rate of intracellular protein retention (qp,intra, U (gcdw)−1 h−1) in initial phase (full symbols) and saturation phase (empty symbols) plotted against specific growth rate (μset). Error bars corresponds to calculated standard error. The grey lines approximate the underlying relationship. Not shown are data for PGA secretion from ENS-D cultivation (from the 50th hour onwards) since they were biased by the post-harvesting treatment
Relationship between saturation of the intracellular environment with PGA and biomass specific growth rate (ENS B-E) during transition phase (II). Full symbols represent the maximum (interpolated) value of the intracellular concentration of active PGA-enzyme per gram of biomass (U (gcdw)−1). Open symbols represent the time point (hours) corresponding to the maximum intracellular saturation relative to the start of induction by methanol, which was set to 0 h. Lines in grey, with 95% confidence bands (in black), were computed by linear regression
Secretion of active enzyme (penicillin G acylase)
For each process, the average specific secretion rate was calculated from two steady-state phases, initial and saturation (Fig. 4a). In practice however, we observed the following three phases:
Initial phase: The specific secretion rate qp,extra of the recombinant product (PGA) increased up to a μset 0.006–0.007 h−1 (14–16.3% of the μmax) and then decreased again. The association between product secretion and growth was described by a bell-shaped curve (Looser et al. 2015), and the highest measured qp,extra = 0.4746 U (gcdw) −1 h−1 was attained at μ 0.0066 h−1 (Fig. 4).
Transition phase: A temporary increase in extracellular productivity during the transition phase was observed (Fig. 3b). This was consistent with a temporary decrease in the level of intracellular PGA protein (data not shown). Cell lysis (measured as the DNA concentration in the supernatant per gram cell dry weight) increased during the transition period, stabilising again in the last saturation phase; this suggests that the temporary increase in active enzyme in the supernatant was caused by cell lysis and release of intracellular enzyme (Figure S2). The proportion of lysed cells was below the detection limit for biomass measurement and we did not record any imbalance in growth characteristics of the culture.
Saturation phase: the specific secretion rates of all processes were 2- to 3.1-fold higher than in the initial phase and the relationship between μ and qp,extra changed (Fig. 4a). The qp,extra and μset showed a direct correlation, with R2 of 0.95. The highest qp,extra was 0.9735 U (gcdw)−1 h−1 at μ 0.0099 h−1 (23% of μmax).
Discussion
Knowledge of product formation kinetics, i.e. the relationship between the specific rate of protein production and the specific growth rate of biomass, is imperative for bioprocess optimisation. Using a mathematical fitting for data analysis, formation kinetics of PGA in P. pastoris was investigated, with the focus on the kinetics of not only PGA secretion, but also its intracellular retention, which has not yet been described in the literature. As the methanol feed was successfully maintained in cultivations and the calculated μ remained stable, the specific rate of total product formation and the specific product secretion rate were expected to be constant throughout the cultivation, as described previously in the literature (Hang et al. 2008; Zhang et al. 2005). However, we observed a dramatic shift in the specific productivities of intracellular and extracellular active enzyme over the production phase in all cultivations with different μset. Generally, three main phases (Fig. 3) with respect to changes in specific productivities of secreted and intracellularly retained PGA were distinguished in each cultivation. In all cultivations, PGA also accumulated inside the cells to a maximum, when the cell machinery was likely saturated with active enzyme. We assume that enzyme retained inside the cells, both in this study and the study of Maresova et al. 2017, was localised exclusively within the secretory pathway compartments, as was proven in other studies for GFP (Love et al. 2012; Sjöblom et al. 2012). Our hypothesis is also supported by results of a study focused on the intracellular production of PGA in P. pastoris X33, as opposed to our “extracellular” production strategy, (Maresova et al. 2010); the intracellular concentration of active PGA did not reach the saturation maximum, but increased until the end of the cultivation, suggesting that the enzyme produced intracellularly was spread throughout the whole intracellular space.
In our work, both the value of the saturation maximum and the time needed to reach the maximum, were shown to decrease with increasing specific growth rate of biomass, meaning that faster growing cells became saturated in a shorter time and retained less intracellular enzyme than slower growing cells (Fig. 5). This might be explained by rapidly growing cells having a shorter time to adapt to increasing amounts of recombinant PGA produced, and therefore becoming saturated faster but to a lesser extent.
In the last saturation phase, i.e. after the point of saturation, the qp,intra decreased significantly (Fig. 3b). Since we did not observe any intracellular accumulation of unprocessed PGA (on SDS gels—data not shown), we suggest two possible explanations for the decrease in qp,intra. Elevated upregulation of the endoplasmic reticulum associated protein degradation (ERAD) pathway may have resulted in rapid degradation of the accumulated product. However, this is rather improbable since the upregulation of this pathway is mostly expected in the first phase of production (Aw and Polizzi 2013; Marsalek et al. 2019; Vogl et al. 2014). The more probable explanation is partial translational arrest, as previously described by Edwards-Jones et al. (2015). The most likely stress factor that could promote translational arrest is a nutritional imbalance, resulting from demands of cells undergoing nutritional limitation and synthesising high level of proteins, leading to a redox imbalance between the cytosol and mitochondria (Edwards-Jones et al. 2015). This state could cause a transient and selective translational arrest, which would significantly affect heterologous protein production. While producing lysozyme I56T, Hesketh et al. (2013) observed significant changes in the levels of transcripts predicted to encode proteins associated with mRNA processing and translation. This may reflect general changes in protein synthesis during recovery from cellular stress, as indicated by the down-regulation of genes associated with ribosome biogenesis (Hesketh et al. 2013). We assume that translational arrest may have helped to relieve the stress, facilitating restoration of the secretory pathway, but this may have also resulted in lower overall productivity of the system. Similarly, intracellular product saturation was described in the work of Barrigón et al. (2013) who suggested that there may be down-regulation of transcription in response to activation of the unfolded protein response pathway (UPR).
The μ-dependency of the specific rate of product secretion in the initial phase (I) was bell-shaped with μ (qp,max) being between 14 and 16.3% of the μmax (Fig. 4a). This is in agreement with previously published data for the pAOX1-based Pichia system (Looser et al. 2015). However, while this relationship is usually valid for the whole production phase (Looser et al. 2015), we observed this qp,extra (μ) relationship only for the initial phase. Then, intracellular saturation with active enzyme, and the physiological responses connected to this phenomenon probably had a serious impact on the secretory capacity of the cells and affected the qp,extra (μ) (Fig. 3b). Later in saturation phase (III), the relationship between qp,extra and μ was not bell-shaped anymore, but linear, and the specific rate of product secretion reached its maximum in this phase, assuming that the limit of the secretory machinery was also reached (Fig. 4a).
Rebnegger et al. (2014) described significant changes in the regulation of important groups of genes at high μ. Specifically, this involved upregulation of translational and UPR genes such as those involved in translocation of nascent proteins to the ER, enhancement of protein folding in the ER and the synthesis of cytosolic chaperones. High μ also led to the downregulation of genes involved in proteolytic degradation of proteins in the secretory pathway and exocytosis (Rebnegger et al. 2014). Such upregulation of genes at high μ could explain the linear relationship between qp,extra and μset observed in this work.
The pAOX1 induction system may generally be challenging because the methanol-induced start of protein production coincides with the extensive reorganisation of cellular metabolism, involving not only the synthesis of enzymes required for methanol catabolism but also a massive proliferation of peroxisomes (van der Klei et al. 2006), which likely drains the cellular resources. As a result, stress responses such as the UPR or ERAD may be significantly upregulated. It was demonstrated in the work of Hesketh et al. (2013) that lysozyme variant I56T invoked intracellular protein aggregation. This was followed by up/downregulation of transcription of genes involved in responses to intracellular stress. Several of these genes were also found to be antisense to genes associated with cell membrane biosynthesis and metabolism. This confirmed the inference from the “sense” transcriptome that overproduction of a misfolded protein has a significant impact on cell wall-associated processes and can therefore significantly affect the secretory abilities of the cell (Hesketh et al. 2013). Camara et al. (2017) supported those results; their observations showed the attenuation of methanol metabolism and peroxisome biogenesis in response to the presence of a recombinant production cassette in P. pastoris, which resulted in reduced secretion (Camara et al. 2017). Moreover, Love et al. (2012) showed that export of proteins from the endoplasmic reticulum appeared to be particularly difficult in the case of pAOX1-controlled expression. Their results indicated that there could be inefficient recycling of the protein export machinery in the presence of excess protein cargo. This phenomenon could be overturned by lowered overall metabolic load, caused by heterologous protein production of the system (Love et al. 2012).
The three phases that we distinguished in own data for PGA with respect to qp,extra (t) (Fig. 3) were also identified from literature data (Fig. 6) that describe the production and secretion of recombinant lipase by P. pastoris (Arnau et al. 2010; Barrigón et al. 2013; Resina et al. 2005; Sha et al. 2013). This comparison suggests that the qp,extra (t) dependency, might be generally valid for a wide spectrum of recombinant proteins produced by either Mut+ or MutsP. pastoris using different promoters, for which the utilisation of methanol is the connecting element. Processes shown in Fig. 6e and f confirm the increase in qp,extra, but the cultures may not have entered the third saturation phase, since the μ of the cultures was not stable at the late stages of the cultivation and therefore was cultivation possibly terminated before the last phase occurred. This demonstration using literature data should inspire further investigations of qp time courses, whereby data of suitable quality and from frequent sampling should be collected, appropriately interpolated and processed further.
Comparison of time courses of specific production rates (with respect to the extracellular product) for different lipases produced in both Mut+ and MutSP. pastoris strains, all being under the control of the pAOX1 promoter, with the exception of one under the pFLD1 promoter. Squares represent the time courses of qp,extra (U (gcdw)−1 h−1) as published by respective authors or calculated from their experimental data. The solid curves represent the data interpolation using equation 5. a Arnau et al. (2010): Mut+ phenotype, pAOX1 promoter, Rhizopus oryzae lipase (ROL) production; b Barrigón et al. (2013): Mut+ phenotype, pAOX1 promoter, ROL production; c Resina et al. (2005) A: Mut+ phenotype, pFLD1 promoter, ROL production; d Resina et al. (2005) B: Muts, phenotype, pAOX1 promoter, ROL production; e Sha et al. (2013) A: Muts, phenotype, pAOX1 promoter, Rhizopus chinensis lipase (r27RCL) production; f Sha et al. (2013) B: Mut phenotype, pAOX1 promoter, r27RCL production, co-expressed with secretion factors ERO1 and PDI
The key achievement in the study presented here is a description of the temporal change in the rate of specific product formation (qp) during the production phase of P. pastoris fedbatch cultivation, while producing PGA under the control of the AOX1 promoter. Our results indicate that initial product secretion is related, in a bell-shaped manner, to growth while after the transition period, the qp,extra (μ) relationship shifted towards a linear production kinetics, which is usually found for constitutive promoters (Fig. 4a). After the described shift, the specific secretion rate of the cells was up to three times higher in the later stages of cultivation. According to our results, a prospective procedure maximising the titres of the product should minimise the duration of the temporary initial phase (I) and maximise the productivity of the system in the saturation phase (III).
This study represents a significant contribution to our understanding of the dynamic changes in qp over time and, as such, may generate opportunities for expanding the biotechnological application potential of the Pichia-AOX1 system for difficult-to-produce products.
References
Ahmad M, Hirz M, Pichler H, Schwab H (2014) Protein expression in Pichia pastoris: recent achievements and perspectives for heterologous protein production. Appl Microbiol Biotechnol 98(12):5301–5317. https://doi.org/10.1007/s00253-014-5732-5
Arnau C, Ramon R, Casas C, Valero F (2010) Optimization of the heterologous production of a Rhizopus oryzae lipase in Pichia pastoris system using mixed substrates on controlled fed-batch bioprocess. Enzym Microb Technol 46(6):494–500. https://doi.org/10.1016/j.enzmictec.2010.01.005
Aw R, Polizzi KM (2013) Can too many copies spoil the broth? Microb Cell Factories 12:128. https://doi.org/10.1186/1475-2859-12-128
Baghban R, Farajnia S, Rajabibazl M, Ghasemi Y, Mafi A, Hoseinpoor R, Rahbarnia L, Aria M (2019) Yeast expression systems: overview and recent advances. Mol Biotechnol 61(5):365–384. https://doi.org/10.1007/s12033-019-00164-8
Balasingham K, Warburton D, Dunnill P, Lilly MD (1972) The isolation and kinetics of penicillin amidase from Escherichia coli. Biochim Biophys Acta 276(1):250–256. https://doi.org/10.1016/0005-2744(72)90027-7
Barrigón JM, Montesinos JL, Valero F (2013) Searching the best operational strategies for Rhizopus oryzae lipase production in Pichia pastoris Mut + phenotype: methanol limited or methanol non-limited fed-batch cultures? Biochem Eng J 75(Supplement C):47–54. https://doi.org/10.1016/j.bej.2013.03.018
Barrigon JM, Valero F, Montesinos JL (2015) A macrokinetic model-based comparative meta-analysis of recombinant protein production by Pichia pastoris under AOX1 promoter. Biotechnol Bioeng 112(6):1132–1145. https://doi.org/10.1002/bit.25518
Camara E, Landes N, Albiol J, Gasser B, Mattanovich D, Ferrer P (2017) Increased dosage of AOX1 promoter-regulated expression cassettes leads to transcription attenuation of the methanol metabolism in Pichia pastoris. Sci Rep 7:44302. https://doi.org/10.1038/srep44302
Delic M, Valli M, Graf AB, Pfeffer M, Mattanovich D, Gasser B (2013) The secretory pathway: exploring yeast diversity. FEMS Microbiol Rev 37(6):872–914. https://doi.org/10.1111/1574-6976.12020
Doran PM (1995) 13 - Reactor engineering bioprocess engineering principles. Academic Press, London, pp 333–391
Edwards-Jones B, Aw R, Barton GR, Tredwell GD, Bundy JG, Leak DJ (2015) Translational arrest due to cytoplasmic redox stress delays adaptation to growth on methanol and heterologous protein expression in a typical fed-batch culture of Pichia pastoris. PLoS One 10(3):e0119637. https://doi.org/10.1371/journal.pone.0119637
Grulich M, Stepanek V, Kyslik P (2013) Perspectives and industrial potential of PGA selectivity and promiscuity. Biotechnol Adv 31(8):1458–1472. https://doi.org/10.1016/j.biotechadv.2013.07.005
Hang HF, Chen W, Guo M, Chu J, Zhuang Y, Zhang S (2008) A simple unstructured model-based control for efficient expression of recombinant porcine insulin precursor by Pichia pastoris. Korean J Chem Eng 25:1065–1069. https://doi.org/10.1007/s11814-008-0174-3
Hellwig S, Emde F, Raven NP, Henke M, van Der Logt P, Fischer R (2001) Analysis of single-chain antibody production in Pichia pastoris using on-line methanol control in fed-batch and mixed-feed fermentations. Biotechnol Bioeng 74(4):344–352. https://doi.org/10.1002/bit.1125
Hesketh AR, Castrillo JI, Sawyer T, Archer DB, Oliver SG (2013) Investigating the physiological response of Pichia (Komagataella) pastoris GS115 to the heterologous expression of misfolded proteins using chemostat cultures. Appl Microbiol Biotechnol 97(22):9747–9762. https://doi.org/10.1007/s00253-013-5186-1
Hyka P, Zullig T, Ruth C, Looser V, Meier C, Klein J, Melzoch K, Meyer HP, Glieder A, Kovar K (2010) Combined use of fluorescent dyes and flow cytometry to quantify the physiological state of Pichia pastoris during the production of heterologous proteins in high-cell-density fed-batch cultures. Appl Environ Microbiol 76(13):4486–4496. https://doi.org/10.1128/AEM.02475-09
Juturu V, Wu JC (2018) Heterologous protein expression in Pichia pastoris: latest research progress and applications. Chembiochem 19(1):7–21. https://doi.org/10.1002/cbic.201700460
Ljubijankic G, Gvozdenovic J, Sevo M, Degrassi G (2002) High-level secretory expression of penicillin amidase from Providencia rettgeri in Saccharomyces cerevisiae: purification and characterization. Biotechnol Prog 18(2):330–336. https://doi.org/10.1021/bp010182g
Looser V, Bruhlmann B, Bumbak F, Stenger C, Costa M, Camattari A, Fotiadis D, Kovar K (2015) Cultivation strategies to enhance productivity of Pichia pastoris: a review. Biotechnol Adv 33(6 Pt 2):1177–1193. https://doi.org/10.1016/j.biotechadv.2015.05.008
Looser V, Luthy D, Straumann M, Hecht K, Melzoch K, Kovar K (2017) Effects of glycerol supply and specific growth rate on methanol-free production of CALB by P. pastoris: functional characterisation of a novel promoter. Appl Microbiol Biotechnol 101(8):3163–3176. https://doi.org/10.1007/s00253-017-8123-x
Love KR, Politano TJ, Panagiotou V, Jiang B, Stadheim TA, Love JC (2012) Systematic single-cell analysis of Pichia pastoris reveals secretory capacity limits productivity. PLoS One 7(6):e37915. https://doi.org/10.1371/journal.pone.0037915
Maresova H, Markova Z, Valesova R, Sklenar J, Kyslik P (2010) Heterologous expression of leader-less pga gene in Pichia pastoris: intracellular production of prokaryotic enzyme. BMC Biotechnol 10:7. https://doi.org/10.1186/1472-6750-10-7
Maresova H, Plackova M, Grulich M, Kyslik P (2014) Current state and perspectives of penicillin G acylase-based biocatalyses. Appl Microbiol Biotechnol 98(7):2867–2879. https://doi.org/10.1007/s00253-013-5492-7
Maresova H, Palyzova A, Plackova M, Grulich M, Rajasekar VW, Stepanek V, Kyslikova E, Kyslik P (2017) Potential of Pichia pastoris for the production of industrial penicillin G acylase. Folia Microbiol 62(5):417–424. https://doi.org/10.1007/s12223-017-0512-0
Marsalek L, Puxbaum V, Buchetics M, Mattanovich D, Gasser B (2019) Disruption of vacuolar protein sorting components of the HOPS complex leads to enhanced secretion of recombinant proteins in Pichia pastoris. Microb Cell Factories 18(1):119. https://doi.org/10.1186/s12934-019-1155-4
Puxbaum V, Mattanovich D, Gasser B (2015) Quo vadis? The challenges of recombinant protein folding and secretion in Pichia pastoris. Appl Microbiol Biotechnol 99(7):2925–2938. https://doi.org/10.1007/s00253-015-6470-z
Raschmanova H, Weninger A, Glieder A, Kovar K, Vogl T (2018) Implementing CRISPR-Cas technologies in conventional and non-conventional yeasts: current state and future prospects. Biotechnol Adv 36(3):641–665. https://doi.org/10.1016/j.biotechadv.2018.01.006
Rebnegger C, Graf AB, Valli M, Steiger MG, Gasser B, Maurer M, Mattanovich D (2014) In Pichia pastoris, growth rate regulates protein synthesis and secretion, mating and stress response. Biotechnol J 9(4):511–525. https://doi.org/10.1002/biot.201300334
Reichelt WN, Haas F, Sagmeister P, Herwig C (2017) Bioprocess development workflow: transferable physiological knowledge instead of technological correlations. Biotechnol Prog 33(1):261–270. https://doi.org/10.1002/btpr.2377
Resina D, Cos O, Ferrer P, Valero F (2005) Developing high cell density fed-batch cultivation strategies for heterologous protein production in Pichia pastoris using the nitrogen source-regulated FLD1 Promoter. Biotechnol Bioeng 91(6):760–767. https://doi.org/10.1002/bit.20545
Senerovic L, Stankovic N, Spizzo P, Basso A, Gardossi L, Vasiljevic B, Ljubijankic G, Tisminetzky S, Degrassi G (2006) High-level production and covalent immobilization of Providencia rettgeri penicillin G acylase (PAC) from recombinant Pichia pastoris for the development of a novel and stable biocatalyst of industrial applicability. Biotechnol Bioeng 93(2):344–354. https://doi.org/10.1002/bit.20728
Sevo M, Degrassi G, Skoko N, Venturi V, Ljubijankic G (2002) Production of glycosylated thermostable Providencia rettgeri penicillin G amidase in Pichia pastoris. FEMS Yeast Res 1(4):271–277. https://doi.org/10.1111/j.1567-1364.2002.tb00045.x
Sha C, Yu XW, Zhang M, Xu Y (2013) Efficient secretion of lipase r27RCL in Pichia pastoris by enhancing the disulfide bond formation pathway in the endoplasmic reticulum. J Ind Microbiol Biotechnol 40(11):1241–1249. https://doi.org/10.1007/s10295-013-1328-9
Sjöblom M, Lindberg L, Holgersson J, Rova U (2012) Secretion and expression dynamics of a GFP-tagged mucin-type fusion protein in high cell density Pichia pastoris bioreactor cultivations. Adv Biosci Biotechnol 3(3):238–248. https://doi.org/10.4236/abb.2012.33033
Srirangan K, Orr V, Akawi L, Westbrook A, Moo-Young M, Chou CP (2013) Biotechnological advances on penicillin G acylase: pharmaceutical implications, unique expression mechanism and production strategies. Biotechnol Adv 31(8):1319–1332. https://doi.org/10.1016/j.biotechadv.2013.05.006
van der Klei IJ, Yurimoto H, Sakai Y, Veenhuis M (2006) The significance of peroxisomes in methanol metabolism in methylotrophic yeast. Acta Biochim Biophys 1763(12):1453–1462. https://doi.org/10.1016/j.bbamcr.2006.07.016
Vogl T, Glieder A (2013) Regulation of Pichia pastoris promoters and its consequences for protein production. New Biotechnol 30(4):385–404. https://doi.org/10.1016/j.nbt.2012.11.010
Vogl T, Thallinger GG, Zellnig G, Drew D, Cregg JM, Glieder A, Freigassner M (2014) Towards improved membrane protein production in Pichia pastoris: general and specific transcriptional response to membrane protein overexpression. New Biotechnol 31(6):538–552. https://doi.org/10.1016/j.nbt.2014.02.009
Zhang W, Sinha J, Smith LA, Inan M, Meagher MM (2005) Maximization of production of secreted recombinant proteins in Pichia pastoris fed-batch fermentation. Biotechnol Prog 21(2):386–393. https://doi.org/10.1021/bp049811n
Acknowledgements
The authors gratefully acknowledge Zdenek Knejzlik and Fermenta Biotech Ltd. (Thane, India) for support in strain development as well as Anton Glieder for fruitful discussions. Thanks are also due to Béla Brühlmann, Marcel Straumann, Fabian Breitenstein, Matthias Barmettler and Lukas Neutsch for their help in the preparation and performance of long-term cultivations. Further thanks go to John Brooker for language improvement and proofreading.
Funding
This project was financially supported by the PEGAS 14.176 project in the SCIEX-NMSCH-Programme by swissuniversities in association with the Swiss Development and Cooperation Agency (Switzerland). Strain construction and design was funded by an industry grant (Fermenta Biotech Ltd., Thane, India) and by project RV061388971 of the Institute of Microbiology, The Czech Academy of Sciences v.v.i. (Prague, Czech Republic).
Author information
Authors and Affiliations
Contributions
KK and PK enabled and supervised this research. MB, VL, PK and KK conceived of the study. MB, HM and HR constructed the used strains. MB designed and MB, HR and IZ performed the bioreactor experiments. MB and HR performed product analyses. IZ, SH and KK designed and IZ prepared the descriptive mathematical model. MB and VL analysed and interpreted the experimental data. MB wrote and all authors approved the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary materials
ESM 1
(PDF 472 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Borčinová, M., Raschmanová, H., Zamora, I. et al. Production and secretion dynamics of prokaryotic Penicillin G acylase in Pichia pastoris. Appl Microbiol Biotechnol 104, 5787–5800 (2020). https://doi.org/10.1007/s00253-020-10669-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00253-020-10669-x