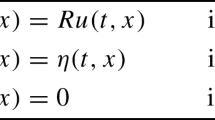1 Problem Statement and Optimality Conditions

We consider optimal control problems of the form

(1a)
(1b)
(1c)
(1d)
(1e)

where \(t_0\) and \(t_\textrm{f}\) define a fixed and finite time horizon, \(x: [t_0, t_\textrm{f}] \rightarrow \mathbb {R}^n\) is a state function, \(u: [t_0, t_\textrm{f}] \rightarrow \mathbb {R}^m\) is a control function, and U is an arbitrary subset of \(\mathbb {R}^m\). The functions \(\chi _j, \psi _j: \mathbb {R}^n \rightarrow \mathbb {R}\) impose constraints on the initial and terminal state, respectively, and the functions \(\varphi _0, \varphi _\textrm{f}: \mathbb {R}^n \rightarrow \mathbb {R}\) model initial and terminal costs. The minimum is taken over all absolutely continuous functions \(x(\cdot )\) as well as over all measurable and essentially bounded functions \(u(\cdot )\).

Such problems are numerically solved predominantly by gradient-based optimization methods. Firstly, because of their close relation to classic problems from the calculus of variations leading to multiplier-based optimality conditions such as Pontryagin’s principle, which then in turn can be solved using Newton-type shooting approaches. Secondly, because of the difficulty that their discretization naturally leads to large-scale finite-dimensional problems being typically solved locally based on finite-dimensional optimality conditions. Hence, these problems are mostly studied for compact and convex constraints on the control values.

In this work, it is important to observe that we do not impose any connectivity or convexity assumptions on the control constraint set U. Thus, (1) includes integrality constraints for, e.g., modeling discrete decisions on some components of u. Such optimal control problems exhibit combinatorial aspects and received a lot of attention in recent years. Indeed, many applications require to include integer restrictions on the control value as to model, e.g., decisions such as opening or closing valves in gas network operation [21]. Similar logical restrictions occur, e.g., in autonomous driving in case of vehicles with gear shifting [13], in contact problems such as robotic multi-arm transport [6], or in the control of chemical reactors in process engineering [53].

Due to the discrete nature of U, these problems cannot be solved directly with gradient-based methods from optimal control. Therefore, several approaches have been proposed in the literature to overcome this limitation such as partial outer convexification and combinatorial integral approximation [26, 47], alternating direction methods [16], extended multi-interval Legendre–Gauß–Radau pseudospectral methods [38], multiple shooting [46], bilevel approaches [7], adaptive wavelet methods [11], model reduction [25], genetic algorithms [54], mixed-integer linear programming techniques [19], instantaneous control [18], time-transformation methods [14, 32, 44], hybrid extensions of the maximum principle [15, 51, 52], the competing Hamiltonian approach [4], or outer-approximation, Benders-type decomposition, etc. for linear-quadratic problems [43]. Available analytical results concern, e.g., turnpike properties [10] and value-function regularity [17].

Similar to solution approaches based on hybrid extensions of the maximum principle, we consider in this work the infinite-dimensional optimality conditions of (1) for discrete U. To this end, our goal will be to find a Pontryagin-minimum of (1), i.e., an admissible state-control point \((x^*, u^*)\), such that for any constant N there exists an \(\varepsilon = \varepsilon (N) > 0\) with the properties that for any admissible point (x, u) satisfying

$$\begin{aligned} \Vert x^*-x\Vert _{\mathcal {C}^0([t_0,t_\textrm{f}];\mathbb {R}^n)}< \varepsilon , \quad \Vert u^*-u\Vert _{\mathcal {L}^1(t_0,t_\textrm{f};\mathbb {R}^m)}<\varepsilon , \quad \Vert u^*-u\Vert _{\mathcal {L}^\infty (t_0,t_\textrm{f};\mathbb {R}^m)} \le N, \end{aligned}$$

it holds

$$\begin{aligned} \varphi _0(x^*(t_0)) + \varphi _\textrm{f}(x^*(t_\textrm{f})) \le \varphi _0(x(t_0)) + \varphi _\textrm{f}(x(t_\textrm{f})); \end{aligned}$$

see, e.g., [8, 42]. Note that global minima are Pontryagin-minima.

We suppose that \(f: Q \rightarrow \mathbb {R}^n\) is continuous with a continuous partial derivative \(f_{x}\) on a set \(Q \subseteq \mathbb {R}^{n + m}\) and the functions \(\chi _j, \psi _j, \varphi _0, \varphi _\textrm{f}: P \rightarrow \mathbb {R}\) are continuously differentiable on a set \(P \subseteq \mathbb {R}^{n}\). Here, Q and P are open super-sets of the admissible state-control set and its projection onto the states, respectively.

For \(\lambda \in \mathbb {R}^n\), \(x \in \mathbb {R}^n\), and \(u \in \mathbb {R}^m\) we let

denote the Hamiltonian associated with Problem (1). If \((x^*,u^*)\) is a Pontryagin-minimum of Problem (1), Pontryagin’s maximum principle yields that there exists a collection \(\eta =(\alpha ,\beta ,\lambda )\) with \(\alpha \ge 0\), \(\beta =(\beta _1,\ldots ,\beta _{p+q}) \in \mathbb {R}^{p+q}\), and \(\lambda \) being a Lipschitz-function \(\lambda : [t_0,t_\textrm{f}] \rightarrow \mathbb {R}^n\) such that the following conditions hold:

  1. (i)

    \((\alpha ,\beta ) \ne 0\),

  2. (ii)

    \(\dot{\lambda }(t) = -H_x(\lambda (t),x^*(t),u^*(t)) = - f_x(x^*(t),u^*(t))^\top \lambda (t)\) a. e. in \((t_0,t_\textrm{f})\),

  3. (iii)

    \(\lambda (t_0) = \alpha \varphi _0^\prime (x^*(t_0)) + \sum _{j=1}^p \beta _j \chi _j^\prime (x^*(t_0))\),

  4. (iv)

    \(\lambda (t_\textrm{f}) = -\alpha \varphi _\textrm{f}^\prime (x^*(t_\textrm{f})) - \sum _{j=1}^{q} \beta _{p+j} \psi _j^\prime (x^*(t_\textrm{f}))\),

  5. (v)

    \(\max _{u \in U} H(\lambda (t),x^*(t),u) = H(\lambda (t),x^*(t),u^*(t))\) a. e. in \((t_0,t_\textrm{f})\);

see, e.g., [8, Theorem 1]. Note that these conditions are stated in a non-qualified form, i.e., \(\alpha =0\) is possible. However, it is well-known that these conditions hold with \(\alpha \ne 0\) if the initial- and end-point constraints are regular in the sense that

$$\begin{aligned} \textrm{rank} [\chi _1'(x),\ldots ,\chi _p'(x)]=p \quad \text {for all}~x~\text {such that}~\chi _1(x)=\cdots =\chi _p(x)=0 \end{aligned}$$

and

$$\begin{aligned} \textrm{rank} [\psi _1'(x),\ldots ,\psi _q'(x)]=q \quad \text {for all}~x~\text {such that}~\psi _1(x)=\cdots =\psi _q(x)=0; \end{aligned}$$

see, e.g., [2]. Therefore, we assume in the following that the constraints \(\chi _1,\ldots ,\chi _p\) and \(\psi _1,\ldots ,\psi _q\) are regular.

In particular, under this assumption, the Pontryagin maximum principle together with the constraints of Problem (1) yield the following necessary optimality conditions for (x, u) being a Pontryagin-minimum:

(2)

So far, this is well-known and, indeed, does not require any assumption on U in the original proof in [42] using needle-variations, the terminal cone, and the separating hyperplane theorem as, for instance, also being exploited for the so-called hybrid maximum principle [8]. It is also well-known that Problem (1) being in so-called Mayer form is not restrictive. One can, for instance, include running costs

$$\begin{aligned} \int _{t_0}^{t_\textrm{f}} L(x, u) \,\textrm{d}t \end{aligned}$$

in Problem (1) by defining a new state variable y with

(3)

and adding \(y(t_\textrm{f})\) to the objective function. Nevertheless, we note that our convergence result in Sect. 4 applies to problems in Mayer form with linear dynamics and a quadratic objective function. Hence, nonlinear terms in L(x, u) that depend on x are not covered. For running costs L that are independent of x, however, (3) is equivalent to considering . Besides this, we choose the Mayer form to keep the optimality system as simple as possible. Moreover, a free terminal time can be transformed into a fixed terminal time, etc.; see, e.g., [33]. We also note that the regularity assumptions on f and on the constraint functions can be relaxed [1].

As already indicated above, most approaches in the literature yet focused on solving (2) using further necessary optimality conditions for the pointwise maximization of the Hamiltonian. Additional properties on U are then needed. Most prominently, e.g., for convex sets U, the pointwise maximization of the Hamiltonian can be replaced using Karush–Kuhn–Tucker type optimality conditions and the two-point boundary value problem (2) can then be solved using Newton’s method in the fashion of single or multiple shooting. If U is a discrete-continuous set, switching-time re-parameterization can be used. This, however, leaves a gap on efficient treatments concerning the combinatorial aspects. For an overview of shooting techniques we refer to [5]. In any case, all of these approaches solve (2) to some form of local optimality with respect to the maximization of the Hamiltonian. However, the conditions in (2) hold with global optimality even for (locally optimal) Pontryagin-minima.

This motivates us to consider a solution approach for (2) based on (global) mixed-integer nonlinear programming (MINLP) techniques. This, of course, needs to overcome the difficulty that (2) is an MINLP subject to differential equations with no direct advantage over the original problem (1). Instead, (2) has even more variables for the adjoint equation. In particular, a direct discretization of (2) as, e.g., considered in [20] yields a large-scale MINLP that in many applications becomes computationally intractable.

We overcome this limitation by using time-domain decomposition methods originally developed for partial differential equations (PDEs); see, e.g., [23, 24, 27,28,29,30,31, 34,35,36]. The main idea of these methods is to split the time domain \([t_0,t_\textrm{f}]\) into non-overlapping subintervals and then to iteratively decouple the optimality system (2) such that on each subinterval, subproblems are solved together with conditions at the breakpoints that couple the states over two subsequent iterations. For PDEs, this decomposition approach goes back to the so-called parareal-scheme introduced in [37]. In the following, we show that this approach can also be used to decompose (2) for arbitrary sets U. As in [29,30,31], we exploit that the decomposition yields subproblems that correspond to so-called virtual control problems on the subintervals. For discrete-continuous U, this yields an iterative scheme of mixed-integer optimal control problems on smaller time horizons. For sufficiently fine decompositions, these can eventually be solved using direct transcription methods such as collocation [22] or Runge–Kutta discretizations [49], both resulting in reasonably sized finite-dimensional mixed-integer nonlinear problems. The limit behavior of such approximations are discussed in [20]. The method can be interpreted as an alternating approach [12] or as a structure-exploiting decomposition for MINLPs rather than a generic one [41].

Our main contribution is that we prove convergence of this iterative scheme for the important case of linear-quadratic problems. We support our theoretical result with encouraging numerical results and also include experiments for nonlinear problems. In particular, we demonstrate that the iterative method can provide solutions for problems where the same solver applied to full direct discretization fails to reach an optimal solution within amply time limits.

The remainder of the paper is structured as follows. In Sect. 2, we introduce the time-domain decomposition of the optimality system and discuss the iterative idea to recover the transmission conditions at the boundaries of the subintervals. Afterward, we re-interpret the decomposed (primal-dual) optimality conditions as so-called (primal) virtual control problems in Sect. 3 and state the overall iterative procedure. For the case of linear-quadratic problems, we prove convergence of the method in Sect. 4. We present some case studies for linear as well as nonlinear problems in Sect. 5 to give a numerical proof of concept. Finally, we conclude in Sect. 6.

2 Time-Domain Decomposition of the Optimality System

We now consider the time-domain decomposition

$$\begin{aligned} {[}t_0,t_\textrm{f}]=\bigcup _{k=0}^K [t_k,t_{k+1}] \quad \text {with} \quad t_k < t_{k+1}, \ t_{K+1}=t_\textrm{f}\end{aligned}$$

of the entire time horizon of Problem (1). Accordingly, we define

$$\begin{aligned} x_k:=x|_{[t_k,t_{k+1}]},\quad \lambda _k:=\lambda |_{[t_k,t_{k+1}]},\quad \text {and}~u_k:=u|_{[t_k,t_{k+1}]}\end{aligned}$$

for \(k=0,\ldots ,K\); see Fig. 1.

Fig. 1
figure 1

Schematic illustration of the time-domain decomposition

Full size image

The optimality conditions (2) then are equivalent to the following sets of conditions.

  1. (i)

    For \(k=0\):

    $$\begin{aligned} \dot{x}_0&= f(x_0,u_0) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_0,t_1), \end{aligned}$$
    (4a)
    $$\begin{aligned} \chi _j(x_0(t_0))&= 0, \quad j=1,\ldots ,p,\end{aligned}$$
    (4b)
    $$\begin{aligned} u_0(t)&\in U \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_0,t_1],\end{aligned}$$
    (4c)
    $$\begin{aligned} \dot{\lambda }_0&= - f_x(x_0,u_0)^\top \lambda _0 \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_0,t_1),\end{aligned}$$
    (4d)
    $$\begin{aligned} \lambda _0(t_0)&= \varphi _0^\prime (x_0(t_0)) + \sum _{j=1}^p \beta _j \chi _j^\prime (x_0(t_0)),\end{aligned}$$
    (4e)
    $$\begin{aligned} \max _{u \in U}\ H(\lambda _0(t),x_0(t),u)&= H(\lambda _0(t),x_0(t),u_0(t)) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_0,t_1). \end{aligned}$$
    (4f)
  2. (ii)

    For \(k=1,\ldots ,K-1\):

    $$\begin{aligned} \dot{x}_k&= f(x_k,u_k) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}),\end{aligned}$$
    (5a)
    $$\begin{aligned} u_k(t)&\in U \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_k,t_{k+1}],\end{aligned}$$
    (5b)
    $$\begin{aligned} \dot{\lambda }_k&= - f_x(x_k,u_k)^\top \lambda _k \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}),\end{aligned}$$
    (5c)
    $$\begin{aligned} \max _{u \in U}\ H(\lambda _k(t),x_k(t),u)&= H(\lambda _k(t),x_k(t),u_k(t)) \quad \mathrm{a.}\,\mathrm{e.}\, \textrm{in}\ (t_k,t_{k+1}). \end{aligned}$$
    (5d)
  3. (iii)

    For \(k=K\):

    $$\begin{aligned} \dot{x}_K&= f(x_K,u_K) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_K,t_\textrm{f}),\end{aligned}$$
    (6a)
    $$\begin{aligned} \psi _j(x_K(t_\textrm{f}))&= 0, \quad j=1,\ldots ,q,\end{aligned}$$
    (6b)
    $$\begin{aligned} u_K(t)&\in U \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_K,t_\textrm{f}],\end{aligned}$$
    (6c)
    $$\begin{aligned} \dot{\lambda }_K&= - f_x(x_K,u_K)^\top \lambda _K \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_K,t_\textrm{f}),\end{aligned}$$
    (6d)
    $$\begin{aligned} \lambda _K(t_\textrm{f})&= - \varphi _\textrm{f}^\prime (x_K(t_\textrm{f})) - \sum _{j=1}^{q} \beta _{p+j} \psi _j^\prime (x_K(t_\textrm{f})),\end{aligned}$$
    (6e)
    $$\begin{aligned} \max _{u \in U}\ H(\lambda _K(t),x_K(t),u)&= H(\lambda _K(t),x_K(t),u_K(t)) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_K,t_\textrm{f}). \end{aligned}$$
    (6f)

These conditions are completed with the conditions

$$\begin{aligned} x_k(t_{k+1})&= x_{k+1}(t_{k+1}),{} & {} k = 0, \dotsc , K-1,\end{aligned}$$
(7a)
$$\begin{aligned} \lambda _k(t_k)&= \lambda _{k-1}(t_k),{} & {} k = 1, \dotsc , K, \end{aligned}$$
(7b)

which ensure the continuity of the state x and of the adjoint \(\lambda \) at the boundaries of the sub-intervals.

The main idea of the time-domain decomposition method is to decouple the transmission conditions (7) and to construct an iterative procedure that converges to points that satisfy the decomposed optimality system above. To this end, we consider an iteration index \(\ell \), iterates \(x_k^\ell \), \(\lambda _k^\ell \), and \(u_k^\ell \) for \(x_k\), \(\lambda _k\), and \(u_k\), respectively, and a scalar parameter \(\gamma > 0\), to decouple the transmission conditions (7) as

$$\begin{aligned} x_k^\ell (t_{k+1}) + \gamma \lambda _k^\ell (t_{k+1})&= \phi _{k,k+1}^{\ell -1}, \quad k = 0, \ldots , K-1, \end{aligned}$$
(8a)
$$\begin{aligned} x_k^\ell (t_k) - \gamma \lambda _k^\ell (t_k)&= \phi _{k,k-1}^{\ell -1}, \quad k = 1, \ldots , K, \end{aligned}$$
(8b)

with the update rules

$$\begin{aligned} \phi _{k,k+1}^{\ell -1} ={}&(1 - \varepsilon ) \left( x_{k+1}^{\ell -1}(t_{k+1}) + \gamma \lambda _{k+1}^{\ell -1}(t_{k+1})\right) \nonumber \\&+ \varepsilon \left( x_k^{\ell -1}(t_{k+1}) + \gamma \lambda _k^{\ell -1}(t_{k+1})\right) , \quad k = 0, \ldots , K-1, \end{aligned}$$
(9a)
$$\begin{aligned} \phi _{k,k-1}^{\ell -1} ={}&(1 - \varepsilon ) \left( x_{k-1}^{\ell -1}(t_k) - \gamma \lambda _{k-1}^{\ell -1}(t_k)\right) \nonumber \\&+ \varepsilon \left( x_k^{\ell -1}(t_k) - \gamma \lambda _k^{\ell -1}(t_k)\right) , \quad k = 1, \ldots , K \end{aligned}$$
(9b)

for \(\varepsilon \in (0,1)\); see, e.g., [29,30,31, 34,35,36].

Let us make a first observation. To this end, assume that the iterates \(x_k^{\ell -1}\), \(\lambda _k^{\ell -1}\) for \(k = 0, \dotsc , K\) converge for \(\ell \rightarrow \infty \) to \(x_k\) and \(\lambda _k\), respectively. Then, substituting \(\phi _{k,k+1}\) and \(\phi _{k,k-1}\) and dividing by \((1 - \varepsilon )\) yields

$$\begin{aligned} x_k(t_{k+1}) + \gamma \lambda _k(t_{k+1})&= x_{k+1}(t_{k+1}) + \gamma \lambda _{k+1}(t_{k+1}), \end{aligned}$$
(10a)
$$\begin{aligned} x_k(t_k) - \gamma \lambda _k(t_k)&= x_{k-1}(t_k) - \gamma \lambda _{k-1}(t_k). \end{aligned}$$
(10b)

Next, we shift the k-index in Equation (10b) by 1 and obtain

$$\begin{aligned} x_{k+1}(t_{k+1}) - \gamma \lambda _{k+1}(t_{k+1}) = x_{k}(t_{k+1}) - \gamma \lambda _{k}(t_{k+1}). \end{aligned}$$

Adding this to (10a) yields

$$\begin{aligned} \gamma \lambda _k(t_{k+1}) - \gamma \lambda _{k+1}(t_{k+1}) = \gamma \lambda _{k+1}(t_{k+1}) - \gamma \lambda _{k}(t_{k+1}), \end{aligned}$$

which is, for \(\gamma > 0\), equivalent to

$$\begin{aligned} \lambda _{k+1}(t_{k+1}) = \lambda _k(t_{k+1}). \end{aligned}$$

Finally, (10a) implies

$$\begin{aligned} x_k(t_{k+1}) = x_{k+1}(t_{k+1}). \end{aligned}$$

Hence, we have shown that if the state \(x_k^\ell \) and the adjoint \(\lambda _k^\ell \) converge, then the iteratively decoupled transmission conditions (8) tend to the continuity conditions (7).

If we combine the decomposed optimality conditions (4–6) for all \(k=0, \ldots , K\) with the iterative transmission conditions (8), we get

$$\begin{aligned} \dot{x}_k^\ell&= f(x_k^\ell ,u_k^\ell ) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}), \end{aligned}$$
(11a)
$$\begin{aligned} \chi _j(x_0^\ell (t_0))&= 0 \quad \text {if } k = 0, \end{aligned}$$
(11b)
$$\begin{aligned} \psi _j(x_K^\ell (t_\textrm{f}))&= 0 \quad \text {if } k = K, \end{aligned}$$
(11c)
$$\begin{aligned} u_k^\ell (t)&\in U \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_k,t_{k+1}], \end{aligned}$$
(11d)
$$\begin{aligned} \dot{\lambda }_k^\ell&= -f_x(x_k^\ell ,u_k^\ell )^\top \lambda _k^\ell \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}), \end{aligned}$$
(11e)
$$\begin{aligned} \lambda _0^\ell (t_0)&= \varphi _0^\prime (x_0^\ell (t_0)) + \sum _{j=1}^p \beta _j \chi _j^\prime (x_0^\ell (t_0)) \quad \text {if } k = 0, \end{aligned}$$
(11f)
$$\begin{aligned} \lambda _K^\ell (t_\textrm{f})&= - \varphi _\textrm{f}^\prime (x_K^\ell (t_\textrm{f})) - \sum _{j=1}^{q} \beta _{p+j} \psi _j^\prime (x_K^\ell (t_\textrm{f})) \quad \text {if } k = K, \end{aligned}$$
(11g)
$$\begin{aligned} \max _{u \in U}\ H(\lambda _k^\ell (t),x_k^\ell (t),u)&= H(\lambda _k^\ell (t),x_k^\ell (t),u_k^\ell (t)) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}), \end{aligned}$$
(11h)
$$\begin{aligned} x_k^\ell (t_{k+1}) + \gamma \lambda _k^\ell (t_{k+1})&= \phi _{k,k+1}^{\ell -1} \quad \text {if } k \ne K, \end{aligned}$$
(11i)
$$\begin{aligned} x_k^\ell (t_k) - \gamma \lambda _k^\ell (t_k)&= \phi _{k,k-1}^{\ell -1} \quad \text {if } k \ne 0 \end{aligned}$$
(11j)

together with the update rules (9).

3 Virtual Control Problems and the Iterative Procedure

We will now observe that the iteratively decomposed optimality systems (11) have a primal interpretation as other optimal control problems with additional and so-called virtual controls h; see, e.g., [29,30,31, 34,35,36]. For the inner time sub-intervals k, the respective primal problem reads

(12a)
$$\begin{aligned} \text {s.t.}\quad&\dot{x}_k = f(x_k, u_k) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}), \end{aligned}$$
(12b)
$$\begin{aligned}&x_k(t_k) = \phi _{k,k-1}^{\ell -1} + h_k, \end{aligned}$$
(12c)
$$\begin{aligned}&h_k \in \mathbb {R}^n, \end{aligned}$$
(12d)
$$\begin{aligned}&u_k(t) \in U \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_k,t_{k+1}]. \end{aligned}$$
(12e)

The ODE constraint (12b) and the control constraint (12e) carry over from Problem (1) but are now restricted to the time interval \([t_k, t_{k+1}]\). The virtual controls enter in the initial conditions (12c). These controls allow the state to be bounded away from the current transmission conditions at \(t_k\). The violation of the current transmission conditions at \(t_k\) and \(t_{k+1}\) is penalized in the objective function. Since this virtual control problem is defined for the inner time sub-intervals, there are no initial or final conditions as in Problem (1) in the constraints or in the objective function. In order to bring (12) into the form of Problem (1), one can remove (12d) and model the virtual control \(h_k\) as a trivial state variable, i.e.,

$$\begin{aligned} h_k(t_k)=h_k,\quad \dot{h}_k = 0 \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}). \end{aligned}$$

Technically speaking, \(h_k\) is not a control but a constant state. We will, however, keep referring to it as a virtual control to be in line with the pertinent literature; see, e.g., [31, 34]. We use the Hamiltonian

$$\begin{aligned} H(\lambda _k, x_k, u_k) = \lambda _k^\top f(x_k, u_k), \end{aligned}$$

in which we omit the adjoint state corresponding to \(h_k\) because it vanishes. The corresponding optimality conditions are given by

$$\begin{aligned} \dot{x}_k&= f(x_k, u_k) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}), \end{aligned}$$
(13a)
$$\begin{aligned} \dot{h}_k&= 0 \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}), \end{aligned}$$
(13b)
$$\begin{aligned} x_k(t_k)&= \phi _{k,k-1}^{\ell -1} + h_k(t_k), \end{aligned}$$
(13c)
$$\begin{aligned} u_k(t)&\in U \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_k,t_{k+1}], \end{aligned}$$
(13d)
$$\begin{aligned} \dot{\lambda }_k&= - f_x(x_k, u_k)^\top \lambda _k \quad \text {a. e. in}\ (t_k,t_{k+1}), \end{aligned}$$
(13e)
$$\begin{aligned} \lambda _k(t_k)&= \frac{1}{\gamma } h_k(t_k), \end{aligned}$$
(13f)
$$\begin{aligned} \lambda _k(t_{k+1})&= -\frac{1}{\gamma } \left( x_k(t_{k+1}) - \phi _{k,k+1}^{\ell -1} \right) , \end{aligned}$$
(13g)
$$\begin{aligned} \max _{u \in U}\ H(\lambda _k(t),x_k(t),u)&= H(\lambda _k(t),x_k(t),u_k(t)) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}). \end{aligned}$$
(13h)

If we substitute \(h_k(t_k)\) in (13c) with (13f) and rewrite (13g), we obtain

$$\begin{aligned} \dot{x}_k&= f(x_k, u_k) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}),\\ u_k(t)&\in U \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_k,t_{k+1}],\\ \dot{\lambda }_k&= - f_x(x_k, u_k)^\top \lambda _k \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}), \\x_k(t_k) - \gamma \lambda _k(t_k)&= \phi _{k,k-1}^{\ell -1},\\ x_k(t_{k+1}) + \gamma \lambda _k(t_{k+1})&= \phi _{k,k+1}^{\ell -1},\\ \max _{u \in U}\ H(\lambda _k(t),x_k(t),u)&= H(\lambda _k(t),x_k(t),u_k(t)) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}). \end{aligned}$$

This exactly corresponds to the iteratively decomposed optimality system (11) for \(k=1,\ldots ,K-1\). Note that we scaled the objective function (12a) with the factor \(1/(2 \gamma )\) to be in line with with the notation of System (11). However, any other positive factor would be valid as well.

For the first time sub-interval, i.e., \(k = 0\), the respective primal problem reads

(14a)
$$\begin{aligned} \text {s.t.}\quad&\dot{x}_0 = f(x_0, u_0) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_0,t_{1}), \end{aligned}$$
(14b)
$$\begin{aligned}&\chi _j(x_0(t_0)) = 0, \end{aligned}$$
(14c)
$$\begin{aligned}&u_0(t) \in U \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_0,t_{1}], \end{aligned}$$
(14d)

in which we have no transmission conditions at \(t_0\) but the original initial conditions instead. For the last time sub-interval, i.e., \(k=K\), we get

(15a)
$$\begin{aligned} \text {s.t.}\quad&\dot{x}_K = f(x_K, u_K) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_K,t_{K+1}),\end{aligned}$$
(15b)
$$\begin{aligned}&x_K(t_K) = \phi _{K,K-1}^{\ell -1} + h_K, \end{aligned}$$
(15c)
$$\begin{aligned}&\psi _j(x_K(t_\textrm{f}))=0, \end{aligned}$$
(15d)
$$\begin{aligned}&h_K \in \mathbb {R}^n, \end{aligned}$$
(15e)
$$\begin{aligned}&u_K(t) \in U \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_K,t_{K+1}], \end{aligned}$$
(15f)

in which we have no transmission conditions at \(t_{K+1}\) but the original final conditions instead.

figure a

Now we can state the iterative time-domain decomposition method; see Algorithm 1. In Step 3 the virtual control problems (12), (14), and (15) are solved. This is equivalent to solving the iteratively decomposed optimality systems (11) for all \(k=0, \ldots , K\). One can compute the values of the adjoint variables \(\lambda _k^\ell \) at the transmission points \(t_k\) and \(t_{k+1}\) by using (11i) and (11j) in Step 4. In Step 6, the update rules in (9) are used to obtain the transmission conditions for the next iteration.

To conclude this section, also note that the solution of the \(K+1\) problems in Step 3 of Algorithm 1 can be done in parallel.

4 Convergence Analysis for Linear-Quadratic Problems

In this section, we will prove the convergence of Algorithm 1 in the sense of continuity at the boundaries of the sub-intervals, i.e., we show that

$$\begin{aligned} x_k^\ell (t_{k+1}) - x_{k+1}^\ell (t_{k+1})&\rightarrow 0,\\ \lambda _k^\ell (t_{k+1}) - \lambda _{k+1}^\ell (t_{k+1})&\rightarrow 0 \end{aligned}$$

holds for all \(k = 0, \ldots , K-1\) as \(\ell \rightarrow \infty \). To this end, we restrict ourselves to the case of linear dynamics with objective functions being quadratic with respect to the state and include control costs, i.e., we consider

$$\begin{aligned} \min \quad&\frac{1}{2} x(t_0)^\top Q_0 x(t_0) + q_0^\top x(t_0) + \frac{1}{2} x(t_\textrm{f})^\top Q_\textrm{f}x(t_\textrm{f}) + q_\textrm{f}^\top x(t_\textrm{f}) + \int _{t_0}^{t_\textrm{f}} L(u) \,\textrm{d}t \end{aligned}$$
(16a)
$$\begin{aligned} \text {s.t.}\quad&\dot{x}= Ax + Bu + c \quad \text {a. e. in}\ (t_0,t_\textrm{f}),\end{aligned}$$
(16b)
$$\begin{aligned}&R_0 x(t_0) = c_0,\end{aligned}$$
(16c)
$$\begin{aligned}&R_\textrm{f}x(t_\textrm{f}) = c_\textrm{f},\end{aligned}$$
(16d)
$$\begin{aligned}&u(t) \in U \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_0,t_\textrm{f}] \end{aligned}$$
(16e)

with \(U \subseteq \mathbb {R}^m\) arbitrary, \(x: [t_0, t_\textrm{f}] \rightarrow \mathbb {R}^n\), \(u: [t_0, t_\textrm{f}] \rightarrow \mathbb {R}^m\), \(A\in \mathbb {R}^{n \times n}\), \(Q_0, Q_\textrm{f}\in \mathbb {R}^{n \times n}\) being positive semi-definite, \(B \in \mathbb {R}^{n \times m}\), \(c, q_0, q_\textrm{f}\in \mathbb {R}^n\), \(R_0 \in \mathbb {R}^{p \times n}\), \(R_\textrm{f}\in \mathbb {R}^{q \times n}\), \(c_0 \in \mathbb {R}^p\), \(c_\textrm{f}\in \mathbb {R}^q\), and L(u) being continuous on an open super-set of the admissible controls in \(\mathbb {R}^m\). Note, that we are still dealing with an arbitrary control set U. The Hamiltonian is given by

cf. (3) and the subsequent remark.

The decomposed optimality conditions (4–6) of Problem (16) for \(k = 0,\ldots ,K\) read

$$\begin{aligned} \dot{x}_k&= Ax_k + Bu_k + c \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}),\end{aligned}$$
(17a)
$$\begin{aligned} R_0 x_0(t_0)&= c_0 \quad \text {if } k = 0,\end{aligned}$$
(17b)
$$\begin{aligned} R_\textrm{f}x_K(t_\textrm{f})&= c_\textrm{f}\quad \text {if } k = K,\end{aligned}$$
(17c)
$$\begin{aligned} u_k(t)&\in U \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_k,t_{k+1}],\end{aligned}$$
(17d)
$$\begin{aligned} \dot{\lambda }_k&= -A^\top \lambda _k \quad \text {a. e. in}\ (t_k,t_{k+1}),\end{aligned}$$
(17e)
$$\begin{aligned} \lambda _0(t_0)&= Q_0 x_0(t_0) + q_0 + R_0^\top \left( \beta _j\right) _{j=1}^p \quad \text {if } k = 0,\end{aligned}$$
(17f)
$$\begin{aligned} \lambda _K(t_\textrm{f})&= - Q_\textrm{f}x_K(t_\textrm{f}) - q_\textrm{f}- R_\textrm{f}^\top \left( \beta _j\right) _{j=p+1}^{p+q} \quad \text {if } k = K,\end{aligned}$$
(17g)
$$\begin{aligned} \max _{u \in U}\ H(\lambda _k(t),x_k(t),u)&= H(\lambda _k(t),x_k(t),u_k(t)) \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}),\end{aligned}$$
(17h)
$$\begin{aligned} x_k(t_k)&= x_{k-1}(t_k) \quad \text {if } k \ne 0,\end{aligned}$$
(17i)
$$\begin{aligned} \lambda _k(t_{k+1})&= \lambda _{k+1}(t_{k+1}) \quad \text {if } k \ne K. \end{aligned}$$
(17j)

The iterative version (11) is now given by

$$\begin{aligned} \dot{x}_k^\ell&= Ax_k^\ell + Bu_k^\ell + c \quad \text {a. e. in}\ (t_k,t_{k+1}),\end{aligned}$$
(18a)
$$\begin{aligned} R_0 x_0^\ell (t_0)&= c_0 \quad \text {if } k=0,\end{aligned}$$
(18b)
$$\begin{aligned} R_\textrm{f}x_K^\ell (t_\textrm{f})&= c_\textrm{f}\quad \text {if } k=K,\end{aligned}$$
(18c)
$$\begin{aligned} u_k^\ell (t)&\in U \quad \text {a. e. in}\ [t_k,t_{k+1}],\end{aligned}$$
(18d)
$$\begin{aligned} \dot{\lambda }_k^\ell&= -A^\top \lambda _k^\ell \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (t_k,t_{k+1}),\end{aligned}$$
(18e)
$$\begin{aligned} \lambda _0^\ell (t_0)&= Q_0 x_0^\ell (t_0) + q_0 + R_0^\top \left( \beta _j\right) _{j=1}^p \quad \text {if } k=0,\end{aligned}$$
(18f)
$$\begin{aligned} \lambda _K^\ell (t_\textrm{f})&= - Q_\textrm{f}x_K^\ell (t_\textrm{f}) - q_\textrm{f}- R_\textrm{f}^\top \left( \beta _j\right) _{j=p+1}^{p+q} \quad \text {if } k=K,\end{aligned}$$
(18g)
$$\begin{aligned} \max _{u \in U}\ H(\lambda _k^\ell (t),x_k^\ell (t),u)&= H(\lambda _k^\ell (t),x_k^\ell (t),u_k^\ell (t)) \quad \text {a. e. in}\ (t_k,t_{k+1}),\end{aligned}$$
(18h)
$$\begin{aligned} x_k^\ell (t_{k+1}) + \gamma \lambda _k^\ell (t_{k+1})&= \phi _{k,k+1}^{\ell -1} \quad \text {if } k \ne K,\end{aligned}$$
(18i)
$$\begin{aligned} x_k^\ell (t_k) - \gamma \lambda _k^\ell (t_k)&= \phi _{k,k-1}^{\ell -1} \quad \text {if } k \ne 0 \end{aligned}$$
(18j)

for \(\ell \in \mathbb {N}\) with the update rules (9).

We assume that (17) and (18) have a solution. In general, it is not to be expected that this solution is unique, which is one of the main differences to the assumptions made for similar time-domain decompositions of PDEs in, e.g., [29,30,31]. Let \((x_k, u_k, \lambda _k)\) be a solution of (17) and let \((x_k^\ell , u_k^\ell , \lambda _k^\ell )\) be a solution of the iteratively decomposed optimality conditions (18) for \(k=0,\ldots ,K\) and \(\ell \in \mathbb {N}\). We introduce the errors

$$\begin{aligned} \tilde{x}_k^\ell \mathrel {{\mathop :}{=}}x_k^\ell - x_k, \quad \tilde{u}_k^\ell \mathrel {{\mathop :}{=}}u_k^\ell - u_k, \quad \tilde{\lambda }_k^\ell \mathrel {{\mathop :}{=}}\lambda _k^\ell - \lambda _k. \end{aligned}$$

These errors satisfy the conditions

$$\begin{aligned} \dot{\tilde{x}}_k^\ell&= A\tilde{x}_k^\ell + B\tilde{u}_k^\ell \quad \text {a. e. in}\ (t_k,t_{k+1}),\end{aligned}$$
(19a)
$$\begin{aligned} R_0 \tilde{x}_0^\ell (t_0)&= 0 \quad \text {if } k=0,\end{aligned}$$
(19b)
$$\begin{aligned} R_\textrm{f}\tilde{x}_K^\ell (t_\textrm{f})&= 0 \quad \text {if } k=K,\end{aligned}$$
(19c)
$$\begin{aligned} \tilde{u}_k^\ell (t)&\in \tilde{U}\quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [t_k,t_{k+1}],\end{aligned}$$
(19d)
$$\begin{aligned} \dot{\tilde{\lambda }}_k^\ell&= -A^\top \tilde{\lambda }_k^\ell \quad \text {a. e. in}\ (t_k,t_{k+1}),\end{aligned}$$
(19e)
$$\begin{aligned} \tilde{\lambda }_0^\ell (t_0)&= Q_0 \tilde{x}_0^\ell (t_0) \quad \text {if } k = 0,\end{aligned}$$
(19f)
$$\begin{aligned} \tilde{\lambda }_K^\ell (t_\textrm{f})&= - Q_\textrm{f}\tilde{x}_K^\ell (t_\textrm{f}) \quad \text {if } k=K,\end{aligned}$$
(19g)
$$\begin{aligned} \tilde{x}_k^\ell (t_{k+1}) + \gamma \tilde{\lambda }_k^\ell (t_{k+1})&= \tilde{\phi }_{k,k+1}^{\ell -1} \quad \text {if } k \ne K,\end{aligned}$$
(19h)
$$\begin{aligned} \tilde{x}_k^\ell (t_k) - \gamma \tilde{\lambda }_k^\ell (t_k)&= \tilde{\phi }_{k,k-1}^{\ell -1} \quad \text {if } k \ne 0 \end{aligned}$$
(19i)

together with the update rules

$$\begin{aligned} \tilde{\phi }_{k,k+1}^{\ell -1} ={}&(1 - \varepsilon ) \left( \tilde{x}_{k+1}^{\ell -1}(t_{k+1}) + \gamma \tilde{\lambda }_{k+1}^{\ell -1}(t_{k+1})\right) \nonumber \\&+ \varepsilon \left( \tilde{x}_k^{\ell -1}(t_{k+1}) + \gamma \tilde{\lambda }_k^{\ell -1}(t_{k+1})\right) ,\end{aligned}$$
(20a)
$$\begin{aligned} \tilde{\phi }_{k,k-1}^{\ell -1} ={}&(1 - \varepsilon ) \left( \tilde{x}_{k-1}^{\ell -1}(t_k) - \gamma \tilde{\lambda }_{k-1}^{\ell -1}(t_k)\right) \nonumber \\&+ \varepsilon \left( \tilde{x}_k^{\ell -1}(t_k) - \gamma \tilde{\lambda }_k^{\ell -1}(t_k)\right) . \end{aligned}$$
(20b)

Moreover, we set

$$\begin{aligned} \tilde{U}\mathrel {{\mathop :}{=}}U - U = \{u-v:u,v \in U\}. \end{aligned}$$

To derive System (19) we use that both (17) and (18) are linear. This is the case, because Problem (16) has linear dynamics and in the objective function, the only quadratic terms in x are initial and terminal costs. There are approaches to extend this method to more general nonlinear right-hand sides f(x, u) by applying Lipschitz-type conditions on the nonlinearities and their derivatives; see, e.g., [27] where this was done for hyperbolic semilinear PDEs. This, however, exceeds the scope of this work.

First, we prove the following result.

Lemma 1

For all \(k=0, \ldots , K\) and \(\ell \in \mathbb {N}\), it holds

(21)

Proof

From (17h) we have

for all \(u \in U\) a. e. in \((t_k,t_{k+1})\). Analogously, using (18h) we get

(22)

for all \(u \in U\) a. e. in \((t_k,t_{k+1})\). If we set \(u=u_k\) in the last inequality, we can write

a. e. in \((t_k,t_{k+1})\). \(\square \)

Definition 1

We define the state of all updates in iteration \(\ell \) as

$$\begin{aligned} X^\ell \mathrel {{\mathop :}{=}}{}&\left( \left( \tilde{\phi }_{k,k+1}^{\ell -1}\right) _{k = 0}^{K-1}, \left( \tilde{\phi }_{k,k-1}^{\ell -1}\right) _{k = 1}^{K}\right) \\ ={}&\left( \left( \tilde{x}_k^\ell (t_{k+1}) + \gamma \tilde{\lambda }_k^\ell (t_{k+1})\right) _{k = 0}^{K-1}, \left( \tilde{x}_k^\ell (t_k) - \gamma \tilde{\lambda }_k^\ell (t_k)\right) _{k = 1}^{K}\right) . \end{aligned}$$

Moreover, we define the mapping

$$\begin{aligned} T X^\ell \mathrel {{\mathop :}{=}}{}&\left( \left( \tilde{\phi }_{k,k+1}^{\ell }\right) _{k = 0}^{K-1}, \left( \tilde{\phi }_{k,k-1}^{\ell }\right) _{k = 1}^{K}\right) \\ ={}&\left( \left( \tilde{x}_{k+1}^{\ell }(t_{k+1}) + \gamma \tilde{\lambda }_{k+1}^{\ell }(t_{k+1})\right) _{k = 0}^{K-1}, \left( \tilde{x}_{k-1}^{\ell }(t_k) - \gamma \tilde{\lambda }_{k-1}^{\ell }(t_k)\right) _{k = 1}^{K}\right) . \end{aligned}$$

With this notation at hand and \(I\) denoting the identity, the update in Step 6 of Algorithm 1 is given by the relaxed mapping \(T_\varepsilon \mathrel {{\mathop :}{=}}(1 - \varepsilon ) T + \varepsilon I\), i.e.,

$$\begin{aligned} T_\varepsilon X^\ell = (1 - \varepsilon )T X^\ell + \varepsilon X^\ell . \end{aligned}$$

Consequently, we consider the fixed point iteration

$$\begin{aligned} X^{\ell +1} = T_\varepsilon X^\ell . \end{aligned}$$
(23)

Clearly, X is a fixed point of T and \(T_\varepsilon \) if and only if the transmission conditions for the errors

$$\begin{aligned} \tilde{x}_k(t_{k+1})&= \tilde{x}_{k+1}(t_{k+1}),{} & {} k = 0, \dotsc , K-1,\\ \tilde{\lambda }_k(t_k)&= \tilde{\lambda }_{k-1}(t_k),{} & {} k = 1, \dotsc , K, \end{aligned}$$

are satisfied. The errors fulfill these transmission conditions if and only if \(x_k^\ell \) and \(\lambda _k^\ell \) from the iteratively decomposed optimality conditions (18) do, too. This is only the case in a solution of (17). Since we assume that (17) has at least one solution, T and \(T_\varepsilon \) have a fixed point.

Remark 1

For any

$$\begin{aligned} \bar{X} = \left( \left( \bar{\phi }_{k,k+1}\right) _{k = 0}^{K-1}, \left( \bar{\phi }_{k,k-1}\right) _{k = 1}^{K}\right) \in \mathbb {R}^{2K}, \end{aligned}$$

the corresponding right-hand sides of the transmission conditions (18i) and (18j) are given by

$$\begin{aligned} \phi _{k,k+1}&= \bar{\phi }_{k,k+1} + x_k(t_{k+1}) + \gamma \lambda _k(t_{k+1}),\\ \phi _{k,k-1}&= \bar{\phi }_{k,k-1} + x_k(t_k) - \gamma \lambda _k(t_k), \end{aligned}$$

where \((x_k, u_k, \lambda _k)\) is the chosen solution of (17). If System (18) has a solution \((\bar{x}_k, \bar{u}_k, \bar{\lambda }_k)\), then the errors \((\tilde{x}_k, \tilde{u}_k, \tilde{\lambda }_k) = (\bar{x}_k, \bar{u}_k, \bar{\lambda }_k) - (x_k, u_k, \lambda _k)\) are well-defined and, thus, the mapping \(T: \mathbb {R}^{2K} \rightarrow \mathbb {R}^{2K}\) is well-defined, too.

Definition 2

We define the energies

Lemma 2

For all \(\ell \in \mathbb {N}\), the energies \(\mathcal {E}^\ell \) and \(\mathcal {F}^\ell \) are non-negative, i.e.,

$$\begin{aligned} \mathcal {E}^\ell \ge 0, \quad \mathcal {F}^\ell \ge 0 \end{aligned}$$

holds.

Proof

It is clear that \(\mathcal {E}^\ell \) is non-negative because it is a sum of norms. The non-negativity of \(\mathcal {F}^\ell \) follows from Lemma 1 and of \(Q_0\) and \(Q_\textrm{f}\) being positive semi-definite. \(\square \)

Next, we show that we can use the energies to describe the state of all updates.

Lemma 3

It holds

Proof

We multiply the state equation (19a) by \(\tilde{\lambda }_k^\ell \) and integrate to obtain

It follows

and

Now, we can write

\(\square \)

We get a similar result if we apply the mapping T first.

Lemma 4

It holds

Proof

Similarly to the proof of Lemma 3 we can write

\(\square \)

Remark 2

A direct consequence of Lemma 3 and 4 is

Since \(\mathcal {F}^\ell \) is non-negative, it follows

(24)

Hence, it is sufficient for Algorithm 1 to be well-defined that (18) has a solution for instead of for all vectors in \(\mathbb {R}^{2K}\).

Next, we observe that T is a non-expansive mapping.

Lemma 5

The mapping \(T: \mathbb {R}^{2K} \rightarrow \mathbb {R}^{2K}\) satisfies

for all \(X^1, X^2 \in \mathbb {R}^{2K}\).

Proof

Let \((x^1_k, u^1_k, \lambda ^1_k)\) and \((x^2_k, u^2_k, \lambda ^2_k)\) be the the solutions of (18) corresponding to \(X^1\) and \(X^2\). The errors that solve (19) are given by

$$\begin{aligned} (\tilde{x}^1_k, \tilde{u}^1_k, \tilde{\lambda }^1_k)&= (x^1_k, u^1_k, \lambda ^1_k) - (x_k, u_k, \lambda _k),\\ (\tilde{x}^2_k, \tilde{u}^2_k, \tilde{\lambda }^2_k)&= (x^2_k, u^2_k, \lambda ^2_k) - (x_k, u_k, \lambda _k). \end{aligned}$$

We define the differences

$$\begin{aligned} (y_k, v_k, \mu _k) \mathrel {{\mathop :}{=}}(\tilde{x}^1_k, \tilde{u}^1_k, \tilde{\lambda }^1_k) - (\tilde{x}^2_k, \tilde{u}^2_k, \tilde{\lambda }^2_k) = (x^1_k, u^1_k, \lambda ^1_k) - (x^2_k, u^2_k, \lambda ^2_k) \end{aligned}$$

for all \(k = 0, \ldots , K\). Because of the linear nature of (19), these differences fulfill the system

$$\begin{aligned} \dot{y}_k&= Ay_k + Bv_k \quad \text {a. e. in}\ (t_k,t_{k+1}), \end{aligned}$$
(25a)
$$\begin{aligned} R_0 y_0(t_0)&= 0 \quad \text {if } k=0,\end{aligned}$$
(25b)
$$\begin{aligned} R_\textrm{f}y_K(t_\textrm{f})&= 0 \quad \text {if } k=K,\end{aligned}$$
(25c)
$$\begin{aligned} \dot{\mu }_k&= -A^\top \mu _k \quad \text {a. e. in}\ (t_k,t_{k+1}),\end{aligned}$$
(25d)
$$\begin{aligned} \mu _0(t_0)&= Q_0 y_0(t_0) \quad \text {if } k = 0,\end{aligned}$$
(25e)
$$\begin{aligned} \mu _K(t_\textrm{f})&= - Q_\textrm{f}y_K(t_\textrm{f}) \quad \text {if } k=K,\end{aligned}$$
(25f)
$$\begin{aligned} y_k(t_{k+1}) + \gamma \mu _k(t_{k+1})&= \tilde{\phi }^1_{k,k+1} - \tilde{\phi }^2_{k,k+1} \quad \text {if } k \ne K,\end{aligned}$$
(25g)
$$\begin{aligned} y_k(t_k) - \gamma \mu _k(t_k)&= \tilde{\phi }^1_{k,k-1} - \tilde{\phi }^2_{k,k-1} \quad \text {if } k \ne 0. \end{aligned}$$
(25h)

Now, we have

Next, we investigate the relation between and . To this end, we multiply (25a) with \(\mu _k\) and integrate to get

From (22), we have

a. e. in \((t_k,t_{k+1})\). Therefore, it holds

Finally, we can conclude that

holds because \(Q_\textrm{f}\) and \(Q_0\) are positive semi-definite. \(\square \)

We can now apply Schaefer’s theorem to T.

Theorem 1

(Schaefer [48]) Let \(\mathcal {I}\) be a convex, closed, and bounded set in a uniformly convex Banach space \(\mathcal {X}\) and let \(T: \mathcal {I} \rightarrow \mathcal {I}\) be a non-expansive mapping with at least one fixed point. Then, for any \(\varepsilon \in (0, 1)\) the mapping \(T_\varepsilon = (1 - \varepsilon ) T + \varepsilon I\) is asymptotically regular, i.e.,

This theorem allows us to prove convergence for Algorithm 1 applied to the linear-quadratic problem (16).

Theorem 2

If Algorithm 1 is applied to Problem (16), the iterates \((x_k^\ell , \lambda _k^\ell )\) for \(k = 0, \ldots , K\) converge in the sense

$$\begin{aligned} x_k^\ell (t_{k+1}) - x_{k+1}^\ell (t_{k+1})&\rightarrow 0,\\ \lambda _k^\ell (t_{k+1}) - \lambda _{k+1}^\ell (t_{k+1})&\rightarrow 0 \end{aligned}$$

for all \(k = 0, \ldots , K-1\) as \(\ell \rightarrow \infty \).

Proof

By setting , Schaefer’s theorem yields

(26)

as \(\ell \rightarrow \infty \). We rewrite the scalar product of \(TX^\ell \) and \(X^\ell \) as

(27)

Using Lemmas 3,  4, and (27) we get

Because of (26), it follows

$$\begin{aligned} \tilde{x}_k^\ell (t_{k+1}) - \tilde{x}_{k+1}^\ell (t_{k+1})&\rightarrow 0,\\ \tilde{\lambda }_k^\ell (t_{k+1}) - \tilde{\lambda }_{k+1}^\ell (t_{k+1})&\rightarrow 0 \end{aligned}$$

for all \(k = 0, \ldots , K-1\) as \(\ell \rightarrow \infty \). Since this holds for the errors, it is also true for the iterates, i.e.,

$$\begin{aligned} x_k^\ell (t_{k+1}) - x_{k+1}^\ell (t_{k+1})&\rightarrow 0,\\ \lambda _k^\ell (t_{k+1}) - \lambda _{k+1}^\ell (t_{k+1})&\rightarrow 0 \end{aligned}$$

for all \(k = 0, \ldots , K-1\) as \(\ell \rightarrow \infty \). \(\square \)

Remark 3

Note that Theorem 2 states convergence of Algorithm 1 with respect to the error. In order to conclude for convergence of the iterates, further assumptions are needed. To this end, we recall that if we have continuity at the boundaries of the sub-intervals, i.e.,

$$\begin{aligned} x_k^\ell (t_{k+1})&= x_{k+1}^\ell (t_{k+1}),\\ \lambda _k^\ell (t_{k+1})&= \lambda _{k+1}^\ell (t_{k+1}) \end{aligned}$$

for all \(k = 0, \ldots , K-1\), then the optimality conditions (17) are fulfilled as well.

Therefore we can conclude that the iterates \((x_k^\ell , \lambda _k^\ell )\) converge to \((x_k, \lambda _k)\) in \(L^2(t_0, t_\textrm{f})\) for all \(k = 0, \ldots , K\) if (17) has a unique solution \((x_k, \lambda _k)\).

Moreover, we can conclude that there is a subsequence of \((x_k^\ell , \lambda _k^\ell )\) that converges to a solution \((x_k, \lambda _k)\) of (17) if the boundary points \(x_k^\ell (t_{k+1})\), \(x_{k+1}^\ell (t_{k+1})\), \(\lambda _k^\ell (t_{k+1})\), \(\lambda _{k+1}^\ell (t_{k+1})\) are contained in a compact set. This is the case if (17) has more than one but still finitely many solutions.

If System (17) has infinitely many solutions, a similar conclusion can, in general, not be made. However, Algorithm 1 can still be applied in practice, where we have to impose a reasonable stopping criterion anyway such as, e.g.,

(28)

for all \(k = 0, \ldots , K-1\) with given tolerances \(\delta _x, \delta _\lambda > 0\). This way, we can still compute an approximate solution that is arbitrarily close to a solution of (17) by choosing \(\delta _x\) and \(\delta _\lambda \) sufficiently small.

5 Case Studies

In this section, we apply Algorithm 1 to test its practical performance on some exemplary problems. We implemented the algorithm in Julia 1.5.3 [3].Footnote 1 All computations were done on a machine with an Intel(R) Core(TM) i7-8550U CPUwith 4 physical cores (and 8 logical cores), 1.8 GHz to 4.0 GHz, and 16 GB RAM. To solve the virtual control problems in Step 3, we apply a first-discretize-then-optimize approach using a Runge–Kutta method [20, 49]. To this end, we equidistantly partition each time domain \([t_k, t_{k+1}]\), \(k = 0, \dotsc , K\), using \(N + 1 \in \mathbb {N}\) time points

$$\begin{aligned} t_{ki} \mathrel {{\mathop :}{=}}t_k + i \frac{(t_{k+1} - t_k)}{N}, \quad i = 0, \ldots , N. \end{aligned}$$

Runge–Kutta methods approximate the solution of the ODE

$$\begin{aligned} \dot{x}_k = f(x_k, u_k) \end{aligned}$$

of the virtual control problems (12), (14), and (15) as

$$\begin{aligned} x_k(t_{k(i+1)}) = x_k(t_{ki}) + \varDelta t \sum _{j=1}^s b_j l_j, \quad i = 0, \ldots , N, \end{aligned}$$

with the step size \(\varDelta t = (t_{k+1} - t_k) / N\), the intermediate steps

$$\begin{aligned} l_j = f\left( x_k(t_{ki}) + \varDelta t \sum _{m=1}^{s} a_{jm} l_m, \, u_k(t_{ki})\right) , \end{aligned}$$

given coefficients \(a_{jm} \in \mathbb {R}\) and \(b_j \ge 0\) for \(j, m \in \{1, \ldots , s\}\), and the number of stages \(s \in \mathbb {N}\). In what follows, we are using the classic fourth-order Runge–Kutta method with coefficients

$$\begin{aligned} a = \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0\\ \frac{1}{2} &{} 0 &{} 0 &{} 0\\ 0 &{} \frac{1}{2} &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0 \end{bmatrix}, \quad b = \left( \frac{1}{6}, \frac{1}{3}, \frac{1}{3}, \frac{1}{6}\right) ^\top . \end{aligned}$$
(29)

Moreover, we use the initial condition (12c) to solve for the virtual control

$$\begin{aligned} h_k = x_k(t_k) - \phi _{k,k-1}^{\ell -1}. \end{aligned}$$

We can then substitute \(h_k\) in the objective function and remove the constraint (12c). The discretized virtual control problem (12) is thus given by

(30a)
$$\begin{aligned} \text {s.t.}\quad&x_k(t_{k(i+1)}) = x_k(t_{ki}) + \varDelta t \sum _{j=1}^s b_j l_j, \quad i = 0, \ldots , N, \end{aligned}$$
(30b)
$$\begin{aligned}&u_k(t_{ki}) \in U, \quad i = 0, \dotsc , N. \end{aligned}$$
(30c)

The problems (14), (15) can be discretized analogously. Problem (30) is a finite-dimensional optimization problem, which we model using GAMS 25.1.2 [39]. The resulting instances are solved using ANTIGONE 1.1 [40]. All virtual control problems are solved in parallel using

figure b

’s build-in multi-threading capabilities.

In our implementation, the iteration is started with the zero transmission conditions \(\phi _{k,k-1}^0 = 0 \in \mathbb {R}^n\) for \(k=1, \dotsc , K\) and \(\phi _{k,k+1}^0 = 0 \in \mathbb {R}^n\) for \(k=0, \dotsc , K-1\). We initialize the algorithm with all variables set to 0 and after the first iteration, we warmstart all virtual control problems with their solution from the previous iteration. As a stopping criterion for Algorithm 1, we use (28) for all \(k = 0, \dotsc , K-1\) with tolerances \(\delta _x = \delta _\lambda = 10^{-2}\). In addition, we use the time limit of 1000 s for all subproblems unless stated otherwise.

After termination of the algorithm, we fix the resulting control u and compute the corresponding state x on the entire time horizon \((t_0, t_\textrm{f})\) to obtain an accurate objective value.

5.1 A Mixed-Integer Linear-Quadratic Problem

We consider the mixed-integer linear-quadratic problem

$$\begin{aligned} \min \quad&x_1(1)^2 + x_2(1)^2 + \int _{0}^{1} 0.005u^2 \,\textrm{d}t \end{aligned}$$
(31a)
$$\begin{aligned} \text {s.t.}\quad&\dot{x}_1 = 2x_2 \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (0,1),\end{aligned}$$
(31b)
$$\begin{aligned}&\dot{x}_2 = -x_1 + x_2 - u \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (0,1),\end{aligned}$$
(31c)
$$\begin{aligned}&x_1(0) = -2, \quad x_2(0) = 1,\end{aligned}$$
(31d)
$$\begin{aligned}&u \in \{0,1,2,3,4\} \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [0,1]. \end{aligned}$$
(31e)

Note that this problem is of the form (16).

We use the time-domain decomposition with \(t_i = i / 4\) for \(i = 0, \dotsc , 4\) as well as parameters \(\gamma = 1\), \(\varepsilon = 0.5\), and \(\varDelta t = 1/100\).

Figure 2 shows the solution of Problem (31) using the direct discretization and solution approach from above on a single interval [0, 1] (left) and the one computed using the proposed algorithm with 4 time domains (right). Although the controls differ, the resulting states are almost the same. Additionally, the first part of Table 1 lists the number of iterations, the running time, and the objective value for different decompositions of the time domain. Even though the algorithm does not outperform the solution of the original problem (first row of the table), one can see that they are rather comparable w.r.t. the objective value for 2 and 4 domains. This can be explained by the fact that Problem (31) is quite simple to solve. Thus, solving the fully discretized original problem directly using ANTIGONE(on the entire time horizon) is already rather efficient. The worse objective values in the case of 8 and 16 domains can be attributed to the errors we make at the interfaces of the domains because of the tolerances \(\delta _x\) and \(\delta _\lambda \). To show this effect we re-ran the cases of 2, 4, 8, and 16 domains with the smaller tolerances \(\delta _x = \delta _\lambda = 5 \times 10^{-3}\) and \(\delta _x = \delta _\lambda = 10^{-3}\). The corresponding results are shown in the second and third part of Table 1. While these smaller tolerances obviously increase the running time of the algorithm, they have a positive impact on the objective value. This impact increases if more domains are used. Since (31) is a mixed-integer linear-quadratic problem, it is also possible to solve it with the solver Gurobi 9.1.2. However, our preliminary numerical results showed that for almost all cases, ANTIGONEperforms better w.r.t. the running time. For comparison, we include these results in the fourth part of Table 1.

To make sure that our discretization step size \(\varDelta t\) is small enough, we used the resulting controls from the first part of Table 1 to compute the corresponding state \(\hat{x}\) with the halved step size \(\varDelta t / 2\). The subsequent errors are all smaller than \(1.4 \times 10^{-9}\) which is significantly smaller than the tolerances \(\delta _x\) and \(\delta _\lambda \) at the interfaces.

Fig. 2
figure 2

Solutions of Problem (31) solved with (right) and without (left) Algorithm 1

Full size image
Table 1 Results for Problem (31) for different numbers of time domains (first column)
Full size table

Next, we study the impact of the parameter \(\gamma \). It functions as a weighing factor of the state x compared to the adjoint \(\lambda \) in Step 4 of the algorithm. It is thus an important parameter regarding the errors that are made w.r.t. the continuity of the states and adjoints at the interfaces of the time domains. Figure 3 displays these errors for \(\gamma \in \{0.2, 1, 5\}\) and the case of 4 domains. One can clearly see that the smallest value \(\gamma =0.2\) leads to larger errors for the adjoint \(\lambda \) compared to the errors for the state x. For the larger value \(\gamma =5\) it is the other way around. For \(\gamma =1\), both errors have roughly the same size. Since in our case, the tolerances \(\delta _x\) and \(\delta _\lambda \) are the same, it takes less iterations for the algorithm to reach the stopping criterion (28) for \(\gamma = 1\) than for the other values. More precisely, we need 35 iterations instead of 45 for \(\gamma = 0.2\) or 44 for \(\gamma = 5\). Figure 3 also shows the typical convergence behavior of Algorithm 1, i.e., the errors are reduced quickly during the first iterations but only decrease slowly when they are already closer to zero. This suggest that the method has an asymptotically sublinear convergence rate. However, estimates on these rates are beyond the scope of this paper.

Fig. 3
figure 3

The maximum norm of all errors w.r.t. the state x and the adjoint \(\lambda \) for each iteration of Problem (31) for different values of \(\gamma \). Top: \(\gamma = 0.2\). Middle: \(\gamma = 1\). Bottom: \(\gamma = 5\)

Full size image

Lastly for this example, we investigate the role of the parameter \(\varepsilon \), which weighs the boundary data of the domain k against the boundary data of its neighboring domain \(k-1\) or \(k+1\). Table 2 shows the effect of different parameters \(\varepsilon \) on the number of iterations, the running time, and the objective value of Problem (31) when solved using 4 time domains. One can see that \(\varepsilon \) does not have a significant impact on the objective value but on the number of iterations and, thus, the running time. We see that we obtain a roughly monotonically increasing relation between \(\varepsilon \) and the running times of the algorithm. For this example, the fastest algorithm is obtained with \(\varepsilon = 0.1\). We also additional sampling points for \(\varepsilon \) between 0 and 0.2, which confirm that \(\varepsilon = 0.1\) is the best choice for this problem.

Table 2 Results for Problem (31) for different parameters \(\varepsilon \)
Full size table

5.2 Mixed-Integer Nonlinear Problems

The convergence theory from Sect. 4 does not apply to problems with nonlinearities in the differential equation. Nevertheless, we can conclude from considering Algorithm 1 as the fixed-point iteration (23) that upon convergence, the error in the transmission conditions vanishes and a candidate for a Pontryagin minimum is found. We demonstrate this for two nonlinear examples.

As a first nonlinear example we consider Fuller’s initial value problem from the benchmark library mintOC of mixed-integer optimal control problems (see [45] and https://mintoc.de):

$$\begin{aligned} \min \quad&(x_1(1) - 0.01)^2 + x_2(1)^2 + x_3(1) \end{aligned}$$
(32a)
$$\begin{aligned} \text {s.t.}\quad&\dot{x}_1 = x_2 \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (0,1),\end{aligned}$$
(32b)
$$\begin{aligned}&\dot{x}_2 = 1 - 2u \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (0,1),\end{aligned}$$
(32c)
$$\begin{aligned}&\dot{x}_3 = x_1^2 \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (0,1),\end{aligned}$$
(32d)
$$\begin{aligned}&x_1(0) = 0.01, \quad x_2(0) = 0, \quad x_3(0) = 0,\end{aligned}$$
(32e)
$$\begin{aligned}&u \in \{0, 1\} \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [0,1]. \end{aligned}$$
(32f)
Table 3 Results for problem (32) for different numbers of domains
Full size table

Again, we choose the parameters \(\gamma = 1\) and \(\varepsilon = 0.5\) for our computations. For this example the step size for the discretization is \(\varDelta t = 1/50\). We solve Problem (32) with Algorithm 1 using 1, 2, 4, 8, and 16 domains. For a single domain, i.e., without using the presented time-domain decomposition approach, ANTIGONEreaches the time limit and cannot solve the problem. For two domains, our algorithm also reaches the time limit in the first iteration. The remaining results are shown in Table 3. For 4 domains, the algorithm finds a solution in 56 s. Figure 4 shows the solution for 4 domains. For more domains, the number of iterations and the running time increases. The objective values for the last three cases are all close to zero. This shows the potential of Algorithm 1 when applied to nonlinear problems since it can outperform applying a global MINLP solver to the discretized problem directly, i.e., on the entire time horizon. However, let us comment on that this comparison needs to be interpreted carefully since the goal of ANTIGONEas a global MINLP solver is different to the one of our method that aims to compute a Pontryagin minimum of the problem. Thus, we additionally applied ANTIGONEwith a time limit of 56 s, which is the solution time of our method, and compared the feasible point found by ANTIGONEwithin this time limit with the point that our method computed. For the considered instance, ANTIGONEfound a feasible point of comparable quality in 26 s. Note, however, that this point comes with no quality guarantee whereas we can guarantee that we computed a Pontryagin minimum.

Again, we used the resulting controls from Table 3 to compute the corresponding state \(\hat{x}\) with the halved step size \(\varDelta t / 2\). The errors are all smaller than \(1.9 \times 10^{-9}\) which is, again, significantly smaller than the tolerances \(\delta _x\) and \(\delta _\lambda \) at the interfaces.

Fig. 4
figure 4

Solutions of problem (32) solved with Algorithm 1 using 4 domains

Full size image

As for the example in the linear-quadratic case we again test, which values of \(\varepsilon \) lead to the best results. Table 4 contains the results for the case of 4 domains. We skip the case of \(\varepsilon = 0\) since we reached the time limit for this case. The algorithm also takes rather long for \(\varepsilon = 0.1\). For \(\varepsilon \) between 0.2 and 0.7, one achieves the shortest running times. Again, if the value of \(\varepsilon \) is too large, the number of iterations and the running time increase considerably.

Table 4 Results for problem (32) for different parameters \(\varepsilon \)
Full size table

As a second example, we consider a variation of Problem (32), namely Fuller’s initial value multimode problem from mintOC (see again [45] and https://mintoc.de):

$$\begin{aligned} \min \quad&(x_1(1) - 0.01)^2 + x_2(1)^2 + x_3(1) \end{aligned}$$
(33a)
$$\begin{aligned} \text {s.t.}\quad&\dot{x}_1 = x_2\quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (0,1),\end{aligned}$$
(33b)
$$\begin{aligned}&\dot{x}_2 = 1 - 2u_1 - 0.5u_2 - 3u_3 \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (0,1),\end{aligned}$$
(33c)
$$\begin{aligned}&\dot{x}_3 = x_1^2 \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (0,1),\end{aligned}$$
(33d)
$$\begin{aligned}&x_1(0) = 0.01, \quad x_2(0) = 0, \quad , x_3(0) = 0,\end{aligned}$$
(33e)
$$\begin{aligned}&1 = \sum _{i=1}^{4} u_i \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [0,1],\end{aligned}$$
(33f)
$$\begin{aligned}&u \in \{0, 1\}^4 \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [0,1]. \end{aligned}$$
(33g)

Here, we have three more binary controls and an SOS-1 constraint w.r.t. the binary controls. This makes the problem harder to solve, which is why we increased the maximal running time for this example to 2000 s. Note that \(u_4\) does not occur in the ODE system (33b–33d). Therefore, \(u_4(t)=1\) corresponds to not controlling the system at time t.

The parameters \(\gamma = 1\), \(\varepsilon = 0.5\), and \(\varDelta t = 1/50\) stay unchanged and we, again, solve the problem using 1, 2, 4, 8, and 16 domains.

Table 5 Results for problem (33) for different numbers of domains
Full size table

The results are displayed in Table 5 except for a single domain and the case of 16 domains. For a single domain, we again reach the time limit—which is also the case for our algorithm applied to 16 domains, where the time limit is reached in iteration 737. For this example, we achieved the fastest running time (of 209 s) for 8 domains. One can see that the number of iterations for 2 and 4 domains is lower than for 8 domains but the running times are higher. This is the case because, in a few iterations, the solution time of a virtual control problem is much higher than usual. Thus, we can see the trade-off between (i) a usually higher coordination effort of the method to obtain continuity at the interfaces of the time domains for a larger number of domains and (ii) a usually larger running time for less domains since the virtual control problems then are larger. The solution is shown in Fig. 5.

Fig. 5
figure 5

Solutions of Problem (33) solved with Algorithm 1 using 8 domains. Because of the SOS-1 condition (33f) exactly one \(u_i\) (\(i=1,2,3,4\)) is 1 at the same time, thus, we use the aggregated control \(u = u_1 / 3 + 2 u_2 / 3 + u_3 + 0u_4\) to simplify the plot

Full size image

We again compared the solution that we obtain with the best feasible point computed by ANTIGONEwithin the time limit given by the best running time of our method, i.e., within 209 s. In this case, the feasible point found by ANTIGONEis slightly worse than the one we computed. The first feasible point found by ANTIGONEthat is better than our solution needs 899 s to be computed by ANTIGONE.

For this example, we also used the resulting controls from Table 5 to compute the corresponding state \(\hat{x}\) with the halved step size \(\varDelta t / 2\). This time, the errors are all smaller than \(3.1 \times 10^{-9}\) which is, again, significantly smaller than the tolerances \(\delta _x\) and \(\delta _\lambda \) at the interfaces.

An example for which convergence of our implementation of Algorithm 1 was not observed is a reformulation of the highly nonlinear problem “F-8 aircraft” from the mintOC library (see [45] and https://mintoc.de) to a fixed-time horizon problem, where either the time limit of 2000 s was reached or at some point one of the virtual control problems reported infeasibility. This happened for all combinations of parameters \(\varepsilon \in \{0, 0.1, \ldots , 0.9\}\), \(\varDelta t \in \{1/50, 1/100\}\), \(\delta _x, \delta _\lambda \in \{10^{-1}, 10^{-2}\}\) and all numbers of domains in \(\{1, 2, 4, 8, 16\}\) and could be caused by the presence of multiple local minima. See [15] for a successful application of a global maximum principle to the aircraft problem with numerical results.

Remark 4

Another instructive exemplary problem is

$$\begin{aligned} \min \quad&T\end{aligned}$$
(34a)
$$\begin{aligned} \text {s.t.}\quad&\ddot{x} = u \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (0,T), \end{aligned}$$
(34b)
$$\begin{aligned}&x(0) = -7, \quad \dot{x}(0) = 2,\end{aligned}$$
(34c)
$$\begin{aligned}&x(T) = 0, \quad \dot{x}(T) = 0,\end{aligned}$$
(34d)
$$\begin{aligned}&u \in \{-1, 0, 1\} \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [0,T]. \end{aligned}$$
(34e)

The state \(x(t) \in \mathbb {R}\) represents the position of a car with bounded acceleration u. The car starts at \(-7\) and has an initial speed of 2. The goal is to park the car in the origin in the shortest possible time T. The optimal bang-bang solution to this problem is to accelerate (\(u(t) = 1\)) until \(t^*=1\) and to break (\(u(t) = -1\)) after this until \(T=4\). To fit this in our setting we use a time transformation to reformulate the problem as

$$\begin{aligned} \min \quad&x_3^2\end{aligned}$$
(35a)
$$\begin{aligned} \text {s.t.}\quad&\dot{x}_1 = x_2 x_3 \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (0,1),\end{aligned}$$
(35b)
$$\begin{aligned}&\dot{x}_2 = u x_3 \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ (0,1),\end{aligned}$$
(35c)
$$\begin{aligned}&x_1(0) = -7, \quad x_2(0) = 2,\end{aligned}$$
(35d)
$$\begin{aligned}&x_1(1) = 0, \quad x_2(1) = 0,\end{aligned}$$
(35e)
$$\begin{aligned}&u \in \{-1, 0, 1\} \quad \mathrm{a.}\,\mathrm{e.}\,\textrm{in}\ [0,1], \end{aligned}$$
(35f)

where \(x_1\) is the position, \(x_2\) the speed, and \(x_3\) the time T. This is a nonlinear problem with initial and terminal conditions. The optimal solution stays unchanged but the switching point between acceleration and breaking is now \(t^*=1/4\). If we try to solve this problem with \(\varDelta t = 1/100\) using ANTIGONE, no feasible point is found. For 2 domains of equal length, the algorithm reaches the time limit of 1000 s in iteration 19. However, for 4 domains of equal length and the 2 domains [0, 1/4], [1/4, 1] the global optimal solution is found in 60.886 s and 182.550 s, respectively. This can be explained by both decompositions containing the switching point \(t^*=1/4\) in an interface between two subdomains, which decreases the difficulty of the virtual control problems. Therefore, it could be an interesting topic for future research to compute the switching points of a bang-bang solution before applying Algorithm 1. This could be combined with considering constant control decisions for each subdomain, which could further decrease the difficulty of solving the virtual control problems.

6 Conclusion

Our results show that linear-quadratic mixed-integer optimal control problems can be solved iteratively by computing solutions to suitably chosen virtual mixed-integer optimal control problems on smaller time-horizons. In order to reach a certain accuracy of the solution, these subproblems then require less discretization variables and they can be solved in parallel. Both aspects can provide significant computational advantages compared to direct discretization of the original problem on the entire time horizon. We exemplarily demonstrate this with our numerical results, where we also discuss the choice of additional parameters of the proposed algorithm. Our computational experiments show that this advantage also pays off for the case of nonlinear problems if the iterative procedure converges. However, a more detailed numerical study that might also include a comparison with other methods are out of scope of this paper and part of our future work. In particular, the iterative method may even yield solutions where full direct discretization fails. Guarantees for nonlinear problems, however, requires further algorithmic and theoretical investigations.

The presented study is primarily motivated by the need to incorporate integer restrictions on the control values into optimal control problems as to model logical constraints. However, the findings are also interesting for classic optimal control problems with other nonconvex control constraints, because the proposed iterative procedure provides an alternative to shooting-type methods as a solution approach with its well-known limitations such as proper initialization or achieving global optimality in the Hamiltonian maximization condition.

Future work will therefore concern extensions of this approach to more general problem classes including further nonlinearities, state constraints, and also partial differential equations. Moreover, the general type of methods discussed in this paper is known to have slow convergence rates although approximate solutions of acceptable quality might be obtained rather quickly. It is thus another future research topic to consider possible crossover-approaches in which an acceptable solution found with the proposed method is handed over to another method that has favorable local convergence properties. Additionally, investigations on the convergence rates and on accelerating mechanisms would be of great interest. Finally, the method presented in this paper could be combined with techniques that try to compute the time points at which the optimal control switches, see, e.g., [9, 50], and to use this information to set up the time blocks of the domain decomposition.