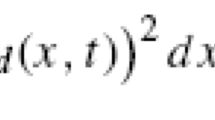A space–time variational method for optimal control problems: well-posedness, stability and numerical solution

Abstract

We consider an optimal control problem constrained by a parabolic partial differential equation with Robin boundary conditions. We use a space–time variational formulation in Lebesgue–Bochner spaces yielding a boundedly invertible solution operator. The abstract formulation of the optimal control problem yields the Lagrange function and Karush–Kuhn–Tucker conditions in a natural manner. This results in space–time variational formulations of the adjoint and gradient equation in Lebesgue–Bochner spaces, which are proven to be boundedly invertible. Necessary and sufficient optimality conditions are formulated and the optimality system is shown to be boundedly invertible. Next, we introduce a conforming uniformly stable simultaneous space–time (tensorproduct) discretization of the optimality system in these Lebesgue–Bochner spaces. Using finite elements of appropriate orders in space and time for trial and test spaces, this setting is known to be equivalent to a Crank–Nicolson time-stepping scheme for parabolic problems. Comparisons with existing methods are detailed. We show numerical comparisons with time-stepping methods. The space–time method shows good stability properties and requires fewer degrees of freedom in time to reach the same accuracy.

1 Introduction

The optimal control of partial differential equations (PDE) is an area of vast growing significance e.g. in fluid flows, crystal growths or medicine, see, e.g. [1, 2]. This explains the huge amount of literature concerning theoretical as well as numerical aspects.

The abstract form of such problems relies on a cost function $J:{{\mathcal {Y}}}\times {{\mathcal {U}}}\rightarrow {\mathbb {R}}$, where ${{\mathcal {Y}}}$ and ${{\mathcal {U}}}$ are function spaces for the state y and the control u. The constrained optimal control problem then takes the form

$$\begin{aligned} J(y,u)\rightarrow \min !\quad \text {s.t.}\quad e(y,u) = 0, \end{aligned}$$

(1.1)

where the constraint $e(y,u) = 0$ is often termed as state equation. At this point, there is a bifurcation concerning the subsequent approach. On the one hand, the first-discretize-then-optimize approach seeks for an appropriate discretization of (1.1) and then derives optimality conditions for the discretized optimal control problem. On the other hand, first-optimize-then-discretize means that optimality conditions are derived directly w.r.t. (1.1) and then the arising optimality system is discretized. We shall follow the second approach.

First-optimize-then-discretize

Within this approach, the first step is a suitable interpretation of the state equation. In case of a PDE-constrained optimal control problem, the state equation is a PDE. Here, we are interested in the case where the PDE is a parabolic problem in space and time. This offers a variety of different formulations of the state equation, e.g.

• Strong form: $e(y,u) = 0$ is interpreted pointwise. This, however does often not allow statements on the well-posedness of the state equation.

• Semi-variational: Using a variational form in either space or time yields either an initial value problem of an ordinary differential equation or a system of elliptic boundary value problems.

• Space-0time variational: Space and time are both treated as variables in a variational sense. In that case, the state equation is tested by space–time test functions $z\in {{\mathcal {Z}}}$, where ${{\mathcal {Z}}}$ is an appropriate Lebesgue–Bochner space, and takes the form, for a right-hand side $f(\cdot ;u)\in {{\mathcal {Z}}}'$

  $$\begin{aligned} \text {find } y\in {{\mathcal {Y}}}:\quad b(y,z) = f(z; u)\quad \text { for all } z\in {{\mathcal {Z}}}. \end{aligned}$$

  (1.2)

Space–time variational formulations and adjoint problem

We follow the last-mentioned method in the above list. In the literature, this approach has already been studied, see e.g. [3,4,5,6,7,8], but with some (partly subtle) differences to our approach to be detailed below. The well-posedness theory for (1.2) dates back (at least) to the 1970s, see e.g. [9,10,11]. In order to describe to which extent our approach differs from the mentioned papers, we first note, that we understand well-posedness in the sense of Hadamard as existence, uniqueness and stability, [12]. Following e.g. [13], we can rephrase this as follows: By ${{\mathcal {L}}}({{\mathcal {Y}}},{{\mathcal {Z}}}')$ we denote the space of bounded linear mappings ${{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}'$ and by ${{{\mathcal {L}}}_{\text {is}}}({{\mathcal {Y}}},{{\mathcal {Z}}}')$ its subset of boundedly invertible mappings ${{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}'$. We call a problem $By=z'$ in ${{\mathcal {Z}}}'$ well-posed if $B\in {{{\mathcal {L}}}_{\text {is}}}({{\mathcal {Y}}},{{\mathcal {Z}}}')$. Hence, we need to detail the choices of the bilinear form $b(\cdot ,\cdot )$ as well as the trial and test spaces ${{\mathcal {Y}}}$ and ${{\mathcal {Z}}}$. We shall see that our subsequent choice allows us to show that the solution operator $B:{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}'$ defined in (2.14) is in ${{{\mathcal {L}}}_{\text {is}}}({{\mathcal {Y}}},{{\mathcal {Z}}}')$. This necessarily implies that ${{\mathcal {Y}}}\not ={{\mathcal {Z}}}$ and requires these spaces to satisfy an inf-sup condition

$$\begin{aligned} \inf _{y \in {{\mathcal {Y}}}} \sup _{z \in {{\mathcal {Z}}}} \frac{b(y, z)}{\Vert y\Vert _{{\mathcal {Y}}}\, \Vert z\Vert _{{\mathcal {Z}}}} =: \beta >0, \end{aligned}$$

(1.3)

which is known to hold, [14, 15]. We postpone a detailed comparison with other space–time methods to Sect. 2.2 (in particular Remark 2.8) below.

Another difference of the known approaches from the literature and our proposed framework is the derivation of an optimality system. For the details, we refer to Sect. 3.2, Remark 3.10 below. We use the variational form (1.2) to derive the reduced problem (w.r.t. the control), which allows us to prove the existence of a unique optimal solution. In a next step, we define the Lagrange function, again using the variational form (1.2), from which we then derive the Karush–Kuhn–Tucker (KKT) conditions. The adjoint problem arises in a natural variational form by the KKT system, see Proposition 3.3 below.

Space–time discretization

In a final step, we propose a conforming space–time discretization, which amounts to construct finite-dimensional spaces ${\mathcal {Y}}_\delta \subset {\mathcal {Y}}$ and ${\mathcal {Z}}_\delta \subset {\mathcal {Z}}$ for a Petrov–Galerkin discretization of (1.2) and later also the control space ${\mathcal {U}}_\delta \subset {\mathcal {U}}$. Since ${{\mathcal {Y}}}\not ={{\mathcal {Z}}}$, the discrete spaces ${\mathcal {Y}}_\delta$ and ${\mathcal {Z}}_\delta$ need to satisfy a discrete inf-sup condition, also known as Ladyshenskaja–Babuška–Brezzi (LBB) condition, i.e.,

$$\begin{aligned} \inf _{y_\delta \in {{\mathcal {Y}}}_\delta } \sup _{z_\delta \in {{\mathcal {Z}}}_\delta } \frac{b(y_\delta , z_\delta )}{\Vert y_\delta \Vert _{{\mathcal {Y}}}\, \Vert z_\delta \Vert _{{\mathcal {Z}}}} {=: {\bar{\beta }}} >0 \end{aligned}$$

(1.4)

uniformly in $\delta$ (where ${\bar{\beta }}$ is independent of $\delta$).¹ The discrete inf-sup constant ${\bar{\beta }}$ is particularly relevant as the Xu–Zikatanov lemma [16] yields an error/residual-relation with the multiplicative factor ${{{\bar{\beta }}^{-1}}}$. In some cases, one can realize optimally stable discretizations, i.e., ${{\bar{\beta }}}=1$ (in particular, the constant is independent of the final time, which is crucial for optimal control problems), [15, 17, 18]. This is a key motivation for our approach. However, there are different stable discretizations described in the literature. For example, in [14, 19, 20] wavelet methods have been used to derive an LBB-stable discretization, [15, 17, 18] propose tensorproduct discretizations (some of them reducing to time-stepping schemes) and [8, 21] introduce unstructured finite element discretizations in space and time. Here, we use a tensorproduct discretization since they allow for efficient numerical solvers and admit optimal stability, [22, 23]; of course, also other schemes could be used instead. Our approach leads to a different discrete system as previous approaches, see Sect. 4.5, Remark 4.4 below.

Until recently it has been believed that a simultaneous discretization of time and space variables would be way too costly since problems in $n+1$ dimensions need to be solved, where n denotes the space dimension. This has changed somehow since it is nowadays known that space–time discretizations yield good stability properties, can efficiently be used for model reduction and can also be treated by efficient numerical solvers, see [14, 17, 22,23,24,25,26,27,28], just to name a few papers in that direction. However, the issues of a suitable discretization and the question if the arising higher-dimensional problem can efficiently be solved remain. Of course, also for space–time approaches different from ours, there are also efficient numerical solvers known, see e.g. [2, 29, 30].

Model problem

We consider the following PDE-constrained optimal control problem.

Problem 1.1

(Model problem in classical form) Let $I=(0,T)\subset {\mathbb {R}}$, $0<T<\infty$ and $\Omega \subset {\mathbb {R}}^n$ be a bounded Lipschitz domain. The outer unit normal vector of $\partial \Omega {=:} \Gamma$ is denoted by $\nu (x) \in {\mathbb {R}}^n$ for almost all $x\in \Gamma$ w.r.t. the surface measure.

The state space ${{\mathcal {Y}}}$ consists of mappings $y:I\times \Omega \rightarrow {\mathbb {R}}$, the control space ${{\mathcal {U}}}$ of functions $u: I \times \Omega \rightarrow {\mathbb {R}}$. We are interested in determining a control ${\overline{u}}\in {{\mathcal {U}}}$ and a corresponding state ${\overline{y}} \in {{\mathcal {Y}}}$ that solve the following optimization problem:

$$\begin{aligned} \min \limits _{ \left( y,u\right) \in {{\mathcal {Y}}}\times {{\mathcal {U}}}} J(y,u) :={\textstyle {\frac{1}{2}}} \int \limits _{\Omega } |y(T,x) - y_d(x) |^2 \mathop {}\!\textrm{d}x + {\textstyle {\frac{\lambda }{2}}} \int \limits _{I} \int \limits _{\Omega } |u(t,x) |^2 \mathop {}\!\textrm{d}x \mathop {}\!\textrm{d}t \end{aligned}$$

s.t.

where the functions $\mu : {\Gamma } \rightarrow {\mathbb {R}}$, $\eta :I \times \Gamma \rightarrow {\mathbb {R}}$ and $y_d: \Omega \rightarrow {\mathbb {R}}$ as well as a scalar $\lambda > 0$ are given. Moreover, R is a linear operator, whose role will be described below. We shall always assume that $\mu (x)>0$² for all $x \in \Omega$ a.e..

Remark 1.2

(a) We could easily extend to a cost function of the form

$$\begin{aligned} J(y,u)&= {\textstyle {\frac{\omega _1}{2}}} \Vert y-y_d\Vert _{L_2(I; L_2(\Omega ))}^2 + {\textstyle {\frac{\omega _2}{2}}} \Vert y(T)-y_d(T)\Vert _{L_2(\Omega )}^2 + {\textstyle {\frac{\omega _3}{2}}} \Vert u\Vert _{L_2(I; L_2(\Omega ))}^2, \end{aligned}$$

with real constants $\omega _1$, $\omega _2\ge 0$, $\omega _1+\omega _2>0$, $\omega _3>0$ and $y_d:I\times \Omega \rightarrow {\mathbb {R}}$.

(b) The extension to inhomogeneous initial conditions $y(0,x)=y_0$ and other types of boundary conditions follows standard lines, e.g. [14] and Remark 2.7.

(c) In the first preprint version of this paper, we considered box constraints for the control. In order to discuss the analysis concerning well-posedness and convergence in full detail, we decided to devote control constraints to future research.

Main contributions

In this paper, we introduce a variational space–time approach which allows us to show that the solution operator for the constraint as well as of the first order optimality system is boundedly invertible. This yields a corresponding choice of the spaces ${{\mathcal {Y}}}$, ${{\mathcal {Z}}}$ and ${{\mathcal {U}}}$ for state, co-state and control, in particular allowing ${{\mathcal {Y}}}\not ={{\mathcal {Z}}}$. As we prove that $B\in {{{\mathcal {L}}}_{\text {is}}}({{\mathcal {Y}}},{{\mathcal {Z}}}')$, which requires ${{\mathcal {Y}}}\not ={{\mathcal {Z}}}'$, there is a unique and stable solution for all $f(\cdot ;u)\in {{\mathcal {Z}}}'$. Hence, ${{\mathcal {Z}}}'$ is the “largest” co-state space allowing for an isomorphism, in particular allowing for minimal regularity (for the right-hand side and the initial state). Moreover, we construct a uniformly stable simultaneous space–time discretization of the optimality system in these arising spaces.

Even though Problem 1.1 is a simple model problem (and there are in fact several articles in the literature covering more general problems), a consideration of more general scenarios (e.g. think of control constraints) is expected to be done following standard paths.

Organization of the paper

The remainder of this paper is organized as follows. In Sect. 2, we recall and collect some preliminaries on PDE-constrained optimization problems in reflexive Banach spaces and on space–time variational formulations of parabolic PDEs. The space–time variational formulation of the optimal control problem under consideration is developed in Sect. 3. In particular, we derive necessary and sufficient optimality conditions. Section 4 is devoted to the space–time discretization of the PDE, the discretization of the control as well as of the adjoint problem. The latter one turns out to be much simpler in our space–time context than in the semi-variational setting as we obtain a linear system whose matrix is just the transposed of the matrix appearing in the primal problem. The fully discretized optimal control problem is then solved numerically. We report on our numerical experiments in Sect. 5 and conclude by a summary, conclusions and an outlook in Sect. 6.

2 Preliminaries

Let us start by collecting some preliminaries that we will need in the sequel.

2.1 Optimal control problems

In this section, we recall the abstract functional analytic framework for optimal control problems in reflexive Banach spaces³ which we will later apply within the space–time setting. The consideration of control and/or state constraints is devoted to future research.

Problem 2.1

Let ${{\mathcal {Y}}}$, ${{\mathcal {U}}}$, ${{\mathcal {Z}}}$ be some real reflexive Banach spaces. Given an objective function $J:{{\mathcal {Y}}}\times {{\mathcal {U}}}\rightarrow {\mathbb {R}}$ and the state operator $e:{{\mathcal {Y}}}\times {{\mathcal {U}}}\rightarrow {{\mathcal {Z}}}'$, we consider the constrained optimization problem

$$\begin{aligned} \min \limits _{ (y,u) \in {{\mathcal {Y}}}\times {{\mathcal {U}}}} J(y,u) \quad \text {subject to (s.t.) the constraint } e(y,u)=0{,} \end{aligned}$$

where we assume J and e to be continuously Fréchet-differentiable.

Remark 2.2

Note, that $e(y,u)=0$ is an equation in the dual space ${{\mathcal {Z}}}'$ of ${{\mathcal {Z}}}$. Since we consider reflexive Banach spaces, it holds ${{\mathcal {Z}}}''\cong {{\mathcal {Z}}}$. Therefore, the constraint is to be interpreted as $\langle e(y,u), z\rangle _{{{\mathcal {Z}}}'\times {{{\mathcal {Z}}}}} = 0$ for all $z\in {{{\mathcal {Z}}}}$, where $\langle \cdot , \cdot \rangle _{{{\mathcal {Z}}}'\times {{{\mathcal {Z}}}}}$ is the duality pairing, and the adjoint state will be in ${{\mathcal {Z}}}$.

A pair $( {\overline{y}},{\overline{u}})\in {\lbrace (y,u)\in {{\mathcal {Y}}}\times {{\mathcal {U}}}:\, e(y,u)=0\rbrace =:{\mathcal {X}}_{\text {ad}}}$ is called local optimum of Problem 2.1 if

$$\begin{aligned} J({\overline{y}},{\overline{u}}) \le J(y,u), \qquad \forall (y,u)\in {\mathcal {N}}({\overline{y}},{\overline{u}}) \cap {{\mathcal {X}}_{\text {ad}}} \text {,} \end{aligned}$$

(2.1)

for some neighborhood ${\mathcal {N}}({\overline{y}},{\overline{u}})$ of $({\overline{y}},{\overline{u}})$; the pair is called global optimum of Problem 2.1 if (2.1) is satisfied for all $(y,u)\in {{\mathcal {X}}_{\text {ad}}}$.

We will be investigating the well-posedness of such optimal control problems in a space–time variational setting. This requires first to study the well-posedness of the state equation $e(y,u)=0$, namely the question if a unique state can be assigned to each admissible control. If so, one defines the control-to-state operator

$$\begin{aligned} S: {{\mathcal {U}}}\rightarrow {{\mathcal {Y}}}\text {, } u \mapsto y(u) = Su, \end{aligned}$$

(2.2)

which allows one to consider the reduced objective function $\hat{J}: {{\mathcal {U}}}\rightarrow {\mathbb {R}}\text {, }\hat{J}(u) :=J(Su,u)$ and the corresponding reduced problem

$$\begin{aligned} {\min \limits _{u\in {\mathcal {U}}} \hat{J}(u)}. \end{aligned}$$

(2.3)

We recall the following well-known result for later reference, [31, Thm. 3.1].

Theorem 2.3

Let ${{\mathcal {U}}}$ be a reflexive Banach space. Moreover, let $\hat{J}:{{\mathcal {U}}}\rightarrow {\mathbb {R}}$ be weakly lower semi-continuous and radially unbounded, i.e.,

$$\begin{aligned} \lim \limits _{\Vert u\Vert _{{\mathcal {U}}}\rightarrow \infty } \hat{J}(u) = +\infty . \end{aligned}$$

(2.4)

Then, (2.3) admits at least one solution.

Necessary first order optimality conditions for optimal control problems are based upon the Euler–Lagrange equation $\hat{J}^\prime ({\overline{u}}) = 0$, e.g. [1]. This, however, involves the derivative of $\hat{J}$, which is often difficult to determine exactly. The well-known way-out is through the adjoint problem. In fact, if $e_y(Su,u){[\cdot ]}: {{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}'$ (the partial derivative of $e(\cdot ,\cdot )$ w.r.t. y) is a bijection, then, $\hat{J}'(u) = J_u(Su,u)-e_u(Su,u)^*\left( e_y(Su,u)^*\right) ^{-1}J_y(Su,u)$, for any $u\in {{\mathcal {U}}}$, where $e_y(Su,u)^*$ and $e_u(Su,u)^*$ denote the adjoint operators of $e_y(Su,u)$ and $e_u(Su,u)$, respectively. In order to avoid the determination of the inverse of the adjoint $e_y(Su,u)^*$, one considers the adjoint equation

$$\begin{aligned} e_y(y,u)^*{z}={-}J_y(y,u), \end{aligned}$$

(2.5)

whose solution ${z} \in {{\mathcal {Z}}}$ is called adjoint state. Then,

$$\begin{aligned} \hat{J}^\prime (u) = J_u(Su,u)+e_u(Su,u)^*{z}. \end{aligned}$$

(2.6)

Theorem 2.4

(KKT system) Let ${\overline{u}}$ be a solution of (2.3) and ${\overline{y}}:=S{\overline{u}}$ the related state. If $e_y({{\overline{y}},{\overline{u}}})[\cdot ]: {{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}'$ is a bijection, then, there exists an adjoint state $\overline{{z}}\in {{\mathcal {Z}}}$, such that the following KKT system is satisfied:

$$\begin{aligned} e({\overline{y}},{\overline{u}})&=0,{} & {} \end{aligned}$$

(2.7a)

$$\begin{aligned} e_y({\overline{y}},{\overline{u}})^*\overline{{z}}&={-}J_y({\overline{y}},{\overline{u}}),{} & {} \end{aligned}$$

(2.7b)

$$\begin{aligned} e_u({\overline{y}},{\overline{u}})^*\overline{{z}}&= {-}J_u({\overline{y}},{\overline{u}}).{} & {} \end{aligned}$$

(2.7c)

The Lagrange function ${\mathcal {L}}: {{\mathcal {Y}}}\times {{\mathcal {U}}}\times {{{\mathcal {Z}}}} \rightarrow {\mathbb {R}}$ to Problem 2.1 reads

$$\begin{aligned} {\mathcal {L}}(y,u,{z}) :=J(y,u) {+} \langle {z}, e(y,u) \rangle _{{{{\mathcal {Z}}}} \times {{\mathcal {Z}}}'}{.} \end{aligned}$$

Then, (2.7) can equivalently be written as $\nabla {\mathcal {L}}({\overline{y}},\overline{{u}},\overline{{z}})=0$.

2.2 Space–time variational formulation of parabolic problems

In order to detail the setting in Sect. 2.1 for the specific Problem 2.1 at hand, we review a variational formulation of the initial boundary value problem (1.5) in space and time, which yields the specific form of the state operator $e(\cdot ,\cdot )$. To this end, let $H:=L_2(\Omega )$, $G:=L_2(\Gamma )$, $V:=H^1(\Omega )$ and $V'$ be the dual of V induced by the H-inner product. Then, we denote the Lebesgue–Bochner spaces by ${{\mathcal {H}}}:=L_2(I;H)$, ${{\mathcal {G}}}:=L_2(I;G)$, ${{\mathcal {V}}}:=L_2(I;V)$ and ${{\mathcal {V}}}':=L_2(I;V')$. Moreover, denoting by $\langle \cdot ,\cdot \rangle _{V'\times V}$ the duality pairing in space only, we obtain inner products and duality pairing in time and space as

$$\begin{aligned} (u,v)_{{\mathcal {X}}}:=\int _I (u(t),v(t))_X\mathop {}\!\textrm{d}t, \qquad \langle u,v\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}} :=\int _I \langle u(t), v(t)\rangle _{V'\times V} \mathop {}\!\textrm{d}t\end{aligned}$$

for the respective u and v and $X\in \{ V',H,V\}$, ${{\mathcal {X}}}\in \{{{\mathcal {V}}}',{{\mathcal {H}}},{{\mathcal {V}}}\}$, respectively.

Then, we start by testing the first equation in (1.5) with functions ${z}(t)\in {V}$, $t\in I$ a.e., integrate over space, perform integration by parts in space and insert the Robin boundary condition of (1.5). Denoting by $a: {V}\times {V}\rightarrow {\mathbb {R}}$ the bilinear form in space, i.e., $a(\phi ,\psi ) :=(\nabla \phi , \nabla \psi )_H + (\mu \,\phi , \psi )_G$, we get

$$\begin{aligned} \langle {\dot{y}}(t), {z}(t) \rangle _{{V'\times V}} + a(y(t),{z}(t)) = {\langle Ru(t),z(t)\rangle _{V'\times V} + (\eta (t), z(t))_G}, \end{aligned}$$

(2.8)

for $t\in I$ a.e. To obtain a variational formulation in space and time we integrate (2.8) over time and obtain

$$\begin{aligned} { \langle {\dot{y}}, z\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}} } + \!\int \limits _{I}\!\! a(y(t),{z}(t)) \mathop {}\!\textrm{d}t = {\langle Ru,z\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}} + (\eta , z)_{{\mathcal {G}}}.} \end{aligned}$$

(2.9)

The trial space for the state y is a Lebesgue–Bochner space defined as

$$\begin{aligned} {\mathcal {Y}} :=\lbrace y \in L_2(I;{V}): {{\dot{y}}} \in L_2(I;{V}'), {y(0)=0} \rbrace = L_2(I;{V})\cap {H^1_{(0)}(I;{V}'}). \end{aligned}$$

(2.10)

As in [15, 18], we choose the norms

$$\begin{aligned} \Vert y\Vert _{{\mathcal {Y}}}^2:=\Vert {\dot{y}}\Vert _{{{\mathcal {V}}}'}^2 + \Vert y\Vert _{{\mathcal {V}}}^2+\Vert y(T)\Vert _H^2 \quad \text {and}\quad \Vert \phi \Vert _V^2:=a(\phi ,\phi ), \end{aligned}$$

but other equivalent norms can also be considered. The test space reads

$$\begin{aligned} {\mathcal {Z}}:={{{\mathcal {V}}}=L_2(I;V), \qquad \Vert \cdot \Vert _{{\mathcal {Z}}}:=\Vert \cdot \Vert _{{\mathcal {V}}}. } \end{aligned}$$

(2.11)

For the well-posedness of (2.9) (see [14]), we need $Ru\in {{\mathcal {V}}}'=L_2(I; V')={{\mathcal {Z}}}'$. However, the definition of the cost function J in Problem 1.1 requires

$$\begin{aligned} {{\mathcal {U}}}:={{{\mathcal {H}}}=L_2(I; H)}, \qquad \Vert \cdot \Vert _{{\mathcal {U}}}:=\Vert \cdot \Vert _{{{\mathcal {H}}}}. \end{aligned}$$

(2.12)

Thus, we can now detail the role of the linear mapping R, namely $R:{{\mathcal {H}}}\rightarrow {{\mathcal {V}}}'$ (which could here also be just the canonical embedding). We introduce the bilinear form $b: {{\mathcal {Y}}}\times {{\mathcal {Z}}}\rightarrow {\mathbb {R}}$ and the linear form $h\in {{\mathcal {Z}}}'$ by

$$\begin{aligned} b(y,z) :=\langle \dot{y}, z\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}} + \int \limits _{I} a(y(t),{z}(t)) \mathop {}\!\textrm{d}t, \quad \,\, h(z):=(\eta ,z)_{{\mathcal {G}}}, \end{aligned}$$

so that (2.9) equivalently can be written as

$$\begin{aligned} b(y,z)=\langle Ru,z\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}} + h(z) \qquad \forall z\in {{\mathcal {Z}}}. \end{aligned}$$

(2.13)

Obviously, (2.13) is a variational problem of the form (1.2), where the right-hand side is a linear form in ${{\mathcal {Z}}}'$ for all $u\in {{\mathcal {U}}}$. For later reference, it will be convenient to reformulate (2.13) in operator form. To this end, we define

$$\begin{aligned} B: {{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}',&\quad \langle By, z\rangle _{{{\mathcal {Z}}}'\times {{\mathcal {Z}}}} :=b(y,z), \end{aligned}$$

(2.14)

so that (2.13) reads $By=Ru+h$. If we define the differential operator in space as $A_x:V\rightarrow V'$ by $\langle A_x\phi ,\psi \rangle _{V'\times V}:=a(\phi ,\psi )$ with its space–time extension $A:{{\mathcal {V}}}\rightarrow {{\mathcal {V}}}'$ defined as $\langle A y, \delta y\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}}:=\int _I a(y(t),\delta y(t))\, dt$, then we get the representation $By={\dot{y}}+A y$.

2.2.1 Well-posedness of the parabolic problem

The proof of the well-posedness of the variational form (2.13) for any given $u\in {{\mathcal {U}}}$ basically follows the lines of [11, 14, 15], namely by verifying the conditions of the Banach–Nečas theorem. For the Robin data we make the usual assumptions $\mu \in L_\infty (I\times \Gamma )$ and $\eta \in {{\mathcal {G}}}=L_2(I;G)$. The surjectivity is shown by proving the convergence of a Faedo–Galerkin approximation, [14, App. A]. Inf-sup-condition and boundedness can be derived by detailing primal and dual supremizers.

Proposition 2.5

The problem (2.13) is well-posed, i.e., $B\in {{{\mathcal {L}}}_{\text {is}}}({{\mathcal {Y}}},{{\mathcal {Z}}}')$, with

$$\begin{aligned} {\beta }&{:=} \inf _{y\in {{\mathcal {Y}}}} \sup _{z\in {{\mathcal {Z}}}} \frac{b(y,z)}{\Vert y\Vert _{{\mathcal {Y}}}\, \Vert z\Vert _{{\mathcal {Z}}}} = \inf _{z\in {{\mathcal {Z}}}} \sup _{y\in {{\mathcal {Y}}}} \frac{b(y,z)}{\Vert y\Vert _{{\mathcal {Y}}}\, \Vert z\Vert _{{\mathcal {Z}}}} \nonumber \\&= {\gamma _B :=} \sup _{y\in {{\mathcal {Y}}}} \sup _{z\in {{\mathcal {Z}}}} \frac{b(y,z)}{\Vert y\Vert _{{\mathcal {Y}}}\, \Vert z\Vert _{{\mathcal {Z}}}} = \sup _{z\in {{\mathcal {Z}}}} \sup _{y\in {{\mathcal {Y}}}} \frac{b(y,z)}{\Vert y\Vert _{{\mathcal {Y}}}\, \Vert z\Vert _{{\mathcal {Z}}}} = 1, \end{aligned}$$

(2.15)

in particular $\Vert B\Vert _{{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}'} = \Vert B^*\Vert _{{{\mathcal {Z}}}\rightarrow {{\mathcal {Y}}}'} = \Vert B^{-1}\Vert _{{{\mathcal {Z}}}'\rightarrow {{\mathcal {Y}}}} = \Vert B^{-*}\Vert _{{{\mathcal {Y}}}'\rightarrow {{\mathcal {Z}}}} = 1$.

Proof

The proof closely follows the lines of [14, Thm. 5.1], [15, Prop. 1] and [18, Prop. 2.6]. In fact, we can identify primal and dual supremizers for given $z\in {{\mathcal {Z}}}$ and $y\in {{\mathcal {Y}}}$, respectively, as follows

$$\begin{aligned} {{\mathcal {Z}}}\ni s_y&:= \arg \sup _{\delta z\in {{\mathcal {Z}}}} \frac{b(y,\delta z)}{\Vert \delta z\Vert _{{\mathcal {Z}}}} = A^{-1} B y = A^{-1}{\dot{y}} + y, \\ {{\mathcal {Y}}}\ni s_z&:= \arg \sup _{\delta y\in {{\mathcal {Y}}}} \frac{b(\delta y,z)}{\Vert \delta y\Vert _{{\mathcal {Y}}}} = B^{-1} A z. \end{aligned}$$

In addition, $\Vert s_y\Vert _{{{\mathcal {Z}}}}^2 = \Vert A^{-1}\dot{y} + y\Vert _{{\mathcal {V}}}^2 = \Vert \dot{y}\Vert _{{{\mathcal {V}}}'}^2 + \Vert y\Vert _{{\mathcal {V}}}^2 + \Vert y(T)\Vert _H^2 =\Vert y\Vert _{{\mathcal {Y}}}^2$ and $\Vert s_z\Vert _{{{\mathcal {Y}}}} = \Vert \dot{s_z} + As_z\Vert _{{{\mathcal {V}}}'} = \Vert Az\Vert _{{{\mathcal {V}}}'}= \Vert z\Vert _{{\mathcal {Z}}}$, which completes the proof. $\square$

Remark 2.6

Even though we have proven optimal stability and continuity, we will later also need the general case, in which we have

$$\begin{aligned} \Vert B\Vert _{{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}'} = \Vert B^*\Vert _{{{\mathcal {Z}}}\rightarrow {{\mathcal {Y}}}'} {=} \gamma _B,\quad&\Vert B^{-1}\Vert _{{{\mathcal {Z}}}'\rightarrow {{\mathcal {Y}}}} = \Vert B^{-*}\Vert _{{{\mathcal {Y}}}'\rightarrow {{\mathcal {Z}}}} = {\textstyle {\frac{1}{\beta }}}. \end{aligned}$$

(2.16)

Remark 2.7

(Inhomogeneous initial conditions) As already mentioned in Remark 1.2, we restrict ourselves to homogeneous initial conditions only for convenience of the presentation. In fact, for $y_0\not =0$, we would set ${{\mathcal {Y}}}:=L_2(I;V)\cap H^1(I;V')$, the test space would be ${{\mathcal {Z}}}:= L_2(I;V)\times H$ and bilinear and linear forms read for $y\in {{\mathcal {Y}}}$, $z=(z_1,z_2)\in {{\mathcal {Z}}}$

$$\begin{aligned} b(y, (z_1,z_2))&:=\langle \dot{y}, z_1\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}} + \int \limits _{I} a(y(t),z_1(t)) \mathop {}\!\textrm{d}t + (y(0),z_2)_H,\\ f((z_1,z_2);u)&:=\langle Ru,z_1\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}} + h(z_1) + (y_0,z_2)_H, \end{aligned}$$

yielding a state equation of the form (1.2). Hence, inhomogeneous initial conditions can be treated analogously, just the notation becomes a bit more heavy, [14].

2.2.2 Comparison with existing space–time methods

As already mentioned in the introduction, our approach is somehow different as existing ones in the literature. We are now going to describe the differences concerning the formulation of the state equation in more detail.

Remark 2.8

(Comparison with existing space–time methods)

• (a) In [3,4,5], Meidner, Neitzel and Vexler use (almost) the same trial space ${{\mathcal {Y}}}$ as in (2.10), namely ${\widetilde{{{\mathcal {Y}}}}}:=L_2(I;V)\cap H^1(I;V')$, but impose the initial condition $y(0)=y_0$⁴ in strong form. The arising problem is not of the form (1.2). In fact, the well-posedness does not follow from the Banach–Nečas theorem but with techniques from semigroup theory, [11]. This requires $y_0\in V$ (but the problem is also well-posed for $y_0\in H$), [3, Prop. 2.1]. In fact, the right-hand side is required to be in $L_2(I;H)$ and the solution is in $L_2(I;V\cap H^2(\Omega ))\cap H^1(I;H)\hookrightarrow C({\bar{I}};V)$, which is significantly stronger than ${{\mathcal {Y}}}$ defined in (2.10).

  Moreover, treating the initial condition as in [3,4,5] allows to use ${\widetilde{{{\mathcal {Y}}}}}$ also as test space, which is another reason for the additional smoothness, but which yields a Galerkin discretization instead of a Petrov–Galerkin one, see below.

• (b) In [6, 7], von Daniels, Hinze and Vierling use the same trial space ${\widetilde{{{\mathcal {Y}}}}}$ for the state equation as [3,4,5], but impose the initial condition in a weak sense, [6, (1.5)]. Moreover, ${\widetilde{{{\mathcal {Y}}}}}$ is chosen also as test space (in a Galerkin spirit).

• (c) In the more recent paper, Langer, Steinbach, Tröltzsch and Yang use the same variational formulation as we do with $y_0=0$, [8]. In [21] (on which [8] is based), non-homogeneous initial conditions are treated by means of reduction to homogeneous initial conditions. Moreover, in [21] it is assumed that $y_0\in V$, whereas we choose $y_0\in H$.

In all cases, there are differences to our approach in the derivation/formulation of the adjoint equation and the adjoint state to be described in the next section.

3 Space–time variational optimal control problem

Next, we formulate the optimal control problem in the variational space–time setting by specifying the above abstract framework. To do so, we are now going to derive a space–time variational formulation of Problem 1.1. The state space is determined by the PDE, i.e., we choose ${{\mathcal {Y}}}$ defined in (2.10). In view of Remark 2.2 and recalling that ${{\mathcal {Z}}}'' \cong {{\mathcal {Z}}}$, we are now in position to formulate the constraint in space–time variational form as follows

$$\begin{aligned} \langle e(y,u), z\rangle _{{{\mathcal {Z}}}'\times {{\mathcal {Z}}}} :=b(y,z) - \langle {R}u,z\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}} - h(z), \qquad z\in {{\mathcal {Z}}}, \end{aligned}$$

(3.1)

i.e., $e(y,u):=By-Ru-h \in {{\mathcal {Z}}}'$. Next, we can detail the control-to-state operator $S: {{\mathcal {U}}}\rightarrow {{\mathcal {Y}}}$ as follows $Su = B^{-1} \left( {R}u+{h} \right)$. Finally, the objective function $J: {{\mathcal {Y}}}\times {{\mathcal {U}}}\rightarrow {\mathbb {R}}$ in Problem 1.1 can now be written as $J(y,u) = \frac{1}{2} \Vert y(T) - y_d \Vert _{{H}}^2 + \frac{\lambda }{2} \Vert u \Vert _{{{{\mathcal {H}}}}}^2$, where $\lambda > 0$ is the regularization parameter.

3.1 Existence of an optimal solution

Problem 3.1

(Reduced problem) Find a control ${{\bar{u}}\in {{\mathcal {U}}}}$ such that

$$\begin{aligned} {{\bar{u}} = \arg }\min \limits _{u\in {{\mathcal {U}}}} \hat{J}(u),&\quad \hat{J}(u):={\textstyle {\frac{1}{2}}} \Vert (Su)(T) - y_d \Vert _{{H}}^2 + {\textstyle {\frac{\lambda }{2}}} \Vert u \Vert _{{{\mathcal {H}}}}^2 . \end{aligned}$$

(3.2)

Proposition 3.2

Problem 3.1 admits a unique solution.

Proof

Since $\hat{J}$ is easily seen to be strictly convex and continuous (by continuity of S and the norms), it follows that $\hat{J}$ is weakly lower semi-continuous, see e.g. [32, p. 15]. In addition, it holds $\hat{J}(u) \ge {\textstyle {\frac{\lambda }{2}}} \Vert u \Vert _{{{\mathcal {H}}}}^2$, and, consequently, $\hat{J}$ is bounded from below and is radially unbounded (i.e., fulfills (2.4)). Since ${{\mathcal {U}}}$ is reflexive as a Hilbert space, Theorem 2.3 proves the claim. $\square$

3.2 First order necessary optimality conditions

Adopting the previous notation, we start by detailing the Lagrange function ${\mathcal {L}}: {{{\mathcal {Y}}}\times {{\mathcal {U}}}\times {{\mathcal {Z}}}} \rightarrow {\mathbb {R}}$ for Problem 1.1, namely

$$\begin{aligned} {\mathcal {L}}({y,u,z})&={\textstyle {\frac{1}{2}}} \Vert y(T) - y_d \Vert _{{H}}^2 + {\textstyle {\frac{\lambda }{2}}} \Vert u \Vert _{{{\mathcal {H}}}}^2 +\langle {z}, By - {R}u - {h}\rangle _{{{{\mathcal {Z}}}\times {{\mathcal {Z}}}'}} . \end{aligned}$$

(3.3)

The partial derivatives can easily be derived as follows: ${\mathcal {L}}_z({y,u,z}) = B{y}-{R}{u} -{h}$, ${\mathcal {L}}_y({y,u,z})= D{y} - g {+} B^*{z}$, where we introduce the bilinear form $d:{{\mathcal {Y}}}\times {{\mathcal {Y}}}\rightarrow {\mathbb {R}}$, $d(y,\delta y):=(y(T),\delta y(T))_H$ and the associated operator⁵$D:{{\mathcal {Y}}}\rightarrow {{\mathcal {Y}}}'$, $\langle Dy,\delta y\rangle _{{{\mathcal {Y}}}'\times {{\mathcal {Y}}}}:=d(y,\delta y)$ as well as the functional $g\in {{\mathcal {Y}}}'$, $g(\delta y) :=(y_d,\delta y(T))_H$. Finally, for $\delta u\in {{\mathcal {U}}}$, we have ${\mathcal {L}}_u(y,u,z)[\delta u] = \lambda \, (u,\delta u)_{{\mathcal {H}}}- \langle z, R\delta u\rangle _{{{\mathcal {V}}}\times {{\mathcal {V}}}'}$. Hence, we obtain the following first order optimality (KKT) system: Find $\left( {\overline{y}}, {\overline{z}}, {\overline{u}} \right) \in {{\mathcal {Y}}}\times {{\mathcal {Z}}}\times {{\mathcal {U}}}$ such that

$$\begin{aligned} b({\overline{y}},\delta z)&- \langle R{\overline{u}},\delta z\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}}{} & {} \quad = h(\delta z)&\forall \delta z\in {{\mathcal {Z}}}, \end{aligned}$$

(3.4a)

$$\begin{aligned} d( {\overline{y}}, \delta y)&+b(\delta y,{\overline{z}}){} & {} \quad = g(\delta y)&\forall \delta y\in {{\mathcal {Y}}}, \end{aligned}$$

(3.4b)

$$\begin{aligned} \lambda ( {\overline{u}}, \delta u)_{{\mathcal {H}}}&- \langle R\delta u, {\overline{z}}\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}}{} & {} \quad = 0&\forall \delta u \in {{\mathcal {U}}}. \end{aligned}$$

(3.4c)

Let us further detail the gradient equation (3.4c). Denote by $R^*:{{\mathcal {V}}}\rightarrow {{\mathcal {H}}}$ the adjoint operator of R defined by $(R^*v,h)_{{\mathcal {H}}}:= \langle R h, v\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}}$ for $v\in {{\mathcal {V}}}$ and $h\in {{\mathcal {H}}}{\cong {{\mathcal {H}}}'}$. Then, (3.4c) reads $\lambda ( {\overline{u}}, \delta u)_{{\mathcal {H}}}- (R^*{\overline{z}},\delta u)_{{\mathcal {H}}}=0$, which means that we can derive a relation of the optimal control ${\bar{u}}$ and the optimal adjoint state ${\bar{z}}$, namely

$$\begin{aligned} {\bar{u}} = \lambda ^{-1}\, R^* {\bar{z}}. \end{aligned}$$

(3.5)

Then, we can formulate the KKT conditions as follows.

Proposition 3.3

(Optimality (KKT) system) Let $\left( {\overline{y}}, {\overline{u}} \right) \in {{\mathcal {Y}}}\times {{\mathcal {U}}}$ be an optimal solution of Problem 1.1. If $B: {{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}'$ is a bijection, then there exists an adjoint state ${\overline{z}} \in {{\mathcal {Z}}}$ such that the following optimality system holds:

$$\begin{aligned} B{\overline{y}} - R {\overline{u}}&= {h}{} & {} \text { in } {{\mathcal {Z}}}'&{\textit{(state equation)}}, \end{aligned}$$

(3.6a)

$$\begin{aligned} {D{\overline{y}} + B^*{\overline{z}}}&= {g }{} & {} \text { in } {{\mathcal {Y}}}'&{\textit{(adjoint equation)}}, \end{aligned}$$

(3.6b)

$$\begin{aligned} \lambda {\overline{u}} {-} {{R^*} {\overline{z}}}&= {0}{} & {} \text { in } {{\mathcal {U}}}'&\text {(gradient equation) }, \end{aligned}$$

(3.6c)

or, in operator form

$$\begin{aligned} \begin{pmatrix} D &{} \quad B^* &{} \quad 0 \\ B &{} \quad 0 &{} \quad -R \\ 0 &{} \quad -R^* &{} \quad \lambda I \end{pmatrix} \begin{pmatrix} {{\bar{y}}} \\ {{\bar{z}}} \\ {{\bar{u}}} \end{pmatrix} = \begin{pmatrix} g \\ h \\ 0 \end{pmatrix}. \end{aligned}$$

Setting $P:=RR^*:{{\mathcal {V}}}\rightarrow {{\mathcal {V}}}'$, inserting (3.5) into (3.4) yields the reduced first order optimality system for determining $({\overline{y}},{\bar{z}})\in {{\mathcal {Y}}}\times {{\mathcal {Z}}}$ such that

$$\begin{aligned} b({\overline{y}},\delta z)&- \lambda ^{-1} \langle P {\bar{z}},\delta z\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}}{} & {} \quad = h(\delta z){} & {} \forall \delta z\in {{\mathcal {Z}}}, \end{aligned}$$

(3.7a)

$$\begin{aligned} d( {\overline{y}}, \delta y)&+b(\delta y,{\overline{z}}){} & {} \quad = g(\delta y){} & {} \forall \delta y\in {{\mathcal {Y}}}, \end{aligned}$$

(3.7b)

or, in operator form (where we reordered the equations)

$$\begin{aligned} L \begin{pmatrix} {\bar{y}} \\ {\bar{z}} \end{pmatrix} = \begin{pmatrix} g \\ h \end{pmatrix}, \quad L:= \begin{pmatrix} D &{} B^* \\ B &{} -\lambda ^{-1} P \end{pmatrix}: {{\mathcal {W}}}:=({{\mathcal {Y}}}\times {{\mathcal {Z}}})\rightarrow {{\mathcal {W}}}'. \end{aligned}$$

(3.8)

For later reference, we equip the space ${{\mathcal {W}}}={{\mathcal {Y}}}\times {{\mathcal {Z}}}$ with the norm

$$\begin{aligned} \Vert w \Vert _{{\mathcal {W}}}:=\Vert y\Vert _{{\mathcal {Y}}}+ \Vert z\Vert _{{\mathcal {Z}}},\quad w= (y,z)\in {{\mathcal {W}}}. \end{aligned}$$

(3.9)

It is easily seen that $L:{{\mathcal {W}}}\rightarrow {{\mathcal {W}}}'$ is bounded, i.e., $\Vert L \Vert _{{{\mathcal {W}}}\rightarrow {{\mathcal {W}}}'} <\infty$.

Remark 3.4

(Well-posedness of the adjoint problem) From (3.4b) we see that the adjoint problem arises from the primal one by exchanging the roles of trial and test spaces—and by a different right-hand side, of course. We recall from Sect. 2.2 that the primal problem (3.4a) is well-posed, see e.g. [11, 14]. This is a consequence of the Banach–Nečas theorem and the fact that the inf-sup condition (2.15) holds. Due to its specific form, this immediately implies well-posedness also of the adjoint problem (3.4b), even with the same inf-sup constant as for (3.4a).

Remark 3.5

Due to the convexity of the objective function as well as the linearity of the state equation, the Problem 1.1 is convex. Hence, every solution of (3.3) is a global optimal solution of the problem, [1].

Theorem 3.6

(Well-posedness of the optimality system) The first order optimality system (3.8) is well-posed, i.e., $L\in {{{\mathcal {L}}}_{\text {is}}}({{\mathcal {W}}},{{\mathcal {W}}}')$, for all $\lambda >0$ with

$$\begin{aligned} L^{-1} = \begin{pmatrix} \lambda ^{-1} B^{-1} P C^{-1} &{} \quad B^{-1} - \lambda ^{-1} B^{-1} P C^{-1} D B^{-1} \\ C^{-1} &{} \quad -C^{-1} D B^{-1} \end{pmatrix} \end{aligned}$$

with $C:= B^{*} + \lambda ^{-1} DB^{-1} P: {{\mathcal {Z}}}\rightarrow {{\mathcal {Y}}}'$. For $\gamma _P:=\Vert P\Vert _{{{\mathcal {V}}}\rightarrow {{\mathcal {V}}}'}$, we have

$$\begin{aligned} \Vert L^{-1} \Vert _{{{\mathcal {W}}}'\rightarrow {{\mathcal {W}}}} \le {\textstyle {\frac{\gamma _P+\lambda \beta + \lambda \beta ^2}{\lambda \beta ^3}}}. \end{aligned}$$

(3.10)

Proof

The fact that $LL^{-1}$ and $L^{-1}L$ are identity maps can be verified by straightforward calculations, as long as $L^{-1}$ exists. This, in turn, boils down to the existence of $C^{-1}$. In order to show this, note that $C=B^*(I+\lambda ^{-1} B^{-*}DB^{-1} P) =: B^* (I+\lambda ^{-1}K)$ and $B^*$ is invertible. The operator $K:{{\mathcal {Z}}}\rightarrow {{\mathcal {Z}}}$ is self-adjoint since

$$\begin{aligned} (Kz, \delta z)_{{\mathcal {Z}}}&= \langle B^{-*} DB^{-1} P z, P \delta z\rangle _{{{\mathcal {Z}}}\times {{\mathcal {Z}}}'} = \langle P z, B^{-*} D B^{-1} P \delta z\rangle _{{{\mathcal {Z}}}'\times {{\mathcal {Z}}}} = (z, K \delta z)_{{\mathcal {Z}}}\end{aligned}$$

since $D^*=D$. Hence, the spectrum $\sigma (K)\subset {\mathbb {R}}_0^+$ is contained in the non-negative reals. This implies $\Vert (I+\lambda ^{-1} K)^{-1}\Vert _{{{\mathcal {Z}}}\rightarrow {{\mathcal {Z}}}} \le 1$ for all $\lambda >0$, so that $\Vert C^{-1}\Vert _{{{\mathcal {Y}}}'\rightarrow {{\mathcal {Z}}}} \le \Vert B^{-*}\Vert _{{{\mathcal {Y}}}'\rightarrow {{\mathcal {Z}}}} = \frac{1}{\beta }$. In order to bound $\Vert L^{-1} \Vert _{{{\mathcal {W}}}'\rightarrow {{\mathcal {W}}}}$, let ${(g,h)}^T\in {{{\mathcal {W}}}'}$. Then,

which proves the claim. $\square$

Remark 3.7

For the optimal solution $(y,z)^\top \in {{\mathcal {W}}}$ of (3.8) we have $\Vert y\Vert _{{\mathcal {Y}}}+ \Vert z\Vert _{{\mathcal {Z}}}=\Vert (y,z)^\top \Vert _{{\mathcal {W}}}\le \Vert L^{-1} \Vert _{{{\mathcal {W}}}'\rightarrow {{\mathcal {W}}}}\Vert (g,h)^\top \Vert _{{{\mathcal {W}}}'}$ and for the corresponding optimal control $u\in {{\mathcal {U}}}$ it holds due to (3.5)

$$\begin{aligned} \Vert u\Vert _{{\mathcal {U}}}&= \textstyle {\frac{1}{\lambda }} \Vert {R^*} z\Vert _{{\mathcal {H}}}\le \textstyle {\frac{1}{\lambda }}{\Vert R^*\Vert _{{{\mathcal {V}}}\rightarrow {{\mathcal {H}}}}} \Vert z\Vert _{{\mathcal {V}}}\le \textstyle {\frac{1}{\lambda }}{\Vert R^*\Vert _{{{\mathcal {V}}}\rightarrow {{\mathcal {H}}}}} \Vert (y,z)^T\Vert _{{{\mathcal {W}}}} \\&\le \textstyle {\frac{1}{\lambda }}{\Vert R^*\Vert _{{{\mathcal {V}}}\rightarrow {{\mathcal {H}}}}} \Vert L^{-1} \Vert _{{{\mathcal {W}}}'\rightarrow {{\mathcal {W}}}} \Vert {(g,h)}^T\Vert _{{{\mathcal {W}}}'}\le \textstyle {\frac{{\gamma _P}}{\lambda }} \Vert L^{-1} \Vert _{{{\mathcal {W}}}'\rightarrow {{\mathcal {W}}}} \Vert {(g,h)}^T\Vert _{{{\mathcal {W}}}'}. \end{aligned}$$

Remark 3.8

Recall that $\Vert L^{-1} \Vert _{{{\mathcal {W}}}'\rightarrow {{\mathcal {W}}}}$ is the inverse of the inf-sup constant of L, i.e.,

$$\begin{aligned} \inf _{w \in {{\mathcal {W}}}} \sup _{v \in {{\mathcal {W}}}} \frac{\langle Lw, v\rangle _{{{\mathcal {W}}}'\times {{\mathcal {W}}}}}{\Vert v\Vert _{{\mathcal {W}}}\Vert w\Vert _{{\mathcal {W}}}} \ge {\textstyle {\frac{\lambda \beta ^3}{\gamma _P+\lambda \beta + \lambda \beta ^2}}}. \end{aligned}$$

(3.11)

Corollary 3.9

For (2.13) we have

$$\begin{aligned} \Vert L^{-1} \Vert _{{{\mathcal {W}}}'\rightarrow {{\mathcal {W}}}} \le { {\textstyle {\frac{\gamma _P+2\lambda }{\lambda }}}=2+{\textstyle {\frac{\gamma _P}{\lambda }}}}, \end{aligned}$$

(3.12)

so that the inf-sup-constant (3.11) of the reduced optimality system is at least $\frac{\lambda }{{\gamma _P}+2\lambda }$.

Proof

Since $\beta =1$ the estimate (3.12) follows from (3.10) and (3.11). $\square$

Remark 3.10

(Comparison with existing space–time methods, continued) We continue Remark 2.8 with highlighting the differences to previous publications.

• (a) In [3,4,5], the adjoint problem is derived directly from the variational formulation, which means that the terminal condition is imposed in strong form. This necessarily implies that ${{\mathcal {Z}}}={{\mathcal {Y}}}$ is the space for the adjoint state. Moreover, the same high regularity requirements apply for the solution of the adjoint problem as for the primal one, [3, Prop. 2.3].

• (b) In [6, 7] the adjoint equation is derived by integration by parts in time, which is possible since ${{\mathcal {Z}}}={{\mathcal {Y}}}$. As in [3,4,5], this implies high (and the same) regularity for y and z, [6, La. 3.2].

• (c) In [8] the adjoint problem and also the gradient equation are derived in strong form, which is then formulated in space–time variational form. This results in a coupled space–time system where primal and adjoint state have the same regularity. Moreover, since the initial condition is imposed in the primal trial space, the terminal condition is part of the definition of the adjoint trial space. In our case, it holds $z \in {{\mathcal {Z}}}$, which is appropriate since $B^*\in {{{\mathcal {L}}}_{\text {is}}}({{\mathcal {Z}}},{{\mathcal {Y}}}')$. Hence, ${{\mathcal {Z}}}$ is the natural space for the adjoint, which effects the required regularity and the sharpness of the error estimates.

The differences concerning discretization will be described in the next section.

4 Space–time discretization

In this section, we are going to describe a conforming discretization of the optimal control problem in space and time. We start by reviewing space–time Petrov–Galerkin methods for parabolic problems from [15, 17, 18] and will extend this to a full space–time discretization of the optimal control problem at hand. This leads us to a tensorproduct-type discretization w.r.t. time and space variables. Of course, the approach is not restricted to tensorproducts; for example, one could also use unstructured space–time finite elements as in [8]. However, w.r.t. stability and efficient solution of the fully discretized problems, the tensorproduct approach turned out to be very promising, see also [20, 22].

4.1 Petrov–Galerkin discretization of the PDE

We consider and construct finite-dimensional spaces ${\mathcal {Y}}_\delta \subset {\mathcal {Y}}$ and ${\mathcal {Z}}_\delta \subset {\mathcal {Z}}$, where—for simplicity—we assume that $n_\delta :=\dim ({{\mathcal {Y}}}_\delta )=\dim ({{\mathcal {Z}}}_\delta )$. The Petrov–Galerkin approximation to (2.13) amounts to find $y_\delta \in {{\mathcal {Y}}}_\delta$ such that (for given $u\in {{\mathcal {U}}}$ to be discretized below)

$$\begin{aligned} {b(y_\delta , z_\delta ) = \langle Ru,z_\delta \rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}} + h(z_\delta ) } \qquad \forall z_\delta \in {\mathcal {Z}}_\delta . \end{aligned}$$

(4.1)

We may think of $\delta =({\Delta {t}},h)$, where ${\Delta {t}}$ is the temporal and h the spatial mesh width. We recall, that there are several ways to select such discrete spaces so that the arising discrete problem is well-posed and stable in the sense of (1.4). An overview of conditionally and unconditionally stable variants can be found in [17, 26, 33]. In [21] a finite element approach is described. Moreover, the authors of [15, 18] show that linear ansatz and constant test functions w.r.t. time lead to the Crank–Nicolson time integration scheme for the special case of homogeneous Dirichlet boundary conditions if the right-hand side is approximated with the trapezoidal rule. A similar approach, but for the case of Robin boundary conditions, is briefly presented in the sequel, where we basically follow [17]. It is convenient (and, as we explained above, also efficient from the numerical point of view) to choose the approximation spaces to be of tensorproduct form,

$$\begin{aligned} {\mathcal {Y}}_\delta = V_{{\Delta {t}}} \otimes {V}_h, \quad {{\mathcal {Z}}}_\delta = { Q_{{\Delta {t}}} \otimes {V}_h } \end{aligned}$$

(4.2)

with the temporal subspaces $V_{{\Delta {t}}} \subset H^1(I)$ and $Q_{{\Delta {t}}} \subset L_2(I)$ as well as the spatial subspace ${V}_h \subset {V}=H^1(\Omega )$. Our particular choice is as follows: The time interval $I=(0,T)$ is discretized according to

$$\begin{aligned} {\mathcal {T}}_{{\Delta {t}}} :=\{0 =:t^{(0)}< t^{(1)}< \cdots < t^{(K)} :=T \} \subset [0,T]\text {,}\quad t^{(k)}=k \cdot {\Delta {t}}, \end{aligned}$$

where $K \in {\mathbb {N}}$ denotes the number of time steps, i.e., ${\Delta {t}}:=T/K$ is the time step size. The temporal subspaces $V_{{\Delta {t}}}$, $Q_{{\Delta {t}}}$ and the spatial subspace ${V}_h$ read

$$\begin{aligned} V_{{\Delta {t}}} :={\mathrm {span \ }} \Theta _{\Delta {t}}\subset H^1(I), \,\,\, Q_{{\Delta {t}}} :={\mathrm {span \ }} \Xi _{\Delta {t}}\subset L_2(I), \,\,\, {V_h} :={\mathrm {span \ }} \Phi _h \subset H^1(\Omega ) \end{aligned}$$

with piecewise linear functions $\Theta _{\Delta {t}}= \{\theta ^k \in H^1(I): k= {1},\ldots , K \}$, piecewise constants $\Xi _{\Delta {t}}= \{\xi ^\ell \in L_2(I): \ell =0,\ldots , K-1 \}$ in time and piecewise linear basis functions in space $\Phi _h = \{\phi _i \in H^1(\Omega ): i=1,\ldots ,n_h\}$. Doing so, we obtain $\dim ({{\mathcal {Y}}}_\delta )=\dim ({{\mathcal {Z}}}_\delta )=n_\delta ={K}n_h$. Such a Petrov–Galerkin discretization for solving (4.1) amounts to determine

$$\begin{aligned} {\mathcal {Y}}_\delta \ni y_\delta = \sum \limits _{k={1}}^K \sum \limits _{i=1}^{n_h} y_i^k \theta ^k \otimes \phi _i\text {,} \end{aligned}$$

(4.3)

with the coefficient vector ${{\varvec{y}}}_\delta :=[y_1^{{1}},\ldots , y_{n_h}^{{1}},\ldots ,y_1^K,\ldots , y_{n_h}^K ]^\top \in {\mathbb {R}}^{n_\delta }$. We are going to derive the arising linear system of equations for (4.1)

$$\begin{aligned} {{\varvec{B}}}_\delta {{\varvec{y}}}_\delta = {({\varvec{R}}{\varvec{u}})_\delta } {+ {\varvec{h}}_\delta }, \end{aligned}$$

(4.4)

with the stiffness matrix ${\varvec{B}}_\delta \in {\mathbb {R}}^{n_\delta \times n_\delta }$ and the vectors $({\varvec{R}}{\varvec{u}})_\delta \in {\mathbb {R}}^{n_\delta }$, ${\varvec{h}}_\delta \in {\mathbb {R}}^{n_\delta }$ to be detailed next. To this end, we use the basis functions for the test space and obtain for $\ell =0,\ldots ,K-1$ and $j=1,\ldots ,n_h$

$$\begin{aligned} b(y_\delta , {\xi ^\ell \otimes \phi _j} )&= \int \limits _I \langle {\dot{y}}_\delta (t), \xi ^\ell \otimes \phi _j \rangle _{{V' \times V}} + a(y_\delta (t),\xi ^l \otimes \phi _j) \mathop {}\!\textrm{d}t\\&= \sum \limits _{k={1}}^K \sum \limits _{i=1}^{n_h} y_i^k \left[ \langle {\dot{\theta }}^k \otimes \phi _i, \xi ^\ell \otimes \phi _j \rangle _{{V}' \times {V}} + a(\theta ^k \otimes \phi _i,\xi ^\ell \otimes \phi _j) \mathop {}\!\textrm{d}t \right] \\&= \sum \limits _{k={1}}^K \sum \limits _{i=1}^{n_h} y_i^k \left[ \left( {\dot{\theta }}^k, \xi ^\ell \right) _{L_2(I)}\, \left( \phi _i, \phi _j \right) _{H} +\left( \theta ^k, \xi ^\ell \right) _{L_2(I)}\, a(\phi _i, \phi _j) \right] \text {.} \end{aligned}$$

Moreover, it holds $({\varvec{R}}{\varvec{u}})_\delta :=[ r^\ell _j(u)]_{\ell =0,\ldots ,K-1; j=1,\ldots ,n_h}\in {\mathbb {R}}^{n_\delta }$ and ${\varvec{h}}_\delta :=[ h^\ell _j]_{\ell =0,\ldots ,K-1; j=1,\ldots ,n_h}\in {\mathbb {R}}^{n_\delta }$, where $r^\ell _j(u) =:\langle Ru, \xi ^\ell \otimes \phi _j\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}}$ and $h^\ell _j =:h(\xi ^\ell \otimes \phi _j)= (\eta , \xi ^\ell \otimes \phi _j )_{{{\mathcal {G}}}}$. The control u will be discretized below. In order to derive a compact form, we introduce a number of matrices

$$\begin{aligned}&{\underline{C}}^{\textrm{time}}_{\Delta {t}}:=\left[ c_{k,\ell } \right] _{k={1}, \ell =0}^{K, K-1}{} & {} \ \in {\mathbb {R}}^{{K} \times K}{} & {} \qquad \text {with } \qquad c_{k,\ell } :=({\dot{\theta }}^k, \xi ^\ell )_{L_2(I)} ,\\&{\underline{N}}^{\textrm{time}}_{\Delta {t}}:=\left[ n_{k,\ell } \right] _{k={{1}}, \ell =0}^{K, K-1}{} & {} \ \in {\mathbb {R}}^{{K} \times K}{} & {} \qquad \text {with } \qquad n_{k,\ell } :=(\theta ^k, \xi ^\ell )_{L_2(I)}, \\&{\underline{M}}^{\textrm{time}}_{\Delta {t}}:=\left[ m_{k,\ell } \right] _{k=0, \ell =0}^{K-1, K-1}{} & {} \ \in {\mathbb {R}}^{K \times K}{} & {} \qquad \text {with } \qquad m_{k,\ell } :=(\xi ^k, \xi ^\ell )_{L_2(I)}, \\&{\underline{A}}^{\textrm{space}}_h :=\left[ a_{i,j} \right] _{i,j=1}^{n_h}{} & {} \ \in {\mathbb {R}}^{n_h \times n_h}{} & {} \qquad \text {with } \qquad a_{i,j} :=a(\phi _i, \phi _j ) ,\\&{\underline{M}}^{\textrm{space}}_h :=\left[ m_{i,j} \right] _{i,j=1}^{n_h}{} & {} \ \in {\mathbb {R}}^{n_h \times n_h}{} & {} \qquad \text {with } \qquad m_{i,j} :=(\phi _i, \phi _j )_{{H}}. \end{aligned}$$

Based upon this, we obtain ${{\varvec{B}}}_\delta :={\underline{C}}^{\textrm{time}}_{{\Delta {t}}} \otimes {\underline{M}}^{\textrm{space}}_h + {\underline{N}}^{\textrm{time}}_{\Delta {t}}\otimes {\underline{A}}^{\textrm{space}}_h \in {\mathbb {R}}^{n_\delta \times n_\delta }$.

Remark 4.1

There are several uniformly inf-sup stable discretizations available, see e.g. [33]. For the above case, there is even an optimal discretization, i.e., where the inf-sup constant $\bar{\beta }$ is unity, [15, 18]. In any case, we have (and shall assume in the sequel) that (1.4) holds uniformly in $\delta \rightarrow 0$, possibly with discrete norms $\Vert \cdot \Vert _{{{\mathcal {Y}}}_\delta }$, $\Vert \cdot \Vert _{{{\mathcal {Z}}}_\delta }$.

4.2 Discretization of the control

So far, we did not discretize the control $u\in {{\mathcal {U}}}= L_2(I;H)$. A natural choice seems to be ${{\mathcal {U}}}_\delta :=Q_{\Delta {t}}\otimes V_h={{\mathcal {Z}}}_\delta$, but other choices are also possible. Thus, set

$$\begin{aligned} u_\delta :=\sum _{k=0}^{K-1} \sum _{i=1}^{{n}_h} u_i^k\, \xi ^k\otimes \phi _i, \qquad {\varvec{u}}_\delta :=[u_i^k]_{k=0,\ldots ,K-1;\, i=1,\ldots ,n_h}\in {\mathbb {R}}^{K{n}_h}. \end{aligned}$$

(4.5)

The next step is to detail $({\varvec{R}}{\varvec{u}})_\delta$ based upon this discretization. We obtain for $\ell = 0,\ldots ,K-1$ and $j=1,\ldots , n_h$

$$\begin{aligned} {r^\ell _j(u_\delta )}&= {\langle Ru_\delta , \xi ^\ell \otimes \phi _j\rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}}} = \sum _{k=0}^{K-1} \sum _{i=1}^{{n}_h} u_i^k\, (\xi ^k, \xi ^\ell )_{L_2(I)}\, {\langle }{R\phi _i}, \phi _j{\rangle _{V'\times V}} \nonumber \\&= [({\underline{M}}^{\textrm{time}}_{\Delta {t}}\otimes {\underline{N}}^{\textrm{space}}_h) {\varvec{u}}_\delta ]_{\ell , j} {=:[ {\tilde{{\varvec{M}}}}_\delta {\varvec{u}}_\delta ]_{\ell , j}}, \end{aligned}$$

(4.6)

where ${\underline{M}}^{\textrm{time}}_{\Delta {t}}\in {\mathbb {R}}^{K\times K}$ is as introduced above and ${\underline{N}}^{\textrm{space}}_h :=\left[ n_{i,j} \right] _{i=1,j=1}^{n_h,{n}_h}$ with $n_{i,j} :={\langle R\phi _i, \phi _j\rangle _{V'\times V}}$.⁶ Putting everything together, the discretized version of the primal problem (4.4) reads

$$\begin{aligned} {{\varvec{B}}}_\delta {{\varvec{y}}}_\delta -\tilde{{\varvec{M}}}_\delta {{\varvec{u}}}_\delta = {\varvec{h}}_\delta . \end{aligned}$$

(4.7)

For later reference, we note that

$$\begin{aligned} \Vert u_\delta \Vert _{{{\mathcal {H}}}}^2 = \sum _{k,\ell =0}^{K-1} \sum _{i,j=1}^{{n}_h} u_i^k\, u_j^\ell \, (\xi ^k, \xi ^\ell )_{L_2(I)}\, (\phi _i, \phi _j)_H&= {\varvec{u}}_\delta ^\top \, ({\underline{M}}^{\textrm{time}}_{\Delta {t}}\otimes {\underline{{M}}^{\textrm{space}}_h})\, {\varvec{u}}_\delta \\&=:{\varvec{u}}_\delta ^\top \,{{\varvec{M}}}_\delta \, {\varvec{u}}_\delta . \end{aligned}$$

Remark 4.2

We stress the fact that we could use any other suitable discretization of the control, both w.r.t. time and space, in particular including adaptive techniques or a discretization arising from implicitly utilizing the optimality conditions and the discretization of the state and adjoint equation, see e.g. [34].

4.3 Petrov–Galerkin discretization of the adjoint problem

We are now going to derive the discrete form of the adjoint problem (3.6b) or (3.4b). Since this problem involves the adjoint operator, it seems reasonable to use the same discretization, so that the (matrix–vector form of the) discrete problem amounts to find ${{\varvec{z}}_\delta }\in {\mathbb {R}}^{n_\delta }$ such that (for given $y_\delta \in {{\mathcal {Y}}}_\delta$)

$$\begin{aligned} {\varvec{B}}_\delta ^\top {{\varvec{z}}_\delta } + {{\varvec{d}}_\delta (y_\delta ) = {\varvec{g}}_\delta } , \end{aligned}$$

(4.8)

with ${\varvec{d}}_\delta (y_\delta )\in {\mathbb {R}}^{n_\delta }$, ${\varvec{g}}_\delta \in {\mathbb {R}}^{n_\delta }$, i.e., $d(y_\delta , \delta y_\delta ) +b(\delta y_\delta ,z_\delta ) = g(\delta y_\delta )$ for all $\delta y_\delta \in {{\mathcal {Y}}}_\delta$. Note, that the stiffness matrix is the transposed of the stiffness matrix of the primal problem. The unknown coefficient vector ${\varvec{z}}_\delta \in {\mathbb {R}}^{Kn_h}$ reads

$$\begin{aligned} {{\mathcal {Z}}}_\delta \ni {z_\delta }&{= \sum _{k=0}^{K-1}\sum _{i=1}^{n_h} z_i^k\, \xi ^k\otimes \phi _i}, \qquad {\varvec{z}}_\delta :=[z_i^k]_{k=0,\ldots ,K-1;\, i=1,\ldots ,n_h}\in {\mathbb {R}}^{K n_h}. \end{aligned}$$

(4.9)

Let us now detail the remaining terms ${\varvec{d}}_\delta (y_\delta )=[d_j^\ell (y_\delta )]_{\ell =1,\ldots ,K;\, j=1,\ldots ,n_h}\in {\mathbb {R}}^{n_\delta }$, ${\varvec{g}}_\delta =[g_j^\ell ]_{\ell =1,\ldots ,K;\, j=1,\ldots ,n_h}\in {\mathbb {R}}^{n_\delta }$. For $\ell =1,\ldots ,K$ and $j=1,\ldots ,n_h$, we get

$$\begin{aligned} g^\ell _j&= g(\theta ^\ell \otimes \phi _j) = (y_d, \theta ^K(T)\otimes \phi _j)_H = \theta ^K(T) \cdot (y_d, \phi _j)_H. \end{aligned}$$

Further, we abbreviate the coefficient vector of $y_\delta (T)$ in terms of the basis $\Phi _h$ as ${{{\varvec{y}}}_{\delta }^K} :=[y_1^K,\ldots , y_{n_h}^K ]^\top$ so that by (4.3) we obtain for $\ell =1,\ldots ,K$ and $j=1,\ldots ,n_h$

$$\begin{aligned} d_j^\ell (y_\delta )&= d(y_\delta , \theta ^\ell \otimes \phi _j) = (y_\delta (T), \theta ^K(T)\otimes \phi _j)_H \\&= \theta ^\ell (T)\cdot \theta ^K(T) \cdot \sum \limits _{i=1}^{n_h} y_i^K (\phi _i, \phi _j)_H = \delta _{\ell ,K}\cdot [{\underline{M}}^{\textrm{space}}_h {\varvec{y}}_\delta ^K ]_{j} =:[{\varvec{D}}_\delta {\varvec{y}}_\delta ]_{\ell ,j}, \end{aligned}$$

where $\delta _{\ell ,K}$ denotes the discrete Kronecker delta and we introduce

$$\begin{aligned} {\varvec{D}}_\delta :=\begin{pmatrix} \varvec{0} &{} \quad \varvec{0} \\ \varvec{0} &{} \quad {\underline{M}}^{\textrm{space}}_h \end{pmatrix}\in {\mathbb {R}}^{n_\delta \times n_\delta }. \end{aligned}$$

We note that it holds $\theta ^\ell (T)=\delta _{\ell ,K}$, i.e., $\theta ^\ell (T)=0$ for $\ell =1,\ldots ,K-1$ and $\theta ^K(T)=1$. With this notation at hand, the fully discretized version of the adjoint problem (4.8) reads

$$\begin{aligned} {\varvec{B}}_\delta ^\top {\varvec{z}}_\delta + {\varvec{D}}_\delta {\varvec{y}}_\delta = {\varvec{g}}_\delta . \end{aligned}$$

(4.10)

4.4 Petrov–Galerkin discretization of the gradient equation

In order to obtain a discrete version of the gradient equation we test (3.4c) with the basis functions of ${{\mathcal {U}}}_\delta$, namely $\lambda \left( u_\delta , \delta u_\delta \right) _{{{\mathcal {H}}}}- \langle R \delta u_\delta , z_\delta \rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}}= 0$ for all $\delta u_\delta \in {{\mathcal {U}}}_\delta$. Recalling the discretizations (4.5) and (4.9) of $u_\delta$ and $z_\delta$, respectively, we obtain for $\ell =0,\ldots ,K-1$ and $j=1,\ldots ,{n}_h$

$$\begin{aligned} 0&= \lambda \left( u_\delta , \xi ^\ell \otimes \phi _j \right) _{{{\mathcal {H}}}} - \langle z_\delta , \xi ^\ell \otimes R\phi _j\rangle _{{{\mathcal {V}}}\times {{\mathcal {V}}}'} \\&=\lambda \sum _{k=0}^{K-1} \sum _{i=1}^{{n}_h} u_i^k\, (\xi ^k\otimes \phi _i, \xi ^\ell \otimes \phi _j )_{{{\mathcal {H}}}} - \sum _{k=0}^{K-1}\sum _{i=1}^{n_h} z_i^k\, \langle \xi ^k\otimes \phi _i, \xi ^\ell \otimes R\phi _j \rangle _{{{\mathcal {V}}}\times {{\mathcal {V}}}'} \\&= \lambda \sum _{k=0}^{K-1} \sum _{i=1}^{{n}_h} u_i^k \, (\xi ^k,\xi ^\ell )_{L_2(I)}\, (\phi _i, \phi _j)_H - \sum _{k=0}^{K-1}\sum _{i=1}^{n_h} z_i^k\,(\xi ^k,\xi ^\ell )_{L_2(I)}\, \langle R\phi _j, \phi _i\rangle _{V'\times V} \\&= \lambda [({\underline{M}}^{\textrm{time}}_{\Delta {t}}\otimes \underline{{M}}^{\textrm{space}}_h) {\varvec{u}}_\delta ]_{\ell , j} - [({\underline{M}}^{\textrm{time}}_{\Delta {t}}\otimes ({\underline{N}}^{\textrm{space}}_h)^\top ) {\varvec{z}}_\delta ]_{\ell , j} \\&=\lambda [{{\varvec{M}}}_\delta {\varvec{u}}_\delta ]_{\ell , j} - [ {\tilde{{\varvec{M}}}}_\delta ^\top {\varvec{z}}_\delta ]_{\ell , j} . \end{aligned}$$

Then, the discrete version of the gradient equation (3.4c) reads

$$\begin{aligned} \lambda {{\varvec{M}}}_{\delta } {\varvec{u}}_\delta - {\tilde{{\varvec{M}}}}_\delta ^\top {\varvec{z}}_\delta = \varvec{0}. \end{aligned}$$

(4.11)

We note, that ${{\varvec{M}}}_{\delta }$ is a square mass matrix, i.e., invertible. For $R=I$, we have ${\tilde{{\varvec{M}}}}_\delta ^\top ={{\varvec{M}}}_{\delta }$, so that ${\varvec{u}}_\delta =\lambda ^{-1} {\varvec{z}}_\delta$.

4.5 The discrete optimality system

We can now put all pieces together and detail the discrete version of the first order optimality system (3.4), namely

$$\begin{aligned} b({\overline{y}}_\delta ,\delta z_\delta ) - \langle R{\overline{u}}_\delta ,\delta z_\delta \rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}}&= h(\delta z_\delta ){} & {} \forall \delta z_\delta \in {{\mathcal {Z}}}_\delta , \end{aligned}$$

(4.12a)

$$\begin{aligned} d( {\overline{y}}_\delta , \delta y_\delta ) +b(\delta y_\delta ,{\overline{z}}_\delta )&= g(\delta y_\delta ){} & {} \forall \delta y_\delta \in {{\mathcal {Y}}}_\delta , \end{aligned}$$

(4.12b)

$$\begin{aligned} \lambda ( {\overline{u}}_\delta , \delta u_\delta )_{{\mathcal {H}}}- \langle R\delta u_\delta , {\overline{z}}_\delta \rangle _{{{\mathcal {V}}}'\times {{\mathcal {V}}}}&= 0{} & {} \forall \delta u_\delta \in {{\mathcal {U}}}_\delta . \end{aligned}$$

(4.12c)

Recalling (4.7), (4.10) and (4.11), the discrete first order optimality system (4.12) can be written in matrix form as

$$\begin{aligned} \begin{pmatrix} {\varvec{D}}_\delta &{} \quad {\varvec{B}}_\delta ^T &{} \quad \varvec{0} \\ {\varvec{B}}_\delta &{} \quad \varvec{0} &{} \quad -{\tilde{{\varvec{M}}}}_\delta \\ \varvec{0} &{} \quad -{\tilde{{\varvec{M}}}}_{\delta }^\top &{} \quad \lambda \,{{\varvec{M}}}_{\delta } \end{pmatrix} \begin{pmatrix} {\varvec{y}}_\delta \\ {\varvec{z}}_\delta \\ {\varvec{u}}_\delta \end{pmatrix} = \begin{pmatrix} {\varvec{g}}_\delta \\ {{\varvec{h}}_\delta } \\ \varvec{0} \end{pmatrix}, \end{aligned}$$

where all involved matrices have tensorproduct structure. In view of (4.11), i.e, $\lambda {{\varvec{M}}}_{\delta } {\varvec{u}}_\delta = {\tilde{{\varvec{M}}}}_{\delta }^\top {\varvec{z}}_\delta$, we can easily eliminate the variable ${\varvec{u}}_\delta$ and obtain the reduced system

$$\begin{aligned} {\varvec{L}}_\delta \begin{pmatrix} {\varvec{y}}_\delta \\ {\varvec{z}}_\delta \end{pmatrix} = \begin{pmatrix} {\varvec{g}}_\delta \\ {{\varvec{h}}_\delta } \end{pmatrix}, \qquad {\varvec{L}}_\delta := \begin{pmatrix} {\varvec{D}}_\delta &{} {\varvec{B}}_\delta ^T \\ {\varvec{B}}_\delta &{} -\textstyle {\frac{1}{\lambda }} {\tilde{{\varvec{M}}}}_\delta {\varvec{M}}_{\delta }^{-1} {\tilde{{\varvec{M}}}}_\delta \end{pmatrix} \end{aligned}$$

(4.13)

which is a discretized version of (3.8). All involved matrices are tensorproducts and for our choice, we have ${\varvec{M}}_{\delta }={\tilde{{\varvec{M}}}}_\delta$. Set $\gamma := \Vert {\tilde{{\varvec{M}}}}_\delta {\varvec{M}}_{\delta }^{-1} {\tilde{{\varvec{M}}}}_\delta \Vert = \Vert {\varvec{M}}_\delta \Vert$, which is bounded uniformly in $\delta \rightarrow 0$.

Theorem 4.3

(Well-posedness of the discrete optimality system) Assume that the discrete inf-sup condition (1.4) holds. Then, the discrete first order optimality system (4.12) is well-posed for all $\lambda >0$ with

$$\begin{aligned} \Vert {\varvec{L}}_\delta ^{-1} \Vert \le {\textstyle {\frac{\gamma +\lambda {{\bar{\beta }}} + \lambda {{\bar{\beta }}}^2}{\lambda {{\bar{\beta }}}^3}}}, \end{aligned}$$

(4.14)

and we have

$$\begin{aligned} \Vert {\varvec{y}}_\delta \Vert + \Vert {\varvec{z}}_\delta \Vert&\le {\textstyle {\frac{\gamma +\lambda {{\bar{\beta }}} + \lambda {{\bar{\beta }}}^2}{\lambda {{\bar{\beta }}}^3}}} (\Vert {\varvec{h}}_\delta \Vert + \Vert {\varvec{g}}_\delta \Vert ),&\Vert {\varvec{u}}_\delta \Vert \le {\textstyle {\frac{\gamma }{\lambda }}} {\textstyle {\frac{\gamma +\lambda {{\bar{\beta }}} + \lambda {{\bar{\beta }}}^2}{\lambda {{\bar{\beta }}}^3}}} (\Vert {\varvec{h}}_\delta \Vert + \Vert {\varvec{g}}_\delta \Vert ). \end{aligned}$$

Proof

We obtain the bound (4.14) by adapting the proof of Theorem 3.6 to the discrete case. This ensures the reduced system (4.13) to be well-posed. Remark 3.7, also adapted to the discrete case, yields the bounds for $\Vert {\varvec{y}}_\delta \Vert +\Vert {\varvec{z}}_\delta \Vert$ and $\Vert {\varvec{u}}_\delta \Vert$. $\square$

Remark 4.4

(Comparison with existing space–time methods, continued) We continue Remarks 2.8 and 3.10 with highlighting the differences to previous publications, now concerning the discretization.

To summarize our approach, we start by an optimally stable Petrov–Galerkin discretization of the state equation based upon tensorproducts, which can be chosen to be equivalent to a Crank–Nicolson time stepping method. In a second step, we chose an appropriate discretization of the control. This automatically yields a Petrov–Galerkin discretization of the adjoint equation and the gradient equation. Putting everything together results in a stable discretization of the optimality system along with a priori and a posteriori error estimates.

• (a) [3,4,5] suggest semi-discretizations for the state by discontinuous Galerkin methods. Since there ${{\mathcal {Z}}}={{\mathcal {Y}}}$, this can also be used for the adjoint state. Stability and approximation results are then given.

• (b) [6, 7] uses a Petrov–Galerkin method with temporal discontinuous trial functions and continuous test functions for primal and adjoint problems. The control is not discretized, but treated in a variational manner.

• (c) In [8], the derivation yields a $2\times 2$ saddle point problem for primal and dual state similar to (3.7), which is discretized in a similar fashion as in our approach for the primal state equation. This means that also here primal and dual states use discretizations of the same order, which is different from our approach.

  Moreover, [8] uses an unstructured space–time discretization, whereas we suggest a tensorproduct approach. However, the tensorproduct discretization was here mainly chosen to allow the use of efficient solvers and can easily be replaced by other discretizations as well, provided that a discrete inf-sup can be proven. Tensorproduct discretizations require typically less storage, but usually do not allow adaptive refinement.

4.6 Error analysis

Corollary 4.5

(A priori estimate) The Xu–Zikatanov Lemma [16, Thm. 2] yields a quasi-best approximation statement, i.e.,

Proof

Due to $\inf _{w_\delta \in {{\mathcal {W}}}_\delta } \sup _{v_\delta \in {{\mathcal {W}}}_\delta } \frac{\langle Lw_\delta , v_\delta \rangle _{{{\mathcal {W}}}'\times {{\mathcal {W}}}}}{\Vert v_\delta \Vert _{{\mathcal {W}}}\Vert w_\delta \Vert _{{\mathcal {W}}}} = \Vert {\varvec{L}}_\delta ^{-1}\Vert ^{-1} \ge {\textstyle {\frac{\lambda \bar{\beta }^3}{\gamma +\lambda \bar{\beta } + \lambda \bar{\beta }^2}}},$ we get by applying [16, Thm. 2] to (4.13) the estimate

$$\begin{aligned} \Vert w-w_\delta \Vert _{{{\mathcal {W}}}} \le \Vert L\Vert _{{{\mathcal {W}}}\rightarrow {{\mathcal {W}}}'} {\textstyle {\frac{\gamma +\lambda {{\bar{\beta }}} + \lambda {{\bar{\beta }}}^2}{\lambda {{\bar{\beta }}}^3}}} \inf _{\tilde{w}_\delta \in {{\mathcal {W}}}_\delta }\Vert w-{{\tilde{w}}}_\delta \Vert _{{\mathcal {W}}}\end{aligned}$$

for $w:=(y,z)\in {{\mathcal {W}}}$, $w_\delta :=(y_\delta ,z_\delta )\in {{\mathcal {W}}}_\delta := {{\mathcal {Y}}}_\delta \times {{\mathcal {Z}}}_\delta$. Finally, Remark 3.7 yields $\Vert u - u_\delta \Vert _{{\mathcal {U}}}\le {\textstyle {\frac{\gamma _P}{\lambda }}} \Vert z - z_\delta \Vert _{{\mathcal {Z}}}$, which, together with the definition (3.9) of the norm on ${{\mathcal {W}}}$, proves the claim. $\square$

Using the above described discretization for ${{\mathcal {Y}}}_\delta$, ${{\mathcal {Z}}}_\delta$ and ${{\mathcal {U}}}_\delta$, we get an error of order ${{\mathcal {O}}}(\max \{ h,\Delta t\})$ in the prescribed norms, which can easily be improved by using higher order discretizations (if the solution is sufficiently regular).

Corollary 4.6

(A posteriori estimate) It holds that

$$\begin{aligned} \Vert y-y_\delta \Vert _{{\mathcal {Y}}}+ \Vert z-z_\delta \Vert _{{\mathcal {Z}}}+ \Vert u-u_\delta \Vert _{{\mathcal {U}}}\le {{(1+{\textstyle {\frac{{\gamma _P}}{\lambda }}})} {\textstyle {\frac{\gamma _P+\lambda {\beta } + \lambda {\beta }^2}{\lambda {\beta }^3}}}} \Vert r_\delta \Vert _{{{\mathcal {W}}}'}, \end{aligned}$$

where $r_\delta := \left( g, h\right) ^\top - L(y_\delta ,z_\delta )^\top \in {{\mathcal {W}}}'$ is the residual of the optimality system (3.8).

Proof

Let $w:=(y,z)\in {{\mathcal {W}}}$ the solution of the reduced optimality system (3.8) and $w_\delta :=(y_\delta ,z_\delta )\in {{\mathcal {W}}}_\delta :={{\mathcal {Y}}}_\delta \times {{\mathcal {Z}}}_\delta \subset {{\mathcal {W}}}$ the discrete solution. Then, denoting the right-hand side of (3.8) by $\ell :=(g,h)^\top \in {{\mathcal {W}}}'$ it holds for $v\in {{\mathcal {W}}}$

$$\begin{aligned} r_\delta (v)&= \ell (v) - \langle Lw_\delta , v \rangle _{{{\mathcal {W}}}'\times {{\mathcal {W}}}} = \langle Lw , v \rangle _{{{\mathcal {W}}}'\times {{\mathcal {W}}}} - \langle Lw_\delta , v \rangle _{{{\mathcal {W}}}'\times {{\mathcal {W}}}} \\ {}&= \langle L(w-w_\delta ), v \rangle _{{{\mathcal {W}}}'\times {{\mathcal {W}}}}. \end{aligned}$$

Using the lower bound (3.11) for the inf-sup constant of L, it holds for $w-w_\delta \in {{\mathcal {W}}}$

$$\begin{aligned} {\textstyle {\frac{\lambda \beta ^3}{\gamma _P+\lambda \beta + \lambda \beta ^2}}} \Vert w-w_\delta \Vert _{{\mathcal {W}}}\le \sup _{v \in {{\mathcal {W}}}} \frac{\langle L(w-w_\delta ), v\rangle _{{{\mathcal {W}}}'\times {{\mathcal {W}}}}}{\Vert v\Vert _{{\mathcal {W}}}} = \sup _{v \in {{\mathcal {W}}}} \frac{r_\delta (v)}{\Vert v\Vert _{{\mathcal {W}}}} = \Vert r_\delta \Vert _{{{\mathcal {W}}}'}. \end{aligned}$$

Moreover, Remark 3.7 yields $\Vert u - u_\delta \Vert _{{\mathcal {U}}}\le {\textstyle {\frac{\gamma _P}{\lambda }}} \Vert z - z_\delta \Vert _{{\mathcal {Z}}}$, which, together with the definition (3.9) of the norm on ${{\mathcal {W}}}$, proves the claim. $\square$

The latter estimate allows us to use residual-based error estimates, which are e.g. particularly relevant for the reduced basis method in the case of parameter-dependent problems, see e.g. [35].

4.7 Discretization of the cost function

Finally, we detail the space–time discretization of the cost function, i.e.,

$$\begin{aligned} {\varvec{\hat{J}}}_\delta ({\varvec{u}}_\delta )&:={\textstyle {\frac{1}{2}}} \Vert y_\delta (T) - y_{d,h} \Vert _H^2 + {\textstyle {\frac{\lambda }{2}}} \Vert u_\delta \Vert _{{\mathcal {H}}}^2 \\&= {\textstyle {\frac{1}{2}}} (\theta ^K(T)\, {\varvec{y}}_{\delta }^K - {\varvec{y}}_{d,h})^\top {\underline{M}}^{\textrm{space}}_h (\theta ^K(T)\, {\varvec{y}}_{\delta }^K - {\varvec{y}}_{d,h}) + {\textstyle {\frac{\lambda }{2}}} {\varvec{u}}_\delta ^\top \,{{\varvec{M}}}_\delta \, {\varvec{u}}_\delta , \end{aligned}$$

where $y_{d,h} = \sum _{i=1}^{n_h} y_{d,i}\, \phi _i$ with the coefficient vector ${\varvec{y}}_{d,h} :=(y_{d,i})_{i=1,\ldots ,n_h}\in {\mathbb {R}}^{n_h}$ is a discretization of $y_d$.⁷

We solve the optimal control problem by numerically solving the reduced $2 \times 2$ block linear system arising from the optimality system (4.13).

5 Numerical results

In this section, we present some results of our numerical experiments. We follow two main goals: (1) We make quantitative comparisons concerning the inf-sup-stability of the optimality system and (2) we compare the above presented space–time variational approach with the standard semi-variational approach (see also [36] for such comparisons for parabolic problems). We do not compare with other state-of-the-art methods as we are mainly interested in investigating the effect of simultaneous space–time discretization. In order to make the comparison fair, we chose an all-at-once method for the semi-variational framework so that the reduced discrete optimality system is built in a similar manner in both approaches. Moreover, we used the Crank–Nicolson scheme for the semi-discrete problem since our choice for trial and test spaces for the primal problem is equivalent to this time-stepping scheme, [15, 18]. Thus, in the semi-variational setting, primal and dual problems amount for a comparable number of operations, with a stability issue for the dual problem, of course. Note that, in the semi-variational case, the Crank–Nicolson scheme for the adjoint problem (i.e., $\partial _t z + \mathop {}\Delta z = 0;\ z(T) = y(T)- y_d$) is backward in time.

All results were obtained with Matlab R2020b on a machine with a quad core with 2.7 GHz and 16 GB of RAM.

5.1 Discrete inf-sup constant

We start by computing the discrete inf-sup constant of the optimality system and compare that with the bound (3.12) in Corollary 3.9. We report the data for a 1d example on $I \times \Omega =(0,1) \times (-1,1)$ with $\mu (x) = x^2 + 0.1$ for $n_h = 40$, $K= 80$, but stress that the results are representative also for other examples.

First, we investigate the dependence of the inf-sup constant w.r.t. the regularization parameter $\lambda$. In Fig. 1, we show the computed discrete inf-sup constant in comparison with the lower bound $(2+{\textstyle {\frac{1}{\lambda }}})^{-1}$.⁸ We observe the same quantitative behaviors of both curves and see that our bound seems to be almost sharp for increasing values of $\lambda$. In particular, we see the optimality (inf-sup is unity) already for $\lambda =10^{-2}$ and larger. For small values of $\lambda$, the bound is too pessimistic by almost two orders of magnitude.

Fig. 1

Discrete inf-sup constant of the optimality system for different values of $\lambda$

Next, we fix $\lambda =10^{-2}$ and investigate the dependence of the discretization. The results are presented in Fig. 2. On the left, we fix $K=60$ and vary $n_h$, whereas on the right, we choose $n_h=60$ and modify K. We see that the lower bound is in fact pessimistic, stability improves as K increases and worsens for $n_h$ – as to be expected. However, we can confirm uniform stability (i.e., for all choices of $n_h$ and K) in all cases.

Fig. 2

Discrete inf-sup constant of the optimality system for $\lambda =10^{-2}$ and different values of $n_h$ and K

5.2 Space-time versus semi-variational method

Our next aim is to compare our space–time method with a semi-variational approach. As already pointed out earlier, we choose the data in such a way that the results are in fact comparable.

5.2.1 One-dimensional example

We start by Problem 1.1 on $I \times \Omega =(0,1) \times (-1,1)$ for $\mu (x) :=x + 1.3$, boundary data $\eta (t,x) :=\frac{\textrm{sign}(x) 50 t^2}{\cosh (50x)} + (1.3 + x) \tanh (50 x) t^2$ and desired state $y_d(x) = \tanh (50 x)$. Again, we note that we got comparable results also for other data. We compare the value of the objective function that we reach by solving the optimality system with the two approaches. The results are shown in Fig. 3 for two values of the regularization parameter $\lambda$. We show the value for increasing number K of time steps and two different spatial discretizations, namely $n_h=101$ and $n_h=1001$. First, we observe that the overall performance is independent of the choice of $\lambda$. Next, we see that both methods converge to the same value of the objective function as K increases. However, the huge benefit of the space–time setting shows off, namely that we reach an almost optimal value also for very coarse temporal discretizations, which offers significant computational savings.

Fig. 3

1d example, values of the objective function for different discretizations (left: $\lambda = 10^{-1}$, right: $\lambda =10^{-3}$, abbreviations: semi-variational (sv), space–time (st))

It is not surprising that this effect is due to the improved stability of the space–time method as we can also see in Fig. 4, where we depict the control for different values of K for $\lambda =10^{-3}$ and $n_h=101$. We can clearly observe the stability issues for the semi-variational approach in the left column, which do not appear in the space–time context.

Fig. 4

Optimal control for $\lambda = 10^{-3}$ and $n_h=101$ (left column: semi-variational, right column: space–time, top row: $K = 50$, bottom row: $K=500$)

5.2.2 Higher dimensional examples

A possible criticism of the space-time-approach is the fact that the size of the optimality system might significantly grow with increasing space dimension. Hence, we realized both approaches also in 2d and 3d and report the results in the 2d case here. We do not monitor CPU-time comparisons, but refer e.g. to [22, 37], where such comparisons have been done for space–time variational formulations of the heat and wave equation, respectively. It was shown there, that appropriate tensorproduct solvers in fact yield competitive CPU times for the arising space–time systems. The adaptation of those approaches to the optimality system (4.13) is subject to ongoing work, see also Remark 5.1 below.

Hence, we are going to report results for $I \times \Omega :=(0,1) \times (0,1)^2$ and boundary data $\mu (x) :=0.25 \cosh (x y) +0.25$ along with a compatible function $\eta$. As desired state, we choose $y_d(x) = \tanh (10 (x-0.5)(y-0.5))$. As in the 1d case, we compare the values of the objective function, see Fig. 5. The overall behavior is very similar to the 1d case, namely we get a significant improvement of the space-approach over the semi-variational one for small number of time steps K. Note, that here we use a linear scale for the horizontal axis as opposed to Fig. 3, where the results are shown in logarithmic scale. Moreover, for large values of $\lambda$, we observe the necessity of a sufficiently fine spatial discretization for both methods.

Fig. 5

2d example, values of the objective function for different discretizations (left: $\lambda = 10^{-1}$, right: $\lambda =10^{-3}$, abbreviations: semi-variational (sv), space–time (st))

Remark 5.1

With the chosen all-at-once approach, we get very similar CPU times for both methods. As already pointed out earlier, a runtime comparison of best possible schemes is not the aim of this paper. Not using efficient tensorproduct solvers yields that the limiting factor is the memory – in both cases.

6 Summary, conclusions and outlook

We have considered a space–time variational formulation for a PDE-constrained optimal control problem. Our first-optimize-then-discretize approach follows the abstract functional analytic framework of such problems, which is then detailed for the space–time variational method. This can be summarized as follows:

• Well-posed space–time variational formulation of the state equation. This yields different trial and test spaces (Petrov–Galerkin style) of minimal regularity;

• Formulation of the optimal control problem in the arising spaces, definition of the Lagrange function and derivation of KKT conditions. This yields the adjoint and gradient equations in natural spaces with minimal regularity requirements;

• Derivation of (necessary and sufficient) optimality conditions and optimality system (still in the infinite-dimensional setting);

• LBB-stable discretization of the optimality system. In special cases, this can be chosen to be equivalent to a Crank–Nicolson semi-discrete discretization, which allows quantitative numerical comparisons.

Moreover, we reported on numerical experiments showing that space–time methods yield the same value of the objective function for significantly smaller number of unknowns. Since the CPU-times for the same number of unknowns turned out to be similar, this offers potential for significant speedup.

Topics for future research include control and state constraints, other types of PDEs for the constraints, improved schemes for solving the optimality system, adaptive discretization of the control, etc. Also efficient solvers that explicitly exploit the Kronecker structures of arising operators should be investigated. Finally, the above setting seems to be a very good starting point for investigating model reduction, e.g. [18].