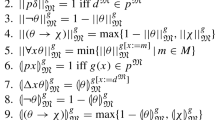An encoding of the $\lambda$-calculus in the String MultiSet Rewriting calculus

Abstract

In this paper, we present an encoding of the $\lambda$-calculus in a multiset rewriting system and provide a few applications of the construction. For this purpose, we choose the calculus named String MultiSet Rewriting, which was introduced in Barbuti et al. (Electron Notes Theor Comput Sci 194:19–34, 2008) by Barbuti et al. With the help of our encoding, we give alternative proofs for the standardization and the finiteness of developments theorems in the $\lambda$-calculus.

1 Introduction

In past years, many formalisms have appeared in order to model biological systems based on interacting components. Most of these systems are high-level abstractions of biological phenomena aiming to describe the organization of the components of a biological system and the possible interactions between the components. For example, we would mention the $\kappa$-calculus of Danos and Laneve [11], which is a formal system modeling protein interaction, and the biochemical Stochastic $\pi$-calculus [16], which allows qualitative and quantitative investigations of composite systems. The Brane Calculus defined by Cardelli [8] is an efficient tool for the exact presentation of cell-level processes, and the same is true for the Calculus of Looping Sequences [3]. Many of the systems mentioned are based on multiset rewriting, and the same is true for membrane systems [10], chemical reaction systems [15] and Petri nets [9]. There are recent investigations concerning the introduction of regulating mechanism to reduce the extent of non-determinism and to enhance the expressive power of these systems [20]. A significant part of the attention devoted to these investigations is due to the effort of providing manageable but general enough modeling frameworks for biologically inspired computational systems [18].

A form of multiset rewriting, which is the Calculus of Looping Sequences, was proposed in [14] offering a simple and easy to implement tool with a clear semantics to model biochemical processes. Translating higher-level systems to this calculus turned out to be difficult, however. Hence, the calculus of String MultiSet Rewriting (SMSR) was developed [4], which proved to be an appropriate intermediate solution: its main invention is the maximal matching operator, which facilitates the representation of higher-level languages. The underlying idea of that calculus is that, by grabbing the tree-like structures of terms of a formal system, a multiset of strings can describe the index paths from root to leaves in a given term and, consequently, substitutions with terms are encoded as replacement of a whole multiset of strings having a common prefix with another multiset in a single step.

In this paper, we introduce first the SMSR system following [4]. Then, we show how to represent $\lambda$-terms with multisets and define the multiset rewriting rule corresponding to $\beta$-reduction. We prove that this multiset calculus correctly simulates the $\lambda$-calculus equipped with $\beta$-reduction. With this in hand, we present two applications of the construction: We give a proof of the standardization theorem of the $\lambda$-calculus and a demonstration of the finiteness of developments theorem. The proofs benefit from the fact that strings in multisets can be considered index sequences identifying subterm occurrences in the corresponding $\lambda$-terms; hence, the statements concerning subterms, contractums and residuals can be formulated in a precise and natural way based on the multiset calculus. The proofs give some insight into the original $\lambda$-calculus notions: For example, we can address every subterm occurrence by some string and, hence, by giving an appropriate ordering to these strings, we can show that a $\beta$-reduction sequence is standard if and only if the sequence of index strings is non-decreasing. That is, the phrase “from left to right” used to explain standardness obtains its meaning. By the proof of the finiteness of developments theorem, we make use of a separation lemma applied in [21], the proof of which can possibly be presented in a more intuitive and clearer way when we resort to multisets. The present encoding can open the way for approaching theorems of the $\lambda$-calculus from a different perspective: It offers a computationally complete “index calculus” that may be the source of further investigations. It seems to be flexible enough to encode different evaluation semantics of the lambda calculus, or, possibly, resource lambda calculus [7], or symmetric lambda calculi [17] or non-deterministic calculi like, for example, the chemical programming model of Bânatre et al [2]. On the other hand, the calculus appears to be simple enough to serve as the foundation for implementations. There is already an ongoing research on the implementation of a multiset rewriting calculus [20] very similar to SMSR calculus. To sum it up, the multiset rewriting calculus provides a powerful tool in the study of rewriting systems, which is capable of both underpinning precise mathematical arguments and of permitting the creation of tools for real-life applications.

2 String MultiSet Rewriting

In this section, we provide a brief overview of the String MultiSet Rewriting (SMSR) calculus following the treatment in [4].

2.1 Strings and multisets

In what follows, we present the String MultiSet Rewriting (SMSR) calculus. Prior to this, we briefly recall the main notions regarding multisets.

Let $\mathbb {N}$ denote the set of natural numbers and $\mathbb {N}^+$ denote the set of positive integers, respectively, and let U be a finite non-empty set. A multiset M over U is a pair $M=(U,f)$, where the mapping $f:U\rightarrow \mathbb {N}$ gives the multiplicity of each element $a\in U$. If $f(a)=0$ for each $a\in U$, then M is the empty multiset. The number of elements in a multiset M, that is, the elements $a\in U$ with positive multiplicity, is denoted by |M|, and we refer to this number as the cardinality of M. In our case, the cardinality of a string multiset M is the number of strings in M.

Next, we define some elementary operations concerning multisets. Let $M_1=(U,f_1),$ $M_2=(U,f_2)$. Then, $(M_1\sqcap M_2)=(O,f)$ where $f(a)=\textrm{min}\{f_1(a),f_2(a)\}$; $(M_1\sqcup M_2)=(O,f')$, where $f'(a)=\textrm{max}\{f_1(a),f_2(a)\}$; $(M_1\oplus M_2)=(O,f'')$, where $f''(a)=f_1(a)+f_2(a)$; $(M_1\ominus M_2)=(O,f''')$ where

$f'''(a)=\textrm{max}{\{f_1(a)-f_2(a),0\}}$; and $M_1\sqsubseteq M_2$, if $f_1(a)\le f_2(a)$ for all $a\in O$.

String MultiSet Rewriting (SMSR) is a term rewriting calculus. Firstly, we will define the syntax of terms, which are the strings and their multisets, and then a structural congruence relation on them. Afterward, a rewrite rule will be introduced which constitutes the instructions for the evolution of terms.

In the sequel, we will assume that an infinite alphabet $\mathcal {E}$ is given.

Definition 1

(Terms) Multisets M and strings S over an alphabet $\mathcal {E}$ are defined by the following Backus–Naur form:

$$\begin{aligned} M \quad&= \quad S \quad \big | \quad (M \; | \; M) \\ S \quad&= \quad \varepsilon \quad \big | \quad e \quad \big | \quad (S \cdot S) \end{aligned}$$

where $\varepsilon$ is the empty string, e is a generic element of the alphabet $\mathcal {E}$, $\cdot$ denotes string concatenation, and | stands for multiset union. The set of all multisets over $\mathcal {E}$ is denoted by $\textbf{M}(\mathcal {E})$, or by $\textbf{M}$ if $\mathcal {E}$ is clear from the context. Similarly for $\textbf{S}(\mathcal {E})$, which is the set of all strings over $\mathcal {E}$. We denote an arbitrary element of $\textbf{S}$ either by the letters $P, Q, S, \ldots$ possibly with indexes, or by smaller case Greek letter $\xi$, $\eta$, $\nu$, etc. Let |M| denote the cardinality of M as a multiset, while let lh(M) denote the total number of occurrences of symbols of $\mathcal {E}$ in M counted with multiplicities.

We introduce a structural congruence relation expressing the associativity of $\cdot$ and |, commutativity of |, and we make sure that $\varepsilon$ is an identity element either considered a string or a multiset.

Definition 2

Let $\xi , \xi _1, \xi _2, \xi _3$ be strings and $M, M_1, M_2, M_3$ be multisets. The structural congruence relation $\equiv$ is the least congruence relation on multisets with the following properties:

$$\begin{aligned}{} & {} (\xi _1 \cdot (\xi _2 \cdot \xi _3)) \equiv ((\xi _1 \cdot \xi _2) \cdot \xi _3) \qquad (\xi \cdot \varepsilon ) \equiv \xi \\{} & {} (M_1 \; | \; M_2) \equiv (M_2 \; | \; M_1) \quad (M_1 \; | \; (M_2 \; | \; M_3)) \equiv ((M_1 \; | \; M_2) \; | \; M_3) \quad (M \; | \; \varepsilon ) \equiv M \end{aligned}$$

Applying this congruence, we abbreviate expressions by omitting parentheses if possible. The outermost parentheses will be frequently omitted. In the sequel, we implicitly understand multiset equality modulo that congruence. We use standard equality to express that on the left- and right-hand side there stand the same objects (in most of the cases by virtue of some definition). Having the syntax and the structural congruence of terms at hand, we can now introduce the concept of patterns. We will assume an infinite set of variables $\mathcal {V} = \mathcal {V}_{\mathcal {E}} \cup \mathcal {V}_{{S}} \cup \mathcal {V}_{{M}}$, where $\mathcal {V}_{\mathcal {E}} = \{x, y, z, \ldots \}$ denotes the infinite set of element variables, $\mathcal {V}_{{S}} = \{\widetilde{x}, \widetilde{y}, \widetilde{z}, \ldots \}$ denotes the infinite set of string variables and $\mathcal {V}_{{M}} = \{X, Y, Z, \ldots \}$ stands for the infinite set of multiset variables. The definition below defines multiset patterns.

Definition 3

(Patterns) Multiset patterns and string patterns over an alphabet $\mathcal {E}$ are defined applying the following Backus–Naur form:

$$\begin{aligned} MP \quad =&\quad SP \quad \big | \quad MP \; | \; MP \quad \big | \quad \{ \! |SP | \! \}_X \quad \big |\\&\quad \{ \! |SP | \! \}_{X}\vartriangleright _e\{ \! |SP | \! \}_{Y}\\ SP \quad =&\quad \varepsilon \quad \big | \quad e \quad \big | \quad SP \cdot SP \quad \big | \quad \widetilde{x} \quad \big | \quad x \end{aligned}$$

In the sequel, we denote by $\textbf{MP}$ the set of multiset patterns and by $\textbf{SP}$ the set of string patterns, respectively.

The above definition of multiset patterns differs from that applied in [4]. Namely, we augmented it with the construction $\{ \! |SP_1 | \! \}_{X}\vartriangleright \{ \! |SP_2 | \! \}_{Y}$ for arbitrary string patterns $SP_1$, $SP_2$. This construction could be circumvented in the original string multiset calculus; however, by this, the encoding of $\lambda$-terms seemed to be more natural and smooth.

Multiset patterns are used to construct rewrite rules, which define the evolution of SMSR terms. A rewrite rule is a pair of multiset patterns, where the first pattern matches the term to be modified by the rule, while the second pattern matches the result of the rule application, which is the new term. Element variables of multiset patterns are substituted by elements of $\mathcal {E}$ and string variables by strings during the reduction.

We call a function $\sigma : \mathcal {V}_{\mathcal {E}}\cup \mathcal {V}_S\rightarrow \textbf{S}$ an instantiation. Given an instantiation $\sigma$, we can extend it to a function $\sigma ':\textbf{SP}\rightarrow \textbf{S}$ in an obvious way, by letting $\sigma '$ agree with $\sigma$ on $\mathcal {V}_{\mathcal {E}}\cup \mathcal {V}_S$ and by demanding that $\sigma '(SP_1\cdot SP_2)=\sigma '(SP_1)\cdot \sigma '(SP_2)$ for any $SP_1$, $SP_2\in \textbf{SP}$ and $\sigma '(e)=e$ if $e\in \mathcal {E}$. In the sequel, we use the notation $\sigma$ for $\sigma '$ as well and call $\sigma '$ an instantiation, also. Hence, to define an instantiation $\sigma : \textbf{SP}\rightarrow \textbf{S}$, it is enough to determine the values assigned by $\sigma$ to the set of element and string variables, respectively. To define the meaning of a multiset pattern, besides the instantiation $\sigma : \textbf{SP}\rightarrow \textbf{S}$, we need a function $\rho : \mathcal {V}_{{M}} \rightarrow \mathbb {N}^+$ and a pattern expansion function $\langle \_ \rangle _{\_}^{-}: \textbf{MP} \times (\mathcal {V}_{{M}} \rightarrow \mathbb {N}^+)\times (\textbf{SP}\rightarrow \textbf{S}) \rightarrow \textbf{M}$.

The pattern expansion function transforms multiset patterns into multisets. Particularly, it assigns to a multiset pattern of the form $\{ \! |SP | \! \}_{X}$ a finite union of multisets all having the same prefix, namely, the common prefix is obtained after evaluating SP with the help of $\rho$ and $\sigma$, where $SP\in \textbf{SP}$ is arbitrary. The patterns of the form $\{ \! |SP_1 | \! \}_{X}\vartriangleright _e\{ \! |SP_2 | \! \}_{Y}$ are evaluated to some “cross-product” of the multisets obtained by evaluating $\{ \! |SP_1 | \! \}_{X}$ and $\{ \! |SP_2 | \! \}_{Y}$ $(SP_1, SP_2\in \textbf{SP})$. The subsequent definitions will provide the exact notions.

Given multisets $M_1$, $M_2$ and element $e\in \mathcal {E}$, we define the operation of substituting the multiset $M_2$ in $M_1$ in place of e when the underlying occurrence of e is the rightmost element of a string in $M_1$.

Definition 4

The multiset substitution function $.[.\leftarrow .]:\textbf{M} \times \mathcal {E}\times \textbf{M} \rightarrow \textbf{M}$ acts in the following way.

• 1. $S_1 [e\leftarrow S_2] = \left\{ \begin{array}{ll}S_1' \cdot S_2,&{}\text { if }S_1=S_1'\cdot e,\\ S_1&{}\text { otherwise}.\end{array}\right.$

• 2. $(M_1 \; | \; M_2) [e\leftarrow S] = (M_1 [e\leftarrow S] \; | \; M_2 [e\leftarrow S])$

• 3. $M_1 [e\leftarrow (M_2 \; | \; M_3)] = (M_1 [e\leftarrow M_2] \; | \; M_1 [e\leftarrow M_3])$

Now, we are in a position to define the pattern expansion itself.

Definition 5

Let $SP, SP_1, SP_2\in \textbf{SP}$ and $MP_1, MP_2\in \textbf{MP}$. The pattern expansion function $\langle \_ \rangle _{\_}^{-}: \textbf{MP} \times (\mathcal {V}_{{M}} \rightarrow \mathbb {N}^+)\times (\textbf{SP}\rightarrow \textbf{S}) \rightarrow \textbf{M}$ is recursively defined as follows:

• 1. $\langle SP \rangle _\rho ^{\sigma } \quad = \quad \sigma (SP),$

• 2. $\langle \{ \! |SP | \! \}_{X}\rangle ^{\sigma } _\rho = \big (\sigma (SP) \cdot \sigma (\widetilde{x}_1) \; | \; \ldots \; | \; \sigma (SP) \cdot \sigma (\widetilde{x}_{n})\big ) \ \textrm{where} \quad \widetilde{x} \in \mathcal {V}_\textbf{S}\ \textrm{and}\ \rho (X)=n,$

• 3. $\langle \{ \! |SP_1 | \! \}_{X}\vartriangleright _e \{ \! |SP_2 | \! \}_{Y}\rangle _\rho ^{\sigma } \quad = \quad \langle \{ \! |SP_1 | \! \}_{X}\rangle _{\rho }^{\sigma } [e\leftarrow \langle \{ \! |SP_2 | \! \}_{Y}\rangle _{\rho }^{\sigma }],$

• 4. $\langle MP_1 \; | \; MP_2 \rangle _\rho ^{\sigma } \quad = \quad \big (\langle MP_1 \rangle _\rho ^{\sigma } \; | \; \langle MP_2 \rangle _\rho ^{\sigma }\big ).$

Observe that the operator $\vartriangleright _e$ acts as a replacement with respect to the occurrences of e which are final occurrences of a string in $\langle \{ \! |SP_1 | \! \}_{X}\rangle _{\rho }^{\sigma }$. We illustrate this in the next example.

Example 6

Let $\mathcal {E}=\{a,b,c,d,e\}$, let $SP_1=a$, $SP_2=\varepsilon$. Let $\rho : \mathcal {V}_{{M}} \rightarrow \mathbb {N}^+$ and $\sigma : \textbf{SP}\rightarrow \textbf{S}$ in the multiset pattern $\{ \! |SP_1 | \! \}_{X}\vartriangleright _c \{ \! |SP_2 | \! \}_{Y}$ be defined as $\rho (X)=\rho (Y)=2$ and $\sigma (\tilde{x}_1)=b$, $\sigma (\tilde{x}_2)=c$ and $\sigma (\tilde{y}_1)=d$, $\sigma (\tilde{y}_2)=e$. Then,

$$\begin{aligned} \langle \{ \! |SP_1 | \! \}_{X}\vartriangleright _c \{ \! |SP_2 | \! \}_{Y}\rangle _\rho ^{\sigma }\equiv & {} (a\cdot b\mid a\cdot c)\vartriangleright _c (d\mid e)\\ {}\equiv & {} (a\cdot b\mid a\cdot c)[c\leftarrow (d\mid e)]\\\equiv & {} ((a\cdot b)[c\leftarrow (d\mid e)]\mid (a\cdot c)[c\leftarrow (d\mid e)])\\\equiv & {} ((a\cdot b)[c\leftarrow d]\mid (a\cdot b)[c\leftarrow e]\mid \\ {}{} & {} (a\cdot c)[c\leftarrow d]\mid (a\cdot c)[c\leftarrow e])\\ {}\equiv & {} (a\cdot b\mid a\cdot b\mid a\cdot d\mid a\cdot e). \end{aligned}$$

2.2 The rewrite rules

We give an account, based on [4], of the reduction rule in the SMSR calculus. Before giving a full-fledged formal description of SMSR reduction, we try to grab the intuition behind it in the next definition.

Definition 7

• 1. Let $M, N\in \textbf{M}$. We apply the notation $N\in M$ if $\exists$ P :  $M\equiv N\mid P$.

• 2. A rewrite rule is a pair $(MP_1,MP_2)$ of multiset patterns such that $MP_1$ is non-empty. As before, we call a function $\sigma : \textbf{SP}\rightarrow \textbf{S}$ an instantiation. We denote the set of rewrite rules by $\textbf{R}$.

• 3. Let M and $M'\in \textbf{M}$. Then, M, $M'$ can be matched by the rule $(MP_1,MP_2)$ if $\langle MP_1\rangle _\rho ^\sigma \equiv M$ and $\langle MP_2\rangle _\rho ^\sigma \equiv M'$, where $\rho :\mathcal {V}_{{S}}\rightarrow \mathbb {N}$ and $\sigma$ is an instantiation. Assume $M\in N$ and M, $M'$ can be matched by $(MP_1,MP_2)\in \textbf{R}$. Then, M can be exchanged for $M'$ only if there is no string U in $N\setminus M$ such that there is a prefix $U'$ of U which is a common prefix of all the strings in M.

We have to deal with some technical questions first. Namely, we make sure that rule applications always generate fresh names. With this aim, we introduce some auxiliary notions. The definition below is based on [4].

Definition 8

• 1. Let Var(MP) denote the set of variables appearing in the multiset pattern MP with the proviso that $Var(\{ \! |SP| \! \}_{X})$ is understood as $Var(SP)\cup \{\widetilde{x}_i\mid i\in \mathbb {N}\}$. For example, $Var(a\cdot \widetilde{x}\mid y\mid \{ \! |\varepsilon | \! \}_{Y})=\{\widetilde{x}, y\}\cup \{\widetilde{y}_i\mid i\in \mathbb {N}\}$.

• 2. Let Symbols(U) denote the set of elements of $\mathcal {E}$ that appear in the multiset pattern or multiset U. For instance, $Symbols(a \cdot x | a \cdot b | \{ \! |d| \! \}_{X}) = \{a, b, d\}$. We assume that Symbols extends to a set of multiset patterns or multisets and we define the set of fresh names for a multiset M as $\mathcal {E}\setminus Symbols(M)$.

• 3. A multiset pattern MP is ground if and only if $Var(MP)=\emptyset$. A rule $R=(MP,MP')$ is ground if and only if both MP and $MP'$ are ground. We write $Var(R)=Var(MP) \cup Var(MP')$ and $Symbols(R) = Symbols(MP) \cup Symbols(MP')$.

• 4. Let $R=(MP,MP')$. Then, $Fv(R)=\{v\mid v\in Var(MP'){\setminus } Var(MP)\}$ and $Bv(R)=Var(R){\setminus } Fv(R)$.

Now, we define the rewrite rules.

Definition 9

Let $R=(MP_1,MP_2)\in \textbf{R}$. An application of R can be described as follows. Assume $M, M'$ are multisets such that $\langle MP_1\rangle _{\rho }^{\sigma } \equiv M$ and $\langle MP_2\rangle _{\rho }^{\sigma } \equiv M'$ for some $\rho$ and instantiation $\sigma$.

• 1. Assume $Symbols(\sigma (Bv(R)) \cup Symbols(R)) \cap Symbols(\sigma (Fv(R))) = \emptyset$. Then, we write

  $$\begin{aligned} \xrightarrow [\text {}]{(\{\sigma (SP)\mid \langle \{ \! |SP| \! \}_{X}\rangle _{\rho }^{\sigma }\in M\}, Symbols(\sigma (Fv(R)))} M'.\end{aligned}$$

  (1)

• 2. If $M\xrightarrow [\text {}]{(\xi ,\zeta )}M'$ and $(\forall S\in \xi )(\not \exists S'\in \textbf{S})((S\cdot S')\in M'')$ and $Symbols(M'')\cap \zeta =\emptyset$, then

  $$\begin{aligned}M''\mid M\xrightarrow [\text {}]{(\xi ,\zeta )}M''\mid M'. \end{aligned}$$

  (2)

The first rule expresses the fact that each submultiset of M with a common prefix must be taken into account in the course of the reduction. The second rule ensures that only maximal submultisets with a common prefix can be exchanged.

The next example illustrates the definition.

Example 10

Let $M \equiv b\;|\;b\cdot c\;|\;b\cdot d$. Let $R_1=(\{ \! |b | \! \}_{X},a)$ and $R_2=(b\cdot \widetilde{x}\;|\;\{ \! |b | \! \}_{X},a)$ be two rules. Then,

• 1. $M\rightarrow ^{(\xi _1,\zeta _1)} a$ is a correct application of $R_1$ with $\rho _1(X)=3$ and $\sigma _1(\widetilde{x}_1)=\epsilon$, $\sigma _1(\widetilde{x}_2)=c$ and $\sigma _1(\widetilde{x}_3)=d$. Regarding the label: $(\xi _1,\zeta _1)=(\{b\}, \emptyset )$.

• 2. Furthermore, $M\rightarrow ^{(\xi _2,\zeta _2)} a$ with $\sigma _2(\widetilde{x})=\epsilon$, $\rho _2(X)=2$ and $\sigma _2(\widetilde{x}_1)=c$, $\sigma _2(\widetilde{x}_2)=d$ is a correct derivation applying $R_2$. Regarding the label: $(\xi _2,\zeta _2)=(\{b\}, \emptyset )$.

• 3. On the contrary,

  $$\begin{aligned} b\;|\;b\cdot c\;|\;b\cdot d\rightarrow _{R_1}a\;|\;b\cdot d,\;\;\;b\;|\;b\cdot c\;|\;b\cdot d\rightarrow _{R_2} b\;|\;a \end{aligned}$$

  would be incorrect derivations, since they violate the stipulation that $\langle \{ \! |b | \! \}_{X}\rangle _{\rho }^\sigma$ should be the maximal subterm of M the strings of which begin with the prefix b.

In general, rewriting affects the maximal submultisets beginning with the common prefix $\sigma (SP)$ for some SP. This ensures that in encodings, where submultisets correspond to subterms, multisets denoting subterms are replaced as a whole. The next subsection clarifies this idea.

3 Encoding of the $\lambda$-calculus in SMSR

In this section, we present an encoding of the $\lambda$-calculus in SMSR. The main idea behind the encoding is to make use of the tree-like representation of $\lambda$-terms. We create an SMSR string for every branch of the syntax tree of a $\lambda$-term. Leaf elements of strings represent variables or constants in the original $\lambda$-terms. We lean on the fact that in the SMSR calculus we can identify submultisets of strings by the pattern expansion function. The next function inserts a string in front of each element of a string multiset.

Definition 11

The injection function $\gg \;: \; \textbf{S} \times \textbf{M} \rightarrow \textbf{M}$ is defined recursively as follows:

• 1. $\xi _1 \gg \xi _2= \xi _1 \cdot \xi _2$

• 2. $\xi \gg (M_1 \; | \; M_2)= (\xi \; \gg \; M_1) \; | \; (\xi \; \gg \; M_2)$

Observe that $\gg$ extends the $\cdot$ operator on strings. In the sequel, by abusing notation, we write $\xi \cdot M$ instead of $\xi \gg M$ even when M is a multiset consisting of more than one string. We assume that $\gg$ associates to the right.

Using the injection function, we can now easily construct SMSR strings representing paths in the syntactic tree. Prior to this, following [5], we provide the inevitable notions for formulating $\lambda$-calculus terms. Given a set of variables $\mathcal {V}_\lambda$, a $\lambda$-term is defined by the following Backus–Naur form:

$$\begin{aligned}\Lambda = \mathcal {V_\lambda }\mid (\lambda \mathcal {V_\lambda }\,\Lambda )\mid (\Lambda \,\Lambda ).\end{aligned}$$

We may agree on the usual ways of applying parentheses in the $\lambda$-calculus: Abstraction associates to the right, while application associates to the left. The dot notation indicates the weakest operation in the subterm surrounded by parentheses. The outermost parentheses can be omitted. Hence, $\lambda x\lambda y. xy\equiv (\lambda x(\lambda y(x\,y)))$, or $\lambda x.xy(\lambda z\,z)\equiv (\lambda x((x\,y)(\lambda z\,z)))$. With this in hand, we can now encode terms by a multiset of strings as the next definition shows.

Definition 12

Let $\mathcal {V}_\lambda$ be the set of $\lambda$-variables. Let $\mathcal {E}_\lambda =\mathcal {V}_\lambda \cup \{l, r\}\cup \{\lambda x\mid x\in \mathcal {V}_\lambda \}$. The encoding function $\lfloor \,\_\rfloor :\Lambda \rightarrow \textbf{M}(\mathcal {E}_\lambda )$ is defined recursively as follows:

• 1. $\lfloor M\;N \rfloor = (l \; \cdot \; \lfloor M \rfloor \; | \; r \; \cdot \; \lfloor N \rfloor )$

• 2. $\lfloor \lambda x.M \rfloor = \lambda x \; \cdot \; \lfloor M \rfloor$

• 3. $\lfloor x \rfloor = x$

In what follows, we mean by strings the elements of the set $\textbf{S}({\mathcal {E}_\lambda })$ and by multisets the elements of the set $\textbf{M}({\mathcal {E}_\lambda })$, respectively. Since we identify congruent multisets according to Definition 2, several possible representations are equivalent for the same $\lambda$-term M. Definition 12, however, prescribes a certain order of the strings of a multiset. We call the multiset $\lfloor M\rfloor$ obtained by Definition 12 the canonical representation of the $\lambda$-term M or, simply, the representation of M. Moreover, if N is a multiset obtained from M by means of this encoding, then N is said to be a $\lambda$-multiset.

Example 13

As a short example, we present the encoding of the well-known term $(\lambda x.xx)(\lambda x.xx)$:

$$\begin{aligned} \lfloor (\lambda x.xx)(\lambda x.xx) \rfloor \equiv l \cdot \lambda x \cdot l \cdot x \; | \; l \cdot \lambda x \cdot r \cdot x \; | \; r \cdot \lambda x \cdot l \cdot x \; | \; r \cdot \lambda x \cdot r \cdot x \end{aligned}$$

3.1 b-reduction

After establishing the encoding of $\lambda$-terms, we proceed with presenting the multiset rewrite rule corresponding to $\beta$-reduction in $\lambda$-calculus. Prior to this, we present the $\beta$-reduction in the $\lambda$-calculus. A $\Lambda$-term of the form $(\lambda \,U)\,V$ is called a $\beta$-redex. A $\beta$-reduction is the smallest binary relation over $\Lambda$ compatible with the term formation rules and containing

$$\begin{aligned}(\lambda \,U)\,V\rightarrow _\beta U[x:=V],\end{aligned}$$

where $U[x:=V]$ is obtained from U by obtaining every free occurrence of x in U by V. In the term $\lambda x.U$, the occurrences of the variable x in U are considered to be bound. If an occurrence of x is free in U, then we say that the abstraction $\lambda x$ binds x in $\lambda x.U$. We adopt Barendregt’s notational conventions here: Terms differing in proper renaming of bound variables are considered equal, and if $M_1,\ldots ,M_n$ occur in a certain mathematical context (e.g., definition, proof), then in these terms all bound variables are chosen to be different from the free variables. With all that being said, we can formulate b-reduction on multiset patterns, which corresponds to $\beta$-reduction.

Definition 14

(b-rule, $b_0$-rule)

• 1. In order to define a reduction on multisets, we introduce the b-rule, which is a relation over multiset patterns.

  $$\begin{aligned} ((\{ \! |l \cdot \lambda x| \! \}_X \; | \; \{ \! |r | \! \}_Y), (\{ \! |\varepsilon | \! \}_{X}\vartriangleright _x \{ \! |\varepsilon | \! \}_{Y}))\;\;\;\;\;(b\text {-}rule) \end{aligned}$$

  We call the multiset pattern $(\{ \! |l \cdot \lambda x| \! \}_X \; | \; \{ \! |r | \! \}_Y)$ a b-redex pattern, and the multiset pattern $(\{ \! |\varepsilon | \! \}_{X}\vartriangleright _x \{ \! |\varepsilon | \! \}_{Y})$ a b-contractum pattern. Note that $x\in \mathcal {E}_\lambda$ by Definition 12.

• 2. We call a given M a $b_0$-redex, and $M'$ its $b_0$-contractum if M, $M'\in \textbf{M}(\mathcal {E}_\lambda )$ is such that $(M,M')$ can be matched with the b-rule, that is, $M\equiv \langle (\{ \! |l \cdot \lambda x| \! \}_X \; | \; \{ \! |r | \! \}_Y)\rangle _{\rho }^{\sigma }$ and $M'\equiv \langle (\{ \! |\varepsilon | \! \}_X \; \triangleright _x \; \{ \! |\varepsilon | \! \}_Y)\rangle _{\rho }^{\sigma }$. In notation: $M\hookrightarrow _{b_0} M'$.

As usual, we define b-reduction as the smallest relation over the set of multisets $\textbf{M}(\mathcal {E}_\lambda )$ that contains $\hookrightarrow _{b_0}$ and is compatible with the term formation rules. In notation: $M\hookrightarrow _b M'$ if M b-reduces to $M'$.

Definition 15

(b-reduction) The $b_0$-rule can be extended to $\hookrightarrow _{b}$-reduction over multisets in $\textbf{M}(\mathcal {E}_\lambda )$. Let U, V and $W\in \textbf{M}(\mathcal {E}_\lambda )$.

• 1. If $U\hookrightarrow _{b_0} V$, then $U\hookrightarrow _b V$.

• 2. If $U\hookrightarrow _b V$, then $\lambda x\cdot U\hookrightarrow _b \lambda x\cdot V$.

• 3. If $U\hookrightarrow _b V$, then $l\cdot U\;|\;r\cdot W\hookrightarrow _b l\cdot V\;|\;r\cdot W$ and $l\cdot W\;|\;r\cdot U\hookrightarrow _b l\cdot W\;|\;r\cdot V$.

We can observe that this is equivalent to the following approach: let U be a submultiset of M such that U is a $b_0$-redex. Then, $M\hookrightarrow _b M'$ if either U is M and $M'$ is the $b_0$-contractum of M, or $\exists$ $\xi$ such that $M\equiv \xi \cdot U$ and $M'\equiv \xi \cdot U'$ and $U'$ is the $b_0$-contractum of U, or $M\equiv N\;|\;V$ and $V\equiv \xi \cdot U$ and $M'\equiv \xi \cdot U'$ and $U'$ is the $b_0$-contractum of U and none of the strings in N begins with $\xi$. The latter part follows from Rule (2) of Definition 9, since it identifies redexes as special from multisets with maximal common prefixes. The key idea behind the rewrite rule is as follows. Given a $\lambda$-term M, assume $(\lambda x\,U)\, V$ is a $\beta$-redex in M. Then, the canonical encoding $\lfloor (\lambda x\,U)\, V\rfloor$ is of the form $l\; \cdot \; (\lambda x\;\cdot \;\lfloor U\rfloor )\;|\;r\;\cdot \;\lfloor V\rfloor$. In this case, we are able to find $\rho$ and $\sigma$ such that $\langle \{ \! |l \cdot \lambda x| \! \}_X\rangle ^\sigma _\rho$ evaluates to $\lfloor \lambda x.U\rfloor$ and $\langle \{ \! |r| \! \}_Y\rangle ^\sigma _\rho$ evaluates to $\lfloor V\rfloor$. But then $(\{ \! |\varepsilon | \! \}_{X}\vartriangleright _x \{ \! |\varepsilon | \! \}_{Y})$ correctly encodes the contractum $U[x:=V]$. This is stated by Theorem 24 in the next subsection.

We term the calculus obtained as above the $\lambda$-SMSR calculus. In what follows, when we talk about a String MultiSet Rewriting calculus, we refer to the $\lambda$-SMSR calculus; hence, we may omit the prefix $\lambda$.

We recall that given $M\in \textbf{M}$, the multiset patterns $(\{ \! |l \cdot \lambda x| \! \}_X \; | \; \{ \! |r | \! \}_Y)$ are matched against the largest possible submultisets of M with a certain common prefix. If M is the $b_0$-redex itself, then Rule (2) of Definition 9 is trivially valid. Then, the values for $\rho (X)$, $\rho (Y)$ are chosen according to the number of strings of the corresponding submultisets representing U and V in $\lfloor (\lambda x\,U)\,V\rfloor$. This is illustrated in the next example.

Example 16

Previously, in Example 13, we showed how the term $(\lambda x.xx)(\lambda x.xx)$ can be encoded. Here, we demonstrate the application of the rewrite rule:

$$\begin{aligned}&\; l \cdot \lambda x \cdot l \cdot x \; | \; l \cdot \lambda x \cdot r \cdot x \; | \; r \cdot \lambda x \cdot l \cdot x \; | \; r \cdot \lambda x \cdot r \cdot x \\&\quad \equiv \; \langle (\{ \! |l\cdot \lambda x| \! \}_X\vartriangleright _x\{ \! |r| \! \}_Y)\rangle _{\rho }^{\sigma } \\&\quad \hookrightarrow _{b} \; \langle (\{ \! |\varepsilon | \! \}_X\vartriangleright _x\{ \! |\varepsilon | \! \}_Y)\rangle _{\rho }^{\sigma }\\&\quad \equiv \; l \cdot \lambda x \cdot l \cdot x \; | \; r \cdot \lambda x \cdot l \cdot x \; | \; l \cdot \lambda x \cdot r \cdot x \; | \; r \cdot \lambda x \cdot r \cdot x, \end{aligned}$$

where $\rho (X)=\rho (Y)=2$ and $\sigma (\widetilde{x}_1)=l\cdot x$, $\sigma (\widetilde{x}_2)=r\cdot x$ and $\sigma (\widetilde{y}_1)=\lambda x\cdot l\cdot x$ and $\sigma (\widetilde{y}_2)=\lambda x\cdot r\cdot x$. Of course, the above rewriting can be continued, because of the non-normalizing property of $(\lambda x.xx)(\lambda x.xx)$.

A few remarks on the correct execution of $\hookrightarrow _b$-reduction are in order here. To preserve the correctness of the encoding between the $\lambda$-calculus and the String MultiSet Rewriting system obtained above, we must keep in mind that in the $\lambda$-calculus bound and free variable occurrences are distinguished and $\lambda$-terms are defined in a way such that the problem of variable collision should be avoided. In order to acquire the same ability for the $\lambda$-SMSR calculus, a solution can be to introduce the analogue of Barendregt’s variable conventions for $\lambda$-SMSR. This means that we identify multisets that are images of $\lambda$-terms differing in the correct renaming of bound variables by extending Definition 2 to these cases. Hence, substitution as defined in Definition 4 is understood via “renaming of bound variables”; therefore, collision of variables does not occur. We omit the technical details, however. In what follows, the notation IH stands for the phrase “the induction hypothesis.”

3.2 Correctness of the encoding

Before stating the theorem on the correctness of the encoding, we introduce some necessary notation and lemmas. We first show that b-redexes in multisets correspond to $\beta$-redexes in $\lambda$-terms. Prior to this, we examine the relation between $\lambda$-terms and their representing multisets. From now on, we mean by multisets the elements of the set $\textbf{M}(\mathcal {E}_\lambda )$. We write $\textbf{M}$ instead of $\textbf{M}(\mathcal {E}_\lambda )$ and $\textbf{S}$ instead of $\textbf{S}(\mathcal {E}_\lambda )$.

Definition 17

(Maximal submultisets, multiset prefixes)

• 1. Let $\xi ,\zeta \in \textbf{S}$. Then, $\xi <\zeta$ if $\exists$ $\nu$ such that $\zeta =\xi \cdot \nu$ and $\nu \ne \varepsilon$.

• 2. Let M, N be multisets. Then, $\xi \in \textbf{S}$ is a multiset prefix of N in M, or, in short, a multiset prefix of N, if, for every $\chi \in N$, $\xi \cdot \chi \in M$. In other words, $(\xi \cdot N)\sqsubseteq M$. in notation: $N\sqsubseteq _\xi M$. Let pref(M) denote the set of multiset prefixes for M, that is, $pref(M)=\{\xi \mid \exists N:\,N\sqsubseteq _\xi M)\}$.

• 3. Let M, U be multisets. Let $\xi \in \textbf{S}$ and assume $\xi$ is a prefix for U. We call U maximal in M with respect to $\xi$, or, in short, maximal, if $\not \exists \zeta$ for which $(\zeta \;|\;\xi \cdot U)\sqsubseteq M$ and $\xi < \zeta$. In notation: $U\preceq _\xi M$. We may omit $\xi$ if it is clear from the context. If we want to emphasize that $\xi$ is the multiset prefix of the maximal multiset U, we write $\xi =pref_M(U)$. We may omit the subscript M. We collect the maximal multisets U of M with respect to some $\xi$ by writing $U\in mm(M)$. Note that if $U\in mm(M)$, U is not a submultiset of M (except for $U\equiv M$); however, there exists $\xi$ such that $(\xi \cdot U)\sqsubseteq M$.

Note that, given $N\sqsubseteq _\xi M$, the multiset prefix $\xi$ is unique if it exists. On the other hand, if $N\sqsubseteq _\xi M$ such that N is maximal, then N is the unique such multiset. The following example illustrates the above notions.

Example 18

Let $M\equiv ((\lambda x. x\,y\,x)\,y)$. Consider the corresponding multiset $U\equiv \lfloor M\rfloor \equiv (l\cdot \lambda x\cdot l\cdot l\cdot x\mid l\cdot \lambda x\cdot l\cdot r\cdot y\mid l\cdot \lambda x\cdot l\cdot x\mid r\cdot y)$.

• 1. The multiset $(\lambda x\cdot l\cdot l\cdot x\mid \lambda x\cdot l\cdot r\cdot y)$ has l as prefix and the multiset $(l\cdot l\cdot x\mid l\cdot r\cdot y)$ has prefix $l\cdot \lambda x$, respectively.

• 2. The multiset $V\equiv (l\cdot x\mid x)$ has prefix $l\cdot \lambda x\cdot l$. However, V is not maximal in M with respect to $l\cdot \lambda x\cdot l$. The multiset $(l\cdot x\mid r\cdot y\mid x)$ is maximal in M with respect to $l\cdot \lambda x\cdot l$, and it is the only such multiset.

Intuitively, U is maximal in N, provided N is the image of some $\lambda$-term M by the encoding, if and only if U collects all the strings of N starting with a certain common prefix. The next lemma identifies the maximal multisets in $\lfloor M\rfloor$ in terms of the encoding. First of all, we give an informal description of what we mean by subterm occurrences. A subterm occurrence of N in M is a pair $(N,C[\;])$ such that $app(C[\;],N)=M$, where $C[\;]$ a one-holed context and $app(C[\;],N)$ yields the result of the substitution of N in $C[\;]$. We recall the fairly straightforward definitions.

Definition 19

Let $[\;]$ be a given symbol called a hole and assume $\mathcal {V}_\lambda$ are the set of $\lambda$-variables.

• 1. Then, the one-holed $\lambda$–contexts are defined by the Backus–Naur form below:

  $$\begin{aligned}C[\;]\,=\,[\;]\mid (\lambda \mathcal {V}_\lambda \,C[\;])\mid (\Lambda \,C[\;])\mid (C[\;]\,\Lambda ),\end{aligned}$$

  where $\Lambda$ denotes the $\lambda$-terms.

• 2. Let $C[\;]$ be a one-holed $\lambda$-context and $N\in \Lambda$. Then, $app(C[\,],N)$ is the result of writing N in place of the hole:

  • (a) $app([\,],N)=N$,

  • (b) $app(\lambda x.C[\,],N)=\lambda x.app(C[\,],N)$,

  • (c) $app((U\,C[\,]),N)=(U\,app(C[\,],N))$,

  • (d) $app((C[\,]\,U),N)=(app(C[\,],N)\,U)$, where $U\in \Lambda$.

Furthermore, by abuse of notation, we may ignore references to contexts when we mention subterms. Namely, we may write $N\le M$ instead of $app(C[\;],N)=M$. Furthermore, we assume in what follows that $[\;]$ is an element of the alphabet $\mathcal {E}_\lambda$ underlying the encoding of the $\lambda$-calculus. The main advantage of the encoding is that the notion of subterm occurrence can be made precise through it and, hence, we can reason on them in exact terms. As we will see later, we can determine the address of a subterm occurrence explicitly by examining its representing strings, hence identifying the subterm occurrence in a unique way. We denote by $N\le M$ the fact that N is a subterm (occurrence) of M, where M is a $\lambda$-term. Given a finite sequence $\sigma$, let the notation $a\in \sigma$ denote the fact that a is one of the elements of $\sigma$.

Lemma 20

Let $\xi \in pref(\lfloor M\rfloor )$, where $M\in \Lambda$. Then, if $\xi '=(\xi \cdot e)\in pref(\lfloor M\rfloor )$, for $e\in \mathcal {E}$, then either $e\in \{l, r\}$ or $e=\lambda x$ or $e=x$ for some $x\in \mathcal {V}_\lambda$ and these possibilities are mutually exclusive.

Proof

Straightforward. $\square$

Lemma 21

Let M be a $\lambda$-term. Then, U is a maximal multiset of $\lfloor M\rfloor$ iff there exists a subterm N of M such that $U\equiv \lfloor N\rfloor$. Moreover, $app(C[\;],N)=M$ iff $U\preceq _\xi \lfloor M\rfloor$ such that $[\;]\preceq _\xi C[\;]$.

Proof

• $(\Rightarrow )$ Let M be a $\lambda$-term, assume U is a maximal multiset of $\lfloor M\rfloor$. Then, $U\preceq _\xi M$ for some $\xi$. We argue by induction on $\xi$.

  • $|\xi |=0$. Then, $U\equiv M$ and the statement is obvious.

  • $\xi =\xi '\cdot \lambda x$ for some $\xi '$ and $\lambda x$. Let $U'=mm(M, \xi ')$. By IH, $\exists$ $V'\le M$ such that $U'\equiv \lfloor V'\rfloor$. By Lemma 20, $V'\equiv \lambda x \cdot V$. Regarding the maximality, let $\xi '\cdot \lambda x < \zeta$ for some $\zeta$. This means $\xi ' < \zeta$, and, by the maximality of $\lfloor V'\rfloor$, $\zeta \in \xi '\cdot \lfloor V'\rfloor$. Since $\lfloor V'\rfloor \equiv \lambda x\cdot \lfloor V\rfloor$, we have $\zeta \in \xi \cdot \lfloor V\rfloor$. Moreover, let $app(C'[\;],V')=M$ and let $U'\preceq _\xi '\lfloor M\rfloor$. Then, $app(C[\;],V)=M$, where $C[\;]$ is obtained from $C'[\;]$ when we exchange $[\;]$ is $C'[\;]$ for $\lambda x\cdot [\;]$.

  • $\xi =\xi '\cdot l$ or $\xi =\xi '\cdot r$. Analogous to the above case.

• $(\Leftarrow )$ Let $N\le M$. Assume $app(C[\;],N)=M$. We argue by induction on $C[\;]$.

  • $C[\;]=[\;]$. Then, $N\equiv M$ and the statement is clear.

  • $C[\;]=(U\,C_1[\;])$. Then, $M=(U\,app(C_1[\;],N))$. By IH, $U\equiv \lfloor N\rfloor$ is a maximal multiset of $\lfloor app(C_1[\;],N)\rfloor$. Let $\xi$ be its multiset prefix. Then, $r\cdot \xi \cdot \lfloor app(C_1[\;],N)\rfloor \sqsubseteq M$. Moreover, let $r\cdot \xi <\zeta$. Then, $\zeta = r\cdot \zeta '$. By the maximality of U in $\lfloor app(C_1[\;],N)\rfloor$, $\zeta '\in \xi \cdot U$, which means, $\zeta \in r\cdot \xi \cdot U$. Hence, $U\in mm(M)$. The remaining cases are similar.

$\square$

We observe that since a b-redex is a maximal submultiset of $\lfloor M\rfloor$ for any M, it corresponds to a subterm of M. Moreover, the above lemma shows that a b-redex must be the image of a $\beta$-redex by the encoding. Hence, b-redexes are the counterparts of $\beta$-redexes. The following lemma is a preparation for Lemma 23.

Lemma 22

Let M,$N\in \Lambda$. Then, $\lfloor M\rfloor [x\leftarrow \lfloor N\rfloor ]\equiv \lfloor M[x:=N]\rfloor$.

Proof

By induction on M. $\square$

The next lemma states that if we start from a b-redex, the result of the reduction is the encoding of the contractum of the corresponding $\beta$-redex.

Lemma 23

Let $M=(\lambda x.M_1)\,M_2$, assume $\lfloor M\rfloor \hookrightarrow _{b} U$ such that $\lfloor M\rfloor$ is the redex reduced. Then, $U\equiv \lfloor M_1[x:=M_2]\,\rfloor$.

Proof

Assume $M=(\lambda x.M_1)\,M_2$ and $\lfloor M\rfloor \hookrightarrow _{b}^{\lfloor M\rfloor } U$ as above. Since $\lfloor M\rfloor =l\cdot \lambda x\cdot \lfloor M_1\rfloor \mid r\cdot \lfloor M_2\rfloor$, by the formulation of b-reduction, we must have $\langle \{ \! |\varepsilon | \! \}_{X}\rangle _{\rho }^\sigma \equiv \lfloor M_1\rfloor$ and $\langle \{ \! |\varepsilon | \! \}_{Y}\rangle _{\rho }^\sigma \equiv \lfloor M_2\rfloor$. We argue by induction on $M_1$.

• $M_1\in \mathcal {V}_\lambda$. If $M_1=x$, then, by Definition 4, $\lfloor M_1\rfloor [x\leftarrow \lfloor M_2\rfloor ]\equiv \lfloor M_2\rfloor \equiv \lfloor M_1[x:=M_2]\rfloor$. When $M_1=y$, then $\lfloor M_1[x:=M_2]\rfloor \equiv y \equiv \lfloor y\rfloor$.

• $M_1=\lambda y.M_3$. Then, $\lfloor M_1\rfloor \equiv \lambda y\cdot \lfloor M_3\rfloor$ and, straightforwardly, $(\lambda y\cdot \lfloor M_3\rfloor )[x\leftarrow \lfloor M_2\rfloor ]\equiv \lambda y\cdot (\lfloor M_3\rfloor [x\leftarrow \lfloor M_2\rfloor ])$. Applying Lemma 22$(\lfloor M_3\rfloor [x\leftarrow \lfloor M_2\rfloor ])$, we obtain the result.

• $M_1=(M_3\,M_4)$. In this case, $\lfloor M_1\rfloor \equiv l\cdot \lfloor M_3\rfloor \mid r\cdot \lfloor M_4\rfloor$ and $(l\cdot \lfloor M_3\rfloor \mid r\cdot \lfloor M_4\rfloor ) [x\leftarrow \lfloor M_2\rfloor ]\equiv l\cdot \lfloor M_3\rfloor [x\leftarrow \lfloor M_2\rfloor ]\mid r\cdot \lfloor M_4\rfloor [x\leftarrow \lfloor M_2\rfloor ]$. The statement follows from Lemma 22 and the fact $(M_3\,M_4)[x:=M_2]=(M_3[x:=M_2]\,M_4[x:=M_2])$.

$\square$

Now, we are in a position to prove the correctness theorem.

Theorem 24

The encoding correctly simulates $\beta$-reduction in the $\lambda$-calculus. That is, the following assertions are valid.

• 1. Let $M\rightarrow _\beta M'$. Then, $\lfloor M\rfloor \hookrightarrow _{b}\lfloor M'\rfloor$.

• 2. Let $\lfloor M\rfloor \hookrightarrow _{b}U$. Then, there exists $M'$ such that $U\equiv \lfloor M'\rfloor$ and $M\rightarrow _\beta M'$.

Proof

• 1. We argue by induction on M.

  • $M=\lambda x.M_1$. Then $M=\lambda xM_1\rightarrow _\beta \lambda x.M_1'=M'$ and $\lfloor M\rfloor \equiv \lambda x\cdot \lfloor M_1\rfloor$. By the induction hypothesis, $\lfloor M_1\rfloor \hookrightarrow _{b}\lfloor M_1'\rfloor$. Then, since $\hookrightarrow _b$ is compatible with the term formation rules, we obtain $\lfloor M\rfloor \equiv \lambda x\cdot \lfloor M_1\rfloor \hookrightarrow _b\lambda x\cdot \lfloor M_1'\rfloor \equiv \lfloor M\rfloor$.

  • $M=(M_1 \,M_2)$. Assume $M_1\rightarrow _\beta M_1'$. The case for $M_2\rightarrow _\beta M_2'$ being similar. Then we apply IH to $M_1$ to obtain $\lfloor M_1\rfloor \hookrightarrow _{b}\lfloor M_1'\rfloor$. The result follows from the compatibility of $\hookrightarrow _b$ with the term formation rules. The case $M=(\lambda x.M_1)\,M_2\rightarrow _\beta M'=M_1[x:=M_2]$ is treated by Lemma 23.

• 2. Let $\lfloor M\rfloor \hookrightarrow _b U$. We proceed by induction on M.

  • $M=\lambda x.M_1$. Then, $\lfloor M\rfloor \equiv \lambda x \cdot \lfloor M_1\rfloor$. Definitions 14 and 15 imply that $\lfloor M_1\rfloor \hookrightarrow _b V$ such that $U\equiv \lambda x\cdot V$. Then, by IH, we obtain $M_1\rightarrow _\beta M_1'$ with $V\equiv \lfloor M_1'\rfloor$. Then, clearly, $M=\lambda x.M_1\rightarrow _\beta \lambda x.M_1'=M'$ and $U\equiv \lfloor M'\rfloor$.

  • $M=(M_1\,M_2)$. Then $\lfloor M\rfloor \equiv l \cdot \lfloor M_1\rfloor \;|\;r \cdot \lfloor M_2\rfloor$. Let $\lfloor M_1\rfloor \hookrightarrow _b U'$, the case $M_2\hookrightarrow _b U''$ being similar. Then, by IH, $\exists$ $M_1'$ such that $M_1\rightarrow _\beta M_1'$ and $U'\equiv \lfloor M_1'\rfloor$. Hence, $M\rightarrow _\beta (M_1'\,M_2)$ and $U\equiv \lfloor (M_1'\,M_2)\rfloor$. In the case when $\lfloor M\rfloor \hookrightarrow _bM'$ and $\lfloor M\rfloor$ is the redex itself, we necessarily have $\lfloor M\rfloor \equiv \langle (\{ \! |l \cdot \lambda x| \! \}_X \; | \; \{ \! |r | \! \}_Y)\rangle ^\sigma _\rho$ with some $\rho$ and $\sigma$. Hence, $\lfloor M\rfloor \equiv (l\cdot \lambda x)\cdot U_1\;|\;r\cdot U_2$ for some multisets $U_1$ and $U_2$. Lemma 21 provides $M_1$ and $M_2$ such that $\lfloor M_i\rfloor \equiv U_i$ $(i\in \{1,2\})$. Then, Lemma 23 yields $U\equiv \lfloor M_1[x:=M_2]\,\rfloor$.

$\square$

4 Applications: proofs of the standardization and finiteness of developments theorems

We demonstrate the applicability and flexibility of the new tool obtained by presenting proofs for two fundamental theorems. We prove the standardization and the finiteness of developments theorems by means of the encoding. The main advantage of the encoding that, by this, we obtain a tool for identifying subterm occurrences in $\lambda$-terms, more precisely, multiset occurrences in the corresponding multisets. The multiset prefixes not only provide an index pointing to that occurrence, but we are also able to manipulate them with the help of the underlying calculus. Firstly, we formulate the necessary notions for the $\lambda$-calculus, then we discuss how these notions transfer to string multisets. We present the usual, more or less, intuitive definitions concerning residuals and developments. Then we turn to the proof of the standardization theorem. The most widespread method for standardization is that introduced in [5]. Several authors have produced somewhat similar variants of Barendregt’s method [1, 13]. In [1], Amadio and Curien define subterm occurrence by giving a sequence of indexes leading to the underlying subterm in a way very similar to that applied here. Their construction, however, does not expand to a full calculus, they make use of it to give the precise interpretation of subterm occurrences. In Sects. 2.1 and 2.2 they present, among the others, a proof of the standardization theorem. The proof when M is strongly normalizing, is relatively easy, on the contrary, the general case is obtained by introducing labeled lambda terms, which makes their treatment a little more involved than that in [5]. In this paper, we chose a method presented in [12]. The present proof is facilitated by Proposition 37 of this section, which gives a characterization of standard reduction sequences.

Next, we briefly recall the notions of residuals and developments in such a form that is customary in the $\lambda$-calculus. If s is an arbitrary sequence of some elements, other than a sequence in the SMSR calculus, a is an element from the same set, we denote by a :  : s the concatenation of the one element sequence (a) and s.

Definition 25

(Residuals in $\lambda$-calculus) Let M be a term, $R=(\lambda x. U)\,V$ be a redex in M. Let $P\le M$. The residual set P[R] of P with respect to R (or $P[R]_M$ if we intend to indicate M) is defined by the following cases.

• 1.

  • $P\le U$: $P[R]=\{P[x:=V]\}$.

  • $P\le V$: $P'\in P[R]$ iff $P'$ is an occurrence P in one of the substituted instances of V.

  • $R\le P$: $P[R]=\{P'\}$, where $P'$ is obtained from P by replacing $(\lambda x.U)\, V$ with $U[x:=V]$.

  • P and R are disjoint: $P[R]=\{P\}$.

  In all the other cases P has no residuals.

• 2. Let $\sigma :M\rightarrow M_1\rightarrow \ldots \rightarrow M_n$ be a reduction sequence starting from M. Let $P\le M$. Then, the residuals of P with respect to $\sigma$ are defined by induction on $|\sigma |$ and are denoted by $P[\sigma ]$ or by $P[\sigma ]_M$ if we intend to emphasize that the original term is M. Assume we have already determined the set $P[\sigma ']$ for each $|\sigma '|<|\sigma |$.

  • $|\sigma |=0$: every term is a residual of itself.

  • $\sigma =\sigma ':: R$: then $P''\in P[\sigma ]$ if, for some $P'\in P[\sigma ']$, $P''$ is a residual of $P'$ with respect to R. That is, $P''\in P'[R]_{M_{n-1}}$.

  We can define the residuals of a set of subterms $\textbf{N}$ with respect to $\sigma$ in an analogous way, which is denoted by $\textbf{N}[\sigma ]$.

• 3. Let $\textbf{R}$ be a set of redexes. A development is a reduction sequence $[R_1,\ldots ,R_n]$, where $R_i\in \textbf{R}[R_1,\ldots ,R_{i-1}]$. A development is complete if there are no more residuals of $\textbf{R}$ left.

We define standard reduction sequences in the usual manner ( [5]).

Definition 26

A $\beta$-redex $R_1=(\lambda x.U_1)\, U_2$ of M is to the left of $R_2=(\lambda y.V_1)\, V_2$ if $\lambda x$ precedes $\lambda y$ when we read M from left to right. In other terms, $R_1=(\lambda x.U_1)\, U_2$ being to the left of $R_2=(\lambda y.V_1)\, V_2$ this means the fulfillment of one of the following cases:

• There are $(M_1\,M_2)\le M$ such that $R_1\le M_1$ and $R_2\le M_2$, or

• $R_2\le U_1$, or

• $R_2\le U_2$.

Definition 27

(Standard reduction sequence) Let $\sigma :M_1\rightarrow ^{R_1}M_2\rightarrow ^{R_2}\ldots \rightarrow ^{R_n}M_{n+1}$ be a reduction sequence. Then $\sigma$ is standard if there are no $1\le i<j\le n+1$ such that $R_j$ is a residual of some R standing to the left of $R_i$. We use the notation $\sigma \in St$ to claim that $\sigma$ is a standard reduction sequence.

We might have the impression that the definition of standard reduction sequences is somewhat imprecise and difficult to handle. We intend to remedy this shortcoming by introducing standard reduction sequences in connection with multisets. We present the necessary notions first.

Definition 28

Let M be a $\lambda$-multiset, assume $P\sqsubseteq _\xi M$, $Q\sqsubseteq _\zeta M$ as defined in Definition 17. We write $P\sqsubseteq _M Q$ if $\zeta \le \xi$. We denote this containment by writing $P\preceq _M Q$ if, in addition, $P, Q\in mm(M)$.

In the sequel, we write $N\preceq M$ if $\xi$ is not known or not interesting to us. We do not omit M from the relation $P\preceq _M Q$. Observe that, if M is such that $M\equiv \lfloor U\rfloor$, and $N\preceq _\xi M$ with an appropriate $\xi$, then, by Lemma 21, there exists $V\le U$ such that $N\equiv \lfloor V\rfloor$. Hence, multiset occurrences in M match subterm occurrences in U provided $M\equiv \lfloor U\rfloor$. We sum up these properties in the next lemma.

Lemma 29

Let U, V, W be multisets. Assume $U\equiv \lfloor M\rfloor$ for some $\lambda$-term M. Then, the following statements hold.

• 1. Let $V\in mm(U)$. Then, $V\preceq _\xi U$ iff $\exists$ $N\le M$ such that $V\equiv \lfloor N\rfloor$.

• 2. Let V, $W\in mm(U)$. Then, ${V}\preceq _{{U}}{W}$ iff $\exists$ N, $P\le M$ such that $V\equiv \lfloor N\rfloor$ and $W\equiv \lfloor P\rfloor$ and $N\le P$.

Proof

• 1. The first part is a simple restatement of Lemma 21.

• 2. Assume V, $W\in mm(U)$ as above. Let ${V}\preceq _{{U}}{W}$. Then, there exist $\xi$, $\zeta$ such that $V\preceq _\xi U$, $W\preceq _\zeta U$ and $\zeta \le \xi$. Since, in addition, V, $W\in mm(U)$, then, by Lemma 21, we obtain N, $P\le M$ such that $V\equiv \lfloor N\rfloor$ and $W\equiv \lfloor P\rfloor$. What remains to prove is that $\zeta \le \xi$ iff $N\le P$. By Lemma 21, there exist $C'[\;]$, $C''[\;]$: $app(C'[\;],N)=M$ and $app(C''[\;],P)=M$ and $[\;]\preceq _\zeta C''[\;]$ and $[\;]\preceq _\xi C'[\;]$. An easy proof by induction on $|\xi |-|\zeta |$ shows that, from $\zeta \le \xi$ and Lemma 20, it follows that $\exists$ $C'''[\;]$ such that $app(C'''[\;],N)=P$, which is the result.

$\square$

Remark 30

Observe that there is a delicate connection between $\lambda$-multisets, that is, multisets that are the images of $\lambda$-terms, and maximal multisets of $\lambda$-multisets. Namely, if U is a maximal multiset of $\lfloor M\rfloor$, that is, $U\preceq _\xi \lfloor M\rfloor$ for some $\xi$, then $U\equiv \lfloor V\rfloor$ such that $V\le M$ as a $\lambda$-term. Moreover, $\xi$ determines the position of $[\;]$ in $C[\;]$, where $app(C[\;],V)=M$. In what follows, if we write “we proceed by induction on P” and $P\equiv \lfloor M\rfloor$ is a $\lambda$-multiset, we understand induction on the number of steps needed to produce P from M by reason of Definition 12.

In order to talk about the relative positions of multisets in a multiset in a more precise way, we define an order on the strings. The next definition extends the relation < on strings.

Definition 31

Let $\xi$, $\eta$ be strings. Then, $\xi$ precedes $\eta$, in notation $\xi \prec \eta$ if, either

• 1. $\xi < \eta$, or

• 2. $\xi =\nu \cdot l\cdot \xi '$ and $\eta =\nu \cdot r\cdot \eta '$ for some $\nu$, $\xi '$, $\eta '\in \textbf{S}$.

We write $\xi \preceq \eta$, if either $\xi \prec \eta$ or $\xi =\eta$.

Before stating the proposition that expresses standardness in terms of maximal prefixes, we formulate some auxiliary lemmas. The next lemma gives the notion of being to the left in the context of multisets.

Lemma 32

Let $R_1$, $R_2\le M$ be two different redex occurrences of M. Then, $R_1$ is to the left of $R_2$ iff $pref(\lfloor R_1\rfloor )\prec pref(\lfloor R_2\rfloor )$ in $\lfloor M\rfloor$.

Proof

Let $R_1=(\lambda x_1.P_1)\,Q_1$ and $R_2=(\lambda x_2.P_2)\,Q_2$.

($\Rightarrow$):

Assume $R_1$ is to the left of $R_2$. We take into account the various cases of Definition 26. Applying Lemma 21, it is easy to check that in each of the cases the assertion holds.

($\Leftarrow$):

Let $pref(R_i)=\xi _i$ $(i\in \{1,2\})$. If $\xi _1\prec \xi _2$ holds by reason of $\xi _2=\xi _1\cdot \nu$, then $\lfloor R_2\rfloor \preceq _M\lfloor R_1\rfloor$, hence $R_2\le R_1$ is valid by Lemma 29. Otherwise, $\xi _1=\nu \cdot l\cdot \xi _1'$ and $\xi _2=\nu \cdot r\cdot \xi _2'$. Let $U_1\preceq \lfloor M\rfloor$ such that $pref(U_1)=\nu \cdot l$ and $U_2\preceq \lfloor M\rfloor$ such that $pref(U_2)=\nu \cdot r$. By Lemma 21, there exist $N_1$, $N_2$ such that $U_i\equiv \lfloor N_i\rfloor$ $(i\in \{1,2\})$. By virtue of Lemma 29, we obtain that $R_i\le N_i$ $(i\in \{1,2\})$, which means that $R_1$ is to the left of $R_2$.

$\square$

We remark that since there is a bijection between $\lambda$-terms and $\lambda$-multisets, which are the images of $\lambda$-terms in the encoding, we do not introduce a different font style for $\lambda$-multisets. We indicate it in most of the cases, however, whether we are dealing with $\lambda$-terms or $\lambda$-multisets.

We can transfer the notions of residuals and standardness to multisets. By the identification of terms with $\lambda$-multisets, $\beta$-redexes can also be matched to b-redexes and the notions like residuals, being to the left and standardness apply mutatis mutandis. In order to define the property of a b-redex lying to the left of another one, we can resort to Lemma 32. We define residuals only for maximal submultisets of the given multiset. Considering the strong analogy, we apply the same notation to multisets in connection with residuals as those introduced for $\lambda$-terms in Definition 25. We repeat the necessary definitions.

Definition 33

(Residuals in the multiset calculus) Let U be a $\lambda$-multiset, assume $R=(l\cdot \lambda x\cdot S\mid r\cdot T)$ is a b-redex in U. Let $P\preceq M$ be a $\lambda$-multiset. The b-residual set P[R] of P with respect to R (or $P[R]_U$ if we intend to indicate U) is defined by the following cases.

• 1.

  • $P\preceq S$: $P[R]=\{P[x\leftarrow T]\}$.

  • $P\preceq T$: $P'\in P[R]$ iff $P'$ is a multiset occurrence of P in one of the substituted instances of T.

  • $R\preceq P$: $P[R]=\{P'\}$, where $P'$ is obtained from P by replacing R with $S[x\leftarrow T]$.

  • P and R are disjoint: $P[R]=\{P\}$.

  In all the other cases P has no residuals.

• 2. Let $\sigma :M\rightarrow M_1\rightarrow \ldots \rightarrow M_n$ be a b-reduction sequence starting from M. Let $P\sqsubseteq M$ be a $\lambda$-multiset. Then, the b-residuals of P with respect to $\sigma$ are defined by induction on $|\sigma |$ and are denoted by $P[\sigma ]$ or by $P[\sigma ]_M$ if we intend to emphasize that the original term is M. Assume we have already determined the set $P[\sigma ']$ for each $|\sigma '|<|\sigma |$.

  • $|\sigma |=0$: every $\lambda$-multiset is a b-residual of itself.

  • $\sigma =\sigma ':: R$: then $P''\in P[\sigma ]$ if, for some $P'\in P[\sigma ']$, $P''$ is a b-residual of $P'$ with respect to R. That is, $P''\in P'[R]_{M_{n-1}}$.

  We can define the b-residuals of a set of submultisets $\textbf{N}$ with respect to $\sigma$ in an analogous way, which is denoted by $\textbf{N}[\sigma ]$.

• 3. Let $\textbf{R}$ be a set of b-redexes. A b-development is a b-reduction sequence $[R_1,\ldots ,R_n]$, where $R_i\in \textbf{R}[R_1,\ldots ,R_{i-1}]$. A b-development is complete if there are no more b-residuals of $\textbf{R}$ left.

We omit the prefix “b” and write “residual” and “development” when it is clear from the context that those are the multiset residuals and multiset developments that are under discussion.

The next lemma describes the previous notions in terms of maximal prefixes.

Lemma 34

Let R, M, N be $\lambda$-multisets. Assume $R\equiv (l\cdot \lambda x\cdot P\mid r\cdot Q)$, $N\sqsubseteq M$ and assume $M\hookrightarrow _b^RM'$. Suppose $N'$ is a residual of N and let $pref_M(R)=\eta$, $pref_M(N)=\xi$ and $pref_{M'}(N')=\chi$. Then, the following assertions hold.

• 1. Let $\xi =\eta \cdot l\cdot \lambda x\cdot \xi '$ for some $\xi '$. Then, $\chi =\eta \cdot \xi '$.

• 2. Let $\xi =\eta \cdot r\cdot \xi ''$ for some $\xi ''$. Then, $\chi \in \{\eta \cdot \nu \cdot \xi ''\mid pref_R(x)=l\cdot \lambda x\cdot \nu \text { for some string }\nu \}$.

• 3. Let $\xi \prec \eta$ and $\xi$ be a substring of $\eta$. Then, $\chi =\xi$.

• 4. Let $\xi \prec \eta$ and assume $\xi$ is not a substring of $\eta$ or $\eta \prec \xi$ and assume $\eta$ is not a substring of $\xi$. Then, $\chi =\xi$.

Proof

We consider the cases of Definition 33 and apply Lemma 29. $\square$

Lemma 35

Let M be a $\lambda$-multiset and assume R is a b-redex. Let $M\hookrightarrow ^R M'$ and assume $R'$ is a b-redex such that $R'$ is not a residual of any b-redex in M. Then, $pref_M(R)\preceq pref_{M'}(R')$.

Proof

We observe that when we turn to $\lambda$-terms instead of multisets, if $P=(\lambda y.U)\, V$ is a redex in a $\lambda$-term N and $N\rightarrow ^P N'$, then Q can be a new redex in $N'$ only if it is of the form $Q=(V\, W[y:=V])$. Hence, $(y\,W)$ is a subterm of U and $V=\lambda z.S$ for some S.

Let M, R be as above. Since M is a $\lambda$-multiset, $\exists$ N such that $M\equiv \lfloor N\rfloor$. Assume $R\equiv \lfloor (\lambda y.U)\,V\rfloor$. Let $W\equiv \lfloor U[y:=V]\,\rfloor$. By the previous discussion we derive that $R'\preceq _{M'} W$, and we know by Lemma 29 that $pref_{M'}(W)\le pref_{M'}(R')$. Moreover, by Lemma 34, $pref_M(R)=pref_{M'}(W)$; hence, we can conclude that $pref_M(R)\le pref_{M'}(R')$. $\square$

The next corollary states that the “order” of redexes will not change after a reduction step.

Corollary 36

Let M be a $\lambda$-multiset and $N\preceq M$ be a b-redex.

• 1. Suppose R is a b-redex of M and assume $M\hookrightarrow ^RM'$. Suppose $N'$ is a residual of N, $R'$ is the contractum of R and assume N is to the left of R (R is to the left of N, respectively). Then $N'$ is to the left of $R'$ ($R'$ is to the left of $N'$, respectively).

• 2. Let $\sigma =[R_1,R_2,\ldots ,R_n]$ and assume $M\equiv M_1\hookrightarrow ^{R_1}M_2\hookrightarrow ^{R_2}\ldots \hookrightarrow ^{R_n}M_{n+1}\equiv M'$. Suppose $N'$ is a residual of N with respect to $\sigma$ and assume that, for every $1\le i\le n$, N is to the left of $R_i$ (N is to the right of $R_i$, resp.). Then, for every $1\le i\le n$, $pref_{M'}(N')\prec pref_M(R_i)$ ($pref_M(R_i)\prec pref_{M'}(N')$, resp.).

Proof

• 1. By Lemmas 32 and 34.

• 2. Follows from Point 1 taking into account Lemma 35.

$\square$

The next proposition gives a surprising characterization of standard reduction sequences: It is enough to check whether the maximal prefixes of the actual redexes form a monotone increasing sequence.

Proposition 37

Let $\sigma :M_1\hookrightarrow ^{R_1}M_2\hookrightarrow ^{R_2}\ldots \hookrightarrow ^{R_n}M_{n+1}$ be a reduction sequence. Then, $\sigma$ is standard iff $pref_{M_1}(R_1)\preceq pref_{M_2}(R_2)\preceq \ldots \preceq pref_{M_n}(R_n)$.

Proof

Let $\sigma :M_1\hookrightarrow ^{R_1}M_2\hookrightarrow ^{R_2}\ldots \hookrightarrow ^{R_n}M_{n+1}$ be a reduction sequence. Assume $\xi _i=pref_{M_i}(R_i)$ $(1\le i\le n)$.

• ($\Rightarrow$) Let $\sigma$ be a standard reduction sequence. Assume $\xi _i=pref_{M_i}(R_i)$ and $\xi _1\preceq \xi _2\preceq \ldots \preceq \xi _j\succ \xi _{j+1}$ for some $1\le j\le n-1$.

  • Suppose $R_{j+1}\in R[R_j]$ for some R. Then, Corollary 36 implies that R is to the left of $R_j$, which contradicts the standardness assumption.

  • Suppose $R_{j+1}$ is a newly created redex, that is, $R_{j+1}$ is not a residual of some redex R with respect to $R_j$. In this case, Lemma 35 involves that $\xi _j\preceq \xi _{j+1}$, contrary to our assumption.

• ($\Leftarrow$) Suppose $\xi _1\preceq \xi _2\preceq \ldots \preceq \xi _j$ and there are $1\le i<j\le n$ such that $R_j$ is a residual of some R standing to the left of $R_i$. Then, by Corollary 36, we would necessarily have $\xi _{j}\prec \xi _i$ contradicting our assumption.

$\square$

We are now in a position to prove the standardization theorem for $\lambda$-multisets. Thus, by reason of the encoding, we obtain the standardization theorem for the $\lambda$-calculus. Prior to this, however, we have to state some more lemmas. The next lemma prepares the proof of the standardization theorem.

Lemma 38

Let P, Q be $\lambda$-multisets. Then, the following assertions are valid.

• 1. If $P\equiv \lambda y\cdot P_1$, then $P[x\leftarrow Q]\equiv \lambda y\cdot P_1[x\leftarrow Q]$.

• 2. If $P\equiv (P_1\mid P_2)$, then $P[x\leftarrow Q]\equiv (P_1[x\leftarrow Q]\mid P_2[x\leftarrow Q])$.

Proof

The proof proceeds by induction on $lh(P)+lh(Q)$ using the previous lemma. $\square$

The analogue of the next lemma is one of the main tools for demonstrating the standardization theorem in the $\lambda$-calculus. The proof exploiting multiset representation might probably seem more precise than the traditional one owing to the characterization of standardness in Proposition 37.

Lemma 39

Let P, Q be $\lambda$-multisets and assume $P\hookrightarrow ^\sigma _{st} P'$ and $Q\hookrightarrow ^\nu _{st} Q'$. Then, there exists $P[x\leftarrow Q]\hookrightarrow ^\tau _{st}P'[x\leftarrow Q']$.

Proof

Let $P\hookrightarrow ^\sigma _{st} P'$, $Q\hookrightarrow ^*_{st} Q'$. We prove that $P[x\leftarrow Q]\hookrightarrow ^{\xi }_{st}P'[x\leftarrow Q']$ by induction on the lexicographically order pair $\langle ||\sigma |,lh(P)\rangle$.

• $|\sigma |=0$. We proceed by induction P.

  • P is a variable. If $P\equiv x$, then we have the result by our assumption on Q. Otherwise, the statement is trivial.

  • $P\equiv \lambda y\cdot P_1$. IH applies together with Lemma 38.

  • $P\equiv (P_1\mid P_2)$. By Lemma 38 and IH, we obtain the result.

• $|\sigma |=k>0$.

  • $P\equiv \lambda y\cdot P_1$. Then $P_1\hookrightarrow ^\sigma P_1'$, and we can use IH.

  • $P\equiv (P_1\mid P_2)$.

    $*$:

    Assume $\exists$ $\sigma _1$, $\sigma _2$ such that $P_i\hookrightarrow ^{\sigma _i}P_i'$ $(i\in \{1,2\})$. Then, by IH, $P_1[x\leftarrow Q]\hookrightarrow ^{\tau _1}P'_1[x\leftarrow Q']$ and $P_2[x\leftarrow Q]\hookrightarrow ^{\tau _2}_{st}P'_2[x\leftarrow Q']$. Applying Proposition 37 we obtain that $\tau =\tau _1\#\tau _2\in St$.

    $*$:

    Let $P\hookrightarrow ^{\sigma _1}(l\cdot \lambda y\cdot U\mid r\cdot V)\hookrightarrow U[y\leftarrow V]$ be an initial reduction sequence of $\sigma$. Then $\sigma _1$ is necessarily empty, otherwise, by Proposition 37, the reduction sequence $\sigma$ would not be standard. Hence, $\sigma$ is $P\equiv (l\cdot \lambda y\cdot U\mid r\cdot V)\hookrightarrow U[y\leftarrow V]\hookrightarrow ^{\sigma '}P'$. Let $P''=U[y\leftarrow V]$. Then, by applying IH, we obtain $P''[x\leftarrow Q]\hookrightarrow ^{\tau '}_{st}P'[x\leftarrow Q']$. Since P is the redex itself, applying Proposition 37 again, we obtain that $\tau =[P]::\tau '\in St$.

$\square$

We can now state and prove the standardization theorem for $\lambda$-multisets.

Theorem 40

(Standardization) Let $M\hookrightarrow ^*M'$. Then, there exists a standard reduction sequence $M\hookrightarrow ^*_{st}M'$.

Proof

Let $\sigma :M_1\hookrightarrow ^{R_1}M_2\hookrightarrow ^{R_2}\ldots \hookrightarrow ^{R_n}M_{n+1}\equiv M'$, and let us write $pref_{M_i}(R_i)=\xi _i$ $(1\le i\le n)$. Suppose $\xi _1\preceq \ldots \preceq \xi _{n-1}\succ \xi _{n}$. Let i be the first index $1\le i\le n$ such that $R_n\in R[R_i,\ldots ,R_{n-1}]$, that is, $R_n$ is a residual of some $R\le M_i$ and, if $pref_{M_i}(R)=\xi$, then $\xi _i\prec \xi \prec \xi _{i+1}$. We prove that there exists a standard reduction sequence $\tau$ such that $M_1\hookrightarrow ^{R_1}M_2\hookrightarrow ^{R_2}\ldots \hookrightarrow ^{R_{i-1}}M_i\rightarrow ^R M'\hookrightarrow ^* M_{n+1}$.

Let $R\equiv \lfloor (\lambda x.P)\,Q\rfloor$. Then, the last redex $R_n$ of $\sigma$ is $\lfloor (\lambda x.P')\,Q'\rfloor$, where, by IH, $P\hookrightarrow ^*_{st}P'$ and $Q\hookrightarrow ^*_{st}Q'$. Lemma 39 provides us with a $\theta \in St$ such that $P[x\leftarrow Q]\hookrightarrow ^\theta _{st}P'[x\leftarrow Q']$. Putting together Lemma 34 and Corollary 36, if $R'\in \sigma$ is such that $\xi '=pref(R')\prec \xi =pref_{M_i}(R)$ or $\xi \prec \xi '$ and $\xi \nless \xi '$, that is, $\xi$ is not a substring of $\xi '$, then $\xi '\preceq \xi ''$ or $\xi ''\preceq \xi '$, resp., for any $\xi ''$, where $\xi ''$ is multiset the prefix of some $R''\in \theta$. Hence, the standardness of the new reduction sequence is guaranteed. $\square$

We turn to the proof of the finiteness of developments theorem. Considering its main idea, our proof is similar to the one given in [21]; however, the development separation theorem, which was the main tool in [21], seems to be more intuitive and easier to handle in our formalism. In order to deal with developments, we apply a well-known construction for distinguishing the abstractions that do not count in the development. The definition of redexes remains the same, we define applications though which do not count as redexes. We introduce $\lambda ^*$-abstractions and stipulate that, as before, only ordinary $\lambda$-abstractions can form a redex. Hence, new redexes do not emerge in the reduction sequence. First of all, we introduce some auxiliary notions and prove some lemmas.

Definition 41

(Starred terms)

• 1. The set of $\lambda ^*$-terms is defined as follows.

  $$\begin{aligned} {\mathcal {T}^*} = x \mid (\lambda ^* x.\mathcal {T}^*)\mid ((\lambda x.\mathcal {T}^*)\,\mathcal {T}^*)\mid (\mathcal {T}^*\,\mathcal {T}^*).\end{aligned}$$

  The terms of the form $(\lambda x.U)\,V$ are considered $\beta$-redexes, as usual.

In what follows, we understand by a term a starred term, unless otherwise stated.

The multiset encoding of $\lambda ^*$-terms goes along the same way as that of $\lambda$-terms. The new elements of the underlying set $\mathcal {E}$ compared to the $\lambda$-terms are the elements $\lambda ^*x$, where x is an arbitrary $\lambda$-variable. As before, we call the multisets forming the image set of $\lambda ^*$-terms $\lambda$-multisets. The following theorem is a version of the development separation theorem in [21]. Before that, we formulate a definition that generalizes the ${M}[x\leftarrow {N}]$ notation. We recall relation $\preceq$ on strings from a total order as defined in Definition 28. With the help of this, we define a term that is obtained by exchanging the occurrences of x in it with certain multisets. Intuitively, the notation ${P}[{Q}_1,\ldots ,{Q}_k]_x$ means that P contains k multisets ending with x and all such occurrences of x are replaced by terms $Q_1,\ldots , Q_k$ respecting the multiset order. Obviously, if we let $Q_i\equiv Q$ $(1\le i\le k)$, then ${P}[{Q}_1,\ldots ,{Q}_k]_x$ is the same as $P[x\leftarrow Q]$. We repeat this construction in the next definition.

Definition 42

Let ${P}, {Q}_1,\ldots ,{Q}_k$ be multisets and assume $\xi _1\prec \ldots \prec \xi _k$ are all the strings in P which end with the element x. Then, let ${P}[{Q}_1,\ldots ,{Q}_k]_x$ denote the multiset which is obtained from P when we exchange $\xi _i=\xi '_i\cdot x$ with $\xi '_i\cdot {Q}_i$ $(1\le i\le k)$.

The next lemma is intuitive and straightforward. It helps us with proving the development separation theorem for multisets.

Lemma 43

Let P, $Q_1,\ldots ,Q_k$ be $\lambda$-multisets such that $U\equiv P[{Q}_1,\ldots ,{Q}_k]_x$. Then, either of the following statements holds.

• 1. $U\equiv \lambda ^* x\cdot U_1$, where $U_1\equiv P_1[{Q}_1,\ldots ,{Q}_k]_x$ for some $P\equiv \lambda ^* x\cdot P_1$.

• 2. $U\equiv (l\cdot U_1\mid r\cdot U_2)$, where $U_1\equiv P_1[{Q}_1,\ldots ,{Q}_i]_x$ and $U_2\equiv P_2[{Q}_{i+1},\ldots ,{Q}_k]_x$ for some $1\le i\le k$ with $P\equiv (l\cdot P_1\mid r\cdot P_2)$.

Proof

Let $U\equiv P[{Q}_1,\ldots ,{Q}_k]_x$. We proceed by induction on P.

• 1. $P\equiv \lambda ^* x\cdot P_1$. We note that every string in $P\equiv \lambda ^* x\cdot P_1$ is of the form $\lambda ^* x\cdot \xi _1$, where $\xi _1$ is a string of $P_1$. From this, Point 1 follows.

• 2. $P\equiv (l\cdot P_1\mid r\cdot P_2)$. Since P is in the canonical representation, the strings of P are in the order prescribed by $\prec$. Hence, there is an $1\le i\le k$ such that $\xi _1\prec \ldots \prec \xi _i$ are all the strings of P falling in $P_1$ and ending in x. By this, we obtain Point 2. Since P must take exactly one of these two forms, these cases exhaust the possibilities for U.

$\square$

Now, we can turn to the proof of the multiset counterpart of the development separation theorem.

Theorem 44

Let ${R}\equiv \lfloor (\lambda x.{P})\,{Q}\rfloor$ be a b-redex. Assume ${R}\hookrightarrow ^*_{b}{R}'$. Then, ${R}'\equiv {P}'[{Q}_1,\ldots ,{Q}_k]_x$ such that ${P}\hookrightarrow ^*_{b}{P}'$ and $Q_i\hookrightarrow ^*_{b}{Q}_i$ for $1\le i\le k$, where k is the number of occurrences of x in $R'$.

Proof

Let ${R}\hookrightarrow ^k_{b}{R}'$. We proceed by induction on k.

• $k=1$. ${R}'\equiv {P}[x\leftarrow Q]$. By this, the assertion is true.

• $k=l+1$. Assume ${R}\hookrightarrow ^l_{b}{R}''\equiv {P}''[{Q}''_1,\ldots ,{Q}''_k]_x\hookrightarrow _{b}{R}'$ with appropriate $P''$ and $Q_1'',\ldots ,Q_k''$. We prove by induction on $P''$ that, if $P''[{Q}_1'',\ldots ,{Q}_k'']_x\hookrightarrow ^T_{b}S$, then S is of the desired form. From this, we can derive our assertion.

  • $P''\equiv x$. Then, $Q_j''\hookrightarrow S$ for some $1\le j\le k$. Then, the case $P''\equiv y$, where $x\ne y$, is impossible.

  • $P''\equiv \lambda ^*y.U$. Then, Definition 15 and Lemma 43 imply that, from $P''[{Q}_1'',\ldots ,{Q}_k'']_x\hookrightarrow _{b}S$, it follows that $U[{Q}_1'',\ldots ,{Q}_k'']_x\hookrightarrow _{b}S_1$ for some $S\equiv \lambda ^*y. S_1$. Then we use IH.

  • $P''\equiv (l\cdot U_1\mid r\cdot U_2)$. Then, by Lemma 43, $P''[Q_1'',\ldots ,Q_k'']_x \equiv (l\cdot U_1[Q_1'',\ldots ,Q_i'']_x\mid r\cdot U_2[Q_{i+1}'',\ldots ,Q_k'']_x)$ for some $1\le i\le k$. If either $U_1[{Q}_1'',\ldots ,{Q}_i'']_x\hookrightarrow ^T_{b}S_1$ or $U_2[{Q}_{i+1}'',\ldots ,{Q}_k'']_x\hookrightarrow ^T_{b}S_2$, where $S\equiv (S_1\mid S_2)$, then we can apply the IH. Otherwise, $U_1[Q_1'',\ldots ,Q_i'']_x\equiv \lambda y.U_1'$. By Lemma 43, $U_1\equiv \lambda y.U_1''\prec P''$. Hence, $P''[Q_1'',\ldots ,Q_k'']_x\hookrightarrow U_1''[{Q}_1'',\ldots ,{Q}_i'']_x[y\leftarrow U_2[{Q}_{i+1}'',\ldots ,{Q}_k'']_x]\equiv U_1''[y\leftarrow U_2][{Q}_1''',\ldots ,{Q}_l''']_x$, where l depends on the number of strings belonging to $U_1''[y\leftarrow U_2]$ ending in x and $Q_j'''\in \{{Q}_1'',\ldots ,{Q}_k''\}$ $(1\le j\le l)$.

Now, we can demonstrate the finiteness of developments theorem for multisets. $\square$

Theorem 45

Let $\textbf{R}$ be a set of b-redexes of the $\lambda$-multiset M. Assume ${M}\hookrightarrow _{b}^\sigma {M}'$ is a development of $\textbf{R}$. Then, the length of $\sigma$ cannot be arbitrarily large.

Proof

We argue by induction on $n=lh(M)$, which is the total number of the elements of $\mathcal {E}$ in M with multiplicities. Let ${M}\hookrightarrow _{b}^\sigma {M}'$, where $\sigma$ is a development of $\textbf{R}$. Let us denote by $l_n$ the maximal number of strings of ${M}'$ and $s_n$ the maximal length of $\sigma$ if any one of them is finite. We assume that $l_t$ and $s_t$ are finite for every $1\le t<n$. Furthermore, let |M| stand for the number of strings in the multiset M, that is, the cardinality of M.

• $M\equiv \lambda ^*y\cdot M_1$. Then ${M}_1\hookrightarrow _{b}^\sigma {M}_1'$ by Definition 15, hence, IH applies.

• $M\equiv (l\cdot M_1\mid r\cdot M_2)$. If $M'\equiv (l\cdot M_1'\mid r\cdot M_2)$ such that $M_1\hookrightarrow ^\sigma M_1'$ or $M'\equiv (l\cdot M_1\mid r\cdot M_2')$ such that $M_2\hookrightarrow ^\sigma M_2'$, respectively, then we can apply IH. Otherwise, ${M}\equiv (l\cdot \lambda y\cdot {M}_1\mid r\cdot {M}_2)$ and ${M}\equiv (l\cdot \lambda x\cdot {M}_1\mid r\cdot {M}_2)\hookrightarrow _{b}^{\sigma _1}(l\cdot \lambda x\cdot {M}'_1\mid r\cdot {M}'_2)\hookrightarrow _{b}^{\mathcal {R}}{M}'_1[x\leftarrow {M}'_2]\hookrightarrow _{b}^{\sigma _2}{M}''$ for some $\sigma _1$ and $\sigma _2$. By Theorem 44, ${M}''\equiv {M}_1''[{M}_2^1,\ldots ,{M}_2^k]_x$, where ${M}'_1\hookrightarrow ^*_b{M}_1''$ and ${M}_2'\hookrightarrow ^*{M}_2^j$ $(1\le j\le k)$. Hence, $|\sigma |\le s_k+s_{m}\cdot l_k+1$, where $lh({M}_1)=k$, $lh({M}_2)=m$ with $1\le k, m < n$ and $|M''|\le l_k+l_k\cdot l_{m}$. The right-hand side of both inequalities has a finite maximum; therefore, since M was arbitrary, $s_n$ and $l_n$ are finite.

$\square$

Corollary 46

Let $\textbf{R}$ be a set of redexes in the $\lambda$-term M. Let $\sigma$ be a development of $\textbf{R}$. Then, the length of $\sigma$ cannot be arbitrarily large.

Proof

It follows from the previous theorem and Theorem 24. $\square$

Remark 47

Theorem 45 gives us a bound for the length of developments and for the size of the result obtained by completing a development. It is not intended in this paper to try to set up an explicit bound for the lengths of reduction sequences, but it could be performed by utilizing the bound provided by Theorem 45 (cf. [6]).

5 Conclusion

Regarding the calculi developed for the simulation of biological processes, the String MultiSet Rewriting calculus proposed by Barbuti et al. is outstanding in the sense that it possesses the full computational strength of a Turing machine [4] while, on the other hand, it preserves a simple structure owing to which it appears to be quite handy on the side of implementation. In order to demonstrate that computational strength and flexibility, we encoded the $\lambda$-calculus in the frames of the SMSR calculus. The encoding allowed us to address each subterm of a $\lambda$-term directly, hence, making the proof of such classical theorems precise and, at the same time, intuitive where the argumentation depends on the behavior of particular subterms. We demonstrated this by proving the standardization and finiteness of developments theorems of the $\lambda$-calculus. Besides shedding light on crucial points of the demonstrations of these well-known theorems, this method can offer an illustrative tool for formalizing and implementing $\lambda$-calculus theorems.