Abstract
I examine notions of equivalence between logics (understood as languages interpreted model-theoretically) and develop two new ones that invoke not only the algebraic but also the string-theoretic structure of the underlying language. As an application, I show how to construe modal operator languages as what might be called typographical notational variants of bona fide first-order languages.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The present essay has two principal parts. The first, consisting of Sect. 2, endeavors to contribute to the study of ways in which two logics can be equivalent. In the second (Sect. 3), I define novel first-order systems that are equivalent, in the strongest non-trivial sense identified in Sect. 2, to various modal operator languages.
In the recent literature on translational equivalence and notational variance, a logic has typically been understood as a pair consisting of a language and a consequence relation, where consequence may be characterized in an abstract fashion or defined either proof-theoretically or model-theoretically. Authors who have provided systematic discussions of ways in which two logics, so conceived, may be equivalent include Wojcicki (1988), Epstein (1990), Pelletier and Urquhart (2003), Caleiro and Gonçalves (2007), Kocurek (2017) and French (2019).
By contrast, I here construe logics as interpreted languages, which are taken to be pairs consisting of a set L of expressions and a function \(\lambda \mathfrak {M}.\lambda \phi .\llbracket {\phi }\rrbracket _{\mathfrak {M}}\) mapping models \(\mathfrak {M}\) to functions \(\lambda \phi .\llbracket {\phi }\rrbracket _{\mathfrak {M}}\) that assign semantic values to expressions relative to models.Footnote 1 This is very roughly the notion of a logic common in the abstract model theory literature since at least Lindström (1969). As Ebbinghaus (1985, 28) points out, Feferman’s (1974) term model-theoretic language seems more appropriate for the concept than logic, and my terminology of “interpreted languages” is intended to reflect this view.
Generally speaking, two interpreted languages are considered “equivalent” just in case there are maps between their sets of expressions that preserve semantic values relative to each model (and perhaps satisfy certain other constraints). Thus where consequence relations are defined model-theoretically, equivalence results in our sense will typically yield equivalence results in the consequence-focused sense as well, with our analysis being more fine-grained since model-theoretic consequence generalizes over all models, while we examine meaning-preservation in a pointwise, model-by-model fashion.
That said, the model-focused approach has its drawbacks, too; most significantly, it is inapplicable to language pairs that do not share a common model space (such as, say, classical and intuitionistic propositional logic). Nevertheless, from the point of view of truth-conditional semantics, if the truth conditions of a sentence are cashed out as the class of models in which it is true, notions of equivalence for interpreted languages in our sense are clearly more immediately relevant than those for languages endowed with consequence relations.
To a large extent, however, the actual innovations proposed in this paper are independent of one’s construal of a logic, since they simply consist in two constraints, which give rise to what I call word-word variance and character-word variance, that maps between languages may or may not satisfy and which can thus be imposed regardless of the approach one follows.
A perhaps interesting feature of these novel equivalence relations between interpreted languages is that they marry two distinct construals of languages. These might be called the free algebraic (or Polish) view of languages as free algebras generated from a set of atoms by various operations (such as the forming of negations, conjunctions, necessitations, etc.) on the one hand, and the semigroup or formal-language theoretic view of languages as sets of strings over an alphabet endowed with the operation of concatenation, on the other.Footnote 2 Since the usual logical languages are plausibly regarded as exhibiting both kinds of structure, it seems apposite to consider structural aspects of both sorts in translating between them.Footnote 3
As an application of our classification of translational equivalence relations in Sect. 2, I show that the basic propositional modal language is a character-word variant of a bona fide quantificational language, relative to models with arbitrary (i.e. not necessarily universal) accessibility relations. Thus, for example, the basic modal logic \(\mathbf {K}\) turns out to be a notational variant, in a strong sense, of a certain first-order logic. The novel universal quantifier required for this result provides an exact first-order analog of the box operator in modal logic. I further show how to generalize this result to polymodal and quantified modal languages, as well as modal languages containing the actuality operator.
2 Equivalence Relations Between Interpreted Languages
Given an alphabet A, we let \(A^{*}\) be the set of all finite strings over A, including the empty string \(\epsilon \). The set \(A^+\) is \(A^*{\setminus } \{ \epsilon \}\), i.e. the set of all non-empty finite strings over A. Where \(n\ge 1\) and \(a_1,\ldots ,a_n\in A\), we write \(a_1\ldots a_n\) for the string whose i-th entry is \(a_i\), for \(1\le i\le n\). For \(\sigma _1,\ldots ,\sigma _n\in A^{*}\), we let \(\sigma _1\,^{\frown }\ldots ^{\frown }\sigma _n\) be the concatenation of \(\sigma _1,\ldots ,\sigma _n\), in that order. A language over the alphabet A is a non-empty subset of \(A^+\); a language is a language over some alphabet. We typically refer to the members of a language L as the L-formulas.
If L is a language, a semantics for L is a family \(\mathscr {S} = (\llbracket {\cdot }\rrbracket _{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}}\) of functions \(\llbracket {\cdot }\rrbracket _{\mathfrak {M}}\) with some (not necessarily proper) superset of L as their common domain, where \(\mathbf {M}\) is a non-empty class whose members are called models for L. For \(\phi \in L\) and \(\mathfrak {M}\in \mathbf {M}\), \(\llbracket {\phi }\rrbracket _{\mathfrak {M}}\) is the semantic value of \(\phi \) relative to \(\mathfrak {M}\) (according to \(\mathscr {S}\)). An interpreted language is a pair \((L,\mathscr {S})\) consisting of a language L and a semantics \(\mathscr {S}\) for L.
Definition 1
(Translation) For \(i\in \{ 0,1\}\), let \(L_i\) be a language, and let \(\mathscr {S}_i = (\llbracket {\cdot }\rrbracket ^i_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}}\) be a semantics for \(L_i\) (note that both semantics must be based on the same model class \(\mathbf {M}\)). A function \(t: L_0 \rightarrow L_1\) is a translation from the interpreted language \((L_0,\mathscr {S}_0)\) to the interpreted language \((L_1,\mathscr {S}_1)\) if, for every \(\phi \in L_0\) and every \(\mathfrak {M}\in \mathbf {M}\), \(\llbracket {\phi }\rrbracket ^0_{\mathfrak {M}} = \llbracket {t(\phi )}\rrbracket ^1_{\mathfrak {M}}\). \(\square \)
When it is obvious from context what the respective semantics are, we sometimes speak simply of a translation from \(L_0\) to \(L_1\).Footnote 4
One obvious notion of equivalence between interpreted languages is mutual translatability, or bi-translatability as we shall call it.
Definition 2
(Bi-translation; bi-translatability) When for \(i\in \{0,1\}\), \(t_i\) is a translation from \((L_i,(\llbracket {\cdot }\rrbracket ^i_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) into \((L_{1-i},(\llbracket {\cdot }\rrbracket ^{1-i}_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\), the pair \((t_0,t_1)\) is a bi-translation from \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) to \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\). \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) and \((L_{1},(\llbracket {\cdot }\rrbracket ^{1}_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) are bi-translatable if there exists a bi-translation from the former to the latter.\(\square \)
Remark 1
If \((t_0,t_1)\) is a bi-translation from \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) to \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\), it follows that \(\llbracket {t_1(t_0(\phi ))}\rrbracket ^0_{\mathfrak {M}} = \llbracket {\phi }\rrbracket ^0_{\mathfrak {M}}\) and \(\llbracket {t_0(t_1(\psi ))}\rrbracket ^1_{\mathfrak {M}} = \llbracket {\psi }\rrbracket ^1_{\mathfrak {M}}\) for all \(\phi \in L_0\), \(\psi \in L_1\), and \(\mathfrak {M}\in \mathbf {M}\). \(\square \)
Example 1
Let \(1{\mathsf {QL}}\) be the language of monadic predicate logic, whose syntax is given by \({\phi }{:}{:=} px\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, {\forall }{x}\phi \), where p ranges over a countably infinite set \(\mathsf {S}\) (whose members we will in this example construe as one-place predicate symbols) and x ranges over the countably infinite set \(\mathsf {Var}= \{ {\mathsf {v}_{0}},{\mathsf {v}_{1}},\ldots ,\mathsf {v}_i,\ldots \}\) of individual variables.
Let \(\delta \) and \(\Delta \) be fresh symbols, and let the languages \(1{\mathsf {QL}}_{\delta }\) and \(1{\mathsf {QL}}_{\Delta }\) be given by \({\phi }{:}{:=} px\, |\, p\delta \, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, {\forall }{x}\phi \) and \({\phi }{:}{:=} px\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, {\forall }{x}\phi \, |\, \Delta x\phi \). The new symbols \(\delta \) and \(\Delta \) thus present syntactically as an individual constant and a quantifier, respectively. The model class \(\mathbf {M}\) consists of structures \(\mathfrak {M}= (M, d^{\mathfrak {M}}, (p^{\mathfrak {M}})_{p\in \mathsf {S}})\) where \(d^{\mathfrak {M}}\in M\) and \(p^{\mathfrak {M}}\subseteq M\) for each \(p\in \mathsf {S}\).
Let \(\mathfrak {M}\) be such a model. A variable assignment in \(\mathfrak {M}\) is a function \(g:\mathsf {Var}\rightarrow M\), and for \(x\in \mathsf {Var}\) and \(m\in M\), \(g[x:= m]\) is the variable assignment in \(\mathfrak {M}\) that agrees with g on \(\mathsf {Var}{\setminus } \{ x\}\) and maps x to m. For \(1{\mathsf {QL}}_{\delta }\)-formulas \(\phi \) and \(1{\mathsf {QL}}_{\Delta }\)-formulas \(\psi \), we define the local values  relative to \(\mathfrak {M}\) and g in familiar Tarskian fashion as follows:
relative to \(\mathfrak {M}\) and g in familiar Tarskian fashion as follows:

For models \(\mathfrak {M}\) and \(\phi \in 1{\mathsf {QL}}_{\delta }\), \(\psi \in 1{\mathsf {QL}}_{\Delta }\), let \(||\phi ||_{\mathfrak {M}} := \lambda g. ||\phi ||_{\mathfrak {M}}^{g}\) and  . Then the following recursively defined functions \(\tau :1{\mathsf {QL}}_{\delta } \rightarrow 1{\mathsf {QL}}_{\Delta }\) and \(\sigma :1{\mathsf {QL}}_{\Delta }\rightarrow 1{\mathsf {QL}}_{\delta }\) translate between the interpreted languages \((1{\mathsf {QL}}_{\delta }, (||\cdot ||_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) and
. Then the following recursively defined functions \(\tau :1{\mathsf {QL}}_{\delta } \rightarrow 1{\mathsf {QL}}_{\Delta }\) and \(\sigma :1{\mathsf {QL}}_{\Delta }\rightarrow 1{\mathsf {QL}}_{\delta }\) translate between the interpreted languages \((1{\mathsf {QL}}_{\delta }, (||\cdot ||_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) and  .Footnote 5
.Footnote 5

The interpreted languages \((1{\mathsf {QL}}_{\delta }, (||\cdot ||_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) and  are thus bi-translatable. \(\square \)
are thus bi-translatable. \(\square \)
Bi-translatability is arguably the weakest relation of semantic equivalence between languages. We can obtain stricter notions by imposing constraints on the translations. Such constraints typically require an additional assumption about the languages at hand; to wit, that they are freely generated by a set of primitive syntactic operations from a set of atoms. This is the case for all the particular languages we will consider. Henceforth it will be assumed in our definitions that a language \(L_i\) is freely generated by the primitive operations in \({\mathsf {O}}_i\) from the atoms in \(\mathsf {S}_i\).
Definition 3
(Compositionality; Atomic Faithfulness; Definitionality) A translation t from \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) into \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) is compositional if, for every n-ary operation \(\circ \in {\mathsf {O}}_0\) there is an n-place \(L_1\)-contextFootnote 6\(\psi ^{\circ }(*_1,\ldots ,*_n)\), called the \(L_1\)-definition of \(\circ \), such that for all \(\phi _1,\ldots ,\phi _n\in L_0\): \(t(\circ (\phi _1,\ldots ,\phi _n)) = \psi ^{\circ }(t(\phi _1),\ldots ,t(\phi _n))\).
A translation t from \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) into \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) is atomically faithful if it maps \(\mathsf {S}_0\) into \(\mathsf {S}_1\); it is definitional if it is compositional and atomically faithful.
A bi-translation \((t_0,t_1)\) from \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) to \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) is definitional if both \(t_0\) and \(t_1\) are definitional. The interpreted languages \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) and \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) are definitionally equivalent if there exists a definitional bi-translation between them.\(\square \)
Example 2
For \(\circ \in \{\wedge ,\vee \}\), let \({\mathsf {PL}}_{\lnot ,\circ }\) be the language of propositional logic over the set \(\mathsf {S}\) (whose members we construe, for the purposes of this example, as sentence letters) with the syntax \({\phi }{:}{:=} p\,|\, \lnot \phi \,|\, (\phi \circ \phi )\). Let \(\delta : {\mathsf {PL}}_{\lnot ,\wedge }\rightarrow {\mathsf {PL}}_{\lnot ,\vee }\) rewrite propositional formulas in \(\lnot \) and \(\wedge \) into formulas in \(\lnot \) and \(\vee \) using the equivalence of \((\phi \wedge \psi )\) with \(\lnot (\lnot \phi \vee \lnot \psi )\). That is, let \(\delta \) be defined recursively by the following equations:
-
\(\delta (p) = p\) when \(p\in \mathsf {S}\)
-
\(\delta (\lnot \phi ) = \lnot \delta (\phi )\)
-
\(\delta ((\phi \wedge \psi )) = \lnot (\lnot \delta (\phi )\vee \lnot \delta (\psi ))\)
Let the model class be the set \(2^{\mathsf {S}}\) of all Boolean valuations \(v:\mathsf {S}\rightarrow \{ 0,1\}\) and let \(\llbracket {\phi }\rrbracket _v\) be the truth value of the propositional formula \(\phi \) relative to the Boolean valuation v. Then \(\delta \) is a translation from \(({\mathsf {PL}}_{\lnot ,\wedge },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\) to \(({\mathsf {PL}}_{\lnot ,\vee },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\), since \(\llbracket {\phi }\rrbracket _v = \llbracket {\delta (\phi )}\rrbracket _v\) for all \({\mathsf {PL}}_{\lnot ,\wedge }\)-formulas \(\phi \) and all valuations v. Obviously \(\delta \) is atomically faithful, since its restriction to \(\mathsf {S}\) is the identity function. Moreover, \(\delta \) is compositional, the \({\mathsf {PL}}_{\lnot ,\vee }\)-definition for negation being \(\lnot *_1\) and the \({\mathsf {PL}}_{\lnot ,\vee }\)-definition for conjunction being \(\lnot (\lnot *_1 \vee \lnot *_2)\). So \(\delta \) is a definitional translation.
Conversely, let \(\gamma :{\mathsf {PL}}_{\lnot ,\vee }\rightarrow {\mathsf {PL}}_{\lnot ,\wedge }\) rewrite propositional formulas in \(\lnot \) and \(\vee \) into formulas in \(\lnot \) and \(\wedge \) using the equivalence of \((\phi \vee \psi )\) with \(\lnot (\lnot \phi \wedge \lnot \psi )\). That is, let \(\gamma \) be defined recursively by the following equations:
-
\(\gamma (p) = p\) for \(p\in \mathsf {S}\)
-
\(\gamma (\lnot \phi ) = \lnot \gamma (\phi )\)
-
\(\gamma ((\phi \vee \psi )) = \lnot (\lnot \gamma (\phi )\wedge \lnot \gamma (\psi ))\)
Then \(\gamma \) is a translation from \(({\mathsf {PL}}_{\lnot ,\vee },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\) to \(({\mathsf {PL}}_{\lnot ,\wedge },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\). It is obviously atomically faithful and compositional, the \({\mathsf {PL}}_{\lnot ,\wedge }\)-definition for negation being \(\lnot *_1\) and the \({\mathsf {PL}}_{\lnot ,\wedge }\)-definition for disjunction being \(\lnot (\lnot *_1 \wedge \lnot *_2)\). So \(\gamma \) is also a definitional translation, \((\delta ,\gamma )\) is a definitional bi-translation, and the interpreted languages \(({\mathsf {PL}}_{\lnot ,\vee },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\) and \(({\mathsf {PL}}_{\lnot ,\wedge },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\) are definitionally equivalent.\(\square \)
Remark 2
Bi-translatability does not entail definitional equivalence: As we saw in Example 1, \(1{\mathsf {QL}}_{\delta }\) and \(1{\mathsf {QL}}_{\Delta }\) are bi-translatable. They are not, however, definitionally equivalent. Indeed, it can be shown that there is no atomically faithful translation from \(1{\mathsf {QL}}_{\delta }\) to \(1{\mathsf {QL}}_{\Delta }\). To see this, suppose that \(t:1{\mathsf {QL}}_{\delta }\rightarrow 1{\mathsf {QL}}_{\Delta }\) is an atomically faithful translation. By atomic faithfulness, \(t(p_{0}\delta )\) must be an atom of \(1{\mathsf {QL}}_{\Delta }\), i.e. some formula of the form qy with \(q\in \mathsf {S}\) and \(y\in \mathsf {Var}\). Moreover, since t is a translation, we must have  for all \(\mathfrak {M}\) and g. But then q must be \(p_{0}\), since otherwise there are models \(\mathfrak {M}\) with \(p_{0}^{\mathfrak {M}} = M\) and \(q^{\mathfrak {M}} = \emptyset \). So \(t(p_{0}\delta ) = p_{0}y\). Now consider any \(\mathfrak {M}\) with \(\emptyset \ne p_{0}^{\mathfrak {M}} \ne M\). We must have
for all \(\mathfrak {M}\) and g. But then q must be \(p_{0}\), since otherwise there are models \(\mathfrak {M}\) with \(p_{0}^{\mathfrak {M}} = M\) and \(q^{\mathfrak {M}} = \emptyset \). So \(t(p_{0}\delta ) = p_{0}y\). Now consider any \(\mathfrak {M}\) with \(\emptyset \ne p_{0}^{\mathfrak {M}} \ne M\). We must have  for all g. However, \(||p_{0}\delta ||_{\mathfrak {M}}^{g}\) is independent of g, while there are h and k such that
for all g. However, \(||p_{0}\delta ||_{\mathfrak {M}}^{g}\) is independent of g, while there are h and k such that  , contradiction.
, contradiction.
It is natural to consider a strengthening of the compositionality constraint on translations that requires the target language definition of a primitive operation to be itself provided by a primitive operation:
Definition 4
(Homomorphism; Bi-Homomorphism; Isomorphism) An atomically faithful translation t from \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) into \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) is homomorphic if there exists a function \(\circ \mapsto \circ ^t\) from \({\mathsf {O}}_0\) into \({\mathsf {O}}_1\) such that, for any n-ary operation \(\circ \in {\mathsf {O}}_0\), the operation \(\circ ^t\in {\mathsf {O}}_1\) is n-ary and satisfies the condition that for any \(\phi _1,\ldots ,\phi _n\) in \(L_0\), \(t(\circ (\phi _1,\ldots ,\phi _n)) = \circ ^t(t(\phi _1),\ldots ,t(\phi _n))\).
A bi-homomorphism from \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) to \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) is a pair \((h_0,h_1)\), where each \(h_i\) is a homomorphism from from \((L_i,(\llbracket {\cdot }\rrbracket ^i_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) to \((L_{1-i},(\llbracket {\cdot }\rrbracket ^{1-i}_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\).
The languages \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) and \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) are homomorphically bi-translatable if there exists a bi-homomorphism from the former to the latter.
A homomorphic translation t from \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) to \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) is an isomorphic translation if t is a bijection from \(L_0\) onto \(L_1\). \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) and \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) are isomorphic languages just in case there is an isomorphic translation from the former to the latter.\(\square \)
Remark 3
Obviously any homomorphic translation is definitional, and hence homomorphically bi-translatable languages are definitionally equivalent. There are, however, definitional translations that are not homomorphisms, e.g. the functions \(\delta \) and \(\gamma \) of Example 2. Indeed, \({\mathsf {PL}}_{\lnot ,\wedge }\) and \({\mathsf {PL}}_{\lnot ,\vee }\), while definitionally equivalent, are not homomorphically bi-translatable, since there are no homomorphic translations between \({\mathsf {PL}}_{\lnot ,\wedge }\) and \({\mathsf {PL}}_{\lnot ,\vee }\). For suppose \(f:{\mathsf {PL}}_{\lnot ,\wedge }\rightarrow {\mathsf {PL}}_{\lnot ,\vee }\) were a homomorphic translation. Since it is then in particular an atomically faithful translation, it must map each sentence letter to itself.Footnote 7 Now homomorphism requires that \(f((p\wedge q)) = (f(p)\vee f(q))\) since disjunction is the only primitive binary operation available in \({\mathsf {PL}}_{\lnot ,\vee }\). So \(f((p\wedge q)) = (p\vee q)\), which contradicts f being a translation. The same argument shows that there are no homomorphic translations in the reverse direction. Thus homomorphic bi-translatability implies definitional equivalence but not conversely.\(\square \)
Remark 4
The inverse of an isomorphism is again an isomorphism; thus if f is an isomorphism, the pair \((f,f^{-1})\) is a bi-homomorphism. Therefore isomorphic interpreted languages are homomorphically bi-translatable. The converse fails, since the languages \({\mathsf {PL}}_{\lnot ,\wedge }\) and \( {\mathsf {PL}}_{\lnot ,\wedge , \& }\), with \(\wedge \) and & given the same truth-tabular interpretation, are homomorphically bi-translatable but not isomorphic: Any homomorphism from \( {\mathsf {PL}}_{\lnot ,\wedge , \& }\) to \({\mathsf {PL}}_{\lnot ,\wedge }\) must map both \((p\wedge q)\) and \( (p\, \& \, q)\) to \((p\wedge q)\).\(\square \)
Remark 5
As the example in the previous remark shows, in order for t to be a homomorphism from \(L_0\) to \(L_1\), the function \(\circ \mapsto \circ ^t\) from \({\mathsf {O}}_0\) to \({\mathsf {O}}_1\) is not required to be \(1\text{- }1\); nor is it required to be surjective: In the case of the homomorphism from \({\mathsf {PL}}_{\lnot ,\wedge }\) to \( {\mathsf {PL}}_{\lnot ,\wedge , \& }\), surjectivity fails, and in the case of the homomorphism from \( {\mathsf {PL}}_{\lnot ,\wedge , \& }\) to \({\mathsf {PL}}_{\lnot ,\wedge }\), injectivity fails. If, however, f is an isomorphic translation from \(L_0\) to \(L_1\), the function \(\circ \mapsto \circ ^f\) from \({\mathsf {O}}_0\) to \({\mathsf {O}}_1\) is easily seen to be a bijection.
Example 3
Let \({\mathsf {PPL}}_{\lnot ,\wedge }\) be the set of propositional formulas in \(\lnot \) and \(\wedge \) over \(\mathsf {S}\) written in Polish notation. That is, let the syntax of \({\mathsf {PPL}}_{\lnot ,\wedge }\) be given by \({\phi }{:}{:=} p\,|\, \lnot \phi \,|\, \wedge \phi \phi \). Then the function \(\pi :{\mathsf {PL}}_{\lnot ,\wedge }\rightarrow {\mathsf {PPL}}_{\lnot ,\wedge }\) defined by the recursion equations
-
\(\pi (p) = p\)
-
\(\pi (\lnot \phi ) = \lnot \pi (\phi )\)
-
\(\pi ((\phi \wedge \psi )) = \wedge \pi (\phi )\pi (\psi )\)
is an isomorphic translation from \(({\mathsf {PL}}_{\lnot ,\wedge },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\) to \(({\mathsf {PPL}}_{\lnot ,\wedge },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\), and hence these interpreted languages are isomorphic.\(\square \)
We next introduce a novel (as far as we’re aware) equivalence relation that is stricter than isomorphism.
Definition 5
(n-Word Basis; n-WW-Replacement; WW-Variance; WW-Variants) Where L is a language over the alphabet A and \(n\ge 1\), a subset \(\Lambda \) of \(A^+\) is an n-word basis for L over A if every member of \(\Lambda \) is of a length \(\le n\), and for every \(\phi \in L\) there is a unique finite sequence \(l_0,\ldots ,l_{n_{\phi }}\) of elements of \(\Lambda \) such that \(\phi \) is the concatenation \(l_0\, ^{\frown }\ldots ^{\frown } l_{n_{\phi }}\) of \(l_0\), ..., \(l_{n_{\phi }}\). (So A, or more precisely, the set of length 1 words over A, is always a 1-word basis for L over A.)
For \(i\in \{0,1\}\), let \(L_i\) be a language over \(A_i\). An n-WW-replacement from \(A_0\) to \(A_1\) relative to \(L_0\) is a pair \((\Lambda ,r)\), where \(\Lambda \) is an n-word basis for \(L_0\) over \(A_0\) and \(r:\Lambda \rightarrow A_1^{*}\) (so r replaces certain Words over \(A_0\) by Words over \(A_1\)).
A function \(f:L_0\rightarrow L_1\) is induced by the n-WW-replacement \((\Lambda ,r)\) from \(A_0\) to \(A_1\) relative to \(L_0\) if, whenever \(\phi \in L_0\) and \(\phi \) is the concatenation \(l_0\, ^{\frown }\ldots ^{\frown } l_{m}\) of \(l_0\), ..., \(l_m\in \Lambda \), \(f(\phi )\) is \(r(l_0)^{\frown } \ldots ^{\frown } r(l_m)\).
An isomorphism f from \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) to \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) is a WW-variance if there are m and n such that f is induced by an m-WW-replacement and its inverse \(f^{-1}\) is induced by an n-WW-replacement (equivalently, if there is an n such that f and \(f^{-1}\) are each induced by n-WW-replacements). The interpreted languages \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) and \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) are WW-variants if there exists a WW-variance from the former to the latter.\(\square \)
Remark 6
We require a finite bound n in the definition of WW-variance in order not to trivialize the definition: If strings of arbitrary lengths were allowed in the basis, any isomorphism f, which is trivially induced by (L, f) as an (unbounded) WW-replacement, would be a WW-variance.\(\square \)
The following example shows that isomorphism does not imply WW-variance.
Example 4
The interpreted languages \({\mathsf {PL}}_{\lnot ,\wedge }\) and \({\mathsf {PPL}}_{\lnot ,\wedge }\) aren’t WW-variants (though they are isomorphic, as shown in Example 3). Indeed no homomorphic translation from \({\mathsf {PPL}}_{\lnot ,\wedge }\) to \({\mathsf {PL}}_{\lnot ,\wedge }\) is induced by an n-WW-replacement, for any n: Suppose that some n-WW-replacement \((\Lambda ,r)\) from \(\mathsf {S}\cup \{\lnot ,\wedge \}\) to \(\mathsf {S}\cup \{\lnot ,\wedge \}\cup \{ (\, ,)\}\) relative to \({\mathsf {PPL}}_{\lnot ,\wedge }\) induces a homomorphic translation \(f: {\mathsf {PPL}}_{\lnot ,\wedge }\rightarrow {\mathsf {PL}}_{\lnot ,\wedge }\). Clearly the only segmentation of an atomic formula p in terms of the n-word basis \(\Lambda \) is as p itself, so \(\mathsf {S}\subseteq \Lambda \) (more precisely, every singleton string over \(\mathsf {S}\) is in \(\Lambda \)). Let \(\phi _0\) be \(p_{0}\) and \(\phi _{k+1}\) be \(\wedge \phi _k p_{k+1}\). Then \(\phi _n\) is \(\wedge \cdots \wedge p_{0}\cdots p_n\), with an initial string of n conjunction symbols. If the unique segmentation of \(\phi _n\) in terms of \(\Lambda \) is \(\sigma _0\), ..., \(\sigma _m\) with \(\sigma _m\) a singleton string consisting only of \(p_n\), then the function induced by \((\Lambda ,r)\) maps \(\phi _n\) to an expression that ends in \(p_n\) (this is because f is an atomically faithful translation, so that \(r(p) = f(p) = p\) for \(p\in \mathsf {S}\)). But if the induced function were a homomorphic translation, it would have to map \(\phi _n\) to a (non-degenerate) conjunction and hence to an expression ending in a closing parenthesis, so this is impossible. Now the only other prima facie possible segmentations of \(\phi _n\) in terms of \(\Lambda \) are of the form \(\sigma _0\), ..., \(\sigma _m\) with \(\sigma _m\) being the length \(k+1\) string \(p_{n-k} \ldots p_n\) for some \(1\le k<n\), since the segmenting words cannot be longer than n. But as each singleton string \(\pi _i\) consisting of a single sentence letter \(p_i\) belongs to \(\Lambda \), this contradicts the uniqueness requirement of \(\Lambda \)’s being an n-word basis, for we could then also segment \(\phi _n\) into \(\sigma _0\), ..., \(\sigma _{m-1}\), \(\pi _{n-k}\), ..., \(\pi _n\).\(\square \)
There are, however, non-identical languages that are WW-variants.
Example 5
Consider the language \(1{\mathsf {QL}}\) of Example 1 whose syntax is given by \({\phi }{:}{:=} px\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, {\forall }{x}\phi \), as well as the language \(1{\mathsf {QL}}^{*}\) that is exactly like \(1{\mathsf {QL}}\) except that it puts decorative parentheses around its quantifier prefixes. More precisely, the syntax of \(1{\mathsf {QL}}^{*}\) is given by \({\phi }{:}{:=} px\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, ({\forall }{x})\phi \).
For both languages, models are standard first-order structures \(\mathfrak {M}= (M, (p^{\mathfrak {M}})_{p\in \mathsf {S}})\), and the semantic value  (respectively,
(respectively,  ) of a \(1{\mathsf {QL}}\)-formula \(\phi \) (respectively, \(1{\mathsf {QL}}^{*}\)-formula \(\phi \)) relative to such a structure \(\mathfrak {M}\) is the function that maps any variable assignment g over \(\mathfrak {M}\) to the usual Tarskian value
) of a \(1{\mathsf {QL}}\)-formula \(\phi \) (respectively, \(1{\mathsf {QL}}^{*}\)-formula \(\phi \)) relative to such a structure \(\mathfrak {M}\) is the function that maps any variable assignment g over \(\mathfrak {M}\) to the usual Tarskian value  (respectively
(respectively  ) of the formula \(\phi \) in the structure \(\mathfrak {M}\) relative to g.
) of the formula \(\phi \) in the structure \(\mathfrak {M}\) relative to g.
Let \(t:1{\mathsf {QL}}\rightarrow 1{\mathsf {QL}}^{*}\) be the function that changes nothing except that it encloses quantifier prefixes in parentheses. Obviously t is an isomorphism, and its inverse \(t^{-1}:1{\mathsf {QL}}^{*}\rightarrow 1{\mathsf {QL}}\) changes nothing except that it erases decorative parentheses around quantifier prefixes. The translation t is induced by the 2-WW-replacement whose 2-word basis contains the singleton strings of every primitive symbol except \({\forall }\) and the length 2 strings \({\forall }{x}\) whenever \(x\in \mathsf {Var}\), and whose replacement function maps each singleton string in the basis to itself, and each string \({\forall }{x}\) to \(({\forall }{x})\). Similarly, \(t^{-1}\) is induced by the 4-WW-replacement whose 4-word basis contains the singleton strings of every primitive symbol except \({\forall }\) as well as, for each \(x\in \mathsf {Var}\), the length 4 string \(({\forall }{x})\), and whose replacement function maps each singleton string in the basis to itself, and each string \(({\forall }{x})\) to \({\forall }{x}\). \(\square \)
We obtain a strengthening of WW-variance if we require that the translations must in fact be 1-WW-replacements; in other words, that translations proceed by replacing individual symbols of the source language’s alphabet by finite strings over the target alphabet. This leads to the notion of CW-variance.
Definition 6
(CW-Replacement; CW-Variance; CW-Variant) For \(i\in \{0,1\}\), let \(L_i\) be a language over the alphabet \(A_i\). A CW-replacement from \(A_0\) to \(A_1\) is a map from \(A_0\) into the set \(A_1^{*}\) of finite strings (including the empty string \(\epsilon \)) over \(A_1\) (so that it replaces Characters from \(A_0\) by Words over \(A_1\)). A function \(f:L_0\rightarrow L_1\) is induced by the CW-replacement r if, whenever \(c_0,\ldots ,c_n\in A_0\) and the length \(n+1\) string \(c_0\ldots c_n\) is in \(L_0\), \(f(c_0\ldots c_n)\) is \(r(c_0)^{\frown } \ldots ^{\frown } r(c_n)\). An isomorphism f from \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) to \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) is a CW-variance if both it and its inverse \(f^{-1}\) are induced by CW-replacements. The interpreted languages \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) and \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) are CW-variants if there exists a CW-variance from the former to the latter.\(\square \)
Remark 7
There are isomorphisms that are induced by CW-replacements but whose inverses are not so induced. Recall the isomorphism \(\pi :{\mathsf {PL}}_{\lnot ,\wedge }\rightarrow {\mathsf {PPL}}_{\lnot ,\wedge }\) of Example 3. It is induced by the CW-replacement that maps every primitive symbol except the opening and closing parentheses and the conjunction symbol to itself, that maps the closing parenthesis as well as the conjunction symbol to the empty string, and the opening parenthesis to the conjunction symbol. The inverse \(\pi ^{-1}\), however, is not induced by any CW-replacement; indeed no atomically faithful translation \(f:{\mathsf {PPL}}_{\lnot ,\wedge }\rightarrow {\mathsf {PL}}_{\lnot ,\wedge }\) can be induced by a CW-replacement r. Otherwise we would have \(p = f(p) = r(p)\) for each \(p\in \mathsf {S}\) and hence \(f(\wedge pq) = r(\wedge )^{\frown } pq\), but no \({\mathsf {PL}}_{\lnot ,\wedge }\)-formula has adjacent sentence letter occurrences.
Remark 8
Obviously CW-variance implies WW-variance, since CW-variances are essentially 1-WW-variances. The converse fails, since \(1{\mathsf {QL}}\) and \(1{\mathsf {QL}}^{*}\) are WW-variants (as shown in Example 5) but not CW-variants.Footnote 8 Indeed there cannot be any atomically faithful translation \(f:1{\mathsf {QL}}\rightarrow 1{\mathsf {QL}}^{*}\) that is induced by a CW-replacement r. Otherwise, by atomic faithfulness, for each \(p\in \mathsf {S}\) and \(x\in \mathsf {Var}\), f(px) must be an atom of \(1{\mathsf {QL}}^{*}\), and by translation, f(px) must be px. But of course we must also have \(f(px) = r(p)^{\frown } r(x)\). It follows that, for every \(p\in \mathsf {S}\) and every \(x\in \mathsf {Var}\), \(r(p) = p\) and \(r(x) = x\).Footnote 9 It then follows that \(f({\forall }{x}px) = r({\forall })^{\frown } xpx\). But there are no \(1{\mathsf {QL}}^{*}\)-formulas in which a variable x occurs directly before a predicate symbol \(p\in \mathsf {S}\).
The next example shows that there are non-trivial cases of CW-variant languages. Since the example provides the motivation for the discussion in the following section, we work through it in some detail.
Example 6
The primitive symbols of the basic modal language \(\mathsf {ML}\) are the members of the set \(\mathsf {S}\) (which in the context of \(\mathsf {ML}\) we’ll again call sentence letters), the connectives \(\lnot \) and \(\rightarrow \), the unary operator \(\Box \), as well as parentheses. The syntax of \(\mathsf {ML}\) is given by \({\phi }{:}{:=} p\, |\, \lnot \phi \,|\, (\phi \rightarrow \phi )\, |\, \Box \phi \), where p ranges over the set \(\mathsf {S}\). The \(\mathsf {ML}\)-formulas are interpreted in models \(\mathfrak {M}= (W,R,{(p^{\mathfrak {M}})_{p\in {\mathsf {S}}}})\), where W is a non-empty set (whose members may be called worlds or indices), R is a binary relation on W (the accessibility relation), and \({(p^{\mathfrak {M}})_{p\in {\mathsf {S}}}}\) is an \(\mathsf {S}\)-indexed family of sets \(p^{\mathfrak {M}}\subseteq W\).
The local value \(\llbracket {\phi }\rrbracket ^w_{\mathfrak {M}}\in \{ 0,1\}\) of an \(\mathsf {ML}\)-formula \(\phi \) at a world w relative to a model \(\mathfrak {M}\) is defined recursively as follows:
-
1.
\(\llbracket {p}\rrbracket ^w_{\mathfrak {M}} = 1\) if \(w\in p^{\mathfrak {M}}\)
-
2.
\(\llbracket {\lnot \phi }\rrbracket ^w_{\mathfrak {M}} = 1-\llbracket {\phi }\rrbracket ^w_{\mathfrak {M}}\)
-
3.
\(\llbracket {(\phi \rightarrow \psi )}\rrbracket ^w_{\mathfrak {M}} = \max \{ 1-\llbracket {\phi }\rrbracket ^w_{\mathfrak {M}},~\llbracket {\psi }\rrbracket ^w_{\mathfrak {M}}\}\)
-
4.
\(\llbracket {\Box \phi }\rrbracket ^w_{\mathfrak {M}} = \min \{ \llbracket {\phi }\rrbracket ^v_{\mathfrak {M}} \,|\, wRv\}\)
The semantic value \(\llbracket {\phi }\rrbracket _{\mathfrak {M}}\) of \(\phi \) in a model \(\mathfrak {M}\) is the function \(\lambda w.\llbracket {\phi }\rrbracket ^w_{\mathfrak {M}}\).
When attention is restricted to models \(\mathfrak {M}= (W,R,{(p^{\mathfrak {M}})_{p\in {\mathsf {S}}}})\) in which R is universal (i.e. \(R = W\times W\)), clause 4 can be simplified to \(\llbracket {\Box \phi }\rrbracket ^w_{\mathfrak {M}} = \min \{ \llbracket {\phi }\rrbracket ^v_{\mathfrak {M}} \,|\, v\in W\}\). No reference is then made to the accessibility relation in any of the semantic clauses, which therefore idles as a component of the model. When this restriction is in place, we may thus take models to be pairs \(\mathfrak {M}= (W,{(p^{\mathfrak {M}})_{p\in {\mathsf {S}}}})\), which we call universal models. For the remainder of this example we impose this universality restriction.
Recall that \(1{\mathsf {QL}}\) is the first-order language over the signature given by the set \(\mathsf {S}\) of sentence letters, reconstrued as one-place predicate symbols. Any universal model \(\mathfrak {M}= (W,{(p^{\mathfrak {M}})_{p\in {\mathsf {S}}}})\) for \(\mathsf {ML}\) is at the same time a first-order structure for \(1{\mathsf {QL}}\).
The local values  and the semantic values
and the semantic values  of \(1{\mathsf {QL}}\)-formulas \(\phi \) in universal models \(\mathfrak {M}\) were defined in Example 1 along familiar Tarskian lines.
of \(1{\mathsf {QL}}\)-formulas \(\phi \) in universal models \(\mathfrak {M}\) were defined in Example 1 along familiar Tarskian lines.
Now let the \({\mathsf {v}_{0}}\)-fragment \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\) of \(1{\mathsf {QL}}\) be the set of all \(1{\mathsf {QL}}\)-formulas in which no variable other than \({\mathsf {v}_{0}}\) occurs. Though defined here as a fragment of \(1{\mathsf {QL}}\), \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\) is an inductively defined first-order language in its own right: With p ranging over \(\mathsf {S}\), its syntax can be given as \({\phi }{:}{:=} p{\mathsf {v}_{0}}\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, {\forall }{\mathsf {v}_{0}}\phi \).
The semantics for \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\) is that of \(1{\mathsf {QL}}\) restricted to formulas in which the only variable is \({\mathsf {v}_{0}}\). In evaluating a \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\)-formula relative to an assignment, we obviously needn’t take into account the values of any variables other than \({\mathsf {v}_{0}}\); so an assignment is simply the specification of a value w for the variable \({\mathsf {v}_{0}}\). But then we might as well say that \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\)-formulas have local values  relative to models \(\mathfrak {M}\) and individual members w of \(\mathfrak {M}\)’s domain, instead of local values
relative to models \(\mathfrak {M}\) and individual members w of \(\mathfrak {M}\)’s domain, instead of local values  relative to \(\mathfrak {M}\) and assignment functions \(\{ \langle {\mathsf {v}_{0}}, w\rangle \}\). So we have the following semantic clauses for
relative to \(\mathfrak {M}\) and assignment functions \(\{ \langle {\mathsf {v}_{0}}, w\rangle \}\). So we have the following semantic clauses for  :
:
-
1.

-
2.

-
3.

-
4.

Now consider the functions \(\lambda :\mathsf {ML}\rightarrow 1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\) and \(\mu : 1{\mathsf {QL}}_{{\mathsf {v}_{0}}} \rightarrow \mathsf {ML}\) defined by the following recursion equations:

Informally, \(\lambda \) appends \({\mathsf {v}_{0}}\) to every sentence letter and replaces \(\Box \) with \({\forall }{\mathsf {v}_{0}}\), while \(\mu \) deletes \({\mathsf {v}_{0}}\) and replaces \({\forall }\) with \(\Box \). It is easy to see that \(\lambda \) and \(\mu \) are isomorphic translations that are inverses of each other. Indeed, both \(\lambda \) and \(\mu \) are induced by CW-replacements: \(\lambda \) is induced by the CW-replacement that maps every \(p\in \mathsf {S}\) to the string \(p{\mathsf {v}_{0}}\), the box \(\Box \) to the string \({\forall }{\mathsf {v}_{0}}\), and every other primitive symbol of \(\mathsf {ML}\) to itself. Its inverse \(\mu \) is induced by the CW-replacement that maps \({\mathsf {v}_{0}}\) to the empty string \(\epsilon \), \({\forall }\) to \(\Box \), and every other primitive character of \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\) to itself. Thus \(\lambda \) is a CW-variance, and the interpreted languages \(\mathsf {ML}\) and \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\) are CW-variants of each other—provided that the model class is restricted to universal models.Footnote 10\(\square \)
There is an obvious strengthening of the notion of CW-variance that can be obtained by requiring of the relevant translations that they be induced by replacement functions that swap primitive symbols of the source language for primitive symbols of the target language (so that single Characters are replaced by single Characters).
Definition 7
(CC-Replacement; CC-Variance; CC-Variant) For \(i\in \{ 0,1\}\), let \(L_i\) be a language over the alphabet \(A_i\). A CC-replacement from \(A_i\) to \(A_{1-i}\) is a function from the former to the latter. A function \(f:L_i\rightarrow L_{1-i}\) is induced by a CC-replacement r from \(A_i\) to \(A_{1-i}\) if, whenever \(c_0,\ldots ,c_n\in A_i\) and the length \(n+1\) string \(c_0\ldots c_n\) is in \(L_i\), \(f(c_0\ldots c_n)\) is the length \(n+1\) string \(r(c_0)\ldots r(c_n)\). An isomorphism f from \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) to \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) is a CC-variance if f is induced by a CC-replacement, and its inverse \(f^{-1}\) is also induced by a CC-replacement. The interpreted languages \((L_0,(\llbracket {\cdot }\rrbracket ^0_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) and \((L_1,(\llbracket {\cdot }\rrbracket ^1_{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) are CC-variants if there exists a CC-variance from the former to the latter.\(\square \)
Example 7
Let \(\rho \) be the function from \({\mathsf {PL}}_{\lnot ,\wedge }\) to \( {\mathsf {PL}}_{\thicksim , \& }\) that is induced by the CC-replacement mapping every primitive symbol of \({\mathsf {PL}}_{\lnot ,\wedge }\) except \(\lnot \) and \(\wedge \) to itself, \(\lnot \) to \(\thicksim \), and \(\wedge \) to&. The inverse of \(\rho \) is induced by the CC-replacement that maps every primitive symbol of \( {\mathsf {PL}}_{\thicksim , \& }\) except \(\thicksim \) and & to itself, \(\thicksim \) to \(\lnot \), and & to \(\wedge \). Then \(\rho \) is a CC-variance from \(({\mathsf {PL}}_{\lnot ,\wedge },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\) to \( ({\mathsf {PL}}_{\thicksim , \& },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\), and so \(({\mathsf {PL}}_{\lnot ,\wedge },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\) and \( ({\mathsf {PL}}_{\thicksim , \& },(\llbracket {\cdot }\rrbracket _v)_{v\in 2^{\mathsf {S}}})\) are CC-variants.\(\square \)
Remark 9
Obviously every CC-variance is a CW-variance. The converse fails, for (relative to the class of universal models) the translation \(\lambda :\mathsf {ML}\rightarrow 1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\) is a CW-variance (as shown in Example 6) but not a CC-variance. Indeed no function from \(\mathsf {ML}\) to \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\) is induced by a CC-replacement: If \(f:\mathsf {ML}\rightarrow 1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\) were induced by the CC-replacement r, \(f(p) = r(p)\) would have to be a \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\)-formula consisting of a single character; but no such \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\)-formulas exist.\(\square \)
3 Boxes Versus Quantifiers: Arbitrary Accessibility Relations
3.1 The Basic Modal Language
Once we permit models with non-universal accessibility relations, the functions \(\lambda \) and \(\mu \) between \(\mathsf {ML}\) and \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\) defined in Example 6 are no longer translations: They match \(\Box p\) with \({\forall }{\mathsf {v}_{0}}p{\mathsf {v}_{0}}\), but the former will be true at w just in case p is true at all worlds accessible from w, whereas the latter will be satisfied by the assignment of w to \({\mathsf {v}_{0}}\) just in case \(p{\mathsf {v}_{0}}\) is satisfied by all assignments (not just those that map \({\mathsf {v}_{0}}\) to a world accessible from w).
In this section we will see that even relative to the class of all possible-world models it is possible to identify a bona fide first-order, monadic language whose one-variable fragment is a CW-variant of \(\mathsf {ML}\). Before we turn to this task, let us briefly recall a folklore result, if only to realize that it does not help in the search for a first-order language that is CW-variant with \(\mathsf {ML}\).
Let \(1{\mathsf {QL}}R\) be the extension of \(1{\mathsf {QL}}\) by a single two-place predicate symbol R, so that its formulas are given by \({\phi }{:}{:=} px\, |\, Rxy\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, {\forall }{x}\phi \), where p ranges over \(\mathsf {S}\), and x and y range over \(\mathsf {Var}\). For any \(\mathsf {ML}\)-formula \(\phi \), define auxiliary translations \(\phi ^{{\mathsf {v}_{0}}}\) and \(\phi ^{{\mathsf {v}_{1}}}\) like so:
-
\(p^{\mathsf {v}_{i}}:= p{\mathsf {v}_{i}}\)
-
\((\lnot \phi )^{\mathsf {v}_{i}}:= \lnot \phi ^{\mathsf {v}_{i}}\)
-
\((\phi \wedge \psi )^{\mathsf {v}_{i}}:= (\phi ^{\mathsf {v}_{i}}\wedge \psi ^{\mathsf {v}_{i}})\)
-
\((\Box \phi )^{\mathsf {v}_{i}} := {\forall }\mathsf {v}_{1-i} (R\mathsf {v}_i \mathsf {v}_{1-i} \!\rightarrow \! ~ \phi ^{\mathsf {v}_{1-i}})\)
The so-called standard translation from \(\mathsf {ML}\) into \(1{\mathsf {QL}}R\) is then the function \({\mathsf {st}}\) that maps each \(\mathsf {ML}\)-formula \(\phi \) to \(\phi ^{{\mathsf {v}_{0}}}\).
Given any object w, let \(\mathbf {w}\) be the constant function on \(\mathsf {Var}\) with value w. Define the semantic value  of a \(1{\mathsf {QL}}R\)-formula \(\phi \) in a model \(\mathfrak {M}= (W, R, (p^{\mathfrak {M}})_{p\in \mathsf {S}})\) to be the function that maps any \(w\in W\) to the local value
of a \(1{\mathsf {QL}}R\)-formula \(\phi \) in a model \(\mathfrak {M}= (W, R, (p^{\mathfrak {M}})_{p\in \mathsf {S}})\) to be the function that maps any \(w\in W\) to the local value  . Then \({\mathsf {st}}\) is indeed a translation from \((\mathsf {ML}, (\llbracket {\cdot }\rrbracket _{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) to
. Then \({\mathsf {st}}\) is indeed a translation from \((\mathsf {ML}, (\llbracket {\cdot }\rrbracket _{\mathfrak {M}})_{\mathfrak {M}\in \mathbf {M}})\) to  , where \(\mathbf{M} \) is the class of all models. Since \({\mathsf {st}}\) is injective, it follows that \(\mathsf {ML}\) is bi-translatable with the range of the standard translation.
, where \(\mathbf{M} \) is the class of all models. Since \({\mathsf {st}}\) is injective, it follows that \(\mathsf {ML}\) is bi-translatable with the range of the standard translation.
That, however, is about as much as we can get out of the standard translation, for it is clearly not an isomorphism, since it is not compositional: Suppose there were a \(1{\mathsf {QL}}R\)-formula context \(\chi (\cdot )\) such that \({\forall }{\mathsf {v}_{1}}\,(R{\mathsf {v}_{0}}{\mathsf {v}_{1}}\rightarrow p{\mathsf {v}_{1}}) = {\mathsf {st}}(\Box p) = \chi ({\mathsf {st}}(p)) = \chi (p{\mathsf {v}_{0}})\). Then, since \(p{\mathsf {v}_{0}}\) does not occur in \({\forall }{\mathsf {v}_{1}}\,(R{\mathsf {v}_{0}}{\mathsf {v}_{1}}\rightarrow p{\mathsf {v}_{1}})\), \(\chi (\cdot )\) would have to be \({\forall }{\mathsf {v}_{1}}\,(R{\mathsf {v}_{0}}{\mathsf {v}_{1}}\rightarrow p{\mathsf {v}_{1}})\) itself—a context with no gap. But then \({\mathsf {st}}(\Box \Box p) = {\forall }{\mathsf {v}_{1}}\,(R{\mathsf {v}_{0}}{\mathsf {v}_{1}}\rightarrow {\forall }{\mathsf {v}_{0}}\, (R{\mathsf {v}_{1}}{\mathsf {v}_{0}}\rightarrow p{\mathsf {v}_{0}}))\) would have to be \(\chi ({\mathsf {st}}(\Box p))\), i.e. just \({\forall }{\mathsf {v}_{1}}\, ({\mathsf {v}_{0}}R{\mathsf {v}_{1}}\rightarrow p{\mathsf {v}_{1}})\), contradiction.Footnote 11
Moreover, the range of the standard translation is not freely generated from any subset of the \(1{\mathsf {QL}}R\)-atoms by any subset of the primitive \(1{\mathsf {QL}}R\)-operations, i.e. not a well-behaved fragment of \(1{\mathsf {QL}}R\). This follows immediately from the fact that the range of \({\mathsf {st}}\) is not closed under the subformula-relation of \(1{\mathsf {QL}}R\): While the formula \({\forall }{\mathsf {v}_{1}}\,(R{\mathsf {v}_{0}}{\mathsf {v}_{1}}\,{\rightarrow }\,p{\mathsf {v}_{1}}) = {\mathsf {st}}(\Box p)\) is in the range, its \(1{\mathsf {QL}}R\)-subformulas \(R{\mathsf {v}_{0}}{\mathsf {v}_{1}}\), \(p{\mathsf {v}_{1}}\), and \((R{\mathsf {v}_{0}}{\mathsf {v}_{1}}\,{\rightarrow }\,p{\mathsf {v}_{1}})\) are not.
Nor is \({\mathsf {st}}\) induced by a CW-replacement: Suppose that \({\mathsf {st}}\) were induced by such a replacement function r. Then we would have \(p{\mathsf {v}_{0}}= {\mathsf {st}}(p) = r(p)\), and the formula \({\forall }{\mathsf {v}_{1}}\, (R{\mathsf {v}_{0}}{\mathsf {v}_{1}}\,{\rightarrow }\,p{\mathsf {v}_{1}}) = {\mathsf {st}}(\Box p)\) would have to be the concatenation of \(r(\Box )\) and r(p), i.e. of \(r(\Box )\) and \(p{\mathsf {v}_{0}}\). This is clearly not the case.
So the standard translation merely shows \(\mathsf {ML}\) to be bi-translatable with a subset of \(1{\mathsf {QL}}R\) that does not present itself, in any natural way, as a sublanguage of \(1{\mathsf {QL}}R\) in its own right. This is of no help to us.Footnote 12
But now consider the language \(1{\mathsf {QL}}^R\), which is very similar to \(1{\mathsf {QL}}\) except for the unusual syntax of its quantifier. Its formulas are given by \({\phi }{:}{:=} px\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, {\forall }yx\phi \), where p ranges over \(\mathsf {S}\) and x and y range over \(\mathsf {Var}\).
Call expressions of the form \({\forall }yx\) accessibility quantifiers.Footnote 13
The \(1{\mathsf {QL}}^R\)-formulas are interpreted in models \(\mathfrak {M}= (W, R, (p^{\mathfrak {M}})_{p\in \mathsf {S}})\), understood as first-order structures for \(1{\mathsf {QL}}\) equipped with an additional relation \(R\subseteq W\times W\); call such structures accessibility structures.Footnote 14 The local value  of a \(1{\mathsf {QL}}^R\)-formula \(\phi \) in such a structure \(\mathfrak {M}\) relative to a variable assignment g is defined recursively much as one would expect. The only noteworthy clause is the one for the new quantifier:Footnote 15
of a \(1{\mathsf {QL}}^R\)-formula \(\phi \) in such a structure \(\mathfrak {M}\) relative to a variable assignment g is defined recursively much as one would expect. The only noteworthy clause is the one for the new quantifier:Footnote 15

So g satisfies \({\forall }yx\phi \) in \(\mathfrak {M}\) just in case for every w accessible from g(y), the x-variant \(g[x:=w]\) of g satisfies \(\phi \) in \(\mathfrak {M}\).Footnote 16 It follows that we may define the set \(\mathsf {FV}(\phi )\) of variables occurring free in an \(1{\mathsf {QL}}^R\)-formula \(\phi \) recursively as follows: \(\mathsf {FV}(px) = \{ x\}\); \(\mathsf {FV}(\lnot \phi ) = \mathsf {FV}(\phi )\); \(\mathsf {FV}((\phi \rightarrow \psi )) = \mathsf {FV}(\phi )\cup \mathsf {FV}(\psi )\); \(\mathsf {FV}({\forall }yx\phi ) = (\mathsf {FV}(\phi ){\setminus } \{ x\}) \cup \{ y\}\). Thus in \({\forall }yx\phi \), the leading accessibility quantifier binds any free occurrences of x in \(\phi \) but introduces a new free occurrence of y.
The accessibility quantifier may initially seem to be nothing but a restricted quantifier, with \(\forall yx \phi \) simply a fancy notation for \({\forall }{x} (Ryx \rightarrow \phi )\). That would be a misconstrual. In the case where x and y are the same variable, the standard restricted quantifier \({\forall }{x} (Rxx \rightarrow \phi )\) overwrites the value of x everywhere whereas \(\forall xx \phi \) does not overwrite the value of the first displayed occurrence of x. As a consequence, relative to an assignment g, \(\forall xx \phi \) generalizes over all points accessible from g(x), whereas \({\forall }{x} (Rxx \rightarrow \phi )\) ends up generalizing over self-accessible points. This difference is crucial for the modal language’s translatability into the one-variable fragment of the first-order language \(1{\mathsf {QL}}^R\).
For let \(1{\mathsf {QL}}^R_{{\mathsf {v}_{0}}}\) be the \({\mathsf {v}_{0}}\)-fragment of \(1{\mathsf {QL}}^R\). With only one variable in the language, we may again write  instead of
instead of  , construing w as the g-value of the language’s sole variable. We then have that \((\mathsf {ML}, \llbracket {\cdot }\rrbracket _{\mathfrak {M}})\) and
, construing w as the g-value of the language’s sole variable. We then have that \((\mathsf {ML}, \llbracket {\cdot }\rrbracket _{\mathfrak {M}})\) and  are CW-variants: The translation from \(\mathsf {ML}\) to \(1{\mathsf {QL}}^R_{{\mathsf {v}_{0}}}\) is induced by the CW-replacement that maps \(\Box \) to \({\forall }{\mathsf {v}_{0}}{\mathsf {v}_{0}}\), sentence letters p to \(p{\mathsf {v}_{0}}\), and every other primitive symbol of \(\mathsf {ML}\) to itself. Its inverse is induced by the CW-replacement that maps \({\mathsf {v}_{0}}\) to \(\epsilon \), \({\forall }\) to \(\Box \), and every other primitive symbol of \(1{\mathsf {QL}}^R_{{\mathsf {v}_{0}}}\) to itself. Thus, in the general setting too, we have found a monadic first-order language, viz. \(1{\mathsf {QL}}^R_{{\mathsf {v}_{0}}}\), of which the modal operator language \(\mathsf {ML}\) is a CW-variant.
are CW-variants: The translation from \(\mathsf {ML}\) to \(1{\mathsf {QL}}^R_{{\mathsf {v}_{0}}}\) is induced by the CW-replacement that maps \(\Box \) to \({\forall }{\mathsf {v}_{0}}{\mathsf {v}_{0}}\), sentence letters p to \(p{\mathsf {v}_{0}}\), and every other primitive symbol of \(\mathsf {ML}\) to itself. Its inverse is induced by the CW-replacement that maps \({\mathsf {v}_{0}}\) to \(\epsilon \), \({\forall }\) to \(\Box \), and every other primitive symbol of \(1{\mathsf {QL}}^R_{{\mathsf {v}_{0}}}\) to itself. Thus, in the general setting too, we have found a monadic first-order language, viz. \(1{\mathsf {QL}}^R_{{\mathsf {v}_{0}}}\), of which the modal operator language \(\mathsf {ML}\) is a CW-variant.
To be sure, the accessibility quantifiers are not the standard first-order quantifiers, but they are in a precise sense generalizations of them: The class of standard first-order structures for a given signature can be construed as that subclass of the accessibility structures for the same signature in which the accessibility relation is universal. Over this subclass, the accessibility quantifiers coincide with the standard quantifiers. In this sense the CW-variance of Example 6 is a special case of our general result.
3.2 Temporal Language
The CW-variance established in the previous section generalizes easily to polymodal languages, as long as the first-order language is given a separate accessibility quantifier \({\forall }^i yx\) for each of the accessibility relations \(R_i\).Footnote 17 As a case in point, we will look briefly at the bi-modal language \(\mathsf {TL}\) of propositional tense logic.
The syntax of \(\mathsf {TL}\) is given by \({\phi }{:}{:=} p\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, {\mathsf {H}}\phi \, |\, {\mathsf {G}}\phi \). The models for \(\mathsf {TL}\) are the possible-world models \(\mathfrak {M}= (W, R, {(p^{\mathfrak {M}})_{p\in {\mathsf {S}}}})\) for \(\mathsf {ML}\). Of course, in the context of \({\mathsf {TL}}\) one usually speaks of the members of W not as worlds but as times, and notates the accessibility relation as < rather than R.
The local value \(\llbracket {\phi }\rrbracket ^w_{\mathfrak {M}}\in \{ 0,1\}\) of a \({\mathsf {TL}}\)-formula \(\phi \) at a time w in a model \(\mathfrak {M}= (W, <, {(p^{\mathfrak {M}})_{p\in {\mathsf {S}}}})\) is defined by recursion on \(\phi \) in the familiar way:
-
\(\llbracket {p}\rrbracket ^w_{\mathfrak {M}} = 1\) if \(w\in p^{\mathfrak {M}}\)
-
\(\llbracket {\lnot \phi }\rrbracket ^w_{\mathfrak {M}} = 1-\llbracket {\phi }\rrbracket ^w_{\mathfrak {M}}\)
-
\(\llbracket {(\phi \rightarrow \psi )}\rrbracket ^w_{\mathfrak {M}} = \max \{ 1-\llbracket {\phi }\rrbracket ^w_{\mathfrak {M}}, \llbracket {\psi }\rrbracket ^w_{\mathfrak {M}}\}\)
-
\(\llbracket {{\mathsf {H}}\phi }\rrbracket ^w_{\mathfrak {M}} = \min \{ \llbracket {\phi }\rrbracket _{\mathfrak {M}}^v\, |\, v<w \}\)
-
\(\llbracket {{\mathsf {G}}\phi }\rrbracket ^w_{\mathfrak {M}} = \min \{ \llbracket {\phi }\rrbracket _{\mathfrak {M}}^v\, |\, v>w \}\)
Let \(\mathfrak {T}\) be the first-order language whose primitive symbols are the variables, the parentheses, the members of \(\mathsf {S}\) qua one-place predicate symbols, \(\lnot \) and \(\rightarrow \), the retrograde accessibility quantifier \(\underline{{\forall }}\) and the forward-looking accessibility quantifier \(\overline{{\forall }}\). The \(\mathfrak {T}\)-formulas are given by \({\phi }{:}{:=} px\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, \underline{{\forall }}yx\phi \, |\, \overline{{\forall }}yx\phi \), where p ranges over \(\mathsf {S}\) and x and y range over \(\mathsf {Var}\).Footnote 18
The local value  of a \(\mathfrak {T}\)-formula \(\phi \) in a model \(\mathfrak {M}\) relative to a variable assignment g is defined recursively, the interesting clauses being those for \(\underline{{\forall }}\) and \(\overline{{\forall }}\):
of a \(\mathfrak {T}\)-formula \(\phi \) in a model \(\mathfrak {M}\) relative to a variable assignment g is defined recursively, the interesting clauses being those for \(\underline{{\forall }}\) and \(\overline{{\forall }}\):
The one-variable fragment \(\mathfrak {T}_{{\mathsf {v}_{0}}}\) of \(\mathfrak {T}\) is a CW-variant of \({\mathsf {TL}}\), since the function \(\mathscr {T}\) from \({\mathsf {TL}}\) to \(\mathfrak {T}_{{\mathsf {v}_{0}}}\) that is induced by the CW-replacement mapping sentence letters p to \(p{\mathsf {v}_{0}}\), the retrograde temporal operator \({\mathsf {H}}\) to \(\underline{{\forall }}{\mathsf {v}_{0}}{\mathsf {v}_{0}}\), the forward-looking temporal operator \({\mathsf {G}}\) to \(\overline{{\forall }}{\mathsf {v}_{0}}{\mathsf {v}_{0}}\), and every other primitive symbol to itself, is a CW-variance (its inverse is induced by the CW-replacement that maps \({\mathsf {v}_{0}}\) to \(\epsilon \), \(\underline{{\forall }}\) to \({\mathsf {H}}\), \(\overline{{\forall }}\) to \({\mathsf {G}}\), and every other primitive symbol to itself).
3.3 Quantified Modal Logic
For each \(n\ge 1\), let \(\mathscr {P}^n\) be a (possibly empty) set of n-ary predicate symbols, and let \(\mathscr {P}\) be the union of the \(\mathscr {P}^n\). Let \(\mathscr {C}\) be a (possibly empty) set of individual constants. Let \(\Sigma \) be the signature \((\mathscr {P},\mathscr {C})\). Then the primitive symbols of the language \(\mathsf {QML}_{\Sigma }\) of quantified modal logic over \(\Sigma \) are the members of \(\mathscr {P}\) and \(\mathscr {C}\), the members of the countably infinite set \({\mathsf {Z}} = \{ {\mathsf {z}}_0, {\mathsf {z}}_1, {\mathsf {z}}_2, \ldots \}\) of individual variables, the propositional connectives \(\lnot \) and \(\rightarrow \), the necessity operator \(\Box \), the actualist individual quantifier \({\forall }\), the possibilist individual quantifier \(\Pi \), as well as opening and closing parentheses.Footnote 19 The \(\mathsf {QML}_{\Sigma }\)-terms are the members of \(\mathscr {C}\cup \mathsf {Z}\). The \(\mathsf {QML}_{\Sigma }\)-formulas are generated inductively as follows: Whenever \(P\in \mathscr {P}^n\) and \(t_1,\ldots ,t_n\) are \(\mathsf {QML}_{\Sigma }\)-terms, \(Pt_1\ldots t_n\) is an atomic \(\mathsf {QML}_{\Sigma }\)-formula. Whenever \(\phi \) and \(\psi \) are \(\mathsf {QML}_{\Sigma }\)-formulas and \(r\in \mathsf {Z}\), all of \(\lnot \phi \), \((\phi \rightarrow \psi )\), \(\Box \phi \), \({\forall }r\phi \), and \(\Pi r\phi \) are \(\mathsf {QML}_{\Sigma }\)-formulas.
A model for \(\mathsf {QML}_{\Sigma }\) is a quintuple \(\mathfrak {M}= (W, (D_w)_{w\in W}, R, (P^{\mathfrak {M}})_{P\in \mathscr {P}}, (c^{\mathfrak {M}})_{c\in \mathscr {C}})\), where \(W\ne \emptyset \) is called the set of worlds, \((D_w)_{w\in W}\) is a W-indexed family of sets \(D_w\), not all of which are empty (so that the union D of all the \(D_w\) is non-empty), \(R\subseteq W\times W\) is the accessibility relation, for each \(P\in \mathscr {P}^n\), \(P^{\mathfrak {M}}\) maps worlds to subsets of \(D^n\), and \((c^{\mathfrak {M}})_{c\in \mathscr {C}}\) is a \(\mathscr {C}\)-indexed family of members \(c^{\mathfrak {M}}\) of the union D of all the \(D_w\). An individual variable assignment in such a model \(\mathfrak {M}\) is a function \(g:\mathsf {Z}\rightarrow D\).
The local value \(\llbracket {t}\rrbracket ^{w,g}_{\mathfrak {M}}\) of a \(\mathsf {QML}_{\Sigma }\)-term t relative to a world w, an individual variable assignment g and a model \(\mathfrak {M}\) is \(c^{\mathfrak {M}}\), if t is a constant symbol c, and is g(r), if t is an individual variable r. The local value \(\llbracket {\phi }\rrbracket ^{w,g}_{\mathfrak {M}}\in \{0,1\}\) of a \(\mathsf {QML}_{\Sigma }\)-formula \(\phi \) relative to a world w, an individual variable assignment g, and a model \(\mathfrak {M}\), is defined by recursion on \(\phi \) as follows.
-
\(\llbracket {Pt_1\ldots t_n}\rrbracket ^{w,g}_{\mathfrak {M}} = 1\) if \(\langle \llbracket {t_1}\rrbracket ^{w,g}_{\mathfrak {M}},\ldots ,\llbracket {t_n}\rrbracket ^{w,g}_{\mathfrak {M}}\rangle \in P^{\mathfrak {M}}(w)\)
-
\(\llbracket {\lnot \phi }\rrbracket ^{w,g}_{\mathfrak {M}} = 1-\llbracket {\phi }\rrbracket ^{w,g}_{\mathfrak {M}}\)
-
\(\llbracket {(\phi \rightarrow \psi )}\rrbracket ^{w,g}_{\mathfrak {M}} = \max \{ 1-\llbracket {\phi }\rrbracket ^{w,g}_{\mathfrak {M}}, \llbracket {\psi }\rrbracket ^{w,g}_{\mathfrak {M}}\}\)
-
\(\llbracket {\Box \phi }\rrbracket ^{w,g}_{\mathfrak {M}} = \min \{ \llbracket {\phi }\rrbracket ^{v,g}_{\mathfrak {M}} \, |\, wRv\}\)
-
\(\llbracket {{\forall }r\phi }\rrbracket ^{w,g}_{\mathfrak {M}} = \min \{ \llbracket {\phi }\rrbracket _{\mathfrak {M}}^{w,g[r:=o]}\, |\, o\in D_w\}\)
-
\(\llbracket {\Pi r\phi }\rrbracket ^{w,g}_{\mathfrak {M}} = \min \{ \llbracket {\phi }\rrbracket _{\mathfrak {M}}^{w,g[r:=o]}\, |\, o\in D\}\)
The two-sorted first-order language \(\mathfrak {Q}_{\Sigma }\) is based on the sorts \({\mathsf {i}}\) (individuals) and \({\mathsf {w}}\) (worlds). Its primitive symbols are:
-
the members of the set \(\mathsf {Z}\) of individual variables, which are of sort \({\mathsf {i}}\)
-
the members of the set \(\mathsf {Var}\) of world variables, which are of sort \({\mathsf {w}}\)
-
for each \(n\ge 1\), the members of the set \(\mathscr {P}^n\), but construed as \(n+1\)-ary rather than n-ary predicate symbols, where the first argument place of \(P\in \mathscr {P}^n\) is of sort \({\mathsf {w}}\) and the next n places are of sort \({\mathsf {i}}\)
-
the members of the set \(\mathscr {C}\), which are of sort \({\mathsf {i}}\)
-
the propositional connectives \(\lnot \) and \(\rightarrow \)
-
the actualist individual quantifier \({\forall }^{\mathsf {i}}\)
-
the possibilist individual quantifier \(\Pi ^{\mathsf {i}}\)
-
the accessibility quantifier \({\forall }^{\mathsf {w}}\)
-
opening and closing parentheses
The \(\mathfrak {Q}_{\Sigma }\)-terms of sort \({\mathsf {i}}\) are the members of \(\mathsf {Z}\cup \mathscr {C}\); the \(\mathfrak {Q}_{\Sigma }\)-terms of sort \({\mathsf {w}}\) are the members of \(\mathsf {Var}\). Whenever \(P\in \mathscr {P}^n\), \(x\in \mathsf {Var}\), and \(t_1,\ldots ,t_n\) are \(\mathfrak {Q}_{\Sigma }\)-terms of individual sort, \(Pxt_1\ldots t_n\) is an atomic \(\mathfrak {Q}_{\Sigma }\)-formula. Compound \(\mathfrak {Q}_{\Sigma }\)-formulas are generated by way of negation and the conditional, as well as the following formation rules for the various quantifiers:
-
Whenever \(\phi \) is a \(\mathfrak {Q}_{\Sigma }\)-formula, \(x\in \mathsf {Var}\), and \(r\in \mathsf {Z}\), \({\forall }^{\mathsf {i}}xr\phi \) is a \(\mathfrak {Q}_{\Sigma }\)-formula.
-
Whenever \(\phi \) is a \(\mathfrak {Q}_{\Sigma }\)-formula and \(r\in \mathsf {Z}\), \(\Pi ^{\mathsf {i}}r\phi \) is a \(\mathfrak {Q}_{\Sigma }\)-formula.
-
Whenever \(\phi \) is a \(\mathfrak {Q}_{\Sigma }\)-formula and \(x, y\in \mathsf {Var}\), \({\forall }^{\mathsf {w}} yx\phi \) is a \(\mathfrak {Q}_{\Sigma }\)-formula.
The local value  of a \(\mathfrak {Q}_{\Sigma }\)-term t relative to a model \(\mathfrak {M}= (W, (D_w)_{w\in W}, R\), \((P^{\mathfrak {M}})_{P\in \mathscr {P}}, (c^{\mathfrak {M}})_{c\in \mathscr {C}})\), an individual variable assignment g, and a world variable assignment \(\omega : \mathsf {Var}\rightarrow W\), is \(c^{\mathfrak {M}}\) if t is the individual constant \(c\in \mathscr {C}\), is g(z) if t is the individual variable z, and is \(\omega (x)\) if t is the world variable x. The local value
of a \(\mathfrak {Q}_{\Sigma }\)-term t relative to a model \(\mathfrak {M}= (W, (D_w)_{w\in W}, R\), \((P^{\mathfrak {M}})_{P\in \mathscr {P}}, (c^{\mathfrak {M}})_{c\in \mathscr {C}})\), an individual variable assignment g, and a world variable assignment \(\omega : \mathsf {Var}\rightarrow W\), is \(c^{\mathfrak {M}}\) if t is the individual constant \(c\in \mathscr {C}\), is g(z) if t is the individual variable z, and is \(\omega (x)\) if t is the world variable x. The local value  of a \(\mathfrak {Q}_{\Sigma }\)-formula \(\phi \) relative to g, \(\omega \), and \(\mathfrak {M}\) is defined by recursion on \(\phi \) as follows.Footnote 20
of a \(\mathfrak {Q}_{\Sigma }\)-formula \(\phi \) relative to g, \(\omega \), and \(\mathfrak {M}\) is defined by recursion on \(\phi \) as follows.Footnote 20
-
 if
if 
-

-

-

-

-

Now let \(\mathfrak {Q}^{{\mathsf {v}_{0}}}_{\Sigma }\) be the one-variable fragment of \(\mathfrak {Q}_{\Sigma }\), and let \(\mathfrak {q}:\mathsf {QML}_{\Sigma }\rightarrow \mathfrak {Q}^{{\mathsf {v}_{0}}}_{\Sigma }\) be the function induced by the CW-replacement that maps \(P\in \mathscr {P}^n\) to \(P{\mathsf {v}_{0}}\), \(\Box \) to \({\forall }^{\mathsf {w}}{\mathsf {v}_{0}}{\mathsf {v}_{0}}\), \({\forall }\) to \({\forall }^{\mathsf {i}}{\mathsf {v}_{0}}\), \(\Pi \) to \(\Pi ^{\mathsf {i}}\), and all other primitive symbols of \(\mathsf {QML}_{\Sigma }\) to themselves. Then \(\mathfrak {q}\) is a CW-variance, its inverse being induced by the CW-replacement that maps \({\mathsf {v}_{0}}\) to \(\epsilon \), \({\forall }^{\mathsf {i}}\) to \({\forall }\), \(\Pi ^{\mathsf {i}}\) to \(\Pi \), \({\forall }^{\mathsf {w}}\) to \(\Box \), and all other primitive \(\mathfrak {Q}_{\Sigma }\)-symbols to themselves.Footnote 21
3.4 Actuality
In this section we consider the generalization of our CW-variance result to the propositional modal language augmented with the actuality operator.
The language \(\mathsf {AML}\) of actuality modal logic is the language \(\mathsf {ML}\) extended by a single one-place operator \(\mathsf {A}\), the actuality operator, and therefore has the additional formation rule that \(\mathsf {A}\) may be prefixed to any \(\mathsf {AML}\)-formula: \({\phi }{:}{:=} p\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, \Box \phi \, |\, \mathsf {A}\phi \). These formulas are interpreted in “pointed” models, which are quadruples \(\mathfrak {M}= (W,{a^{\mathfrak {M}}}, R, {(p^{\mathfrak {M}})_{p\in {\mathsf {S}}}})\), where \((W,R,{(p^{\mathfrak {M}})_{p\in {\mathsf {S}}}})\) is a model in our original sense, and \({a^{\mathfrak {M}}}\) is a distinguished member of W (the “actual world” of \(\mathfrak {M}\)). The recursive clauses defining local values at worlds in pointed models are as for \(\mathsf {ML}\), with the addition of a clause for formulas governed by \(\mathsf {A}\): \(\llbracket {\mathsf {A}\phi }\rrbracket ^w_{\mathfrak {M}} = \llbracket {\phi }\rrbracket ^{{a^{\mathfrak {M}}}}_{\mathfrak {M}}\); in other words, \(\mathsf {A}\phi \) is true at w just in case \(\phi \) is true at \({a^{\mathfrak {M}}}\), the actual world of \(\mathfrak {M}\).Footnote 22
Let \(1{\mathsf {QL}}\mathbb {A}^R\) be the extension of \(1{\mathsf {QL}}^R\) by a quantifier symbol \(\mathbb {A}\) that denotes, in each model \(\mathfrak {M}= (W,{a^{\mathfrak {M}}}, R, {(p^{\mathfrak {M}})_{p\in {\mathsf {S}}}})\), the generalized quantifier \(\{ X\subseteq W\, |\, {a^{\mathfrak {M}}}\in X\}\); in other words, \(\mathbb {A}\) stands for the Montagovian individual obtained by type-lifting \({a^{\mathfrak {M}}}\) from type e to type \(\langle \langle e,t\rangle , t\rangle \).Footnote 23
The \(L^{\mathbb {A}}\)-formulas are, accordingly, given by \({\phi }{:}{:=} px\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, {\forall }yx\phi \, |\, \mathbb {A}x\phi \), where p ranges over \(\mathsf {S}\) and x and y range over \(\mathsf {Var}\). The semantic clause for the new quantifier symbol \(\mathbb {A}\) reads:

which, as mentioned, just means that the interpretation of \(\mathbb {A}\) is the distinguished world \({a^{\mathfrak {M}}}\), lifted to quantifier type.
Now let \(1{\mathsf {QL}}\mathbb {A}^R_{{\mathsf {v}_{0}}}\) be the one-variable fragment of \(1{\mathsf {QL}}\mathbb {A}^R\). Then \(\mathsf {AML}\) is a CW-variant of \(1{\mathsf {QL}}\mathbb {A}^R_{{\mathsf {v}_{0}}}\) via the translations induced by the CW-replacements defined in the previous section, supplemented by the following clauses for \(\mathsf {A}\) and \(\mathbb {A}\), respectively:
-
The CW-replacement for the translation \(\mathsf {AML}\rightarrow 1{\mathsf {QL}}\mathbb {A}^R_{{\mathsf {v}_{0}}}\) maps \(\mathsf {A}\) to \(\mathbb {A}{\mathsf {v}_{0}}\).
-
The CW-replacement for the translation \(1{\mathsf {QL}}\mathbb {A}^R_{{\mathsf {v}_{0}}}\rightarrow \mathsf {AML}\) maps \(\mathbb {A}\) to \(\mathsf {A}\) (and of course still maps \({\mathsf {v}_{0}}\) to \(\epsilon \)).
We thus translate from \(\mathsf {AML}\) to \(1{\mathsf {QL}}\mathbb {A}^R_{{\mathsf {v}_{0}}}\) by appending \({\mathsf {v}_{0}}\) to every sentence letter and replacing sans-serif \(\mathsf {A}\) with \(\mathbb {A}{\mathsf {v}_{0}}\) and \(\Box \) with \({\forall }{\mathsf {v}_{0}}{\mathsf {v}_{0}}\). Conversely, we translate from \(1{\mathsf {QL}}\mathbb {A}^R_{{\mathsf {v}_{0}}}\) to \(\mathsf {AML}\) by switching every \({\forall }\) to \(\Box \), every \(\mathbb {A}\) to \(\mathsf {A}\), and deleting every \({\mathsf {v}_{0}}\).Footnote 24
4 Conclusion
We’ve isolated seven levels of language equivalence that are strictly weaker than literal identity; and for each of these levels we’ve found pairs of languages that are semantically equivalent at that level but not at a higher one. The results of our investigation can be summed up in the following table, which lists the equivalence notions in order of strictly ascending strictness:
Equivalence relation | Representative pair |
|---|---|
Bi-translatability | \(1{\mathsf {QL}}_{\delta }\) versus \(1{\mathsf {QL}}_{\Delta }\) |
Definitional equivalence | \({\mathsf {PL}}_{\lnot ,\wedge }\) versus \({\mathsf {PL}}_{\lnot ,\vee }\) |
Homomorphic bi-translatability | \({\mathsf {PL}}_{\lnot ,\wedge }\) versus \( {\mathsf {PL}}_{\lnot ,\wedge , \& }\) |
Isomorphism | \({\mathsf {PL}}_{\lnot ,\wedge }\) versus \({\mathsf {PPL}}_{\lnot ,\wedge }\) |
WW-variance | \(1{\mathsf {QL}}\) versus \(1{\mathsf {QL}}^{*}\) |
CW-variance | \(\mathsf {ML}\) versus \(1{\mathsf {QL}}_{{\mathsf {v}_{0}}}\) |
CC-variance | \({\mathsf {PL}}_{\lnot ,\wedge }\) versus \( {\mathsf {PL}}_{\thicksim , \& }\) |
I’ve deliberately chosen more or less neutral terms for these various equivalence relations so as not to intermingle, in the main body of the paper, purely technical observations with philosophical judgments. This concluding section, however, would seem to be an appropriate place to reflect on the intuitive significance of these equivalence relations, and tentatively to propose a more memorable nomenclature.
Let us begin with CC-variance. CC-variant languages differ at most in trivial ways, namely in the shapes of the primitive symbols they employ (think English written in lower-case letters versus English written in upper-case letters). These are such uninteresting differences that some logic textbooks don’t even bother to define languages more specifically than up to CC-variance (see e.g. Bell and Machover 1977, 8). It therefore seems appropriate to propose the more intuitive term trivial notational variance for CC-variance.
At the next level down there is CW-variance, which might also be called strict or, more descriptively, typographical notational variance. This designation seems apt because one can enable an agent to translate a language into a CW-variant by simply reprogramming the keys of their keyboard according to the relevant CW-replacement.Footnote 25 In our hierarchy, typographical notational variance would be the strictest non-trivial notion of notational variance.
Taking another step down the hierarchy, we have WW-variance, to which we might refer as linear notational variance since, in contradistinction to mere isomorphism (compare the case of \({\mathsf {PL}}_{\lnot ,\wedge }\) and \({\mathsf {PPL}}_{\lnot ,\wedge }\)), no re-arranging of elements of the strings can occur. It should be noted that, unlike typographical notational variance and trivial notational variance, linear notational variance requires some parsing of the input string, if only into linear, contiguous segments.
This conveniently leaves the unqualified notational variance as an alternative term for what we’ve been calling language isomorphism. Our paradigmatic cases of the isomorphic languages \({\mathsf {PL}}_{\lnot ,\wedge }\) and \({\mathsf {PPL}}_{\lnot ,\wedge }\) on the one hand, and the merely homomorphically bi-translatable languages \({\mathsf {PL}}_{\lnot ,\wedge }\) and \( {\mathsf {PL}}_{\lnot ,\wedge , \& }\) makes this usage plausible: Whether one employs ordinary, parenthesis-based notation or Polish notation is indeed a purely notational, non-substantive matter. On the other hand, a language like \( {\mathsf {PL}}_{\lnot ,\wedge , \& }\) that contains distinct but synonymous primitives differs not just notationally from the result of excising this synonymy, \({\mathsf {PL}}_{\lnot ,\wedge }\); the languages have distinct conceptual structures, one containing a redundancy, the other not.
That talk of notational variance is inappropriate in the case of the definitionally equivalent languages \({\mathsf {PL}}_{\lnot ,\wedge }\) and \({\mathsf {PL}}_{\lnot ,\vee }\) is, I take it, even less controversial, since the adequacy of the target language definitions rests on De Morgan’s laws, substantive principles of classical logic rather than merely conventional, notational choices.
In light of the fact that, in these latter cases, more than notation is at stake, it might make sense to use terms not containing “notational”, like homomorphic variants and definitional variants, for homomorphically bi-translatable and definitionally equivalent language pairs, respectively. Bi-translatability, finally, seems sufficiently descriptive to warrant adoption as such.Footnote 26
Besides developing the beginnings of a theory of model-focused language equivalence, we considered the special case of the basic modal language \(\mathsf {ML}\). It has been known for a long time that, relative to universal models, \(\mathsf {ML}\) is a typographical notational variant (i.e. a CW-variant) of \(1{\mathsf {QL}}\)’s one-variable fragment. In the general case, where models with arbitrary accessibility relations are permitted, extant techniques do not establish more than mere bi-translatability of \(\mathsf {ML}\) with a subset of \(1{\mathsf {QL}}R\) that is neither freely generated nor closed under subformulas in the sense of \(1{\mathsf {QL}}R\). With the single conceptual innovation of the accessibility quantifier, we were able to exhibit a bona fide first-order, monadic language whose one-variable fragment is likewise a typographical notational variant of \(\mathsf {ML}\). Modal operator language is thus equivalent to explicitly quantificational language in the strictest non-trivial sense of semantic equivalence.
Notes
The way I use the term “interpreted language” (basically: formal language with a model theory) thus differs from another popular usage, where it is assumed that every lexical item of the language in question has one fixed interpretation in a single model.
See Humberstone (2011, 100) for additional discussion.
For the purposes of this paper, we will assume that the relevant algebras are one-sorted and total. A more general approach would allow the algebras to either be many-sorted or partial.
In the abstract model theory literature mentioned in the Introduction, the existence of a translation from \(L_0\) to \(L_1\), given the axiom of choice, amounts to \(L_1\) being at least as strong as \(L_0\) (often written \(L_0 \le L_1\)). Similarly, bi-translatability, defined below, corresponds to \(L_0\) and \(L_1\) being equally strong, \(L_0 \equiv L_1\).
In clause (\(\sigma 2\)) below, \(\sigma (\theta )_x[\delta ]\) is the result of replacing, in \(\sigma (\theta )\), every free occurrence of x with \(\delta \). Note that, in clause (\(\tau 2\)), we pick one particular variable, \({\mathsf {v}_{0}}\).
For our purposes, we can take an n-place \(L_1\)-context to be a non-empty string \(\theta \) over the alphabet \(A_1 \cup \{ *_1,\ldots ,*_n\}\) such that, for any \(\phi _1,\ldots ,\phi _n\in L_1\), the result \(\theta (\phi _1,\ldots ,\phi _n)\) of simultaneously substituting \(\phi _i\) for \(*_i\) in \(\theta \) is an \(L_1\)-formula. We sometimes suggestively write \(\theta (*_1,\ldots ,*_n)\) for such n-place \(L_1\)-contexts \(\theta \).
Atomic faithfulness requires that sentence letters be mapped to sentence letters; translation then requires that each sentence letter be mapped to itself.
Here we are assuming that, in \(1{\mathsf {QL}}\), the string \({\forall }{x}\) is not an atom but consists of two characters, \({\forall }\) and x, and that in \(1{\mathsf {QL}}^{*}\), the string \(({\forall }{x})\) analogously isn’t atomic but consists of four characters.
If for some \(p_{0}\), \(r(p_{0})\) were not \(p_{0}\), it would have to be either \(\epsilon \) or identical to \(p_{0}x\) for every \(x\in \mathsf {Var}\). The latter is plainly impossible. In the former case r(y) would be \(p_{0} y\) for every \(y\in \mathsf {Var}\); but then \(qx = f(qx) = r(q)^{\frown } r(x) = r(q)^{\frown } p_{0} x\) for every \(q\in \mathsf {S}\), which is impossible.
We shall return to the universality constraint in Sect. 3.1.
If we let \( [y|x]\phi \) be the result of switching all occurrences (free and bound) of y and x in \(\phi \), we can define \({\mathsf {st}}\) very simply by means of the clauses \({\mathsf {st}}(p) = p{\mathsf {v}_{0}}\), \({\mathsf {st}}(\lnot \phi ) = \lnot {\mathsf {st}}(\phi )\), \({\mathsf {st}}((\phi \wedge \psi )) = ({\mathsf {st}}(\phi )\wedge {\mathsf {st}}(\psi ))\), and \({\mathsf {st}}(\Box \phi ) = {\forall }{\mathsf {v}_{1}}(R{\mathsf {v}_{0}}{\mathsf {v}_{1}}\rightarrow [{\mathsf {v}_{1}}|{\mathsf {v}_{0}}]{\mathsf {st}}(\phi ))\). It is tempting to conclude that \({\mathsf {st}}\) is compositional after all, the required \(1{\mathsf {QL}}R\)-context for \(\Box \) being \({\forall }{\mathsf {v}_{1}}(R{\mathsf {v}_{0}}{\mathsf {v}_{1}}\rightarrow [{\mathsf {v}_{1}}|{\mathsf {v}_{0}}]*_1)\). Note, however, that the latter is not a \(1{\mathsf {QL}}R\)-context, since [x|y] is not an object-linguistic \(1{\mathsf {QL}}R\)-operator but a metalinguistically defined function on \(1{\mathsf {QL}}R\)-formulas.
This observation should not be taken as criticism of the standard translation. Quite to the contrary, the standard translation is an immensely useful metatheoretical tool, as is evident e.g. from van Benthem’s (1976) characterization theorem, according to which a first-order formula is bisimulation-invariant just in case it is logically equivalent to the standard translation of a modal formula. See also van Benthem (1985) as well as the seminal Andréka et al. (1998), in which it is shown that the range of \({\mathsf {st}}\) is included in the (syntactically well-behaved and decidable) guarded fragment of first-order logic.
For practical purposes, it seems advisable to notate accessibility quantifiers as \({\forall }^y x\) or even \(^y{\forall }{x}\) to avoid confusion with the more familiar meanings “for all y and x” or “for all pairs \(\langle y,x\rangle \)” of the symbol combination \({\forall }yx\). I nevertheless choose the slightly awkward latter notation here simply because superscripts do not sit all that well with the string-theoretic construal of expressions.
Note that unlike in the case of the standard translation, R is not considered to be the interpretation of a relation symbol in the language’s signature.
More generally, in languages whose signatures may include individual constants and function symbols, we would have
 , where \(\llbracket {t}\rrbracket ^g_{\mathfrak {M}}\) is the local value of the term t relative to the assignment g in \(\mathfrak {M}\). Here, of course, \(\llbracket {c}\rrbracket ^g_{\mathfrak {M}}\) is the interpretation \(c^{\mathfrak {M}}\) of c in \(\mathfrak {M}\) if c is a constant symbol, and \(\llbracket {ft_1\ldots t_n}\rrbracket ^g_{\mathfrak {M}}\) is \(f^{\mathfrak {M}}(\llbracket {t_1}\rrbracket ^g_{\mathfrak {M}},\ldots ,\llbracket {t_n}\rrbracket ^g_{\mathfrak {M}})\) for n-place function symbols f and terms \(t_1\), ..., \(t_n\).
, where \(\llbracket {t}\rrbracket ^g_{\mathfrak {M}}\) is the local value of the term t relative to the assignment g in \(\mathfrak {M}\). Here, of course, \(\llbracket {c}\rrbracket ^g_{\mathfrak {M}}\) is the interpretation \(c^{\mathfrak {M}}\) of c in \(\mathfrak {M}\) if c is a constant symbol, and \(\llbracket {ft_1\ldots t_n}\rrbracket ^g_{\mathfrak {M}}\) is \(f^{\mathfrak {M}}(\llbracket {t_1}\rrbracket ^g_{\mathfrak {M}},\ldots ,\llbracket {t_n}\rrbracket ^g_{\mathfrak {M}})\) for n-place function symbols f and terms \(t_1\), ..., \(t_n\).The accessibility quantifier is perhaps not as unusual as it at first seems. Under certain circumstances, free logic’s inner and outer quantifiers \({\forall }^{\mathsf {i}}\) and \({\forall }^{\mathsf {o}}\) can be regarded as instances of accessibility quantifiers: Let a free-logical model \(\mathfrak {M}\) have inner domain \(M_{\mathsf {i}}\) and outer domain \(M_{\mathsf {o}} \supseteq M_{\mathsf {i}}\), and suppose \(c_{\mathsf {i}}^{\mathfrak {M}}\in M_{\mathsf {i}}\) and \(c_{\mathsf {o}}^{\mathfrak {M}}\in M_{\mathsf {o}}{\setminus } M_{\mathsf {i}}\). In \(\mathfrak {M}\), \({\forall }^{\mathsf {i}}\) ranges over \(M_{\mathsf {i}}\) and \({\forall }^{\mathsf {o}}\) ranges over \(M_{\mathsf {o}}\). Recarve \(\mathfrak {M}\) into a model \(\mathfrak {N}\) suitable for interpreting accessibility quantifiers as follows: \(\mathfrak {N}\)’s domain is \(M_{\mathsf {o}}\), and \(R := (\{{c_{\mathsf {i}}}^{\mathfrak {M}}\} \times M_{\mathsf {i}})\cup (\{{c_{\mathsf {o}}}^{\mathfrak {M}}\}\times M_{\mathsf {o}})\). Now the inner quantifier \({\forall }^{\mathsf {i}}x\) is the accessibility quantifier \({\forall }c_{\mathsf {i}}x\) and the outer quantifier \({\forall }^{\mathsf {o}} x\) is \({\forall }c_{\mathsf {o}}x\). Obviously, the standard universal quantifier can similarly be construed as an instance of the accessibility quantifier: Let \(\mathfrak {M}\) be a model and define R as \(M\times M\). Then \({\forall }{x}\) is just \({\forall }{xx}\).
Alternatively: As long as the accessibility quantifier is endowed with an additional parameter i and the semantic clause
 .
.Alternatively, in the spirit of footnote 17, we could have a single accessibility quantifier \({\forall }\) in the lexicon but allow it to take an additional parameter from \(\{ f,b\}\) (mnemonic for “forward” and “backward”) as follows: \({\phi }{:}{:=} px\, |\, \lnot \phi \, |\, (\phi \rightarrow \phi )\, |\, {\forall }iyx\phi \), where i ranges over \(\{ f,b\}\) and \({\forall }fyx\) (resp. \({\forall }byx\)) is given the semantic behavior of \(\overline{{\forall }} yx\) (resp. \(\underline{{\forall }} yx\)).
To be sure, quantified modal languages do not typically contain both actualist and possibilist quantifiers. We include both here just to show that both varieties can be translated in the appropriate fashion.
Note that the \(\mathfrak {Q}_{\Sigma }\)-equivalent \({\forall }^{{\mathsf {i}}}\) of the actualist quantifier \({\forall }\) of \(\mathsf {QML}_{\Sigma }\) naturally presents itself as the accessibility quantifier for the accessibility relation between worlds and individuals that holds between w and o just in case \(o\in D_w\).
It should be noted that some of our equivalence relations are sensitive to quite subtle design decisions. For example, if we had constructed the \(\mathfrak {Q}_{\Sigma }\)-atomic formulas from the \(\mathsf {QML}_{\Sigma }\)-atomic formulas by adding the world argument place after all the individual argument places rather than before, we would not have gotten a CW-variant, and indeed, if \(\mathscr {P}^n\ne \emptyset \) for infinitely many n, not even a WW-variant.
The first appearance of the actuality operator is, as far as I am aware, in Kamp (1971), in the form of the now operator of tense logic. The locus classicus for the modal actuality operator is Crossley and Humberstone (1977). In a propositional environment, the actuality operator is eliminable relative to real-world validity (Hazen et al. 2013), though not relative to general validity. In a quantificational environment, it is not even eliminable relative to real-world validity (Kamp 1971; Hazen 1976; Hodes 1984; Wehmeier 2003).
The possibility of replacing individuals with generalized quantifiers is familiar from Montague semantics; cf. e.g. Dowty et al. (1981: 193). The notation used here resembles more closely the one suggested by Barwise and Cooper (1981: 166). We’ve already encountered this type of quantifier in the shape of \(\Delta \) in Example 1.
Note that, in contradistinction to the languages \(1{\mathsf {QL}}^R\) and \(1{\mathsf {QL}}^R_{{\mathsf {v}_{0}}}\) of the previous section, \(1{\mathsf {QL}}\mathbb {A}^R\) and \(1{\mathsf {QL}}\mathbb {A}^R_{{\mathsf {v}_{0}}}\) do have closed formulas, since \(\mathbb {A}\) can bind variables without at the same time introducing new free occurrences.
To be sure, we would have to allow for macros, i.e. for each single key to be reprogrammed so as to produce a fixed finite string, possibly the empty string, of characters from the target alphabet. If the keys can only be reprogrammed so as to produce a single character from the target alphabet, we end up with CC-variance, or as we now also call it, trivial notational variance.
A reviewer for this journal has pointed out that, while I suggest to draw the line between notational and non-notational variance between homomorphic bi-translatability and language isomorphism, another natural cleavage point is between those equivalence relations that do not invoke string-theoretic structure and those that do, i.e. between language isomorphism and WW-variance. There is no doubt that this latter boundary is theoretically significant; nevertheless my own sense is that it does not coincide with the notational/non-notational divide, given pairs like \({\mathsf {PL}}_{\lnot ,\wedge }\) and \({\mathsf {PPL}}_{\lnot ,\wedge }\).
References
Andréka, H., Németi, I., & van Benthem, J. (1998). Modal languages and bounded fragments of predicate logic. Journal of Philosophical Logic, 27, 217–274.
Barwise, J., & Cooper, R. (1981). Generalized quantifiers and natural language. Linguistics and Philosophy, 4(2), 159–219.
Bell, J. L., & Machover, M. (1977). A course in mathematical logic. Amsterdam: North Holland.
Caleiro, C., & Gonçalves, R. (2007). Equipollent logical systems. In J.-Y. Béziau (Ed.), Logica universalis (pp. 97–109). Basel: Birkhäuser.
Crossley, J. N., & Humberstone, L. (1977). The logic of “actually”. Reports on Mathematical Logic, 8, 11–29.
Dowty, D. R., Wall, R. E., & Peters, S. (1981). Introduction to Montague semantics. Dordrecht: Kluwer.
Ebbinghaus, H.-D. (1985). Extended logics: The general framework. In J. Barwise & S. Feferman (Eds.), Model-theoretic logics (pp. 25–76). New York: Springer.
Epstein, R. (1990). The semantic foundations of logic: Propositional logics. Dordrecht: Kluwer.
Feferman, S. (1974). Two notes on abstract model theory I: Properties invariant on the range of definable relations between structures. Fundamenta Mathematicae, 82, 153–165.
French, R. (2019). Notational variance and its variants. Topoi, 38(2), 321–331.
Hazen, A. P. (1976). Expressive completeness in modal language. Journal of Philosophical Logic, 5, 25–46.
Hazen, A. P., Rin, B. G., & Wehmeier, K. F. (2013). Actuality in propositional modal logic. Studia Logica, 101, 487–503.
Hodes, H. (1984). Some theorems on the expressive limitations of modal languages. Journal of Philosophical Logic, 13, 13–26.
Humberstone, L. (2011). The connectives. Cambridge: MIT Press.
Kamp, H. (1971). Formal properties of “now”. Theoria, 37(3), 227–273.
Kocurek, A. (2017). On the concept of a notational variant. In A. Baltag, J. Seligman, & T. Yamada (Eds.), Logic, rationality and interaction: 6th international workshop (pp. 284–298). Berlin: Springer.
Lindström, P. (1969). On extensions of elementary logic. Theoria, 35, 1–11.
Pelletier, F., & Urquhart, A. (2003). Synonymous logics. Journal of Philosophical Logic, 32, 259–285.
van Benthem, J. (1976). Modal correspondence theory. Doctoral dissertation, University of Amsterdam.
van Benthem, J. (1985). Modal logic and classical logic. Napoli: Bibliopolis.
Wehmeier, K. F. (2003). World travelling and mood swings. In B. Löwe, W. Malzkorn, & T. Räsch (Eds.), Foundations of the formal sciences II (pp. 257–260). Dordrecht: Kluwer Academic Publishers.
Wojcicki, R. (1988). Theory of logical calculi. Dordrecht: Kluwer.
Acknowledgements
This paper has its origins in conversations with my late colleague and friend Aldo Antonelli about the relationship between modal and first-order language. It would undoubtedly be a better paper had I had the chance to discuss it with him. I am grateful to Johan van Benthem for correspondence over an early version of a predecessor of this paper. Many thanks, moreover, to Rohan French, Allen Hazen, Maciej Kłeczek, Jan Köpping, Fabio Lampert, Heinrich Wansing, Ede Zimmermann, and especially Lloyd Humberstone, for feedback on various drafts or presentations of the material. Audiences at the Frankfurt Semantics Colloquium and the workshop Logic in Bochum V in July of 2019 provided helpful comments and asked productive questions, for which I owe them thanks. Anonymous reviewers made several insightful suggestions that improved the paper, even if I was unable to accommodate them all. Funding was provided by the National Endowment for the Humanities (Grant No. FA-232235-16). Any views, findings, conclusions, or recommendations expressed in this article do not necessarily represent those of the National Endowment for the Humanities.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by .
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wehmeier, K.F. On Equivalence Relations Between Interpreted Languages, with an Application to Modal and First-Order Language. Erkenn 88, 193–213 (2023). https://doi.org/10.1007/s10670-020-00346-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-020-00346-w


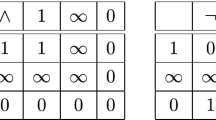








 if
if 





 , where
, where  .
.