On the Separation Question for Tree Languages

Abstract

We show that the separation property fails for the classes Σ _n of the Rabin-Mostowski index hierarchy of alternating automata on infinite trees. This extends our previous result (obtained with Szczepan Hummel) on the failure of the separation property for the class Σ ₂ (i.e., for co-Büchi sets). The non-separation result is also adapted to the analogous classes induced by weak alternating automata.

To prove our main result, we first consider the Rabin-Mostowski index hierarchy of deterministic automata on infinite words, for which we give a complete answer (generalizing previous results of Selivanov): the separation property holds for Π _n and fails for Σ _n -classes. The construction invented for words turns out to be useful for trees via a suitable game.

It remains open if the separation property holds for all classes Π _n of the index hierarchy for tree automata. To give a positive answer it would be enough to show the reduction property of the dual classes—a method well-known in descriptive set theory. We show that it cannot work here, because the reduction property fails for all classes in the index hierarchy.

1 Introduction

The separation question is whether two disjoint sets A and B can be separated by a set C (i.e., A⊆C and B∩C=∅) which is in some sense simpler. Separation is one of the main issues in descriptive set theory. A fundamental result due to Lusin is that two analytic sets can always be separated by a Borel set, but two co-analytic sets in general cannot. The former implies that if a set is simultaneously analytic and co-analytic then it is necessarily Borel, which is the celebrated Suslin Theorem (see, e.g., [11] or [9]).

A well-known fact in automata theory exhibits a similar pattern: if a set of infinite trees as well as its complement are both recognizable by Büchi automata then they are also recognizable by weak alternating automata (weakly recognizable, for short). This result was first proved by Rabin [13] in terms of monadic second-order logic; the automata-theoretic statement was given by Muller, Saoudi, and Schupp [12] in terms of weak alternating automata. It is not difficult to adapt Rabin’s proof to obtain a—slightly stronger—separation property: any two disjoint Büchi recognizable sets of trees can be separated by a weakly recognizable set (see, e.g., [7]). Quite analogical to the co-analytic case, the separation property fails in general for the dual class of co-Büchi tree languages (i.e., the complements of Büchi recognizable sets). In [7], a pair of such sets is presented that cannot be separated by any Borel set, hence a fortiori by any weakly recognizable set.

A systematic study of the separation property for tree automata has been undertaken by Santocanale and Arnold [14]. They asked if the above-mentioned result of Rabin can be shifted to the higher levels of the index hierarchy of alternating automata with an appropriate generalization of weak recognizability. The question stems naturally from the μ-calculus version of Rabin’s result which states that if a tree language is definable both by a Π ₂-term (i.e., with a pattern νμ) and a Σ ₂-term (μν), then it is also definable by an alternation free term, i.e., one in Comp(Π ₁∪Σ ₁) [3]. Somewhat surprisingly, Santocanale and Arnold [14] discovered that the equation

$$\varPi_{n} \cap\varSigma_{n} = \mathrm{Comp}( \varPi_{n-1} \cup\varSigma_{n-1}), $$

which amounts to Rabin’s result for n=2, fails for all n≥3. Consequently, it is in general not possible to separate two disjoint sets in the class Σ _n by a set in Comp(Π _n−1∪Σ _n−1); similarly for Π _n .

There is however another plausible generalisation of Rabin’s result suggested by the analogy with descriptive set theory. Letting

$$\Delta_{n} = \varPi_{n} \cap\varSigma_{n}, $$

we may ask if two disjoint sets in a class Σ _n can be separated by a set in Δ _n ; a similar question can be stated for Π _n . By remarks above, we know that the separation property in this sense holds for Π ₂ (Büchi) and fails for Σ ₂ (co-Büchi) class, in a perfect analogy with the properties of analytic vs. co-analytic classes in the descriptive set theory.¹

In the present paper we answer the question negatively for all classes Σ _n of the Rabin–Mostowski index hierarchy for alternating automata on infinite trees. (The classes Σ _n correspond to the indices (i,k) with k odd; see the definition in Sect. 2 below.) By an analogy with the Borel hierarchy [9, 11], one is tempted to conjecture that the separation property actually does hold for all classes Π _n , but this question seems to be difficult already for n=3.

To prove our main result, we first study a conceptually simpler case of infinite words and the Rabin–Mostowski index hierarchy of deterministic automata. In this case we give a complete answer: the separation property holds for classes Π _n and fails for classes Σ _n . The argument is based on a uniform construction of an inseparable pair in each class Σ _n . It should be noted that the separation property of the class (1,2) was proved earlier by Selivanov [15], who also gave a hint [16] how this result can be generalized for all classes Π _n in the index hierarchy of deterministic automata on infinite words.

The construction made for words is further used in the case of trees. More specifically, we consider labeled trees whose vertices are divided between two players: Eve and Adam, who wish to form a path in a tree. Given a set on infinite words L, we consider the set Win^∃(L) of those trees where Eve has a strategy to force a path into L. The operation Win^∃ allows us to shift the witness family from words to trees.

The main result is completed by two further observations. We show that the non-separation result holds for the analogous classes in the index hierarchy of the weak alternating automata. Next, in quest to solve the aforementioned conjecture about the classes Π _n , we investigate reduction property for tree automata. Roughly, this property means that any union A∪B can be refined to a disjoint union A′∪B′ of sets of the same complexity. In descriptive set theory, the reduction property of a class of sets is often used to show the separation property of the dual class (see [9]). We show that this method cannot be used here, because the reduction property fails for all non-trivial classes in the index hierarchy of alternating automata on trees.

The preliminary version of this paper was presented to the conference STACS 2012 [2]. The results about weak automata and about reduction property are new and presented for the first time in this paper.

2 Index Hierarchy

Throughout the paper, ω stands for the set of natural numbers, and notations n∈ω and n<ω are interchangeable. We identify a natural number n<ω with the set {0,1,…,n−1}; in particular 2={0,1}. An alphabet is any set, which is finite but non-empty.

We will consider deterministic automata on infinite words and alternating automata on infinite trees. The latter will be introduced via games. For more background on automata, we refer the reader to a survey by W. Thomas [17].

2.1 Automata on Infinite Words

A deterministic parity automaton on infinite words over an input alphabet A can be presented by $\mathcal{A} = \langle A, Q,q_{I}, \delta, \mathrm{rank}\rangle$, where Q is a finite set of states ranked by the function rank:Q→ω, and δ:Q×A→Q is a transition function. A run of $\mathcal{A}$ on a word u∈A ^ω is a word r∈Q ^ω whose first element r ₀ is the initial state q _I , and r _n+1=δ(r _n ,u _n ), for n<ω. It is accepting if the highest rank occurring infinitely often (i.e., lim sup _n→∞rank(r _n )) is even. The language $L(\mathcal{A})$ recognized by $\mathcal{A}$ consists of those words u∈A ^ω which admit an accepting run.

The Rabin-Mostowski index of $\mathcal{A}$ is the pair (minrank(Q),maxrank(Q)). It should be clear that moving all ranks up by an even number would not change the recognized language; therefore we may assume without loss of generality that minrank(Q) is 0 or 1. It is useful to partially order the indices as represented on Fig. 1. That is, we let (ι,κ)⊑(ι′,κ′) if either {ι,…,κ}⊆{ι′,…,κ′}, or ι=0, ι′=1, and {ι+2,…,κ+2}⊆{ι′,…,κ′}. We consider the indices (1,κ) and (0,κ−1) as dual, and let $\overline{(\iota,\kappa)}$ denote the index dual to (ι,κ).

Fig. 1

The Mostowski–Rabin index hierarchy

To better understand the structure of indices, we can think of a structure 〈{ι,…,κ},≤,Even〉 associated with an index (ι,κ), where Even stands for the evenness predicate. We identify indices whose structures are isomorphic. The ordering of indices corresponds to inclusion of isomorphism types, and the types of dual indices differ only by the monadic predicates, which are complement to each other.

The ordering of indices induces a hierarchy of languages, that is, if a language L is recognized by an automaton of index (ι,κ) and (ι,κ)⊑(ι′,κ′) then L is also recognized by an automaton of index (ι′,κ′). The hierarchy is known to be strict in the sense that, for any index (ι,κ), there is a language recognized by an automaton of index (ι,κ), but not by any (deterministic) automaton of the dual index $\overline{(\iota,\kappa)}$ [8, 18]. Indeed, the witness can be the parity condition itself:

(1)

2.2 Games

A graph game is a perfect information game of two players, say Eve and Adam, where plays may have infinite duration. It can be presented by a tuple

$$\langle V_\exists,V_\forall,\mathrm{Move},p_I,\ell, A, L_\exists, L_\forall \rangle. $$

Here V _∃ and V _∀ are (disjoint) sets of positions of Eve and Adam, respectively, Move⊆V×V is the relation of possible moves, with V=V _∃∪V _∀, p _I ∈V is a designated initial position, and ℓ:V→A is a labelling function, with some alphabet A. These items constitute an arena of the game. Additionally, L _∃,L _∀⊆A ^ω are two disjoint sets representing the winning criteria for Eve and Adam, respectively. In a special case of A={ι,…,κ}, L _∃=L _ι,κ (see Eq. (1)), and $L_{\forall}= \overline {L_{\exists}} = \{ u \in\{ \iota,\ldots, \kappa\}^{\omega}: \limsup_{n \rightarrow\infty} u_{n} \mbox{ is odd} \}$, we refer to the game as to a parity game of index (ι,κ).

The players in a graph game start a play in the position p _I and then move the token according to the relation Move (always to a successor of the current position), thus forming a path in the arena. The move is selected by Eve or Adam, depending on who the owner of the current position is. If a player cannot move, she/he looses. Otherwise, the result of the play is an infinite path v ₀,v ₁,v ₂,… , inducing the sequence of labels ℓ(v ₀),ℓ(v ₁),ℓ(v ₂),… . If this sequence belongs to L _∃ then Eve wins the play, if it belongs to L _∀ then Adam is the winner; otherwise there is a draw.

In the games considered in this paper, we always have L _∀=A ^ω−L _∃, hence a draw cannot occur.

Intuitively, a strategy is an oracle that tells the player her/his next move in the play, depending on the current history of the game. A history is any finite path in the arena starting from the initial position, i.e., a sequence π=(v ₀,v ₁,v ₂,…,v _k ), with v ₀=p _I , and (v _i ,v _i+1)∈Move, for i<k. We let last(π)=v _k .

We represent a strategy for Eve as a set S of histories, such that

• 1. p _I is the unique history of length 1 belonging to S,

• 2. each history π∈S with last(π)∈V _∃ has a unique prolongation πw _π in S (where (last(π),w _π )∈Move),

• 3. each history π∈S with last(π)∈V _∀ has a prolongation πw in S, for each w, such that (last(π),w)∈Move,

• 4. S is closed under initial segments.²

Note that the condition 2 induces a (partial) mapping π↦w _π , which can be used as an alternative representation of the strategy.

A play (finite or infinite) is consistent with a strategy S if all its finite prefixes are in S. A strategy S is winning for Eve, if every play consistent with S is won by Eve. That is, either the play is finite and ends in a position from which Adam has no move, or it is infinite, and the sequence of labels belongs to L _∃.

Analogically we define a strategy and a winning strategy for Adam. We say that Eve wins the game $\mathcal{G}$ if she has a winning strategy in this game, the similar for Adam.

In this paper we will often consider games whose arenas are infinite binary trees. A (full) binary tree over a finite alphabet Alph is a mapping t:2^∗→Alph. For a finite alphabet A, we denote by GTr(A) the set of binary trees over the alphabet Alph={∃,∀}×A. Any tree in GTr(A) constitutes an arena, where the labels {∃,∀} induce a partition of the nodes of the tree into positions of Eve and Adam, the moves go to the successors of a current node, and the initial position is the root.

A language L⊆A ^ω can serve as a winning criterion for either of the players. We will therefore consider two classes of games: L-∃ games, and L-∀ games.

An L-∃ game over a tree t∈GTr(A) is given by the following items:

(2)

An L-∀ game over t is defined similarly with the winning criteria L _∀=L, and $L_{\exists}= \overline{L}$.

We let

(3)

(4)

2.3 Automata on Trees

For a finite alphabet A, let Tr(A) denote the set of all binary trees over A (please note the difference with the notation GTr(A) introduced in the previous section).

An alternating parity automaton of index (ι,κ) on infinite binary trees over an input alphabet A can be presented by

(5)

where Q is a finite set of states with an initial state q _I , partitioned into existential states Q _∃ and universal states Q _∀, δ⊆Q×A×{0,1,ε}×Q is a transition relation, and rank:Q→ω with ι=minrank(Q), and κ=maxrank(Q). An input tree t is accepted by $\mathcal{A}$ iff Eve has a winning strategy in the parity game

(6)

where Move={((p,v),(q,vd)):v∈dom(t), (p,t(v),d,q)∈δ} and ℓ(q,v)=rank(q). The language $L(\mathcal{A})$ recognized by $\mathcal{A}$ consists of those trees t∈Tr(A), for which Eve has a winning strategy in the game $G(\mathcal{A},t)$.

Intuitively, players in this game follow a path in the tree t, additionally annotated by the states. A transition is always selected by the owner of the state. The automaton accepts the tree if Eve can make sure that the sequence of ranks encountered during an infinite play satisfies the parity condition (and she wins all finite plays if any).

Similarly as for deterministic automata on infinite words discussed in Sect. 2.1, the hierarchy of tree languages induced by the Rabin-Mostowski indices of alternating parity automata is strict, as showed by Bradfield [5]. An alternative proof of this difficult result was later given [1] based on the Banach Fixed-Point Theorem. Both proofs [1, 5] use the same witness family of sets of binary trees, which can be expressed in terms of the winning sets defined in Eq. (3)

(7)

In the present paper, we will consider sets Win^∃(L) (and occasionally Win^∀(L)), for other sets L recognized by word automata. It is useful to note the following.

Lemma 1

If a language L of infinite words is recognized by a deterministic automaton of index (ι,κ) then both languages Win^∃(L) and Win^∀(L) can be recognized by an alternating ³ tree automaton of index (ι,κ).

Proof

Let ${\mathcal{B}}$ be a deterministic automaton on infinite words of index (ι,κ), such that $L({\mathcal{B}}) = L$. The alternating tree automaton ${\mathcal{A}}$ accepting Win^∃(L) will have three copies of the states of the automaton ${\mathcal{B}}$, say Q ^∃, Q ^∀, and Q ^ε. The states in Q ^∃ are existential and the states in Q ^∀ are universal. We let the states in Q ^ε be also universal (for concreteness), but they will not leave Adam any choice; these states will be used only in ε-moves. Let q ^∇ denote a respective copy of a state q. We let rank(q ^∇)=rank(q).

The initial state is $q_{I}^{\varepsilon}$. For any state q and letter a, there are transitions (q ^ε,(∃,a),ε,q ^∃) and (q ^ε,(∀,a),ε,q ^∀). Whenever (p,a,q) is a transition in ${\mathcal{B}}$, there are moreover transitions (p ^∃,(∃,a),0,q ^ε), (p ^∃,(∃,a),1,q ^ε), and (p ^∀,(∀,a),0,q ^ε), (p ^∀,(∀,a),1,q ^ε). Now it can easily be verified that a winning strategy for Eve in the L-∃-game on t can be transferred to a winning strategy of Eve in the automaton game $G(\mathcal{A},t)$, and vice-versa.

An analogous construction works for Win^∀(L) (by interchanging the players). □

We now explain the Σ/Π terminology for the index hierarchy, which we have used informally in Introduction. It originates from the μ-calculus (see, e.g., [4]), and will be convenient to handle dualities. For each m≥1, we consider two indices: (1,m) and (0,m−1), and associate the symbol Σ _m with this index whose maximum is odd, and Π _m with the one whose maximum is even. For example, (0,1)≈Σ ₂, (1,2)≈Π ₂, (1,3)≈Σ ₃, (0,2)≈Π ₃, (1,4)≈Π ₄, (0,3)≈Σ ₄, etc. We will then refer to an automaton (of any kind) of index (ι,κ) as to Σ _m -automaton or Π _m -automaton with an appropriate m.

This terminology extends to classes of languages of infinite words and trees. A language of infinite words is in the class Σ _m if it is recognized by a deterministic Σ _m -automaton; similarly for Π _m . A language is in the class Δ _m if it is simultaneously in the classes Σ _m and Π _m .

For trees, we use the analogical terminology for alternating automata.

3 Tinkering with Infinite Words

The following property of languages will be useful. Informally, a language is stuttering if it does not distinguish between a single letter a and an nonempty block a ^ℓ.

Definition 2

A language L⊆A ^ω is stuttering if, for any a∈A, the following holds.

• For any infinite sequence of finite words (w _n ) _n<ω ,

  

• For any finite sequence of finite words w _n (n=0,…,k) and any infinite word v,

  

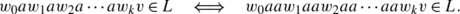
Directly from the definition we get the following.

Fact 3

If L is stuttering, then $\overline{L}$ is stuttering too.

Fact 4

Each language L _ι,κ is stuttering.

In the sequel we consider words over a product alphabet E ². We identify a pair of words 〈(u _n ),(v _n )〉∈(E ^ω)² with a single word over (E ²)^ω via a mapping 〈(u _n ),(v _n )〉↦〈(u _n ,v _n )〉.

A deterministic automaton $\mathcal{A}$ of index (ι,κ) over an alphabet A induces a mapping $g_{\mathcal{A}}: A^{\omega}\to\{ \iota ,\ldots,\kappa\}^{\omega}$ defined as follows. For a word u∈A ^ω, let r∈Q ^ω be the unique run of $\mathcal{A}$ on u (c.f. Sect. 2.1), and let

That is, $g_{\mathcal{A}}(u)$ is the sequence of ranks encountered in the run of $\mathcal{A}$ on u. Note that $u \in L(\mathcal{A})$ iff $g_{\mathcal{A}} (u) \in L_{i,k}$, i.e., $L(\mathcal{A})=g_{\mathcal{A}}^{-1}(L_{i,k})$.

If $\mathcal{B}$ is another deterministic automaton of index (ι,κ) over A, we define $g_{\mathcal{A}\times\mathcal{B}}: A^{\omega}\to(\{ \iota,\ldots,\kappa \}^{2})^{\omega}$ by $g_{\mathcal{A}\times\mathcal{B}}(u)= (g_{\mathcal{A}}(u),g_{\mathcal{B}}(u))$.

Lemma 5

Let $\mathcal{A}$ and $\mathcal{B}$ be automata of index (ι,κ) over some alphabet A, such that $L(\mathcal{ A})\cap L(\mathcal{ B}) = \emptyset$, and let L=L _ι,κ .

Then, for each word u∈A ^ω,

• 1. if $u \in L(\mathcal{ A})$ then $g_{\mathcal{A} \times\mathcal{B}} (u) \in{L\times{\overline{L}}}$,

• 2. if $u \in L(\mathcal{ B})$ then $g_{\mathcal{A} \times \mathcal{B}} (u) \in{\overline{L}\times L}$,

• 3. $g_{\mathcal{A} \times\mathcal{B}} (u) \in{\overline {L\times L}}$.

Proof

As mentioned above $u \in L(\mathcal{ A}) \Rightarrow g_{\mathcal{A}} (u) \in L$, and $u \notin L(\mathcal{ B}) \Rightarrow g_{\mathcal{B}} (u) \in\overline{L}$. As $L(\mathcal{ A})$ and $L(\mathcal{ B})$ are disjoint, $u \in L(\mathcal{ A})$ implies $u\notin L(\mathcal{B})$ hence $g_{\mathcal{A} \times\mathcal{B}} (u) \in L \times\overline{L }$.

The argument for 2 is similar. Finally, again by disjointness of $L(\mathcal{ A})$ and $L(\mathcal{ B})$, we have $g_{\mathcal{A} \times \mathcal{B}} (u) \in\overline{L \times L}$, for any u, which completes the proof. □

4 Separation Property of ω-Languages

We recall the main concept of the paper.

Definition 6

A set Z separates a pair of sets X,Y if X⊆Z and Y∩Z=∅ or, symmetrically, Y⊆Z and X∩Z=∅.

We say that the separation property holds for a class Γ _m ∈{Σ _m ,Π _m } if any two disjoint languages⁴ from this class are separable by a language in class Δ _m ; otherwise the separation property fails for Γ _m .

In this section we show that the separation property holds for classes Π _m and fails for classes Σ _m , for m≥1. In fact, both properties will follow from a single construction (parametrized by m≥2).

The level 1 is somewhat exceptional. The class Σ ₁ consists of a single language ∅, and the class Π ₁ consists of languages of all words (for each finite alphabet). Therefore the class Δ₁ is empty. For any alphabet A, there are no disjoint languages in the class Π ₁, hence the separation property holds trivially. On the other hand, there is a pair of disjoint sets in the class Σ ₁ (namely ∅ and ∅), which is inseparable because the class Δ₁ is empty. From now on, we will only consider classes with m≥2.

The following is the first non-separability result.

Lemma 7

Let L=L _i,k ⊆{i,…,k}^ω (with ⁵ i∈{0,1}) and let m=k+1−i. Then $L\times\overline{L}$ and $\overline{L}\times L$ (which are obviously disjoint) are not separable by a set in Δ _m .

Proof

Suppose to the contrary that there is a set C recognizable by an automaton of index (i,k), such that $\overline{L}\times L \subseteq C$ and $L\times\overline{L}\subseteq \overline{C}$.

By Lemma 5,

• if u∈C then $g_{\mathcal{A} \times\mathcal{B}} (u) \in L\times{\overline{L}}\subseteq \overline{C}$,

• if $u \in\overline{C}$ then $g_{\mathcal{A} \times\mathcal{B}} (u) \in{\overline{L}\times L}\subseteq C$.

Note that in this case the function $g_{\mathcal{A} \times\mathcal{B}}$ maps ({i,…,k}²)^ω into itself. We will show that it has a fixed point. Indeed, a fixed point f can be defined⁶ by an inductive formula

where $\hat{\delta}$ is the standard extension of δ from letters to finite words.

For this fixed point f, we have $f\in C \Rightarrow f\in\overline{C}$ and $f\in\overline{C} \Rightarrow f\in{C}$, a contradiction which completes the proof. □

The subsequent lemma is the heart of our proof.

Lemma 8

Let E={i,…,k}, where k is even, and let m=k+1−i. Let L=L _i,k ⊆E ^ω (hence L is in Π _m ), and let I⊆L _i,k consist of the words that contain infinitely many occurrences of k. Then there exist disjoint sets U ₁,U ₂⊆(E ²)^ω in the class Σ _m , satisfying the following.

Proof

The automata for U ₁ and U ₂ will only differ by their ranks. Their set of states is {up}×{i,…,k}×{i,…,k+1}∪{down}×{i,…,k+1}×{i,…,k}, the initial state is 〈up,i,i〉, and the transitions are

(8)

(9)

Figure 2 represents the table of the automata.

Fig. 2

The table for the automata for U ₁ and U ₂

With each state s we assign two ranks: rank₁(s) and rank₂(s), for U ₁ and U ₂, respectively, by

Each word u∈(E ²)^ω induces the same run in both automata up to the rankings. Clearly, a word u causes infinitely many changes of the level if and only if it contains infinitely many occurrences of k on both left and right track if and only if it visits infinitely often a state 〈up,r,k+1〉 and a state 〈down,k+1,s〉. By the definition of the rank functions such a word is accepted by neither of the automata. On the other hand, if the run on u stabilizes on some level then only one of the automata necessarily accepts as the ranks they assume in their runs (after stabilization) differ precisely by 1.

This shows that U ₁ and U ₂ are disjoint and $U_{1} \cup U_{2} = \overline{I \times I }$. The inclusion $\overline{L \times L } \subseteq\overline{I \times I }$ is obvious.

If $u \in L \times\overline{L }$ then the run on u stabilizes in the upper or lower component (as clearly u∉I×I). Then the automaton for U ₁, from some moment on, either reads a word in L in the upper component or a word in $\overline{L }$ in the lower component; in either case it accepts. An argument for the inclusion involving U ₂ is similar. □

We are now ready to state the main result of this section. Recall that the separation property for the class Π ₂ was proved earlier by Selivanov [15], who also gave⁷ a hint [16] on how this result can be generalized for all classes Π _n .

Theorem 9

The separation property holds for classes Π _m and fails for classes Σ _m of the index hierarchy of deterministic word automata.

Proof

We will show that any pair of disjoint languages of class Π _m over some finite alphabet A is separable by a language of class Δ _m , whereas this property fails for the pair of sets U ₁,U ₂ constructed in Lemma 8, for any class Σ _m , m≥2.

Let $\mathcal{A}$ and $\mathcal{B}$ be as in Lemma 5. It follows from 1 and 2 that the inverse image of U ₁ under the mapping $g_{\mathcal{A} \times\mathcal{B}}$, i.e.,

separates $L(\mathcal{A})$ and $L(\mathcal{B})$. Let us see that this set is recognizable by an Σ _m -automaton. For an input u, we just use the automaton for U ₁ reading the subsequent values of the function $g_{\mathcal{A} \times\mathcal{B}}$; the construction is straightforward. In a similar vein we can show that $( g_{\mathcal{A} \times\mathcal{B}} )^{-1} (U_{2})$ is in the class Σ _m as well. Clearly these sets are disjoint as U ₁ and U ₂ are disjoint. But it follows from condition 3 of Lemma 5 that they sum up to A ^ω, hence they both are of class Δ _m .

Now, by Lemma 8, $L\times{\overline{L}}\subseteq U_{1}$ and $\overline{L}\times L \subseteq U_{2}$, where L is the parity language in Π _m . If the sets U ₁ and U ₂ in Σ _m were separable by a set in Δ _m , then $L\times{\overline{L}}$ and $\overline {L}\times L$ would be separable, a contradiction with Lemma 7. □

5 Tinkering with Trees

5.1 Contractions

Definition 10

Let 2^<n={v∈2^∗:|v|<n} and 2^≤n={v∈2^∗:|v|≤n}. We say that a mapping g:Tr(A)→Tr(B) (for some alphabets A and B) is contracting if, for all n<ω, and t, t′∈Tr(A),

where F↾X denotes the restriction of a function F to a set X.

In the sequel, we will often use⁸ the celebrated Banach Fixed-Point Theorem: If g is a contracting mapping over the same domain Tr(A), it has a (unique) fixed point.

For ι≤κ<ω, we will use an abbreviation GTr({ι,…,κ})=GTr _ι,κ . The following fact, first noted in [1], is very useful in analysis of tree automata.

Theorem 11

[1]

Let $\mathcal{A}$ be an alternating tree automaton of index (ι,κ) over the alphabet A. There exists a contracting mapping g:Tr(A)→GTr _ι,κ such that $t\in L(\mathcal{A})$ iff g(t)∈W _ι,κ .

Proof (sketch)

In the first step we replace ${\mathcal{A}}$ with another automaton ${\mathcal{A}}'$ of the same index (ι,κ) such that $L({\mathcal{A}})=L({\mathcal{A}}')$ and in every state of ${\mathcal{A}}'$ the player has exactly two possible moves. We fix a map h which assigns to a given tree t a tree h(t) of all possible gameplays between Adam and Eve on t on ${\mathcal{A}}'$. That is, for every label of h(t) the first coordinate indicates who the owner of the state is (this is ∃ or ∀) and the second coordinate is the rank of the state q. The sons of a given vertex are induced by transitions from the state q.

This is almost what we need, that is $t\in L(\mathcal{A})$ if and only if h(t)∈W _ι,κ . In order to make h contracting, we add a dummy initial level to h(t), that is g(t)(ϵ)=g(t)(∃,ι) and g(t)(iv)=h(t)(v) for i=0,1. □

The above theorem also implies its dual variant.

Corollary 12

Let $\mathcal{A}$ be a tree automaton of index (ι,κ) over the alphabet A. There exists a contracting mapping g:Tr(A)→GTr _ι,κ such that $t\in L(\mathcal{A})$ iff g(t)∈W ^∀(L _ι,κ ).

Proof

Since W _ι,κ =W ^∃(L _ι,κ ), it is enough to compose a contraction from Theorem 11 with a mapping which switches roles between Eve and Adam. □

5.2 Product of Trees

In this section we define the product of two trees in the sets GTr—a crucial technical concept needed later in Sect. 6. In a sense, it is a notion similar to the direct product of infinite words.

Consider two alphabets, A and B. Recall that the label of a vertex of a tree t ₀∈GTr(A) has two coordinates, the first one tells us who the owner of the state is, and the second coordinate is a letter from A; similarly, for a tree in t ₁∈GTr(B). The product operation on trees assigns to a pair t ₀,t ₁ a tree t ₀⊗t ₁∈GTr(A×B). A vertex of the tree t ₀⊗t ₁ is also labeled by two coordinates, but the second coordinate is a pair of two letters, one from A and one from B. The following inductive definition of the tree t ₀⊗t ₁∈GTr(A×B) defines precisely the labeling of the vertices (see Fig. 3). We use the notation α(t,s) for a tree with the root labeled by α and the left and right subtrees t,s, respectively.

Fig. 3

Product of trees

As usual we can extend this operation to sets of trees; U⊗V={t⊗s:t∈U,s∈V}.

Lemma 13

If L ₀⊆A ^ω and L ₁=B ^ω are stuttering, then Win^∃(L ₀)⊗Win^∃(L ₁)⊆Win^∃(L ₀×L ₁) and Win^∀(L ₀)⊗Win^∀(L ₁)⊆Win^∀(L ₀×L ₁).

Proof

First let us observe that the sequence of labels in A×B along any infinite path $d_{1}d'_{1}d_{2}d'_{2}\cdots d_{n}d'_{n}\cdots$ in the product tree t=t ₀⊗t ₁ is 〈a ₀,b ₀〉〈a ₀,b ₀〉〈a ₁,b ₁〉⋯, where path d ₁ d ₂⋯d _n ⋯ has labels a ₀ a ₁⋯ in t ₀, and path $d'_{1}d'_{2}\cdots d'_{n}\cdots$ has labels b ₀ b ₁⋯ in t ₁.

Now let σ _i be a strategy for Eve in t _i . In the case of games on trees, we can simplify the presentation of a strategy (c.f. Sect. 2.2) and view it just as a mapping from positions of Eve (i.e., nodes marked ∃) to {0,1}, indicating a move to the left or right successor of the current node. We construct the strategy σ for Eve on t below. For any v such that t(v)=〈∃,a,b〉, let

$$\sigma(v)= \left \{ \begin{array}{l@{\quad}l} \sigma_0(\varepsilon)&\mbox{if $v=\varepsilon$}\\[4pt] \sigma_1(\varepsilon)&\mbox{if $v=d_{1}$}\\[4pt] \sigma_0(d_1d_2\cdots d_{n})&\mbox{if $v=d_{1}d'_{1}\cdots d_{n}d'_{n}$ }\\[4pt] \sigma_1(d'_1d'_2\cdots d'_{n})&\mbox{if $v=d_{1}d'_{1}\cdots d_{n}d'_{n}d_{n+1}$. } \end{array} \right . $$

If $d_{1}d'_{1}d_{2}d'_{2}\cdots$ is any path played along the strategy σ on t then d ₁ d ₂⋯ is played along σ ₀ in t ₀ and $d'_{1}d'_{2}\cdots$ is played along σ ₁ in t ₁.

To prove that Win^∃(L ₀)⊗Win^∃(L ₁)⊆Win^∃(L ₀×L ₂), we have to show that if σ ₀ and σ ₁ are winning then so is σ. Let τ be any strategy for Adam and let w=〈a ₀,b ₀〉〈a ₁,b ₁〉〈a ₂,b ₂〉⋯ be the label of the path $d_{1}d'_{1}d_{2}d'_{2}\cdots$ played along σ and τ. Then a ₀ a ₁ a ₂⋯ is the label of the path d ₁ d ₂⋯ played along the winning strategy σ ₀, thus it belongs to L ₀, and since L ₀ is stuttering, w ₀=a ₀ a ₀ a ₁ a ₁⋯∈L ₀ as well. Similarly w ₁=b ₀ b ₀ b ₁ b ₁⋯∈L ₁. Thus w=w ₀×w ₁∈L ₀×L ₁, which proves that σ is winning.

The proof for Win^∀ is very similar. □

6 Inseparable Pairs in Σ _m

Recall that, for trees, we use the notation Σ _m ,Π _m for classes of tree languages recognized by alternating automata of appropriate indices; a tree language is in the class Δ _m if it is simultaneously in the classes Σ _m and Π _m .

We let m≥2; the case of m=1 will be considered in Sect. 6.1. Let $U^{m}_{1}$ and $U^{m}_{2}$ be the sets constructed in Lemma 8. By Lemma 1, the sets $\mathrm{Win}^{\exists}(U^{m}_{1})$ and $\mathrm{Win}^{\forall}(U^{m}_{2})$ are in the class Σ _m of the tree automata hierarchy. We will show that they are inseparable by a set in Δ _m . Let us first verify that these two sets are disjoint: if $t\in\mathrm{Win}^{\exists}(U^{m}_{1})\cap \mathrm{Win}^{\forall}(U^{m}_{2})$ then t has a branch labelled by a word in $U^{m}_{1}\cap U^{m}_{2}$, a contradiction.

Lemma 14

Let (ι,κ) be the index corresponding to the class Π _m and let L=L _ι,κ . If T and T′ are two disjoint subsets of GTr _ι,κ in class Π _m then there exists a contracting mapping h such that

$$t\in T\Rightarrow h(t)\in\mathrm{Win}^\exists(L\times\overline{L}) $$

and

$$t\in T'\Rightarrow h(t)\in\mathrm{Win}^\forall(\overline{L} \times L). $$

Proof

Since T is in the class Π _m , there exists (by Theorem 11) a contracting mapping g such that t∈T iff g(t)∈Win^∃(L). From Corollary 12 we get a contracting mapping g′ such that t∈T′ iff g′(t)∈Win^∀(L).

Since T and T′ are disjoint, t∈T implies t∉T′ and thus g(t)∈Win^∃(L) and $g'(t)\in\mathrm{Win}^{\exists}(\overline{L})$. Hence by Lemma 13 we have $g(t)\otimes g'(t)\in\mathrm{Win}^{\exists}(L\times\overline{L})$.

Similarly, if t∈T′ then $g(t)\in\mathrm{Win}^{\forall}(\overline {L})$, g′(t)∈Win^∀(L), and $g(t)\otimes g'(t)\in\mathrm{Win}^{\forall}( \overline{L}\times L)$. Now let us define h by h(t)=g(t)⊗g′(t). It is easy to check that h is contracting. □

Lemma 15

Let (ι,κ) be the index corresponding to the class Π _m and let L=L _ι,κ . Then $\mathrm{Win}^{\exists}(L\times\overline{L})$ and $\mathrm {Win}^{\forall}(\overline{L}\times L)$ cannot be separated by a set C∈Δ _m .

Proof

Suppose there is such a set C∈Δ _m . Note that both sets $C, \overline{C}$ are in Π _m . Then, by the previous lemma with $T = \overline{C}$, T′=C, there exists a contracting h such that $t\in\overline{C}\Rightarrow h(t)\in \mathrm{Win}^{\exists}(L\times\overline{L}) \subseteq C$, $t\in{C}\Rightarrow h(t)\in \mathrm{Win}^{\forall}(\overline{L}\times L) \subseteq\overline{C}$. Since h is contracting, it has a fixed point t=h(t), and for this t, $t\in\overline{C}\Rightarrow t\in C$, and $t\in{C}\Rightarrow t \in\overline{C}$, a contradiction. □

Theorem 16

The sets $\mathrm{Win}^{\exists}(U^{m}_{1})$ and $\mathrm{Win}^{\forall}(U^{m}_{2})$ are not separable by a set in Δ _m , for m≥2.

Proof

Let (ι,κ) be the index corresponding to the class Π _m . Since, by Lemma 8, $\mathrm{Win}^{\exists}(L_{\iota,\kappa} \times\overline{L_{\iota,\kappa}})\subseteq\mathrm{Win}^{\exists}(U_{1}^{m})$ and $\mathrm{Win}^{\forall}(\overline{L_{\iota,\kappa}}\times L_{\iota,\kappa})\subseteq\mathrm{Win}^{\forall}(U_{2}^{m})$, a separator of $\mathrm{Win}^{\exists}(U_{1}^{m})$ and $\mathrm{Win}^{\forall}(U_{2}^{m})$ would also separate $\mathrm{Win}^{\exists}(L_{\iota,\kappa} \times\overline {L_{\iota,\kappa}})$ and $\mathrm{Win}^{\forall}(\overline{L_{\iota ,\kappa}}\times L_{\iota,\kappa})$, a contradiction with Lemma 15. □

6.1 Level 1

In contrast to deterministic automata for words, the classes Σ ₁ and Π ₁ for alternating automata on trees are not completely trivial. For example, an automaton $\mathcal{A}$ of index (1,1) may accept a tree t if Eve wins the game $G(\mathcal{A},t)$ in finite time. Similarly, an automaton of index (0,0) may fail to accept a tree if Adam wins the game in finite time. Not surprisingly, the separation question for classes Σ ₁ and Π ₁ is not difficult to solve. We use, however, different methods than for higher levels, including some basic topology.

For a finite alphabet Alph, we equip the set Tr(Alph) with a topology à la Cantor, which can be defined by pointwise convergence: a set of trees t _n converges to a tree t if, for any vertex v, the sequence t _n (v) stabilizes on some letter in Alph. It is well known that this space is compact and the family of closed-open sets of the form

(10)

where I⊆2^∗ is finite and f:I→Alph is an arbitrary function, forms its basis. It is a folklore knowledge⁹ that tree languages accepted by alternating automata of index (0,0) (i.e., with trivial acceptance condition) are closed in this topology. Consequently, the languages accepted by automata of index (1,1) are open, and the languages in the class Δ₁ clopen (closed-open).

Proposition 17

The separation property fails for the class Σ ₁ and holds for the class Π ₁.

Proof

For the negative result, we construct automata A ₁ and A ₂ as follows. Both automata read the leftmost branch of a given tree over the alphabet {a,b}. A ₁ accepts a tree t if and only if the first appearance of the letter a is at an even level, and A ₂ accepts t iff the first appearance of the letter a is at an odd level. Formally speaking, the automaton A ₁ has two existential states q ₀,q ₁ of rank 1 and one “dead” universal state (with no move) also of rank 1. The initial state is q ₀. In the game $G(\mathcal{A},t)$, Eve alternates between her two states q ₀,q ₁ moving to the left when she reads letters b unless she is in the state q ₀ and reads letter a. In this case she moves to the “dead” state of Adam, and thus wins the game. The same description works for A ₂ except that the roles of q ₀ and q ₁ are switched.

Clearly the languages L(A ₁) and L(A ₂) are disjoint and of index (1,1). Suppose L(A _i ) is contained in a certain language K _i of index (0,0) for i=1,2. We claim that a tree t with every vertex labeled b belongs to K ₁∩K ₂. For, let t _n be a tree with every vertex labelled b except of the vertex 0ⁿ (i.e., the n-th vertex on the leftmost branch), which is labeled a. Clearly, t is a pointwise limit of trees t _2n ∈L(A ₁) (n<ω) and it is also a pointwise limit of trees t _2n+1∈L(A ₂) (n<ω). But, as we have noted above, the sets K _i are closed, and hence t∈K ₁∩K ₂. This shows that it is impossible to separate L(A ₁) and L(A ₂) by a set in Δ₁.

Now let L ₁,L ₂⊆Tr(Alph) be two disjoint languages recognizable by automata of index (0,0). We will show that they can be separated by a language C in class Δ₁.

For each tree t∈L ₁ we fix a finite set of vertices I _t ⊂2^∗ and a set

$$U_t = \bigl\{ s\in\mathrm{Tr}(\mathit{Alph} ): s(v) = t(v) \mbox{ for } v\in I_t\bigr\}, $$

such that U _t ∩L ₂=∅. One can find such set I _t , since the set L ₂ is closed and for a fixed t∉L ₂ the family

$$\bigl\{ \bigl\{ s\in \mathrm{Tr}: s(v) = t(v) \ \mbox{for}\ v\in I \bigr\}: I \subseteq2^*,\ I\ \mbox{finite}\bigr\} $$

is a basis of open sets in the point t (c.f. Eq. (10)).

Since the space is compact and sets U _t are open, one can find t ₀,…,t _k , such that $L_{1}\subseteq C = U_{t_{0}}\cup\cdots\cup U_{t_{k}}$; by definition C separates L ₁ and L ₂. We claim that C is in the class Δ₁; clearly it is enough to show that this holds for each set of the form (10) (each U _t,i is of such form).

The (0,0) and (1,1) automata recognizing U _f are identical except ranks. We describe them in terms of the respective games. Adam first makes an ε-move: he chooses a vertex in the finite set I, say v. Once the decision is made, the automaton moves from the root to v in a deterministic manner and then verifies whether the label t(v) agrees with f(v). If it is the case, the automaton enters a “dead” state of Adam, and Adam looses. Otherwise, it enters a “dead” state of Eve, and Eve looses. Note that any play in this game is finite (bounded by max{|v|:v∈I}+2), hence the ranks of the states do not matter.

This remark completes the proof. □

Remark

From the above considerations, it is not hard to infer a simple characterizations of languages in the class Δ₁. Namely, the following conditions are equivalent for a tree language L⊆Tr(Alph).

• L is simultaneously recognized by an automaton of index (0,0) and by an automaton of index (1,1),

• L is closed and open in the above topology,

• L is accepted by an alternating automaton B (of any index), such that every gameplay between Adam and Eve in B is finite,

• L is accepted by an alternating automaton B, and there is a constant N such that every gameplay between Adam and Eve in B ends in less than N moves.

We now summarize the results of this section, Theorem 16 above, and the results on level 2 mentioned in Introduction [7, 13].

Corollary 18

Consider the Rabin-Mostowski index hierarchy for alternating automata on trees. Separation property fails for all classes Σ _m , m≥1, and holds for the classes Π ₁ and Π ₂.

The status of the classes Π _m , m≥3, remains open.

7 Weakly Recognizable Tree Languages

A weak alternating parity tree automaton of index (ι,κ) can be presented as an ordinary automaton introduced in Sect. 2.3, subject to an extra monotonicity condition: if (p,a,d,q) is a transition in δ then rank(q)≥rank(p). The Rabin-Mostowski indices of weak automata induce a hierarchy of tree languages similarly as for the ordinary automata; however we will not associate letters Σ/Π with this hierarchy. The strictness of the weak hierarchy has been established prior to the “strong” one by A.W.Mostowski [10]; an alternative proof can be given via the weak versions of languages W _ι,κ (see, e.g., [4]).

Note that the weak automata with indices (0,0) and (1,1) coincide with the ordinary ones, and we have already considered the respective classes in Sect. 6.1.

From now on we fix a pair (ι,κ) (ι<κ<ω) and define M=M _ι,κ to be the set of all non–decreasing sequences in {ι,…,κ}^ω. We let $\mathbb{A}M$ be the set of all trees in ${\mathcal{T}}_{\iota,\kappa}$, such that the labeling of any path projected at the second component is in M. Let L=L _ι,κ . The mapping g constructed in Theorem 11 has the following property in the weak case (see, e.g., [4] Theorem 8.3.1).

Fact 19

Let T⊆GTr _ι,κ be a weak language of index (ι,κ). Then there exists a contracting mapping g such that $t\in{\mathcal{T}}\Leftrightarrow g(t)\in\mathrm{Win}^{\exists}(L)$ and moreover, for all t, $g(t)\in\mathbb{A}M$. The analogous claim holds for Win^∀(L).

Now, as in the general case (c.f. Lemma 14), if T,T′⊆GTr _ι,κ are two weak languages of index (ι,κ) then there exist g and g′ such that

• if t∈T then $g(t)\in\mathrm{Win}^{\exists}(L)\cap\mathbb{A}M$ and $g'(t)\in\mathrm{Win}^{\exists}(\overline{L})\cap\mathbb{A}M$; it follows that $g(t)\otimes g'(t)\in\mathrm{Win}^{\exists}(L\times\overline{L})\cap \mathbb{A}M^{2} \subseteq\mathrm{Win}^{\exists}((L\times\overline{L})\cap M^{2})$;

• analogously, if t′∈T′ then $g(t')\otimes g'(t')\in\mathrm{Win}^{\forall}((\overline{L}\times L)\cap M^{2})$.

Since g⊗g′ is contracting, we get the following, for the same reasons as in Lemma 15.

Fact 20

$\mathrm{Win}^{\exists}((L\times\overline{L})\cap M^{2})$ and $\mathrm{Win}^{\forall}((\overline{L}\times L)\cap M^{2})$ cannot be separated by a set C such that C and $\overline{C}$ are weak languages of index (ι,κ).

From now on we assume that ι=1, hence L=L _1,κ and M=M _1,κ , with 1<κ<ω. We will prove an analogue of Lemma 8. We call a deterministic automaton on infinite words weak if its transitions do not decrease ranks.

Lemma 21

There exist two disjoint sets V ₁,V ₂⊆({1,…,κ}²)^ω, satisfying the following.

The languages V ₁,V ₂ are accepted by weak deterministic automata of index (1,κ).

Proof

Let ⊤={1,…,κ}^ω. For any language Z⊆⊤ and i∈{1,…,κ}, we abbreviate Z _i =Z∩{i,…,κ}^ω.

Let us first consider the case of κ odd.

Let X=L∩M and $Y = \overline{L} \cap M$.

We let

(11)

(12)

Note that X _p ∩Y _p =∅, for any p, which follows that V ₁ and V ₂ are disjoint. It is also straightforward to verify the inclusions claimed in the lemma.

We now describe a weak deterministic automaton of index (1,κ) recognizing V ₁. We use notation $p \stackrel{s}{\to} q$ to mean δ(p,s)=q. The automaton has states 1,2,…,κ, $\overline{2}, \ldots, \overline{\kappa}$, and ♠. The rank of state i is i, the rank of state $\overline{i}$ is i−1, and the rank of ♠ is κ. The initial state 1 has transitions

The states 2≤i “read” the first component as long as monotonicity is preserved, i.e., the transitions are $i \stackrel{j,k}{\to} j$, for j≥i. However, violating monotonicity is “punished” by entering ♠, i.e., $i \stackrel{j,k}{\to} \spadesuit$, whenever j<i. Similarly, the states $\overline{i}$ read the second component, i.e., $\overline{i} \stackrel{j,k}{\to} \overline{j}$, for j≥i; but violating monotonicity is again punished by ♠. The state ♠ loops in itself independently of the input letter.

By definition, the automaton is weak of index (1,κ); We leave it to the reader to check that it recognizes V ₁. The construction of the automaton for V ₂ is analogous.

For κ even, we again consider two cases. Let us first consider κ≥4. The sets V ₁ and V ₂ are defined by the formulas (11) and (12) above, but we change the definition of X, which is now

Note that X _p ∩Y _p =∅ continues to hold, and hence the sets V ₁ and V ₂ are disjoint. They clearly satisfy the inclusions claimed in the lemma.

An automaton recognizing V ₁ is similar as in the previous case, except for the rank of ♠ which is now κ−1 (which is odd and greater than 1). Moreover, the automaton has a new self-looping state ♡ with the rank κ. The transitions are similar as before whenever monotonicity is preserved. The violation of monotonicity in state $\overline{i}$ is again punished by entering the state ♠. In contrast, the violation of monotonicity in a state i is not punished at all, but instead it is granted by entering a “winning” state ♡. Again, it is straightforward to verify that the automaton satisfies all requirements. An automaton for V ₂ is analogous.

Finally for the index (1,2), we let

It is immediate to see that the sets V ₁ and V ₂ are disjoint and the inclusions of the lemma are satisfied. An automaton recognizing V ₁ has an initial state 1 and two self-looping states ♠ and ♡ ranked as before. The transitions for 1 are

An automaton for V ₂ is analogous. □

Now, by reading the proof of Lemma 1, we can easily see if a deterministic automaton recognizing a set of infinite words is weak of index (ι,κ) then the alternating automata recognizing sets Win^∃(L) and Win^∀(L) are also weak of index (ι,κ). Hence we can note the following.

Fact 22

For languages V ₁,V ₂ constructed in Lemma 21, the sets of trees Win^∃(V ₁) and Win^∀(V ₂) can be recognized by weak alternating automata of index (1,κ).

Thus we obtain the following analogue of

Theorem 23

For every κ≥1, the separation property fails for the class of weak regular languages of index (1,κ).

Proof

For index (1,1), the weak automata coincide with the ordinary ones, and this case has been already settled in Proposition 17.

For κ>1, we claim that the sets Win^∃(V ₁) and Win^∀(V ₂) are inseparable. Indeed, as $\mathrm {Win}^{\exists}(({L}\times\overline{L})\cap M^{2})\subseteq\mathrm {Win}^{\exists}(V_{1})$ and $\mathrm{Win}^{\forall}((\overline{L}\times L)\cap M^{2})\subseteq\mathrm{Win}^{\forall}(V_{2})$ (by Lemma 21), a separator of Win^∃(V ₁) and Win^∀(V ₂) would also separate $\mathrm{Win}^{\exists}((L\times \overline{L})\cap M^{2})$ and $\mathrm{Win}^{\forall}((\overline{L}\times L)\cap M^{2})$, contradicting Fact 20. □

8 Reduction Property

Sets C,D reduce a given pair of sets A,B if C⊆A, D⊆B, C∪D=A∪B and C∩D=∅. The reduction property holds for a class ${\mathcal{C}}$ of sets, if for every $A,B\in{\mathcal{C}}$, there exist $C,D\in{\mathcal{C}}$ which reduce A,B. The reduction property for a class ${\mathcal{C}}$ implies readily the separation property for the dual class $\{ \overline{C}: C\in{\mathcal{C}}\}$. In set-theoretic hierarchies, usually the converse also holds, that is the separation property for a class ${\mathcal{C}}$ implies the reduction property for the dual class (see [9]). We will see that it is not the case for the index hierarchy of the alternating automata on trees.

Theorem 24

The reduction property fails for all classes Σ _m and Π _m , for m≥1.

The rest of this section is devoted to the proof of this theorem. We consider a class Σ _m with m≥2; the proof for Π _m is analogous.

Let us start with a simple combinatorial lemma.

Lemma 25

Let ⊤ be any set and W⊆⊤. Assume that

$$(\top\times W) \cup(W \times\top) = X \cup Y , $$

where X⊆⊤×W, Y⊆W×⊤, and the sets X and Y are disjoint. Suppose further that

for some sets a _i ,b _i ,c _i ,d _i ⊆⊤. Then the set $\overline{W} = \top- W$ can be generated from the sets a ₁,…,a _m ,d ₁,…,d _n , by (finite) union and intersection.¹⁰

Proof

Let, for t∈⊤,

where A _t =⊤ if the set {a _i :t∈a _i } is empty. If

(13)

then we are done, as there are only finitely many distinct sets A _t . Note that the inclusion ⊆ in (13) always holds as t∈A _t , for any t. Thus (13) may fail only if there are some $t \in\overline{W}$, t′∈W, such that t′∈A _t . We will show that, in this case,

(14)

(⊇) If $s \in\overline{W}$ then (t′,s)∈X∪Y (because t′∈W) but (t′,s)∉X (because s∉W), hence (t′,s)∈Y.

(⊆) Let (t′,s)∈Y. Suppose s∈W; then (t,s)∈X. (For, it is in X∪Y because of s, but not in Y because of t.) Now the assumption that t′∈A _t implies that (t′,s)∈X as well. (For, if (t,s)∈a _i ×b _i then (t′,s)∈a _i ×b _i as well.) But this is impossible as X and Y are disjoint; the contradiction proves that $s \in\overline{W}$.

To complete the proof, note that the right-hand side of (14) amounts to

 □

The next lemma will introduce a decomposition of a recognizable tree language into “rectangles” in the same class. We fix an alphabet A and a letter d∈A. Recall that d(t ₀,t ₁) denotes a tree with the root labeled by d, and the left and right subtrees t ₀ and t ₁, respectively. For sets of trees K,L, let d(K,L)={d(t ₀,t ₁):t ₀∈K,t ₁∈L}. Clearly, if K and L are in the class Σ _m , so is d(K,L).

Let ⊤=Tr(A) stand for all trees over alphabet A.

Lemma 26

Let T⊆d(⊤,⊤) be in the class Σ _m . Then

for some finite set of pairs (A _i ,B _i ) _i∈I of sets in Σ _m .

Proof

Let $\mathcal{A}$ be an alternating tree automaton of index (ι,κ) recognizing T (like in (5)). For a state q∈Q, let $\mathcal{A}_{q}$ be an automaton which differs from $\mathcal{A}$ only in that its initial state is q.

Let t=d(t ₀,t ₁)∈T, and let S be a winning strategy of Eve in the game $G(\mathcal{A},t)$ (c.f. Sect. 2.3). Recall that nodes in the arena of this game have form (q,v), where q is a state of the automaton and v is a node of the tree; in particular the initial position of the game is (q _I ,ε). Let L(t) be the set of those histories in S, where the left successor of the root of the tree t (i.e., the node 0) is reached for the first time (possibly after a sequence of ε-moves). That is, π is in L(t) if it is in the form (v ₀,v ₁,…,v _k ), where v ₀=(q _I ,ε), v _k =(q,0), for some q, and v _i =(p _i ,ε), for i<k, for some states p _i . Let R(t) be defined similarly for the right subtree.

Let L _state (t)={q:last(π)=(q,0),for some π∈L(t)}, and let R _state (t) be defined similarly. Note that $t_{0} \in L( \mathcal{A}_{q} )$, whenever q∈L _state (t), as Eve can use a sub-strategy of S (starting from an appropriate history) to win the game $G(\mathcal{A}_{q},t_{0} )$. The similar holds for t ₁ and R _state (t). We claim that a kind of converse also holds: if $t_{0}' \in\bigcap_{q \in L_{\mathit{state}}(t)} L(\mathcal{A}_{q})$ and $t_{1}' \in\bigcap_{q \in L_{\mathit{state}}(t)} R(\mathcal{A}_{q})$ then $d (t_{0}' , t_{1}') \in T$. Indeed, for each q∈L _state (t), Eve has a winning strategy S _q,0 in the game $G(\mathcal{A}_{q},t_{0}' )$, and the similar holds for $t_{1}'$. Hence, Eve can combine these strategies with the strategy S. That is, she plays S until the play reaches a history π∈L(t) with last(π)=(q,0), for some q (or π∈R(t) with last(π)=(q,1)), in which case she switches to the strategy S _q,0 (or S _q,1). Symbolic presentation of this new strategy in terms of concatenation of sets of histories is easy but cumbersome, and we omit it here.

Hence

Obviously, the number of pairs of sets which may occur as arguments of d in the formula above is finite. It is well-known (and easy to verify) that the class Σ _m is closed under finite meets. Hence the formula gives us a decomposition required in the lemma. □

We now fix an alphabet A and a tree language W over A belonging to the class Σ _m , but not in Π _m . For concreteness, for ι<κ, we can take the set W _ι,κ for appropriate ι,κ, c.f. Sect. 2.3. For the classes Σ ₁ and Π ₁ (c.f. Sect. 6.1), we leave the construction of the respective examples to the reader. We claim that the pair d(⊤,W),d(W,⊤) is not reducible.

For, suppose that

for some sets X,Y in class Σ _m , such that X⊆d(⊤,W), Y⊆d(W,⊤), and the sets X and Y are disjoint. Let

be decompositions given by Lemma 26; in particular all sets a _i ,b _i ,c _j ,d _j are in class Σ _m . We apply Lemma 25 via an obvious correspondence between a tree d(t ₀,t ₁) and a pair (t ₀,t ₁); hence $\overline{W}$ can be presented as a ∪∩–combination of sets in Σ _m . By the closure properties of Σ _m , this would imply that $\overline{W}$ is in this class itself, contradicting the choice of W. This remark completes the proof of Theorem 24.