Abstract
We obtain new quantitative estimates on Weyl Law remainders under dynamical assumptions on the geodesic flow. On a smooth compact Riemannian manifold (M, g) of dimension n, let \(\Pi _\lambda \) denote the kernel of the spectral projector for the Laplacian, \(\mathbb {1}_{[0,\lambda ^2]}(-\Delta _g)\). Assuming only that the set of near periodic geodesics over \({W}\subset M\) has small measure, we prove that as \(\lambda \rightarrow \infty \)
where B is the unit ball. One consequence of this result is that the improved remainder holds on all product manifolds, in particular giving improved estimates for the eigenvalue counting function in the product setup. Our results also include logarithmic gains on asymptotics for the off-diagonal spectral projector \(\Pi _\lambda (x,y)\) under the assumption that the set of geodesics that pass near both x and y has small measure, and quantitative improvements for Kuznecov sums under non-looping type assumptions. The key technique used in our study of the spectral projector is that of geodesic beams.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let (M, g) be a smooth compact connected Riemannian manifold of dimension n, \(\Delta _g\) be the negative definite Laplace-Beltrami operator acting on \(L^2(M)\), and \(\{\lambda _j^2\}_{j=0}^\infty \) be the eigenvalues of \(-\Delta _g\), repeated with multiplicity, \(0=\lambda _0^2 < \lambda _1^2 \le \lambda _2^2 \le \dots \). In this article we obtain improved asymptotics for both pointwise and integrated Weyl Laws. That is, we study asymptotics for the Schwartz kernel of the spectral projector
i.e. \(\Pi _\lambda \) is the orthogonal projection operator onto functions with frequency at most \(\lambda \). If \(\{\phi _{\lambda _j}\}_{j=1}^\infty \) is an orthonormal basis of eigenfunctions, \(-\Delta _g \phi _{\lambda _j}=\lambda _j^2 \phi _{\lambda _j}\), the Schwartz kernel of \(\Pi _\lambda \) is
Asymptotics for the spectral projector play a crucial role in the study of eigenvalues and eigenfunctions for the Laplacian, with applications to the study of physical phenomena such as wave propagation and quantum evolution. One of the oldest problems in spectral theory is to understand how eigenvalues distribute on the real line. Let \(N(\lambda ):=\#\{{j:\;}\lambda _j\le \lambda \}\) be the eigenvalue counting function. Motivated by black body radiation, Hilbert conjectured that, as \(\lambda \rightarrow \infty \),
Here, \({{\,\textrm{vol}\,}}_{{\mathbb {R}}^n}(B)\) is the volume of the unit ball \(B \subset {\mathbb {R}}^n\), \({{\,\textrm{vol}\,}}_g(M)\) is the Riemannian volume of M, and \({{\,\mathrm{{\text {dv}}}\,}}_g\) is the volume measure induced by the Riemannian metric. The conjecture was proved by Weyl [46] and is known as the Weyl Law. We refer to \(E(\lambda )\) as a Weyl remainder. In 1968, Hörmander [25], provided a framework for the study of \(E(\lambda )\) and generalized the works of Avakumović [1] and Levitan [35], who proved \(E(\lambda )=O(\lambda ^{n-1})\); a result that is sharp on the round sphere and is thought of as the standard remainder.
The article [25] provided a framework for the study of Weyl remainders which led to many advances, including the work of Duistermaat–Guillemin [17] who showed \(E(\lambda )=o(\lambda ^{n-1})\) when the set of periodic geodesics has measure 0. Recently, [27] verified this dynamical condition on all product manifolds. A striking application of our main theorem on Weyl remainders is:
Theorem 1
Let \((M_i,g_i)\) be smooth compact connected Riemannian manifolds of dimension \(n_i\ge 1\) for \(i=1,2\). Then, with \(M=M_1\times M_2\), \(g=g_1\oplus g_2\), and \(n:=n_1+n_2\),
For future reference, we note that \( {N(\lambda )=\int _{M}\Pi _{\lambda }(x,x){{\,\mathrm{{\text {dv}}}\,}}_g(x)} \) and thus \(N(\lambda )\) can be studied by understanding the kernel of \(\Pi _{\lambda }\) restricted to the diagonal. We study both on and off diagonal Weyl remainders in this article. The main idea is to adapt the geodesic beam techniques developed by authors [9, 11, 22] to study Weyl remainders. These techniques were originally used to study averages of quasimodes over submanifolds by decomposing the quasimodes into geodesic beams and controlling the averages in terms of the \(L^2\) norms of these beams. In this work the key point is to study the eigenvalue counting function by viewing it as a sum of quasimodes averaged over the diagonal in \(M\times M\). We start our exposition in the setting of the on diagonal estimates.
1.1 On diagonal Weyl remainders
The connection between the spectrum of the Laplacian and the properties of periodic geodesics on M has been known since at least the works [15, 16, 45], with their relation to Weyl remainders first explored in the seminal work [17]. To control \(E(\lambda )\) we impose dynamical conditions on the periodicity properties of the geodesic flow \(\varphi _t:T^*M \setminus \{0\} \rightarrow T^*M{\setminus \{0\}}\), i.e., the Hamiltonian flow of \((x,\xi )\mapsto |\xi |_{g(x)}\). For \(t_0>0\), \(T>0\), and \(R>0\), define the set of near periodic directions in \(U \subset S^*M\) by
Given two sets \(U\subset V\subset T^*M\), and \(R>0\), we write \(B_{_{V}}(U,R):=\{\rho \in V:\; d(U, \rho )<R\}\), where d is the distance induced by some fixed metric on \(T^*M\), \(B(U,R)=B_{_{T^*\!M}}(U,R)\), and \(B_{_{V}}(\rho ,R)=B_{_{V}}(\{\rho \},R)\). The set \(\mathcal {P}^R_{_{U}}(t_0,T)\) represents those points which come R close to being periodic with period between \(t_0\) and T and will be used to give a quantitative measure of how many near periodic geodesics there are.
We phrase our dynamical conditions in terms of a resolution function \(\textbf{T}=\textbf{T}(R)\). This is a function of the scale, R, at which the manifold is resolved, which increases as \(R\rightarrow 0^+\). We use \(\textbf{T}\) to measure the time for which balls of radius R can be propagated under the geodesic flow while satisfying a given dynamical assumption, e.g. being non periodic.
Definition 1.1
We say a decreasing, continuous function \({\textbf{T}}:(0,\infty )\rightarrow (0,\infty )\) is a resolution function. In addition, we say a resolution function \(\textbf{T}\) is sub-logarithmic, if it is differentiable and
We measure how close \(\textbf{T}\) is to being logarithmic through
Simple examples of sub-logarithmic resolution functions are \(\textbf{T}(R)=\alpha (\log R^{-1})^\beta \) for any \(\alpha >0\) and \(0<\beta \le 1\). For an explanation for our use of resolution functions, see Remark 1.6.
For improved integrated Weyl remainders, we need a condition on the geodesic flow. We will use the notation that for \({U}\subset T^*\!M\) we write \(\mu _{_{\!{U}}}\) for the Liouville measure induced on U.
Definition 1.2
Let \(\textbf{T}\) be a resolution function. Then \(U\subset S^*M\) is said to be \(\textbf{T}\) non-periodic with constant \(C_{_{\!{\text {np}}}}\) provided there exists \(t_0>0\) such that

We say U is \(\textbf{T}\) non-periodic if there is such \(C_{_{\!{\text {np}}}}\), and \({W}\subset M\) is \(\textbf{T}\) non-periodic if \(S^*_{{W}}M\) is.
Below, for \(U\subset T^*\!M\), we write \(\dim _{box }{U}\) for the Minkowski box dimension of U (see e.g. [42, Page 333]). Note that if \({W}\subset M\) is open with smooth boundary then \(\dim _{box }\partial {W}=n-1\).
Theorem 2
Let (M, g) be a smooth compact connected Riemannian manifold of dimension n, \({W}\subset M\) be an open subset with \(\dim _{box }\partial {W}<n\), and \({\Omega _0}>0\). There exists \(C_{_{0}}>0\) such that if \(\textbf{T}\) is a sub-logarithmic rate function with \(\Omega (\textbf{T})<{\Omega _0}\) and \({W}\) is \(\textbf{T}\) non-periodic, then there is \(\lambda _0\) such that for all \(\lambda >\lambda _0\)
In particular, if M is \(\textbf{T}\) non-periodic, then there is \(\lambda _0\) such that for all \(\lambda >\lambda _0\)
We illustrate an application of Theorem 2 in Fig. 1. In this example we construct a surface of revolution with both a periodic and a non-periodic set (see Definition 1.2). In particular, Theorem 2 applies with \({W}\) contained in the non-periodic (green) set. One can obtain little oh improvements for the statement in Theorem 2, but this requires the more general version given in Theorem 6 instead (see Remark 1.8). See Table 1 in Sect. 1.3 for some additional examples.
An example of a perturbation of the sphere with both a non-periodic (green) and a periodic (orange) physical space set. The perturbed metric coincides with the round metric outside the strip (a, b). Trajectories which remain in the spherical strip are \(2\pi \) periodic, while those which enter the non-periodic set are mostly non-periodic. See Sect. B.2.1 for a precise description of this example (color figure online)
The assumptions of Theorem 2 apply to a wide variety of Riemannian manifolds. Indeed, in addition to the concrete examples in Sect. 1.3, the authors [12] use Theorem 2 to give a logarithmic improvement in the remainder for the Weyl law that works for ‘typical’ metrics on any smooth manifold. This result is the first quantitative estimate for the remainder in Weyl laws that holds for most metrics.
We next discuss \(E_\lambda (x)\), the remainder in the on diagonal pointwise Weyl law
The Weyl remainder in [25] comes from the estimate \(E_{\lambda }(x)=O(\lambda ^{n-1})\) for \(x\in M\) (again, sharp on the round sphere). The connection between \(E_\lambda (x)\) and geodesic loops through x is studied in the works of Safarov, Sogge–Zelditch [38, 41] and often appears in estimates for sup-norms of eigenfunctions. To control the pointwise remainder \( E_\lambda (x)\) we impose dynamical conditions on the looping properties of geodesics joining x with itself. For \(t_0>0\), \(T>0\), \(R>0\), and \(x,y\in M\), define
Similar to \(\mathcal {P}^R_{_{U}}(t_0,T)\), the set \({\mathcal {L}}_{x,y}^{{R}}(t_0, T)\) represents those points, \(\rho \), that are R close to x and such that the geodesic through \(\rho \) comes R close to passing through to y in some time between \(t_0\) and T. The set will be used to give a quantitative measure of how many near looping geodesics there are.
Definition 1.3
Let \(\textbf{T}\) be a resolution function, \(t_0> 0\), \(C_{_{\!{\text {nl}}}}>0\), and \(x, y \in M\). Then, (x, y) is said to be a \((t_0, \textbf{T})\) non-looping pair with constant \(C_{_{\!{\text {nl}}}}\) when

We say x is \((t_0,\textbf{T})\) non-looping with constant \(C_{_{\!{\text {nl}}}}\) if (x, x) is a \((t_0,\textbf{T})\) non-looping pair with constant \(C_{_{\!{\text {nl}}}}\).
Note that if \(t_0<{{\,\textrm{inj}\,}}(M)\), where \({{\,\textrm{inj}\,}}(M)\) is the injectivity radius of M, then for x to be \((t_0, \textbf{T})\) non-looping is the same as being \((\varepsilon , \textbf{T})\) non-looping for any \(0<\varepsilon \le t_0\). In this case, we write x is \((0, \textbf{T})\) non-looping.
To state our estimates on the pointwise Weyl remainder, we let \(\lambda >0\), and, for points \(x,y \in M\) with \(d(x,y)<{{\,\textrm{inj}\,}}M\), define
Here, the integral is over \(T_y^*M\), \(\exp _x:T_x^*M\rightarrow M\) is the the exponential map, and \(|g_y|\) denotes the determinant of the metric g at y, when g is thought of as matrix in local coordinates.
Theorem 3
Let \(\alpha ,\beta \in {\mathbb {N}}^n\), \(0< \delta <\frac{1}{2}\), \(C_{_{\!{\text {nl}}}}>0\), and \({\Omega _0}>0\). There exists \(C_{_{0}}>0\) such that the following holds. If \(\textbf{T}\) is a sub-logarithmic resolution function with \(\Omega (\textbf{T})<{\Omega _0}\), there is \(\lambda _0>0\) such that if \(x_0\in M\) is \((0,\textbf{T})\) non-looping with constant \(C_{_{\!{\text {nl}}}}\), then for all \(\lambda >\lambda _0\)
See Table 2 in Sect. 1.3 for some examples to which Theorem 3 applies.
Remark 1.4
At first it may not be obvious that (1.6) is the correct remainder to estimate for off-diagonal Weyl asymptotics. However, one can check that the term we subtract comes from the singularities corresponding to the shortest geodesic from x to y and, when there are few additional loops from x to y, one expects these to give the main contribution. See also the discussion after Theorem 4.
Theorems 2 and 3 fit in a long history of work on asymptotics of the kernel of the spectral projector and the eigenvalue counting function. Many authors considered pointwise Weyl sums [1, 21, 25, 35, 36, 39], eventually proving the sharp remainder estimates. The article [25] provided a method which was used in many later works: [17] showed \(E(\lambda )=o(\lambda ^{n-1})\) under the assumption that the set of periodic trajectories has measure 0, [38, 41] improved estimates on \(E_\lambda (x)\) to \(o(\lambda ^{n-1})\) under the assumption that the set of looping directions through x has measure 0 (see also the book of Safarov–Vassiliev [37]). See [13, 14] for corresponding estimates that are uniform in a small neighborhood of the diagonal and Ivrii [28] for the case of manifolds with boundaries.
While o(1) improvements were available under dynamical assumptions, until now, quantitative improvements in remainders were available in geometries where one has an effective parametrix to \(\log \lambda \) times e.g. manifolds without conjugate points [2, 4, 31] or non-Zoll convex analytic rotation surfaces [43, 44]. We point out that the closest results to ours are those of Volovoy [43]. There, quantitative estimates on \(E(\lambda )\) are obtained under stronger assumptions than those of Theorem 2. In particular, \({W}\) is required to be equal to M and the volume in (1.3) is required to be bounded by a positive power of R, rather than \(\textbf{T}(R)^{-1}\).
The estimates in this article are available without additional geometric assumptions. This comes from our use of the ’geodesic beam techniques’ developed in the authors’ work [9, 11, 22] and which in turn draw upon the semiclassical approach of Koch–Tataru–Zworski [33]. Theorems 2 and 3 can be thought of as the quantitative analogs of the main results in [17] and of [38], [41] respectively. In fact, these results can be recovered from Theorems 2 and 3 by allowing \(\textbf{T}(R)\) to grow arbitrarily slowly as \(R\rightarrow 0^+\) (see [11, Appendix B]). We also note that our estimates include both \(C^\infty \) asymptotics for \(\Pi _\lambda (x,y)\) and uniformity in certain shrinking neighborhoods of the diagonal without any additional effort and hence include the results from [13, 14].
Remark 1.5
To recover the results of [13, 14, 38, 41] one needs uniformity in o(1) neighborhoods of points of interest. As stated, Theorem 3 does not quite include this since it works in a \(\lambda ^{-\delta }\) neighborhood of x. However, the full version of our estimates, Theorem 9, allows for the neighborhood of x to shrink arbitrarily slowly and thus recovers these earlier results.
Remark 1.6
(Resolution functions) There are several reasons why we state our theorems in terms of a general resolution function. First, it is necessary to allow \(\textbf{T}(R)\) to grow arbitrarily slowly as \(R\rightarrow 0\) to recover the o(1) results of [17, 38, 41] (see Remark 1.8). Second, while it may appear from Tables 1 and 2, that \(\textbf{T}(R)\) is always either \(c\log R^{-1}\) or the trivial case of \({{\,\textrm{inj}\,}}(M)\), this is not always true. In fact, one can check that many integrable examples are non-looping or non-periodic for \(\textbf{T}(R)\gg \log R^{-1}\). At the moment, the authors are not aware of concrete examples with \(\textbf{T}(R)\ll \log R\). However, it is likely that for any sub-logarithmic resolution function \(\textbf{T}\), with \(\textbf{T}(R)\rightarrow \infty \) as \(R\rightarrow 0^+\), a modification of the construction from [6] yields a metric on the sphere for which there is a point x such that x is not \((t_0,\textbf{T})\) non-looping for any \(t_0>0\), but there is a resolution function \(\textbf{T}_1\) with \(\textbf{T}_1(R){\longrightarrow } \infty \) as \(R\rightarrow 0^+\) and \(t_0>0\) such that x is \((t_0,\textbf{T}_1)\) non-looping. Also, note that our non-periodic, non-looping, and non-recurrent conditions are all monotonic in \(\textbf{T}\) in the sense that if \(\textbf{T}_1(R)\le \textbf{T}_2(R)\), and one of these conditions hold with the resolution function \(\textbf{T}_2\), then it also holds with \(\textbf{T}_1\).
1.2 Off diagonal Weyl remainders
The off diagonal behavior of \(\Pi _\lambda (x,y)\) plays a crucial role in understanding monochromatic random waves (see e.g. [7]) as well as in estimates for \(L^p\) norms of Laplace eigenfunctions (see e.g. [40, Section 5.1]). This problem is more complicated than the on diagonal situation since understanding the far off diagonal (i.e., \(d(x,y)>{{\,\textrm{inj}\,}}(M)\)) regime typically involves parametrices for \(e^{it\sqrt{-\Delta _g}}\) for \(t>{{\,\textrm{inj}\,}}(M)\), which are difficult to control. Notably, our geodesic beam techniques allow us to overcome this difficulty when estimating errors.
To control \(\Pi _\lambda (x,y)\) off-diagonal, we introduce a dynamical condition on the non-recurrence properties of the geodesics joining a point x with itself. To our knowledge, this is the first time non-recurrence is used in understanding off-diagonal Weyl remainders. For \(x \in M\), \({U} \subset S_x^*M\), \(t_0>0\), \(T>0\), and \(R>0\), let
Definition 1.7
Let \({\mathfrak {t}}\) and \(\textbf{T}\) be resolution functions and \(R_0>0\). We say \(x \in M\) is \({({\mathfrak {t}},}\textbf{T})\) non-recurrent at scale \(R_0\) if for all \(\rho \in S^*_xM\) there exists a choice of ± such that for all \(A\subset B_{_{S^*_xM}}(\rho ,R_0)\), \(\varepsilon >0\), \(r>0\) with \(\textbf{T}(r)>{{\mathfrak {t}}(\varepsilon )}\), and \(0<R<R_0\),

Heuristically, the way to think about Definition 1.7 is as follows. Recall that the standard definition of recurrence of a set \(A\subset S^*_xM\) is that that for all \(B\subset A\) and \(\mu _{_{S^*_xM}}\)-almost every \(\rho \in B\), the geodesic through \(\rho \) returns to B infinitely often. Definition 1.7 is a strengthening of the statement that no recurrent set exists. Indeed, the set \(\mathcal {R}^{R}_{_{{U},{\pm }}}(t_0,T)\) consists of those points in U which return R close to U in times between \(t_0\) and T. Thus, a set is non-recurrent according to Definition 1.7 if every subset A of \(S^*_xM\) has the property that the collection of points which are close to A and almost return to A in time \({\mathfrak {t}}(\varepsilon )\) has volume smaller than \(\varepsilon \) times that of the ball of radius R around A. Thus, in particular, most points eventually do not come close to A and hence A is also non-recurrent in the traditional sense.
If (x, y) is a \((t_0, \textbf{T})\) non looping pair for some \(t_0>0\) we measure the difference between \(\Pi _\lambda (x,y)\) and its smoothed version which takes into account propagation up to time \(t_0\). Let \(\rho \in \mathcal {S}({\mathbb {R}})\) with \({\hat{\rho }}(0)\equiv 1\) on \([-1,1]\) and \({{\,\textrm{supp}\,}}{\hat{\rho }}\subset [-2,2]\). For \(\sigma >0\) we define
For \(x,y \in M\), \(t_0>0\), and \(\lambda >0\), let
where the convolution is taken in the \(\lambda \) variable. The quantity \(E_{\lambda }^{t_0}\) is the appropriate one to estimate since, under non-looping type assumptions, one expects the main contribution to the kernel of the spectral projector to come from short (fixed) time wave propagation.
Below is our first off diagonal result.
Theorem 4
Let \(\alpha ,\beta \in {\mathbb {N}}^n\), \(0<\delta <\frac{1}{2}\), \(C_{_{\!{\text {nl}}}}>0\), \({R_0>0}\), \({\Omega _0}>0\), \({\varepsilon }>0\), and \({\mathfrak {t}}\) be a resolution function, there is \(C_{_{0}}>0\) such that if \(\textbf{T}_j\) is a sub-logarithmic resolution function with \(\Omega (\textbf{T}_j)<{\Omega _0}\) for \(j=1,2\) and \(\textbf{T}_{\max }=\max (\textbf{T}_1,\textbf{T}_2)\), then there is \(\lambda _0>0\) such the following holds. If \(x_0,y_0 \in M\) and \(t_0>0\) are such that \(x_0\) and \(y_0\) are respectively \(({\mathfrak {t}},\textbf{T}_1)\) and \(({\mathfrak {t}},\textbf{T}_2)\) non-recurrent at scale \(R_0\), and \((x_0,y_0)\) is a \((t_0,{\textbf{T}_{\max }})\) non-looping pair with constant \(C_{_{\!{\text {nl}}}}\), then for \(\lambda >\lambda _0\)
See Table 2 in Sect. 1.3 for some examples to which Theorem 4 applies.
To compare Theorems 3 and 4, note that for \(x,y\in M\) with \(d(x,y)<\varepsilon <{{\,\textrm{inj}\,}}(M)\),
where \(q_{{\lambda }}(x,y, \xi ){=} 1+\lambda ^{-1}q_{-1}(x,y,\xi )\) and \(q_{-1}(x,y,\xi )=O(d(x,y))\) (see e.g. [13, Proof of Proposition 10]). Then, for points x, y with \(d(x,y)<\lambda ^{-\delta }\), modulo terms smaller than our remainder, \(E^0_\lambda (x,y)\) as defined in (1.6) is the same as \(E^\varepsilon _\lambda (x,y)\).
For any \(t_0<\infty \), it is possible to write an oscillatory integral expression for \(\rho _{t_0}*\Pi _{\lambda }(x,y)\). However, its precise behavior in \(\lambda \) depends heavily on the geometry of (M, g); in particular, on the structure of the set of geodesics from x to y. This explains why we state our estimates in terms of \(E_{\lambda }^{t_0}\).
More generally, our results apply to averages of \(\Pi _\lambda (x,y)\) with \(x \in H_1\) and \(y \in H_2\), where \(H_1,H_2\) are any two smooth submanifolds of M. This type of integral is known as a Kuznecov sum [47] and appears in the analytic theory of automorphic forms [5, 23, 24, 29, 34]. All our dynamical assumptions for points \(x,y \in M\) above may be defined for the submanifolds \(H_1,H_2 \subset M\) instead. In doing so, the only change needed is to use the sets of unit co-normal directions \(S\!N^*\!H_1\) and \(S\!N^*\!H_2\), instead of \(S_x^*M\) and \(S_y^*M\). See Definitions 1.12 and 1.13 for a detailed explanation. In what follows \(d\sigma _{_{\!H_1}}\) and \(d\sigma _{_{\!H_2}}\) denote the volume measures induced by the Riemannian metric on \(H_1\) and \(H_2\) respectively.
Theorem 5
Let \(\alpha ,\beta \in {\mathbb {N}}^n\), \({1}\le k_1\le n\), \({1}\le k_2\le n\), \(C_{_{\!{\text {nl}}}}>0\), \({\Omega _0}>0\), \({\varepsilon }>0\), \({R_0}>0\), and \({\mathfrak {t}}\) be a resolution function. There is \(C_{_{0}}{=C_{_{0}}(\alpha ,\beta ,k_1,k_2,n,C_{_{\!{\text {nl}}}},\Omega _0,\varepsilon ,R_0,{\mathfrak {t}})}>0\) such that if \(\textbf{T}_j\) is a sub-logarithmic resolution function with \(\Omega (\textbf{T}_j)<{\Omega _0}\) for \(j=1,2\) and \(\textbf{T}_{\max }=\max (\textbf{T}_1,\textbf{T}_2)\) the following holds. If \(t_0>0\), and \(H_j\subset M\) are submanifolds of codimension \(k_j\) such that \((H_1,H_2)\) is a \((t_0,{\textbf{T}_{\max }})\) non-looping pair with constant \(C_{_{\!{\text {nl}}}}\), and \(H_j\) is \(({\mathfrak {t}},\textbf{T}_j)\) non-recurrent at scale \(R_0\) for \(j=1,2\), then there is \(\lambda _0>0\) such that for \(\lambda >\lambda _0\)
See Table 2 in Sect. 1.3 for some examples to which Theorem 5 applies.
To our knowledge, Theorem 5 is the first theorem to give improved remainders for Kuznecov sum remainders under dynamical assumptions. Theorems 3, 4, and 5 are consequences of our results for general semiclassical pseudodifferential operators (see Theorems 8 and 9).
1.3 Applications
In this section we present some examples to which our theorems apply. For each of them we give a reference for the detailed proofs that the relevant assumptions are satisfied. Note that Appendix B contains many examples not listed in Tables 1 and 2, and that the results from [8] can be used to find additional examples. With the exception of the final three rows of Table 1 with \(W=M\), all the estimates in Tables 1 and 2 are new.
In Table 1, we list examples where the assumptions of Theorem 2 hold. The final two examples are due to Volovoy [44].
In Table 2 we list some examples for which Theorems 4 and 5 hold. In each case there exists \(t_0>0\) such that \((H_1, H_2)\) is a \((t_0, {\max (\textbf{T}_1,\textbf{T}_2)})\) non-looping pair. Note that we omit labeling points for which \(\textbf{T}_2={{\,\textrm{inj}\,}}(M)\) since being \({{\,\textrm{inj}\,}}(M)\) non-recurrent is an empty statement. In these cases the gain in the pointwise Weyl law is \(\sqrt{\log \lambda }\) instead of \(\log \lambda \).
1.4 Further improvements
Many experts believe that, for a Baire generic Riemannian metric on a smooth compact manifold, there is \(\delta >0\) such that \(E(\lambda )=O(\lambda ^{n-1-\delta })\). Presently, this type of improved remainder is only available when the geodesic flow has special structure e.g. the flat torus, non-Zoll convex analytic surfaces of revolution, or compact Lie groups of rank \(>1\) with bi-invariant metric [44]. Specifically, the geodesic flow must expand only polynomially in time, \(\Vert d\varphi _t\Vert _{L^\infty (TS^*\!M)}\le C\langle t\rangle ^N\) for some \(N>0\). Typically, geodesics will instead expand exponentially in some places and, because of this, Egorov’s theorem generally only holds to logarithmic times. In fact, the only ingredient in our proof which restricts us to logarithmic improvements is Egorov’s theorem. Under the assumption of polynomial expansion one can prove an Egorov theorem to polynomial times and hence obtain polynomially improved remainders using our methods. We do not pursue this here since the present article is intended to apply on a general manifold and the polynomial times involved in such an Egorov theorem are not explicit. We instead plan to address the integrable case specifically in a future article.
1.5 Weyl laws for general operators
Let \(\Psi ^m(M)\) denote the class of semiclassical pseudodifferential operators of order \(m>0\) and \(P(h) \in \Psi ^m(M)\) be self-adjoint, with principal symbol p, that is positive and classically elliptic in the sense that there is \(C>0\) such that
Let \(\{E_j(h)\}_j\) be the eigenvalues of P repeated with multiplicity. For \(s\in {\mathbb {R}}\) we work with \(\Pi _h(s):=\mathbb {1}_{(-\infty ,s]}(P(h)),\) which is the orthogonal projection operator
For \(x,y \in M\) we write \(\Pi _h(s; x,y)\) for its kernel
where \(\{\phi _{_{E_j(h)}}\}_j\) is an orthonormal basis for \(L^2(M)\) with \( P(h)\phi _{_{E_j(h)}}=E_j(h)\phi _{_{E_j(h)}}. \) Note that one integrates (1.10) against the Riemannian volume density \({{\,\mathrm{{\text {dv}}}\,}}_g(y)\).
Let \( \varphi _t:T^*M \rightarrow T^*M \) denote the Hamiltonian flow for p at time t. We recall the maximal expansion rate for the flow and the Ehrenfest time at frequency \(h^{-1}\) respectively:
Note that \(\Lambda _{\max }\in [0,\infty )\) and if \(\Lambda _{\max }=0\), we may replace it by an arbitrarily small constant.
Remark 1.8
(Little oh improvements) When the expansion rate \(\Lambda _{\max }=0\) (see (1.11)) and our dynamical assumptions hold for \(\textbf{T}(R)\gg \log R^{-1}\), our theorems can be used to obtain \(o(1/\log \lambda )\) improvements over standard remainders. In special situations where the geodesic flow has sub-exponential expansion, we expect similar results with improvements beyond \(o(1/\log \lambda )\).
Definition 1.9
Let \(a, b \in {\mathbb {R}}\) with \(a\le b\). Let \(t_0>0\) and \(\textbf{T}\) be a resolution function. A set \(U\subset T^*M\) is said to be \( \textbf{T}\) non-periodic for p in the window [a, b] provided that for all \(E\in [a,b]\) Definition 1.2 holds with \(\varphi _t\) being the Hamiltonian flow for p, and with \(S^*M\) replaced by \(p^{-1}(E)\).
The following is our most general version of the Weyl Law. We write \(\pi _{_{M}}:T^*M \rightarrow M\) for the natural projection and \({{\textsf{H}}_p}\) for the Hamiltonian vector field for p.
Theorem 6
Let \(0< \delta <\frac{1}{2}\), \(\ell \in {\mathbb {R}}\), and \(\mathcal {V}\subset \Psi ^\ell (M)\) a bounded subset, \(U\subset T^*M\) open, \(t_0>0\), \(C_{_{U}}>0\), and \(a,b\in {\mathbb {R}}\) with \(a\le b\). Suppose \(d\pi _{_{M}}{{\textsf{H}}_p}\ne 0\) on \(p^{-1}([a,b])\cap {\overline{U}}\). Then, there is \(C_{_{0}}>0\) such that the following holds. Let \(K>0\), \(A\in \mathcal {V}\) with \({\hbox {WF}}_{\textrm{h}}(A)\subset U\), \(\Lambda >\Lambda _{\max }\), \(\textbf{T}\) be a sub-logarithmic resolution function with \(\Lambda \Omega (\textbf{T})<1-2\delta \), and suppose U is \(\textbf{T}\) non-periodic in the window [a, b] with
Then, there is \(h_0>0\) such that for all \(0<h<h_0\), and \(E\in [a,b+Kh]\)
Since the second term in (1.13) involves only short time propagation for the Schrödinger group \(e^{itP/h}\), its asymptotic expansion in powers of h can in principle be obtained. This calculation is routine, but long, so we do not include it here. For the details when \(P=-h^2\Delta _g\), we refer the reader to [17, Proposition 2.1]. In addition, if \(U\subset T^*M\) has smooth boundary which intersects \(p^{-1}(E)\) transversally for \(E\in [a,b]\), then (1.12) holds. Although the statement of Theorem 6 is cumbersome when U with rough boundary is allowed, it is natural to consider dynamical assumptions on this type of set. Indeed, many dynamical systems exhibit the so-called ‘chaotic sea’ with ‘integrable islands’ behavior where the dynamics are aperiodic in the sea; a set which typically has very rough boundary.
Next, we consider generalized Kuznecov [34] type sums of the form
where \(A_1,A_2\in \Psi ^\infty (M)\) and \(H_1, H_2 \subset M\) are two submanifolds of M.
Let \(H\subset M\) be a smooth submanifold. For \(a,b \in {\mathbb {R}}\), \(a \le b\), define
Definition 1.10
We say a submanifold \(H\subset M\) of codimension k is conormally transverse for p in the window [a, b] if given \(f_1,\dots , f_{k}\in C_c^\infty (M;{{\mathbb {R}}})\) locally defining H, i.e. with \(H= \bigcap _{i=1}^k\{f_i=0\}\) and \(\{df_i\}\text { linearly independent on }H,\) we have
Here, we interpret \(f_i\) as a function on the cotangent bundle by pulling it back through the canonical projection map.
Remark 1.11
If \(P(h)=-h^2\Delta _g\), then \(p(x,\xi )=|\xi |^2_{g(x)}\). Working with \(a=b=1\), we have \( \Sigma _{_{[a,b]}}^H= S\!N^*H\). In this setup every submanifold \(H \subset M\) is conormally transverse for p.
Definition 1.12
Let \(H_1, H_2 \subset M\) be two smooth submanifolds. Let \(a, b \in {\mathbb {R}}\) with \(a\le b\). Let \(t_0>0\), \(\textbf{T}\) a resolution function, and \(C_{_{\!{\text {nl}}}}>0\). We say \((H_1,H_2)\) is a \((t_0, \textbf{T})\) non-looping pair in the window [a, b] with constant \(C_{_{\!{\text {nl}}}}\) provided that Definition 1.3 holds for all \(E\in [a,b]\) with \(\varphi _t\) being the Hamiltonian flow for p and with \({\mathcal {L}}_{x,y}^{{R}}\) changed to
and with \({S_x^*M}\) and \({S_y^*M}\) replaced with \( \Sigma _{_{E}}^{H_1} \) and \( \Sigma _{_{E}}^{H_2}\) respectively. We say H is \((t_0,\textbf{T})\) non-looping if (H, H) is a \((t_0,\textbf{T})\) non-looping pair.
Definition 1.13
Let \(H \subset M\) be a smooth submanifold. Let \(a, b \in {\mathbb {R}}\) with \(a\le b\). Let \(t_0>0\), \(R_0>0\), \(0<C_{_{\!{\text {nr}}}}<1\), and let \(\textbf{T}\) be a resolution function. H is said to be \(\textbf{T}\) non-recurrent in the window [a, b] with constants \({(R_0,C_{_{\!{\text {nr}}}})}\) provided Definition 1.7 holds for any \(E\in [a,b]\) with \( S^*_xM\) replaced by \( \Sigma _{_{E}}^H\) and where \(\varphi _t\) is the Hamiltonian flow for p.
To state our main estimate for Kuznecov sums, let \(\rho \in \mathcal {S}({\mathbb {R}})\) with \({\hat{\rho }}(0)\equiv 1\) on \([-1,1]\) and \({{\,\textrm{supp}\,}}{\hat{\rho }}\subset [-2,2]\). For \(T>0\) we define
We then introduce the remainder
Theorem 7
Let \(P(h) \in \Psi ^m(M)\) be a self-adjoint semiclassical pseudodifferential operator with classically elliptic symbol p. Let \({\mathfrak {t}}\) be a resolution function and \({\varepsilon >0}\). For \(j=1,2,\) let \(H_j\subset M\) be submanifolds with co-dimension \(k_j\). Let \(a, b\in {\mathbb {R}}\) such that \(H_j\) is conormally transverse for p in the window [a, b] for \(j=1,2\). Let \({R_0}>0,\) \(t_0>0\), and for \(j=1,2\), let \(\textbf{T}_j\) be sub-logarithmic resolution functions and \(\textbf{T}_{\max }=\max (\textbf{T}_1,\textbf{T}_2)\). Suppose \(H_j\) is \({({\mathfrak {t}},\textbf{T}_j)}\) non-recurrent in the window [a, b] with constant \({R_0}\) for each \(j=1,2\), and \((H_1,H_2)\) is a \((t_0, {\textbf{T}_{\max }})\) non-looping pair in the window [a, b] with constant \(C_{_{\!{\text {nl}}}}\). Then, for all \(A_1, A_2\in \Psi ^\infty (M)\), there exist \(h_0>0\) and \(C_{_{0}}>0\) such that for all \(0<h\le h_0\), \(K>0\), and \({s}\in [a-Kh,b+Kh]\)
Remark 1.14
We omit the precise dependence of the constant \(C_{_{0}}\) on various parameters in Theorem 7. Instead, we refer the reader to our main theorem on averages, Theorem 8, where we have introduced notation to handle uniformity in families of submanifolds \(H_1\) and \(H_2\).
1.6 Outline of the paper and ideas from the proof
In Sect. 2 we introduce the notion of good coverings by tubes and various assumptions on these coverings which allow us to adapt the results of [11] to our setup. We also state our main averages theorem in its full generality (Theorem 8). Section 3 studies how the dynamical assumptions in the introduction relate to the assumptions on coverings by tubes from Sect. 2. In Sect. 4 we adapt the crucial estimates coming from the geodesic beam techniques [11] so that they can be applied to the study of Weyl remainders. Next, in Sect. 5, we estimate the scale (in the energy) at which averages of the spectral projector behave like Lipschitz functions in the spectral parameter. With this in hand, we are able to approximate \(\Pi _h\) using \(\rho _{_{h,T(h)}}*\Pi _h\) with \(T(h)=\sqrt{\textbf{T}_1(h)\textbf{T}_2(h)}\). Finally, Sect. 6 shows that the \(\rho _{_{h,T(h)}}*\Pi _h\) approximation is close to \(\rho _{h,t_0}*\Pi _h\), finishing the proof of our main theorem on averages. Section 7 contains the proof of our theorems on the Weyl remainder. This section follows the same strategy as that for averages: an estimate for the Lipschitz scale of the trace of the spectral projector, followed by relating \(\rho _{_{h,T(h)}}*\Pi _h\) to \(\rho _{_{h,t_0}}*\Pi _h\). In Appendix A we present an index of notation and in Appendix B we give examples including those from Table 2 to which our theorems can be applied.
The main idea of this article is to view the kernel of the spectral projector \(\mathbb {1}_{[t-s,t]}(P)\) as a quasimode for P. This allows us to use the geodesic beam techniques from [11] to control the energy scale at which the projector behaves like a Lipschitz function and hence to estimate the error when the projector is smoothed at very small scales. This idea is used a second time when controlling \((\rho _{h,T(h)}-\rho _{h,t_0}) *\Pi _h\) to estimate the contribution from small volumes of the possibly looping tubes. A simple argument using Egorov’s theorem controls the remaining non-looping tubes. The crucial insight used to handle the Weyl law is to view the kernel of the spectral projector as a distribution on \(M\times M\), where it is a quasimode for \({\textbf{P}}:=P\otimes 1\), and to study the Weyl Law via integration of the kernel over the diagonal. By doing this, we are able to reduce the problem to bounding an average of a quasimode over a submanifold, a setting in which geodesic beam techniques apply.
Note that Theorems 2 and 6 are proved in Sects. 7.1.4 and 7.1.3 respectively. Theorem 1 is a corollary of Theorem 2; the necessary dynamical properties are proved in Appendix B.1.1. Theorems 3, 4, 5, and 7 follow from an application of Theorem 9 (See Sect. 2.4 for Theorems 3, 4, and 5. Theorem 7 is a direct corollary of Theorem 9.). The fact that Theorem 9 follows from Theorem 8 is proved in Sect. 9 and Theorem 8 is proved in Sect. 6.2.
Acknowledgements. The authors would like to thank Dmitry Jakobson, Iosif Polterovich, John Toth, Dmitri Vassiliev and Steve Zelditch for helpful comments on the existing literature and Maciej Zworski for suggestions on how to improve the exposition and presentation, and Leonid Parnovski for comments on a previous draft. Thanks also to the anonymous referee who’s comments improved the exposition. The authors are grateful to the National Science Foundation for partial support under grants DMS-1900434 and DMS-1502661 (JG) and DMS-1900519 (YC). Y.C. is grateful to the Alfred P. Sloan Foundation.
2 Results with dynamical assumptions via coverings by tubes
We divide this section in four parts. In Sect. 2.1 we introduce the analogues of Definitions 1.12 and 1.13 via the use of coverings by bicharacteristic tubes. Microlocalization to these tubes will eventually be used to generate bicharacteristic beams. In Sect. 2.2 we introduce the uniformity assumptions that allow us to obtain uniform control of the constants in all our results. In Sect. 2.3 we state the most general version of our results, using the definitions via coverings by tubes, and the uniformity assumptions.
2.1 Dynamical assumptions via coverings by tubes
Let \(H\subset M\) be a smooth submanifold that is conormally transverse for p in the window [a, b]. Let \({\mathcal {Z}}\subset T^*M\) with
be a hypersurface that is transverse to the flow, and \( \varphi _t \) continue to denote the Hamiltonian flow for p at time t. Given \(A \subset \Sigma _{_{[a,b]}}^{H}\), \(\tau >0\), and \(r>0\), we define
Let \(\tau _{_{{{\,\textrm{inj}\,}}_H}}>0\) be small enough so that the map
is injective. Given \(r>0\), \(0<\tau <\tau _{_{{{\,\textrm{inj}\,}}_H}}\), and a collection of points \(\{\rho _j\}_{j\in \mathcal {J}(r)}\), we will work with the tubes
A \((\tau , r)\)-cover for \(A\subset T^*M\) is a collection of tubes \(\{\mathcal {T}_j(r)\}_{j\in \mathcal {J}(r)}\) where \(\mathcal {J}(r)\subset {\mathbb {N}}\) for which
Let \({\mathfrak {D}}>0\). We say a \((\tau ,r)\)-cover is a \(({\mathfrak {D}},\tau ,r)\)-good cover, if there is a splitting \(\mathcal {J}(r)=\sqcup _{i=1}^{{\mathfrak {D}}}\mathcal {J}_i(r)\) such that for all \(1\le i\le {\mathfrak {D}}\) and \(k{\ne }\ell \in \mathcal {J}_i(r)\),
For \(E\in {\mathbb {R}}\) and \(r>0\), we adopt the notation
We are now ready to introduce the definitions via coverings of our dynamical assumptions. First, for \(0<t_0<T_0\), we say \(A\subset T^*\!M\) is \([t_0,T_0]\) non-self looping if
Definition 2.1
(non looping pairs via coverings) Let \(t_0>0\), \({\tau _0}>0\), \({{\mathfrak {D}}}>0\), and \(\textbf{T}\) be a resolution function. Let \(H_1, H_2\) be two submanifolds and \(U_1\subset {N^*H_1}\), \(U_2\subset N^*H_2\). We say \((U_1,U_2)\) is a \((t_0, \textbf{T})\) non-looping pair in the window [a, b] via \({\tau _0}\)-coverings with constant \({C_{_{\!{\text {nl}}}}}\) provided for all \(0<\tau <\tau _0\) there exists \(r_0>0\) such that for \(0<r<{r_0}\), any two \(({{\mathfrak {D}}},\tau , r)\)-good covers of \(U_1\cap \Sigma _{_{[a,b]}}^{H_1}\) and \(U_2\cap \Sigma _{_{[a,b]}}^{H_2}\), \(\{\mathcal {T}_j^1(r)\}_{j\in \mathcal {J}^1(r)}\) and \(\{\mathcal {T}_j^2(r)\}_{j\in \mathcal {J}^2(r)}\) respectively, and every \(E\in [a,b]\), there is splittings of indices
satisfying
-
(1)
for each \({i,k\in \{1,2\}}\), \(i\ne k\) every \(\ell \in \mathcal {G}_{_{E}}^i(r)\),
$$\begin{aligned} \Bigg (\bigcup _{{t_0+\tau \le |t|\le \textbf{T}(r)-\tau }} \varphi _t \Big (\mathcal {T}_\ell ^i(r)\Big ) \Bigg ) \bigcap \Bigg ( \bigcup _{j \in \mathcal {J}^k_{_{E}}(r)} \mathcal {T}_j^k(r) \Bigg )=\emptyset , \end{aligned}$$ -
(2)
\(r^{2({n-1})}|\mathcal {B}_{_{E}}^1(r)||\mathcal {B}_{_{E}}^2(r)|\textbf{T}(r)^2\le {{\mathfrak {D}}^2}C_{_{\!{\text {nl}}}}.\)
We will say \((H_1,H_2)\) is a \((t_0,\textbf{T})\) non-looping pair in the window [a, b] via \(\tau \)-coverings if \((N^*H_1,N^*H_2)\) is. We will also say H is \((t_0, \textbf{T})\) non-looping in the window [a, b] via \(\tau \) coverings whenever (H, H) is a non-looping pair.
In Definition 2.1, the sets \(\mathcal {B}_{_{E}}\) and \(\mathcal {G}_{_{E}}\) should be thought of as respectively ‘bad’ and ‘good’ tubes. The tubes \(\mathcal {B}_{_{E}}\) are ‘bad’ in the sense that they may connect \( \Sigma _{_{[a,b]}}^{H_1}\) and \( \Sigma _{_{[a,b]}}^{H_2}\) under the Hamiltonian flow for p in a relatively short time, while the tubes \(\mathcal {G}_{_{E}}\) are ‘good’ in the sense that they do not connect these two sets for some controlled amount of time (see part (1) of the definition). Part (2) of the definition guarantees that there are not too many bad tubes connecting \( \Sigma _{_{[a,b]}}^{H_1}\) and \( \Sigma _{_{[a,b]}}^{H_2}\).
In Sect. 3, we prove that non looping in the sense of Definition 1.12 is equivalent to non looping by coverings in the sense of Definition 2.1.
Definition 2.2
(non-recurrence via coverings) Let \({\tau _0}>0\), \({{\mathfrak {D}}}>0\), and \(\textbf{T}\) be a resolution function. We say H is \(\textbf{T}\) non-recurrent in the window [a, b] via \({\tau _0}\)-coverings with constant \(C_{_{\!{\text {nr}}}}\) provided for all \(0<\tau <\tau _0\) there exists \(r_0>0\) such that for \(0<r<{r_0}\), every \(({{\mathfrak {D}}},\tau , r)\)-good cover of \( \Sigma _{_{[a,b]}}^{H}\), \(\{\mathcal {T}_j(r)\}_{j\in \mathcal {J}(r)}\), and \(E\in [a,b]\), there exists a finite collection of sets of indices \(\{\mathcal {G}_{_{E,\ell }}(r)\}_{\ell \in {\mathcal {L}_{_{E}}(r)}}\) with \( \mathcal {J}_{_{E}}(r)=\bigcup _{\ell \in {\mathcal {L}_{_{E}}(r)}}\mathcal {G}_{_{E,\ell }}(r), \) and so that for every \(\ell \in {\mathcal {L}_{_{E}}(r)}\) there exist functions \(t_\ell (r)>0\) and \({T_\ell (r)}>0\), with \(0\le t_\ell (r)\le T_\ell (r)\le \textbf{T}(r)\), so that
-
(1)
\(\bigcup _{j\in \mathcal {G}_{_{E,\ell }}(r)}\mathcal {T}_j(r)\;\;\text { is }\;\;[t_\ell (r),T_{\ell }(r)]\text { non-self looping},\)
-
(2)
\(r^{\frac{n-1}{2}}\sum _{\ell \in {{\mathcal {L}}_{_{E}}(r)}} {\big (|\mathcal {G}_{_{E,\ell }} (r)|t_\ell (r){T_\ell (r)}^{-1}\big )^{\frac{1}{2}}} \le {{\mathfrak {D}}^{\frac{1}{2}}}C_{_{\!{\text {nr}}}}\,\textbf{T}(r)^{-\frac{1}{2}}.\)
In Definition 2.2, the sets \(\mathcal {B}_{_{E}}\) and \(\mathcal {G}_{_{E}}\) should again be thought of as respectively ‘bad’ and ‘good’ tubes. The tubes \(\mathcal {B}_{_{E}}\) are ‘bad’ in the sense that they may self intersect under the Hamiltonian flow for p in a relatively short time, while the tubes \(\mathcal {G}_{_{E}}\) are ‘good’ in the sense that they do not self intersect these two sets for some controlled amount of time (see part (1) of the definition). Part (2) of the definition again guarantees that there are not too many bad tubes.
In Lemma 3.5 below we prove that non recurrence in the sense of Definition 1.13 implies non recurrence by coverings in the sense of Definition 2.2. At the moment, we are unable to determine whether these two definitions are equivalent.
2.2 Uniformity assumptions
Let \(H\subset M\) be a smooth submanifold. In practice, we prove estimates on \(\{{\tilde{H}}_h\}_h\), where \(\{{\tilde{H}}_h\}_h\) is a family of submanifolds such that
where \(R(h)>0\) and for every multi-index \(\alpha \) there is \({\mathcal {K}}_{_{\alpha }}>0\) such that for all \(h>0\)
Here \(\textbf{R}_{_{{{\tilde{H}}}_h}}\) and \(\mathbf{\Pi }_{_{{{\tilde{H}}}_h}}\) denote the sectional curvature and the second fundamental form of \({{\tilde{H}}}_h\). Without loss of generality, we will assume \({\mathcal {Z}}\) is chosen so that there exist \(N>0\), \(C=C(p,a,b,\{{\mathcal {K}}_\alpha \}_{|\alpha |\le N})>0,\) and \(r_0>0\) such that for all \(E\in [a,b]\), \(A\subset \Sigma _{_{E}}^H\) and \(0<r<r_0\),
We may do this since \(\dim {\mathcal {Z}}=2n-1\), \(\dim \Sigma _{_{E}}^{H}=n-1\), and \( \Sigma _{_{E}}^{H} \subset {\mathcal {Z}}\).
Note that when \(H=\{x_0\}\) is a point, the curvature bounds become trivial, and so in place of (2.7) we work with \(d(x_0,{\tilde{x}}_h)<{R(h)}\) and may take \({{\mathcal {K}}_{_{\alpha }}}\) to be arbitrarily close to 0. In what follows, let \(r_{_{H}}:T^*M\rightarrow {\mathbb {R}}\) be the geodesic distance to H, i.e., \(r_{_{H}}(x,\xi )=d(x,H)\) for \((x,\xi )\in T^*M\), and write \(\pi _{_{M}}:T^*M \rightarrow M\) for the natural projection.
Definition 2.3
(regular families) We will say a family of submanifolds \(\{H_h\}_{h}\) is regular in the window [a, b] if it satisfies (2.8) and there is \(\varepsilon >0\) so that for all \(h>0\), the map \((-\varepsilon ,\varepsilon )\times { \Sigma _{_{[a,b]}}^H}\rightarrow M\),
Then, define \(|{{\textsf{H}}_p}r_{_{\!H}}|: \Sigma _{_{[a,b]}}^H\rightarrow {\mathbb {R}}\) by
Definition 2.4
(uniformly conormally transverse submanifolds) A family of submanifolds \(\{{{\tilde{H}}}_h\}_{h}\) is said to be uniformly conormally transverse for p in the window [a, b] provided
-
(1)
\({{\tilde{H}}}_h\) is conormally transverse for p in the window [a, b] for all \(h>0\),
-
(2)
there exists \({\mathfrak {I}}_{_{\!0}}>0\) so that for all \(h>0\)
$$\begin{aligned} \inf \Big \{|{{\textsf{H}}_p}r_{_{\!{{\tilde{H}}}_{\!h}}}|(\rho )\,\,\big |\,\,{\rho \in \Sigma _{_{[a,b]}}^H}\Big \} \ge {\mathfrak {I}}_{_{\!0}}. \end{aligned}$$(2.11)
When the constants involved in our estimates depend on \(\{{{\tilde{H}}}_h\}_h\), they will do so only through finitely many of the \({\mathcal {K}}_{_{\alpha }}\) constants and the constant \({\mathfrak {I}}_{_{\!0}}\).
Remark 2.5
We note that for \(p(x, \xi )=|\xi |^2_{g(x)}\), \( {a=b=1,}\) and \( \Sigma _{_{[a,b]}}^H=S\!N^*\!H\), we have \(|{{\textsf{H}}_p}r_{_{\!H}}|(\rho )=2\) for all \(\rho \in S\!N^*\!H\). It follows that every family of submanifolds is uniformly conormally transverse and we may take \({\mathfrak {I}}_{_{\!0}}=2\).
2.3 Main results
We now state the main results from which all of our Kuznecov type asymptotics follow. Throughout the text, the notation \(C=C(a_1,\dots , a_k)\) means that the constant C depends only on \(a_1, \dots , a_k\).
Theorem 8
For \(j=1,2\), let \(k_j\in \{1,\dots ,n\}\), \({\mathfrak {I}}_{_{\!0}}^j>0\), \(A_j\in \Psi ^\infty (M)\). Let \(C_{_{\!{\text {nr}}}}^1>0\), \(C_{_{\!{\text {nr}}}}^2>0\) and \(C_{_{\!{\text {nl}}}}>0\). There is
such that the following holds.
Let \(P(h) \in \Psi ^m(M)\) be a self-adjoint semiclassical pseudodifferential operator, with classically elliptic symbol p. Let \(0<\delta <\frac{1}{2}\), \(K>0\), \(a,b \in {\mathbb {R}}\) with \(a\le b\), and for \(j=1,2\) let \(H_j{\subset M}\) be a submanifold with co-dimension \(k_j\) that is regular and uniformly conormally transverse for p in the window [a, b] (with constant \({\mathfrak {I}}_{_{\!0}}^j\) as in (2.11)). Then, there exists \(\tau _0>0\) with the following property. Let \(\Lambda >\Lambda _{\max }\), and \(t_0>0\). For \(j=1,2\) let \(\textbf{T}_j\) be a sub-logarithmic resolution function with \(\Lambda \Omega (\textbf{T}_j)<1-2\delta \) and such that the submanifold \(H_j\) is \(\textbf{T}_j\) non-recurrent in the window [a, b] via \({\tau _0}\)-coverings with constant \(C_{_{\!{\text {nr}}}}^j\). Suppose \((H_1,H_2)\) is a \((t_0,\textbf{T}_{\max })\) non-looping pair in the window [a, b] via \({\tau _0}\)-coverings with constant \(C_{_{\!{\text {nl}}}}\) where \(\textbf{T}_{\max }=\max (\textbf{T}_1,\textbf{T}_2)\). Let \(h^\delta \le R(h)=o(1)\) and for \(j=1,2\) let \(\{{\tilde{H}}_{j,h}\}_h\) be a family of submanifolds of codimension \(k_j\) that is regular, uniformly conormally transverse for p in the window [a, b], and satisfies
Then, there is \(h_0>0\) such that for all \(0<h\le h_0\) and \({s}\in [a-Kh,b+Kh]\),
We also have the following corollary involving the definitions of non-looping (Definition 1.12) and non-recurrence (Definition 1.13).
Theorem 9
Let \({\mathfrak {t}}\) be a resolution function, \(\Lambda >\Lambda _{\max }\), \(K>0\), \({\varepsilon }>0\), \(R_0>0\), \(0< \delta <\frac{1}{2}\), and for \(j=1,2\) let \(\textbf{T}_j\) be a sub-logarithmic resolution function with \(\Lambda \Omega (\textbf{T}_j)<1-2\delta \) and let \(\textbf{T}_{\max }=\max (\textbf{T}_1,\textbf{T}_2)\). Suppose the same assumptions as Theorem 8, but assume instead that for \(j=1,2\) the submanifold \(H_j\) is \({({\mathfrak {t}},\textbf{T}_j)}\) non-recurrent in the window [a, b] at scale \(R_0\), and \((H_1,H_2)\) is a \((t_0, {\textbf{T}_{\max }})\) non-looping pair in the window [a, b] with constant \(C_{_{\!{\text {nl}}}}\). Then, there exist \(C_{_{0}}={C_{_{0}}(n, k_1, k_2, A_1, A_2, {\mathfrak {I}}_{_{\!0}}^1, {\mathfrak {I}}_{_{\!0}}^2, {{\mathfrak {t}}}, C_{_{\!{\text {nl}}}})}\) and \(h_0>0\) such that for all \(0<h\le h_0\) and \({s}\in [a-Kh,b+Kh]\)
For the proof of Theorem 8, see Sect. 6.2 and for the proof of Theorem 9 see Sect. 9.
2.4 Application to the Laplacian
In this section we show how to obtain Theorems 3, 4, and 5 from Theorem 9. It will be convenient here and below to use semiclassical Sobolev spaces defined for \(s\in {\mathbb {R}}\) by the norms
To pass from Theorem 9 to theorems about the Laplacian, we work with an operator Q such that \(\sigma (Q)(x,\xi )=|\xi |_{g(x)}\) near \(\{(x,\xi ):\,|\xi |_{g(x)}=1\}\), Theorem 9 applies with \(P=Q\), and for \(\lambda =h^{-1}\) and all \(N>0\)
Recall that \(\rho _{_{h,t_0}}\) is defined as in (1.16). To build Q, let \(\psi _1,\psi _2\in C_c^\infty ({\mathbb {R}};[0,1])\) with \({{\,\textrm{supp}\,}}\psi _1\subset (-1/4,1/4)\), \({{\,\textrm{supp}\,}}\psi _2\subset [-16,16]\), \(\psi _1 \equiv 1\) on \([-1/16,1/16]\) and \(\psi _2 \equiv 1\) on \([-4,4]\). We claim
satisfies the desired properties. Observe that the second term in (2.14) is added to make Q classically elliptic, and that we use \(-h^2\Delta _g\) rather than \(\sqrt{-h^2\Delta _g}\) in order to apply [48, Theorem 14.9] to obtain \(Q\in \Psi ^2(M)\). Note also that Q is self-adjoint and \(\sigma (Q)=|\xi |_g\) on \(\{\frac{1}{2}\le |\xi |_g\le 2\}\),
and \(\mathbb {1}_{(-\infty ,s]}(Q)=\mathbb {1}_{(-\infty ,s]}(\sqrt{-h^2\Delta _g})=0\) for \(s<0\). Finally, we use the ellipticity of both Q and \(-h^2\Delta _g\) to obtain that for \(N\ge 0\)
Now, for all \(N>0\) and \(L>1\) there is \(C_{_{N,L}}>0\) so that \(|\rho \Big (\frac{t_0}{h}(1-s)\Big )|\le C_{_{N,L}} h^{2N+L}\langle s\rangle ^{-2N-L}\) on \(|s-1|>\frac{1}{2}\). Therefore
Combining (2.15) with (2.16) and (2.17), we obtain (2.13).
Now, every submanifold is conormally transverse for \(p(x,\xi )=|\xi |_{g(x)}\) at \(p^{-1}(1)\) with constant \({\mathfrak {I}}_{_{\!0}}=1\). Therefore, Theorems 3, 4, and 5 follow from Theorem 9. To see this, we set \(P=Q\), \(a=b=1\), and observe that the Hamiltonian flow for \(\sigma (Q)\) near \(S^*_xM\) is equal to the geodesic flow. In particular, the dynamical definitions 1.12 and 1.13 applied to Q at \(E=1\) are exactly Definitions 1.3 and 1.7 with \(S^*_xM\) replaced by \(SN^*H\). This is true because Definitions 1.3 and 1.7 are stated with \(\varphi _t\) being the homogeneous geodesic flow, i.e., the flow generated by \(|\xi |_{g(x)}\). Next, we apply Theorem 5 with \(\Lambda =2\Lambda _{\max }{+1}\), \(h=\lambda ^{-1}\), and work with the resolution functions \({\widetilde{\textbf{T}}}_j=(\Lambda {\Omega _0})^{-1}(1-2\delta )\textbf{T}_j\) for \(j=1,2\).
3 Dynamical assumptions and coverings
In this section we relate the non-looping and non-recurrence concepts introduced in Definitions 1.12 , 1.13, to their analogues via coverings given in Definitions 2.1, 2.2.
Proposition 3.1
Let \(H_1, H_2 \subset M\) be smooth submanifolds. Let \(a,b \in {\mathbb {R}}\) be such that \(H_1, H_2\) are conormally transverse for p in the window [a, b], and \(\tau _0>0\). Let \(t_0>0\), \(\textbf{T}\) a resolution function, and suppose \((H_1,H_2)\) is a \((t_0,\textbf{T})\) non-looping pair in the window [a, b] with constant \(C_{_{\!{\text {nl}}}}\). Then, there is \({\widetilde{C_{_{\!{\text {nl}}}}}}={\widetilde{C_{_{\!{\text {nl}}}}}}(p,a,b,n, C_{_{\!{\text {nl}}}},{H_1, H_2})>0\) such that \((H_1,H_2)\) is a \((t_0{+{3}\tau _0}, {{\widetilde{\textbf{T}}}})\) non-looping pair in the window [a, b] via \(\tau _0\)-coverings with constant \({\widetilde{C_{_{\!{\text {nl}}}}}}\) and with \({\widetilde{\textbf{T}}}(R)=\textbf{T}(4R){-{3}\tau _0}\).
Before proving the proposition, we record some facts about sub-logarithmic resolution functions.
Lemma 3.2
Suppose \(\textbf{T}\) is a sub-logarithmic resolution function.
-
(1)
For \(0<a<b<1\),
$$\begin{aligned} {\textbf{T}(b)\le \textbf{T}(a)}\le \frac{\log a}{\log b}\,{\textbf{T}(b)}. \end{aligned}$$In particular, \(\textbf{T}(R)\le \frac{\log R}{\log \mu +\log R} \textbf{T}(\mu R)\) for \(0<\mu <R^{-1}\).
-
(2)
Let \(f(s):=-\log (\textbf{T}^{-1}(s))\). Then, f extends to a differentiable function on \([0,\infty )\), \(f(0)=0\), and \(f(a)\le \frac{a}{b}f(b)\) for \(0<a<b\).
-
(3)
Let \(0<\delta <\frac{1}{2}\), and \(R(h)\ge h^\delta \) with \(R(h)=o(1)\). Then for all \(\Lambda >\Lambda _{\max }\), \(\varepsilon >0\), there is \(h_0>0\) such that for \(0<h<h_0\)
$$\begin{aligned} \textbf{T}(R(h))\le (\Omega (\textbf{T})\Lambda +\varepsilon )T_e(h). \end{aligned}$$
Proof
Note that
and hence the first claim holds. For the second claim, observe that since \(\textbf{T}\) is sub-logarithmic, \( f'(s)\ge -\frac{\log (\textbf{T}^{-1}(s))}{s}=\frac{f(s)}{s}. \)
To prove the last claim, observe that since \(R(h)=o(1)\), for all \(\Lambda >\Lambda _{\max }\) and \(\varepsilon >0\), there is \(h_0>0\) such that for \(0<h<h_0\),
The second inequality follows from definitions (1.2), (1.11), and \(R(h)\ge h^\delta \) with \(0<\delta <\frac{1}{2}\). \(\square \)
In the following lemma we explain how to partition a \(({\mathfrak {D}},\tau ,r)\)-good cover for \( \Sigma _{_{E}}^{H_1}\) into tubes that do not loop through \( \Sigma _{_{E}}^{H_2}\) for times in \((t_0, T)\), and tubes that are ‘bad’ in the sense that they do loop through \( \Sigma _{_{E}}^{H_2}\). We do this while controlling the number of ‘bad‘ tubes in terms of the size of the set \( {{\mathcal {L}}_{_{{H_1,H_2}}}^{{S},E}(t_0, T)}\) for \(S>4r\).
Lemma 3.3
Let \(a,b\in {\mathbb {R}}\), \(H_1, H_2 \subset M\) be smooth submanifolds such that \(H_1, H_2\) are conormally transverse for p in the window [a, b]. Then there is \(C_{_{0}}=C_{_{0}}(p,a,b,n,{H_1,H_2})\) such that the following holds. Let \(\tau _0>0\), \(r>0\), and \(0<\tau <\tau _0\). For \(i=1,2\) let \(\{\mathcal {T}_{j}^i(r)\}_{j\in {\mathcal {J}}^i(r)}\) be a \(({\mathfrak {D}},\tau ,r)\)-good cover of \(\Sigma ^{H_i}_{[a,b]}\). Let \(t_0>0\), \(T>0\). Then, for all \(E\in [a,b]\) and \( S\ge 4r \) there is a splitting \(\mathcal {J}_{_{E}}^1(r)=\mathcal {B}_{_{E}}^1(r)\cup \mathcal {G}_{_{E}}^1(r)\) such that
-
(1)
for \(j\in \mathcal {G}_{_{E}}^1(r)\) and \(k\in \mathcal {J}_{_{E}}^2(r)\)
$$\begin{aligned} \bigcup _{t_0+{{2}(\tau +r)}\le |t|\le T-{{2}(\tau +r)}}\varphi _t(\mathcal {T}_{j}^1(r))\cap \mathcal {T}_{k}^2(r)=\emptyset , \end{aligned}$$ -
(2)
 .
.
Proof
For \(j=1,2\) let \({\mathcal {Z}}_j\subset T^*M\) be the hypersurface transverse to the flow, with \( \Sigma _{_{[a,b]}}^{H_j} \subset {\mathcal {Z}}_j\), used to build the tubes of the cover, as explained in (2.1). Let \(E\in [a,b]\) and for \(S>0\) set
Then, for \(j\in \mathcal {B}_{_{E}}^{1}(r)\),
In particular, there exists \(C_{_{0}}={C_{_{0}}(p,a,b,n,{H_1,H_2})}>0\) such that for all \(S\ge 4r\)

This proves the claim in (2).
To see the claim in (1), let \(j\in \mathcal {G}_{_{E}}^1(r):=\mathcal {J}_{_{E}}^1(r)\setminus \mathcal {B}_{_{E}}^1(r)\). Then, \({{\mathcal {T}}_j^{{1}}}(r)={\Lambda _{\rho _j}^\tau }(r)\) for some \(\rho _j\in {\mathcal {Z}}_{1}\) with \(d(\rho _j, \Sigma _{_{E}}^{H_1})<2r\) and  . This yields that there is \(\rho _0\in \Sigma _{_{E}}^{H_1}\setminus \mathcal {L}_{_{H_1,H_2}}^{{S,E}}(t_0,T)\) such that \(d(\rho _0,\rho _j)<2r\). In particular, since \( \underset{t_0\le |t|\le T}{\bigcup }\varphi _t(B(\rho _0,S))\cap B( \Sigma _{_{E}}^{H_2},S)=\emptyset \) and \( {\mathcal {T}}_j^1(r)\subset \underset{|t|\le {\tau +r}}{\bigcup }\varphi _t(B(\rho _0,3r)), \) this yields
. This yields that there is \(\rho _0\in \Sigma _{_{E}}^{H_1}\setminus \mathcal {L}_{_{H_1,H_2}}^{{S,E}}(t_0,T)\) such that \(d(\rho _0,\rho _j)<2r\). In particular, since \( \underset{t_0\le |t|\le T}{\bigcup }\varphi _t(B(\rho _0,S))\cap B( \Sigma _{_{E}}^{H_2},S)=\emptyset \) and \( {\mathcal {T}}_j^1(r)\subset \underset{|t|\le {\tau +r}}{\bigcup }\varphi _t(B(\rho _0,3r)), \) this yields
for \(S\ge 4r\). On the other hand, since for all \(k \in \mathcal {J}_{_{E}}^2(r)\), we have \( {\mathcal {T}}_k^2(r)\cap {\mathcal {Z}}_{2}\subset B( \Sigma _{_{E}}^{H_2},3r), \)
In particular, combining (3.1) and (3.2) we have
Thus, the claim (1) holds, provided \(S\ge 4r\). \(\square \)
With Lemmas 3.2 and 3.3 in place, we are now ready to prove Proposition 3.1.
Proof of Proposition 3.1
Let \(C_{_{0}}=C_{_{0}}(p, a, b,n,{H_1,H_2})\) be as in Lemma 3.3. We apply Lemma 3.3 with \(r=R\), \(T=\textbf{T}(S)\), \(S=4R\), \(0<R<\frac{1}{2}\tau _0\). This shows that \((H_1,H_2)\) is a \([t_0{+{3}\tau _0}, {\widetilde{\textbf{T}}}]\) non-looping pair in the window [a, b] via \(\tau \)-coverings with constant \({\widetilde{C_{_{\!{\text {nl}}}}}}=C_0^2 C_{_{\!{\text {nl}}}}\). \(\square \)
Lemma 3.4
There is a constant \(C_n>0\), depending only on n, such that the following holds. Let \(\tau _0>0\), \(t_0>0\), \(H_1,H_2\subset M\) be smooth submanifolds such that \(H_1\) and \(H_2\) are conormally transverse for p in the window [a, b]. Let \(\textbf{T}\) be a resolution function. If \((H_1,H_2)\) is a \((t_0,\textbf{T})\) non-looping pair in the window [a, b] via \(\tau _0\)-coverings with constant \(C_{_{\!{\text {nl}}}}\), then \((H_1,H_2)\) is a \((t_0,{{\widetilde{\textbf{T}}}})\) non-looping pair in the window [a, b] with constant \(C_{_{\!{\text {nl}}}}{C_n}\) and \({\widetilde{\textbf{T}}}(R)=\textbf{T}(2R)\).
Proof
Let \(E\in [a,b]\) and fix \(i,j \in \{1,2\}\), \(i\ne j\). For each \(R>0\) consider the non-looping partition \(\mathcal {J}_{_{E}}^i({R})=\mathcal {G}_{_{E}}^i(R)\sqcup \mathcal {B}_{_{E}}^i({R})\) given by Definition (2.1). Let \(\rho \in \mathcal {L}_{_{H_i,H_j}}^{{{R}/2,E}}(t_0,{\textbf{T}(R)})\). Then, there are \(\rho _1\in B(\rho ,{R}/2)\) and \(t_0\le |t|\le {\textbf{T}(R)}\) such that \(\varphi _t(\rho _1)\in B( \Sigma _{_{E}}^{H_j},{R}/2)\). Hence, there is \(\ell \in {\mathcal {B}_{_{E}}^i}({R})\) such that \(\rho _1\in {\mathcal {T}}^i_\ell ({R})\) and hence \(\rho \in {\mathcal {T}}^i_\ell (2{R})\). This implies \( B_{_{{ \Sigma _{_{E}}^{H_i}}}}(\rho ,{R}/2)\subset {{\mathcal {T}}^i_\ell (3{R})}. \) Thus,

In particular, there exists \(C_{{n}}>0\) such that

Therefore,

The lemma follows from Definition 1.12 after taking the limit \(R \rightarrow 0^+\) and redefining \(C_n\). \(\square \)
Proposition 3.5
Let \({\mathfrak {t}}\), \(\textbf{T}\) be resolution functions and \(H \subset M\) be a smooth submanifold. Let \(a,b \in {\mathbb {R}}\) be such that H is conormally transverse for p in the window [a, b]. Suppose H is \({({\mathfrak {t}},\textbf{T})}\) non-recurrent in the window [a, b] at scale \(R_0\).
Then, there exists \({C_{_{\!{\text {nr}}}}=C_{_{\!{\text {nr}}}}}(M,p,{{\mathfrak {t}}},{R_0})>0\) such that for all \(\tau _0>0\), there is a resolution function \({\widetilde{\textbf{T}}}\) such that the submanifold H is \({\widetilde{\textbf{T}}}\) non-recurrent in the window [a, b] via \(\tau _0\)-coverings with constant \({C_{_{\!{\text {nr}}}}}\). Moreover, there is \(c>0\) such that if \(\textbf{T}\) is sub-logarithmic, then \({\widetilde{\textbf{T}}}(R)\ge c\textbf{T}(R)\) for all R.
The proof of this result hinges on two lemmas. To state the first one, we introduce a slight adaptation of [8, Definition 3]. Let \(\varepsilon _0>0\), \(\digamma >0\), \({\mathfrak {t}}_0:[\varepsilon _0, +\infty ) \rightarrow [1, +\infty )\), and \(f:[0,\infty )\rightarrow [0,\infty )\). We say a set \(A_0\) is \((\varepsilon _0,{\mathfrak {t}}_0,\digamma , f)\) controlled up to time T provided it is \((\varepsilon _0, {\mathfrak {t}}_0, \digamma )\) controlled up to time T in the sense of [8, Definition 3] except that we replace the condition on r by
and replace point (3) by
Next, fix \(E \in [a,b]\). Since H is \( {({\mathfrak {t}},}\textbf{T})\) non-recurrent in the window [a, b] at scale \({R_0}\), for all \(\rho \in \Sigma _{_{E}}^H\) there exists a choice of ± such that for all \(A \subset {B_{_{ \Sigma _{_{E}}^H}}(\rho ,R_0)}\), \(0<R<R_0\), \(\varepsilon >0\), and \(T>{{\mathfrak {t}}(\varepsilon )}\)

with f as in Lemma 3.2. Then, extract a finite cover of \( \Sigma _{_{E}}^H\) by balls \({\tilde{B}}_\rho =B(\rho ,R_{{0}}/2)\) and set
where \({B}_\rho =B(\rho ,R_{{0}})\). Note that, again using that H is non-recurrent with at scale \(R_0\), we may assume \(K\le C_n R_0^{1-n}\) where \(C_n\) is a constant depending only on n.
Lemma 3.6
Let H, \({\mathfrak {t}}\) and \(\textbf{T}\) be as in Proposition 3.5 and \(f(T):= -\log (\textbf{T}^{-1}(T))\). Then, there exist \(c_n>0\) depending only on n and \(\digamma >0\) such that for all \(E\in [a,b]\) and \({T>1}\) every ball in \(\mathcal {A}_{_{E}}\) is \((0,{{\mathfrak {t}}_0},\digamma , f)\) controlled up to time T with \({\mathfrak {t}}_0(\varepsilon )={\mathfrak {t}}(c_n\varepsilon )\).
Proof
Let \(E\in [a,b]\). Let \(A_0:=B_{\rho _0}\) for some \(B_{\rho _0}\in \mathcal {A}_{_{E}}\), \(\varepsilon _1>0\), \(\Lambda {>} \Lambda _{\max }\), and \(0<\tau <\tfrac{1}{2}\tau _{_{{{\,\textrm{inj}\,}}_H}}\). Let \(T> {1}\) and \(0\le {{\tilde{R}}}_0 \le \frac{1}{\digamma }e^{-\digamma \Lambda T }\) for \(\digamma >{2R_0^{-1}}\) to be determined later. Let \(0<r_0<{{\tilde{R}}}_0\). Suppose \(A_1\subset A_0\) and \(\{B_{0,i}\}_{i=1}^N\) are balls centered in \(A_0\) with radii \(R_{0,i}\in [r_0,{{\tilde{R}}}_0]\) such that \( A_1\subset \cup _{i=1}^N B_{0,i}\subset A_0. \)
Let \(R:=\tfrac{1}{2}\inf _i R_{0,i}\). There exist \(C_n>0\), depending only on n, and a collection of balls \(\{{\tilde{B}}_{0,i}\}_{i=1}^{N_0}\) of radius R, such that
Fix \(0\le r \le \frac{1}{\digamma }e^{-\digamma \Lambda T{-f(T)} }r_0\). Next, let \(\{B(q_j, r)\}_{j\in \mathcal {J}} \subset \Sigma _{_{E}}^H\) be a cover of \( \Sigma _{_{E}}^H\) by balls of radius r such that there are at most \({\mathfrak {D}}_n\) balls over each point in \( \Sigma _{_{E}}^H\), where \({\mathfrak {D}}_n>0\) depends only on n. Assume, without loss of generality, that (3.5) holds for \(\rho _0\) with the choice \(\pm =+\). Next, set \(\mathcal {J}_{_{\!A_1}}:=\{j \in \mathcal {J}:\; B(q_j, {\frac{1}{2}}e^{-f(T)}R)\cap \mathcal {R}^{{e^{-f(T)}}R}_{_{{A_1, +}}}({\mathfrak {t}}{(\varepsilon _1)},T)\ne \emptyset \}\). Defining the collection
we have  . Then, letting \(R_{1,i}:=\tfrac{1}{2}e^{-f(T)}R\), we have \(R_{1,i}\in [0,\tfrac{1}{4}{{\tilde{R}}}_0]\), and using that \(R<R_0/2\) the bound in (3.5) applied to \(A_1\) yields
. Then, letting \(R_{1,i}:=\tfrac{1}{2}e^{-f(T)}R\), we have \(R_{1,i}\in [0,\tfrac{1}{4}{{\tilde{R}}}_0]\), and using that \(R<R_0/2\) the bound in (3.5) applied to \(A_1\) yields
Next, by (3.7) note that \( B_{_{ \Sigma _{_{E}}^H}}(A_1,R)\subset \bigcup _{i=1}^{N_0}2{\tilde{B}}_{0,i}, \) where \(2{\tilde{B}}_{0,i}\) denotes the ball with the same center as \({\tilde{B}}_{0,i}\) but with radius 2R. Using (3.7) again there is \(C_n>0\) such that
Let \({\varepsilon :=\varepsilon _1} C_n {\mathfrak {D}}_n\). Combining (3.8) and (3.9) yields point (2) of [8, Definition 3] with \({\mathfrak {t}}_0(\varepsilon )={\mathfrak {t}}(\varepsilon /(C_n{\mathfrak {D}}_n))\). By the definition of R, we also note that point (3), which was replaced by (3.4), also holds.
It remains to check point (1) i.e. there is \(\digamma >0\) such that \(\Lambda ^\tau _{A_1\setminus \cup _{k}B_{1,k}}(r)\) is \([{\mathfrak {t}}_0{(\varepsilon )},T]\) non-self looping for \( 0<r<\frac{1}{\digamma }e^{-\digamma \Lambda T{-f(T)}}R. \) For this, suppose \(\rho _1,\rho _2\in \Lambda ^{\tau }_{A_1\setminus \cup _{k}B_{1,k}}(r)\) and \(t\in [{{\mathfrak {t}}_0(\varepsilon )},T]\) such that \( \varphi _t(\rho _1)=\rho _2. \) Then, there are \(s_1,s_2\in {[-\tau -r,\tau +r]}\), \(q_1,q_2\in A_1\setminus \cup _k B_{1,k}\) such that \(d(\rho _i,\varphi _{s_i}(q_i))<{r}\). In particular, there is \(C_{_{0}}>0\) depending only on \((M,p,a,b,\Lambda )\) such that
Finally, let \(\digamma >0\) be large enough so that \(\frac{1}{\digamma }e^{-\digamma \Lambda T}< \min ((1+C_{_{0}} e^{\Lambda (|T|+{2\tau +2r})})^{-1},R_0/2)\). Note that the choice of \(\digamma \) does not need to depend on T. Then, since \( r<(1+C_{_{0}}e^{\Lambda (|{T}|+{2\tau +2r})})^{-1}{e^{-f(T)}}R, \) we have \(q_2\in \mathcal {R}^{{e^{-f(T)}}R}_{_{A_1{,+}}}({{\mathfrak {t}}_0(\varepsilon )},T)\), which is a contradiction since \( \mathcal {R}^{{e^{-f(T)}}R}_{_{A_1{,+}}}({{\mathfrak {t}}_0(\varepsilon )},T)\subset \cup _i B_{1,i}\). \(\square \)
In what follows we fix \(1<\beta _0 < \varepsilon _0^{-1}\) and define
Lemma 3.7
Let \(B\subset \Sigma _{_{E}}^H\) be a ball of radius \(\delta >0\). Let \({0<\varepsilon _0<1}\), \({\mathfrak {t}}_0:[\varepsilon _0, +\infty ) \rightarrow [1, +\infty )\), \(f:[0,\infty )\rightarrow [0,\infty )\) increasing with \(f(e^{-x})\in L^1([0,\infty ))\), \(T_0>0\), and \(\digamma >0\), such that B can be \((\varepsilon _0, {{\mathfrak {t}}_0}, \digamma ,f)\)-controlled up to time \(T_0\). Let \(0<m<\frac{\log T_0-\log {{\mathfrak {t}}_0({\varepsilon _0})}}{\log \beta _0}\) be a positive integer, \(\Lambda > \Lambda _{\max }\),
and \(B_0\subset B\) with \(d(B_0, B^c)>{{\tilde{R}}}_0\). Let \(0<\tau <\tau _0\) and suppose \(\{\Lambda _{_{\rho _j}}^\tau (r_1)\}_{j=1}^{N_{r_1}}\) is a \(({{\mathfrak {D}}},\tau , r_1)\) good cover of \(\Sigma _{_{\!H\!,p}}\) and set \( \mathcal {E}:=\{j \in \{1, \dots , {N_{r_1}}\}: \Lambda _{\rho _j}^\tau (r_1)\cap \Lambda ^\tau _{B_0}(\tfrac{r_1}{5})\ne \emptyset \}. \)
Then, there exist \(C_{_{\!M,p}}>0\) depending only on (M, p) and sets \(\{\mathcal {G}_{_{E,\ell }}\}_{\ell =0}^m\subset \{1,\dots N_{r_1}\}\), \(\mathcal {B}_{_{E}}\subset \{1,\dots N_{r_1}\}\) so that \(\mathcal {E}\;\subset \; \mathcal {B}_{_{E}}\cup \displaystyle \cup _{\ell =0}^m \mathcal {G}_{_{E,\ell }}\) and
Proof
The proof is the same as that of [8, Lemma 3.2], with a very minor modification. Namely, we replace \(R_0\) by \({\tilde{R}}_0\) and put \(r_0=e^{-{\textbf{F}}(T_0)}{{\tilde{R}}}_0\) instead of \(r_0=e^{2\textbf{D}\Lambda T_0}{{\tilde{R}}}_0\). We then obtain the following instead of the leftmost equation in [8, (3.21)]
Which in turn changes the leftmost equation in [8, (3.22)] to
This follows from the argument below [8, Remark 8], that yields, since \(\ell \le m\),
\(\square \)
With Lemmas 3.6 and 3.7 in place, we are now ready to prove Proposition 3.5.
Proof of Proposition 3.5
Let \(\{{\mathcal {T}}_j(R)\}_{j \in \mathcal {J}(h)}=\{\Lambda _{_{\rho _j}}^\tau (R)\}_{j\in \mathcal {J}(h)}\) be a \(({\mathfrak {D}}, \tau , R)\) good covering of \( \Sigma _{_{[a,b]}}^H\). Let \(E \in [a,b]\) and \(\mathcal {A}_{_{E}}:=\{B_{\rho _i}\}_{i=1}^K\) be the covering of \( \Sigma _{_{E}}^H\) as described in (3.6). Let \({\mathfrak {t}}_0\) be as in Lemma 3.6 and fix \(0<\varepsilon _0<\frac{1}{2}\). There exists \(\digamma >0\) such that each ball in \(\mathcal {A}_{_{E}}\) can be \((\varepsilon _0,{\mathfrak {t}}_0, \digamma , f)\) controlled for time \(T>1\).
We then apply Lemma 3.7 to each ball in \(\mathcal {A}_{_{E}}\). Let \(\delta _0:={R_0/2}\) be the radius of the balls in \(\mathcal {A}_{_{E}}\), and \({\textbf{T}_0=\textbf{T}_0(R)}\) such that \(\textbf{T}_0>{\mathfrak {t}}_0(\varepsilon _0)\) and
Without loss of generality, we may assume \(\digamma \) is large enough so that \({\tfrac{1}{\digamma }}e^{-{\digamma }\Lambda {{\mathfrak {t}}_0(\varepsilon _0)}}\le {\tfrac{\delta _0}{10}}\). Then, putting \( {{\tilde{R}}}_0= \tfrac{1}{\digamma }e^{-{\digamma }\Lambda T_0}\) in Lemma 3.7, and using condition (3.13) allows us to set \(r_1={R}\) in Lemma 3.7 and apply it to each ball \(B_{\rho _0}\) in \(\mathcal {A}_{_{E}}\). Let \({{\tilde{B}}}_{\rho _0}\) be the ball with the same center as \(B_{\rho _0}\) but with a radius \({R_{{0}}/2}\) so that \(d({{\tilde{B}}}_{\rho _0}, B_{\rho _0}^c){=}R_0/2>{{\tilde{R}}_0}\). Let \(\tau _0>0\), \(0<\tau <\tau _0\), and set \(\mathcal {J}_{_{E}}^{\rho _0}({R})=\{j \in \mathcal {J}_{_{E}}({R}):\; \Lambda _{_{\rho _j}}^\tau (R) \cap \Lambda _{_{{{\tilde{B}}}_{\rho _0}}}^\tau (\tfrac{1}{5}R)\ne \emptyset \}\), there is \(C_{_{\!M,p}}>0\) and sets \(\{{\mathcal {G}_{_{E,\ell }}}\}_{\ell =0}^m\subset \mathcal {J}_{_{E}}({R})\), \(\mathcal {B}_{_{E}}\subset \mathcal {J}_{_{E}}({R})\) so that \(\mathcal {J}_{_{E}}^{\rho _0}({R})\;\subset \; \mathcal {B}_{_{E}}\cup \displaystyle \cup _{\ell =0}^m{\mathcal {G}_{_{E,\ell }}}\), and (3.10), (3.11), (3.12) hold.
Therefore, letting \(T_\ell = \beta _0^{-\ell } {\textbf{T}_0}\) and \(t_\ell ={\mathfrak {t}}_0(\varepsilon _0)\) for \(1 \le \ell \le m\), and setting \(\mathcal {G}_{m+1}:=\mathcal {B}_{_{E}}\), \(T_{m+1}=t_{m+1}=1\), yields that there exists \({C_{_{\!{\text {nr}}}}=C_{_{\!{\text {nr}}}}(M,p{,{\mathfrak {t}}})>0}\) such that
The existence of \(C_{_{\!{\text {nr}}}}>0\) is justified since \(\beta _0\varepsilon _0<1\). Repeating for each ball \(B_{\rho _i} \in \mathcal {A}_{_{E}}\) and using \(K\le C_nR_0^{1-n}\), proves that H is \(\textbf{T}_0\) non-recurrent in the window [a, b] via \(\tau _0\)-coverings with constant \(C_{_{\!{\text {nr}}}}C_nR_0^{1-n}\).
By Lemma 3.2, when \(\textbf{T}\) is sub-logarithmic and \(0<a<b\) we have \( f(b)\ge \frac{b}{a}f(a). \) In particular,
Therefore, using \(f(T)=-\log (\textbf{T}^{-1}(T))\), there exists \(c>0\) such that we may define
\(\square \)
Remark 3.8
We note that our definition of recurrence (Definition 1.13) is equivalent to the following. There is \(\digamma >0\) such that for all \(\rho \in \Sigma _{_{E}}^{H}\) there is \(R_0>0\) such that \(B(\rho ,R_0)\) is \((\varepsilon _0,{\mathfrak {t}}_0,\digamma ,f)\) controlled with an additional small modification of the definition of \((\varepsilon _0,{\mathfrak {t}}_0,\digamma ,f)\) controlled (see (3.3) and (3.4)): One needs to replace (1) by
To see these are equivalent, we identify \({B(\rho ,R_0)}\) with \(A_0\) and A with \(A_1\).
One can check that all of the proofs of being \((\varepsilon _0,{\mathfrak {t}}_0,\digamma , f)\) controlled in [8] actually prove this slightly stronger condition with \(f(T)=CT\) for some \(C>0\).
4 Basic estimates for averages over submanifolds
Let \(P(h) \in \Psi ^m(M)\) be a self-adjoint semiclassical pseudodifferential operator, with classically elliptic symbol p. Throughout this section we assume \(H \subset M\) is a smooth submanifold of co-dimension k, and \(a, b\in {\mathbb {R}}\) are such that H is conormally transverse for p in the window [a, b].
As explained in Sect. 1.6, we crucially view the kernel of the spectral projector \(\mathbb {1}_{[t-s,t]}(P)\) as a quasimode for P. We are then able to use estimates from [11] to estimate the error when the projector is smoothed at very small scales. This section is dedicated to adapting the estimates from [11] to the current setup.
All our estimates are made in terms of \(({\mathfrak {D}},\tau , R(h))\)-good covers and \(\delta \)-partitions associated to them. For the definition of a good cover see (2.4). Note, in addition, that there is a constant \({\mathfrak {D}}_n\) depending only on n such that we may work with a \(({\mathfrak {D}}_n,\tau , R(h))\) good cover [10, Lemma 2.2] [11, Proposition 3.3].
We now define the concept of \(\delta \)-partitions. For \(0\le \delta <\frac{1}{2}\), we write
and write \(\Psi _\delta ^m(M)\) for the corresponding semiclassical pseudodifferential operators. We refer the reader to [11, Appendix A.2], [48, Chapters 4,9], [19, Appendix E] for more detailed accounts of these operators.
Let \(\tau >0\), \(0< \delta <\tfrac{1}{2}\), and \(R(h)\ge {h^\delta }\). Let \(\{{\mathcal {T}}_j\}_{_{j\in \mathcal {J}(h)}}\) be a \((\tau ,R(h))\)-cover for \( \Sigma _{_{[a,b]}}^H\) with \({\mathcal {T}}_j=\Lambda _{\rho _j}^\tau (R(h))\), and for \(E\in [a,b]\) let \(\mathcal {J}_{_{E}}(h):=\mathcal {J}_{_{E}}(R(h))\) as defined in (2.5). We say
is a \(\delta \)-partition for \( \Sigma _{_{E}}^H\) associated to \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}(h)}\) provided the families \(\{\chi _j\}_{j\in \mathcal {J}_{_{E}}(h)}\) and \( \{h^{-1}[P,\chi _j]\}_{j\in \mathcal {J}_{_{E}}(h)}\) are bounded in \(S_\delta (T^*M;[0,1])\) and
For the construction of such a partition we refer the reader to [11, Proposition 3.4].
The next lemma controls the average of Au over a submanifold H in terms of the \(L^2\) masses of the bicharacteristic beams intersecting the microsupport of A. Here, u is a quasimode for P and A is a pseudodifferential operator. When we apply this lemma, u will be the kernel of the spectral projector onto a small window, and A will either represent a localizer to a family of tubes or differentiation in one of the coordinates.
To ease notation, for \({E} \in {\mathbb {R}}\) we write \(P_{_{E}}=P_{_{E}}(h)\)
In addition, given \(A \in \Psi _\delta ^\infty (M)\), \(\psi \in C^\infty _0({\mathbb {R}};[0,1])\), \(E\in {\mathbb {R}}\), \(h>0\), \(C>0\), \(C_{_{N}}>0\), and \(u \in \mathcal {D}'(M)\) we set \(\alpha :=\frac{k-2m+1}{2}\) and
We fix \(\varepsilon _0>0\) and a continuous family \([a-\varepsilon _0,b+\varepsilon _0]\ni E\mapsto B_{_{E}}\in \Psi _\delta ^0(M)\) such that
This will serve as a microlocalizer to the region of interest. We recall the constants \(\mathcal {K}_0\), \(\tau _{{{\,\textrm{inj}\,}}}\), \({\mathfrak {I}}_{_{\!0}}\) defined in (2.8), (2.3), and (2.11) respectively.
Lemma 4.1
There exist \( \tau _0=\tau _0(M,p,\tau _{{{\,\textrm{inj}\,}}},{\mathfrak {I}}_{_{\!0}})>0\) and \(R_0=R_0(M,p,k, \mathcal {K}_0, \tau _{{{\,\textrm{inj}\,}}}, {\mathfrak {I}}_{_{\!0}})>0, \) such that the following holds.
Let \(0<\tau <\tau _0\), \(0<\delta <\tfrac{1}{2}\) and \({h^\delta } \le R(h) \le R_0\). For \(h>0\) let \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}(h)}\) be a \(({\mathfrak {D}}_n, \tau , R(h))\) good cover of \( \Sigma _{_{[a,b]}}^H\). Let \(\mathcal {V}\subset S_\delta (T^*M;[0,1])\) be bounded. Let \(\psi \in C^\infty _0({\mathbb {R}};[0,1])\) with \(\psi (t)=1\) for \(|t| \le \tfrac{1}{4}\) and \(\psi (t)=0\) for \(|t| \ge 1\). Let \(\ell \in {\mathbb {R}}\), \(\mathcal {W}\) and \(\widetilde{\mathcal {W}}\) be bounded subsets of \(\Psi _\delta (M)\) and \(\Psi ^{\ell }_\delta (M)\) respectively, and \(B_{_{E}}\) be as in (4.5).
Then, there exist \(C_{_{0}}=C_{_{0}}(n,k,{\mathfrak {I}}_{_{\!0}},\mathcal {V},\mathcal {W},\widetilde{\mathcal {W}})\), \(C>0\), and for all \(K>0\) there is \(h_0>0\), such that for all \(N>0\) there exists \(C_{_{N}}>0\), with the following properties. For all \(u\in \mathcal {D}'(M)\), \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\), every \(\delta \)-partition \(\{\chi _{_{{\mathcal {T}}_j}}\}_{j\in \mathcal {J}_{_{E}}(h)}\subset {\mathcal {V}}\) associated to \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}_{_{E}}(h)}\), and every \(A\in \widetilde{\mathcal {W}}\) such that \(B_{_{E}}\frac{1}{h}[P,A]\in \mathcal {W}\),
Here, \(\mathcal {I}_{_{E}}(h):=\{j \in \mathcal {J}_{_{E}}(h): {\mathcal {T}}_j \cap {\hbox {MS}}_{\textrm{h}}(A) \cap \Lambda _{ \Sigma _{_{E}}^H}^\tau (R(h)/2) \ne \emptyset \}\), \(\psi \in S_\delta \cap C^\infty _c(T^*M;[0,1])\) is any symbol with \({{\,\textrm{supp}\,}}\psi \subset \big (\Lambda ^\tau _{\Sigma ^H_{_{E}}}(2h^\delta )\big )^c\), and for each \(j \in \mathcal {J}_{_{E}}(h)\) we let \({\tilde{\chi }}_{_{{\mathcal {T}}_j}}\) be any symbol in \(S_\delta (T^*M;[0,1])\cap C^\infty _c(T^*M;[0,1])\) such that \({\tilde{\chi }}_{_{{\mathcal {T}}_j}}\equiv 1 \) on \({{\,\textrm{supp}\,}}\chi _{_{{\mathcal {T}}_j}}\) and \({{\,\textrm{supp}\,}}{\tilde{\chi }}_{_{{\mathcal {T}}_j}}\subset {\mathcal {T}}_j.\) In addition, if \({\widetilde{\mathcal {W}}}\subset \Psi _0^{\ell }(M)\), then \(C_{_{0}}=C_{_{0}}(n,k,{\mathfrak {I}}_{_{\!0}},\mathcal {V},\widetilde{\mathcal {W}})\).
Proof
First, we prove the statement for the case \(A=I\). Note that in this case the sets \(\mathcal {W}\) and \(\widetilde{\mathcal {W}}\) play no role. The result for \(A=I\) is a direct combination of the estimate in [11, (3.16)] and [11, Proposition 3.2]. We recall the estimate [11, (3.16)] with \(w\equiv 1\) here:

In (4.7), \(C_{n,k}>0\) is a constant depending only on n and k, and \(\beta _\delta :T^*H \rightarrow {{\mathbb {R}}}\) is a localizer to near conormal directions defined by \(\beta _\delta (x', \xi ')=\chi \big (h^{-\delta }|\xi '|_{_{H}} \big )\) where \(\chi \in C^\infty _0({\mathbb {R}};[0,1])\) is a smooth cut-off with \(\chi (t)=1\) for \(t \le \tfrac{1}{2}\) and \(\chi (t)=0\) for \(t \ge 1\).
Indeed, [11, Proposition 3.2] yields the existence of \(\tau _0, R_0, h_0>0\) as claimed, and the estimate [11, (3.16)] yields the same bound as above, but with three modifications.
To obtain the desired estimate, observe that the constant \(C_{_{0}}=C_{_{0}}(n,k, {\mathfrak {I}}_{_{\!0}})>0\) is the constant \(C_{n,k}\) divided by \({\mathfrak {I}}_{_{\!0}}\), because we absorb the \(|{{\textsf{H}}_p}r_H(\rho _j)|\) factors in (4.7). Second, in (4.7) the estimate is given for for \(\Big |\int _{H} Op_h(\beta _{\delta }) u\,d\sigma _{_{\!H}}\Big |\). It turns out that this estimate is all we need since [11, Proposition 3.2] yields that for every \(N>0\) there exists \(c_{_{N}}>0\) such that for all \(u \in \mathcal {D}'(M)\)
The third modification is that in (4.7) the first error term is \(Ch^{-\frac{1}{2}-\delta } \big \Vert P_{_{E}}u\big \Vert {_{\!H_{{\text {scl}}}^{\!\!\frac{k-2m+1}{2}}\!\!\!(M)}}\) instead of \(Ch^{-\frac{1}{2}-\delta }\big \Vert \big (1-\psi \big (\tfrac{P_{_{E}}}{h^\delta }\big )\big )P_{_{E}}u\big \Vert {_{\!H_{{\text {scl}}}^{\!\!\frac{k-2m+1}{2}}\!\!\!(M)}}\). The operator \(\big (1-\psi \big (\tfrac{P_{_{E}}}{h^\delta }\big )\big )\) can be added since the error term is a consequence of the application of an elliptic parametrix applied to an operator supported away from \(P_{_{E}}=0\), in particular of the bound in [11, (3.10)], which is for \(Op_h(\chi ) u\) where \(\chi \) is supported in \(\{(x, \xi ):\; |p_{_{E}}(x, \xi )|\ge \tfrac{1}{3}h^\delta \}\). One then uses \({{\,\textrm{supp}\,}}\chi \subset {{\,\textrm{supp}\,}}\big (1-\psi \big (\tfrac{p_{_{E}}}{h^\delta }\big ) \big )\).
We note that the desired bound holds for every \(\delta \)-partition \(\{\chi _{_{{\mathcal {T}}_j}}\}_{j\in \mathcal {J}_{_{E}}(h)}\subset {\mathcal {V}}\) associated to \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}_{_{E}}(h)}\), since the constants \(C, C_{_{N}}, h_0\) provided by [11, Proposition 3.5] are uniform for \(\chi _{_{{\mathcal {T}}_j}}\) in bounded subsets of \(S_\delta \).
Given \(\varepsilon _0>0\) we note that the statement holds for every \(E \in [a-\varepsilon _0, b+\varepsilon _0]\) since the constants \(C, C_{_{N}}, h_0\) provided by [11, Proposition 3.5] depend on \(P_{_{E}}\) only through P. Therefore, given \(K>0\), the statement for \(A=I\) holds for \(E \in [a-Kh, b+Kh]\) provided \(h_0\) depends on K.
We now treat the case \(A \ne I\). Let \(\mathcal {V},\mathcal {W}, \widetilde{\mathcal {W}}\), and \(\{B_{_{E}}\}_{E\in [a-\varepsilon _0, b+\varepsilon _0]}\) be as in the assumptions. Let \(E\in [a-\varepsilon _0, b+\varepsilon _0]\). Let \(X\in \Psi _\delta (M)\) with \({\hbox {MS}}_{\textrm{h}}(I-X)\cap \Lambda _{ \Sigma _{_{E}}^H}^\tau (\tfrac{1}{3}R(h))=\emptyset \), \({\hbox {MS}}_{\textrm{h}}(X)\subset \Lambda _{ \Sigma _{_{E}}^H}^{\tau _0+{\varepsilon _0}}(\tfrac{1}{2}R(h))\) and \(B_{_{E}}[P,X]\in \Psi _\delta (M)\). Then, for all \(N>0\) there is \(C_{_{N}}>0\) depending on \(\mathcal {V}\)
so we may replace A by XA and assume \({\hbox {MS}}_{\textrm{h}}(A)\subset \Lambda _{ \Sigma _{_{E}}}^{{\tau _0+{\varepsilon _0}}}(R(h)/2)\) from now on. Since the estimate holds when \(A=I\), there exist \(C_{_{0}}=C_{_{0}}(n,k,{\mathfrak {I}}_{_{\!0}})\), \(C>0\), and for all \(K>0\) there is \(h_0>0\) such that for all \(N>0\) there exists \(C_{_{N}}>0\) with the following properties. For all \(u\in \mathcal {D}'(M)\), \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\), and every \(\delta \)-partition \(\{\chi _{_{{\mathcal {T}}_j}}\}_{j\in \mathcal {J}_{_{E}}(h)}\subset {\mathcal {V}}\) associated to \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}_{_{E}}(h)}\), the bound in (4.6) holds with I in place of A, and with Au in place of u:
We may sum over \(j \in \mathcal {I}_{_{E}}(h)\) instead of \(j \in \mathcal {J}_{_{E}}(h)\) since \({\hbox {MS}}_{\textrm{h}}(A){\cap \Lambda _{ \Sigma _{_{E}}^H}^\tau (\tfrac{1}{2}R(h))}\subset \cup _{j \in \mathcal {I}_{_{E}}(h)} {\mathcal {T}}_j\).
Next, we explain how to write u in place of Au in each of the terms of the sum over \(j \in \mathcal {I}_{_{E}}(h)\) in (4.6). To replace the term \(\Vert Op_h({ \chi }_{_{{\mathcal {T}}_j}})Au\Vert _{_{\!L^2(M)}}\) with \(\Vert Op_h({{\tilde{\chi }}}_{_{{\mathcal {T}}_j}})u\Vert _{_{\!L^2(M)}}\), we use \({\hbox {MS}}_{\textrm{h}}(Op_h(\chi _{_{{\mathcal {T}}_j}})A) \subset {\text {Ell}}(Op_h({{\tilde{\chi }}}_{_{{\mathcal {T}}_j}}))\) and apply the elliptic parametrix construction to find \(F_1\in \Psi _\delta (M)\) with
Next, to replace the term \(\Vert Op_h({ \chi }_{_{{\mathcal {T}}_j}})P_{_{E}}Au\Vert _{_{\!L^2(M)}}\) with \(\Vert Op_h({{\tilde{\chi }}}_{_{{\mathcal {T}}_j}})P_{_{E}}u\Vert _{_{\!L^2(M)}}\), we decompose
for each \(j \in \mathcal {I}_{_{E}}(h)\), and apply the elliptic parametrix construction and find \( F_2\in \Psi _\delta (M)\) with
To do this we used the assumptions: \(B_{_{E}}\) is microlocally the identity on \(\Lambda _{{ \Sigma _{_{E}}^H}}^{\tau _0+{\varepsilon _0}}({2R(h)})\), \({\hbox {MS}}_{\textrm{h}}({A}) \subset \Lambda _{{ \Sigma _{_{E}}^H}}^{\tau _0+{\varepsilon _0}}(\tfrac{1}{2}R(h))\), and A is such that \(B_{_{{E}}}\tfrac{1}{h}[P,A]\in \mathcal {W}\subset \Psi _\delta (M)\). This allows us to apply the parametrix construction to \(Op_h(\chi _{_{{\mathcal {T}}_j}})B_{_{E}}\tfrac{1}{h}[P_{_{E}},A]\).
Using (4.9) and (4.10), we may modify \(C_{_{0}}\), and having it now also depend on A, \(\mathcal {V}\) and \(\mathcal {W}\), to obtain the claim. Note that if \(A \in \Psi _0^\infty (M)\), then \(\tfrac{1}{h}[P_{_{E}},A] \in \Psi _\delta ^\infty (M)\) and so we may apply the elliptic parametrix construction to obtain (4.10) without the need of introducing the operator \(B_{_{{E}}}\) or the set \(\mathcal {W}\). In this case, we have \(C_{_{0}}=C_{_{0}}(n,k,{\mathfrak {I}}_{_{\!0}},\mathcal {V}, {\widetilde{\mathcal {W}}})\) as claimed. \(\square \)
Definition 4.2
Low density tubes Let \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}(h)}\) be a cover by tubes of \( \Sigma _{_{[a,b]}}^H\) and \(0<\delta <\tfrac{1}{2}\). Let \({{\mathcal {G}}}(h)\subset \mathcal {J}(h)\) and for each \(j \in {{{\mathcal {G}}}(h)}\) let \(1<t_j(E,h)\le T_j(E,h)\), where \(h>0\) and \(E\in {\mathbb {R}}\).
We say \(\{{\mathcal {T}}_j\}_{j \in {{\mathcal {G}}}(h)}\) has \(\{(t_j, T_j)\}_{j\in {{\mathcal {G}}}(h)}\) density on [a, b] if the following holds. For all \(\mathcal {V}\subset S_\delta \) bounded, \(K>0\) there is \(h_0>0\) such that for all \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\), every \(\delta \)-partition \(\{\chi _j\}_{j\in \mathcal {G}_{_{E}}(h)}\subset \mathcal {V}\) associated to \(\{{\mathcal {T}}_j\}_{j \in \mathcal {G}_{_{E}}(h)}\), and all \(u \in \mathcal {D}'(M)\),
where \(\mathcal {G}_{_{E}}(h)={{\mathcal {G}}}(h)\cap \mathcal {J}_{_{E}}(h)\).
The statement of [11, Lemma 4.1] can be reformulated as: if a collection of families of tubes is non self-looping for different times, then the tubes have a low density dictated by those times. More precisely, the following lemma is a restatement of [11, Lemma 4.1].
Lemma 4.3
Let \(R_0,\) \(\tau _0\), \(\delta \), R(h), \(\tau \), and \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}(h)}\) be as in Lemma 4.1. Let \(0< \alpha < 1-\limsup _{h\rightarrow 0^+} 2\tfrac{\log R(h)}{\log h}\) and \(K>0\). There exists \(h_0>0\) such that the following holds. Let \(0<h<h_0\), \(E\in [a-Kh, b+Kh]\), and \(\mathcal {G}_{_{E}}(h)\subset \mathcal {J}_{_{E}}(h)\) with \({\mathcal {G}_{_{E}}(h)=\sqcup _{\ell \in \mathcal {L}_{_{E}}(h)} \mathcal {G}_{_{E,\ell }}}(h)\). For every \(\ell \in {\mathcal {L}}_{_{E}}(h)\) suppose \(t_\ell (E,h)>0\), \(0<{T_\ell (E,h)}\le 2\alpha \, T_e(h),\) and
Then, \(\{{\mathcal {T}}_j\}_{j \in {{\mathcal {G}}}(h)}\) has \(\{(t_j, T_j)\}_{j\in {{\mathcal {G}}}(h)}\) density on [a, b], where for \(0<h<h_0\), \(j \in \mathcal {J}(h)\), and \(E\in [a-Kh, b+Kh]\), we set \((t_j(E,h), T_j(E,h)):=(t_\ell (E,h), T_\ell (E,h))\) whenever \(j \in \mathcal {G}_{_{E,\ell }}(h)\).
We note that the statement of [11, Lemma 4.1] does not provide the requisite uniformity for \(E\in [a-Kh,b+Kh]\); however, this follows from the same argument.
Our next estimate shows that if a family of tubes has low density, then averages of a quasimode over H can be controlled in terms of the density times.
Lemma 4.4
Let \(R_0,\) \(\tau _0\), \(\delta \), R(h), \(\tau \), \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}(h)}\), \(\mathcal {W}\), \(\widetilde{\mathcal {W}}\), and \(\psi \) be as in Lemma 4.1. Then, there exist \(C_{_{0}}=C_{_{0}}(n,k,p,{\mathfrak {I}}_{_{\!0}},\mathcal {W})\) and \(C>0\), and for all \(N>0\), \(K>0\) there are \(h_0>0\) and \(C_{_{N}}>0\), such that the following holds.
Suppose that for all \(0<h<h_0\) and \(E\in [a-Kh, b+Kh]\) there exists \(\mathcal {G}_{_{E}}(h)\subset \mathcal {J}_{_{E}}(h)\) with \({\mathcal {G}_{_{E}}(h)=\sqcup _{\ell \in {\mathcal {L}}_{E}(h)} \mathcal {G}_{_{E,\ell }}}(h)\), such that for every \(\ell \in {\mathcal {L}}_{_{E}}(h)\) there exist \(t_\ell =t_\ell (E,h)>0\) and \({T_\ell =T_\ell (E,h)}>0\) so that, with \((t_j, T_j):=(t_\ell , T_\ell )\) for every \(j \in \mathcal {G}_{_{E,\ell }}(h)\), then
Then, for all \(u\in \mathcal {D}'(M)\), \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\), and every \(A\in {\widetilde{\mathcal {W}}}\) with \(B_{_{E}}\frac{1}{h}[P,A]\in \mathcal {W}\),
In addition, if \({\widetilde{\mathcal {W}} \subset } \Psi _0^\infty (M)\), the estimate holds with \(C_{_{0}}=C_{_{0}}(n,k,p,{\mathfrak {I}}_{_{\!0}},{\widetilde{\mathcal {W}}})\).
Proof
Let \(\mathcal {V}\) a bounded subset of \(S_\delta (T^*M;[0,1])\). By Lemma 4.1 there exist \(C_{_{0}}=C_{_{0}}(n,k,{\mathfrak {I}}_{_{\!0}},\mathcal {V},\mathcal {W})\), \(C>0\), and \(h_0>0\), such that for all \(N>0\) there exist \(C_{_{N}}>0\), with the following properties. For all \(u\in \mathcal {D}'(M)\), \(K>0\), \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\), and every \(\delta \)-partition \(\{\chi _{_{{\mathcal {T}}_j}}\}_{j\in \mathcal {J}_{_{E}}(h)}\subset {\mathcal {V}}\) associated to \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}_{_{E}}(h)}\),
where \(\mathcal {I}_{_{E}}(h):=\bigcup _{\ell \in {\mathcal {L}}_{h,E}}{\mathcal {G}_{_{E,\ell }}}\). Note that if \(A\in \Psi _0^\infty (M)\), then the estimate holds with \(C_{_{0}}=C_{_{0}}(n,k,p, {\mathfrak {I}}_{_{\!0}}, \mathcal {V}, {\widetilde{\mathcal {W}}})\). Next, note that
and so, since \(|\mathcal {J}_{_{E}}(h)| \le C_n{{\,\textrm{vol}\,}}({ \Sigma _{_{E}}^H})R(h)^{{1-n}}\) for some \(C_n>0\), we have, after adjusting \(C>0\), that for all \(0<h<h_0\)
Since we are working with a \(({{\mathfrak {D}}_n},\tau ,R(h))\)-good cover, we split each \({\mathcal {G}_{_{E,\ell }}}\) into \({\mathfrak {D}}_n\) families \(\{\mathcal {G}_{_{E,\ell , i}}\}_{i=1}^{{\mathfrak {D}}_n}\) of disjoint tubes. Note that
Next, since \(\{{\mathcal {T}}_j\}_{j \in {{\mathcal {G}}}(h)}\) has \(\{(t_j, T_j)\}_{j\in {{\mathcal {G}}}(h)}\) density on [a, b], after possibly shrinking \(h_0\) (depending on the \(S_\delta \) bounds for \({\tilde{\chi }}_j\) and \(K>0\)), Cauchy-Schwarz yields that for all \(0<h<h_0\)
The result follows from combining (4.13) and (4.12), and feeding this to (4.11). Note that \(C_{_{0}}\) needs to be modified, but only in a way that depends on n via \({\mathfrak {D}}_n\). \(\square \)
We also need the following basic estimate for averages over submanifolds to control averages of \(u={\textbf{1}}_{(-\infty , s]}(P)\) when s is large.
Lemma 4.5
Suppose \(H\subset M\) is a submanifold of codimension k and \(P\in \Psi ^m(M)\), with \(m>0\), is such that there exists \(C>0\) for which
Let \(\psi \in S^0(T^*M; [0,1])\) with \(\psi \equiv 1\) on \(N^*H\), and let \(\ell \in {\mathbb {R}}\). Let \(A\in \Psi _\delta ^{\ell }(M)\) and \(r>\frac{k+2\ell }{2m}\). Then, there are \(C_{_{0}}>0\) and \(h_{0}>0\) such that for all \(N>0\) there is \(C_{_{N}}>0\) satisfying
Proof
Let \({{\tilde{\psi }}} \in S^0(T^*M; [0,1])\) with \({\tilde{\psi }}\equiv 1\) on \(N^*H\), \({{\,\textrm{supp}\,}}{\tilde{\psi }}\subset \{\psi \equiv 1\}\), and such that
Then, since \({\hbox {WF}}_{\textrm{h}}(\delta _{H})=N^*\!H\), for any \(N>0\) there is \(C_{_{N}}>0\) such that
Next, by the Sobolev embedding theorem, for any \(\varepsilon >0\) there exists \(C_{_{0}}>0\) such that
Taking r with \(rm>\frac{k}{2}+\ell \) and using an elliptic parametrix, for any \(N>0\) there is \(C_{_{N}}>0\) with
Indeed, this follows from letting \(\chi \in S^0(T^*M;[0,1])\) so that \( |\sigma (P_{_{E}})(x,\xi )|\ge \tfrac{1}{C}|\xi |^m\) in the support of \({{\tilde{\psi }}} (1-\chi )\), and then using the elliptic parametrix construction to find \(F_1, F_2 \in \Psi ^0(M)\) such that
Combining with (4.14) and (4.15) completes the proof. \(\square \)
5 Lipschitz scale for spectral projectors
In this section we estimate the scale at which averages of the spectral projector behave like Lipschitz functions of the spectral parameter, and use this to approximate \(\Pi _h\) using \(\rho _{h,T(h)}*\Pi _h\).
Throughout this section we assume \(H_1,H_2 \subset M\) are two smooth submanifolds of co-dimension \(k_1\) and \(k_2\) respectively. The goal for this section is to prove the following proposition.
Proposition 5.1
Suppose \(a, b\in {\mathbb {R}}\) such that \(H_1, H_2\) are uniformly conormally transverse for p in the window [a, b]. Let \(\tau _0, R_0\) be as in Lemma 4.1. Let \(0<\tau <\tau _0\) and \(0<\delta <\tfrac{1}{2}\). For \(i=1,2\), let \(\textbf{T}_i\) be sub-logarithmic resolution functions with \(\Omega (\textbf{T}_i)\Lambda <1-2\delta \) and suppose \(H_i\) is \({\textbf{T}_i}\) non-recurrent in the window [a, b] via \(\tau \)-coverings with constant \(C_{_{\!{\text {nr}}}}^i\).
Let \(A_1,A_2\in \Psi ^\infty (M)\), \({K>0}\), \( R(h)\ge {h^\delta }\), and \(\textbf{T}:=\sqrt{\textbf{T}_1\textbf{T}_2}\). Then, there exist \(h_0>0\) and
such that for all \(0<h\le h_0\) and \(E\in [a-Kh,b+Kh]\),
Remark 5.2
To ease notation, throughout this section we write \(T_i(h):=\textbf{T}_i(R(h))\), \(T(h):=\textbf{T}(R(h))\), and \({T_{\max }(h):=\max (\textbf{T}_1(R(h),\textbf{T}_2(R(h))))}.\)
Proof
We split the proof into Lemmas 5.3, 5.4, and 5.5 below. Lemmas 5.4 and 5.5 show that there exist \(C_{_{0}}=C_{_{0}}(n, k_1, k_2, {\mathfrak {I}}_{_{\!0}}^1,{\mathfrak {I}}_{_{\!0}}^2, A_1, A_2, C_{_{\!{\text {nr}}}}^1, C_{_{\!{\text {nr}}}}^2)>0\), \(C_1>0\), and \(h_0>0\) such that \(w_h(E):=\Pi _{_{H_1,H_2}}^{^{A_1,A_2}}(E)\) satisfies the hypotheses of Lemma 5.3 with \(I_h:= [a-Kh,b+Kh]\), \(\rho _h:=\rho _{_{h,T_{\max }(h)}}\), \(\sigma _h:= T_{\max }(h)/h\),
and \(0<h<h_0\). Next, let \(\{K_j\}_{j=1}^\infty \subset {\mathbb {R}}_+\) be given by the choice of \(\rho \) in (1.16). Since \(\Big \langle \frac{T_1(h)s}{h}\Big \rangle ^{\frac{1}{2}}\Big \langle \frac{T_2(h) s}{h}\Big \rangle ^{\frac{1}{2}}\le \langle \sigma _{_{h}} s\rangle \) for all \(s\in {\mathbb {R}}\), Lemma 5.3 yields that there exists \(C_{_{\rho }}>0\) and for all \(N>0\) there exists \(C_{_{N}}>0\) such that
for all \(0<h<h_0\). This completes the proof after choosing \(h_0\) small enough. \(\square \)
We now present the lemmas used in the proof of Proposition 5.1. The first shows that if a family of functions \(\{w_h\}_h\) is Lipstchitz at scale \(\sigma _h^{-1}\) with (at most) polynomial growth at infinity, then the family can be well approximated by its convolution \(\rho _{h} *w_h\) where \(\{\rho _h\}_h\) is a family of Schwartz functions
Lemma 5.3
Let \(\{K_j\}_{j={0}}^\infty \subset {\mathbb {R}}_+\). Then, there exists \(C>0\) and for all \(N_0\in {\mathbb {R}}\), \(N>0\) there exists \(C_{_{N}}>0\), such that the following holds. Let \(\{\rho _{h}\}_{h>0}\subset {\mathcal {S}}({\mathbb {R}})\) be a family of functions and \(\{\sigma _h\}_{h>0}\subset {\mathbb {R}}_+\) such that for all \(j\ge 1\) and \(h>0\),
Let \(\{L_h\}_{h>0}\subset {\mathbb {R}}_{+}\), \(\{B_h\}_{h>0}\subset {\mathbb {R}}_{+}\), \(\{w_h:{\mathbb {R}}\rightarrow {\mathbb {R}}\}_{h>0}\), \(I_h\subset [-K_0,K_0]\), \(h_0>0\) and \(\varepsilon _0>0\), be so that for all \(0<h<h_0\)
-
\(|w_h(t-s)-w_h(t)|\le L_h\langle \sigma _h \,s\rangle \) for all \(t\in I_h\) and \({|s|\le \varepsilon _0}\),
-
\(|w_h(s)|\le B_h\langle s\rangle ^{N_0}\) for all \(s\in {\mathbb {R}}\).
Then, for all \(0<h<h_0\) and \(t\in I_h\)
Proof
For all \(0<h<h_0\) and \(t\in I_h\)
The existence of C and \(C_{_{N}}\) follows from integrability of each term and the boundedness of \(I_h\). \(\square \)
The next lemma shows that the family of functions \(w_h(t)=\Pi _{_{H_1,H_2}}^{^{A_1,A_2}}(t)\) is Lipschitz at scales dictated by the non-recurrence times for \(H_1\) and \(H_2\).
Lemma 5.4
Suppose \(a,b\in {\mathbb {R}}\), \(\varepsilon _0>0\) are such that \(H_1\), \(H_2\) are conormally transverse for p in the window \([a-\varepsilon _0,b+\varepsilon _0]\). Let \(A_1\), \(A_2\), \(\tau _0\), \(R_0\), \(\tau \), \(\delta \), R(h), and \(\alpha \) be as in Proposition 5.1. Let \(C_{_{\!{\text {nr}}}}>\) and \(K>0\). Then, there exist \(h_0>0\) and
such that the following holds.
For \(i=1,2\), let \(\textbf{T}_i\) be a sub-logarithmic resolution function with \(\Omega (\textbf{T}_i)\Lambda <1-2\delta \). Suppose \(H_i\) is \(\textbf{T}_i\) non-recurrent in the window [a, b] via \(\tau \)-coverings with constant \(C_{_{\!{\text {nr}}}}^i{\le C_{_{\!{\text {nr}}}}}\). Then for all \(0<h\le h_0\), \(|s|\le \varepsilon _0\), and \(t\in [a-Kh,b+Kh]\),
Proof
We first assume the statement for \(|s| \le 2h\). Suppose \(s\ge 2h\). The case of \(s\le -2h\) being similar. Define \(k_0:=\lfloor \frac{s}{h}\rfloor \) and \(t_k:=t-s+kh\) for \(0\le k\le k_0-1,\) and \(t_k:=t\) for \(k=k_0\). Then
Using \(|t_{k+1}-t_k|\le 2h\), and putting \(t=t_{k+1}\), \(s=t_{k+1}-t_k\), we apply the case \(|s|\le 2h\) with \(T_1=T_2=1\) for each term to obtain
and this proves the claim provided the statement holds for \(|s| \le 2h\).
We proceed to prove the statement for \(|s| \le 2h\). First, note that by (1.10) and Cauchy-Schwarz
Now, for each \(i=1,2,\)
where \(\delta _{_{H_i}}\) is the delta distribution at \(H_i\) and the last equality follows by duality.
We now use the non-recurrence assumption on \(H_1\) and \(H_2\). Since for each \(i=1,2\), the submanifold \(H_i\) is \(\textbf{T}_i\) non-recurrent in the window [a, b] via \(\tau _0\)-coverings, there is \(h_0>0\) small enough depending on R(h), K so that for all \(0<h<h_0\) and \(t \in {[E-Kh,E+Kh]}\) there is a partition of indices \(\mathcal {J}_{_{t}}^i(h)=\cup _{\ell \in {\mathcal {L}}_{_{t}}^i(h)} {{\mathcal {G}}}_{_{t,{\ell }}}^i(h)\), and times \(\{T_\ell ^i(h)\}_{\ell \in {\mathcal {L}}_{_{t}}^i(h)}\), and \(\{t_\ell ^i(h)\}_{\ell \in {\mathcal {L}}_{_{t}}^i(h)}\) as in Definition 2.2.
Note that we have chosen \(h_0\) small enough so that \(\mathcal {J}_{_{E}}^i(h)\) is a \((\tau ,R(h))\) good covering of \(\Sigma ^{H_i}_t\) for \(t \in [E-Kh,E+Kh]\). In particular, for \(i=1, 2\) and \(t\in [E-Kh,\,E+Kh]\)
The first bound is condition (2) in Definition 2.2, and the second bound follows from the first one together with the \(T_\ell ^i \le T_i\) for all \(\ell \in \mathcal {L}^i_{h,E}\). Next, for \(\ell \in \mathcal {L}^i_{E}\) let
and note that \(\sum _{{\tilde{t}}_\ell ^i={\tilde{T}}_\ell ^i=1}|{{\mathcal {G}}}_{_{t,{\ell }}}^i|^{\frac{1}{2}}\le C_{_{\!{\text {nr}}}}^i \sqrt{\frac{1}{T_i}\Big \langle \frac{T_i s}{h}\Big \rangle }. \) In particular,
Then, since for each \(\ell \in \mathcal {L}_{_{E}}^i(h)\) the union of tubes with indices in \({\mathcal {G}^i_{_{E,\ell }}}\) is also \([{\tilde{t}}_\ell ^i(h),{{\tilde{T}}}_{\ell }^i(h)]\) non-self looping, we may apply Lemma 4.3 with the sets \(\{{{\mathcal {G}}}_{_{t,{\ell }}}^i(h)\}_{\ell \in \mathcal {L}_{_{E}}^i(h)}\), \(\{{{\tilde{T}}}_\ell ^i(h)\}_{\ell \in \mathcal {L}_{_{E}}^i(h)}\), \(\{t_\ell ^i(h)\}_{\ell \in \mathcal {L}_{_{E}}^i(h)}\) to see that \(\{{\mathcal {T}}_j\}_{j\in {{\mathcal {G}}}_{_{t,{\ell }}}^i(h)}\) has \(\{(t_j,T_j)\}\) density on [a, b] where \(t_j={\tilde{t}}_j^i(h)\), \(T_j={\tilde{T}}_j^i(h)\). Then, using Lemma 4.4 with operators \(A_i \in \Psi ^\infty (M)\), \(\psi \in C^\infty _0({\mathbb {R}};[0,1])\) with \(\psi (t)=1\) for \(|t| \le \tfrac{1}{4}\) and \(\psi (t)=0\) for \(|t| \ge 1\), and for \(s \in {\mathbb {R}}\) let \(u=\mathbb {1}_{[t-s,t]}(P)w\), where w is any function in \(L^2(M)\) with \(\Vert w\Vert _{_{\!L^2(M)}}=1\). Next, by Lemma 4.4, for \(i=1,2\), there exist \(C_{_{0}}^i=C_{_{0}}(n,k_i,{\mathfrak {I}}_{_{\!0}}^i, A_i)\), \(C>0\), and for all N there is \(C_{_{N}}>0\) such that for all \(0<h<h_0\), \(s\in {\mathbb {R}}\), and \(t \in [E-Kh, E+Kh]\)
Note that for all N there is \(C_{_{N}}>0\) such that for all \(t\in [a{-Kh},b{+Kh}]\), \(|s|\le 10\) and \(0<h<1\)
In addition, we use the elliptic parametrix construction, together with \(|s|\le 2h\) to obtain
We combine these estimates with (5.3) and the definition of \({{\tilde{T}}}_\ell ^i\) into (5.2) to obtain that for all \(0<h<h_0\), \(|s|\le 2h\), \(K>0\), and \(t \in [E-Kh, E+Kh]\),
In particular, since \(\tau <1\), using this estimate in (5.2) we conclude that for all \(0<h<h_0\), \(|s|\le 2h\), \(K>0\), and \(t \in [E-Kh, E+Kh]\)
Combining estimates for \(H_1\) and \(H_2\) using (5.1), and \(C_{_{\!{\text {nr}}}}^i\le C_{_{\!{\text {nr}}}}\) completes the proof. \(\square \)
The last lemma shows that \(w_h(s)=\Pi _{_{H_1,H_2}}^{^{A_1,A_2}}(s)\) has at most polynomial growth at infinity.
Lemma 5.5
Let \(\ell _1, \ell _2\in {\mathbb {R}}\). Then, there is \(N_0>0\) such that for all \(A_1\in \Psi ^{\ell _1}_\delta (M)\), \(A_2\in \Psi ^{\ell _2}_\delta (M)\), there are \(C_{_{1}}>0\), \(h_0>0\), such that for all \(0<h<h_0\) and \(s\in {\mathbb {R}}\),
Proof
Arguing as in (5.1), and (5.2), it is enough to prove that there is \(C_{_{1}}>0\) such that for each \(i=1,2\) there is \(N_i>0\) for which
Applying Lemma 4.5 with \(u=\mathbb {1}_{(-\infty ,s]}(P) w\) yields that for any \(\psi \in S^0(T^*M;[0,1])\) with \(\psi \equiv 1\) on \(N^*\!H\) and \(r_i> \tfrac{k_i+2\ell _i}{2m}\) there exist \(C_{_{1}}>0\) and \(h_0>0\) such that for all \(N>0\) there is \(C_{_{N}}>0\) satisfying for \(0<h<h_1\) and \(s\in {\mathbb {R}}\),
Finally, the last term is bounded by \(C_{_{1}} (1+|s|^{r_i})\) since \(\Vert f(P)\Vert _{L^2\rightarrow L^2}\le \Vert f\Vert _{L^\infty }.\) \(\square \)
6 Smoothed projector with non-looping condition
This section is dedicated to the proof of Theorems 8 and 9. The crucial step, completed in Sect. 6.1, is to bound \( (\rho _{_{h,{\widetilde{T}}(h)}}-\rho _{_{h,t_0}})*\Pi _{_{H_1,H_2}}^{^{A_1,A_2}}\) when the pair \((H_1,H_2)\) is \((t_0,\textbf{T})\) non-looping and \({\widetilde{T}}(h)=\frac{1}{2}\textbf{T}(R(h))\). In Sect. 6.2 we prove Theorem 8 by combining the estimates from §6.1 with Proposition 5.1. In §6.3 we derive Theorem 9 from Theorem 8.
6.1 Comparing against a short fixed time
Throughout this section we continue to assume \(H_1 \subset M\) and \(H_2\subset M\) are two submanifolds of co-dimension \(k_1\) and \(k_2\) respectively. The goal is to show that, under the assumption \((H_1,H_2)\) is a \((t_0,\textbf{T})\) non-looping pair in the window [a, b], we can control \(\rho _{\sigma _{h,{\widetilde{T}}(h)}}*\Pi _h\) by comparing it to \(\rho _{_{h,t_0}}*\Pi _h\). For the rest of the section we write
Proposition 6.1
Suppose \(a, b\in {\mathbb {R}}\) are such that \(H_1, H_2\) are conormally transverse for p in the window [a, b]. Let \(\tau _0, R_0\) be as in Lemma 4.1. Let \(0<\tau <\tau _0\), \(0<\delta <\tfrac{1}{2}\), and \(\textbf{T}\) a sub-logarithmic resolution function with \(\Omega (\textbf{T})\Lambda <1-2\delta \).
Suppose \((H_1,H_2)\) is a \((t_0, {\textbf{T}})\) non-looping pair in the window [a, b] via \(\tau \)-coverings with constant \(C_{_{\!{\text {nl}}}}\). Let \(A_1,A_2\in \Psi ^\infty (M)\), \( {h^\delta } \le R(h) \le R_0\), and \(K>0\). There exist
and \(h_0>0\) such that for all \(0<h<h_0\) and all \(E\in [a-Kh,b+Kh]\),
We prove the proposition at the end of the section. The proof hinges on four lemmas. The first one, Lemma 6.3, rewrites the left hand side in (6.1) in terms of the function
where S, T are two positive constants with \(S<T\), and \(\rho \) is as in (1.16)
Remark 6.2
We note that for all \(N>0\)
Lemma 6.3
Suppose \(k>0\) and \(P\in \Psi ^k(M)\) is self-adjoint with symbol satisfying (1.9). Then, for all \(N>0\),
Proof
First, we prove that if P is self-adjoint \(E_1, E_2 \in {\mathbb {R}}\), then
To ease notation write \({\widetilde{T}}\) for \({\widetilde{T}}(h)\). To prove (6.4) we write
where we use \({\hat{\rho }}\big (\tfrac{w}{\sigma _{_{h,t_0}}}\big )={\hat{\rho }}\big (\tfrac{w}{\sigma _{_{h,{\widetilde{T}}}}}\big ){\hat{\rho }}\big (\tfrac{w}{\sigma _{_{h,t_0}}}\big )\). Putting \(\tau :=hw\), (6.4) follows.
Next, let \(N>0\). By (6.4) it suffices to find \(E_1 \in {\mathbb {R}}\) such that for all \({t>c>0}\)
To prove the first claim in (6.5), note that by (6.3) for all \(N>0\) there is \(C_{_{N}}>0\) such that
Next, since P satisfies (1.9), there is \(a>0\) such that \(p(x,\xi )>-a\) for all \((x, \xi ) \in T^*M\). In particular, for \(E_1\le -2a\), \(P_{_{E_1}}\) is elliptic and we have \( P_{_{E_1}}^{-1}:H_{scl }^s(M)\rightarrow H_{scl }^{s+k}(M)=O_s(1) \) for all \(s \in {\mathbb {R}}\). Then, for \(E_1\le {-2a}\) the first claim in (6.5) follows.
Next, by the sharp Gårding inequality, there is \(C>0\) such that \(\Pi _h(s)\equiv 0\) for \(s\le -a-Ch\). Thus, for \(E_1\le -3a\) and all \(N,M\ge 0\) there is \(C_{_{M,N}}>0\) such that
The claim follows after choosing M large enough. \(\square \)
Let \(H_1, H_2\), \(t_0, T(h)\), \(\tau ,\) and R(h) be as in Proposition 6.1. Since \((H_1,H_2)\) is a \((t_0, \textbf{T})\) non-looping pair in the window [a, b] via \(\tau _0\)-coverings, for \(i=1,2\) and \(h>0\) we let
We study \(A_1{f_{_{t_0,{\widetilde{T}},h}}\big (P_{_{E}}\big )}\,A_2^*\) by understanding the behavior of
for \(j \in \mathcal {J}^1(h)\) and \(k \in \mathcal {J}^2(h)\). Next, we study the case when \({\mathcal {T}}_j^1\) does not loop through \({\mathcal {T}}_k^2\).
Lemma 6.4
Assume \(H_1\) and \(H_2\) are conormally transverse for p in the window [a, b]. For \(i=1,2\) let \(\{{\mathcal {T}}_j^i\}_{j\in \mathcal {J}^i(h)}\) as in (6.6) and \(j \in \mathcal {J}^1(h)\), \(\ell \in \mathcal {J}^2(h)\) be such that
Let \(K>0\) and \(\mathcal {V}\) be a bounded subset of \(S_\delta (T^*M;[0,1])\). Then, there exists \(h_0>0\) and for all \(N>0\) there exists \(C_{_{N}}>0\) such that for all \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\), and every \(\delta \)-partition \(\{\chi _{_{{\mathcal {T}}_j^i}}\}_{j\in \mathcal {J}_{_{E}}^i(h)}\subset {\mathcal {V}}\) associated to \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}_{_{E}}^i(h)}\), \(i=1,2\),
Proof
By Egorov’s theorem, for all \(N>0\) there exist \(h_0>0\) and \(C_{_{N}}>0\) such that for all \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\), and \(|t|\in [t_0+\tau , T(h)-\tau ]\)
(see e.g. [18, Proposition 3.9]). The claim follows from the definition (6.2) together with the facts that by (6.3) the support of its integrand has \(\tau \in [t_0, 2 {\widetilde{T}}(h)]\), and \({\widetilde{T}}(h)=\tfrac{1}{2}T(h)\). \(\square \)
The next lemma provides an estimate for \({F_{{j,\ell }}^{^{A_1,A_2}}(E,h)}\) based on volumes of tubes.
Lemma 6.5
Assume \(H_1\) and \(H_2\) are conormally transverse for p in the window [a, b]. Let \(A_1\), \(A_2\), \(\tau _0\), \(R_0\), \(\tau \), \(\delta \), and R(h) be as in Proposition 6.1. For \(i=1,2\) let \(\{{\mathcal {T}}_j^i\}_{j\in \mathcal {J}^i(h)}\) be a \(({\mathfrak {D}}_n, \tau , R(h))\)-good covering of \( \Sigma _{_{[a,b]}}^{H_i}\). Let \(K>0\) and \(\mathcal {V}\) a bounded subset of \(S_\delta (T^*M;[0,1])\). Then, there are \(C_{_{0}}=C_{_{0}}(n,k_1, k_2,{\mathfrak {I}}_{_{\!0}}^1, {\mathfrak {I}}_{_{\!0}}^2, A_1,A_2,\mathcal {V})\) and \(h_0>0\), and for all \(N>0\) there exists \(C_{_{N}}>0\) such that the following holds. For all \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\), all \(\delta \)-partitions \(\{\chi _{_{{\mathcal {T}}_j^i}}\}_{j\in \mathcal {J}_{_{E}}^i(h)}\subset {\mathcal {V}}\) and \(\mathcal {I}_i \subset \mathcal {J}_{_{E}}^i(h)\) for \(i=1,2\), and all \(t_0, {{\tilde{T}}}\) with \(0<t_0<{\widetilde{T}}\),
Proof
The first step in our proof is to define for \(0<t_0<{\widetilde{T}}\) the functions
where \(N_0 \ge 1\) will be chosen later. Note that by (6.3) for all \(L>0\) there is \(C_{L}>0\) such that
Since \({f_{_{t_0,{\widetilde{T}},h}}\big (P_{_{E}}\big )= g^1_{_{t_0,{\widetilde{T}},h}}\big (P_{_{E}}\big )g^2_{_{t_0,{\widetilde{T}},h}}\big (P_{_{E}}\big )},\) we may use Cauchy-Schwarz to bound
Next, we use that for \(i=1,2\),
Thus, let \(w \in L^2(M)\) and fix \(i \in \{1,2\}\). We next apply Lemma 4.4 to the function \(u={g^i_{_{t_0,{\widetilde{T}},h}}\big (P_{_{E}}\big )}w\) and operator \(A=\sum _{j\in \mathcal {I}_i}Op_h(\chi _{_{{\mathcal {T}}_{j}^i}}) A_i\in \Psi _\delta ^\infty (M)\). Here, we use that \({\hbox {MS}}_{\textrm{h}}(A) \subset \cup _{j \in \mathcal {I}_i}{\mathcal {T}}_j^i\) and that \(\tfrac{1}{h}[P_{_{E}},A] \in \Psi ^\infty _\delta (M)\) (see the definition of a \(\delta \)-partition (4.2)). In particular, we may fix \(\mathcal {W}\subset \Psi ^\infty _\delta (M)\) such that \(\tfrac{1}{h}[P_{_{E}},A] \in \mathcal {W}\) regardless of the choice of cover and \(\delta \)-partition contained in \(\mathcal {V}\). Then, the constant \(C_{_{0}}^i\) provided by the Lemma depends on \(A_i\) instead of \(\mathcal {W}\).
Fix \(\psi \in C^\infty _0({\mathbb {R}};[0,1])\) with \(\psi (t)=1\) for \(|t| \le \tfrac{1}{4}\) and \(\psi (t)=0\) for \(|t| \ge 1\). By Lemma 4.4 with \(t_1=t_0\), \(T_1=t_0\), and \({{\mathcal {G}}}_\ell =\emptyset \) for all \(\ell >1\), we obtain that there are \(C_{_{0}}^i=C_{_{0}}^i(n,k_i,{\mathfrak {I}}_{_{\!0}}^i,A_i)>0\), \(C>0\), there exist \(h_0>0\) and for all \(N>0\) there is \(C_{_{N}}>0\) such that for all \(0<h<h_0\)
By the definitions \(g^i_{_{t_0,{\widetilde{T}}}}\), \(i=1,2\) and (6.8) there exists \(C>0\) such that for all \(t_0,{\widetilde{T}}\) with \(t_0<{\widetilde{T}}\),
In addition, note that for \(i=1,2\) there exists \(C_{_{N_0}}>0\) such that
The claim follows from choosing \(N_0\) large enough that \(N_0(1-\delta )+\delta \ge N\). \(\square \)
Lemma 6.6
Assume the same assumptions as in Proposition 6.1. For \(i=1,2\) let \(\{{\mathcal {T}}_j^i\}_{j\in \mathcal {J}^i(h)}\) be as in (6.6), \(\mathcal {V}\) be a bounded subset of \(S_\delta (T^*M;[0,1])\) and \(K>0\). There exists \(h_0>0\), and for all \(N>0\) there exists \(C_{_{N}}>0\) such that for all \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\), and every \(\delta \)-partition \(\{\chi _{_{{\mathcal {T}}_j^i}}\}_{j\in \mathcal {J}_{_{E}}^i(h)}\subset {\mathcal {V}}\) associated to \(\{{\mathcal {T}}_j^i\}_{j\in \mathcal {J}_{_{E}}^i(h)}\),
Proof
Let \(K>0\) and \(\psi \in C^\infty _c((-1,1);[0,1])\) with \(\psi (t)=1\) for \(|t| \le \tfrac{1}{4}\). We claim there exists \(h_0>0\) such that for all \(N>0\) there is \(C_{_{N}}>0\) so that for \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\).
To see this, first note that for \({{{\tilde{\psi }}}}\in C_c^\infty \) with \({{\,\textrm{supp}\,}}{{\tilde{\psi }}} \subset \{{\psi }\equiv 1\}\) and \(L>0\),
Now, since \(P_{_{E}}\) is classically elliptic in \(\Psi ^m(M)\), for all \(s\in {\mathbb {R}}\),
Note that (6.10) also holds with \({{\tilde{\psi }}}\) in place of \(\psi \). In addition, by (6.3)
Taking \(L>\max (N/m,N/(2(1-\delta )))\) and combining (6.10) and (6.11) we obtain (6.9).
Next, for \(i=1,2\) we define \( {G_i}:={\text {Id}}-\sum _{j \in \mathcal {J}_{_{{E}}}^i(h)} \!\!\!Op_h(\chi _{_{\mathcal {T}^i_j}}), \) and note that \({\hbox {MS}}_{\textrm{h}}(G_i)\cap \Lambda ^\tau _{ \Sigma _{_{E}}^{H_i}}(R(h)/2)=\emptyset \). Therefore, combining Lemma 4.1 together with (6.9), there exists \(h_0>0\) such that for all \(N>0\) there is \(C_{_{N}}>0\) so that for all \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\).
In particular, the lemma follows from applying (6.12) and its analogs since
\(\square \)
Proof of Proposition 6.1. Since \((H_1,H_2)\) is a \((t_0, \textbf{T})\) non-looping pair in the window [a, b] via \(\tau _0\)-coverings, for \(i=1,2\) and \(h>0\) we may work with \(\{{\mathcal {T}}_j^i\}_{j\in \mathcal {J}^i(h)}\), as in (6.6) and \(\{\chi _{_{{\mathcal {T}}_j^i}}\}_{j\in \mathcal {J}^i(h)}\) a \(\delta \)-partition associated \(\{{\mathcal {T}}^i_j\}\) For each \(E\in [a,b]\) and \(i=1,2,\) let \(\mathcal {J}^i_{_{E,h}}=\mathcal {B}_{_{E}}^i(h)\cup \mathcal {G}^i_{_{E}}(h)\) be a partition of indices such that property (1) of Definition 2.1 with \(r=R(h)\). Then, by Lemma 6.4, for \(K>0\) there exists \(h_0>0\) such that the following holds: For all \(N>0\) there is \(C_{_{N}}>0\) so that for all \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\), and \(i,k=1,2\) with \(i\ne k\),
Therefore, considering the remaining term, and applying Lemma 6.5 we obtain the following. There is \(C_{_{0}}=C_{_{0}} (n,k_1, k_2,{\mathfrak {I}}_{_{\!0}}^1, {\mathfrak {I}}_{_{\!0}}^2,A_1,A_2)>0\) and for \(K>0\) there exists \(h_0>0\) such that the following holds: For all \(N>0\) there is \(C_{_{N}}>0\) so that for all \(0<h<h_0\), \(E\in [a-Kh,b+Kh]\),
To get the last line we used that our covering satisfies property (2) of Definition 2.1. Combining Lemma 6.6 with (6.6), (6.13), and (6.14), we obtain the claim.
6.2 Proof of Theorem 8
Since for \(i=1,2\) the submanifold \(H_i\) is \( T_i(h)\) non-recurrent in the window [a, b] via \({\tau _0}\)-coverings with constant \(C_{_{\!{\text {nr}}}}^i\), we may apply Proposition 5.1 to obtain the existence of \(C_{_{0}}=C_{_{0}}(n,k_1, k_2,{\mathfrak {I}}_{_{\!0}}^1, {\mathfrak {I}}_{_{\!0}}^2,A_1,A_2,C_{_{\!{\text {nr}}}}^1, C_{_{\!{\text {nr}}}}^2)\) and for all \(K>0\) obtain \(h_0>0\) such that for all \(0<h\le h_0\) and \({s}\in [a-Kh,b+Kh]\),
where \(T(h)=(T_1(h)T_2(h))^{\tfrac{1}{2}}\) and \(T_{\max }(h)=\max (T_1(h),T_2(h))\). Note that we are actually applying the proposition only using that \(H_i\) is \(\tfrac{1}{2} T_i(h)\) non-recurrent.
On the other hand, since \((H_1,H_2)\) is a \((t_0, {\textbf{T}_{\max }})\) non-looping pair in the window [a, b] via \(\tau _0\) coverings, we may apply Proposition 6.1 to obtain that there exist \(C_{_{1}}=C_{_{1}}(n,k_1, k_2,{\mathfrak {I}}_{_{\!0}}^1, {\mathfrak {I}}_{_{\!0}}^2,A_1,A_2,C_{_{\!{\text {nl}}}})>0\) and for all \(K>0\) there is \(h_0>0\) such that for all \(0<h<h_0\) and all \(s\in [a-Kh,b+Kh]\)
The result follows from combining (6.15) with (6.16). We note that \(H_1\) and \(H_2\) may be replaced by \({{\tilde{H}}}_{1,h}\) and \({{\tilde{H}}}_{2,h}\) since \(C_{_{\!{\text {nl}}}}\), \(C_{_{\!{\text {nr}}}}^1\), and \(C_{_{\!{\text {nr}}}}^2\) are uniform for \(\{{{\tilde{H}}}_{1,h}\}_h\) and \(\{{{\tilde{H}}}_{2,h}\}_h\).
6.3 Proof of Theorem 9
Let \(0<\tau {<\min (\tau _0,\varepsilon /3)}\). By Proposition 3.5 there exists \(c_0>0\), \(C_{_{\!{\text {nr}}}}=C_{_{\!{\text {nr}}}}(M,p,{\mathfrak {t}},R_0)>0\) such that for \(j=1,2\), the submanifold \(H_j\) is \(c \textbf{T}_i(R)\) non-recurrent in the window [a, b] via \(\tau \) coverings with constant \(C_{_{\!{\text {nr}}}}\).
Now, since \((H_1,H_2)\) is a \((t_0,{\textbf{T}}_{\max })\) non-looping pair in the window [a, b] with constant \(C_{_{\!{\text {nl}}}}\). Proposition 3.1 implies there is \({\widetilde{C_{_{\!{\text {nl}}}}}}={\widetilde{C_{_{\!{\text {nl}}}}}}(p,a,b,n,C_{_{\!{\text {nl}}}}, H_1, H_2)\) such that \((H_1,H_2)\) is a \((t_0+3\tau _0,{\tilde{\textbf{T}}})\) non-looping pair in the window [a, b] via \(\tau _0\)-coverings with constant \({\widetilde{C_{_{\!{\text {nl}}}}}}\) where \({\tilde{\textbf{T}}}(R)=\textbf{T}_{\max }(4R)-3\tau _0\). Since \(\textbf{T}_j\) are sub-logarithmic, there is \(c_1>0\) such that \({\tilde{\textbf{T}}}(R)\ge c_1 \textbf{T}_{\max }(R)\). The proof now follows from a direct application of Theorem 8 with \(\textbf{T}_j\) replaced by \(\min (c_0,c_1)\textbf{T}_j\) and \(t_0\) by \(t_0+\varepsilon \).
7 The Weyl law
In order to improve remainders in the Weyl law itself, we let \({\mathbf {\Delta }} \subset M \times M\) be the diagonal, and for \(A_1, A_2\in \Psi ^\infty (M)\) consider the integral
where \(d\sigma _{_{\!{\mathbf {\Delta }}}}\) is the Riemannian volume form induced on \(\Delta \) by the product metric on \(M \times M\). To ease notation, we write \({\textbf{P}}_t=(P-t)\otimes 1={P\otimes 1-t{\text {Id}}}.\) We will view \({\mathbf {\Delta }}\) as a hypersurface of codimension n in \(M\times M\), and the kernel of \(\mathbb {1}_{[t-s,t]}(P)\) as a quasimode for \({\textbf{P}}_t\). In particular, observe that for any operator \(B:L^2(M)\rightarrow L^2(M)\)
In addition, note that for \((x,\xi ,y,\eta ) \in T^*M \times T^*M\)
Therefore, for all \(c>0\), there is \(C>0\) such that if \(c|\eta |\le |\xi |\) and \(|\xi |\ge C\), then
In particular, since we work near the \({\textbf{p}}\) flow-out of \( N^*{\mathbf {\Delta }}\cap \{{\textbf{p}}=t\} \) where \(t\in [a,b]\), and
we may work as though \({\textbf{P}}_t\) were elliptic in \(\Psi ^m(M\times M)\), and apply the results of the previous sections by accepting \(O(h^\infty )\) errors. We will do this without further comment.
We next describe the tubes relevant in this section. We will work microlocally near a point \(\rho _0\in N^*{\mathbf {\Delta }}\cap {\textbf{p}}^{-1}([a,b])\). Let \(\pi _{_{R}},\pi _{_{L}}:T^*(M\times M)\rightarrow T^*M\) denote the projections to the right and left factor, and let \({\mathcal {Z}}_{\pi _{_{L}}(\rho _0)}\subset T^*M\) be a transversal to the flow for p containing \(\pi _{_{L}}(\rho _0)\). (Such a hypersurface exists since \(dp(\rho )\ne 0\) on \(p^{-1}([a,b])\).) Define a transversal to the flow for \({\textbf{p}}\) by
and let U be a neighborhood of \(\rho _0\) in \(N^*{\mathbf {\Delta }}\) such that \( U\cap {\textbf{p}}^{-1}([a,b])\subset {\mathcal {Z}}_{\rho _0}. \) We will use the metric \({{\tilde{d}}}\) on \(T^*M\times M\) defined by \( {{\tilde{d}}}\Big ((\rho _{_{L}},\rho _{_{R}}),(q_{_{L}},q_{_{R}})\Big ):=\max \Big ( d(\rho _{_{L}},q_{_{L}}), d(\rho _{_{R}},q_{_{R}})\Big ), \) for \((\rho _{_{L}},\rho _{_{R}}),(q_{_{L}},q_{_{R}})\in T^*M \times M.\) With this definition, for \(\rho =(\rho _{_{L}},\rho _{_{R}})\in N^*{\mathbf {\Delta }}\cap \{{\textbf{p}}_t=0\}\),
where \(\Lambda _A^\tau (r)\) is defined by (2.2) with \(\varphi _t\) the Hamiltonian flow for \({\textbf{p}}\) and \({{\tilde{{\mathcal {T}}}}}={\tilde{\Lambda }}_{\rho _{_{L}}}^\tau (r)\) denotes a tube with respect to p and the hypersurface \({\mathcal {Z}}_{\pi _{_{L}}(\rho _0)}\). In particular, when we use cutoffs with respect to a tube \({\mathcal {T}}\), we will always work with cutoffs of the form
We will refer only to this tube in \(T^*M\), leaving the other implicit and will think of the kernel of \(A_1\mathbb {1}_{[a,b]}(P)A_2\) as that of \(\mathbb {1}_{[a,b]}(P)\) acted on by \(A_1\otimes A_2^{{t}}.\) Before we start our proof of the improved Weyl remainder, we need a dynamical lemma.
Lemma 7.1
Let \(C_{_{\!{\text {np}}}}>0\), \(a\le b\), and \(U\subset T^*M\) satisfying \(d\pi _{_{M}}{{\textsf{H}}_p}\ne 0\) on \(p^{-1}([a,b])\cap {\overline{U}}\). Then there are \(\tau _0>0\) and \({\widetilde{C_{_{\!{\text {np}}}}}}={\widetilde{C_{_{\!{\text {np}}}}}}(p,U,C_{_{\!{\text {np}}}})\) such that the following holds. If U is \((t_0,\textbf{T})\) non-periodic for p in the window [a, b] with constant \(C_{_{\!{\text {np}}}}\), then \(N^*\mathbf{\Delta }\cap (U\times T^*M)\) is \((t_0+{3}\tau _0,\textbf{T}({16}R)-{3}\tau _0)\) non-looping for \({\textbf{p}}\) via \(\tau _0\)-coverings in the window [a, b] with constant \({\widetilde{C_{_{\!{\text {np}}}}}}\).
Proof
Let \(E\in [a,b]\). We work with \(\mathcal {L}_{_{\mathbf{\Delta },\mathbf{\Delta }}}^{{R,E}}(t_0,T)\) as defined in Definition 1.12 but with p replaced by \({\textbf{p}}\), \(\varphi _t^{{\textbf{p}}}:=\exp (t H_\textbf{p})\), and \(\Sigma _{_{E}}^{\mathbf{\Delta }}=N^*\!\mathbf{\Delta } \cap \{{\textbf{p}}=\!E\}\). First, we claim
Here, through a slight abuse of notation, we write \(\mathcal {L}^{R,E}_{_{{\mathbf {\Delta }_U},{\mathbf {\Delta }_U}}}\) for (1.5) with \(S^*_xM\) and \(S^*_yM\) replaced by \({\mathbf {\Delta }_U}:=N^*\mathbf{\Delta } \cap (U\times T^*M)\) and \(\varphi _t=\exp (tH_{\textbf{p}})\). To prove (7.2) suppose \(\rho _0\in B_{_{\Sigma _{_{E}}^{{\mathbf {\Delta }}}}}\!\big ({\scriptstyle \mathcal {L}_{_{{\mathbf {\Delta }_U},{\mathbf {\Delta }_U}}}^{{R,E}}\!(t_0,T)}, R\big )\). Then, there are \(\rho _1 \in \Sigma _{_{E}}^{\mathbf{\Delta }}{\cap {\mathbf {\Delta }_U}}\) and \(\rho _1'\in T^*(M\times M)\) such that
Therefore, there is \(\rho _2 \in \Sigma _{_{E}}^{\mathbf{\Delta }}\) such that \({{\tilde{d}}}\big (\varphi _t^{\textbf{p}}(\rho _1'), \rho _2\big )<R\) for some \(t_0\le |t|\le T\). Let \(\rho _1'=(x',\xi ',y',-\eta ')\) with \((x',\xi '),(y',\eta ')\in T^*M\). Then, since \(\rho _1=(x,\xi ,x,-\xi )\) and \(\rho _2=(y,\eta ,y,-\eta )\) for some \((x,\xi )\in T^*M\) and \((y,\eta )\in T^*M\), we have \(d(\varphi _t(x',\xi '),(x',\xi '))<4R\) and \(\pi _{_{L}}({\rho _1'})=({x',\xi '})\in \mathcal {P}^{{4}R}_{_{U}}(t_0,T).\) On the other hand, since \(d(\pi _{_{L}}(\rho _0),\pi _{_{L}}({\rho '_1}))<{2}R\) we obtain \(\pi _{_{L}}(\rho _0)\in B_{_{S^*\!M}}\!\big ({\scriptstyle \mathcal {P}_U^{{4}R}(t_0,T)}, {2}R\big )\). This proves claim (7.2).
Next, note that since \(\pi _{_{L}}:{{\mathbf {\Delta }_U}}\cap { \Sigma _{_{E}}^{{\mathbf {\Delta }}} \rightarrow \{p=E\}\cap U}\) is a diffeomorphism for \(E\in [a,b]\), it follows that there exists \(C={C(p)}>0\) such that for all \(E \in [a,b]\)
Hence, if U is \((t_0,{\textbf{T}})\) non-periodic for p at energy E, we have
and so \({\mathbf {\Delta }_U}\) is \((t_0,\textbf{T}({4}R))\) non-looping for \(\textbf{p}\) at energy E. The result follows from Corollary 3.1. \(\square \)
In what follows, we write \(\Vert \cdot \Vert _{_{HS}}\) for the Hilbert-Schmidt norm.
Lemma 7.2
Let \(\mathcal {V}\subset S_\delta (T^*M;[0,1])\) be a bounded subset. Then, there are \(C>0\) and \(h_0>0\), and for all \(N>0\) there exists \(C_{_{N}}>0\), such that for all \(t \in [a,b]\), \(\chi \in \mathcal {V}\), \(0<h<h_0\), and \(|s|\le 2h\),
Proof
We follow the proof of [18, Lemma 3.11]. Let \(\psi \in \mathcal {S}({\mathbb {R}})\) with \(\psi (0)=1\) and \({{\,\textrm{supp}\,}}{\hat{\psi }}\subset [-1,1]\). Define \(\psi _\varepsilon (s):=\psi (\varepsilon s).\) Then, there is \(\varepsilon _0>0\) small enough so that \(\psi _{\varepsilon _0}(s)>\frac{1}{2}\) on \([-2,2]\). Abusing notation slightly, put \(\psi =\psi _{\varepsilon _0}\). Then, there exists an operator \(Z_s\) such that \( \mathbb {1}_{[t-s,t]}(P)={Z_s}\psi \big (\tfrac{P_t}{h}\big ), \) \([Z_s,P]=0\), and \(\Vert Z_s\Vert _{L^2\rightarrow L^2}\le 3\) for \(|s|\le 2h\). Therefore, \( \Vert \mathbb {1}_{[t-s,t]}(P)Op_h(\chi )\Vert _{_{HS}}\le {3}\big \Vert \psi \big (\tfrac{P_t}{h}\big )Op_h(\chi )\big \Vert _{_{HS}} \) and the Hilbert–Schmidt norm is the \(L^2\) norm of the kernel. Next, we recall that after application of a microlocal partition of unity, we may write
for a symbol \(a\sim \sum _j h^ja_j\) and phase \(\varphi \) solving \( \partial _t\varphi =p(x,\partial _x\varphi ) \) and \( \varphi (0,x,\eta )=\langle x,\eta \rangle . \) At this point the proof of (7.3) follows exactly as in [18, Lemma 3.11].
To obtain (7.4), we write \( P_t\mathbb {1}_{[t-s,t]}(P)=Z_sP_t\psi \big (\tfrac{P_t}{h}\big ) \) and note that \( \tfrac{P_t}{h}\psi \big (\tfrac{P_t}{h}\big )=(t\psi )\big (\tfrac{P_t}{h}\big ). \) Hence the same argument applies with \(\widehat{t\psi }(\tau )=-i\partial _\tau {\hat{\psi }}(\tau )\) replacing \({\hat{\psi }}(\tau )\). \(\square \)
We will also need the following trace bound for \(\mathbb {1}_{[t-s,t]}\).
Lemma 7.3
Suppose \(a,b\in {\mathbb {R}}\), \(\varepsilon _0>0\), \(\ell _1,\ell _2\in {\mathbb {R}}\), \(\mathcal {V}_1\subset \Psi ^{\ell _1}(M)\), and \(\mathcal {V}_2\subset \Psi _\delta ^{\ell _2}(M)\) bounded subsets, \(U\subset T^*M\) open such that \(|d\pi _{_{M}}{{\textsf{H}}_p}|>c >0\) on \(p^{-1}([a-\varepsilon _0,b+\varepsilon _0])\cap U\). Let \(\tau _0\),\(R_0\), \(\delta \), R(h), and \(\tau \) be as in Lemma 4.1. Let \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}(h)}\) be a \(({\mathfrak {D}},\tau ,R(h))\) good covering of \({\textbf{p}}^{-1}([a,b])\cap N^*{\mathbf {\Delta }}{\cap (U\times T^*M)}\) and \(\mathcal {V}\subset S_\delta (T^*M\times T^*M; [0,1])\) bounded. Then, there is \(C_{_{0}}>0\) such that for all \(\{\chi _{_{{\mathcal {T}}_j}}\}_{j\in \mathcal {J}(h)}\subset \mathcal {V}\) partitions for \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}(h)}\), \(j \in \mathcal {J}(h)\), \(A_1\in \mathcal {V}_1\), \(A_2\in \mathcal {V}_2\), and \(|s|\le \varepsilon _0\)
Proof
We first note that it suffices to prove the statement for \(|s|\le 2h\). Indeed, this is because we may apply the arguments from Lemma 5.4 and decompose \( \mathbb {1}_{[t-s,t]}(P)=\sum _{k=0}^{k_0-1}\mathbb {1}_{[t_k,t_{k+1}]}(P), \) with \(|t_{k+1}-t_k|\le 2h\). This allows us to obtain the result for \(|s|\le \varepsilon _0\).
Suppose \(|s|\le 2h\). Let \({{\tilde{U}}} \supset {B(U,2R(h))}\), \(j \in \mathcal {J}(h)\), and \(A:=Op_h(\chi _{_{{\mathcal {T}}_j}})(A_1 \otimes A_2)\). Note that
with seminorms bounded by those of \(\chi _{_{{\mathcal {T}}_j}}\), \(A_1\), and \(A_2\). We next apply Lemma 4.1 with \(A:=Op_h(\chi _{_{{\mathcal {T}}_j}})(A_1 \otimes A_2)\), \(\mathbf{P_t}\) in place of \(P_t\), \(k=n\), \(M\times M\) in place of M, and \( u:=\mathbb {1}_{[t-s,t]}(P){Op_h(\chi _{_{{\tilde{U}}}})}, \) where the latter is viewed as a kernel on \(M \times M\). Here, \(\chi _{_{{\tilde{U}}}}\in S_\delta (T^*M)\) with \(\chi _{_{{\tilde{U}}}}\equiv 1\) on B(U, R(h)), \({{\,\textrm{supp}\,}}\chi _{_{{\tilde{U}}}}\subset {\tilde{U}}\). Let \({\tilde{\chi }}_{_{{\mathcal {T}}_j}}\in \mathcal {V}\) with \({{\,\textrm{supp}\,}}{\tilde{\chi }}_{_{{\mathcal {T}}_j}}\subset {\mathcal {T}}_j\) and \({\tilde{\chi }}_{_{{\mathcal {T}}_j}}\equiv 1\) on \({{\,\textrm{supp}\,}}\chi _{_{{\mathcal {T}}_j}}\). Then, since \({\hbox {MS}}_{\textrm{h}}(A) \subset {\mathcal {T}}_j\), by Lemma 4.1 there exist \(C_{_{0}}>0\) and \(C>0\), such that
Note that we omit the analogous error terms appearing in the estimate of Lemma 4.1 since these error terms can be dealt with by applying the bounds in (5.7) and (5.8) in combination with (7.1).
Next, since \(Op_h({\tilde{\chi }}_{_{{\mathcal {T}}_j}})=Op_h({\tilde{\chi }}_{_{{\widetilde{{\mathcal {T}}}}_j}})\otimes Op_h({\tilde{\chi }}_{\rho _j})\), where \({\tilde{\chi }}_{\rho _j}\) and \({\tilde{\chi }}_{_{{\widetilde{{\mathcal {T}}}}_j}}\) are bounded in \(S_\delta (T^*M;[0,1])\) by the seminorms in the set \(\mathcal {V}\), we obtain
where u is now viewed as an operator. In the last line we used Lemma 7.2 and the existence of \(C>0\) such that \( \mu _t\Big (({{\,\textrm{supp}\,}}{\tilde{\chi }}_{\rho _j})\cap p^{-1}(t)\Big )\le CR(h)^{2n-1}. \) This finishes the proof when \(|s|\le 2h\). \(\square \)
Lemma 7.4
Let \(a,b,\varepsilon _0\), \(\tau _0\), \(\mathcal {V}_1,\mathcal {V}_2\) \(R_0\), \(\tau \), \(\delta \), R(h) and \(\alpha \) as in Lemma 4.4. Let \({N^*{\mathbf {\Delta }}\cap (U\times T^*M)}\) be \(\textbf{T}\) non-looping for \({\textbf{p}}\) in the window [a, b] via \(\tau \)-coverings and let \(C_{_{\!{\text {np}}}}\) be the constant \(C_{_{\!{\text {nl}}}}\) in Definition 2.1. Then, there is \(C_{_{0}}=C_{_{0}}(n,P, {\mathcal {V}_1, \mathcal {V}_2}, C_{_{\!{\text {np}}}},\varepsilon _0)>0\) and for all \(K>0\) there is \(h_0>0\) such that for all \(0<h\le h_0\), \(A_1\in \mathcal {V}_1\), \(A_2 \in \mathcal {V}_2\) with \({{\hbox {MS}}_{\textrm{h}}(A_2)\subset U}\), \(|s|\le 2h\), and \(t\in [a-Kh,b+Kh]\),
where \({\tilde{U}}(h)\supset B(U,2R(h))\), \(\chi _{_{{\tilde{U}}}}\in S_\delta \), \(\chi _{_{{\tilde{U}}}}\equiv 1\) on B(U, R(h)), and \({{\,\textrm{supp}\,}}\chi _{_{{\tilde{U}}}}\subset {\tilde{U}}\).
Proof
Since \(N^*{\mathbf {\Delta }} \cap (U\times T^*M)\) is \(\textbf{T}\) non-looping in the window [a, b] via \(\tau _0\)-coverings, for all \(t\in [a-Kh,b+Kh]\), there is a partition of indices \(\mathcal {J}_{_{t}}(h)={{\mathcal {G}}}_{_{t,0}}(h)\sqcup {{\mathcal {G}}}_{_{t,1}}(h)\) as described in Definition 2.1 (with \(H={\mathbf {\Delta }}\)). Let \(t_0=t_0\), \(t_1=1\), \(T_0(h)=T(h)\) and \(T_1(h)=1\). Then, there is \(C_{_{\!{\text {np}}}}>0\) such that for all \(t\in [a-Kh,b+Kh]\)
Next, we argue as in (5.5), and then apply a combination of Lemma 4.3 and Lemma 4.4 with \(A:=A_1 \otimes A_2\), \(\mathbf{P_t}\) in place of \(P_{_{E}}\), 2n in place of n, \(M\times M\) in place of M, \(k=n\), and \(u:=\mathbb {1}_{[t-s,t]}(P){Op_h(\chi _{_{{\tilde{U}}}})}\), where u is viewed as a kernel on \(M \times M\). Then, there is \(C_{_{0}}>0\) so that
where \({\tilde{t}}_\ell \) and \({\tilde{T}}_\ell \) are as in (5.4). We have used that, since \({\hbox {MS}}_{\textrm{h}}(A)\subset U \times T^*M\) and the tubes are a covering for \({\textbf{p}}^{-1}([a,b])\cap N^*{\mathbf {\Delta }}{\cap (U\times T^*M)}\), then \({\hbox {MS}}_{\textrm{h}}(A)\cap \Lambda _{\Sigma ^{{\mathbf {\Delta }}}_t}^\tau (R(h)/2) \subset \bigcup _{j \in \mathcal {J}_{_{t}}(h)}{\mathcal {T}}_j\). Also, note that we omit the analogous error terms appearing in the estimate of Lemma 4.4 since these error terms can be dealt with by applying the bounds in (5.7) and (5.8) in combination with (7.1).
The proof follows from applying the bounds in (5.5) in combination with (7.1). \(\square \)
Lemma 7.5
Let \(\ell _i \in {\mathbb {R}}\), \(\mathcal {V}_i\subset \Psi _\delta ^{\ell _i}(M)\) bounded for \(i=1,2\). Then, there are \(N_0>0\), \(C>0\), \(h_0>0\) such that for all \(A_1\in \mathcal {V}_1\) and \(A_2\in \mathcal {V}_2\), \(s\in {\mathbb {R}}\) and \(0<h<h_0\)
Proof
We apply Lemma 4.5 with \(H={\mathbf {\Delta }}\), \(A=A_1 \otimes A_2\), and \(u=\mathbb {1}_{(-\infty ,s]}(P)\). Then, for \(r>\frac{n+2(\ell _1+\ell _2)}{2m}\), there is \(C>0\) such that for all \(N>0\) there is \(C_N>0\) such that
It follows from (7.1) that the last term can be bounded by \(C(1+|s|^r) \Vert \mathbb {1}_{(-\infty ,s]}(P)\Vert _{L^2}\). \(\square \)
7.1 Proofs of Theorems 2 and 6
We claim that for \({E}\in [a-Kh,b+Kh]\) and \(A_1\in \mathcal {V}_1\), and \(A_2\in \mathcal {V}_2\) with \({\hbox {MS}}_{\textrm{h}}(A_2)\subset U\),
We start by showing under the same assumptions that
for some \(t_0\) independent of h. At the end of the section we will derive Theorems 2 and 6 from (7.7).
7.1.1 Proof of (7.8).
Let \({{\tilde{U}}},U_0 \subset T^*M\) with \(B(U_0,2R(h))\subset U\subset B(U_0,4R(h)) \subset {{\tilde{U}}}\). Then, let \(\chi _{_{{\tilde{U}}}},\chi _{_{U_0}},\chi _{_{{\tilde{U}}\setminus {U_0}}}\in S_\delta (T^*M;[0,1])\) with \(\chi _{_{{\tilde{U}}}}\equiv 1\) on U, \({{\,\textrm{supp}\,}}\chi _{_{{\tilde{U}}}}\subset B(U_0,3R(h))\), \(\chi _{_{U_0}}\equiv 1\) on \(B(U_0, R(h))\), \({{\,\textrm{supp}\,}}\chi _{_{U_0}}\subset U\), \(\chi _{_{{\tilde{U}}\setminus {U_0}}}\equiv 1\) on \({{\,\textrm{supp}\,}}\chi _{_{{\tilde{U}}}}(1-\chi _{_{U_0}})\), \({{\,\textrm{supp}\,}}\chi _{_{{\tilde{U}}\setminus {U_0}}}\subset {\tilde{U}}\setminus U_0\). By Lemma 7.2 and (1.12) there exists \(C_0>0\) such that for \(|s|\le 2h\),
Note that when \(U=T^*M\) this is an empty statement. Then, for \({|s|\le 2h}\), by Lemma 7.4
Then, applying the quadratic formula with \(x={\text {tr}}\mathbb {1}_{[t-s,t]}(P){Op_h(\chi _{_{U_0}})}\), for \(|s|\le 2h\) we have
Next, for \(|s|\le \varepsilon _0\), splitting \(\mathbb {1}_{[t-s,t]}(P)=\sum _{k=0}^{k_0-1}\mathbb {1}_{[t_k,t_{k+1}]}(P)\) as before, we have by Lemma 7.4 and Lemma 7.5 that there exists \(N_0>0\) such that
where to get the last inequality, we use Lemma 7.5 with \(U=M\), \(A_1=A_2={\text {Id}}\).
In particular, combining (7.11) and (7.12) together with Lemma 5.3 implies (7.8) holds.
7.1.2 Proof of (7.9).
Using Lemma 6.3, the proof of (7.9) amounts to understanding
where \(f_{S,T,h}\) is given by (6.2), and \({\tilde{T}}(h)=\frac{T(h)}{2}\). In particular, for \(E\in [a-Kh,b+Kh]\), we consider \( {\text {tr}}A_1{f_{t_0,{\tilde{T}},h}\big (P_E\big )}A_2.\) For this, we let \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}(h)}\) be a \(({\mathfrak {D}},\tau ,R(h))\)-good covering of \({\textbf{p}}^{-1}([a,b])\cap N^*{\mathbf {\Delta }}\cap (U\times T^*M)\) and \(\mathcal {V}\subset S_\delta (T^*M\times M;[0,1])\) a bounded subset. Let \(\{\chi _{_{{\mathcal {T}}_j}}\}_{j\in \mathcal {J}(h)}\subset \mathcal {V}\) be a partition associated to \(\{{\mathcal {T}}_j\}_{j\in \mathcal {J}_{_{E}}(h)}\).
Lemma 7.6
Let \(\mathcal {I}\subset \mathcal {J}_{_{E}}(h)\), \(\mathcal {V}_1\subset \Psi ^{\ell _1}(M)\), \(\mathcal {V}_2\subset \Psi _\delta ^{\ell _2}(M)\) bounded subsets. Then, there exist \(C_{_{0}}>0\) and \(h_0>0\) such that for all \(A_1\in \mathcal {V}_1\), \(A_2\in \mathcal {V}_2\), \(0<h<h_0\)
Proof
We first note that \( {f_{t_0,{\widetilde{T}}(h),h}(P_{_{E}})}= {\varrho _h}*\partial _s \mathbb {1}_{(-\infty ,\,\cdot \,]}({P})({E}), \) where \( {\varrho _h(s)}:={f_{t_0,{\widetilde{T}}(h),h}(-s)}. \) Then, since \(\widehat{f_{t_0,{\widetilde{T}}(h)}}(0)=0\), we have \(\int _{\mathbb {R}}\partial _s\varrho _h(s)ds=0\). In particular, by the estimates (6.3), Lemma 5.3 applies with \(\sigma _h=h^{-1}\). Note that by Lemma 7.3, for \(t\in [a-Kh,b+Kh]\), and \(|s|\le 1\),
Also, by Lemma 7.5, there exists \(N_0\) such that for \(s\in {\mathbb {R}}\),
The proof follows from Lemma 5.3 using (7.13) and (7.14), and by summing in \(j\in {\mathcal {I}}\). \(\square \)
Lemma 7.7
Let \(\mathcal {V}_1, \mathcal {V}_2\) as in Lemma 7.6 and suppose \({\mathcal {T}}_j\) is a tube such that \({\tilde{{\mathcal {T}}}}_j\), its corresponding tube in \(T^*M\), satisfies \( \varphi _t({\tilde{{\mathcal {T}}}}_j)\cap {\tilde{{\mathcal {T}}}}_j=\emptyset \) for \(|t|\in [t_0,T(h)].\) Then for all \(N>0\) there is \(C_{_{N}}>0\) such that for all \(A_1\in \mathcal {V}_1\), and \(A_2\in \mathcal {V}_2\),
Proof
Note that the assumption on \({\tilde{{\mathcal {T}}}}_j\) implies \( \exp (tH_{\textbf{p}})({\mathcal {T}}_j)\cap N^*{\mathbf {\Delta }} =\emptyset \) for \( |t|\in [t_0,T(h)]. \) Therefore, the same application of Egorov’s theorem as in Lemma 6.4, completes the proof. \(\square \)
Since U is \(\textbf{T}\) non-periodic in the window [a, b] via \(\tau \)-coverings, for all \(E\in [a-Kh,b+Kh]\), there is a splitting \( \mathcal {J}_{_{E}}(h)=\mathcal {B}_{_{E}}(h)\cup \mathcal {G}_{_{E}}(h) \) such that \(\varphi _t({\tilde{{\mathcal {T}}}}_j)\cap {\tilde{{\mathcal {T}}}}_j=\emptyset \) for \(|t|\in [t_0,T(h)]\) for \(j\in \mathcal {G}_{_{E}}(h)\), and \( |\mathcal {B}_{_{E}}(h)|R(h)^{2n-1}\le T^{-1}(h). \) We write, using \({\hbox {MS}}_{\textrm{h}}(A_1\otimes A_2)\cap \Lambda _{\Sigma ^{{\mathbf {\Delta }}}_t}^\tau (R(h)/2)\subset \bigcup _{j\in \mathcal {J}_{h,E}}{\mathcal {T}}_j,\)
Applying Lemma 7.7 to the sum over \(\mathcal {G}_{_{E}}(h)\) and Lemma 7.6 to the sum over \(\mathcal {B}_{_{E}}(h)\), we have
for any \(E\in [a-Kh,b+Kh]\). In particular (7.9) holds.
7.1.3 Completion of the proof of Theorem 6
In order to complete the proof of Theorem 6, we take \(A_1={\text {Id}}\) and \(A_2=A^{{t}}\) and apply (7.7) to obtain the theorem. \(\square \)
7.1.4 Proof of Theorem 2
We assume \({W}\subset M\) is \(\textbf{T}\) non-periodic and let \(P=Q\) as in (2.14). Then \(|d\pi _{_{M}}{{\textsf{H}}_p}|>c>0\) on \(|\xi |_g>\frac{1}{2}>0\) so we may apply (7.7) for \(E>\frac{1}{2}\). Let \(0<\delta <\tfrac{1}{2}\). Let \(\chi _h\in C_c^\infty (M)\) as in [9, (19)] i.e. such that \(\chi _h\equiv 1\) in a neighborhood of \(\partial {W}\), \({{\,\textrm{supp}\,}}\chi _h\subset \{ d(x,\partial {W})<2h^\delta \}\), \(|\partial _x^\alpha \chi |\le C_\alpha h^{-|\alpha |\delta },\) \({{\,\textrm{vol}\,}}_{_{\!M}}({{\,\textrm{supp}\,}}\chi _h)\le C h^{\delta (n-\dim _{box }\partial {W})}.\)
Let \(R(h)\ge {h^\delta }\), and \(T(h)=\textbf{T}(R(h))\). Then, put \(A_1=1\) and \(A_2=(1-\chi _h)1_{{W}}\) in (7.7) to obtain
Next, since \( \rho _{h,t_0}*\mathbb {1}_{(-\infty ,\cdot ]}(P)({1})(x,x)=\frac{{{\,\textrm{vol}\,}}_{{\mathbb {R}}^n}(B^n)}{(2\pi h)^{n}}+O(h^{-n+2}) \) (apply Theorem 3 with \(\textbf{T}=1\)),
Also, since \(\Pi _h(1,x,x)=(2\pi h)^{-n}{{\,\textrm{vol}\,}}_{{\mathbb {R}}^n}(B^n)|= O(h^{1-n})\) (apply Theorem 3 with \(\textbf{T}={{\,\textrm{inj}\,}}M\)),
where we used \( {{\,\textrm{vol}\,}}({{\,\textrm{supp}\,}}\chi _h)\le h^{\delta (n-\dim _{box }(\partial {W}))}\). In particular,
\(\square \)
References
Avakumović, V.G.: Über die Eigenfunktionen auf geschlossenen Riemannschen Mannigfaltigkeiten. Math. Z. 65, 327–344 (1956)
Bérard, P.H.: On the wave equation on a compact Riemannian manifold without conjugate points. Math. Z. 155(3), 249–276 (1977)
Besse, A.L.: Manifolds all of whose geodesics are closed, volume 93 of Ergebnisse der Mathematik und ihrer Grenzgebiete [Results in Mathematics and Related Areas]. Springer-Verlag, Berlin-New York (1978). With appendices by D. B. A. Epstein, J.-P. Bourguignon, L. Bérard-Bergery, M. Berger and J. L. Kazdan
Bonthonneau, Y.: The \(\Theta \) function and the Weyl law on manifolds without conjugate points. Doc. Math. 22, 1275–1283 (2017)
Bruggeman, R.W.: Fourier coefficients of automorphic forms, volume 865 of Lecture Notes in Mathematics. Springer-Verlag, Berlin-New York, 1981. Mathematische Lehrbücher und Monographien, II. Abteilung: Mathematische Monographien [Mathematical Textbooks and Monographs, Part II: Mathematical Monographs], 48
Burns, K., Paternain, G.P.: On the growth of the number of geodesics joining two points. In: International Conference on Dynamical Systems (Montevideo, 1995), volume 362 of Pitman Res. Notes Math. Ser., pp. 7–20. Longman, Harlow (1996)
Canzani, Y.: Monochromatic random waves for general riemannian manifolds. In: Frontiers in Analysis and Probability. Springer (2020)
Canzani, Y., Galkowski, J.: Improvements for eigenfunction averages: an application of geodesic beams. arXiv:1809.06296, to appear in J. Differential Geom. (2019)
Canzani, Y., Galkowski, J.: On the growth of eigenfunction averages: microlocalization and geometry. Duke Math. J. 168(16), 2991–3055 (2019)
Canzani, Y., Galkowski, J.: Growth of high \({L}^p\) norms for eigenfunctions: an application of geodesic beams. arXiv:2003.04597 to appear in Anal. PDE (2020)
Canzani, Y., Galkowski, J.: Eigenfunction concentration via geodesic beams. J. Reine Angew. Math. 775, 197–257 (2021)
Canzani, Y., Galkowski, J.: Logarithmic improvements in the Weyl law and exponential bounds on the number of closed geodesics are predominant. arXiv:2204.11921 (2022)
Canzani, Y., Hanin, B.: Scaling limit for the kernel of the spectral projector and remainder estimates in the pointwise Weyl law. Anal. PDE 8(7), 1707–1731 (2015)
Canzani, Y., Hanin, B.: \(C^\infty \) scaling asymptotics for the spectral projector of the Laplacian. J. Geom. Anal. 28(1), 111–122 (2018)
Chazarain, J.: Formule de Poisson pour les variétés riemanniennes. Invent. Math. 24, 65–82 (1974)
Colin de Verdière, Y.: Spectre du laplacien et longueurs des géodésiques périodiques. II. Compos. Math. 27(2), 159–184 (1973)
Duistermaat, J.J., Guillemin, V.W.: The spectrum of positive elliptic operators and periodic bicharacteristics. Invent. Math. 29(1), 39–79 (1975)
Dyatlov, S., Guillarmou, C.: Microlocal limits of plane waves and Eisenstein functions. Ann. Sci. Éc. Norm. Supér. (4) 47(2), 371–448 (2014)
Dyatlov, S., Zworski, M.: Mathematical theory of scattering resonances. 200, xi+634 (2019)
Eberlein, P.: When is a geodesic flow of Anosov type?. I. J. Differ. Geom. 8, 437–463 (1973)
Gårding, L.: On the asymptotic distribution of the eigenvalues and eigenfunctions of elliptic differential operators. Math. Scand. 1, 237–255 (1953)
Galkowski, J.: Defect measures of eigenfunctions with maximal \(L^\infty \) growth. Ann. Inst. Fourier (Grenoble) 69(4), 1757–1798 (2019)
Good, A.: Local analysis of Selberg’s trace formula, volume 1040 of Lecture Notes in Mathematics. Springer-Verlag, Berlin (1983)
Hejhal, D.A.: Sur certaines séries de Dirichlet associées aux géodésiques fermées d’une surface de Riemann compacte. C. R. Acad. Sci. Paris Sér. I Math. 294(8), 273–276 (1982)
Hörmander, L.: The spectral function of an elliptic operator. Acta Math. 121, 193–218 (1968)
Horozov, E.: On the isoenergetical nondegeneracy of the spherical pendulum. Phys. Lett. A 173(3), 279–283 (1993)
Iosevich, A., Wyman, E.: Weyl law improvement for products of spheres. Anal. Math. 47(3), 593–612 (2021)
Ivriĭ, V.J.: The second term of the spectral asymptotics for a Laplace-Beltrami operator on manifolds with boundary. Funktsional. Anal. i Prilozhen. 14(2), 25–34 (1980)
Iwaniec, H.: Nonholomorphic modular forms and their applications. In: Modular forms (Durham, 1983), Ellis Horwood Ser. Math. Appl.: Statist. Oper. Res., pp. 157–196. Horwood, Chichester (1984)
Katok, A., Hasselblatt, B.: Introduction to the modern theory of dynamical systems, volume 54 of Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge (1995). With a supplementary chapter by Katok and Leonardo Mendoza
Keeler, B.: A logarithmic improvement in the two-point weyl law for manifolds without conjugate points. arXiv:1905.05136 (2019)
Klingenberg, W.: Riemannian manifolds with geodesic flow of Anosov type. Ann. Math. 2(99), 1–13 (1974)
Koch, H., Tataru, D., Zworski, M.: Semiclassical \(L^p\) estimates. Ann. Henri Poincaré 8(5), 885–916 (2007)
Kuznecov, N.V.: The Petersson conjecture for cusp forms of weight zero and the Linnik conjecture. Sums of Kloosterman sums. Mat. Sb. (N.S.) 111(153)(3), 334–383, 479 (1980)
Levitan, B.M.: On the asymptotic behavior of the spectral function of a self-adjoint differential equation of the second order. Izvestiya Akad. Nauk SSSR. Ser. Mat. 16, 325–352 (1952)
Minakshisundaram, S., Pleijel, A.: Some properties of the eigenfunctions of the Laplace-operator on Riemannian manifolds. Can. J. Math. 1, 242–256 (1949)
Safarov, Y., Vassiliev, D.: The asymptotic distribution of eigenvalues of partial differential operators, volume 155 of Translations of Mathematical Monographs. American Mathematical Society, Providence, RI (1997). Translated from the Russian manuscript by the authors
Safarov, Y.G.: Asymptotic of the spectral function of a positive elliptic operator without the nontrap condition. Funct. Anal. Appl. 22(3), 213–223 (1988)
Seeley, R.T.: Complex powers of an elliptic operator. pp. 288–307 (1967)
Sogge, C.D.: Fourier integrals in classical analysis, volume 105 of Cambridge Tracts in Mathematics. Cambridge University Press, Cambridge (1993)
Sogge, C.D., Zelditch, S.: Riemannian manifolds with maximal eigenfunction growth. Duke Math. J. 114(3), 387–437 (2002)
Stein, E.M., Shakarchi, R.: Real analysis, volume 3 of Princeton Lectures in Analysis. Princeton University Press, Princeton, NJ (2005). Measure theory, integration, and Hilbert spaces
Volovoy, A.V.: Improved two-term asymptotics for the eigenvalue distribution function of an elliptic operator on a compact manifold. Commun. Partial Differ. Equ. 15(11), 1509–1563 (1990)
Volovoy, A.V.: Verification of the Hamilton flow conditions associated with Weyl’s conjecture. Ann. Global Anal. Geom. 8(2), 127–136 (1990)
Weinstein, A.: Fourier integral operators, quantization, and the spectra of Riemannian manifolds. In: Géométrie symplectique et physique mathématique (Colloq. Internat. CNRS, No. 237, Aix-en-Provence, 1974), pp. 289–298. (1975) With questions by W. Klingenberg and K. Bleuler and replies by the author
Weyl, H.: Das asymptotische Verteilungsgesetz der Eigenwerte linearer partieller Differentialgleichungen (mit einer Anwendung auf die Theorie der Hohlraumstrahlung). Math. Ann. 71(4), 441–479 (1912)
Zelditch, S.: Kuznecov sum formulae and Szegő limit formulae on manifolds. Commun. Partial Differ. Equ. 17(1–2), 221–260 (1992)
Zworski, M.: Semiclassical analysis, volume 138 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI (2012)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Index of notation
In general we denote points in \(T^*\!M\) by \(\rho \). When position and momentum need to be distinguished we write \(\rho =(x,\xi )\) for \(x\in M\) and \(\xi \in T_x^*M\). The natural projection is \(\pi _{_{M}}:T^*M \rightarrow M\). Sets of indices are denoted in calligraphic font (e.g., \(\mathcal {J}\)). Next, we list symbols that are used repeatedly in the text along with the location where they are first defined.
\(\rho _\sigma \) | (1.7) | \(E_{_{H_1,H_2}}^{A_1,A_2}\) | (1.17) | \(\mathcal {K}_\alpha \) | (2.8) |
\(E_\lambda ^{t_0}\) | (1.8) | \(\Lambda _{_{\!A}}^\tau (r)\) | (2.2) | \(|{{\textsf{H}}_p} r_{_{H}}|\) | (2.10) |
\(\Lambda _{\max }\) | (1.11) | \(\mathcal {Z}\) | (2.1) | \({\mathfrak {I}}_{_{\!0}}\) | (2.11) |
\(T_e(h)\) | (1.11) | \(\tau _{{{\,\textrm{inj}\,}}}\) | (2.3) | \(\rho _{_{h, T}}\) | (1.16) |
\( \Sigma _{_{[a,b]}}\) | (1.14) | \(\mathcal {J}_{_{E}}(h)\) | (2.5) | \(P_{_{E}}\) | (4.3) |
For \(U\subset V \subset T^*M\) we write \(B_V(U, R)=\{\rho \in V: d(U, \rho )<R\}\) and \(B(U,R)=B_{_{T^*M}}(U,R)\). For \(A \subset T^*M\) we write \(\mu _A\) for the Liouville measure induced on A. The injectivity radius of M is denoted by \({{\,\textrm{inj}\,}}M\). For the definitions of the semiclassical objects \(\Psi ^\ell (M)\), \(\Psi ^\ell _\delta (M)\), \(S^\ell (T^*M)\), \(S^\ell _\delta (T^*M)\), \({\hbox {WF}}_{\textrm{h}}\), \({\hbox {MS}}_{\textrm{h}}\), \(H^N_{\text {scl}}(M)\), we refer the reader to [11, Appendix A.2]. See also (2.12) and (4.1) for the definitions of \(H^N_{\text {scl}}(M)\) and \(S_\delta ,\Psi _\delta \) respectively. For the definition of [t, T] non-self looping, see (2.6), that of \(({\mathfrak {D}},\tau ,r)\) good covers, see (2.4). Non-periodic, non-looping, and non-recurrent are defined in Definitions 1.9, 1.12, and 1.13 respectively. For non-looping via coverings and non-recurrent via coverings, see Definitions 2.1 and 2.2.
Appendix B: Examples
In this section, we verify our dynamical conditions in some concrete examples (some of which are displayed in Tables 1 and 2). In particular, we verify that certain subsets of manifolds are non-periodic (see Definition 1.2), that various pairs of submanifolds \((H_1,H_2)\) are non-looping (see Definition 1.3), and that certain submanifolds are non-recurrent either via coverings (see Definition 2.2) or simply non-recurrent (see Definition 1.7). Recall also that if \((H_1,H_1)\) is a non-looping pair, then \(H_1\) is non-looping and hence also non-recurrent. Once these conditions are verified, one can directly apply the relevant theorems (Theorem 2, 3, 4, and 5).
1.1 Manifolds without conjugate points and generalizations
Let \({\Xi }\) denote the collection of maximal unit speed geodesics for (M, g). For m a positive integer, \(R>0\), \(T\in {{\mathbb {R}}}\), and \(x \in M\) define
where we count conjugate points with multiplicity. Next, for a set \({W}\subset M\) write
Note that if \(\textbf{T}(R) \rightarrow \infty \) as \(R\rightarrow 0^+\), then saying \(y \in \mathcal {C}_{x}^{n-1,R,\textbf{T}(R)}\) for R small indicates that x behaves like a point that is maximally conjugate to y. Note that if (M, g) has no conjugate points, then \(\mathcal {C}_{x}^{m,r,T} =\emptyset \) for all \(x \in M\) and \(r<|T|\).
Lemma B.1.1
Let \(\alpha >0\), \(t_0>0\) and \(\textbf{T}(R)=\alpha \log R^{-1}\). Then there are \(C_{_{\!{\text {nl}}}}>0\) and \(c>0\) such that if \(H_1,H_2\subset M\) of co-dimension \({k_1},{k_2}\), and
for all \(R<e^{-t_0/\alpha }\), then \((H_1,H_2)\) is a \((t_0,c\log R^{-1})\) non-looping pair with constant \(C_{_{\!{\text {nl}}}}\), for \(p(x,\xi )=|\xi |_{g(x)}\).
Proof
By [8, Proposition 2.2, Lemma 4.1] there exist \(\tau >0\), \(\delta >0\), \(C_{_{\!{\text {nl}}}}>0\), \(C>0\), such that the pair \((H_1,H_2)\) is a \((t_0,T(h))\) non-looping via \((\tau ,h^\delta )\) coverings with constant \(C_{_{\!{\text {nl}}}}\) in the window [a, b] for any \(0<a<b\), where \( T(h)=c\log h^{-1} \) for some \(c>0\) depending on \((M,g,\alpha )\). Combining this result with Lemma 3.4 completes the proof. \(\square \)
Remark B.1.2
We note that [8, Proposition 2.2] was only proved for \(H_1=H_2\). However, the same argument works for the general case.
1.1.1 Product manifolds
Let \((M_i,g_i)\), \(i=1,2\), be two compact Riemannian manifolds. Let \(M=M_1\times M_2\) endowed with the product metric \(g=g_1\oplus g_2\). By [11, Lemma 1.1] we have \(\mathcal {C}^{n-1,r,T}_{x}=\emptyset \) for \(0<r<|T|\). Therefore, by Lemma B.1.1 for every \(\alpha ,t_0>0\) there is \(C_{_{\!{\text {nl}}}}\) such that every \(x\in M\) is \((t_0,\alpha \log R^{-1})\) non-looping with constant \(C_{_{\!{\text {nl}}}}\) for \(|\xi |_{g(x)}\). Note that, integrating over M, and using
this also implies M is \(\alpha \log R^{-1}\) non-periodic. We point out that although \(\mathcal {C}^{{n-1},r,T}_x\) is empty for \(0<r<|T|\), M may, and often does, have conjugate points. For example, this is the case when \(M^1=S^{n_1}\) with \(n_1\ge 2\).
1.1.2 Flow invariance of non-looping condition
In this section, we show that non-looping properties of a pair \((H_1,H_2)\) are inherited by their flow-outs \(H^t:=\pi (\varphi _t(S\!N^*\!H)).\) Note, for example, that a geodesic sphere is given by \(H^t\) when \(H=\{x\}\) is a point for some \(t>0\).
Lemma B.1.3
Suppose \((H_1,H_2)\) is a \((t_0,\textbf{T})\) non-looping pair. Then, for all \(s,t\in {\mathbb {R}}\) there exists \(C>0\) such that \((H^t_1,H^s_2)\) is a \((t_0+|t|+|s|,{\tilde{\textbf{T}}})\) non-looping pair where \({\tilde{\textbf{T}}}(R)=\textbf{T}(CR)-(|t|+|s|).\)
Proof
First, note that \(S\!N^*\!H^t_j=\varphi _t(S\!N^*\!H_j)\cup \varphi _{-t}(S\!N^*\!H_j)\) for \(j=1,2\). Let \(T>0\) and suppose  . Then, there is \(q_1\in \mathcal {L}^{{R,1}}_{_{H^t_1,H^s_2}}(t_0,T)\) such that \(d(q_{{1}},\rho )<R\). In particular, there are \(q_2\in T^*M\) and \(t_0\le |t_1|\le T\) such that \(d(q_1,q_2)< R\) and \( d(\varphi _{t_1}(q_2), S\!N^*\!H^s_2)<R. \)
. Then, there is \(q_1\in \mathcal {L}^{{R,1}}_{_{H^t_1,H^s_2}}(t_0,T)\) such that \(d(q_{{1}},\rho )<R\). In particular, there are \(q_2\in T^*M\) and \(t_0\le |t_1|\le T\) such that \(d(q_1,q_2)< R\) and \( d(\varphi _{t_1}(q_2), S\!N^*\!H^s_2)<R. \)
Now, either \(\varphi _{-t}(q_1)\in S\!N^*\!H_1\) or \(\varphi _t(q_1)\in S\!N^*\!H_1\). We consider the case \(\varphi _{t}(q_1)\in S\!N^*\!H_1\), the other begin similar. Then, there exist \(C_t,C_s>0\) such that
In particular, letting \(C=\max (C_t,C_s)\), \( \varphi _t(q_1)\in \mathcal {L}_{_{H_1,H_2}}^{CR}(t_0+|t|+|s|,T-(|t|+|s|)), \) and, since \(d(\varphi _t(\rho ),\varphi _t(q_1))<CR\),

Repeating this argument when \(\varphi _{-t}(q_1)\in S\!N^*\!H_1\), we obtain

In particular, there is \(C>0\) such that

Therefore, since \((H_1,H_2)\) is a \((t_0,\textbf{T})\) non-looping pair, \((H_1^t,H_2^s)\) is a \((t_0+|t|+|s|,{\tilde{\textbf{T}}})\) non-looping pair with \({\tilde{\textbf{T}}}(R)=\textbf{T}(CR)-|t|-|s|.\) \(\square \)
Now, by Lemma B.1.1, in the case \( d\big (y,\mathcal {C}_x^{n-1,R,\textbf{T}(R)}\big )>R, \) for \(R<e^{-t_0/\alpha }\) and \(\textbf{T}(R)=\alpha \log R^{-1}\), we have (x, y) is a \((t_0,c\log R^{-1})\) non-looping pair. Hence, by Lemma B.1.3 that the geodesic spheres generated by x and y form a non-looping pair with resolution function \(\textbf{T}(R)={\tilde{C}}\log R^{-1}\) for some \({{\tilde{C}}}>0\).
1.2 Surfaces of revolution
Consider \(M=S^2\) with the metric a \( \iota ^*g \) where
and \(\iota :[-\frac{\pi }{2},\frac{\pi }{2}]\times {\mathbb {R}}/2\pi {\mathbb {Z}}\rightarrow S^2\), with \( \iota (s,\theta )=(\cos (s)\cos (\theta ),\cos (s)\sin (\theta ), \sin (s)).\) Here, \(\alpha \) is a smooth function satisfying \(\alpha (\pm \frac{\pi }{2})=0\) and \(\pm \alpha '(\pm \pi /2)=1\). This assumption implies g is a smooth Riemannian metric. Furthermore, we assume \(-s\alpha '(s)>0\) for \(s\ne 0\) and \(\alpha ''(0)<0\). Note that the round sphere is given by \(\alpha (s)=\cos (s)\).
For a unit speed geodesic, \(t \mapsto (s(t),\theta (t))\) with \((s(0),\theta (0))=(0,0)\), \({\dot{\theta }}(0)>0\), \({\dot{s}}(0)>0\), we have by the Clairaut formula (see e.g. [3, Proposition 4.7])
where \(s_+\) is the maximal value of s on the geodesic. In particular, putting \(t(s_+)\) for the first time when \(s(t)=s_+\), we have \(s:[0,t(s_+)]\rightarrow [0,s_+]\) is invertible,
and, changing variables to \(w=s(t)\) and using \( \dot{s}(t)=\sqrt{1-\frac{\alpha ^2(s_+)}{\alpha ^2(s(t))}}, \) we have
We then define \(\theta _+(s_+):=2\theta (t(s_+))\). If we instead suppose \({{\dot{\theta }}}>0\) and \({\dot{s}}<0\), we can define \(\theta _-(s_-)\) analogously where \(s_-\) is the minimal s value on the trajectory. Now, there is a smooth function
such that if \(s_+\) is the maximal s value of a trajectory, then \(s_-(s_+)\) is the minimal s value. Moreover, \(\partial _{s_+}s_-<0\).
Finally, note that for a trajectory with maximal s value \(s_+\), \(s(0)=0\), \({\dot{s}}\ne 0\), if T is the second return time to \(s(0)=0\), then
Note that apriori, \(\theta (T)-\theta (0)\) could depend on the precise geodesic whose maximal s value is \(s_+\). However, the integrable torus, \({\mathbb {T}}_{s_+}\), consisting of all such geodesics has the same \(\theta (T)-\theta (0)\) up to sign.
In the next lemmas, we reduce the study of dynamical properties on (M, g) to the Poincaré section \(\{s(0)=0,{\dot{s}}(0)>0\} \subset TM\). The function \(\Theta _0:(0, \pi /2] \rightarrow {\mathbb {R}}\) is the change in \(\theta \) after a return to the Poincaré section. In particular, \({\mathbb {T}}_{s_+}\) is a periodic torus (i.e. all its trajectories are periodic) if and only if for some \(p,q\in {\mathbb {Z}}\), \(q\ne 0\),
Lemma B.2.1
Suppose there exists \(b> 0\) such that
Then, there are \(C_{_{\!{\text {np}}}},c>0\) such that every subset \(U\subset \{s>b\}\cup \{s<s_-(b)\}\) is \(\textbf{T}\) non-periodic for \(\textbf{T}(R)=cR^{-1/3}\) with constant \(C_{_{\!{\text {np}}}}\).
Proof
Suppose \(\rho \in S^*M\) with \(s_+(\rho )>b\), and let \(t\in {\mathbb {R}}\) be such that
Then, there is \(|t_1|\le R\) such that \( d(\varphi _{t+t_1}(\rho ),\rho )< (1+C (|t|+|t_1|))R. \) Now, for some \(0\le t_2\le c\), we have \( {s}(\varphi _{t_2}(\rho ))=0 \) and
Let \(s_+\) be the maximal s value for the trajectory through \(\rho \). Then, there are \(p,q\in {\mathbb {Z}}\) with \(|p|,|q|\le C(1+|t|)\), \(|q|\ge c(1+|t|)\) such that
We have shown that if \(\rho \in S^*M\) is such that (B.2) holds, then \(\rho \in \bigcup _{s_+ \in A(t)} {\mathbb {T}}_{s_+}\), where
Next, we claim
Indeed, \({\#}\{r \in [0,1]:\; \exists p,q \in {{\mathbb {Z}}},\; r=p/q,\;\; |p|,|q|\le C(1+|t|)\} \le C(1+|t|)^2\) and hence, the volume of possible values of \(\Theta _0(s_+)\) such that (B.3) holds is bounded by \( C(1+|t|)^2R. \) The claim in (B.4) then follows from the assumption \(\partial _{s_+} \Theta _0(s_+)\ne 0\) on \(s_+\ge b\).
Our next goal is to show that the bound in (B.4) translates to a bound on the set of \(\rho \) with (B.2). To see this, note that \({\mathbb {T}}_{s_+}=\{ |\xi _\theta |=\alpha (s_+)\}{\cap S^*M}\) where we work in the cotangent bundle with coordinates \((s, \theta , \xi _s,\xi _\theta )\). Therefore, when \(\alpha (s_+)<\alpha (s_0)\), the intersection \({\mathbb {T}}_{s_+}\cap S^*_{(s_0,\theta )}M\) is transversal for any \(\theta \). In particular, for any \(\varepsilon >0\) and \(s_0\ge 0\), there exists \(C_\varepsilon >0\) such that for any \(A\subset [s_0+\varepsilon , \pi /2]\)
Moreover, since there is \(T>0\) such that the restriction of the map \( (t,q)\mapsto \varphi _t(q)\)
is a surjective local diffeomorphism,
In particular, by (B.4), since \(b>0\), there exists \(C_b>0\) such that
Hence, for \(U\subset \{s>b\}\cup \{s<s_-(b)\}\),

So, provided \(\textbf{T}(R)\le R^{-1/3}\), U is \(\textbf{T}(R)\) non-periodic with constant \(C_{_{\!{\text {np}}}}=C/2\). \(\square \)
Lemma B.2.2
Suppose \(x_0\) is a pole, and \(x_1=(s_1,\theta _1)\) for \(-\pi /2<s_1<\pi /2\). Then, there is \(C_{_{\!{\text {nl}}}}>0\) such that \((x_0,x_1)\) is a \(\textbf{T}(R)=R^{-1}\) non-looping pair.
Proof
Suppose \(x_0\) is the pole with \(s=\pi /2\). Suppose \(\rho \in S^*_{x_1}M\) and there exists \(\rho _1\in S^*_{x_1}M\) such that \(d(\rho ,\rho _1)<R\) and \(\varphi _t(B(\rho _1,R))\cap B(S^*_{x_0}M,R)\ne \emptyset \). Then, there is \(\rho _2\in B(\rho _1,R)\) such that \(s_+(\rho _2)>\pi /2-R\). Therefore, there is \(C>0\) such that \(s_+(\rho )>\pi /2-CR\) and (since \(|s_1|<\pi /2\)),
In particular, for any \(t_0>0\), \(T>0\),

and hence \((x_0,x_1)\) is a \(\textbf{T}(R)=R^{-1}\) non-looping pair. \(\square \)
Lemma B.2.3
Suppose the assumptions of Lemma B.2.1 hold and \(x_0=(s_0,\theta _0)\) with \(s\in (-\pi /2, s_-(b))\cup (b,\pi /2).\) Then there is \(\delta >0\) such that \(x_0\) is \(\textbf{T}(R)=R^{-\delta }\) non-looping.
Proof
The proof is identical to [11, Lemma 5.1]. \(\square \)
1.2.1 Perturbed spheres
Next, we construct examples which have large (positive measure) periodic sets as well as large non-periodic sets. In particular, we find examples where the assumptions of Lemma B.2.1 hold and such that there is \(c>0\) with the property that the flow is periodic on \(-c<s<c\). If \(s_0>0\), we will call \((s_0,\theta _0)\) aperiodic if
In the case \(s_0<0\), we require the same condition on \(\{\alpha (s_+)\le \alpha (s)\}\). We define the aperiodic set to be the set of aperiodic points and Theorem 2 holds for any U inside this set.
In order to do this, we make a small perturbation of the round metric (\(\alpha (s)=\cos s\)). First, we compute
Let \(0<a<b<\pi /2\) and \(\alpha _\varepsilon =\alpha _0+\varepsilon (f_++f_-)\), with \({{\,\textrm{supp}\,}}f_+\subset (a,b)\) and \({{\,\textrm{supp}\,}}f_- \subset (-\pi /2,0)\). We have for \(s_+\ge b\),
Arguing identically for \(\theta _-\), if \(\alpha _\varepsilon =\alpha _0+\varepsilon (f_++f_-)\) with \({{\,\textrm{supp}\,}}f_-\subset (s_-(b),s_-(a))\) and \({{\,\textrm{supp}\,}}f_+\subset (0,\pi /2)\), then
To construct an example where the assumptions of Lemma B.2.1 hold, let \(\alpha _0(s)=\cos (s)\) so that \(\alpha _0\) induces the standard round metric. Let \(0<a<b<\frac{\pi }{2}\), \(f_+\) not identically 0 and \(f_+\ge 0\) with \({{\,\textrm{supp}\,}}f_+\subset (a,b)\), and let \(f_-\ge 0\) with \({{\,\textrm{supp}\,}}f_-\subset (s_-(b),s_-(a))\). Then, we have for \(s_+\ge b\), and \(\Theta _{0,\varepsilon }\) corresponding to the perturbed metric with \(\alpha _\varepsilon \),
In particular, we may choose \(\varepsilon _0>0\) small enough such that for \(0<\varepsilon <\varepsilon _0\) and \(\alpha =\alpha _{\varepsilon }\), we have \(-s\alpha _\varepsilon '(s)>0\) when \(s\ne 0,\) and
Moreover, since \(\alpha _0\) is the round metric on the sphere, the flow is periodic for trajectories not leaving \((s_-(a),a)\). (See Fig. 1)
1.2.2 The spherical pendulum
We now recall the spherical pendulum on \(S^2\) whose Hamiltonian is given in the \((s,\theta )\) coordinates by
This Hamiltonian describes the movement of a pendulum of mass 1 moving without friction on the surface of a sphere of radius 1. When \(E>2\), up to reparametrization of the integral curves, the dynamics for the spherical pendulum are equivalent to those for the Hamiltonian \(p=|\xi |^2_{\iota ^*g}\) and g is given by
Making a further change of variables in the s variable, we can put the metric in the form (B.1) and, moreover, by [26] for \(E\ge \frac{14}{\sqrt{17}}\), \(|\partial _{s_+}\Theta _0|> c>0\) for \(s_+\in (0,\pi /2]\). Note that the failure of this condition at the torus \({\mathbb {T}}_{0}\) is due to the fact that this torus is singular, consisting of the two curves \(\{s=0,\theta \in {\mathbb {R}}/2\pi {\mathbb {Z}}, \xi _r=0,|\xi _\theta |=\alpha (0)\}\). In fact, it is easy to see that \(|\Theta _0(s_+)|>cs_+^{1/2}\) for \(s_+\) near 0. This, together with Lemmas B.2.1 and [11, Lemma 5.1] are enough to obtain the results in Table 2 and that Theorem 2 applies to the spherical pendulum with \(U=M\).
1.3 Submanifolds of manfiolds with Anosov geodesic flow
We next recall some examples when (M, g) has Anosov geodesic flow. The geodesic flow is Anosov if there is \({\textbf{B}}>0\) such that for all \(\rho \in T^*M\) there is a splitting
such that
where \(|\cdot |\) is the norm induced by a Riemannian metric on \(T^*M\). Here, \(E_+(\rho )\) is called the stable space and \(E_-(\rho )\), the unstable space.
We also note (see [20, 32]) that a manifold with non-positive sectional curvature has no conjugate points and that
Note that these implications are not equivalences. Indeed, there exist manifolds with Anosov geodesic flow containing sets with strictly positive sectional curvature as well as manifolds with no conjugate points which do not have Anosov geodesici flow.
One of the main goals of [8] was to prove that various submanifolds of manifolds with the Anosov or non-focal property are non-recurrent via coverings. We will review only some of these results here, referring the reader to [8] for further examples. In what follows we present several dynamical lemmas which yield the statements from Table 2.
Define for a submanifold \(H\subset M\), and for every \(\rho \in S\!N^*\!H\)
Note that in two dimensions \(m_{\pm }(H,\rho )\ne 0\) is equivalent to H being tangent to, and having the same curvature as, a stable/unstable horosphere with conormal \(\rho \). In fact, in any dimension, a generic \(H \subset M\) satisfies \(m_{\pm }(H,\rho )=0\) for all \(\rho \in S\!N^*\!H\).
Lemma B.3.1
Let \(H\subset M\) be a smooth submanifold . Suppose (M, g) is a manifold with Anosov geodesic flow and for all \(\rho \in S\!N^*\!H\)
Then there are \(c,\delta ,\tau >0\) such that for all \(0<a<b\), H is \(c\log h^{-1}\) non-recurrent via \((\tau ,R(h))\) coverings for the symbol \(p(x,\xi )=|\xi |_{g(x)}\) in the window [a, b].
Proof
The proof of this result is that of [8, Theorem 6], see [8, Section 5.1]. \(\square \)
Lemma B.3.2
Suppose (M, g) is a manifold with Anosov geodesic flow and \(H_1,H_2\subset M\) are a smooth submanifolds such that for \(i=1,2,\) \( \sup _{\rho \in S\!N^*\!H_i}m_{\pm }(H_i,\rho )=0. \) Then there are \(c,t_0>0\) such that for all \(0<a<b\), \((H_1,H_2)\) is a \((t_0,c\log R)\) non-looping pair for \(p(x,\xi )=|\xi |_{g(x)}\) in the window [a, b].
Proof
By [8, Proposition 2.2, Lemma 5.1] (in particular, adapting the arguments in [8, “Treatment of \(D\in \{D_i\}_{i\in \mathcal {I}_K}\)”, page 38]) there exist \(\tau >0\), \(\delta >0\), \(C_{_{\!{\text {nl}}}}>0\), \(C>0\), such that the pair \((H_1,H_2)\) is a \((t_0,T(h))\) non-looping via \((\tau ,h^\delta )\) coverings with constant \(C_{_{\!{\text {nl}}}}\) in the window [a, b] for any \(0<a<b\), where \( T(h)=c\log h^{-1} \) for some \(c>0\) depending on \((M,g,\alpha )\). Combining this result with Lemma 3.4 yields the claim. \(\square \)
Recall that a stable/unstable horosphere is defined by the property that \(T_\rho S\!N^*\!H=E_\pm (\rho )\) for all \(\rho \in S\!N^*\!H\).
Lemma B.3.3
Suppose (M, g) is a manifold with Anosov geodesic flow, \(H_{\pm }\subset M\) is a compact subset of a stable/unstable horosphere and \(H_2\subset M\) is a submanifold with \(m_{\pm }(H_2,\rho )<n-1\) for all \(\rho \in S\!N^*\!H_2\). Then, there are \(c,t_0>0\) such that for all \(0<a<b\), \((H_\pm ,H_2)\) is a \((t_0,c\log R)\) non-looping pair for \(p(x,\xi )=|\xi |_{g(x)}\) in the window [a, b].
For simplicity, we prove only Lemma B.3.3 but point out that the arguments similar to those in [8, Lemma 5.1] can be used to obtain much more general statements.
Proof
We consider the case \(H_+\). The other case following identically. By Lemma 3.4 it suffices to show \((H_{+},H_2)\) is a non-looping pair via coverings. Thus, by [8, Proposition 2.2] and Lemma 3.4 it suffices to show there exists \(\alpha >0\) such that for all \((t, \rho ) \in [t_0, T_0]\times S\!N^*\!H_+\) such that \(d(\varphi _t(\rho ),S\!N^*\!H_2)\le \, e^{-{\alpha }|t|}/\alpha \), there exists \(\textbf{w} \in T_{\rho }S\!N^*\!H_+\) for which the restriction
has left inverse \(L_{(t, \rho )}\) with \(\Vert L_{(t, \rho )}\Vert \le \alpha e^{ \alpha |t|}\). Here, \(\psi :{\mathbb {R}}\times S\!N^*\!H_+\rightarrow {\mathbb {R}}^{n+1}\) is given by \( \psi (t,\rho )=F\circ \varphi _t(\rho ) \) and \(F:T^*M \rightarrow {{\mathbb {R}}}^{n+1}\) is a defining function for \(S\!N^*\!H_2=F^{-1}(0)\).
Note that \(T_\rho S\!N^*\!H_+=E_+(\rho )\) and there is \({\textbf{D}}>0\) such \(d\varphi _t:E_+(\rho )\rightarrow E_+(\varphi _t(\rho ))\) is invertible with inverse satisfying
Since \(H_2\) is compact, and \(m_+(H_2,q)<n-1\) for all \(q\in S\!N^*\!H_2\), there is \(c>0\) such that for all \(q\in S\!N^*\!H_2\) there is \({\textbf{u}}\in E_+(q)\) with \(|{\textbf{u}}|=1\) such that \(|dF{\textbf{u}}|\ge c|{\textbf{u}}|.\)
Since \(\rho \mapsto E_+(\rho )\) is \(\nu \)-Hölder continuous for some \(\nu >0\) [30, Theorem 19.1.6], there is \(C_M>0\) and \({{\tilde{\textbf{u}}}}\in E_+({\tilde{q}})\) with
Therefore,
Let \({\tilde{q}}=\varphi _t(\rho )\), so that \(d(q,{\tilde{q}})<e^{-\alpha t}/\alpha \) and set \(\textbf{w}=(d\varphi _t)^{-1}({{\tilde{\textbf{u}}}})\). The claim follows provided \(\alpha >1\) is large enough (depending on \({\textbf{D}},\nu , c,C\)). \(\square \)
Lemma B.3.4
Suppose (M, g) has Anosov geodesic flow and non-positive curvature. Then if \(H\subset M\) is a totally geodesic submanifold, \(m_\pm (H,\rho )\equiv 0\).
Proof
We need only show that for a totally geodesics submanifold \(m_+(H,\rho )=m_-(H,\rho )=0\). It is easier to work on the tangent space side, so we will do so, denoting \(E^\sharp _{\pm }(\rho ^\sharp )\) for the dual stable and unstable bundles.
Suppose \(\rho ^{\sharp } \in SNH\). Then, arguing as in [8, Proof of Theorem 4.C], and using that H is totally geodesic, we have for all \(v\in T_{\rho ^\sharp }SNH\)
Here \(N:(-\varepsilon ,\varepsilon )\rightarrow NH\) is a smooth vectorfield with \(N(0)=\rho ^\sharp \) and \(N'(0)=v\), \({\tilde{\nabla }}\) is the Levi-Civita connection on M, and \(\Pi _H\) is the second fundamental form to H. On the other hand, by [8, (5.46)], for \(v_\pm \in E^\sharp _\pm (\rho ^\sharp )\),
where \(\mathcal {W}_{\pm }\) is a stable/unstable horosphere with normal vector \(\rho ^\sharp \). Therefore, \(T_{\rho ^\sharp }SNH\cap E^\sharp _\pm (\rho ^\sharp )=\emptyset \) and in particular \(m_{\pm }(H,\rho )=0\). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Canzani, Y., Galkowski, J. Weyl remainders: an application of geodesic beams. Invent. math. 232, 1195–1272 (2023). https://doi.org/10.1007/s00222-023-01178-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-023-01178-5




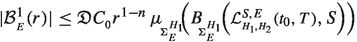 .
.