Abstract
This paper studies the structure and stability of boundaries in noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) spaces, that is, metric-measure spaces \((X,{\mathsf {d}},{\mathscr {H}}^N)\) with Ricci curvature bounded below. Our main structural result is that the boundary \(\partial X\) is homeomorphic to a manifold away from a set of codimension 2, and is \(N-1\) rectifiable. Along the way, we show effective measure bounds on the boundary and its tubular neighborhoods. These results are new even for Gromov–Hausdorff limits \((M_i^N,{\mathsf {d}}_{g_i},p_i) \rightarrow (X,{\mathsf {d}},p)\) of smooth manifolds with boundary, and require new techniques beyond those needed to prove the analogous statements for the regular set, in particular when it comes to the manifold structure of the boundary \(\partial X\). The key local result is an \(\varepsilon \)-regularity theorem, which tells us that if a ball \(B_{2}(p)\subset X\) is sufficiently close to a half space \(B_{2}(0)\subset {\mathbb {R}}^N_+\) in the Gromov–Hausdorff sense, then \(B_1(p)\) is biHölder to an open set of \({\mathbb {R}}^N_+\). In particular, \(\partial X\) is itself homeomorphic to \(B_1(0^{N-1})\) near \(B_1(p)\). Further, the boundary \(\partial X\) is \(N-1\) rectifiable and the boundary measure  is Ahlfors regular on \(B_1(p)\) with volume close to the Euclidean volume. Our second collection of results involve the stability of the boundary with respect to noncollapsed mGH convergence \(X_i\rightarrow X\). Specifically, we show a boundary volume convergence which tells us that the \(N-1\) Hausdorff measures on the boundaries converge
is Ahlfors regular on \(B_1(p)\) with volume close to the Euclidean volume. Our second collection of results involve the stability of the boundary with respect to noncollapsed mGH convergence \(X_i\rightarrow X\). Specifically, we show a boundary volume convergence which tells us that the \(N-1\) Hausdorff measures on the boundaries converge  to the limit Hausdorff measure on \(\partial X\). We will see that a consequence of this is that if the \(X_i\) are boundary free then so is X.
to the limit Hausdorff measure on \(\partial X\). We will see that a consequence of this is that if the \(X_i\) are boundary free then so is X.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper studies structural and stability properties for noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) spaces with boundary. In particular, we give affirmative answers to some of the recent conjectures presented in [37, 59].
Most of the statements are new and of interest even for noncollapsed limits of smooth Riemannian manifolds with convex boundary and interior lower Ricci curvature bounds.
Our main results can be grouped into
-
Structure results for boundaries and spaces with boundary;
-
Stability/gap theorems about the absence/presence of boundary.
In particular, we obtain the rectifiable structure of the boundary together with measure estimates. Moreover we prove that noncollapsed \({{\,\mathrm{RCD}\,}}\) spaces are homeomorphic to topological manifolds (possibly with boundary) up to sets of codimension two.
On the side of stability/gap results we are going to prove that the absence of boundary is preserved under noncollapsed (pointed) Gromov–Hausdorff convergence and that the boundary volume measures converge in full generality. We also show that the presence of boundary is stable, under an additional assumption which is satisfied for sequences of smooth manifolds with boundary.
Below, after briefly introducing the relevant terminology and background, we outline the main achievements of the paper.
The Riemannian Curvature Dimension condition \({{\,\mathrm{RCD}\,}}(K,\infty )\) was introduced in [6] (see also [5]) coupling the Curvature Dimension condition \({{\,\mathrm{CD}\,}}(K,\infty )\), previously proposed in [85, 86] and independently in [67], with the infinitesimally Hilbertian assumption, corresponding to the Sobolev space \(H^{1,2}\) being Hilbert.
The natural finite dimensional refinements subsequently led to the notions of \({{\,\mathrm{RCD}\,}}(K,N)\) and \({{\,\mathrm{RCD}\,}}^*(K, N)\) spaces, corresponding to \({{\,\mathrm{CD}\,}}(K, N)\) (resp. \({{\,\mathrm{CD}\,}}^*(K, N)\), see [15]) coupled with linear heat flow. The class \({{\,\mathrm{RCD}\,}}(K,N)\) was proposed in [43], motivated by the validity of the sharp Laplacian comparison and of the Cheeger–Gromoll splitting theorem, proved in [41]. The (a priori more general) \({{\,\mathrm{RCD}\,}}^*(K,N)\) condition was thoroughly analysed in [39] and (subsequently and independently) in [11] (see also [24] for the equivalence betweeen \({{\,\mathrm{RCD}\,}}^*\) and \({{\,\mathrm{RCD}\,}}\) in the case of finite reference measure).
Several geometric and analytic properties have been proved for \({{\,\mathrm{RCD}\,}}(K,N)\) spaces in the last years, often inspired by the theory of (weighted) Riemannian manifolds with lower Ricci bounds and of Ricci limits. Without the aim of being complete, let us mention the heat kernel estimates [54], the rectifiability [69], the constancy of the dimension in the almost everywhere sense [19] (cf. with [33] dealing with Ricci limit spaces) and the existence of a second order differential calculus [44].
In the theory of Ricci limit spaces, further regularity properties are satisfied under the noncollapsing assumption. If the approximating sequence of smooth Riemannian manifolds, besides the lower Ricci bound
verifies also the lower volume bound
then by volume convergence [28, 32] the volume measures converge to the \({\mathscr {H}}^N\)-measure on the limit metric space. Noncollapsed Ricci limit spaces are much more regular than general Ricci limits, see [28,29,30,31].
Motivated by this refinement in the theory of Ricci limits, a notion of noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure space \((X,{\mathsf {d}},{\mathfrak {m}})\) has been proposed in [37] by asking that \({\mathfrak {m}}={\mathscr {H}}^N\) (a weaker definition had been previously suggested in [64]). In the same work some properties valid for noncollapsed Ricci limits have been generalized to the synthetic framework, such as the volume convergence and the stratification of the singular set. More recent contributions dealt with topological regularity [59], volume bounds for the singular strata [14] and differential characterizations [53].
1.1 Singular strata and boundaries
On a noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure space \((X,{\mathsf {d}},{\mathscr {H}}^N)\) any tangent cone is a metric cone (see [27, 28, 36, 37]). Moreover, there is a natural stratification of the singular set
where
is the set of regular points of \((X,{\mathsf {d}},{\mathscr {H}}^N)\) and, for any \(0\le k\le N-1\),
This stratification was first introduced in [28] for noncollapsed Ricci limits. Therein it was proven that
and that the following Hausdorff dimension estimate holds:
A more quantitative analysis of singular strata was initiated in [30], based on quantitative differentiation arguments and yielding to Minkowski-type estimates for the quantitative singular strata
and
We recall that \(B_s(x)\) is said to be a \((k,\varepsilon )\)-symmetric ball provided
where \(z\in C(Z)\times {\mathbb {R}}^k\) is a tip of the metric cone \(C(Z)\times {\mathbb {R}}^k\). We refer to Sect. 2 for the precise introduction of metric cones and of the Gromov–Hausdorff distance \({\mathsf {d}}_{GH}\).
Later on, in [29] the estimates for the quantitative singular strata have been sharpened, and the k-rectifiable structure of \({\mathcal {S}}^k\) has been shown for any \(0\le k\le N-2\).
In the framework of \({{\,\mathrm{RCD}\,}}\) spaces, the top dimensional singular stratum \({\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\) is not empty in general, since Riemannian manifolds with convex boundary and lower Ricci curvature bounds in the interior belong to this class (here by convex boundary we intend that the second fundamental form with respect to the interior unit normal must be non negative definite). Still, the Hausdorff dimension estimate (1.7) holds for any \(0\le k\le N-1\) (see [37]). The same phenomenon happens in the theory of Alexandrov spaces, where the top dimensional singular stratum is strictly linked to the boundary of the space [22, 75]. Elementary examples suggest that this is the case also for noncollapsed \({{\,\mathrm{RCD}\,}}\) spaces.
In [37, 59] two different notions of boundary for an \({{\,\mathrm{RCD}\,}}(K,N)\) space \((X,{\mathsf {d}},{\mathscr {H}}^N)\) have been proposed (see also [58] for another notion introduced for Alexandrov spaces). For the sake of this introduction we are going to deal with the one introduced in [37], where the authors define
Above we denoted by \(\overline{{\mathcal {S}}^{N-1}\setminus {\mathcal {S}}^{N-2}}\) the topological closure of \({\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\).
Let us point out that, since the density of \({\mathscr {H}}^N\) at any point in \({\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\) equals 1/2, by lower semicontinuity of the density it holds
in particular
A comparison with the notion of boundary introduced in [59] will be investigated subsequently in the paper (cf. Theorem 6.6 (i)).
Given the above definition of boundary it sounds natural to introduce the following.
Definition 1.1
We say that an \({{\,\mathrm{RCD}\,}}(K,N)\) space \((X,{\mathsf {d}},{\mathscr {H}}^N)\) has boundary in \(B_1(p)\) if
otherwise we say that \((X,{\mathsf {d}},{\mathscr {H}}^N)\) has no boundary in \(B_1(p)\).
1.2 An \(\varepsilon \)-regularity theorem for top dimensional singularities
For all the subsequent developments of the paper, the building block is an \(\varepsilon \)-regularity theorem, dealing with the structure of balls sufficiently close in the GH sense to a ball centered on the boundary of a half-space.
Let us preliminarily recall that a set \(E\subset X\) is said to be \((N-1)\)-rectifiable provided
where \({\mathscr {H}}^{N-1}(M)=0\) and each \(E_i\) is biLipschitz to a Borel subset of \({\mathbb {R}}^{N-1}\) for any \(i\in {\mathbb {N}}\).
Theorem 1.2
(\(\varepsilon \)-regularity) Let \(1\le N<\infty \) be a fixed natural number and let \(\varepsilon >0\). If \(\delta \le \delta (N,\varepsilon )\), then for any \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) m.m.s. \((X,{\mathsf {d}},{\mathscr {H}}^N)\) with \(p\in X\) such that
it holds that \(\partial X\cap B_1(p)\ne \emptyset \). Moreover
-
(i)
(Ahlfors regularity) for any \(x\in \partial X\cap B_1(p)\) and for any \(0<r<1\)
$$\begin{aligned}&(1-\varepsilon )\omega _{N-1}r^{N-1} \le {\mathscr {H}}^{N-1}(\partial X\cap B_r(x))\le (1+\varepsilon )\omega _{N-1}r^{N-1};\qquad \qquad \end{aligned}$$(1.13) -
(ii)
(Rectifiable structure) \(\partial X\cap B_1(p)\) is \((N-1)\)-rectifiable;
-
(iii)
(Topological structure) there exists a map \(F:B_1(p)\rightarrow {\mathbb {R}}_+^N\) satisfying
-
(a)
\((1-\varepsilon ) {\mathsf {d}}(x,y)^{1+\varepsilon } \le |F(x) - F(y)| \le C(N) {\mathsf {d}}(x,y)\) for any \(x,y\in B_1(p)\);
-
(b)
\(F(p)=0\) and \(\partial {\mathbb {R}}_+^N \cap B_{1-2\varepsilon }(0) \subset F(\partial X \cap B_1(p)) = \partial {\mathbb {R}}^N_+\cap F(B_1(p))\);
-
(c)
F is open and a homeomorphism with its image;
-
(d)
\( B_{1-2\varepsilon }^{{\mathbb {R}}_+^N}(0) \subset F(B_1(p))\).
-
(a)
Remark 1.3
In view of the volume \(\varepsilon \)-regularity for the boundary Theorem 8.2 the conclusions of Theorem 1.2 hold by assuming \(p\in \partial X\) and the volume pinching condition
in place of (1.12).
The proof of Theorem 1.2 requires most of the tools developed in the paper and will be split into several intermediate results.
One of the building blocks to prove the boundary measure estimates in Theorem 1.2 is a weaker \(\varepsilon \)-regularity theorem, Theorem 6.1. There we prove that there exist constants \(c(N)>1\) and \(\eta (N)>0\) such that if
then
Stability is a key feature of the top dimensional singular stratum. It is well known that codimension two singularities might appear even for limits of smooth manifolds. The easiest example of this being that of a two dimensional singular cone, which can be obtained as a limit of smooth manifolds with uniform lower Ricci bounds by rounding off the tip.
Among the other things, Theorem 1.2 (and even its weaker version Theorem 6.1) implies that the top dimensional singular stratum \({\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\) is empty for noncollapsed Ricci limits of manifolds without boundary, as known from the seminal paper [28]. It is worth stressing that our strategy is completely different from the original one, which is based on a topological argument and seems not suitable to handle the general case of \({{\,\mathrm{RCD}\,}}\) spaces. A previous attempt in this direction has been made in [59], where the authors extended Cheeger–Colding’s result to the setting of noncollapsed \({{\,\mathrm{RCD}\,}}\) spaces verifying an additional topological regularity assumption. In contrast, our proof is quantitative in nature and does not require any topological argument. Moreover, the statement we achieve is stronger, and new even in the smooth framework. Indeed we prove that closeness to the model boundary ball implies the presence of a definite amount of boundary points.
The Ahlfors regularity for the boundary measure in sharp form, Theorem 1.2 (i), will be established through several steps. The key step is the improved structure theorem for boundary balls Theorem 8.1, which when combined with Theorem 6.1 yields to Ahlfors regularity in weaker form, with a constant \(c(N)>1\) and 1/c(N) in place of \(1+\varepsilon \) and \(1-\varepsilon \), respectively. The sharp version of the bound will be obtained later in Corollary 8.7 by combining the stability of Theorem 8.1 and the rectifiable and biHölder structure of Theorem 8.4 (ii), (iii) and (iv).
The topological regularity part of Theorem 1.2 is new and of interest even in the case of limits of smooth Riemannian manifolds. At its heart, the proof is based on two key points, (cf. with the proof of Theorem 8.1). The first is the stability of Lemma 7.1 which tells us that if a ball \(B_r(x)\) is Gromov–Hausdorff close to a half space, then the boundary singularities \(\partial X\cap B_r(x)\) must be \(\varepsilon \)-close to a ball in \({\mathbb {R}}^{n-1}\cap B_r(0^{n-1})\). The second is a boundary volume \(\varepsilon \)-regularity Theorem 8.2, based in turn on Lemma 6.5, which roughly tells us that if there are two balls \(B_r(x)\subseteq B_R(x)\), both close to half spaces and centered at a boundary point, then the smaller ball \(B_r(x)\) must be at least as close to a half-space as the larger ball \(B_R(x)\). The effect of these two results is that once boundary singularities start to appear, they cannot stop appearing and we can eventually put them together into a topological structure.
1.3 Structure of boundaries and of spaces with boundary
The \(\varepsilon \)-regularity Theorem 1.2, when combined with a covering argument, yields a structural result for noncollapsed \({{\,\mathrm{RCD}\,}}\) spaces with boundary.
Here and throughout the paper we shall adopt the notation
to indicate the tubular neighbourhood of a set on a metric space.
Theorem 1.4
(Boundary Structure) Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be an \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) space with \(p\in X\) such that \({\mathscr {H}}^{N}(B_1(p))>v>0\). If \(({\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2})\cap B_2(p)\ne \emptyset \), then the following hold
-
(i)
(Rectifiability and volume estimates) \(\partial X\) is \((N-1)\)-rectifiable and
$$\begin{aligned} {\mathscr {H}}^{N-1}(B_r(x)\cap \partial X)\le C(N,v) r^{N-1} \quad \text {for any }x\in \partial X\cap B_1(p)\text { and }r\in (0,1); \end{aligned}$$ -
(ii)
(Volume estimate for the tubular neighbourhood)
$$\begin{aligned} {\mathscr {H}}^N(B_r(\partial X)\cap B_1(p)) \le C(N,v) r \quad \text {for any }r\in (0,1), p\in X, \end{aligned}$$(1.15) -
(iii)
(Uniqueness of tangents) for any \(x\in {\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\) the tangent cone at x is unique and isomorphic to \({\mathbb {R}}^{N}_+\);
-
(iv)
(Topological regularity) for any \(0<\alpha <1\) there exists a closed set \(C_\alpha \subset {\mathcal {S}}^{N-2}(X)\) such that
-
(a)
\(\dim _H(X{\setminus } C_{\alpha })\le N-2\);
-
(b)
\(X{\setminus } C_\alpha \) is a topological manifold with boundary and \(C^{\alpha }\)-charts.
-
(a)
The rectifiability of the top dimensional singular stratum was conjectured both in [59, Conjecture 4.10] and in [37], together with the local finiteness of the \({\mathscr {H}}^{N-1}\)-measure. Moreover, with (1.15) we sharpen the volume bound for the tubular neighbourhood of the top dimensional singular set obtained in [14, Corollary 2.7] by adapting the techniques developed in [30] to the synthetic framework. The topological regularity part of Theorem 1.4 improves upon [59, Theorem 4.11], including the boundary in the statements.
The regularity results above are mostly peculiar of codimension one singularities:
-
Volume estimates for the tubular neighbourhood and the measure estimate for the full singular stratum, and not only for the quantitative one, fail in codimension higher than one. Indeed there are examples of two dimensional Alexandrov spaces where the singular set \({\mathcal {S}}^0\) has not locally finite \({\mathscr {H}}^0\)-measure, see for instance [29, Section 3.4].
-
In [34, Theorem 1.2] a noncollapsed Ricci limit space \((X,{\mathsf {d}},{\mathscr {H}}^N)\) with a point \(x\in {\mathcal {S}}^{N-2}{\setminus }{\mathcal {S}}^{N-3}\) with non unique tangent cone is constructed (actually tangents with maximal splitting \({\mathbb {R}}^k\) for any \(0\le k\le N-2\) appear at that point).
-
As pointed out in [29, Remark 1.11, Example 3.2] based on [66], there is an example of N-dimensional Alexandrov space such that the singular set \({\mathcal {S}}^{N-2}\) is a Cantor set, and in particular no point has a neighbourhood in which \({\mathcal {S}}^{N-2}\) is topologically a manifold.
In the case of Ricci limits, Theorem 1.4 (iv) can be sharpened to a finite \({\mathscr {H}}^{N-2}\)-measure estimate for the topologically singular set, relying on [29]:
Theorem 1.5
Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be an \({{\,\mathrm{RCD}\,}}\) m.m.s. arising as noncollapsed limit of a sequence of smooth Riemannian manifolds with convex boundaries and Ricci curvature bounded from below in the interior by \(-(N-1)\). Then, for any \(0<\alpha <1\), there exist a constant \(C=C(N,\alpha ,{\mathscr {H}}^N(B_1(p)))\) and a closed set of codimension two \(C_\alpha \subset {\mathcal {S}}^{N-2}(X)\) such that
and \(X{\setminus } C_\alpha \) is a topological manifold with boundary and \(C^{\alpha }\)-charts.
1.4 Stability and gap theorems for boundaries
The following stability theorem gives an affirmative answer to [59, Conjecture 5.11] (see Remark 6.7 for more explanations). Its proof follows directly from (a weak form of) the \(\varepsilon \)-regularity theorem for boundary balls, Theorem 1.2 (i).
Theorem 1.6
(Stability) Let \(N\in {\mathbb {N}}^+\) and \(K\in {\mathbb {R}}\) be fixed. Let \((X_n,{\mathsf {d}}_n,{\mathscr {H}}^N,x_n)\) be a sequence of pointed \({{\,\mathrm{RCD}\,}}(K,N)\) spaces with no boundary on \(B_2(x_n)\) converging in the pmGH topology to \((Y,{\mathsf {d}}_Y,{\mathscr {H}}^N,y)\). Then Y has no boundary on \(B_1(y)\).
While the above tells that spaces without boundary converge to spaces without boundary under non collapsing pGH convergence, stability of boundary points (i.e whether boundary points converge to boundary points) remains an open question in the general case.
The analysis of the Laplacian of the distance from the boundary performed in Sect. 7 allows us to prove the local Ahlfors regularity of the boundary volume measure, together with stability of boundary points in the case of Ricci limits with boundary.
Theorem 1.7
Let \((X,{\mathsf {d}},{\mathscr {H}}^N,p)\) be the noncollapsed pGH limit of a sequence of smooth N-dimensional Riemannian manifolds \((X_n,{\mathsf {d}}_n, p_n)\) with convex boundary and Ricci curvature bounded from below by K in the interior. Then:
-
(i)
if \(B_1(p_n) \cap \partial X_n \ne \emptyset \) for every n then \(\partial X \ne \emptyset \). Moreover if points \(x_n\in \partial X_n\) converge to \(x\in X\), then \(x\in \partial X\);
-
(ii)
for any \(x\in \partial X\) one has
$$\begin{aligned} {\mathscr {H}}^{N-1}(B_2(x)\cap \partial X) > C(K) {\mathscr {H}}^N(B_1(x)); \end{aligned}$$(1.17) -
(iii)
 is locally Ahlfors regular and for any \(x\in \partial X\) any tangent cone at x has boundary.
is locally Ahlfors regular and for any \(x\in \partial X\) any tangent cone at x has boundary.
We conjecture that the gap estimate (1.17) holds for general noncollapsed \({{\,\mathrm{RCD}\,}}\) spaces without further assumptions, which would also prove stability of boundary points and the equivalence between the two notions of boundary in [37] and [59] in full generality.
Our last result is a version of Colding’s volume convergence theorem (cf. [28, 32]) for boundary measures:
Theorem 1.8
(Boundary Volume Convergence) Let \(1\le N<\infty \) be a fixed natural number. Assume that \((X_n,{\mathsf {d}}_n,{\mathscr {H}}^N,p_n)\) are \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) spaces converging in the pGH topology to \((X,{\mathsf {d}},{\mathscr {H}}^N,p)\). Then

In particular
whenever \(X_n\ni x_n\rightarrow x\in X\) and \({\mathscr {H}}^{N-1}(\partial X\cap \partial B_r(x))=0\).
1.5 Comparison with the Alexandrov theory
In [78, 90] it has been proved that if \((X,{\mathsf {d}})\) is an N-dimensional Alexandrov space with curvature bounded from below by k, then \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is an \({{\,\mathrm{RCD}\,}}(k(N-1),N)\) metric measure space. Below we compare the results of the present paper with the literature about Alexandrov spaces:
-
(i)
on Alexandrov spaces, interior regular points have neighbourhoods bi-Lipschitz homeomorphic to Euclidean balls and regular boundary points have open neighbourhoods bi-Lipschitz homeomorphic to boundary balls in the Euclidean half-space. This was proved in [23], see in particular Remark 12.9.1 for a remark dealing with boundary points and the more recent [40, Theorem 1.1] for a detailed proof.
-
(ii)
While in the Alexandrov theory topological regularity near to regular interior and boundary points was already known, the existence of biHölder homeomorphisms with harmonic components (apart from the last coordinate in the case of boundary points) is new also in this case. Indeed it answers to an open question in [76], cf. with Remark 9.6.
-
(iii)
The non collapsing of boundaries under non collapsing convergence of Alexandrov spaces is proved in [57, Theorem 9.2, Remark 9.13] where the more general case of extremal subsets is considered. The volume convergence for the boundary measure is considered in the more recent [40, Theorem 1.3].
-
(iv)
When \(N=2\), it has been proved in [68] that \({{\,\mathrm{RCD}\,}}(K,2)\) spaces \((X,{\mathsf {d}},{\mathscr {H}}^2)\) are Alexandrov spaces. In particular, most of the results of the present paper follow from the Alexandrov theory if \(N=2\).
-
(v)
Relying on [66, Corollary 1.4] instead of [29] it is possible to prove that Theorem 1.5 holds also when \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is an Alexandrov space with curvature bounded from below.
1.6 The remainder of the paper
The rest of the paper is divided in eight sections.
The first two aim at presenting preliminary results which will be used throughout the paper. In Sect. 2 we recall the main definitions and basic results of the theory of \({{\,\mathrm{RCD}\,}}\) spaces. In Sect. 3 we prove a local version of the almost splitting theorem, originally due to Cheeger–Colding (see [27, 31] for the present form on Ricci limit spaces) and previously proved on \({{\,\mathrm{RCD}\,}}\) spaces only in a weaker form (see [17, 18]). Moreover we adapt the proof of the transformation theorem [29] (see also [31]) by Cheeger–Jiang–Naber to the \({{\,\mathrm{RCD}\,}}\) framework.
In Sect. 4 we introduce and study neck regions tailored for the analysis of boundaries on noncollapsed \({{\,\mathrm{RCD}\,}}\) spaces. This study is the key ingredient for all the developments of the paper: rectifiable regularity, topological regularity and stability.
The role of this tool has been prominent in the recent literature about spaces with lower Ricci curvature bounds and bounded Ricci curvature, see [29, 56], and also in several other frameworks, see for instance [71, 72].
The analysis of neck regions is made in two steps. After their introduction in Definition 4.3, we first describe their structure in Theorem 4.9. In the second step we prove existence of neck regions in Theorem 4.13 under geometric assumptions, guaranteeing in particular the non triviality of the previous structural result.
In the analysis of the structure of neck regions there are several simplifications with respect to the study in [29, 56]. Instead non trivial new ideas are needed to deal with the stability of codimension one singularities and the existence of neck regions.
In Sect. 5, following closely the neck decomposition theorems in [29, 56], we prove that any noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) space can be decomposed into neck-regions, \((N,\varepsilon )\)-symmetric balls and a set of codimension at least 2, with quantitative summability control over the radii of balls appearing in the covering.
In Sect. 6 we combine the previously obtained existence and structure of neck regions with the neck decomposition theorem to prove the weak \(\varepsilon \)-regularity Theorem 6.1. In particular, we show the stability Theorem 1.6 for spaces without boundary, and the \((N-1)\)-rectifiable structure of the boundary together with local finiteness estimates for the boundary measure (cf. Theorem 1.4 (i)).
We dedicate Sect. 7 to the study of the distance function from the boundary. We show how upper bounds on the absolutely continuous part of its Laplacian imply noncollapsing estimates on the boundary measure, see Theorem 7.4. We present an open question concerning the case of general noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) spaces that we are able to verify for smooth manifolds with boundary and their noncollapsed pGH limits, as well as Alexandrov spaces with curvature bounded below. As a consequence we prove Theorem 1.7.
In Sect. 8 we improve the structure of neck regions by a bootstrap argument based on the stability of the boundary. In Theorem 8.1 we prove that, on a ball sufficiently close in the GH sense to the model ball of the half-space, balls centered at boundary points are close to the model ball in the half-space and balls centered at interior points are close to the model ball in the Euclidean space at any sufficiently small scale.
The improved neck structure Theorem 8.1 has a number of consequences: the topological regularity of the boundary up to sets of ambient codimension two (see Theorem 8.4), the improved volume estimate Corollary 8.7 and the boundary volume convergence Theorem 1.8. In Sect. 9 we deal with the topological regularity up to the boundary of noncollapsed \({{\,\mathrm{RCD}\,}}\) spaces proving Theorem 1.2 (iv), Theorem 1.4 (iv) and Theorem 1.5.
2 Preliminaries
A metric measure space will be a triple \((X,{\mathsf {d}},{\mathfrak {m}})\) where \((X,{\mathsf {d}})\) is a complete and separable metric space and \({\mathfrak {m}}\) is a locally finite Borel measure.
We will denote by \(B_r(x)=\{{\mathsf {d}}(\cdot ,x)<r\}\) and \(\bar{B}_r(x)=\{{\mathsf {d}}(\cdot ,x)\le r\}\) the open and closed balls respectively. By \({{\,\mathrm{Lip}\,}}(X)\) (resp. \({{\,\mathrm{Lip_b}\,}}(X)\)) we denote the space of Lipschitz (resp. bounded) functions and for any \(f\in {{\,\mathrm{Lip}\,}}(X)\) we shall denote its slope by
We will use the standard notation \(L^p(X,{\mathfrak {m}})\), for the \(L^p\) spaces and \({\mathscr {L}}^n,{\mathscr {H}}^n\) for the n-dimensional Lebesgue measure on \({\mathbb {R}}^n\) and the n-dimensional Hausdorff measure on a metric space, respectively. The Hausdorff measure is always normalised in such a way that it coincides with the Lebesgue measure on Euclidean spaces. We shall also denote by \({\mathscr {H}}^{n}_{\infty }\) the pre-Hausdorff measure in dimension n (obtained with no upper bounds on the radii of the covering sets). We shall denote by \(\omega _n\) the Lebesgue measure of the unit ball in \({\mathbb {R}}^n\).
We will also deal with pointed metric measure spaces \((X,{\mathsf {d}},{\mathfrak {m}},x)\) in case a reference point \(x\in X\) has been fixed. We will say that a pointed metric measure space is normalised whenever
We will deal with the Gromov–Hausdorff (GH), measured Gromov–Hausdorff (mGH) and pointed measured Gromov–Hausdorff (pmGH) convergence of (pointed) metric measure spaces. We refer to [46] for the relevant background about these notions. The associated distances will be denoted by \({\mathsf {d}}_{GH}\), \({\mathsf {d}}_{mGH}\) and \({\mathsf {d}}_{pmGH}\).
A basic reference about analysis on metric space is the book [22]. Given a proper metric space \((X,{\mathsf {d}})\) and two bounded subsets \(F,E\subset X\) we denote by
their Hausdorff distance in \((X,{\mathsf {d}})\).Footnote 1
We recall a simple connection between convergence in the Hausdorff distance and behaviour of pre-Hausdorff measures \({\mathscr {H}}_{\infty }^{\alpha }\), for any \(\alpha \ge 0\). If \({\mathsf {d}}_H(A_n,A)\rightarrow 0\) and A is compact, then
When the sets are subsets of metric spaces converging in the pGH topology we will understand the convergence as realized in a common background proper metric space and the Hausdorff convergence of compact sets has to be understood as Hausdorff convergence in the ambient space. All the spaces considered in this paper are proper.
Remark 2.1
We recall that in a proper metric space \((Z,{\mathsf {d}}_Z)\) with a sequence of uniformly bounded compact sets \(K_n\subset Z\) and \(K\subset Z\), the following conditions are equivalent:
-
(i)
\(K_n\) converge to K in the Hausdorff distance;
-
(ii)
\(K_n\) converge to K in the Kuratowski sense, i.e. any limit point x of a subsequence \(x_n\in K_n\) belongs to K and for any \(y\in K\) there exists a sequence \(y_n\in K_n\) such that, up to subsequence, \(y_n\rightarrow y\);
-
(iii)
setting \({\mathsf {d}}_C:Z\rightarrow [0,\infty )\) to be the distance function from any closed set \(C\subset Z\), it holds that \({\mathsf {d}}_{K_n}\rightarrow {\mathsf {d}}_K\) uniformly as \(n\rightarrow \infty \).
We refer to [16] for a treatment of these equivalences and we remark that they hold also for subsets of a pGH converging sequence of metric spaces (once the convergence is realized in a common proper metric space).
2.1 Calculus tools
The Cheeger energy \(\mathsf{Ch}:L^2(X,{\mathfrak {m}})\rightarrow [0,+\infty ]\) associated to a m.m.s. \((X,{\mathsf {d}},{\mathfrak {m}})\) is the convex and lower semicontinuous functional defined through
and its finiteness domain will be denoted by \(H^{1,2}(X,{\mathsf {d}},{\mathfrak {m}})\). Looking at the optimal approximating sequence in (2.4), it is possible to identify a canonical object \(\left|\nabla f\right|\), called minimal relaxed slope, providing the integral representation
Definition 2.2
Any metric measure space such that \(\mathsf{Ch}\) is a quadratic form is said to be infinitesimally Hilbertian.
Let us recall from [6, 43] that, under the infinitesimally Hilbertian assumption, the function
defines a symmetric bilinear form on \(H^{1,2}(X,{\mathsf {d}},{\mathfrak {m}})\times H^{1,2}(X,{\mathsf {d}},{\mathfrak {m}})\) with values into \(L^1(X,{\mathfrak {m}})\).
It is possible to define a Laplacian operator \(\Delta :{\mathcal {D}}(\Delta )\subset L^{2}(X,{\mathfrak {m}})\rightarrow L^2(X,{\mathfrak {m}})\) in the following way. We let \({\mathcal {D}}(\Delta )\) be the set of those \(f\in H^{1,2}(X,{\mathsf {d}},{\mathfrak {m}})\) such that, for some \(h\in L^2(X,{\mathfrak {m}})\), one has
and, in that case, we put \(\Delta f=h\). It is easy to check that the definition is well-posed and that the Laplacian is linear (because \(\mathsf{Ch}\) is a quadratic form).
Definition 2.3
(Perimeter and sets of finite perimeter) Given a Borel set \(E\subset X\) and an open set \(A\subset X\) the perimeter \({{\,\mathrm{Per}\,}}(E,A)\) is defined as
We say that E has locally finite perimeter if \({{\,\mathrm{Per}\,}}(E,K)<\infty \) for any compact set K. In that case it can be proved that the set function \(A\mapsto {{\,\mathrm{Per}\,}}(E,A)\) is the restriction to open sets of a locally finite Borel measure \({{\,\mathrm{Per}\,}}(E,\cdot )\) defined by
The following coarea formula is taken from [70, Proposition 4.2].
Theorem 2.4
(Coarea formula) Let \((X,{\mathsf {d}},{\mathfrak {m}})\) be a locally compact metric measure space and \(v\in {{\,\mathrm{Lip}\,}}(X)\). Then, \(\{v>r\}\) has locally finite perimeter for \({\mathscr {L}}^1\)-a.e. \(r\in {\mathbb {R}}\) and, for any Borel function \(f:X\rightarrow [0,\infty ]\), it holds
2.2 \({{\,\mathrm{RCD}\,}}\) spaces
Let us start by recalling the so-called curvature dimension condition \({{\,\mathrm{CD}\,}}(K,N)\). Its introduction dates back to the seminal and independent works [67, 85, 86], while in this presentation we closely follow [15].
Below \({\mathscr {P}}(X)\) denotes the set of probability measure over X while
We define the operator \(e_t: \text {Geo}(X) \rightarrow X\) as \(e_t(\gamma ):= \gamma (t)\). Given \(\mu _0, \mu _1\in {\mathscr {P}}(X)\), an optimal geodesic plan is any \(\Pi \in {\mathscr {P}}(\text {Geo}(X))\) such that \((e_0,e_1)_{\sharp }\Pi \) is an optimal plan, i.e.
for any \(\pi \in {\mathscr {P}}(X\times X)\) such that \(\pi (A\times X) = \mu _0(A)\) and \(\pi (X\times A) = \mu _1(A)\) for any Borel set \(A\subset X\).
Definition 2.5
(Curvature dimension bounds) Let \(K\in {\mathbb {R}}\) and \(1\le N<\infty \). We say that a m.m.s. \((X,{\mathsf {d}},{\mathfrak {m}})\) is a \({{\,\mathrm{CD}\,}}(K,N)\) space if, for any \(\mu _0,\mu _1\in {\mathscr {P}}(X)\) absolutely continuous w.r.t. \({\mathfrak {m}}\) with bounded support, there exists an optimal geodesic plan \(\Pi \in {\mathscr {P}}(\text {Geo}(X))\) such that for any \(t\in [0,1]\) and for any \(N'\ge N\) we have
where \((e_t)_{\sharp }\Pi =\rho _t{\mathfrak {m}}\), \(\mu _0=\rho _0{\mathfrak {m}}\), \(\mu _1=\rho _1{\mathfrak {m}}\) and the distortion coefficients \(\tau _{K,N}^{t}(\cdot )\) are defined as follows. First we define the coefficients \([0,1]\times [0,\infty )\ni (t,\theta )\mapsto \sigma _{K,N}^{(t)}(\theta )\) by
then we set \(\tau _{K,N}^{(t)}(\theta ) := t^{1/N}\sigma _{K,N-1}^{(t)}(\theta )^{1-1/N}\).
Definition 2.6
We say that a metric measure space \((X,{\mathsf {d}},{\mathfrak {m}})\) satisfies the Riemannian curvature-dimension condition for some \(K\in {\mathbb {R}}\) and \(1\le N<\infty \) (it is an \({{\,\mathrm{RCD}\,}}(K,N)\) m.m.s. for short) if it is a \({{\,\mathrm{CD}\,}}(K,N)\) infinitesimally hilbertian metric measure space.
Note that, if \((X,{\mathsf {d}},{\mathfrak {m}})\) is an \({{\,\mathrm{RCD}\,}}(K,N)\) m.m.s., then so is \(({{\,\mathrm{supp}\,}}{\mathfrak {m}},{\mathsf {d}},{\mathfrak {m}})\), hence in the following we will always tacitly assume \({{\,\mathrm{supp}\,}}{\mathfrak {m}}= X\).
Remark 2.7
(Compatibility with the smooth case) The \({{\,\mathrm{RCD}\,}}(K,N)\) notion is compatible with the smooth case of weighted Riemannian manifolds with (weighted-)Ricci curvature bounded from below [67, 85,86,87]. It means that a Riemannian manifold meets the \({{\,\mathrm{RCD}\,}}(K,N)\) condition if and only if it has dimension smaller than N and the N-dimensional Bakry-Ricci tensor is bounded below by K.
Remark 2.8
(Stability) A fundamental property of \({{\,\mathrm{RCD}\,}}(K,N)\) spaces, that will be used several times in this paper, is the stability w.r.t. pmGH convergence, meaning that a pmGH limit of a sequence of (pointed) \({{\,\mathrm{RCD}\,}}(K,N)\) spaces is still an \({{\,\mathrm{RCD}\,}}(K,N)\) m.m.s.
The basic references for the theory of convergence and stability of Sobolev functions on converging sequences of \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure spaces are [46] and [7, 8].
We recall that any \({{\,\mathrm{RCD}\,}}(K,N)\) m.m.s. \((X,{\mathsf {d}},{\mathfrak {m}})\) satisfies the Bishop-Gromov inequality:
for any \(0<r< R\) and for any \(x\in X\), where \(v_{K,N}(r):= N\omega _N\int _0^r \left( s_{K,N}(s)\right) ^{N-1}\mathop {}\!\mathrm {d}s\) and
In particular \((X,{\mathsf {d}},{\mathfrak {m}})\) is locally uniformly doubling, that is to say, for any \(R>0\) there exists \(C(K,N,R)>0\) such that
Moreover, in [80, 88] has been proven that \({{\,\mathrm{RCD}\,}}(K,N)\) spaces verify a local Poincaré inequality, therefore they fit in the general framework of PI spaces considered for instance in [26].
2.2.1 Structure theory
From the point of view of geometric measure theory a notion of k-regular point for an \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure space \((X,{\mathsf {d}},{\mathfrak {m}})\) can be introduced in the following terms.
Definition 2.9
(Regular points) We say that \(x\in {\mathcal {R}}_k\) whenever
as \(r\downarrow 0\), where \(\omega _k:={\mathscr {H}}^k(B_1(0^k))\).
In [19] (see also the very recent [35]), generalizing a previous result obtained for Ricci limits in [33], it has been proved that for any \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure space \((X,{\mathsf {d}},{\mathfrak {m}})\) there exists an integer \(1\le n\le N\), that we shall call essential dimension of \((X,{\mathsf {d}},{\mathfrak {m}})\) from now on, such that
In this generality we also know after [69] that X is \(({\mathfrak {m}},n)\)-rectifiable as metric space. Moreover, the representation formula \({\mathfrak {m}}=\theta {\mathscr {H}}^n\), for some locally integrable nonnegative density \(\theta \), has been obtained in the independent works [38, 47, 60].
2.2.2 Calculus on \({{\,\mathrm{RCD}\,}}\) spaces
We refer to [6, 43, 44] for the basic background about first and second order differential calculus on \({{\,\mathrm{RCD}\,}}\) spaces.
Here and in the following we denote by \({{\,\mathrm{Hess}\,}}u\) the Hessian of a function \(u\in H^{2,2}(X,{\mathsf {d}},{\mathfrak {m}})\), referring to [44] for the study of its main properties in this framework. Thanks to locality, we will be dealing also with functions that are defined only locally. Following the notation of [44], we denote the space of test functions as
The existence of many test functions within this framework is one of the outcomes of [82].
We will also rely repeatedly on the following existence result for good cut-off functions.
Lemma 2.10
(Good cut-off functions [10]) Let \((X,{\mathsf {d}},{\mathfrak {m}})\) be an \({{\,\mathrm{RCD}\,}}(K,N)\) space. Let \(p\in X\) be fixed. Then there exists \(\eta \in \mathrm{Test}(X,{\mathsf {d}},{\mathfrak {m}})\) such that \(0\le \eta \le 1\) on \(X\), the support of \(\eta \) is compactly contained in \(B_5(p)\), and \(\eta =1\) on \(B_4(p)\).
In Sect. 3 we will rely on some tools from optimal transportation on \({{\,\mathrm{RCD}\,}}(K,N)\) spaces. Mainly we will be concerned with first and second derivatives of (sufficiently regular) potentials along Wasserstein geodesics. We will denote by \(W_2\) the Wasserstein distance induced by optimal transport with cost equal to the distance squared on the space \({\mathscr {P}}_2(X)\) of probabilities with finite second moment. We refer to [6, 87] for the basic terminology about this topic and to [49] for a more detailed account about optimal transportation on \({{\,\mathrm{RCD}\,}}(K,N)\) spaces.
The next result follows by combining Proposition 5.15 and Corollary 5.7 in [41].
Proposition 2.11
Let \((X,{\mathsf {d}},{\mathfrak {m}})\) be an \({{\,\mathrm{RCD}\,}}(K, N)\) space for some \(K\in {\mathbb {R}}\) and \(1\le N<\infty \). Consider a \(W_2\)-geodesic \((\eta _s)_{s\in [0,1]}\in {\mathscr {P}}_2(X)\), satisfying \(\eta _s\le C{\mathfrak {m}}\) and \({{\,\mathrm{supp}\,}}\eta _s \subset B_R(p)\) for any \(s\in [0,1]\), for some \(C>0\), \(R>0\) and \(p\in X\). Then, for any \(u\in {{\,\mathrm{Lip}\,}}(X,{\mathsf {d}})\), the function \(s\mapsto \int u\mathop {}\!\mathrm {d}\eta _s\) is \(C^1\) and one has
where \(\varphi _s\) is any Lipschitz Kantorovich potential from \(\eta _s\) to \(\eta _0\).
2.3 Continuity equation and flow maps
Let us recall that given any function \(u\in \mathrm{Test}(X,{\mathsf {d}},{\mathfrak {m}})\) a solution to the continuity equation induced by \(\nabla u\) is any absolutely continuous curve \((\rho _t)_{t\in [0,1]}\subset {\mathscr {P}}_2(X)\) such that the following holds: for any \(f\in {{\,\mathrm{Lip}\,}}_c(X,{\mathsf {d}})\) the function \(t\mapsto \int f\mathop {}\!\mathrm {d}\rho _t\) is absolutely continuous and it satisfies
We refer to [12, 45] for the treatment of the continuity equation on (\({{\,\mathrm{RCD}\,}}\)) metric measure spaces.
The next result is a particular case of [45, Proposition 3.11].
Lemma 2.12
Let \((X,{\mathsf {d}},{\mathfrak {m}})\) be an \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure space for some \(K\in {\mathbb {R}}\) and \(1\le N<\infty \). Let \(u\in \mathrm{Test}(X,{\mathsf {d}},{\mathfrak {m}})\) and let \((\rho _t)_{t\in [0,1]}\subset {\mathscr {P}}_2(X)\) be a solution of the continuity equation associated to \(\nabla u\). If we further assume that \(\rho _t\le C{\mathfrak {m}}\) for any \(t\in [0,T]\) for some \(C>0\), then for any \(\nu \in {\mathscr {P}}_2(X)\) it holds
where \(\varphi _t\) is any optimal Kantorovich potential for the transport problem between \(\rho _t\) and \(\nu \).
The theorem below is taken from [50] where the second order differentiation formula along \(W_2\)-geodesics has been proved on \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure spaces.
Theorem 2.13
Let \((X,{\mathsf {d}},{\mathfrak {m}})\) be an \({{\,\mathrm{RCD}\,}}(K,N)\) m.m.s. for some \(1\le N<\infty \). Let \((\eta _s)_{s\in [0,1]}\) be a \(W_2\)-geodesic connecting probability measures \(\eta _0\) and \(\eta _1\) absolutely continuous w.r.t. \({\mathfrak {m}}\) and with bounded densities and assume that \(u\in \mathrm{Test}(X,{\mathsf {d}},{\mathfrak {m}})\). Then, the curve
is \(C^1\) on [0, 1], where \(\varphi _s\) is any function such that for some \(r\in [0,1]\) with \(s\ne r\) it holds that \(-(r-s)\varphi _s\) is an optimal Kantorovich potential from \(\eta _s\) to \(\eta _r\). Moreover
In the context of \({{\,\mathrm{RCD}\,}}(K,\infty )\) spaces a general theory of flows for Sobolev vector fields has been developed in [12]. Here we only collect some simplified statements relevant for our purposes.
Definition 2.14
Let \(u\in \mathrm{Test}(X,{\mathsf {d}},{\mathfrak {m}})\). We say that a Borel map \({\varvec{X}}:[0,\infty )\times X\rightarrow X\) is a Regular Lagrangian flow (RLF for short) associated to \(\nabla u\) if the following conditions hold true:
-
(1)
\({\varvec{X}}(0,x)=x\) and \({\varvec{X}}(\cdot ,x)\in C([0,\infty );X)\) for every \(x\in X\);
-
(2)
there exists \(L\ge 0\), called compressibility constant, such that
$$\begin{aligned} {\varvec{X}}(t,\cdot )_{\sharp } {\mathfrak {m}}\le L{\mathfrak {m}},\qquad \text {for every }t\ge 0; \end{aligned}$$(2.23) -
(3)
for every \(f\in \mathrm{Test}(X,{\mathsf {d}},{\mathfrak {m}})\) the map \(t\mapsto f({\varvec{X}}(t,x))\) is locally absolutely continuous in \([0,\infty )\) for \({\mathfrak {m}}\)-a.e. \(x\in X\) and
$$\begin{aligned} \frac{\mathop {}\!\mathrm {d}}{\mathop {}\!\mathrm {d}t} f({\varvec{X}}(t,x))= \nabla u\cdot \nabla f({\varvec{X}}(t,x)) \quad \quad \text {for a.e.}\ t\in (0,\infty ). \end{aligned}$$(2.24)
In the next theorem we state some general results concerning Regular Lagrangian flows that will be used in the sequel.
Theorem 2.15
Let \((X,{\mathsf {d}},{\mathfrak {m}})\) be an \({{\,\mathrm{RCD}\,}}(K,\infty )\) space for some \(K\in {\mathbb {R}}\). Let us fix a function \(u\in \mathrm{Test}(X,{\mathsf {d}},{\mathfrak {m}})\) with \(\Delta u\in L^{\infty }(X,{\mathfrak {m}})\). Then
-
(i)
there exists a unique regular Lagrangian flow \({\varvec{X}}:{\mathbb {R}}\times X\rightarrow X\) associated to \(\nabla u\)Footnote 2 (uniqueness is understood in the following sense: if \({\varvec{X}}\) and \({\bar{{\varvec{X}}}}\) are Regular Lagrangian flows associated to \(\nabla u\), then for \({\mathfrak {m}}\)-a.e. \(x\in X\) one has \({\varvec{X}}_t(x)={\bar{{\varvec{X}}}}_t(x)\) for any \(t\in {\mathbb {R}}\));
-
(ii)
\({\varvec{X}}\) satisfies the semigroup property: for any \(s\in {\mathbb {R}}\) it holds that, for \({\mathfrak {m}}\)-a.e. \(x\in X\),
$$\begin{aligned} {\varvec{X}}(t,{\varvec{X}}(s,x))={\varvec{X}}(t+s,x) \qquad \forall t\in {\mathbb {R}}, \end{aligned}$$(2.25)and the following bound is verified:
$$\begin{aligned} e^{-t\left\Vert \Delta u\right\Vert _{L^{\infty }}}{\mathfrak {m}}\le \left( {\varvec{X}}_t\right) _{\sharp }{\mathfrak {m}}\le e^{t\left\Vert \Delta u\right\Vert _{L^{\infty }}}{\mathfrak {m}}; \end{aligned}$$(2.26) -
(iii)
if \(\Delta u=0\), \({{\,\mathrm{Hess}\,}}u=0\) and \(|\nabla u|\le 1\) in \(B_4(p)\) for some \(p\in X\) then, for any \(x\in B_1(p)\) and \(t\in (-1,1)\) the map \({\varvec{X}}\) admits a pointwise representative satisfying
$$\begin{aligned} {\mathsf {d}}({\varvec{X}}_t(x),{\varvec{X}}_t(y))={\mathsf {d}}(x,y) \quad \text {for any }x,y\in B_1(p)\text {, and }t\in (-1,1).\qquad \end{aligned}$$(2.27)
Proof
We refer to [4, Theorem 1.12] for the proof of (i) and (ii), while (iii) follows just localising the argument in [20, Theorem 2.7]. \(\square \)
Remark 2.16
(Continuity equations and flow maps) Solutions to the continuity equations and flow maps are strictly related. Indeed, given a function \(u\in \mathrm{Test}(X,{\mathsf {d}},{\mathfrak {m}})\) with \(\Delta u\in L^{\infty }(X,{\mathfrak {m}})\) and \({\varvec{X}}\) a RLF associated to \(\nabla u\) one has that
is the unique solution to the continuity equation with initial datum \(\rho _0\in L^{\infty }(X)\) and velocity field \(\nabla u\).
2.4 Noncollapsed spaces
In [37] the notion of noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure space has been proposed motivated by the theory of noncollapsed Ricci limit spaces, studied since [28] (see also a similar, though a priori weaker, notion suggested in [64]). We say that \((X,{\mathsf {d}},{\mathfrak {m}})\) is a noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) space if N is an integer and \({\mathfrak {m}}={\mathscr {H}}^N\).
We point out that another relevant class to consider would be that of \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure spaces for which the essential dimension equals N (called weakly noncollapsed in [37]). In the compact case it is known that these spaces are noncollapsed in the above sense [53] and it is conjectured that this should be true also in the general case.
On top of the usual structure of \({{\,\mathrm{RCD}\,}}(K,N)\) spaces, noncollapsed spaces have additional regularity properties.
Let us begin by pointing out the following powerful result [37, Theorem 1.2], generalizing a previous statement due to Cheeger–Colding [28] (see also [32]).
Theorem 2.17
(Volume convergence) Let \((X_n,{\mathsf {d}}_n,{\mathscr {H}}^N,x_n)\) be pointed noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure spaces and assume that they converge in the pGH topology to \((X,{\mathsf {d}},x)\). Then, if
they also converge in the pmGH topology to \((X,{\mathsf {d}},{\mathscr {H}}^N,x)\).
We refer to [22, Definition 3.6.16] for the definition of metric cone \((C(Y),{\mathsf {d}}_C)\) over a metric space \((Y,{\mathsf {d}}_Y)\). Here we just recall that for points \((r_1,x_1)\) and \((r_2,x_2)\) such that \(r_1,r_2\ge 0\) and \({\mathsf {d}}_Y(x_1,x_2)\le \pi \) the cone distance is given by the law of cosines:
In [37], generalizing [28] and relying on [36] (which extends in turn one of the key results in [27]) it has been proven that for a noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure space \((X,{\mathsf {d}},{\mathscr {H}}^N)\) any tangent cone is a metric cone over a noncollapsed \({{\,\mathrm{RCD}\,}}(N-2,N-1)\) metric measure space \((Y,{\mathsf {d}}_Y,{\mathscr {H}}^{N-1})\). This amounts to say that any pGH limit of \((X,r_i^{-1}{\mathsf {d}},x)\), for some sequence of radii \(r_i\downarrow 0\), is a metric cone in the sense above.
Given any noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) metric measure space \((X,{\mathsf {d}},{\mathscr {H}}^N)\) and any \(x\in X\) let us denote by
the density of \({\mathscr {H}}^N\) at x (when there is no risk of confusion we will drop the dependence on the ambient space X). The existence of the limit above follows from the Bishop-Gromov inequality. Moreover, the lower semicontinuity of the density (cf. [37, Lemma 2.2 (i)]) together with a standard result about differentiation of measures allow to infer that \(\Theta (x)\le 1\) for every \(x\in X\) and \(\Theta (x)=1\) for \({\mathscr {H}}^N\)-a.e. \(x\in X\).
By volume rigidity (see [37, Theorem 1.6] after [32]) we recognize that \(\Theta (x)=1\) if and only if the tangent cone is unique and isometric to \(({\mathbb {R}}^N,{\mathsf {d}}_{eucl})\).
More generally, Colding’s volume convergence theorem [28, 32] (see also [37, Theorem 1.3]) yields that for any \(x\in X\) any cross section \((Y,{\mathsf {d}}_Y)\) of a tangent cone C(Y) at x satisfies
2.5 Cone splitting via content
Let us start by restating a quantitative version of the cone splitting lemma [30, Lemma 4.1] tailored for \({{\,\mathrm{RCD}\,}}(K,N)\) spaces (see [14] for the present version).
Definition 2.18
We define the \(\varepsilon -(t,r)\) conical set in \(B_{\frac{1}{2}}(x_0)\) as
Theorem 2.19
For all \(K\in {\mathbb {R}}\), \(N\in [2,\infty )\), \(0<\gamma <1\), \(\delta <\gamma ^{-1}\), and for all \(\tau ,\psi >0\) there exist \(0<\varepsilon =\varepsilon (N,K,\gamma ,\delta ,\tau ,\psi )<\psi \) and \(0<\theta =\theta (N,K,\gamma ,\delta ,\tau ,\psi )\) such that the following holds. Let \((X,{\mathsf {d}},{\mathfrak {m}})\) be an \({{\,\mathrm{RCD}\,}}(K,N)\) m.m.s., \(x\in X\) and \(r\le \theta \) be such that there exists an \(\varepsilon r\)-GH equivalence
for some cone \({\mathbb {R}}^l\times C(Z)\), with \((Z,{\mathsf {d}}_Z,{\mathfrak {m}}_Z)\) an \({{\,\mathrm{RCD}\,}}(N-l-2,N-l-1)\) m.m.s.. If there exists
with
then for some cone \({\mathbb {R}}^{l+1}\times C({\tilde{Z}})\), where \(({\tilde{Z}},{\mathsf {d}}_{{\tilde{Z}}},{\mathfrak {m}}_{{\tilde{Z}}})\) is an \({{\,\mathrm{RCD}\,}}(N-l-3,N-l-2)\) m.m.s.,
Theorem 2.19 is a quantitative version of the following statement: if a metric cone with vertex z is a metric cone also with respect to \(z'\ne z\), then it contains a line.
Let us now present a quantitative version of the cone splitting theorem via content, taken from [29, Theorem 4.9]. We begin by defining the notion of the pinching set.
Definition 2.20
Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be an \({{\,\mathrm{RCD}\,}}(-\xi (N-1),N)\) and \(p\in X\), we set
where \({\mathcal {V}}_{r}(x):= \frac{{\mathscr {H}}^N(B_r(x))}{v_{K,N}(r)}\) is the volume ratio appearing in (2.13).
We define the set with small volume pinching accordingly to be
Theorem 2.21
Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be an \({{\,\mathrm{RCD}\,}}(-\xi (N-1),N)\) space with \({\mathscr {H}}^N(B_1(p))>v>0\). If for some \(r\in (0,1)\) it holds that \({\mathscr {H}}^{N}(B_{\gamma r}({\mathcal {P}}_{r,\xi }))\ge \varepsilon \gamma r^{N}\), with \(0<\delta \), \(\varepsilon <\delta (N,v)\), \(\gamma \le \gamma (N,v,\varepsilon )\) and \(\xi \le \xi (\delta ,\varepsilon ,\gamma ,N,v)\), then there exists \(q\in B_{4r}(p)\) such that either
or
The proof of Theorem 2.21 easily follows from Theorem 2.19, see for instance [56, Theorem 7.6].
3 Splitting maps on \({{\,\mathrm{RCD}\,}}\) spaces
In the development of the structure theory of Ricci limit spaces a prominent role has been played by the \(\delta \)-splitting maps [27,28,29, 31]. After the construction of a second order differential calculus on \({{\,\mathrm{RCD}\,}}\) spaces in [44] this tool, which provides a way to turn analytic information into geometric information, has also begun to play a role in the synthetic framework [17].
All the works mentioned above rely on the equivalence between the existence of an \({\mathbb {R}}^k\)-valued \(\delta \)-splitting map and the (pointed measured)GH-closeness to a product with factor \({\mathbb {R}}^k\). Below we state the definition of a \(\delta \)-splitting map relevant for the sake of this paper.
Definition 3.1
Let \((X,{\mathsf {d}},{\mathfrak {m}})\) be an \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) m.m.s., \(p\in X\) and \(\delta >0\) be fixed. We say that \(u:=(u_1,\ldots ,u_k):B_r(p)\rightarrow {\mathbb {R}}^k\) is a \(\delta \)-splitting map provided it is harmonic and it satisfies:
-
(i)
\(|\nabla u_a|< C(N)\);
-
(ii)
 ;
; -
(iii)
 ;
;
for any \(a,b=1,\ldots ,k\).
Remark 3.2
(About the scale invariant smallness of the Hessian) If we make the stronger assumption that the ambient space is \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\), then condition (ii) is unnecessary once we strengthen the harmonicity assumption to harmonicity on \(B_{2r}(p)\), since it follows from conditions (i) and (iii) integrating the Bochner inequality against a good cut-off function, see for instance [18].
Remark 3.3
(Sharper gradient bounds) If we assume that \((X,{\mathsf {d}},{\mathfrak {m}})\) is an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) metric measure space then the gradient bound in (i) can be sharpened to the conclusion
In particular, if \(u:B_r(x)\rightarrow {\mathbb {R}}^{k}\) is a \(\delta \)-splitting map according to Definition 3.1 and the ambient space is \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\), then \(u:B_{r/2}(x)\rightarrow {\mathbb {R}}^{k}\) is a \(C(N)\delta \)-splitting map and we can replace condition (i) in the definition with the sharper gradient bound (3.1).
Moreover the following Lipschitz estimate holds
The validity of (3.1) has been pointed out for the first time in the framework of smooth Riemannian manifolds in [31, equations (3.42)–(3.46)], we report here a slightly modified argument tailored for the \({{\,\mathrm{RCD}\,}}\) framework.
Let us fix \(a\in \{1,\dots ,k\}\) and drop the dependence on the chosen component, writing just u.
Observe that, by volume doubling and (iii), for any \(y\in B_{r/2}(p)\) it holds that

Now we consider a regular cut-off function \(\varphi :X\rightarrow [0,1]\) such that \(\varphi =1\) on \(B_{3/4r}(x)\) and \(\varphi =0\) outside of \(B_r(x)\), \(r^2\left|\Delta \varphi \right|\le C(N)\) and \(r\left|\nabla \varphi \right|\le C(N)\) (see Lemma 2.10) and the one parameter family
Differentiating with respect to time, taking into account the heat kernel estimate
which follows from [54] and volume doubling, for any \(y\in B_{r/2}(x)\) and \(t\in [0,r^2]\) we can estimate
Above the first inequality follows from the bounds for the cut-off function and from Bochner’s inequality.
Given (3.6), observing that, for \({\mathfrak {m}}\)-a.e. \(y\in B_{r/2}(x)\) it holds
we can integrate between 0 and \(r^2\) to obtain

From this we easily infer that
In order to show (3.2) it is enough to check that for any \(v\in {\mathbb {R}}^k\) with \(|v|=1\) it holds
Indeed (3.9) yields
which implies (3.2) by taking the supremum w.r.t. \(v\in {\mathbb {S}}^{k-1}\).
Now the key observation to prove (3.9) is that \(v\cdot u\) verifies (up to a constant) the same bounds of the components of the original \(\delta \)-splitting map. In particular it is harmonic and it satisfies

therefore applying the argument already described for \(u_a\) we get (3.10).
The first main result of this section will be Theorem 3.8 below, where we prove the equivalence between the existence of an \({\mathbb {R}}^k\)-valued \(\delta \)-splitting map on a ball and the measured GH closeness of the ball with same center and comparable radius to the ball of a product with \({\mathbb {R}}^k\). This statement will be proved arguing by compactness, starting from its rigid version Theorem 3.4.
The second key result is Proposition 3.13, a version of the transformation theorem [29, Proposition 7.7] (see also [31] for a previous version with different assumptions) tailored for our purposes.
3.1 Functional splitting theorem, local version
In the rest of the note we will rely on the following functional version of the (iterated) splitting theorem in local form. With respect to the present literature the main novelty is the locality of the statement, which requires some cut-off arguments and the use of Theorem 2.13, which relies in turn on [50]. The proof combines techniques from [27, 41].
Theorem 3.4
Let \((X,{\mathsf {d}},{\mathfrak {m}})\) be an \({{\,\mathrm{RCD}\,}}(0,N)\) m.m.s. for some \(N\ge 1\) and let \(p\in X\) be fixed. Assume that for some positive \(k\in {\mathbb {N}}\) there exists \(u=(u_1,\ldots , u_k):B_6(p)\rightarrow {\mathbb {R}}^k\) satisfying
-
(i)
\(u(p)=0\);
-
(ii)
\(|\nabla u_a|=1\) and \(\Delta u_a=0\), \({\mathfrak {m}}\)-a.e. in \(B_5(p)\) for any \(a=1,\ldots , k\);
-
(iii)
\(\nabla u_a\cdot \nabla u_b=0\), \({\mathfrak {m}}\)-a.e. in \(B_5(p)\), for any \(a\ne b\).
Then there exist a m.m.s. \((Z,{\mathsf {d}}_Z,{\mathfrak {m}}_Z)\) and a function \(f:B_1(p)\rightarrow Z\) such that
is an isomorphism of metric measure spaces with its image.
Proof
Let \(\eta \in \mathrm{Test}(X,{\mathsf {d}},{\mathfrak {m}})\) be a good cut-off function (see Lemma 2.10) satisfying \(\eta =1\) on \(B_4(p)\) and \(\eta =0\) on \(X{\setminus } B_5(p)\). Let us define the vector fields \(b_{a}:=\nabla (\eta u_a)\) and denote by \(X^{a}\) their Regular Lagrangian flows, for \(a=1,\ldots ,k\). Notice that by the improved Bochner inequality with Hessian term [44, Theorem 3.3.8], \({{\,\mathrm{Hess}\,}}(\eta u_a)=0\) in \(B_4(p)\). Therefore thanks to Theorem 2.15 (iii) we have a pointwise defined representative of \(X^a_t(x)\) for \(t\in (-1,1)\) and \(x\in B_1(p)\) satisfying (2.27). Building upon [48, Theorem 3.24] we conclude that \(X_{t_a}^a \circ X_{t_b}^b = X_{t_b}^b\circ X_{t_a}^a\) whenever \(X^a_{t_a}, X^b_{t_b}\in B_{1}(p)\), \(a,b=1, \ldots , k\). Moreover, it holds
Let us now set \(Z:=\{u=0\}\), \({\mathsf {d}}_Z(x,y):={\mathsf {d}}(x,y)\) for \(x,y\in Z\), and

In order to conclude the proof it is enough to show that there exists a pointwise representative
Indeed, if it the case, we can conclude as follows. Observe that \(B_{1/k}(p)\subset \Phi ((-1/k,1/k)^k\times (B_1(p)\cap Z))\), since for any \(y\in B_{1/k}(p)\) we can set
and check, by means of (3.13), that \(\Phi (t_1,\ldots ,t_k, \pi (y))=y\). Finally we notice that \(\Phi ^{-1}: B_{1/k}(p)\rightarrow {\mathbb {R}}^k\times Z\) is the sought map, since it is an isometry and can be written as \(\Phi ^{-1}=(u,f)\) for some \(f:B_{1/k}(p)\rightarrow Z\), thanks to (3.13). Moreover setting  , one can easily check that
, one can easily check that
The proof of (3.15) is divided in three steps.
Step 1. There exists a pointwise representative of \(\Phi \) on \((-1/k,1/k)^{k}\times (B_1(p)\cap Z)\) such that, for any \(x,y\in B_{1}(p)\cap Z\) and \((t_1,\ldots ,t_k)\in (-1/k,1/k)^k\) it holds
for \(a=1,\ldots ,k\).
As we have already remarked, there exists a pointwise defined representative of \(X^a_t(x)\) for \(t\in (-1,1)\) and \(x\in B_1(p)\) satisfying (2.27), therefore the first identity in (3.16) follows.
Concerning the second equality, observe that, since \(|\nabla (\eta u_a)|=1\) in \(B_4(p)\) we have that \({\mathsf {d}}(X^a_t(x),x)\le t\) for \(t\in (-1,1)\) and \(x\in B_1(p)\). Moreover (3.13) and the fact that \(u_a\) is 1-Lipschitz in \(B_1(p)\) give
Combining the two inequalities also the second equality in (3.16) follows.
Step 2. In this step we are going to prove that for any \(a\in \{1,\ldots ,k\}\), any \(x,y\in B_1(p)\) and any \(t\in (0,1)\) it holds
To this aim let us fix \(a\in \{1,\ldots ,k\}\), \(x,y\in B_1(p)\) and \(r>0\) with the property that \(B_r(x)\cup B_r(y)\subset B_1(p)\). Then let us define

Let us set \(\rho _t^r:=\left( {X^a_t}\right) _{\#}\mu ^r\) and observe that for any function \(f \in {{\,\mathrm{Lip}\,}}(X,{\mathsf {d}})\) we have
namely \(\rho _t^r=\left( {X^a_t}\right) _{\#}\mu ^r\) solves the continuity equation associated to \(\nabla u\) (cf Remark 2.16). Therefore Lemma 2.12 guarantees that \(t\mapsto \frac{1}{2}W_2^2(\rho _t^r,\nu _r)\) is absolutely continuous and
where \(\varphi _t\) is any optimal Kantorovich potential from \(\rho _t^r\) to \(\nu ^r\).
Let us now fix \(t\in (0,1)\) such that (3.21) holds true. Denote by \((\eta ^{r,t}_s)_{s\in [0,t]}\) the \(W_2\)-geodesic connecting \(\nu _r\) to \(\rho _t^r\). From Proposition 2.11 we get

where \(\varphi _t\) is any optimal Kantorovich potential from \(\rho _t^r\) to \(\nu ^r\).
Combining (3.21) and (3.22) we deduce

Moreover, since \({{\,\mathrm{Hess}\,}}u=0\) in \({{\,\mathrm{supp}\,}}\eta _s^{r,t}\) for any \(0\le s\le t\le 1\), Theorem 2.13 implies that \(s\mapsto \int u \mathop {}\!\mathrm {d}\eta ^{r,t}_s\) is affine. Therefore
that, along with (3.23), yields
Finally, (3.18) follows from (3.25) by continuity letting \(r\rightarrow 0\).
Step 3. We conclude the proof of (3.15) by showing that
for any \(x,y\in Z\cap B_1(p)\) and any \(s_a,t_a\in (-1/k,1/k)\), for \(a=1,\dots ,k\).
In order to do so let us assume without loss of generality that \(t_1\ge s_1\) and set \({\bar{x}}:=X^2_{t_2}\circ \ldots \circ X^k_{t_k}(x)\) and \({\bar{y}}:=X^2_{s_2}\circ \ldots \circ X^k_{s_k}\) if \(k\ge 2\) and \({\bar{x}}:=x\), \({\bar{y}}:=y\) otherwise.
By exploiting the semigroup property (ii) in Theorem 2.15, Step 1 and Step 2, we get
Observe now that \(u_1({\bar{x}})=u_1({\bar{y}})=0\) since the function \(t\mapsto u_1(X^a_t(z))\) is constant for \(t\in (-1,1)\), \(z\in B_2(p)\) and \(a\ne 1\). Indeed, taking the derivative w.r.t. \(t\in (-1,1)\) and using (iii) in our assumptions we have
for a.e. \(t\in (-1,1)\) and for a.e. \(z\in B_2(p)\). The statement can then be proved for any time and starting point by a continuity argument. It follows that
and a simple induction argument gives (3.26). \(\square \)
Below we specialize Theorem 3.4 to the case in which \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is a noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) space and the splitting map has \(N-1\) components. In this case we are going to prove that, as expected, the factor Z is one dimensional.
Theorem 3.5
Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be an \({{\,\mathrm{RCD}\,}}(0,N)\) m.m.s. for some natural \(2\le N<\infty \) and let \(p\in X\) be fixed. Assume that there exists a 0-splitting map
Then there exist a m.m.s. \((Z,{\mathsf {d}}_Z,{\mathscr {H}}^1)\), with \((Z,{\mathsf {d}}_Z)\) isometric to the ball of a one dimensional Riemannian manifold (possibly with boundary), and a map \(f:B_{1/(N-1)}(p)\rightarrow Z\) such that
is an isomorphism of metric measure spaces.
Moreover, up to an additive constant, f coincides with the signed distance function from the level set \(\{f=z_0\}\).
Remark 3.6
In particular, Z is isometric, in the sense of Riemannian manifolds, to either a circle or a connected closed interval \(I\subseteq {\mathbb {R}}\), possibly with infinite length.
Proof
Let us start by applying the local functional splitting Theorem 3.4 to get the metric measure space \((Z,{\mathsf {d}}_Z,{\mathfrak {m}}_Z)\) and the map \(f:B_{1/(N-1)}(p)\rightarrow Z\).
By a slight modification of the proof of [41, Corollary 5.30], we can prove a weaker version of the \({{\,\mathrm{CD}\,}}(0,N)\) condition for the space \((Z,{\mathsf {d}}_Z,{\mathfrak {m}}_Z)\). More precisely we can check that, for any \(\mu _0\in {\mathscr {P}}_2(Z)\) satisfying \(\mu _0\ll {\mathfrak {m}}_Z\) and \({{\,\mathrm{supp}\,}}\mu _0 \subset B_{1/(N-1)}(z_0)\) there exists \(r>0\) such that for any \(\mu _1\in {\mathscr {P}}_2(X)\) absolutely continuous w.r.t. \({\mathfrak {m}}_Z\) and supported on \(B_r({{\,\mathrm{supp}\,}}\mu _0)\) one has a unique \(W_2\)-geodesic connecting \(\mu _0\) and \(\mu _1\) which satisfies the defining inequality for the \({{\,\mathrm{CD}\,}}(0,N)\) condition.
Next we observe that, as a consequence of the discussion above, of the isometry between \(B_{1 /(N-1)}(p)\) and the split ball and of the noncollapsing assumption, all the metric measured tangents to \((Z,{\mathsf {d}}_Z,{\mathfrak {m}}_Z)\) are either lines or half lines as metric spaces. By the structure theory of \({{\,\mathrm{RCD}\,}}\) spaces, the tangent is unique and a line for \({\mathfrak {m}}_Z\)-a.e. \(z\in B_1^Z(z_0)\). Moreover, by the noncollapsing assumption, at points where there is a line in the tangent the tangent is unique, since they correspond to points on the starting space where the tangent is \({\mathbb {R}}^N\).
Adapting the arguments of [63] (see also [84] for a recent generalization with simplified arguments relying on optimal transport tools), it is possible to prove that at points of Z where there is a line in the tangent there is a small ball isometric to the Euclidean one. Moreover, at the other points the tangent is still unique and isometric to a half line pointed at the extreme (otherwise there would be a full line in the tangent and we would be in the previous case). Arguing as in the proof of [84, Theorem 3.1] we conclude that each point in Z has a neighborhood isometric either to \((-\varepsilon ,\varepsilon )\) or to \([0,\varepsilon )\). Hence the metric conclusion follows from the characterization of one dimensional Riemannian manifolds.
The conclusion about the measure can be achieved relying on the fact that
is an isomorphism of metric measure spaces and the measure on \((X,{\mathsf {d}})\) is \({\mathscr {H}}^N\).
The last conclusion in the statement can be easily proved given the previous ones. \(\square \)
Remark 3.7
The converse of Theorem 3.4 is trivially verified. Indeed, if the space is locally isomorphic to a product with Euclidean factor then the coordinates of the Euclidean factor are easily seen to verify properties (i)–(iii).
3.2 \(\delta \)-Splitting maps and \(\varepsilon \)-GH isometries
Arguing by compactness we now obtain an approximated version of Theorem 3.4. As in the rigid case the novelty with respect to the literature of \({{\,\mathrm{RCD}\,}}\) spaces is the ease of producing locality of the statement, cf. with [17]. We refer to [31, Lemma 1.21] and [29, Theorem 4.11] for similar statements for Ricci limits.
Theorem 3.8
(\(\delta \)-splitting vs \(\varepsilon \)-GH isometry) Let \(1\le N<\infty \) be fixed.
-
(i)
For every \(0<\delta <1/2\) and \(\varepsilon \le \varepsilon (N,\delta )\) the following holds. If \((X,{\mathsf {d}},{\mathfrak {m}})\) is an \({{\,\mathrm{RCD}\,}}(-\varepsilon (N-1),N)\) m.m.s. satisfying
$$\begin{aligned} {\mathsf {d}}_{mGH}(B_2(p),B_2^{{\mathbb {R}}^k\times Z}(0,z))\le \varepsilon \end{aligned}$$(3.29)for some integer k, some \(p\in X\) and some pointed m.s. \((Z,{\mathsf {d}}_Z)\), then there exists a \(\delta \)-splitting map \(u=(u_1,\ldots ,u_k):B_1(p)\rightarrow {\mathbb {R}}^k\).
-
(ii)
For every \(\varepsilon >0\) and \(\delta < \delta (N,\varepsilon )\) the following holds. If \((X,{\mathsf {d}},{\mathfrak {m}})\) is a normalised \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) m.m.s. and there exists a \(\delta \)-splitting map \(u:B_6(p)\rightarrow {\mathbb {R}}^k\) for a given \(p\in X\), then
$$\begin{aligned} {\mathsf {d}}_{GH}(B_{1/k}(p),B^{{\mathbb {R}}^k\times Z}_{1/k}(0,z))< \varepsilon \end{aligned}$$(3.30)for some pointed metric space \((Z,{\mathsf {d}}_Z,z)\). Moreover, there exists \(f:B_{1}(p)\rightarrow Z\) such that
$$\begin{aligned} (u-u(p),f):B_{1/k}(p)\rightarrow B_{1/k}^{{\mathbb {R}}^k\times Z}(0,z) \quad \text {is an }\varepsilon \text {-GH isometry.\qquad } \end{aligned}$$(3.31) -
(iii)
If we additionally assume that \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) noncollapsed with \({\mathscr {H}}^N(B_1(p))>v>0\), \(k=N-1\), and \(\delta <\delta (N,v,\varepsilon )\), then \((Z,{\mathsf {d}}_Z,{\mathscr {H}}^1)\) in (ii) can be chosen to be the ball of a one dimensional Riemannian manifold, possibly with boundary.
Proof
The first part of the statement can be proved arguing as in the proof of [17, Proposition 3.9], relying on the local convergence and stability results obtained in [8].
Let us now prove the second conclusion. Arguing by contradiction, for any \(n\in {\mathbb {N}}\), we can find a normalised pointed \({{\,\mathrm{RCD}\,}}(-1/n,N)\) m.m.s. \((X_{n},{\mathsf {d}}_n,{\mathfrak {m}}_n,p_n)\) and a 1/n-splitting map \(u_n:B_6(p_n)\rightarrow {\mathbb {R}}^k\) such that \(u_n(p_n)=0\) and the following property holds: for any pointed metric space \((Z,{\mathsf {d}}_Z,z)\) and any function \(f:B_{1/k}(p_n) \rightarrow B_{1/k}^Z(z)\), the map
Thanks to the stability and compactness of the \({{\,\mathrm{RCD}\,}}\) condition we can find a pointed \({{\,\mathrm{RCD}\,}}(0,N)\) m.m.s. \((X_{\infty },{\mathsf {d}}_{\infty },{\mathfrak {m}}_{\infty },p_{\infty })\) such that, up to extract a subsequence (that we do not relabel), it holds
Arguing as in [17, Proposition 3.7] we can assume that \(u_n\rightarrow u\) uniformly in \(B_6(p_{\infty })\), where u is a C(N)-Lipschitz and harmonic function in \(B_6(p_{\infty })\) satisfying \(\nabla u_a\cdot \nabla u_b=\delta _{ab}\), \({\mathfrak {m}}_{\infty }\)-a.e. in \(B_2(p_{\infty })\) for \(a,b=1,\ldots ,k\). Thanks to Theorem 3.4 we can find a m.s. \((Z,{\mathsf {d}}_Z)\) and a function \(f:B_{1/k}(p_{\infty })\rightarrow Z\) such that
Let us conclude the proof by showing that (3.34) contradicts (3.32). Let us consider a sequence of 1/n-isometries \(\Psi _n:B_{1/k}(p_n)\rightarrow B_{1/k}(p_{\infty })\). By [87, Lemma 27.4] we can suppose that \(\Psi _n\) converge to an isometry from \(B_{1/k}(p_{\infty })\) into itself. Up to composing with the inverse of this isometry we assume that the maps \(\Psi _n\) converge to the identity map of \(B_{1/k}(p_{\infty })\). Set \(f_n:= f\circ \Psi _n\). Next we claim that
which will contradict (3.32) yielding the sought conclusion.
Being f continuous (actually 1-Lipschitz since (u, f) is an isometry with its image), one can easily prove that \((u_n,f_n)\rightarrow (u,f)\), therefore the image of \((u_n,f_n)\) is \(\varepsilon \)-dense in \(B_{1/k}^{{\mathbb {R}}^k\times Z}((0,z))\) for any n big enough. It remains just to check that
when n is big enough. We argue by contradiction. If the conclusion were false we could find sequences \((x_n)\) and \((y_n)\) in \(B_{1/k}(p_n)\) such that the defining condition of \(\varepsilon \)-isometries does not hold for these points, i.e.
By compactness, up to extracting a subsequence that we do not relabel, we can assume that \(x_n\) converge to \(x\in B_{1/k}(p_{\infty })\) and \(y_n\) converge to \(y\in B_{1/k}(p_{\infty })\). It is easily verified that \(x\ne y\), thanks to (3.37) and to the Lipschitz regularity of \(u_n\) and f. Passing to the limit (3.37), taking into account the uniform convergence of \(u_n\) to u and the convergence of \(\Psi _n\) to the identity map together with the continuity of f, we get
that contradicts (3.34).
The additional conclusion under the noncollapsing assumption can be obtained relying on Theorem 3.5. Taking into account the lower bound on the volume, the pmGH convergence in the contradiction argument above improves to noncollapsed convergence. Therefore the limit space is \({{\,\mathrm{RCD}\,}}(0,N)\) noncollapsed. \(\square \)
Remark 3.9
When \((X,{\mathsf {d}}, {\mathscr {H}}^N)\) is a noncollapsed \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) space satisfying \({\mathscr {H}}^N(B_1(p))>v\), then in Theorem 3.8 we can relax (3.29) to
provided \(\delta \le \delta (N,v,\varepsilon )\).
Remark 3.10
In the case of maximal dimension we can slightly improve upon the implication between \(\delta \)-splitting and \(\varepsilon \)-isometry. In particular the following holds: for any \(\varepsilon >0\) there exists \(\delta =\delta (\varepsilon ,N)>0\) such that if \((X,{\mathsf {d}},{\mathfrak {m}})\) is an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) space, \(B_{3/2}(p)\subset X\),
and \(u:B_1(p)\rightarrow {\mathbb {R}}^N\) is a \(\delta \)-splitting map, then \(u:B_1(p)\rightarrow {\mathbb {R}}^N\) is an \(\varepsilon \)-isometry.
The same statement holds for splitting maps with \(N-1\) components in case we put \({\mathbb {R}}^N_+\) in place of \({\mathbb {R}}^N\).
This statement can be proved relying on the local convergence and stability results of [8], taking into account the fact that local spectral convergence holds for all radii when the limit space is the Euclidean space (or, more in general, a metric measure cone).
Notice that the main improvement is that we do not need to worsen the radius to pass from the \(\delta \)-splitting condition to the \(\varepsilon \)-isometry. Moreover we can allow not only for harmonic \(\delta \)-splitting functions but also for functions with small Laplacian in \(L^2(B_1(p))\), cf. with Definition 3.11 below.
For the study of the topological structure of \({{\,\mathrm{RCD}\,}}\) spaces with boundary in section 9 we will need a slightly less restrictive notion of \(\delta \)-splitting map.
Definition 3.11
Fix \(\delta >0\). Let \((X,{\mathsf {d}},{\mathfrak {m}})\) be an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) m.m.s. and \(p\in X\). We say that \(u:=(u_1,\ldots ,u_k) :B_r(p)\rightarrow {\mathbb {R}}^k\) is a \(\delta \)-almost splitting map provided it satisfies
-
(i)
\(|\nabla u_a|< C(N)\);
-
(ii)
 (3.41)
(3.41)
Arguing as in Remark 3.2 one can easily check through Bochner’s inequality that a \(\delta \)-almost splitting map \(u: B_{2r}(p)\rightarrow {\mathbb {R}}^k\) satisfies

Therefore, the only meaningful difference between the notion of \(\delta \)-splitting map and \(\delta \)-almost splitting map is that the latter is not harmonic but enjoys a scale invariant \(L^2\)-smallness of the Laplacian.
Remark 3.12
It is immediately seen that Theorem 3.8 and Remark 3.10 still hold when relaxing the assumptions by considering \(\delta \)-almost splitting maps in place of \(\delta \)-splitting maps.
3.3 Transformation theorem
In [31] a key result in order to prove the codimension 4 conjecture for noncollapsed limits of manifolds with bounded Ricci curvature was the so-called transformation theorem. Given an \((N-2,\delta (\varepsilon ))\)-splitting map \(u:B_1(p)\rightarrow {\mathbb {R}}^{N-2}\), [31, Theorem 1.32] provides conditions guaranteeing the existence of a lower triangular matrix with positive entries \(T_r\) such that \(T_ru:B_r(x)\rightarrow {\mathbb {R}}^{N-2}\) is an \((N-2,\varepsilon )\)-splitting map for \(0<r<1\).
In [29] (see in particular Proposition 7.8) a geometric version of the transformation theorem was proved, in order to study singular strata of any codimension on Ricci limits. In particular, the weak version of the estimate proven in [29] was that given a \((k,\delta )\)-splitting map on \(B_1(p)\), there is a lower triangular matrix with positive entries \(T_r\) such that \(T_ru:B_r(x)\rightarrow {\mathbb {R}}^k\) remains \((k,\varepsilon )\)-splitting as long as \(B_s(p)\) is k-symmetric and far from being \((k+1)\)-symmetric, for any \(r\le s \le 2\).
Here we provide a version of the geometric transformation theorem tailored for the purpose of studying the structure of noncollapsed \({{\,\mathrm{RCD}\,}}\) spaces with boundary. We focus the attention only on \(\delta \)-boundary balls (see Definition 4.1) and \((N,\delta )\)-symmetric balls (corresponding to \(k=n-1,n\) in [29]) and, for technical reasons, we work with possibly non harmonic \(\delta \)-splitting maps (cf. with Definition 3.11) rather than harmonic \(\delta \)-splitting maps. Up to these small variants the argument presented here is the one from [29].
Proposition 3.13
(Transformation) Let \(1\le N<\infty \) be a fixed natural number. For any \(\varepsilon >0\) there exists \(\delta (N,\varepsilon )>0\) such that for any \(\delta <\delta (N,\varepsilon )\), for any \({{\,\mathrm{RCD}\,}}(-\delta ^2(N-1),N)\) space \((X,{\mathsf {d}},{\mathscr {H}}^N)\), for any \(x\in X\) and \(0<r_0<1\) the following hold.
-
If \(B_s(x)\) is a \(\delta ^2\)-boundary ball for any \(r_0\le s\le 1\) and \(u:B_2(x)\rightarrow {\mathbb {R}}^{N-1}\) is a \(\delta \)-almost splitting map, then for each scale \(r_0\le s\le 1\) there exists an \((N-1)\times (N-1)\) lower triangular matrix \(T_{s}\) such that
-
(i)
\(T_su:B_s(x)\rightarrow {\mathbb {R}}^{N-1}\) is an \(\varepsilon \)-almost splitting map on \(B_s(x)\);
-
(ii)
 ;
; -
(iii)
\(\left|T_s\circ T_{2s}^{-1}-\mathrm {Id}\right|\le \varepsilon \).
-
(i)
-
If \(B_s(x)\) is an \((N,\delta ^2)\)-symmetric ball for any \(r_0\le s\le 1\) and \(u:B_2(x)\rightarrow {\mathbb {R}}^{N}\) is a \(\delta \)-almost splitting map, then for each scale \(r_0\le s\le 1\) there exists an \(N\times N\) lower triangular matrix \(T_{s}\) such that
-
(i)
\(T_su:B_s(x)\rightarrow {\mathbb {R}}^{N}\) is an \(\varepsilon \)-almost splitting map on \(B_s(x)\);
-
(ii)
 ;
; -
(iii)
\(\left|T_s\circ T_{2s}^{-1}-\mathrm {Id}\right|\le \varepsilon \).
-
(i)
We postpone the proof of the transformation Proposition 3.13 after some technical lemmas. The first one is about the very rigid form of harmonic functions with almost linear growth on the Euclidean space and half-space. It can be easily proved thanks to the explicit knowledge of entire harmonic functions (cf. with [29, Lemma 7.8], dealing with a much more general case) and we omit the details.
Lemma 3.14
Let \(1\le N<\infty \) be a fixed natural number, then there exists \(\varepsilon =\varepsilon (N)>0\) such that the following holds. Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be isomorphic either to the Eucildean space \({\mathbb {R}}^N\) or to the half-space \({\mathbb {R}}^N_+\). Then any harmonic function \(u:X\rightarrow {\mathbb {R}}\) with almost linear growth, \(\left|u(x)\right|\le C\left|x\right|^{1+\varepsilon }+C\) for any \(x\in X\), is linear and induced by an \({\mathbb {R}}\) factor.
The second lemma is about estimates for the transformation matrixes, given their existence. We refer to [29, Lemma 7.9] for its proof, which is a simple inductive argument relying on the uniqueness of Cholesky decompositions [51].
Below we shall denote by \(\left|\cdot \right|_{\infty }\) the \(L^{\infty }\)-norm on matrixes.
Lemma 3.15
Under the assumptions of Proposition 3.13, there exists a constant \(C=C(N)>0\) such that, if \(T_{s}\) and \(T_{2s}\) are matrixes verifying (i) and (ii) at scale s and 2s respectively, then automatically
Given Lemma 3.15 and arguing inductively as in [29] it is then possible to prove a growth estimate for the transformation matrixes, once we assume that they exist.
Corollary 3.16
Under the assumptions of Proposition 3.13, there exists a constant \(C=C(N)>0\) such that, if \(T_{\bar{r}}\) and \(T_{r}\) are matrixes verifying (i) and (ii) at scales \(0<\bar{r}<r\) respectively, then
Proof of Proposition 3.13
Let us treat first the second case of \((N,\delta ^2)\)-symmetric balls. Observe also that we only need to prove (i) and (ii), since (iii) will follow from Lemma 3.15.
We wish to get the sought conclusion arguing by contradiction. We suppose that there exists \(0<\varepsilon _0\ll 1\) such that the following hold:
-
(a)
there exist pointed \({{\,\mathrm{RCD}\,}}(-\delta _i,N)\) spaces \((X_n,{\mathsf {d}}_n,{\mathscr {H}}^N,x_n)\) such that the balls \(B_r(x_n)\) are \((N,\delta _i^2)\)-symmetric for any \(r_n\le r\le 1\), and \(\delta _n\)-almost splitting maps \(u_n:B_2(x_n)\rightarrow {\mathbb {R}}^N\), for a sequence \(\delta _n\downarrow 0\);
-
(b)
there exist \(s_n>r_n\) such that for any \(s_n<r\le 1\) there exist lower triangular matrixes \(T_{x_n,r}\) such that \(T_{x_n,r}u:B_r(x_n)\rightarrow {\mathbb {R}}^{N}\) is an \(\varepsilon _0\)-splitting map on \(B_r(x_n)\) and
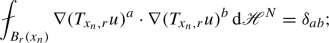 (3.44)
(3.44) -
(c)
no such mapping \(T_{x_n,s_n/10}\) exists on \(B_{s_n/10}(x_i)\).
Let us start by noticing that it must hold \(s_{n}\downarrow 0\) as \(n\rightarrow \infty \), otherwise we would easily reach a contradiction.
Then let us consider the scaled pointed spaces \({\tilde{X}}_n:=(X_n,s_n^{-1}{\mathsf {d}}_n,{\mathscr {H}}^N,x_n)\). Observe that, since \(B^{X_n}_r(x_n)\) is \((N,\delta _n)\)-symmetric for any \(r_i\le r\le 1\), on the scaled space it holds that \(B_{r}^{{\tilde{X}}_n}(x_n)\) is \((N,\delta _n)\)-symmetric for any \(r_n/s_n\le 1\le r\le s_n^{-1}\). Since \(s_n\rightarrow 0\) as \(n\rightarrow \infty \), we infer that \({\tilde{X}}_n\) converge to \({\mathbb {R}}^N\) in the pGH (and a posteriori pmGH) topology.
Let us now set
Observe that

thanks to Corollary 3.16 and the fact that \(u_n\) is a \(\delta _n\)-almost splitting map ( cf. Definition 3.11 (ii)). Moreover \(v_n\) has almost linear growth, \(\left|v_n(x)\right|\le C{\mathsf {d}}(x_n,x)^{1+\varepsilon }+C\) for any x such that \({\mathsf {d}}(x_n,x)\le s_n^{-1}\), thanks to Corollary 3.16, and it verifies

by (3.44).
By [8] and (3.46) we obtain that \(v_n\) converge locally in \(W^{1,2}\) and locally uniformly to a harmonic function \(v:{\mathbb {R}}^N\rightarrow {\mathbb {R}}^N\) with almost linear growth. Passing to the limit (3.47) and taking into account Lemma 3.14, we get that v is an orthogonal transformation of \({\mathbb {R}}^N\).
Localizing the \(W^{1,2}\)-convergence (see [7, Theorem 1.5.7, Proposition 1.3.3.]), we obtain

Therefore, taking into account also (3.46), we infer that \(v_i:B_1^{{\tilde{X}}_n}(x_n)\rightarrow {\mathbb {R}}^N\) becomes an \(\varepsilon _n\)-almost splitting map where \(\varepsilon _n\rightarrow 0\) as \(n\rightarrow \infty \).
Hence for each \(1/10\le r\le 1\) and any sufficiently large n there exists a lower triangular \(N\times N\) matrix \(A_{n,r}\) with \(\left|A_{n,r}-\mathrm {Id}\right|\le C(N)\varepsilon _n\) and

In particular, for any sufficiently large n, \(A_{n,r}v_n:B_r^{{\tilde{X}}_n}(x_n)\rightarrow {\mathbb {R}}^N\) is an \(\varepsilon _0\)-splitting map for any \(1/10\le r\le 1\) satisfying the orthogonality condition (ii) in the statement. This contradicts the minimality of \(s_i\) (cf. with condition (c)), scaling back to the starting spaces \(X_n\). This finishes the proof of the existence of transformation matrixes, the growth estimate (iii) can be obtained by Lemma 3.15, as we already argued.
The case of boundary balls can be handled by the very same argument. The only difference is that the sequence \({{\tilde{X}}}_n\) converges in the pmGH topology to the Euclidean half space \({\mathbb {R}}^N_+\), instead of \({\mathbb {R}}^N\). As before, we pass to the limit in the sequence \(v_n\) to get a harmonic function \(v: {\mathbb {R}}^N_+ \rightarrow {\mathbb {R}}^{N-1}\). Then we apply Lemma 3.14 to infer that v is linear and depends only on the Euclidean factor \({\mathbb {R}}^{n-1}\). \(\square \)
4 Neck regions
This section is dedicated to the introduction and the analysis of neck regions. We first provide the relevant definition tailored for the study of singularities of codimension one for noncollapsed \({{\,\mathrm{RCD}\,}}\) spaces. Then in Sects. 4.1 and 4.2 we provide structural results for neck regions and an existence result, respectively.
The notion of neck region has been introduced in [56, 72] to study \(L^2\)-curvature bounds for spaces with bounded Ricci curvature and the energy identity for Yang–Mills connections. Its use has been crucial also in [71] and, more recently, in [29], for the rectifiability of singular sets in arbitrary codimension on noncollapsed Ricci limits.
In the following we shall denote by \({\mathbb {R}}_+^N:=\{x\in {\mathbb {R}}^N:\ x_N\ge 0\}\) the Euclidean half space of dimension \(N\ge 1\).
Definition 4.1
(Boundary ball) Let \(1\le N<\infty \) and \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be an \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) metric measure space. Given \(x\in X\) and \(r>0\) we say that \(B_r(x)\) is a \(\delta \)-boundary ball if it is \(\delta r\)-GH close to \(B_r^{{\mathbb {R}}_+^N}(0)\).
Given a \(\delta \)-boundary ball \(B_1(x)\) and a \(\delta \)-isometry \(\Psi : B_1^{{\mathbb {R}}_+^N}(0)\rightarrow B_1(x)\) we set
When \(B_{r}(x)\) is a \(\delta \)-boundary ball we will consider the approximate singular set \({\mathcal {L}}_{x,r}\) that can be introduced in the analogous way.
Remark 4.2
The following property is an easy consequence of definitions. Given a \(\delta \)-boundary ball \(B_1(x)\), a \(\delta \)-isometry
and \(y\in {\mathcal {L}}_{x,1}\), any ball \(B_s(y)\subset B_r(x)\) is a \(\delta s^{-1}\)-boundary ball.
We now introduce the relevant notion of a neck region for this paper:
Definition 4.3
(Neck region) Fix \(\varepsilon ,\delta \in (0,1/2)\), an integer \(N\ge 1\) and \(\tau :=10^{-10N}\). Let \((X,{\mathsf {d}},{\mathscr {H}}^N,p)\) be a pointed noncollapsed \({{\,\mathrm{RCD}\,}}(-\varepsilon (N-1),N)\) metric measure space. We say that \({\mathcal {N}}\subset B_2(p)\) is an \((\varepsilon ,\delta )\)-neck region if there exist a closed set \({\mathcal {C}}\subset B_1(p)\) and a function \(r:{\mathcal {C}}\rightarrow [0, 1/8]\) such that \({\mathcal {N}}:=B_2(p){\setminus } \cup _{x\in {\mathcal {C}}}\bar{B}_{r_x}(x)\) and, setting \({\mathcal {C}}_0:=\{x\in {\mathcal {C}}:\ r_x=0\}\) and \({\mathcal {C}}_+:={\mathcal {C}}{\setminus }{\mathcal {C}}_0\), the following hold:
-
(i)
the family \(\{\bar{B}_{\tau ^2 r_x}(x)\}_{x\in {\mathcal {C}}}\subset B_2(p)\) is disjoint;
-
(ii)
for any \(x\in {\mathcal {C}}\) and \(r_x\le r\le \tau ^{-3}\), \(B_r(x)\) is an \(\varepsilon ^2\)-boundary ball, i.e. there exists an \(\varepsilon ^2 r\)-GH isometry
$$\begin{aligned} \Psi _{x,r}: B_r^{{\mathbb {R}}_+^N}(0)\rightarrow B_r(x); \end{aligned}$$(4.2) -
(iii)
setting \({\mathcal {L}}_{x,r}:=\Psi _{x,r}(\{x_N=0\})\)
$$\begin{aligned} {\mathcal {C}}\cap B_r(x)\subset B_{2\varepsilon r}({\mathcal {L}}_{x,r}) \quad \text {and}\quad {\mathcal {L}}_{x,r}\cap B_r(x)\subset B_{10^3 \tau r}({\mathcal {C}}) \end{aligned}$$(4.3)for any \(x\in {\mathcal {C}}\) and \(r_x< r < \tau ^{-3}\);
-
(iv)
there exists a \(\delta ^4\)-splitting map \(u:B_{\tau ^{-4}}(p)\rightarrow {\mathbb {R}}^{N-1}\) such that, for any \(x\in {\mathcal {C}}\) and \(r_x< r <\tau ^{-3}\) it holds that
$$\begin{aligned} u:B_r(x)\rightarrow {\mathbb {R}}^{N-1} \quad \text {is a }\delta \text {-splitting map } \end{aligned}$$(4.4)and
 (4.5)
(4.5)
Remark 4.4
In fact, it will follow from the construction that \({{\,\mathrm{Lip}\,}}r_x\le \tau ^2\).
As in [29, 56] we introduce the packing measure as an approximation of the Hausdorff measure restricted to the top dimensional singular stratum.
Definition 4.5
Given any neck region \({\mathcal {N}}=B_2(p){\setminus } \cup _{x\in {\mathcal {C}}}\bar{B}_{r_x}(x)\) we shall denote by \(\mu \) the associated packing measure defined by

Remark 4.6
Informally, a neck region \({\mathcal {N}}:=B_2(p){\setminus } \cup _{x\in {\mathcal {C}}}\bar{B}_{r_x}(x)\) is the portion of the boundary ball \(B_2(p)\) that we are able to control at any scale and location. It comes with a closed set \({\mathcal {C}}\), which approximates the boundary of the space, and good harmonic splitting maps \(u: B_2(p)\rightarrow {\mathbb {R}}^{N-1}\). Any ball centered at \(x\in {\mathcal {C}}\) with radius \(r> r_x\) looks like a ball in the Euclidean half space, and \(u: B_r(x) \rightarrow {\mathbb {R}}^{N-1}\) is a \(\delta \)-splitting map.
The union of balls \(\{\bar{B}_{r_x}(x)\, : \, x\in {\mathcal {C}}_+\}\) is the set where we are not able to control neither the space nor the harmonic splitting functions. A fundamental step in our work is to prove that \(\cup _{x\in {\mathcal {C}}}\bar{B}_{r_x}(x)\) is small (cf. Theorem 4.13).
The packing measure \(\mu \) has to be understood as an approximation of the volume measure of the boundary.
Let us explain the meaning of each item in Definition 4.3. Condition (i) guarantees that we do not overly cover the bad set. Conditions (ii) and (iii) play the role of a Reifenberg condition on the singular set, still they are not sufficient alone to prove rectifiability, which requires the combination with (ii) and (iv). Condition (iv) says that \(u: B_2(p) \rightarrow {\mathbb {R}}^{N-1}\) is well-behaved on any ball \(B_{r}(x)\), where \(x\in {\mathcal {C}}\) and \(r>r_x\).
Remark 4.7
With respect to the notions of neck region adopted in [29, 56] here we chose to put the harmonic \(\delta \)-splitting map directly into the definition. Building \(\delta \)-splitting maps that control the geometry of neck regions requires a great amount of efforts and several ideas in codimension greater or equal than two, as in [29, 56]. Here instead we heavily rely on the fact that we are working in codimension one and the \(L^2\)-Hessian bounds for harmonic \(\delta \)-splitting maps propagate well thanks to a weighted maximal function argument, as pointed out in [31].
Remark 4.8
It follows from Colding’s volume convergence theorem [37, Theorem 1.3] (see also [28, 32]) that there exists a function \(\Psi :=\Psi (\varepsilon ,N)\) depending only on N and going to 0 as \(\varepsilon \rightarrow 0\) such that, if \(B_r(x)\) is an \(\varepsilon \)-boundary ball, then
In particular, if \({\mathcal {N}}=B_2(p){\setminus }\cup _{x\in {\mathcal {C}}}\bar{B}_{r_x}(x)\) is an \((\varepsilon ,\delta )\)-neck region, then (4.7) holds for any \(x\in {\mathcal {C}}\) and for any \(r_x\le r\le \tau ^{-3}\).
4.1 Structure of neck regions
The aim of this subsection is to prove a structure theorem for neck regions, its relevance will be clear after Sect. 4.2 where we are going to prove that neck regions can be built on any ball sufficiently close to a ball of the model half-space.
Let us recall that the main goal of the present paper is to prove rectifiability and measure bounds for the singular stratum of codimension one on noncollapsed \({{\,\mathrm{RCD}\,}}\) spaces together with stability under noncollapsing convergence. In this regard Theorem 4.9 is a key building block since, together with Theorem 4.13, it tells that our desired properties hold, up to a controlled error, on balls close to the model ball.
Theorem 4.9
(Neck structure theorem) Let \(N\in {\mathbb {N}}\), \(v>0\), \(0<\varepsilon <1\) be fixed, and let \(\eta <\eta (N,\varepsilon )\) and \(\delta <\delta (N,v,\varepsilon )\). Then for any \((\eta ,\delta )\)-neck region \({\mathcal {N}}=B_2(p){\setminus } {\overline{B}}_{r_x}({\mathcal {C}})\) of an \({{\,\mathrm{RCD}\,}}(-\eta (N-1),N)\) space \((X,{\mathsf {d}},{\mathscr {H}}^N)\) satisfying \({\mathscr {H}}^N(B_1(p))\ge v\) it holds that:
-
(i)
\(u:{\mathcal {C}}\rightarrow {\mathbb {R}}^{N-1}\) is bi-Lipschitz with its image, more precisely
$$\begin{aligned} ||u(x)-u(y)|-{\mathsf {d}}(x,y)|\le \varepsilon {\mathsf {d}}(x,y) \quad \text {for any }x,y\in {\mathcal {C}}, \end{aligned}$$(4.8)where \(u:B_{\tau ^{-4}}(p)\rightarrow {\mathbb {R}}^{N-1}\) is as in Definition 4.3 (iv);
-
(ii)
there exists \(c=c(N)\ge 1\) such that, denoting by \(\mu \) the packing measure as in (4.6), we have
$$\begin{aligned} c^{-1}r^{N-1}\le \mu (B_r(x))\le c r^{N-1} \quad \text {for any }x\in {\mathcal {C}}\text { and }r_x \le r\le 2; \end{aligned}$$(4.9) -
(iii)
at any \(x\in {\mathcal {C}}_0\) the tangent cone is unique and isometric to \({\mathbb {R}}_+^N\).
Remark 4.10
Let us comment on the different parts of the statement of Theorem 4.9.
The combination of points (i) and (ii) is the analogue of [56, Theorem 3.10] and [29, Theorem 2.9]. Together with the existence of neck regions and the neck decomposition theorem it can be summed up to obtain rectifiability of the top dimensional singular stratum and measure estimates.
Point (iii) has an analogue in the context of lower Ricci bounds for the codimension two stratum [29] and in the context of two sided Ricci bounds for the codimension four stratum [56], where the tangent cones are also uniquely determined by the neck structure. There is no analogue in case of general stratum under a lower Ricci bound [29] however, where uniqueness of symmetries holds in the neck region but not of the whole tangent cone.
In order to provide the reader with an intuition about the notion of neck region and about the neck structure theorem, we present two elementary examples below. They are the counterparts of [29, Example 2.11, Example 3.1] in the present context.
Example 4.11
(Simplest) Let \((X,{\mathsf {d}},{\mathscr {H}}^N)=({\mathbb {R}}^N_+,{\mathsf {d}}_{\mathrm {eucl}},{\mathscr {H}}^N)\) be the Euclidean half-space. Let \(u:{\mathbb {R}}^N_{+}\rightarrow {\mathbb {R}}^{N-1}\) be the map whose components are the coordinates of the \({\mathbb {R}}^{N-1}\) factor of \({\mathbb {R}}^{N}_+={\mathbb {R}}^{N-1}\times {\mathbb {R}}_+\). Let \({\mathcal {C}}\subset B_2(0^{N-1})\times \{0\}\) be any closed subset and \(r:{\mathcal {C}}\rightarrow [0,1/8]\) be any function with \({{\,\mathrm{Lip}\,}}r\le \tau ^2\) and such that the family \(\{\bar{B}_{\tau ^2 r_x}(x)\}_{x\in {\mathcal {C}}}\subset B_2(0^N)\) is disjoint. Then it is straightforward to check that \({\mathcal {N}}:=B_2(p){\setminus } \cup _{x\in {\mathcal {C}}}\bar{B}_{r_x}(x)\) is a (0, 0)-neck region with associated splitting map u.
Notice that in this case the rectifiability and the Ahlfors regularity of the packing measure follow since \({\mathcal {C}}\subset {\mathbb {R}}^{N-1}\) canonically and \(\{B_{\tau r_x}(x)\}\) form a Vitali covering. Moreover, if one looks for a maximal neck region the natural choice in this case would be to consider \({\mathcal {C}}= B_2(0^{N-1})\times \{0\}\) and \(r\equiv 0\).
Example 4.12
(Conical) A less elementary example of neck region can be constructed considering a conical singularity.
If we denote by \(I_t\) the closed interval of length \(0<t\le \pi \), then the cone \(C(I_r)\) endowed with cone distance and Hausdorff measure \({\mathscr {H}}^2\) is an \({{\,\mathrm{RCD}\,}}(0,2)\) space with boundary. For \(t=\pi \) we obtain a half-space, while for \(0<t<\pi \) it corresponds to a convex region inside \({\mathbb {R}}^2\) with boundary \(\partial C(I_t)\) and a singularity at the origin \(0\in C(I_t)\).
If \(\pi -t<\varepsilon ^2\) then we can find a harmonic \(\delta ^4\)-splitting map \(u:B_{\tau ^{-4}}(0)\rightarrow {\mathbb {R}}\), thanks to Theorem 3.8. A first important difference with the previous elementary situation is that \(\left|\nabla u(x)\right|\rightarrow 0\) as \({\mathsf {d}}(x,0)\rightarrow 0\). Therefore u cannot remain \(\delta \)-splitting at all scales \(r>0\) on \(B_r(0)\).
Nevertheless, if we consider \(\pi -t<\varepsilon ^2\), choose any \(\tau ^2\)-Lipschitz function \(r:\partial C(I_t)\rightarrow [0,1/8]\) such that \(r(0)>\varepsilon \) and any closed set \({\mathcal {C}}\subset \partial C(I_t)\) such that \(\{B_{\tau ^2r_x}(x)\}\) is a disjoint family, then it is possible to check that \({\mathcal {N}}:=B_2(0){\setminus } \cup _{x\in {\mathcal {C}}}\bar{B}_{r_x}(x)\) is an \((\varepsilon ,\delta )\)-neck region.
The construction can be generalized to any dimension by taking the product with \({\mathbb {R}}^{N-2}\).
Proof of Theorem 4.9
(i). Let us fix \(x,y\in {\mathcal {C}}\) and set \(r:= (2\tau ^2)^{-1}{\mathsf {d}}(x,y)\). Assuming without loss of generality that \(r_y\ge r_x\), we have \(r_x<r<\tau ^{-3}\) as a consequence of (i) in Definition 4.3. Therefore, by (iv) in Definition 4.3
Let \(\varepsilon '<\varepsilon \) to be fixed later. Assuming \(\delta <\delta (\varepsilon ',N)\), Theorem 3.8 yields the existence of a one dimensional manifold \((Z,{\mathsf {d}}_Z,z)\) and a function \(f:B_{2{\mathsf {d}}(x,y)}(x)\rightarrow Z\) such that
is a \(2{\mathsf {d}}(x,y) \varepsilon '\text {-GH isometry}\). Since \(2{\mathsf {d}}(x,y)\ge \tau ^2r_x\), taking into account Definition 4.3 (ii) and Remark 4.2 we know that \(B_{2{\mathsf {d}}(x,y)}(x)\) is a \(\tau ^{-2}\eta \)-boundary ball. Therefore the triangle inequality gives
Hence, choosing \(\eta ,\varepsilon ' \le \varepsilon (N)\), we can apply Lemma 4.15 below concluding that
is a \(2\mathsf{d}(x,y)\varepsilon \)’-GH isometry. In order to get (i) it suffices to check that
Indeed (4.14), when plugged in the defining condition of GH-isometries
gives the sought conclusion provided \(\varepsilon ', \eta \le C(\varepsilon ,N)\).
To check (4.14) we rely on (iii) in Definition 4.3. Set \(s:=\frac{3}{2}{\mathsf {d}}(x,y)\) to ease notation and recall that \(2\tau ^{-2}s\ge r_x\). Observe that
therefore Lemma 4.15 gives
By (iii) in Definition 4.3\({\mathcal {C}}\,{\cap }\, B_{2\tau ^{-2}s}(x) \,{\subset }\, B_{10 \eta \tau ^{-2} s}(\Psi _{x,2\tau ^{-2}s}(\{x_N=0\}))\), we conclude that
yielding (4.14).
(ii). We begin by showing that
Fix \(z\in {\mathcal {C}}\) and \(r_z<r<2\). Recall that by i) in Definition 4.3,
In view of (i) we know that \(u:B_r(z)\cap {\mathcal {C}}\rightarrow B_{3r}(u(z))\) is a \((1+\varepsilon )\)-Lipschitz map, therefore
and
Then we can estimate
Let us now show the opposite inequality:
Observe that, by the very definition of packing measure (4.6), it is sufficient to verify (4.21) for radii r such that \(r_z<r<2\).
Let us fix \(z\in {\mathcal {C}}\) and \(r_z<r<2\) as above. It suffices to prove that
Indeed (4.22) gives
Let us check (4.22) arguing by contradiction. Set for simplicity \(u(z)=0\). If the conclusion is false we can find \(w\in B_{r/8}(0)\) such that \(w\notin {\bar{B}}_{r_x}(u(x))\) for any \(x\in {\mathcal {C}}\cap {\bar{B}}_r(z)\). Then we can set
Observe that, by the very definition of s, it holds that \(r/8>s=s_x>r_x\) for some \(x\in {\mathcal {C}}\cap {\bar{B}}_r(z)\). Therefore the ball \(B_s(x)\) is an \(\eta \)-boundary ball and \(u:B_{s}(x)\rightarrow {\mathbb {R}}^{N-1}\) is \(\delta \)-splitting. Hence, arguing as in the first part of the proof, we can complete u to an \(s\varepsilon '\)-GH isometry
provided \(\delta < \delta (N,\varepsilon ')\), for some \(\varepsilon '<1/8\). Since \((w,0)\in {\bar{B}}_s^{{\mathbb {R}}_+^N}((u(x),0))\) we can find \(y\in {\mathcal {L}}_{x,s}\) such that \(|u(y)-w|\le 2s \varepsilon '\).
Moreover, thanks to the second inclusion in (iii) of Definition 4.3 there exists \(y'\in {\mathcal {C}}\cap B_{2s}(x)\) such that \({\mathsf {d}}(y,y')\le 10^3\tau s\). This implies that
since u is \((1+C(N)\sqrt{\delta } )\)-Lipschitz and \(\tau < 10^{-4}\), cf. with Remark 3.3.
We claim that \(B_{2s}(x)\subset B_r(z)\). In order to prove this claim let us first point out that
Hence, since by the result of the previous step,
we can infer that, if \(\varepsilon <\varepsilon (N)\), then \({\mathsf {d}}(x,z)<2r/4=r/2\). In particular, since we already pointed out that \(s<r/8\), we obtain that \(B_s(x)\subset B_r(z)\), as we claimed.
This gives (4.22), since (4.25) and the inclusion \(B_{2s}(x)\subset B_r(z)\) contradicts the minimality of s.
(iii). Let \((Y,\varrho ,{\mathscr {H}}^N,y)\) be a tangent cone at \(x\in {\mathcal {C}}_0\), originating from a sequence \(r_n\downarrow 0\). From (iv) in Definition 4.3 we know that there exists \(u_{\infty }: Y \rightarrow {\mathbb {R}}^{N-1}\) satisfying
-
(a)
\({{\,\mathrm{Hess}\,}}u_{\infty }=0\),
-
(b)
\(\int _{B_1(y)}|\nabla (u_{\infty })_{a} \cdot \nabla (u_{\infty })_{b}- \delta _{ab}| \mathop {}\!\mathrm {d}{\mathscr {H}}^N \le C(N)\delta \), for \(a,b=1,\ldots ,N-1\),
as a limit of the sequence
This can be easily checked with a by now standard argument, relying on the convergence and stability results of [7, 8].
By the functional splitting theorem (cf. [14, Lemma 1.20]), Y splits off a factor \({\mathbb {R}}^{N-1}\). Moreover, it is a metric cone and it is not isometric to \({\mathbb {R}}^N\), thanks to Definition 4.3 (ii). Therefore it is isometric to \({\mathbb {R}}^N_{+}\). \(\square \)
4.2 Existence of neck regions
The aim of this subsection is to prove that on any ball of a noncollapsed \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) space, which is sufficiently GH-close to the model ball on the half space
it is possible to build a neck region.
It is worth noting that, for the sake of proving stability results, it is key to construct neck regions quite carefully. If we were to build neck regions that are much smaller than they should be, then the construction would not force the presence of boundary points in \({\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\) on regions which look like half spaces.
For this reason below we are going to prove that neck regions verifying an additional maximality condition exist, once we assume closeness to the model boundary ball.
Theorem 4.13
(Existence of maximal neck regions) Let \(\tau :=10^{-10N}\), \(0<\varepsilon \le \varepsilon (N)\), \(\delta <\delta (\varepsilon ,N)\) and \(\eta <\eta (\varepsilon ,\delta ,N)\). If \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is an \({{\,\mathrm{RCD}\,}}(-\eta (N-1),N)\) m.m.s., \(p\in X\) and \(B_{4\tau ^{-4}}(p)\) is an \(\eta \)-boundary ball, then there exists an \((\varepsilon ,\delta )\)-neck region \({\mathcal {N}}=B_2(p){\setminus } \cup _{x\in {\mathcal {C}}}\bar{B}_{r_x}(x)\) on \(B_2(p)\) which additionally verifies the following maximality condition:
Remark 4.14
The combination of (4.29) with the lower Ahlfors bound in Theorem 4.9 (ii) and Theorem 4.9 (iii) implies that on \(\eta \)-boundary balls there exists a bunch of boundary points in \({\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\).
This is the starting point of our rigidity and stability and it is unique to the codimension one setting. Indeed, as it is pointed out in [29], for neck regions on smooth Riemannian manifolds, \({\mathcal {C}}_0\) is always empty (there is no singular set). Instead, the combination of (4.29) and Theorem 4.9 above provides an analytic proof of a quantitative (and more general) version of the fact, proved in [28], that smooth Riemannian manifolds with lower Ricci curvature bounds cannot converge without volume collapse to a half-space.
4.2.1 Auxiliary results
Before proving Theorem 4.13, we prove three key lemmas. The first one deals with en elementary property of one dimensional Riemannian manifolds with boundary, the second one deals with the propagation of the \(\delta \)-splitting property, the last one is the fundamental iteration step in the proof of Theorem 4.13.
Lemma 4.15
(One dimensional rigidity) There exists \(\varepsilon _0>0\) such that, if a pointed one dimensional Riemannian manifold (possibly with boundary) \((Z,{\mathsf {d}}_Z,z)\) satisfies
then there exist \(0\le a\le \varepsilon \le 1-\varepsilon \le b \le \infty \) such that \(B_1^Z(z)\) is isometric to the ball of radius one centered at \(a\in [0,b)\).
Proof
Observe that \(\partial Z \ne \emptyset \), since any ball of radius one in \({\mathbb {S}}^1(r)\) for some \(r>0\), or in \({\mathbb {R}}\) is \(\varepsilon _0\) far from \(B_1^{{\mathbb {R}}_+}(0)\), provided \(\varepsilon _0\) is small enough. This implies that Z is isometric to [0, b) for some \(b \le \infty \). It is now immediate to check that a ball of radius one in [0, b) is \(\varepsilon \)-close to \(B_1^{{\mathbb {R}}_+}(0)\) if and only if it is centered at some point \(0\le a \le \varepsilon \) and \(b\ge 1-\varepsilon \). \(\square \)
Next we give a general auxiliary result about the propagation of the \(\delta \)-splitting property. Basically, it amounts to saying that given a \(\delta \)-splitting map at a certain location and scale, the \(\delta \)-splitting property, up to slightly worsening \(\delta \), propagates if we can control the Hessian in a slightly better than scale invariant sense. We refer to [56, Lemma 5.91] and to [17] for previous appearances of this argument.
Lemma 4.16
Let \(1\le N<\infty \) be fixed. There exists \(C=C(N)>0\) such that for any \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) metric measure space \((X,{\mathsf {d}},{\mathfrak {m}})\) with \(p\in X\) the following holds. If \(u:B_2(p)\rightarrow {\mathbb {R}}^{k}\) is a \(\delta \)-splitting map with \(x\in B_1(p)\) such that

then \(u: B_s(x)\rightarrow {\mathbb {R}}^{k}\) is a \(C(N)\delta ^{1/4}\)-splitting map for any \(r<s<1\).
Proof
It is enough to check that

for \(a,b=1,\ldots ,k\).
Let us set \(f_{a,b}:= |\nabla u_a\cdot \nabla u_b-\delta _{ab}|\) and note that \(|\nabla f_{a,b}|\le 2 C(N)(|{{\,\mathrm{Hess}\,}}u_a|+|{{\,\mathrm{Hess}\,}}u_b|)\), here we have used (i) in Definition 3.1. Using this bound, the local Poincaré inequality (cf. [80, 88]) and (4.31) we deduce

for any \(0<r<s<1\). Applying a telescopic argument it is simple to see that

Therefore, using that \(u:B_2(p)\rightarrow {\mathbb {R}}^k\), is a splitting map we deduce

therefore yielding (4.32). \(\square \)
The next lemma is the main iterative step in the construction of maximal neck regions over boundary balls.
Lemma 4.17
(Iteration step) Let \(\tau =10^{-10N}\) and \(\gamma \in (0,1/4)\) be fixed with \(\varepsilon _0\) as in Lemma 4.15. For any \(\varepsilon < 2\gamma \wedge \varepsilon _0/2\) and \(\delta \le \delta (\varepsilon ,\gamma , N)\) the following property holds. Given an \({{\,\mathrm{RCD}\,}}(-\varepsilon (N-1),N)\) m.m.s. \((X,{\mathsf {d}},{\mathscr {H}}^N)\), an \(\varepsilon ^2\)-boundary ball \(B_2(p)\subset X\) and \(k\in {\mathbb {N}}\), if there exists a \(\delta ^4\)-splitting map \(u:B_{2 \gamma ^{-k}}(p)\rightarrow {\mathbb {R}}^{N-1}\) such that

then there exists a covering
where
-
(i)
the family \(\{B_{\tau ^4 \gamma }(x_{\alpha })\}\cup \{B_{\tau ^4 \gamma }(x_{\beta })\}\) is disjoint;
-
(ii)
for any \(\alpha \), \(B_{2\gamma }(x_{\alpha })\) is an \(\varepsilon ^2\)-boundary ball such that

with
$$\begin{aligned} u:B_s(x_{\alpha })\rightarrow {\mathbb {R}}^{N-1} \quad \text {a }C_{\gamma , N}\delta \text {-splitting map for any }s\in [\tau ^2 \gamma , \gamma ^{-k}];\nonumber \\ \end{aligned}$$(4.36) -
(iii)
for any \(\beta \),
 (4.37)
(4.37) -
(iv)
\(x_{\alpha }\in B_{2\gamma \varepsilon }({\mathcal {L}}_{p,2})\) for any \(\alpha \), and \(x_{\beta }\in {\mathcal {L}}_{p,2}\) for any \(\beta \).
Proof
We choose \(\delta =\delta (\varepsilon ,\gamma ,N)\) given by Theorem 3.8 such that any ball endowed with a \(C_{\gamma ,N}\delta \)-splitting map is \(\varepsilon ^2/2\)-close to a ball in a space splitting \({\mathbb {R}}^{N-1}\), where \(C_{\gamma ,N}\) is the constant in (4.40) below.
Let \(\{B_{\tau ^3 \gamma }(x_{\xi })\}\) be any covering of \(B_1(p)\cap {\mathcal {L}}_{p,2}\) with \(x_{\xi }\in {\mathcal {L}}_{p,2}\) and such that \(\{B_{\tau ^4\gamma }(x_{\xi })\}\) is a disjoint maximal collection.
Given \(\xi \) such that

one has

as a consequence of (4.34). Therefore, by Lemma 4.16,
In order to conclude the proof we just need to prove the existence of \(x_{\alpha }\in B_{2\gamma \varepsilon }(x_{\xi })\) such that \(B_{2\gamma }(x_{\alpha })\) is an \(\varepsilon ^2\)-boundary ball.
To do so notice that the following properties hold:
-
(a)
\(B_{4\gamma }(x_{\xi })\) is a \(2^{-1}\gamma ^{-1}\varepsilon ^2 \)-boundary ball;
-
(b)
there exists a one dimensional manifold (possibly with boundary) \((Z,{\mathsf {d}}_Z)\) such that
$$\begin{aligned} {\mathsf {d}}_{GH}(B_{4\gamma }(x_{\xi }),B^{{\mathbb {R}}^{N-1}\times Z}_{4\gamma }((0,z)))\le 2\gamma \varepsilon ^2. \end{aligned}$$(4.41)
The property (a) follows from Remark 4.2 while (b) comes from (4.40) and Theorem 3.8.
Let us finally prove that (a) and (b) imply the existence of \(x_{\alpha }\in B_{2\gamma \varepsilon }(x_{\xi })\) such that \(B_{2\gamma }(x_{\alpha })\) is an \(\varepsilon ^2\)-boundary ball.
By exploiting (a), (b), the triangular inequality and our choice of \(\varepsilon \), we deduce
Therefore by Lemma 4.15 (in scale invariant form) there exist \(0\le a\le 8\gamma \varepsilon \le 4\gamma -8\gamma \varepsilon \le b\le \infty \) such that
Denoting by \(\Psi : B^{{\mathbb {R}}^{N-1}\times [0,b]}_{4\gamma }((0,a))\rightarrow B_{4\gamma }(x_{\xi })\) any \(2\gamma \varepsilon ^2\)-GH isometry, we set \(x_{\alpha }:=\Psi (0)\). It is easily seen that \(x_{\alpha }\in B_{2\gamma \varepsilon }(x_{\xi })\) and \(B_{2\gamma }(x_{\alpha })\) is an \(\varepsilon ^2\)-boundary ball (compare with Remark 4.2).
Changing \(x_{\xi }\) into \(x_{\alpha }\) in the above considered case and relabelling \(x_{\xi }\) as \(x_{\beta }\) in the other one, it is easily verified that the family \(\{B_{\gamma }(x_{\alpha })\}\cup \{B_{\gamma }(x_{\beta })\}\) has the sought properties. \(\square \)
4.3 Strategy of proof of Theorem 4.13
The overall strategy is similar to those [29, Proposition 10.5], [56, Proposition 7.13, Proposition 7.26] and [72, Theorem 5.4]. The key difference with respect to [29] and [56] is that we wish to build neck regions whose geometry is controlled by the same \(\delta \)-splitting map. Moreover, as we already pointed out, we need to prove that bad-balls \(B_{r_x}(x)\) with \(x\in {\mathcal {C}}_+\) have small \((N-1)\)-dimensional content.
The first step in the construction is based on the iterative application of Lemma 4.17. It turns that the outcome of this construction is a decomposition which shares most of the properties of neck regions with a subtle difference: there might be nearby balls with uncontrollably different sizes. This implies in turn that the second inclusion in condition (iii) of Definition 4.3 needs to be relaxed to a slightly weaker inclusion, where we do not look below the scale \(r_y\) near to a point \(y\in {\mathcal {C}}_+\), cf. with (4.45) below.
Definition 4.18
(Weak neck region) Fix \(\varepsilon ,\delta \in (0,1/2)\), an integer \(N\ge 1\) and \(\tau :=10^{-10N}\). Let \((X,{\mathsf {d}},{\mathscr {H}}^N,p)\) be a pointed \({{\,\mathrm{RCD}\,}}(-\varepsilon (N-1),N)\) metric measure space. We say that \({\mathcal {N}}\subset B_2(p)\) is a weak \((\varepsilon ,\delta )\)-neck region if there exist a closed set \({\mathcal {C}}\subset B_1(p)\) and a function \(r:{\mathcal {C}}\rightarrow [0, 1/8]\) such that \({\mathcal {N}}:=B_2(p){\setminus } \cup _{x\in {\mathcal {C}}}\bar{B}_{r_x}(x)\) and, setting \({\mathcal {C}}_0:=\{x\in {\mathcal {C}}:\ r_x=0\}\) and \({\mathcal {C}}_+:={\mathcal {C}}{\setminus }{\mathcal {C}}_0\), the following hold:
-
(i)
the family \(\{\bar{B}_{\tau ^4 r_x}(x)\}_{x\in {\mathcal {C}}}\subset B_2(p)\) is disjoint;
-
(ii)
for any \(x\in {\mathcal {C}}\) and \(r_x\le r\le \tau ^{-4}\), \(B_r(x)\) is an \(\varepsilon ^2\)-boundary ball, i.e. there exists an \(\varepsilon ^2 r\)-GH isometry
$$\begin{aligned} \Psi _{x,r}: B_r^{{\mathbb {R}}_+^N}(0)\rightarrow B_r(x); \end{aligned}$$(4.44) -
(iii)
setting \({\mathcal {L}}_{x,r}:=\Psi _{x,r}(\{x_N=0\})\), it holds that
$$\begin{aligned} {\mathcal {C}}\cap B_r(x)\subset B_{2\varepsilon r}({\mathcal {L}}_{x,r}) \quad \text {and}\quad {\mathcal {L}}_{x,r}\cap B_r(x)\subset B_{100\tau ^3 \max \{r,r_y\}}({\mathcal {C}}), \end{aligned}$$(4.45)for any \(x\in {\mathcal {C}}\) and \(r_x< r < \tau ^{-4}\), where we denoted by
$$\begin{aligned} B_{100\tau ^3 \max \{r,r_y\}}({\mathcal {C}}):=\bigcup _{y\in {\mathcal {C}}}B_{100\tau ^3 \max \{r,r_y\}}(y) ; \end{aligned}$$(4.46) -
(iv)
there exists a \(\delta ^4\)-splitting map \(u:B_{2\tau ^{-4}}(p)\rightarrow {\mathbb {R}}^{N-1}\) such that, for any \(x\in {\mathcal {C}}\) and \(r_x< r <\tau ^{-4}\) it holds that
$$\begin{aligned} u:B_r(x)\rightarrow {\mathbb {R}}^{N-1} \quad \text {is a }\delta \text {-splitting map } \end{aligned}$$(4.47)and
 (4.48)
(4.48)
The packing measure associated to a weak neck region is defined as in the case of neck regions, cf. with Definition 4.5.
The outcome of this first step will be a weak neck region for which we can additionally prove a small content bound for bad-balls, cf. with (4.49) below. This is due to the fact that in Lemma 4.17 we only stop the decomposition when the Hessian bound fails. Since we start with a Hessian bound on the ambient ball, this allows to get a content bound for bad-balls via a standard weighted maximal argument.
Proposition 4.19
(Existence of weak neck regions with content estimates) Let \(\tau :=10^{-10N}\). For any \(0<\varepsilon \le \varepsilon (N)\), for any \(\delta <\delta (\varepsilon ,N)\) and \(\eta <\eta (\varepsilon ,\delta ,N)\) the following holds. If \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is an \({{\,\mathrm{RCD}\,}}(-\eta (N-1),N)\) m.m.s., \(p\in X\) and \(B_{4\tau ^{-4}}(p)\) is an \(\eta \)-boundary ball, then there exists a weak \((\varepsilon ,\delta )\)-neck region \({\mathcal {N}}=B_2(p){\setminus } \cup _{x\in {\mathcal {C}}}\overline{B}_{r_x}(x)\) on \(B_2(p)\) which additionally verifies
Once we have built a weak neck region we need to refine the construction to get a neck region out of it, also keeping the small content bound for bad balls. This will be achieved refining the approximate singular set and regularizing the radius function \(r_x\).
Via this procedure we might be enlarging the set \({\mathcal {C}}_+\) of centers of bad balls and the new bad balls might not verify anymore the maximality condition (4.37). The key observation will be that the new center points are all near to old center points at the right scale. Then the structure Theorem 4.9 allows to turn the small content bound for the weak neck region into a small content bound for the neck region.
4.3.1 Proof of Proposition 4.19
Base step. Let us fix a scale parameter \(\gamma =1/8\), \(\varepsilon \le \varepsilon (N)\) and \(\delta <\delta (\varepsilon ,\gamma ,N)\) as in Lemma 4.17. We consider \(\eta < \eta (N,\delta ^4)\) such that, by Theorem 3.8 (i), there exists a \(\delta ^4\)-splitting map \(u:B_{2\tau ^{-4}}(p)\rightarrow {\mathbb {R}}^{N-1}\).
Let us apply Lemma 4.17 with \(k=0\) to obtain a covering
where
-
(i)
the family \(\{B_{\tau ^4\gamma }(x_{\alpha }^1)\}\cup \{B_{\tau ^4 \gamma }(x^1_{\beta })\}\) is disjoint;
-
(ii)
\(\alpha \)-balls \(B_{2\gamma }(x^1_{\alpha })\) and \(\beta \)-balls \(B_{2\gamma }(x^1_{\beta })\) verify the following:
-
(\(\alpha \)-balls) for any \(\alpha \), \(B_{2\gamma }(x^1_{\alpha })\) is an \(\varepsilon ^2\)-boundary ball and
$$\begin{aligned} u:B_s(x^1_{\alpha })\rightarrow {\mathbb {R}}^{N-1} \quad \text {is a }C_{\gamma , N}\delta \text {-splitting map for any }s\in [\tau ^3 \gamma , 1];\qquad \qquad \end{aligned}$$(4.51) -
(\(\beta \)-balls) for any \(\beta \),
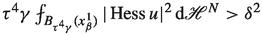 ;
;
-
-
(iii)
\(x^1_{\alpha }\in B_{2\gamma \varepsilon }({\mathcal {L}}_{p,2})\) for any \(\alpha \), and \(x^1_{\beta }\in {\mathcal {L}}_{p,2}\) for any \(\beta \).
Iteration steps. Observe that
is easily seen to be a neck region. However, it could be that this neck region is not nearly maximal and can be extended. Therefore we wish to iteratively refine the construction by decomposing the \(\alpha \)-balls in the decomposition via Lemma 4.17.
To this aim, let us apply Lemma 4.17 with \(k=1\) and same choice of parameters as in the base step of the iteration to any approximate singular set \({\mathcal {L}}_{x_{\alpha }^1,\gamma }\) (after scaling the scale \(\gamma \) to scale 1).
We obtain a covering
such that \(B_{\tau ^4\gamma ^2}(x^2_{\alpha })\) and \(B_{\tau ^4\gamma ^2}(x^2_{\beta })\) are disjoint,
and
Moreover, the balls in the covering are labeled as \(\alpha \)-balls or \(\beta \)-balls according to the convention of Lemma 4.17. In particular:
-
for any center of \(\alpha \)-ball \(x^2_{\alpha }\), it holds that \(B_{r}(x^2_{\alpha })\) is a \(\gamma ^{-1}\varepsilon ^2\)-boundary ball for any \(\gamma ^2<r< \tau ^{-4}\) and
 (4.56)
(4.56) -
for any \(k=1,2\) and any centre of \(\beta \)-ball \(x^k_{\beta }\), it holds that
 (4.57)
(4.57)
Moreover, being \(\gamma \le 1/4\), the balls \(B_{\tau ^4\gamma ^2}(x_{\alpha }^2)\) and \(B_{\tau ^4\gamma ^2}(x_{\beta }^2)\) are also mutually disjoint with all the balls \(B_{\tau ^4\gamma }(x_{\beta }^1)\).
At this stage of the decomposition we have a weak neck region
Observe that after this second step we pass from a neck region to a weak neck region since there might already be balls of different sizes nearby. As we already pointed out this motivates the necessity for a refinement of the construction later on.
After repeating this decomposition i times, decomposing at each step the \(\alpha \)-balls via Lemma 4.17 (applied with \(k=i\) after scaling each \(\alpha \)-ball to radius 2), we get an approximate weak neck region
The balls in the covering in particular satisfy the following:
-
for any centre of \(\alpha \)-ball \(x^i_{\alpha }\), it holds that \(B_{r}(x^i_{\alpha })\) is a \(\gamma ^{-1}\varepsilon ^2\)-boundary ball for any \(\gamma ^i<r<\tau ^{-4}\) and
 (4.60)
(4.60) -
for any \(k=1,2,\dots , i\), and any centre of \(\beta \)-ball \(x^k_{\beta }\), it holds that
 (4.61)
(4.61)
Limiting argument. Set
By construction (cf. with (4.54) and (4.55)) we have
Therefore, we can define the Hausdorff limit
By letting \(i\rightarrow \infty \) and passing to the limit the weak neck regions \({\mathcal {N}}^i\) in (4.59), letting
we get
By construction, the balls \(B_{\tau ^4r_x}(x)\) are disjoint for \(x\in {\mathcal {C}}_+\),

Passing to the limit the bounds in the intermediate steps of the construction it is possible to infer that \({\mathcal {N}}\) is a \((\gamma ^{-1}\varepsilon ,\delta )\)-weak neck region.
Content bound. Let us now verify the small content bound (4.49). Taking into account the disjointness of the balls \(B_{\tau ^4r_x}(x)\) for \(x\in {\mathcal {C}}_+\) and (4.67) we can estimate

The sought conclusion follows from Remark 4.8, which yields \({\mathscr {H}}^N(B_{\tau ^4 r_x}(x))\ge \frac{1}{4}\omega _N(\tau ^4 r_x)^{N}\).
4.3.2 Proof of Theorem 4.13
We can now complete the proof of the existence of neck regions, together with the small content estimate. First we are going to apply Proposition 4.19. Then we refine the approximate singular set and the radius function to get a neck region. In the last step of the proof we prove the content bound relying on (4.49) and on the structure of neck regions Theorem 4.9.
Refinement of approximate singular set and radius. Let \(\varepsilon ',\delta '>0\) to be chosen later in terms of \(\varepsilon \), \(\delta \) and N. Given \(\eta <\eta (\varepsilon ',\delta ',N)\) we apply Proposition 4.19 with \(\varepsilon '\) and \(\delta '\) in place of \(\varepsilon \) and \(\delta \) to obtain a weak neck region
Let \(\gamma =1/8\) be the iteration scale in the proof of Proposition 4.19.
In order to refine the weak neck region \(\tilde{{\mathcal {N}}}\), let us build an approximate singular set \(\tilde{{\mathcal {S}}}\) as follows. For any \(x\in B_2(p)\) we denote by \({\tilde{x}}\in \tilde{ {\mathcal {C}}}\) a point verifying \({\mathsf {d}}(\tilde{ {\mathcal {C}}},x) = {\mathsf {d}}({\tilde{x}},x)\) and set \(s_x:= 2\max \{{\mathsf {d}}({\mathcal {C}}, x), {\tilde{r}}_{{\tilde{x}}}\}\).
We say that \(x\in B_2(p)\) belongs to \(\tilde{ {\mathcal {S}}}\) if \(x\in \cup _{{\tilde{y}}\in \tilde{{\mathcal {C}}}} B_{ \tau {\tilde{r}}_{{\tilde{y}}}}({\tilde{y}})\) and
Now, let us define a radius function on \(\tilde{{\mathcal {S}}}\) as
It is easily seen that \({{\,\mathrm{Lip}\,}}r_x\le \tau ^2\), \(\tilde{{\mathcal {C}}}\subset \tilde{{\mathcal {S}}}\) and \(r_x=0\) for any \(x\in \tilde{ {\mathcal {C}}}_0\).
Choose a maximal disjoint collection \(\{B_{\tau ^2 r_x}(x),x\in \tilde{{\mathcal {S}}}\}\) whose set of centers \({\mathcal {C}} = {\mathcal {C}}_0 \cup {\mathcal {C}}_+\) satisfies \({\mathcal {C}}_0 = \tilde{ {\mathcal {C}}}_0\) and \(\tilde{{\mathcal {C}}}_{+}\subset {\mathcal {C}}_+\).
We claim that
is an \((\varepsilon ,\delta )\)-neck region for \(\varepsilon '\le \varepsilon '(\varepsilon ,N)\) and \(\delta '\le \delta '(\varepsilon ,\delta ,N)\).
Proof of the neck region properties for \({\mathcal {N}}\). The Vitali covering condition (i) in the neck region Definition 4.3 is satisfied by the construction. Moreover, as we already pointed out, it holds \({{\,\mathrm{Lip}\,}}r_x\le \tau ^2\).
Next, note that \(B_{r}(x)\) is an \((\varepsilon '^2\tau ^{-6})\)-boundary ball for all \(x\in {\mathcal {C}}\) and \(r_x \le r \le \gamma \tau ^{-4}\). This follows from Remark 4.2 thanks to the following observation: with this choice of parameters, all the balls \(B_r({\tilde{x}})\) for \({\tilde{x}}\in \tilde{{\mathcal {C}}}\) and \(r>{\tilde{r}}_{{\tilde{x}}}\) in the weak neck region are \(\gamma ^{-1}\varepsilon '^2\)-boundary balls and the center point x belongs to the approximate singular set by (4.69).
Since \(\gamma ^{-1}\varepsilon '^2\tau ^{-6}\le \varepsilon ^2\) for \(\varepsilon '\le \varepsilon '(N,\varepsilon )\), this proves condition (ii) in Definition 4.3.
The first inclusion in Definition 4.3 (iii) is also satisfied by the very construction of \(\tilde{{\mathcal {S}}}\), since the center points all belong to the approximate singular set above their own scale.
Let us now verify the second inclusion in (iii) of Definition 4.3, which is the main reason for the refinement of the weak neck region \(\tilde{{\mathcal {N}}}\) into \({\mathcal {N}}\).
Let \(x\in {\mathcal {C}}\) and \(r_x \le r \le \tau ^{-3}\). Then, if \({\tilde{x}}\in \tilde{{\mathcal {C}}}\) is such that \({\mathsf {d}}(x,{\tilde{x}})={\mathsf {d}}(x,\tilde{{\mathcal {C}}})\),
since \(r\ge r_x \ge \tau ^{2}{\mathsf {d}}(x,{\tilde{x}})\) by (4.70).
The cone splitting Theorem 2.19 gives
for \(\varepsilon \le \varepsilon (N)\). The application of the cone splitting theorem is justified by the fact that, as we already pointed out above, the balls \(B_s(x)\) and \(B_t({\tilde{x}})\) are \(\varepsilon ^2\)-boundary balls for \(s\ge r_x\) and \(t\ge r_x\).
In order to get (iii) of Definition 4.3 it is enough to see that
Indeed, if (4.74) holds, then the Lipschitz property \({{\,\mathrm{Lip}\,}}r_x \le \tau ^{2}\) gives
Let us prove (4.74).
The property (iii) in the definition of weak neck region \(\tilde{{\mathcal {N}}}\) (see Definition 4.18) gives the inclusion
Moreover, the cone splitting Theorem 2.19 implies
for any \(\varepsilon '\le \varepsilon '(\varepsilon ,N)\).
To finish the proof of (4.74) we are going to prove that
Let us first check (4.77). In particular we claim that \({\mathcal {L}}_{{\tilde{y}}, \tau ^2 {\tilde{r}}_{{{\tilde{y}}}}} \subset B_{\tau ^{20}{\tilde{r}}_{{{\tilde{y}}}}}({{\tilde{S}}})\).
Given \(z\in {\mathcal {L}}_{{\tilde{y}}, \tau ^2 {\tilde{r}}_{{{\tilde{y}}}}}\) we consider \({{\tilde{z}}} \in {\mathcal {C}}\) such that \({\mathsf {d}}(z,{\tilde{z}})={\mathsf {d}}(z,\tilde{{\mathcal {C}}})\). If \({\mathsf {d}}(z,{{\tilde{z}}})\le \tau ^{20} {\tilde{r}}_{{\tilde{y}}}\) then \(z\in B_{\tau ^{20}{\tilde{r}}_{{{\tilde{y}}}}}({{\tilde{S}}})\), since \({{\tilde{z}}}\in {{\tilde{S}}}\). If \({\mathsf {d}}(z,{{\tilde{z}}}) > \tau ^{20} {\tilde{r}}_{{\tilde{y}}}\) then
as a consequence of the cone splitting Theorem 2.19. This implies \(z\in {\tilde{S}}\) by (4.69), since we already know that \(z\in B_{\tau ^{2}{\tilde{r}}_{{{\tilde{y}}}}}({{\tilde{y}}}) \subset \cup _{{\tilde{w}}\in \tilde{{\mathcal {C}}}} {\bar{B}}_{\tau {\tilde{r}}_{{{\tilde{w}}}}}({{\tilde{w}}})\).
To prove (4.78) we rely on the inequalities \(\tau ^{20} {\tilde{r}}_{{{\tilde{y}}}} \le \tau ^{10} r_y\), \(r_{{{\tilde{x}}}} \le r\) and the Lipschitz bound \({{\,\mathrm{Lip}\,}}r_y \le \tau ^2\). The last inclusion (4.79) follows from the definition of \({\mathcal {C}}\).
Let us now verify condition (iv) in Definition 4.3. For any \(x\in {\mathcal {C}}\) we consider a point in \({\tilde{x}}\in \tilde{{\mathcal {C}}}\) such that \({\mathsf {d}}(x,\tilde{{\mathcal {C}}})={\mathsf {d}}(x,{\tilde{x}})\). Observe that, for any \(r_x\le r\le \tau ^3\), it holds \(B_r(x)\subset B_{\tau ^{-6}r}({\tilde{x}})\). The sought conclusion follows from


by choosing \(\delta '\le \delta '(N,\delta )\).
If \(r\ge \tau ^3\) instead, the sought bound can be easily obtained by recalling that \(u: B_{4\tau ^{-4}}(p)\rightarrow {\mathbb {R}}^{N-1}\) is a \(\delta '\)-splitting map and, again, choosing \(\delta '\le \delta '(\delta ,N)\).
Proof of the small content bound (4.29). By the very construction of the neck region \({\mathcal {N}}\), the following holds:
Moreover, for any \({\tilde{x}}\in \tilde{{\mathcal {C}}}_+\) and for any \(x\in {\mathcal {C}}_+\cap B_{\tau {\tilde{r}}_{{\tilde{x}}}}({{\tilde{x}}})\) it holds that
by definition of radius function (4.70).
Denoting by \(\mu \) the packing measure of the neck region \({\mathcal {N}}\) as in Definition 4.5, it holds
5 Neck Decomposition
The main result of this part is Theorem 5.1 below. Its proof is based on the combination of the following three ingredients:
-
the boundary-interior decomposition Theorem 5.2, dealing with a decomposition of the space into a singular part, regular balls and boundary balls with content bounds;
-
the existence of neck regions Theorem 4.13;
-
the structure theorem for neck regions Theorem 4.9.
The covering arguments needed in the proof are essentially those of [56, Section 7] (see also [29, Section 10]) and we will only sketch them in most cases.
Theorem 5.1
(Neck decomposition theorem) Let \(\eta >0\) with \(\delta <\delta (N,v,\eta )\) and consider a noncollapsed \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) m.m.s. \((X,{\mathsf {d}},{\mathscr {H}}^N)\). For any \(p\in X\) such that \({\mathscr {H}}^N(B_1(p))\ge v\), there exists a decomposition
such that the following hold:
-
(i)
for any a, the set \({\mathcal {N}}_a=B_{2r_a}(x_a){\setminus }\bar{B}_{r_x}({\mathcal {C}}_a)\) is an \((\eta ,\delta )\)-neck region with \((N-1)\)-singular set \({\mathcal {C}}_{0,a}\subset B_{2r_a}(x_a)\);
-
(ii)
for any b, the ball \(B_{2r_b}(x_b)\) is \((N,\eta )\)-symmetric and \(r_b^2\le \eta \);
-
(iii)
\(\sum _ar_a^{N-1}+\sum _br_b^{N-1}+{\mathscr {H}}^{N-1}({\mathcal {S}}^{\delta ,\eta })\le C(N,v,\delta ,\eta )\);
-
(iv)
it holds \({\mathscr {H}}^{N-1}(\tilde{{\mathcal {S}}}^{\delta ,\eta })=0\);
-
(v)
the singular set \({\mathcal {S}}^{\delta ,\eta }\) is \((N-1)\)-rectifiable;
-
vi)
if \(\eta <\eta (N,v)\) and \(\delta <\delta (N,v,\eta )\), then \({\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2}\subset {\mathcal {S}}^{\delta ,\eta }\).
The Neck decomposition theorem provides a quantitative covering of \(B_1(p)\) in terms of sets that we know how to control at any scale. In the decomposition we have:
-
(a)
\((N,\eta )\)-symmetric balls \(B_{r_b}(x_b)\). They cover the “interior” of the space and look Euclidean at any scale and location;
-
(b)
neck regions \({\mathcal {N}}_a = B_{2r_a}(x_a){\setminus }\bar{B}_{r_x}({\mathcal {C}}_a)\), where balls centred at \(x_a\in {\mathcal {C}}_a\) look like boundary balls at any scale above \(r_a\);
-
(c)
the set \({\mathcal {S}}^{\delta ,\eta }\). This is an \((N-1)\)-dimensional set covering the actual boundary of the space up to an \({\mathscr {H}}^{N-1}\)-negligible set.
What makes our covering quantitative is the content bound (c). This is the key ingredient to prove sharp estimates on the size of tubular neighbourhoods of the boundary.
The essence of the Neck decomposition theorem is well illustrated in the case of the convex region \(C(I_t)\) introduced in Example 4.12, where \(I_t\) is an interval with very small length t. In this case neither interior 2-symmetric balls of fixed size, nor 1-symmetric boundary balls of fixed size can get too close to the singular point. Therefore one is led to consider a covering with infinitely many regular balls (whose radii become smaller and smaller when the centres get close to the singular point) and infinitely many neck regions (whose radii become smaller and smaller as the centres get close to the singular point).
We refer to [29, Example 2.14 and 2.15] for other examples of neck decompositions in any codimension.
The next theorem is typically the first step in the proof of the Neck Decomposition Theorem 5.1. We emphasize it here, as once we have proven the \(\varepsilon \)-regularity Theorem 1.2 this leads to our Boundary Structure Theorem 1.4:
Theorem 5.2
(Boundary-Interior decomposition theorem) For any \(\eta >0\) and \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) m.m.s. \((X,{\mathsf {d}},{\mathscr {H}}^N)\) with \(p\in X\) such that \({\mathscr {H}}^N(B_1(p))\ge v\), there exists a decomposition
such that the following hold:
-
(i)
the balls \(B_{4\tau ^{-4}r_a}(x_a)\) are \(\eta \)-boundary balls and \(r_a^2\le \eta \);
-
(ii)
the balls \(B_{2r_b}(x_b)\) are \((N,\eta )\)-symmetric and \(r_b^2\le \eta \);
-
(iii)
\(\tilde{{\mathcal {S}}}\subset {\mathcal {S}}\) and \({\mathscr {H}}^{N-1}(\tilde{{\mathcal {S}}})=0\);
-
(iv)
\(\sum _br_b^{N-1}\le C(N,v,\eta )\);
-
(v)
\(\sum _ar_a^{N-1}\le C(N,v)\).
The proof of Theorem 5.2 proceeds via an iterative recovering argument. In the next subsection, we introduce various rougher decompositions which include different types of balls, and we show how we can iteratively get rid of them. The arguments are those of [29, Section 10], with some simplifications due to the strong rigidity of singularities in codimension one. We only sketch the proofs, omitting the details and referring to [29] for all the details.
5.1 Proof of the neck decomposition theorem
Let us state an intermediate decomposition result and show how it can be used to derive the boundary-interior decomposition Theorem 5.2. Here a different type of balls appears, which are not \(\eta \)-boundary balls nor \((N,\eta )\)-symmetric balls but have a definite volume drop with respect to the background scale.
Proposition 5.3
For any \(\eta >0\) there exists \({\nu }^0(N,v,\eta )>0\) such that, if \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is an \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) m.m.s. and \(B_1(p)\subset X\) verifies \({\mathscr {H}}^N(B_1(p))\ge v\), then there exists a decomposition
such that the following hold:
-
(i)
for any a, the ball \(B_{4\tau ^{-4}r_a}(x_a)\) is an \(\eta \)-boundary ball and \(r_a^2\le \eta \);
-
(ii)
for any b, the ball \(B_{2r_b}(x_b)\) is \((N,\eta )\)-symmetric and \(r_b^2\le \eta \);
-
(iii)
\(\sum _br_b^{N-1}+\sum _{\nu }r_{\nu }^{N-1}\le C(N,\eta ,v)\);
-
(iv)
\(\sum _ar_a^{N-1}\le C(N,v)\);
-
(v)
\(\tilde{{\mathcal {S}}}\subset {\mathcal {S}}\) and \({\mathscr {H}}^{N-1}(\tilde{{\mathcal {S}}})=0\);
-
(vi)
for any \(\nu \), \(\inf _{y\in B_{4r_{\nu }}(x_{\nu })}{\mathcal {V}}_{r_{\nu }}(y)\ge \inf _{y\in B_4(p)}{\mathcal {V}}_1(y)+\nu ^0\).
Let us now prove the boundary-interior decomposition Theorem 5.2. In order to do so we just need to iteratively apply a finite number of times Proposition 5.3 to get rid of \(\nu \)-balls in the decomposition.
Proof of Theorem 5.2
In order to prove Theorem 5.2 given Proposition 5.3 we just need to follow the first part of the proof of [29, Theorem 2.12]. After a finite number of iterations of the induction step decomposition we get a decomposition with only a-balls, b-balls and a subset of the singular stratum \({\mathcal {S}}^{N-2}\). \(\square \)
The remainder of this subsection is devoted to the proof of Proposition 5.3.
We are going to consider constants \(\xi ,\delta ,\gamma ,\varepsilon \) which in general will satisfy
We will assume additionally that \((X,{\mathsf {d}},{\mathscr {H}}^{N})\) is an \({{\,\mathrm{RCD}\,}}(-\xi (N-1),N)\) space. The general cases of all the statements can be achieved via additional covering arguments.
Let us introduce the notation for the various families of balls we will use in the intermediate steps of our arguments.
We recall that the set with small volume pinching has been introduced in (2.37) and the almost cone splitting via content Theorem 2.21, to which we refer for the various constants appearing below.
Any ball \(B_r(x)\) will be of one or more of these types, indexed by letters b, c, d and e:
-
(i)
b-balls \(B_{r_b}(x_b)\) are balls such that \(B_{2r_b}(x_b)\) is \((N,\eta )\)-symmetric;
-
(ii)
c-balls \(B_{r_c}(x_c)\) are balls which are not b-balls but satisfy
$$\begin{aligned} {\mathscr {H}}^{N}(B_{\gamma r_c}({\mathcal {P}}_{r_c,\xi }(x_c)))\ge \varepsilon \gamma r_c^N; \end{aligned}$$(5.6) -
(iii)
d-balls are balls \(B_{r_d}(x_d)\) for which \({\mathcal {P}}_{r_d,\xi }(x_d)\ne \emptyset \) but
$$\begin{aligned} {\mathscr {H}}^{N}(B_{\gamma r_d}({\mathcal {P}}_{r_d,\xi }(x_d)))<\varepsilon \gamma r_d^N; \end{aligned}$$(5.7) -
(iv)
e-balls \(B_{r_e}(x_e)\) for which \({\mathcal {P}}_{r_e,\xi }(x_e)=\emptyset \).
Remark 5.4
Let us point out that any e-ball \(B_{r_e}(x_e)\) can be covered by \(\nu \)-balls as in (vi) of Proposition 5.3 in such a way that
and \(\sum _{\nu }r_{\nu }^{N-1}\le C(N,v)r_e^{N-1}\).
In order to do so it is sufficient to consider a Vitali covering of \(B_{r_e}(x_e)\) with balls \(B_{\xi r_e}(x_e^i)\) such that \(x_e^i\in B_{r_e}(x_e)\) and the balls \(B_{\xi r_e/5}(x_e^i)\) are disjoint. At the end of the proof of [29, Proposition 10.2] it is verified that the balls \(B_{\xi r_e}(x_e^i)\) are \(\nu \)-balls with \(\nu _0=\xi \) and the content estimate follows from the Vitali covering property.
Remark 5.5
Let us see how to recover boundary balls starting from c-balls.
We wish to prove that, for \(\delta \) sufficiently small, any c-ball \(B_{r_c}(x_c)\) is such that \(B_{\tau ^{-6}r_c}(x'_c)\) is an \(\eta \)-boundary ball for some \(x'_c\in B_{4r_c}(x_c)\), in particular \(B_{r_c}(x_c)\subset B_{\tau ^{-6}r_c}(x_c')\).
In order to do so we argue by contradiction. Recall that the parameters are set in such a way that the assumptions of the cone splitting via content Theorem 2.21 are satisfied. Observe that, if \(B_{r_c}(x_c)\) is a c-ball (see (5.6)), then there exists \(x_c'\in B_{4r_c}(x_c)\) such that \(B_{\delta ^{-1}r_c}(x_c')\) is \((N-1,\delta ^2)\)-symmetric. Since by assumption \(B_{r_c}(x_c)\) is not \((N,\eta )\)-symmetric, it is easy to check arguing by contradiction that, for \(\delta \) sufficiently small, \(B_{\tau ^{-6}r_c}(x'_c)\) is an \(\eta \)-boundary ball.
Proposition 5.6
Let \(v>0\) be fixed. For any \(\varepsilon \le \varepsilon (N,v)\), \(\gamma \le \gamma (N,v,\varepsilon )\), \(\delta \le \delta (N,v,\eta )\) and \(\xi \le \xi (N,v,\varepsilon ,\gamma ,\delta ,\eta )\) and for any \({{\,\mathrm{RCD}\,}}(-\xi (N-1),N)\) m.m.s. \((X,{\mathsf {d}},{\mathscr {H}}^N)\) and \(B_1(p)\subset X\) such that \({\mathscr {H}}^N(B_1(p))\ge v\) the following holds. There exists a decomposition
where we are adopting the usual notation for the various types of balls,
and \(\tilde{{\mathcal {S}}}\subset {\mathcal {S}}\), with \({\mathscr {H}}^{N-1}(\tilde{{\mathcal {S}}})=0\).
Proof
Specializing [29, Proposition 10.3] to the case \(k=N-1\), we obtain that there exist \(\varepsilon \le \varepsilon (N,v)\), \(\gamma \le \gamma (N,v,\varepsilon )\) and \(\delta \le \delta (N,v,\eta )\) such that, if the additional assumption \({\mathscr {H}}^N(B_{\gamma }({\mathcal {P}}_{1,\xi }(p)))<\varepsilon \gamma \) is satisfied (that is to say \(B_1(p)\) is a d-ball), the following holds: there exists a decomposition
where
-
(i)
\({\mathscr {H}}^{N-1}(\tilde{{\mathcal {S}}}_d)=0\);
-
(ii)
\(\sum _br_b^{N-1}+\sum _{e}r_e^{N-1}\le C(N,\gamma )\);
-
(iii)
\(\sum _cr_c^{N-1}\le C(N,v)\).
To conclude, let us observe that, if \(B_1(p)\) is either a b-ball, a c-ball or an e-ball, then the statement is trivially verified. Therefore we can assume that \(B_1(p)\) is a d-ball and the conclusion follows from what we observed in the first part of the proof. \(\square \)
Proof of Proposition 5.3
We divide the proof into two steps.
In the first one we reduce ourselves to balls such that, after rescaling of the space at the scale of their radii the lower Ricci curvature bound is \(-\xi (N-1)\). Then, relying on Remark 5.4 and Remark 5.5, we get the sought decomposition starting from Proposition 5.6.
Step 1. Considering a Vitali covering of \(B_1(p)\) with balls of sufficiently small radius we reduce to balls that, when rescaled to radius one, verify the assumptions of Proposition 5.6. The number of these balls can be controlled due to the Vitali property.
Step 2. Given any ball arising from the first step, we apply Proposition 5.6. Thanks to Remark 5.4 we cover any e-ball with \(\nu \)-balls keeping to content bound. Next, relying on Remark 5.5, for any c-ball \(B_{r_c}(x_c)\) we find \(x_a\in B_{4r_c}(x_c)\) such that \(B_{\tau ^{-6}r_c}(x_a)\) is an \(\eta \)-boundary ball and we substitute the given c-ball with the a-ball \(B_{4\tau ^{-4}r_c}(x_a)\). Since \(B_{r_c}(x_c)\subset B_{r_a}(x_a)\) we keep the covering property and also the content bound is preserved. \(\square \)
The proof of the neck decomposition Theorem 5.1 with properties i) to iv) relies on the iterative application of the boundary-interior decomposition Theorem 5.2 together with the existence of neck regions Theorem 4.13 and the structure Theorem 4.9 to take care of the content and \({\mathscr {H}}^{N-1}\)-measure estimates.
Proof of Theorem 5.1
In the following we are going to denote by \(B_{r_f}(x_f)\) a ball which has not been identified with an a-ball or b-ball yet.
Let us start combining and rephrasing Theorem 4.13 and Theorem 4.9 in a way convenient for our purposes: for any \(\varepsilon >0\), \(\eta <\eta (\varepsilon ,N)\) and \(\delta \le \delta (N,\eta )\) there exists \(\eta '>0\) such that, if a ball \(B_{4\tau ^{-4}r}(p)\) is an \(\eta '\)-boundary ball, then there exists an \((\eta ,\delta )\)-neck region \({\mathcal {N}}=B_{2r}(p){\setminus }\bar{B}_{r_x}({\mathcal {C}})\) over \(B_{2r}(p)\) such that
-
(i)
\( B_r(p)\subset \left( {\mathcal {N}}\cap B_{r}(p)\right) \cup {\mathcal {C}}_0\cup \bigcup _f B_{2r_f}(x_f);\)
-
(ii)
\({\mathscr {H}}^{N-1}({\mathcal {C}}_0)\le A(N)r^{N-1}\);
-
(iii)
the singular set \({\mathcal {C}}_0\) is biLipschitz to a subset of \({\mathbb {R}}^{N-1}\);
-
(iv)
and \(\sum _{f}r_f^{N-1}\le \varepsilon r^{N-1}\);
-
(v)
for any f it holds that
$$\begin{aligned} {\mathscr {H}}^N(B_{r_f}(x_f))\le \frac{2}{3}\omega _Nr^N. \end{aligned}$$(5.13)
Let us just point out that item (v) above follows from Remark 4.8.
In order to get the sought covering we proceed inductively. First we apply Theorem 5.2 with \(\eta =\eta '\) given in the discussion above. Then we build \((\eta ,\delta )\)-neck regions verifying (i) to (v) above on any ball \(B_{2r_a}(x_a)\) of the decomposition. After this first stage of the procedure we get
with
-
(i)
\(\sum _br_b^{N-1}\le C(N,v,\eta )\);
-
(ii)
\(\sum _a{\mathscr {H}}^{N-1}({\mathcal {C}}_{0,a})\le A(N)\sum _{a}r_a^{N-1}\le C'(N,v)\);
-
(iii)
\(\tilde{{\mathcal {S}}}\subset {\mathcal {S}}\) and \({\mathscr {H}}^{N-1}(\tilde{{\mathcal {S}}})=0\);
-
(iv)
\(\sum _{f}r_f^{N-1}\le \varepsilon \sum _{a}r_a^{N-1}\le C(N,v)\varepsilon .\)
Next we apply again the procedure above to the balls \(B_{r_f}(x_f)\): first we perform the boundary-interior decomposition of Theorem 5.2, then we build neck regions on any new \(\eta \)-boundary ball appearing. At the first iteration we get
with
-
(i)
\(\sum _{b_1}(r_{b_1})^{N-1}\le C(N,v,\eta )(1+C(N,v)\varepsilon )\);
-
(ii)
\(\sum _{a_1}(r_{a_1})^{N-1}\le C(N,v)(1+\varepsilon C(N,v))\);
-
(iii
\(\sum _{a_1}{\mathscr {H}}^{N-1}({\mathcal {C}}_{0,{a_1}})\le A(N)C(N,v)(1+\varepsilon C(N,v))\);
-
(iv)
\(\tilde{{\mathcal {S}}}_1\subset {\mathcal {S}}\) and \({\mathscr {H}}^{N-1}(\tilde{{\mathcal {S}}}_1)=0\);
-
(v)
\(\sum _{f_1}(r_{f_1})^{N-1}\le \varepsilon \sum _{f}r_{f}^{N-1}\le C(N,v)\varepsilon ^2.\)
Arguing by induction, after n iterations of the scheme we get
with
-
(n-i)
\(\sum _{b_n}(r_{b_n})^{N-1}\le C(N,v,\eta )(1+C(N,v)\varepsilon +\dots +(C(N,v)\varepsilon )^n)\);
-
(n-ii)
\(\sum _{a_n}(r_{a_n})^{N-1}\le C(N,v)(1+C(N,v)\varepsilon +\dots +(C(N,v)\varepsilon )^n)\);
-
(n-iii)
\(\sum _{a_n}{\mathscr {H}}^{N-1}({\mathcal {C}}_{0,a_n})\le C(N,v)(1+C(N,v)\varepsilon +\dots +(C(N,v)\varepsilon )^n)\);
-
(n-iv)
\(\tilde{{\mathcal {S}}}_n\subset {\mathcal {S}}\) and \({\mathscr {H}}^{N-1}(\tilde{{\mathcal {S}}}_n)=0\);
-
(n-v)
\(\sum _{f_n}(r_{f_n})^{N-1}\le C(N,v)\varepsilon ^n.\)
Next we wish to pass to the limit in the construction above.
To this aim choose \(\varepsilon \) small enough to ensure that \(C(N,v)\varepsilon <1\), \(\eta \) and \(\delta \) accordingly and let us set
Furthermore we denote by a any index belonging to \(\cup _n\left\{ a_n\right\} \) and by b any index belonging to \(\cup _n\left\{ b_n\right\} \). Observe that \(\left\{ a_n \right\} \subset \left\{ a_m\right\} \) if \(n\le m\) and analogous inclusion holds for the indexes b.
Then it is easy to check that
Passing to the limit (n-i), (n-ii) and (n-iii) we can easily verify that:
-
(i)
\(\sum _ar_a^{N-1}+\sum _br_b^{N-1}\le C(N,v,\eta )\);
-
(ii)
\(\sum _a{\mathscr {H}}^{N-1}({\mathcal {C}}_{0,a})\le C(N,v)\)
-
(iii)
\(\cup _{n\ge 1}\tilde{{\mathcal {S}}}_n\subset {\mathcal {S}}\) and \({\mathscr {H}}^{N-1}(\cup _{n\ge 1}\tilde{{\mathcal {S}}}_n)=0\).
To conclude we are left to verify that
The first conclusion can be checked relying on (n-iv) above, taking into account the definition of the Hausdorff pre-measures \({\mathscr {H}}^{N-1}_{\xi }\).
The second conclusion can be verified since the balls \(B_{r_{f_n}}(x_{f_n})\) satisfy the volume bounds (5.13). Therefore, at any point \(x\in \tilde{{\mathcal {S}}}_f\), it holds that \(\lim _{r\rightarrow 0}{\mathscr {H}}^{N}(B_r(x))/\omega _Nr^N<1\), hence \(x\in {\mathcal {S}}\).
All in all, letting
we get the neck decomposition verifying the sought properties in the statement.
To address v) we just point out that, by (5.18), \({\mathcal {S}}^{\delta ,\eta }\) is covered by the countable union
up to \({\mathscr {H}}^{N-1}\)-negligible sets. Therefore it is \((N-1)\)-rectifiable by the neck structure Theorem 4.9.
Now we deal with vi). In order to do so we follow the last part of the proof of [29, Theorem 2.12], with simplifications due to the rigidity of codimension one.
We claim that the following hold:
-
(a)
if \(\eta <\eta (N)\) and \(B_{\tau ^{-1}r_b}(x_b)\) is an \((N,\eta )\)-symmetric ball such that \(r_b^2(N-1)\le \eta \), then there is no point of \({\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\) in \(B_{r_b}(x_b)\);
-
(b)
if \(\eta <\eta (N)\) and \(\delta <\delta (\eta ,N)\) then no \((\eta ,\delta )\)-neck region \({\mathcal {N}}_a=B_{2r_a}(x_a){\setminus }\bar{B}_{r_x}({\mathcal {C}})\) can contain points of \({\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\).
This will certainly suffice to establish (vi), so let us prove (a) and (b) above.
To prove (a) let us fix \(\varepsilon <{\mathsf {d}}_{GH}(B_1^{{\mathbb {R}}^N}(0),B_1^{{\mathbb {R}}^N_+}(0))/2\). Then by volume convergence, volume monotonicity and volume rigidity, if \(\eta <\eta (\varepsilon )=\eta (N)\), any tangent cone at any point \(x\in B_{r_b}(x_b)\) has unit ball \(\varepsilon \)-close to the unit ball of \({\mathbb {R}}^N\), therefore \(x\notin {\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\).
In order to prove (b) let us consider \(x\in {\mathcal {N}}_a=B_{2r_a}(x_a){\setminus }\bar{B}_{r_x}({\mathcal {C}}_a)\) and let \(y\in {\mathcal {C}}_a\) be such that \({\mathsf {d}}(x,y)={\mathsf {d}}(x,{\mathcal {C}}_a)\). Then by the first defining condition of neck region \(B_{4{\mathsf {d}}(x,y)}(y)\) is an \(\eta \)-boundary ball. Therefore, \(B_{{\mathsf {d}}(x,y)/2}(x)\) is \((N,\varepsilon )\)-symmetric if \(\eta <\eta (\varepsilon )\). Then, arguing as in the proof of (a) we infer that, if \(\varepsilon <\varepsilon (N)\), then \(x\notin {\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\). \(\square \)
6 Boundary rectifiability and stability
This section is dedicated to the proofs of the rectifiability and first stability results for boundaries of noncollapsed \({{\,\mathrm{RCD}\,}}\) spaces by means of the tools developed in section 5 and section 4.
6.1 Proof of the stability results
Let us start with a weak \(\varepsilon \)-regularity result. Basically, it amounts to saying that balls sufficiently close in the GH sense to a model boundary ball have a definite amount of boundary points. This will be sharpened later on in Corollary 8.7.
Theorem 6.1
Let \(N\ge 1\) be fixed. There exists \(\eta (N)>0\) and \(c(N)>1\) such that, if \(\eta \le \eta (N)\) and
where \(B_1(p)\) is a ball of an \({{\,\mathrm{RCD}\,}}(-\eta (N-1),N)\) space \((X,{\mathsf {d}},{\mathscr {H}}^N)\), then
Proof
The lower bound in (6.2) follows by combining Theorem 4.9 and Theorem 4.13. Indeed by means of the latter, for \(\eta >0\) small enough, we can build an \((\varepsilon ,\delta )\)-neck region over \(B_{4^{-1}\tau ^4}(p)\) and from (ii), (iii) in Theorem 4.9 and (4.29) we deduce that, up to take \(\varepsilon , \delta \) sufficiently small, it holds
The upper bound in (6.2) instead follows from Theorem 5.1. Indeed, it is sufficient to apply the neck decomposition with parameters \(\eta \) and \(\delta \) sufficiently small in such a way that, thanks to (vi) of Theorem 5.1, \({\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\subset {\mathcal {S}}^{\delta ,\eta }\) and then to rely on (iii) of the same statement to infer that
To conclude we observe that the dependence of the constant on the volume can be removed taking into account the volume convergence Theorem 2.17 and (6.1). \(\square \)
The \(\varepsilon \)-regularity theorem above directly yields a stability result for the absence of boundary under noncollapsing pGH convergence.
Theorem 6.2
Let \((X_n,{\mathsf {d}}_n,{\mathscr {H}}^N,x_n)\) be a sequence of noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) spaces with no boundary on \(B_2(x_n)\) in the sense of Definition 1.1. Assume that
Then \((Y,{\mathsf {d}}_Y,{\mathscr {H}}^N)\) has no boundary on \(B_1(y)\).
Proof
Let us argue by contradiction. Assume that there exists \(z\in B_1(y)\cap {\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2}\). Then we can find \(r\in (0,1/5)\) such that \({\mathsf {d}}_{GH}(B_r(z),B^{{\mathbb {R}}_+^N}_r(0))\le \frac{\eta (N)}{2} r\) where \(\eta (N)\) is as in Theorem 6.1. Let \(X_n\ni z_n\rightarrow z\in Y\). Then we have
for n big enough. Thanks to Theorem 6.1 above we can infer that
contradicting the assumption that \(X_n\) has no boundary in \(B_2(x_n)\supset B_r(z_n)\). \(\square \)
6.2 Rectifiable structure and volume estimates
The main goal of this section is to prove Theorem 1.4 (i), (ii) and (iii). This will be achieved through some intermediate steps.
Theorem 6.3
Let \(1\le N<\infty \) and \(v>0\) be fixed. Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be a noncollapsed \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) space and \(p\in X\) be such that \({\mathscr {H}}^N(B_1(p))>v>0\). Then the following hold:
-
(i)
the singular set \({\mathcal {S}}^{N-1}\) is \((N-1)\)-rectifiable;
-
(ii)
there exists a constant \(C=C(N,v)>0\) such that
$$\begin{aligned} {\mathscr {H}}^N(B_r({\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2})\cap B_1(p)) \le C r \quad \text {for any }r\in (0,1), p\in X. \end{aligned}$$(6.4)In particular
$$\begin{aligned} {\mathscr {H}}^{N-1}({\mathcal {S}}^{N-1}\cap B_1(p))\le C \quad \text {for any }p\in X; \end{aligned}$$(6.5) -
(iii)
at any \(x\in {\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2}\), the tangent cone is unique and isomorphic to the Euclidean half space \({\mathbb {R}}_+^{N-1}:=\{x\in {\mathbb {R}}^N:\, x_N\ge 0\}\).
Proof of Theorem 6.3 (i)
The rectifiability of \({\mathcal {S}}^{N-1}\) immediately follows from Theorem 5.1. Indeed
where \({\mathscr {H}}^{N-1}({\mathcal {S}}^{\delta ,\eta })=0\) and \({\mathcal {C}}_{0,a}\) is \((N-1)\)-rectifiable by (iv), (v) and (vi) of Theorem 5.1. \(\square \)
Proof of Theorem 6.3 (ii)
We divide the proof of (6.4) in three steps: volume estimate for the tubular neighbourhood intersected with neck regions (Step 1), volume estimate for the tubular neighbourhood intersected with regular balls (Step 2) and combination of the previous estimates (Step 3).
Let us point out that (6.5) can be obtained either as a consequence of Theorem 5.1, or as a consequence of the volume bound for the tubular neighbourhood (6.4) by a standard argument (cf. [14, Lemma 2.5]).
Step 1. We claim that if \(\varepsilon \le \varepsilon (N)\) and \(\delta \le \delta (N,v,\varepsilon )\), then for any \((\varepsilon ,\delta )\)-neck region \({\mathcal {N}}_a=B_{2r_a}(x_a){\setminus } {\overline{B}}_{r_x}({\mathcal {C}}_a)\) it holds
Observe that (6.6) is trivially verified when \(r> r_a/2\). Indeed
Therefore let us assume \(r \le r_a/2\). Notice that
Indeed, if this is not the case we could find \(x\in B_r({\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2}) \cap {\mathcal {N}}_a\cap B_{r_a}(x_a)\) and \(y\in {\mathcal {C}}_a\) such that \(2r\le {\mathsf {d}}(x,{\mathcal {C}}_a)={\mathsf {d}}(x,y)=:s\). Observe that \(B_{2s}(y)\) is an \(\varepsilon \)-boundary ball and
as a consequence of (iii) in Definition 4.3 (recall that we set \(\tau :=10^{-10N}\)). Being \(x\in B_r({\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2}) \cap {\mathcal {N}}_a\cap B_{r_a}(x_a)\) there exists
such that \({\mathsf {d}}(x,z)\le r\). This yields to a contradiction since
With (6.7) at our disposal let us conclude the proof of (6.6). Let \(x_1,\ldots ,x_m\in {\mathcal {C}}_a\) be such that \(\{B_{r}(x_i)\}\) is a disjoint family, \(2r> r_{x_i}\) for any \(i=1,\dots ,m\) and
It is immediate to check that
Hence from (6.7) we deduce
It remains only to show that \(m\le C(N) r^{1-N} r_a^{N-1}\). In order to do so we use (ii) in Theorem 4.9 which gives
with \(\mu \) packing measure associated to the neck region as in (4.6).
Step 2. We claim that, for any \(\varepsilon <\varepsilon (N)\), it holds
whenever \(B_{2r_b}(x_b)\) is an \((N,\varepsilon )\)-symmetric ball.
Let us choose \(\varepsilon (N)\) small enough to ensure that
whenever \(B_{2r_b}(x_b)\) is \((N,\varepsilon )\)-symmetric for some \(\varepsilon \le \varepsilon (N)\). This choice gives the implication
that easily leads to (6.15).
Step 3. Let us conclude the proof of (6.4) relying on Theorem 5.1 and the previous two steps. Let \(\varepsilon (N)>0\) be smaller than the ones in Step 1 and Step 2, and let \(\delta \le \delta (N,v,\varepsilon (N))\), smaller than the one in Step 2 and in Theorem 5.1. By Theorem 5.1 we can find a covering
where any \(B_{2r_b}(x_b)\) is an \((N,\varepsilon (N))\)-symmetric ball, \({\mathcal {N}}_a=B_{2r_a}{\setminus } {\overline{B}}_{r_x}({\mathcal {C}}_a)\) is an \((\varepsilon (N), \delta )\) neck region and \({\mathcal {S}}^{\delta ,\eta }\) is \({\mathscr {H}}^N\)-negligible. Then we can estimate
where the first inequality follows from (6.17), the second one from Step 1 and Step 2 and the last one from (iii) in Theorem 5.1. \(\square \)
Proof of Theorem 6.3 (iii)
When \(x\in {\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2}\) any tangent cone has the density at the tip equal to \(\Theta _X(x)=1/2\) since \(({\mathbb {R}}_+^N,{\mathsf {d}}_{\text {Eucl}},{\mathscr {H}}^N,0)\in {{\,\mathrm{Tan}\,}}_x(X,{\mathsf {d}},{\mathscr {H}}^N)\). Hence, Lemma 6.5 below implies that if \((Y,\varrho ,{\mathscr {H}}^N,y)\in {{\,\mathrm{Tan}\,}}_x(X,{\mathsf {d}},{\mathscr {H}}^N)\) then, either \(Y={\mathbb {R}}_+^{N}\) or it has no boundary according to Definition 1.1.
This along with a classical result (see for instance [29, Theorem 4.2]) ensuring that the set of tangent cones at given point \(x\in X\) is connected with respect to the pmGH topology, implies the sought conclusion. Indeed the set of pointed \({{\,\mathrm{RCD}\,}}(K,N)\) spaces without boundary is closed with respect to noncollapsed pGH convergence by Theorem 6.2. \(\square \)
Remark 6.4
It follows from the lower semicontinuity of the density \(\Theta \) and the observation that \(\Theta (x)=1/2\) for any \(x\in {\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\), that for any noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) m.m.s. \((X,{\mathsf {d}},{\mathscr {H}}^N)\), it holds that \(\Theta (x)\le 1/2\) for any \(x\in \partial X\).
Lemma 6.5
Let C(Y) be a noncollapsed \({{\,\mathrm{RCD}\,}}(0,N)\) m.m.s. which is a cone over an \({{\,\mathrm{RCD}\,}}(N-2,N-1)\) m.m.s. \((Y,{\mathsf {d}}_Y,{\mathscr {H}}^{N-1})\) with tip p. If C(Y) has boundary according to Definition 1.1 then \(\Theta (p)\le \frac{1}{2}\). Moreover, the equality holds if and only if C(Y) is isometric to the Euclidean half-space \({\mathbb {R}}_+^N\).
Proof
It is simple to verify that if C(Y) has boundary then Y has boundary as well. Observe that \((Y,{\mathsf {d}}_Y,{\mathscr {H}}^{N-1})\) is an \({{\,\mathrm{RCD}\,}}(N-2,N-1)\) space, therefore by [61] it has diameter less than \(\pi \). Let \(y\in {\mathcal {S}}^{N-2}{\setminus } {\mathcal {S}}^{N-3}(Y)\). Then the Bishop-Gromov inequality for the \({{\,\mathrm{CD}\,}}(N-2,N-1)\) condition ensures that
Therefore
where the second equality follows from the definition of metric measure cone while the inequality follows from (6.18) (cf. with (2.30)).
Let us now deal with the equality case. Assume that \(\Theta (p)=\frac{1}{2}\). We claim that C(Y) is a cone with respect to any \(x\in {\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2}\). Indeed, for any \(x\in C(Y)\), it holds
since
where we set \(R:={\mathsf {d}}(x,p)\) and the converse inequality can be obtained switching the roles of x and p.
Therefore, if we additionally assume that \(x\in {\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\), then
The volume cone implies metric cone theorem [36] (see also [27] for the previously considered case of Ricci limits) gives then the claimed conclusion.
Arguing inductively and relying on the cone splitting theorem we can now conclude that \(C(Y)={\mathbb {R}}_+^N\). \(\square \)
6.3 A second notion of boundary and further regularity properties
Recall that our working definition of boundary \(\partial X\), taken from [37], is as topological closure of the top dimensional singular stratum:
In [59] an alternative definition of boundary has been proposed, inspired by the one adopted for Alexandrov spaces [75]:
where cones with boundary are cones for which the cross section, that is a noncollapsed \({{\,\mathrm{RCD}\,}}(N-2,N-1)\) space thanks to [37, 61], has boundary. Arguing recursively we reduce to \({{\,\mathrm{RCD}\,}}(0,1)\) spaces and, thanks to the classification in [63], we know that they are isometric to manifolds of dimension one, possibly with boundary (in the topological sense). In this case we say that the space has boundary if and only if it is a manifold with boundary.
Theorem 6.6
Let \(1\le N<\infty \) and \(v>0\) be fixed. Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be an \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) space and \(p\in X\) be such that \({\mathscr {H}}^{N}(B_1(p))>v\). Then, \({\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2} = \emptyset \) if and only if \({\mathcal {F}}X = \emptyset \). Moreover the following hold:
-
(i)
\({\mathcal {F}} X\subset \partial X\);
-
(ii)
\(\partial X\) is \((N-1)\)-rectifiable and
$$\begin{aligned} {\mathscr {H}}^{N-1}(\partial X\cap&B_r(x))\le C(N,v) r^{N-1} \text {for any }x\in \partial X\cap B_1(p)\text { and }r\in (0,1);\qquad \end{aligned}$$ -
(iii)
$$\begin{aligned} {\mathscr {H}}^N(B_r(\partial X)\cap B_1(p)) \le C(N,v) r \quad \text {for any }r\in (0,1), p\in X, \end{aligned}$$(6.24)
Proof
From the inclusion \({\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2} \subset {\mathcal {F}}X\) we deduce that \({\mathcal {F}}X = \emptyset \) implies \({\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2}= \emptyset \). To prove the converse implication we show the following
by induction on N. The case \(N=1\) is trivial, thanks to the classification of \({{\,\mathrm{RCD}\,}}(0,1)\) spaces [63]. Let us deal with the inductive step. Given a noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) m.m.s. \((X,{\mathsf {d}},{\mathscr {H}}^N)\) and \(x\in {\mathcal {F}}X\) there exists a cone \((C(Y),\varrho ,{\mathscr {H}}^N,y)\in {{\,\mathrm{Tan}\,}}_x(X,{\mathsf {d}},{\mathfrak {m}})\) where the cross section \((Y,{\mathsf {d}}_Y,{\mathscr {H}}^{N-1})\) is an \({{\,\mathrm{RCD}\,}}(N-2,N-1)\) space such that \({\mathcal {F}} Y \ne \emptyset \). The inductive assumption gives
which easily yields the claimed conclusion.
Let us now prove the inclusion \({\mathcal {F}} X \subset \partial X\). Being \(\partial X\) closed, for any \(x\in X{\setminus } \partial X\) there exists \(r>0\) such that
Therefore any tangent cone \((Y,\varrho , {\mathscr {H}}^N,y)\) at x satisfies \({\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2}=\emptyset \) as a consequence of Theorem 6.1. Hence, from (6.25) we deduce \({\mathcal {F}} Y=\emptyset \) which, by definition, yields \(x\notin {\mathcal {F}} X\).
The rectifiability and the measure estimate in (ii) follow from Theorem 6.3 (i) and (6.5) respectively, taking into account the dimension estimate \(\dim {{\mathcal {S}}^{N-2}}\le N-2\). The volume bound for the tubular neighbourhood is a consequence of (6.4) and the very definition of \(\partial X\). \(\square \)
Remark 6.7
Thanks to Theorem 6.6, the notion of having boundary for a noncollapsed \({{\,\mathrm{RCD}\,}}\) space is independent of the definition of boundary we choose, between the ones in [37, 59]. This gives a positive answer to [59, Question 4.8].
Moreover, we can employ the stability result in Theorem 1.6 to prove that any pmGH limit \((X,{\mathsf {d}},{\mathscr {H}}^N,x)\) of a sequence of pointed \({{\,\mathrm{RCD}\,}}(K,N)\) spaces \((X_n, {\mathsf {d}}_n, {\mathscr {H}}^N,x_n)\) with \({\mathcal {F}}X_n = \emptyset \) satisfies \({\mathcal {F}}X=\emptyset \). This answers positively to [59, Question 5.11].
Remark 6.8
With the techniques of this paper we are not able to show the identity \({\mathcal {F}}X = \partial X\) in full generality, which would give a positive answer to [59, Question 4.9].
Nevertheless the analysis of the Laplacian of the distance from the boundary performed in section 7 allows us to prove this identity, together with the local Ahlfors regularity of the boundary volume measure, in the case of Ricci limits with boundary. Moreover, the improved neck structure Theorem 8.1 gives the same conclusion on \(\delta \)-boundary balls whenever \(\delta < \delta (N)\).
Corollary 6.9
Let \(1\le N<\infty \) be a fixed natural number. Then, for any \(v>0\) there exists a constant \(C=C(N,v)>0\) such that the following holds. If \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is an \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) space and \(x\in X\) is such that \({\mathscr {H}}^N(B_1(x))>v\), then

Proof
The first inequality above is true in great generality by the very definition of the Hausdorff and pre-Hausdorff measures.
Let us pass to the verification of the second one.
In order to do so let C(N, v) be such that \({\mathscr {H}}^{N-1}(\partial X\cap B_r(x))\le C(N,v) r^{N-1}\) for any \(x\in \partial X\cap B_1(p)\) and \(r\in (0,1)\) given by Theorem 1.4 (i). Let \(B_{r_i}(x_i)\) be any covering of a Borel set \(A\subset \partial X\cap B_1(x)\). Then, up to worsening the constant C(n, v) we can estimate
Passing to the infimum on the family of all coverings of A we get the sought estimate
\(\square \)
Corollary 6.10
Let \(1\le N<\infty \) be a fixed natural number and \(v>0\), then the following holds. Assume that \((X_n,{\mathsf {d}}_n,{\mathscr {H}}^N,p_n)\) are noncollapsed \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) spaces converging in the pGH topology to \((X,{\mathsf {d}},{\mathscr {H}}^N,p)\) and verifying the noncollapsing assumption \({\mathscr {H}}^N(B_1(p_n))>v\) for any \(n\in {\mathbb {N}}\). Then
where \(C(N,v)>0\) is the constant appearing in Corollary 6.9 above.
Proof
Let us denote by \(C\subset X\) the limit of the sequence of compact sets \(\partial X_n\cap \overline{B}_1(p_n)\) in the Hausdorff topology, possibly after passing to a subsequence. Here it is understood that the convergence of the ambient spaces is realized in a common proper metric space \((Z,{\mathsf {d}}_Z)\). Since, as we already remarked, any boundary point has density less than 1/2 and the density is lower semicontinuous along pGH converging sequences, we infer that \(\Theta _X(x)\le 1/2\) for any \(x\in C\). In particular \(C\subset {\mathcal {S}}\cap \overline{B}_1(p)\). Moreover, it easily follows from the Hausdorff dimension estimate \(\dim _H({\mathcal {S}}^{N-2})\le N-2\) that \({\mathscr {H}}^{N-1}_{\infty }(C)\le {\mathscr {H}}^{N-1}_{\infty }(\partial X\cap \overline{B}_1(p))\).
Taking into account the general inequality \({\mathscr {H}}^{N-1}_{\infty }\le {\mathscr {H}}^{N-1}\) and the discussion above, in order to prove (6.29) it suffices now to observe that
where the first inequality is a consequence of (2.3) while the second one follows from Corollary 6.9. \(\square \)
7 Distance from the boundary and noncollapsing of boundaries
In this section we are going to study some key properties of the distance function from the boundary. They will be useful to better understand the convergence of boundaries of \({{\,\mathrm{RCD}\,}}\) spaces under noncollapsing pGH convergence and their topological regularity in the next sections.
Given a noncollapsed \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) space \((X,{\mathsf {d}},{\mathscr {H}}^N)\) with boundary we denote by
the distance function from \(\partial X\).
Let us start with a key lemma regarding convergence of distance functions from the boundary in case the limit space is the model half space.
Lemma 7.1
Let \(1\le N<\infty \) be a fixed natural number. For any sequence of pointed \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) spaces \((X_n,{\mathsf {d}}_n,{\mathscr {H}}^N,x_n)\) such that \(B_8(x_n) \rightarrow B_8^{{\mathbb {R}}_+^N}(0)\) in the GH-topology one has that
Moreover \({\mathsf {d}}_{\partial X_n} \rightarrow {\mathsf {d}}_{\partial {\mathbb {R}}_+^N}\) uniformly and in \(W^{1,2}\) on \(B_2(0)\).
Proof
Taking into account Remark 2.1 it is sufficient to prove that the convergence holds in the Kuratowski sense.
Let us first prove that any limit point of a sequence of points \(y_n\in \partial X_n\cap {\overline{B}}_3(p_n)\) belongs to \(\partial {\mathbb {R}}^N_+\cap {\overline{B}}_3(0)\). To this aim it is sufficient to take into account Remark 6.4 and the lower semicontinuity of the density along pGH converging sequences of noncollapsed spaces. We conclude that the limit point has density less than 1/2 and therefore it belongs to the boundary of the half space, since those are the only singular points.
Next we wish to prove that any point in \(\partial {\mathbb {R}}^N_+\cap {\overline{B}}_3(0)\) is the limit of a sequence of points in \(\partial X_n\cap {\overline{B}}_3(p_n)\). To prove this claim we rely on the stability of the boundary. If the claim were false then we could find a scale \(r>0\) and points \(y_n\in X_n\) such that \(y_n\rightarrow 0\in {\mathbb {R}}^N_+\) and \(B_r(y_n)\subset X_n\) has no boundary for any \(n\in {\mathbb {N}}\). The contradiction follows by Theorem 6.1, since the ball \(B_r(0)\subset {\mathbb {R}}^N_+\) has boundary.
The uniform convergence \({\mathsf {d}}_{\partial X_n} \rightarrow {\mathsf {d}}_{\partial {\mathbb {R}}_+^N}\) on \(B_2(0)\) is a simple consequence of (7.1) (see again Remark 2.1).
To obtain the \(W^{1,2}\) convergence it is sufficient to observe that, as pointed out in [9], for uniformly continuous functions the uniform and the \(L^2\) convergence are equivalent. Moreover, \(\left|\nabla {\mathsf {d}}_{\partial X_n}\right|=\left|\nabla {\mathsf {d}}_{\partial X}\right|=1\) \({\mathscr {H}}^N\) a.e., therefore the \(W^{1,2}\) convergence follows from the volume convergence Theorem 2.17, since
\(\square \)
Given the stability Theorem 6.1 and Lemma 7.1 we can provide a useful improvement upon the form of the \(\varepsilon \)-isometry in Theorem 3.8 in the case of \(\delta \)-boundary balls.
Corollary 7.2
Let \(1\le N<\infty \) be a fixed natural number. Then for any \(\varepsilon >0\) there exists \(\delta =\delta (\varepsilon ,N)>0\) such that, if \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is a noncollapsed \({{\,\mathrm{RCD}\,}}(-\delta (n-1),N)\) space and \(B_2(x)\subset X\) is a \(\delta \)-boundary ball, then for any \(\varepsilon \)-splitting map \(u:B_1(x)\rightarrow {\mathbb {R}}^{N-1}\) such that \(u(x)=0\) one has that
and

Proof
Both conclusions can be obtained arguing by contradiction as in the proof of Theorem 3.8 and relying on Lemma 7.1. \(\square \)
7.1 Laplacian of the distance from the boundary
Next we study the Laplacian of the distance function from the boundary, which plays a fundamental role in establishing noncollapsing estimates for the boundary measure.
Let us begin by recalling that \({\mathsf {d}}_{\partial X}\) has locally measure valued Laplacian \(\varvec{\Delta }{\mathsf {d}}_{\partial X}\) on \(X{{\setminus }}\partial X\) as a consequence of the general representation theorem for Laplacians of distance functions [25, Corollary 4.16]. Moreover in [25, Corollary 4.16] it is also proved that the singular part of \(\varvec{\Delta }{\mathsf {d}}_{\partial X}\) on \(X{\setminus }\partial X\) is non positive. The following conjecture regards the absolutely continuous part.
Open Question 7.3
Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be a noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) m.m.s. for some \(K\in {\mathbb {R}}\) and \(1\le N<\infty \). Assume that \(\partial X\ne \emptyset \). Then
where \(\varvec{\Delta }^{\text {ac}}{\mathsf {d}}_{\partial X}\) denotes the absolutely continuous part of \(\varvec{\Delta }{\mathsf {d}}_{\partial X}\) on \(X{\setminus } \partial X\).
As we shall see below, Open Question 7.3 can be verified for Alexandrov spaces with curvature bounded from below, Riemannian manifolds with convex boundary and interior lower Ricci curvature bounds and their noncollapsed pGH limits. Notice that in this paper manifolds with convex boundary are those for which the second fundamental form with respect to the interior normal vector is non negative definite. Thanks to [89, Theorem 1.2.1] this condition implies that the interior part of the manifold is geodesically convex.
The main difficulty in order to answer to Open Question 7.3 in full generality is that a geometric condition needs to be turned into an analytic information: the fact that \(\partial X\) is the boundary of an \({{\,\mathrm{RCD}\,}}(K,N)\) space \((X,{\mathsf {d}},{\mathscr {H}}^N)\), therefore it is convex to some extent, should imply a bound on the Laplacian of the distance function.
In the case of Alexandrov spaces this difficulty can be circumvented since the distance from the boundary is concave (in the case of non negative sectional curvature) see [1] and [77, Theorem 3.3.1]. For smooth manifolds, instead, the regularity of the boundary is key to turn the non negativity of the second fundamental form into non negativity of the mean curvature of the boundary.
Let us first present the main analytic and geometric implications of a positive answer to Open Question 7.3.
Theorem 7.4
Let \(N\in {\mathbb {N}}\), \(N\ge 1\) and \(K\in {\mathbb {R}}\) be fixed. Given an \({{\,\mathrm{RCD}\,}}(K,N)\) m.m.s. \((X,{\mathsf {d}},{\mathscr {H}}^N)\) with \(\partial X\ne 0\) such that Open Question 7.3 is verified, the following hold:
-
(i)
\({\mathsf {d}}_{\partial X}\) has measure valued Laplacian on X and
 ;
; -
(ii)
for any \(p\in \partial X\) one has
$$\begin{aligned} {\mathscr {H}}^{N-1}(B_2(p)\cap \partial X) > C(K) {\mathscr {H}}^N(B_1(p)); \end{aligned}$$(7.6) -
(iii)
any tangent cone at \(x\in \partial X\) has boundary, in particular \({\mathcal {F}}X = \partial X\) (recall that \({\mathcal {F}}X\) is defined in (6.23)).
Let us state and prove a lemma that is independent of the validity of Open Question 7.3 and will play a role in the proof of Theorem 7.4.
Lemma 7.5
Let \(1\le N<\infty \) be a natural number and \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be a noncollapsed \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) metric measure space. Assume that \(\partial X\ne \emptyset \). Then \({\mathsf {d}}_{\partial X}:X\rightarrow [0,\infty )\) has locally measure valued Laplacian on \(X{\setminus }\partial X\) and the singular part of \(\varvec{\Delta }{\mathsf {d}}_{\partial X}\) is non positive on \(X{\setminus }\partial X\). Moreover
for some sequence \(r_i\downarrow 0\) and locally finite measure \(\mu \) on X (a priori depending on the chosen sequence).
Proof
We have already observed that \(\varvec{\Delta }{\mathsf {d}}_{\partial X}\) has locally measure valued Laplacian on \(X{\setminus }\partial X\) and the singular part of \(\varvec{\Delta }{\mathsf {d}}_{\partial X}\) is non positive on \(X{\setminus }\partial X\) as a consequence of [25, Corollary 4.16].
Let us verify that \({\mathsf {d}}_{\partial X}\) verifies (7.7). We treat only the case when \((X,{\mathsf {d}})\) (and a fortiori \(\partial X\)) is compact, the general one can be handled with an additional cut-off argument.
In order to do so we wish to pass to the limit in the integration by parts formula on (sufficiently regular) superlevel sets of the distance from the boundary.
Observe that, by the coarea formula Theorem 2.4, for almost every \(r>0\), the superlevel set \(\{{\mathsf {d}}_{\partial X}>r\}\) has finite perimeter. Moreover, the volume bound for the tubular neighbourhood of the boundary
obtained thanks to Theorem 6.6 (iii) via a covering argument, together with a further application of the coarea formula, yield the existence of a sequence \((r_i)\) with \(r_i\downarrow 0\) as \(i\rightarrow \infty \) and
Since \({\mathsf {d}}_{\partial X}\) has measure valued Laplacian on \(X{\setminus }\partial X=\{{\mathsf {d}}_{\partial X}>0\}\), the bounded vector field \(\nabla {\mathsf {d}}_{\partial X}\) has measure valued divergence on the same domain. Therefore, applying the Gauss Green theorem [21, Section 6] to the vector field \(\varphi \nabla {\mathsf {d}}_{\partial X}\) on the domain \(\{{\mathsf {d}}_{\partial X}>r_i\}\) we infer that
for some function \(f_i\) verifying
Thanks to (7.9) and (7.11) we can assume that, up to extracting a subsequence, the measures \(f_i{{\,\mathrm{Per}\,}}(\{{\mathsf {d}}_{\partial X}>r_i\})\) weakly converge to a finite measure \(\nu \) on X in duality with continuous functions. Therefore we can pass to the limit in (7.10) as \(i\rightarrow \infty \) to get that
as we claimed. \(\square \)
Proof of Theorem 7.4
Let \(\mu \) and \(r_i\downarrow 0\) be as in Lemma 7.5. If Open Question 7.3 holds then we deduce that
In particular \(\varphi \mapsto \int \nabla \varphi \cdot \nabla {\mathsf {d}}_{\partial X}\mathop {}\!\mathrm {d}{\mathscr {H}}^N + \int \varphi \mathop {}\!\mathrm {d}\mu + K\int \varphi {\mathsf {d}}_{\partial X}\mathop {}\!\mathrm {d}{\mathscr {H}}^N\) is a negative linear map. Hence there exists a nonnegative locally finite measure \(\nu \) such that
This implies that \({\mathsf {d}}_{\partial X}\) has measure valued Laplacian on X.
Let us now prove that

Observe first that \(\varvec{\Delta }{\mathsf {d}}_{\partial X}\ll {\mathscr {H}}^{N-1}\) as a consequence of the following more general observation, applied to \(b=\nabla {\mathsf {d}}_{\partial X}\): if b is a bounded vector field with measure valued divergence \(\varvec{\mathrm {div}}\,b\) on a noncollapsed \({{\,\mathrm{RCD}\,}}\) space \((X,{\mathsf {d}},{\mathscr {H}}^N)\), then \(\varvec{\mathrm {div}}\,b\ll {\mathscr {H}}^{N-1}\).
In order to prove the property above we rely on the integration by parts formula for bounded vector fields with measure valued divergence proved in this framework in [21], taking into account the bound \({{\,\mathrm{Per}\,}}(B_r(x))\le C_{K,N}r^{N-1}\) for any \(0<r<1\) and following the Euclidean strategy in [73]. Relying on these tools we infer that
which suffices to conclude that \(\varvec{\mathrm {div}}\,b\ll {\mathscr {H}}^{N-1}\).
Next observe that  is absolutely continuous with respect to
is absolutely continuous with respect to  , which is a locally finite measure on an \((N-1)\)-rectifiable set by Theorem 6.6. By standard differentiation of measures tools we infer that, in order to prove (7.13), we need to show that
, which is a locally finite measure on an \((N-1)\)-rectifiable set by Theorem 6.6. By standard differentiation of measures tools we infer that, in order to prove (7.13), we need to show that
The validity of (7.15) can be checked at any regular boundary point \(x\in {\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\), applying Lemma 7.1 to the sequence of scaled spaces converging to the tangent half-space. Indeed the \(W^{1,2}\) convergence of the distance functions, yields the weak convergence of their Laplacians, which yields in turn (7.15) by scaling.
We can now pass to the proof of (ii). Let \(\varphi \in {{\,\mathrm{Lip}\,}}(X)\) be nonnegative with bounded support. The coarea formula Theorem 2.4 yields
Using again the Coarea formula, the \({\mathscr {H}}^N\)-a.e. identity \(|\nabla {\mathsf {d}}_{\partial X}|^2=1\) and integrating by parts, we get
for any \(a\in C^{\infty }_c(0,\infty )\). A simple approximation and Lebesgue points argument allows plugging \(a(s)=\chi _{\{s\le r\}}\) on (7.16) for almost every \(r>0\), yielding
All in all we have
for a.e. \(s\ge 0\).
Let \(t\in (0,1)\). An additional approximation argument allows to plug \(\varphi = \chi _{B_t}(p)\) in the previous inequality. Setting \(f(s,t):= {\mathscr {H}}^N(B_s(\partial X)\cap B_t(p))\), we then infer that \(s\mapsto f(s,t)\) is absolutely continuous and
for a.e. \(s\in (0,1)\). This yields in turn
for a.e. \(s\in (0,1)\), thanks to the coarea formula and the bound
By using (7.17) and (7.19) it is simple to verify that \(s\mapsto \int _0^{1-s}f(s,1-r)\mathop {}\!\mathrm {d}r\) is absolutely continuous in (0, 1). We now prove that
for a.e. \(s\in (0,1)\).
For any \(t\in (0,1)\) we denote by \(I_t\subset [0,1]\) the set of \(s\in (0,1)\) such that (7.17) holds true. Given \(s\in \cap _{t\in {\mathbb {Q}}\cap (0,1)} I_t=:I\) and \(\varepsilon >0\) we consider \(q\in {\mathbb {Q}}\) such that \(s<q<s+\varepsilon \). Then we have
for any \(0<h<1\) small enough, as a consequence of (7.17). Therefore, using the fact that \(s<q\), we get
for any \(s\in I\). Letting \(\varepsilon \rightarrow 0\) we conclude
for any \(s\in I\).
Using once more (7.19) we easily deduce
which along with (7.22) gives (7.20) for any \(s\in I\) such that the derivative \(\frac{\mathop {}\!\mathrm {d}}{\mathop {}\!\mathrm {d}s} \int _0^{1-s}f(s,1-r)\mathop {}\!\mathrm {d}r\) exists.
We can finally conclude the proof of (7.6) by integrating (7.20) in (0, 1/2):
Let us now address (iii). This assertion can be obtained by combining Corollary 6.10 and the inequality
which follows in turn from the scaling invariant version of (7.6). \(\square \)
7.2 Alexandrov spaces and noncollapsed Ricci limits with boundary
We are able to verify Open Question 7.3 in the setting of Alexandrov spaces with curvature bounded below and in the case of Ricci limits with boundary.
Let us recall that an N-dimensional Alexandrov space with curvature bounded from below by k and equipped with the measure \({\mathscr {H}}^N\) is a noncollapsed \({{\,\mathrm{RCD}\,}}(k(N-1),N)\) space, see [78, 90].
Proposition 7.6
Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be an Alexandrov space with curvature bounded from below by k and assume that \(\partial X\ne \emptyset \). Then \({\mathsf {d}}_{\partial X}\) has locally measure valued Laplacian,
In particular, there exists a constant \(C(k,N)>0\) such that the following holds: if \(p\in \partial X\), then
Next we deal with the case of \({{\,\mathrm{RCD}\,}}\) spaces with boundary that are also smooth Riemannian manifolds, see [52]. This is a key tool in order to address the case of limits of Riemannian manifolds with boundary later. Let us point out that bounds for the Laplacian on the distance from the boundary in the sense of barriers and under different assumptions have been considered in [74] (see also the references therein).
Proposition 7.7
Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be a smooth N-dimensional Riemannian manifold with convex boundary \(\partial X\) (in the sense that the second fundamental form with respect to the interior normal is non negative definite) and Ricci curvature bounded from below by K in the interior. Then \({\mathsf {d}}_{\partial X}\) has locally measure valued Laplacian,
In particular
The lower bound for the volume of the boundary in the case of smooth \({{\,\mathrm{RCD}\,}}\) spaces with boundary allows us to get a more complete picture about their pGH limits. The last result of this section provides, in particular, a positive answer to [59, Questions 4.4, 4.7, 4.9] in this setting.
Theorem 7.8
Let \((X,{\mathsf {d}},{\mathscr {H}}^N,p)\) be the noncollapsed pGH limit of a limit of smooth N-dimensional pointed Riemannian manifolds \((X_n,{\mathsf {d}}_n, p_n)\) with convex boundary and Ricci curvature bounded from below by K in the interior. Assume that there exists \(R>0\) such that \(B_R(p_n)\cap \partial X_n\ne \emptyset \) for any \(n\in {\mathbb {N}}\). Then
-
(i)
\(\partial X\ne \emptyset \). Moreover, if points \(x_n\in \partial X_n\) converge to \(x\in X\), then \(x\in \partial X\);
-
(ii)
\({\mathsf {d}}_{\partial X}\) has measure valued Laplacian,
$$\begin{aligned} \varvec{\Delta }^{ac}{\mathsf {d}}_{\partial X}\le - K {\mathsf {d}}_{\partial X}\;\;\text {and}\;\; \varvec{\Delta }^{s}{\mathsf {d}}_{\partial X}\le 0 \quad \text {on }X{\setminus }\partial X. \end{aligned}$$(7.29)and
 (7.30)
(7.30) -
(iii)
\(\partial X={\mathcal {F}}X\),
 is locally Ahlfors regular and for any \(x\in \partial X\) any tangent cone at x has boundary.
is locally Ahlfors regular and for any \(x\in \partial X\) any tangent cone at x has boundary.
The remaining part of this subsection is devoted to the proof of Proposition 7.6, Proposition 7.7 and Theorem 7.8.
Proof of Proposition 7.6
We avoid introducing all the relevant background about calculus on Alexandrov spaces, since this is not the main topic of the paper. We refer to [3, 22] for the relevant notions and references.
In [1] (see also [77, Theorem 3.3.1]) it is proved that on any Alexandrov space with curvature bounded from below by k and non empty boundary, the distance function from the boundary is \({\mathcal {F}}k\)-concave, that is to say its restriction to any unit speed geodesic \(\gamma :[0,1]\rightarrow X\) verifies
in the sense of barriers. We already know that the singular part of \(\varvec{\Delta }{\mathsf {d}}_{\partial X}\) is non positive on \(X{\setminus }\partial X\) (see Lemma 7.5). It is then sufficient to prove that its absolutely continuous part verifies
Combining (7.31) with Alexandrov’s theorem (see [3, Proposition 7.5] for its proof in the setting of DC functions on Alexandrov spaces) and the fact that the restriction of \({\mathsf {d}}_{\partial X}\) to a minimizing geodesic connecting a regular point to a point of minimal distance on the boundary is affine, we infer that
where \({{\,\mathrm{Hess}\,}}^{\mathrm{{ac}}}{\mathsf {d}}_{\partial X}\) denotes the absolutely continuous part of the Hessian of \({\mathsf {d}}_{\partial X}\). Indeed, we recall that the tangent cone on an Alexandrov space can be equivalently characterised as the set of initial velocities of geodesics. Then (7.33) follows by tracing, since there is a direction v along which \({{\,\mathrm{Hess}\,}}^{\mathrm{{ac}}}{\mathsf {d}}_{\partial X}(v,v)=0\), while along all the others the estimate \({{\,\mathrm{Hess}\,}}^{\mathrm{{ac}}}{\mathsf {d}}_{\partial X}(v,v)\le -k{\mathsf {d}}_{\partial X}\) holds by (7.31).
The conclusion (7.32) follows from the fact that the Laplacian is the trace of the Hessian in this context, see [3, Proposition 5.8, 5.9].
The second conclusion of Proposition 7.6 follows from Theorem 7.4. \(\square \)
Proof of Proposition 7.7
Observe that, as pointed out in [52], smooth Riemannian manifolds with convex boundary and Ricci curvature bounded from below in the interior are \({{\,\mathrm{RCD}\,}}\) spaces.
Also in this case it is sufficient to deal only with the absolutely continuous part of the Laplacian. The bound (7.27) can be obtained starting from the following observation: since the boundary is smooth and convex it has non positive second fundamental form with respect to the exterior normal. Therefore by tracing we infer that it has nonpositive mean curvature with respect to the exterior normal. By smoothness again we infer that the restriction of the a.c. part of the Laplacian of the distance from the boundary on the boundary is non positive (it coincides with the mean curvature). By the localization technique [25] we can then propagate the non positivity of the Laplacian on the boundary to the interior to obtain (7.27).
More in detail, we recall that \({\mathsf {d}}_{\partial X}\) induces a decomposition of the Riemannian manifold into rays \((X_{\alpha },{\mathfrak {m}}_{\alpha },{\mathsf {d}})\) and an associated disintegration of the volume measure:
where \({\mathcal {Q}}\) is a set parametrizing the rays in the decomposition and \(\mathrm {q}\) is a suitable weight on \({\mathcal {Q}}\).
Moreover, for \(\mathrm {q}\)-a.e. ray \((X_{\alpha })\) the one dimensional metric measure space \((X_{\alpha },{\mathfrak {m}}_{\alpha },{\mathsf {d}})\) is a \({{\,\mathrm{CD}\,}}(K,N)\) space, hence \({\mathfrak {m}}_{\alpha }=h_{\alpha }{\mathscr {H}}^1\) for some density \(h_{\alpha }\) which is \(\log -K\) concave, once we parametrize the ray \(X_{\alpha }\) with a geodesic \(\gamma _{\alpha }\) such that its ending point belongs to \(\partial X\).
By [25] we also know that
with canonical identifications. The sought conclusion follows observing that since \(h_{\alpha }\) is \(\log -K\) concave, it holds that
Let \(p=\gamma _{\alpha }(t)\) and \(\gamma _{\alpha }(s)\) is the footpoint on \(\partial X\) of the minimizing geodesic for the distance to the boundary \(\gamma _{\alpha }\). Since we already pointed out that the convexity of the boundary yields \((-\log h_{\alpha })'(\gamma _{\alpha }(s))\le 0\) when \(\gamma _{\alpha }(s)\in \partial X\), we infer from (7.36) and (7.35) that,
The inequality (7.28) and the fact that \({\mathsf {d}}_{\partial X}\) has measure valued Laplacian globally now follow from Theorem 7.4. \(\square \)
Remark 7.9
For general \({{\,\mathrm{RCD}\,}}(K,N)\) spaces \((X,{\mathsf {d}},{\mathscr {H}}^N)\), the missing ingredient for the Riemannian strategy above is a counterpart of the non positive mean curvature condition with respect to the exterior normal along the boundary.
Proof Theorem 7.8
Let us start by proving the second part of (ii). The first part will directly follow. In order to do so we observe that, if \(x_n\in \partial X_n\), then by (the scale invariant version of) (7.28) we infer that
Therefore we can apply Corollary 6.10 to get that
where \(v>0\) is a noncollapsing bound for \({\mathscr {H}}^N(B_1(x_n))\). From (7.40) we infer in particular that \(x\in \partial X\).
By the stability Theorem 1.6 we know that if \(x\in \partial X\) then there exists a sequence \(\partial X_n\ni x_n\rightarrow x\), as \(n\rightarrow \infty \). Therefore \({\mathsf {d}}_{\partial X_n}\) converge locally uniformly and locally in \(W^{1,2}\) to \({\mathsf {d}}_{\partial X}\). Hence we can pass to the limit their measure valued Laplacians and the bounds obtained in Proposition 7.7 to infer that \({\mathsf {d}}_{\partial X}\) has measure valued Laplacian satisfying the bound (7.29).
The remaining conclusions follow immediately from Theorem 7.4. \(\square \)
8 Improved neck structure and boundary measure convergence
In this section we are going to improve upon the regularity of balls sufficiently close to the model boundary ball on the half-space. This will provide a key tool in order to obtain topological regularity of boundaries, away from sets of ambient codimension two, and convergence of the boundary measures under noncollapsing pGH convergence as stated in Theorem 1.8.
8.1 Improved neck structure theorem and boundary volume rigidity
Below we state the key result we will rely on. As in the case of \((N,\delta )\)-symmetric balls, where regularity propagates at all locations and scales, in the case of a \(\delta \)-boundary ball we shall see that balls centered at boundary points are still \(\delta '\)-boundary balls at any scale, while balls centered at interior points become \((N,\delta ')\)-symmetric at sufficiently small scales.
Theorem 8.1
Let \(1\le N<\infty \) be a fixed natural number. For any \(0<\varepsilon <\varepsilon (N)\), \(\delta \le \delta (N,\varepsilon )\) and for any \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) m.m.s. \((X,{\mathsf {d}},{\mathscr {H}}^N)\), \(p\in X\) such that \(B_2(p)\) is a \(\delta \)-boundary ball, the following properties hold:
-
(i)
for any \(x\in \partial X\cap B_1(p)\) and any \(r\in (0,1)\) there exists an \(\varepsilon r\)-GH isometry
$$\begin{aligned} \Psi _{x,r}:B_r^{{\mathbb {R}}_+^N}(0) \rightarrow B_r(x); \end{aligned}$$ -
(ii)
for any \(x\in \partial X\cap B_1(p)\) and for any \(0<r<1\), setting \({\mathcal {L}}_{x,r}:= \Psi _{x,r}(\{x_N=0\})\) it holds
$$\begin{aligned} {\mathsf {d}}_H(\partial X\cap B_r(x), {\mathcal {L}}_{x,r}\cap B_r(x)) \le \varepsilon r. \end{aligned}$$(8.1)It follows in particular that
$$\begin{aligned} {\mathsf {d}}_{GH}(\partial X\cap B_r(x),B^{{\mathbb {R}}^{N-1}}_r(0))\le 2\varepsilon r; \end{aligned}$$(8.2) -
(iii)
for any \(x\in B_{1/2}(p){\setminus } \partial X\) and \(r\in (0, {\mathsf {d}}_{\partial X}(x)/2)\) the ball \(B_r(x)\) is \((N,\varepsilon )\)-symmetric.
The proof of Theorem 8.1 builds upon the following \(\varepsilon \)-regularity results for the boundary, which is based in turn on the stability of boundaries Theorem 6.1 and the volume rigidity for cones with boundary Lemma 6.5.
Theorem 8.2
(Volume \(\varepsilon \)-regularity for the boundary) Let \(N\in {\mathbb {N}}\), \(N\ge 1\) be fixed. For any \(\varepsilon >0\), if \(\delta \le \delta (N,\varepsilon )\) and \((X,{\mathsf {d}},{\mathscr {H}}^N,x)\) is an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) pointed m.m.s., \(x\in \partial X\) and \({\mathscr {H}}^N (B_1(x)) \ge \frac{1}{2}\omega _N-\delta \), then
Proof
We divide the proof into two steps, first proving a weak version of the statement, where we additionally assume a definite size of boundary points in the given ball, and then passing to the strong form via bootstrap.
Step 1. We claim that the following holds: for any \(\varepsilon >0\) and \(c>0\), if \(\delta \le \delta (N,\varepsilon ,c)\) and \((X,{\mathsf {d}},{\mathscr {H}}^N,x)\) is an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) pointed m.m.s., \(x\in \partial X\), \({\mathscr {H}}^N (B_1(x)) \ge \frac{1}{2}\omega _N-\delta \) and \({\mathscr {H}}^{N-1}(\partial X\cap B_{1/2}(x))\ge c\), then
We argue by contradiction. Let us assume that for some \(\varepsilon >0\) and \(c>0\) there is a sequence \((X,{\mathsf {d}}_n,{\mathscr {H}}^N,x_n)\) of \({{\,\mathrm{RCD}\,}}(-1/n,N)\) p.m.m.s. with \(x_n\in \partial X_n\), such that \({\mathscr {H}}^N(B_1(x_n))\ge \frac{1}{2}\omega _N -\frac{1}{n}\), \({\mathscr {H}}^{N-1}(\partial X_n\cap B_{1/2}(x_n))\ge c\) and
Up to extracting a subsequence \((X_n, {\mathsf {d}}_n,{\mathscr {H}}^N, x_n) \rightarrow (X,{\mathsf {d}},{\mathscr {H}}^N,x)\) in the pmGH topology.
Notice that, by Corollary 6.10 and the uniform lower bound on the boundary measure, we infer that \(\partial X\cap \bar{B}_{1/2}(x)\ne \emptyset \).
Since x is limit of boundary points it holds \(\Theta _X(x)\le 1/2\), by lower semicontinuity of the density. Therefore, by volume convergence and thanks to the volume pinching assumption, \({\mathscr {H}}^N(B_r(x)) = \omega _N/2\) for any \(r\in [0,1]\). Hence the volume cone implies metric cone theorem (see [36]) gives that \(B_{1/2}(x)\) is isometric to the ball of radius 1/2 of a cone C(Z) centered at a tip point \(z\in C(Z)\) with isometry sending x to z. The sought contradiction comes from Lemma 6.5. Indeed Z has boundary and \(\Theta (z)=\frac{1}{2}\), therefore C(Z) is isometric to \({\mathbb {R}}^N_+\).
Step 2. Next we wish to remove the lower volume boundary assumption. In order to do so we first observe that, by a limiting argument, it is sufficient to prove the statement under the assumption that \(x\in {\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\).
Let us set \(c:=4^{-N}c(N)^{-1}\) and assume without loss of generality that \(\varepsilon <\eta (N)\), where c(N) and \(\eta (N)\) are as in Theorem 6.1. We wish to prove that \(\delta (N,\varepsilon )=\delta (N,\varepsilon ,c)\) given by the previous step does the right job. Let us argue by contradiction. If this is not the case then we can find \(0<r<1\) such that
but
since we know that the only element of the tangent cone at x is \({\mathbb {R}}^N_+\) (cf. with Theorem 6.3 (iii)).
Observe that
by our choice of c and (the scale invariant version of) Theorem 6.1.
Moreover, by volume monotonicity,
Applying the result of Step 1 (in scale invariant form) we infer that
therefore reaching a contradiction with (8.7). \(\square \)
Remark 8.3
Under the same assumptions of Theorem 8.2, it follows by volume monotonicity and scaling that (8.4) can be slightly improved to the statement
for any \(0<r<1\).
Proof of Theorem 8.1
Let us begin by observing that for any \(\delta \le \delta (\delta _0,N)\) if \(B_2(p)\) is a \(\delta \)-boundary ball of an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) space then
This claim can be checked arguing by contradiction and exploiting the fact that boundary points converge to boundary points when the limit ball is isometric to a ball centered on the boundary of the half space \({\mathbb {R}}_+^N\) (cf. with Lemma 7.1).
Next, by volume convergence, choose \(\delta _0=\delta _0(\varepsilon ,N)<\varepsilon /2\) such that if \(B_1(x)\) is a \(\delta _0\)-boundary ball on an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) and \(x\in \partial X\), then the assumptions of Theorem 8.2 are satisfied.
If we choose \(\delta \) accordingly given by the observations above, then by Theorem 8.2 we infer that, for any \(x\in \partial X\) and for any \(0<r<1\), \(B_r(x)\) is an \(\varepsilon \)-boundary ball.
From now on we let
be \(\varepsilon r\)-isometries, for any \(x\in \partial X\) and any \(0<r<1\).
Let us prove (ii). We first prove that for any \(z\in B_r^{{\mathbb {R}}^N_+}(0)\cap \{x_N=0\}\) there exists \(y\in B_r(x)\cap \partial X\) such that \({\mathsf {d}}(\Psi _{x,r}(z),y)\le C(N)\varepsilon r\). In order to do so it is sufficient to observe that for any \(s>0\) the ball \(B_{sr}(\Psi _{x,r}(z))\) is an \(s^{-1}\varepsilon \)-boundary ball. By Theorem 6.1, if \(s^{-1}\varepsilon <\eta (N)\), then there exists a boundary point \(y\in B_{rs}(\Psi _{x,r}(z))\cap \partial X\). Therefore, minimizing we infer that there exists a boundary point \(y\in B_r(x)\cap \partial X\) such that \({\mathsf {d}}(\Psi _{x,r}(z),y)\le C(N)\varepsilon r\), where \(C(N):=1/\eta (N)\).
It remains to prove that for any \(y\in B_r(x)\cap \partial X\) there exists \(z\in B_r^{{\mathbb {R}}^N_+}(0)\cap \{x_N=0\}\) such that \({\mathsf {d}}(y,\Psi _{x,r}(z))\le C(N)\varepsilon r\). In order to do so it is sufficient to observe that, by elementary considerations, if \(B_1(p)\subset {\mathbb {R}}^N_+\) is an \(\varepsilon \)-boundary ball, then \({\mathsf {d}}(p,\{x_N=0\})\le C(N)\varepsilon \), therefore by scaling invariance of the half-space, if \(B_r(p)\) is an \(\varepsilon \)-boundary ball, then \({\mathsf {d}}(p,\{x_N=0\})\le C(N)\varepsilon r\).
Let us finally prove (iii). In order to obtain the conclusion it is sufficient to prove the following statement: for any \(\varepsilon >0\) there exists \(\delta >0\) such that if \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) m.m.s., \(p\in X\) and \(B_4(p)\) is a \(\delta \)-boundary ball, then for any \(x\in B_1(p){\setminus }\partial X\) the ball \(B_{{\mathsf {d}}_{\partial X}(x)/2}(x)\) is \((N,\varepsilon )\)-symmetric. Indeed, if \(B_{{\mathsf {d}}_{\partial X}(x)/2}(x)\) is \((N,\varepsilon )\)-symmetric, then by volume convergence Theorem 2.17 it has almost Euclidean volume and by volume almost rigidity [37, Theorem 1.6] we infer that \(B_r(x)\) is \((N,\varepsilon )\)-symmetric for any \(0<r<{\mathsf {d}}_{\partial X}(x)/2\), up to worsening \(\varepsilon \).
Let us now prove the claimed conclusion. Let \(q\in \partial X\) be such that \({\mathsf {d}}_{\partial X}(x) = {\mathsf {d}}(q,x)\) and set \(r:= 2{\mathsf {d}}_{\partial X}(x)\). As a consequence of (i) and (ii) we know that there exists an \(\varepsilon r\)-GH isometry \(\Psi _{x,r}: B_r^{{\mathbb {R}}_+^N}(0) \rightarrow B_r(q)\).
By elementary considerations we can find \(z\in {\mathbb {R}}_+^N\) such that
and
is an \(8\varepsilon r\)-GH isometry. \(\square \)
8.2 Topological regularity of the boundary
Thanks to Theorem 8.1 we better understand the geometry of \(\delta \)-boundary balls. Below we build a parametrization of the boundary of a \(\delta \)-boundary ball well suited for its geometry. In particular this parametrization will put us in position to control both the topology and the volume near to sufficiently regular boundary points (cf. with [13, 28, 59] in the case of interior regular points).
With respect to Theorem 4.9 here we heavily rely on Theorem 8.1 and on the transformation Proposition 3.13 to get bi-Hölder continuity of the splitting map, as in [29].
Theorem 8.4
Let \(1\le N<\infty \) be a fixed natural number. Then for each \(0<\varepsilon <1/5\) there exists \(\delta =\delta (\varepsilon ,N)>0\) such that for any \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) space \((X,{\mathsf {d}},{\mathscr {H}}^N)\) and for any \(\delta \)-boundary ball \(B_{16}(p)\subset X\), \(\partial X\cap B_8(p)\) is homeomorphic to a smooth \((N-1)\)-dimensional manifold without boundary.
Moreover, there exists a map \(u:B_8(p)\rightarrow {\mathbb {R}}^{N-1}\) verifying the following properties:
-
(i)
\(u:B_8(p)\rightarrow {\mathbb {R}}^{N-1}\) is an \(\varepsilon \)-splitting map;
-
(ii)
there exists a closed set \(U\subset B_1(p)\cap \partial X\) such that
$$\begin{aligned} {\mathscr {H}}^{N-1}\left( (B_1(p)\cap \partial X){\setminus } U\right) \le \varepsilon \end{aligned}$$(8.16)and
$$\begin{aligned} (1-\varepsilon ){\mathsf {d}}(x,y)\le \left|u(x)-u(y)\right|\le (1+\varepsilon ){\mathsf {d}}(x,y) \quad \text {for any }x,y\in U;\qquad \end{aligned}$$(8.17) -
(iii)
for any \(x,y\in \partial X\cap B_1(p)\) it holds that
$$\begin{aligned} (1-\varepsilon ){\mathsf {d}}(x,y)^{1+\varepsilon }\le \left|u(x)-u(y)\right|\le (1+\varepsilon ){\mathsf {d}}(x,y); \end{aligned}$$(8.18) -
(iv)
\(u(B_1(p)\cap \partial X)\supset B_{1-2\varepsilon }^{{\mathbb {R}}^{N-1}}(0)\).
Proof
The fact that \(B_8(p)\cap \partial X\) is homeomorphic to a smooth \(N-1\)-dimensional manifold without boundary follows from Theorem 8.1 (ii) thanks to Reifenberg’s theorem for metric spaces [28, Theorem A.1.1], see also [13, 59, 81].
Let us fix \(0<\eta <\varepsilon \) to be specified later. Choosing \(\delta \) small enough we can build an \(\eta \)-splitting map \(u:B_8(p)\rightarrow {\mathbb {R}}^{N-1}\) by Theorem 3.8. This in particular proves (i).
Let us now show (ii). We set

Notice that U is closed and \(u: B_s(x) \rightarrow {\mathbb {R}}^{N-1}\) is a \(C(N)\eta ^{1/4}\)-splitting map for any \(s\in (0,5)\), by Lemma 4.16. For \(\delta \) and \(\eta \) small enough we deduce from Corollary 7.2 that
for any \(x\in U\) and \(s\in (0,5/2)\). In particular, given \(x,y\in U\) and \(s={\mathsf {d}}(x,y)(1+\varepsilon )\), it holds
therefore yielding (8.17).
Let us prove (8.16). A standard Vitali’s covering argument produces a disjoint family of balls \(\{B_{s_i}(x_i)\}_{i\in {\mathbb {N}}}\) with \(x_i\in B_1(p)\cap \partial X\), \(s_i\in (0,1)\) such that

Relying on (8.19), the Bishop-Gromov inequality, Remark 4.8 and Theorem 1.4 (i) (see also Theorem 6.6 (ii)), we conclude that
for \(\eta \) sufficiently small.
The Hölder estimate (8.18) will follow from Theorem 5.1 (i) and the transformation Proposition 3.13, arguing as in the proof of [29, Theorem 7.10].
More precisely, if \(x,y\in B_1(p)\cap \partial X\) we set \(r:={\mathsf {d}}(x,y)\). Then by Theorem 8.1 (i) we infer that \(B_r(x)\) is an \(\eta \)-boundary ball, for \(\eta \) small to be chosen later, if \(\delta \le \delta (N,\eta )\). Then we apply the transformation Proposition 3.13 to obtain existence of a lower triangular matrix \(T_{x,r}\) such that \(T_{x,r}u:B_r(x)\rightarrow {\mathbb {R}}^{N-1}\) is an \(\varepsilon '\)-splitting map for \(\varepsilon '\) small to be chosen later and for any \(\eta \le \eta (N,\varepsilon ')\). Taking into account Corollary 7.2 we obtain that
Taking into account the matrix growth estimate \(\left|T_{x,r}\right|\le r^{-\varepsilon }\) (cf. Corollary 3.16) and that \(r=d(x,y)\) we get that
The upper bound in (8.18) follows from Remark 3.3.
To prove the last assertion we argue as in [59, Remark 2.10]. We claim that there exists \(0<s<1\) such that
To this aim we observe that \(u({\overline{B}}_s(p)\cap \partial X) \cap {\overline{B}}_{1-2\varepsilon }^{{\mathbb {R}}^{N-1}}(0)\) is non empty and closed in \({\overline{B}}_{1-2\varepsilon }^{{\mathbb {R}}^{N-1}}(0)\). Moreover, it holds
whenever \(s^{1+\varepsilon }(1-\varepsilon )>1-2\varepsilon \). Indeed for any \(q\in \partial B_s(p)\cap \partial X\) one has
as a consequence of (8.18). Therefore, for such a choice of s the set \(u({\overline{B}}_s(p)\cap \partial X) \cap {\overline{B}}_{1-2\varepsilon }^{{\mathbb {R}}^{N-1}}(0)\) is also open in \({\overline{B}}_{1-2\varepsilon }^{{\mathbb {R}}^{N-1}}(0)\) as a consequence of the invariance of the domain (here we are using that \(B_8(p)\cap \partial X\) is an \((N-1)\)-dimensional topological manifold, as we already pointed out). \(\square \)
Remark 8.5
In the smooth case, i.e. when \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is a Riemannian manifold with convex boundary and Ricci curvature bounded below by \(-\delta (N-1)\), the map \(u:B_1(p)\cap \partial X\rightarrow {\mathbb {R}}^{N-1}\) obtained in Theorem 8.4 is also a diffeomorphism onto its image. This follows by observing that u is smooth and
Observe that \(u:B_2(p) \rightarrow {\mathbb {R}}^{N-1}\) is a \(\varepsilon \)-splitting map where \(\varepsilon \le \varepsilon (N)\). Let \(x\in B_1(p)\cap \partial X\). By the transformation Proposition 3.13 for any \(r\le 1\), there exists an \(N\times N\) matrix \(A_{x,r}\) such that \(A_{x,r}\circ u : B_r(x) \rightarrow {\mathbb {R}}^{N-1}\) is a \(\delta \)-splitting map, where \(\delta \le \delta (\delta ',N)\). For \(r\le r_x\) small enough, standard elliptic regularity estimates up to the boundary give
which implies that \(\mathop {}\!\mathrm {d}u_x\) is nondegenerate.
Corollary 8.6
Let \(1\le N<\infty \) be a natural number and \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be an \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) metric measure space. Assume that \(\partial X\ne \emptyset \), then for any \(0<\alpha <1\) there exists \(U_{\alpha }\subset \partial X\) such that:
-
(i)
\(U_{\alpha }\) is relatively open and dense in \(\partial X\);
-
(ii)
\(\dim _{H}(\partial X{\setminus } U_{\alpha })\le N-2\);
-
(iii)
\(U_{\alpha }\) is an \((N-1)\)-dimensional \(\alpha \)-Hölder topological manifold without boundary and the charts can be chosen with components that are restriction of harmonic maps (on the ambient space).
Proof
Fix \(\alpha \in (0,1)\). Thanks to Theorem 8.4 we can find \(\delta <\delta (N,\alpha )\) with the property that if \(B_{16}(p)\) is a \(\delta \)-boundary ball of an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) m.m.s. \((X,{\mathsf {d}},{\mathscr {H}}^N)\), then \(\partial X\cap B_1(p)\) is a \(C^{\alpha }\) manifold of dimension \((N-1)\).
For any \(x\in {\mathcal {S}}^{N-1}{\setminus }{\mathcal {S}}^{N-2}\) we consider \(r_x\in (0,\delta )\) such that \(B_{16 r_x}(x)\) is a \(\delta \)-boundary ball and we set
By construction \(U_\alpha \) satisfies (iii). Notice that \(U_{\alpha }\) is open and dense in \(\partial X\) and \(\partial X{\setminus } U \subset {\mathcal {S}}^{N-2}\), yielding (i) and (ii). \(\square \)
Corollary 8.7
Let \(1\le N<\infty \) be a fixed natural number. For any \(\varepsilon >0\) and \(\delta <\delta (\varepsilon ,N)>0\) the following holds. If \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) space and \(B_{16}(p)\) is a \(\delta \)-boundary ball, then
Moreover, \({\mathcal {F}}X\cap B_1(p)=\partial X\cap B_1(p)\) and for any \(x\in \partial X\cap B_1(p)\), any tangent cone at x has boundary.
Proof
Let \(\varepsilon '<\varepsilon \) to be fixed later. For \(\delta \le \delta (N,\varepsilon ')\) we find a \(\varepsilon '\)-splitting function \(u:B_8(p)\rightarrow {\mathbb {R}}^{N-1}\) satisfying (i)-(iv) in Theorem 8.4 with \(\varepsilon '\) in place of \(\varepsilon \). Let in particular \(U\subset B_1(p)\cap \partial X\) be the good set appearing in Theorem 8.4 (ii).
The inclusion \(u(U)\subset B_{1+\varepsilon '}(0)\) implies
On the other hand since \(u(B_1(p)\cap \partial X)\supset B_{1-2\varepsilon '}^{{\mathbb {R}}^{N-1}}(0)\), \(u((\partial X\cap B_1(p)){\setminus } U)\le C(N)\varepsilon '\) and u is bi-Lipschitz on U we infer that
The sought conclusion (8.24) follows from (8.25) and (8.26) by choosing \(\varepsilon '\) small enough.
The second part of the statement follows from (8.24) taking into account the following general property: given a noncollapsed \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) space \((X,{\mathsf {d}},{\mathscr {H}}^N)\) and a point \(x\in \partial X\) such that
then any tangent cone to \((X,{\mathsf {d}})\) at x has boundary.
The verification of the claim above follows from Corollary 6.10, taking into account the scaling properties of \({\mathscr {H}}^{N-1}\). \(\square \)
8.3 Convergence of boundary measures
Let us recall that for measures defined on sequences of metric spaces converging in the pGH sense, weak convergence is understood in duality with continuous functions with bounded support once the pGH converging metric spaces are embedded in a common proper metric space (cf. [7, 8]).
In this framework, two standard consequences of weak convergence are the lower semicontinuity of the evaluation on open sets and the upper semicontinuity of the evaluation on closed sets: if \(\mu _n\) are locally finite measures on Z weakly converging to \(\mu \) in duality with continuous functions with bounded support as \(n\rightarrow \infty \) and \(A\subset Z\) and \(C\subset Z\) are an open and a closed subset respectively, then
From the two properties above one can easily infer the full convergence \(\lim _{n\rightarrow \infty }\mu _n(O)=\mu (O)\), for any Borel set \(O\subset Z\) such that \(\mu (\partial O)=0\), where we denoted by \(\partial O\) the topological boundary of O.
We now prove Theorem 1.8 which is restated below for reader’s convenience.
Theorem 8.8
(Boundary Volume Convergence) Let \(1\le N<\infty \) be a fixed natural number. Assume that \((X_n,{\mathsf {d}}_n,{\mathscr {H}}^N,p_n)\) are \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) spaces converging in the pGH topology to \((X,{\mathsf {d}},{\mathscr {H}}^N,p)\). Then

In particular
whenever \(X_n\ni x_n\rightarrow x\in X\) and \({\mathscr {H}}^{N-1}(\partial X\cap \partial B_r(x))=0\).
Proof
Set  . Up to extracting a subsequence one has that \(\nu _n \rightarrow \nu \) weakly, where \(\nu \) is a nonnegative measure on X satisfying
. Up to extracting a subsequence one has that \(\nu _n \rightarrow \nu \) weakly, where \(\nu \) is a nonnegative measure on X satisfying
-
(i)
\(\nu (B_r(x)) \le C(N) r^{N-1}\) for any \(x\in X\) and a.e. \(r\in (0,2)\);
-
(ii)
\({{\,\mathrm{supp}\,}}\nu \subset {\mathcal {S}}^{N-1}\).
Here we have used standard compactness theorem for measures along with Theorem 1.4 (i), the lower semicontinuity of the density \(\Theta _{X_n}\) w.r.t. the GH convergence, and Remark 6.4. We need to prove that  .
.
Let us begin by observing that, as a consequence of (i) and (ii), it holds that  . In particular if \({\mathcal {S}}^{N-1}(X){\setminus } {\mathcal {S}}^{N-2}(X) = \emptyset \) then
. In particular if \({\mathcal {S}}^{N-1}(X){\setminus } {\mathcal {S}}^{N-2}(X) = \emptyset \) then  . We can therefore assume that \({\mathcal {S}}^{N-1}(X){\setminus } {\mathcal {S}}^{N-2}(X) \ne \emptyset \). To get the claimed conclusion it is enough to verify that
. We can therefore assume that \({\mathcal {S}}^{N-1}(X){\setminus } {\mathcal {S}}^{N-2}(X) \ne \emptyset \). To get the claimed conclusion it is enough to verify that
thanks to a classical result about differentiation of measures [62]. Here we used that \(\partial X\) is \((N-1)\)-rectifiable with locally finite \({\mathscr {H}}^{N-1}\)-measure.
To prove (8.30) we rely on Corollary 8.7. Observe that we can check (8.30) just considering regular boundary points \(x\in {\mathcal {S}}^{N-1}{\setminus } {\mathcal {S}}^{N-2}\) for which the limit
exists.
Let us fix \(\delta >0\). For any \(x\in \partial X\) as above there exists \(r_x<1\) such that \(B_r(x)\) is a \(\delta /2\)-boundary ball for every \(r\in (0,r_x)\), thanks to Theorem 8.1 (i). In particular, if \(\partial X_n\ni x_n\rightarrow x\in \partial X\) then \(B_r(x_n)\) is a \(\delta \)-boundary ball for any \(r\in (0,r_x]\), and n big enough (here we rely again on Theorem 8.1 (i) to handle radii in \((0,r_x)\)). Notice that the existence of the sequence \((x_n)\) verifying the property above for \(r=r_x\) is a consequence of the stability Theorem 6.1. Let us now fix \(\varepsilon >0\) and assume that \(\delta \le \delta (N,\varepsilon )\) so that Corollary 8.7 holds true. We get
Footnote 3 which yields (8.30), being \(\varepsilon \) arbitrary. \(\square \)
9 Topological regularity up to the boundary
In [59, Corollary 3.2], following the arguments of [28] (see also the previous [13]) and relying on Reifenberg’s theorem for metric spaces, it has been proved that on any noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) space \((X,{\mathsf {d}},{\mathscr {H}}^N)\) and for any \(\alpha \in (0,1)\) there exists an open and dense subset \(U\subset X\) such that:
-
\(\dim _H(X{\setminus } (U\cup \partial X))\le N-2\);
-
U is an N-dimensional topological manifold with no boundary and \(C^{\alpha }\)-charts.
The aim of this section is to sharpen this result including the boundary in the topological regularity statement. We shall prove that any noncollapsed \({{\,\mathrm{RCD}\,}}(K,N)\) is space (with boundary) is homeomorphic, up to a set of codimension two, to a topological manifold (with boundary) with \(\alpha \)-biHölder charts for any \(0<\alpha <1\).
In view of [59, Theorem 4.11] and of Theorem 5.1 the main tool needed to get topological regularity up to the boundary are biHölder topological charts on \(\delta \)-boundary balls.
Theorem 9.1
Let \(N\in {\mathbb {N}}\), \(N \ge 1\) and \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) space, \(p\in X\) such that \(B_{16}(p)\) is a \(\delta \)-boundary ball. Then, for any \(0<\varepsilon <1/5\) if \(\delta <\delta (N,\varepsilon )\) there exists \(F:B_1(p)\rightarrow {\mathbb {R}}_+^N\) such that
-
(i)
\((1-\varepsilon ) {\mathsf {d}}(x,y)^{1+\varepsilon } \le |F(x) - F(y)| \le C(N) {\mathsf {d}}(x,y)\) for any \(x,y\in B_1(p)\);
-
(ii)
\(F(p)=0\) and \(\partial {\mathbb {R}}_+^N \cap B_{1-2\varepsilon }(0) \subset F(\partial X \cap B_1(p)) = \partial {\mathbb {R}}^N_+\cap F(B_1(p))\);
-
(iii)
F is open and a homeomorphism onto its image;
-
(iv)
\( B_{1-2\varepsilon }^{{\mathbb {R}}_+^N}(0) \subset F(B_1(p))\).
By combining [59, Theorem 4.11] and Theorem 9.1 we infer that on a noncollapsed \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) m.m.s., if \(\varepsilon <\varepsilon (N)\) then any point in \(X{\setminus }{\mathcal {S}}^{N-2}_{\varepsilon }\) has a neighbourhood which is \(C^{\alpha }\)-homeomorphic either to an open set in \({\mathbb {R}}^N\) or to an open set in \({\mathbb {R}}^N_+\) (see (1.8) for the definition of the quantitative singular stratum \({\mathcal {S}}^{N-2}_{\varepsilon }\)). It is then easy to infer the following.
Theorem 9.2
Let \(N\in {\mathbb {N}}\), \(N\ge 1\) be fixed and \(0<\alpha <1\). If \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is a \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) metric measure space, then there exists a closed set of codimension at least two \(C_\alpha \subset {\mathcal {S}}^{N-2}_{\varepsilon }(X)\), for some \(0<\varepsilon <\varepsilon (N,\alpha )\), such that \(X{\setminus } C_\alpha \) is a topological manifold with boundary and \(C^{\alpha }\)-charts.
Let us begin by proving Theorem 9.2 assuming the validity of Theorem 9.1. The latter will be proven at the end of this section.
Proof
It is sufficient to prove that if \(\varepsilon <\varepsilon (N,\alpha )\), then any point in \(X{\setminus }{\mathcal {S}}^{N-2}_{\varepsilon }\) admits a neighbourhood which is either \(C^{\alpha }\)-homeomorphic to an open subset of \({\mathbb {R}}^N\), or \(C^{\alpha }\)-homeomorphic to an open subset of \({\mathbb {R}}^N_+\).
In order to do so we just observe that, if \(x\in X{\setminus }{\mathcal {S}}^{N-2}_{\varepsilon }\), then there exists \(0<r<1\) such that either \(B_r(x)\) is \((N,\varepsilon )\)-symmetric, or \(B_r(x)\) is an \(\varepsilon \)-boundary ball. In the first case x has a neighbourhood \(C^{\alpha }\)-homeomorphic to an open subset of \({\mathbb {R}}^N\) by [59, Theorem 4.11] (see also [13, 28]), for \(\varepsilon <\varepsilon (\alpha ,N)\). In the second case, by Theorem 9.1x has a neighbourhood \(C^{\alpha }\)-homeomorphic to an open subset of \({\mathbb {R}}^N_{+}\), if \(\varepsilon <\varepsilon (\alpha ,N)\). \(\square \)
In the framework of limits of N-dimensional manifolds with convex boundary and Ricci tensor bounded below by \(-(N-1)\) in the interior we can improve Theorem 9.2 with the following.
Theorem 9.3
Let \((X,{\mathsf {d}},{\mathscr {H}}^N)\) be an \({{\,\mathrm{RCD}\,}}\) m.m.s. arising as noncollapsed limit of a sequence of smooth Riemannian manifolds with convex and Ricci curvature bounded from below in the interior by \(-(N-1)\). Then for any \(0<\alpha <1\) there exists a constant \(C=C(N,\alpha ,{\mathscr {H}}^N(B_1(p)))\) and a closed set of codimension at least two \(C_\alpha \subset {\mathcal {S}}^{N-2}(X)\) such that
and \(X{\setminus } C_\alpha \) is a topological manifold with boundary and \(C^{\alpha }\)-charts.
The improvement will follow from the sharp measure estimates for the effective singular stratum \({\mathcal {S}}^{N-2}_{\varepsilon }\) on noncollapsed Ricci limit spaces obtained in [29]. The conclusion is almost straightforward once we point out that the verbatim arguments of [29] allow to treat also the case of noncollapsed limits of smooth Riemannian manifolds with convex boundary (and interior lower Ricci curvature bounds). Since that case was not considered therein, we also give a detailed proof relying on a gluing procedure (see [83]) in order to reduce the study of singularities in the boundary to that of interior singularities.
Proof of Theorem 9.3
First let us point out that, the analogue of [29, Theorem 1.9] in the case of non collapsed limits of smooth manifolds with convex boundary and interior lower Ricci curvature bounds yields that, under our assumptions,
The conclusion then follows from Theorem 9.2, where we proved that the topologically singular set is included in \({\mathcal {S}}^{N-2}_{\varepsilon }\). The validity of [29, Theorem 1.9] in the case of manifolds with boundary can be checked with the verbatim arguments therein indicated.
However, since the case of manifolds with boundary is not considered in [29], below we provide an alternative proof under the additional technical assumption that the smooth approximating manifolds have boundaries with uniformly bounded diameter.
Let us start by pointing out that
-
(i)
if \(x\in \partial X\) and \(\Theta _X(x)\ge 1/2-\eta (N,\alpha )\), then x has a neighbourhood \(C^{\alpha }\)-homeomorphic to an open set in \({\mathbb {R}}^N_+\);
-
(ii)
if \(x\in X\) verifies \(\Theta _X(x)\ge 1-\eta (N,\alpha )\), then x has an open neighbourhood \(C^{\alpha }\)-homeomorphic to an open subset of \({\mathbb {R}}^N\).
We refer to [13, 28, 59] for the proof of (ii), which is based on Reifenberg’s theorem for metric spaces.
Property (i) instead directly follows from the Boundary volume rigidity Theorems 8.2 and 9.1.
It follows from the discussion above that, letting
it suffices to prove
Let now \(({\hat{X}}, {\hat{{\mathsf {d}}}}, {\mathscr {H}}^N)\) be the doubling of \((X,{\mathsf {d}},{\mathscr {H}}^N)\) gluing along \(\partial X\), see for instance [79] for the precise definition. We claim that it is noncollapsed Ricci limit (of a sequence of smooth N-dimensional Riemannian manifolds with no boundary and Ricci curvature bounded from below by \(-N\)).
Before proving the claim let us see how it implies (9.4). In order to do so we let \(\iota :X\rightarrow \hat{X}\) be one of the canonical immersions of the starting space into its double. Since \(\iota \) is isometric, in order to prove (9.4) it suffices to prove that
It is easy to check that, for any \(\hat{x}\in \iota (I\cup P)\) it holds
Hence, there exists \(\varepsilon =\varepsilon (N,\alpha )\) such that
Applying [29, Theorem 1.9] to \((\hat{X},\hat{{\mathsf {d}}})\) we infer that
which yields the sought estimate.
Let us pass to the verification of the claim. In order to do so we let \((X_n,{\mathsf {d}}_n)\) be the sequence of smooth manifolds with boundary converging to \((X,{\mathsf {d}})\). We then let \((\hat{X}_n,\hat{{\mathsf {d}}}_n)\) be the doubling along the boundary of \((X_n,{\mathsf {d}}_n)\). From [83] (see also the previous [65]) we deduce that \((\hat{X}_n,\hat{{\mathsf {d}}}_n)\) is a noncollapsed limit of a sequence of smooth Riemannian manifolds with no boundary and Ricci curvature bounded below by \(-N\), for any \(n\in {\mathbb {N}}\). Then it is easy to check that \((\hat{X}_n,\hat{{\mathsf {d}}}_n)\) converge in the pGH topology to \((\hat{X},\hat{{\mathsf {d}}})\) without collapse. To conclude we observe that a diagonal argument yields that \((\hat{X},\hat{{\mathsf {d}}})\) is a noncollapsed Ricci limit space. \(\square \)
Remark 9.4
Relying on [29, Remark 1.10] we can improve (9.1) by showing a stronger packing type estimate: for any collection of disjoint balls \(\{B_{r_i}(x_i)\}_{i\in {\mathbb {N}}}\) with \(x_i\in C_\alpha \cap B_1(p)\) it holds
The remaining part of this section is devoted to the proof of Theorem 9.1. Let us first introduce a regularization result for the distance to the boundary on \(\delta \)-boundary balls.
Lemma 9.5
Let \(N\in {\mathbb {N}}\), \(N\ge 1\) be fixed. For any \(\varepsilon >0\), if \(\delta <\delta (N,\varepsilon )\) then the following holds. Given an \({{\,\mathrm{RCD}\,}}(-\delta (N-1),N)\) m.m.s. \((X,{\mathsf {d}},{\mathscr {H}}^N)\) and \(p\in X\) such that \(B_8(p)\) is a \(\delta \)-boundary ball, there exists a \((1+\varepsilon )\)-Lipschitz function \(b: B_4(p) \rightarrow {\mathbb {R}}_+\) satisfying:
-
(i)
\(|b(x) - {\mathsf {d}}_{\partial X}(x)| \le \varepsilon {\mathsf {d}}_{\partial X}(x)\) for any \(x\in B_2(p)\);
-
(ii)
\(b\in D_{\mathrm{loc}}(\Delta , B_4(p){\setminus } \partial X )\) and
 (9.9)
(9.9)for any \(x\in B_2(p){\setminus }\partial X\), and \(r={\mathsf {d}}_{\partial X}(x)/3\).
Proof
We divide the proof into four steps. The first one aims at building a partition of unity suitable for the geometry of our problem. In the second step we build harmonic approximations of \({\mathsf {d}}_{\partial X}\) on balls with radius proportional to their distance from the boundary and prove good estimates as in the theory of Ricci limits (cf. [27]). The sought function is obtained averaging the harmonic approximations of the distance obtained in Step 2 by the partition of unity built in Step 1. The third step is devoted to the proof of (i) while in the last step we obtain (ii).
Step 1. There exist a family of functions \(\{\varphi _k: B_8(p)\rightarrow {\mathbb {R}}_+\}_{k\in {\mathbb {N}}}\) and a family of balls \(\{B_{r_k}(x_k)\}_{k\in {\mathbb {N}}} \) satisfying the following conditions:
-
(a)
\(r_k:= {\mathsf {d}}_{\partial X}(x_k)/8\), \(B_4(p){\setminus } \partial X \subset \bigcup _k B_{\frac{2}{3} r_k}(x_k)\);
-
(b)
if \(B_{\frac{3}{2}r_{k_1}}(x_{k_1})\cap \ldots \cap B_{\frac{3}{2}r_{k_m}}(x_{k_m})\ne \emptyset \) then \(m\le C(N)\) and \(r_{k_i}\le C(N) r_{k_j}\) for any \(i,j=1,\ldots ,m\);
-
(c)
\(\varphi _k\in {{\,\mathrm{Lip}\,}}(X)\cap D(\Delta )\), \({{\,\mathrm{supp}\,}}\varphi _k \subset B_{r_k}(x_k)\) and
$$\begin{aligned} \varphi _k + r_k |\nabla \varphi _k| + r_k^2 |\Delta \varphi _k| \le C(N); \end{aligned}$$ -
(d)
\(\sum _k \varphi _k = 1 \) on \(B_4(p){\setminus }\partial X\).
Let us briefly explain how to build a family of balls satisfying (a) and (b). For any \(\alpha \in {\mathbb {N}}\) we cover \(B_4(p)\cap \{2^{-\alpha } \le {\mathsf {d}}_{\partial X} \le 2^{-\alpha + 2}\}\) using balls \(\{B_{2^{-\alpha -1}}(x_{\alpha ,i}):\, i=1,\ldots ,m_{\alpha }\}\) with \(x_{\alpha ,i}\in \{2^{-\alpha } \le {\mathsf {d}}_{\partial X} \le 2^{-\alpha + 2}\}\) such that \(\{B_{2^{-\alpha - 3}}(x_{\alpha ,i})\, i=1,\ldots ,m_{\alpha }\}\) is a disjoint family. The verification of the fact that \(\{B_{2^{-\alpha -1}}(x_{\alpha ,i}):\, \alpha =1,\ldots ,m_\alpha ,\, i\in {\mathbb {N}}\}\) satisfies (a) and (b) follows from the following simply verified observations:
-
\(m_{\alpha } \le C(N)\) for any \(\alpha \in {\mathbb {N}}\);
-
if \(B_{\frac{3}{2}\cdot 2^{-\alpha -1}}(x_{\alpha ,i})\cap B_{\frac{3}{2}\cdot 2^{-\beta -1}}(x_{\beta ,j})\ne \emptyset \) then \(|\alpha - \beta | \le 2\).
We build now the partition of unity \(\{\varphi _k\}\) satisfying (c) and (d) following a standard procedure. For any \(k\in {\mathbb {N}}\) we use Lemma 2.10 to get a nonnegative function \(\eta _k\) satisfying \(\eta _k=1\) on \(B_{\frac{2}{3}r_k}(x_k)\) and \(\eta _k=0\) on \(X{\setminus } B_{ r_k}(x_k)\) along with the bound
Then we set
The verification of (c) and (d) is straightforward and builds upon the observation that \(1\le \sum _i \eta _i \le C(N)\) on \(B_4(p){\setminus }\partial X\).
Step 2. If \(\delta <\delta (N,\varepsilon )\), \(x\in B_4(p)\), \(s={\mathsf {d}}_{\partial X}(x)/5\) then there exists a unique solution \(b_{x,s}\) to the Dirichlet boundary value problemFootnote 4
which satisfies moreover the estimates
-
(1)
\(b_{x,s}>0\), \(|\nabla b_{x,s}|\le C(N)\) and \(|\nabla b_{x,s}|\le 1+\varepsilon \) on \(B_{s/2}(x)\);
-
(2)
\(|b_{x,s} - {\mathsf {d}}_{\partial X}| \le \varepsilon s\) on \(B_s(x)\);
-
(3)
 .
.
Existence and uniqueness of solutions to (9.10) follow from classical functional analytic arguments (cf. [26, (4.5)] and [8, (4.11)]) since \(X{\setminus } B_{(1+\varepsilon )s}(x)\ne \emptyset \). The positivity of \(b_{x,s}\) in (1) is a consequence of the maximum principle, while the gradient bounds follow from [55] (for the non sharp one) and Remark 3.3, for the sharp one given (iii).
In order to verify (2) and (3) let us consider a point \(q\in B_4(p)\cap \partial X\) such that \({\mathsf {d}}(x,q) \le 5s\) and notice that \(B_{6s}(q)\) is a \(\delta '\)-boundary ball for \(\delta \le \delta (N,\delta ')\), thanks to Theorem 8.1 (i). Since \(B_s(x) \subset B_{6s}(q)\) we can scale the space by a factor 3/2s and verify (2) and (3) in the special case \({\mathsf {d}}_{\partial X}(x)/5 =s=2/3\). In order to do so we rely on the continuity of the harmonic replacement (see [8]) arguing by contradiction.
First we observe that 1/n-boundary balls \(B_2(q_n)\) converge to \(B_2^{{\mathbb {R}}^N_+}(0)\) as \(n\rightarrow \infty \). Then we recall that Lemma 7.1 yields uniform and \(W^{1,2}\) convergence of the distance functions from the boundaries along the converging sequence, and on any converging sequence of balls \(B_{2/3}(x_n)\).Footnote 5 To conclude we observe that on the half space the distance from the boundary is harmonic away from the boundary and local spectral convergence holds for any ball far away from the boundary. Therefore the harmonic replacements of the distance from the boundary verify:
as \(n\rightarrow \infty \), yielding the sought estimates (2) and (3).
Step 3. Let \(\varphi _k\) and \(B_{r_k}(x_k)\) be as in Step 1. We set \(b_k:= b_{x_k,2r_k}\), where \(b_{x_k,2r_k}\) is obtained by Step 2, and we define
Let us show that \(|b(x) - {\mathsf {d}}_{\partial X}(x)| \le C(N) \varepsilon {\mathsf {d}}_{\partial X}(x)\) for any \(x\in B_2(p)\).
First let us consider \(x\in B_2(p){\setminus }\partial X\). Using (1), (2), (b) and (d) we get
Then we can estimate
for \({\mathscr {H}}^N\)-a.e. \(x\in B_4(p)\). Above we exploited the very definition of b, together with (a)–(d) and (1), (2).
This gradient estimate, together with the previous one, allows to infer that b is Lipschitz once we set \(b=0\) on \(\partial X\).
Step 4. We now verify that \(b\in D_{\mathrm{loc}}(\Delta , B_4(p){\setminus } \partial X )\) and

For \({\mathscr {H}}^N\)-a.e. \(x\in B_2(p)\) one has
where we have used (b), (c) and (2).
Let us now observe that on \(B_4(p){\setminus }\partial X\) it holds
The first sum in (9.14) can be easily bounded by using (b), (c), (d) and (2)
The estimate of the second sum in (9.14) uses (b) and (d):
By combining (9.13), (9.15) and (9.16) we find out

which easily yields the sought conclusion as a consequence of (b) and (3). \(\square \)
Before entering into the proof of Theorem 9.1 we outline its strategy for the reader’s convenience. In a nutshell: we perform a Reifenberg type argument with two model sets, the Euclidean space \({\mathbb {R}}^N\) and the Euclidean half space \({\mathbb {R}}_+^N\), instead of the single model of the usual statement.
The homeomorphism \(F: B_1(p) \rightarrow {\mathbb {R}}_+^N\) is built by setting \(F:=(u,b)\) where \(u: B_8(p)\rightarrow {\mathbb {R}}^{N-1}\) is a \(\delta \)-splitting map with \(u(p)=0\) and b is given by Lemma 9.5. The latter has to be understood as a suitable regularization of \({\mathsf {d}}_{\partial _X}\). It is straightforward to check that F is a Lipschitz map, the delicate part of our argument is to prove that
To this aim, we distinguish two cases.
Case 1: x, y are far away from the boundary. More precisely, \(r:={\mathsf {d}}(x,y)\) is much smaller than \({\mathsf {d}}_{\partial X}(y)\) and \({\mathsf {d}}_{\partial X}(x)\). In this case, \(x,y\in B_{2r}(x)\) and the ball \(B_{2r}(x)\) looks Euclidean at any scale. We can then run a transformation argument as in [29, Theorem 7.10] to find a transformation matrix A such that
Using that \(\delta \)-almost splitting maps are \(\varepsilon \)-isometries we conclude
Case 2: x, y are close to the boundary. In this case \(B_{2r}(x)\) is a boundary ball, where \(r:={\mathsf {d}}(x,y)\), and we can apply a transformation argument on \(u: B_{2r}(x)\rightarrow {\mathbb {R}}^{N-1}\). We can find A such that
Arguing as above, we deduce that \(v:=(A\circ u, b) : B_r(x) \rightarrow {\mathbb {R}}^N_+\) is an \(\varepsilon \)-isometry and
Proof of Theorem 9.1
For \(\delta <\delta (N,\delta ')\) we build a \(\delta '\)-splitting map \(u: B_8(p) \rightarrow {\mathbb {R}}^{N-1}\) with \(u(p)=0\) and a function \(b:B_8(p)\rightarrow {\mathbb {R}}_+\) satisfying (i) and (ii) in Lemma 9.5 with \(\delta '\) in place of \(\varepsilon \). We claim that \(F := (u,b)\) verifies (i)–(iv).
Let \(x,y \in B_1(p)\) and set \(r:={\mathsf {d}}(x,y)\). The inequality \(|F(x) - F(y)|\le C(N){\mathsf {d}}(x,y)\) follows from the Lipschitz regularity of u and b.
Aiming at proving the inequality \(|F(x) - F(y)| \ge (1-\varepsilon ) {\mathsf {d}}(x,y)^{1+\varepsilon }\) we are going to argue as in the proof of [29, Theorem 7.10] (see also the proof of (8.18)), relying on the transformation theorem. Since in this case the target is the half-space and not the Euclidean space, we need to study separately the two cases \(r\le {\mathsf {d}}_{\partial X}(x)/3\) and \(r > {\mathsf {d}}_{\partial X}(x)/3\).
Assume first \(r\le {\mathsf {d}}_{\partial X}(x)/3\). Let \(q\in \partial X\cap B_1(p)\) such that \({\mathsf {d}}(x,q)= {\mathsf {d}}_{\partial X}(x)\). For \(\delta <\delta (N,\delta ')\) the ball \(B_s(q)\) is a \(\delta '\)-boundary ball for any \(s\in (0,8)\), by Theorem 8.1 (i). The transformation theorem Proposition 3.13 (see also the matrix growth estimate in Corollary 3.16) applied to \(u: B_{2{\mathsf {d}}_{\partial X}(x)}(q) \rightarrow {\mathbb {R}}^{N-1}\) (taking into account the fact that \(u:B_2(q)\rightarrow {\mathbb {R}}^{N-1}\) is a \(\delta '\)-splitting map) implies the existence of a matrix \(T_x\) such that
-
\(T_x \circ u : B_{2{\mathsf {d}}_{\partial X}(x)}(q) \rightarrow {\mathbb {R}}^{N-1}\) is an \(\varepsilon '\)-splitting map;
-
\(|T_x| \le (2{\mathsf {d}}_{\partial X}(x))^{-\varepsilon '}\le (6r)^{-\varepsilon '}\),
whenever \(\delta '<\delta '(N,\varepsilon ')\). Assume \(\delta '\le \varepsilon '\). Setting \(v:=(T_x\circ u, b)\), thanks to Corollary 7.2 and (9.9), we have

for \(s:= {\mathsf {d}}_{\partial X}(x)/3\) and \(\varepsilon '\le \varepsilon '(N,\varepsilon '')\).
Applying again Proposition 3.13 to \(v: B_s(x)\rightarrow {\mathbb {R}}^{N}\) taking into account that \(B_t(x)\) is a \((N,\delta ')\)-symmetric ball for any \(r\le t<3/2s\) (see Theorem 8.1 (iii)) when \(\delta \le \delta (N,\delta ')\), we get the existence of a matrix \(A_x\) such that
-
\(w:=A_x\circ v : B_{r}(x) \rightarrow {\mathbb {R}}^N\) is a \(\varepsilon ''\)-almost splitting map;
-
\(|A_x|\le r^{-\varepsilon ''}\),
for \(\varepsilon ' \le \varepsilon '(N,\varepsilon '')\). Hence, if \(\varepsilon ''\le \varepsilon ''(N,\varepsilon ''')\), \(w: B_r(x)\rightarrow {\mathbb {R}}^N\) is a \(\varepsilon '''\)-GH isometry thanks to Remark 3.10 and Remark 3.12, yielding that
This implies in turn
being \(w := B\circ F\), where B is a matrix satisfying \(|B|\le (1+\varepsilon )r^{-\varepsilon }\) for \(\varepsilon ',\varepsilon '',\varepsilon '''\) small enough.
Let us now deal with the case \(r > {\mathsf {d}}_{\partial X}(x)/3\). Let \(q\in \partial X\cap B_1(p)\) such that \({\mathsf {d}}(x,q)= {\mathsf {d}}_{\partial X}(x)\). Notice that \(B_{8r}(q)\) is a \(\delta '\)-boundary ball for \(\delta \le \delta (N,\delta ')\) as a consequence of Theorem 8.1 (i). We apply the transformation theorem Proposition 3.13 to get a matrix \(A_x\), such that \(|A_x|\le (8r)^{-\varepsilon '}\) and \(A_x\circ u:B_{8r}(q)\rightarrow {\mathbb {R}}^{N-1}\) is an \(\varepsilon '\)-splitting map. Relying now on Corollary 7.2 and on Lemma 9.5 (i) we infer that, when \(\delta \le \delta (N,\varepsilon '')\), \(v:=(A\circ u, b):B_{4r}(q)\rightarrow {\mathbb {R}}_+^N\) is an \(\varepsilon ''\)-GH isometry. Notice that \(y\in B_{4r}(q)\), hence
Arguing as above we deduce \(|F(x) - F(y)|\ge (1-\varepsilon ){\mathsf {d}}(x,y)^{1+\varepsilon }\), for \(\varepsilon ''\) small enough.
The assertion (ii) follows from the fact that \(\{b=0\}\cap B_4(p)=\partial X\cap B_4(p)\) and Theorem 8.4 (iv).
Observe that \(F:B_1(p){\setminus }\partial X\rightarrow {\mathbb {R}}^{N}_+{\setminus } \{x_N=0\}\) is an open mapping by invariance of the domain. Indeed, under our assumptions \(B_1(p){\setminus }\partial X\) is homeomorphic to a topological manifold thanks to Theorem 8.1 (iii) and Reifenberg’s theorem. Being F continuous and injective, to prove that \(F:B_1(p)\rightarrow {\mathbb {R}}^N_+\) is an homeomorphism with its image it is sufficient to prove (iv). If this is the case, to prove that the image of any open set in \(B_1(p)\) is open in \({\mathbb {R}}^N_+\) we just need to observe that on any boundary ball, up to an invertible matrix, the restriction of F verifies the same properties that F verifies on the ball of radius 1.
Let us therefore move to the verification of (iv). In order to do this it is sufficient to prove that
for any \(\delta >0\). This claim can be verified arguing as we did in the proof of Theorem 8.4 (iv), relying once more on the invariance of the domain and on the fact that \(F(x)\in \{x_N=0\}\) if and only if \(x\in \partial X\). \(\square \)
Remark 9.6
Arguing as in the proof of [29, Theorem 7.10] (see also the proof of Theorem 9.1 above) and relying on the transformation Proposition 3.13 it is possible to obtain the following regularity result, which is worth pointing out.
If \((X,{\mathsf {d}},{\mathscr {H}}^N)\) is a noncollapsed \({{\,\mathrm{RCD}\,}}(-(N-1),N)\) space and \(x\in X\) is a regular point, then for any \(0<\alpha <1\) there exists an open neighbourhood of x which is \(C^{\alpha }\)-homeomorphic to an open subset of \({\mathbb {R}}^N\), and the homeomorphism can be chosen with harmonic coordinate maps.
This observation gives in particular a positive answer to a question raised in [76, Question 2.1] about existence of homeomorphisms from a neighbourhood of a regular point of an Alexandrov space with curvature bounded from below to an open set in \({\mathbb {R}}^N\) with harmonic coordinates. Notice that the regularity of the harmonic map cannot be improved to biLipschitz, due to the presence of singular points where harmonic maps do degenerate, see [31, Example 2.14].
Notes
We remark that to obtain a distance one should restrict to bounded and closed sets, but this will cause no troubles for our aims.
To be more precise, there exist unique Regular Lagrangian flows \({\varvec{X}}^+,{\varvec{X}}^-:[0,+\infty )\times X\rightarrow X\) associated to \(\nabla u\) and \(-\nabla u\) respectively and we let \({\varvec{X}}_t={\varvec{X}}^+_t\) for \(t\ge 0\) and \({\varvec{X}}_t={\varvec{X}}_{-t}^-\) for \(t\le 0\).
The inequality (8.32) holds for all those radii such that \(\nu (\overline{B}_r(x){\setminus } B_r(x))=0\), a property which fails in at most countable cases.
The Dirichlet boundary condition below is understood as \(b_{x,s}-{\mathsf {d}}_{\partial X}\in H^{1,2}_0(B_s(x))\).
This stronger statement can be checked arguing as in the case of balls centered at boundary points, given the uniform convergence of the distance functions.
References
Alexander, S., Bishop, R.: \({\cal{F}}K\)-convex functions on metric spaces. Manuscripta Math. 110(1), 115–133 (2003)
Ambrosio, L.: Calculus, heat flow and curvature-dimension bounds in metric measure spaces. In: Proceedings of the International Congress of Mathematicians—Rio de Janeiro 2018. Vol. I. Plenary Lectures, pp. 301–340. World Sci. Publ., Hackensack (2018)
Ambrosio, L., Bertrand, J.: DC calculus. Math. Z. 288(3–4), 1037–1080 (2018)
Ambrosio, L., Brué, E., Semola, D.: Rigidity of the 1-Bakry-Émery inequality and sets of finite perimeter in RCD spaces. Geom. Funct. Anal. 19(4), 949–1001 (2019)
Ambrosio, L., Gigli, N., Mondino, A., Rajala, T.: Riemannian Ricci curvature lower bounds in metric measure spaces with \(\sigma \)-finite measure. Trans. Am. Math. Soc. 367, 4661–4701 (2015)
Ambrosio, L., Gigli, N., Savaré, G.: Metric measure spaces with Riemannian Ricci curvature bounded from below. Duke Math. J. 163, 1405–1490 (2014)
Ambrosio, L., Honda, S.: New stability results for sequences of metric measure spaces with uniform Ricci bounds from below. Measure Theory in Non-Smooth Spaces, De Gruyter Open, Warsaw, pp. 1–51 (2017)
Ambrosio, L., Honda, S.: Local spectral convergence in \(\text{ RCD}^*(K, N)\) spaces. Nonlinear Anal. Part A 177, 1–23 (2018)
Ambrosio, L., Honda, S., Tewodrose, D.: Short-time behavior of the heat kernel and Weyl’s law on \(\text{ RCD}^*(K, N)\)-spaces. Ann. Global Anal. Geom. 53, 97–119 (2018)
Ambrosio, L., Mondino, A., Savaré, G.: On the Bakry–Émery condition, the gradient estimates and the local-to-global property of \(\text{ RCD}^*(K, N)\) metric measure spaces. J. Geom. Anal. 26, 1–33 (2014)
Ambrosio, L., Mondino, A., Savaré, G.: Nonlinear diffusion equations and curvature conditions in metric measure spaces. Mem. Am. Math. Soc. 262(1270), v+121 (2019)
Ambrosio, L., Trevisan, D.: Well posedness of Lagrangian flows and continuity equations in metric measure spaces. Anal. PDE 7, 1179–1234 (2014)
Anderson, M.: Convergence and rigidity of manifolds under Ricci curvature bounds. Invent. Math. 102(2), 429–445 (1990)
Antonelli, G., Bruè, E., Semola, D.: Volume bounds for the quantitative singular strata of noncollapsed \(\text{ RCD }\) metric measure spaces. Anal. Geom. Metr. Spaces 7(1) (2019)
Bacher, K., Sturm, K.-T.: Localization and tensorization properties of the curvature-dimension condition for metric measure spaces. J. Funct. Anal. 259(1), 28–56 (2010)
Beer, G.: On convergence of closed sets in a metric space and distance functions. Bull. Austral. Math. Soc. 31(3), 421–432 (1985)
Bruè, E., Pasqualetto, E., Semola, D.: Rectifiability of the reduced boundary for sets of finite perimeter over \(\text{ RCD }(K,N)\) spaces, Preprint arXiv:1909.00381
Bruè, E., Pasqualetto, E., Semola, D.: Rectifiability of \(\text{ RCD }(K, N)\) spaces via \(\delta \)-splitting maps. Ann. Fenn. Math. 46(1), 465–482 (2021)
Brué, E., Semola, D.: Constancy of the dimension for \(RCD(K, N)\) spaces via regularity of Lagrangian flows. Commun. Pure Appl. Math. 73(6), 1141–1204 (2020)
Brué, E., Semola, D.: Regularity of Lagrangian flows over \(\text{ RCD}^*(K, N)\) spaces. J. Reine Angew. Math. 765, 171–203 (2020)
Buffa, V., Comi, G., Miranda, M., jr: On BV functions and essentially bounded divergence-measure fields in metric spaces, to appear on Rev. Mat. Ibero., preprint arXiv:1906.07432
Burago, D., Burago, Y., Ivanov, S.: A course in metric geometry. Graduate Studies in Mathematics, 33. American Mathematical Society, Providence (2001)
Burago, Y., Gromov, M., Perelman, G.: AD Aleksandrov spaces with curvatures bounded below, Uspekhi Mat. Nauk 47(2,284), 3–51, 222 (1992) (translation in Russian Math. Surveys 47 (1992), no. 2, 1–58)
Cavalletti, F., Milman, E.: The globalization theorem for the curvature-dimension condition. Invent. Math. 226(1), 1–137 (2021)
Cavalletti, F., Mondino, A.: New formulas for the Laplacian of distance functions and applications. Anal. PDE 13(7), 2091–2147 (2020)
Cheeger, J.: Differentiability of Lipschitz functions on metric measure spaces. Geom. Funct. Anal. 9, 428–517 (1999)
Cheeger, J., Colding, T.-H.: Lower bounds on Ricci curvature and the almost rigidity of warped products. Ann. Math. 2(144), 189–237 (1996)
Cheeger, J., Colding, T.-H.: On the structure of spaces with Ricci curvature bounded below. I. J. Differ. Geom. 46, 406–480 (1997)
Cheeger, J., Jiang, W., Naber, A.: Rectifiability of singular sets in noncollapsed spaces with Ricci curvature bounded below. Ann. Math. (2) 193(2), 407–538 (2021)
Cheeger, J., Naber, A.: Lower bounds on Ricci curvature and quantitative behavior of singular sets. Invent. Math. 191(2), 321–339 (2013)
Cheeger, J., Naber, A.: Regularity of Einstein manifolds and the codimension 4 conjecture. Ann. Math. (2) 182(3), 1093–1165 (2015)
Colding, T.-H.: Ricci curvature and volume convergence. Ann. Math. (2) 145(3), 477–501 (1997)
Colding, T.-H., Naber, A.: Sharp Hölder continuity of tangent cones for spaces with a lower Ricci curvature bound and applications. Ann. Math. (2) 176(2), 1173–1229 (2012)
Colding, T.-H., Naber, A.: Characterization of tangent cones of noncollapsed limits with lower Ricci bounds and applications. Geom. Funct. Anal. 23(1), 134–148 (2013)
Deng, Q.: Hölder continuity of tangent cones on \(\text{ RCD }(K,N)\) spaces and applications to non branching Preprint arXiv:2009.07956
De Philippis, G., Gigli, N.: From volume cone to metric cone in the nonsmooth setting. Geom. Funct. Anal. 26, 1526–1587 (2016)
De Philippis, G., Gigli, N.: Non-collapsed spaces with Ricci curvature bounded from below. J. Éc. Polytech. Math. 5, 613–650 (2018)
De Philippis, G., Marchese, A., Rindler, F.: On a conjecture of Cheeger. Measure theory in non-smooth spaces, Partial Differ. Equ. Meas. Theory, pp. 145–155. De Gruyter Open, Warsaw (2017)
Erbar, M., Kuwada, K., Sturm, K.-T.: On the equivalence of the entropic curvature-dimension condition and Bochner’s inequality on metric measure spaces. Invent. Math. 201, 993–1071 (2015)
Fujioka, T.: Regular points of extremal subsets in Alexandrov spaces, preprint arXiv:1905.05480
Gigli, N.: The splitting theorem in non-smooth context. Preprint arXiv:1302.5555
Gigli, N.: An overview of the proof of the splitting theorem in spaces with non-negative Ricci curvature. Anal. Geom. Metr. Spaces 2, 169–213 (2014)
Gigli, N.: On the differential structure of metric measure spaces and applications. Mem. Am. Math. Soc. 236, vi–91 (2015)
Gigli, N.: Nonsmooth differential geometry: an approach tailored for spaces with Ricci curvature bounded from below. Mem. Am. Math. Soc. 251, v–161 (2018)
Gigli, N., Han, B.-X.: The continuity equation on metric measure spaces. Calc. Var. Partial Differ. Equ. 53, 149–177 (2015)
Gigli, N., Mondino, A., Savaré, G.: Convergence of pointed non-compact metric measure spaces and stability of Ricci curvature bounds and heat flows. Proc. Lond. Math. Soc. 3(111), 1071–1129 (2015)
Gigli, N., Pasqualetto, E.: Behaviour of the reference measure on \(\text{ RCD }\) spaces under charts, to appear on Communications in Analysis and Geometry, preprint arXiv:1607.05188
Gigli, N., Rigoni, C.: Recognizing the flat torus among \(\text{ RCD}^*(0, N)\) spaces via the study of the first cohomology group (Paper No. 104). Calc. Var. Partial Differ. Equ. 57(4), 39 (2018)
Gigli, N., Rajala, T., Sturm, K.-T.: Optimal maps and exponentiation on finite-dimensional spaces with Ricci curvature bounded from below. J. Geom. Anal. 26(4), 2914–2929 (2016)
Gigli, N., Tamanini, L.: Second order differentiation formula on \(\text{ RCD}^*(K, N)\) spaces. J. Eur. Math. Soc. (JEMS) 23(5), 1727–1795 (2021)
Golub, G.-H., Van Loan, C.-F.: Matrix Computations. Johns Hopkins Studies in the Mathematical Sciences, 4th edn. Johns Hopkins University Press, Baltimore (2013)
Han, B.-X.: Measure rigidity of synthetic lower Ricci curvature bound on Riemannian manifolds. Adv. Math. 373, 107327 (2020)
Honda, S.: New differential operator and non-collapsed \(\text{ RCD }\) spaces. Geom. Topol. 24(4), 2127–2148 (2020)
Jiang, R., Li, H., Zhang, H.: Heat kernel bounds on metric measure spaces and some applications. Potential Anal. 44, 601–627 (2016)
Jiang, R.: Cheeger-harmonic functions in metric measure spaces revisited. J. Funct. Anal. 266(3), 1373–1394 (2014)
Jiang, W., Naber, A.: \(L^2\) curvature bounds on manifolds with bounded Ricci curvature. Ann. Math. (2) 193(1), 107–222 (2021)
Kapovitch, V.: Perelman’s Stability Theorem. Surveys in Differential Geometry, vol. XI, pp. 103–136. Int Press, Somerville (2007)
Kapovitch, V., Lytchak, A., Petrunin, A.: Metric-measure boundary and geodesic flow on Alexandrov spaces. J. Eur. Math. Soc. (JEMS) 23(1), 29–62 (2021)
Kapovitch, V., Mondino, A.: On the topology and the boundary of \(N\)-dimensional \(\text{ RCD }(K, N)\) spaces. Geom. Topol. 25(1), 445–495 (2021)
Kell, M., Mondino, A.: On the volume measure of non-smooth spaces with Ricci curvature bounded below. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 18(2), 593–610 (2018)
Ketterer, C.: Cones over metric measure spaces and the maximal diameter theorem. J. Math. Pures Appl. (9) 103(5), 1228–1275 (2015)
Kirchheim, B.: Rectifiable metric spaces: local structure and regularity of the Hausdorff measure. Proc. Am. Math. Soc. 121(1), 113–123 (1994)
Kitabeppu, Y., Lakzian, S.: Characterization of low dimensional \(\text{ RCD}^*(K, N)\) spaces. Anal. Geom. Metr. Spaces 4(1), 187–215 (2016)
Kitabeppu, Y.: A sufficient condition to a regular set being of positive measure on \(\text{ RCD }\) spaces. Potential Anal. 51(2), 179–196 (2019)
Kosovski, N.-N.: Gluing of Riemannian manifolds of curvature \(\ge k\). Algebra i Analiz 14(3), 140–157 (2002) (translation in St. Petersburg Math. J. 14(3), 467–478 (2003))
Li, N., Naber, A.: Quantitative estimates on the singular sets of Alexandrov spaces. Peking Math. J. 3(2), 203–234 (2020)
Lott, J., Villani, C.: Ricci curvature for metric-measure spaces via optimal transport. Ann. Math. 2(169), 903–991 (2009)
Lytchak, A., Stadler, S.: Ricci curvature in dimension 2, to appear on JEMS, preprint arXiv:1812.08225
Mondino, A., Naber, A.: Structure theory of metric measure spaces with lower Ricci curvature bounds. J. Eur. Math. Soc. (JEMS) 21(6), 1809–1854 (2019)
Miranda, M., Jr.: Functions of bounded variation on “good’’ metric spaces. J. Math. Pures Appl. 82, 975–1004 (2003)
Naber, A., Valtorta, D.: Rectifiable-Reifenberg and the regularity of stationary and minimizing harmonic maps. Ann. Math. (2) 185(1), 131–227 (2017)
Naber, A., Valtorta, D.: Energy identity for stationary Yang Mills. Invent. Math. 216(3), 847–925 (2019)
Phuc, N.-C., Torres, M.: Characterizations of the existence and removable singularities of divergence-measure vector fields. Indiana Univ. Math. J. 57(4), 1573–1597 (2008)
Perales, R.: Volumes and limits of manifolds with Ricci curvature and mean curvature bounds. Differ. Geom. Appl. 48, 23–37 (2016)
Perelman, G.: A.D. Alexandrov’s spaces with curvatures bounded from below, II. http://www.math.psu.edu/petrunin/papers/alexandrov/perelmanASWCBFB2+.pdf (1991)
Petrunin, A.: Harmonic functions on Alexandrov spaces and their applications. Electron. Res. Announc. Am. Math. Soc. 9, 135–141 (2003)
Petrunin, A.: Semiconcave Functions in Alexandrov’s Geometry. Surveys in Differential Geometry, vol. XI, pp. 137–201. Int Press, Somerville (2007)
Petrunin, A.: Alexandrov meets Lott–Villani–Sturm. Münster J. Math. 4, 53–64 (2011)
Profeta, A., Sturm, K.-T.: Heat flow with Dirichlet boundary conditions via optimal transport and gluing of metric measure spaces. Calc. Var. Partial Differ. Equ. 59(4), 117 (2020)
Rajala, T.: Local Poincaré inequalities from stable curvature conditions on metric spaces. Calc. Var. Partial Differ. Equ. 44(3–4), 477–494 (2012)
Reifenberg, E.R.: Solution of the plateau problem for m-dimensional surfaces of varying topological type. Acta Math. 104, 1–92 (1960)
Savaré, G.: Self-improvement of the Bakry–Émery condition and Wasserstein contraction of the heat flow in \(\text{ RCD }(K,\infty )\) metric measure spaces. Discrete Contin. Dyn. Syst. 34(4), 1641–1661 (2014)
Schlichting, A.: Gluing Riemannian manifolds with curvature operators at least k, ArXiv e-prints. arXiv:1210.2957
Schultz, T.: On one-dimensionality of metric measure spaces. Proc. Am. Math. Soc. 149, 383–396 (2021)
Sturm, K.-T.: On the geometry of metric measure spaces I. Acta Math. 196, 65–131 (2006)
Sturm, K.-T.: On the geometry of metric measure spaces II. Acta Math. 196, 133–177 (2006)
Villani, C.: Optimal Transport. Old and New. Grundlehren der Mathematischen Wissenschaften, vol. 338. Springer, Berlin (2009)
Von Renesse, M.-K.: On local Poincaré via transportation. Math. Z. 259, 21–31 (2008)
Wang, F.-Y.: Analysis for Diffusion Processes on Riemannian Manifolds. Advanced Series on Statistical Science & Applied Probability, vol. 18. World Scientific Publishing Co. Pte Ltd., Hackensack (2014)
Zhang, H.-C., Zhu, X.-P.: Ricci curvature on Alexandrov spaces and rigidity theorems. Commun. Anal. Geom. 18(3), 503–553 (2010)
Acknowledgements
The first author is supported by the Giorgio and Elena Petronio Fellowship at the Institute for Advanced Study. The second author was partially supported by the National Science Foundation Grant No. DMS-1809011. The third author is supported by the European Research Council (ERC), under the European’s Union Horizon 2020 research and innovation programme, via the ERC Starting Grant “CURVATURE”, Grant Agreement No. 802689. Most of this work was developed while the first and third authors were Ph.D. students at Scuola Normale Superiore. They wish to express their gratitude to this institution for the excellent working conditions and the stimulating atmosphere. The authors are grateful to Alexander Lytchak for useful comments on a preliminary version of the note and to the anonymous reviewers for their careful reading and remarks.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bruè, E., Naber, A. & Semola, D. Boundary regularity and stability for spaces with Ricci bounded below. Invent. math. 228, 777–891 (2022). https://doi.org/10.1007/s00222-021-01092-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-021-01092-8



 is locally Ahlfors regular and for any
is locally Ahlfors regular and for any  ;
; ;
;
 ;
; ;
;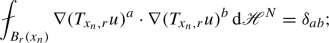




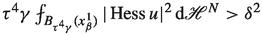 ;
;



 ;
;
 is locally Ahlfors regular and for any
is locally Ahlfors regular and for any 
 .
.