Doubly Intermittent Full Branch Maps with Critical Points and Singularities

Abstract

We study a class of one-dimensional full branch maps admitting two indifferent fixed points as well as critical points and/or unbounded derivative. Under some mild assumptions we prove the existence of a unique invariant mixing absolutely continuous probability measure, study its rate of decay of correlation and prove a number of limit theorems.

1 Introduction

The purpose of this paper is to study the ergodic properties of a large class of full branch interval maps with two branches, including maps with two indifferent fixed points (which, as we shall see below, affects both the results and the construction of the induced map which we require). We also allow the derivative to go to zero as well as to infinity at the boundary between the two branches, and we do not assume any symmetry, even the domains of the branches can be of arbitrary length. Such maps are known to exhibit a wide range of behaviour from an ergodic point of view and many of them have been extensively studied, we give a detailed literature review below.

In Sect. 1.1 we give the precise definition of the class of maps we consider, which includes many cases already studied in the literature as well as many cases which have not yet been studied; in section 1.2 we give the precise statements of our results; in section 1.3 we give a literature review of related results and include specific examples of maps in our family; in Sect. 2 we give a detailed outline of our proof, emphasising several novel aspects of our construction and arguments. Then in Sect. 3 we give the construction and estimates related to our “double-induced” map and in Sect. 4 apply these estimates to complete the proofs of our results

1.1 Full branch maps

We start by defining the class of maps which we consider in this paper. Let $I, I_-, I_+$ be compact intervals, let $\mathring{I}, \mathring{I}_-, \mathring{I}_+$ denote their interiors, and suppose that $I = I_{-}\cup I_{+}$ and $\mathring{I}_-\cap \mathring{I}_+=\emptyset$.

(A0):

$g: I \rightarrow I$ is full branch: the restrictions $g_{-}: \mathring{I}_{-}\rightarrow \mathring{I}$ and $g_{+}: \mathring{I}_{+}\rightarrow \mathring{I}$ are orientation preserving $C^{2}$ diffeomorphisms and the only fixed points are the endpoints of $I$.

To simplify the notation we will assume that

$$\begin{aligned} I=[-1, 1], \quad I_{-}=[-1, 0], \quad I_{+}=[0,1] \end{aligned}$$

but our results and proofs will be easily seen to hold in the general setting.

(A1):

There exists constants $\ell _1,\ell _2 \ge 0$, $\iota , k_1,k_2, a_1,a_2,b_1,b_2 > 0$ such that:

• (i) if $\ell _{1}, \ell _{2}\ne 0$ and $k_{1}, k_{2} \ne 1$, then

  $$\begin{aligned} g(x) = {\left\{ \begin{array}{ll} x+b_1{(1+x)}^{1+\ell _1} &{} \text {in } U_{-1},\\ 1-a_1{|x|}^{k_1} &{} \text {in } U_{0-}, \\ -1+a_2{x}^{k_2} &{} \text {in } U_{0+}, \\ x-b_2{(1-x)}^{1+\ell _2} &{} \text {in } U_{+1}, \end{array}\right. } \end{aligned}$$

  (1)

  where

  $$\begin{aligned} U_{0-}:=(-\iota , 0], \quad U_{0+}:=[0, \iota ), \quad U_{-1}:=g(U_{0+}), \quad U_{+1}:=g(U_{0-}). \end{aligned}$$

  (2)

• (ii) If $\ell _{1}=0$ and/or $\ell _2=0$ we replace the corresponding lines in (1) with

  $$\begin{aligned} g|_{U_{\pm 1}}(x) {:}{=}\pm 1 + (1 + b_1) ( x + 1) \mp \xi (x), \end{aligned}$$

  (3)

  where $\xi$ is $C^2$, $\xi (\pm 1)= 0, \xi '(\pm 1)=0$, and $\xi ''(x)>0$ on $U_{-1}$ and $\xi ''(x)<0$ on $U_{+1}$. If $k_1 = 1$ and/or $k_2 = 1$, then we replace the corresponding lines in (1) with the assumption that $g'(0_-) = a_1>1$ and/or $g'(0_+) = a_2>1$ respectively, and that $g$ is monotone in the corresponding neighbourhood.

Remark 1.1

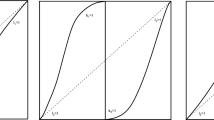
It is easy to see that the definition in (1) yields maps with dramatically different derivative behaviour depending on the values of $\ell _1, \ell _2, k_1, k_2$, including having neutral or expanding fixed points and points with zero or infinite derivative, see Remark 1.3 for a detailed discussion. For the moment we just remark that the assumptions described in part ii) of condition (A1) are consistent with (1) but significantly relax the definition given there as in these cases (1) would imply that the map is affine in the corresponding neighbourhood, whereas we only need expansivity. In particular this allows us to include uniformly expanding maps in our class of maps. In the calculations below we will explicitly consider the cases $\ell _{1}=0$ and/or $\ell _2=0$, which correspond to assuming that one or both the fixed points are expanding instead of neutral, since they yield different estimates (several quantities decay exponentially rather than polynomially in these cases) and different results, and still include some maps which, as far as we know, have not been studied in the literature. For simplicity, on the other hand, we will not consider explicitly the cases $k_1 = 1$ and/or $k_2 = 1$, which just correspond to assuming the derivative at one or both sides of the discontinuity is finite instead of being zero or infinite. These correspond to much simpler special cases and the required estimates follow by arguments which are very similar to arguments and calculations we give here, and which are essentially already considered in the literature, but treating them explicitly would require a significant amount of additional notation and calculations.

Our final assumption can be intuitively thought of as saying that $g$ is uniformly expanding outside the neighbourhoods $U_{0\pm }$ and $U_{\pm 1}$. This is however much stronger than what is needed, and therefore we formulate a weaker and more general assumption for which we need to describe some aspects of the topological structure of maps satisfying condition (A0). First of all we define

$$\begin{aligned} \Delta ^-_0:= g^{-1}(0,1)\cap I_- \quad \text { and } \quad \Delta ^+_0:= g^{-1}(-1,0)\cap I_+. \end{aligned}$$

(4)

Then we define iteratively, for every $n \ge 1$, the sets

$$\begin{aligned} \Delta _n^{-}:= g^{-1}(\Delta _{n-1}^{-})\cap I_{-} \quad \text { and } \quad \Delta _n^{+}:= g^{-1}(\Delta _{n-1}^{+})\cap I_{+} \end{aligned}$$

(5)

as the $n$’th preimages of $\Delta _0^-, \Delta _0^+$ inside the intervals $I_{-}, I_{+}$. It follows from (A0) that $\{ \Delta _n^{-}\}_{n\ge 0}$ and $\{ \Delta _n^{+}\}_{n\ge 0}$ are $\bmod \;0$ partitions of $I_{-}$ and $I_{+}$ respectively, and that the partition elements depend monotonically on the index in the sense that $n > m$ implies that $\Delta _n^{\pm }$ is closer to $\pm 1$ than $\Delta _m^{\pm }$, in particular the only accumulation points of these partitions are $-1$ and $1$ respectively. Then, for every $n \ge 1$, we let

$$\begin{aligned} \delta _{n}^{-}:= g^{-1}(\Delta _{n-1}^{+}) \cap \Delta _0^{-} \quad \text { and } \quad \delta _{n}^{+}:= g^{-1}(\Delta _{n-1}^{-}) \cap \Delta _0^{+}. \end{aligned}$$

(6)

Notice that $\{ \delta _n^{-}\}_{n\ge 1}$ and $\{ \delta _n^{+}\}_{n\ge 1}$ are $\bmod \; 0$ partitions of $\Delta _0^-$ and $\Delta _0^+$ respectively and also in these cases the partition elements depend monotonically on the index in the sense that $n > m$ implies that $\delta _n^{\pm }$ is closer to $0$ than $\delta _m^{\pm }$, (and in particular the only accumulation point of these partitions is 0). Notice moreover, that

$$\begin{aligned} g^{n}(\delta _{n}^{-})= \Delta _{0}^{+} \quad \text {and} \quad g^{n}(\delta _{n}^{+})= \Delta _{0}^{-}. \end{aligned}$$

We now define two non-negative integers $n_{\pm }$ which depend on the positions of the partition elements $\delta _{n}^{\pm }$ and on the sizes of the neighbourhoods $U_{0\pm }$ on which the map $g$ is explicitly defined. If $\Delta _0^{-} \subseteq U_{0-}$ and/or $\Delta _0^{+} \subseteq U_{0+}$, we define $n_{-}= 0$ and/or $n_{+}=0$ respectively, otherwise we let

$$\begin{aligned} n_{+}:= \min \{n:\delta _{n}^{+} \subset U_{0+} \} \quad \text { and } \quad n_{-}:= \min \{n:\delta _{n}^{-} \subset U_{0-} \}. \end{aligned}$$

(7)

We can now formulate our final assumption as follows.

(A2):

There exists a $\lambda > 1$ such that for all $1\le n\le n_{\pm }$ and for all $x \in \delta _n^{\pm }$ we have $(g^n)'(x) > \lambda$.

Notice that (A2) is an expansivity condition for points outside the neighbourhoods $U_{0\pm }$ and $U_{\pm 1}$ but is much weaker than assuming that the derivative of $g$ is greater than 1 outside these neighbourhoods, which would be unnatural and unnecessarily restrictive in the presence of critical points. This completes the set of conditions which we require, and for convenience we let

$$\begin{aligned} \widehat{\mathfrak {F}} {:}{=}\{ g: I \rightarrow I \text { which satisfy~(A0)-(A2)}\} \end{aligned}$$

The class $\widehat{\mathfrak {F}}$ contains many maps which have been studied in the literature, including uniformly expanding maps and various well known intermittency maps with a single neutral fixed point. We will give a more in-depth literature review in Sect. 1.3. Here we make a few technical remarks concerning these assumptions before proceeding to state our results in the next subsection.

Remark 1.2

(Remark on notation). To simplify many statements which will be made through the paper, it will be useful to recall some relatively standard notation as follows. Given sequences $(s_{n})$ and $(t_{n})$ of non-negative terms, we write $s_{n} = O(t_{n})$, or $s_{n} \lesssim t_{n}$, if $s_{n}/t_{n}$ is uniformly bounded above; $s_{n}\approx t_{n}$ if $s_{n}/t_{n}$ is uniformly bounded away from 0 and $\infty$; $s_{n} = o(t_{n})$ if $s_{n}/t_{n} \rightarrow 0$ as $n \rightarrow \infty$; and $s_{n}\sim t_{n}$ if $s_{n}/t_{n}= 1+o(1)$, i.e. if $s_{n}/t_{n}$ converges to 1 as $n \rightarrow \infty$.

Remark 1.3

Changing the parameter values $\ell _{1}, \ell _{2}, k_{1}, k_{2}$ gives rise to maps with quite different characteristics. For example, if $\ell _{1}>0$, we have

$$\begin{aligned} g'|_{U_{-1}}(x)= 1+b_1(1+\ell _1)(1+x)^{\ell _1} \quad \text { and } \quad g''|_{U_{-1}}(x) = b_1(1+\ell _1)\ell _1 (1+x)^{\ell _1-1}. \quad \end{aligned}$$

(8)

Then $g'(-1)= 1$ and the fixed point $-1$ is a neutral fixed point. Similarly, when $\ell _{2}>0$ the fixed point $1$ is a neutral fixed point. On the other hand, when $\ell _1=0$, from (3) we have

$$\begin{aligned} g'|_{U_{-1}}(x)= 1+b_1 + \xi '(x) \quad \text { and } \quad g''|_{U_{-1}}(x) =\xi ''(x) \end{aligned}$$

(9)

and thus the fixed point $-1$ is hyperbolic repelling with $g'(-1)=1+b$. When $k_{1}\ne 1$ we have

$$\begin{aligned} g'|_{U_{0-}}(x)= a_1k_1|x|^{k_1-1} \quad \text { and } \quad g''|_{U_{0-}}(x)= a_1k_1(k_1-1)|x|^{k_1-2}. \end{aligned}$$

(10)

Then $k_{1} \in (0,1)$ implies that $|g'|_{U_{0-}}(x)|\rightarrow \infty$ as $x \rightarrow 0$, in which case we say that $g|_{U_{0-}}$ has a (one-sided) singularity at 0, whereas $k_{1} > 1$ implies that $|g'|_{U_{0-}}(x)|\rightarrow 0$ as $x \rightarrow 0$, and therefore we say that $g|_{U_{0-}}$ has a (one-sided) critical point at 0. Analogous observations hold for the various values of $\ell _2$ and $k_2$ and Fig. 1 shows the graph of $g$ for various combinations of these exponents.

Fig. 1

Graph of g for various possible values of parameters

For future reference we mention also some additional properties which follow from (A1). First of all notice that if $\ell _1 \in (0,1)$ we have $g''(x) \rightarrow \infty$ but if $\ell _1 >1$ we have $g''(x) \rightarrow 0$, as $x\rightarrow -1$ and, as we shall see, this qualitative difference in the higher order derivative plays a crucial role in the ergodic properties of $g$. Analogous observations apply to $g|_{U_{1}}$ when $\ell _{2}>0$. Secondly, notice also that for every $x\in U_{-1}$ we have

$$\begin{aligned} {g''(x)}/{g'(x)} \lesssim (1+x)^{\ell _1-1} \end{aligned}$$

(11)

and an analogous bound holds for $x\in U_{1}$. Similarly, in $U_0$ we have

$$\begin{aligned} {|g''(x)|}/{|g'(x)|} \lesssim x^{-1}, \end{aligned}$$

(12)

and notice that in this case the bound does not actually depend on the value of $k_1$ or $k_2$ and in particular does not depend on whether we have a critical point or a singularity. Finally, we note that when $\ell _1=0$, it follows from (9) and from the assumption that $\xi ''(x) > 0$ that

$$\begin{aligned} \xi '(x) > \xi (x)/(1+x) \end{aligned}$$

(13)

for every $x \in U_{-1}$. Indeed, notice that $1+x$ is just the distance between $x$ and $-1$ and thus $\xi (x)/(1+x)$ is the slope of the straight line joining the point $(-1, 0 )$ to $(x, \xi (x))$ in the graph of $\xi$, which is exactly the average derivative of $\xi$ in the interval $[-1, x]$. Since $\xi '' > 0$, the derivative is monotone increasing and thus the derivative $\xi '$ is maximal at the endpoint $x$, which implies (13). The same statement of course holds for $\ell _2=0$ and for all $x\in U_{+1}$.

1.2 Statement of results

Our first result is completely general and applies to all maps in $\widehat{\mathfrak {F}}$.

Theorem A

Every $g \in \widehat{\mathfrak {F}}$ admits a unique (up to scaling by a constant) invariant measure which is absolutely continuous with respect to Lebesgue; this measure is $\sigma$-finite and equivalent to Lebesgue.

This is perhaps not completely unexpected but also certainly not obvious in the full generality of the maps in $\widehat{\mathfrak {F}}$, especially for maps which admit critical points (which can, moreover, be of arbitrarily high order). Our construction gives some additional information about the measure given in Theorem A, in particular the fact that its density with respect to Lebesgue is locally Lipschitz and unbounded only at the endpoints $\pm 1$. We will show that, depending on the exponents $k_{1}, k_{2}, \ell _{1}, \ell _{2}$, the density may or may not be integrable and so the measure may or may not be finite. More specifically, let

$$\begin{aligned} \beta _1 {:}{=}k_2 \ell _1,\quad \beta _2 {:}{=}k_1 \ell _2, \quad \text { and } \quad \beta {:}{=}\max \{ \beta _{1}, \beta _{2} \}. \end{aligned}$$

We will show that the density is Lebesgue integrable at -1 or 1 respectively if and only if $\beta _{1}$ and $\beta _{2}$ respectively are $<1$. In particular, letting

$$\begin{aligned} {\mathfrak {F}}:= \{ g\in \widehat{{\mathfrak {F}}} \text { with } \beta < 1 \} \end{aligned}$$

we have the following result.

Theorem B

A map $g \in \widehat{{\mathfrak {F}}}$ admits a unique ergodic invariant probability measure $\mu _g$ absolutely continuous with respect to (indeed equivalent to) Lebesgue if and only if $g \in {\mathfrak {F}}$.

Notice that the condition $\beta <1$ is a restriction only on the relative values of $k_{1}$ with respect to $\ell _{2}$ and of $k_{2}$ with respect to $\ell _{1}$. It still allows $k_{1}$ and/or $k_{2}$ to be arbitrarily large, thus allowing arbitrarily “degenerate” critical points, as long as the corresponding exponents $\ell _{2}$ and/or $\ell _{1}$ are sufficiently small, i.e. as long as the corresponding neutral fixed points are not too degenerate.

We now give several non-trivial results about the statistical properties maps $g \in {\mathfrak {F}}$ with respect to the probability measure $\mu _g$. To state our first result recall that the measure-theoretic entropy of $g$ with respect to the measure $\mu$ is defined as

$$\begin{aligned} h_{\mu }(g):= \sup _{{\mathcal {P}}} \left\{ \lim _{n\rightarrow \infty } \frac{1}{n} \sum _{\omega _{n}\in {\mathcal {P}}_{n}} - \mu (\omega _{n})\ln \mu (\omega _{n})\right\} \end{aligned}$$

where the supremum is taken over all finite measurable partitions ${\mathcal {P}}$ of the underlying measure space and ${\mathcal {P}}_{n}:= {\mathcal {P}} \vee f^{-1}{\mathcal {P}}\vee \cdots \vee f^{-n}{\mathcal {P}}$ is the dynamical refinement of ${\mathcal {P}}$ by $f$.

Theorem C

Let $g \in {\mathfrak {F}}$. Then $\mu _g$ satisfies the Pesin entropy formula: $h_{\mu _g}(g)=\int \log |g'|d\mu _g.$

For Hölder continuous functions $\varphi , \psi : [-1,1] \rightarrow \mathbb {R}$ and $n \ge 1$, we define the correlation function

$$\begin{aligned} {\mathcal {C}}_{n}(\varphi , \psi ):= \left| \int \varphi \psi \circ g^{n} d\mu - \int \varphi d\mu \int \psi d\mu \right| . \end{aligned}$$

It is well known that $\mu _g$ is mixing if and only if ${\mathcal {C}}_n(\varphi , \psi ) \rightarrow 0$ as $n \rightarrow \infty$. We say that $\mu _g$ is exponentially mixing, or satisfies exponential decay of correlations if there exists a $\lambda > 0$ such that for all Hölder continuous functions $\varphi , \psi$ there exists a constant $C_{\varphi , \psi }$ such that ${\mathcal {C}}_{n}(\varphi , \psi ) \le C_{\varphi , \psi } e^{-\lambda n}$. We say that $\mu _g$ is polynomially mixing, or satisfies polynomial decay of correlations, with rate $\alpha >0$ if for all Hölder continuous functions $\varphi , \psi$ there exists a constant $C_{\varphi , \psi }$ such that ${\mathcal {C}}_{n}(\varphi , \psi ) \le C_{\varphi , \psi } n^{-\alpha }$.

Theorem D

Let $g \in {\mathfrak {F}}$. If $\beta = 0$ then $\mu _g$ is exponentially mixing, if $\beta \in (0,1)$ then $\mu _g$ is polynomially mixing with rate $(1-\beta )/\beta$.

Notice that the polynomial rate of decay of correlations $(1-\beta )/\beta$ itself decays to 0 as $\beta$ approaches 1, which is the transition parameter at which the invariant measure ceases to be finite. Intuitively, as $\beta \rightarrow 1$, the measure, while still equivalent to Lebesgue, is increasingly concentrated in neighbourhoods of the neutral fixed points, which slow down the decay of correlations.

Our final result concerns a number of limit theorems for maps $g \in {\mathfrak {F}}$, which depend on the parameters of the map and, in some cases, also on some additional regularity conditions. These are arguably some of the most interesting results of the paper, and those in which the existence of two indifferent fixed points, instead of just one, really comes into play, giving rise to quite a complex scenario of possibilities. We start by recalling the relevant definitions. For integrable functions $\varphi$ with $\int \varphi d\mu = 0$ we define the following limit theorems.

CLT:

$\varphi$ satisfies a central limit theorem with respect to $\mu$ if there exists a $\sigma ^2 \ge 0$ and a $\mathcal {N}(0,\sigma ^2)$ random variable $V$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty } \mu \left( \frac{ \sum _{ k = 0 }^{ n - 1 } \varphi \circ g^k }{ \sqrt{n} } \le x \right) = \mu ( V \le x ), \end{aligned}$$

for every $x \in \mathbb {R}$ for which the function $x \mapsto \mu ( V_{\sigma ^2} \le x )$ is continuous.

CLT_ns:

$\varphi$ satisfies a non-standard central limit theorem with respect to $\mu$ if there exists a $\sigma ^2 \ge 0$ and a $\mathcal {N}(0,\sigma ^2)$ random variable $V$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty } \mu \left( \frac{ \sum _{ k = 0 }^{ n - 1 } \varphi \circ g^k }{ \sqrt{n\log n} } \le x \right) = \mu ( V \le x ), \end{aligned}$$

for every $x \in \mathbb {R}$ for which the function $x \mapsto \mu ( V_{\sigma ^2} \le x )$ is continuous.

SL${}_\alpha$:

$\varphi$ satisfies a stable law of index $\alpha \in (1,2)$, with respect to a measure $\mu$, if there exists a stable random variable $W_{\alpha }$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty } \mu \left( \frac{ \sum _{ k = 0 }^{ n - 1 } \varphi \circ g^k }{ n^{1/\alpha } } \le x \right) = \mu ( W_{\alpha } \le x ), \end{aligned}$$

for every $x \in \mathbb {R}$ for which the function $x \mapsto \mu ( W_{\alpha } \le x )$ is continuous.

Finally, we say that an observable $\varphi : [-1,1] \rightarrow \mathbb {R}$ is a co-boundary if there exists a measurable function $\chi : [-1,1] \rightarrow \mathbb {R}$ such that $\varphi = \chi \circ g - \chi$. We are now ready to state our result on the various limit theorems which hold under some conditions on the parameters and on the observable $\varphi$. In order to state these conditions it is convenient to introduce the following variable:

$$\begin{aligned} \beta _\varphi {:}{=}{\left\{ \begin{array}{ll} 0 &{}\text {if } \varphi ( -1 ) = 0 \text { and } \varphi ( 1 ) = 0 \\ \beta _1 &{}\text {if } \varphi ( -1 ) \ne 0 \text { and } \varphi ( 1 ) = 0 \\ \beta _2 &{}\text {if } \varphi ( -1 ) = 0 \text { and } \varphi ( 1 ) \ne 0 \\ \beta &{} \text {if } \varphi ( -1 )\ne 0 \text { and } \varphi ( 1 )\ne 0, \end{array}\right. } \end{aligned}$$

(14)

We can then state our results in all cases in a clear and compact way as follows.

Theorem E

Let $g \in \mathfrak {F}$ and $\varphi : [ -1, 1 ] \rightarrow \mathbb {R}$ be Hölder continuous with $\int \varphi d\mu = 0$ and satisfying

(${\mathcal {H}}$):

$\nu _1> (\beta _{1} - 1/2)/ k_{2} \quad \text { and } \quad \nu _{2} > ( \beta _{2} - 1/2)/ k_{1 },$

where $\nu _{1}, \nu _{2}$ are the Hölder exponents of $\varphi |_{[-1,0]}$ and $\varphi |_{(0,1]}$ respectively. Then

• 1. if $\beta _{\varphi } \in [0,1/2 )$ then $\varphi$ satisfies CLT,

• 2. if $\beta _{\varphi } = 1/2$ then $\varphi$ satisfies CLT${}_{\textrm{ns}}$,

• 3. if $\beta _{\varphi } \in (1/2,1 )$ then $\varphi$ satisfies  SL${}_{1/ \beta _\varphi }$.

In case 3 we can replace the Hölder continuity condition $({\mathcal {H}})$ by the weaker (in this case) condition

(${\mathcal {H}}'$):

$\nu _1> (\beta _{1} - \beta _{\varphi })/ k_{2 } \quad \text { and } \quad \nu _{2} > (\beta _{2} - \beta _{\varphi } )/ k_{1 }.$

Moreover, in all cases where (CLT) holds we have that $\sigma ^2 = 0$ if and only if $\varphi$ is a coboundary.

Remark 1.4

Our results highlight the fundamental significance of the value of the observable $\varphi$ at the two fixed points, and how the fixed point at which $\varphi$ is non-zero, in some sense dominates, and determines the kind of limit law which the observable satisfies. If $\varphi$ is non-zero at both fixed points, then it is the larger exponent which dominates.

Remark 1.5

Note that $({\mathcal {H}})$ and (${\mathcal {H}}'$) are automatically satisfied for various ranges of $\beta _{1}, \beta _{2}$, for example if $\beta \le 1/2$ then $({\mathcal {H}})$ always holds and if $\beta = \beta _{\varphi }$ then (${\mathcal {H}}'$) always holds. These Hölder continuity conditions arise as technical conditions in the proof and it is not clear to us if they are really necessary and what could be proved without them. It may be the case, for example, that some limit theorems still hold under weaker regularity conditions on $\varphi$.

Remark 1.6

We remark also that the compact statement of Theorem E somewhat “conceals” quite a large number of cases which express an intricate relationship between the map parameters and the values and regularity of the observable. For example, the case $\beta _{\varphi }=0$ allows all possible values $\beta _1, \beta _2\in [0,1)$ and the case $\beta _{\varphi }=\beta _1$ allows all possible values of $\beta _2\in [0,1)$. We therefore have a huge number of possible combinations which do not occur in the case of maps with just a single intermittent fixed point.

1.3 Examples and literature review

There is an extensive literature on the dynamics and statistical properties of full branch maps, which have been studied systematically since the 1950s. Their importance stems partly from the fact that they occur very naturally, for example any smooth non-invertible local diffeomorphism of ${\mathbb {S}}^1$ is a full branch map, but also, and perhaps most importantly, because many arguments in Smooth Ergodic Theory apply in this setting in a particularly clear and conceptually straightforward way. Indeed, arguably, most existing techniques used to study hyperbolic (including non-uniformly hyperbolic) dynamical systems are essentially (albeit often highly non-trivial) extensions and generalisations of methods first introduced and developed in the setting of one-dimensional full branch maps.

Our class of maps $\widehat{{\mathfrak {F}}}$ is quite general and includes many one-dimensional full branch maps which have been studied in the literature as well as many maps which have not been previously studied. We give below a brief survey of some of these examples and indicate for which choices of parameters these correspond to maps in our family.¹

Arguably one of the very first and simplest general class of maps for which the existence of an invariant ergodic and absolutely continuous probability measure was proved are uniformly expanding full branch maps with derivatives uniformly bounded away from 0 and infinity, a result often referred to as the Folklore Theorem and generally attributed to Renyi. Some particularly simple examples of uniformly expanding maps are piecewise affine maps such as those given by

$$\begin{aligned} g (x) = {\left\{ \begin{array}{ll} ax &{}\text {for } x \in [0,1/a] \\ \frac{a}{a-1} \left( x - \frac{1}{a} \right) &{}\text {for } x \in (1/a, 1] \end{array}\right. } \end{aligned}$$

(15)

for parameters $a > 1$, see Fig. 2a. These are easily seen to be contained in the class $\widehat{\mathfrak {F}}$ with parameters $(\ell _1,\ell _2,k_1,k_2,a_1,a_2,b_1,b_2) = ( 0, 0, 1, 1, a, {a}/({a-1}), a - 1, {a}/({a-1}) - 1)$.

In the late ’70 s, physicists Maneville and Pomeau [PM80] introduced a simple but extremely interesting generalisation consisting of a class of full branch one-dimensional maps $g: [0, 1] \rightarrow [0,1]$, which they called intermittency maps, defined by

$$\begin{aligned} g (x) = x( 1 + x^{\alpha } )\mod 1 \end{aligned}$$

(16)

for $\alpha > 0$, see Fig. 2b (notice that for $\alpha = 0$ this just gives the map $g(x) = 2x$ mod 1, which is just (15) with $a =2$). These maps can be seen to be contained in our class $\widehat{\mathfrak {F}}$ by taking the parameters $(\ell _1,\ell _2,k_1,k_2,a_1,a_2,b_1,b_2) = ( \alpha , 0, 1, 1, a, a, 1, 1)$, where $a = g'(x_0)$, and $x_0 \in (0,1)$ is the boundary of the intervals on which the two branches of the map are defined. The Maneville-Pomeau maps are interesting because the uniform expansivity condition fails at a single fixed point on the boundary of the interval, where we have $g'(0)=1$ Their motivation was to model fluid flow where long period of stable flow is followed with an intermittent phase of turbulence, and they showed that this simple model indeed seemed to exhibit such dynamical behaviour. It was then shown in [Pia80] that for $\alpha >2$, the intermittency maps failed to have an invariant ergodic and absolutely continuous probability measure and satisfies the extremely remarkable property that the time averages of Lebesgue almost every point converge to the Dirac-delta measure $\delta _0$ at the neutral fixed point, even though these orbits are dense in $[0,1]$ and the fixed point is topologically repelling.

Fig. 2

a Graph of (15) with $a = 5$. b Graph of (16) with $\alpha = 9/10$. Graphs of a piecewise affine, Manneville–Pomeau, and Liverani–Saussol—Vaienti maps

Various variations of intermittency maps have been studied extensively from various points of views and with different techniques yielding quite deep results, see e.g. [LSV99, You99, Sar01, Mel09, PS09, FL01, Gou04a, Gou04b, NTV18, CHT21, Fre+16, Kor16, BS16, Ter16, SS13, Zwe03]. One well known version is the so-called Liverani-Saussol-Vaienti (LSV) map $g: [0, 1] \rightarrow [0,1]$ introduced in [LSV99] and defined by

$$\begin{aligned} g (x) = {\left\{ \begin{array}{ll} x (1 + 2^\alpha x^{\alpha }) &{} \text {for } x\in [0,1/2] \\ 2x - 1 &{}\text {for } x \in (1/2,1) \end{array}\right. } \end{aligned}$$

(17)

with parameter $\alpha > 0$, see Fig. 3a. This maintains the essential features of the Maneville-Pomeau maps (16), i.e. it is uniformly expanding except at the neutral fixed point at the origin, but in slightly simplified form where the two branches are always defined on the fixed domains $[0,1/2]$ and $1/2, 1)$ and the second branch is affine, both of which make the map family easier to study, including the effect of varying the parameter. The family of LSV maps (17) can be seen to be contained in our class $\widehat{\mathfrak {F}}$ by taking the parameters $(\ell _1,\ell _2,k_1,k_2,a_1,a_2,b_1,b_2) = ( \alpha , 0, 1, 1, 2, 2, 2^{\alpha }, 1)$.

In an earlier paper [Pik91], Pikovsky had introduced the maps $g: \mathbb {S}^1 \rightarrow \mathbb {S}^1$, defined (in a somewhat unwieldy way) by the implicit equation

$$\begin{aligned} x = {\left\{ \begin{array}{ll} \frac{1}{2 \alpha } (1 + g(x))^{\alpha } &{} \text {for } x\in [0, 1/2\alpha ] \\ g(x) + \frac{1}{2 \alpha } ( 1 - g(x) )^{\alpha } &{}\text {for } x \in (1/2\alpha ,1) \end{array}\right. } \end{aligned}$$

(18)

for $x\in [0,1)$, and then by the symmetry $g(x) = g(-x)$ for $x\in (-1, 0]$, see Fig. 3b. These maps have a neutral fixed point at the left end point, like in (16) and (17) but with the added complication of having unbounded derivative at the boundary between the domains of the two branches. On the other hand the definition is specifically designed in such a way that the order of intermittency is the inverse of the order of the singularity and, together with the symmetry of the two branches, this implies that Lebesgue measure is invariant for all values of the parameter $\alpha > 0$. Ergodic and statistical properties of these maps were studied in [AA04, Cri+10, BM14] and they can be seen to be contained within our class $\widehat{\mathfrak {F}}$ by taking the parameters $(\ell _1,\ell _2,k_1,k_2,a_1,a_2,b_1,b_2) = ( \alpha - 1, \alpha - 1, 1/\alpha , 1/\alpha , (2\alpha )^{1/\alpha }, (2\alpha )^{1/\alpha }, 1/2\alpha , 1/2\alpha )$.

Finally, [Ino92, Cui21] consider a class of maps, see Fig. 3c for an example, with a single intermittent fixed point and multiple critical points with each critical point mapping to the fixed point. These include some maps which are more general than those we consider here as they are defined near the fixed and critical points through some bounds rather than explicitly as we do here, but are also more restrictive as they only allow for a single neutral fixed point. Under a condition on the product of the orders of the neutral and (the most degenerate) critical point which is exactly analogous to our condition $\beta <1$, the existence of an invariant ergodic probability measure is proved which exhibits decay of correlations but no bounds are given for the rate of decay and no limit theorems are obtained.

Fig. 3

a Graph of (17) with $\alpha = 9/10$. b Graph of (18) with $\alpha = 3$. c An example from [Cui21]. Graphs of previsously studied generalisations of the Manneville-Pomeau map

2 Overview of the Proof

We discuss here our overall strategy and prove our Theorems modulo some key technical Propositions which we then prove in the rest of the paper. Our argument can be naturally divided into three main steps which we describe in some detail in the following three subsections.

2.1 The induced map

The first step of our arguments is the construction of an induced full branch Gibbs-Markov map, also known as a Young Tower. This is relatively standard for many systems, including intermittent maps, however, the inducing domain which we are obliged to use here due to the presence of two indifferent fixed points is different from the usual inducing domains and requires a more sophisticated double inducing procedure, which we outline here and describe and carry out in detail in Sect. 3. Recall the definition of $\Delta _0^-$ in (4) and, for $x\in \Delta _0^-$, let

$$\begin{aligned} \tau (x) {:}{=}\min \{ n > 0: g^{n} (x) \in \Delta _0^{-}\} \end{aligned}$$

be the first return time to $\Delta _0^-$. Then we define the first-return induced map

$$\begin{aligned} G: \Delta _0^- \rightarrow \Delta _0^- \quad \text { by } \quad G(x) {:}{=}g^{\tau (x)} (x). \end{aligned}$$

(19)

We say that a first return map (or, more generally, any induced map), saturates the interval $I$ if

$$\begin{aligned} \bigcup _{n\ge 0} \bigcup _{i= 0}^{n-1} g^{i}(\{\tau = n \}) = \bigcup _{n\ge 0} g^{n}(\{\tau > n \}) = I \ (\text {mod} \ 0). \end{aligned}$$

(20)

Intuitively, saturation means that the return map “reaches” every part of the original domain of the map $g$, and thus the properties and characteristics of the return map reflect, to some extent, all the relevant characteristics of $g$.

Remark 2.1

If $G$ is a first return induced map, as in our case, then all sets of the form $g^{i}(\{\tau = n \})$ are pairwise disjoint and therefore form a partition of $I$ mod 0.

The first main result of the paper is the following.

Proposition 2.2

Let $g \in \widehat{\mathfrak {F}}$. Then $G: \Delta _0^- \rightarrow \Delta _0^-$ is a first return induced Gibbs-Markov map which saturates $I$.

We give the precise definition of Gibbs-Markov map, and prove Proposition 2.2, in Sect. 3. In Sect. 3.1 we describe the topological structure of $G$ and show that it a full branch map with countably many branches which saturates $I$ (we will define $G$ as a composition of two full branch maps, see (37) and (40), which is why we call the construction a double inducing procedure); in Sect. 3.2 we obtain key estimates concerning the sizes of the partition elements of the corresponding partition; in Sect. 3.3 we show that $G$ is uniformly expanding; in Sect. 3.4 we show that $G$ has bounded distortion. From these results we get Proposition 2.2 from which we can then obtain our first main Theorem.

Proof of Theorem A

By standard results $G$ admits a unique ergodic invariant probability measure $\hat{\mu }_-$, supported on $\Delta _0^-$, which is equivalent to Lebesgue measure $m$ and which has Lipschitz continuous density ${\hat{h}}_-= d{\hat{\mu }}_-/dm$ bounded above and below. We then “spread” the measure over the original interval $I$ by defining the measure

$$\begin{aligned} {\tilde{\mu }} {:}{=}\sum _{n=0}^{\infty } g^n_*({\hat{\mu }}_-|\{\tau \ge n\}) \end{aligned}$$

(21)

where $g^n_*({\hat{\mu }}_-|\{\tau \ge n\})(E):= \hat{\mu }_- ( g^{-n} ( E ) \cap \{ \tau \ge n \} ).$ Again by standard arguments, we have that ${\tilde{\mu }}$ is a sigma-finite measure which is ergodic and invariant for $g$ and, using the non-singularity of $g$, it is absolutely continuous with respect to Lebesgue. The fact that $G$ saturates $I$ implies moreover that ${\tilde{\mu }}$ is equivalent to Lebesgue, which completes the proof. $\square$

Remark 2.3

We emphasize that we are not assuming any symmetry in the two branches of the map $g$. It is not important that the branches are defined on intervals of the same length and, depending on the choice of constants, we might even have a critical point in one branch and a singularity with unbounded derivative on the other. Interestingly, however, there is some symmetry in the construction in the sense that for $x\in \Delta _0^+$, we can define the first return map $G_+: \Delta _0^+ \rightarrow \Delta _0^+$ in a completely analogous way to the definition of $G$ above (see discussion in Sect. 3.1). Moreover, the conclusions of Proposition 2.2 hold for $G_+$ and thus $G_+$ admits a unique ergodic invariant probability measure $\hat{\mu }_+$ which is equivalent to Lebesgue measure $m$ and such that the density ${\hat{h}}_+:= d{\hat{\mu }}_+/dm$ is Lipschitz continuous and bounded above and below. The two maps $G$ and $G_+$ are clearly distinct, as are the measures ${\hat{\mu }}_-$ and ${\hat{\mu }}_+$, but exhibit a subtle kind of symmetry in the sense that the corresponding measure ${\tilde{\mu }}$ obtained by substituting ${\hat{\mu }}_-$ by ${\hat{\mu }}_+$ in (21) is, up to a constant scaling factor, exactly the same measure.

Corollary 2.4

The density ${\tilde{h}}$ of ${\tilde{\mu }}|_{\Delta _0^- \cup \Delta _0^+}$ is Lipschitz continuous and bounded and ${\tilde{\mu }} |_{\Delta _0^-} = {\hat{\mu }}$.

Proof

Since $G$ is a first return induced map it follows that the measure ${\tilde{\mu }}$ defined in (21) satisfies ${\tilde{\mu }} |_{\Delta _0^-} = {\hat{\mu }}$ and so the density ${\tilde{h}}$ of ${\tilde{\mu }}$ is Lipchitz continuous and bounded away from both $0$ and infinity on $\Delta _0^-$. Moreover, as mentioned in Remark 2.3, ${\tilde{\mu }} | _{\Delta _0^+}$ is equal, up to a constant, to the measure ${\hat{\mu }}_{+}$ and so the density of ${\tilde{\mu }} |_{\Delta _0^+}$ is also Lipschitz continuous and bounded away from 0 and infinity. $\square$

Remark 2.5

We have used above the notation $G$ rather than $G_{-}$ for simplicity as this is the map which plays a more central role in our construction, see Remark 3.3 below. Similarly, we will from now on simply use the notation ${\hat{\mu }}$ to denote the measure ${\hat{\mu }}_-$.

2.2 Orbit distribution estimates

The second step of the argument is aimed at establishing conditions under which the measure ${\tilde{\mu }}$ is finite, and can therefore be renormalized to a probability measure $\mu := {\tilde{\mu }}/ {\tilde{\mu }}(I),$ and aimed at studying the ergodic and statistical properties of $\mu$. Our approach here differs even more significantly from existing approaches in the literature, although it does have some similarities with the argument of [Cri+10]: rather than starting with estimates of the tail of the inducing time (which would themselves anyway be significantly more involved than in the usual examples of intermittency maps with a single critical point due to our double inducing procedure), we carry out more general estimates on the distribution of iterates of points in $I_-$ and $I_+$ before they return to $\Delta _{0}^{-}$. More precisely, we define the functions $\tau ^\pm (x): \Delta _0^-\rightarrow {\mathbb {N}}$ by

$$\begin{aligned} \tau ^+(x):= \#\{1\le i \le \tau : g^i(x)\in I_+ \}, \quad \text { and } \quad \tau ^-(x):= \#\{1\le j \le \tau : g^j(x)\in I_- \}.\nonumber \\ \end{aligned}$$

(22)

These functions count the number of iterates of $x$ in $I_-$ and $I_+$ respectively before returning to $\Delta _0^-$. Then for any $a,b\in {\mathbb {R}}$ we define weighted combination $\tau _{a,b}: \Delta _-^0 \rightarrow {\mathbb {R}}$ by

$$\begin{aligned} \tau _{a,b} (x) = a\tau ^+(x) + b \tau ^-(x) \end{aligned}$$

(23)

As we shall see as part of our construction of the induced map, both of these functions are unbounded and their level sets have a non-trivial structure in $\Delta _-^0$ and, moreover, the inducing time function $\tau : \Delta ^{-}_{0}\rightarrow {\mathbb {N}}$ of the induced map $G_{-}$ corresponds exactly to $\tau _{1,1}$ so that

$$\begin{aligned} \tau (x) = \tau _{1,1}(x) = \tau ^+(x) + \tau ^-(x). \end{aligned}$$

(24)

The key results of this part of the proof consists of explicit and sharp asymptotic bounds for the distribution of $\tau _{a,b}$ for different values of $a,b$, from which we can then obtain as an immediate corollary the rates of decay of the inducing time function $\tau$, and which will also provide the core estimates for the various distributional limit theorems. To state our results, let

$$\begin{aligned} B_1:= a_1^{-1/k_1} (\ell _2 b_2)^{-1/\beta _{2}} \quad \text { and } \quad B_2:= a_2^{-1/k_2} (\ell _1 b_1)^{-1/\beta _{1}}, \end{aligned}$$

(25)

(the expressions defining the constants $B_{1}, B_{2}$ will appear in the proof of Proposition 3.5 below).

Recall from Corollary 2.4 that the density ${\tilde{h}}$ of ${\tilde{\mu }}$ is bounded on ${\Delta _0^- \cup \Delta _0^+}$ and let ${\tilde{h}}(0^-)$ and ${\tilde{h}}(0^+)$ denote the values of this density on either side of $0$. Then, for any $a,b \ge 0$, we let

$$\begin{aligned} C_a {:}{=}{\tilde{h}}(0^-) B_1 a^{{1}/{\beta _2}}, \quad \text { and } \quad C_b {:}{=}{\tilde{h}}(0^+) B_2 b^{{1}/{\beta _1}}. \end{aligned}$$

(26)

Then we have the following distributional estimates.

Proposition 2.6

Let $g \in \widehat{\mathfrak {F}}$. Then for every $a, b \ge 0$ we have the following distribution estimates.

For every $\gamma \in [0,1)$

$$\begin{aligned} {\tilde{\mu }}( a\tau ^+ + b\tau ^-> t )&= {\left\{ \begin{array}{ll} C_b t^{-1/\beta _1} + C_a t^{-1/\beta _2} + o ( t^{ - \gamma - 1 / \beta }) &{}\text {if } \ell _1, \ell _2> 0 \\ C_b t^{-1/\beta _1} + o( t^{ - \gamma -1/\beta _1} ) &{}\text {if } \ell _1> 0, \ell _2 = 0 \\ C_a t^{-1/\beta _2} + o( t^{-\gamma -1/\beta _2} ) &{}\text {if } \ell _1 = 0, \ell _2 > 0 \\ O \left( (1 + b_1)^{-t/k_2} + (1 + b_2)^{-t/k_1} \right) &{}\text {if } \ell _1 = 0 , \ell _2 = 0 \end{array}\right. } \end{aligned}$$

(27)

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^+ - b\tau ^-> t )&= {\left\{ \begin{array}{ll} C_a t^{-1/\beta _2} + o( t^{- \gamma - 1/\beta } ) &{}\text {if } \ell _2 > 0 \\ O\left( (1 + b_2)^{-t/k_1}\right) , &{}\text {if } \ell _2 = 0 \end{array}\right. } \end{aligned}$$

(28)

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^+ - b\tau ^- < - t )&= {\left\{ \begin{array}{ll} C_b t^{-1/\beta _1} + o( t^{-\gamma - 1/\beta } ) &{}\text {if } \ell _1 > 0 \\ O\left( (1 + b_1)^{-t/k_2}\right) , &{}\text {if } \ell _1 = 0. \end{array}\right. } \end{aligned}$$

(29)

Remark 2.7

We have assumed in Proposition 2.6 that $a,b \ge 0$ to avoid stating explicitly too many cases, but one can easily read off the tails for $\tau _{a,b}$ for arbitrary $a,b \in \mathbb {R}$. For example, if $a<0$ and $b>0$ we can write ${\tilde{\mu }} ( -a\tau ^+ + b \tau ^- > t ) = {\tilde{\mu }} ( a\tau ^+ - b \tau ^- < -t )$ and get the corresponding estimate from (29). Notice moreover, that the estimates for $\ell _{1}=0$ and/or $\ell _{2}=0$ are exponential.

Recall from Corollary 2.4 that ${\hat{\mu }} = {\tilde{\mu }}$ on the inducing domain $\Delta _{0^{-}}$ and therefore all the above estimates hold for ${\hat{\mu }}$ with exactly the same constants. In particular by Proposition 2.6 and (24), we immediately get the corresponding estimates for the tail ${\hat{\mu }} ( \tau> t ) = {\tilde{\mu }} ( \tau > t )$.

Corollary 2.8

If $\beta = 0$ then ${\hat{\mu }} ( \tau > t )$ decay exponentially as $t \rightarrow +\infty$. If $\beta > 0$ then there exists a positive constant $C_{\tau }$ (which can be computed explicitly) such that

$$\begin{aligned} {\hat{\mu }} ( \tau > t ) \sim C_{\tau } t^{-1/\beta }. \end{aligned}$$

Proposition 2.6 will be proved in Sect. 4.1, here we show how it implies Theorems B, C, D.

Proof of Theorems B, C, and D

From the definition of ${\tilde{\mu }}$ in (21) and since $g^{-n}(I)=I$ we have

$$\begin{aligned} {\tilde{\mu }}(I) {:}{=}\sum _{n=0}^{\infty } {\hat{\mu }}_-(g^{-n}(I)\cap \{\tau> n\}) =\sum _{n=0}^{\infty } {\hat{\mu }}_-(I\cap \{\tau> n\}) =\sum _{n=0}^{\infty } {\hat{\mu }}_-(\tau > n). \end{aligned}$$

By Corollary 2.8, if $\beta =0$, the quantities ${\hat{\mu }}_-(\tau > n)$ decay exponentially and, if $\beta >0$ we have

$$\begin{aligned} {\tilde{\mu }}(I) = C\sum _{n=1}^{\infty }n^{-\frac{1}{\beta } } ( 1 + o(1) ), \end{aligned}$$

for some $C > 0$. This implies that ${\tilde{\mu }}(I) < \infty$ if and only if $\beta \in [0,1)$, i.e. if and only if $g \in {\mathfrak {F}}$. Thus, for $g \in {\mathfrak {F}}$ we can define the measure $\mu _{g}:={\tilde{\mu }}/{\tilde{\mu }}(I)$, which is an invariant ergodic probability measure for $g$, and is unique because it is equivalent to Lebesgue, thus proving Theorem  B. Theorem C follows from Theorem A in [AM21] by noticing that $\mathcal {P}=\{(-1,0),(0,1)\}$ is a Lebesgue mod 0 generating partition such that $H_{\mu _g}(\mathcal {P})<\infty$ and $h_{\mu _g}(g,\mathcal {P})<\infty$, and therefore $h_{\mu _g}(g)<\infty$. Finally, Theorem D follows by well known results [You99] which show that the decay rate of the tail of the inducing times provides upper bounds for the rates of decay of correlations as stated. $\square$

2.3 Distribution of induced observables

The last part of our argument is focused on obtaining the limit theorems stated in Theorem E. When $\beta =0$ the decay of correlations is exponential and the result follows from [YouRecurrenceTimesRates1999]. Similarly, after having established Proposition 2.2 and Corollary 2.8, the case that only one of $\ell _{1}, \ell _{2}$ is positive implies that there is only one intermittent fixed point, and thus essentially reduces to the argument given in [Gou04a, Theorem 1.3] for the LSV map. We only therefore need to consider the case that both $\ell _{1}, \ell _{2} > 0$, which implies in particular that $\beta \in (0,1)$.

Given an observable $\varphi : [0,1] \rightarrow \mathbb {R}$, we define the induced observable $\Phi : \Delta _0^- \rightarrow \mathbb {R}$ by

$$\begin{aligned} \Phi (x) {:}{=}\sum _{ k = 0 }^{ \tau (x) - 1 } \varphi \circ g^k. \end{aligned}$$

Definition 2.9

We write $\Phi \in \mathcal {D}_{\alpha }$ if $\exists c_{1}, c_{2} \ge 0$, with at least one of $c_1,c_2$ non-zero, such that

$$\begin{aligned} \hat{ \mu } ( \Phi > t ) = c_{1}t^{-\alpha } + o( t^{-\alpha } ) \quad \text { and } \quad \hat{ \mu } ( \Phi < -t ) = c_{2}t^{-\alpha } + o( t^{-\alpha } ), \end{aligned}$$

(30)

In certain settings, limit theorems can be deduced from properties of the induced observable $\Phi$. In particular, it is proved in Theorems 1.1 and 1.2 of [Gou04a] that, precisely in our setting²:

$$\begin{aligned}&\text { if } \Phi \in L^2 ( \hat{\mu }) \text { then } \varphi \text { satisfies }~(CLT), \end{aligned}$$

(31)

$$\begin{aligned}&\text { if } \Phi \in \mathcal {D}_{2} \text { then } \varphi \text { satisfies }(CLT_{\textrm{ns}}), \end{aligned}$$

(32)

$$\begin{aligned}&\text { if } \Phi \in \mathcal {D}_{\alpha } \text { with } \alpha \in (1, 2) \text { then } \varphi \text { satisfies }~SL_{\alpha }. \end{aligned}$$

(33)

We will argue that in each case of Theorem E, the induced observable $\Phi$ satisfies one of the above. To prove this, we first decompose a general observable $\varphi : [-1, 1]\rightarrow {\mathbb {R}}$ by letting $a:= \varphi (1)$ and $b:= \varphi (-1)$ and writing

$$\begin{aligned} \varphi = \varphi _{a,b} + {\tilde{\varphi }} \quad \text { where } \quad \varphi _{a,b} {:}{=}b \chi _{[-1,0)} + a \chi _{[0,1]} \ \text {and}\ {\tilde{\varphi }} {:}{=}\varphi - \varphi _{a,b}, \end{aligned}$$

(34)

where $\chi _{[-1,0)}, \chi _{[0,1]}$ are the characteristic functions of the intervals $[-1,0)$ and $(0,1]$ respectively. The induced observable of $\varphi$ is the sum of the induced observables of $\varphi _{a,b}$ and ${\tilde{\varphi }}$ giving

$$\begin{aligned} \Phi (x) = \sum _{ k = 0 }^{ \tau (x) - 1 } \varphi _{a,b} \circ g^{k} (x) +\sum _{ k = 0 }^{ \tau (x) - 1 } \tilde{ \varphi } \circ g^{k} (x) = \tau _{a,b} + {\tilde{\Phi }}, \end{aligned}$$

(35)

where $\tilde{\Phi }$ denote the induced observable of ${\tilde{\varphi }}$, and $\tau _{a,b}$ is defined in (23), indeed, $\varphi _{a,b}\circ g^k(x)$ takes only two possible values, $a$ or $b$, depending on whether $g^k(x)\in (0,1]$ or $g^k(x)\in [-1,0)$, and therefore the corresponding induced observable is precisely $\tau _{a,b}$.

To prove Theorem E we obtain regularity and distribution results for the induced observables $\tau _{a,b}$ and ${\tilde{\Phi }}$ and substitute them into (35) to get the various cases (31)-(33). The motivation for the decomposition (34) is given by the observation that ${\tilde{\varphi }} (-1) = {\tilde{\varphi }} (1) = 0$, which allows us to prove the following estimate for the corresponding induced observable ${\tilde{\Phi }}$.

Proposition 2.10

Let $g \in \mathfrak {F}$ with $\beta \in (0,1)$ and let ${\tilde{\varphi }}: [-1,1]\rightarrow {\mathbb {R}}$ be a Hölder continuous observable such that ${\tilde{\varphi }} (-1)={\tilde{\varphi }} (1) = 0$. Then

$$\begin{aligned} ({\mathcal {H}}) \implies {\tilde{\Phi }} \in L^2 \quad \text { and } \quad ({\mathcal {H}}') \implies {\hat{\mu }}( \pm {\tilde{\Phi }} > t ) = o( t^{ -1/\beta _\varphi }). \end{aligned}$$

(36)

Proposition 2.6 gives results for $\tau _{a,b}$.

Corollary 2.11

(Corollary to Proposition 2.6). If at least one of $a {:}{=}\varphi (1)$, $b {:}{=}\varphi (-1)$ is non-zero then:

$$\begin{aligned} \beta _{\varphi } \in [0,1/2) \implies \tau _{a,b} \in L^2( \hat{\mu } ), \quad \text { and } \quad \beta _{\varphi } \in [1/2, 1) \implies \tau _{a,b} \in \mathcal {D}_{1/\beta _{\varphi }}. \end{aligned}$$

We prove Corollary  2.11 and Proposition 2.10 in Sect. 4.2. For now we show how they imply Theorem E.

Proof of Theorem E

If $\varphi (-1) = \varphi (1) = 0$ then $\tau _{a,b} \equiv 0$ and so $\Phi = {\tilde{\Phi }}$, Proposition 2.10 implies that $\Phi \in L^{2}( {\hat{\mu }} )$ and so (31) holds. If at least one of $\varphi (-1), \varphi (1)$ is non-zero, we have two cases. If $\beta _{\varphi } \in (0,1/2)$, Proposition 2.10 and Corollary 2.11 give that both $\tau _{a,b}, {\tilde{\Phi }} \in L^{2} ( {\hat{\mu }} )$, which implies that $\Phi \in L^{2} ( {\hat{\mu }} )$ and therefore (31) holds. If $\beta _{\varphi } \in [1/2, 1)$ then $\tau _{a,b} \in \mathcal {D}_{1/\beta _{\varphi }}$ by Corollary 2.11 and ${\hat{\mu }} ( \pm {\tilde{\Phi }} > t ) = o( t^{-1/\beta _{\varphi }} )$ by Proposition 2.10, and therefore $\Phi = \tau _{a,b} + \tilde{\Phi } \in \mathcal {D}_{1/\beta _{\varphi }}$ since the tail of ${\tilde{\Phi }}$ is negligible compared to that of $\tau _{a,b}$. Whence, (32) holds when $\beta _{\varphi } = 1/2$ and (33) holds otherwise. $\square$

Remark 2.12

The relation between $\Phi$ and $\tau _{a,b}$ is given formally in (35) but it can be useful to have a heuristic idea of this relationships. Given a point $x \in \delta _{i,j}$ with $i,j$ both large we know that most of the first $i$ iterates $x, g(x), \dots , g^{ i - 1 } (x)$ will lie near the fixed point $1$. Similarly, most of the next $j$ iterates $g^{ i } (x), \dots , g^{ i + j - 1 }$ will lie near the fixed point $-1$. Thus, if we assume that $\varphi$ is “sufficiently well behaved” near $1$ and $-1$ (in a sense that is made precise by conditions $({\mathcal {H}})$ and  (${\mathcal {H}}'$)), it is reasonable to hope that the induced observable $\Phi$ at the point $x$ will behave like $\Phi (x) = \sum _{ k = 0 }^{ n - 1} \varphi \circ g^k \approx a i + b j = \tau _{a,b}(x)$ when $a= \varphi (1), b=\varphi (-1)$ are not both zero.

3 The Induced Map

In this section we prove Proposition 2.2. We begin by recalling one of several essentially equivalent definitions of Gibbs-Markov map.

Definition 3.1

An interval map $F: I \rightarrow I$ is called a (full branch) Gibbs-Markov map if there exists a partition ${\mathcal {P}}$ of $I$ (mod 0) into open subintervals such that:

• 1. $F$ is full branch: for all $\omega \in {\mathcal {P}}$ the restriction $F|_{\omega }: \omega \rightarrow int(I)$ is a $C^{1}$ diffeomorphism;

• 2. $F$ is uniformly expanding: there exists $\lambda > 1$ such that $|F'(x)|\ge \lambda$ for all $x\in \omega$ for all $\omega \in {\mathcal {P}}$;

• 3. $F$ has bounded distortion: there exists $C>0, \theta \in (0,1)$ s.t. for all $\omega \in {\mathcal {P}}$ and all $x, y\in \omega$,

  $$\begin{aligned} \log \bigg |\frac{F'(x)}{F'(y)}\bigg |\le C\theta ^{s(x,y)}, \end{aligned}$$

  where $s ( x, y ) {:}{=}\inf \{ n \ge 0: F^n x \text { and } F^n y$ lie in different elements of the partition $\mathscr {P} \}.$

We will show that the first return map $G$ defined in (19) satisfies all the conditions above as well as the saturation condition (20). In Sect. 3.1 we describe the topological structure of $G$ and show that it is a full branch map with countably many branches which saturates $I$; this will require only the very basic topological structure of $g$ provided by condition (A0). In Sect. 3.2 we obtain estimates concerning the sizes of the partition elements of the corresponding partition; this will require the explicit form of the map $g$ as given in (A1). In Sect. 3.3 we show that $G$ is uniformly expanding; this will require the final condition (A2). Finally, in Sect. 3.4 we use the estimates and results obtained to show that $G$ has bounded distortion.

3.1 Topological construction

In this section we give an explicit and purely topological construction of the first return maps $G^{-}: \Delta _0^- \rightarrow \Delta _0^-$ and $G^{+}: \Delta _0^- \rightarrow \Delta _0^-$ which essentially depends only on condition (A0), i.e. the fact that $g$ is a full branch map with two orientation preserving branches. Recall first of all the definitions of the sets $\Delta _{n}^{\pm }$ and $\delta _{n}^{\pm }$ in (5) and (6). It follows immediately from the definitions and from the fact that each branch of $g$ is a $C^{2}$ diffeomorphism, that for every $n \ge 1$, the maps $g:\delta _{n}^{-} \rightarrow \Delta _{n-1}^{+}$ and $g:\delta _{n}^{+} \rightarrow \Delta _{n-1}^{-}$ are $C^{2}$ diffeomorphisms, and, for $n \ge 2$, the same is true for the maps $g^{n-1}: \Delta _{n-1}^{-}\rightarrow \Delta _0^{-},$ and $g^{n-1}: \Delta _{n-1}^{+}\rightarrow \Delta _0^{+},$ which implies that for every $n \ge 1$, the maps

$$\begin{aligned} g^{n}: \delta _n^{-} \rightarrow \Delta _0^+ \quad \text { and } \quad g^{n}: \delta _n^{+} \rightarrow \Delta _0^- \end{aligned}$$

are $C^{2}$ diffeomorphisms. We can therefore define two maps

$$\begin{aligned} {\widetilde{G}}^-:\Delta _{0}^{-} \rightarrow \Delta _{0}^{+} \quad \text { and } \quad {\widetilde{G}}^+:\Delta _{0}^{+} \rightarrow \Delta _{0}^{-} \quad \text { by } \quad {\widetilde{G}}^\pm |_{\delta _{n}^{\pm } }:= g^{n}. \end{aligned}$$

(37)

Notice that these are full branch maps although they have different domains and ranges, indeed the domain of one is the range of the other and viceversa. The fact that they are full branch allows us to pullback the partition elements $\delta _{n}^{\pm }$ into each other: for every $m, n \ge 1$ we let

$$\begin{aligned} \delta ^-_{m,n}:= g^{-m}(\delta ^+_n) \cap \delta ^-_m \quad \text { and } \quad \delta ^+_{m,n}:= g^{-m}(\delta ^-_n) \cap \delta ^+_m. \end{aligned}$$

Then, for $m \ge 1$, the sets $\{ \delta _{m,n}^{-}\}_{n\ge 1}$ and $\{ \delta _{m,n}^{+}\}_{n\ge 1}$ are partitions of $\delta _m^-$ and $\delta _m^+$ respectively and so

$$\begin{aligned} {\mathscr {P}}^-:= \{ \delta _{m,n}^{-}\}_{m,n\ge 1} \quad \text { and } \quad {\mathscr {P}}^+:= \{ \delta _{m,n}^{+}\}_{m,n\ge 1} \end{aligned}$$

(38)

are partitions of $\Delta _0^-, \Delta _0^+$ respectively, with the property that for every $m,n \ge 1$, the maps

$$\begin{aligned} g^{m+n}: \delta _{m,n}^{-} \rightarrow \Delta _{0}^{-} \quad \text { and } \quad g^{m+n}: \delta _{m,n}^{+} \rightarrow \Delta _{0}^{+} \end{aligned}$$

(39)

are $C^2$ diffeomorphisms. Notice that $m+ n$ is the first return time of points in $\delta _{m,n}^{-}$ and $\delta _{m,n}^{+}$ to $\Delta _{0}^{-}$ and $\Delta _{0}^{+}$ respectively and we have thus constructed two full branch first return induced maps

$$\begin{aligned} G^-:={\widetilde{G}}^+ \circ {\widetilde{G}}^-:\Delta _{0}^{-} \rightarrow \Delta _{0}^{-} \quad \text { and } \quad G^+:={\widetilde{G}}^- \circ {\widetilde{G}}^+:\Delta _{0}^{+} \rightarrow \Delta _{0}^{+}. \end{aligned}$$

(40)

for which we have $G^-|_{\delta _{m,n}^{-} }= g^{m+n}$ and $G^+|_{\delta _{m,n}^{+} }= g^{m+n}.$

Lemma 3.2

The maps $G^{-}$ and $G^{+}$ are full branch maps which saturate $I$

Proof

The full branch property follows immediately from (39). It then also follows from the construction that the families

$$\begin{aligned} \{g^j(\delta ^-_{m,n})\}_{\begin{array}{c} m,n\ge 1 \\ 0\le j< m+n \end{array}} \quad \text { and } \quad \{g^j(\delta ^+_{m,n})\}_{\begin{array}{c} m,n\ge 1 \\ 0\le j < m+n \end{array}} \end{aligned}$$

of the images of the partition elements (38) are each formed by a collection of pairwise disjoint intervals which satisfy

$$\begin{aligned} \bigcup _{\delta ^-_{m,n}\in {\mathcal {P}}^-} \bigcup _{j=0}^{m+n-1} g^j(\delta ^-_{m,n}) = \bigcup _{\delta ^+_{m,n}\in {\mathcal {P}}^+} \bigcup _{j=0}^{m+n-1} g^j(\delta ^-_{m,n}) = I \mod 0 \end{aligned}$$

and therefore clearly satisfy (20), giving the saturation. $\square$

Remark 3.3

Notice that the map $G^{-}$ is exactly the first return map $G$ defined in (19) and therefore Lemma 3.2 implies the first part of Proposition 2.2.

3.2 Partition estimates

The construction of the full branch induced maps $G^{\pm }: \Delta _0^\pm \rightarrow \Delta _0^\pm$ in the previous section is purely topological and works for any map $g$ satisfying condition (A0). In this section we proceed to estimate the sizes and positions of the various intervals defined above, and this will require more information about the map, especially the forms of the map as given in (A1). Before stating the estimates we introduce some notation. First of all, we let $( x_n^{-} )_{n \ge 0} \text { and } ( x_{n}^+ )_{ n \ge 0}$ be the boundary points of the intervals $\Delta _n^{-}, \Delta _n^{+}$ so that $\Delta _0^{-}=(x_{0}^{-}, 0), \Delta _0^{+}=(0, x_{0}^{+})$ and, for every $n \ge 1$ we have

$$\begin{aligned} \Delta _0^{-}=(x_{0}^{-}, 0), \quad \Delta _0^{+}=(0, x_{0}^{+}), \quad \Delta _n^{-} = ( x_{n}^{-}, x_{n-1}^{-} ), \quad \Delta _n^{+} = ( x_{n-1}^{+}, x_n^{+}). \end{aligned}$$

(41)

The following proposition gives the speed at which the sequences $(x_n^+), (x_n^-)$ converge to the fixed points $1, -1$ respectively and gives estimates for the size of the partition elements $\Delta _n^{\pm }$ for large $n$ in terms of the values of $\ell _1$ and $\ell _2$. To state the result we let

$$\begin{aligned} C_1 = \left( \ell _1 b_1\right) ^{- {1}/{\ell _1}}, \quad C_2 = \left( \ell _2 b_2 \right) ^{-{1}/{\ell _2}}, \quad C_3 = \ell _1^{-(1 + 1/\ell _1)} b_1^{-1/\ell _1} \quad C_4 = \ell _2^{- (1 + 1/\ell _2)} b_2^{-1/\ell _2}. \end{aligned}$$

Proposition 3.4

If $\ell _1 = 0$, then

$$\begin{aligned} (1+b_1+\epsilon )^{-n}\lesssim 1 + x_n^{-} \lesssim (1+b_1)^{-n} \quad \text { and } \quad |\Delta _n^{-}| \lesssim (1+b_1)^{-n}. \end{aligned}$$

(42)

If $\ell _1> 0$, then

$$\begin{aligned} 1 + x_n^{-} \sim C_1 n^{-{1}/{\ell _1}} \quad \text { and } \quad |\Delta _n^-| \sim C_3 n^{-\left( 1 +{1}/{\ell _1}\right) }. \end{aligned}$$

(43)

If $\ell _2 = 0$, then

$$\begin{aligned} (1+b_2+\epsilon )^{-n}\lesssim 1 - x_n^{+} \lesssim (1+b_2)^{-n} \quad \text { and } \quad |\Delta _n^{+}| \lesssim (1 + b_2)^{-n}. \end{aligned}$$

(44)

If $\ell _2 > 0$, then

$$\begin{aligned} 1- x_n^{+} \sim C_2 n^{- {1}/{\ell _2}} \quad \text { and } \quad |\Delta _n^+| \sim C_4 n^{-\left( 1 + {1}/{\ell _2}\right) }. \end{aligned}$$

(45)

Proof

We will prove (42) and (43) and then (44) and (45) follow by exactly the same arguments. Notice first of all that from (7) we have $\delta ^{+}_{n} \subset U_{0+}$ for all $n > n_{+}$ and, since from (2) we have that $U_{-1}:=g(U_{0+})$, this implies that $\Delta _{n-1}^{-}:=g(\delta _{n}^{+}) \subset U_{-1}$ for all $n > n_{+}$, and thus $\Delta _{n}^{-} \subset U_{-1}$ for all $n \ge n_{+}$ which, by the definition of $x_{n}$ in (41), implies that $x_n^{-}\in U_{-1}$ for $n \ge n_+$.

Now suppose that $\ell _1>0$. For $n \ge n_+$, by definition of the $x_{n}^{-}$, we have that $g(x_{n+1}^{-}) = x_n^{-}$, and so $1 + x_{n}^{-} = 1 + x_{n+1}^{-} + b_1 ( 1 + x_{n+1}^- )^{1 + \ell _1}$. Setting $z_n = 1 + x_n^{-}$ we can write this as $z_n = z_{n+1} (1 + b_1 z_{n+1}^{\ell _{1}})$ and, taking the power $-\ell _{1}$ and expanding we get

$$\begin{aligned} \frac{1}{z_n^{\ell _{1}}}&= \frac{1}{z_{n+1}^{\ell _{1}}} (1 + b_1 z_{n+1}^{\ell _{1}})^{-\ell _{1}} = \frac{1}{z_{n+1}^{\ell _{1}}} \left( 1 - \ell _{1} b_1z_{n+1}^{\ell _{1}} + O(z_{n+1}^{2\ell _1})\right) = \frac{1}{z_{n+1}^{\ell _{1}}} - \ell _{1}b_1 + o(1). \end{aligned}$$

From the above we know that $z_n^{-\ell _1} = z_{n-1}^{-\ell _1} + b_1\ell _1 + o(1)$ and applying this relation recursively we obtain that $z_{n}^{-\ell _1} = \ell _1 b_1 n + o (n)$ which yields $x_n^{-} + 1 = ( \ell _1 b_1 n )^{ -{1}/{\ell _1} } (1 + o (1) )$, thus giving the first statement in (43). Now, by definition $\Delta _n^{-} = [ x_{n}^-, x_{n-1}^- ) = [ x_{n}^-, g(x_n^-) )$, so, for all $n$ large enough, $|\Delta _n^{-}| = g(x_n^-) - x_n^{-} = b_1 (1 + x_n^{-} )^{ 1 + \ell _1}$. Inserting $x_n^- + 1 \sim C_1 n^{ - 1 / \ell _1 }$ into this expression for $|\Delta _n^-|$ then yields $|\Delta _n^-| \sim \ell _1^{-(1 + {1}/{\ell _1})} b_1 n^{ -1 - 1/\ell _1}$, completing the proof of (45).

Now, for $\ell _1=0$, since $g(x_n^-)=x_{n-1}^-$, the mean value theorem implies $(1+b_1)\le (x_{n-1}^-+1)/(x_{n}^-+1)\le (1+b_1+o(1))$ which can be written as $(1+b_1+o(1))^{-1}(x_{n-1}^-+1)\le x_{n}^-+1\le (1+b_1)^{-1}(x_{n-1}^-+1)$. Iterating this relation we obtain the claimed bounds for $x_n^{-} + 1$. As in the previous case we may calculate using (3) that $|\Delta _n^-| = g(x_{n}^{-}) - x_{n}^{-} = -1 + (1 + b_1) ( 1 + x_n^{-} ) + \xi ( x_n^{-} ) - x_{n-1} = b_1 ( 1 + x_n^{-} ) + o(1) \lesssim (1 + b_1 )^{-n}$, which concludes the proof. $\square$

To get analogous estimates for the intervals $\delta _n^{-}, \delta _n^{+}$, we let $(y_n^{-})_{ n \ge 0 }$ and $(y_n^{+} )_{ n \ge 0 }$ be the boundary points of the intervals $\delta _n^{-}, \delta _n^{+}$ respectively, so that for every $n\ge 1$ we have

$$\begin{aligned} \delta _n^{-} = ( y_{n-1}^{-}, y_{n}^- ) \quad \text { and } \quad \delta _n^{+} = ( y_{n}^{+}, y_{n-1}^{+}). \end{aligned}$$

In particular, $y_{0}^{-} = x_0^-$, $y_{0}^{+} = x_0^+$, and $g(y^-_n) = x^+_{n-1}$, $g(y^+_n) = x^-_{n-1}$ for $n \ge 1$. Then we let

$$\begin{aligned} B_1 = a_1^{-1/k_1} (\ell _2 b_2)^{-1/\beta _{2}}, \quad B_2 = a_2^{-1/k_2} (\ell _1 b_1)^{-1/\beta _{1}}, \quad B_3 = B_1/\beta _{2}, \quad B_4 = B_2/\beta _{1}. \end{aligned}$$

Recall that $B_{1}, B_{2}$ have already been defined in (25).

Proposition 3.5

If $\ell _1= 0$, then for every $\varepsilon > 0$

$$\begin{aligned} \left( \frac{1}{1+b_2+\varepsilon }\right) ^{\frac{n}{k_1}} \lesssim -y_n^{-} \lesssim \left( \frac{1}{1+b_2}\right) ^{\frac{n}{k_1}} \quad \text { and } \quad |\delta _n^{-}| \lesssim \left( \frac{1}{1+b_2}\right) ^{n}. \end{aligned}$$

(46)

If $\ell _1> 0$, then

$$\begin{aligned} y_n^{-} \sim - B_1 n^{-\frac{1}{\beta _{2}}}, \quad \text { and } \quad |\delta _n^{-}| \sim B_3 n^{-\left( 1 + \frac{1}{\beta _{2}} \right) }. \end{aligned}$$

(47)

If $\ell _2 = 0$, then for every $\varepsilon > 0$

$$\begin{aligned} \left( \frac{1}{1+b_1+\varepsilon }\right) ^{\frac{n}{k_2}} \lesssim y_n^{+} \lesssim \left( \frac{1}{1+b_1}\right) ^{\frac{n}{k_2}}, \quad \text { and } \quad |\delta _n^{+}| \lesssim \left( \frac{1}{1+b_1}\right) ^{n}. \end{aligned}$$

(48)

If $\ell _2 > 0$, then

$$\begin{aligned} y_n^{+} \sim B_2 n^{-\frac{1}{\beta _{1}}}, \quad \text { and } \quad |\delta _n^{+}| \sim B_4 n^{-\left( 1 + \frac{1}{\beta _{1}} \right) }, \end{aligned}$$

(49)

Proof

We will prove (46) and (47), as (48) and (49) follow by analogous arguments. Suppose first that $\ell _1 > 0$. As $x_n^+ \rightarrow 1$, and as $g_{-}(y_n^-) = x_{n-1}^{+}$ we know that for all $n$ sufficiently large we have $g_{-} (y_n^-) = 1 - a_1 (-y_n^-)^{k_1} = x_{n-1}^{+}$. Solving for $y_n$ this gives

$$\begin{aligned} y_{n}^{-} = - \left( { (1 - x_{n-1}^{+}) }/{a_1} \right) ^{1/k_1} = - a_1^{-1/k_1} \left( \ell _2 b_2 n\right) ^{-{1}/{\ell _2 k_1}} (1 + o(1)) \end{aligned}$$

which is the first statement in (47). Now we turn our attention to the size of the intervals $\delta _n^{-}$. First let us note that for any $\gamma > 0$ we have that $n^{-\gamma } - (n + 1)^{-\gamma } = n^{-\gamma } \left[ 1 - (1 + 1/n)^{-\gamma }\right] = n^{-\gamma } \left[ 1 - \left( 1 - \gamma /{n} + O(n^{-2})\right) \right] = \gamma n^{-(1 + \gamma )} (1 + O(1/n))$ and therefore

$$\begin{aligned}{} & {} |\delta _n| = y_n^{-} - y_{n+1}^{-} = B_1 ( n^{-1/\ell _2 k_1} - (n+1)^{-1/\ell _2 k_1}) (1 + o(1)) = \frac{B_1}{\ell _2 k_1} n^{-(1 + 1/\ell _2 k_1)}(1 + o(1)) \end{aligned}$$

which completes the proof of (47). Now for $\ell _2=0$ we proceed as before, and by (42) we get

$$\begin{aligned} (1 + b_2 + \varepsilon )^{-n/k_1} \lesssim - y_n^- = \left( ({ 1 - x_{n-1}^{+} })/{a_1} \right) ^{1/k_1} \lesssim (1 + b_2)^{-n/k_1}. \end{aligned}$$

For the size of the interval $\delta _n^-$, we may use the mean value theorem to conclude that

$$\begin{aligned} g'(u_n) = \frac{ x_{n-2}^+ - x_{n-1}^+ }{ y_{n-1}^{-} - y_{n}^{-} } = \frac{ | \Delta _{n-1 }^+|}{ |\delta _n^-| }, \end{aligned}$$

for some $u_n \in \delta _n^-$. As $g'$ is monotone on $U_{0}^-$ we know, from the above and (44), that

$$\begin{aligned} |\delta _n^-| \lesssim {|\Delta _{n-1}^+|}/{g'(y_n^{-})} \lesssim (1 + b_2 + \varepsilon )^{-n/k_1} ( 1 + b_2 )^{-n} \lesssim ( 1 + b_2 )^{-n}. \end{aligned}$$

which concludes the proof. $\square$

3.3 Expansion estimates

Proposition 3.6

For every $g \in \widehat{{\mathfrak {F}}}$ the first return map $G: \Delta _0^- \rightarrow \Delta _0^-$ is uniformly expanding.

It is enough to prove uniform expansivity for the two maps ${\widetilde{G}}^-, {\widetilde{G}}^+$, recall (37), since this implies the same property for their composition $G= G^{-}$, recall (40). To simplify the notation we will only prove the statement for ${\widetilde{G}}^+$, i.e. we will prove that $x \in \delta _{n}^+ \Rightarrow (g^n)'(x) > \lambda$. The fact that $x \in \delta _{n}^- \Rightarrow (g^n)'(x) > \lambda$ follows by an identical argument.

Notice first of all that if $k_2 \in (0,1)$, the derivative in $\Delta _0^+$ is greater than 1 and therefore the uniform expansion of ${\widetilde{G}}^+$ is immediate. So throughout this section we will assume that $k_2 \ge 1$ which means that $g$ has a critical point and the derivative of $g$ in $\Delta _0^+$ can be arbitrarily small. For points outside the neighourhood $U_{0+}$ on which the map $g$ has a precise form, more precisely for $1\le n \le n_+$ and for $x \in \delta _{n}^+$, the expansivity is automatically guaranteed by condition (A2), but for points close to 0 where the derivative can be arbitrarily small the statement is non-trivial. It ultimately depends on writing ${\widetilde{G}}^+(x):= g^n(x)$ for $x \in \delta _{n}^+$, so that $( {\widetilde{G}}^+)'(x) = (g^n)'(x) = (g^{n-1})'(g(x)) g'(x)$, and then showing that the small derivative $g'(x)$ near the critical point is compensated by sufficiently large number of iterates where the derivative is $> 1$. This clearly relies very much on the partition estimates in Sect. 3.2 which provide a relation between the position of points, and therefore their derivatives, and the corresponding values of $n$. A relatively straightforward computation using those estimates shows that we get expansion for sufficiently large $n \ge 1$, which is quite remarkable but not enough for our purposes as it does not give a complete proof of expansivity for ${\widetilde{G}}^+$ at every point in $\Delta _0^+$. We therefore need to use a somewhat more sophisticated approach that shows that the derivative of ${\widetilde{G}}^+$ has a kind of “monotonicity” property in the following sense. Define the function $\phi : \Delta _0^+ {\setminus } \delta _1^+ \rightarrow \Delta _0^+$ given implicitly by $g^2 = g \circ \phi$ and explicitly by

$$\begin{aligned} \phi {:}{=}(g|_{U_{0+}})^{-1} \circ g|_{U_{-1}} \circ g|_{U_{0+}} \end{aligned}$$

(50)

Notice that $\phi$ is the bijection which makes the diagram in Fig. 4 commute.

Fig. 4

Definition of the map $\phi : \Delta _{0}^+{\setminus } \delta _{1}^+ \rightarrow \Delta _{0}^+$

The key step in the proof of Proposition 3.6 is the following lemma.

Lemma 3.7

For all $n \ge n^+$ and $x \in \delta _{n+1}^+$ we have

$$\begin{aligned} (g^{2})'(x) > g'(\phi (x)). \end{aligned}$$

Remark 3.8

Lemma 3.7 is equivalent to ${(g^2)' (x)}/{g'(\phi (x))} > 1$ which is equivalent to

$$\begin{aligned} \frac{ g'(x) }{ g'(\phi (x))} g'(g(x)) > 1. \end{aligned}$$

(51)

Notice that the ratio ${ g'(x) }/{ g'(\phi (x)) }$ is $< 1$ and measures how much derivative is “lost” when choosing the initial condition $x$ instead of the initial condition $\phi (x)$ (since $\phi (x) > x$ and the derivative is monotone increasing), whereas $g'(g(x)) > 1$ measures how much derivative is “gained” from performing an extra iteration of $g$. The Lemma says that the gain is more than the loss.

Proof

To simplify the notation let us set $a = a_{2}$, $b = b_1$, $k = k_2$, and $\ell = \ell _1$. Notice first of all that by the form of $g$ in $U_{0+}$ given in (A1) we have

$$\begin{aligned} \frac{g'(x)}{g'(\phi (x))} = \left( \frac{ x }{ \phi (x) }\right) ^{k - 1} = \left( \frac{ \phi (x) }{ x }\right) ^{1-k} \end{aligned}$$

(52)

Recall that $k > 1$ and $x< \phi (x)$ and so the ratio above is $< 1$. To estimate $g'(g(x))$ we consider two cases depending on $\ell$. If $\ell > 0$, using the form of $g$ given in (A1) and plugging into 50 we get

$$\begin{aligned} \phi (x) = \left[ x^{k} + b a^\ell x^{ k ( \ell + 1 )} \right] ^{{1}/{k}} \quad \text { and therefore } \quad \left( \frac{\phi (x)}{x} \right) ^k = 1 + b a^\ell x^{ k \ell } \end{aligned}$$

and, therefore, using the form of $G$ in $U_{-1}$, this gives

$$\begin{aligned} g'(g(x)) = g'( -1 + a x^k ) = 1 + b a^\ell x^{k \ell } + b \ell a^{\ell } x ^{k \ell } = \left( \frac{\phi (x)}{x} \right) ^k + b\ell a^\ell x^{k \ell }. \end{aligned}$$

(53)

From (52) and (53) and the fact that $x< \phi (x)$ we immediately get

$$\begin{aligned} \frac{g'(x)}{g'(\phi (x))} g'(g(x)) = \left( \frac{\phi (x)}{x} \right) ^{1-k} \left[ \left( \frac{ \phi (x)}{ x} \right) ^k + b \ell a^{\ell } x^{ k \ell } \right]> \frac{\phi (x)}{x} > 1 \end{aligned}$$

which establishes (51) and completes the case that $\ell > 0$. For $\ell = 0$, proceeding as above we obtain

$$\begin{aligned}{} & {} \phi (x) = \left[ (1 + b)x^k + \xi (g(x))/a \right] ^{1/k} \quad \text { and therefore }\nonumber \\ {}{} & {} \quad \left( \frac{\phi (x)}{x} \right) ^k = (1 + b) + \frac{\xi (g(x))}{ax^k}. \end{aligned}$$

(54)

Since $g(x) {=} -1{+}ax^k$, from (13) we have $\xi '(g(x)) \ge \xi (g(x))/(1{+}g(x)){=} \xi (g(x))/ax^k)$, and so

$$\begin{aligned} g'(g(x)) = (1 + b) + \xi '(g(x)) \ge (1 + b) + \frac{\xi (g(x))}{ax^k} = \left( \frac{\phi (x)}{x} \right) ^k. \end{aligned}$$

Together with (52), as above, we get the statement in this case also. $\square$

As an almost immediate consequence of Lemma 3.7 we get the following.

Corollary 3.9

For all $n \ge n^+$ and $x \in \delta _{n+1}^+$ we have

$$\begin{aligned} ({\widetilde{G}}^{+}){'}(x) > ({\widetilde{G}}^{+}){'}(\phi (x)). \end{aligned}$$

Proof

By Lemma 3.7 and (51), for any $1 \le m \le n$ we have

$$\begin{aligned}{} & {} (g^{m+1}) ' (x) = g'(x) g'(g(x)) \cdots g'(g^{m} (x)) = \frac{ g'(x) g'(g (x))}{ g'( \phi (x)) } (g^{m})'(\phi (x)) > (g^{m})'(\phi (x)).\nonumber \\ \end{aligned}$$

(55)

$\square$

Proof of Proposition 3.6

Condition (A2) implies that $({\widetilde{G}}^{+}){'}(x)\ge \lambda$ for all $x\in \delta ^{+}_{n}$ for $1\le n \le n^{+}$. Then, for $x \in \delta ^{+}_{n^{+}+1}$ we have $\phi (x) \in \delta ^{+}_{n^{+}}$ and therefore

$$\begin{aligned} ({\widetilde{G}}^{+}){'}(x) > ({\widetilde{G}}^{+}){'}(\phi (x)) \ge \lambda \end{aligned}$$

Proceeding inductively we obtain the result. $\square$

3.4 Distortion estimates

Proposition 3.10

For all $g \in \widehat{ \mathfrak {F} }$ there exists a constant ${\mathfrak {D}}>0$ such that for all $0\le m < n$ and all $x, y\in \delta ^{\pm }_n$,

$$\begin{aligned} \log \dfrac{\left( g^{n-m}\right) '(g^m(x))}{\left( g^{n-m}\right) '(g^m(y))} \le {\mathfrak {D}} |g^n(x) - g^n(y)|. \end{aligned}$$

As a consequence we get that $G$ is a Gibbs-Markov map with constants $C= {\mathfrak {D}}\lambda$ and $\theta =\lambda ^{-1}$.

Corollary 3.11

For all $x, y\in \delta _{i,j}\in {\mathcal {P}}$ with $x \ne y$ we have

$$\begin{aligned} \log \bigg |\frac{G'(x)}{G'(y)}\bigg |\le {\mathfrak {D}} \lambda ^{-s(x,y)+1}. \end{aligned}$$

Proof

Let $n {:}{=}s(x,y)$. Since G is uniformly expanding, we have $1\ge |G^{n}(x)-G^{n}(y)|=|(G^{n-1})'(u)||G(x)-G(y)|\ge \lambda ^{n-1}|G(x)-G(y)|$ and therefore $|G(x)-G(y)|\le \lambda ^{-n+1}.$ By Proposition 3.10 this gives $\log |G'(x)/G'(y)| \le {\mathfrak {D}}|G(x)-G(y)| \le {\mathfrak {D}} \lambda ^{-n+1} = {\mathfrak {D}} \lambda ^{-s(x,y)+1}$. $\square$

Proof of Proposition 3.10

We begin with a couple of simple formal steps. First of all, by the chain rule, we can write

$$\begin{aligned} \log \dfrac{\left( g^{n-m}\right) '(g^m(x))}{\left( g^{n-m}\right) '(g^m(y))}=\log \prod _{i=m}^{n-1}\dfrac{g'(g^i(x))}{g'(g^i(y))} =\sum _{i=m}^{n-1}\log \dfrac{g'(g^i(x))}{g'(g^i(y))}. \end{aligned}$$

Then, since $g^i(x), g^i(y)$ are both in the same smoothness component of $g$, by the Mean Value Theorem, there exists $u_i\in (g^i(x),g^i(y))$ such that

$$\begin{aligned} \log \dfrac{g'(g^i(x))}{g'(g^i(y))} = \log g'(g^i(x))-\log g'(g^i(y)) = \dfrac{g''(u_i)}{g'(u_i)} |g^i(x)-g^i(y)|. \end{aligned}$$

Substituting this into the expression above, and writing ${\mathfrak {D}}_i:= {g''(u_i)}/{g'(u_i)}$ for simplicity, we get

$$\begin{aligned} \log \dfrac{\left( g^{n-m}\right) '(g^m(x))}{\left( g^{n-m}\right) '(g^m(y))} = \sum _{i=m}^{n-1} {\mathfrak {D}}_i |g^i(x)-g^i(y)| \le \sum _{i=0}^{n-1} {\mathfrak {D}}_i |g^i(x)-g^i(y)|. \end{aligned}$$

(56)

We will bound the sum above in two steps. First of all we will show that it admits a uniform bound $\widehat{{\mathfrak {D}}}$ independent of $m,n$. We will then use this bound to improve our estimates and show that by paying a small price (increasing the uniform bound to a larger bound ${\mathfrak {D}}:= \widehat{{\mathfrak {D}}}^2/{|\Delta _0^-|}$) we can include the term $|g^n(x)-g^n(y)|$ as required. Ultimately this gives a stronger result since it takes into account the closeness of the points $x,y$.

Let us suppose first for simplicity that $x, y\in \delta ^{+}_n$, the estimates for $\delta ^{-}_n$ are identical. Then for $1\le i < n$ we have that $g^i(x), g^i(y), u_i\in \Delta ^{-}_{n-i}$ and therefore we can bound (56) by

$$\begin{aligned} \sum _{i=0}^{n-1} {\mathfrak {D}}_i |g^i(x)-g^i(y)| \le {\mathfrak {D}}_0 |x-y| + \sum _{i=1}^{n-1} {\mathfrak {D}}_i |g^i(x)-g^i(y)| \le {\mathfrak {D}}_0 \delta ^{+}_n + \sum _{i=1}^{n-1} {\mathfrak {D}}_i |\Delta ^{-}_{n-i}|.\nonumber \\ \end{aligned}$$

(57)

From (12) and using the relationship between the $y_n^+$ and the $x_n^-$ we may bound the first term by

$$\begin{aligned} {\mathfrak {D}}_0 |\delta _n^{+}| \lesssim u_0^{-1} |\delta _n^{+}| \lesssim \frac{ y_n^+ - y_{n+1}^+}{y_{n+1}^+} \lesssim \left( \frac{ 1 + x_n^- }{1 + x_{n+1}^{-}}\right) ^{1/k} - 1 \rightarrow c < \infty \end{aligned}$$

(58)

where we have used the fact that that for some sequence $\xi _n \rightarrow -1$ we have ${ (1 + x_n^- )}/{(1 + x_{n+1}^{-})} = g' ( \xi _n )$ which converges to $1$ if $\ell > 0$ (and therefore $c = 0$) or $1 + b_1$ otherwise (and therefore $c = b_{1}$). If $\ell _1 = 0$ then ${\mathfrak {D}}_i$ is uniformly bounded for $i > 0$, if $\ell _1 > 0$, then from (11) and (43) we know that

$$\begin{aligned} {\mathfrak {D}}_i |\Delta _{n-i}^-| \lesssim (1+u_i)^{\ell _1-1} |\Delta _{n-i}^-| \lesssim (n-i)^{-\frac{\ell _1-1}{\ell _1}} (n-i)^{-\left( 1 + \frac{1}{\ell _1}\right) } = (n-i)^{-2}. \end{aligned}$$

(59)

Then by (58) and (59) we find that

$$\begin{aligned} \widehat{ {\mathfrak {D}} } {:}{=}\exp \left\{ {\mathfrak {D}}_0 \delta _{n}^+ + \sum _{i = 1}^\infty {\mathfrak {D}}_i \Delta _{ n - i } \right\} \le \exp \left\{ {\mathfrak {D}}_0 + \sum _{i = 1}^\infty {\mathfrak {D}}_i \Delta _{ n - i } \right\} < \infty . \end{aligned}$$

(60)

Substituting this back into (57) and then into (56) we get

$$\begin{aligned} \log \bigg |\dfrac{\left( g^{n-m}\right) '(g^m(x))}{\left( g^{n-m}\right) '(g^m(y))}\bigg | \le \log \widehat{{\mathfrak {D}}} \end{aligned}$$

(61)

which completes the first step in the proof, as discussed above. We now take advantage of this bound to improve our estimates as follows. By a standard and straightforward application of the Mean Value Theorem, (61) implies that the diffemorphisms $g^{n}: \delta _{n}^+ \rightarrow \Delta _0^-$ and $g^{n-m}: \Delta _{n-m}^- \rightarrow \Delta _0^-$ all have uniformly bounded distortion in the sense that for every $x,y \in \delta ^+_n$ and $1\le m < n$ we have

$$\begin{aligned} \dfrac{|x-y|}{|\delta _{n}^+|} \le \widehat{{\mathfrak {D}}} \dfrac{|g^n(x)-g^n(y)|}{|\Delta _0^-|} \end{aligned}$$

(62)

and

$$\begin{aligned} \dfrac{|g^m(x)-g^m(y)|}{|\Delta _{n-m}^+|} \le \widehat{{\mathfrak {D}}} \dfrac{|g^{n-m}(g^m(x))-g^{n-m}(g^m(y))|}{|\Delta _0^-|}=\widehat{{\mathfrak {D}}} \dfrac{|g^n(x))-g^n(y)|}{|\Delta _0^-|}. \end{aligned}$$

(63)

Therefore

$$\begin{aligned}{} & {} |x-y| \le \frac{\widehat{{\mathfrak {D}}}}{|\Delta _0^-|} |g^n(x)-g^n(y)|{|\delta _{n}^+|} \quad \text { and } \quad |g^m(x)-g^m(y)| \le \frac{\widehat{{\mathfrak {D}}}}{|\Delta _0^-|} |g^n(x)-g^n(y)| {|\Delta _{n-m}^-|}. \end{aligned}$$

Substituting these bounds back into (56) (with $i=m$), and letting ${\mathfrak {D}}:= \widehat{{\mathfrak {D}}}^2/{|\Delta _0^-|}$, we get

$$\begin{aligned} \begin{aligned} \log \frac{\left( g^{n-m}\right) '(g^m(x))}{\left( g^{n-m}\right) '(g^m(y))}&\le \sum _{i=0}^{n-1} {\mathfrak {D}}_i |g^i(x)-g^i(y)| = {\mathfrak {D}}_0 |x-y| + \sum _{i=1}^{n-1} {\mathfrak {D}}_i |g^i(x)-g^i(y)| \\ {}&\le {\mathfrak {D}}_0 \frac{\widehat{{\mathfrak {D}}}}{|\Delta _0^-|} |g^n(x)-g^n(y)| {|\delta _{n}^+|} + \sum _{i=1}^{n-1} {\mathfrak {D}}_i \frac{\widehat{{\mathfrak {D}}}}{|\Delta _0^-|} |g^n(x)-g^n(y)|{|\Delta _{n-i}^-|} \\ {}&= \frac{\widehat{{\mathfrak {D}}}}{|\Delta _0^-|} \left[ {\mathfrak {D}}_0 {|\delta _{n}^+|} + \sum _{i=1}^{n-1} {\mathfrak {D}}_i {|\Delta _{n-i}^-|} \right] |g^n(x)-g^n(y)| \\ {}&\le \frac{\widehat{{\mathfrak {D}}}^2}{|\Delta _0^-|} |g^n(x)-g^n(y)| = {\mathfrak {D}} |g^n(x)-g^n(y)|. \end{aligned} \end{aligned}$$

Notice that the last inequality follows from (60). This completes the proof. $\square$

We state here also a simple corollary of Propositions 3.5 and 3.10 which we will use in Sect. 4.

Lemma 3.12

For all $i,j \ge 1$ we have

$$\begin{aligned} {\tilde{\mu }}( \delta _{i,j} ) \lesssim {\left\{ \begin{array}{ll} i^{ -(1 + 1/\beta _{2}) } j^{ -( 1 + 1/\beta _{1})},&{}\text {if } \ell _1, \ell _2> 0 \\ (1 + b_2)^{-i}, &{}\text {if } \ell _1 =0, \ell _2> 0 \\ (1 + b_1)^{-j}, &{}\text {if } \ell _2 =0, \ell _1 > 0 \\ \min \{ (1 + b_1), (1 + b_2) \}^{-i -j}, &{}\text {if } \ell _1 =0, \ell _2 = 0 \end{array}\right. } \end{aligned}$$

(64)

Proof

Proposition 3.10 implies that $|\delta _{ij}| \approx |\delta _{i}^{-}| |\delta _{j}^{+}|$ uniformly for all $i,j \ge 1$. Indeed, more precisely, it implies ${\mathfrak {D}}^{-1} {|g^{i}(\delta _{ij})|}/{|g^{i}(\delta _{i})|} \le {|\delta _{ij}|}/{|\delta _{i}|} \le {\mathfrak {D}} {|g^{i}(\delta _{ij})|}/{|g^{i}(\delta _{i})| }$ which implies $|\delta _{i}^{-}| |\delta _{j}^{+}|/{\mathfrak {D}} |\Delta _{0}^{+}| \le |\delta _{ij}| \le {\mathfrak {D}} |\delta _{i}^{-}| |\delta _{j}^{+}|/ |\Delta _{0}^{+}|.$ As ${\tilde{\mu }}$ is equivalent to Lebesgue on $\Delta _0^-\cup \Delta _{0}^{+}$ we obtain the Lemma immediately from Proposition 3.5. $\square$

4 Statistical Properties

In Sect. 4.1 we prove Proposition 2.6 and in Sect. 4.2 we prove Proposition 2.10 and Corollary 2.11. As discussed in Sect. 2.3 this completes the proof of Theorem E.

4.1 Distribution and tail estimates

In this section we prove Proposition 2.6. We will only explicitly prove (27) and (28) as the proof of (29) is identical to that of (28). For $a, b \ge 0$ consider the following decompositions

$$\begin{aligned} {\tilde{\mu }}( a\tau ^{+} + b \tau ^{-}> t )&= {\tilde{\mu }}( a\tau ^{+}> t) + {\tilde{\mu }}( b\tau ^{-} > t) \end{aligned}$$

(65)

$$\begin{aligned}&\quad - {\tilde{\mu }} ( a\tau ^{+}> t, b\tau ^{-}> t) + {\tilde{\mu }} ( a\tau ^{+} + b \tau ^{-} > t, \max \{a\tau ^{+}, b\tau ^{-}\} \le t ) \end{aligned}$$

(66)

and

$$\begin{aligned} {\tilde{\mu }} ( a \tau ^+ - b\tau ^-> t ) =&{\tilde{\mu }} ( a\tau ^{+} > t) \end{aligned}$$

(67)

$$\begin{aligned}&- {\tilde{\mu }}( a\tau ^{+} > t, a\tau ^{+} - b \tau ^{-} \le t ). \end{aligned}$$

(68)

We can then reduce the proof to two further Propositions. First of all we give precise asymptotic estimates of the terms $\mu ( a \tau ^+ > t )$, $\mu ( b \tau ^- > t )$ which make up (65) and (67).

Proposition 4.1

For every $a,b \ge 0$ and for every $\gamma \in ( 0, 1 )$

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^+> t ) = {\left\{ \begin{array}{ll} C_a t^{-1/\beta _2} + o( t^{-\gamma - 1/\beta _2} ) &{} \text {if } \ell _1 > 0 \\ O \left( ( 1 + b_2 )^{-t/ak_1} \right) &{} \text {if } \ell _1 = 0 \end{array}\right. } \end{aligned}$$

(69)

and

$$\begin{aligned} {\tilde{\mu }} ( b\tau ^-> t ) = {\left\{ \begin{array}{ll} C_b t^{-1/\beta _1} + o( t^{-\gamma - 1/\beta _1} ) &{} \text {if } \ell _2 > 0 \\ O \left( ( 1 + b_1 )^{-t/bk_2} \right) &{} \text {if } \ell _2 = 0 \end{array}\right. } \end{aligned}$$

(70)

Then, we show that the remaining terms (66) and (68) in the decompositions above have negligible contribution to the leading order asymptotics of the tail.

Proposition 4.2

If at least one of $\ell _1, \ell _2$ are not zero, then for every $a, b \ge 0$, $\gamma \in ( 0, 1 )$ we have

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^{+}> t, b\tau ^{-}> t ) + {\tilde{\mu }} ( a\tau ^{+} + b \tau ^{-} > t, \max \{a\tau ^{+}, b\tau ^{-}\} \le t ) = o( t^{-\gamma -1/\beta }) \end{aligned}$$

(71)

and

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^{+} > t, a\tau ^{+} - b \tau ^{-} \le t ) = o( t^{ - \gamma - 1/\beta }) \end{aligned}$$

(72)

As we shall see, (72) actually holds for all $\gamma \in (0,1/\beta )$ (where $1/\beta > 1$ since $\beta \in (0,1)$ by assumption) but we will not need this stronger statement. We prove Proposition 4.1 in Sect. 4.1.1 and Proposition 4.2 in Sect. 4.1.2, but first we show how they imply Proposition 2.6.

Proof of Proposition 2.6

To prove (27), first suppose that least one of $\ell _1, \ell _2$ is non-zero. Substituting the corresponding lines of (69) and (70) into (66) and substituting (71) into (68) we obtain (27) in this case. If $\ell _1 = \ell _2 = 0$ we only need to establish an upper bound for ${\tilde{\mu }} ( a \tau ^+ + b \tau ^- > t)$ rather than an asymptotic equality and therefore, instead of the decomposition in (65) and (66), we can use the fact that

$$\begin{aligned} {\tilde{\mu }} ( a \tau ^+ + b \tau ^-> t ) \le {\tilde{\mu }} ( a \tau ^+> t ) + {\tilde{\mu }} ( b \tau ^- > t ) \end{aligned}$$

(73)

The result then follows by inserting the corrsponding lines of (69) and (70) into (73).

To prove (28), if $\ell _2 > 0$ the result follows by substituting the corresponding line of (69) into (67) and substituting (72) into (68). Again, if $\ell _2 = 0$ we only need to establish an upper bound for ${\tilde{\mu }} ( a \tau ^+ - b \tau ^- > t)$ rather than an asymptotic equality and therefore, instead of the decomposition in (67) and (68), we can use the fact that

$$\begin{aligned} {\tilde{\mu }} ( a \tau ^+ - b \tau ^-> t ) \le {\tilde{\mu }} ( a \tau ^+ > t ) \end{aligned}$$

(74)

The result then follows by inserting the corresponding line of (70) into (74). $\square$

4.1.1 Leading order asymptotics

We prove Proposition 4.1 via two lemmas which show in particular how the values ${\tilde{h}}(0^-), {\tilde{h}}(0^+)$ of the density of the measure ${\tilde{\mu }}$ turn up in the constants $C_a, C_b$ defined in (26). Our first lemma shows that the tails of the distributions ${\tilde{\mu }}( \tau ^{+} > t )$ and ${\tilde{\mu }}( \tau ^{-} > t )$ have a very geometric interpretation.

Lemma 4.3

For every $t > 0$ we have

$$\begin{aligned} {\tilde{\mu }}( \tau ^{+}> t ) = {\tilde{\mu }} (y_{\lceil t \rceil }^-, 0) \quad \text { and } \quad {\tilde{\mu }}( \tau ^{-} > t ) = {\tilde{\mu }} (0, y_{\lceil t \rceil }^+ ). \end{aligned}$$

(75)

Remark 4.4

While the first statement in (75) is relatively straightforward, the second statement is not at all obvious since $\tau ^-$ is defined on $\Delta _0^-$ and there is no immediate connection with the interval $(0, y_{\lceil t \rceil }^+)$ in $\Delta _0^+$. As we shall see, the proof of Lemma 4.3 requires a subtle and interesting argument.

Remark 4.5

Since ${\tilde{\mu }}$ is equivalent to Lebesgue measure on $\Delta _0^-$ and $\Delta _0^+$, we immediately have that ${\tilde{\mu }} ( y_{\lceil t \rceil }^-, 0) \approx |y_{\lceil t \rceil }^-|$ and ${\tilde{\mu }} (0, y_{\lceil t \rceil }^+ ) \approx y_{\lceil t \rceil }^+$, and we can then use (47) and (49), and Lemma 4.3, to get upper bounds for the distributions ${\tilde{\mu }}( \tau ^{+} > t )$ and ${\tilde{\mu }}( \tau ^{+} > t )$. This is however not enough for our purposes as we require sharper estimates for the distributions, and we therefore need a more sophisticated argument which yields the statement in the following lemma.

Lemma 4.6

For every $t > 0$ we have

$$\begin{aligned} {\tilde{\mu }} ( y_{\lceil t \rceil }^-, 0 ) = y_{\lceil t \rceil }^- {\tilde{h}}( 0^-) + O( (y_{\lceil t \rceil }^-)^2) \quad \text { and } \quad {\tilde{\mu }} ( y_{\lceil t \rceil }^+, 0 ) = y_{\lceil t \rceil }^+ {\tilde{h}}( 0^+) + O( (y_{\lceil t \rceil }^+)^2). \end{aligned}$$

Before proving these two lemmas we show how they imply Proposition 4.1.

Proof of Proposition 4.1

Let us first show (69). Recall from the definition of $C_a$ in (26) that $a = 0 \Rightarrow C_a = 0$, so if $a = 0$ there is nothing to prove. Let us suppose then that $a > 0$. By Lemmas 4.3 and 4.6 we have

$$\begin{aligned} {\tilde{\mu }}( a\tau ^{+}> t ) = {\tilde{\mu }}( \tau ^{+} > t/a ) = y_{\lceil t/a \rceil }^- {\tilde{h}}( 0^-) + O( (y_{\lceil t/a \rceil }^-)^2). \end{aligned}$$

Then, using the asymptotic estimates (46) and (47) for $y_{n}^-$ in Proposition 3.5; and since $O ( t^{-2/\beta _1} ) = o ( t^{ - \gamma - 1 / \beta _1 } )$ for every $\gamma \in ( 0, 1 )$; and by the definition of $C_a$ in (26), we obtain

$$\begin{aligned} \mu ( a\tau ^+> t ) = {\left\{ \begin{array}{ll} B_1 {\tilde{h}} (0^-) (t / a)^{-1/\beta _2} + O ( t^{-2/\beta _2}) = C_a t^{-1/\beta _2} + o( t^{-\gamma - 1/\beta _2} ) &{} \text {if } \ell _1 > 0 \\ O \left( ( 1 + b_2 )^{-t/ak_1} \right) &{} \text {if } \ell _1 = 0 \end{array}\right. } \end{aligned}$$

yielding (70). To show (69) we can proceed similarly to the above. As before, if $b = 0$ there is nothing to prove so we assume $b > 0$ in which case Lemmas 4.3 and 4.6 we have ${\tilde{\mu }}( b\tau ^{-}> t ) = {\tilde{\mu }}( \tau ^{-} > t/b ) = y_{\lceil t/b \rceil }^+ {\tilde{h}}( 0^-) + O( (y_{\lceil t/b \rceil }^+)^2)$. Now using (48) and (49), and arguing as above we find that (29) holds for every $\gamma \in ( 0, 1)$. $\square$

We complete this section with the proofs of Lemmas 4.3 and 4.6.

Proof of Lemma 4.3

By definition, recall (22), $\tau ^{+}(x)=i, \tau ^{-}(x)=j$ for all $x\in \delta _{i,j}$, and therefore

$$\begin{aligned} {\tilde{\mu }} ( \tau ^{+}> t) = \sum _{i> t } \sum _{j = 1}^{\infty } {\tilde{\mu }}(\delta _{i,j}) \quad \text { and } \quad {\tilde{\mu }} ( \tau ^{-}> t ) = \sum _{j > t } \sum _{i = 1}^{\infty } {\tilde{\mu }}(\delta _{i,j}). \end{aligned}$$

(76)

We claim that for every $i, j \ge 1$ we have

$$\begin{aligned} \sum _{j = 1}^{\infty } {\tilde{\mu }} (\delta _{i,j}) = {\tilde{\mu }}(\delta _i^-) \quad \text { and } \quad \sum _{i = 1}^{\infty } {\tilde{\mu }} (\delta _{i,j}) = {\tilde{\mu }}(\delta _j^+). \end{aligned}$$

(77)

Then, substituting (77) into (76) we get

$$\begin{aligned} {\tilde{\mu }} ( \tau ^{+}> t) = \sum _{i> t} \sum _{j = 1}^{\infty } {\tilde{\mu }}( \delta _{i,j} ) = \sum _{i > t} {\tilde{\mu }} ( \delta _{i}^{-} ) = {\tilde{\mu }} ( y_{\lceil t \rceil }^-, 0 ), \end{aligned}$$

(78)

and

$$\begin{aligned} {\tilde{\mu }} ( \tau ^{-}> t ) = \sum _{j> t } \sum _{i = 1}^{\infty } {\tilde{\mu }}(\delta _{i,j}) = \sum _{j > t} {\tilde{\mu }} ( \delta _{i}^{+} ) = {\tilde{\mu }} ( 0, y_{\lceil t \rceil }^+ ) \end{aligned}$$

which is exactly the statement (75) in the Lemma.

Thus it only remains to prove (77). As already mentioned in Remark 4.4, despite the apparent symmetry between the two statements, the situation in the two expressions is actually quite different. Indeed, from the topological construction of the induced map, for each $i \ge 1$ we have

$$\begin{aligned} \delta _{i}^{-}= \bigcup _{j=1}^{\infty } \delta _{i,j} \end{aligned}$$

(79)

which, since the intervals $\delta _{i,j}$ are pairwise disjoint, clearly implies the first equality in (77). The second equality is not immediate since, for each fixed $j \ge 1$, the intervals $\delta _{i,j}$ are spread out in $\Delta _0^-$, with each $\delta _{i,j}$ lying inside the corresponding interval $\delta _i^-$, and indeed the $\delta _{i,j}$ do not even belong to $\delta _j^+$ and therefore we cannot just substitute $i$ and $j$ to get a corresponding version of (79). We use instead a simple but clever argument inspired by a similar argument in [Cri+10, Lemma 8] which takes advantage of the invariance of the meaure ${\tilde{\mu }}$. Recall first of all from the construction of the induced map, that $g^{-1} (\delta _{ j }^+)$ consists of exactly two connected components, one is exactly the interval $\delta _{1,j}$ and the other one is a subinterval of $\Delta _1^+$. So for any $j \ge 1$ we have

$$\begin{aligned} g^{-1} (\delta _{ j }^+) = \delta _{1,j} \cup \{ x: \Delta _1^+: g(x) \in \delta _j^{+}\}. \end{aligned}$$

By the invariance of the measure ${\tilde{\mu }}$, and since these two components are disjoint, this implies

$$\begin{aligned} {\tilde{\mu }}(\delta _{ j }^+) = {\tilde{\mu }}(g^{-1} (\delta _{ j }^+)) = {\tilde{\mu }}(\delta _{1,j}) + {\tilde{\mu }}( \{ x: \Delta _1^+: g(x) \in \delta _j^{+}\}) \end{aligned}$$

(80)

The preimage of the set $\{ x: \Delta _1^+: g(x) \in \delta _j^{+}\}$ itself also has two disjoint connected components

$$\begin{aligned} g^{-1} \{ x \in \Delta _1^+: g(x) \in \delta _j^{+} \} = \delta _{2,j} \cup \{ x \in \Delta _2^+: g^2(x) \in \delta _j^{+} \} \end{aligned}$$

and therefore, again by the invariance of ${\tilde{\mu }}$, we get

$$\begin{aligned} {\tilde{\mu }}(g^{-1} \{ x \in \Delta _1^+: g(x) \in \delta _j^{+} \}) = {\tilde{\mu }}(\delta _{2,j}) + {\tilde{\mu }}(\{ x \in \Delta _2^+: g^2(x) \in \delta _j^{+} \}) \end{aligned}$$

and, substituting this into (80), we get

$$\begin{aligned} {\tilde{\mu }}(\delta _{ j }^+) = {\tilde{\mu }}(g^{-1} (\delta _{ j }^+)) = {\tilde{\mu }}(\delta _{1,j}) + {\tilde{\mu }}(\delta _{2,j}) + {\tilde{\mu }}(\{ x \in \Delta _2^+: g^2(x) \in \delta _j^{+} \}). \end{aligned}$$

Repeating this procedure $n$ times gives

$$\begin{aligned} {\tilde{\mu }}(\delta _{ j }^+) = \sum _{i = 1}^{n} {\tilde{\mu }}(\delta _{i,j}) + {\tilde{\mu }}(\{ x \in \Delta _n^+: g^n(x) \in \delta _j^{+} \}) \end{aligned}$$

and therefore inductively, we obtain (77), thus completing the proof. $\square$

Proof of Lemma 4.6

From Lemma 4.3 we can give precise estimates for ${\tilde{\mu }} ( \tau ^{\pm } > t )$ in terms of the $y_{\lceil t \rceil }$ by making use of the fact that ${\tilde{h}}$ is Lipschitz on $\Delta _0^{\pm }$ (see Corollary 2.4). Indeed,

$$\begin{aligned} {\tilde{\mu }} ( \tau ^- > t ) = {\tilde{\mu }} ( 0, y_{\lceil t \rceil }^+) = \int _0^{y_{\lceil t \rceil }^+} {\tilde{h}} (x) dx = y_{\lceil t \rceil }^+ {\tilde{h}}( 0^+) + \int _0^{y_{\lceil t \rceil }^+} {\tilde{h}} (x) - {\tilde{h}} (0^+) dx. \end{aligned}$$

Using the fact that the density is Lipschitz we have

$$\begin{aligned} \left| \int _0^{y_{\lceil t \rceil }^+} {\tilde{h}} (x) - {\tilde{h}} (0^+) dx \right| \lesssim \int _0^{y_{\lceil t \rceil }^+}x dx \lesssim (y_{\lceil t \rceil }^+)^2 \end{aligned}$$

and so ${\tilde{\mu }} ( \tau ^- > t ) = y_{\lceil t \rceil }^+ {\tilde{h}}( 0^+) + O( (y_{\lceil t \rceil }^+)^2).$ The statement for $\mu ( \tau ^+ > t )$ follows in the same way. $\square$

4.1.2 Higher order asymptotics

In this subsection we prove Proposition 4.2. For clarity we prove (71) and (72) in two separate lemmas. We will make repeated use of some upper bounds for the measure ${\tilde{\mu }} ( \delta _{i,j} )$ of the partition elements which are given in Lemma 3.12

Lemma 4.7

If at least one of $\ell _1, \ell _2$ are not zero, then for every $a, b \ge 0$

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^{+}> t, b\tau ^{-}> t ) + {\tilde{\mu }} ( a\tau ^{+} + b \tau ^{-} > t, \max \{ a\tau ^{+}, b\tau ^{-}\} \le t ) = o( t^{-\gamma -1/\beta }) \end{aligned}$$

(81)

for any $\gamma \in ( 0, 1 )$.

Proof

First note that if one of $a,b$ is $0$ then (81) is automatically satisfied.

Now suppose that $a, b > 0$. For the first term in (81), from Lemma 3.12 we get

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^{+}> t, b\tau ^{-} > t ) = \sum _{ i = t/a }^{\infty }\sum _{j = t/b }^{\infty } {\tilde{\mu }} (\delta _{i,j}) \lesssim \sum _{i = t/a }^{\infty }\sum _{j = t/b }^{\infty } (ij)^{-(1 + 1/\beta )} \lesssim t^{-2/\beta } \end{aligned}$$

(82)

which is $o( t^{-\gamma -1/\beta })$ for every $\gamma \in (0, 1/\beta )$ and therefore in particular for every $\gamma \in (0, 1)$.

For the second term in (81) we obtain from Lemma 3.12 that

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^{+} + b \tau ^{-} > t, \max \{ a\tau ^{+}, b\tau ^{-}\} \le t )&= \sum _{ i = 1 }^{t/a} \sum _{j = \frac{t - ai + 1}{b}}^{t/b} {\tilde{\mu }}(\delta _{i,j}) \lesssim \sum _{ i = 1 }^{t/a} \sum _{ j = \frac{ t - ai + 1}{b}}^{t/b} i^{-1 - 1/\beta } j ^{-1 - 1/\beta } \nonumber \\&\lesssim \sum _{ i = 1 }^{t/a} i^{-1-1/\beta } \left[ \left( \frac{t - ai + 1}{b} \right) ^{-1/\beta } - \left( \frac{t}{b}\right) ^{-1/\beta } \right] \nonumber \\&\lesssim t^{-1/\beta } \sum _{ i = 1 }^{ t / a } i^{- 1 - 1/\beta } \left[ \left( 1 - \frac{ ai - 1 }{t} \right) ^{1/\beta } - 1 \right] \nonumber \\ \end{aligned}$$

(83)

Making the change of variables $k = \lceil ai - 1 \rceil$ and using that the first term in the sum is $0$ we obtain

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^{+} + b \tau ^{-} > t, \max \{a\tau ^{+}, b\tau ^{-}\} \le t ) \lesssim t^{-1/\beta } \sum _{ k = 1 }^{ t - 1 } k^{- 1 - 1/\beta } \left[ \left( 1 + \frac{k}{t} \right) ^{1/\beta } - 1 \right] . \end{aligned}$$

Let us set $a_k (t) {:}{=}k^{- 1 - 1/\beta } \left[ \left( 1 + \frac{k}{t} \right) ^{1/\beta } - 1 \right]$ and use the binomial theorem to get

$$\begin{aligned} a_{k}(t) = \frac{1}{k^{1+1/\beta }} \sum _{ m = 1 }^{ \infty } \left( {\begin{array}{c} - 1/\beta \\ m \end{array}}\right) \left( - \frac{ k }{ t } \right) ^m = \frac{1}{t k^{1/\beta }} \sum _{ m = 1 }^{ \infty } \left( {\begin{array}{c} - 1/\beta \\ m - 1 \end{array}}\right) \left( \frac{1}{m} \left( \frac{1}{\beta } - 1 \right) + 1 \right) \left( - \frac{ k }{ t } \right) ^{ m - 1 }. \end{aligned}$$

As $\left( \frac{1}{\beta } - 1 \right) /m$ is uniformly bounded above by some constant depending only on $\beta$ we obtain

$$\begin{aligned} a_{k} (t) \lesssim k^{-1/\beta } t^{ -1 } \sum _{ k = 0 }^{\infty } \left( {\begin{array}{c} - 1/\beta \\ m - 1 \end{array}}\right) \left( - \frac{ k }{ t } \right) ^{ m - 1 } = k^{-1/\beta } t^{-1} \left( 1 - \frac{k}{t} \right) ^{-1/\beta }. \end{aligned}$$

Using the fact that $n/( n - 1) < 2$ and that $1/\beta > 1$ we may conclude

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^{+} + b \tau ^{-} > t, \max \{a \tau ^{+}, b\tau ^{-}\} \le t )&\lesssim t^{- 1 -1/\beta } \sum _{ k = 1 }^{ t - 1 } \left( \frac{ t }{ k ( t - k ) }\right) ^{1/\beta } \lesssim t^{- 1 -1/\beta } \sum _{ k = 1 }^{ t - 1 } \frac{ t }{ k ( t - k ) } \\&\lesssim t^{- 1 -1/\beta } \int _{ 1 }^{ t - 1 } \frac{ t }{ x ( t - x ) } dx \lesssim t^{-1 -1/\beta } \log (t) = o( t^{-\gamma -1/\beta }) \end{aligned}$$

for any $\gamma \in ( 0, 1 )$. $\square$

Lemma 4.8

If $\ell _1, \ell _2$ are not both zero, then for every $a, b \ge 0$, $\gamma \in (0,1/\beta )$ we have

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^{+} > t, a\tau ^{+} - b \tau ^{-} \le t ) = o( t^{ - \gamma - 1/\beta }). \end{aligned}$$

Proof

By Lemma 3.12 we get

$$\begin{aligned} {\tilde{\mu }} ( a\tau ^{+}> t , a\tau ^{+} - b \tau ^{-} \le t )&= \sum _{ i> t/a } {\tilde{\mu }} ( \tau ^{+} = i, b\tau ^{-} \ge ai - t ) = \sum _{ i> t/a } \sum _{ j \ge (ai - t)/b } {\tilde{\mu }}( \delta _{i, j}) \\&\lesssim \sum _{ i > t/a } i^{- (1 + 1/\beta ) }(ai - t )^{-1/\beta } \lesssim \sum _{ i = 1}^{\infty } ( i + t )^{-(1 + 1/\beta )}i^{-1/\beta }. \end{aligned}$$

We claim that

$$\begin{aligned} \sum _{ i = 1}^{ \infty } ( t + i )^{ - 1 - 1/\beta }i^{ -1/\beta } \lesssim t^{- \gamma - 1/\beta } \end{aligned}$$

for every $0< \gamma < 1/\beta$, which is equivalent to showing that

$$\begin{aligned} \sum _{ i = 1}\frac{t^{\gamma + 1/\beta }}{(t + i)^{1 + 1/ \beta }i^{ 1 / \beta }} \le C \end{aligned}$$

for some $C > 0$ independent of $t$. Indeed, for every $i$,

$$\begin{aligned} \frac{t^{\gamma + 1/\beta }}{(t + i)^{1 + 1/ \beta }i^{ 1 / \beta }} \le \frac{ ( t + i )^{ \gamma + 1 / \beta } }{ (t + i)^{1 + 1 / \beta } i^{1/\beta } } = \frac{ 1 }{ ( t + i )^{ 1 - \gamma } i^{1/\beta } } = \frac{ 1 }{ ( t/i + 1 )^{ 1 - \gamma } i^{ 1 - \gamma + 1/\beta } } \le \frac{1}{ i^{ 1 - \gamma + 1/\beta } } \end{aligned}$$

which is summable for every $0< \gamma < 1/\beta$. This implies the claim and thus the lemma. $\square$

4.2 Estimates for the induced observables

In this section we prove Corollary 2.11 and Proposition 2.10. We recall (see paragraph at the beginning of Sect. 2.3) that we will only explicitly treat the case that $\ell _{1}, \ell _{2} > 0$ (and thus in particular $\beta > 0$). Throughout this section we will assume that $\varphi$ is a Hölder obervable and define $a = \varphi (1)$, $b = \varphi (-1)$.

4.2.1 Proof of Corollary 2.11

We first consider the case where $\beta _{\varphi } = \beta$. Recall from (14) that $\beta _{\varphi } = \beta$ occurs when $\varphi$ is non-zero at a fixed point corresponding to the maximum of $\beta _{1}, \beta _{2}$; and that $\beta _{\varphi } \ne \beta$ occurs when $\beta _{1} \ne \beta _{2}$ and $\varphi$ is zero at the fixed point corresponding to the minimum of $\beta _{1}, \beta _{2}$.

Lemma 4.9

If $\beta _{\varphi } = \beta$, then $\tau _{a,b} \in \mathcal {D}_{1/\beta _{\varphi }}$. In particular, if $\beta _{\varphi } \in (0,1/2)$ then $\tau _{a,b} \in L^2( {\hat{\mu }} )$.

Proof

Notice first of all that if $\tau _{a,b} \in \mathcal {D}_{1/\beta _\varphi }$ then, in particular, ${\tilde{\mu }} ( \pm \tau _{a,b} > t ) \lesssim t^{-1/\beta _{\varphi }}$ and so, if $\beta _{\varphi } \in (0,1/2)$ we obtain that $\tau _{a,b} \in L^2 ( {\hat{\mu }} )$. Thus we just need to prove that $\tau _{a,b} \in \mathcal {D}_{1/\beta _\varphi }$.

Suppose first that $a, b$ do not have opposite signs, i.e. either $a,b \ge 0$ or $a,b \le 0$, in which case the distribution of $\tau _{a,b}$ is determined by the first case of (27). Therefore, taking $\gamma = 0$ we get

$$\begin{aligned} {\tilde{\mu }} ( \tau _{a,b} > t ) = C_a t^{-1/\beta _2} + C_b t^{-1/\beta _1} + o ( t^{- 1/\beta } ) = c t^{-1/\beta } + o ( t^{-1/\beta }) \end{aligned}$$

for some constant $c > 0$, which may be equal to $C_{a}$, $C_{b}$, or $C_{a}+C_{b},$ depending on the relative values of $\beta _{1}, \beta _{2}$. If $a,b\ge 0$, and exactly the same tail for ${\tilde{\mu }} ( \tau _{a,b} < - t)$ if $a, b \le 0$. By (30) and the fact that $\beta _{\varphi } = \beta$ we get that $\tau _{a,b} \in \mathcal {D}_{1/\beta _\varphi }$, thus proving the result in this case. If $a \ge 0$, $b \le 0$ the distribution of $\tau _{a,b}$ is given by (28) and (29) and so, taking $\gamma = 0$ gives

$$\begin{aligned} {\tilde{\mu }} ( \tau _{a,b} > t ) = C_a t^{-1/\beta _2} + o (t^{-1/\beta }) = c_1 t^{-1/\beta } + o(t^{-1/\beta }) \end{aligned}$$

and

$$\begin{aligned} {\tilde{\mu }} ( \tau _{a,b} < - t ) = C_{|b|} t^{-1/\beta _1} + o (t^{-1/\beta }) = c_2 t^{-1/\beta } + o(t^{-1/\beta }) \end{aligned}$$

where $c_{1} = C_{a}$ and $c_{2}= C_{|b|}$ if $\beta _2 = \beta$ and $\beta _1 = \beta$ respectively, and equal to 0 otherwise. At least one of the $c_1, c_2$ has to be non-zero as $\beta _{\varphi } = \beta$ implies that $\varphi$ is non-zero at a fixed point corresponding to the largest of $\beta _1, \beta _2$ and so if $\beta _1 = \max \{ \beta _1, \beta _2 \}$ we know from (26) that $c_2 = C_{|b|} > 0$ and if $\beta _2 = \max \{ \beta _1, \beta _2 \}$ we know from (26) that $c_1 = C_a > 0$. Thus, since $\beta =\beta _{\varphi }$, we get $\tau _{a,b} \in \mathcal {D}_{1/\beta _{\varphi }}$. If $a \le 0$, $b \ge 0$ the same argument holds exchanging the roles of the positive and negative tails. $\square$

Proof of Corollary 2.11

We have already proved the result for $\beta _{\varphi }=\beta$ in Lemma 4.9 so we can assume that $\beta _{\varphi } \ne \beta$. This implies that $\beta _1 \ne \beta _2$ and that $\varphi$ is only non-zero at the fixed point corresponding to the smallest of the $\beta _1, \beta _2$. This situation can arrise in two ways: either (i) $a \ne 0$, $b = 0$ and $\beta _{\varphi } = \beta _2 < \beta _1$; or (ii) $a = 0$, $b \ne 0$ and $\beta _\varphi = \beta _1 < \beta _2$. We will assume (i) and give an explcit proof of the Lemma. The proof of the Lemma in situation (ii) then follows in the same way.

Under our assumptions we know from Proposition 2.6 that the tail of $\tau _{a,b}$ is determined by (27), and we recall from (26) that $C_b = 0$. If $\beta _{\varphi } = \beta _2 = 0$ then we know from the second line of (27) that

$$\begin{aligned} {\hat{\mu }} ( \pm \tau _{a,b} > t ) \lesssim t^{-\gamma -1 /\beta _1 }. \end{aligned}$$

Since $\beta = \beta _1 < 1$ by assumption, we may choose $\gamma \in [0,1 )$ such that $\gamma + 1 / \beta _1 > 2$ yielding $\tau _{a,b} \in L^2( {\hat{\mu }} )$. If $\beta _{\varphi } \in (0,1/2)$ then the first line of (27) gives that

$$\begin{aligned} {\hat{\mu }} ( \pm \tau _{a,b} > t ) \lesssim \max \{ t^{-1/\beta _{\varphi }}, t^{-\gamma - 1/\beta } \} \end{aligned}$$

for any $\gamma \in [0,1)$. Choosing $\gamma$ as before so that $\gamma + 1 /\beta _1 > 2$ we again obtain that $\tau _{a,b} \in L^2( {\hat{\mu }} )$. If $\beta _\varphi = \beta _2 \in [1/2,1)$ then, choosing $\gamma \in [0,1)$ so that $\gamma + 1 / \beta _1 > 1 / \beta _{2}$ we know from (27) that the non-zero tail of $\tau _{a,b}$ is given by

$$\begin{aligned} {\hat{\mu }} ( \pm \tau _{a,b} > t ) \lesssim C_a t^{-1/\beta _2} + o ( t^{-\gamma - 1/\beta _1 } ) = C_a t^{-1/\beta _2} + o ( t^{-1/\beta _2}) \end{aligned}$$

yielding $\tau _{a,b} \in \mathcal {D}_{1/\beta _\varphi }$. $\square$

4.2.2 Proof of Proposition 2.10

Proof of Proposition 2.10

For a point $x \in \delta _{i,j}^{-}$ we know that $\tau (x) = i + j$ and that

$$\begin{aligned} g^{k}(x) \in \Delta _{i-k}^+ \quad \forall \ 1 \le k \le i;\quad \text { and } \quad g^{i + k}(x) \in \Delta _{j-k}^{-} \quad \forall \ 1 \le k \le j - 1. \end{aligned}$$

(84)

Recall that by Proposition  3.4 we have $1- x_n^{+} \lesssim n^{- {1}/{\ell _2}},$ and $|\Delta ^{+}_{n}| \lesssim n^{-(1+1/\ell _{2})} \ll 1- x_n^{+}$, which means that we can use the fact that ${\tilde{\varphi }} (1) = 0$ and the Hölder continuity of ${\tilde{\varphi }}_{(0,1]}$ to obtain

$$\begin{aligned} |{\tilde{\varphi }} \circ g^{k}(x)| \lesssim (1- x_{i-k}^{+})^{\nu _{2}}\le (i-k)^{-\nu _{2}/\ell _{2}}, \end{aligned}$$

(85)

for all $1 \le k \le i-1$. Similarly, using the fact that ${\tilde{\varphi }} (-1) = 0$ and the Hölder continuity of ${\tilde{\varphi }}_{[-1,0)}$,

$$\begin{aligned} |{\tilde{\varphi }} \circ g^{i+k}(x)| \lesssim (1+x_{j-k}^{+})^{\nu _{1}}\le (j-k)^{-\nu _{1}/\ell _{1}}, \end{aligned}$$

(86)

for all for $1 \le k \le j - 1$. For $x \in \delta _{i,j}$ we know from (85) and (86) that

$$\begin{aligned} |{\tilde{\Phi }}(x)| \lesssim \sum _{k=1}^{i-1} (i-k)^{-\frac{\nu _2}{\ell _2}} + \sum _{k=1}^{j-1} (j-k)^{-\frac{\nu _1}{\ell _1}}. \end{aligned}$$

(87)

We now consider two cases. Suppose first that $\ell _1 < \nu _1$ and $\ell _2 < \nu _2$. Then $|{\tilde{\Phi }} (x)|$ is uniformly bounded in $x$, as both (85) and (86) are summable in $k$ and therefore the sums in (87) both converge. Therefore ${\tilde{\Phi }} \in L^q ( \hat{\mu } )$ for every $q > 0$, in particular ${\tilde{\Phi }} \in L^2 ( \hat{\mu } )$ giving the first implication in (36), and by Chebyshev’s inequality, ${\hat{\mu }} ( \pm {\tilde{\Phi }} > t ) = O(t^{-q})$ for every $q > 0$, giving the second implication in (36). Notice that we have not required in this case the conditions $({\mathcal {H}})$ and (${\mathcal {H}}'$).

Now suppose that $\ell _1 \ge \nu _1$ and/or $\ell _2 \ge \nu _2$ and suppose also that

$$\begin{aligned} \nu _{1}> \frac{ \beta _{1} - 1/q }{ k_{2} } \quad \text { and } \quad \nu _{2} > \frac{ \beta _{2} - 1/q }{ k_{1} }. \end{aligned}$$

(88)

Notice that for $q = 2$ this gives exactly condition $({\mathcal {H}})$ and for $q = 1/ \beta _{\varphi }$ this gives exactly (${\mathcal {H}}'$). We can also suppose without loss of generality that in fact $\ell _1 > \nu _1$ and/or $\ell _2 > \nu _2$ since we can decrease slightly the Hölder exponent while still satisfying (88). In this case the sums in (87) diverge but admit the following bounds:

$$\begin{aligned} |{\tilde{\Phi }}(x)| \lesssim \sum _{k=1}^{i-1} (i-k)^{-\frac{\nu _2}{\ell _2}} + \sum _{k=1}^{j-1} (j-k)^{-\frac{\nu _1}{\ell _1}} \lesssim i^{1 -\frac{\nu _2}{\ell _2}} + j^{1 - \frac{\nu _1}{\ell _1}}. \end{aligned}$$

We can then bound the integral by

$$\begin{aligned} \int _{\Delta _0^-} |\tilde{\Phi } (x) |^q dm&\lesssim \left[ \sum _{i = 1}^{\infty }\sum _{j=1}^{\infty } |\delta _{i,j}| \left( i^{1 - \frac{\nu _2}{\ell _2}} + j^{1 - \frac{\nu _1}{\ell _1}} \right) ^q \right] \end{aligned}$$

Then, since $| \delta _{i,j}| = O( i^{- ( 1 + 1/\beta _2 )} j^{ -( 1 + 1 / \beta _1 )})$ we get

$$\begin{aligned} \int _{\Delta _0^-} |\tilde{\Phi } (x) |^q dm&\lesssim \left[ \sum _{i,j = 1}^{\infty } \frac{ i^{q - \frac{q\nu _2}{\ell _2}} }{ i^{1 + \frac{1}{\beta _2}} j^{1 + \frac{1}{\beta _1}} } + \sum _{i,j=1}^{\infty } \frac{ j^{q - \frac{q\nu _1}{\ell _1}} }{ i^{1 + \frac{1}{\beta _2}} j^{1 + \frac{1}{\beta _1}} } \right] \lesssim \sum _{i = 1}^{\infty } i^{q - \frac{q\nu _2}{\ell _2} - 1 - \frac{1}{\beta _2}}\\&\quad + \sum _{j=1}^{\infty } j^{q - \frac{q\nu _1}{\ell _1} - 1 - \frac{1}{\beta _1}} \end{aligned}$$

The latter sums are bounded exactly when (88) holds. As mentioned above, for $q= 2$ this is exactly condition $({\mathcal {H}})$ and therefore we get that ${\tilde{\Phi }} \in L^{2} ( {\hat{\mu }} )$. For $q = 1/\beta _{\varphi }$ this is exactly condition (${\mathcal {H}}'$) and therefore we get that ${\tilde{\Phi }} \in L^{q} ( {\hat{\mu }} )$. In fact if (88) holds for $q = 1/\beta _{\varphi }$ then there exists some $\varepsilon > 0$ such that (88) holds for all $q \in [1/\beta _{\varphi }, 1/\beta _{\varphi } + \varepsilon )$ and therefore ${\tilde{\Phi }} \in L^{q} ( {\hat{\mu }} )$ for every $q \in [1/\beta _{\varphi }, 1/\beta _{\varphi } + \varepsilon )$. From this and Chebyschev’s inequality we get ${\hat{\mu }} ( \pm {\tilde{\Phi }} > t ) = o ( t^{ - 1 / \beta _{\varphi } } )$. $\square$