Disconnection and Entropic Repulsion for the Harmonic Crystal with Random Conductances

Abstract

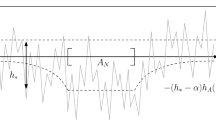
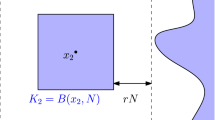
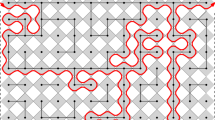
We study level-set percolation for the harmonic crystal on ${\mathbb {Z}}^d$, $d \ge 3$, with uniformly elliptic random conductances. We prove that this model undergoes a non-trivial phase transition at a critical level that is almost surely constant under the environment measure. Moreover, we study the disconnection event that the level-set of this field below a level $\alpha$ disconnects the discrete blow-up of a compact set $A \subseteq {\mathbb {R}}^d$ from the boundary of an enclosing box. We obtain quenched asymptotic upper and lower bounds on its probability in terms of the homogenized capacity of A, utilizing results from Neukamm, Schäffner and Schlömerkemper (SIAM J Math Anal 49(3):1761–1809, 2017). Furthermore, we give upper bounds on the probability that a local average of the field deviates from some profile function depending on A, when disconnection occurs. The upper and lower bounds concerning disconnection that we derive are plausibly matching at leading order. In this case, this work shows that conditioning on disconnection leads to an entropic push-down of the field. The results in this article generalize the findings of Nitzschner (Electron J Probab 23:105, 2018) and Chiarini and Nitzschner (Probab Theory Relat Fields 177(1–2):525–575, 2020) which treat the case of constant conductances. Our proofs involve novel “solidification estimates” for random walks, which are similar in nature to the corresponding estimates for Brownian motion derived by Nitzschner and Sznitman (J Eur Math Soc. 22:2629–2672, 2020).

Proof of Theorem 4.7

In this appendix we prove Theorem 4.7. The proof proceeds as the one in [44] using “I-families” with the respective modifications. We introduce these I-families in the discrete case and sketch the proof, focusing on the part where Proposition 4.6 is applied. Let us first prove the maximality property (4.43). Note that for $U_0 \in {\mathcal {U}}_{\ell _*, A}$, $x \in A$, one has $U_0 - x \in {\mathcal {U}}_{\ell _*, \{ 0\}}$ and $\text {Res}(U_0 - x,I,J,L, \ell _*) =\text {Res}(U_0 ,I,J,L, \ell _*) - x$. For a given $\omega \in \varOmega _\lambda$, one has

$$\begin{aligned} P^\omega _x[H_{\text {Res}} = \infty ] = P^{\tau _x\omega }_0[H_{\text {Res} - x} = \infty ] \le \varPhi _{J,I,L}, \end{aligned}$$

(A.1)

so the maximality follows. We turn to (discrete) I-families. Let $I, J \ge 1$ and $L \ge L(J)$ be fixed, $\ell _*\ge 0$ (I, J, L)-compatible, $\omega \in \varOmega _\lambda$ and $U_0 \in {\mathcal {U}}_{\ell _*, \{ 0 \} }$ (we refer to (4.24) and (4.39) for the respective definitions). Recall also the definition of $\ell _{\text {min}}(\cdot )$ from (4.18). An I-family consists of stopping times $(S_i)_{i = 0}^I$, a random finite subset ${\mathcal {L}}\subseteq (J+1) L {\mathbb {N}}\cap [\ell _{\min }((200J)^{-1}) +LJ, \infty )$, and integer valued random variables ${\widehat{\ell }}_i$, $1 \le i \le I$, such that

$$\begin{aligned} \left\{ \begin{array}{rl} \mathrm{(i)} &{} 0 \le S_0 \le S_1 \le \cdots \le S_I,\ P^\omega _0\text{-a.s. } \text{ finite } \text{ stopping } \text{ times, } \\ \mathrm{(ii)} &{} {\mathcal {L}} \text{ is } \text{ an } {\mathcal {F}}_{S_0}\text{-measurable } \text{ finite } \text{ subset } \text{ of } \\ &{} {\mathcal {L}}\subseteq (J+1) L {\mathbb {N}}\cap [\ell _{\min }((200J)^{-1}) +LJ, \infty )\text{, } \text{ and } |{\mathcal {L}}| \ge I, \\ {\mathrm{(iii)}} &{} {\widehat{\ell }}_i,\ 1 \le i \le I \text{ are } {\mathcal {F}}_{S_i}\text{-measurable, } \text{ pairwise } \text{ distinct } \text{ and } {\mathcal {L}}\text{-valued }, \\ {\mathrm{(iv)}} &{} P^\omega _0\text{-a.s., } \sigma _{{\widehat{\ell }}_i }(X_{S_i}) \in [\tfrac{1}{2} - \tfrac{1}{2^{\ell _{\min }((200J)^{-1}) } }, \tfrac{1}{2} + \tfrac{1}{2^{\ell _{\min }((200J)^{-1}) } }],\ 1 \le i \le I. \end{array}\right. \end{aligned}$$

(A.2)

The “canonical” I-family as defined in (2.12) of [44] also exists in the discrete case, if we replace the conditions $\sigma _\ell (X_{S_i}) = \tfrac{1}{2}$ by $\sigma _{\ell _i }(X_{S_i}) \in [\tfrac{1}{2} - \tfrac{1}{2^{\ell _{\min }((200J)^{-1}) } }, \tfrac{1}{2} + \tfrac{1}{2^{\ell _{\min }((200J)^{-1}) } }]$. Given a general I-family as above, we also define for $1 \le i \le I$ the stopping times

$$\begin{aligned} T_i = \inf \{ s \ge S_i \, : \, |X_s - X_{S_i}|_\infty \ge 2 \cdot 2^{{\widehat{\ell }}_i} \}, \end{aligned}$$

(A.3)

and “intermediate labels” and “labels”

$$\begin{aligned} {\mathcal {L}}_{\text {int}} = \{ \ell - jL \, : \, \ell \in {\mathcal {L}}, 1 \le j \le J \}, \qquad {\mathcal {L}}_*= {\mathcal {L}}\cup {\mathcal {L}}_{\text {int}}. \end{aligned}$$

(A.4)

Finally, we will need for $1 \le k \le J$ the $({\mathcal {L}}_*,k)$-resonance set

$$\begin{aligned} \text {Res}_{({\mathcal {L}}_*,k)} = \bigg \{ x \in {\mathbb {Z}}^d \, : \, \sum _{\ell \in {\mathcal {L}}_*} \mathbb {1}_{ \{ {\widetilde{\sigma }}_\ell (x) \in [{\widetilde{\alpha }}, 1 - {\widetilde{\alpha }} ] \} } \ge k \bigg \}, \end{aligned}$$

(A.5)

and the quantity

$$\begin{aligned} \varGamma ^{\omega ,(J)}_{k}(I) = \sup P^\omega _0[\inf \{ s \ge S_0 \, : \, X_s \in \text {Res}_{({\mathcal {L}}_*,k)} \} > \max _{1 \le i \le I} T_i ], \end{aligned}$$

(A.6)

for $1 \le k \le J$, $I \ge 1$ (with the supremum over all I-families) and $\varGamma ^{\omega , (J)}_k(I) =1$ whenever $I \le 0$. The following discrete analogue of Lemma 2.2 in [44] is the main ingredient of the proof of Theorem 4.7.

Lemma A.1

For $\omega \in \varOmega _\lambda$, one has

$$\begin{aligned} \varGamma ^{\omega ,(J)}_1(I) = 0, \qquad \text {for all } I \ge 1 \end{aligned}$$

(A.7)

and for $1 \le k < J$, $I \ge 1$, $\varDelta = \lfloor \sqrt{I} \rfloor$,

$$\begin{aligned} \varGamma ^{\omega , (J)}_{k+1}(I) \le (1 - c_7(J))^{\sqrt{I} - 1} + I^{1 + \tfrac{k-1}{2}} \varGamma ^{\omega , (J)}_k( \varDelta - k + 1). \end{aligned}$$

(A.8)

Proof

We only sketch the proof. The first part follows by noting that $P^\omega _0$-a.s., $\sigma _{{\widehat{\ell }}_1}(X_{S_1}) \in [\tfrac{1}{2} - \tfrac{1}{2^{\ell _{\min }((200J)^{-1}) } }, \tfrac{1}{2} + \tfrac{1}{2^{\ell _{\min }((200J)^{-1}) } }]$, and since $J \ge 1$, $2^{-\ell _{\min }(1/(200J)) } \le \tfrac{1}{1600}$, hence $U_1$ and $U_0$ have relative volumes in $B(X_{S_1}, 2^{{\widehat{\ell }}_1})$ at least $\tfrac{799}{1600}$ and at most $\tfrac{801}{1600}$, or in other words, ${\widetilde{\sigma }}_{{\widehat{\ell }}_1}(X_{S_1}) \in [{\widetilde{\alpha }}, 1- {\widetilde{\alpha }}]$ and $\varGamma ^{\omega ,(J)}_1(I) = 0$ is immediate since $\inf \{s \ge S_0\,: X_s \in \text {Res}_{({\mathcal {L}}_*,1)} \} \le S_1 \le \max _{1 \le i \le I} T_i$, $P^\omega _0$-a.s., proving (A.7).

We set $m_\varDelta = \lfloor \tfrac{I - 1}{\varDelta } \rfloor$, such that $i_\varDelta = 1 + m_\varDelta \varDelta \le I < 1 + (m_\varDelta + 1)\varDelta$. For $I \ge 2$, we have

$$\begin{aligned} P^\omega _0[\inf \{ s \ge S_0 : X_s \in \text {Res}_{({\mathcal {L}}_*,k+1)} \} > \max _{1 \le i \le I} T_i ] \le a_1^\omega + a_2^\omega , \end{aligned}$$

(A.9)

where

$$\begin{aligned} a_1^\omega&= P^\omega _0[T_i < S_{i + \varDelta } \text { for all } 1 \le i \le I - \varDelta , \inf \{ s \ge S_0 : X_s \in \text {Res}_{({\mathcal {L}}_*,k+1)} \} > \max _{1 \le i \le I} T_i ], \end{aligned}$$

(A.10)

$$\begin{aligned} a_2^\omega&= P^\omega _0[T_i \ge S_{i + \varDelta } \text { for some } 1 \le i \le I - \varDelta , \inf \{ s \ge S_0 \, : \, X_s \in \text {Res}_{({\mathcal {L}}_*,k+1)} \}\nonumber \\&> \max _{1 \le i \le I} T_i ]. \end{aligned}$$

(A.11)

For $a_2^\omega$, one has the bound

$$\begin{aligned} a_2^\omega \le I^{1 + \frac{k-1}{2}} \varGamma ^{\omega , (J) }_k(\varDelta - k + 1). \end{aligned}$$

(A.12)

Its proof proceeds exactly as in the Brownian case, see (2.29)–(2.33) of [44] and is thus omitted. For the bound on $a_1^\omega$, note that one has

$$\begin{aligned} \begin{aligned} a_1^\omega&\le E^\omega _0\big [S_1< T_1< \cdots< S_{i_\varDelta }< T_{i_\varDelta }< \inf \{s \ge S_0\, : \, X_s \in \text {Res}_{({\mathcal {L}}_*,k+1)} \}] \\&\le E^\omega _0\big [S_1< T_1< \cdots< S_{i_\varDelta }< \inf \{s \ge S_0\, : \, X_s \in \text {Res}_{({\mathcal {L}}_*,k+1)} \}, \\&{\widetilde{P}}^\omega _{X_{S_{i_\varDelta }}}[ \inf \{s \ge 0\, : \, |{\widetilde{X}}_s - {\widetilde{X}}_0|_\infty \ge 2 \cdot 2^{{\widehat{\ell }}_{i_\varDelta } } \} < \inf \{ s \ge 0\, : \, {\widetilde{X}}_s \in \text {Res}_{({\mathcal {L}}_*,k+1)} \} ] \big ], \end{aligned} \end{aligned}$$

(A.13)

having used the strong Markov property at time $S_{i_\varDelta }$ for the second bound, and where $({\widetilde{X}}_\cdot )$ denotes the canonical process which behaves as a random walk among conductances $\omega$, starting from $X_{S_{i_\varDelta }}$ under ${\widetilde{P}}^\omega _{X_{S_{i_\varDelta }}}$, and ${\mathcal {L}}_*$ and ${\widehat{\ell }}_{i_\varDelta }$ are not integrated under ${\widetilde{P}}^\omega _{X_{S_{i_\varDelta }}}$.

We use now Proposition 4.6: Choose $x = X_{S_{i_\varDelta }}$ and recall that ${\widehat{\ell }}_{i_\varDelta } - LJ \ge \ell _{\text {min}}((200J)^{-1})$ (by (A.2), (ii)) as well as $|\sigma _{\ell _{i_\varDelta }}(X_{S_{i_\varDelta }}) -\frac{1}{2}| \le 2^{-\ell _{\text {min}}((200J)^{-1}) }$, see (A.2), (iv). Since $k + 1 \le J$, we have on an event that has ${\widetilde{P}}_{X_{S_{i_\varDelta }}}^\omega$-probability bigger or equal to $c_7(J)$ that ${\widetilde{X}}_{\gamma _J} \in \text {Res}_{({\mathcal {L}}_*,k+1)}$, but $\sup \{ |{\widetilde{X}}_s - {\widetilde{X}}_0| \, : \, 0 \le s \le \gamma _J \} \le \tfrac{3}{2} \cdot 2^{{\widehat{\ell }}_{i_\varDelta }}$, so on this event, the event within ${\widetilde{P}}^\omega _{X_{S_{i_\varDelta }}}$ in the last line of (A.13) does not occur. We obtain that the expression in the last line of (A.13) is bounded above by

$$\begin{aligned} \begin{aligned} a_1^\omega&\le E^\omega _0\big [S_1< T_1< \cdots< T_{i_\varDelta - \varDelta } < \inf \{s \ge 0\, : \, X_s \in \text {Res}_{({\mathcal {L}}_*,k+1)} \}] (1-c_7(J)) \\&{\mathop {\le }\limits ^{\text {(induction)}}} (1 - c_7(J))^{m_\varDelta + 1} \le (1 - c_7(J))^{\sqrt{I} - 1}, \end{aligned} \end{aligned}$$

(A.14)

using in the last step that $m_\varDelta > \frac{I - 1}{\sqrt{I}} \ge \sqrt{I} -1$. By combining the bounds (A.12) and (A.14), we obtain:

$$\begin{aligned}&P^\omega _0[\inf \{ s \ge S_0 : X_s \in \text {Res}_{({\mathcal {L}}_*,k+1)} \} > \max _{1 \le i \le I} T_i ]\nonumber \\&\quad \le (1 - c_7(J))^{\sqrt{I} - 1} + I^{1 + \tfrac{k-1}{2}} \varGamma ^{\omega , (J)}_k( \varDelta - k + 1) \end{aligned}$$

(A.15)

Finally, we take the supremum over all I-families, which yields (A.8) in the case where $I \ge 2$. For $I = 1$, the claim of (A.8) is true, since the right-hand side is bigger or equal to 1. $\quad \square$

We now turn to the proof of (4.43) of Theorem 4.7. Similar to (2.34) of [44], we set

$$\begin{aligned} {\widetilde{\varGamma }}^{(J)}_k(I) = {\left\{ \begin{array}{ll} \sup \limits _{\ell _*} \sup \limits _{U_0 \in {\mathcal {U}}_{\ell _*, \{0 \}} }\sup \limits _{\omega \in \varOmega _\lambda } \varGamma ^{\omega , (J)}_k(I), &{} \text { for }1 \le k \le J \text { and } I \ge 1, \\ 1, &{} \text { for } 1\le k \le J \text { and } I \le 0. \end{array}\right. } \end{aligned}$$

(A.16)

where in the first case, the supremum in $\ell _*$ is over all (I, J, L)-compatible $\ell _*\ge 0$. Using the “canonical” I-family, one has that

$$\begin{aligned} \varPhi _{J,I,L} \le {\widetilde{\varGamma }}^{(J)}_J(I). \end{aligned}$$

(A.17)

Using (A.7) and (A.8) of Lemma A.1, we receive upon taking the suprema over $\omega \in \varOmega _\lambda$, $U_0 \in {\mathcal {U}}_{\ell _*,\{ 0\}}$ and (I, J, L)-compatible $\ell _*\ge 0$:

$$\begin{aligned} \begin{aligned}&{\widetilde{\varGamma }}^{(J)}_1(I) = 0, \text { for } I \ge 1, \\&{\widetilde{\varGamma }}^{(J)}_{k+1}(I) \le (1 - c_7(J))^{\sqrt{I} - 1} + I^{1 + \tfrac{k-1}{2}} {\widetilde{\varGamma }}^{(J)}_k( \varDelta - k + 1), \text { for }1 \le k \le J, I \ge 1. \end{aligned} \end{aligned}$$

(A.18)

The proof of (4.43) now follows by induction on k, in exactly the same way as (2.37)–(2.38) of [44].